Magnetic field–driven assembly and reconfiguration of multicomponent supraparticles

We design the magnetic energy landscapes around microparticles and guide their assembly into low-symmetry clusters.

Abstract

Suprastructures at the colloidal scale must be assembled with precise control over local interactions to accurately mimic biological complexes. The toughest design requirements include breaking the symmetry of assembly in a simple and reversible fashion to unlock functions and properties so far limited to living matter. We demonstrate a simple experimental technique to program magnetic field–induced interactions between metallodielectric patchy particles and isotropic, nonmagnetic “satellite” particles. By controlling the connectivity, composition, and distribution of building blocks, we show the assembly of three-dimensional, multicomponent supraparticles that can dynamically reconfigure in response to change in external field strength. The local arrangement of building blocks and their reconfigurability are governed by a balance of attraction and repulsion between oppositely polarized domains, which we illustrate theoretically and tune experimentally. Tunable, bulk assembly of colloidal matter with predefined symmetry provides a platform to design functional microstructured materials with preprogrammable physical and chemical properties.

INTRODUCTION

Assembly of building block molecules/particles into higher-order structures is the origin of all mesoscopic matter around us. Supraparticles are one such class of colloidal matter, in which discrete cluster units are assembled with defined design criteria. The synergy between these structural motifs is unique to their local symmetry and encodes functionality otherwise absent from the unassembled component particles (1). Nature offers various examples in which structure-property-function relationships of supraparticles are dictated by the self-assembled architecture of living systems and their interaction with the surrounding environment. For example, viruses need highly directional interactions to bind on specific cell sites (2), while functional domains on antibodies allow them to bind pathogens (3). Embedding such biomimetic recognition and binding within artificial supraparticles lies in our ability to precisely control the local arrangement of their colloidal building blocks (4). Materials synthesized wielding such degree of control over connectivity, composition, and distribution will give access to a variety of functional devices with unusual microarchitectonics (5).

Diverse colloidal structures have been synthesized over recent years with the goal of tuning assembly size, shape, and intrinsic properties. Self-assembly of colloids is traditionally driven by nonspecific interactions such as van der Waals, depletion, and electrostatic (6–8). Attractive pair potentials and spatial confinement drive particles through a thermodynamic pathway toward highly symmetric close-packed crystals with minimized ensemble energy (9–11). One current approach for the fabrication of anisotropic supraparticles relies on the specific base-pair interactions between DNA-functionalized particles (12). Despite the success of the technique, its necessity for complex synthetic steps, high ionic concentration, and slow assembly kinetics limit its widespread applicability. Such limitations in DNA-mediated assembly have spurred research into alternative mechanisms for encoding stronger and longer-ranged binding interactions (13). One robust method of inducing long-range directional interactions between colloidal particles is via the application of external electromagnetic fields (14–22). However, the external field–driven assembly does not offer intrinsic control over the local arrangement of supraparticles. Lack of control over the local assembled configuration of the colloids has limited the variety of suprastructures to one-dimensional chains, two-dimensional crystals, and other globally isotropic clusters. Thus, assembly of discrete supraparticles of well-defined structural and compositional symmetry using long-range field-driven interactions remains a challenge.

Here, we describe the dynamic assembly of discrete anisotropic supraparticles composed of patchy “cores” and nonmagnetic “satellites.” We use an external magnetic field to supply tunable and long-range directional interaction energy in a chemically noninvasive fashion. Concurrently, we control the local distribution of building blocks and reduce the overall symmetry of supraparticles through an iron patch. We take advantage of the previously introduced concept of magnetic hole (23, 24), which showed that particles less polarizable than their medium behave diamagnetically. This allows us to manipulate nonmagnetic particles immersed in ferrofluid using external magnetic fields. We find that the presence of a ferromagnetic patch further reduces the symmetry of the cluster from previously reported D_∞h to a less symmetric C_2v point group. We show how the surface anisotropy of patchy colloids is combined with directional magnetic interactions to form shape anisotropic supraparticles. Discrete assemblies are reversible in suspension, and their structures are controllable by experimental parameters such as applied field strength, patch characteristics, and relative concentration of building blocks. While assembly is governed by long-range magnetic interactions, we are also able to photochemically manipulate the short-range interparticle electrostatics. Thus, we demonstrate a method to permanently link the assembled blocks into stable anisotropic supraparticles that are readily recovered out of suspension. These may be used as “steerable microswimmers” (25, 26) or further assembled into higher-order colloidal materials (27).

RESULTS AND DISCUSSION

Building blocks for supraparticles

Our experimental model system consists of a mixture of nonmagnetic polystyrene microspheres that act as satellites (radius R_S = 1.0 μm; green fluorescent) and metallodielectric patchy particles composed of a polystyrene core (radius R_C = 2.5 μm; red fluorescent) with an iron patch (size distributions available in fig. S1). The particles are suspended in an aqueous ferrofluid containing ~1.1 volume % of superparamagnetic Fe₃O₄ nanoparticles of radius ~5 nm. The surface of polystyrene microspheres was prefunctionalized with carboxylate groups, which induced a net negative charge on the particles at pH 6 (28). Thus, the building blocks are stable in aqueous ferrofluid solution due to electrostatic double layer repulsion. The patchy particles were fabricated by controlled deposition of iron vapors on a substrate containing a close-packed monolayer of the core microspheres. In a typical batch synthesis, a monolayer of microspheres was deposited on a glass substrate using a Langmuir-Blodgett trough (29). The metal patch was introduced on the particles by controlled vapor deposition of a 5-nm chromium layer followed by a 30-nm iron layer (Fig. 1, A and B). Further details on the synthesis of metallodielectric patchy particles can be found elsewhere (30).

Fig. 1. Supraparticle assembly and experimental setup.

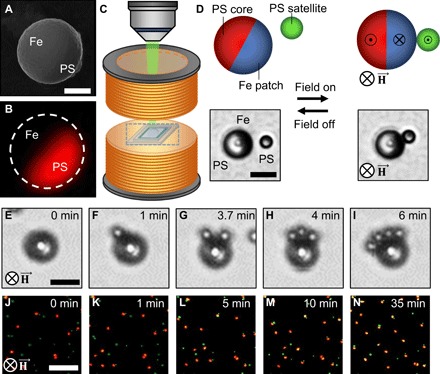
(A) Scanning electron microscopy (SEM) and (B) fluorescence light microscopy images of freestanding Janus particle. Fe and PS represent the magnetic iron patch and nonmagnetic polystyrene, respectively. Scale bar, 2 μm. (C) Representation of the Helmholtz coil setup used for assembly on microscope stage. The particle dispersion is placed at the center of the electromagnet to guarantee a uniform magnetic field over the suspension. (D) Schematic representation and corresponding brightfield images of model assembly system: Under magnetic field, the iron patch (blue) aligns ferromagnetically, while the polystyrene microsphere (green) and the core of the patchy particle (red) align diamagnetically due to the ferrofluid suspension. Brightfield images demonstrating the spontaneous assembly and disassembly of the cluster by cycling the magnetic field on and off. Scale bar, 5 μm. (E to I) Sequence of multistep supraparticle growth as four isotropic satellite particles assemble on the patchy particle, one microsphere at a time. Scale bar, 5 μm. (J to N) Fluorescence micrographs showing the dynamics of the assembly process in bulk ferrofluid at τ = 2. The supraparticle structures approach a near-equilibrium state after 35 min of field application (2500 A m⁻¹). Red hemispheres are Fe-patched Janus particles (red region, polystyrene; dark region, Fe), and green particles are isotropic polystyrene satellite particles. Scale bar, 40 μm.

The mixture of the metallodielectric patchy particles and nonmagnetic microspheres in ferrofluids is a precursor for directed assembly of the supraparticles. We represent the relative concentration of building blocks in terms of a particle number ratio (τ) defined as the excess number of satellites per patchy particle, i.e., τ = N_B/N_A, where N_A and N_B are the numbers of patchy and isotropic particles, respectively. In a typical experiment, 0.5 μl of the mixture of microspheres in ferrofluid at a desired τ was placed between a glass substrate and a coverslip and then sealed with a hydrophobic barrier pen into a liquid film of thickness ~25 μm. This experimental chamber was transferred to an electromagnetic Helmholtz coil setup shown in Fig. 1C. The assembly process was initiated by applying a uniform magnetic field to the dispersion, which was produced by passing direct current through the electromagnetic coils (fig. S2). The intensity of the magnetic field was measured using a gaussmeter and precisely maintained at 2500 A m⁻¹ (30 Oe). The in situ assembly process was visualized using an upright light microscope. We use both brightfield and fluorescence modes to monitor the dynamics of supraparticle formation.

Assembly of supraparticles in magnetic field

Exposing the suspension to a uniform external field leads to the assembly of discrete anisotropic supraparticles formed by the attachment of satellite particles onto a patchy particle. The ferromagnetic patch provides strong directionality to the assembly, as most satellites appear to attach on the iron layer. A large number of satellites attaches to the nonmagnetic hemisphere of the patchy particles, which appear yellow in fluorescence due to colocalization of green on red fluorophores. The assembled structures are transient and will break apart upon turning off the external magnetic field, as shown in Fig. 1D and movie S1. All particles in the suspension initially repel each other, as a result of their negative surface charge. Once the external field is applied, the assembly follows a multistep growth mechanism, i.e., it proceeds in multiple steps as nonmagnetic microspheres are “magnetically captured” by the patchy particles, as shown in Fig. 1 (E to I) and the corresponding movie S2. The assembly mechanism is described as follows

$$\begin{array}{c}\mathrm{A}+\mathrm{B}\to \text{AB}\\ \text{AB}+\mathrm{B}\to {\text{AB}}_2\\ \cdots \\ {\text{AB}}_{n-1}+\mathrm{B}\to {\text{AB}}_n\end{array}$$

where A represents the patchy particle, B represents the nonmagnetic satellite microspheres, and the subscript n is the final number of blocks B assembled on A, which determines the supraparticle cluster size. The growth rate of the supraparticles is proportional to the number of building blocks B: The higher the number of satellites in suspension, the faster the structure will grow to a specific cluster size. Furthermore, concentration of B also dictates the maximum size that the supraparticles can reach. We find that the clusters attain a near-equilibrium state after ~35 min of exposure to magnetic field and do not significantly change beyond that time. The condition of near equilibrium is associated with the end of the supraparticle growth process, but it is a steady state due to its inherent dependence on external energy input via external field. Fully formed supraparticles are disassembled and reassembled in a single reversible step of turning the field off and on again

$${\text{AB}}_n\rightleftarrows \mathrm{A}+n\mathrm{B}$$

Supraparticles in solution experience competition between attractive and repulsive magnetic forces: Multipolar interactions lead to assembly, while long-range magnetic repulsion tends to keep the clusters separate and restrict the formation of a closed packed crystal-like phase (see movie S3). Self-avoidance among formed supraparticles is caused by A-A dipolar repulsion (31). This self-limiting magnetic behavior in thin films leads to the ordered arrangement of supraparticles into hexagonal arrays as shown in Fig. 2A.

Fig. 2. Colloidal clusters and effect of particle bulk ratio τ.

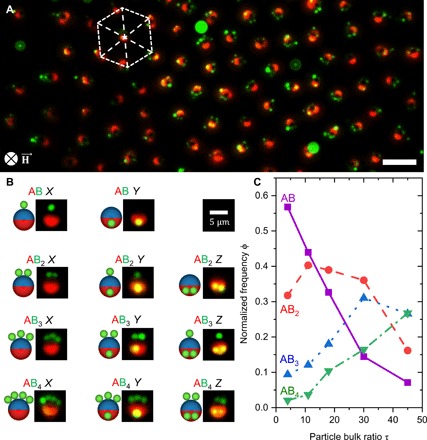
(A) 2D hexagonal arrangement of supraparticles. Scale bar, 25 μm. (B) Classification of colloidal clusters: From top to bottom, the number of satellites increases as supraparticles vary from AB to AB₄; from left to right, the fraction of satellites on the nonmagnetic hemisphere increases corresponding to isomers X, Y, and Z. (C) With increasing τ, the frequency of assembly of smaller clusters decreases in favor of larger supraparticles. All experiments were performed at H = 2500 A m⁻¹.

Near-equilibrium supraparticle structures

Clusters appear in a variety of structures depending on factors including field intensity, patch size, and ferrofluid concentration. By fixing these parameters, it is possible to control, classify, and analyze the different assemblies. Initial control over the assembly may be achieved by controlling the cluster size, which, as mentioned above, is highly dependent on the number of satellites (blocks B) initially present in solution. We find that the fraction of core Janus particles attaching with satellites to form supraparticle nearly doubles from 0.5 to 0.95 upon increasing τ from 4 to 30 (see fig. S3). The extent of cluster growth is determined by the quantity of building blocks within the capture radius of the patchy particle, i.e., the distance at which magnetic attraction overcomes self-diffusion of satellites when the Peclet number equals 1 (32).

The assembled supraparticles can be classified based on their final stoichiometry, from AB to AB_n (i.e. 1:1 to 1:n stoichiometry). Within each observed supraparticle stoichiometry, we identified different geometrical configurations: In some cases, satellites assemble not only on the metal patch but also on the nonmagnetic hemisphere of the patchy particle. Clusters of identical composition and differing configuration are colloidal isomers, which we classify based on the local arrangement of satellite particles as shown in Fig. 2B. Going from top to bottom in a column, we represent supraparticles of increased cluster size. From left to right in a column are isomers of a supraparticle of a given cluster size. These isomers are labeled as X, Y, and Z, which have 0, 1, or 2 satellites, respectively, on the nonmagnetic hemisphere of the patchy particle. We varied τ, i.e., the ratio of initial freestanding blocks B to blocks A, and monitored the growth of supraparticles upon initiating assembly. Upon allowing 1 hour of field exposure to reach equilibrium in cluster growth, ~2800 clusters were analyzed for their local configuration. All structures observed are classified as in Fig. 2B, and the normalized frequency of assembly ϕ into clusters AB to AB₄ is plotted as a function of τ (Fig. 2C). Here, ϕ represents the number of supraparticles assembled in a given structure, divided by the total number of assemblies. At the low building block ratio of 4, around 0.57 of the assembled supraparticles are AB, 0.31 are AB₂, 0.09 are AB₃, and 0.03 are AB₄. Increasing τ leads to a drastic reduction in AB structures in favor of all the larger cluster sizes. AB₂ and AB₃ clusters have maxima of frequency of 0.4 near τ = 11 and 0.3 near τ = 30, respectively, after which their frequency decreases in favor of AB₄. Increasing the overall ratio of B to A in the bulk leads to an increase in the number of nonmagnetic particles within the characteristic capture volume of the Janus particle. The effect of particle bulk ratio on supraparticles is consistent with the chemical analogy. The assembly process is comparable to a reaction scheme in which A is the limiting reactant that will determine the extent of reaction (33) (34).

Interactions driving the assembly process

The assembly of patchy and nonpatchy particles into supraparticle clusters is driven by the magnetic interactions between the building blocks. The magnetic energy landscape and the assembly kinetics determine the relative population of a given isomer of the cluster. Here, we use a point-dipole approximation to estimate the magnetic ensemble energy of a supraparticle and their isomers (U_mag) composed of the iron patch (P), the satellite particle/s (S), and the core of the patchy particle (C)

$$U_{\text{mag}}=U_{P-S}+U_{S-C}+U_{P-C}$$ (1)

Note that the interaction between patch and core U_P−C is constant with respect to the distance and the angle between the domains. The net magnetic interaction energy (U_ij) between two point dipoles is given as (35)

$${\mathbf{U}}_{\text{ij}}=\frac{1}{{\mathrm{r}}_{\text{ij}}^3}[{\mathbf{m}}_{\mathbf{i}}\cdot {\mathbf{m}}_{\mathbf{j}}-3\frac{({\mathbf{m}}_{\mathbf{i}}\cdot {\mathbf{r}}_{\text{ij}})({\mathbf{m}}_{\mathbf{j}}\cdot {\mathbf{r}}_{\text{ij}})}{{\mathrm{r}}_{\text{ij}}^2}]$$ (2)

where the subscripts i and j are two point dipoles representing the magnetized domains, r_ij is the interdipolar distance, and m is the magnetic dipole moment given as m_i = J V_i K_CM,iH. Here, J is the patch size defined as the fraction of the surface area of the particle that is covered by the metal patch, and V_i is the volume of the magnetized domain. K_{CM, i} is the real part of the Clausius-Mossotti function expressed in terms of magnetic susceptibility χ as

$$K_{\text{CM},\mathrm{i}}=\frac{{\mathrm{\chi }}_{\mathrm{i}}-{\mathrm{\chi }}_{\text{FF}}}{{\mathrm{\chi }}_{\mathrm{i}}+2{\mathrm{\chi }}_{\text{FF}}+3}$$ (3)

where the subscript FF represents the ferrofluid medium. Note that while the ferrofluid is composed of discrete Fe₃O₄ superparamagnetic nanoparticles (~5 nm in radius) dispersed in water, at micrometer length scale, this dispersion can be considered as a continuous medium of constant susceptibility χ_FF. Equation 3 mathematically illustrates that if χ_i > χ_FF, the dipole moment m (positive) of the particle will be aligned parallel to the direction of H, and if χ_i < χ_FF, m (negative) will be antiparallel to H. In our case, iron-patched particles contain both magnetic and nonmagnetic domains and show a more complex polarization pattern in the external field. In aqueous ferrofluid, χ > χ_FF for the iron patch, and χ < χ_FF for the nonmagnetic core of the particle. Therefore, the dipoles in the magnetic patch and nonmagnetic core are mutually antiparallel, making the patchy particle quadrupolar instead of dipolar (Fig. 1D). The multipolar nature of the patchy particle, and its interactions with the surrounding dipolar particles, is key in directing the symmetry of the multicomponent cluster.

The magnetization of each domain was calculated from the Clausius-Mossotti function using χ_S = 0, χ_FF = 0.15 (equivalent to the ferrofluid susceptibility at ~1.1 volume %) and χ_P = 0.49 as interpolated from SQUID measurements (figs. S4 and S5). In particular, the magnetic permeability of the patch was approximated to a concentric hemisphere composed of a thin iron layer surrounded by vacuum as calculated in the Supplementary Materials (note S1). For a given cluster, we evaluated U_mag as a function of the satellite orientation angle θ from 0° to 180°, in the plane of applied magnetic field (Fig. 3A). The change in ensemble energy for a Janus particle with one assembled satellite is shown in Fig. 3B. The calculations show a global minimum in magnetic energy at θ = 0° equivalent to U_mag ≈ −53.4 kT (k is the Boltzmann constant and T is the temperature), which corresponds to the apex of the metal hemisphere. This finding is expected because previous work has shown that assemblies involving iron-coated Janus particles are governed primarily by the strong polarization of the metal hemisphere (36). Unexpectedly, the magnetic energy shows a local minimum at θ = 109° with U_mag ≈ −21.2 kT. The presence of such local energy minima is a result of a delicate balance of attraction between the satellite particle and magnetic patch, combined with the repulsion between nonmagnetic core and satellite particle. During assembly, a nonmagnetic block approaching the Janus particle from the side of the nonmagnetic hemisphere (between angles 90° and 180°) experiences high repulsion from the 90° pole and a weak repulsion from the equator at 180°. At the same time, it experiences attraction from the metal patch across the Janus particle. The orientation angle of local minimum depends on the balance between these magnetic interactions. The thermodynamic significance stems from the lower enthalpy of cluster formation associated with lower ensemble energies. Therefore, for a given cluster size, assembly in which all satellites attach on the metal patch, i.e., isomer X, is more favorable than isomer Y, which has one particle attached on the nonmagnetic hemisphere (Fig. 2B). In turn, isomers Y are more thermodynamically favorable than isomers Z. The calculated results are in agreement with our experimental findings (see fig. S6).

Fig. 3. Magnetic energy landscape of Janus particle.

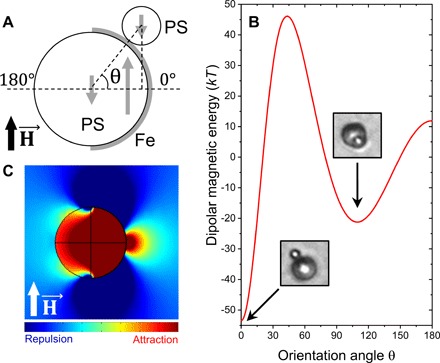
(A) Positioning of satellite relative to Janus particle as described by the orientation angle θ. The 0° angle corresponds to the apex of the metal patch, and the 90° angle corresponds to the “center” of the particle as seen from the top. Arrows indicate the position and direction of magnetic dipoles. (B) Plot of calculated dipolar magnetic energy U_mag as a function of θ, with fixed applied field intensity H = 2500 A m⁻¹. The global energy minimum is found at θ = 0°, and a local minimum is also found at θ = 109°. (C) Magnetic flux density distribution around a Janus particle as calculated using COMSOL Multiphysics 5.3.

Finite element analysis provides an alternative approach to study the magnetic energetics without relying on point-dipole approximated models. Alongside the calculation discussed above, we used COMSOL Multiphysics to solve the Maxwell equations and integrate the local magnetic energy over small finite domains (more details regarding this method are found in note S2). Similar results are obtained, validating our calculations: A 2D slice of magnetic field density is plotted in Fig. 3C, which shows strong attraction (dark red colored) at the apex of the patch and a weaker attraction (green colored) on the nonmagnetic hemisphere at θ ≈ 110° (figs. S7 and S8).

Determining the energy landscape around the Janus particle clarifies the multiplicity of configurations observed in experiments. Supraparticle formation is enthalpically driven by the supply of energy in the form of an external magnetic field, and it presents both a thermodynamic ground state and metastable states. Initial spatial distribution of building blocks and their orientation play a fundamental role as nonmagnetic particles are attracted not only to the ferromagnetic coating but also to nonmagnetic “patches” found on the Janus particle (see movie S5). As clusters form, particles may be dynamically trapped into metastable state within a few minutes, forming multiple isomeric supraparticles.

Controlling the local assembly

The local configuration of supraparticles is preprogrammed by the choice of building blocks: In particular, we have shown the crucial role of the metallo-dielectric patchy particle in originating multipolar interactions. As described above and in note S3, the magnitude of the ferromagnetic moment scales directly with J, modifying the energetic landscape around the patchy particle surface, as calculated in Fig. 4A. A nonpatchy particle immersed in ferrofluid presents a single global minimum at the poles (90°), which leads to chaining in the direction of field as shown previously (24). Introduction of an iron patch drastically modifies the plot, with the new global minimum moved to the equator on the patch (0°). The minimum traditionally found at 90° for isotropic particles (D_∞h symmetry) is geometrically pushed further toward the nonmagnetic hemisphere (C_2v symmetry). The position of this now local minimum is shifted from 93° with J = 0.1 to 109° for Janus particles (i.e., J = 0.5). We define the distance δ between the center of the satellite and the polar axis of the patchy particle as δ = (R_C + R_S) cos (180 ° − θ_lmin) and calculated it as a function of the orientation angle of local minimum θ_lmin. Starting from δ = 0 μm for nonpatchy particles (J = 0.0), the value increases up to δ = 1.1 μm with Janus particles (J = 0.5). We synthesized building blocks of different patch sizes (i.e., J = 0.1, 0.3, and 0.4) by the method of glancing angle deposition and assembled AB supraparticles with τ = 4 for each patch size. We used the ImageJ software package (37) to determine δ for each assembly by measuring it for 15 s, equivalent to 200 frames. The average value for each experiment is plotted in Fig. 4B with high agreement with the theoretical line. The fluorescence micrographs of the AB supraparticles (Y isomer) with a dotted line running through the poles of each core particle are shown in Fig. 4C. By increasing patch size from J = 0 to J = 0.5, the position of the satellite on the local minimum changes from δ = 0.05 μm to δ = 1.1 μm. This occurs as the fine balance of attraction to the patch against repulsion from the core is tuned by J. The patchy particle is an asymmetric quadrupole with a highly polarizable ferromagnetic domain. The iron patch attracts satellites at the equator (where they align antiparallel) and repels them near the poles. Increasing the volume of iron implies the strengthening of both interactions: satellites being repelled further from the poles with J. As J decreases, the strength of the interactions decreases and approaches the isotropic case.

Fig. 4. Effect of patch size J.

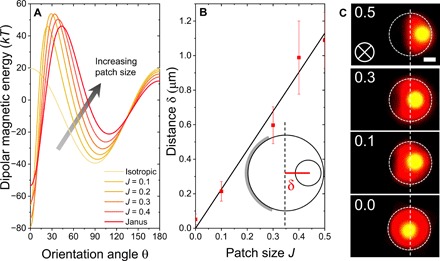
(A) Calculated dipolar magnetic energy as a function of θ for different patch sizes. The minimum found at θ = 90° for an isotropic particle is relocated to θ_lmin = 93°, 97°, 101°, 105°, and 109° for J = 0.1, 0.2, 0.3, 0.4, and 0.5, respectively. (B) Measured and calculated values of distance δ increasing as a function of J, i.e., the fraction of the surface covered by the metal patch. Error bars represent the SD of the location of the satellite particle on the surface of a patchy particle. This is due to the inherent surface diffusion of the satellite on the core particle. (C) From bottom to top, images of AB Y supraparticles of varying structure as obtained by increasing iron patch size. δ ranges from 0.05 μm for an isotropic core particle to 1.1 μm for a Janus particle. The symmetry point group of the supraparticle changes from D_∞h to C_2v upon increasing the patch size from J = 0.0 to 0.5. Scale bar, 2.0 μm.

Reconfiguration of supraparticle clusters

Control of the shape and symmetry of clusters is achieved both by preprogramming of the building blocks and by in situ reconfiguration of assembled structures. One possible reconfiguration consists in transitioning kinetically trapped isomers into their thermodynamically preferred counterparts, i.e., moving satellite particles from the weakly attractive nonmagnetic hemisphere to form a stronger magnetic bond with the iron patch (fig. S9). Pseudo-isomerization can be done by lowering the energy barrier between metastable and ground states seen in Fig. 3B. From Eq. 2, we know that the dipolar energy is directly proportional to the magnetization of two particles and by transitive property to the magnetic field intensity squared H². Therefore, reducing the field intensity will minimize the “saddle point” and create a pathway for satellite particles to move from the nonmagnetic hemisphere to the metal patch. We show five stages of the pseudo-isomerization of an AB₆ supraparticle in Fig. 5A (see movie S6). Initially, the cluster has three B blocks on the patch and three on the nonmagnetic hemisphere. By decreasing the field intensity from 4000 A m⁻¹ to below 700 A m⁻¹, we reduced the interaction potential between the building blocks. The already weak attraction provided on the nonmagnetic hemisphere is no longer enough to bind three satellites: Two of them escape the region and attach on the iron patch. Enough energy is maintained for a single satellite to stay on the nonmagnetic hemisphere, even at very low fields. Note that at no point did we reduce the field to 0 A m⁻¹, which would cause the supraparticle to disassemble completely. We performed colloidal isomerization on a multitude of supraparticles and observed that ~68% of satellites initially assembled on the polymer hemisphere will diffuse toward the iron patch upon decreasing H (see fig. S10). The ensemble energy of each configuration is estimated by combining the dipolar energy contributions of six isotropic satellites, the iron patch, and the nonmagnetic core. We calculated the difference between configurational magnetic energies for the initial and final states (ΔU) as a function of H (Fig. 5A). The results are plotted in Fig. 5B, showing that, at H = 4000 A m⁻¹, the ensemble energy of state 1 is higher than that of state 2 by ~50 kT. Decreasing applied field intensity comes with a drastic reduction in the energy difference between the initial and final states, down to ~ 1 kT at H < 700 A m⁻¹. At larger values of applied field, the high magnitude of the magnetic interactions dominates assembly. By contrast, lower H allows satellites to thermally fluctuate in their position, thus transitioning to the ground configurational state. Further indication of the relationship between H and structures is found in fig. S11. We observed that performing the assembly at high field intensity increases the fraction of metastable isomers. Higher-energy input allows metastable states to form and be maintained, because the high enthalpic “price” can be paid. On the other hand, a lower initial field intensity leads to a higher fraction of isomers X, as it does not provide enough attraction to pay the energy price of state 1. The isomerization here described is a phenomenon that only occurs when releasing satellites from the kinetic trap by reducing the applied energy. Supraparticles assembled in their ground state will not undergo field-driven reconfiguration.

Fig. 5. Supraparticle reconfiguration by lowering field intensity.

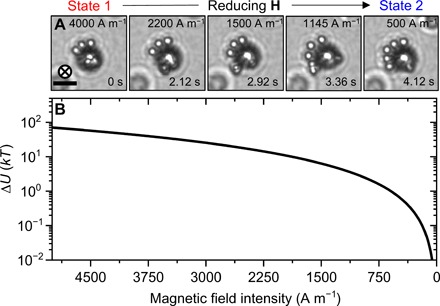
(A) Brightfield micrographs of AB₆ supraparticle from state 1 to state 2 through five stages of reconfiguration. Decreasing the applied field intensity from 4000 to 500 A m⁻¹ allows relocation of two satellites from the nonmagnetic hemisphere to the iron patch. Scale bar, 5.0 μm. (B) Ensemble energy difference between state 1 and state 2 (ΔU) as a function of applied field intensity H. At 4000 A m⁻¹, the energy difference is ~50 kT and is reduced to ~1 kT at 700 A m⁻¹.

Permanent locking of supraparticle structures

All supraparticles discussed above require exposure to magnetic field to assemble and to maintain their structure. If, on the one hand, the dependence on field-supplied energy provides the element of reversibility in the assembly process, it also impedes the possibility of making materials using these unusual low-symmetry supraparticles as building blocks. Permanent binding of particles forming a supraparticle requires further processing of the system. We introduce a simple, minimally intrusive method for tuning the physical interactions between the building blocks. We replaced the carboxylated nonmagnetic particles with aminated nonmagnetic particles (radius R_AM = 1.0 μm; green fluorescent), which have their isoelectric point at pH ~3. We used 15 mM diphenyliodonium nitrate as a photo-acid generator capable of producing protons when exposed to ultraviolet (UV) light (38). After assembly under magnetic field was completed, we irradiated the sample with UV light (λ = 365 nm) for 1 hour at a distance of 10 cm. The photo-acid generator induced a decrease in pH and the subsequent reversal in surface charge density of the amine-functionalized particles from negative at pH 5 to positive at pH 2 (39).

Three types of interparticle interactions are at play, as plotted in Fig. 6A, to which three separate physical states correspond, as represented by Fig. 6B. At the initial pH of 5, DLVO (electrostatic + van der Waals) repulsion dominates the system, as all surfaces are negatively charged (sample calculation can be found in note S4). Once the field is turned on, long-range magnetic attraction overwrites the repulsion and building blocks dynamically arrange into supraparticles with near-equilibrium energetics discussed in the above sections. With the final pH of ~2 obtained after UV exposure, electrostatic attraction takes place instead of repulsion: Supraparticles in their magnetic configurations are now locked in a DLVO minimum, regardless of field exposure (see movie S7). The proposed method of electrostatic binding of particles by inverting surface charges is not limited to the amine-carboxyl functionalized microparticle pair, but it can be extended to any particle precursor with dissimilar isoelectric points.

Fig. 6. Manipulation of DLVO interactions by photo-acid generator.

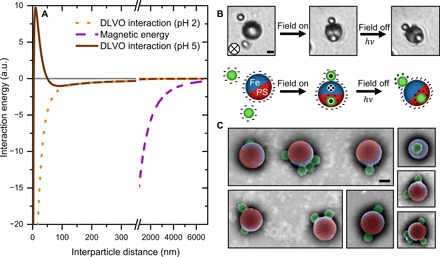
(A) Plot of interaction energy against interparticle distance: At the initial pH of 5, particles experience repulsion (brown line). Magnetic field induces long-range attraction even at a distance beyond 5 μm (purple dashed line). Exposure to UV light reduces the pH to 2, at which particles experience short-range electrostatic attraction (orange dotted line). (B) Brightfield images and corresponding schematic of the three conditions in the suspension: initial repulsion of negatively charged surfaces, attraction into supraparticle via magnetic field, and permanent locking into DLVO minimum after reversal of surface charge on satellites. Scale bar, 2 μm. (C) False-colored SEM images of dried and recovered structures. Scale bar, 2 μm.

Taking advantage of the photochemically induced stability, we have applied this process in bulk, i.e., we performed magnetic assembly on a small vial containing our dispersion of building blocks in ferrofluid, exposed it to 365-nm light within a UV chamber. The induced electrostatic interactions are strong enough to trap the clusters into DLVO minima capable of withstanding thermal and mechanical forces operational in post-assembly processing of the supraparticles. We filtered the clusters from the suspension to remove the magnetite nanoparticles. Thus, by adding a single step mechanism of photo-protonation to the assembly process, we recovered complex supraparticles of varying anisotropy as shown in Fig. 6C (more available in fig. S12). Supraparticles with a wide range of preprogrammed structures are readily obtainable through this mechanism. The yield of the overall process from discrete particles to washed and filtered supraparticles was found to be ~55%. We believe that the supraparticle production using this method can be scaled up by designing a continuous flow process, where the magnetic assembly and surface charge inversion are sequential steps along a synthesis line. However, the current bottleneck of the large-scale production of these clusters is the synthesis of patchy core particles, where further work is necessary to scale up the fabrication process.

CONCLUSION

We demonstrate how the multipolar nature of metallodielectric patchy particles can be programmed to magnetically assemble supraparticles with defined structure and configuration. Parameters such as the relative concentration of building block particles, the field strength, and the size of the metal patch were tested as means to achieve control over the assembly of supraparticle in bulk. We complemented the experimental findings with theoretical analysis of the assembly, using the point-dipolar model for magnetic interactions. In addition, we introduced a facile method for the in situ manipulation of DLVO interactions using a photo-acid generator, which allows the permanent binding of assembled clusters into recoverable supraparticles. The article presents an approach to controlling three structural motifs of supraparticles: connectivity via exposure to magnetic field, composition via suspension of nonmagnetic particles in ferrofluid, and distribution via adoption of patchy colloids as building blocks. The resulting colloidal clusters are formed with isomeric configurations and a controllable variety of structures. Techniques for the tuning of colloidal interactions constitute the toolset for future development of functional applications. In that context, this study bridges two research currents in the field of supraparticle engineering: the simple, scalable methods obtained at the cost of repeatability, and the highly defined, precise structures assembled through multiple complex stages.

MATERIALS AND METHODS

Materials

The ferrofluid used is a commercially available aqueous suspension of magnetite (Fe₃O₄) nanoparticles ~5 nm in diameter (Ferrotec EMG 707). The nanoparticles are coated with anionic surfactant and have a saturation magnetization of ~5000 A m⁻¹ at room temperature (fig. S4). Polystyrene latex microspheres were acquired from Magsphere Inc.: red fluorescent carboxylated (R_C = 2.5 μm), green fluorescent carboxylated (R_S = 1.0 μm), and green fluorescent aminated particles (R_AM = 1.0 μm). Janus particles were fabricated by coating a monolayer of polystyrene beads deposited on a glass slide via Langmuir-Blodgett trough (surface pressure, 8 mN m⁻¹), with a 5-nm chromium layer (deposition rate, 0.5 nm s⁻¹) followed by a 30-nm iron layer (deposition rate, 0.10 nm s⁻¹) under vacuum (1 × 10⁻⁶ torr) in a thermal evaporator. More details on patchy particles are available in the Supplementary Materials (figs. S13 and S14). The coated particles were transferred into a vial using a spatula and redispersed in deionized water by gentle sonication before experiments. The concentration of the patchy particle stock suspensions was ~0.15 volume %. The mixtures of ferrofluid, polystyrene, and Janus particles used were diluted using ultrapure water of resistivity 18.2 megaohm·cm.

Supraparticle assembly setup

Assembly experiments were performed under the microscope by sealing 0.5 μl of suspension between a glass slide and a coverslip using a hydrophobic barrier pen. A custom-built magnetic field setup was constructed from a single cylindrical air-core solenoid electromagnet (TEMCo Industrial 14 AWG Copper Magnet Wire; 36 m long, 0.08 cm thick, approximately 450 turns). The samples were placed on the sample holder at the center, forming a vertical Helmholtz coil arrangement that provided a uniform magnetic field. Supraparticle assembly was monitored via brightfield and fluorescence microscopy using a Leica DM6 microscope equipped with DFC9000 GTC camera and EL 6000 fluorescence light source. The objectives used were Leica ×20/0.40 and ×40/0.55 in conjunction with green fluorescent protein (GFP) and Texas Red filter cubes. Further processing of images was done with the ImageJ software package.

Scanning electron microscopy

Samples for scanning electron microscopy (SEM) imaging were prepared by deposition of filtrate containing supraparticles on carbon tape. A Quanta 3D DualBeam FEG FIB-SEM was used for high-resolution imaging in vacuum, with an accelerating voltage of 20 kV, at a working distance of ~10 mm. Both a secondary electron and backscattered electron detectors were used. Note that higher electron density of the iron patch relative to polystyrene makes it appear brighter.

Finite element analysis

Magnetic flux distribution and total magnetic energy were calculated using the AC/DC package with COMSOL Multiphysics 5.3a, specifically the Magnetic Fields interface. A 3D representation of the assembly was built with a Janus particle and a single or multiple nonmagnetic particle (relative permeability μ_r = 1 + χ_S = 1) as needed, surrounded by a 100 × 100 × 100 μm volume of ferrofluid (relative permeability μ_r = 1 + χ_FF = 1.15). The metal coating of the patchy particle was built as a Boolean difference between a metal sphere (relative permeability μ_r = 5000) and the nonmagnetic core (relative permeability μ_r = 1) of the Janus particle. A uniform magnetic field of 2500 A m⁻¹ was input in the z direction. The built geometry was divided into a fine mesh (minimum element size, 0.02 μm; maximum element size, 2 μm; maximum element growth rate, 1.3 μm) of free tetrahedral shapes over which the Maxwell-Ampere equations were solved to obtain the magnetic flux distributions. Subsequently, the total magnetic energy of the assemblies was calculated by integrating the local magnetic energy over each subdomain.

SQUID magnetometry

Measurement of magnetic properties was done using a “MPMS XL” SQUID magnetometer (Quantum Design). Samples are inserted in a 5 mm × 5 mm × 5 mm volume within a plastic enclosing and centered with respect to the pickup coils. The instrument detects changes in magnetic flux created by mechanically sliding the sample through a superconducting coil. The diamagnetic contribution due to the plastic container is subtracted from the resulting data, available in the Supplementary Materials.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/19/eaba5337/DC1