Passenger mutations in 2500 cancer genomes: Overall molecular functional impact and consequences

Summary

The dichotomous model of “drivers” and “passengers” in cancer posit that only a few mutations in a tumor strongly affect its progression, with the remaining ones being inconsequential. Here, we leveraged the comprehensive variant dataset from the Pan-cancer Analysis of Whole Genomes project to demonstrate that – in addition to the dichotomy of high- and low-impact variants – there is a third group of medium-impact putative passengers. Moreover, we also found that molecular impact correlates with subclonal architecture (i.e., early vs. late mutations) and that different signatures encode for mutations with divergent impact. Furthermore, we adapted an additive-effects model from complex-trait studies to show that the aggregated effect of putative passengers, including undetected weak drivers, provides significant additional power (~12% additive variance) for predicting cancerous phenotypes, beyond PCAWG-identified driver mutations. Finally, this framework allowed us to estimate the frequency of potential weak-driver mutations in PCAWG samples lacking any well-characterized driver alterations.

Graphical Abstract

Introduction

Previous studies have characterized variants within coding regions of cancer genomes (Ding et al., 2018; Weinstein et al., 2013). However, given that the majority of cancer variants occupy non-coding regions (Khurana et al., 2016), investigation into the overall molecular functional impact of variants influencing both coding and non-coding genomic elements are needed. The extensive Pan-cancer Analysis of Whole Genomes (PCAWG) variant dataset (Campbell et al., 2017) includes >2,500 uniformly processed whole-genome sequences of cancer samples. Moreover, this dataset contains a full spectrum of variants, including somatic copy number alterations, structural variants (SVs), single-nucleotide variants (SNVs), and small insertions and deletions (INDELs).

Of the 44 million SNVs in the PCAWG variant dataset, thousands of mutations have been identified as drivers (i.e., positively selected variants that favor tumor growth), with most tumors having ~5 driver mutations in total (Campbell et al., 2017; Vogelstein and Kinzler, 2015). The remaining ~99% of SNVs are termed passenger variants (referred to as putative passengers in this work), with poorly understood molecular consequences and fitness effects. Recent studies have proposed that some putative passengers may weakly affect tumor cell fitness by promoting or inhibiting tumor growth. In prior studies, these variants have been described as “mini-drivers” (Castro-Giner et al., 2015) and “deleterious passengers” (McFarland et al., 2013), respectively.

In this work, we explored the landscape of putative passengers in various cancer cohorts by leveraging the comprehensive information in the PCAWG project on variant calls (Campbell et al., 2017; Li et al., 2017), driver mutations (Campbell et al., 2017; Rheinbay et al., 2017a), transcriptome profiles (Fonseca et al., 2017), mutational signatures (Alexandrov et al., 2018), and subclonal status (Gerstung et al., 2017). More specifically, we built upon and applied existing tools (Balasubramanian et al., 2017; Fu et al., 2014) to annotate and predict the molecular functional impact of variants. This effort generated a comprehensive resource of annotated PCAWG variants, which we leveraged to quantify the aggregated burden and molecular impact of putative passengers on various genomic elements in different cancer cohorts. We observed that disruption of regulatory elements in non-coding regions correlated with altered gene expression. Moreover, our analysis of signatures indicated that various mutational processes have differential impacts on coding genes and regulatory elements. Similarly, we found that the predicted molecular functional impact of variants correlated with patient survival time and tumor clonality.

All the above observations potentially could be explained by alterations in the mutational processes in various cancers and/or by the action of selection. Additionally, we note that selection acting on somatic cells is dynamic throughout tumor progression. Thus, putative passengers that initially have no fitness impact could provide cellular fitness advantages at a later phase, when treatment is given or when cancer spreads to another organ. Hence, we assessed possible non-neutral roles for putative passengers. We found that the aggregated impact of putative passengers provides significant predictive power – beyond common driver mutations – to distinguish cancer from non-cancer phenotypes, even after controlling for known mutational processes and background mutation rates. This observation is particularly prominent among tumors without known drivers (Campbell et al., 2017; Rheinbay et al., 2017a) or with fewer driver variants than expected. Although the non-neutral effects of these putative passengers can only be detected in aggregate (by our model), our findings motivate future studies aimed at identifying such weak drivers, especially within non-coding regions of the genome.

Results

Molecular functional impact of putative passengers

In this work, we restricted the majority of our analyses to the core set of non-driver mutations that were absent from the PCAWG driver mutation catalog (Campbell et al., 2017). Briefly, the PCAWG driver and functional interpretation group integrated results from multiple driver detection methods to identify a consensus set of driver genes and non-coding elements including promoters, untranslated regions, and enhancers. Subsequently, a comprehensive workflow was applied to distinguish driver mutations from putative passengers within these predicted driver genes and elements (Campbell et al., 2017). Additionally, this approach nominated mutations as drivers based on their presence in previously known driver genes (based on predictive methods, and experimental or clinical validation) (Campbell et al., 2017; Rheinbay et al., 2017a) (STAR method section 10.2).

To characterize the landscape of putative passenger mutations in PCAWG, we first surveyed the predicted molecular functional impact (quantified by FunSeq score (Fu et al., 2014)) of somatic variants at the pan-cancer level. Briefly, the FunSeq tool assigns a molecular functional impact score to a mutation based on various features. These features include interspecies conservation; gain or break of transcription factor (TF) motifs; disruption of known enhancer-gene interactions; and centrality in the gene-regulatory or protein-interaction network. The predicted functional impact distribution varied among cancer types and genomic elements.A closer inspection of the pan-cancer impact score distribution for non-coding mutations demonstrated three distinct regions. The upper and the lower extremes of this distribution were enriched with high-impact strong drivers and low-impact neutral passengers, respectively. In contrast, the middle range of this distribution corresponded to putative passengers with intermediate molecular functional impacts (Fig. 1a & supplement Fig. S1a). A majority of these medium-impact putative passengers were found in metabolic, immune response, and essential genes. (We highlight this finding specifically for nonsynonymous and promoter mutations in supplement Fig. S1d.)

Figure 1: Overall functional impact of PCAWG variants:

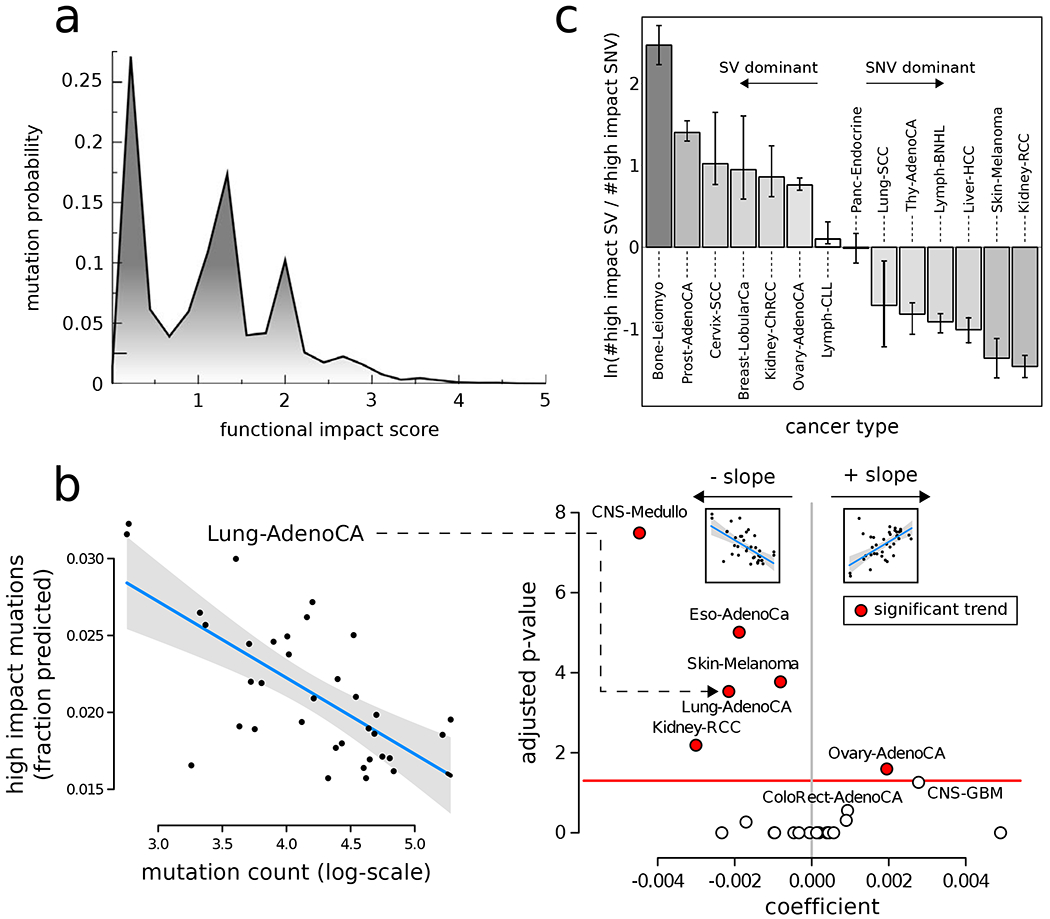
a) Functional impact distribution in non-coding (DNase hypersensitive sites averaged across multiple cell lines) regions: three peaks correspond to low-, medium-, and high-impact mutations. b) Correlation between the fraction of high- and medium-impact non-coding SNVs and the total mutational counts for lung adenocarcinoma cohort (left). Scatter plot for correlation coefficient (x-axis) and FDR-corrected p-value for various cancer cohorts (right). c) Log ratio between high-impact SV and SNV frequency in different cancer cohorts. Error bars correspond to variation within the cohort. See also supplement Fig. S1.

Subsequently, we investigated how the fraction of higher impact passenger mutations (STAR Method section 3.2 for classification) related to total mutational burden (i.e., number of mutations). Naively, we would expect this fraction to remain constant, assuming that passengers were not under selection. In contrast, we observed a decrease in higher-impact putative passenger frequency for tumors with a high mutational burden, which could be construed as evidence of weak negative selection. Alternatively, one might explain this in terms of changed mutational signatures in such tumor samples. This trend was particularly strong in central nervous system (CNS) medulloblastoma (p < 4e-8), lung adenocarcinoma (p < 3e-4), and other specific cancer cohorts (Fig. 1b & supplement Fig. S1c).

In addition to SNVs, SVs play an essential role in cancer progression. Thus, we quantified the functional impact of putative passenger SVs after excluding driver deletions and duplications (Rheinbay et al., 2017a). Briefly, we built a machine-learning framework, which utilized conservation, epigenomic signals, and overlaps with known cancer genes to assign an SV impact score (STAR method section 4.2). A close inspection of both putative passenger SV and SNV impact scores suggested that some cancer subtypes harbor many high-impact SVs, while others contain a large number of high-impact SNVs (Fig. 1c). Many of these correlations have previously been observed (Ciriello et al., 2013). For example, large deletions are known to act as the predominant drivers in ovarian cancer; in contrast, SNVs often exclusively drive clear cell kidney cancer (Ciriello et al., 2013). However, the comprehensive PCAWG call sets allowed us to find new associations, such as the predominance of high-impact large deletions compared to impactful SNVs in the bone leiomyoma cohort. Similarly, a close inspection of high-impact large duplications and high-impact SNVs suggested their differential association with different cancer cohorts (supplement Fig. S1e).

Putative passenger burden among different genomic elements

Next, we investigated the overall putative passenger burden among different genomic elements in various cancer cohorts and observed differential burdening of specific gene categories and their regulatory elements. This is most straightforward to interpret for coding loss-of-function mutations (LoFs), where molecular impact is most intuitive. We thus examined the fraction of deleterious LoFs affecting genes belonging to several cancer-related gene categories (Fig. 2a). Driver LoFs (i.e., LoFs included in the PCAWG driver catalog) showed significant enrichment among cancer-related gene categories (DNA repair, immune response, and essential genes, all with p < 0.001 and relative to uniform genome-wide expectation) (Fig. 2a); in contrast, putative passenger LoFs were significantly depleted among DNA repair genes (compared to the uniform case, Fig. 2a). As mutational signatures might influence these observations, we also employed signature-corrected background randomization; using this, we observed that putative passenger LoFs were significantly depleted in additional cancer-related gene categories beyond DNA repair (including cell cycle, cancer pathway, and apoptosis) (supplement Fig. S2a). Finally, we note that a differential tendency towards mutation generation or mutation repair among gene categories may contribute to these observations (e.g., higher expression among essential genes may lead to both increased transcription-coupled damage and transcription-coupled repair (Hanawalt and Spivak, 2008)).

Figure 2: Overall functional burdening of different genomic elements:

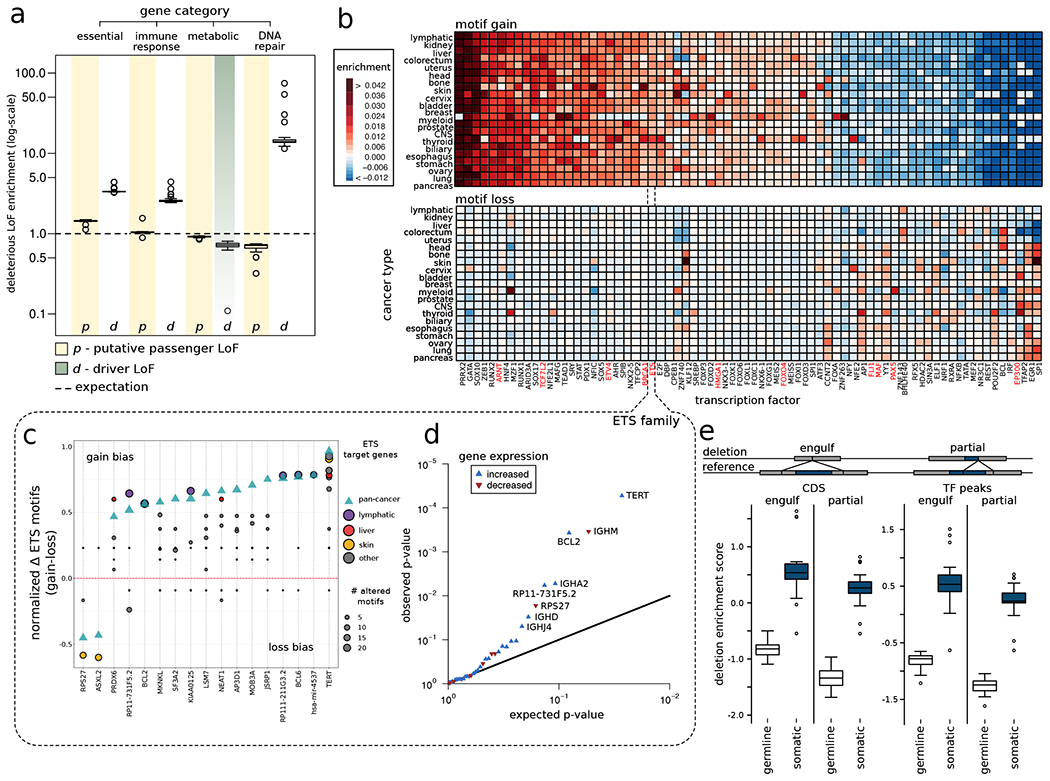
a) Percentage of genes in different gene categories affected by driver (grey band) and putative passenger (faded yellow band) LoFs compared to uniform background expectation (dashed black line). Data points in boxplot correspond to different tumor types. b) Heatmap showing enrichment (red color) and depletion (blue color) of motif gain (upper panel) and loss (bottom panel) events induced by putative passenger mutations for various TFs compared to a uniform genomic background. TFs highlighted in red are well-known cancer genes. c) Gain (positive alteration bias) and loss (negative alteration bias) of motif events observed among target genes (on x-axis) regulated by the ETS TF family. The green triangle denotes alteration bias on the pan-cancer level, whereas colored circles correspond to alteration bias for different cancer cohorts. The size of the circles corresponds to the frequency of motif-altering events. d) Q-Q plot showing genes that are differentially expressed due to gain-of-motif events in TFs belonging to the ETS TF family. e) Enrichment of germline and somatic large deletions that can engulf or partially delete coding regions and TF binding peaks. See also supplement Fig. S2.

As with LoFs, we quantified the overall molecular impact burden of the non-coding SNVs in a cancer genome. For the majority of non-coding SNVs, the predicted molecular functional impact is less easy to gauge. An important exception is TF binding sites (TFBSes), where the impact of variants is clearly manifested through the creation or destruction of binding motifs (gain or loss-of-motif) (Melton et al., 2015; Yiu Chan et al., 2019). In both cases (gain or loss in a TFBS), we observed significant differential burdening of putative passenger mutations among different cancer cohorts (STAR method section 6.1). For instance, based on a uniform background model, we detected significant enrichment of mutations creating binding motifs for various TFs including GATA, PRRX2, and SOX10 (Fig. 2b, Supplement Table S1) across major cancer types, compared with genome-wide expectation. Similarly, in many cancer cohorts, mutations breaking motifs were highly enriched for TFs such as SP1, EGR1, EP300, and ETS (Fig. 2b, Supplement Table S1). Additionally, we quantified the overall burdening of TFs that undergo gain- or loss-of-motif events due to presence of INDELs (supplement Fig. S2c).

This overall enrichment or depletion provides insight into the particular regulatory subsystems most differentially affected in each cancer, via the action of mutational processes. Furthermore, to investigate the role of selection, we refined the analysis by repeating it using a signature-corrected background model. We observed significant enrichment of motif-gain events for the TFBSes of STAT in addition to PRRX2 and SOX10; similarly, loss-of-motif events were enriched for HNF4, ETS, and SP1 (Supplement Table S1 & supplement Fig. S2b). In contrast to the previous analysis with a uniform background, here the enrichment and depletion potentially suggests the role of selection. We note that the definitions of these motifs are derived from the ENCODE project (Dunham et al., 2012) and they may represent direct as well as indirect associations with corresponding TFs.

For a given TF, one can identify the associated target genes that are affected due to the bias towards the creation or disruption of specific motifs in their regulatory elements (promoters and enhancers). For instance, putative passengers that induced motif creation events among TFBSes belonging to the ETS TF family influenced their target TERT genes across multiple cancer types (Fig. 2c). Similarly, motif alteration bias events among ETS TFBSes also influenced other genes (including BCL6), albeit in fewer cancer types. Moreover, the enrichment of putative passenger mutations in select motifs led to gain and break events in promoter, significantly perturbing the overall expression of downstream genes (Fig. 2d & supplement Fig. S2d–S2e). For example, mutations in many cancers are strongly biased to create new motifs for TFs belonging to the ETS family, which, in turn, drive expression changes in their target genes including TERT and BCL2 (with p-values of TERT=5.49e-5 and BCL2=3.4e-4). In contrast, in skin-melanoma, mutations break many ETS motifs, and this is associated with the downregulation of the RPS27 gene.

Finally, we analyzed the overall burden of SVs (specifically, large deletions and duplications) in various genomic elements and compared the pattern of somatic SVs in cancer genomes to those in the germline (Fig. 2e). Using a uniform background model, we observed that somatic SVs were more enriched within functional elements compared to germline SVs (Fig. 2e & supplement Fig. S2f); this was expected, because the latter will be under negative selection against functional disruption. Furthermore, we observed a distinct pattern of enrichment for SVs that split a functional element versus those that “engulf” an entire element. As previously noted (Khurana et al., 2013; Sudmant et al., 2015), we found a greater enrichment of germline SVs that entirely engulf an entire element rather than for those that partially break one. Interestingly, here, we observed the same pattern among somatic SVs (Fig. 2e & supplement Fig. S2f).

Characterizing mutational processes underlying putative passengers

Mutational processes underlying putative passengers have a stochastic but unevenly distributed nature, which can potentially explain the differential burdening of various genomic elements. Thus, we carefully inspected the mutational processes generating putative passengers in both coding and non-coding regions. Among coding mutations, we found that the LoF mutation spectra in many cancers were reasonably close to what one would expect from a possible theoretical mutational spectrum generating all potential premature stops in coding regions. However, there were differences between different cancers. In particular, variants creating premature stops showed a higher percentage of T>As in renal cell carcinomas (RCCs) compared to the pan-cancer average (18% vs. 8%) (Fig. 3a & supplement Fig. S3a). Furthermore, a close inspection of the penta-nucleotide spectrum associated with premature stops suggested a high correlation between the frequency of observed LoF mutations and in- or out-of-frame mutational stop patterns within specific cancer cohorts (supplement Fig. S3b). Moreover, there are fewer LoFs than we expect from the theoretical distribution in kidney-RCC and skin-melanoma cohorts (supplement Fig. S3b).

Figure 3. Mutational signatures associated with different categories of impactful variants:

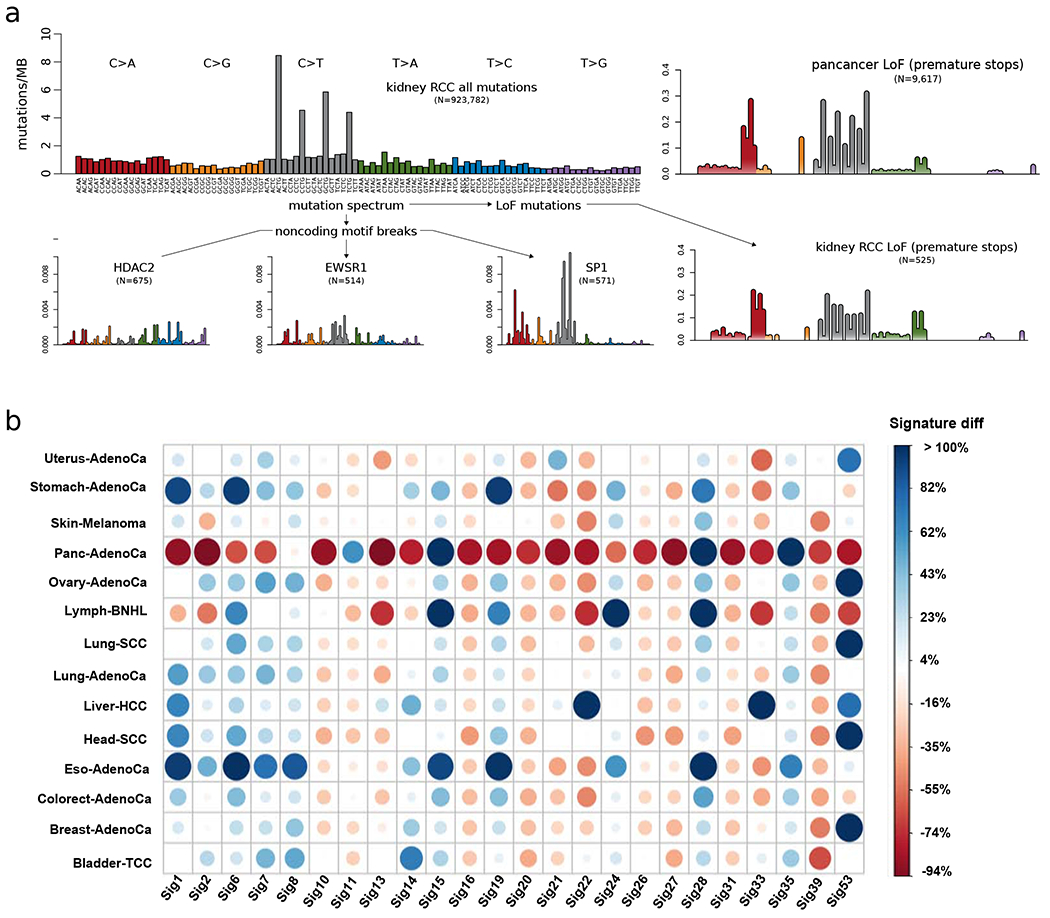
a) Mutation spectra associated with premature stops and TF binding motif-breaking events in the kidney-RCC cohort. b) Comparison of underlying signature distribution between high- and low-impact putative passengers in different cancer cohorts for a subset of signatures. For a given signature, the size of a dot corresponds to the percent increase or decrease in their contribution to describe high-impact mutations compared to low-impact mutations. Blue and red colored dots represent positive and negative signature differences, respectively. See also supplement Fig. S3.

Similarly, we analyzed the mutational spectrum underlying variants in TFBSes. We note that different TFs tend to have different nucleotide contexts in their TFBSes, making them differentially sensitive to different mutational processes. For instance, the mutational spectrum of SP1 motif-breaking events suggested a predominant contribution from C>T and C>A mutations (Fig. 3a). In contrast, motif-breaking events for HDAC2 and EWSR1 have a relatively uniform mutational spectrum (Fig. 3a).

Based on the mutational context, we can further decompose observed mutations into a linear combination of signatures, each of which represents different mutational processes (Alexandrov et al., 2013; Helleday et al., 2014). Each signature (Alexandrov et al., 2018) has a different contribution towards the mutational processes in a given cancer type. We compared the signature distributions of low- and high-impact putative passengers in different cancer cohorts. Briefly, for each cancer cohort we compared the contribution of individual signatures underlying high- and low-impact putative passengers using a non-parametric statistical test (method section 7.4). We identified a subset of signatures that had significant differential contributions for low- and high-impact putative passengers across multiple cancer types. In particular, we observed distinct signatures for the low-and high-impact putative passengers in pancreatic, esophageal, lymphoma, and ovary cohorts (Fig. 3b). A few signatures (1, 6, 7,19, 28, and 35) consistently had a higher contribution toward high-impact putative passengers across multiple cohorts; in contrast, other signatures (20, 22, 27, and 39) had consistent lower contributions. These observations imply that differing mutational processes could potentially explain the divergence of functional impacts among a subset of putative passengers.

Finally, we observed that cancer samples with microsatellite instability (due to the failure of DNA mismatch repair) have a higher percentage of high-impact non-coding putative passengers compared to those with stable microsatellites (supplement Fig. S3c).

Subclonal architecture and mutational heterogeneity of putative passengers

Cancer is an evolutionary process, often characterized by the presence of different sub-clones. We can categorize these subclones as early and late based on the overall subclonal architecture of a cancer sample (STAR method section 8.1). Here, we explored the relative population of high- and low-impact putative passengers in different sub-clones of a tumor sample (Gerstung et al., 2017). Intuitively, one might hypothesize that high-impact mutations achieve greater prevalence in tumor cells if they are advantageous to the tumor, and a lower prevalence if they are deleterious. As expected, we observed this to be true among driver variants (Fig. 4a). Interestingly, we found that high-impact putative passengers in coding regions had greater prevalence among parental subclones (STAR method section 8.1) – an effect consistent with their presence in tumor suppressor and apoptotic genes (Fig. 4a). In contrast, high-impact putative passengers in oncogenes appeared slightly depleted in parental subclones. Similarly, we observed a depletion of higher impact putative passengers overlapping with DNA repair genes and cell cycle genes in early subclones (Fig. 4a). We obtained similar results when we categorized mutations by variant allele frequency (VAF) (supplement Fig. S4). We note that a prior analysis (Gerstung et al., 2017) suggested that there are small differences in signatures between early and late subclone mutations. Thus, signature differences between early and late subclones could potentially contribute to our observations.

Figure 4: Correlating functional burdening with subclonal information and patient survival:

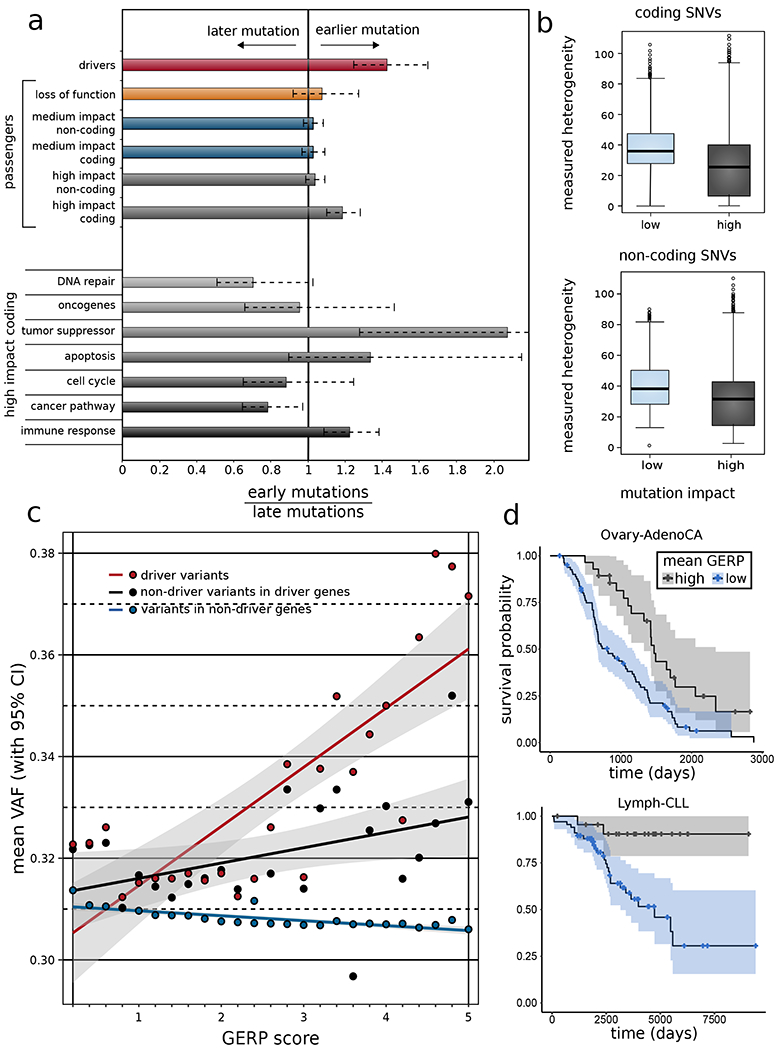
a) Subclonal ratio (early/late) for different categories of SNVs (coding and non-coding) based on their impact scores. Subclonal ratios for high-impact SNVs occupying distinct gene sets. b) Mutant tumor allele heterogeneity difference comparison between high-, and low-impact SNVs for coding (top) and non-coding (bottom) regions. c) Correlation between mean VAF and GERP score of different categories of variants on a pan-cancer level. d) Survival curves in CLL (left panel) and RCC (right panel) with 95% confidence intervals, stratified by mean GERP score. See also supplement Fig. S4.

In non-rearranged genomic intervals, the VAF of a mutation is expected to be proportional to the fraction of tumor cells bearing that mutation. Previous studies (Mroz and Rocco, 2013) have used variability in VAFs as a proxy to quantify overall intra-tumor heterogeneity. In particular, we used this approach to quantify heterogeneity amongst low- and high-impact putative passengers for different cancer cohorts (STAR method section 8.2). Overall, we observed lower mutational heterogeneity among high-impact putative passengers for both coding (with p-value < 2e-5) and non-coding regions (with p-value < 2e-5) (Fig. 4b). Furthermore, we correlated the predicted molecular functional impact (measured by GERP score) of each variant with their cellular prevalence estimated by VAF (STAR method section 8.3). Our VAF-GERP correlation analysis indicated that within driver genes and their regulators, variants that disrupt more conserved positions (high GERP score) tend to have higher VAF values (Fig. 4c). This trend remained even after excluding SNVs that have been individually classified as driver variants, suggesting that within cancer driver genes, there is either a presence of weak drivers or yet-uncalled standard drivers (potentially among high-impact putative passengers). We also found that outside of driver genes, variants that disrupt more conserved positions tend to have lower VAF values (Supplement Table 2A). This observation could be potentially related to the presence of a subset of putative passengers undergoing weak negative selection in tumor cells.

Beyond the clonal status of a tumor, clinical outcomes (such as patient survival) provide an alternative measure of tumor progression. Therefore, we performed a survival analysis to determine if somatic molecular impact burden – measured as the mean GERP of putative passenger mutations per patient – predicts patient survival within individual cancer subtypes (STAR method section 9). We used patient age at diagnosis as a covariate in the survival analysis. We obtained significant correlations between somatic molecular impact burden and patient survival in two cancer subtypes after multiple test correction (Supplement Table 2B). More specifically, we observed that somatic molecular impact burden predicted patient survival well in lymphocytic leukemia (Lymph-CLL, p-value 2.3e-4) and ovary adenocarcinoma (Ovary-AdenoCA, p-value 2e-3) (Fig. 4d). The use of average impact ensures that these results do not merely reflect more advanced progression (i.e., more mutations) of cancer at the time of sequencing. The prolonged survival of high mean GERP patients in these subtypes is consistent with the possibility that an important subset of mutations at conserved positions are deleterious to tumor cells and benefit the patient. We note that unmeasured patient clinical characteristics or tumor molecular subtypes may partially influence these correlations.

Categorizing putative passenger variants

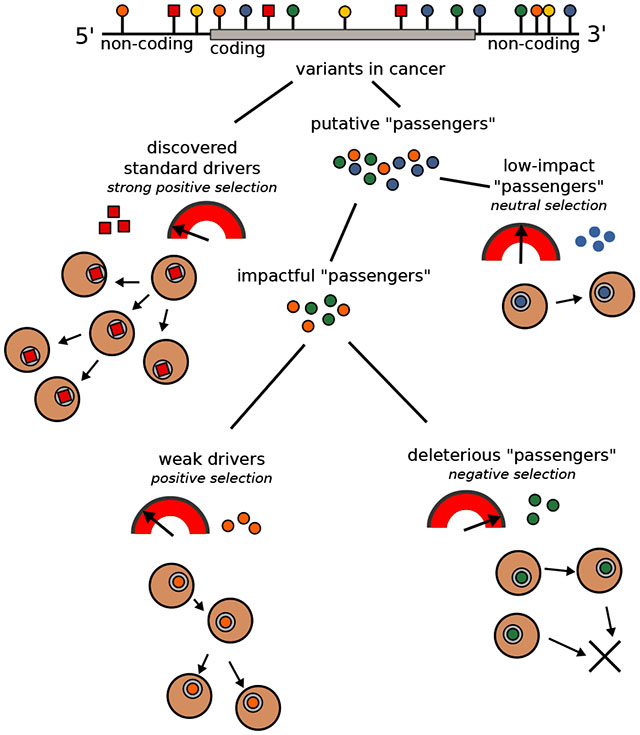
The comprehensive characterization of the passenger mutational landscape in PCAWG highlighted many key attributes of putative passengers. Some of these results provide mechanistic insights and potentially reflect the underlying mutational processes. In addition, they may be indicative of selective effects among a subset of these mutations. If a subset of putative passengers indeed possesses fitness effects, then we can extend the dichotomous model of drivers and passengers into a continuum. Conceptually, in such a model, somatic variants can be classified into multiple categories while considering their impact on tumor cell fitness: drivers with strong positive selective effects and putative passengers with neutral, weak positive, and weak negative selective effects. We can further refine this broad classification into subcategories based on ascertainment-bias and the putative molecular functional impact of different variants (Fig. 5a). Previous power analyses (Kumar and Gerstein, 2017; Lawrence et al., 2014; Rheinbay et al., 2017b) suggest that existing cohort sizes only allow the identification of strong, positively selected driver variants, common within a cohort, but are underpowered to detect many weaker drivers and even some rare (low frequency) strong drivers. However, these missing driver variants can also provide a fitness advantage to tumor cells. Further, we note that weak drivers possibly include variants with a small effect size that can contribute to cancer progression through epistatic interactions or aggregated/additive effects.

Figure 5. Conceptual classification of SNVs based on their functional impact and selection characteristics, and additive effects model:

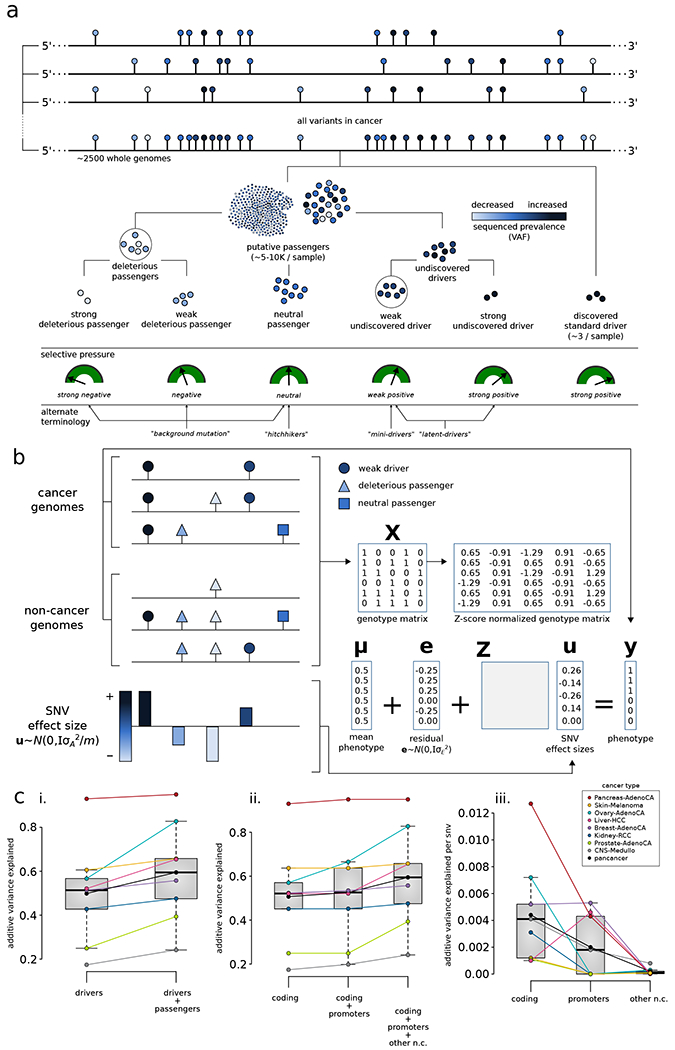
a) In addition to canonical drivers, deleterious passengers (weak and strong) and mini drivers (weak and strong) represent additional categories of cancer mutations in the extended model. b) Additive effects model for putative passengers: The combined effect of many nominal passengers is modeled linearly and predicts whether a genotype arises from an observed cancer sample or from a null (neutral) model. c) Predictive power of known drivers and putative passengers using the additive effects model: (i) compares the maximum possible variance that can be explained using known drivers; (ii) further splits the variance into contributions from coding, non-coding, and promoter variants; (iii) presents normalized additive variance explained exclusively by putative passengers in coding regions, by promoters, and by other non-coding elements of the genome. See also supplement Fig. S5.

Concerning the functional-impact-based classification, any positively or negatively selected variants will have some impact in terms of molecular function (e.g., an effect on gene expression). The relevance of molecular functional impact is intuitive for driver mutations (under positive selection) and deleterious passengers (under negative selection) (McFarland et al., 2013). However, the potential for a dissociation between impact and selective effect on tumorigenicity also exists. For instance, variants with strong functional impact may be selectively neutral because they alter gene expression or activity in ways that are not ultimately relevant for tumor fitness. Likewise, variants with weak molecular functional impact may be selectively relevant due to the particular cellular systems they impact (Castro-Giner et al., 2015). Thus, a full continuum of positive and negative selective effects can be used to generate various subcategories of cancer mutations (Fig. 5a).

Additive-effects model: Aggregated effects of putative passengers

It is interesting to note that in a cancer genome the presence of a few drivers (with high positive fitness effects) and large numbers of putative passengers (with weak or neutral fitness effects) could be considered analogous to prior observations in genome-wide association studies (GWAS) that implicated a handful of variants in complex traits. These modest numbers of variants explained only a small proportion of the genetic variance, thus contributing to the “missing heritability” problem in GWAS for traits such as height or schizophrenia (International Schizophrenia Consortium et al., 2009; Yang et al., 2010). However, studies subsequently found that aggregating the remaining variants with weak effects could explain a significant part of the “missing heritability” (Yang et al., 2010) and was predictive of phenotype (Furlong, 2013). In a similar fashion, subclonal growth rate may be considered a “subclonal trait” in a cancer in which the genetic architecture may be polygenic to varying extents across cancer subtypes. In general, the subclonal heritability of growth rate may depend on both genetic and epigenetic factors (STAR method section 10). Although the degree of “missing heritability” in subclonal growth rates has not been directly assessed experimentally, the lack of driver mutations in a subset (~10%) of PCAWG samples suggests (Campbell et al., 2017) the importance of investigating the cumulative effect of putative passengers.

To address this problem, we adapted an additive-effects model (Yang et al., 2010, 2011), initially used in complex trait analysis to quantify the relative size of the aggregated effect of putative passengers compared to known drivers for a proxy binarized trait (cancer vs. no cancer) (Fig. 5b, STAR method section 10). Briefly, we created a balanced dataset of the observed tumor and matched neutral (null) model samples, using a background model that preserves mutational signatures, local mutation rates, and coverage bias (STAR method section 1.1.b). Subsequently, we used an additive effects model to implicitly associate a positive or negative effect (coefficient) to each SNV, considering all the coefficients to be sampled from a normal distribution (STAR method section 10.1). Furthermore, in this model the individual effects of SNVs were not explicitly estimated; instead, their overall contributions to the total variance of phenotype were evaluated using the restricted maximum likelihood (REML) approach (Yang et al., 2011), where separate variance components can be associated with SNVs falling into distinct categories. We further utilized two additional local background models to validate the robustness of our findings (STAR method section 1.1.a–c).

We compared several versions of the additive effects model in eight cancer cohorts with a sample size >100. In the first model, we separated the mutations into two categories, corresponding to drivers (from PCAWG) and putative passengers (Fig. 5ci). We included putative passengers in the model only if they were found in at least two samples from a cohort (any combination of observed and simulated samples). Additionally, to maximize the predictive potential of the driver mutations, we used a binary variable, which indicated if any driver mutation was present in a sample, as a predictor (STAR method section 10.1). This approach effectively isolates the effect of putative passengers in tumors without driver mutations. In this model, we observed an increase in the variance from ~49.9% using drivers alone to ~59.4% with putative passengers included, when averaged across all cohorts. The putative passenger contribution was significant at FDR<0.1 in all cohorts (except kidney-RCC), further supporting that non-neutral effects are present among the putative passenger mutations (Supplement Table 3A). We further tested a different model in which we split mutations into coding, promoter, and other non-coding categories, where coding mutations are a superset of the PCAWG drivers (Fig. 5cii). As expected, the coding mutations accounted for most of the overall variance (~50.7% averaged across cohorts), while promoter and other non-coding mutations contributed less but still significant amounts of extra variance (~1.9% and 6.9%, respectively, with cohort-specific contributions from each category at FDR<0.1, Supplement Table 3B). Although the total contribution of the promoters was lowest in this model, the additive variance per SNV, which we call “normalized variance,” was substantially higher in promoters than other non-coding mutations (Fig. 5ciii). As expected, the normalized variance for coding mutations was the highest. We also evaluated the sensitivity of our analysis for the influence of null models and possible overfitting effects using double-null samples and observed near-zero additive variance for all such cases (STAR method section 10.3).

Additive-effects model: Analysis of samples without strong drivers

By including a binary indicator for known drivers in our model, we expected the contribution of the putative passengers toward the additive variance to be higher among samples without known drivers (as well as all null samples). To confirm that the putative passengers were indeed contributing to the discrimination of samples without known drivers, we further calculated the additive variance exclusively for such samples in PCAWG. In particular, we repeated the analysis of the eight cohorts above, while excluding samples with known drivers (including known SNV drivers, and any SNVs falling in known driver elements such as the TERT promoter). We observed an average of 12.5% additive variance in this calculation (Supplement Table 3C), which was higher than the 9.5% additive variance estimates based on putative passengers among all samples (with and without known drivers; p=0.01, 1-tailed paired t-test for an increase in per-cohort additive variance, all cohorts ≥ 20 samples). This observation is consistent with a more critical role for the putative passengers among samples without a known driver, since they may have partially redundant effects in the samples harboring known drivers. To test the robustness of this result, we calculated the additive variance after excluding samples with driver SVs and copy number alterations (CNAs) in addition to samples with known driver SNVs, using a pan-cancer meta-cohort that pools all such samples (Supplement Table 3D). We observed a lower amount of additive variance (6.8%) for the pan-cancer meta-cohort, which may be due to tissue-specific effects that are lost at the meta-cohort level.

Additive-effects model: Recasting the model in a predictive form

All of the above analyses use a random-effects model to estimate the overall variance attributable to different categories of mutations. However, this model does not identify specific mutations as having large or small absolute effects. To determine a subset of key mutations, the additive-effects model can be recast in predictive form by calculating the best linear unbiased predictor (BLUP), which provides a point estimate of the effects associated with each variant. We used this approach first to test for overfitting, by calculating a BLUP predictor for each cohort on a subset of the data. We observed a correlation between predictive accuracy of the predictor on held-out data and additive variance of the SNVs on the training data. This approach showed that the additive variance is predictive of generalization on held-out data in the sense of crossvalidation (STAR method section 10.3).

Furthermore, we performed a BLUP calculation for individual cohorts after excluding samples with predicted SNV, SV, and CNA drivers (STAR method section 10.2), and used this calculation to estimate the number of weak drivers among samples lacking predicted PCAWG drivers (Campbell et al., 2017) (Supplement Table 3G, supplement Fig. 5a). This method conservatively predicted an average of 8.4 weak drivers per cohort. Furthermore, we identified putative weak driver genes based on the highest (absolute value) BLUP estimates for SNVs and compared them with the PCAWG driver element catalog for orthogonal support (STAR method section 10.2). We specifically looked for overlap between our weak driver genes and the PCAWG driver discovery set (Rheinbay et al., 2017a), particularly where the latter did not satisfy the statistical significance criterion during the driver discovery process, observing a substantial overlap between these two lists (Supplement Table 3H). Finally, we also tested for possible inflation of BLUP coefficients on the q arm of chromosome1(1q) due to the gain of 1q events (arm-level aneuploidy) in the samples without known drivers and found no effect (Supplement Table 3I–J).

Comprehensive resource for cancer genomics

In addition to exhaustively characterizing putative passengers, our work has generated multiple uniformly processed datasets. These derived datasets can serve as valuable resources in future cancer studies. In contrast to previous investigations into a limited set of driver variants, we comprehensively characterized each mutation cataloged by PCAWG. Our analysis thus includes an exhaustive list of annotations and predicted molecular impact scores for each coding and noncoding mutation. Furthermore, we identified putative LoF mutations and their associated molecular impact scores. In addition to these primary resources, we generated various derived datasets that can be leveraged for future work. Finally, using a predictive recasting of our additive-effects model, we identified genes and genomic elements that are predicted to be weak drivers. Note that a subset of these elements – which we call putative weak drivers – were not previously identified as standard drivers, as they failed to meet the standard FDR threshold in the PCAWG driver discovery analyses despite being implicated in our approach through their combined effects. Thus, our list of putative weak drivers complements the PCAWG driver discovery exercise and potentially may be useful for testing in future functional assays (Supplement Table S4). These experimental studies could help decipher the roles of weak drivers in cancer progression. We have compiled these resources into an easy-to-use portal through a project-specific webpage. We note that in addition to resources generated through our study, other PCAWG studies have also created multiple resources (supplement Fig. S5b). We list these on our study’s resource website (http://pcawg.gersteinlab.org/).

Discussion

Although a typical tumor has thousands of genomic variants, very few (~5/tumor) are thought to drive tumor growth (Campbell et al., 2017; Vogelstein and Kinzler, 2015). The remaining putative passengers represent the overwhelming majority of mutations in each tumor, and their functional consequences are poorly understood. In this work, we comprehensively characterized putative passengers in the PCAWG dataset. We then quantified the cumulative fitness effects of these putative passengers on tumor growth through an additive-effects model.

Overall, we observed that the molecular functional impact has a multimodal distribution suggesting that the canonical dichotomy of drivers and passengers might not necessarily reflect the complex mutational landscape in cancer genomes (supplement Fig. S1b). Moreover, we observed a reduced fraction of high-impact putative passengers with an increase in the total mutation frequency. This could be attributed to the underlying mutational signatures or might signify the presence of weak negative selection among a subset of putative passengers. Additionally, we found a depletion of putative passenger LoFs in key gene categories, including DNA repair and cell-cycle, potentially suggesting the presence of weak negative selection (McFarland et al., 2013).

Furthermore, we detected differential mutational burdening for early and late sub-clonal mutations at the pan-cancer level. More specifically, we observed an opposing enrichment and depletion of putative passengers among tumor suppressors and oncogenes, respectively. This suggests that the subset of putative passengers in tumor suppressors may confer weak driver activity, while those in oncogenes may impair oncogenic activity to the detriment of tumor fitness. However, we note that the difference in signatures between early and late subclones can also contribute to these differences. Similarly, we observed a negative correlation between conservation and VAF for putative passengers in non-driver genes, which also suggests negative selection (or could be attributed to the underlying mutational signatures). We note that even if mutational signatures are neutral with respect to direct-offspring fitness (i.e. number of daughter cells generated by a given parent cell), they can acquire an emergent fitness value over longer timescales through the action of the mutations they generate over several generations (Warrell and Gerstein, 2019).

In the context of germline variants, mutations found significant in current GWAS studies typically only explain a small proportion of total heritability of quantitative traits. However, the remaining mutations can account for a large percentage of the heritability through additive effects. Inspired by this observation, here we quantified the degree to which the overall additive-effect of putative passengers explained the total variance between observed and null genomes in a cancer cohort better than known drivers alone. Our additive-effects model demonstrated that aggregating putative passengers in a cancer genome can indeed provide strong predictive performance in distinguishing between cancer and non-cancerous phenotypes. Moreover, this model can be utilized to obtain a conservative estimate of the number of putative passengers with weak positive and negative effects in various cancer cohorts.

We note that discussion of these selective effects is meaningful only in the context of a proper background (null) model. In this work, we applied multiple background models that were also applied in the PCAWG driver discovery work. Overall, our additive variance analysis was robust for these background models and suggested a clear role for a subset of putative passengers in tumor progression through cumulative effects. That said, our current background models of mutational processes may have some limitations; for example, unmodeled mutation processes might result in confounding effects.

Further, we note that our additive-effects models did not incorporate the effects of epistatic interactions. Hence, although some variants may have context-specific effects, the additive-effects model can only capture a mean effect across all genetic backgrounds; thus, it may represent only the lower bound of the genetic contribution towards the cancerous phenotype. Moreover, our current framework can be extended by using more complex models that capture both additive and epistatic variance. This is an important future direction. Additionally, with larger cohort sizes and a clearer understanding of mutational processes underlying SVs, we can extend our additive effects model to capture the aggregated effects of putative passenger SVs in tumor growth.

Finally, our analyses further complement the PCAWG driver discovery study (Rheinbay et al., 2017a) by identifying key alterations beyond strong drivers. We have identified multiple genomic elements where the aggregated effects of putative passengers may play roles in tumor progression. In conclusion, our work highlights that an essential subset of SNVs currently identified as passengers nonetheless may not merely be going for the ride and may in fact have important functional roles in driving cancer.

STAR Methods

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and request for resources and reagent should be directed to and will be fulfilled by the lead contact, Mark Gerstein(pi@gersteinlab.org).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All primary datasets included in this manuscript were generated as part of the PCAWG project. The PCAWG project uniformly processed more than 2500 cancer whole-genome sequences for multiple cancer types. PCAWG project created various cancer genomics resources based on analyses of these samples. In this work, we cite the appropriate reference to these works and guide readers to obtain more information on those primary analyses. Moreover, these primary datasets including variant calls and gene expression data are accessible through PCAWG data portals (http://docs.icgc.org/pcawg).

METHOD DETAILS

This section describes resources and methods that are common to many analyses, including the use of randomized datasets, the exclusion of blacklisted samples, and the use of different cancer-associated gene categories (e.g., apoptosis genes, essential genes, oncogenes/tumor suppressor genes (TSGs), etc.).

1. Data Preparation

1.1. Randomized dataset

1.1.a. Signature preserving randomized datasets

PCAWG group generated randomized mutation datasets for each cancer cohort. Here, observed mutations were randomly shuffled within a 50,000-base pair (bp) window for every patient in a given cancer type. During the shuffling process, the tri-nucleotide context of a mutation was preserved. Mutations affecting known cancer driver genes were excluded from the generation of these randomized mutation sets. The result of this process is a control dataset, specific to a given cancer type, to be used for comparison concerning the observed cancer mutations. These shuffled mutation sets (synapseId: syn7187923) preserve mutational signatures associated with cancer while removing the local position-specific effects of cancer mutations within the range of the 50,000bp window.

1.1.b. Signature and coverage preserving randomized dataset

In this randomization approach, the entire genome was divided into 50kb segments. For each segment, the mutation rate was calculated as a ratio of mutation frequency in that region across PCAWG to the total mutation frequency in PCAWG. The randomized mutation dataset was generated based on the region’s mutation rate. Furthermore, the permuted position was accepted if the trinucleotide context of the shuffled variant was the same as the original variant. Additionally, based on 1111 tumor and normal WGS pairs, each nucleotide in the genome was assigned a frequency quantifying the extent of coverage in PCAWG. While shuffling the mutation, the fraction of samples with enough coverage at the site was used as the nucleotide’s probability of being mutated (synapseId: syn7152699).

1.1.c. Covariate corrected randomized datasets

Prior parametric approaches to model variant distributions are useful when various whole genome signals that co-vary with the mutation density (i.e., covariates) are known. Furthermore, it is required that their contributions to the highly heterogeneous whole genome background mutation rate (BMR) are accurately modeled (Lawrence et al., 2013). However, there are potentially hundreds of covariates to model not all of which may be known or fully understood. Furthermore, some of the requisite covariate data is not available for some genomic regions, leaving the model incomplete.

For these reasons, we created a somatic variant simulation framework to generate distributions of background variants. Our approach uses an empirical, nonparametric method to derive the expected distribution of these variants. Our model doesn’t rely on fully defining every relevant influence, but instead only assumes that the BMR is substantially constant over sufficiently small genomic regions.

To define the size of the genomic regions over which we could safely assume a constant BMR, we analyzed a few of the covariates with the most substantial influence on the BMR. These covariates include DNA replication timing, GC content, Dnase I Hypersensitivity Sites (DHS), and gene expression. We obtained DNA replication timing data acquired by Chen et al. (Chen et al., 2010), which used bromodeoxyuridine-(BrdU) labelling to track each genome region’s timing in the synthesis phase (S-phase) in HeLa cells. Guanine-cytosine content (GC-content) data was obtained from the University of California, Santa Cruz (UCSC) Genome Browser (Rosenbloom et al., 2013), which offers a range of publicly available whole genome resources. Moreover, we used a DHS signal track for the HeLa cell line. Finally, we used the average gene expression values from the Cancer Cell Line Encyclopedia (CCLE), as reported previously (Lawrence et al., 2013).

The first part of our analysis was to evaluate each covariate’s variance over genomic regions of varying spatial resolution. Our goal was to find the smallest resolution at which all three covariates can be considered constant. We first binned the human genome at a range of resolutions spanning 500kb, 100kb, 50kb, 10kb, 5kb, and 1kb. Then we calculated the standard deviation of each covariate’s value within each bin using the bigWigAverageOverBed tool available from UCSC’s genome utilities website (Rosenbloom et al., 2013). From this data, the mean standard deviation of DNA replication timing plateaus at a resolution of 10kb or less. DHS sensitivity appears to have a steadily decreasing mean standard deviation at all resolutions. Thus, we decided to use a 10kb resolution, as it turns out to be the smallest resolution at which we would still have computational tractability for the subsequent steps.

Subsequently, we divided the genome into 10kb bins. These bins were assigned to a cluster in the covariate space by k-means clustering. The number of groups was chosen, such that 95% of the total variance in the covariates is captured. Randomized mutation datasets were generated by shuffling the original mutations to a 10kb bin on the same chromosome (including the bin it originates from). The shuffled position was accepted if the corresponding bin was present in the same cluster as the bin of the original mutation.

Moreover, the permuted position was accepted if the underlying trinucleotide context was the same as the trinucleotide context of the original mutation. Finally, the shuffled position was disallowed if the position’s probability for being mutated was less than 80%. The probability value of being mutated was derived from the driver group study (Rheinbay et al., 2017a). Briefly, the frequency of every base with sufficient read coverage was obtained by counting how many times it was covered sufficiently in the sub-selected PCAWG samples (1111 samples).

2. Annotation and functional impact score calculations

2.1. SNV annotation and functional impact calculation

We applied FunSeq2 (Fu et al., 2014) to annotate and predict the molecular functional impact of each somatic mutation for each of the 2548 samples from PCAWG (syn12176719). Our predicted molecular functional impact scores were then further used for various downstream analyses. In this work, we applied the annotation dataset defined by the PCAWG annotation subgroup instead of using the default annotation data context as described in the original FunSeq2 work. The PCAWG annotation set was derived primarily from the GENCODE v.19 annotation resource (Harrow et al., 2012). In addition, for annotating the noncoding RNAs, additional annotations were gathered from multiple noncoding RNA databases including miRBase (Griffiths-Jones, 2006), snoRNABase (Lestrade and Weber, 2006), MiTranscriptome (Iyer et al., 2015), rfam (Griffiths-Jones et al., 2003), and tRNAscan-SE (Lowe and Chan, 2016).

Furthermore, the original annotations were collapsed to obtain the consensus definition of various genomic elements including protein-coding parts (CDS), untranslated regions (UTR) and other noncoding regions of the genome. This annotation collapse was necessary to avoid complexities due to the presence of multiple transcripts for a gene. For example, for a given gene with multiple transcripts, the promoter was defined by taking the union of promoter regions for all individual transcripts. The promoter region for each transcript was defined as 1,000 bases upstream of the transcription start site. Additionally, nucleotides falling in CDS, UTR, and other noncoding regions were subtracted. Definitions of transcription factor binding sites (transcription factor (TF) peaks and TF motifs) were based on the Encyclopedia of DNA Elements (ENCODE) Phase II Project annotation set (Dunham et al., 2012). Similarly, enhancer region definitions were obtained from the Roadmap Epigenomics Project (Roadmap Epigenomics Consortium et al., 2015).

In addition to annotating each mutation, we also generated the core funseq score for these mutations. Briefly, the core funseq score is determined based on a weighted scoring scheme. In this approach, multiple features are used including functional annotations (regulatory elements, coding regions, HOT regions), inter-species conservation (GERP score), network-related features (centrality in gene regulatory or PPI networks), and nucleotide level analysis for TF binding sites (motif gain or break events). These core funseq score for each mutation was utilized further for downstream analyses.

2.2. Annotation of Loss-of-Function Transcripts (ALoFT)

In addition to FunSeq based annotation, we also applied the ALoFT tool to annotate and evaluate the impact of the loss-of-function (LoF) mutations. We note that not all LoF mutation results in total gene loss of function. The factors influencing the effect of a LoF mutation include the location at which a LoF mutation occurs within the coding sequence of a gene and the network centrality of a gene among its binding partners. For instance, a LoF mutation that truncates a functional domain, or loss of a protein that plays a central role in a gene regulatory network, is more likely to have a harmful effect.

ALoFT is a tool developed to identify the harmfulness of LoF mutations (Balasubramanian et al., 2017). ALoFT uses feature data associated with a LoF variant to predict the deleterious consequence associated with that variant. These features include variant frequency in population-scale databases (Exome Aggregation Consortium (Lek et al., 2016), and 1000 Genomes (1000 Genomes Project Consortium et al., 2015), the distance of the LoF mutation from the CDS stop site and cross-species conservation of region truncated by the LoF mutation. LoF variant annotation data is taken as feature input to a random forest machine learning algorithm trained to predict the functional impact associated with a given LoF mutation.

The output of the ALoFT machine learning algorithm is a predicted classification for each LoF variant input. ALoFT classifies somatic mutations as either tolerated or deleterious. For our analysis, all insertions and deletions (INDELs) and single nucleotide variant (SNV) LoF variants from the PCAWG cancer dataset were analyzed using the ALoFT annotation tool (syn12176699). Those LoF mutations that were predicted to have deleterious consequences via ALoFT were then carried forward for further analysis. Comparisons between the ALoFT mutation data set were made with a randomly generated data sets using a uniform randomization and signature corrected background models.

3. Sample selection and mutation categorization

3.1. Sample Inclusion criteria

In this work, we only considered variants from PCAWG samples which satisfy Pan Cancer Analysis of Whole Genomes-(PCAWG)wide quality control (QC) criteria and were included in the final release (Campbell et al., 2017). Additionally, certain cohorts such as prostate adenocarcinoma and lymphomas had replicates for certain patients. Among patients with multiple replicate samples, only one sample with the best overall QC metric was included per patient. Moreover, 38 hyper-mutated melanoma and lymphoma samples were excluded in this work. In total, we used variant calls from 2548 PCAWG samples for our analysis.

3.2. Putative passenger categorization

In classical models of cancer, driver mutations exert a positive selective effect on cancer cells that is necessary for tumor growth. In this framework, non-driver mutations are considered either as the product of background mutation, or as the product of a functional process unrelated to cancer growth and development. Non-driver mutations are often termed passenger mutations (“putative passengers” in the current study), in relation to their dependency on driver mutations for reproduction and in relation to the hypothesis that these non-driver mutations do not affect cancer growth and development.

To the extent that these theoretical categories of selection are found in tumors, we hypothesized that the scale of the PCAWG cohort (~2500 patients with whole-genome sequencing results) would allow for the detection of these categories of selective effect. Furthermore, whole genome sequencing would allow for the detection of these selective effects in non-coding regions, where the bulk of mutations in cancer are found.

In this work, we employed a predicted molecular functional impact based on the FunSeq software tool, to further categorize putative passengers as high impact and low impact putative passengers. For coding putative passengers, we classify them as high impact (FunSeq score >= 5.0), medium impact (FunSeq score >= 2.0 and Funseq score < 5.0) and low impact (FunSeq score < 2.0). Similarly, noncoding putative passengers are classified as high impact (FunSeq score >= 3.5), medium impact (FunSeq score > 1.0 and FunSeq score < 3.5) and low impact (FunSeq score <= 1.0), respectively.

3.3. Various cancer-associated gene categories

In this work, we employed common set of gene list belonging to different functional categories to perform various downstream analyses. Most of these gene categories were obtained from prior studies or existing databases. For instance, essential gene set were obtained from previous study looking at CRISPR knockout in different cancer cell lines (Wang et al., 2015). Similarly, genes were categorized as oncogenes or TSG based on previous study (Vogelstein et al., 2013). Finally, genes involved in apoptosis, DNA repair and metabolic genes were derived from the Reactome pathway database (Croft et al., 2011).

QUANTIFICATION AND STATISTICAL ANALYSIS

This section describes various statistical analyses that were performed to analyze putative passenger landscape in PCAWG.

4. Annotation and impact of structural variations (SVs) in cancer

4.1. Burdening of structural variants in different genomic elements

We quantified the overlap between PCAWG defined annotated genomic elements (CDS, intronic regions, promoters, UTRs, ultra-conserved regions) and structural variations (SVs) to test the significance of enrichment (or depletion) compared to genome-wide background. We measured partial overlap as the number of genomic elements with at least 1bp of overlap with the SV(s) (syn7596712). Engulfing SVs were defined as the full embedding of a genomic element within an SV. Significance level (2-tailed empirical p-value) was determined by comparing the observed count with the null distribution count, calculated from intersecting genomic elements with randomly shuffled SVs (Sudmant et al., 2015). For SVs in each cancer subtype, we shuffled the SVs per sample 1,000 times, requiring that shuffled simulated SVs still locate on the same chromosome, and that grch37 gap regions are avoided. For somatic SVs, we filtered out the SVs that overlap with long arm deletions.

Part of genomic element annotation used in the analysis (including gencode.v19.cds.bed, gencode.v19.intron.bed, gencode.v19.promoter.bed, gencode.v19.utr.bed, ultra.conserved.hg19.bed) was based on a PCAWG-wide genome annotation as described earlier in section 1.3 (syn5259890). The rest of annotation files were obtained from data sources such as GENCODE (Harrow et al., 2012) and other literature (Fu et al., 2014).

4.2. Functional Prioritization of Somatic SVs using Machine Learning Algorithms

To systematically prioritize structural variants in PCAWG, we have developed a machine-learning based framework (Kumar et al., 2019). Briefly, in this framework, we utilize structural variants from the 1000 Genomes Project (1KG) (Sudmant et al., 2015) and the somatic (Li et al., 2017) and germline SVs (Campbell et al., 2017) from PCAWG cohorts. The 1KG SVs are treated as probable low impact variants that do not have a high functional consequence for tumor progression. Here, we assume that the majority of 1KG SVs are polymorphic variants that are seen in healthy individuals and are expected to have a neutral effect on cancer progression. Similarly, the PCAWG germline SVs are considered as a mixture of high and low impact SVs that are dominated by low impact SVs with little or no consequence for tumor growth. The somatic SVs, on the other hand, is expected to include a comparatively large number of high impact variants, including driver SVs.

These training classes are quite diverse. For example, the 1KG SVs and somatic SVs may have different molecular mechanisms of formation. We, however, hypothesize that the impact of an SV depends purely on the functional elements that it affects. We speculate further that any somatic SV that resembles a 1KG SV most probably will have low impact. We use the machine learning-based framework to classify any SV into these SV classes. The algorithm learns to discriminate the somatic SVs from germline SVs and the 1KG SVs. After the model is trained, if it assigns a high probability of being in the somatic SV class to a new SV, we assume that this SV does not resemble the low impact SVs and therefore potentially has high impact score.

In our scoring framework, we utilized a random-forest machine-learning methodology, with features based on functional genomics datasets from the ENCODE Project (Dunham et al., 2012) (H3K36me3, H3K4me3, H3K27ac, H3K27me3 marks) and annotated genomic elements from the GENCODE project (Harrow et al., 2012). We chose to use these features because they mark important coding and non-coding functional elements in the genome. In addition, we built an extended model including features like conservation and overlap with COSMIC cancer census genes (Futreal et al., 2004). Note that unlike the SNV impact evaluation framework, SVs have variable lengths that can span over very large regions of the genome. This makes it hard to create a feature set for SVs with different lengths. To get around this issue, we first divided SVs into windows of 10 base pairs and computed the features over these windows. For instance, given an SV [a, b] which starts at genomic position a and ends at position b, we divide the interval into 10 base pair bins, i.e., $n=\frac{b-a}{10}$ bins. For the i^th bin (n ≥ i ≥ 1), we compute the total H3K36me3, H3K4me3, H3K27ac, and H3K27me3 signals using the ENCODE Project datasets within the bin, which we denote, for example, by s_H3K27ac(i). In addition, we computed the total PhyloP conservation signal (Pollard et al., 2010) over each bin. Furthermore, we calculated the maximum and average of the histone levels over all 10bp bins.

For H3K27ac, we compute these features as following:

$$\max (s_{H3K27ac}(1),s_{H3K27ac}(2),\dots ,s_{H3K27ac}(n))$$

and

$$\frac{(s_{H3K27ac}(1)+s_{H3K27ac}(2)+\dots +s_{H3K27ac}(n))}{n}\text{.}$$

In addition, we overlapped each bin with the exon annotations from the GENCODE project and COSMIC cancer census genes. For each overlap, we computed the fraction of the bin that overlaps with the annotation element. Similar to the signal levels, we recorded the maximum and average of the overlap fractions. Putting these together, the total set of features can be summarized as:

$$\mathit{SV}[a,b]\to \left(\begin{array}{c}\hfill {š}_{H3K27ac},{\stackrel{‒}{s}}_{H3K27ac},\hfill \\ \hfill {š}_{H3K4me3},{\stackrel{‒}{s}}_{H3K4me3},\hfill \\ \hfill {š}_{H3K36me3},{\stackrel{‒}{s}}_{H3K36me3},\hfill \\ \hfill {š}_{H3K27me3},{\stackrel{‒}{s}}_{H3K27me3},\hfill \\ \hfill {š}_{PhyloP},{\stackrel{‒}{s}}_{PhyloP},\hfill \\ \hfill {š}_{\text{GENCODE}},{\stackrel{‒}{s}}_{\text{GENCODE}},\hfill \\ \hfill {š}_{\text{COSMIC}},{\stackrel{‒}{s}}_{\text{COSMIC}},\hfill \end{array}\right)$$

where š denotes the maximum of the signal over all the 10-bp bins within [a, b] and $\stackrel{‒}{s}$ denotes the average signal over all the bins. We generate these 14 features and use them to build the model.

In order to train the model, we created a training set that included 3000 SVs (1000 SVs from each SV datasets including somatic, germline and 1KG) and built the model using 5000 trees. Furthermore, for the training of the model, we required that SVs are less than 100,000 bps. The size restriction of SVs is essential as large SVs tend to saturate the features, i.e. every feature has high values, which is not very informative for building the model. Subsequently, we scored the remaining SVs that were shorter than 10 mega-bases using the trained random forest algorithm. The random forest computes a probability for each SV class. When scoring an SV, we use the probability computed for the somatic SV class as the SV impact score (SVIS). This scoring is used for the SVs that are shorter than 10 mega-bases long. We assumed that any SV longer than 10 mega-bases had a very high impact, i.e., impact score of 1.0.

After the model was built, we used the model to compute SVIS for the PCAWG somatic SVs. At this step, we need to assign a score for all the SVs, including the 3000 SVs that were used for training. This may introduce a bias because SVs used in the training will be assigned perfect scores to their respective classes. To get around this bias, we applied the following strategy: We generated 5 different training sets (Using 5x3,000=15,000 SVs in total) and we built a model using each training set, which yielded 5 random forest models. We then scored all the somatic SVs using these 5 models (Each SV received 5 scores). Next, for each SV, we computed the average of the 5 scores assigned to this SV. The average SVIS score for each SV was used as the final impact score.

We utilized the SVIS and Funseq score to identify cancer cohorts harboring high impact SVs or SNVs. For this analysis, we classified an SV with impact score above 0.85 as a high impact SV. As mentioned earlier, coding SNVs with Funseq score >= 5.0 and non-coding SNVs with Funseq score >= 3.5 were identified as high impact SNVs. Subsequently, we plotted the log ratio of high impact SVs and SNVs in multiple cancer cohorts.

5. Loss of function mutation (LoF) analysis

5.1. Enrichment and depletion of LoF mutations by functional category

The percentage of observed and predicted deleterious LoF mutations impacting genes associated cancer growth. The percentage of genes harboring LoF mutations was compared between the original and randomized dataset. These percentages were calculated on a per-cancer type basis. Gene categories with a significant difference were identified using a Kolmogorov-Smirnov (KS) test for each of the cancer cohorts. We also performed a similar comparison using driver LoF mutations – as determined by the PCAWG driver variant group – as well as a contrast to genome-wide expectation (using uniform and signature corrected background models) normalized to all possible LoF mutation locations.

5.2. Gene-level enrichment of predicted deleterious LoF mutations

Gene-level enrichment of deleterious LoF mutations was calculated across cancer types as well as for Individual cancer-types. For each cancer type, the number of patients with at least one LoF mutation in a given gene was determined to calculate the enrichment of mutations. For the enrichment analysis, we performed comparisons between original and randomized mutation data. A chi-square test was used to evaluate the statistical significance of the difference in LoF prevalence between the observed dataset and the randomized dataset.

6. Impact of somatic variants on the transcription factor binding landscape

In this section, we describe all relevant analyses to evaluate the impact of somatic variants influencing different transcription factors and their target genes.

6.1. TFBS landscape mutational burden

We evaluated the putative impact of SNVs and INDELs affecting transcription factor binding motifs (TFMs) that may lead to creation or disruption of TFMs. The annotation of SNVs and INDELs that break or create TFM was obtained from the output of FunSeq2 (Fu et al., 2014). Briefly, FunSeq evaluates the significance of the changes in the score of the corresponding position weight matrix (PWM) for each putative TFM (as measured between the TFM with the reference allele compared to the alternative allele). Based on this annotation, for each TF we get the observed proportion of TFM gain ${\mathit{pTFM}}_G=\frac{{\mathit{TFM}}_G(\mathit{TF})}{{\mathit{TFM}}_G({\mathit{TF}}_{\text{Total}})}$, where pTFM_G corresponds to the proportion of TFMs gained. This proportion is defined as the ratio between frequency of motif gain events observed for a particular transcription factor TF (TFM_G(TF)) to the total frequency of gain events across all transcription factor (TFM_G(TF_Total)). Similarly, we can compute analogous proportion for the TFM break(loss) events, where observed proportion of TFM loss ${\mathit{pTFM}}_L=\frac{{\mathit{TFM}}_L(\mathit{TF})}{{\mathit{TFM}}_L({\mathit{TF}}_{\text{Total}})}$.

The expected naïve genome-wide background for each TF was assessed as the proportion of coverage of each TFM sequences among the total number of entries from all TFs, ${\mathit{pTFM}}_E=\frac{\mathit{TFM}(\mathit{TF})}{\mathit{TFM}({\mathit{TF}}_{\text{Total}})}$. Whole-genome motif scanning generally discovers millions of motifs including a large fraction of false positives. Therefore, we focused our analysis on variants occurring within promoter regions as defined by the PCAWG annotation subgroup. Furthermore, we required that all motif coordinates should be located in regions corresponding to Chromatin Immunoprecipitate (ChIP-Seq) peaks or DNase hypersensitive (DHS) peaks, as defined by ENCODE (Dunham et al., 2012). The TF PWMs were obtained from ENCODE project, which include TRANScription FACtor database (TRANSFAC (Wingender et al., 1996)) and JASPAR (Mathelier et al., 2016) motifs.

We measured the depletion or enrichment of motif loss for each TF by computing the deviation between the above observed and expected values Δ_L(TF) = pTFM_L − pTFM_E. Similarly, for motif gain, we compute the deviation Δ_G(TF) = pTFM_G − pTFM_E. For loss of motif and gain of motif, a positive value indicates enrichment (higher proportion of impacted motifs) while negative value shows depletion (lower proportion of impacted motifs). Moreover, we utilized same framework to quantify enrichment of TF gain and loss event in PCAWG data using a signature corrected background model.

6.2. Alteration bias score and target gene analysis

We defined an alteration bias score to quantify the overall mutational burden associated with TF binding alteration events (gain/loss of TFM) influencing their corresponding target genes. Since the counts of transcription binding alteration events vary with respect to the localized mutational frequency, it can be challenging to compare mutational burden of transcription factor binding sites associated with different target genes. In order to solve this problem, we used the number of creation and disruption alteration events as a relative control to compute an alteration bias score. Creation and disruption counts were first normalized as the number of nucleotides available to disrupt or create a binding site differs significantly.

The relative difference between the creation and disruption counts were then computed as the alteration bias score. All mutations located within the promoter region of each gene together with the associated gene specific enhancer region (defined by the PCAWG) were matched against the ENCODE transcription factor binding motifs (Kheradpour and Kellis, 2014) to detect significant changes in binding affinity. For a given transcription factor family, alterations influencing TF binding sites were aggregated to compute the alteration bias score. In this framework, TF motifs undergoing gain of event will be assigned a positive alteration bias score, whereas those with large number of break events will be assigned negative alteration bias score. Motif-gene pairs with alteration bias score greater than 0.4 (absolute value) and with at least 15 alteration events were identified to perform the gene expression analysis described in the next section.

6.3. Target gene expression analysis

Since the level of expression differs both across genes and tissue types associated with the cancer cohorts, normalization of expression values is needed (syn3104297). Expression values were z-score transformed, leaving expression distributions across cohorts and genes with means equal 0 and standard deviations equal 1. This allows for a direct comparison of expression values associated with subsets of TFBS mutation events across cohorts and genes in comparison to a background of all expression values for the same set of genes in all patients. We used non-parametric tests (Kolmogorov-Smirnov or Wilcoxon rank sum tests) to evaluate the statistical significance of gene expression changes.

7. Mutation spectrum and signature analysis

7.1. Mutation spectrum of LoF mutations

We analyzed the full mutation spectrum in all coding regions, specifically looking at those sequence alterations that lead to loss of function mutations (LoFs). We performed this analysis for both the pan-cancer cohort and the kidney renal cell carcinoma (Kidney-RCC) cohort.

7.2. Mutation spectrum of TF breaking mutations

For this analysis, we used the most common motif break events in the Kidney-RCC cohort, according to FunSeq assigned annotation. The spectrum is the result of mutations normalized by the number of each trinucleotide in the genome, ordered alphabetically by the mutational context in trinucleotides. That is, from A[C>A] A to T[T>G] T.

7.3. MSI/MSS analysis

We used the microsatellite stability assessment from PCAWG (syn8016399), where the majority of microsatellite instable (MSI) samples were observed in colorectal adenocarcinoma and uterine adenocarcinoma. We then compared the fractions of high-impact passengers between and microsatellite stable (MSS) and MSI cohorts in these two cancer types. We conducted a two-sided rank sum test in order to distinguish between MSI and MSS in these cohorts.

7.4. Signature comparison between different categories of putative passengers

We used signatures identified by the signature working group in the PCAWG (syn8366024). Briefly, signature group assigns signature contribution to each mutation identified in PCAWG. For each cancer cohort, we classify mutations as high- or low-impact based on FunSeq2 threshold defined above. Subsequently, we plot two distributions corresponding to contributions of high- and low-impact mutations for a given signature in a specific cancer cohort. We perform two-sided KS test to obtain a p-value for the signature contribution comparison. We repeat this analysis for every signature and all cancer cohort in PCAWG. We only display a subset of signatures in specific cancer cohort with significant differences.

8. Subclone architecture, tumor evolution, and functional impact score

8.1. Selecting and comparing early vs. late subclones

To identify subclones within bulk tumors we used the PhyloSub (Jiao et al., 2014) assignments from the PCAWG consortium. To ensure that we distinguished between early vs. late subclones, we defined early subclones as those that do not have any parental subclones. Moreover, we defined late subclones as those that were assigned a parental subclone but do not bear any children subclones. For example, between three subclones with parentage in the order A -> B -> C, we select ‘A’ as early and ‘C’ as late subclone. Conversely, if A->B and A->C, both C and B are considered as late subclones. To enhance the quality of the subclone comparison and sample, we have only selected samples that contain both early and late subclones with at least 100 mutations assigned for each early and late subclone. Classification of mutations as high, medium, and low impact was based on the FunSeq score threshold described earlier (method section 1.4).

To determine whether higher impact putative passenger mutations are differentially selected compared with low impact putative passengers, we first compared the early vs. late subclone ratio of high impact putative passenger mutations. Furthermore, we characterized the early vs. late subclone ratio for high impact coding putative passenger mutations based on different gene categories. In addition to this subclone analysis, we obtained similar results when we divided each individual tumor sample into equal-size groups of higher and lower VAF.

8.2. Tumor heterogeneity measured through divergence in variant allele frequency (VAF)

In order to correlate predicted molecular functional impact with underlying tumor heterogeneity, we categorized putative passengers as low, medium, and high predicted impact as described earlier. Furthermore, we quantified tumor heterogeneity by computing the mutant-allele tumor heterogeneity (MATH) score (Mroz and Rocco, 2013) for each of the three categories of putative passengers. For each category, the MATH score was computed by considering the median absolute deviation (MAD) and median of the variant allele frequencies belonging to a particular category.

MATH score = α x (100 * MAD/ median), where α = 1.4826 is a scaling factor as described in previous work.

8.3. Correlation between somatic VAF and conservation as measured by Genomic Evolutionary Rate Profiling (GERP)

We further correlated prevalence (measured through VAF) of mutations with their putative functional impact (measured based on GERP score). The variant allele frequency (VAF) of a mutation is an estimate of the fraction of sample alleles bearing the alternate allele based on the relative abundance of sequencing products. Similarly, GERP is a measure of the degree of evolutionary conservation among mammals at a genomic site (Cooper et al., 2005). Variants were divided into two major classes: 1) variants in driver genes and their noncoding regulators; and 2) remaining putative passenger variants. Variants overlapping deletions or duplications were removed, since such copy number alterations complicate the interpretation of VAF. Variants in copy number altered regions were identified by applying intersectBed from Bedtools (Quinlan and Hall, 2010) to the PCAWG structural variant call set and SNP call sets. Within each major class, variants with similar GERP were aggregated to increase the signal to noise ratio. Specifically, each variant was assigned to one of 30 GERP bins (evenly spaced intervals), representing successive degrees of conservation.

9. Correlating functional impact of variants and survivability

We were interested in investigating whether functional impact of somatic variants was correlated with patient survivability as a descriptive exploration. A Cox proportional hazards model was used to predict patient survival as a function of the mean GERP (Cooper et al., 2005) of the patient’s somatic SNVs. As a measure of the degree of evolutionary conservation of a sites across mammals, GERP score is part of the FunSeq framework, with the advantage of direct comparability between coding and noncoding regions. In any cancer survival model, among the most important confounders are 1) tumor type/subtype, 2) degree of tumor progression at diagnosis, and 3) patient age at diagnosis.

First, to control for the fact that some tumor types are more aggressive than others, separate survival models were trained for each eligible tumor type. 9 cancer types met the inclusion criteria of having 10 or more patient deaths: Breast-AdenoCa, CNS-GBM, Eso-AdenoCa, Kidney-RCC, Liver-HCC, Lymph-CLL, Ovary-AdenoCA, Panc-AdenoCA, and Skin-Melanoma. While this stratification follows the official PCAWG histological categories, there may nonetheless be unmeasured subtypes with different risk profiles and genomic features. Of course, even if subtypes or sub-subtypes do carry different risk profiles, it could very well be the case that those different risk profiles are due to their differing underlying genomic features. Second, we sought to control for degree of tumor progression. Ideally, we would have stratified tumors by TNM staging. However, the PCAWG clinical data did not uniformly annotate the TNM staging of tumors. Therefore, we used somatic mutational load as a proxy for degree of tumor progression, since tumors tend to accumulate mutations with time. The way we incorporated mutational load was by normalizing the aggregate GERP of somatic variants against the number of mutations by tumor. This was equivalent to using mean GERP instead of summed GERP by tumor. Third, patient age at diagnosis was included as a direct covariate in the Cox proportional hazards model. The model was fit using the Survival package, version 2.40-1 in R 3.3.2. The supplemental table 2 below lists the obtained hazard ratios and associated p-values corresponding a one-quartile increase in mean somatic GERP and to 1 year of patient advanced age at diagnosis.

10. Additive effects model for detection of non-neutral aggregated effects

We adapted an additive model with random effects, which has recently been applied to detect the contribution of germline variants to complex traits, to detect the aggregated non-neutral effects of multiple somatic variants in cancer (International Schizophrenia Consortium et al., 2009; Yang et al., 2011). For a given cancer cohort, we generated a balanced sample set consisting of all observed somatic mutations and corresponding matched null (neutral) sample. The neutral sample set was generated by applying three distinct randomization schemes, designed to preserve mutational signatures and the dependence of mutation rate on local covariates. In particular, we use the Broad and Sanger randomization schemes, along with our own scheme designed to explicitly model local covariates (all randomization schemes described above in section 1.1). These multiple background models allow us to study the robustness of our approach.

We evaluated the existence of non-neutral aggregate effects among a set of variants by a test against the null hypothesis that their additive variance with respect to a binary phenotype (cancerous versus null) is zero, implying they have non-zero power to predict true cancer genotypes from ones generated from the neutral model. We note that our test is analogous to that for single driver discovery against a background model, and in the single variant case is equivalent to a test for whether the distributions of the variant in the cancer samples and neutral model are identical.

We first note some differences between our use of the random effects model and its use in germline complex trait analysis. In the latter case, the additive variance can be used as an estimate of the narrow-sense (additive) heritability, which directly determines the response to selection in germline traits (Hartl and Clark, 2007). When modelled as an evolutionary process, somatic variants with non-neutral effects (e.g. drivers, weak drivers and deleterious passengers) determine the growth rate of a subclone, and hence the heritability of the fitness (or tumorigenicity) of the subclone, possibly along with epigenetic modifications and other non-genetic factors. The binary phenotype we construct can be thought of as a discretization of subclonal fitness into two levels, represented by the null samples (low) and the observed samples (high). However, the additive variance in our model does not directly estimate the heritability of this discretized trait in a given tumor, since it is estimated from a synthetic sample which is balanced to contain equal numbers of null and observed samples. The additive variance estimated could potentially be related to the narrow-sense heritability. However, only by monotonic rescaling if the proportions of subclones with fitness in the low and high categories in a given tumor were known (as in the case of balanced case-control designs (Lee et al., 2011)). Assuming therefore that the randomization model is sufficiently close to the mutational processes operating in a given tumor, we expect non-zero additive variance in our balanced sample to indicate non-zero narrow-sense heritability. In addition, we expect the relative amounts of additive variance assigned to categories of mutations to be informative about their contributions to narrow-sense heritability due to the implicit monotonic scaling relationship. This rationale can equally be applied to individual variants and is implicit when the impacts of individual drivers are compared using their departure from a null model. Finally, we note that since the response to selection is determined primarily by broad-sense heritability in clonal evolution as opposed to narrow-sense heritability in the germline (Hartl and Clark, 2007), higher-order epistatic interactions may significantly affect the differences in fitness among tumor sub-clones, which will necessarily be ignored by an additive model.

10.1. General and specific forms of the additive-effects model

For each SNV the additive-effects model implicitly associates a positive or negative effect (coefficient), considering them to be sampled from a normal distribution. The model has the form:

$$y_j=\mu +\sum _{ik}{z}_{ijk}{u}_{ik}+e_j,$$ (1)

where y_j is the phenotype (0 for null/1 for tumor) of sample j, z_ijk is the normalized SNV dosage (z-scored) of the i’th SNV belonging to category k in sample j (with each category indexed independently), e_j is the residual effect for sample j, and μ is the mean phenotype (where μ = 0.5 for a balanced sample). u_ik’s are normally distributed with variance ${\sigma }_k^2∕m_k$, where ${\sigma }_k^2$ is the additive variance and m_k the number of SNVs in category k (where the categories represent, for instance, coding, promoter and other non-coding mutations), and the e_j’s are normally distributed with variance ${\sigma }_E^2$(the ‘residual effects’ variance). The variance of y is denoted ${\sigma }_P^2$ (the ‘phenotypic’ variance), where ${\sigma }_P^2={\Sigma }_k{\sigma }_k^2+{\sigma }_E^2$. The individual effects u_i are not explicitly estimated; instead the hyper-parameters ${\sigma }_k^2$ and ${\sigma }_E^2$ are optimized using restricted maximum-likelihood (REML) (Yang et al., 2011), and the estimator ${\sigma }_A^2={\Sigma }_k{\sigma }_k^2$ can be used to predict the proportion of the phenotypic variance explained by the SNVs as ${\sigma }_A^2∕{\sigma }_P^2$.

The model in Eq. 1 measures the additive variance on the ‘observed scale’, since although the variables y_j are discrete, they are treated directly as a continuous trait, where the estimators ${\widehat{y}}_j=\mu +{\Sigma }_{\mathit{ik}}{z}_{\mathit{ijk}}{u}_{\mathit{ik}}$ can take any real value. As pointed out earlier (Lee et al., 2011), this underestimates the additive variance, since probability mass is wasted on values that the trait cannot take. An alternative is to measure the additive variance on the ‘liability scale’, using a probit linking function and threshold:

$$y_j=\mathrm{I}[\Phi (\mu +\sum _{ik}{z}_{ijk}{u}_{ik})>t],$$ (2)

where I[.] is the indicator function which is 1 for a true proposition and 0 otherwise, Φ(.) is the standard normal cumulative density function, and t is a threshold set according to the prevalence of the binary trait (we set t = 0, using the balanced sample as our reference). The quantity l_j = μ + ∑_ikz_ijku_ik models the liability of genotype j to give rise to a cancerous phenotype. In general, we find that the additive variance estimates are slightly higher on the liability than the observed scale, although the relative sizes between the variance assigned to different categories is qualitatively similar. (We note that, since our analysis is on a synthetic balanced sample, the absolute value of the additive variance on either the observed or liability scale is only indirectly related to narrow-sense heritability as outlined above.)

We now outline three variations of the additive-effects model which were used in our analyses. In each variation, SNVs are only included in the model if they appear in at least two samples of the cohort (either observed or null genotypes), all germline variants are removed, and we filter variants lying in hyper-mutated regions.

Model 1:

Here, we divide the SNVs into two categories, k ∈ {1,2}, where k = 1 implies the variant is a PCAWG driver, and k = 2 includes all other variants. Rather than including the z-score normalized driver variants individually in the model, we first construct a summary indicator which is 1 if any driver is present in a sample, and 0 otherwise:

$$x_j^{\mathrm{drv}}={\vee }_i{x}_{ij1},$$ (3)

where x_ij1 is the SNV dosage (0 or 1) of SNV i in sample j belonging to category k = 1 (drivers). We ensure that $x_j^{\mathrm{drv}}=0$ for all null samples by removing the PCAWG drivers in the simulations; the indicator $x_j^{\mathrm{drv}}$ thus represents an optimal predictor on the basis of the PCAWG drivers. The z-scores $z_j^{\mathrm{drv}}$ are then calculated using these indicators. Additionally, we allow the non-drivers in the model to be restricted to a subset S_f including only those variants whose functional impact score (calculated using Funseq, as described above) exceeds f:

$$y_j=\mu +z_j^{\mathrm{drv}}{u}_1+\sum _{i\in S_f}{z}_{ij2}{u}_{i2}+e_j.$$ (4)

We optimize $({\sigma }_1^2,{\sigma }_2^2,{\sigma }_E^2)$ at the Funseq thresholds f ∈ {0,1,2,3,4,5,6}, and choose the threshold which optimizes ${\sigma }_2^2$ for each cohort independently. A p-value for the contribution of the nondivers is then calculated by performing a log-likelihood ratio test for the full model against the constrained model in which ${\sigma }_2^2=0$.

Model 2:

We also test a version of the model in which we split SNVs into three categories, k ∈ {1,2,3}, corresponding to those appearing in coding sequence regions, promoter regions, and all other non-coding regions respectively. Additionally, we let each category restrict the variants to those exceeding a functional impact threshold, so that the full model is:

$$y_j=\mu +\sum _{\begin{array}{c}k\in \{1,2,3\},\\ i\in S_{f_k}^k\end{array}}{z}_{ijk}{u}_{ik}+e_j.$$ (5)

We optimize the model in piecewise fashion over $({\sigma }_1^2,{\sigma }_2^2,{\sigma }_3^2,{\sigma }_E^2)$ and (f₁,f₂,f₃) ∈ {0,1,2,3,4,5,6}³. In the first step, we fix (${\sigma }_2^2=0$, ${\sigma }_3^2=0$) and optimize $({\sigma }_1^2,{\sigma }_E^2)$ for each value f₁ ∈ {0,1,2,3,4,5,6}, and choose the value $f_1^{\ast }$ for which ${\sigma }_1^2$ is maximized. In the second step, we fix (${\sigma }_3^2=0$, $f_1=f_1^{\ast }$) and optimize $({\sigma }_1^2,{\sigma }_2^2,{\sigma }_E^2)$ for each value f₂ ∈ {0,1,2,3,4,5,6}, and choose the value f²* for which ${\sigma }_2^2$ is maximized. Finally, we fix ($f_1=f_1^{\ast }$, $f_2=f_2^{\ast }$) and optimize $({\sigma }_1^2,{\sigma }_2^2,{\sigma }_3^2,{\sigma }_E^2)$ for f₃ ∈ {0,1,2,3,4,5,6}, choosing the value $f_3^{\ast }$ for which ${\sigma }_3^2$ is maximized. Having fixed ($f_1=f_1^{\ast }$, $f_2=f_2^{\ast }$, $f_3=f_3^{\ast }$), a p-value for the contribution of category k is calculated by performing a log-likelihood ratio test for the full model against the constrained model in which ${\sigma }_k^2$. Further, we evaluate the ‘normalized additive variance’ per SNV in category k as: ${\sigma }_k^2∕({\sigma }_P^2\cdot \mid S_{f_k^{\ast }}^k\mid )$.

Model 3:

Finally, we also test a version of the model with four categories, k ∈ {1,2,3,4}, where category 1 consists of the PCAWG drivers and uses the single summary indicator from Eq. 3, category 2 consists of all remaining non-driver coding sequence variants, and categories 3 and 4 consist of SNVs appearing in promoter regions and other non-coding regions respectively. The model thus has the form:

$$y_j=\mu +z_j^{\mathrm{drv}}{u}_1+\sum _{\begin{array}{c}k\in \{2,3,4\},\\ i\in S_{f_k}^k\end{array}}{z}_{ijk}{u}_{ik}+e_j,$$ (6)

and we use a similar piecewise optimization to model 2 in order to set the thresholds $(f_2^{\ast },f_3^{\ast },f_4^{\ast })$.

10.2. BLUP to estimate the SNVs frequency with non-neutral effects and predict phenotype

In order to provide a conservative estimate of the number of SNVs with non-neutral effects, for a given cohort we find the size of the smallest set of SNVs for which the estimated additive variance exceeds a lower-bound on the additive variance from the model where all SNVs are included (defined using the lowest value of the 95% confidence interval). More specifically, we first exclude all samples from the cohort with a known SNV driver, or an SV or CNA variant occurring in a driver gene as explained in the main text. We then estimate the total additive variance, ${\sigma }_{A,\mathit{tot}}^2$ explained by all SNVs in the remaining samples using Eq. 1 with all SNVs belonging to a single category. To estimate the size of the smallest set of SNVs necessary to capture the total variance, we first calculate the Best Linear Unbiased Predictor (BLUP), $\widehat{u}={\mathrm{argmax}}_{\mathrm{u}}\left(\mathrm{Pr}\left(u\mid x,y,\mu ,{\sigma }_{A,E,\mathit{tot}}^2\right)\right)$, using GCTA (Yang et al., 2011). We then define an ordering of the SNVs according to the absolute values of their BLUP coefficients, writing π(r) for the index of the r’th SNV in the ordering, so that $\mid \widehat{u_{\pi (1)}}\mid \ge \mid \widehat{u_{\pi (2)}}\mid \ge \dots$, where ties are broken arbitrarily, and define associated nested subsets S_r consisting of the first r SNVs in the ordering, S_r = {π(1), π(2), … π(r)}. Finally, we take |S_r*| as a conservative estimate for the number of SNVs with non-neutral effects, where:

$$r^{*}=\min \{r;{\sigma }_A^2(S_r)\ge {\sigma }_{A,tot}^{2,†}\}$$

and ${\sigma }_A^2(S_r)$ is an estimate of the additive variance explained using only SNVs in S_r, calculated by running REML for a single category model containing only SNVs in S_r, and ${\sigma }_{A,\mathit{tot}}^{2,†}$ is the lowest value of the 95% confidence intervals (CI) around the estimate of ${\sigma }_{A,\mathit{tot}}^2$ calculated using all SNVs. This approach attempts to find the smallest set of SNVs having an estimated additive variance of at least ${\sigma }_{A,\mathit{tot}}^{2,†}$ (which, with 95% confidence, will not be more than the total additive variance) by greedily adding those SNVs with the highest predictive value (as measured by the BLUP scores) into the model first. We note that this approach assumes that there are not strong dependencies among the SNVs aside from those induced by the phenotype variable. In general, finding the smallest subset would require an exhaustive search over all subsets. However, if independence is assumed the greedy approach is sufficient, since the r SNVs which are individually most predictive will be those with the highest BLUP scores. Moreover, these will also be the most predictive in combination as a set of size r. Further, we can specifically estimate the number of SNVs with positive and negative effects (weak drivers and deleterious passengers respectively) by counting the number of SNVs in S_r* with positive and negative BLUP coefficients. To estimate the number of weak driver events per tumor, we subtract the per-sample average number of SNVs in S_r* in the null samples from the per-sample average in the observed samples (with positive BLUP coefficients).

As detailed in the main text, we estimated the BLUP for individual cohorts after samples with predicted SNV, SV and CNA drivers were excluded, including SNVs contained in predicted driver elements and used this to derive an estimate of the number of weak drivers among samples lacking predicted PCAWG drivers (Campbell et al., 2017) (Supplement Table 3G). We conservatively estimated the number of weak drivers by finding the smallest set of SNVs whose additive variance is equal to the additive variance of all the SNVs. A per sample estimate of driver events is then derived by comparing the average number of SNVs from this set in the observed versus random samples. Using this approach, we estimated an average of 8.4 weak drivers per cohort, corresponding to approximately 0.81 weak driver events per tumor. We expect that these estimates are limited by sample size, and thus represent conservative lower bounds.

We also use the BLUP predictor to cast the model in a predictive form. In this form, we partition the data into training and testing partitions. We estimate the BLUP predictor on the training partition as above and predict the phenotypes on the testing partition using $y=[(\mu +x\cdot \widehat{u})>0.5]$, where [.] is the indicator function. The predictive accuracy is proportion of correctly predicted test phenotypes.

Finally, we use the smallest subset analysis above to create a list of genes containing putative weak drivers. Since GCTA provides an estimate of the variance of ${\sigma }_{A,\mathit{tot}}^2$, we use this to form the 99% and 95% confidence intervals (CI) around the estimate of ${\sigma }_{A,\mathit{tot}}^2$ under the assumption of normality, and form a list of putative weak driver genes for the lower-bounds on the additive variance associated with each CI (the 99% CI list nested inside the 95% list). The lists are formed by taking the smallest subset of SNVs necessary to explain the variance associated with each lower-bound and taking the union of the genes associated with each SNV (for all SNVs that can be associated with a coding or non-coding element of a gene). We compare our putative weak driver lists with various PCAWG driver discovery gene sets using the hyper-geometric test (Supplemental Table 3H). For this purpose, the union of the putative weak driver gene sets was taken across cohorts, and the PCAWG sets included candidate drivers at the cohort, meta-cohort and pan-cancer levels, from all elements of a gene, or coding sequence drivers only. We note that the PCAWG driver group has integrated results from multiple state-of-the-art cancer driver discovery tools. A very rigorous integration procedure was adopted to nominate elements as a driver using the FDR threshold of 0.1 (Rheinbay et al., 2017a). We note that the FDR cutoff used here is a standard in the field and was agreed upon by more than 800 researchers in the PCAWG. Overall, we observed a substantial overlap across these tests, providing orthogonal validation for our approach. Considering only those genes with PCAWG FDR thresholds between 0.1 and 0.25, the overlap with our weak driver genes is significant at p=1e-5 for all elements, and p=2e-4 for coding elements only (p-values using the hypergeometric test). For all elements under the 0.25 FDR threshold, the overlap is significant at p=3e-13. Presumably, some of the genes with FDR thresholds between 0.1 and 0.25 are weak drivers and failed the statistical significance criterion due to limited cohort size and thus insufficient power in PCAWG.

10.3. Sensitivity analysis

We tested the sensitivity of our results to the choice of null model by repeating the analyses in (Fig. 5 c) using two other randomization schemes, and compared the variance on observed and liability scales, with quantitatively similar results (Supplement Tables 5A–I). We also verified that our model effectively controls for overfitting by observing near zero additive variance when a second randomized sample is substituted for the observed genotypes, and that the sensitivity of the results to changes in the randomization window size is small (Supplemental Table 5J–K). To further verify that the model controls for overfitting, we split the data into test and training partitions, and showed that the additive variance on the training partition correlates with predictive accuracy on the test partition, using the Best Linear Unbiased Predictor (BLUP) to cast the model in predictive form as above (Supplemental Table 5L and method section 10.2).

DATA AND CODE AVAILABILITY

All primary datasets including mutations and gene expressions in this manuscript are made available to the community via ICGC and TCGA associated PCAWG data portals (http://docs.icgc.org/pcawg) using controlled data access. Alternatively, one can use the synapse repository (https://www.synapse.org) to access primary and intermediate data. We specify appropriate synapse accession codes in the method section for each dataset utilized or generated during our analyses. Software and workflows used to perform major analyses in the manuscript are properly cited in the resource table of the manuscript. Finally, all derived data and code used in this manuscript are also available from the resource website for this manuscript (http://pcawg.gersteinlab.org).

ADDITIONAL RESOURCES

http://pcawg.gersteinlab.org/

Supplementary Material

TS1

SI Table S1: P-values associated with enrichment or depletion of motif-gain and motif-break events observed in different cancer cohorts in PCAWG using a uniform and signature-corrected background model, related to Fig. 2.

TS2

SI Table S2: This table presents the correlation between somatic impact burden and tumor prevalence (quantified by mean VAF). Additionally, it also reports p-values and hazard ratio for survival analysis for tumor classified based on somatic impact burden, related to Fig. 2.

TS3

SI Table S3: P-values for additive variance analyses performed on all samples as well as samples lacking any drivers. Moreover, it also reports the result for the comparison of weak driver candidates from BLUP analysis with the PCAWG driver discovery set, related to Fig. 5.

TS4

SI Table S4: List of weak driver genes/elements based on different additive variance confidence intervals and different FDR thresholds.

FS3

SI Fig S3: Analyses of mutational processes underlying putative passengers in PCAWG, Related to Fig. 3.

a) Distribution of mutational signatures in the kidney-chRCC cohort for impactful non-coding SNVs (top), low-impact non-coding SNVs (middle), and premature stops (bottom); b) Stop coding mutational spectrum and in-frame versus out-frame ratios. A pentaplet (with positions 12345) consists of 3 triplets (tr123; tr234; tr345). A particular SNV in middle position (3) is capable of inducing a stop codon in any of these three triplets if the stop triplet is in its corresponding frame (in-frame). Different color of the bar in the plot correspond to difference cancer cohort. We also plot the ratio between observed in-frame to observed out-frame mutations normalized by the theoretical number of in-frame versus out-frame mutations in exonic regions (shown as inset in the plot); c) This plot quantifies fraction of high- and medium-impact mutations for micro-satellite stable (MSS) and instable (MSI) cancers. Each data point on boxplot correspond to samples belonging to MSS or MSI cancer cohorts. We note that MSI samples tend to have high percentage of high- and medium-impact non-coding mutations than MSS tumors. Significance in differences was evaluated using one-sided Wilcoxon rank sum test.

FS1

SI Fig S1: Functional impact characterization for putative passengers in PCAWG, Related to Fig. 1.

a) The functional impact distribution for mutations falling in any non-coding regions; three peaks correspond to low-, medium-, and high-impact variants. Similar to DHS region shown in main Fig 1a, we observe trimodal distribution for the entire non-coding impact distribution; b) This schematic represents functional impact distribution for different models, including canonical (green), continuous (blue), and multimodal (red). The canonical model has two peak corresponding to low-impact passengers and high-impact drivers. In contrast, the continuous model consists of a continuum of mutations with functional impact following a continuous distribution. Finally, the multimodal distribution corresponds to a model with an intermediate group of mutations with medium impact score in addition to high and low functional impact mutations. Our observation suggests the presence of mutations with multimodal functional impact distribution in PCAWG; c) The correlation between fraction of high- and medium-impact noncoding mutations and total noncoding mutations for each cancer cohort. Blue line represents the linear fitting, whereas grey area indicates 95% confidence interval; d) Fraction of pan-cancer low- and medium-impact passenger SNVs influencing various gene categories in the coding (nonsynonymous) and non-coding regions (promoters). Gene categories include metabolic, immune related, essential, and non-essential genes. We normalize the SNV fraction by total number of genes in each category to allow proper comparison. Medium-impact putative passengers are more prevalent compared to low-impact passengers for each gene category except non-essential genes. This trend is true for nonsynonymous as well as promoter mutations; e) Log plot of the ratio of high impact duplication events to high impact SNVs. Similar to deletions, cohorts such as bone-leiomyoma, uterus adenocarcinoma and breast lobular carcinoma harbor high impact duplications compared to high impact SNVs. In contrast, colorectal, melanoma and kidney-RCC cancers are dominated by high impact SNVs compared to large duplications;

FS4

SI Fig S4: Analysis of early and late putative passengers, Related to Fig. 4.

Top plot shows overall early/late ratio (VAF based classification) for high impact SNVs in coding (light brown) and non-coding regions (light pink). Additionally, we also plot early/late mutation ratio for high impact putative passenger mutations affecting TSG and oncogenes. Bottom plot shows loss-of-function (LoF) mutation per sample on pan-cancer level for early and late subclones. Moreover, this plot also displays the LoF mutation density for mutations with high and low VAFs.

TS5

SI Table S5: P-value corresponding to the potential overfitting and sensitivity test for additive-effect models based on different background simulations.

FS2

SI Fig S2: Coding and non-coding putative passenger burden for different genomic elements, Related to Fig. 2.

a) Percentage of genes in different gene categories (apoptosis, cell cycle, cancer pathway, dna repair, metabolic and essential genes) affected by non-driver LoFs (LoFs not present in PCAWG driver mutation catalog) in observed samples (white box plot) and signature corrected background (brown box plot). Data point in box plot correspond to different cancer cohorts; b) Heat map presenting enrichment (red color) or depletion (blue color) of various TFs: SNVs leading to motif gain events in different cohorts compared to the signature corrected background model (top plot). SNVs leading to motif breaking events in different cohorts compared to the signature corrected background model (bottom plot). Each row corresponds to a particular cancer cohort and column correspond to a specific TF. Bold TFs in the column are well known cancer genes. c) Heat map presenting enrichment (red color) or depletion (blue color) of various TFs: INDELs leading to motif gain events in different cohorts compared to a uniform background model (top plot). INDELs leading to motif breaking events in different cohorts compared to the uniform background model (bottom plot). Each row corresponds to a particular cancer cohort and column correspond to a specific TF. Red TFs in the column are well known cancer genes; d) Top plot shows target genes affected due to motif gain and loss events in ZNF transcription factor family. The X-axis correspond to affected target genes and colored dot represents alteration bias score for those genes in different cancer cohorts. Size and color of circle correspond to alteration event frequency and cancer cohort identity, respectively. Bottom q-q plot showing genes such as BCL2, TERT and HOXC13, which are differentially expressed due to gain of motif event in ZNF TFs; e) Pan-cancer analysis of downstream gene expression changes due to motif alteration events (both gain and loss of motif). Top panel includes p-values of the target genes with lymphoma cohort samples included. The bottom panel excludes the lymphoma cohort. TERT, PRF1 and ERBB3 show significant differential gene expression due to TF alteration events; f) Enrichment of somatic duplications in coding region (CDS) and transcription factor binding peaks (TFPs). Large duplications like deletions are highly enriched for engulf events compared to partial overlap events. Data points in box plots correspond to different cancer cohorts.

FS5

SI Fig S5: Schematic of Best Linear Unbiased Predictor to identify weak drivers in PCAWG, Related to Fig. 5.

a) Schematic shows the method used for estimating a lower bound on the number of weak drivers per cohort using the Best Linear Unbiased Predictor (BLUP). The SNVs are ordered by their descending absolute BLUP coefficients, and the additive variance calculated cumulatively using this ordering. The minimal subset of weak-drivers for the cohort is estimated using the point at which the cumulative additive variance crosses the 95% lower-bound of the confidence interval for the total additive variance calculated on all SNVs for the cohort. See Method Section 10.2 for full details, b) This schematic presents different resources generated in our study and their navigation through our resource webpage. Our resource page consists of multiple datasets and software. These resource datasets can be broadly divided as resources generated a part of our study and other PCAWG associated datasets that we utilize to perform our investigation. Moreover, these data resources include both public and private data. Publicly available data can be downloaded from our resource webpage. However, to access private data, users will require appropriate authentication. Accordingly, we redirect users to the relevant website hosted on the ICGC data portal for downloading the private data. Moreover, we also provide information on how to obtain necessary access to download private data. Finally, we also offer link and downloadable code utilized in our study.

KEY RESOURCES TABLES

REAGENT or RESOURCE	SOURCE	IDENTIFIER
SNV & INDEL dataset	ICGC data portal	https://dcc.icgc.org/releases/PCAWG/consensus_snv_indel
SV dataset	ICGC data portal	https://dcc.icgc.org/releases/PCAWG/consensus_sv
Subclonal reconstruction	ICGC data portal	https://dcc.icgc.org/releases/PCAWG/subclonal_reconstruction
Driver mutations	ICGC data portal	https://dcc.icgc.org/releases/PCAWG/driver_mutations
Gene expression	ICGC data portal	https://dcc.icgc.org/releases/PCAWG/transcriptome/gene_expression
Mutation signatures	PCAWG synapse page	https://www.synapse.org/#!Synapse:syn11738306
Driver elements	PCAWG driver paper	biorxiv pcawg driver elemnts
SNV funseq output	PCAWG synapse page	https://www.synapse.org/#!Synapse:syn15574565
SNV ALoFT output	PCAWG synapse page	https://www.synapse.org/#!Synapse:syn12176699
Weak drivers	Passenger resource webpage	http://pcawg.gersteinlab.org/Datasets/Derived/weakDriver/weak_drivers_95_CI_cutoff.xlsx
Software and Algorithms
FunSeq2	Gerstein lab Github	https://github.com/gersteinlab/FunSea2
ALoFT	Gerstein lab Github	https://github.com/gersteinlab/aloft
Additive variance analysis code	Gerstein lab Github	https://github.com/gersteinlab/pcawgAdditiveVariance
Other
Derived resource files	Passenger resource webpage	http://pcawg.gersteinlab.org

Highlights.

• We characterize the passenger landscape in more than 2500 whole-genome tumors.

• Molecular impact correlates with the mutational signature and subclonal architecture.

• The aggregated effect of passengers plays role in tumorigenesis beyond standard drivers.

• Additive-effects model from germline studies can be repurposed for cancer genomics.