A network-based feature response matrix as a brain injury metric

Abstract

Conventional brain injury metrics are scalars that treat the whole head/brain as a single unit but do not characterize the distribution of brain responses. Here, we established a network-based “response feature matrix” to characterize the magnitude and distribution of impact-induced brain strains. The network nodes and edges encoded injury risks to the gray matter regions and their white matter interconnections, respectively. The utility of the metric was illustrated in injury prediction using three independent, real-world datasets: two reconstructed impact datasets from the National Football League (NFL) and Virginia Tech, respectively, and measured concussive and non-injury impacts from Stanford University. Injury predictions with leave-one-out cross-validation were conducted using the two reconstructed datasets separately, and then by combining all datasets into one. Using support vector machine (SVM), the network-based injury predictor consistently outperformed four baseline scalar metrics including peak maximum principal strain of the whole brain (MPS), peak linear/rotational acceleration, and peak rotational velocity across all five selected performance measures (e.g., maximized accuracy of 0.887 vs. 0.774 and 0.849 for MPS and rotational acceleration with corresponding positive predictive values of 0.938, 0.772, and 0.800, respectively, using the reconstructed NFL dataset). With sufficient training data, real-world injury prediction is similar to leave-one-out in-sample evaluation, suggesting the potential advantage of the network-based injury metric over conventional scalar metrics. The network-based response feature matrix significantly extends scalar metrics by sampling the brain strains more completely, which may serve as a useful framework potentially allowing for other applications such as characterizing injury patterns or facilitating multi-scale modeling in the future.

1. Introduction

Understanding the biomechanical mechanisms of traumatic brain injury (TBI) is critical for the prevention, detection, and clinical management of this growing public health problem (NRC 2014). To date, much of the TBI biomechanical work has centered on developing a scalar injury metric, i.e., a single number such as peak linear or rotational acceleration, to correlate with the occurrence of injury. Other more sophisticated injury metrics include the head injury criterion (HIC) derived solely from linear acceleration (Versace 1971) and rotation-based metrics such as brain injury criterion (BrIC (Takhounts et al. 2013)), rotational injury criterion (RIC), power rotational head injury criterion (PRHIC) (Kimpara and Iwamoto 2012), and rotational velocity change index (RVCI (Yanaoka et al. 2015)). Regardless, these metrics remain scalar that effectively treat the whole head as a single unit to indirectly infer the magnitude of brain strains thought to be responsible for mild TBI (mTBI) (King et al. 2003).

Impact-induced brain strains can be estimated using a finite element (FE) model of the human head. Numerous head injury models have been developed, with ever-increasing model sophistication. For example, the number of brain elements increased from thousands in earlier models (Kleiven 2007; Sahoo et al. 2014) to hundreds of thousands (Mao et al. 2013; Ji et al. 2015) or even ~1–2 millions comparable to typical MR voxel resolution (Ho and Kleiven 2009; Miller et al. 2016; Zhao and Ji 2019a), with accurate mesh geometry conforming to individual anatomy (Ho and Kleiven 2009; Ji et al. 2015; Zhao and Ji 2019a). The brain material property has also evolved from relatively simple isotropic models to incorporating white matter (WM) anisotropy (Giordano and Kleiven 2014) using whole-brain tractography derived from advanced neuroimaging (Zhao and Ji 2019b). These sophisticated head injury models provide unparalleled rich information of brain tissue responses that are almost impossible to measure directly. Surprisingly, however, little effort exists to understand how best to utilize the rich information or to effectively sample the simulated brain responses for subsequent injury analysis (Zhao and Ji 2019b). Without an effective response sampling, the advantage of a sophisticated head injury model is lost, especially considering the substantial simulation runtime typically required in the first place.

The most widely used response samplings are the peak maximum principal strain (MPS) of the entire brain, regardless of the incidence location, and the percentage of brain volume experiencing strains above a threshold (i.e., cumulative strain damage measure; CSDM) (Takhounts et al. 2008)). Similar to kinematic counterparts, these scalar metrics treat the entire brain as a single unit and cannot inform the location or distribution of brain strains, even though such information is already available from model simulation. Thus, using an oversimplified MPS of the whole brain may not improve concussion prediction over accelerations (Beckwith et al. 2018), which would defeat the purpose of developing a head injury model in the first place. Further, an oversimplified scalar response variable may not be sufficient to study injury in specific regions or to offer a more graded characterization of mTBI beyond a binary status, where brain strain distribution may seem critical given the widespread neuroimaging alterations (Bigler and Maxwell 2012) and a diverse spectrum of signs and symptoms (Duhaime et al. 2012). These clinical observations of concussion suggest individualized “signature of injury” (Rowson et al. 2018), which requires a more complete sampling of brain responses than conventional scalar metrics.

Extending scalar injury metrics at the whole-brain level to specific regions of interest (ROIs) would mitigate the limitation to some degree. For example, MPS in generic (e.g., brainstem, midbrain, gray or white matter) or more targeted regions (e.g., corpus callosum and thalamus) has been proposed to better predict injury (Zhang et al. 2004; Kleiven 2007; Giordano and Kleiven 2014). A recent study extended the concept of localized strain measures even further, by investigating strain responses of the 50 deep WM ROIs derived from a co-registered neuroimaging atlas (Zhao et al. 2017). The strain variable itself has also been extended from direction-insensitive MPS to WM fiber or axonal strain to characterize the stretch along WM fibers (Giordano and Kleiven 2014; Ji et al. 2015; Sahoo et al. 2016). An ROI-specific injury susceptibility measure analogous to CSDM was also proposed to quantify the fraction of above-threshold (i.e., “injured”) sampling points from tractography (Zhao et al. 2017).

Still, these ROI-specific strain metrics remain scalar that would inevitably discard information in other ROIs, and without a clear rationale. Although they were found to improved injury prediction performance over scalar metrics in other ROIs (Zhang et al. 2004; Kleiven 2007; Giordano and Kleiven 2014), data reanalysis is necessary because the underlying reconstructed National Football League (NFL) head impacts (Newman et al. 2005) had errors (Sanchez et al. 2018). In addition, these earlier studies all reported an injury “training” performance rather than a “cross-validation” measure for a more objective comparison (Zhao et al. 2017).

The other extreme relative to scalar injury metrics was to use strains at every FE element or voxel (Cai et al. 2018), by effectively forming a “response feature vector” to characterize strain magnitude and distribution. Still, it only considered WM but not gray matter (GM) ROIs, or perhaps equally importantly, WM interconnections between GM ROIs that serve as a structural substrate to brain function. In addition, a response vector at every voxel location may be excessive and inefficient, as responses in spatially neighboring locations were likely to be highly correlated.

To address these limitations, here we established a “response feature matrix” based on an organized brain structural network. This was motivated and supported by network-based brain injury analysis common in neuroimaging (Bigler 2016), but which was only starting to emerge in biomechanics (Kraft et al. 2012). Conceptually, this approach transformed conventional brain response sampling using a scalar value into a much higher resolution strain representation or a higher dimensional feature space, where a “feature” in this study represented strain-based injury risk in a specific brain region. The resulting “response signature” would enable subsequent use of advanced feature-based classification via machine learning (Cai et al. 2018). Potentially, this could improve over conventional logistic regression that effectively utilizes a single feature, which is the de facto approach in TBI biomechanics to date (Kimpara and Iwamoto 2012; Rowson and Duma 2013; Takhounts et al. 2013; Giordano and Kleiven 2014).

Advanced machine learning including support vector machine (SVM) (Rathore et al. 2017) and deep learning (Khvostikov et al. 2018) has been used extensively in other related neurological disease classification problems such as Alzheimer’s disease. However, its application in TBI biomechanics has remained rather limited (Hernandez et al. 2015; Cai et al. 2018; Wu et al. 2018), despite the recognized importance and potential in this research field (Agoston and Langford 2017).

To illustrate the use of the structural network-based response sampling scheme, we employed three real-world injury datasets to evaluate and compare its injury prediction performances against representative scalar metrics. We also illustrated how the response sampling, as a brain injury metric, could be employed to characterize “injury patterns” between concussive and non-injury impacts, which may allow comparing with advanced neuroimaging in the future (Koerte et al. 2015). The network-based response feature matrix developed here significantly extends scalar metrics by sampling the brain strains more completely, which may be important for future brain injury studies.

2. Methods

2.1. Worcester Head Injury Model (WHIM)

We used the recent anisotropic version of the Worcester Head Injury Model (WHIM; Fig. 1) for all impact simulations in this study. This model incorporates WM material property anisotropy based on whole-brain tractography (Zhao and Ji 2019b) using the same mesh and brain-skull boundary conditions in the previous isotropic version (Ji et al. 2015). The upgraded model was successfully validated against six cadaveric impacts and an in vivo head rotation (Zhao and Ji 2019b). Validating a head injury model at both ends of the impact severity spectrum may be important to maximize simulation confidence for the majority of real-world head impacts such as those in contact sports (Zhao et al. 2018).

Fig. 1.

The Worcester Head Injury Model (WHIM) showing the exterior features (a), intracranial components, (b), the 50 deep WM ROIs (c), and a subset of WM tractography fibers color-coded by their fractional anisotropy (FA) values (d).

2.2. Injury datasets

We employed three injury datasets to illustrate the use of the network-based brain injury metric and to evaluate its injury prediction performances. They included (1) laboratory reconstructed (and recently corrected) head impacts from the NFL (N=53; 20 concussions and 33 non-injuries (Sanchez et al. 2018)); (2) reconstructed head impacts from Virginia Tech (VT; N=55, 11 concussions and 44 non-injuries (Rowson 2016)); and (3) measured head impacts using mouthguards from Stanford University (SF; N=110, 2 concussions and 108 non-injuries (Hernandez et al. 2015)).

The reconstructed NFL dataset has been extensively used in the past to train an injury predictor (Zhang et al. 2004; Viano et al. 2005; Kleiven 2007; Zhao et al. 2017). In this study, a reanalyzed dataset was employed (Sanchez et al. 2018), which evaluated the accelerometer consistency and corrected errors related to a problematic sensor in the original tests. The updated dataset included 53 impacts (vs. 58 previously (Newman et al. 2005)).

The VT dataset was reconstructed based on impacts measured by the HIT System (Greenwald et al. 2008). While the HIT System provides valuable data that has been used to characterize head accelerations in football, it provides an incomplete kinematic characterization of impact. Specifically, the HIT System does not compute the six degree of freedom accelerations throughout an impact event needed to model brain response. The HIT System is optimized to compute resultant linear acceleration and provide an estimate of peak resultant rotational accelerations (Crisco et al. 2004; Rowson et al. 2012). The reconstructions aimed to fill in the missing kinematic data by impacting a headform in the lab at matched locations to produce the same peak linear and rotational accelerations computed by the HIT System. On-field head impacts measured by the HIT System were reconstructed (Rowson 2016) using a pneumatic ram (Biokinetics, Ottawa, Canada). The impactor struck a modified medium NOCSAE headform mounted on a Hybrid III 50th percentile male neck. The headform was instrumented with three linear accelerometers (7264B-2000, Endevco, San Juan Capistrano, CA) and three angular rate sensors (ARS3 PRO-18K, DTS, Seal Beach, CA). All data were collected at a sampling frequency of 20,000 Hz. Linear accelerations were filtered to channel frequency class (CFC) 1000, and angular/rotational velocity data were filtered to CFC 155 using a 4-pole phaseless Butterworth low-pass filter. Rotational acceleration was obtained by differentiating the angular velocity for each impact.

Eleven concussive and 44 subconcussive impacts were selected from a pool of 15,850 impacts to create a dataset with 4 subconcussive impacts for every concussive impact. The subconcussive head impacts were randomly selected from all recorded impacts greater than 40 g to ensure overlap in impact severity with the concussive impacts. While the dataset might be skewed towards concussive impacts relative to real-world injury rates, this approach attempted to minimize the bias by limiting subconcussive inclusion to high magnitude impacts given the practical challenges of recreating many impacts in the lab.

The SF dataset consisted of two concussive head impacts (a loss of consciousness and a self-reported injury). Its 108 non-injury impacts consisted of 50 randomly selected impacts and 58 additional impacts with at least one translational or rotational acceleration component exceeding an injury threshold (Hernandez et al. 2015). Fig. 2 compares the peak magnitudes of linear acceleration, rotational acceleration, and rotational velocity (a_lin, a_rot and v_rot, respectively) for the three injury datasets.

Fig. 2.

Mean and 75^th percentile quantiles for peak linear acceleration, rotational acceleration, and rotational velocity (a_lin, a_rot and v_rot, respectively) for the three injury datasets.

For each head impact, the six degree-of-freedom linear acceleration and rotational velocity were prescribed to the head center of gravity. The skull, scalp, and facial components of the WHIM were simplified as rigid bodies as they did not influence strain responses of the intracranial components when the kinematic profiles were applied to the rigid skull. A typical simulation runtime for one impact of 100 ms was ~30 min (double precision with 15 CPUs and GPU acceleration; Intel Xeon E5-2698 with 256 GB memory, and 2 NVidia Tesla K20 GPUs with 12 GB memory). All data analyses were conducted in MATLAB (R2018a; MathWorks, Natick, MA).

2.3. Structural network-based response feature matrix

This section describes procedures to use a GM atlas and tractography to encode impact-induced brain strains via a brain structural network. Fig. 3 provides a flow chart for the whole process. Each step is subsequently described in more detail.

Fig. 3.

Flow chart to generate an impact-induced brain strain response feature matrix based on a brain structural network derived from a neuroimage atlas and whole-brain tractography.

Brain structural network

A brain structural network describes the anatomical connections linking a set of neural processing units, generally, cortical and subcortical ROIs (Sporns 2013). The apparently fixed structural network is thought to constrain the dynamic functional network that underlie cognition and behavior (Park and Friston 2013). However, there is no universally-accepted, standard approach to establishing a brain network (Qi et al. 2015). Here, we chose to employ the LONI Probabilistic Brain Atlas (LPBA40) (Shattuck et al. 2008) to construct a brain structural network because it has the fewest number of GM ROIs among those commonly adopted (Qi et al. 2015). Such a choice was calculated to mitigate concerns of using a generic model to study a population that may have significant individual variabilities while allowing us to establish a brain structural network for application in TBI biomechanics. An individualized study was not feasible here, as no MRI was available. Conceivably, nevertheless, a more refined neuroimaging atlas can be employed in the future with subject-specific head injury models and their corresponding neuroimaging and tractography to reduce individual variabilities (Giordano et al. 2017).

Specifically, 54 cortical/subcortical GM ROIs of the cerebrum (excluding cerebellum and brainstem, as no experimental data were available to validate the head injury model in these regions at injury levels) were determined from the LPBA40/AIR probabilistic atlas (a labeled atlas from 40 healthy, normal volunteers (Shattuck et al. 2008)). The LPBA40 GM atlas was transformed into the WHIM space by non-linearly registering with the neuroimages based on which WHIM was created (FNIRT in FSL (Smith et al. 2004)), similarly to a recent study involving the ICBM WM atlas (Zhao et al. 2017). The transformed atlas allowed localizing GM ROIs within the WHIM space (neuroimaging and head injury model mesh, respectively), as well as the WM fiber interconnections between pairs of GM ROIs based on whole-brain tractography (See subsection Response feature matrix). The tractography was previously reconstructed using default parameters in ExploreDTI (Leemans et al. 2009), from which a total of ~35 k fibers were generated (Zhao et al. 2016). Fig. 4 provides an overview of the steps involved in generating a response feature matrix for a head impact, which are subsequently described in further detail.

Fig. 4.

Strain responses of the cerebral GM ROIs (a) and tractography (b; color-coded by WM fiber strains) are used to construct a brain structural network (c) in order to characterize the magnitude and distribution of the MPS in GM ROIs and injury susceptibilities between each pair of GM ROIs (color-coded nodes and edges, respectively; size of nodes indicates the number of traversing WM fibers). The strain-encoded brain structure network is represented as a symmetric feature response matrix shown as a full matrix (d). See text for details.

The smallest structural network

Interregional connections between each pair of the GM ROIs were first identified by testing each fiber in the whole-brain tractography whether it traversed the two GM ROIs under scrutiny (network nodes; Fig. 5). The number of traversing fibers then served as the weight of the corresponding network edge (zero if no connections existed). This led to a symmetric, uni-directional connectivity or adjacency matrix with 1046 non-zero edges, with an average of 79±184 fiber connections (range of 1–2949; ROI pairs with zero connections excluded; Fig. 6a). To focus on the strongest links for subsequent injury analysis, a global density-based thresholding was applied to the connectivity matrix (Fornito et al. 2016). This method retained the top strongest links so that to remove weaker and spurious interconnections. A density threshold of 0.18 was used, as it retained the smallest network with the fewest edges without generating an isolated node. This led to a final adjacency matrix containing 516 non-zero edges in the matrix (258 unique ones), with an average of 153±241 fiber connections (range of 24–2949; Fig. 6bc). The resulting network was subsequently used to develop a response feature matrix by encoding strain-based injury risks.

Fig. 5.

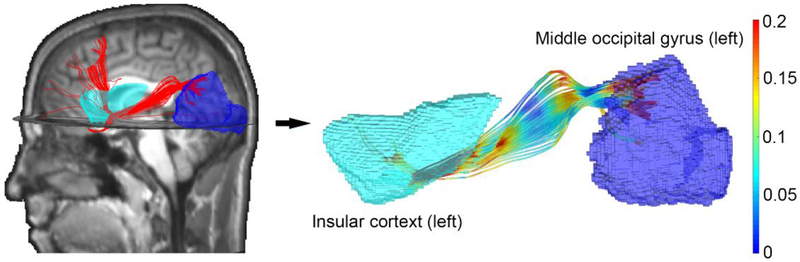
Illustration of how WM fibers from tractography are determined to interconnect two GM ROIs. The number of interconnecting fibers is first used to encode the edge strength between the two ROIs or nodes in the adjacency matrix (Fig. 6). After deriving the smallest network, the surviving edges are then encoded by injury susceptibilities of the corresponding WM fibers (Fig. 7; see text for details).

Fig. 6.

Binary adjacency matrix for the WM (a) before and (b) after a global density-based thresholding (at a threshold of 0.18) to generate the smallest network with the fewest edges without leading to an isolated node. (c) Nonzero edges in the resulting adjacency matrix are encoded by the corresponding number of WM connecting fibers between each pair of WM ROIs (capped at 200 to improve visualization). A node or nonzero edge is called a “feature,” and its location is represented by a matrix coordinate, (i,j)(for nodes, i = j not shown here; otherwise, i ≠ j for edges).

Response feature matrix

To describe mechanical “response features” in the context of brain injury, the resulting brain structural network was encoded by using injury risks for each network node and edge (GM ROI and WM connection, respectively). This allowed characterizing impact-induced strain magnitude and distribution. In theory, any response variable could be used to derive features for encoding. These included MPS, WM fiber strain, strain rate, or volume fractions of above-threshold metrics such as injury susceptibility for the given region (Zhao et al. 2017). Here, we chose to use injury susceptibility based on WM fiber strains to encode injury risks to the network edges, due to its potential improvement in injury prediction (Giordano and Kleiven 2014; Zhao et al. 2017). For network nodes or GM ROIs, we chose to use the peak maximum principal Green strain (evaluated at the 95^th percentile level) to encode their strain responses, as fiber strain relying on WM fiber bundles was undefined in these isotropic regions.

Specifically, for each network edge off the matrix diagonal, WM fiber tracts traversing the pair of GM ROIs, and subsequently, the sampling points linking the two ROIs, were first identified (Fig. 4) (Zhao et al. 2017). The corresponding injury susceptibility (φ) was then calculated as the percentage of tractography sampling points experiencing fiber strains above a threshold of 0.09 – the lower bound of a conservative injury threshold from an in vivo study (Bain and Meaney 2000) as adopted before (which achieved the best injury prediction performance via logistic regression (Zhao et al. 2017)). Edges with no ROI interconnections had φ of zeros. Similar to the binarized connectivity matrix (Fig. 6bc), the response feature matrix was also symmetric as the order of the GM ROI pairs was irrelevant. Collectively, the network nodes and edges represented the strain state of the entire cerebrum for a given head impact. Fig. 7 illustrates the response feature matrices for two representative impacts drawn from each injury dataset, where each non-zero response represents a unique feature. It was important to note that the network edges encoded a percentage of WM fiber tractography sampling points exceeding a strain threshold, while the nodes represented an actual strain value obtained from impact simulation.

Fig. 7.

Representative response feature matrices that encode both peak maximum principal strains in GM regions (node) and injury susceptibilities of their interconnecting WM fibers (edges) for a pair of head impacts obtained from the NFL (a: with concussion; b: without concussion; impact pair in Case 118 (Sanchez et al. 2018)), VT (c: with concussion; d: without concussion), and Stanford datasets (e and f : loss of consciousness and self-reported concussion, respectively). The upper triangle is not shown due to symmetry. The feature matrix is a much higher resolution representation of brain strains compared to scalar metrics such as the maximum principal strain of the whole brain shown in the inset (312 unique features vs. 1). The latter is equivalent to one node along the diagonal but discards information about other nodes or edges.

2.4. Injury prediction

In-sample cross-validation

The utility of the network-based brain injury metric for concussion prediction was illustrated using the two reconstructed injury datasets to measure in-sample performances via the LOOV framework (Cai et al. 2018). The Stanford dataset was not used individually here because of the rather limited number of concussion cases. Then, the three injury datasets were combined into one dataset, and an additional in-sample performance comparison was conducted (N=218; 33 concussions and 185 non-injuries).

Support vector machine (SVM) with a radial basis kernel (RBF) was used for feature-based injury prediction (Hastie et al. 2008). Feature selection is generally necessary for machine learning classifiers to reduce redundant information and to remove irrelevant and/or spurious features so that to maximize classification performance. Here, we chose a sequential forward feature selection (SFFS) method (Hira and Gillies 2015) to identify an optimal subset from nonzero elements in the response feature matrix according to a desired classification performance criterion. This method was chosen because of its generally better performance than others (Hira and Gillies 2015) and was computationally appropriate here due to the relatively few features (vs. every voxel (Cai et al. 2018)). The technique started with an empty feature set, and sequentially added a new feature that led to the greatest increase in a given prediction performance criterion. Feature set update would stop when no further improvement was observed. The parameters related to SVM penalty and RBF kernel function were optimized following a grid search strategy to maximize the generalization ability (Chen and Lin 2006).

Three commonly used performance criteria were adopted, including accuracy, sensitivity and the area under the receiver operating characteristics curve (AUC (Šimundić 2009)). They were obtained from the LOOV procedure based on testing (as opposed to training) data to avoid overfitting. The performances of the network-based injury metric via SVM were compared with those from four baseline scalar metrics using logistic regression, including MPS of the whole brain and basic kinematic variables (a_lin, a_rot and v_rot). CSDM was not used here because the required strain threshold established from SIMon (Takhounts et al. 2008) could not be readily applied to WHIM due to significant model response differences even under identical impact conditions (Ji et al. 2014). For all testing, we also reported specificity and positive predictive value (PPV (Šimundić 2009)).

Out-of-sample prediction

It was important to evaluate the performance of an injury predictor using impacts not previously used in training (Sanchez et al. 2017). To achieve this goal, each injury metric was re-trained using all of the samples in one reconstructed dataset to predict injury using impacts from the other reconstructed dataset as well as the Stanford dataset. This process was enumerated for the two reconstructed datasets. Similarly, accuracy, sensitivity, specificity, AUC and PPV were reported and compared with those from the four baseline scalar metrics. They are reported in the Appendix as secondary results.

2.5. Injury pattern

Finally, we used the NFL dataset to explore “injury pattern” by comparing the feature magnitudes, as similarly conducted before on the earlier versions of the same dataset (Zhang et al. 2004; Kleiven 2007). Specifically, average values of each feature (GM MPS and WM injury susceptibility) for the concussive and non-injury impacts were obtained, respectively. One-tailed unpaired t-tests were performed to identify features that were statistically larger in the concussive group (significance level of 0.05, with Bonferroni correction for multiple comparisons (Hastie et al. 2008)).

3. Results

In-sample injury prediction performances

In-sample cross-validation performances for the two reconstructed datasets are reported in Tables 1 and 2, respectively. Depending on the desired performance criterion, the feature-based predictor was always trained to achieve the best accuracy, sensitivity, or AUC. Maximizing accuracy also consistently led to the highest specificity and PPV. Interestingly, among the four scalar metrics, peak rotational acceleration (a_rot) always outperformed MPS of the whole brain across all performance criteria, for both reconstructed injury datasets.

Table 1.

In-sample cross-validation performance comparisons using the reconstructed NFL dataset via a LOOV procedure. The network-based metric was trained to achieve either the best AUC, accuracy or sensitivity based on the testing dataset. Performances are compared with those from four baseline scalar metrics, including peak maximum principal strain of the whole brain (MPS), linear (a_lin) and rotational (a_rot) acceleration, and rotational velocity (v_rot). For each performance category, the best performer is identified (bold). Among all scalar metrics, a_rot consistently outperformed MPS across all performance measures (shaded).

	network (acc.)	network (sen.)	network (AUC)	MPS	alin (g)	arot (rad/s2)	vrot (rad/s)
Accuracy	0.887	0.811	0.811	0.774	0.755	0.849	0.793
Sensitivity	0.750	0.850	0.750	0.650	0.650	0.800	0.700
Specificity	0.970	0.788	0.849	0.849	0.818	0.879	0.849
Testing AUC	0.838	0.833	0.909	0.852	0.826	0.877	0.824
PPV	0.938	0.708	0.750	0.722	0.684	0.800	0.737
Selected features	(37,37) and (38,38)	(43,35)	(33, 29) and (53, 33)	MPS	alin	arot	vrot
Injury threshold	N/A	N/A	N/A	0.33 ± 0.003	83.10 ± 0.86	5623.17 ± 46.42	38.05 ± 0.34

Table 2.

In-sample cross-validation performance comparisons using the reconstructed VT dataset via a LOOV procedure. Among all scalar metrics, a_rot consistently outperformed MPS across almost all performance measures (shaded).

	network (acc.)	network (sens.)	network (AUC)	MPS	alin (g)	arot (rad/s2)	vrot (rad/s)
Accuracy	0.891	0.855	0.836	0.800	0.873	0.836	0.782
Sensitivity	0.455	0.546	0.182	0.273	0.546	0.455	0.273
Specificity	1.000	0.932	1.000	0.932	0.955	0.932	0.909
Testing AUC	0.626	0.777	0.909	0.789	0.88	0.872	0.773
PPV	1.000	0.667	1.000	0.500	0.750	0.800	0.737
Selected features	(5, 3) and (23, 1)	(6, 6)	(6, 4), (8, 4), (40, 26) and (44, 38)	MPS	alin	arot	vrot
Injury threshold	N/A	N/A	N/A	0.25 ± 0.004	107.00 ± 1.25	5068.77 ± 69.12	31.09 ± 0.52

Both network nodes and edges (GM ROIs and WM interconnections, respectively) could be identified as the most injury predictive features by the SFFS procedure. This is illustrated in Fig. 8 for the NFL dataset. Features that were selected to offer the best accuracy, in general, did not necessarily lead to the best sensitivity or AUC, and vice versa.

Fig. 8.

Illustration of identified features to maximize SVM performance. (a) An axial T1-weighted MRI of the subject used to create the WHIM. (b) LPBA40 GM atlas nonlinearly registered via the corresponding MRI to match with the T1-weighted MRI (slight asymmetry due to the asymmetry in the subject’s MRI). (c) Selected GM ROIs based on the NFL dataset (with numbers representing region indices; Table 1). (d) The identified two nodal features (isolated regions (37, 37) and (38, 38), arrows) to maximize accuracy, one edge feature to maximize sensitivity (yellow; interconnection (43, 35)), and the two edge features to maximize AUC (green; interconnections (33, 29) and (53, 33)). The identified features can be considered as “active” features that are used in SVM for classification.

In-sample injury prediction performances using the combined dataset

Consistent with the previous results, the network-based predictor always achieved the best accuracy, sensitivity, or AUC when so trained, and the network predictor that maximized accuracy also achieved the highest specificity and PPV (Table 3). However, the identified response features were again different from those when each reconstructed injury dataset was used separately. In addition, peak rotational velocity (v_rot) consistently outperformed MPS of the whole-brain across all performance measures.

Table 3.

In-sample cross-validation performances using all of the injury datasets combined via a LOOV procedure. Among all scalar metrics, a_lin and v_rot consistently outperformed MPS across almost all performance measures (shaded).

Combined dataset	network (acc.)	network (sens.)	network (AUC)	MPS	alin (g)	arot (rad/s2)	vrot (rad/s)
Accuracy	0.904	0.881	0.853	0.844	0.867	0.821	0.872
Sensitivity	0.455	0.515	0.212	0.212	0.364	0.061	0.333
Specificity	0.984	0.946	0.968	0.957	0.957	0.957	0.968
Testing AUC	0.824	0.837	0.930	0.818	0.818	0.890	0.837
PPV	0.833	0.630	0.539	0.467	0.600	0.200	0.647
Selected features	(8,1), (5,5) and (51,51)	(8,1), (40,18) and (43,35)	(5,5)	MPS	alin	arot	vrot
Injury threshold	N/A	N/A	N/A	0.40 ± 0.002	110.06 ± 0.57	9461.0 ± 94.06	41.20 ± 0.16

Group-wise “injury pattern”

Fig. 9 compares the average feature magnitudes between the concussive and non-injury groups using the NFL dataset (average MPS magnitude in diagonal nodes and average white matter injury susceptibility measures in off-diagonal edges). Approximately 90% of the features (281 out of 312) in the former were statistically larger than their latter counterparts. Within each group, all features did not have the same magnitude, suggesting a graded regional vulnerability.

Fig. 9.

Average magnitudes of features (i.e., average strains for nodes, and average white matter injury susceptibilities for edges) for concussive (a) and non-injury (b) impacts based on the NFL dataset. Features in the former statistically larger than those in the latter are identified (c; red, vs. green otherwise).

4. Discussion

Traumatic brain injury (TBI) is a complex neurological disorder ranging from concussion of mild symptoms (Duhaime et al. 2012; Bigler 2016) to more severe forms including diffuse axonal injury with damages throughout the brain (Levin et al. 1988). A sophisticated brain injury metric or response sampling scheme is necessary to characterize regional response magnitude and distribution. This, however, is unlikely achievable with scalar injury metrics, whether in kinematics or response-based metrics such as MPS of the whole brain. These scalar injury metrics treat the entire head or brain as a single unit, which inevitably lose critical information on the spatial distribution of brain mechanical responses important to characterize the “signature of injury” (Rowson et al. 2018).

The network-based brain injury metric developed here is a compact matrix form to represent the combined injury risk statuses of GM ROIs and their WM interconnections. A response-based scalar metric, such as MPS of the whole brain or CSDM, is analogous to a degenerated response feature matrix with only one node representing the whole brain but without any edges. Therefore, the response feature matrix significantly extends current scalar metrics by providing more complete information about brain regional injury risks. It also extends the previous “response feature vector” (Cai et al. 2018; Zhao and Ji 2019a), by further informing injury susceptibilities of WM interconnections.

The network-based injury metric is dramatically more sophisticated than conventional scalar metrics (312 unique features vs. 1; Fig. 7), which requires justification. Here, we first discuss its potential advantages in binary injury prediction (concussion vs. non-injury) over conventional scalar metrics as explored in this study. Then, we briefly discuss its potential for future applications in TBI biomechanics.

4.1. In-sample injury prediction performance

An ultimate goal of a sophisticated brain injury metric is to predict the occurrence of injury more reliably. SVMs and the SFFS feature selection procedure employed here always identified appropriate network features (nodes and edges) to yield the highest prediction accuracy, sensitivity or AUC when trained to do so. This was true for all LOOV cross-validations (Tables 1–3). When maximized for accuracy, the network-based injury metric also consistently achieved the best specificity and PPV, for all in-sample LOOV cross-validations. The consistency in performance gain over baseline scalar metrics via conventional logistic regression supported the use of multiple features and machine learning to improve injury prediction performance.

Interestingly, among the four scalar injury metrics, peak rotational acceleration (velocity) always outperformed MPS of the whole brain for the two reconstructed datasets (combined dataset), across all performance measures. This confirmed that if the simulation result was oversimplified (e.g., MPS of the whole brain), a head injury model may not necessarily be better in injury prediction than kinematics (Beckwith et al. 2018). This was not surprising given the substantial loss of information as clearly illustrated in Fig. 7. Collectively, these findings supported the use of a structural network-based response feature matrix and feature-based machine learning for improved concussion prediction performance.

Both network nodes and edges could be selected as the most “injury predictive” features (Fig. 8d). However, the exact features selected depended on the training dataset and the performance criterion. Therefore, it may be ill-advised to pre-select specific response metrics (variable and location) for injury prediction training while assuming the best performance would always follow. This also suggested distinction between injury vulnerability (frequency in sustaining large strains, e.g., the corpus callosum (Zhao et al. 2016; Zhao et al. 2019; Hernandez et al. 2019)) and predictability (the ability to correlate with diagnosed injury).

Nevertheless, it was important to note that these in-sample performances were based on testing rather than training datasets as commonly used (Kleiven 2007; Rowson and Duma 2013; Giordano and Kleiven 2014; Beckwith et al. 2018). Therefore, the performance measures reported here would be more objective (otherwise, a perfect training AUC of 100% can be reached (Cai et al. 2018)). However, it was also important to recognize that the “best features” (Tables 1–3) were selected by maximizing a given performance criterion based on testing datasets, which effectively served as feedback. This was in contrast to an earlier study where the testing dataset was used for cross-validation only without feedback for feature selection (Cai et al. 2018).

4.2. Out-of-sample injury prediction performance

Based on the two reconstructed injury datasets for training, it was clear that out-of-sample injury prediction performance was effectively a “three-way” fitting relying on both the training and testing datasets as well as the injury metric, itself. Not a single injury predictor consistently achieved the best out-of-sample performance across all datasets, regardless of the performance category selected for comparison (Tables A1 and A2).

The dependency on the testing dataset for a trained injury predictor indicated that the testing and training datasets might not have been drawn from the same population. Although both NFL and VT datasets were reconstructed in the laboratory, the former was drawn from professional players while the latter was drawn from college football athletes. Their injury thresholds in terms of peak linear acceleration, rotational acceleration, and angular velocity differed significantly (by 28.8%, −9.9%, −18.3%, respectively, using those from NFL dataset as the baseline). While the SF dataset was also drawn from college football athletes, it was directly measured on-field (vs. reconstructed), and it differed from the VT dataset in ways how the impacts were sampled from the population. As a result, the ratio of the number of concussive/non-injury impacts differed greatly between the two datasets (2/108 vs. 11/44). The sampling differences among the three impact datasets (NFL, VT, and SF) were further confirmed by non-parametric Kolmogorov–Smirnov two-sample tests conducted between each pair of them based on peak linear/rotational acceleration and rotational velocity. All injury dataset pairs, except for two pairs, NFL vs. VT and VT vs. SF when compared using peak linear acceleration, were found to significantly differ (p<0.05; i.e., not from the same population). The observed differences may have also been exacerbated by their relatively small sample sizes.

4.3. Real-world applications

The uncertainty in out-of-sample injury prediction performance may seem to discourage the use of the substantially more complex network-based metric. However, for real-world applications, it would be important to first maximize the training dataset. Therefore, similar injury datasets would have been combined first to train an injury predictor. With sufficient training samples, injury prediction on a new, unseen impact would be closer to in-sample LOOV rather than out-of-sample prediction (i.e., 100 training samples vs. 1 unseen impact). Regardless of the prediction success outcome, once tested, the unseen sample could be combined with the existing training dataset to re-train the injury predictor. Given the consistent performance gain for all in-sample evaluations, the network-based injury metric likely would continue to outperform conventional scalar metrics in real-world applications, especially as training samples could grow along with data collection to iteratively update the predictor.

To support this notion, we randomly selected M% samples (M ranged from 10 to 90, with a step size of 10) from the combined dataset (N=218) and compared the LOOV accuracy using the network-based injury predictor and the four scalar metrics. With 50 random trials and paired t-tests, the former statistically and consistently outperformed MPS, a_lin, a_rot, and v_rot when M% exceeded 40%, 60%, 20%, and 60%, respectively, corresponding to 87, 131, 40, and 131 samples, respectively.

Regardless, the observed injury prediction dependency on both training and testing datasets in out-of-sample evaluations may also provide insight into whether different injury datasets should be combined. For example, professional players may arguably have a higher injury tolerance than young adolescence; thus, their injury datasets might not be combined. Similarly, data from contact sports athletes whose many sub-concussive head impacts could have amounted to significant cumulative effects on injury risks (Beckwith et al. 2013; Montenigro et al. 2017; Stemper et al. 2018; Rowson et al. 2019) may not be readily combined with data from falls, assaults or vehicle crashes, where injury is most likely the result of a single impact event. Admittedly, determining “similar” injury datasets may inevitably be somewhat subjective (as in the current study), particularly given limited injury data available at present.

4.4. Potential applications beyond binary injury prediction

One potential use of the network-based injury metric is to enable the exploration of injury patterns. This was explored using the NFL dataset, as similarly investigated before on a few ROIs (Kleiven 2007). The feature magnitude differences between and within the groups (Fig. 9) suggested graded brain regional vulnerability. It was possible to further identify the most vulnerable GM ROIs and/or WM connections (e.g., with permutation tests (Zhao et al. 2017; Zhao et al. 2019)), which could be reported in the future.

For impact simulation, itself, the compact summary of macro-scale response distribution within the whole brain may allow for a more targeted multi-scale modeling (Cloots 2011; Cloots et al. 2012; Zhu et al. 2016; Mohammadipour and Alemi 2017; Montanino and Kleiven 2018; Zhao and Ji 2019b). In addition, the biomechanical injury pattern from the response feature matrix may also offer a convenient bridge to correlate with observed neuroimaging alterations (Bigler and Maxwell 2012; Koerte et al. 2015) in the future. Finally, the response feature matrix may potentially open a new avenue to relate impact-induced brain strains to subsequent brain dysfunction (Duhaime et al. 2012), in which case a function-specific structural subnetwork could be adapted to summarize brain strain distribution. These potential applications are largely outside of the scope of the current study. Nevertheless, establishing a response sampling framework such as the network-based response feature matrix is an important first step.

4.5. Feature-based classification in neuroimage applications

This study spans across conventional TBI biomechanics, neuroimaging, and machine learning. It is worthwhile getting insight from numerous neuroimage classification studies that employ feature-based machine learning. A close analogue is Alzheimer’s disease (AD) classification from mild cognitive impairment and normal controls using various SVM (Rathore et al. 2017) and more recently, deep learning (Khvostikov et al. 2018) techniques. Several important steps for feature-based AD classification include the generation and extraction of meaningful features and conducting feature selection and dimension reduction to avoid overfitting. Various neuroimage modalities have been utilized to generate features; however, no single modality appears sufficient, and multimodal approaches are gaining attention (Rathore et al. 2017).

In the current TBI study, head impact simulation essentially transformed 6-degree-of-freedom head motion into a strain-based feature space. Constructing the feature response matrix was analogous to extracting features from the simulation result based on domain knowledge of the brain structural network and specific strain response variables. The choice of using the smallest network was also to reduce the number of features, somewhat empirically (Fig. 6) to avoid overfitting. We only used strain-based features, which was analogous to using a single neuroimage modality for AD classification. As impact simulations could also produce other mechanical responses such as strain rate, a similar response feature matrix could be established, analogous to additional neuroimage modalities. It merits further investigation whether combining response feature matrices from strain and strain rate could improve injury prediction performance, similarly to multimodal AD classification.

4.6. Accuracy of the network-based response feature matrix

The accuracy of the network-based response feature matrix is likely more sensitive to model simulation fidelity than scalar metrics because it characterizes both magnitude and distribution of regional strains. The simulation fidelity relies on head injury model biofidelity and the accuracy of impact kinematics. For model biofidelity, there is an ongoing debate on what experimental data to use for validation (e.g., concern on data quality (Wu et al. 2019) in cadaveric strains (Zhou et al. 2018); whether or not strains from in vivo tests (Sabet et al. 2008) are relevant to injury (Giordano and Kleiven 2016; Ganpule et al. 2017; Zhao et al. 2018)). Therefore, even “validated” head injury models produce significant disparities in strains (Ji et al. 2014; Giordano and Kleiven 2016).

On the other hand, current head impact sensor technologies only consider the accuracy of peak linear and/or rotational accelerations or rotational velocity at present (Beckwith et al. 2012; Wu et al. 2015). Investigating the impact sensor accuracy in terms of model-estimated brain strains only emerged recently (Kuo et al. 2017). While peak rotational velocity is most relevant to brain strains, the velocity profile shape could significantly influence brain strain as well (Zhao and Ji 2017). In addition, current head impact sensors focus on peak acceleration magnitudes, but not yet deceleration critical for brain strain as well.

Because of these limitations in injury model validation and impact kinematic measurement, we chose to use the smallest network to characterize brain strain responses. This was a calculated tradeoff between method sophistication and the significance of individual variability (Giordano et al. 2017) as a generic head injury model was used for an athletic population (to avoid “overfitting”). However, similarly to a previous study (Zhao et al. 2017), the current work was a critical stepping-stone towards a more individualized integration of neuroimaging with TBI biomechanical modeling in the future.

4.7. Other limitations

First, the number of impact cases especially for each injury dataset, was limited. For the NFL and VT reconstructed impacts, the over-sampling of concussive impacts and under-sampling of non-injury cases were well-known (Rowson 2016; Sanchez et al. 2018). For the SF dataset, while the relative distribution of concussive vs. non-injury impacts appeared more reflective of real-world impacts, the number of injury cases was low. These practical limitations on the data availability, to some degree, hampered more effective evaluation and comparison of injury prediction performances in this study.

Second, we only used two response variables to encode the response feature matrix for illustration, although other strain (e.g., 9 (Zhao et al. 2017)) and strain rate variables as well as additional weighting factors based on fiber numbers could be explored in the future. The tractography fibers limited to ~35 k were also a rather coarse representation of WM fibers (albeit, no significant differences expected for the overall response matrix because the WM fibers were uniformly sampled across the brain). Importantly, nevertheless, the network-based feature response matrix as a framework could potentially be adapted for specific injury analysis using the techniques developed here.

Third, we recognize the diverse choices of scalar brain injury metrics available (e.g., Hernandez et al. compared 18 metrics (Hernandez et al. 2015) and Sanchez et al., employed 14 risk functions (Sanchez et al. 2017)). Here, we intentionally limited the comparison to four basic and representative scalar metrics to avoid distraction from the focus on developing the network-based response feature matrix. A future study will systematically compare the network-based injury predictor with the diverse scalar injury metrics, perhaps more objectively (i.e., cross-validation vs. training performance).

Finally, we emphasize that as a framework, the network-based response feature matrix developed here is independent of a specific head injury model or injury dataset used. Efforts to improve model biofidelity and accuracy in injury dataset will surely continue, which may render model- or data-specific results different from those presented here. Nevertheless, the response sampling framework, with further enhancement, may provide an improved avenue for more effective injury analysis than those currently available.

5. Conclusion

Based on three independent real-world injury datasets, we found that the network-based brain injury predictor using SVM consistently outperformed other baseline scalars relying on logistic regression for all in-sample evaluations. We also illustrated how the network-based response feature matrix could be used to investigate injury patterns. Future studies are necessary to confirm that the new metric outperforms other conventional scalar metrics using prospective injury data. Nevertheless, the response feature matrix may serve as an important stepping-stone towards a structural network-based approach to elucidating TBI biomechanical mechanism in the future.

Appendix: Out-of-sample prediction performance

The network-based injury metric was re-trained using the entire NFL or VT dataset. Tables A1 and A2 report the out-of-sample performances when predicting injury occurrences for impacts in the other reconstructed and SF dataset. For each injury predictor trained on the same training dataset, the injury prediction performance depended on the testing dataset used. For example, the network-based metric trained on the NFL dataset to maximize accuracy achieved a rather poor sensitivity with VT dataset (0.091; i.e., only one of the 11 concussion cases was correctly predicted), but a perfect score of 1.000 for the SF dataset (both concussions correctly predicted).

On the other hand, when using the same SF dataset for testing, the performance of each injury metric in most categories also depended on the training dataset used. For example, the best performer in terms of out-of-sample prediction accuracy was v_rot when trained on the NFL dataset, but it was a_lin when trained on the VT dataset (accuracy of 0.936 vs. 0.927; Tables A1 and A2). The dependency on the training dataset was also evident when comparing the injury thresholds established. Using those from the NFL dataset as baselines, the injury thresholds for MPS, a_lin, a_rot and v_rot differed by −24.2%, 28.8%, −9.9%, −18.3%, respectively.

Interestingly, the majority of “best performers” were baseline kinematic variables across many categories. For example, a_rot trained on the NFL dataset achieved the best prediction accuracy and testing AUC for the VT dataset (Table A1), and the same variable trained on VT dataset also achieved the best accuracy and AUC when predicting the NFL impacts (Table A2). However, the same predictor did not receive the best accuracy or AUC when predicting impacts in the SF dataset, regardless of which training dataset used. This observation confirmed that the injury prediction performance depended on the testing dataset. Further, kinematic variables could also yield the worst performances. For example, a_lin trained on the VT dataset had a sensitivity of zero for the SF dataset (i.e., none of the two concussions were corrected predicted).

To summarize, these findings suggest that the performance of a specific injury predictor depend not only on the injury metric itself, but also on the training and testing datasets as well. Therefore, out-of-sample injury prediction is effectively a “three-way” fitting process.

Table A1.

Out-of-sample prediction performances using NFL-trained predictors to predict injury on the VT and SF datasets.

	Performance category	network (acc.)	network (sens.)	network (AUC)	MPS	alin (g)	arot (rad/s2)	vrot (rad/s)
VT	Accuracy	0.818	0.855	0.836	0.818	0.800	0.873	0.818
	Sensitivity	0.091	0.364	0.182	0.091	0.727	0.455	0.091
	Specificity	1.000	0.977	1.000	1.000	0.818	0.977	1.000
	Testing AUC	0.822	0.849	0.765	0.833	0.901	0.901	0.816
	PPV	1.000	0.800	1.000	1.000	0.500	0.833	1.000
SF	Accuracy	0.873	0.709	0.773	0.873	0.918	0.818	0.936
	Sensitivity	1.000	1.000	0.500	0.500	1.000	1.000	0.500
	Specificity	0.870	0.704	0.778	0.880	0.917	0.815	0.944
	Testing AUC	0.912	0.926	0.806	0.889	0.935	0.926	0.889
	PPV	0.125	0.059	0.040	0.071	0.182	0.091	0.143
	Injury threshold	N/A	N/A	N/A	0.33	83.10	5623.11	38.05

Table A2.

Out-of-sample prediction performances using VT-trained predictors to predict injury on the NFL and SF datasets.

	Performance category	network (acc.)	network (sens.)	network (AUC)	MPS	alin (g)	arot (rad/s2)	vrot (rad/s)
NFL	Accuracy	0.755	0.623	0.643	0.640	0.755	0.830	0.774
	Sensitivity	0.850	0.900	0.900	0.850	0.350	0.850	0.850
	Specificity	0.697	0.455	0.485	0.515	1.000	0.818	0.727
	Testing AUC	0.829	0.753	0.846	0.876	0.858	0.905	0.849
	PPV	0.630	0.500	0.514	0.515	1.000	0.739	0.654
SF	Accuracy	0.782	0.627	0.636	0.782	0.927	0.736	0.855
	Sensitivity	1.000	1.000	1.000	1.000	0.000	1.000	0.500
	Specificity	0.778	0.620	0.630	0.778	0.944	0.732	0.861
	Testing AUC	0.894	0.898	0.917	0.889	0.935	0.926	0.889
	PPV	0.077	0.047	0.048	0.077	0.000	0.065	0.063
	Injury threshold	N/A	N/A	N/A	0.25	107.00	5068.89	31.08