Imitation dynamics in the mitigation of the novel coronavirus disease (COVID-19) outbreak in Wuhan, China from 2019 to 2020

Abstract

Background

The coronavirus disease 2019 (COVID-19) was first identified in Wuhan, China on December 2019 in patients presenting with atypical pneumonia. Although ‘city-lockdown’ policy reduced the spatial spreading of the COVID-19, the city-level outbreaks within each city remain a major concern to be addressed. The local or regional level disease control mainly depends on individuals self-administered infection prevention actions. The contradiction between choice of taking infection prevention actions or not makes the elimination difficult under a voluntary acting scheme, and represents a clash between the optimal choice of action for the individual interest and group interests.

Methods

We develop a compartmental epidemic model based on the classic susceptible-exposed-infectious-recovered model and use this to fit the data. Behavioral imitation through a game theoretical decision-making process is incorporated to study and project the dynamics of the COVID-19 outbreak in Wuhan, China. By varying the key model parameters, we explore the probable course of the outbreak in terms of size and timing under several public interventions in improving public awareness and sensitivity to the infection risk as well as their potential impact.

Results

We estimate the basic reproduction number, R₀, to be 2.5 (95% CI: 2.4−2.7). Under the current most realistic setting, we estimate the peak size at 0.28 (95% CI: 0.24−0.32) infections per 1,000 population. In Wuhan, the final size of the outbreak is likely to infect 1.35% (95% CI: 1.00−2.12%) of the population. The outbreak will be most likely to peak in the first half of February and drop to daily incidences lower than 10 in June 2020. Increasing sensitivity to take infection prevention actions and the effectiveness of infection prevention measures are likely to mitigate the COVID-19 outbreak in Wuhan.

Conclusions

Through an imitating social learning process, individual-level behavioral change on taking infection prevention actions have the potentials to significantly reduce the COVID-19 outbreak in terms of size and timing at city-level. Timely and substantially resources and supports for improving the willingness-to-act and conducts of self-administered infection prevention actions are recommended to reduce to the COVID-19 associated risks.

Introduction

The coronavirus disease 2019 (COVID-19) was first identified in Wuhan, China on December 2019 in patients presenting with atypical pneumonia and is considered life-threatening (1,2). Common symptoms of the infection include fever, cough and shortness of breath (3). Since December 31 of 2019, Wuhan has officially released the situation report of the outbreak of COVID-19. The cumulative number of officially reported cases remained constant at 41 cases until January 15, and rapidly increased afterward (4,5). As of February 6 (11:59 PM, GMT+8), the still ongoing outbreak has resulted in a reported 28,139 (10,117 in Wuhan) confirmed cases including 564 (414 in Wuhan) deaths and 1,344 (459 in Wuhan) discharges in mainland China (4). Sporadic cases exported from Wuhan were reported in many Asian, Oceanian, North American and European countries or regions (6), and the case number is still increasing, which suggests travel-related spreading risks as indicated by (7-12).

A number of studies used modelling techniques to explore and project the trends of the COVID-19 outbreak. By using the number of exported cases, a research group at the Imperial College London estimated that there had been 1,723 (95% CI: 427−4,471) infections in Wuhan by January 12 and this would increase to 4,000 (95% CI: 1,000−9,700) by January 18. They also estimated the basic reproduction number (R₀) to be 2.6 (95% CI: 1.5−3.5) (13). Leung et al. drew a similar conclusion and estimated the number of cases exported from Wuhan to other major cities in China (14). Most existing estimates of the R₀ of COVID-19 lie between 1.5 and 4 (10,13,15-19), and is in the same scale as the other two well-known coronavirus diseases: severe acute respiratory syndrome (SARS) and Middle East respiratory syndrome (MERS) (20-22).

The ‘city-lockdown’ policy was firstly implemented in Wuhan and suspended all public traffic within the city and all inbound and outbound transportations from or to Wuhan as of January 23, 2020 (23). Similar policies were also implemented in many other Chinese cities subsequently. This effectively reduced the spatial spreading of the COVID-19 in terms of the number of exported cases domestically and internationally, but the city-level (within each isolated city) outbreaks remain a major concern to be addressed.

With increasing public information about COVID-19 and outbreak released since the second half of January 2020, see Box 1, there has been an increasing number of individuals at risk seeking healthcare supports most commonly in the form of self-administered disease infection prevention actions, i.e., infection risk averse actions. And by the first week of February, most people in the cities seriously affected by COVID-19 chose to take infection prevention actions. On the one hand, taking disease control actions can reduce the morbidity and mortality risks involved with the COVID-19 outbreak. However, on the other hand, the infection prevention actions are usually very constraining and difficult to adhere to, and involve giving up to some degree of a normal lifestyle. For example, they may include major mobility restrictions, the continuous wearing of uncomfortable facemasks, frequent cleaning and sterilization, and there is also the financial and mental ‘cost’ required to implement these kinds of measures. Due to the many possible ‘losses’ in utility associated with disease infection prevention actions, this contradiction between choice of actions makes the elimination difficult under a voluntary acting scheme. There is clearly a clash between the optimal choice of action for the individual and the coverage of infection prevention actions uptake that is best for the population as a whole. In other words, the total coverage of infection prevention actions uptake under a voluntary policy is the collective result of individual decisions to take or not to take actions. Similar to the game theory of vaccination proposed in the literature (27), when this coverage increases, an increasing number of ‘free-rider’ individuals will no longer have the incentive to take control actions, since non-action-takers can enjoy the herd immunity without suffering the costs associated with the strict infection prevention actions. This game theoretical contradiction in vaccination decision-making is a well-known phenomenon (27-30).

Table 1. Descriptions of model parameters and compartmental classes.

Class or parameter	Description	Value	Range	Remarks	Unit	Source
R 0	Basic reproduction number	2.5	2.4–2.7	Estimated	Unit-free	(10,13,15,16,19)
β (= R0γ)	Transmission rate	1.1	1.0–1.2	Determined by R0	Per day	None
ξ	Strategy switching rate	1	>0	Assumed	Per day	None
α	Transmission reduction scale	0.33	0–1	None	Unit-free	(36)
σ −1	Incubation period	5.2	Fixed	None	Day	(15)
γ −1	Infectious period	2.3	Fixed	None	Day	(10,15)
η	Symptomatic ratio	0.875	Fixed	None	Unit-free	(38-40)
U	Unmasked population	Time-varying	0-N	None	Person	Eqn [6]
M	Masked population	Time-varying	0-N	None	Person	Eqn [6]
E	Exposed population	Time-varying	0-N	None	Person	Eqn [6]
I	Infectious population	Time-varying	0-N	None	Person	Eqn [6]
R	Removed population	Time-varying	0-N	None	Person	Eqn [6]
K	Combined imitation rate	Time-varying	0-N	None	Unit-free	Eqn [4]
N	Total population	11,000,000	fixed	As of 2019	Person	(10)
Δe	Scaled payoff gain	Time-varying	NA	None	Unit-free	Eqn [3]
κ	Sensitivity to payoff gain	115.5	>0	Estimated, baseline	Unit-free	None
Φ	Perceived infection probability	Time-varying	0–1	None	Unit-free	None
p	Probability (willingness) of taking facemask	Time-varying	0–1	None	Unit-free	Eqn [5]
r (= r1/r0)	Ratio of payoff	1×10−5	0–1	Close to 0, assumed	Unit-free	None

During the outbreak, the action-taking game evolves through time, and individuals cannot precisely determine their probability and possible (negative) consequences of becoming infected.

Moreover, people adopt updated information and new strategies through learning, by imitating others who appear to have adopted more successful strategies (31). Hence, an imitation dynamical behavior with a learning process between individuals, is proposed, which captures the evolutionary process of the frequencies of strategic choices in the population, with respect to disease infection prevention actions. In this study, we develop a compartmental epidemic model incorporated with a behavioral imitation through a game theoretical decision-making process in order to study the dynamics of COVID-19 outbreak in Wuhan, China. We project the future trends and patterns of this outbreak in Wuhan under the most realistic settings. From a public health control viewpoint, we explore the probable courses of the outbreak in terms of size and timing under several public interventions in improving public awareness and sensitivity to the infection risk as well as their potential impact.

Methods

Surveillance data

Due to late reporting or under reporting of the cases in the situation reports in the early outbreak (5,32), which is also indicated by (10,13,16), the officially reported time series data of cases will introduce biases into the estimation and simulation without reasonable adjustment for varying reporting rates (19,33,34). Therefore, we adopt the time series of laboratory confirmed cases from Li et al. (15). All cases were laboratory confirmed following the case definition by the National Health Commission of China (35) indicated in (15). Specifically the cases ‘were collected onto standardized forms through interviews of infected persons, relatives, close contacts, and health care workers’, and aggregated by the date of symptoms onset (15). The data should cover most of symptomatic pneumonia of unknown etiology if not all from December 1, 2019 to early January 8, 2020. We choose to use the data up to January 8, one day before the decline of epidemic curve in Figure 1 of (15), for model fitting and parameter estimation. The decline after January 8, 2020 in their figure was ‘likely to be due to delays in diagnosis and laboratory confirmation’ (15).

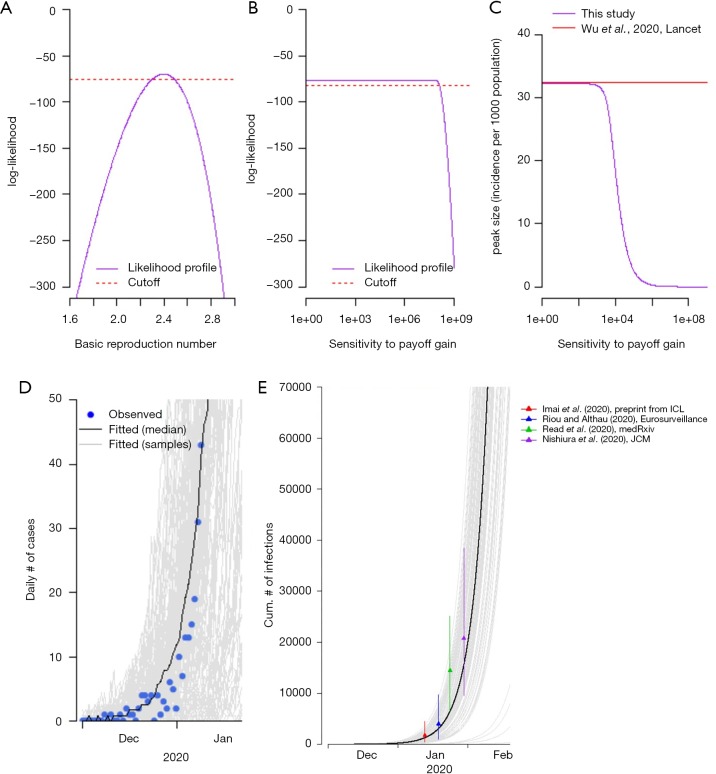
Figure 1.

The estimation of basic reproduction number (R₀) and sensitivity to payoff gain (κ), and the fitting results of the early outbreak. (A,B) likelihood profiles (purple curve) of R₀ and κ, and the cutoff threshold (red dashed line) respectively; (C) comparison between the peak sizes of our simulation (varying with κ) and that of Wu et al. (10); (D) fitting results (curves) to the cases data (blue dots) in Wuhan from Li et al. (15), where the black curve is the simulation median and the grey curves are the 1,000 simulation samples; (E) comparison between our simulation on cumulative number of infections and those from other literatures (9,13,16,17).

Game of taking infection prevention actions

Due to the emergency of the COVID-19 outbreak in Wuhan, a number of infection prevention actions were promoted to individuals at risk, including wearing facemasks, maintaining hand hygiene and reducing outdoor mobility (or activities), etc. Existing literatures suggest that these infection prevention actions could well have reduced the risk of infection in past outbreaks of infectious diseases (22,36). The model of “imitation dynamics” presented here was previously used for predicting the decision-making of vaccination uptake to prevent pediatric infections during the vaccine scare era (27,37). We develop an imitation behavioral modelling framework of two types of strategies for individuals:

• ❖ those willing to take disease infection prevention actions associated with a payoff at E₀, and

• ❖ those not willing to take disease infection prevention actions associated with a payoff at E₁.

For each individual, we assume that his or her willingness (or probability) to take disease infection prevention actions, denoted by p, is controlled by the payoff profile (E₀ and E₁) and the sensitivity of this payoff profile (κ), as explained shortly.

Considering the possibility of being infected, denoted by Φ ranging from 0 to 1, during an outbreak, we account for the prevalence of infections, denoted by I/N. Since N is the total population size and fixed to be a constant, we model Φ as an increasing function of I, i.e., Φ(I). If we denote r₀ (>0) as the cost of being infected by COVID-19, the payoff for an individual that does not take infection prevention actions is given by Eq. [1]:

$$E_0=-\varphi \left(I\right)r_0$$ [1]

For an individual who takes infection prevention actions, the possibility of being infected is reduced by a scalar α, and the possibility is αΦ. At the same time, the cost for taking infection prevention actions is r₁, which is expected to be much smaller than r₀, i.e., r₁ << r₀. Thus, the payoff for an individual that takes infection prevention actions is given by Eq. [2]:

$$E_1=-\mathrm{\alpha \varphi }\left(I\right)r_0-r_1$$ [2]

The payoff gains for one not taking infection prevention actions who then switches to the strategy of taking infection prevention actions is ΔE, such that

$$\mathrm{\Delta E}=E_1-E_0=\left(1-\alpha \right)\varphi \left(I\right)r_0-r_1$$ [3]

Since r₁ << r₀, we rescale the ΔE by r₀ and define r = r₁/r₀ such that 0 < r < 1 and r is expected being close to 0. With the tradeoff of the game holding, we have the scaled ΔE, denoted by Δe, in Eq. [4].

$$\mathrm{\Delta e}=\mathrm{\Delta E}/r_0=\left(1-\alpha \right)\varphi \left(I\right)-r$$ [4]

As Φ(I) measures the risk of being infected, it is proportional to the force of infection that is approximately the product of transmission rate (β) and the instantaneous prevalence rate (I), i.e., Φ(I) is proportional to βI/N. Since the β usually is a constant and its effects can be controlled by other terms, we simply define Φ(I) = I/N throughout this study.

For the imitation dynamics, it is assumed that individuals randomly sample other members of the population at a constant rate. If the strategy of the sampled members provides a higher payoff, then the strategy is adopted with a probability proportional to the expected gain in payoff. Let p denote the probability of an individual who is willing to take infection prevention actions. We further model the imitation rate, K (>0), at which individuals sample others and switch strategies, as a function of Δe, i.e., K(Δe). Therefore, the time evolution of p is given by Eq. [5].

$$p^{\prime }=K\left(\mathrm{\Delta e}\right)p\left(1-p\right)$$ [5]

Since K(Δe) is expected to be an increasing function with respect to Δe, for simplicity, we further define K(Δe) = κΔe. The term κ is a proportionality constant that controls the sensitivity of the imitation rate in response to the perceived payoff gain (Δe). Thus, Eq. [5] can be refined as in Eq. [6].

$$\begin{array}{l}{p}^{\prime }=\mathrm{\kappa \Delta e}\cdot p\left(1-p\right)\\ =\mathrm{\kappa p}\left(1-p\right)\left[\left(1-\alpha \right)\varphi \left(I\right)-r\right]\\ =\mathrm{\kappa p}\left(1-p\right)\left[\left(1-\alpha \right)I/N-r\right]\end{array}$$ [6]

As the term κ controls the sensitivity of the imitation rate in response to the perceived payoff gain, larger κ means that the population is more sensitive to be motivated to take the disease prevention infection prevention actions. When the prevalence of infections (I/N) increases, the combined imitation rate (κΔe) will also increase. The term Δe is the payoff gain, and it measures the ‘cost’ (risk) of being infected due to lack of infection prevention actions based on the real-world facts. The sensitivity term (κ) adjusts and rescales this cost level (Δe) from the public perception side.

Epidemic model

We develop a compartmental model based on the classic susceptible-exposed-infectious-recovered (‘SEIR’) modelling structure. The susceptible population is separated into two groups of population, and they are the people not taking infection prevention actions, denoted by U, and the people taking infection prevention actions, denoted by M. The infectious population is denoted by I, and the removed (by recovery or death) population denoted by R. In addition to the classic compartmental framework, we include the game of taking infection prevention actions or not in the model by allowing switching status (of the action-taking strategy) between U and M at a considerably large rate, ξ.

The switching status is also controlled by the probability of willingness to take infection prevention actions (p) as modelled in Eq. [6]. Hence, we have the following epidemic model as in Eq. [7].

$$\{\begin{array}{c}{U}^{\prime }=-\mathrm{\beta I}\frac{U}{N}+\xi \left[\left(1-p\right)M-\mathrm{pU}\right],\\ M^{\prime }=-\mathrm{\alpha \beta I}\frac{M}{N}-\xi \left[\left(1-p\right)M-\mathrm{pU}\right],\\ E^{\prime }=\mathrm{\beta I}\frac{U+\mathrm{\alpha M}}{N}-\mathrm{\sigma E},\\ I^{\prime }=\mathrm{\sigma E}-\mathrm{\gamma I},\\ R^{\prime }=\mathrm{\gamma I},\\ p^{\prime }=\mathrm{\kappa p}\left(1-p\right)\left[\left(1-\alpha \right)\frac{I}{N}-r\right].\end{array}$$ [7]

The total population N = U + M + E + I + R is a constant. The descriptions of model parameters and the associated references are summarized in Table 1.

Reproduction numbers

At the disease-free equilibrium, with initially 100% of the population in the ‘U’ class, the basic reproduction number can be formulated as R₀ = β/γ, by using the next generation matrix approach (41). Using the same technique, the time-varying effective reproduction number can be defined as R_eff = R₀(U + αM)/N.

Fitting framework

We fit the model (6) to the daily number of cases collected in (15), and incorporate with a symptomatic ratio, denoted by η, to only fit the symptomatic infections to the observed data. We model the theoretical value of daily number of symptomatic cases, z_i, for the i-th day as in Eq. [8].

$$z_i={\displaystyle {\int }_{\text{day }i}\mathrm{\eta \sigma E}\text{d}t}$$ [8]

Following previous studies (10,42), with the observed daily number of symptomatic cases denoted by ci for the i-th day, the likelihood can be calculated under a Poisson distribution with rate at z_i, and denoted by L_i(c_i|z_i). Therefore, the overall likelihood for parameter estimation can be formulated as in Eq. [9]:

$$l\left(\text{Θ}\right)={\displaystyle {\sum }_i\ln L_i(\text{Θ}|c_i,z_i)}$$ [9]

Here, Θ denotes the vector of parameters to be estimated, c_i is the observation from the data, and z_i is defined in Eq. [8] and regarded as the theoretical value of c_i. The L_i(·) is the Poisson distribution for the i-th day, and thus namely, the measurement noises are addressed by the Poisson-distributed likelihood framework.

The stochastic variant of the model simulation is implemented as a continuous-time Markov process approximated via a multinomial process with a fixed time step of 0.1 day. We estimate the model parameters by maximizing the likelihood function defined in Eq. [9], as well as by comparing the key modelling outcomes of the outbreak in Wuhan with Wu et al. (10). Following previous studies (19,42-46), the 95% confidence intervals (95% CI) of estimates are obtained by using the profile likelihood approach with the Chi-squared quantile as the cutoff threshold (47). We conduct 1,000 simulation samples and calculate the median and 95% CI.

Initial condition

Since this is the first outbreak of COVID-19 in history, we assume the initial susceptible population is relatively large, and take it to be 100% as of December 1, 2019. This means that U(0) = N − 1, and we set the 1 infection as the seed at the start of the outbreak. The initial value of p is taken to be 0.01, that is, only 1% of the population was willing to take infection prevention actions at the early stage of the outbreak.

Simulation schemes under different scenarios

We explore the impacts of the changes in

• ❖ sensitivity to payoff gain (κ), and

• ❖ effectiveness of control measures (measured by α).

This will include examining how theses parameters affect the epidemiological features of the COVID-19 outbreak in Wuhan, including

• ❖ peak size (as in incidence rate);

• ❖ final size (in percentage infection), and

• ❖ timing of effective control (i.e., the first time at which R_eff <1).

The baseline scenario is the fitting results with the maximum likelihood estimates of each parameter summarized in Table 1. We vary κ by per 10-fold change for 5 times, and thus this means we have 6 settings including 0-fold (baseline), 10-, 100-, 1,000-, 10,000- and 100,000-fold increase in κ. Similarly, we vary α by per 0.5-fold change for 3 times, and thus this means we have 4 settings including 0-fold (baseline), 1/2-, 1/4- and 1/8-fold decrease in α. Therefore, we have (6×4=) 24 different scenarios including the baseline.

We select a scenario regarding κ that is most approaches to the real situation for further simulation analysis. The timing of key outbreak-related information released that were concentrated at the second half of January 2020, see Box 1. Hence, p is expected to start increasing since the second half of January 2020. Referring to the real-world fact, almost every people in Wuhan and elsewhere affected by increasing number of cases is willing to take or has already took infection prevention actions against COVID-19. Thus, p is also expected to approach 1 in the first week of January. By examining the trends of the time-varying p, we consider a scenario regarding κ that has the desired changing dynamics of p as an approximation of the real-world situation. Details of the κ selection can be found in Supplementary files.

The disease surveillance data during the early phase of the outbreak were obtained from Li et al. (15).

Results

We estimated the basic reproduction number, R₀, at 2.5 (95% CI: 2.4−2.7), see Figure 1A, which is consistent with previous estimates from 1.5 to 4 (10,13,15-19). Although the sensitivity to the payoff gain, κ, does not have significant difference to the data from early outbreak, see Figure 1B, we choose the baseline value of κ by comparing the estimated peak size with the previous estimate in Wu et al. (10). As shown in Figure 1C, when κ becomes larger than 115.5, the estimated peak size starts to become lower than the previous estimate in (10), and thus we treat κ =115.5 as the baseline value. Figure 1D shows the fitting results to the symptomatic cases data published in (15) at the early phase of the outbreak. Figure 1E shows the comparison between our simulation on cumulative number of infections and those from other literatures (9,13,16,17), and they are largely in line with each other.

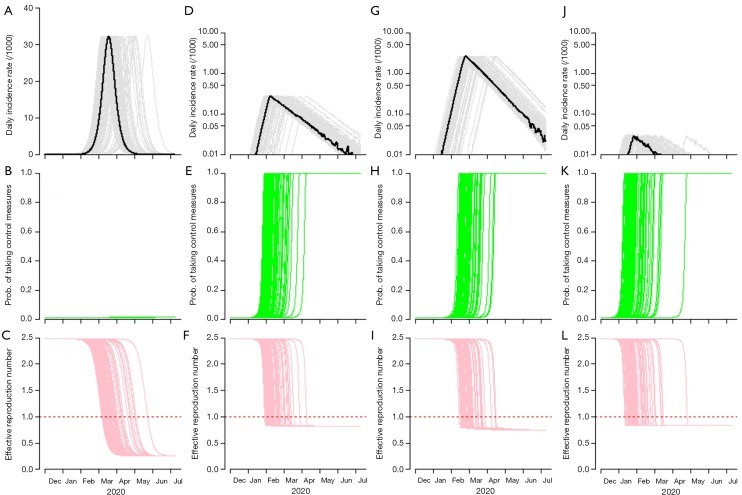
Figure 2 summarizes the simulation results under different scenarios with, from left to right, 0-fold (baseline), 1,000-, 10,000- (the most realistic) and 100,000-fold increase in κ. The simulated epidemic curve under the baseline scenario, in Figure 2A, is consistent with that in the Figure 4 of Wu et al. (10). The fold-increase in κ is likely to mitigate the COVID-19 outbreak in terms of peak level and total infections, see top panels in Figure 2. The middle panels in Figure 2 show the changing dynamics of the willingness (or probability) to take infection prevention actions, i.e., the time-varying p in Eqn (5). This time evolution of p is expected to be largely associated with the situation of the outbreak-related information spread and individuals’ behaviors. By examining the changing dynamics of p, we select the scenario in Figure 2D with 10,000-fold of the baseline κ as an approximation of the real situation, and this scenario will also be used for further simulation analysis. Details of and more reasoning on the selection of scenarios can be found in Supplementary files. For the bottom panels in Figure 2, we found the point in time when R_eff first reduces below unity, i.e., R_eff <1, which implies the epidemic curve will decrease. Figure 2 shows this point in time becomes earlier as κ increase. This finding implies that increasing the sensitivity to take infection risk averse actions would help control the epidemic efficiently.

Figure 2.

The simulation results with, from left to right, 0-fold (baseline, A, B and C), 10,000-fold (the most realistic scenario, D, E and F), 1,000-fold (10-fold less sensitive, G, H and I) and 100,000-fold (10-fold more sensitive, J, K and L) increase in κ and α unchanged at baseline level. The top panels (A, D, G and J) show the daily incidence rate with unit at per 1,000 population. (A) is in the same scale as in Figure 4 of Wu et al. (10), and (D,G,J) are in log scale. The middle (B,E,H,K) show the changing dynamics of the willingness to take infection prevention actions (p). The bottom (C,F,I,L,O) show the changing dynamics of the effective reproduction number (R_eff), and the level 1 is highlighted by the horizonal red dashed line. The curves in light colors represent 1,000 simulation samples.

We summarized the estimates of the key outbreak features under real-world approximation as highlighted in Table 2. We estimate the peak size at 0.28 (95% CI: 0.24−0.32) infections per 1,000 population in Wuhan. The final size of the outbreak is likely to infect 1.35% (95% CI: 1.00−2.12%) of the whole population in Wuhan, see Figure 2D. The outbreak is likely to be under control in terms of the R_eff <1 on February 9 (95% CI: January 31−March 27), 2020. By multiplying the sensitivity of taking infection risk averse actions (κ) by an additional 10-fold (from the real situation), the peak size is likely to reduce at 0.03 (95% CI: 0.03−0.03) infections per 1,000 population, and the final size at 0.15% (95% CI: 0.10−0.22%). However, if κ decreases 10-fold from the real situation, the peak size is likely to rise at 2.65 (95% CI: 2.29−3.07) infections per 1,000 population, and the final size at 10.53% (95% CI: 8.35−13.69%).

Table 2. Summary of the epidemiology features estimation.

Scenario interpretation	Key settings in parameters			Epidemiology features
	Sensitivity to payoff gain	Effectiveness of control measures		Peak size (/1,000 population)	Final size (%)	Date of under control
With 10-fold less sensitive to the risk	1,000-fold of baseline	Baseline (1-fold)		2.65 (2.29, 3.07)	10.53 (8.35, 13.69)	Feb 28 (Feb 14, Apr 18)
		(1/2)-fold of baseline		1.94 (1.70, 2.26)	3.89 (3.51, 4.29)	Feb 24 (Feb 14, Apr 15)
		(1/4)-fold of baseline		1.70 (1.48, 1.99)	2.90 (2.77, 3.21)	Feb 24 (Feb 13, Apr 3)
		(1/8)-fold of baseline		1.60 (1.39, 1.88)	2.58 (2.47, 2.82)	Feb 24 (Feb 13, Apr 3)
The most probable real situation	10,000-fold of baseline	Baseline (1-fold)		0.28 (0.24, 0.32)	1.35 (1.00, 2.12)	Feb 9 (Jan 31, Mar 27)
		(1/2)-fold of baseline		0.20 (0.17, 0.24)	0.40 (0.36, 0.46)	Feb 9 (Jan 28, Mar 21)
		(1/4)-fold of baseline		0.18 (0.15, 0.21)	0.30 (0.28, 0.33)	Feb 6 (Jan 27, Mar 17)
		(1/8)-fold of baseline		0.16 (0.14, 0.19)	0.26 (0.24, 0.29)	Feb 6 (Jan 27, Mar 17)
With additional 10-fold more sensitive to the risk	100,000-fold of baseline	Baseline (1-fold)		0.03 (0.03, 0.03)	0.15 (0.10, 0.22)	Jan 24 (Jan 14, Mar 26)
		(1/2)-fold of baseline		0.02 (0.02, 0.03)	0.04 (0.04, 0.05)	Jan 22 (Jan 10, Mar 10)
		(1/4)-fold of baseline		0.02 (0.02, 0.02)	0.03 (0.03, 0.03)	Jan 21 (Jan 10, Mar 10)
		(1/8)-fold of baseline		0.02 (0.01, 0.02)	0.03 (0.03, 0.03)	Jan 21 (Jan 10, Feb 26)

The ‘date of under control’ is the date when the effective reproduction number (R_eff) firstly decreases below 1, which is consistent with the bottom panels of both Figures 2,3. The highlighted estimates are under the selected scenario as the approximation to the real-world situation.

In Table 2, we also project the outbreak features under several derivative scenarios from the real-world approximation. These ‘what if’ scenarios allow us to evaluate the effect of a certain factor of interest on mitigating the COVID-19 outbreak. By holding other factors unchanged, if the effectiveness of the control measures increases by 2-fold, which means the term α is reduced to be 1/2-fold of its baseline value, the peak size will be likely to reduce to 0.20 (95% CI: 0.17−0.24) infections per 1,000 population in Wuhan, and the final size at 0.40% (95% CI: 0.36−0.46%).

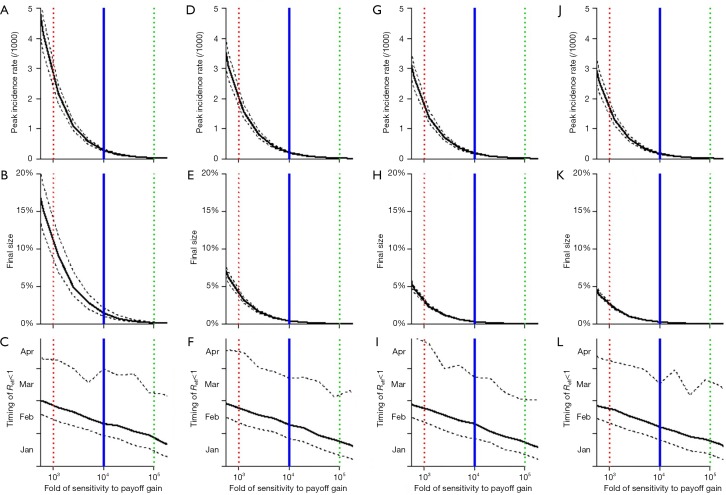
Although we find that the timing of the disease under control (i.e., R_eff <1) is unlikely to change significantly even by increasing as much as 8-fold in the effectiveness of the control measures, see bottom panels in Figure 3, the outbreak size can be successfully reduced, see top and middle panels in Figure 3. The estimates shown in Figure 3 also allow us to further check the sensitivity of results and explore the impacts of varying κ and α on the outbreak features. Both increasing κ and decreasing α are likely to mitigate the COVID-19 outbreak scale in Wuhan.

Figure 3.

The estimation of the key epidemiology features of the COVID-19 outbreak in Wuhan, including peak size (A,D,G,J), final size (B,E,H,K), and timing of effective control (C,F,I,L). The estimation is shown, from left to right, with 0-fold (baseline, A, B and C), 1/2-fold (D,E,F), 1/4-fold (G, H and I) and 1/8-fold (J,K,L) of α. In all panels, the vertical red dashed line is at 1,000-fold of baseline κ (10-fold less sensitive compare to the most realistic situation), the vertical blue bold line is at 10,000-fold of baseline κ (the most realistic situation) and vertical green dashed line is at 100,000-fold of baseline κ (additional 10-fold more sensitive compare to the most realistic situation). The horizontal axes of all panels are the same to be the fold-change in the sensitivity (κ) to the payoff gain of switching from not taking to taking infection prevention actions. The black bold curves are the simulation medians, and the black dashed curves are the 95% CIs. The results shown in this figure are consistent with those in Table 2.

Discussion

The R₀ of COVID-19 is estimated at 2.5 that is in the same magnitude as many other well-known respiratory infections, including SARS and pandemic influenza H1N1 in 2009 (22,48). We estimate there will be some 148.5 (95% CI: 110.0−233.2) thousand infections under the most realistic scenario (i.e., with 10,000-fold of κ from its baseline) by the end of May 2020, given a total of 11 million population in Wuhan. The outbreak will most likely peak in the first half of February (which matches the fact that the daily new confirmations started showing a sign of decreasing these days), and eventually drop to a level of daily new infections of 10 in June 2020, see Figure 2D.

The compartmental model we adopted is similar to those used by other researchers (8,10,13,16,18,19,49-53). Thus, our analyses are based on validated baseline model and approaches and our estimated characteristics are consistent with previous estimates, see Figure 1C,E. Our modelling framework incorporates human reaction and behavior change to the risk and allows us to understand and evaluate the effects of these factors on mitigating the outbreak. We demonstrate that increasing the level of public awareness (in terms of κ) would significantly reduce the outbreak size, see Table 2. Increasing public perception to avert infection risk (κ) and willingness to take infection prevention actions (p) would be helpful to mitigate the on-going COVID-19 outbreak. To achieve this, substantial measures that improve public awareness and willingness for self-protection are strongly desired at the earliest phase locally and domestically. Timely outbreak information updates are crucial. Prevention actions (e.g., avoiding risky contacts and reducing their frequency, avoiding gatherings, and working at home), i.e., moving from class U to M in model (6), would drastically reduce transmission rates, i.e., reduction from β to αβ, As more individuals becoming willing to take actions, the supply and quality of the resources and well-being in supporting for the implementation of the infection prevention actions, become important issues. For example, the availability, cost, quality and quantity of the necessary equipment, e.g., facemask and alcohol sterilizer, sufficient room for self-quarantine and routine supply during mobility restriction, e.g., food and power, are crucially needed to win the combat.

This study has limitations. Our model simulation is conducted under the assumption that the resource for infection prevention actions, e.g., facemasks, can be sufficiently supplied once demanded. This may not always be true during the outbreak, especially when the demand from the population rapidly increase (reflected by p), see Figure 2K,N. However, it appears the charity contribution of the disease prevention resources, which currently occurs in mainland China to support the ‘anti-COVID-19’ campaign in Wuhan, is to some extent alleviating this problem of ‘lack of resources’. Thus, our results still provide legitimate insights on projection and forecasting of the outbreak. Our analysis did not include extreme changes from the side of healthcare providers, e.g., public health service, hospital and use of new drugs or vaccine. Previous modelling analysis demonstrated that large improvement in COVID-19 infection detecting and development and coverage of effective vaccination would reduce the number of cases from the theoretical point of view (53). The timely infections detection associated with isolation could decrease the effective infectious period (γ⁻¹) of transmission, and effective mass vaccination would largely reduce the susceptible pool (U + M). Although these improvements in public health service would mitigate the outbreak by reducing R_eff, the development procedure and delivery of such services or products may be time consuming. Hence, we note that the large changes in healthcare services and products commonly requires relatively long period of time for clinical testing and evaluation, and thus it is unlike to bring significant impacts to current situation. As also pointed out by Wu et al. (10), ‘precisely what and how much should be done is highly contextually specific and there is no one-size-fits-all set of prescriptive interventions that would be appropriate across all settings’. Our imitation framework considers the improvement in the human reaction to take infection risk averse measures in a self-sustaining manner, which demonstrates only by increasing the level of public awareness would largely reduce the outbreak size, see top panels of Figure 3. With the knowledges of the detailed travelling patterns, the number and timing of seed infections in other localities, our modelling framework can be extended to a complex metapopulation version to explore the outbreaks on a spatial level. We remark that as shown in Figure 2 of Wu et al. (10), the outbreak patterns in different places in China are almost the same in peak size, final size and timing of peak as that generated by our model here.

Supplementary

The article’s supplementary files as

Supplementary

Selection of the scenario regarding κ for the real-world situation

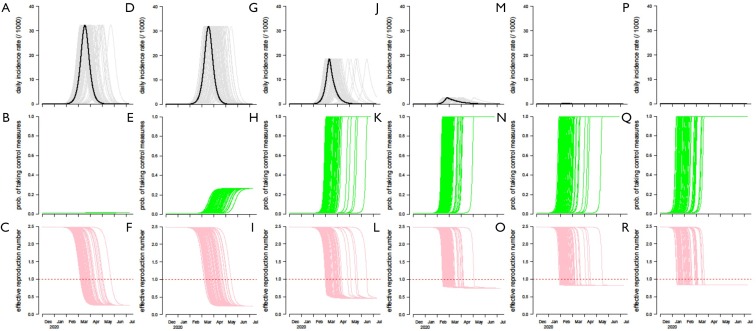
In the main text, we vary κ by per 10-fold change for 5 times including 0-fold (baseline), 10-, 100-, 1,000-, 10,000- and 100,000-fold increase in κ for simulation. Figure S1 summarizes the simulation results under different scenarios with 0-fold (baseline), 10-, 100-, 1,000-, 10,000- and 100,000-fold increase in κ. The fold-increase in κ is likely to mitigate the 2019-nCoV outbreak in terms of peak level and total infections, see top panels in Figure S1.

The middle panels in Figure S1 show the changing dynamics of the willingness (or probability) to take infection prevention actions, i.e., the time-varying p. We select a scenario regarding κ that is most approaches to the real situation for further simulation analysis. The timing of key outbreak-related information released that were concentrated at the second half of January 2020, see Box 1 in the main text. Hence, p is expected to start increasing since the second half of January 2020. Referring to the real-world fact, almost everyone in Wuhan and elsewhere affected by increasing number of cases is willing to take or has already took infection prevention actions against 2019-nCoV. Thus, p is also expected to approach 1 in the first week of January. Therefore, we consider a scenario regarding κ that has the desired changing dynamics of p as an approximation of the real-world situation. By examining the trends of the time-varying p in the middle panels of Figure S1, we confirm that the scenario in Figure S1N associated with 10,000-fold of the baseline κ is probably the closest to the real-world situation. Therefore, we regard this scenario as an approximation of the real situation for further simulation analysis in the main text.

The bottom panels of Figure S1 show the changing dynamics of the R_eff, and we found increasing κ will shorten the period to control the outbreak in terms of the first date when R_eff <1 occurs. We remark that the results of 0-fold (baseline), 1,000-, 10,000- and 100,000-fold are same as in the main results, but only in different scale and sequence.

Figure S1.

The simulation results with 0-fold (baseline, A,B,C), 10-fold (D,E,F), 100-fold (G,H,I), 1000-fold (J, K and L), 10,000-fold (the most realistic scenario, M,N,O) and 100,000-fold (P,Q,R) increase in κ and α unchanged at baseline level. The top panels (A,D,G,J,M,P) show the daily incidence rate with unit at per 1,000 population, which is the same scale as in Figure 4 of Wu et al. (10). The middle panels (B,E,H,K,N,Q) show the changing dynamics of the willingness to take infection prevention actions (p). The bottom panels (C,F,I,L,O,R) show the changing dynamics of the effective reproduction number (R_eff), and the level 1 is highlighted by the horizonal red dashed line. The curves in light colors represent 1,000 simulation samples.

Box 1 Summary of the timing of key outbreak-related information released at the early phase of the outbreak.

The cumulative number of reported cases slowly increased to 41 cases until January 1, 2020 and then rapidly increased after January 16 (4-6), as the official diagnosis protocol was released by the World Health Organization (WHO) on January 17 (24). The exported cases were increasingly detected in many foreign countries and regions globally since the second half of January 2020 (6). The ‘human-to-human’ transmission path was rarely reported until the second half of January (2), and only officially confirmed later (25). In recognition of increased human-to-human transmission on January 23, the local government of Wuhan suspended all public traffic within the city and closed all inbound and outbound transportations (23). The WHO declared the novel coronavirus outbreak to be a public health emergency of international concern on January 30, 2020 (26).

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.