Nonparametric inference on bivariate survival data with interval sampling: association estimation and testing

Summary

In many biomedical applications, interest focuses on the occurrence of two or more consecutive failure events and the relationship between event times, such as age of disease onset and residual lifetime. Bivariate survival data with interval sampling arise frequently when disease registries or surveillance systems collect data based on disease incidence occurring within a specific calendar time interval. The initial event is then retrospectively confirmed and the subsequent failure event may be observed during follow-up. In life history studies, the initial and two consecutive failure events could correspond to birth, disease onset and death. The statistical features and bias of observed data in relation to interval sampling were discussed by Zhu & Wang (2012). Here we propose nonparametric estimation of the association between bivariate failure times based on Kendall’s tau for data collected with interval sampling. A nonparametric estimator is given, where the contribution of each comparable and orderable pair is weighted by the inverse of the associated selection probability. Analysis methods for bivariate survival data with interval sampling rely on the assumption of quasi-independence, i.e., that bivariate failure times and the time of the initial event are independent in the observable region. This paper develops a nonparametric test of quasi-independence based on a bivariate conditional Kendall’s tau for such data. Simulation studies demonstrate that the association estimator and testing procedure perform well with moderate sample sizes. Illustrations with two real datasets are provided.

1. Introduction

In natural history studies of diseases, interest often lies in two or more consecutive failure events and the relationship between event times. For instance, in HIV progression through successive stages, birth is the initial event, and HIV infection and death are the consecutive bivariate failure events. Disease registries or surveillance systems commonly collect data with onset of disease constrained to lie within a specific calendar time interval. This type of sampling is referred to as interval sampling, where the initial event is retrospectively identified and the subsequent bivariate failure events are observed during follow-up. Interval sampling occurs because only individuals diagnosed with disease within a specific time interval can be included, and the data represent a nonrandomly screened subset of a population. For example, for individuals having a fixed date of birth, those with an early age of disease onset cannot be sampled. Therefore, methods of analysis must account for biased sampling.

Examples of such data are seen in a study of HIV seroconversion and subsequent death, and in a study of the natural history of ovarian cancer. In the first example, over 800 subjects aged 15–49 years were ascertained with HIV seroconversion between 1995 and 2003 (Lutalo et al., 2007). Investigators recorded the date of birth, date of HIV seroconversion and subsequent time of death or censoring. The second example involves a cohort of patients, from the Surveillance, Epidemiology and End Results database, diagnosed with ovarian cancer between 1995 and 2002 (Ries et al., 2005). The patients’ dates of birth were ascertained retrospectively, and dates of death were recorded prospectively until the end of 2002.

A common feature of data collected with interval sampling is that the study cohort under interval sampling is made up of subjects experiencing the first failure event within a specific calendar time interval [0, t₀]. Let us denote the calendar time of the initial event by B, the time from the initial event to the first failure event by X, the time from the first event to the second event by Y, and the time from the initial event to the time of censoring by C, where C ⩽ t₀ – B. The bivariate failure times of interest are (X, Y). Under interval sampling, a subject is included in the sample only if 0 ⩽ X + B ⩽ t₀; that is, observation of the first failure time X is doubly truncated. The observation of the second failure time Y could be further complicated by right censoring. Conditional on 0 ⩽ X + B ⩽ t₀, the observed data include independent and identically distributed copies of (B, X, $\tilde{Y}$, δ), where $\tilde{Y}$ = min(Y, C – X) and δ = I (Y ⩽ C – X). The primary aim of this paper is to investigate the dependence structure of the triplet (B, X, Y).

The measurement of association has long been a major topic in bivariate survival analysis. For example, in HIV studies, the dependence between age at HIV infection and residual lifetime reveals useful information about HIV progression. However, analyses of such consecutive failure times, commonly termed gap times, are challenging because within-subject gap time associations induce dependent censoring for the second and subsequent failure times (Lin et al., 1999). It is appealing to develop methods with simple measures of association between gap times in life history processes in order to quantitatively describe the dependence between the two consecutive event times, taking into account disease virulence and possibly natural ageing. This suggests estimation of Kendall’s tau, a popular measure of association between two random variables which does not depend on the marginal distribution. Because of its rank-invariance, Kendall’s tau is suitable for measuring dependence in lifetime models. Lakhal-Chaieb et al. (2010), for example, discussed the analysis of the association between gap times based on Kendall’s tau for follow-up data from a randomized trial of patients with colon cancer (Moertel et al., 1990), with respect to the lifetime process from randomization to cancer recurrence to death. Alternatively, copulas have become an attractive tool for the semiparametric modelling of bivariate survival data. For bivariate right-censored data, Shih & Louis (1995) developed a semiparametric association estimator through a copula model-based two-stage procedure. This method was extended to bivariate survival data with interval sampling to study the association, and it was applied to the ovarian cancer data (Ries et al., 2005) for a joint analysis of age of cancer onset and residual lifetime (Zhu & Wang, 2012). For complete data, Kendall’s tau can be consistently estimated by an empirical estimator. For bivariate right-censored data, several nonparametric estimators have been developed (Oakes, 1982; Wang & Wells, 2000; Lakhal-Chaieb et al., 2010). Nevertheless, nonparametric estimation of Kendall’s tau in the presence of both censoring and truncation has not been systematically investigated. In this paper, we propose a nonparametric estimate of Kendall’s tau as a measure of association between bivariate failure times for data collected with interval sampling.

Most methods proposed in the literature on survival data under truncation (Tsui et al., 1988; Efron & Petrosian, 1999) make the key assumption of independence or a weaker assumption of quasi-independence, namely that the truncation time and failure time are independent, or independent in the observable region. Kendall’s tau serves as the basis of popular nonparametric tests of independence between two random variables. Most survival data are subject to censoring and/or truncation, so Kendall’s tau is not directly applicable. For survival data under truncation, several authors have proposed tests for quasi-independence between truncation and failure times via a conditional Kendall’s tau; see Martin & Betensky (2005) for a review. In analysing bivariate survival data with interval sampling, we have adopted a similar assumption of independence between B and (X, Y), which supposes that the disease process does not depend on when the initial event occurs. However, this independence assumption may be questionable when, for example, an improved screening strategy has been developed which potentially leads to earlier disease detection, or an effective treatment has become available during the observation interval. Further, since we only observe data in the region − B ⩽ X ⩽ t₀ − B due to interval sampling, we cannot identify the relationship between B and (X, Y) outside the region, and so cannot determine whether they are independent. Quasi-independence between B and (X, Y) in the observable region implies that the joint density of (B, X, Y) factors into a product proportional to the density of B and the joint density of (X, Y) in the region − B ⩽ X ⩽ to − B. Methods for bivariate survival data with interval sampling still work under quasi-independence. The second purpose of this paper is to develop a procedure to test nonparametrically the assumption of quasi-independence based on a bivariate conditional Kendall’s tau which quantifies the association between B and (X, Y). The two major issues considered in this paper, association estimation and quasi-independence testing, centre on the dependence structure of the triplet (B, X, Y).

2. Nonparametric estimation of unconditional Kendall’s tau

Kendall’s tau (Kendall & Gibbons, 1990) quantifies any association between random variables X and Y. Let (X₁, Y₁) and (X₂, Y₂) be independent and identically distributed copies of (X, Y). Kendall’s tau is defined as

$$\tau =E[\text{sgn}\{(X_1-X_2)(Y_1-Y_2)\}],$$

where sgn(u) is the sign of u. The pair (1, 2) is said to be concordant if (X₁ − X₂)(Y₁ − Y₂) > 0, and discordant if (X₁ − X₂)(Y₁ − Y₂) < 0. Clearly, −1 ⩽ τ ⩽ 1, and this association measure equals zero when X and Y are independent. For completely observed data {(X_i, Y_i): i = 1,…, n}, τ can be consistently estimated by

$$\widehat{\tau }={\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}\sum _{i<j}\text{sgn}\{(X_i-X_j)(Y_i-Y_j)\},$$

which is an unbiased U-statistic (Randles & Wolfe, 1991) with the property that $n^{1∕2}(\widehat{\tau }-\tau )$ converges weakly to a normal distribution as n → ∞. For bivariate data under censoring, various estimates of τ have been developed. With censored observations, the concordance status can be established only for orderable pairs, making estimation of τ difficult. Oakes (1982) suggested an estimator using only orderable pairs, which is inconsistent when bivariate survival data are not independent and also ignores partial information provided by censored data. Lakhal-Chaieb et al. (2010) introduced a modification of Oakes’s estimator by a Horvitz–Thompson-type correction, where the contribution of each orderable pair is weighted by the inverse of the associated selection probability; this estimator enjoys consistency and asymptotic normality.

For bivariate survival data with interval sampling, Zhu & Wang (2012) considered semiparametric association estimation of bivariate failure times (X, Y) based on a copula model under the assumption that B is independent of (X, Y), although this independence assumption can be relaxed to quasi-independence. In the present paper, we focus on an unconditional Kendall’s tau, τ_XY = E[sgn{X₁ − X₂)(Y₁ − Y₂)} ], as a measure of association between X and Y. For bivariate survival data with interval sampling, to handle the selection bias from the truncation effect and the uncertainty of pair ranking from censoring, attention should be further restricted to pairs that are comparable in addition to orderable. Under quasi-independence, we adopt inverse-probability weighting to adjust for interval sampling bias, and propose a nonparametric estimate of τ_XY where the contribution of each comparable and orderable pair is weighted by the inverse selection probability. In fact, one can consider the comparable and orderable pairs as a sample selected from the population, and a common way to correct the bias in survey sampling is to weight each pair by the inverse of the estimated selection probability.

The challenge is to identify the comparable and orderable pairs and to compute the associated probability. The concept of a comparable pair was first introduced by Bhattacharya et al. (1983). In our setting, the pair (i, j) is comparable if $\{-B_{ij}^{\max }⩽X_{ij}^{\text{min}},X_{ij}^{\max }⩽-B_{ij}^{\text{min}}+t_0\}$, owing to the dual double truncation on B and X, where $-B_{ij}^{\max }=\max (-B_i,-B_j)$, $-B_{ij}^{\text{min}}=\text{min}(-B_i,-B_j)$, $X_{ij}^{\max }=\max (X_i,X_j)$, and $X_{ij}^{\text{min}}=\text{min}(X_i,X_j)$. In the presence of censoring, the order of (Y_i, Y_j) and the concordance or discordance status of the pair (i, j) may not be clear. Following Oakes (1982), the pair (i, j) is orderable if $\{Y_{ij}^{\text{min}}<\text{min}(C_i-X_i,C_j-X_j)\}$, where $Y_{ij}^{\text{min}}=\text{min}(Y_i,Y_j)$. Let λ_ij denote the indicator of comparability and orderability. For ease of exposition, we assume that the censoring time and bivariate failure times are conditionally independent given the calendar time of the initial event and the observable region, written as C ⫫ (X, Y) ∣ (B, − B ⩽ X ⩽ t₀ − B), and that the calendar time of the initial event B and the censoring time C are independent. For such a comparable and orderable pair, $Y_{ij}^{\text{min}}$ is observed, so the conditional probability of a pair being comparable and orderable is

$$\begin{gathered} p_{ij}=\text{pr}(-B_{ij}^{\max }⩽X_{ij}^{\text{min}},X_{ij}^{\max }⩽-B_{ij}^{\text{min}}+t_0,Y_{ij}^{\text{min}}<\text{min}(C_i-X_i,C_j-X_j)\mid \\ {X}_i,X_j,Y_{ij}^{\text{min}}) \\ =\text{pr}(-X_{ij}^{\text{min}}⩽B⩽t_0-X_{ij}^{\max }\mid X_i,X_j{)}^2\times \text{pr}(C_i>X_i+Y_{ij}^{\text{min}}\mid X_i,X_j,Y_{ij}^{\text{min}}) \\ \times \text{pr}(C_j>X_j+Y_{ij}^{\text{min}}\mid X_i,X_j,Y_{ij}^{\text{min}}). \end{gathered}$$

Denote the distribution function of B by G(·), and denote the survival function of C by K(·). Then p_ij can be expressed as

$$p_{ij}=\{G(t_0-X_{ij}^{\max })-G(-X_{ij}^{\text{min}}){\}}^2\times K(X_i+Y_{ij}^{\text{min}})\times K(X_j+Y_{ij}^{\text{min}}),$$

which can be estimated by replacing G and K with estimators. Since the overall follow-up process is assumed to be under independent censoring, K(·),the survival function of C, can be estimated by the Kaplan–Meier estimator $\widehat{K}(\cdot )$ based on $\{(X_i+{\tilde{Y}}_i,1-{\delta }_i):i=1,\dots ,n\}$.

We now discuss estimation of G(·), the distribution function of B, which is essentially dual to estimation of the distribution function of the failure time X, because B is also doubly truncated with the constraint − X ⩽ B ⩽ t₀ − X. For doubly truncated data, Shen (2010) provided an algorithm to jointly compute the nonparametric maximum likelihood estimators for the distribution functions of truncation and failure time variables. Under the assumption of quasi-independence, the full likelihood of the (B_i, X_i) can be expressed as

$$L(g,f)=\prod _{j=1}^n\frac{g_j}{G_j}\times \prod _{j=1}^n\frac{G_j{f}_j}{{\sum }_{i=1}^n{G}_i{f}_i}=L_1(g)\times L_2(g,f),$$

where g = (g₁, …, g_n) and f = (f₁,…, f_n) are probability masses assigning probability g_i to B_i and f_i to X_i, respectively, and $G_i={\sum }_{m=1}^n{g}_{m}I(-B_m⩽X_i⩽t_0-B_m)$ for i = 1, …, n. Here L₁(g) refers to the conditional likelihood of the B_i given the X_i, and L ₂(g, f) is the marginal likelihood of the X_i. Interchanging the roles of the B_i and X_i, the full likelihood can also be decomposed into a product of the conditional likelihood $L_1^{\ast }(f)$ of the X_i given the B_i and the marginal likelihood $L_2^{\ast }(g,f)$ of the B_i. An iterative algorithm can be used to compute the nonparametric maximum likelihood estimators $\widehat{g}$ and $\widehat{f}$ by maximizing L₁(g) and $L_1^{\ast }(f)$, and the corresponding nonparametric estimator of G(·) is denoted by ${\widehat{G}}_{\text{non}}(\cdot )$. Although $\widehat{g}$ and $\widehat{f}$ have no explicit form and must be computed iteratively, the estimation procedure has been implemented in an R (R Development Core Team, 2014) package DTDA (Moreira et al., 2010). Alternatively, if parametric information about the distribution of B is available, we may consider a joint model of (B, X) and parameterize the distribution of B by G(·, θ). Under quasi-independence, the joint sampling density of (B, X) can be expressed as

$$\begin{gathered} p_{B,X}(b,x)=\frac{g(b)f_X(x)I(-x⩽b⩽t_0-x)}{\text{pr}(-B⩽X⩽t_0-B)} \\ =\frac{g(b)I(-x⩽b⩽t_0-x)}{G(t_0-x)-G(-x)}\times \frac{\{G(t_0-x)-G(-x)\}{f}_X(x)}{\int \{G(t_0-u)-G(-u)\}{f}_X(u)\mathrm{d}u} \\ =p_{B\mid X}(b\mid x)\times p_X(x), \end{gathered}$$

where g(·) and f_X(·) are the population densities of B and X, respectively, and p_X(·) is the sampling density of X. Then the conditional likelihood function of the B_i given the X_i eliminates f_X(·) by conditioning, and involves only the parameter θ:

$$L_{\mathrm{c}}(\theta )=\prod _i{p}_{B\mid X}(B_i\mid X_i,\theta )=\prod _i\frac{g(B_i,\theta )}{G(t_0-X_i,\theta )-G(-X_i,\theta )}.$$

Maximizing L_c(θ) leads to an estimator of θ, and the corresponding parametric estimator of G(·) is $\widehat{G}(\cdot ,\theta )$.

Therefore, with G(·) being either nonparametrically estimated by ${\widehat{G}}_{\text{non}}(\cdot )$ or parametrically estimated by $\widehat{G}(\cdot ,\theta )$, and with K(·) estimated by the Kaplan–Meier estimator $\widehat{K}(\cdot )$, an estimator of P_ij is ${\widehat{p}}_{ij}=\{\widehat{G}(t_0-X_{ij}^{\max })-\widehat{G}(-X_{ij}^{\text{min}}){\}}^2\times \widehat{K}(X_i+Y_{ij}^{\text{min}})\times \widehat{K}(X_j+Y_{ij}^{\text{min}})$. The unconditional Kendall’s tau is estimated by

$${\widehat{\tau }}_{XY}={\left(\sum _{i<j}\frac{{\lambda }_{ij}}{{\widehat{p}}_{ij}}\right)}^{-1}\sum _{i<j}\frac{{\lambda }_{ij}\text{sgn}\{(X_i-X_j)({\tilde{Y}}_i-{\tilde{Y}}_j)\}}{{\widehat{p}}_{ij}}.$$

Define an un-rescaled estimator as

$${\widehat{\tau }}_{\mathrm{u}}={\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}\sum _{i<j}\frac{{\lambda }_{ij}\text{sgn}\{(X_i-X_j)({\tilde{Y}}_i-{\tilde{Y}}_j)\}}{{\widehat{p}}_{ij}}.$$

The parameter τ_XY is defined on the domain {(x, y) : x + y ⩽ t₀ − b₋}, where b₋ = inf{b : G(b) > 0}. In the Appendix it is shown that under suitable regularity conditions, $n^{1∕2}({\widehat{\tau }}_{\mathrm{u}}-{\tau }_{XY})$ is asymptotically equivalent to a zero-mean U-statistic of order 2 as n →∞, and a similar result holds for $n^{1∕2}({\widehat{\tau }}_{XY}-{\tau }_{XY})$. Consistency and asymptotic normality follow the lines of van der Vaart (1998) and are summarized in Theorem 1, whose proof is given in the Appendix.

Theorem 1. As n → ∞, ${\widehat{\tau }}_{XY}$ is a consistent estimator of τ_XY, and $n^{1∕2}({\widehat{\tau }}_{XY}-{\tau }_{XY})$ converges weakly to a normal distribution with mean zero and variance ${\sigma }_{XY}^2$.

While the asymptotic variance ${\sigma }_{XY}^2$ may be estimated by its empirical version, the computation is rather complicated. Since the asymptotic normality has been established, it is more convenient to use the bootstrap. The performance of the proposed estimator is evaluated in § 4.

3. Test of quasi-independence via conditional Kendall’s tau

Analysis methods for bivariate survival data with interval sampling rely on the assumption of independence between B and (X, Y). Using the Surveillance, Epidemiology and End-Results ovarian cancer data as an illustrative example, independence implies that the age of cancer diagnosis and the residual lifetime are both independent of the birth cohort. In a nonparametric model, the independence between B and (X, Y) cannot be identified due to the incompleteness of observed data. Nevertheless, quasi-independence between B and (X, Y) in the observable region −B ⩽ X ⩽ t₀ − B, expressedas B ⫫ _Q (X, Y), can be tested. A test is then developed for hypothesis testing based on the fact that violation of quasi-independence implies dependence. Kendall’s tau is not directly applicable to survival data subject to censoring and truncation effects, and a consistent estimate of an unconditional Kendall’s tau cannot be obtained without adjustment. As an extension, a conditional Kendall’s tau has been widely used for tests of quasi-independence for survival data under truncation (Tsai, 1990; Martin & Betensky, 2005), based on comparability of truncated data. Since both B and X are doubly truncated, we adapt this method to the context of interval sampling and define a bivariate conditional Kendall’s tau to test the association between B and (X, Y). Additionally, the second failure time Y is subject to right censoring and may not be observed exactly, so we consider the testing of quasi-independence under censoring rather than testing for independence.

We construct a test statistic from comparable and orderable paired observations. As discussed in § 2, the pair (1, 2) is comparable if $\{-B_{12}^{\max }⩽X_{12}^{\text{min}},X_{12}^{\max }⩽-B_{12}^{\text{min}}+t_0\}$, where $-B_{12}^{\max }=\max (-B_1,-B_2)$, $-B_{12}^{\text{min}}=\text{min}(-B_1,-B_2)$, $X_{12}^{\max }=\max (X_1,X_2)$, and $X_{12}^{\text{min}}=\text{min}(X_1,X_2)$. The pair (1, 2) is orderable if $\{Y_{12}^{\text{min}}<\text{min}(C_1-X_1,C_2-X_2)\}$, where $Y_{12}^{\text{min}}=\text{min}(Y_1,Y_2)$. To test quasi-independence between B and (X, Y) under censoring, we assume that the censoring time and bivariate failure times are conditionally independent given the calendar time of the initial event and the observable region, i.e., C ⫫ (X, Y) ∣ (B, − B ⩽ X ⩽ t₀ − B), which is a weaker condition than C ⫫ (X, Y). The parameter of interest is a bivariate conditional Kendall’s tau for the association between B and (X, Y),

$${\tau }_{\mathrm{c}}=\{\begin{array}{c}{\tau }_{BX}^{\mathrm{c}}=E[\text{sgn}\{(B_1-B_2)(X_1-X_2)\}\mid {\Omega }_{12}],\hfill \\ {\tau }_{BY}^{\mathrm{c}}=E[\text{sgn}\{(B_1-B_2)(Y_1-Y_2)\}\mid {\Lambda }_{12}],\hfill \end{array}\phantom{\}}$$

where (B₁, X₁, Y₁, C₁) and (B₂, X₂, Y₂, C₂) are observations from the distribution of (B, X, Y, C) ∣ (−B ⩽ X ⩽ t₀ − B), Ω₁₂ denotes the event that the pair (1, 2) is comparable in the observable region of (B, X), i.e.,

$${\Omega }_{12}=\{-B_{12}^{\max }⩽X_{12}^{\text{min}},X_{12}^{\max }⩽-B_{12}^{\text{min}}+t_0\},$$

and Λ₁₂ denotes the event that the pair (1, 2) is both comparable and orderable in the observable region of (B, Y), i.e.,

$${\Lambda }_{12}=\{-B_{12}^{\max }⩽X_{12}^{\text{min}},X_{12}^{\max }⩽-B_{12}^{\text{min}}+t_0\}\cap \{Y_{12}^{\text{min}}<\text{min}(C_1-X_1,C_2-X_2)\}.$$

We give the proof of the following theorem in the Appendix.

Theorem 2. Under the hypothesis of quasi-independence, H₀: B ⫫ _Q(X, Y), and the assumption that C ⫫ (X, Y) ∣ (B, −B ⩽ X ⩽ t₀ − B), the bivariate conditional Kendall’s tau satisfies ${\tau }_{\mathrm{c}}=({\tau }_{BX}^{\mathrm{c}},{\tau }_{BY}^{\mathrm{c}}{)}^{\mathrm{T}}=0$.

A consistent estimator of τ_c based on the observed data {(B_i, X_i, ${\tilde{Y}}_i$, δ_i) : i = 1, … , n} is

$${\widehat{\tau }}_{\mathrm{c}}=\{\begin{array}{c}\sum _{i<j}I({\Omega }_{ij})\text{sgn}\{(B_i-B_j)(X_i-X_j)\}∕N_{\Omega },\hfill \\ \sum _{i<j}I({\Lambda }_{ij})\text{sgn}\{(B_i-B_j)({\tilde{Y}}_i-{\tilde{Y}}_j)\}∕N_{\Lambda },\hfill \end{array}\phantom{\}}=\{\begin{array}{c}{U}_1\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)/N_{\Omega },\hfill \\ U_2\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)/N_{\Lambda },\hfill \end{array}\phantom{\}}=\{\begin{array}{c}{U}_1∕U_{\Omega },\hfill \\ U_2∕U_{\Lambda },\hfill \end{array}\phantom{\}}$$

where U_c = (U₁, U₂)^T is a vector of U-statistics, N_ω is the number of comparable pairs for (B, X), and N_Λ is the number of comparable and orderable pairs for (B, Y). The expected values of U_Ω, U_Λ and U_c = (U₁, U₂)^T are pr(Ω_ij) = μ_Ω, pr(Λ_ij) = μ_Λ and $E(U_{\mathrm{c}})=({\tau }_{BX}^{\mathrm{c}}{\mu }_{\Omega },{\tau }_{BY}^{\mathrm{c}}{\mu }_{\Lambda }{)}^{\mathrm{T}}$. Following a theorem on the joint distribution of U-statistics, n^1/2{U_c − E(U_c)} is asymptotically N(0, 4η), where the elements of the matrix η are

$$\begin{gathered} {\eta }_{11}=E[\text{sgn}\{(X_1-X_2)(B_1-B_2)\times (X_1-X_3)(B_1-B_3)\}I({\Omega }_{12}\cap {\Omega }_{13})]-({\tau }_{BX}^{\mathrm{c}}{\mu }_{\Omega }{)}^2, \\ {\eta }_{12}=E[\text{sgn}\{(X_1-X_2)(B_1-B_2)\times (Y_1-Y_3)(B_1-B_3)\}I({\Omega }_{12}\cap {\Lambda }_{13})]-{\tau }_{BX}^{\mathrm{c}}{\mu }_{\Omega }{\tau }_{BY}^{\mathrm{c}}{\mu }_{\Lambda }, \\ {\eta }_{22}=E[\text{sgn}\{(Y_1-Y_2)(B_1-B_2)\times (Y_1-Y_3)(B_1-B_3)\}I({\Lambda }_{12}\cap {\Lambda }_{13})]-({\tau }_{BY}^{\mathrm{c}}{\mu }_{\Lambda }{)}^2, \end{gathered}$$

provided that η₁₁ and η₂₂ are positive as n → ∞. Similarly, $n^{1∕2}({\widehat{\tau }}_{\mathrm{c}}-{\tau }_{\mathrm{c}})$ is asymptotically N(0, 4D⁻¹ηD⁻¹) as n → ∞, where D is a diagonal matrix with [μ_Ω, μ_Λ] on the diagonal. A consistent estimator of the matrix η is obtained by averaging over all possible observations of (B, X, Y), and its exact form is given in the Appendix. Estimating η, μ_Ω and μ_Λ based on the data, the statistic $n{\widehat{\tau }}_{\mathrm{c}}^{\mathrm{T}}\widehat{\mathrm{D}}{\widehat{\eta }}^{-1}\widehat{\mathrm{D}}{\widehat{\tau }}_{\mathrm{c}}∕4$ is asymptotically distributed as a ${\chi }_2^2$ distribution as n → ∞, under H₀ : B ⫫ _Q(X, Y).

4. Simulations

The first simulation was conducted to examine the performance of the estimation method proposed in § 2 with moderate sample sizes. In measuring the association between X and Y, we compare the proposed nonparametric estimator ${\widehat{\tau }}_{XY}^{\mathrm{n}}$ with the copula model-based semiparametric estimator ${\widehat{\tau }}_{XY}^{\mathrm{s}}$. A set of data {(B₁, X₁, Y₁), …, (B_n, X_n, Y_n)} is generated with interval sampling, where B = 9 − 13 W with W ~ Un(0, 1) and correlated pairs (X, Y) are generated from three Archimedean copula models: the Clayton (1978), Gumbel (1960) and Frank (1979) copulas. For each, we use unit exponential margins and choose three values of τ_XY to accommodate different levels of dependence between X and Y. An observation (B_i, X_i, Y_i) is included in the dataset if and only if − B_i ⩽ X_i ⩽ −B_i + 10, and is censored if X_i + Y_i ⩾ −B_i + 10. The censoring fraction is around 20–25%. For each value of τ_XY, 1000 simulated samples are generated with n = 400. Table 1 shows the empirical bias, standard error, average bootstrap standard error and 95% coverage probability for ${\widehat{\tau }}_{XY}^{\mathrm{n}}$ and ${\widehat{\tau }}_{XY}^{\mathrm{s}}$, based on asymptotic normality, in which the standard error is computed using 500 bootstrap resamples. The empirical 95% coverage probability is based on the 1000 confidence intervals. Under all the simulation scenarios, the nonparametric estimator ${\widehat{\tau }}_{XY}^{\mathrm{n}}$ works well, with the bias of ${\widehat{\tau }}_{XY}^{\mathrm{n}}$ being comparable to that of ${\widehat{\tau }}_{XY}^{\mathrm{s}}$. The variance of ${\widehat{\tau }}_{XY}^{\mathrm{n}}$ is much smaller, which demonstrates the inefficiency of the two-stage estimation procedure for ${\widehat{\tau }}_{XY}^{\mathrm{s}}$. The empirical standard error of ${\widehat{\tau }}_{XY}^{\mathrm{n}}$ is very close to the average bootstrap standard error, and the empirical coverage probabilities of ${\widehat{\tau }}_{XY}^{\mathrm{n}}$ are close to 95%, which may imply that the nonparametric inference about τ_XY is reasonably good, and that the bootstrap estimator of the variance ${\sigma }_{XY}^2$ provides an appropriate measure of the variability of ${\widehat{\tau }}_{XY}^{\mathrm{n}}$.

Table 1.

Nonparametric and semiparametric estimators of τ_XY for bivariate survival data with interval sampling

	τXY	$\text{Bias}({\widehat{\tau }}_{XY}^{\mathrm{n}})$	${\text{SE}}_{\mathrm{e}}({\widehat{\tau }}_{XY}^{\mathrm{n}})$	${\text{SE}}_{\mathrm{b}}({\widehat{\tau }}_{XY}^{\mathrm{n}})$	$\text{CP}({\widehat{\tau }}_{XY}^{\mathrm{n}})$	$\text{Bias}({\widehat{\tau }}_{XY}^{\mathrm{s}})$	${\text{SE}}_{\mathrm{e}}({\widehat{\tau }}_{XY}^{\mathrm{s}})$	${\text{SE}}_{\mathrm{b}}({\widehat{\tau }}_{XY}^{\mathrm{s}})$	$\text{CP}({\widehat{\tau }}_{XY}^{\mathrm{s}})$
Clayton	0·2	1·6	4·5	4·4	95·2	1·5	14·4	14·2	96·1
	0·5	2·8	3·6	3·6	94·4	1·7	9·9	9·7	96·3
	0·8	1·8	1·6	1·7	95·5	1·2	4·2	4·0	96·6
Gumbel	0·2	0·6	4·4	4·1	94·3	2·4	14·3	13·9	94·5
	0·5	0·9	3·6	3·4	94·6	−0·3	10·2	9·8	94·9
	0·8	1·1	1·5	1·3	94·8	−0·8	4·5	4·1	95·2
Frank	0·2	0·7	4·4	4·2	95·3	−1·8	15·6	15·3	95·7
	−0·1	−0·3	4·6	4·3	95·6	1·4	17·9	17·5	96·0
	−0·2	−1·0	4·6	4·4	95·4	2·0	15·7	15·3	96·3

${\widehat{\tau }}_{XY}^{\mathrm{n}}$, nonparametric estimator; ${\widehat{\tau }}_{XY}^{\mathrm{s}}$, copula model-based semiparametric estimator; Bias, empirical bias (× 10²); SE_e, empirical standard error (× 10²); SE_b, average bootstrap standard error (× 10²); CP, coverage probability.

The second simulation was carried out to evaluate the test of quasi-independence between B and (X, Y) described in § 3. The power is calculated from 500 replications. For each replication, we generate a dataset of size n = 400 under interval sampling, assuming a trivariate normal distribution of a random vector (B, X, Y) with E{(B, X, Y)} = (1, 0, 0), and vary the population correlation (ρ_BX, ρ_BY) to yield different values of the parameter of interest, ${\tau }_{\mathrm{c}}=({\tau }_{BX}^{\mathrm{c}},{\tau }_{BY}^{\mathrm{c}}{)}^{\mathrm{T}}$. The population correlation between X and Y, ρ_XY, is a nuisance parameter corresponding to the parameter ${\tau }_{XY}^{\mathrm{c}}=E[\text{sgn}\{(X_1-X_2)(Y_1-Y_2)\}\mid {\Lambda }_{12}]$, which is a conditional Kendall’s tau for the association between X and Y. An observation (B_i, X_i, Y_i) is included in the dataset if and only if −B_i ⩽ X_i ⩽ −B_i + 2, and is censored if X_i + Y_i ⩾ −B_i + 2. Figure 1 displays contour plots of test power. For each panel, the contours are based on a linear interpolation of the estimated probability, with interpolation neighbours determined by a Delaunay triangulation of the points in the $({\tau }_{BX}^{\mathrm{c}},{\tau }_{BY}^{\mathrm{c}})$ plane. The orientation of the power surface with respect to ${\tau }_{BX}^{\mathrm{c}}$ and ${\tau }_{BY}^{\mathrm{c}}$ reflects the association between X and Y. For positive ρ_XY, the power to detect quasi-dependence is greatest when ${\tau }_{BX}^{\mathrm{c}}$ and ${\tau }_{BY}^{\mathrm{c}}$ have opposite signs; for negative ρ_XY, the power to detect quasi-dependence is greatest when ${\tau }_{BX}^{\mathrm{c}}$ and ${\tau }_{BY}^{\mathrm{c}}$ have the same sign.

Fig. 1.

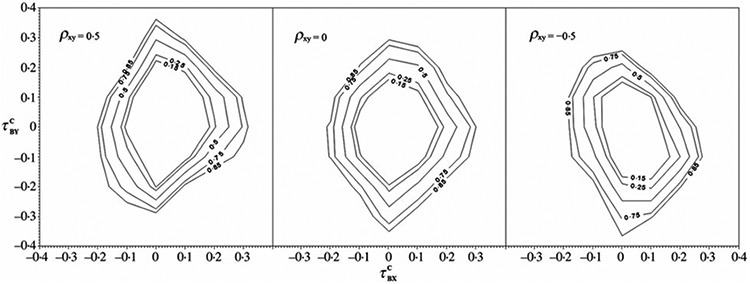
Contour plots of quasi-independence test power versus ${\tau }_{BX}^{\mathrm{c}}$ on the horizontal axis and ${\tau }_{BY}^{\mathrm{c}}$ on the vertical axis. The values of the nuisance parameter ρ_XY are 0·5, 0 and −0·5 from left to right. The power contours are 0·15, 0·25, 0·50, 0·75 and 0·85 from innermost to outermost.

5. Illustrative examples

The proposed nonparametric methods are applied to two sets of real data to test quasi-independence and study the relationships for bivariate survival data with interval sampling. The first dataset is from the Rakai AIDS study of HIV seroconverted subjects (Lutalo et al., 2007). The study cohort consists of 837 subjects with a documented date of HIV seroconversion between 1995 and 2003, and followed until their death or the end of 2003. Among these subjects, 120 died and others were censored by outmigration or administrative censoring at the end of 2003. Clearly, the observed data could be biased due to interval sampling. Estimation or analytical methods that do not consider this fact could yield biased results. Information on the date of birth, date of death, sex, place of residence and HIV subtype is available. In the analysis, the calendar time of birth is denoted by B, and the bivariate failure times are age at HIV infection X and residual lifetime Y; the times are measured in years. Under interval sampling, X is doubly truncated with the constraint −B ⩽ X ⩽ −B + 9, and Y is dependently right censored. Here the null hypothesis of quasi-independence corresponds to HIV progression not depending on birth time in the observable region, i.e., that B is independent of (X, Y) in the region of −B ⩽ X ⩽ −B + 9, written as B ⫫ _Q(X, Y).

We first perform a test of quasi-independence for the HIV seroconversion data. The bivariate conditional Kendall’s tau for testing the association between B and (X, Y) is estimated as ${\widehat{\tau }}_{\mathrm{c}}=({\widehat{\tau }}_{BX}^{\mathrm{c}},{\widehat{\tau }}_{BY}^{\mathrm{c}}{)}^{\mathrm{T}}=(0\cdot 225,0\cdot 067{)}^{\mathrm{T}}$. The quasi-independence test statistic ${\chi }_2^2=2\cdot 156$ and the p-value of 0·340 indicate that there is insufficient evidence to reject quasi-independence between B and (X, Y), which suggests the stability of HIV infection for those diagnosed incidences occurring between 1995 and 2003. Next, given quasi-independence, we quantify the association between X and Y in terms of the unconditional Kendall’s tau, τ_XY, estimated by the inverse-probability weighting method. Studies suggest that progression of HIV infection is affected by HIV subtype (Kaleebu et al., 2001). Therefore, to illustrate the method, we focus on the entire cohort and three subgroups of patients with infection of A subtype, non-A subtype, and unknown subtype. A preliminary Cox regression analysis of residual lifetime conditional on age at HIV infection suggests a significant negative association, but this does not account for interval sampling bias, nor does it give an explicit measure of the association. We compute the nonparametric estimate ${\widehat{\tau }}_{XY}^{\mathrm{n}}$ together with the semiparametric estimate ${\widehat{\tau }}_{XY}^{\mathrm{s}}$ by fitting the Frank copula model. Table 2 shows a negative overall association; interestingly, there is a comparable negative association for non-A and unknown subtypes but a positive association for the A subtype, although the associations are not significant. The results suggest that the HIV epidemic is likely to have a predominance of non-A subtype infection, and subtype A appears to be a very different virus subtype from the others in terms of HIV progression, which is consistent with conclusions from other studies (Kaleebu et al., 2001).

Table 2.

Association estimations of τ_XY for HIV seroconversion data

Cohort	Group size	${\widehat{\tau }}_{XY}^{\mathrm{n}}$	${\text{SE}}_{\mathrm{b}}({\widehat{\tau }}_{XY}^{\mathrm{n}})$	$\text{CI}({\widehat{\tau }}_{XY}^{\mathrm{n}})$	${\widehat{\tau }}_{XY}^{\mathrm{s}}$	${\text{SE}}_{\mathrm{b}}({\widehat{\tau }}_{XY}^{\mathrm{s}})$	$\text{CI}({\widehat{\tau }}_{XY}^{\mathrm{s}})$
All	837	−0·018	0·047	(−0·110, 0·074)	−0·022	0·053	(−0·126, 0·082)
A	64	0·297	0·156	(−0·011, 0·603)	0·303	0·153	(−0·063, 0·538)
Non-A	349	−0·038	0·057	(−0·150, 0·074)	−0·041	0·071	(−0·179, 0·101)
Unknown	424	−0·034	0·040	(−0·112, 0·044)	−0·039	0·046	(−0·129, 0·053)

${\widehat{\tau }}_{XY}^{\mathrm{n}}$, nonparametric estimator; ${\widehat{\tau }}_{XY}^{\mathrm{s}}$, copula model-based semiparametric estimator; SE_b, bootstrap standard error; CI, 95% confidence interval.

The second dataset is from the Surveillance, Epidemiology and End-Results database. The study cohort consists of 1814 nonwhite ovarian cancer patients diagnosed between 1995 and 2002, who were followed until 2002 (Ries et al., 2005). Their dates of birth were ascertained retrospectively, and their dates of death were recorded prospectively. By the end of 2002, 1018 patients had died and the others were right censored. As women tend to have relatively short residual lifetime after diagnosis of ovarian cancer, the competing cause of death due to other risks is relatively small or ignorable. The birth time is denoted by B, and the bivariate failure times of interest are age at cancer onset X and residual lifetime Y. For the quasi-independence test, the bivariate conditional Kendall’s tau is estimated as ${\widehat{\tau }}_{\mathrm{c}}=({\widehat{\tau }}_{BX}^{\mathrm{c}},{\widehat{\tau }}_{BY}^{\mathrm{c}}{)}^{\mathrm{T}}=(0\cdot 016,0\cdot 073{)}^{\mathrm{T}}$, the test statistic is ${\chi }_2^2=0\cdot 308$, and the p-value is 0·857, which indicates no evidence to reject quasi-independence. The association between X and Y is assessed by τ_XY, and a significant negative association between the age of cancer onset and residual lifetime is detected by both the nonparametric and the semiparametric methods. Specifically, ${\widehat{\tau }}_{XY}^{\mathrm{n}}=-0\cdot 275$ with confidence interval (−0·313, −0·218) and ${\widehat{\tau }}_{XY}^{\mathrm{s}}=-0\cdot 372$ with confidence interval (−0·434, −0·302). Our analyses show that, compared with the semiparametric estimate ${\widehat{\tau }}_{XY}^{\mathrm{s}}$, the nonparametric estimate ${\widehat{\tau }}_{XY}^{\mathrm{n}}$ generally suggests slightly smaller negative associations. Further, the semiparametric method depends on a specific copula, the Frank model; thus it is less robust and possibly subject to model misspecification.

6. Discussion

This paper establishes nonparametric inference on bivariate survival data with interval sampling through Kendall’s tau and an extension of it. There is growing interest in assessing the relationship between bivariate failure times, but conditional Kendall’s tau can be a poor measure of dependence. Moreover, frailty models for bivariate survival data suggest that the conditional Kendall’s tau depends on the marginal distribution of each failure time, as well as the copula governing their dependence.

To quantify the dependence between bivariate failure times based on the observed data with interval sampling, we focus on an unconditional Kendall’s tau as a measure of association. Further, since the association parameters in copula models are closely related to Kendall’s tau, the copula association parameter can then be identified via tau. Potentially, the nonparametric estimate of tau may be used to develop a model selection procedure or a goodness-of-fit test of copulas, which could increase the practical utility of copula models. In addition, for bivariate failure times, we can derive estimators for the joint survival function and conditional survival function of the second failure time based on a standard copula formulation, where the copula association parameter is estimated by inverting the proposed estimator of tau. Generally, the proposed methods can be used to help understand the time course of life history processes with an initial event and first and second failure events where transitions between these events represent a progression, for which data are collected with the first event occurring within a time interval and the second event observed subject to right censoring.

Appendix

Proof of Theorem 1

First, we develop asymptotic results for ${\widehat{\tau }}_{\mathrm{u}}$. For convenience of discussion, let us write $\text{sgn}\{(X_i-X_j)({\tilde{Y}}_i-{\tilde{Y}}_j)\}=a_{ij}{b}_{ij}$, where a_ij = 2I(X_i − X_j > 0) − 1 and $b_{ij}=2I({\tilde{Y}}_i-{\tilde{Y}}_j>0)-1$, with $(X_i,{\tilde{Y}}_i)$ and $(X_j,{\tilde{Y}}_j)$ being two observed bivariate failure times. We have

$$\begin{gathered} n^{1∕2}({\widehat{\tau }}_{\mathrm{u}}-{\tau }_{XY})=n^{1∕2}\left\{{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}\sum _{i<j}\frac{{\lambda }_{ij}{a}_{ij}{b}_{ij}}{{\widehat{p}}_{ij}}-{\tau }_{XY}\right\} \\ =n^{1∕2}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}\sum _{i<j}\left(\frac{{\lambda }_{ij}{a}_{ij}{b}_{ij}}{p_{ij}}-{\tau }_{XY}\right)+n^{1∕2}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}\sum _{i<j}{\lambda }_{ij}{a}_{ij}{b}_{ij}\left(\frac{1}{{\widehat{p}}_{ij}}-\frac{1}{p_{ij}}\right). \end{gathered}$$ (A1)

For comparable and orderable pairs, $Y_{ij}^{\text{min}}$ is observed and ${\tilde{Y}}_{ij}^{\text{min}}=Y_{ij}^{\text{min}}$. The first term in (A1) is a U-statistic of order 2, and

$$\begin{gathered} E\left\{\sum _{i<j}\left(\frac{{\lambda }_{ij}{a}_{ij}{b}_{ij}}{p_{ij}}-{\tau }_{XY}\right)\right\}=\sum _{i<j}E\left(\frac{{\lambda }_{ij}{a}_{ij}{b}_{ij}}{p_{ij}}-{\tau }_{XY}\right) \\ =\sum _{i<j}\left[E\left\{E\left(\phantom{\mid }\frac{{\lambda }_{ij}{a}_{ij}{b}_{ij}}{p_{ij}}\mid X_i,X_j,Y_{ij}^{\text{min}}\right)\right\}-{\tau }_{XY}\right] \\ =\sum _{i<j}\left[E\left\{\frac{1}{p_{ij}}E\phantom{(}({\lambda }_{ij}{a}_{ij}{b}_{ij}\mid X_i,X_j,Y_{ij}^{\text{min}})\right\}-{\tau }_{XY}\right]. \end{gathered}$$

Similarly to the discussion in Lakhal-Chaieb et al. (2010), we can show that the concordance or discordance status is conditionally independent of the comparability and orderability event. Once X_i, X_j and $Y_{ij}^{\text{min}}$ are fixed, by the formula for the conditional probability p_ij of the comparability and orderability event, described in § 2, the comparability and orderability event depends only on the initial event time B and the censoring time C. The concordance or discordance status depends only on the original pairs, so these events are conditionally independent, and

$$\begin{gathered} E({\lambda }_{ij}{a}_{ij}{b}_{ij}\mid X_i,X_j,Y_{ij}^{\text{min}})=E({\lambda }_{ij}\mid X_i,X_j,Y_{ij}^{\text{min}})E(a_{ij}{b}_{ij}\mid X_i,X_j,Y_{ij}^{\text{min}}) \\ =p_{ij}E(a_{ij}{b}_{ij}\mid X_i,X_j,Y_{ij}^{\text{min}}). \end{gathered}$$

Then E{∑_i<j (λ_ija_ijb_ij/p_ij − τ_XY)} = 0, so the first term in (A1) is a zero-mean U-statistic of order 2. By the standard theory of U-statistics, the asymptotic variance of the first term in (A1) is equal to

$$\begin{gathered} \underset{n\to \infty }{\text{lim}}\frac{4}{n^3}\{\sum _{i<j<k}\left(\frac{{\lambda }_{ij}{a}_{ij}{b}_{ij}}{p_{ij}}-{\tau }_{XY}\right)\left(\frac{{\lambda }_{ik}{a}_{ik}{b}_{ik}}{p_{ik}}-{\tau }_{XY}\right)+\left(\frac{{\lambda }_{ij}{a}_{ij}{b}_{ij}}{p_{ij}}-{\tau }_{XY}\right)\left(\frac{{\lambda }_{jk}{a}_{jk}{b}_{jk}}{p_{jk}}-{\tau }_{XY}\right)\phantom{\}} \\ \phantom{\{}+\left(\frac{{\lambda }_{ik}{a}_{ik}{b}_{ik}}{p_{ik}}-{\tau }_{XY}\right)\left(\frac{{\lambda }_{jk}{a}_{jk}{b}_{jk}}{p_{jk}}-{\tau }_{XY}\right)\}. \end{gathered}$$

The variation in the second term of (A1) is due to the estimation of p_ij, the conditional probability that a pair is comparable and orderable. We have ${\widehat{p}}_{ij}^{-1}-p_{ij}^{-1}=\{(\Delta \widehat{G}{)}^2{\widehat{K}}_i{\widehat{K}}_j{\}}^{-1}-\{(\Delta G{)}^2{K}_i{K}_j{\}}^{-1}$, where $\Delta G=G(t_0-X_{ij}^{\max })-G(-X_{ij}^{\text{min}})$, $K_i=K(X_i+Y_{ij}^{\text{min}})$, $K_j=K(X_j+Y_{ij}^{\text{min}})$,$\Delta \widehat{G}=\widehat{G}(t_0-X_{ij}^{\max })-\widehat{G}(-X_{ij}^{\text{min}})$, ${\widehat{K}}_i=\widehat{K}(X_i+Y_{ij}^{\text{min}})$ and ${\widehat{K}}_j=\widehat{K}(X_j+Y_{ij}^{\text{min}})$. To be specific, $\widehat{G}$ is either the nonparametric maximum likelihood estimator ${\widehat{G}}_{\text{non}}(\cdot )$(·) (Shen, 2010) or the parametric estimator $\widehat{G}(\cdot ,\theta )$ from the conditional likelihood, and $\widehat{K}$ is the Kaplan–Meier estimator. Note that $\Delta \widehat{G}-\Delta G$ and $\widehat{K}$ – K can be approximated by a sum of independent and identically distributed zero-mean terms. Therefore,

$$\begin{gathered} G(b)-\widehat{G}(b)=\sum _{k=1}^n\frac{{\psi }_1(B_k,X_k,b)}{n}+o_{\mathrm{p}}(n^{-1∕2}), \\ K(s)-\widehat{K}(s)=\sum _{k=1}^n\frac{{\psi }_2(X_k,{\tilde{Y}}_k,{\delta }_k,s)}{n}+o_{\mathrm{p}}(n^{-1∕2}), \end{gathered}$$

where E{ψ₁ (B_k, X_k, b)} = 0 and E{ψ₂ (X_k, ${\tilde{Y}}_k$, δ_k, s)} = 0. Then we have

$$\begin{gathered} n^{1∕2}\left(\frac{1}{{\widehat{p}}_{ij}}-\frac{1}{p_{ij}}\right)=n^{1∕2}\left\{\frac{(\Delta G{)}^2{K}_i{K}_j-(\Delta \widehat{G}{)}^2{\widehat{K}}_i{\widehat{K}}_j}{(\Delta G{)}^2{K}_i{K}_j(\Delta \widehat{G}{)}^2{\widehat{K}}_i{\widehat{K}}_j}\right\} \\ =n^{1∕2}\left[\frac{\Delta G\{K_i(K_j-{\widehat{K}}_j)+{\widehat{K}}_j(K_i-{\widehat{K}}_i)\}+2{\widehat{K}}_i{\widehat{K}}_j(\Delta G-\Delta \widehat{G})}{\Delta G{K}_i{K}_j(\Delta \widehat{G}{)}^2{\widehat{K}}_i{\widehat{K}}_j}\right]+o_{\mathrm{p}}(1) \\ =n^{-1∕2}\left[\frac{\Delta G\{K_i{\sum }_{k=1}^n{\psi }_{2j}+{\widehat{K}}_j{\sum }_{k=1}^n{\psi }_{2i}\}+2{\widehat{K}}_i{\widehat{K}}_j{\sum }_{k=1}^n({\psi }_{1,\text{min}}-{\psi }_{1,\max })}{\Delta G{K}_i{K}_j(\Delta \widehat{G}{)}^2{\widehat{K}}_i{\widehat{K}}_j}\right] \\ +o_{\mathrm{p}}(1), \end{gathered}$$

where

$$\begin{gathered} {\psi }_{1,\text{min}}={\psi }_1(B_k,X_k,X_{ij}^{\text{min}}),{\psi }_{1,\max }={\psi }_1(B_k,X_k,X_{ij}^{\max }-t_0), \\ {\psi }_{2i}={\psi }_2(X_k,{\tilde{Y}}_k,{\delta }_k,X_i+Y_{ij}^{\text{min}}),{\psi }_{2j}={\psi }_2(X_k,{\tilde{Y}}_k,{\delta }_k,X_j+Y_{ij}^{\text{min}}). \end{gathered}$$

Therefore, the second term in (A1) can be expressed as

$$\begin{gathered} n^{-1∕2}\sum _{k=1}^n{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}\sum _{i<j}{\lambda }_{ij}{a}_{ij}{b}_{ij}\left\{\frac{{\psi }_{2j}}{K_j(\Delta \widehat{G}{)}^2{\widehat{K}}_i{\widehat{K}}_j}+\frac{{\psi }_{2i}}{K_i{K}_j(\Delta \widehat{G}{)}^2{\widehat{K}}_i}+\frac{2({\psi }_{1,\text{min}}-{\psi }_{1,\max })}{\Delta G{K}_i{K}_j(\Delta \widehat{G}{)}^2}\right\}+o_{\mathrm{p}}(1) \\ =n^{-1∕2}\sum _{k=1}^{n}E\left[{\lambda }_{12}{a}_{12}{b}_{12}\left\{\frac{{\psi }_{22}}{K_2(\Delta \widehat{G}{)}^2{\widehat{K}}_1{\widehat{K}}_2}+\frac{{\psi }_{21}}{K_1{K}_2(\Delta \widehat{G}{)}^2{\widehat{K}}_1}+\frac{2({\psi }_{1,\text{min}}^{12}-{\psi }_{1,\max }^{12})}{\Delta G{K}_1{K}_2(\Delta \widehat{G}{)}^2}\right\}\right]+o_{\mathrm{p}}(1) \end{gathered}$$

where ${\psi }_{1,\text{min}}^{12}={\psi }_1(B_k,X_k,X_{12}^{\text{min}})$ and ${\psi }_{1,\max }^{12}={\psi }_1(B_k,X_k,X_{12}^{\max }-t_0)$, and it is a sum of independent and identically distributed zero-mean terms. Thus $n^{1∕2}({\widehat{\tau }}_{\mathrm{u}}-{\tau }_{XY})$ is asymptotically equivalent to a zero-mean U-statistic of order 2.

Next, we derive the asymptotic properties of ${\widehat{\tau }}_{XY}$. We have

$$\begin{gathered} n^{1∕2}({\widehat{\tau }}_{XY}-{\tau }_{XY})=n^{1∕2}\left\{\frac{(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}{)}^{-1}{\sum }_{i<j}\frac{{\lambda }_{ij}{a}_{ij}{b}_{ij}}{{\widehat{p}}_{ij}}}{(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}{)}^{-1}{\sum }_{i<j}\frac{{\lambda }_{ij}}{{\widehat{p}}_{ij}}}-{\tau }_{XY}\right\} \\ =n^{1∕2}({\widehat{\tau }}_{\mathrm{u}}-{\tau }_{XY})-n^{1∕2}{\tau }_{XY}\left\{{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}\sum _{i<j}\frac{{\lambda }_{ij}}{{\widehat{p}}_{ij}}-1\right\}+o_{\mathrm{p}}(1) \\ =n^{1∕2}({\widehat{\tau }}_{\mathrm{u}}-{\tau }_{XY})-n^{1∕2}{\tau }_{XY}\left\{{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}\sum _{i<j}\frac{{\lambda }_{ij}}{p_{ij}}-1\right\} \\ -n^{1∕2}{\tau }_{XY}\left\{{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}\left(\sum _{i<j}\frac{{\lambda }_{ij}}{{\widehat{p}}_{ij}}-\sum _{i<j}\frac{{\lambda }_{ij}}{p_{ij}}\right)\right\}+o_{\mathrm{p}}(1). \end{gathered}$$ (A2)

The first term in (A2) has been shown to be asymptotically equivalent to a zero-mean U-statistic of order 2. The second term in (A2) is a sum of n independent and identically distributed zero-mean terms. Similar to the derivation of asymptotic results for the second term in (A1), the third term in (A2) is also asymptotically equivalent to a sum of independent and identically distributed zero-mean terms. These three terms together imply that $n^{1∕2}({\widehat{\tau }}_{XY}-{\tau }_{XY})$ converges weakly to a normal distribution with mean zero and variance ${\sigma }_{XY}^2$ as n → ∞.

Proof of Theorem 2

Under (i) the null hypothesis of quasi-independence, H₀ : B ⫫ _Q(X, Y), and (ii) the assumption of independence between the censoring time and bivariate failure times conditional on the time of the initial event and the observable region, i.e., C ⫫ (X, Y) ∣ (B, −B ⩽ X ⩽ −B + t₀), we show that ${\tau }_{\mathrm{c}}=({\tau }_{BX}^{\mathrm{c}},{\tau }_{BY}^{\mathrm{c}}{)}^{\mathrm{T}}=0$. First, we consider ${\tau }_{BX}^{\mathrm{c}}=E[\text{sgn}\{(B_1-B_2)(X_1-X_2)\}\mid {\Omega }_{12}]$. Notice that

$$\begin{gathered} {\tau }_{BX}^{\mathrm{c}}\propto E[\text{sgn}\{(B_1-B_2)(X_1-X_2)\}I({\Omega }_{12})] \\ =\text{pr}(X_2-t_0⩽-B_1<-B_2⩽X_1<X_2)-\text{pr}(X_1-t_0⩽-B_1<-B_2⩽X_2<X_1) \\ +\text{pr}(X_1-t_0⩽-B_2<-B_1⩽X_2<X_1)-\text{pr}(X_2-t_0⩽-B_2<-B_1⩽X_1<X_2). \end{gathered}$$ (A3)

Given (i) H₀ : B ⫫ _Q(X, Y), the joint density of (X, B) in the observable region −B ⩽ X ⩽ −B + t₀ can be expressed as f_X(x)g*(t) for −b ⩽ x ⩽ −b + t₀, where f_X is the population marginal density of X and g* is proportional to the density of B ∣ (−B ⩽ X ⩽ −B + t₀). Each probability in (A3) equals

$$\text{pr}(-B⩽X⩽-B+t_0{)}^2{\int }_{b=-\infty }^{\infty }{\int }_{s=b}^{\infty }{\int }_{u=s}^{s+t_0}{S}_X(u)f_X(u)g^{\ast }(s)g^{\ast }(b)\mathrm{d}u\mathrm{d}s\mathrm{d}b,$$

where S_X is the marginal survival function of X. Therefore ${\tau }_{BX}^{\mathrm{c}}=0$ under (i).

Next, we focus on ${\tau }_{BY}^{\mathrm{c}}=E[\text{sgn}\{(B_1-B_2)(Y_1-Y_2)\}\mid {\Lambda }_{12}]$. Suppose that (B₁, X₁, Y₁, C₁) and (B₂, X₂, Y₂, C₂) are observations from the distribution (B, X, Y, C) ∣ (−B ⩽ X ⩽ −B + t₀) where pr(−B < C) = 1. Let (X,, ${\tilde{Y}}_i$, δ_i, T_i) and (X_j, ${\tilde{Y}}_j$, δ_j, T_j), where $\tilde{Y}=\text{min}(Y,C-X)$ and δ = I(Y ⩽ C − X), denote two observations with interval sampling. We have

$$\begin{gathered} {\tau }_{BY}^{\mathrm{c}}\propto E[\text{sgn}(B_i-B_j)({\tilde{Y}}_i-{\tilde{Y}}_j)\}I({\Lambda }_{ij})] \\ =\text{pr}({\delta }_i=1,X_j-t_0⩽-B_i<-B_j⩽X_i<X_j,Y_i<{\tilde{Y}}_j) \\ +\text{pr}({\delta }_j=1,X_i-t_0⩽-B_i<-B_j⩽X_j<X_i,Y_i<{\tilde{Y}}_j) \\ -\text{pr}({\delta }_j=1,X_j-t_0⩽-B_i<-B_j⩽X_i<X_j,Y_j<{\tilde{Y}}_i) \\ -\text{pr}({\delta }_j=1,X_i-t_0⩽-B_i<-B_j⩽X_j<X_i,Y_j<{\tilde{Y}}_i) \\ +\text{pr}({\delta }_j=1,X_j-t_0⩽-B_j<-B_i⩽X_i<X_j,Y_j<{\tilde{Y}}_i) \\ +\text{pr}({\delta }_j=1,X_i-t_0⩽-B_j<-B_i⩽X_j<X_i,Y_j<{\tilde{Y}}_i) \\ -\text{pr}({\delta }_i=1,X_j-t_0⩽-B_j<-B_i⩽X_i<X_j,Y_i<{\tilde{Y}}_j) \\ -\text{pr}({\delta }_i=1,X_i-t_0⩽-B_j<-B_i⩽X_j<X_i,Y_i<{\tilde{Y}}_j). \end{gathered}$$ (A4)

Given (i) H₀ : B ⫫ _Q(X, Y), and (ii) C ⫫ (X, Y) ∣ (B, −B ⩽ X ⩽ −B + t₀), the joint density of (B, X, Y, C) in the observable region −B ⩽ X ⩽ −B + t₀ can be expressed as f_XY(x, y)q (b, c) for −b ⩽ x ⩽ −b + t₀, −b < c, where f_XY is the population joint density of (X, Y) and q is proportional to the joint density of (B, C) ∣ (−B ⩽ X ⩽ −B + t₀). Then, each probability in (A4) equals

$$\text{pr}(-B⩽X⩽-B+t_0{)}^2{\int }_{b=-\infty }^{\infty }{\int }_{s=b}^{\infty }{\int }_{u=s}^{s+t_0}{\int }_{v=0}^{\infty }{S}_{XY}(u,v)f_{XY}(u,v)Q(b,v)Q(s,v)\mathrm{d}v\mathrm{d}u\mathrm{d}s,\mathrm{d}b,$$

where S_XY is the joint survival function of (X, Y) and $Q(b,v)={\int }_{c=v}^{\infty }q(b,c)\mathrm{d}c$. Therefore, ${\tau }_{BY}^{\mathrm{c}}=0$ under (i) and (ii). In summary, we have proved that ${\tau }_{\mathrm{c}}=({\tau }_{BX}^{\mathrm{c}},{\tau }_{BY}^{\mathrm{c}}{)}^{\mathrm{T}}=0$ under quasi-independence and the assumption (ii).

Estimation of asymptotic variance and covariance in matrix η

The estimators of the asymptotic variance and covariance in matrix η derived in § 3 are of the form $\{n(n-1)(n-2){\}}^{-1}{\sum }_{i<j<k}{\beta }_{ij}{\gamma }_{ik}=\{n(n-1)(n-2){\}}^{-1}{\sum }_{i=1}^n({\beta }_{i.}{\gamma }_{i.}-{ϵ}_{i.})$, where ${\beta }_{i.}={\sum }_{j\ne i}{\beta }_{ij}$, ${\gamma }_{i.}={\sum }_{j\ne i}{\gamma }_{ij}$, ${ϵ}_{i.}={\sum }_{j\ne i}{\beta }_{ij}{\gamma }_{ij}$, and n is the sample size. For example, in § 3, the estimator of the covariance term η₁₂ is obtained by using βij = sgn{(X_i − X_j)(B_i − B_j)}I(Ω_ij) and γ_ij = sgn{(Y_i − Y_j)(B_i − B_j)}I(Λ_ij).