Exploring cardiac form and function: A length-scale computational biology approach

Abstract

The ability to adequately pump blood throughout the body is the result of tightly regulated feedback mechanisms that exist across many spatial scales in the heart. Diseases which impede the function at any one of the spatial scales can cause detrimental cardiac remodeling and eventual heart failure. An overarching goal of cardiac research is to use engineered heart tissue in vitro to study the physiology of diseased heart tissue, develop cell replacement therapies, and explore drug testing applications. A commonality within the field is to manipulate the flow of mechanical signals across the various spatial scales to direct self-organization and build functional tissue. Doing so requires an understanding of how chemical, electrical and mechanical cues can be used to alter the cellular microenvironment. We discuss how mathematical models have been used in conjunction with experimental techniques to explore various structure-function relations that exist across numerous spatial scales. We highlight how a systems biology approach can been employed to recapitulate in vivo characteristics in vitro at the tissue, cell, and sub-cellular scales. Specific focus is placed on the interplay between experimental and theoretical approaches. Various modeling methods are showcased to demonstrate the breadth and power afforded to the systems biology approach. An overview of modeling methodologies exemplifies how the strengths of different scientific disciplines can be used to supplement and/or inspire new avenues of experimental exploration.

INTRODUCTION

The primary function of the heart is to pump blood in a stable and efficient manner. Native heart tissue consists of aligned interlocking cardiac cells. These individual cardiomyocytes contain myofibrils composed of patterns of repeating sarcomeres, which themselves incorporate a variety of organized interacting proteins (Sheehy, Grosberg, & Parker, 2012; Alberts et al., 2002; Chien, Domian, & Parker, 2008) (Figure 1). Each of these individual components work in concert to induce a contraction (Golob, Moss, & Chesler, 2014; Pong et al., 2011), from the laminar sheets that make up the heart’s four chambers (Rohmer, Sitek, & Gullberg, 2007) to the individual proteins within the actin-mysoin motors (Cooper, 2000). Recapitulating the cooperative nature of this multi-scale coordination is a cornerstone of cardiac tissue engineering (Zhang, Xiao, Hsieh, Thavandiran, & Radisic, 2011; Thavandiran, Nunes, Xiao, & Radisic, 2013). To build tissue that is functional and adaptable requires an understanding of how chemical and biomechanical signals are translated across hierarchical scales as well as the relation between form and function within an individual scale. Through development of in vitro models that mimic the appearance and pathology of native healthy tissue, researchers can explore the factors that influence the various structural patterns present in vivo such as myofibril alignment and sarcomeric registration (Pong et al., 2011; Dasbiswas, Majkut, Discher, & Safran, 2015). However, while these studies suggest correlations between structural parameters and cell morphology, they do not address how physical cues drive self-organization. An ideal method to study the causal relation between proposed parameters is to use computational modeling. In this way, researchers can target specific variables and explore their roles, providing insight into how the identified components cooperate to guide self-assembly. Numerous computational models have been proposed and they can be broadly classified based on the spatial scale of interest.

Figure 1:

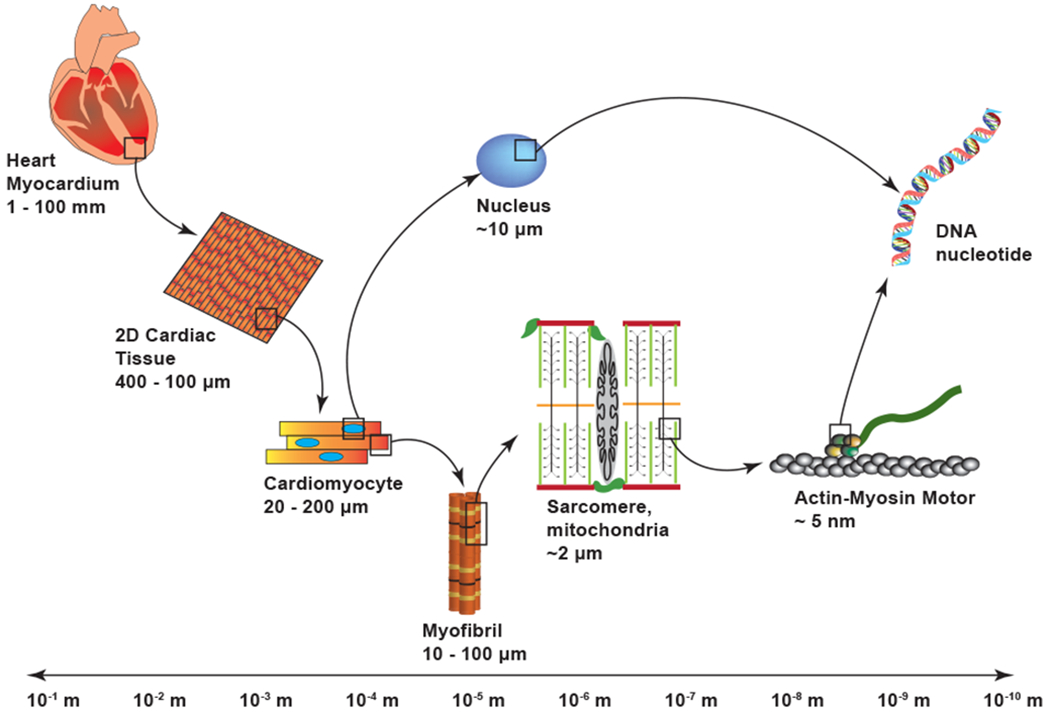
Length scale separation within the heart. Spatial scales can be broken down into a hierarchical structure that spans several orders of magnitude. The various functional components can be studied either independently or in relation to one another.

Models at the organ and tissue scale typically focus on funcationality and explore the influence of cell-cell interactions on tissue-level characteristics such as orientation, beating rate, and contractile strength (Cohen & Safran, 2018; Drew, Johnsen, Core, & Grosberg, 2016; Hayashi, Tokihiro, Kurihara, & Yasuda, 2017; Böl, Reese, Parker, & Kuhl, 2009). In single cells, the ability to self-organize depends on extracellular matrix (ECM) interactions. As such, models at this scale are often concerned with the mechanical cues that influence these interactions (Drew & Grosberg, 2015; Nicolas, Besser, & Safran, 2008; Schwarz & Bischofs, 2006). At the sub-cellular scale, however, the proper computational approach depends on the structure of interest (Edelstein-Keshet, 1998; Versaevel, Grevesse, & Gabriele, 2012; Friedrich, Fischer-Friedrich, Gov, & Safran, 2012). This results in a wide variety of modeling techniques and considerations. To adequately contribute to the held using a modeling approach requires one to not only identify areas which may benefit from computational modeling but also utilize methodologies that are appropriate for the area of interest. Considering the breadth of approaches that have been employed, new researchers with a desire to utilize computational modeling may find the task daunting. We will provide the first step to tackling this problem by identifying common model types that are used at certain spatial scales and summarizing their strengths and weaknesses.

This review will explore the cardiac structure hierarchy through the lens of systems biology, which can be described as an amalgamation of principles from fields such as biology, engineering, and computer science. Beginning at the organ (centimeter to millimeter) scale and continuing to the sub-cellular (nanometer) scale, we will provide an overview of common modeling techniques found in the literature and some of the notable results that those techniques have provided. We then give an overview of the advantages and drawbacks associated with combining models from several scales into a singular multi-scale model. Emphasis will be placed on the interplay between the experimental observations and the modeling approaches since the feedback between experimental techniques and theoretical testing is core to the systems biology approach.

Since the heart is a highly complex, multi-scaled organ, we have chosen to focus our attention towards specific areas of cardiovascular research related to mechanical function. As such, there are numerous areas of active research that will not be covered in this review and are left to the references. These include ionic channel kinetics and their association with contractile function (Yarov-Yarovoy, Allen, & Clancy, 2014; Silva, 2018), models focusing on cardiac electrophysiology (Mayourian, Sobie, & Costa, 2018), and application of fluid mechanics to blood flow and circulation (Safaei et al., 2016), to name a few.

MODELING APPROACHES AT THE ORGAN AND TISSUE SCALE

Heart failure, due to some form of cardiovascular disease, is frequently cited as a leading cause of death worldwide (Bui, Horwich, & Fonarow, 2010; Vunjak-Novakovic et al., 2009; Perreault, Bing, Brooks, Ransil, & Morgan, 1990; Ritchie & Roser, 2019) and once sever damage has occurred, a heart transplant may be the only form of repair. Due to a limited supply of donor hearts (Stehlik et al., 2011; Manas & Brett, 2014), efforts have been made to develop protocols for exploring regenerative and preventative medicines. This has led many to study how alterations to cardiac properties, processing, and structure affect the heart’s performance, summarized by the materials science tetrahedron (Figure 2). Specifically, focus is often placed on two separate yet interconnected properties: construct development and functionality. While it is useful to address the interplay between these two fundamental characteristics, organ and tissue scale models tend to emphasize the impact on functionality. An overarching goal of organ level modeling is to create a mathematical representation of the heart with tunable parameters that are patient-specific. The hope is that these whole-heart computational models will allow physicians to explore ventricular remodeling, electrophysiology and blood flow in a non-invasive manner so that customizable therapies can be developed. To adequately cover the progress that has been made at this level, we feel an entire review is warranted. As such, we refer the reader to the work being done by McCulloch and colleagues (Cranford et al., 2018; Villongco, Krummen, Omens, & McCulloch, 2016), Trayanova and associates (Yu et al., 2019; Trayanova & Winslow, 2011), as well as Peskin and McQueen (Kaiser, McQueen, & Peskin, 2019), among many others, for advancements at this scale.

Figure 2:

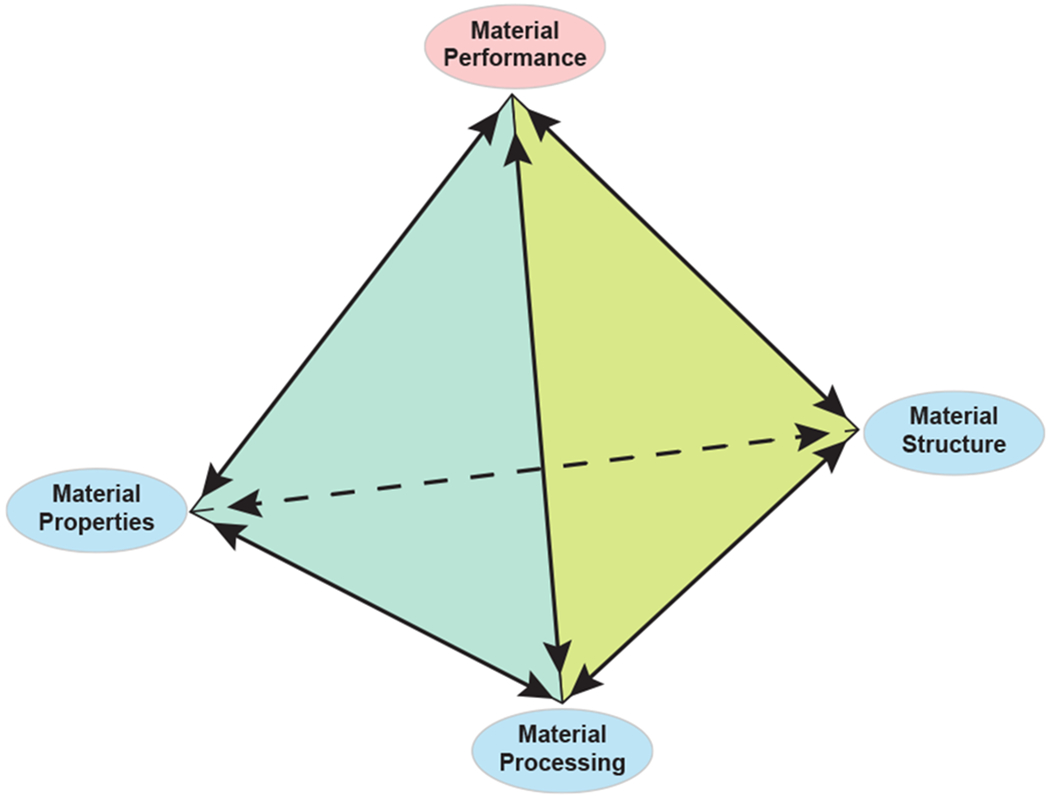
The materials science tetrahedron. There are four interconnected categories that can be used to study the behavior of a material: structure, processing, properties, and performance. Changes in any one category will invariable influence the other three categories. This same categorization may be used to study the heart. (Adapted from (Golob et al., 2014))

Engineering a functional tissue in vitro entails guiding cell assembly through targeted changes in the cellular environment. These changes can be achieved, for example, by using microfabrication to control substrate architecture. Many studies have employed this technique to demonstrate how topographical changes can induce cellular pattern formation (Singhvi, Stephanopoulos, & Wang, 1994; Deutsch, Motlagh, Russell, & Desai, 2000; Kim et al., 2010). To further our understanding of the materials science tetrahedron, computational models have been employed to synthesize existing measurements at the micrometer scale and provide mechanistic explanations for the topology-induced organization that has been observed experimentally. The desire to guide tissue assembly through manipulation of control variables such as substrate topology has provided a platform for efficient model parameter exploration and, more importantly, model validation.

A key feature of cardiovascular disease is cellular remodeling resulting in impaired contractile strength (Shimkunas et al., 2013). Two-dimensional studies are often employed to study contractility of tissue engineered structures since they are less computationally complex than three-dimensional studies yet yield insight into the experimental conditions that can recapitulate properties seen in native cardiac tissue. Biohybrid muscular thin films (MTFs) provide a route for studying contractile function of cultured cardiomyocytes while also bridging the gap between two- and three-dimensional systems (Feinberg et al., 2007; Alford, Feinberg, Sheehy, & Parker, 2010). They incorporate various mechanical properties observed in a healthy myocardium as tunable parameters. To properly identify the impact of the various design parameters, free energy equations and finite-element modeling has been employed to study the deformation behavior in constrained cardiac muscular thin films (Böl et al., 2009). This simulation tool allowed for the identification of material parameters that could be used to optimize fiber orientation in multi-layered patches for future implantation. This approach was later extended as a 3D phenomenological model that was more simplistic than previously proposed models yet captured both the active and passive behavior of unconstrained cardiac cells (Shim, Grosberg, Nawroth, Parker, & Bertoldi, 2012). These techniques allowed the researchers to decouple MTF properties and study the nature of their interactions. By isolating specific parameters, they were able to predict how MTFs respond when mechanical properties are perturbed. From a systems biology point of view, these studies have helped researchers develop innovations to the heart-on-a-chip platform. This platform has been utilized to assess contractile stresses in diseased tissue as well study the toxicity of nanomaterials (Agarwal, Goss, Cho, McCain, & Parker, 2013; Ahn et al., 2018; Feinberg et al., 2007; Grosberg, Alford, McCain, & Parker, 2011).

In native heart tissue, individual cells synchronize their beating rates so that the tissue contracts in a rhythmic fashion. Synchronization occurs, in part, due to mechanical interactions between neighboring cells through intracellular gap junctions (van der Velden & Jongsma, 2002). While isolated cardiomyocytes beat independently and spontaneously, synchronicity in beating rates may be observed when as few as two cells are grouped together (Kojima, Kaneko, & Yasuda, 2005; Kaneko, Kojima, & Yasuda, 2007). However, while it is known that the mechanosensitivity of cells plays a role in modulating beating rates, the mechanism that leads to a group of cells beating with regularity is not entirely understood. Focusing on the electrophysiological processes associated with contractions, beating frequency in a population of cells can be modeled using a small number of ordinary differential equations. Such models typically rely on equations describing electrical currents and action potentials such as Hodgkin-Huxley and Van der Pol equations. One approach explored the temporal behavior of synchronization by implementing a Markov chain process in conjunction with a deterministic Hodgkin-Huxley type model that had been previously proposed (Wilders, Jongsma, & van Ginneken, 1991; Hamada, Nomura, Kaneko, Yasuda, & Okamoto, 2013). This demonstrated that the time needed for synchronization depends on cell-cell conductance. In particular, when cell junctions are formed, a community effect is engaged whereby individual beating fluctuations decrease in favor of group stability. To explore the mechanism of synchronization stability in a network of pulsatile cells, a system of one-dimensional, interacting nonlinear oscillators was utilized (Hayashi et al., 2017). It was shown that pairs of cardiomyocytes tend to beat synchronously with the cell that has a stable beating rhythm rather than the cell with the faster beating rate. This is an important consideration when dealing with a heterogeneous population of cardiomyocytes, as may be the case when performing pharmacological studies. Analyzing the properties of a complex system by manipulating the known properties of a smaller, simpler system is a common systems biology approach. This is emphasized by these synchronicity studies whereby researchers hope to take advantage of the community effect to control of a collection of cardiomyocytes with varying phenotypes, which may be indispensable to the development of therapeutic drugs (Asahi et al., 2018; Zadorozhnyi et al., 2019).

MODELING APPROACHES AT THE CELLULAR SCALE

Morphological changes resulting from heart disease have been shown to influence the geometry and resulting functionality of the individual cells that make up the cardiac tissue. Patients with ischemic cardiomyopathy, for example, have individual myocytes with significantly longer lengths compared to myocytes in healthy tissue (Gerdes et al., 1992). Alterations in cellular geometry have been shown to influence the organization of internal structures such as the actin filaments and sarcomeres as well as impact cell contractility (Ribeiro et al., 2015; Kuo et al., 2012; Vishavkarma et al., 2014). The ability of individual cells to self-assemble under different boundary conditions has been explored by using microcontact printing to create individual cardiomyocytes of particular sizes and shapes. Some common shapes considered include square, rectangular, and circular geometries of varying sizes (Ribeiro et al., 2015; Oakes, Banerjee, Marchetti, & Gardel, 2014). In addition to boundary cues, cell morphology may be influenced by the physical properties of the substrate. Specifically, modification to substrate elastic moduli have been found to affect cell contraction rates, contractile strength, and myofibril organization (Ribeiro et al., 2015; Hersch et al., 2013). These changes may be linked to the cells inability to adequately convert mechanical cues to chemical signals near the cell-substrate interface (Bershadsky, Balaban, & Geiger, 2003). Such a process is regulated by an assortment of proteins collectively known as focal adhesions, suggesting the stability of these protein complexes are a key component in the contractile apparatus (Coyer et al., 2012). While experimental data has demonstrated that self-organization in cardiomyocytes can be induced through proper manipulation of boundary cues and substrate composition, computational models have provided insight into the exact nature of these interactions. Self-assembly can be enhanced or hindered by tunable parameters that may vary depending on cell type or morphology. Computational models are ideally suited for identifying these regulatory parameters and determining regimes which alter cytoskeletal dynamics in a way that optimizes self-assembly and contractility.

In a continuum model, several phenomena related to the cytoskeleton were coupled together (Deshpande, McMeeking, & Evans, 2006). This biochemical approach demonstrated the influence of cell shape on fiber orientation while simultaneously showing contractile forces decreasing when substrate rigidity was increased. A key outcome of the model is its ability to provide guidance for future experiments that aim to explore the cytoskeletal response to mechanical perturbations. As a simplification, this model did not consider focal adhesions, the anchoring sites for myofibrils which transmit mechanical cues between the cytoskeleton and the substrate. However, their dynamics were the central component to a phenomenological model that was developed to explore why focal adhesion proteins can be seen accumulating in the corners of stationary square cells (Novak, Slepchenko, Mogilner, & Loew, 2004). Using deterministic integrin protein density equations linked to force generating stress fibers, the evolution of focal adhesion development was tracked. Allowing feedback between integrin clustering and force production was enough to produce the focal adhesion patterns observed experimentally. The model was validated using square fibroblasts and gave a mechanistic explanation for focal adhesion clustering in the corners of cells. Specifically, it predicted that integrin concentrations in the corners of the cell are increased because these high curvature regions allow stress fiber forces to be amplified. An extension of this model to cardiomyocytes of various cell shapes was later employed (Grosberg, Kuo, et al., 2011). This deterministic model differed from previous approaches by incorporating myofibril maturation through pseudo-labeled integrin densities. The model demonstrated that myofibril length and parallel coupling work cooperatively to produce accurate focal adhesion localization and cell polarization for both homogeneous and heterogeneous boundary conditions. This work exemplifies the systems biology approach where the interplay between experiments and model construction is utilized to fit parameters, validate the model, make testable predictions, and generate new hypotheses for further studies.

The approaches described above either do not consider the elasticity of the substrate or treat it as a fixed parameter. However, since cells actively respond to variations in substrate composition (Ribeiro et al., 2015), several computational models have been used to propose mechanisms that drive cell contractility in response to altered substrate rigidity. An early model was proposed to address how focal adhesion signaling events were linked to substrate elasticity (Schwarz & Bischofs, 2006). In this formulation, focal adhesions were treated as mechanosensors, represented as two harmonic springs in series, and it was assumed that signaling events were triggered once a sufficient amount of force had been built up in the focal adhesions. Doing so, researchers were able to demonstrate how the mechanical properties of the environment could regulate focal adhesion growth by varying the stiffness of the substrate. The two-spring model was later extended to allow for cell migration and proliferation in response to matrix elasticity changes (Moreo, García-Aznar, & Doblaré, 2008). In particular, the extended model predicts that cell migration is linked to the deformability of the substrate, where cells are more likely to migrate to regions that produce higher cellular stresses. These results have been built on and generalized by incorporated rate-dependent effects while simultaneously considering extracellular rigidity (Borau, Kamm, & García-Aznar, 2014). The one-dimensional phenomenological model used a three-spring configuration to predict the mechanosensing behavior of single cells. Specifically, the model allowed for time-dependent cellular response so that researchers could observe how the cell responds to step changes in substrate rigidity during migration. These studies have provided insight into how cell-material interactions regulate cellular response and growth. Specifically, these results can be used to develop scaffolds that may enhance tissue formation (Aznar, Valero, Borau, & Garijo, 2016). This demonstrates how interactions at one spatial scale can be used to influence dynamics at a larger scale, a core principle in understanding multi-scale problems via the systems biology approach.

MODELING APPROACHES AT THE SUB-CELLULAR SCALE

A defining characteristic of the heart is that it undergoes consistent rhythmic contractions at the cellular (and tissue) scale. Cardiac muscle cells contain acto-myosin bundles consisting of myosin filaments crosslinked by α-actinin. These recurring clusters of proteins, referred to as z-bodies or z-bands, appear in regularly spaced intervals and mark the endpoints of the sarcomeres, the fundamental contractile units of myofibrils (Dabiri, Turnacioglu, Sanger, & Sanger, 1997). Optimal contractile function occurs when sarcomere length is approximately 2 μm, but this can be disrupted by morphological changes like cell elongation due to cardiac hypertophy (Mansour, de Tombe, Samarel, & Russell, 2004; Russell, Motlagh, & Ashley, 2000). When myofibrils are elongated, the initial increase in sarcomere length is followed by the addition of filaments and creation of new sarcomeres (Russell et al., 2000). Despite returning the sarcomere length to its resting value, the elongated boundary leads to an increase in myofibril length and a decrease in cell contractility (Kuo et al., 2012). While numerous scaffolding proteins have been identified as potential instigators/regulators of the striation patterns (Chopra et al., 2018; Fraley, Pereira, Tran, Singleton, & Greenwood, 2005; Wang et al., 2005), the mechanisms controlling self-assembly at this scale, including sarcomere addition and filament insertion, still remain elusive. Complicating matters is the challenge of visualizing pattern formation in early development. Despite these limitations, models of various forms have been proposed to address the formation of striations in myofibrils and the dynamics of actin filaments in the cytoskeleton.

The sequence of events that lead to the assembly of mature myofibrils has been outlined (Dabiri et al., 1997). Briefly, sporadic clusters of α-actinin are observed on premyofibrils near the cell periphery. As maturation occurs, clusters on neighboring myofibrils align and striations are formed. Utilizing this observed sequence, a mechanical model was developed to explain the appearance of sarcomeric order in an initially unstriated bundle (Friedrich et al., 2012). Investigators demonstrated the formation and coalescence of actin clusters via crosslinking and treadmilling of actin filaments. Assuming a collection of parallel actin and myosin filaments crosslink via physical interactions, spontaneous pattern formation occurred within their simulated bundle. Their approach suggested that cytoskeletal order may be obtained even without external scaffolding. While this approach demonstrated pattern formation within a single filament bundle, it did not consider how neighboring bundles might behave. Using a phase-order parameter, the degree of pattern alignment (registry) across neighboring myofibrils was modeled and quantified (Dasbiswas et al., 2015). The researchers were also interested in the influence of this alignment on the cell’s contractile function since changes in sarcomeric registry have been correlated with changes in substrate rigidity (Majkut et al., 2013). A key result was the ability to link z-band registration data with contractile strain measurements in beating cells. This suggested that the beating of cardiac cells may be related to the registration of the cell’s myofibrils. The study concluded that contractility could be optimized by appropriately altering the elasticity of the substrate. In this way, the beating of the cell, and hence the registration of z-bands in the cell, could be affected. Consequently, an optimal substrate stiffness may drive self-organization and registration within the cell. In the systems biology framework, these models primarily focus on making testable predictions. Dasbiswas and colleagues, for instance, based their model on experimental observations (Majkut et al., 2013) and their conclusion was validated by the experimental findings of other researchers (Ribeiro et al., 2015).

The cytoskeleton consists of a network of crosslinked actin filaments and provides shape and stability to cells. The mechanical properties of the cytoskeleton, and actin filaments in particular, have been well documented (Lieleg, Claessens, & Bausch, 2010; Lu, Oswald, Ngu, & Yin, 2008). However, some properties may be difficult to discover without hypotheses generated by computational models. For instance, a system of differential equations was constructed to investigate the role of actin polymerization in the distribution of filament lengths (Edelstein-Keshet, 1998). Using kinetic equations, the model provided insight into why the relative levels of actin and gelsolin monomers may lead to actin fiber length distributions that tend to be either exponential or reach a stable size distribution. Furthermore, the conditions under which interacting filaments would align, cluster or form filament bundles was explored. It was demonstrated that longer filaments were more likely to align into bundle-like structures while shorter filaments formed unaligned clusters, consistent with previous observations of actin networks crosslinked with α-actinin. The identification of several network behavior regimes provided a means through which actin polymerization could be manipulated to generate various types of crosslinked networks. This influenced future experiments related to fibrillization. The results for actin filament nucleation were lated used, for instance, to explore molecular mechanisms associated with neurodegenerative diseases (Necula & Kuret, 2004). This closes the experiment-model-experiment loop that is common in the systems biology methodology.

MULTI-SCALE INTEGRATIVE MODELING

An ongoing challenge in computational physiology is linking mathematical models across several spatial scales. While many of the models discussed in previous sections consider other physical scales implicitly, there is much to be gained by considering them explicitly. For instance, cardiac arrhythmias may occur due to a problem associated with the heart’s electrophysiology. The complication is linked to the mishandling of electrical interactions by the individual cells that make up the contractile tissue. These electrical imbalances may be related to genetic mutations that cause alterations in ionic channels on the cell membrane (Chen et al., 1998). In the systems biology sense, multi-scale modeling can be utilized to develop medical therapies on a patient-specific basis to target genetic abnormalities or mutations.

Since the interconnectivity of the heart can be studied in numerous ways, there is little restriction in how one might decide to couple scales together computationally. For instance, while it is difficult to obtain data of electrical and mechanical activity simultaneously at high resolution, it is possible to obtain insights into this link via multi-scale computational models. One such model considered the human ventricle as an organ-sized geometry with fiber-sheet architecture and employed an electromechanical approach that coupled membrane kinetics with a continuum mechanics model of the ventricles (Hu, Gurev, Constantino, Bayer, & Trayanova, 2013). This approach allowed the researchers to study the influence of stretch-activated channel recruitment on fibrillation via alterations in channel conductance.

A notable mutliscale model was developed to understand the functional cues that guide tissue formation (Yan, Nair, & Sun, 2010). They combined a single cell model with a tissue level model and used finite element techniques to quantify cell deformations when subjected to mechanical load. This approach exemplifies a central component to multi-scale modeling techniques. Namely, the utilization and combination of models at individual scales that capture known phenomena while not exacerbating an already high computational cost. Several groups in the cardiac modeling community have attempted to address this obstacle by developing advanced multi-scale simulators that combine, for instance, heart mechanics and electrophysiology (Watanabe, Sugiura, Kafuku, & Hisada, 2004; Usyk & McCulloch, 2003; Nickerson, Smith, & Hunter, 2005). Additionally, other fields have provided computational insights that have led to improved numerical schemes and reduced the computational expense that may be accrued when employing such methodologies (Dada & Mendes, 2011).

OPEN QUESTIONS

We have demonstrated that there are many different types of models that can be used to address questions that would be difficult to explore through experimentation alone. While there has been much progress afforded to experimentalists, many open questions remain from the genetics scale to the organ. Despite the abundance of information obtained from scaled models, synthesizing the data across the many layers of the heart has proven difficult. At the genetic level, an as-yet unresolved issue concerns how the failure of ionic channel inactivation can influence cellular polarization and lead to arrhythmogenesis (Clancy & Rudy, 1999; Noble & Noble, 1999). There is much interest in exploring how various ionic channels might have their function impeded as the result of genetic mutations (Clancy & Rudy, 1999). How are proteins transcriptionally regulated and how do various genetic abnormalities influence protein structure? We know that there’s an interdependence between various ionic channels (Ottolia, Torres, Bridge, Philipson, & Goldhaber, 2013) but how do these abnormalities influence mechanical and electrophysical properties at the organ level? Can we target protein functions at the subcellular scale to influence electrical activity at the organ scale? These question are a key driving force behind the development of drug therapies and computational modeling will be integral to guiding researchers towards effective intervention techniques.

In regards to the single cell level, it has been shown experimentally that native cardiomyocytes tend to exhibit a 7:1 aspect ratio (Gerdes et al., 1992; Gerdes, 2002) and we have discussed different modeling approaches that explore why this aspect ratio may be ideal. Yet, how the optimal aspect ratio is obtained in native cardiac tissue remains elusive. We also provided models that give insight into the events that influences myofibril alignment but it is still unclear how the various components work in concert to create the detailed architecture that is found in native cardiac cells. Currently, there is no consensus on whether the alignment within individual cells results from a top-down cascade, a bottom-up cascade, or even a middle-out cascade, all of which may be possible. This mystery is compounded when we compare myofibril alignment in immature and mature cardiomyocytes. Specifically, we do not yet know why immature and mature cardiomyocytes, subject to the same substrate and cell shape conditions, may produce substantially different organization in the central region of the cell (Sheehy et al., 2012). This exemplifies the current gap in our understanding of stem cell differentiation and maturation in vivo.

The bidirectional influence of larger and smaller spatial scales has also not been resolved at the tissue level. Of particular interest at this scale is cellular and fiber orientation within cardiac tissue and how it may influence contractility. This has led to studies which consider not only the orientation of individual structures (Sun, Tang, & Ding, 2009; Umeno & Ueno, 2003) but also how multiple structures might be correlated with one another (Drew, Eagleson, Jr., Parker, & Grosberg, 2015). These studies have yielded several questions yet to be resolved: What are the dynamics of various correlated structures and how do they influence each other? If multiple constructs are not oriented correctly, how does that affect function? How can the observed correlations be used to enhance protocols for engineering tissue? Some of the models outlined previously were set up so that they can be extended in the future to address these questions.

While there are many open questions at the organ level, particular attention has been paid to analyzing the left ventricular wall. The left ventricle is a highly-organized structure with a smooth transition in fiber angle distribution, which has been used to identify different layers within the ventricular wall (D. D. Streeter, Spotnitz, Patel, Ross, & Sonnenblick, 1969; Greenbaum, Ho, Gibson, Becker, & Anderson, 1981). This complication in myocardial fiber organization has limited our understanding of how the heart employs strain, torsion, and twisting to function efficiently. For instance, we have not been able to properly explore layer-specific strain due in part to data acquisition constraints. This has also restricted our understanding of strain distribution patterns within the various layers and how it might influence global strain measurements. How these layers modulate their coordination and are able to distribute shear stress during contractions is still being explored both computationally and experimentally.

In addition to the modeling techniques discussed, several models use an optimization approach when describing the dynamics at the spatial scale of interest (Washio et al., 2016; Savadjiev et al., 2012). This is often motivated by the observation that the heart structure appears to be organized in a mechanically optimal way (D. Streeter, 1979). Accordingly, it is not uncommon to find theoretical optimization approaches in computational models of the cardiac system. This invites its own sets of computational questions such as the types of optimization constraints that are appropriate for implementation as well as which energetic considerations accurately describe the energy transfer involved. The answers to these types of questions vary depending on the implementation procedure and problem of interest.

CONCLUSIONS

In order to understand the biological complexity of the heart, we must explore how the heart is structured and the physical processes that occur within each spatial scale. To accomplish this, structure-function relations are studied using in vitro models with the intent of recapitulating in vivo characteristics. Since the stiffness of the substrate has been shown to influence cellular development and contractility, a common approach to guiding assembly across the various hierarchical length scales is to adjust the properties of the ECM. This suggests that cardiac tissue structure and function can be altered by manipulating specific biochemical and mechanical processes. However, controlling these mechanical cues requires an understanding of the mechanism at play and how perturbations of that mechanism can cascade bidirectionally in the spatial length scale.

A variety of computational models have been implemented to address this mechanism connectivity problem. In order for computational models to be effective, they must not only mimic experimental observations but also provide insight into the mechanism of interest. It is essential that they both mimic and predict experimental outcomes. This is especially important as a means of hypothesis generation since models allow for exploration of biological parameters and trends that may be time consuming or difficult to discover through experiments alone. While a powerful tool, due to the complexity of most biological systems, modeling requires assumptions and simplifications which can impact its effectiveness at generating testable hypotheses. Hence, an understanding of the system being modeled and what can meaningfully be reproduced and tested experimentally is critical.

The systems biology approach combines the strengths from both modeling and experimentation to provide a more complete view of the phenomena of interest. This is often exemplified by an experiment-model-experiment loop in which an observation drives the construction of a computational model which then generates a hypothesis that can be experimentally tested. This creates a positive feedback loop in which theoretical considerations and practical applications work in tandem to heighten our understanding of the mechanisms driving a biological system. This approach is especially useful when applied to the cardiac system since the heart is a complex multi-layered organ that coordinates its actions across multiple spatial and temporal scales. To tackle the problem requires a multi-pronged approach in which computational modeling provides insight into how mechanisms coordinate their efforts across length scales and experiments utilize those mechanistic links to develop functional tissue. This review can serve as a foundation for new researchers interested in using computational modeling to study the heart’s emergent properties. We have highlighted some common modeling approaches within individual spatial scales and identified how each approach fits within the multi-scale dynamics of the heart. In this way, new computational models may be built, and experiments proposed, to provide mechanistic explanations of how interactions within one of the hearts sub-systems affect the heart in its entirety.