Abstract
It is well established that the chemistry in microdroplets has been found to be radically different from reactions in bulk, particularly in the case of water. It has also been established that there is a threshold size for microdroplets to behave differently than droplets near the 10 µm diameter range. We present a three-dimensional electrostatic treatment in the spirit of the Gouy–Chapman model for double layers at interfaces. Our treatment predicts a strong concentration of charged molecules toward the surface of the droplet. As the droplet size deceases, the majority of the volume of the liquid experiences a large DC electric field. Such electric fields are highly unusual in a conducting fluid such as water. We believe that this unique environment helps to explain the reaction rate acceleration and new chemistry that have been observed in microdroplets compared to bulk phase.
INTRODUCTION
Chemistry often relies on the assumption that the size and shape of a reaction’s container have little effect on the reaction itself. Recently, studies of reactions taking place in volumes on the micrometer scale have been shown to be an exception to this rule. Cooks’ group, our group, and others have shown increases in reaction rate as large as 106 for reactions taking place in microdroplets relative to the bulk solution. A good review of this topic already exists.1 It is readily apparent that a strong understanding of the underlying principles of this phenomenon could lead to a breakthrough in catalysis design. Unfortunately, the mechanism of rate acceleration in small volumes is not yet fully established. This paper models the concentration gradients inside microdroplets and the resulting electric field so that their effects can be considered when discussing mechanisms of reaction rate acceleration.
A notable feature of microdroplets is their high surface-to-volume ratio. For a 5 µm diameter droplet, about half (48.8%) of the droplet’s volume is found within 500 nm of the surface. This study focuses on microdroplets of water. In this case, another distinctive feature is the existence of charges pinned to the surface when the water droplet is in some hydrophobic medium, such as air or oil2 (see Fig. 1). The exact value of the surface charge density and the source of the charges are both matters of debate. Recent work suggests that these surface charges arise from trace impurities in the water, which may explain the variation in the reported experimental results. These trace impurities often act as an anionic surfactant.3 It is the authors’ opinion that bicarbonate anion resulting from a brief exposure of “pure” water to atmosphere is a major player in this phenomenon. In order to sidestep this controversy, the mathematical model used in this paper is agnostic toward the source of the charged surfactant, its sign, and its identity. A spherical shell charge distribution gives rise to no electric field inside the shell. Therefore, the main parameter of the calculation is the average charge density of the liquid—excluding the surface monolayer. Furthermore, the model can be easily adapted to solvents other than water merely by changing the dielectric constant.
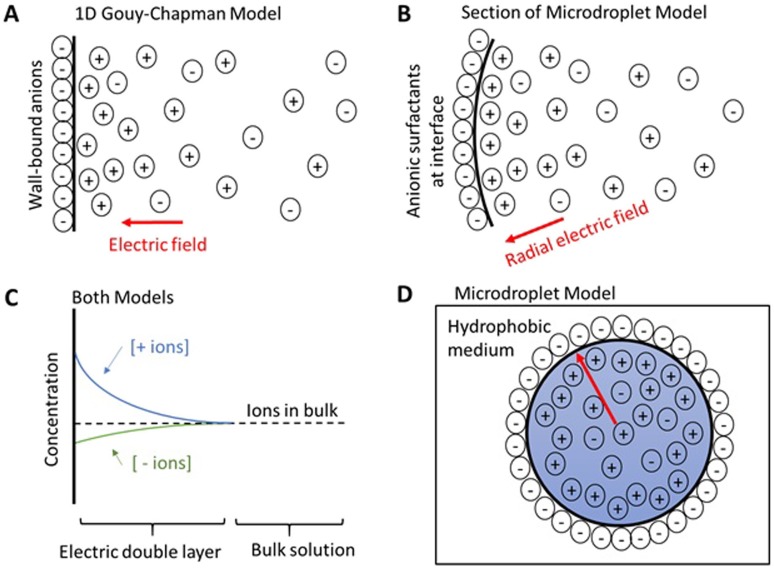
FIG. 1.
(a) Sketch of the electric double layer from an infinite plane of wall-bound anions. (b) Section of the microdroplet showing an electric double layer from a surface monolayer of anionic surfactants. (c) Concentrations of ions in solution from a negatively charged surface, which applies to both models. (d) Cross section of the microdroplet ion distribution (not to scale). The red arrow represents a radial electric field terminating at the wall of anionic surfactants.
It is quite difficult to describe different layers of a surface as the terminology varies between disciplines. We are using conventions from microfluidics. In order to draw parallels between microdroplets and microfluidics, we briefly digress in giving a short description of the one-dimensional Gouy–Chapman model. A more detailed description can be found in the work of Probstein.4
The Gouy–Chapman model describes the surface between a liquid and its container. The wall of the container typical has charged functional groups, a classic example being deprotonated silanol groups on glass when placed in water. There is a surface charge density of charged functional groups chemically bound or adsorbed to the wall of the container. The nearby liquid responds to the charged wall by setting up an electric double layer [Figs. 1(a) and 1(c)]. The electric double layer contains water with a net charge density. All electric field lines from the charged wall terminate within the electric double layer so that the bulk of the water has zero electric field, as would be expected inside a conductor. The charges in the electric double layer balance the charges on the wall, so the system is net neutral. The thickness of the electric double layer varies with ionic strength, but it can range from a few nanometers up to a micrometer. The Gouy–Chapman model is used to determine the concentration gradient of the ions within the electric double layer as well as the electric field strength. In Fig. 1, for simplicity, we have assumed a negative surface charge density so that the electric double layer of the droplet is positively charged. The opposite assumption can be made with no loss of generality to the model, but the sign of the electric field changes while maintaining its magnitude.
As previously discussed, there are charged surfactant molecules of unknown origin at the periphery of the microdroplet. These charged surfactant molecules are diffusing in only two dimensions at the surface monolayer between water and a hydrophobic medium. We consider the surface charge density of these surfactant molecules analogous to the wall’s surface charge density in the one-dimensional Gouy–Chapman model [Figs. 1(b)–1(d)]. It is assumed that the charged surfactant molecules are evenly distributed around the microdroplet’s periphery by two-dimensional diffusion under the action of Coulomb’s law.
Next, we model the electric double layer of the microdroplet arising from the “wall” of charged surfactant molecules. For the droplet to be net neutral in charge, the electric double layer of the microdroplet must contain excess charge that balances the charge on the “wall.” We refer to the ions that make up the excess charge in the electric double layer as “unpaired ions,” as they do not have an ion pair within the electric double layer. The average concentration of “unpaired ions” in the electric double layer is a major parameter of the model.
Recall that a spherical shell charge distribution gives rise to no electric field inside the shell. The “wall” surface charge density does not matter to the calculation other than that it sets the average unpaired ion concentration for the microdroplet. Thus, for charged droplets—commonly created by electrospraying—the important parameter is merely the average unpaired ion concentration. Two microdroplets that differ only in net charge but have the same average unpaired ion concentration have the same ion distribution in their electric double layers. They are mathematically equivalent in this model.
There is one important difference between the two cases. For electrosprayed droplets, the Rayleigh limit5 constrains the amount of unpaired ions in the droplet. In the neutral microdroplet case, both the charged surfactant molecules and the amount of unpaired ions need to be included when evaluating the Rayleigh limit. Thus, in the neutral molecule case, it is possible for the concentration of “unpaired ions” to exceed the Rayleigh limit seen for charged microdroplets. From a physical standpoint, the electric field pulling in on the charged surfactant molecules helps counteract the repulsion of the “unpaired ions” in the interior of the droplet.
For both electrosprayed and neutral droplets, repulsion of unpaired ions in the volume of the microdroplet generates an electric double layer at the surface of the microdroplet. Electric double layers are well known for water solutions and are commonly treated by the Gouy–Chapman model, which has an analytical solution only in one dimension. The one-dimensional solution requires two assumptions: (1) the dimension of the system is much larger than the double layer, and (2) the bulk solution is unperturbed by the existence of the double layer. Both of these assumptions are invalid for micrometer-sized droplets. Assumption 1 is false because the curvature of the microdroplet is at a similar scale to the thickness of the electric double layer. The “wall” of the microdroplet cannot be approximated well by an infinite flat plane. Assumption 2 is false because there is not a point for the solution that is far enough away from the wall to be unaffected by the concentration changes occurring in the electric double layer. The farthest distance from the “wall” of the microdroplet is the center of the droplet. For the one-dimensional Gouy–Chapman model, the bulk solution is an infinite reservoir of ions that remains unchanged by the increases and decreases in ion concentration taking place in the electric double layer. In a microdroplet, the bulk is not an infinite reservoir of ions. Changes in the concentration of ions in the electric double layer alter the remaining concentration of ions at the center of the microdroplet.
We present here a computational solution for micrometer-sized droplets in the spirit of the Gouy–Chapman model. We start with the same equations as those of the Gouy–Chapman model, but we employ a different mathematical route with different boundary conditions prior to analytically integrating the resulting system of differential equations. One might wonder why little work has been done in this area. It may be the lack of interest in microdroplets until recently and the fact that the equations have no known analytical solution in spherical coordinates.
The solutions we find have the following notable features: (1) as expected, the droplet has a very strong electric field; (2) as the size of the droplet decreases, the electric field penetrates surprisingly deeply into the droplet; and (3) the electric field drives charged molecules to the surface. We suggest that both the concentration enhancement and the electric field itself can accelerate chemical reactions.
It is worth noting that strong DC electric fields in bulk water are a highly unusual phenomenon. Water is a conductor with hydroxide (OH−) and hydronium (H+) ions as its charge carriers. Like all conductors, when experiencing an electric field, water rearranges its charge carriers at the surface to cancel all the electric field within the bulk of the liquid. There are two main exceptions. First, a small DC electric field exists in the bulk during electrochemical reactions, which drives the ion current through the liquid. Second, high frequency AC electric fields, which vary faster than the ions can rearrange, permit large electric fields in the bulk.6,7 Large DC electric fields in water are commonly found only in the electric double layer at the surface and not in the bulk of the liquid. While electric double layers are common, they typically compose a negligible amount of the liquid’s total volume. Thus, aqueous microdroplets, where the majority of the volume can be in the double layer, are a rather unique reaction system.
RESULTS AND DISCUSSION
A brief summary of the calculations made in this paper is as follows: Similar to the Gouy–Chapman treatment, a continuum model is assumed for the concentration of species throughout the droplet and, at steady state, the flux from electrophoresis and diffusion balance. This balance of driving forces allows us to write the electric field as a differential function of ion concentration. Substitution of the electric field into Gauss’s law creates a second-order differential equation in ion concentration, which can be numerically solved in spherical coordinates. This strategy is later further expanded to include multiple ionic species, the full details of which are discussed in the section titled Calculations.
Case 1: Singly charged species in a droplet
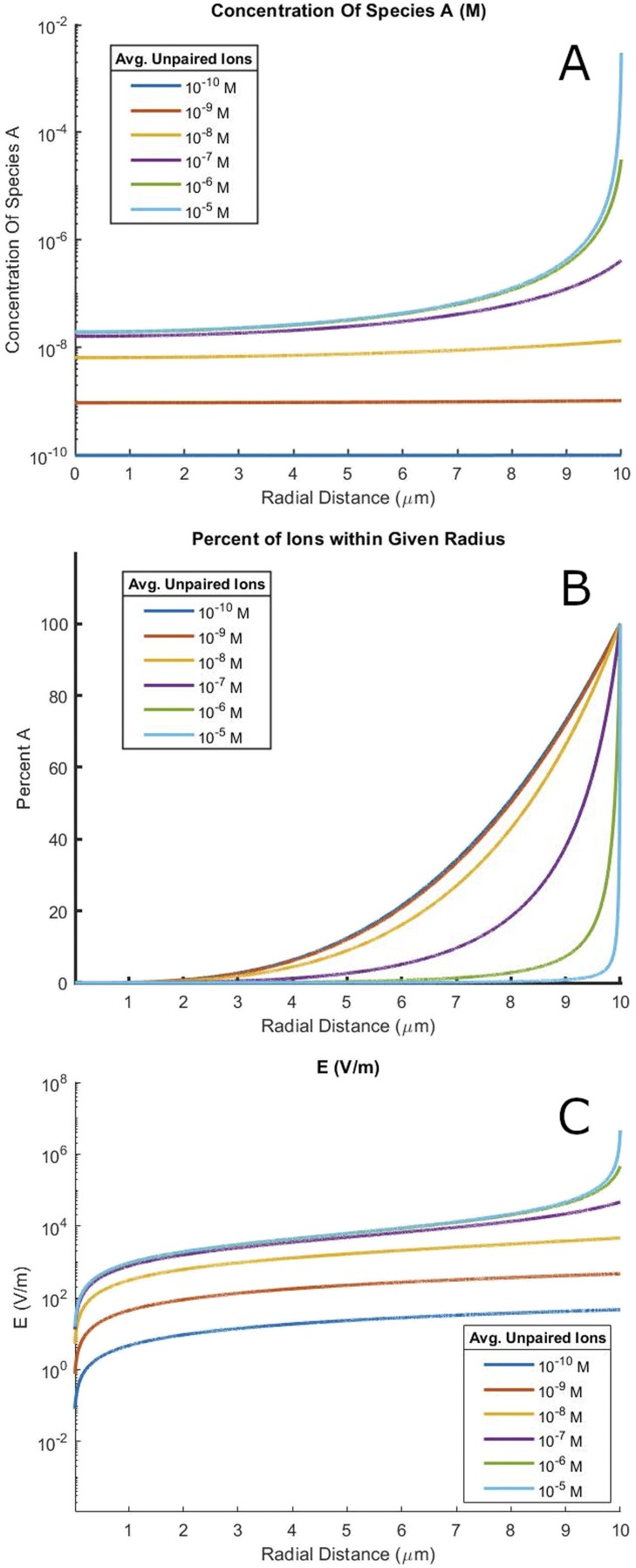
A major contributor to reaction rate acceleration is increased reactant concentrations in microdroplets. In situations with very few charged ions, the ions distribute evenly throughout the droplet. As more ions are added, the electric field grows. The electric field eventually overwhelms entropy, resulting in ions being packed almost entirely close to the surface, and the ion concentration at the center is depleted. The concentration at the edges of the droplet is greatly increased from the concentration of the premicrodroplet bulk solution. This behavior can be clearly seen in Fig. 2(a). Although a much smaller system, a similar ion concentration behavior has been seen in atomistic simulations with nanodroplets containing 3 × 104 water molecules.8
FIG. 2.
(a) The radial dependence of ion concentration for a 20 µm diameter water droplet at 25 °C. The distribution of ions changes markedly with different average concentrations of unpaired ions. (b) Data from (a) graphed in terms of the percentage of ions within a given radius. (c) The radial dependence of electric field strength for a 20 µm diameter water droplet at 25 °C for a variety of different average unpaired ion concentrations.
The source of the unpaired ion is ions in a microdroplet where the counterion is pinned either to the monolayer surface or to a system where the ion does not have a counterion as the droplet is carrying intrinsic charge. This second case is often invoked for advective current when electrospraying into a mass spectrometer. Both cases are mathematically analogous via this treatment, and the results shown below are true of both systems. All calculations were performed assuming a singly charged positive ion (zA = +1) at 25 °C with ε of water at 25 °C in a 20 µm diameter droplet. Equivalent figures for droplets of other sizes are included in the supplementary material (Figs. S2–S4).
There is also work done by Malevanets and Consta using an expansion of Jacobi polynomials to solve for the radial pH in a charged microdroplet.9 For micrometer-sized charged droplets, they find large changes in pH, corresponding to a change of several orders of magnitude in the H+ concentration along the radius of the microdroplet. If we take our positive ion to be H+ in Fig. 2(a), we similarly find a change of several orders of magnitude in the H+ concentration along the radius of the microdroplet. Furthermore, the shape of the radial pH gradient is quite similar. We find good agreement between our work and that of Malevanets and Consta.
Consider a reaction with second-order reaction kinetics in A, with rate constant k and concentration 1 µM. In bulk solution, it would have a reaction rate of k * 10−12 M/s. Using the concentrations calculated for a 20 µm diameter microdroplet with 1 µM average concentration of charged species A, the average reaction rate in the microdroplet would be k * 1.09 * 10−11 M/s—a 10-fold increase. For a 10 µM system, we obtain a reaction rate of k * 10−10 M/s in bulk and k * 1.02 * 10−8 M/s in microdroplets; these values correspond to an ∼100-fold increase in the microdroplet compared to the bulk,
| (1) |
This calculation does not fully explain the reaction rate acceleration seen in some reactions. We have neglected the effect of the electric field. The electric field strength is shown in Fig. 2(c). The effect of electric field on reaction rate is discussed later in this paper.
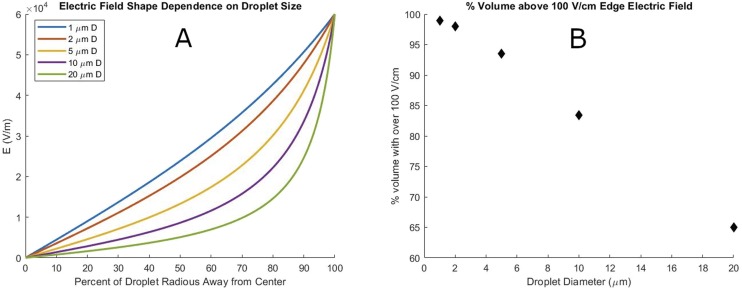
The electric field in a droplet covers a larger volume of the droplet as the size decreases, as is shown in Fig. 3(a). To better quantify this effect, Fig. 3(b) shows the percentage of the droplet’s volume with a field greater than one-sixth of the edge electric field for a droplet with a 600 V/cm edge electric field at 25 °C.
FIG. 3.
(a) Size dependence of the electric field shape in a water microdroplet with 600 V/cm edge electric field at 25 °C. (b) Percentage of microdroplet volume with greater than one-sixth (100 V/cm) of edge electric field strength (600 V/cm) as a function of droplet size.
The change in electric field shape denotes an important regime change for microdroplets vs larger bodies of water. The electric field of the double layer stretches across most of the volume of the droplet and interacts with the double layer on the other side of the droplet, giving rise to a much wider double layer than provided by the traditional one-dimensional Gouy–Chapman model. It also causes molecules in microdroplets to experience a standing electric field throughout most of the volume of the droplet. This situation is not the case in larger reaction containers as typically the electric double layer makes up a negligible percentage of the total volume. We propose that this radial electric field contributes strongly to give microdroplets their unique reaction environment.
Case 2: Uni-univalent electrolyte in a droplet
A uni-univalent electrolyte has two ionic species in the droplet, of +1 and −1 charge, respectively. As can be seen in the section titled Calculations, the final equations have no dependence on the specific ion other than sign and charge. We lump equivalent ions into a single concentration, provided all ions obey the Nernst–Einstein relation.4 The distribution of a given species is then its mole fraction times the combined equivalent ion distribution. For simplicity, all combinations of equivalent ions are referred to as if they are a single species in this paper.
It is helpful to think of the problem in two separate pieces. First, there are paired ions in the solution, which can be thought of as the concentration of salt in the solution. Second, there are unpaired ions, which we define as the excess of whichever species is more abundant. The “unpaired ions” have counterions pinned on the surface of the droplet, or the droplet is carrying advective current.
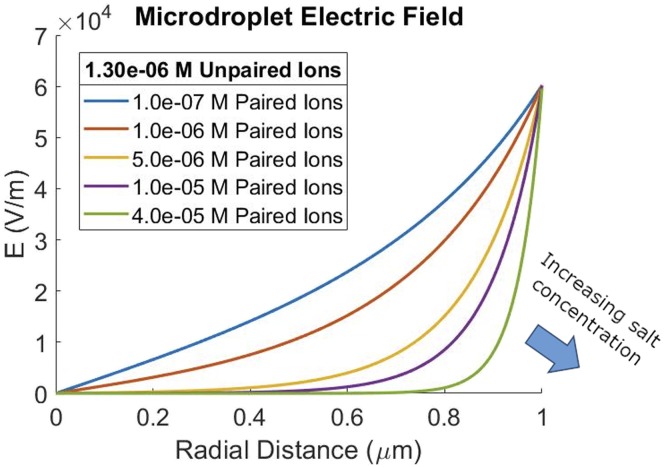
Assuming that a hydroxide anion goes to the surface of the droplet, as was discussed earlier in the paper, and that we have some uni-univalent electrolyte, such as sodium chloride, we get the results shown in Fig. 4.
FIG. 4.
Shape change of the electric field in a 2 µm diameter microdroplet with an increase in salt concentration. Unpaired ion concentration is held constant at 1.3 × 106 M to give a 600 V/cm edge field strength.
The 2 µm diameter droplet shows two regimes at different ionic strengths—a less pronounced similar effect is seen in larger droplets (Figs. S5 and S6). At low ionic strengths, the electric field of the double layer stretches across most of the volume of the droplet. At high ionic strengths, the electric double layer stays close to the surface with a relatively low or no electric field in the bulk.
Similar to the Gouy–Chapman one-dimensional case, where increasing ionic strength shortens the Debye length of the double layer, increasing the ionic strength in the droplet thins the double layer. Because interactions between double layers on opposite sides of the droplet define the two regimes, increasing paired ion concentration takes the first regime slowly toward the second regime.
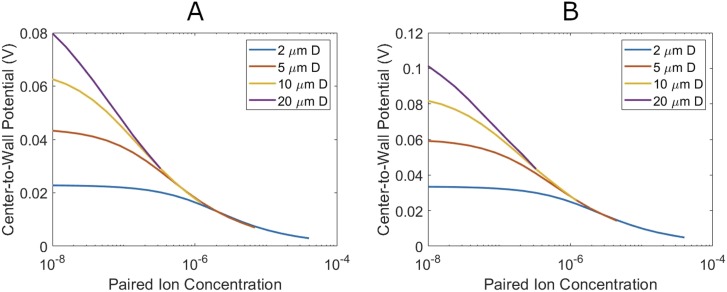
The potential drop from the center to the edge of the droplet provides a good visualization of this effect (Fig. 5). Droplets in the second regime have the potential drop take place almost entirely across the thin double layer at the surface. In the limit that the radius is much greater that the double-layer thickness, this reduces to the one-dimensional wall potential in the Gouy–Chapman model. Thus, droplets in the second regime have the same center-to-wall potential, regardless of droplet size.
FIG. 5.
Center-to-wall potential as a function of different paired ion concentrations for differently sized microdroplets. Edge electric field is maintained at 600 V/cm (plot A) and 1000 V/Cm (plot B).
Droplets in the first regime show a pronounced size dependence. The electric field is stretched out to fill the droplet. As potential is the integral of the electric field, this increases the center-to-wall potential above that of the second regime droplets. The amount of this increase is capped by the radius, as smaller droplets have a smaller distance to integrate the electric field over. Figure 5 shows this effect at two different edge potentials.
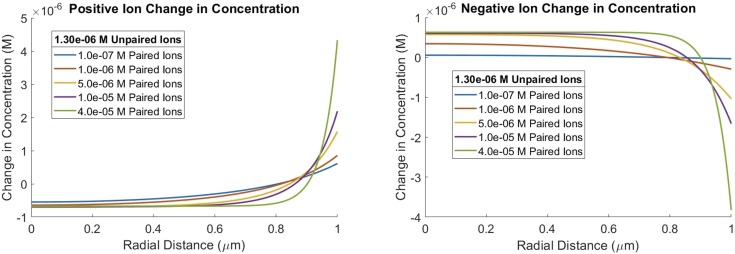
There are two different ion concentrations, one for positive species and the other for negative species. Based on the electric fields in Fig. 4, Fig. 6 shows the expected result that the positive ions are increased in the double layer being drawn in by the electric field, and negative ions are depleted in the double layer having been repelled. Of note, Fig. 6 shows that the change is concentration away from the average concentration. This behavior reverses in cases where the unpaired ion is negatively charged. Whichever ion is in excess is concentrated in the double layer toward the periphery of the droplet, while the other ion is driven toward the center. Once again, atomistic simulations with nanodroplets containing 3 × 104 water molecules exhibit a similar ion behavior with the excess ion concentrated at the edge and the other ion depleted at the edge and forced to the center.8 Not all the negative ions are concentrated toward the center. Note that the formal counterion to the “unpaired ions” is the anionic surfactant at the interface between water and hydrophobic medium as previously discussed. The extent of these effects again depends on the ionic strength of the liquid.
FIG. 6.
Change in ion concentration from average ion concentration in a 2 µm D microdroplet with an increase in ionic strength. Unpaired ion concentration is held constant at 1.3 × 106 M to maintain a 600 V/cm edge field strength.
Just as in the single ion case, the increases in ion concentration result in reaction rate acceleration for bimolecular reactions in the droplet.
Interestingly, the concentration effect on the reaction rate is slower for regime 1 than regime 2 in droplets of the same size. This fact suggests a methodology for experimentally separating the electrical field effects on the reaction rate from the ion concentrating effects on the reaction rate by varying the ionic strength.
Concentration of neutral species
Neutral species are also affected by electric fields through interactions of their dipoles (and induced dipoles) with the gradient of the electric field. The possibility of this leading to unevenly distributed neutral molecules in the droplet was considered.
The distribution of the neutral species is important as a common reaction is one between a neutral species and a charged species that is first order in both reactants. If the neutral species is distributed evenly throughout the droplet, then no average reaction rate acceleration will be seen from the changes in charged species concentration as it is only first order in that reactant.
The concentration gradient depends greatly on the considered molecule. We look at acetonitrile using its gas-phase dipole and polarizability.10 Acetonitrile was chosen because of its large dipole moment and water solubility.
Using the single charged ion electric field found earlier and sweeping from 10 −10M up to 10−4M of unpaired ions, no large changes were seen in the distribution of the neutral species. At the rather absurd 10−4M of unpaired ions, there is a slight 14% increase in the neutral species concentration localized at the edge of the droplet. The graph can be found in the supplementary material (Fig. S1).
Essentially, the divergence of the electric fields in the droplets is insufficiently large to overcome entropy. Thus, we see no significant change in the concentration of the neutral species, even at quite large concentrations of unpaired ions. It seems safe to approximate neutral species as being in one of two regimes. They are either evenly distributed in the droplet or pinned to the surface by hydrophobic forces. Importantly, neutral species have no strong concentration gradient in the volume of the droplet.
Mechanisms of rate acceleration
The reaction rate equation consists of two parts: a rate constant term and a term containing the concentrations of the reactants. Both are affected by the double layer in microdroplets as follows:
| (2) |
The double layer in the droplet acts to accelerate the reaction rate via two different mechanisms. In the first mechanism, the double layer contains gradients of reactant concentrations such that the reactant concentration term can be increased far beyond the reaction rates calculated using the average concentrations of reactants. In the second mechanism, the electric field of the double layer can alter the rate constant of the reaction. We discuss each mechanism separately.
Concentration gradient mechanism
A common bimolecular reaction is that of a neutral species with charged species with first-order kinetics for both reagents. Now that we understand the concentration gradients in microdroplets, we can consider concentration gradient effects on such a reaction.
First, we consider the case of both reagents being distributed in the double layer of the microdroplet. Let us briefly approximate the neutral species as evenly distributed in the double layer, which is reasonable, given the minimal concentration gradient from the double layer on neutral species, as shown above. In this case, the reaction is not accelerated by the concentration gradient mechanism. All gains in the reaction rate from higher concertation areas are exactly offset by slower reaction rates at places depleted of reactants. This is only strictly true when the neutral species is homogeneously distributed. Thus, in this case, the observed increase in reaction rate must be attributed to factors other than concentration gradients.
Next, we consider the case where the neutral species acts as a surfactant and is pinned to the outer surface monolayer and reacts with an ion in the double layer. The ion concentration gradient is largest right where the double layer touches the outer surface monolayer, which is also where the neutral species is located. This case should show large increases in reaction rates from the concentration gradient mechanism. Given that many neutral organic reactants have poor water solubility for at least some portion of the molecule, we hypothesize that this case is quite common for reactions that are accelerated in microdroplets.
For completeness, we briefly discuss the other two cases. When the neutral species is in the double layer and reacts with the ion pinned to the surface monolayer, there is little increase in reaction rate from the concertation gradient mechanism as the neutral species has very little increase at the wall above the average concentration. This is not to say that reaction will not be accelerated, as the reaction rate constant can be very different for reaction with one reactant pinned to a surface. The last case, where both reactants are pinned to the surface monolayer, has no species in the double layer, and thus, the concentration gradient mechanism does not apply.
We have looked at a simple reaction between the neutral and charged species, but similar statements can be made about other reaction systems.
Electric field effect on reaction rate constants
The second mechanism is that the electric double layer in the microdroplet alters the reaction rate constant in the presence of the strong electric field that the double layer generates. This field in the double layer orients molecules based on their dipoles, including the orientation of the solvent cages around the reactants as well as the orientation of the reactants themselves. Orienting the reactants changes the pre-exponential factor in the Arrhenius equation. Orientation of the solvent cage alters the solvent stabilization of the transition states and the reactants, which changes the activation energy of the reaction and thus its rate.
Furthermore, strong electric fields alter the electronic states of the reactant molecules. Recent experimental results in molecular beams have shown that strong AC electric fields from nonresonant light can alter reaction pathways giving different product ratios.11–13 The electric double layer has a DC electric field as opposed to an AC field that has been studied experimentally; however, the underlying mechanism of a Stark shift of the molecule’s energy levels is well known to occur with both AC and DC fields.
There is mounting evidence that the environment in microdroplets is highly unique. Work in our group has shown that reaction thermodynamics are different in microdroplets.14 A recent paper by Pestana and co-workers on the acceleration of Diels–Alder reaction in microdroplets stated, “Our results also suggest that significant acceleration of Diels−Alder reactions in microdroplets or on-water conditions cannot arise from local microsolvation when water is present but instead must come from highly altered reaction environments that drastically change the reaction mechanisms.”15 We hypothesize that the electric field from the double layer may provide the necessary highly altered reaction environment, although a more detailed study would be needed to show this conclusively.
Model limitations
A continuum model assumes that the ion concentration is infinitely divisible. Continuum models break down when applied to very small concentrations or on very short length scales as they require sufficient ions to average over. For example, a 1 µm diameter droplet has a volume of 0.524 pl. A 1 pM solution of ions, in a 1 µm diameter droplet, averages roughly 0.31 ions per droplet. Obviously, this model does not apply well to such a droplet. Care should be taken that the number of ions in the microdroplet remains reasonable. Note that droplet volume decreases with the cube of the radius. Thus, nanoscale clusters of water are particularly prone to this issue when treated with this model.
The model also breaks down for values taken very close to the edge of the droplet. At distances from the edge of the droplet smaller than the distance between ions pinned to the surface, local atomistic fluctuations in the electric field dominate over the field predicted by the continuum model. These fluctuations are rapidly averaged out at larger distances, but they do present an issue for values taken near the microdroplet surface.
For large concentrations of charged ions, a different issue arises. At high surface potentials, the one-dimensional Gouy–Chapman model has to be corrected by the inclusion of a Stern layer.4 The Stern layer consists of a layer of partially or fully dehydrated ions sitting against the charged surface held there by the electric field. The ions in the Stern layer are not freely diffusing, thereby causing the Gouy–Chapman model to break down. Taking a new wall potential as the wall potential minus the Stern layer allows the Gouy–Chapman model to be applied to the remaining ions in the system.
Similarly, in microdroplets, at large unpaired ion concentrations, we suspect that a Stern layer can form at the microdroplet surface. In such an event, our model can still be used with the correction that the surface monolayer needs to be expanded to include both the surface monolayer and the Stern layer.
CONCLUSIONS
We have shown that the solution inside microdroplets is not homogeneous. We propose that microdroplets may be described well by a three-dimensional model consisting of a surface monolayer of charged surfactant molecules and then an electric double layer at the periphery of the microdroplet. Our results show that the electric double layer penetrates deeply into the droplet much farther than would be predicted by the one-dimensional Gouy–Chapman model. As the microdroplet size decreases, the double layers on opposite sides of the microdroplet interact, which causes the electric field to penetrate deeply into the volume of the microdroplet much more deeply than would be predicted by the traditional one-dimensional Gouy–Chapman model. For small microdroplets, the double layer causes a large concentration gradient of ions and a large DC electric field throughout the volume of the microdroplet. The effects of the electric field and concentration gradients must be taken into account in understanding reaction rate acceleration in microdroplets as compared to bulk solutions.
CALCULATIONS
A similar continuum solution for microdroplets has been provided by Malevanets and Consta using an expansion of Jacobi polynomials to solve for the potential in the microdroplet.9 In this work, we instead express the system of equations in terms of the ion concentrations. The electric field can then be extracted from the ion distribution using Eq. (7). We start by writing the electric field as a differential function of ion concentration. Substitution of the electric field into Gauss’s law creates a second-order differential equation in ion concentration, which can be numerically solved in spherical coordinates.
Ion distributions with no reactive species
At equilibrium, the concentration of species A (cA) throughout a droplet does not change in time. From this fact, we conclude that the ion flux is equal to zero at equilibrium. Implicit in this is the assumption that there are no loops of ion current at equilibrium. This is a fair assumption as the drag on the ions from such a loop would require an exterior force to maintain the ion motion,
| (3) |
We also restrict the system to a droplet where the water in the droplet is still with respect to the droplet’s frame of reference; furthermore, there are no external applied forces such as external electric or magnetic fields. Ion flux is attributed to only two factors: flux from the electric field generated by the ions and diffusion. These factors must balance to prevent any net flux. Hence, we obtain the result
| (4) |
where
and
We solve the following equation for the electric field:
| (5) |
We then use the Nernst–Einstein relation to relate ion diffusivity to ion mobility,
| (6) |
Upon substitution, we find
| (7) |
The ion mobility cancels out of the equation, so this result is general to any combination of charged ions of same charge provided that they obey the Nernst–Einstein relation. In cases where ions do not follow the Nernst–Einstein relation, the same equation holds, but with a different coefficient.
Next, we consider the differential form of Gauss’s law
| (8) |
where
and
ε = dielectric constant.
Next, we replace E using Eq. (7) to obtain
| (9) |
Up to this point, the equations are general with regard to the shape of the system. We now assume a spherical droplet in which cA depends only on the radial distance (r). Converting to spherical coordinates and assuming that ε is a scalar whose value is independent of the electric field strength, we find that
| (10) |
Any charge density ρ will typically include Faraday’s constant (F) times a concentration. For simplicity, we now define a new constant K with the unit of meters per mole, which also incorporates Faraday’s constant,
| (11) |
for non-Nernst–Einstein cases
| (12) |
This treatment gives the following equation:
| (13) |
This is a second-order differential equation and thus has two boundary conditions. The concentration of species A and its derivative must be continuous in the droplet. This gives the first boundary condition
| (14) |
The moles of ion A in the droplet gives the second boundary condition. Presumably this constant is known experimentally as it can be calculated from the concentration of A in the liquid before it is formed into a droplet and the resulting volume of the droplet,
| (15) |
Case 1: Singly charged species in a droplet
We consider a droplet with only one charged species in the bulk. Presumably the counterion of this charged species is fixed to the surface of the droplet or the droplet is charged. The charge density is directly related to the concentration with
| (16) |
Using this charge density in Eq. (13) gives the following:
| (17) |
The boundary conditions were previously discussed and are as follows:
| (18) |
| (19) |
Equations (17)–(19) were evaluated using MATLAB’s® ODE45 differential equation solver. Full details of the integration are in the supplementary material. Calculations were performed assuming a singly charged positive ion (zA = +1) at 25 °C with a value of ε of water at 25 °C. The results of the calculated distribution of species A in the droplet are shown in Figs. 2 and 3. Other sizes of droplets are shown in the supplementary material.
Case 2: Uni-univalent electrolyte in a droplet
Next, we consider a uni-univalent electrolyte, wherein there are two ionic species in the droplet, of +1 and −1 charge, respectively. Note that as z = ±1, for simplicity, z has been replaced in the following equation with the appropriate sign. Charge density is related to the difference in concentration of the two species at any point as shown in the following equation:
| (20) |
where c+ and c− are the concentrations of the positive and negative ions, respectively. Substituting ρ into Eq. (13) for each ion results in the following pair of differential equations:
| (21) |
| (22) |
This set of two second-order differential equations has four boundary conditions as follows:
| (23) |
| (24) |
| (25) |
| (26) |
Note that the number of negative and positive ions in the system is different by the net charge on the droplet and the number of ions pinned to the surface monolayer. Again, Eqs. (21)–(26) were evaluated using MATLAB’s ODE45 differential equation solver. Full details of the integration are in the supplementary material. Calculations were performed assuming 25 °C with the value of ε of water at 25 °C. The results of the calculated distribution species A in the droplet are shown in Figs. 4, 5, and 6. Other sizes of droplets are shown in the supplementary material.
Neutral molecules
A neutral molecule’s dipole interacts with the gradient of the electric field to concentrate the molecule in solution. In the case of neutral nonpolar molecules, the electric field will induce a dipole from the molecule’s polarizability.
The force on a molecule depends on its dipole and the electric field gradient as well as any induced dipole from the polarizability,
| (27) |
Furthermore, we assume that the dipole is aligned with the field such that it points in the r direction,
| (28) |
Force times general mobility of a molecule in a liquid gives the terminal velocity,
| (29) |
Combining this result with the concentration at a given r gives the molecular flux arising from the dipole, which we set equal to the flux from diffusion,
| (30) |
The Nernst–Einstein relation written in terms of general mobility is
| (31) |
Substitution gives
| (32) |
which can be rearranged to yield
| (33) |
Integrating gives
| (34) |
Solve for CN,
| (35) |
We solve for C using the boundary condition,
| (36) |
SUPPLEMENTAL MATERIAL
See the supplementary material for figures of several other sizes of microdroplets, the distribution of neutral molecules due to their dipole and induced dipole, the MATLAB code for both the single ion and uni-univalent electrolyte cases, and documentation explaining the shooting method integration used in the MATLAB code. Note that the MATLAB code for uni-univalent electrolyte case will not display results without MATLAB’s mapping toolbox installed. The MATLAB code for the single ion case will run on the base version of MATLAB.
DATA AVAILABILITY
The data and MATLAB codes that support the findings of this study are available within the article (and its supplementary material).
ACKNOWLEDGMENTS
C.F.C. thanks Juan Santiago for his excellent class “Advanced Topics in Electrokinetics,” which inspired this work. We also acknowledge Juan Santiago, Styliani Constas, Maria Dulay, and Carlos Aguilar for helpful discussions. Research in this work was supported by a fellowship from the Center for Molecular Analysis and Design at Stanford and the National Institutes of Health under Award No. 1R01EB025867.
REFERENCES
- 1.Yan X., Bain R. M., and Cooks R. G., “Organic reactions in microdroplets: Reaction acceleration revealed by mass spectrometry,” Angew. Chem., Int. Ed. 55, 12960–12972 (2016). 10.1002/anie.201602270 [DOI] [PubMed] [Google Scholar]
- 2.Nirmalkar N., Pacek A. W., and Barigou M., “On the existence and stability of bulk nanobubbles,” Langmuir 34, 10964–10973 (2018). 10.1021/acs.langmuir.8b01163 [DOI] [PubMed] [Google Scholar]
- 3.Uematsu Y., Bonthuis D. J., and Netz R. R., “Impurity effects at hydrophobic surfaces,” Curr. Opin. Electrochem. 13, 166–173 (2019). 10.1016/j.coelec.2018.09.003 [DOI] [Google Scholar]
- 4.Probstein R. F., Physicochemical Hydrodynamics (John Wiley & Sons, Inc., 1994). [Google Scholar]
- 5.Lord Rayleigh and Lord X. X., “On the equilibrium of liquid conducting masses charged with electricity,” London, Edinburgh, Dublin Philos. Mag. J. Sci. 14, 184–186 (1882). 10.1080/14786448208628425 [DOI] [Google Scholar]
- 6.Ramos A., Morgan H., Green N. G., and Castellanos A., “Ac electrokinetics: A review of forces in microelectrode structures,” J. Phys. D. Appl. Phys. 31, 2338–2353 (1998). 10.1088/0022-3727/31/18/021 [DOI] [Google Scholar]
- 7.Kao K. C., “Electric polarization and relaxation,” in Dielectric Phenomena in Solids, edited by Kao K. C. (Academic Press, 2004), Vol. 77. [Google Scholar]
- 8.Kwan V. and Consta S., “Bridging electrostatic properties between nanoscopic and microscopic highly charged droplets,” Chem. Phys. Lett. 746, 137238 (2020). 10.1016/j.cplett.2020.137238 [DOI] [Google Scholar]
- 9.Malevanets A. and Consta S., “Variation of droplet acidity during evaporation,” J. Chem. Phys. 138, 184312 (2013). 10.1063/1.4804303 [DOI] [PubMed] [Google Scholar]
- 10.Computational Chemistry Comparison and Benchmark DataBase Standard Reference Database 101. Technology National Institute of Standards and Technology.
- 11.Hilsabeck K. I., Meiser J. L., Sneha M., Balakrishnan N., and Zare R. N., “Photon catalysis of deuterium iodide photodissociation,” Phys. Chem. Chem. Phys. 21, 14195–14204 (2019). 10.1039/c8cp06107f [DOI] [PubMed] [Google Scholar]
- 12.Hilsabeck K. I., Meiser J. L., Sneha M., Harrison J. A., and Zare R. N., “Nonresonant photons catalyze photodissociation of phenol,” J. Am. Chem. Soc. 141, 1067–1073 (2019). 10.1021/jacs.8b11695 [DOI] [PubMed] [Google Scholar]
- 13.Corrales M. E. et al., “Control of ultrafast molecular photodissociation by laser-field-induced potentials,” Nat. Chem. 6, 785–790 (2014). 10.1038/nchem.2006 [DOI] [PubMed] [Google Scholar]
- 14.Nam I., Lee J. K., Nam H. G., and Zare R. N., “Abiotic production of sugar phosphates and uridine ribonucleoside in aqueous microdroplets,” Proc. Natl. Acad. Sci. U. S. A. 114, 12396–12400 (2017). 10.1073/pnas.1714896114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pestana L. R., Hao H., and Head-Gordon T., “Diels-alder reactions in water are determined by microsolvation,” Nano Lett. 20, 606–611 (2019). 10.1021/acs.nanolett.9b04369 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See the supplementary material for figures of several other sizes of microdroplets, the distribution of neutral molecules due to their dipole and induced dipole, the MATLAB code for both the single ion and uni-univalent electrolyte cases, and documentation explaining the shooting method integration used in the MATLAB code. Note that the MATLAB code for uni-univalent electrolyte case will not display results without MATLAB’s mapping toolbox installed. The MATLAB code for the single ion case will run on the base version of MATLAB.
Data Availability Statement
The data and MATLAB codes that support the findings of this study are available within the article (and its supplementary material).