Estimation of airborne viral emission: Quanta emission rate of SARS-CoV-2 for infection risk assessment

Highlights

• •Airborne transmission is a pathway of contagion of an epidemic.
• •Simulating the virus airborne transmission requires viral emission data.
• •A novel approach estimating the quanta emission rate of SARS-CoV-2 infected subject.
• •The approach estimates the quanta emission rate from the viral load in sputum.
• •Vocalization during light activity can lead to quanta emission rate >100 quanta h^−1.

Abstract

Airborne transmission is a pathway of contagion that is still not sufficiently investigated despite the evidence in the scientific literature of the role it can play in the context of an epidemic. While the medical research area dedicates efforts to find cures and remedies to counteract the effects of a virus, the engineering area is involved in providing risk assessments in indoor environments by simulating the airborne transmission of the virus during an epidemic. To this end, virus air emission data are needed. Unfortunately, this information is usually available only after the outbreak, based on specific reverse engineering cases. In this work, a novel approach to estimate the viral load emitted by a contagious subject on the basis of the viral load in the mouth, the type of respiratory activity (e.g. breathing, speaking, whispering), respiratory physiological parameters (e.g. inhalation rate), and activity level (e.g. resting, standing, light exercise) is proposed.

The results showed that high quanta emission rates (>100 quanta h⁻¹) can be reached by an asymptomatic infectious SARS-CoV-2 subject performing vocalization during light activities (i.e. walking slowly) whereas a symptomatic SARS-CoV-2 subject in resting conditions mostly has a low quanta emission rate (<1 quantum h⁻¹).

The findings in terms of quanta emission rates were then adopted in infection risk models to demonstrate its application by evaluating the number of people infected by an asymptomatic SARS-CoV-2 subject in Italian indoor microenvironments before and after the introduction of virus containment measures. The results obtained from the simulations clearly highlight that a key role is played by proper ventilation in containment of the virus in indoor environments.

1. Introduction

Expiratory human activities generate droplets, which can also carry viruses (e.g. influenza, tuberculosis, measles and SARS-CoV (Sze To and Chao, 2010, Watanabe et al., 2010)), through the atomization processes occurring in the respiratory tract when sufficiently high speeds are reached (Chao et al., 2009, Morawska, 2006). Indeed, during breathing, coughing, sneezing or laughing, toques of liquid originating from different areas of the upper respiratory tract are drawn out from the surface, pulled thin, and broken into columns of droplets of different sizes (Hickey and Mansour, 2019). The content of infectious agents expelled by an infected person depends, among other factors, on the location within the respiratory tract from which the droplets originated. In particular, air velocities high enough for atomization are produced when the exhaled air is forced out through some parts of the respiratory tract which have been greatly narrowed. The front of the mouth is the site of narrowing and the most important site for atomization; since most droplets originate at the front of the mouth and to a lesser extent from the larynx (Johnson et al., 2011), the concentration of an infectious agent in the mouth (sputum) is representative of the concentration in the droplets emitted during the expiratory activities (Morawska, 2006). Thus, knowledge of the size and origin of droplets is important to understand transport of the virus via the aerosol route. Contrary to the findings of early investigations (Duguid, 1945, Jennison, 1942, Wells, 1934), subsequent studies involving optical particle detection techniques capable of measurements down to fractions of a micrometer suggested that the majority of these particles are in the sub-micrometer size range (Papineni and Rosenthal, 1997). More recently, the growing availability of higher temporal and spatial visualization methods using high-speed cameras (Tang et al., 2011), particle image velocimetry (Chao et al., 2009) and, above all, increasingly accurate particle counters (Morawska et al., 2009) allowed the detailed characterization and quantitation of droplets expelled during various forms of human respiratory exhalation flows (e.g. breathing, whispered counting, voiced counting, unmodulated vocalization, coughing). Therefore, in recent years a marked development has occurred both in the techniques for detecting the viral load in the mouth and in the engineering area of the numerical simulation of airborne transmission of the viral load emitted.

However, the problem of estimating the viral load emitted, which is fundamental for the simulation of airborne transmission, has not yet been solved. This is a missing “transfer function” that would allow the virology area, concerned with the viral load values in the mouth, to be connected with the aerosol science and engineering areas, concerned with the spread and mitigation of contagious particles.

A novel approach is here presented for estimating the viral load emitted by an infected individual. This approach, based on the principle of conservation of mass, represents a tool to connect the medical area, concerned with the concentration of the virus in the mouth, to the engineering area, dedicated to the simulation of the virus dispersion in the environment. On the basis of the proposed approach, the quanta emission rate data of SARS-CoV-2 were calculated as a function of different respiratory activities, respiratory parameters, and activity levels.

The quanta emission rate data, starting from the recently documented viral load in sputum (expressed in copies mL⁻¹), were then applied in an acknowledged infection risk model (Gammaitoni and Nucci, 1997) to investigate the effectiveness of the containment measures implemented by the Italian government to reduce the spread of SARS-CoV-2. In particular, airborne transmission of SARS-CoV-2 by an asymptomatic subject within pharmacies, supermarkets, restaurants, banks, and post offices were simulated, and the reduction in the average number of infected people from one contagious person, R₀, was estimated.

2. Materials and methods

2.1. Estimation of the quanta emission rate

The approach proposed in the present work is based on the hypothesis that the droplets emitted by the infected subject have the same viral load as the sputum. Therefore, if the concentration of the virus in the sputum and the quantity of droplets emitted with dimensions less than 10 µm is known, the viral load emitted can be determined through a mass balance. In particular, the viral load emitted is expressed in terms of quanta emission rate (ER_q, quanta h⁻¹) (a quantum is defined as the dose of airborne droplet nuclei required to cause infection in 63% of susceptible persons) and is evaluated as:

$${\mathit{ER}}_q=c_v·c_i·V_{\mathit{br}}·N_{\mathit{br}}·\underset{0}{\stackrel{10\mu m}{\int }}{N}_d\left(D\right)·{\mathit{dV}}_d\left(D\right)$$ (1)

where c _v is the viral load in the sputum (RNA copies mL⁻¹), c_i is a conversion factor defined as the ratio between one infectious quantum and the infectious dose expressed in viral RNA copies, V _br is the volume of exhaled air per breath (cm³; also known as tidal volume), N _br is the breathing rate (breath h⁻¹), N _d is the droplet number concentration (part. cm⁻³), and V _d(D) is the volume of a single droplet (mL) as a function of the droplet diameter (D). The volume of the droplet (V _d) is determined on the basis of data obtained experimentally by Morawska et al. (2009): they measured the size distribution of droplets for different expiratory activities (e.g. breathing, whispered counting, voiced counting, unmodulated vocalization), recognizing that such droplets present one or more modes occurring at different concentrations. Therefore, the total volume of droplets was calculated by multiplying droplet number distribution by the volume of a sphere corresponding to each diameter of the size distribution. In particular, in the study a particle size distribution with four channels was considered with midpoint diameters of D ₁ = 0.8, D ₂ = 1.8, D ₃ = 3.5, and D ₄ = 5.5 μm. As an example, unmodulated vocalization was recognized as producing additional particles in modes near 3.5 and 5.5 μm. Details of the aerosol concentrations at the four channels of the size distribution during each expiratory activity are reported in Table 1 . The midpoint diameters of each channel were used to calculate the corresponding volume of the droplets. The authors point out that the breathing expiratory activity tested by Morawska et al. (2009), and here considered, is a naturally paced breathing with inspiration by nose and expiration by mouth.

Table 1.

Droplet concentrations (N_i, part. cm⁻³) of the different size distribution channels during each expiratory activity measured by Morawska et al. (2009).

Expiratory activity	D1 (0.80 µm)	D2 (1.8 µm)	D3 (3.5 µm)	D4 (5.5 µm)
Voiced counting	0.236	0.068	0.007	0.011
Whispered counting	0.110	0.014	0.004	0.002
Unmodulated vocalization	0.751	0.139	0.139	0.059
Breathing	0.084	0.009	0.003	0.002

Based on the results obtained by Morawska et al. (2009), equation (1) can be simplified as:

$${\mathit{ER}}_{q,j}=c_v·c_i·IR·\sum _{i=1}^4{(N}_{i,j}·V_i)$$ (2)

where j indicates the different expiratory activities considered (namely voiced counting, whispered counting, unmodulated vocalization, breathing) and IR (m³ h⁻¹) is the inhalation rate, i.e. the product of breathing rate (N _br) and tidal volume (V _br), which is a function of the activity level of the infected subject. The quanta emission rate from equation (2) can vary in a wide range depending on the virus concentration in the mouth, the activity level, and the different types of expiration. Regarding the inhalation rate effect, the quanta emission rate calculations are shown for five different activity levels (resting, standing, light exercise, moderate exercise, and heavy exercise) in which the inhalation rates, averaged between males and females, are equal to 0.49, 0.54, 1.38, 2.35, and 3.30 m³ h⁻¹, respectively (Adams, 1993).

2.2. A demonstration application: The containment measures for the spread of SARS-CoV-2 in Italy

The pandemic of a novel human coronavirus, now named Severe Acute Respiratory Syndrome CoronaVirus 2 (SARS-CoV-2 throughout this manuscript), emerged in Wuhan (China) in late 2019 and then spread rapidly in the world (https://www.who.int/emergencies/diseases/novel-coronavirus-2019). In Italy, an outbreak of SARS-CoV-2 infections was detected starting from 16 cases confirmed in Lombardy (a northern region of Italy) on 21 February. The Italian government has issued government a decree dated 11 March 2020 concerning urgent measures to contain the contagion throughout the country. This decree regulated the lockdown of the country to counteract and contain the spread of the SARS-CoV-2 virus by suspending retail commercial activities, with the exception of the sale of food and basic necessities. It represents the starting point of a system with imposed constraints. Among the measures adopted for the containment of the virus in Italy, great importance was placed on the safe distance of 1 m (also known as “droplet distance”). This distance was actually indicated by the World Health Organization as sufficient to avoid transmission by air, without any reference to the possibility of transmission over greater distances indoors (https://www.who.int/emergencies/diseases/novel-coronavirus-2019). With this measure, along with the opening of only primary commercial establishments (such as pharmacies, supermarkets, banks, post offices) and the closure of restaurants, the Italian government has adopted the concept of spacing (known as “social distancing”) to prevent the spread of the infection. Obviously, this limit per se would have no influence on the reduction of airborne transmission of the infection in indoor environments since this distance is compatible with the normal gathering of people in commercial establishments. Actually, on an absolutely voluntary basis, and despite the continuous denials by the government on the risk of indoor airborne transmission, commercial associations have changed the methods of accessing their commercial spaces such as restaurants, pharmacies, supermarkets, post offices, and banks; for example, by forcing customers to queue outside. It is clear that the best choice in containing an epidemic is a total quarantine which, however, appears to have enormous costs and social impacts.

To show the possible effect of the measures imposed by the Italian government (i.e. lockdown), the infection risk in different indoor microenvironments for the exposed population due to the presence of one contagious individual was simulated, adopting the infection risk model described in Section 2.2.1. In particular, the risk expressed in terms of basic reproduction number (R₀) was derived from the quanta concentration and the infection risk; indeed, R₀ represents the average number of infected people from one contagious person in a population where everyone is susceptible (Rothman et al., 2008).

The indoor microenvironments considered here were a pharmacy, supermarket, restaurant, post office, and bank whose dimensions are summarized in Table 2 . Two different exposure scenarios were simulated for each microenvironment: before lockdown (B) and after lockdown (A). In the simulation of the scenario before lockdown, the microenvironments were run with no particular recommendations; thus, people enter the microenvironments and queue indoors, often resulting in overcrowded environments. Since most of the indoor microenvironments in Italy are not equipped with mechanical ventilation systems, the simulations were performed considering two different situations: natural ventilation (a typical value for an Italian building equal to 0.2 h⁻¹ was adopted, with reference to (d’Ambrosio Alfano et al., 2012, Stabile et al., 2017)) and mechanical ventilation (calculated according the national standard, UNI 10,339 (UNI, 1995), as a function of the crowding index and the type of indoor microenvironment). The scenario after lockdown was tested considering the typical solutions adopted (on a voluntary basis) by the owners of stores and offices – reduced personnel, a reduced number of customers inside the microenvironment, customers forced to queue outdoors, and doors kept open. The scenario after lockdown was also tested for both natural ventilation and mechanical ventilation; in this case a slight increase in the air exchange rate (AER) for natural ventilation (0.5 h⁻¹) was considered in order to take into account that the door was always kept open. The restaurant was not tested in the scenario after lockdown since such commercial activity was closed down as a consequence of the lockdown. For all the scenarios considered in the simulations, the infected individual was considered to enter the microenvironment as the first customer (alone or along with other individuals according to the scenarios summarized in Table 2). All the scenarios were simulated taking into account that the virus is able to remain viable in the air for up to 3 h post aerosolization (with an half-life of 1.1 h) as recently detected by van Doremalen et al. (2020); thus, if the infected individual remained inside the environment for 10 min (e.g. pharmacy), the calculation of the quanta concentration, infection risk, and R₀ was performed for up to 3 h and 10 min (named “total exposure time” in Table 2). For restaurants the calculation was performed for 3 h considering that after 3 h (i.e. two groups remaining inside for 1 h and 30 min one after the other) the microenvironment was left empty.

Table 2.

Summary of the exposure scenarios tested for the different microenvironments under investigation: dimensions, ventilation conditions, number of workers and customers.

		Pharmacy	Supermarket	Restaurant	Post office	Bank
Dimensions	Floor area (A, m2)	25	600	100	100	50
	Height (h, m)	3	3	3	3	3
	Volume (V, m3)	75	1800	300	300	150
Exposure scenario before lockdown (B)	Number of workers	5 (always present)	10 (always present)	4 (just the waiters, always present)	8 (always present)	4 (always present)
	Number and activity of the customers	–1 new customer per min entering the pharmacy, –every customer remains 10 min inside (including waiting time), –thus, 10 customers are simultaneously present	–1 new customer every 30 s entering the supermarket, –every customer remains 30 min inside, –thus, 60 customers are simultaneously present	–80 costumers every 1.5 h, –restaurant working for 3 h (evening), –thus, 80 customers are simultaneously present for a total number of 160 customers per evening.	–1 new customer every 30 s entering the post office, –every customer remains 15 min inside (including waiting time), –thus, 30 customers are simultaneously present	–1 new customer per min entering the bank, –every customer remains 15 min inside (including waiting time), –thus, 15 customers are simultaneously present
	Air exchange rate (AER, h−1) for natural ventilation (NV)	0.2	0.2	0.2	0.2	0.2
	Air exchange rate (AER, h−1) for mechanical ventilation (MV)	2.2	1.1	9.6	2.4	2.4
	Total exposure time	3 h and 10 min	3 h and 30 min	3 h	3 h and 15 min	3 h and 15 min
Exposure scenario after lockdown (A)	Number of workers	3 (always present)	10 (always present)	–	4 (always present)	4 (always present)
	Number and activity of the costumers	–2 new customers every five min entering the pharmacy, –every customer remains 5 min inside, –people forced to queue outside the pharmacy, –thus, 2 customers are simultaneously present	–1 new customer per min entering the supermarket, –every customer remains 10 min inside, –people forced to queue outside the supermarket, –thus, 10 customers are simultaneously present	–	–4 new customers every five min entering the post office, –every customer remains 10 min inside, –people forced to queue outside the post office, –thus, 4 customers are simultaneously present	–4 new customers every five min entering the bank, –every customer remains 10 min inside, –people forced to queue outside the bank, –thus, 4 customers are simultaneously present
	Air exchange rate (AER, h−1) for natural ventilation (NV)	0.5	0.2	–	0.5	0.5
	Air exchange rate (AER, h−1) for mechanical ventilation (MV)	2.2	1.1	–	2.4	2.4
	Total exposure time	3 h and 5 min	3 h and 10 min	3 h	3 h and 10 min	3 h and 10 min

2.2.1. The infection risk model

The simulation of airborne transmission of SARS-CoV-2 was performed adopting the infection risk assessment typically implemented to evaluate the transmission dynamics of infectious diseases and to predict the risk of these diseases to the public. The model considered here to quantify the airborne transmitted infection risk was carried out by Gammaitoni and Nucci (1997) which represents an upgrade of an earlier model provided by Riley et al. (1978). This model was successfully adopted in previous papers estimating the infection risk due to other diseases (e.g. influenza, SARS, tuberculosis, rhinovirus) in different indoor microenvironments such as airplanes (Wagner et al., 2009), cars (Knibbs et al., 2011), and hospitals. The Gammaitoni and Nucci model is based on the rate of change in quanta levels through time; in particular, the differential equations for the change of quanta in a control volume as well as the initial conditions (here not reported for the sake of brevity) allowed to evaluate the quanta concentration in an indoor environment at the time t, n(t), as:

$$n(t)=\frac{{\mathit{ER}}_q·I}{\mathit{IVRR}·V}+\left(n_0+\frac{{\mathit{ER}}_q·I}{\mathit{IVRR}}\right)·\frac{e^{-IVRR·t}}{V}(\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{a}{\mathrm{m}}^{-3})$$ (3)

where IVRR (h⁻¹) represents the infectious virus removal rate in the space investigated, n ₀ represents the initial number of quanta in the space, I is the number of infectious subjects, V is the volume of the indoor environment considered, and ER_q is the abovementioned quanta emission rate (quanta h⁻¹) characteristic of the specific disease/virus under investigation. The infectious virus removal rate (IVRR) is the sum of three contributions (Yang and Marr, 2011): the air exchange rate (AER) via ventilation, the particle deposition on surfaces (k, e.g. via gravitational settling), and the viral inactivation (λ). For the demonstration application here described, the AER values were selected according to the ventilation approach as summarized in Table 2, whereas constant values for deposition rate (k) and viral inactivation (λ) were chosen. In particular, the deposition rate was evaluated as ratio between the settling velocity of super-micrometric particles (roughly 1.0 × 10⁻⁴ m s⁻¹ as measured by Chatoutsidou and Lazaridis (2019)) and the height of the emission source (1.5 m), thus k resulted equal to 0.24 h⁻¹. The viral inactivation was evaluated on the basis of the SARS-CoV-2 half-life (1.1 h) detected by van Doremalen et al. (2020), thus λ resulted equal to 0.63 h⁻¹.

The equation (3) was derived considering the following simplifying assumptions: the quanta emission rate is considered to be constant, the latent period of the disease is longer than the time scale of the model, and the droplets are instantaneously and evenly distributed in the room (Gammaitoni and Nucci, 1997). The latter represents a key assumption for the application of the model as it considers that the air is well-mixed within the modelled space. The authors highlight that in epidemic modeling, where the target is the spread of the disease in the community, it is impossible to specify the geometries, the ventilation, and the locations of the infectious sources in each microenvironment. Therefore, adopting the well-mixed assumption is generally more reasonable than hypothesizing about specific environments and scenarios because the results must be interpreted on a statistical basis (Sze To and Chao, 2010).

To determine the infection risk (R, %) as a function of the exposure time (t) of susceptible people, the quanta concentration was integrated over time through the Wells–Riley equation (Riley et al., 1978) as:

$$R=\left(1-e^{-IR\underset{0}{\stackrel{T}{\int }}n\left(t\right)dt}\right)(\%)$$ (4)

where IR is the inhalation rate of the exposed subject (which is, once again, affected by the subject’s activity level) and T is the total time of exposure (h). From the infection risk R, the number of susceptible people infected after the exposure time can be easily determined by multiplying it by the number of exposed individuals. In fact, equations (3), (4) were adopted to evaluate the infection risk of different exposure scenarios of Italian microenvironments hereinafter reported. The inhalation rate of the exposed subjects in the simulations of the different scenarios was considered as the average value between standing and light exercise activity (thus IR = 0.96 h⁻¹). The quanta emission rate used in the simulation of the scenario represents the average value obtained from the four expiratory activities (voiced counting, whispered counting, unmodulated vocalization, breathing); the data are reported and discussed in the result sections. The R₀ for each scenario was calculated by multiplying the infection risk during the exposure time of each susceptible people by the number of the susceptible people exposed.

3. Results and discussions

3.1. The quanta emission rate

As discussed in the Materials and methods section, the quanta emission rate, ER_q, depends on several parameters.

With reference to SARS-CoV-2 viral load in the mouth, researchers have recently found c_v values up to 10¹¹ copies mL⁻¹, also variable in the same patient during the course of the disease (Pan et al., 2020, Rothe et al., 2020, To et al., 2020, Woelfel et al., 2020). In particular, (Rothe et al., 2020) reported a case of SARS-CoV-2 infection acquired outside Asia in which transmission appears to have occurred during the incubation period in the index patient. A high viral load of 10⁸ copies mL⁻¹ was found, confirming that asymptomatic persons are potential sources of SARS-CoV-2 infection. Furthermore, Pan et al. (2020), in a study on 82 SARS-CoV-2 infected patients, found c_v values in the range 10⁸-10⁹ RNA copies mL⁻¹, also in the previous days and in the first days of onset of the disease. Consequently, the concentrations of viral load in the mouth can reach values of 10⁹ RNA copies mL^-1and occasionally up to 10¹¹ RNA copies mL⁻¹ during the course of the disease.

As regard the corrective coefficient of infectivity, c_i, there are currently no values available in the scientific literature and, therefore, the authors will refer to the case of SARS-CoV-1 which has similar characteristics (van Doremalen et al., 2020). In particular, (Watanabe et al., 2010) estimated the SARS-CoV infectious doses received by residents in Amoy Gardens, Hong Kong (Li et al., 2005, Yu et al., 2004) corresponding to a c_i variable in the 0.01–0.1 range.

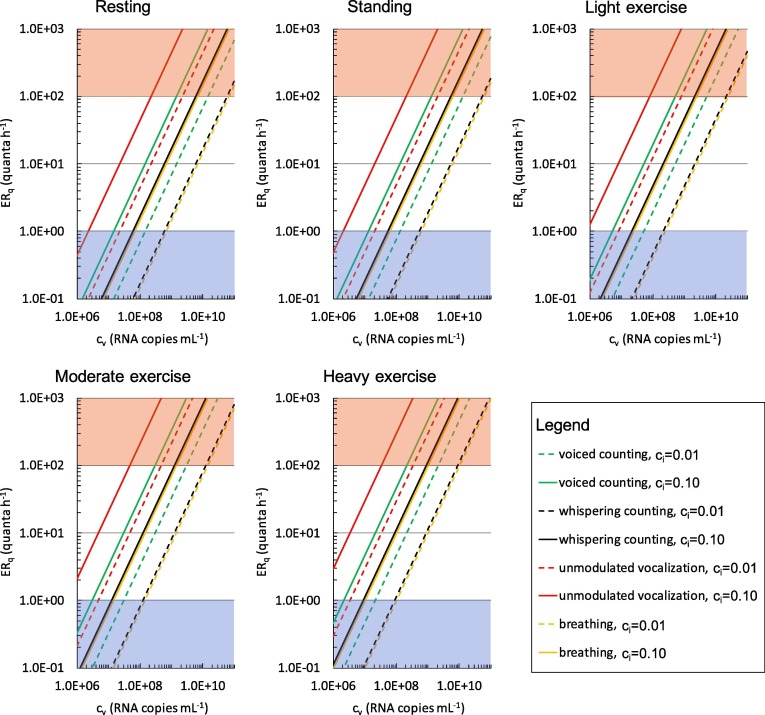
In Fig. 1 the ER_q (quanta h⁻¹) trends for the SARS-CoV-2 are reported as a function of the viral load in the sputum c_v, and the infectious dose, c_i, for different expiratory activities (voiced counting, whispered counting, unmodulated vocalization, breathing) and different activity levels (resting, standing, light exercise, moderate exercise, and heavy exercise). To represent the large variabilities (over several orders of magnitude) of ER_q as a function of c_v, the graph is reported on a bi-logarithmic scale. For the sole purpose of simplifying the discussion, three emission ranges were identified: (i) the low emission zone with values of ER_q < 1 quantum h⁻¹; (ii) the emission zone up to 100 quanta h⁻¹ and (iii) the high emission zone for values greater than 100 quanta h⁻¹.

Fig. 1.

ER_q (quanta h⁻¹) trends as a function of the viral load in sputum (cv, RNA copies mL⁻¹) and quanta-RNA copies correction factor (c_i) for different respiratory activities (voiced counting, whispered counting, unmodulated vocalization, breathing) and different activity levels (resting, standing, light exercise, moderate exercise, and heavy exercise). Zones representative of low (<1 quantum h⁻¹) and high (>100 quanta h⁻¹) quanta emission are indicated as blue and red shaded areas, respectively.

In the case of a resting condition (which could represent the typical condition of a hospitalized patient), with a c_v < 10⁷ copies mL⁻¹ the infectious subject has mostly a low emission (<1 quantum h⁻¹), except in the particular case of unmodulated vocalization and infectivity equal to 0.1. A high emission in the case of oral breathing can be achieved only at very high values of c_v, i.e. higher than 10¹⁰ copies mL⁻¹. While the resting condition is mainly characteristics of a symptomatic hospitalized subject, light exercise activity (e.g. walking slowly, (Adams, 1993)) (Fig. 1c) is of great interest because it represents the typical condition of an asymptomatic person during his daily activities. In this case, a c_v of 10⁶ copies mL⁻¹ is needed to guarantee a low emission. A subject with a c_v equal to 10⁹ copies mL⁻¹ presents an ER_q falling within the emission zone, reaching the high emission zone in the case of vocalization.

Finally, it is interesting to note that in the case of heavy exercise, the high emission zone can theoretically be reached with a c_i equal to 0.10 just during oral breathing. This condition is representative of any person who is engaged in sports.

It is evident from what has been reported how the high emission zone can also be reached for an SARS-CoV-2 asymptomatic subject in the combination of the three parameters c_v, c_i and IR, both in the light exercise condition during speaking and in the heavy exercise with oral breathing.

3.2. Results of the demonstration application: Infection risk and R₀ for different indoor environments and exposure scenarios

In this section, the results of the simulations performed for the microenvironments and exposure scenarios described in Section 2.2 and summarized in Table 2 are reported.

The aim is to analyze the worst case scenario in the presence of an asymptomatic SARS-CoV-2 subject. For this reason, the following input data have been defined: (i) c_i equal to 0.02 (corresponding to the average value of the infectious doses reported for SARS-CoV-2 in Watanabe et al. (2010), (ii) c_v equal to 10⁹ RNA virus copies mL⁻¹, (iii) light exercise as activity level; iv) speaking (considered as mean values between unmodulated vocalization and voiced counting). Using these data, the quanta emission rate estimated through Eq. (1) results equal to 142 quanta h⁻¹.

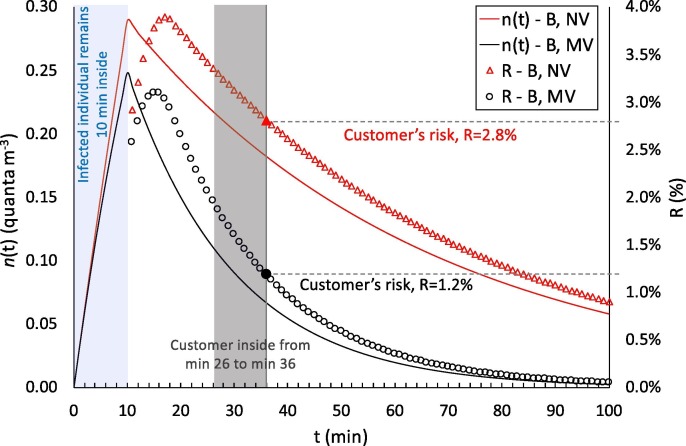
As an illustrative example, Fig. 2 shows the quanta concentration (n(t)) and infection risk (R) trends as a function of time for two different exposure scenarios simulated for the pharmacy, i.e. before lockdown (B) in natural (NV) and mechanical ventilation (MV) conditions. The trends clearly highlight that the presence of the infected individual remaining inside for 10 min leads to an increase in the quanta concentration in the volume: in particular, a higher peak of quanta concentration was recognized, as expected, for reduced ventilation (NV) with respect to the mechanical ventilation (MV). People entering the pharmacy after the infected individual are exposed to a certain quanta concentration during their 10-min time, and the resulting risk for their exposure (evaluated through equation (4)) is just a function of the quanta concentration trend. For example, people entering the microenvironment around the quanta concentration peak are at a higher risk than people entering the pharmacy later. Fig. 2 shows an example of a customer entering at min 26 and leaving at min 36: the risk for this 10-min exposure is 2.8% in natural ventilation conditions and 1.2% in mechanical ventilation conditions. During the entire exposure time of such a scenario (3 h and 10 min), 179 customers (after the infected individual) enter the pharmacy and each of them receive their own risk. In particular, the average risk of the 179 customers is 1.3% for NV conditions and 0.4% for MV conditions, then leading to a R₀ (among the customers) of 2.34 and 0.80, to which must be added the R₀ of the five pharmacists exposed for the entire period. Similar trends, not shown here graphically for the sake of brevity, were obtained for all the scenarios investigated, then leading to the evaluation of the R₀ for each of them as described in the methodology section.

Fig. 2.

Details of application of the proposed approach in the calculation of quanta concentrations, n(t), and infection risks, R, in the pharmacy environment for the exposure scenarios before lockdown (B) in natural (NV) and mechanical ventilation (MV) conditions. The graph shows the entry of the infected individual (first 10 min) and the risk for a customer entering the microenvironment at min 26 and remaining inside for 10 min. The trends are shown for up to 100 min to highlight the peaks of the n(t) and R values.

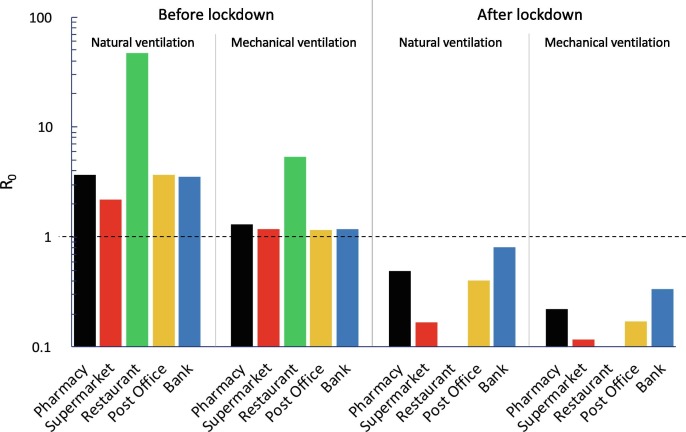
Fig. 3 shows the reproduction number (R₀) data calculated for all the exposure scenarios and microenvironments under investigation (summarized in Table 2) adopting the abovementioned emission data of an asymptomatic SARS-CoV-2 infected subject. The exposed subjects were considered under light exercise and/or standing activity level, thus the average IR amongst these two activity levels was considered as mentioned in the methodology section (IR = 0.96 m³ h⁻¹). The graph clearly highlights some critical exposure scenarios and microenvironments. Indeed, in all the microenvironments, a R₀ > 1 was estimated for all the exposure scenarios before lockdown (B) when the ventilation relied only upon the building being airtight (i.e. natural ventilation conditions): R₀ was equal to 3.70, 2.19, 47.3, 3.64, and 3.52 for pharmacy, supermarket, restaurant, post office, and bank, respectively. The large value for the restaurant is obviously due to the simultaneous co-presence of many people (80 customers and 4 waiters) and to the long exposure time (1 h and 30 min in the current simulations). This situation is obviously improved if mechanical ventilation systems are adopted, but the R₀ is still higher than 1 (R₀ = 5.35). Similar results are obviously expected for all the indoor environments characterized by high crowding indexes and long-lasting exposures such as schools, swimming pools, gyms – venues that, in fact, were also concomitantly locked down by the government. Actually, adopting mechanical ventilation solutions that purportedly provide an adequate indoor air quality (i.e. providing AER values suggested by the standards (UNI, 1995)) did not satisfactorily reduce the R₀ in the other microenvironments investigated. Indeed, the R₀ values obtained from the simulations performed for the pharmacy, supermarket, post office, and bank equipped with mechanical ventilation systems in the conditions before lockdown, with mechanical ventilation in operation, were still slightly > 1 (1.16–1.30).

Fig. 3.

R₀ calculated for all the exposure scenarios (natural ventilation, mechanical ventilation; before lockdown, after lockdown) and microenvironments (pharmacy, supermarket, restaurant, post office, bank) under investigation considering an asymptomatic SARS-CoV-2 infected subject (c_v = 1 × 10⁹ copies mL⁻¹) while performing light exercise activities (ER_q = 142 quanta h⁻¹) and exposed population standing and/or performing light exercise (IR = 0.96 m³ h⁻¹).

The new regulations and methods of accessing the indoor environments that were applied in the conditions after lockdown (i.e. queuing outside, limited time spent in the environments, lower crowding index) were very effective; indeed, the R₀ values were reduced by roughly 80%–90% (for both natural and mechanical ventilation conditions) with respect to the corresponding pre-lockdown scenarios.

As an example, for the natural ventilation scenario, no critical microenvironments were detected as the R₀ values resulted < 1 (0.49, 0.17, 0.41, and 0.81 for pharmacy, supermarket, post office, and bank, respectively). The exposure scenarios after lockdown were further improved for indoor environments equipped with mechanical ventilation systems, as the R₀ were much lower than 1 (0.22, 0.12, 0.17, and 0.34 for pharmacy, supermarket, post office, and bank, respectively). Therefore, if in a single day the infected individual visited different environments, the resulting R₀ would be lower than 1 only if all the microenvironments were equipped with mechanical ventilation systems. Once again, these results highlight the importance of proper ventilation of indoor environments and are in line with the scientific literature that recognizes the importance of ventilation strategies in reducing indoor-generated pollution (Stabile et al., 2017, Stabile et al., 2019).

The values obtained with this approach could vary significantly as a function of (i) the activity levels of both the infected subject and the exposed subjects; and (ii) the viral load in the sputum of the infected subject; therefore, in future studies, more specific exposure scenarios could be simulated on the basis of the findings proposed and discussed in this study.

4. Conclusions

The present study proposed the first approach aimed at filling the gap of knowledge still present in the scientific literature about evaluating the viral load emitted by infected individuals. This information could provide key information for engineers and indoor air quality experts to simulate airborne dispersion of diseases in indoor environments. To this end, an approach to estimate the quanta emission rate (expressed in quanta h⁻¹) is proposed on the basis of the emitted viral load from the mouth (expressed in RNA copies in mL⁻¹), typically available from virologic analyses. Such approach also takes into account the effect of different parameters (including inhalation rate, type of respiratory activity, and activity level) on the quanta emission rate. High emission values have been found for an SARS-CoV-2 asymptomatic subject both in the light exercise condition during speaking and in the heavy exercise with oral breathing.

The proposed approach is of great relevance as it represents an essential tool to be applied in enclosed space and it is able to support air quality experts and epidemiologists in the management of indoor environments during an epidemic just knowing its viral load, without waiting for the end of the outbreak. For this purpose, it has been applied to the Italian case which, at the time of writing, represents the country with the highest number of deaths from SARS-CoV-2 in the world, highlighting the great importance of ventilation in indoor microenvironments to reduce the spread of the infection.

CRediT authorship contribution statement

G. Buonanno: Conceptualization, Methodology, Writing - original draft. L. Stabile: Data curation, Writing - original draft. L. Morawska: Conceptualization, Supervision, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Handling Editor: Xavier Querol