Estimation of the time-varying reproduction number of COVID-19 outbreak in China

Abstract

Background

The 2019 novel coronavirus (COVID-19) outbreak in Wuhan, China has attracted world-wide attention. As of March 31, 2020, a total of 82,631 cases of COVID-19 in China were confirmed by the National Health Commission (NHC) of China.

Methods

Three approaches, namely Poisson likelihood-based method (ML), exponential growth rate-based method (EGR) and stochastic Susceptible-Infected-Removed dynamic model-based method (SIR), were implemented to estimate the basic and controlled reproduction numbers.

Results

A total of 198 chains of transmission together with dates of symptoms onset and 139 dates of infections were identified among 14,829 confirmed cases outside Hubei Province as reported as of March 31, 2020. Based on this information, we found that the serial interval had an average of 4.60 days with a standard deviation of 5.55 days, the incubation period had an average of 8.00 days with a standard deviation of 4.75 days and the infectious period had an average of 13.96 days with a standard deviation of 5.20 days. The estimated controlled reproduction numbers, $R_c$, produced by all three methods in all analyzed regions of China are significantly smaller compared with the basic reproduction numbers $R_0$.

Conclusions

The controlled reproduction number in China is much lower than one in all regions of China by now. It fell below one within 30 days from the implementations of unprecedent containment measures, which indicates that the strong measures taken by China government was effective to contain the epidemic. Nonetheless, efforts are still needed in order to end the current epidemic as imported cases from overseas pose a high risk of a second outbreak.

1. Introduction

On December 29, 2019, four cases of pneumonia with unknown etiology were reported in Wuhan, the capital city of Hubei Province in Central China (Li et al., 2020). Since then, the outbreak has dramatically worsened over a short span of time and has received considerable global attention. On January 7, 2020, the pathogen of the current outbreak was identified as a novel coronavirus (2019-nCoV), and its gene sequence was quickly submitted to the WHO (The coronavirus was renamed COVID-19 by the WHO on February 12, Huang et al., 2020, Wang et al., 2020). On January 30, the WHO announced the listing of this novel coronavirus-infected pneumonia (NCP) as a “public health emergency of international concern”. As of March 31, 2020, the National Health Commission (NHC) of China had confirmed a total of 82,631 cases of COVID-19 in China, including 3,321 fatalities and 76,415 recoveries.

Since January 19, 2020, strict containment measures, including travel restrictions, contact tracing, entry or exit screening, non-hospital isolation, quarantine and awareness campaigns have been implemented by the Wuhan municipal government and quickly adopted by other cities within China with the aim to minimize virus transmission via human-to-human contact. In 2009, similar measures were employed in China in response to the outbreak of H1N1 virus breakout.

This article investigates the change in the basic reproduction number $R_0$ and controlled reproduction number $R_c$ since the outbreak of COVID-19. We have found that the estimated controlled reproduction numbers $R_c$ in all different regions are significantly smaller compared with the basic reproduction numbers $R_0$, which indicates that the containment measures carried out by Chinese government was effective and efficient.

2. Data

A form was designed to collect and standardize information from each individual confirmed case. There were two parts in the designed form:

• (A)Part A directly retrieved pubic available data from provincial or municipal health commissions as well as apps and websites managed by local governments in China. The following details were included on each confirmed case: case ID, region, age, gender, first sign of symptoms, date of symptom onset, date of diagnosis, history of travel or previous residency in Hubei Province, contact history with other confirmed cases and others. See more detail information collected in Part A of the form in Supplement.
• (B)Part B includes probable transmission chains which were inferred based on history of travel to or previous residency in Hubei and other related information. The transmission chain was inferred as follows: (1) if the individual X has not recently been to Hubei Province, but has been in close contact with an imported case Y from Hubei, then the individual X was determined to be infected by this imported case Y and hence formed a transmission chain; (2) if the individual X has not recently been in Hubei province, but has been in close contact with a local case Y who was clearly infected before the contact, then this individual X was determined to be infected by the local case Y. Note: if the individual has been to Hubei Province, the transmission history would not be recorded despite the existence of contact tracing information. See Part B of an empty form in Supplement.

The date of infection was not included in the form but some can be inferred from the form as follows:

• (1)If the individual has not been to Hubei Province recently, but was exposed within a three-day period (i.e., the individual had contact with confirmed cases within three consecutive days), then the corresponding date of infection is inferred as the middle of the exposure period;
• (2)If the individual previously traveled to Hubei Province but returned within three days, then the date of infection is inferred as the middle of the travel period.

All data collection and processing were done manually except that the data from Shenzhen was semi-automated collected (a spreadsheet can be downloaded from an official website for Part A, however information in Part B still needed to be inferred and entered manually). Data collectors were trained and divided into 6 groups according to the regions of confirmed cases with 2 collectors in each group to ensure the efficiency and accuracy of data collection. Data sources, typically the website address, and names of the collectors were also recorded in the form of each case for quality control purposes. The collected data were consistently monitored and spot checked by two assigned supervisors. As of March 31, 2020, we have collected a total of 14,829 confirmed cases detected outside Hubei Province in China.

3. Inference about the generation time, incubation period, serial interval and infectious period

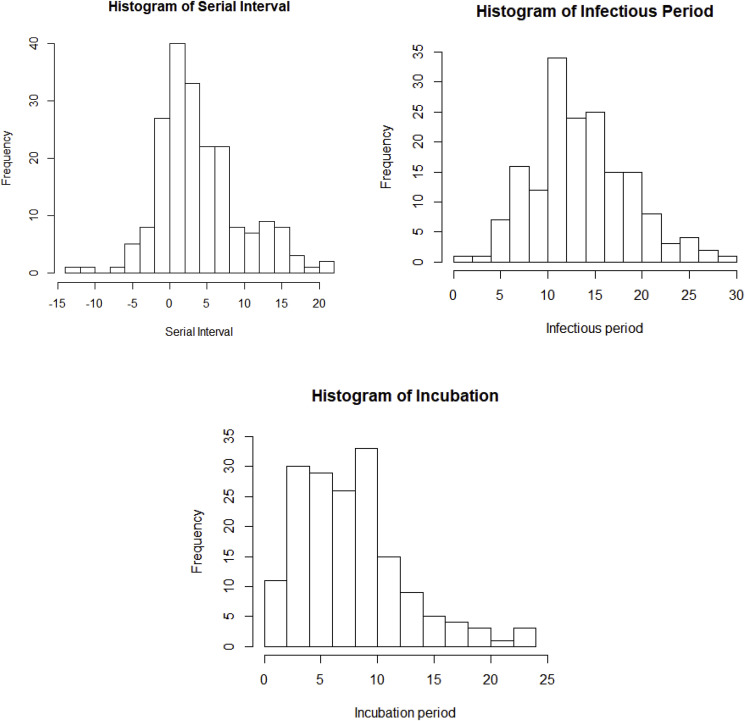
The generation time is the time difference between dates of infection of successive cases in a transmission chain while the serial interval is the difference in dates of symptoms onset between a pair of a primary case and its secondary case. The incubation period is defined as time difference between contraction of the disease and symptoms onsets. The infectious period is the duration of which an infected individual can transmit pathogens to a susceptible host. In this study, the infectious period is defined as the time difference between date of infection and date of diagnosis as there is strong evidence showing that a diseased individual remains infectious even during the incubation period, and would be immediately isolated upon positive diagnosis hence losing the transmissibility (Rothe et al., 2020). All are key quantities that depict an epidemic and are essential to estimate the basic/controlled reproductive number, $R_0$/$R_c$. Among the 645 chains of transmission identified from 14,829 confirmed cases recorded outside Hubei Province as of March 31, 2020, very few of them have their dates of infection acquired, but 198 of them have their dates of symptoms onset available. Hence, we only calculate the serial interval but not the generation time.

We can see that some serial intervals are negative, which suggests that COVID-19 is infectious during incubation and negative values were caused by different lengths of incubation period between individuals. The average of the serial intervals is 4.60 days and the standard deviation is 5.55 days (see Table 1 ). Note that the serial interval of SARS-nCoV in Hongkong was 8.4 days on average (Lipsitch et al., 2003). In fact, the distribution of serial interval may be biased for estimating generation time, especially when the disease is infectious during incubation, in that the variance of generation time could be overestimated (Britton, 2019). In addition, a total of 169 cases in the collected data were able to identify the dates of infection according to the method described in previous section. The histogram of infectious period is in Fig. 1 while the numerical summary is in Table 1. We acknowledge that isolation could occur before the date of diagnosis and suspected cases could be isolated without the formal positive results, hence infectious period could be potentially overestimated. Furthermore, incubation periods of these 169 cases can be identified. See Fig. 1 and Table 1 for the histogram and numerical summary for the incubation period.

Table 1.

Numerical summaries of serial intervals, infectious period, and incubation period.

	Minimum	1st quartile	Median	Mean	3rd quartile	Maximum
Serial intervals	−13.00	1.00	4.00	4.60	7.00	21.00
Infectious period	0.00	11.00	13.50	13.96	17.50	29.00
Incubation period	0.00	4.50	7.00	8.00	10.00	23.50

Fig. 1.

Histograms of serial interval with the median of 4.0 days, infectious period with the median of 13.5 days, and incubation period with the median of 7.0 days.

We found that there were no significant demographical differences between the subset of cases used to estimate serial interval and infectious period and the cases in the full dataset. Therefore, the inference made on serial interval, incubation period and infectious period based on the corresponding subsets should be able to represent the full dataset.

4. Estimation of basic/controlled reproduction number

4.1. Definition

The reproduction number $R_0$ is defined as the (average) number of new infections generated by one infected individual during the entire infectious period in a fully susceptible population (Anderson et al., 1992). The basic reproduction number reflects the ability of an infection spreading under no control. When the size of susceptible population is limited, the quantity, effective reproduction number $R_e$, is used instead of $R_0$. Similarly, the quantity, controlled reproduction number $R_c$, should be used to describe the ability of disease spreading when interventions (such as quarantine, isolation, or traffic control) are taking place. Hence a good measure of any intervention is to reduce $R_c$. Note that the disease will decline and eventually die out if $R_c\le 1$.

4.2. Methods

The basic reproduction number can be estimated through a variety of models (Nikbakht et al., 2019). In this section, we have compared three most popular estimates of $R_0$ or $R_c$ as shown below.

4.2.1. Poisson likelihood-based (ML) method

This method assumes that the total number of secondary cases infected by a single primary case follows a Poisson distribution. The number of individuals infected on Day $t$ is usually approximated by the number of new reported confirmed cases on Day $t$, and the generation time is approximated by its corresponding serial interval. Let $N_t$ be the number of reported new confirmed cases on Day $t$. Suppose that the serial interval has a maximum of $k$ days and the number of new cases generated by an infected individual is assumed to follow a Poisson distribution with parameter $R$ (Forsberg White and Pagano, 2008). The probability that the serial interval of an individual lies in $j$ days is $w_j$, which can be estimated from the empirical distribution of serial interval or by setting up a discretized Gamma prior on it. Note only the non-negative values of serial interval are used here. Thus, the likelihood function can be reduced into a thinned Poisson

$$L\left(R,w\right)=\prod _{t=1}^T\frac{e^{-{\mu }_t}{\mu }_t^{N_t}}{N_t!}$$

where

$${\mu }_t=R\sum _{j=1}^{\min \{k,t\}}{N}_{t-j}{w}_j.$$

The reproduction number $R_{\cdot }$ can be estimated by maximizing the likelihood function. Note that if the empirical distribution of serial interval is used or $w_j$’s is given, then

$${\hat{R}}_{\cdot }=\frac{{\sum }_{t=1}^T{N}_t}{{\sum }_{t=1}^T{\sum }_{j=1}^{\min \{k,t\}}{N}_{t-j}{w}_j}.$$

4.2.2. Exponential growth rate-based (EGR) method

At the early period of an epidemic, the number of infected cases rises exponentially. Similar to the ML method, the number of individuals infected on Day $t$ is approximated by the number of new reported confirmed cases, and the generation time is approximated by its corresponding serial interval. Suppose the exponential epidemic growth rate (Malthusian coefficient) is $r$, which can be estimated by fitting a least square line to the daily number of reported new confirmed cases in a log-scale, namely, $\text{log}\left(N_t\right)$. Let $f_G\left(t\right)$ denote the probability density function of serial interval. Hence the reproduction number can be calculated according to the Euler-Lotka equation in a moment generating form (Wallinga and Lipsitch, 2007)

$${\hat{R}}_{\cdot }=\frac{1}{{\int }_0^{\infty }{e}^{-rt}{f}_G\left(t\right)dt}.$$

4.2.3. Stochastic dynamic model-based method

Here we consider a stochastic Susceptible-Infected-Removed (SIR) model rather than a standard deterministic one. The major advantage of using a stochastic dynamic model is that it affords improved accounting for real variabilities and increases opportunity for quantifying uncertainties (King Aaron et al., 2015). Here we denote $S\left(t\right)$, $I\left(t\right)$ and $R\left(t\right)$ as the number of susceptible, infected but not lab-confirmed cases (including those in incubation period) and removed population (including recoveries, fatalities and confirmed cases) at time $t$ respectively, and note that $N=S\left(t\right)+I\left(t\right)+R\left(t\right)$ is a constant. There was some evidence indicating that the COVID-19 is infectious during its incubation period (Rothe et al., 2020). Due to this unique nature of COVID-19, individuals in state $I$ is contagious during even the incubation period. With the assumption of equal transmissibility during the whole infectious period, individuals in state $I$ pass pathogens to susceptible population with a constant transmission rate $\beta$. The removed individuals are no longer infectious since they have been isolated in hospital. Suppose that the infectious period of an individual is a random variable $T~\text{Exp}\left(\gamma \right)$, then the reproduction number $R_{\cdot }=\beta E\left(T\right)=\beta /\gamma$, where $\gamma$ and $\beta$ are the removing rate and transmission rate. Note that the following mean-field Differential Equation System serves as a deterministics counterpart of the stochastic model,

$$\frac{d\tilde{S}}{dt}=-\frac{\beta \tilde{I}\tilde{S}}{N},$$

$$\frac{d\tilde{I}}{dt}=\frac{\beta \tilde{I}\tilde{S}}{N}-\gamma \tilde{I},$$

$$\frac{d\tilde{R}}{dt}=\gamma \tilde{I},$$

where $\tilde{\text{S}}\left(\text{t}\right)$, $\tilde{\text{I}}\left(\text{t}\right)$ and $\tilde{\text{R}}\left(\text{t}\right)$ are the deterministic counterparts of $\tilde{\text{S}}\left(\text{t}\right)$, $\tilde{\text{I}}\left(\text{t}\right)$ and $\tilde{\text{R}}\left(\text{t}\right)$.

The maximum likelihood method is used to estimate model parameters where the likelihood is obtained by sequential Monte Carlo method, and parameters are estimated using the Iterated Filtering algorithm (IF2) implemented as mif in the R package pomp (Ionides et al., 2015, King et al., 2010). Here we set $S\left(0\right)$ equals the population of the region, $R\left(0\right)=0$, $I\left(0\right)$ is 14 times the average number of confirmed cases from Day 0 to Day 7, and $\gamma =1/13.96$, the inverse of mean infectious period, obtained from the collected data described before.

It is arguable that the transmission rate $\beta$ is a constant over the whole infectious period, some studies indicate that $\beta$ may vary and possibly peak on or before symptoms onset (He et al., 2020). However, it is beyond the scope of this study. In addition, this model does not consider asymptomatic and undocumented case, quarantine measures and human mobility, a more sophisticated and realistic model to reflect unique features of COVID-19 is worth of another paper itself. Nonetheless, this SIR model should at least provide some useful insight into reproduction numbers and is a better alternative of the popular SEIR model which assumes noninfectious incubation period.

5. Results

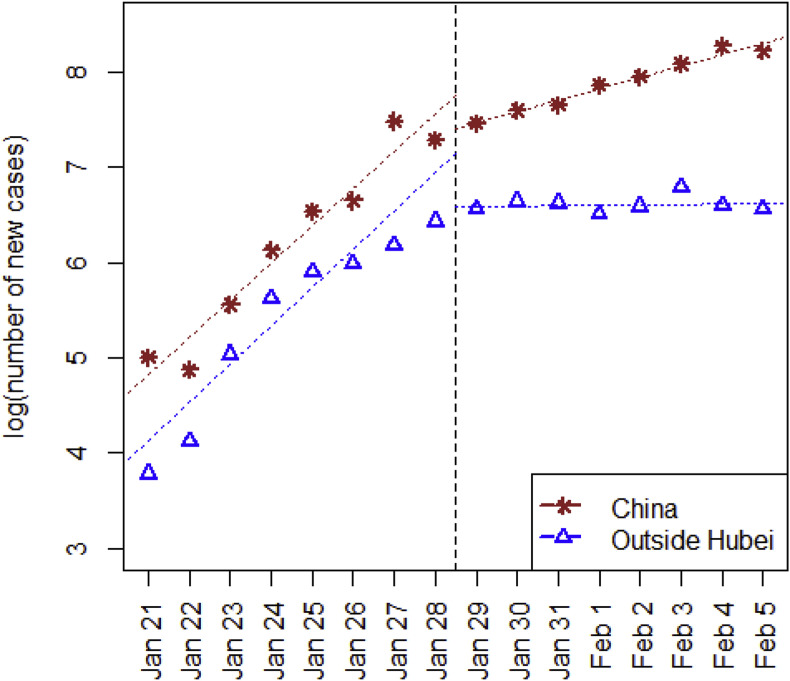
In this section we have estimated the basic reproduction number $R_0$ and the controlled reproduction number $R_c$. Since January 19, 2020, various containment measures have been strictly implemented, especially after the State Council agreed to include COVID-19 into the Management of the Infectious Diseases Law and the Health and Quarantine Law on January 20. Wuhan was locked down on January 23, and the inter-provincial flow of people was greatly reduced (https://qianxi.baidu.com). which effectively controlled the exportation of infected individuals. Based on an average 13.91-day infectious period estimate from our collected data, we expect a flatter rate of increment starting from the end of January. Fig. 2 plots the number of daily new cases on a log-scale against date, and, as anticipated, the trend supports this estimate. Therefore, the basic reproduction number $R_0$ and the early-phase controlled reproduction number $R_c$, are estimated based on collected data in two separate periods, i.e., from January 21 (the starting date of daily updates of confirmed cases nationwide) to January 28, and from January 29 to February 5 respectively.

Fig. 2.

Visualization of daily numbers of new confirmed case along with date, as obvious change of rate occurred on January 29 as expected.

The estimates of $R_0$ and $R_c$ by Poisson likelihood (ML), exponential growth rate (EGR) and Susceptible-Infected-Removed (SIR) model in selected regions of China are listed in Table 2 and Table 3 . Despite the disagreement between different estimation methods, all three methods indicate notable reductions from $R_0$ to $R_c$ which suggests an improvement from January 21 to February 5. This is possibly due to the effective interventions and prompt actions by the local and central governments to minimize further spreading. We also notice that EGR yields smaller estimates of $R_c$ compared to other methods. This might be because the number of infected patients does not grow exponentially after such strict containment measures, hence EGR is only recommended to estimate $R_c$ in early stage of an epidemic.

Table 2.

Estimates and 95% confidence intervals of basic reproduction number in some selected provinces (or cities) of China, from Jan 21 to Jan 28, 2020.

	ML	EGR	SIR
Hubei	2.73 (2.06, 3.61)	3.63 (2.56, 5.22)	6.8 (5.1, 8.5)
Beijing	2.13 (1.53, 2.81)	1.74 (0.57, 3.26)	2.7 (1.0, 4.6)
Shanghai	2.24 (1.56, 2.95)	1.92 (0.88, 3.30)	2.8 (1.0, 4.5)
Guangdong	2.44 (1.82, 3.15)	2.77 (1.59, 4.40)	4.5 (3.2, 6.0)
Zhejiang	2.67 (2.02, 3.48)	3.03 (1.43, 5.26)	6.2 (3.9, 8.7)
Henan	2.38 (1.80, 3.10)	3.41 (1.45, 6.03)	7.8 (4.1, 12.8)

Table 3.

Estimates and 95% confidence intervals of controlled reproduction number in some selected provinces (or cities) of China, from Jan 29 to Feb 5, 2020.

	ML	EGR	SIR
Hubei	2.34 (1.93, 2.83)	1.78 (1.40, 2.27)	3.3 (3.0, 3.7)
Beijing	1.96 (1.53, 2.45)	1.29 (0.33, 2.61)	2.3 (0.9, 4.0)
Shanghai	1.78 (1.39, 2.21)	0.77 (0.40, 1.18)	1.1 (0.4, 2.2)
Guangdong	1.88 (1.54, 2.25)	0.92 (0.52, 1.38)	1.1 (0.5, 2.0)
Zhejiang	1.56 (1.27, 1.86)	0.58 (0.21, 1.03)	0.8 (0.1, 1.6)
Henan	1.93 (1.58, 2.36)	1.08 (0.75, 1.47)	1.6 (1.0, 2.3)

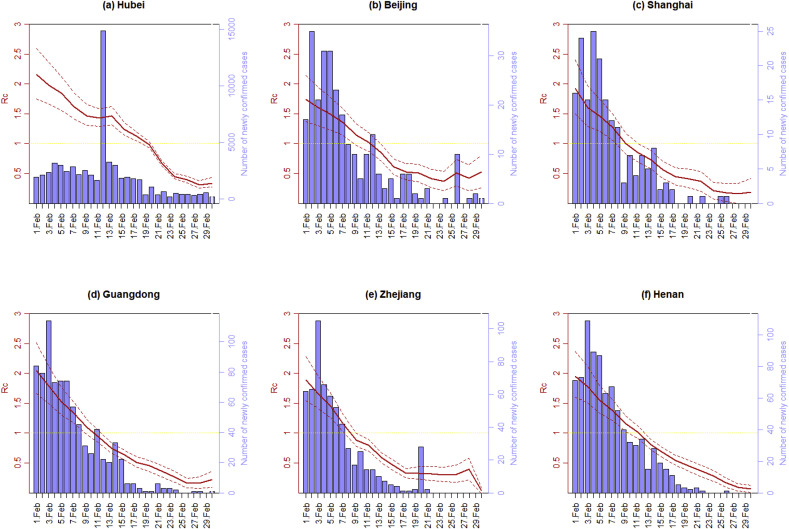
Furthermore, the time-varying controlled reproduction number $R_c\left(t\right)$ can be estimated through the Poisson likelihood (ML) method where $t$ is from February 1 to 29, 2020. Note that there were very few new cases confirmed outside Hubei Province since March 1, 2020, hence we only updated $R_c\left(t\right)$ up to February 29, 2020. For each Day $t$, the number of daily reported new cases from Day $t-9$ to Day$t$ is used to estimate ${\hat{R}}_c\left(t\right)$. Fig. 3 plots the estimated controlled reproduction number ${\hat{R}}_c\left(t\right)$ along with its 95% confidence interval (CI) for selected regions of China. Note that the estimated ${\hat{R}}_c\left(t\right)$ reflects the average spreading ability of the epidemic in a short period prior to Day $t$. As a result, the real-time $R_c\left(t\right)$ might be overestimated if the general trend of $R_c\left(t\right)$ is declining.

Fig. 3.

The number of daily confirmed cases and estimated controlled reproduction number in (a) Hubei, (b) Beijing, (c) Shanghai, (d) Guangdong, (e) Zhejiang, and (f) Henan. The dashed line is the 95% confidence interval.

6. Conclusion

Despite the continuous increase in new confirmed cases between January 21, 2020 and February 5, 2020, the estimated controlled reproduction numbers $R_c$ produced by all three methods in all analyzed regions are significantly smaller compared with the basic reproduction numbers $R_0$. We can see that outside Hubei Province, $R_c\left(t\right)$ dropped below 1 around February 11, 2020 while in Hubei $R_c\left(t\right)$ fell below 1 around February 19, 2020, which indicates that the containment measure carried out by Chinese government was effective and efficient. The controlled reproduction numbers $R_c$ is now much lower than one in all regions of China for quite a time, however, it has yet reached zero. A possible explanation is that the number of foreign imported cases has grown significantly since late February, and posed a high risk of a second outbreak. Efforts are needed in order to end the current epidemic, especially improving quarantine measures at the border.

7. Discussion

In this study, we estimated the reproduction number of COVID-19 in China based on three approaches, namely Poisson likelihood-based method (ML), exponential growth rate-based method (EGR) and stochastic Susceptible-Infected-Removed dynamic model-based method (SIR). The EGR method can be only used at the early period of an epidemic, when the number of confirmed cases grows exponentially. The SIR method is not able to provide a time-varying reproduction number, and as existing literature on COVID-19 showed that SIR model is likely to overestimate the basic reproduction number since a large proportion of susceptible cases were isolated due to the strong control measures implemented (Wu et al., 2020, Tang et al., 2020a, Tang et al., 2020b). Hence, ML method is preferred in this study. Note that this study omits the effect of human mobility before the lockdown starting from January 23, 2020, which may cause an overestimation of the basic reproduction outside Hubei. A more realistic transmission model with spatial spread such as metapopulation disease model can be used but this is beyond the scope of this study (Balcan et al., 2010).

The dataset used in this study is based on the confirmed cases reported by the NHC of China. However, during our period of data collection, the official guidelines for diagnosis and treatment of COVID-2019 underwent six updates. The criteria of confirmation have evolved from the original “whole genome sequencing of the respiratory excretion” to “positive viral nucleic acid results by the RT-PCR of the respiratory excretion or viral gene sequence” in the 5th edition, and, as of now, the inclusion of positive nucleic acid results of the blood sample. The confirmation process has been simplified by the removal of the accreditation process by the national expert committee for confirmed cases. The fourth edition of the official guidelines for diagnosis and treatment granted the accrediting authority to municipalities (National Health Commission of, 2020). In addition, the medical resources in Hubei Province especially in Wuhan received a remarkable boost from early February 2020. All of these changes might result in a temporary surge of confirmed cases and lead to an overestimation of $R_c$ during mid of February, especially in Hubei Province.

The current containment measures in China mainly aim to cut the transmission from human to human via respiratory droplets and have received a significant success by reducing the reproduction number below one in 30 days from the implementation of measures (namely February 19, 2020). However, other transmission pathways, including fecal-oral transmission and aerosol transmission, could not yet be excluded based on current evidence. If other transmission mechanisms do exist, the $R_c$ values could increase in the future unless further measures would intersect these transmission pathways. China NHC have started to report the number of asymptomatic cases since April 1. The asymptomatic cases are typically hard to detect. If asymptomatic cases are not isolated, there may be a second chance of outbreak. Note the incubation period, serial intervals and infectious period estimated in this study only apply to symptomatic patients. Furthermore, despite that the outbreak has been effectively contained currently in China, the number of imported cases will potentially grow with the development of global pandemic. As reported by China NHC, there are totally 788 confirmed imported cases and 4 domestic cases related to these imported cases during March 2020. In brief, the main goal of epidemic prevention in China has shifted from preventing the transmission of domestic confirmed cases to prevention of the spread of asymptomatic cases and foreign imported cases.

Funding information

This research is supported by National Natural Science Foundation of China grant 8204100362 and Zhejiang University special scientific research fund for COVID-19 prevention and control.

Role of funding source

NA.

Ethics committee approval

Not required.

Authors’ contributions

Chong You: data collection, writing. Yuhao Deng: writing, data analysis. Wenjie Hu: data analysis. Jiarui Sun: data analysis. Qiushi Lin: data collection. Feng Zhou: data collection. Cheng Heng Pang: writing. Yuan Zhang: writing. Zhengchao Chen: wrting. Xiao-Hua Zhou: overall design.

Declaration of competing interest

We have no financial relationships (regardless of amount of compensation) with any entities. There is no conflict of interest.