Large H₂O solubility in dense silica and its implications for the interiors of water-rich planets

Significance

Astrophysical observations have shown that Neptune-like planets are common in our galaxy (sub-Neptunes). Some of these exoplanets are believed to be covered with a thick ${\mathrm{H}}_2$O layer (100 to 1,000 km in thickness) above the rocky mantle (“waterworlds”). In order to understand the inner workings of the water-rich planets, it is important to understand the state of matter incorporating ice- and rock-forming elements at high-pressure and high-temperature conditions. Here, we report experimental evidence that silica and water have significant mutual solubility at high pressure and high temperature, forming new phases containing substantial amounts of both H and Si in oxide forms. Therefore, the boundary between rock and ice layers may be “fuzzy” at the deep interiors of water-rich planets.

Abstract

Sub-Neptunes are common among the discovered exoplanets. However, lack of knowledge on the state of matter in ${\mathrm{H}}_2$O-rich setting at high pressures and temperatures ($P-T$) places important limitations on our understanding of this planet type. We have conducted experiments for reactions between ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ and ${\mathrm{H}}_2$O as archetypal materials for rock and ice, respectively, at high $P-T$. We found anomalously expanded volumes of dense silica (up to 4%) recovered from hydrothermal synthesis above $\sim$24 GPa where the ${\mathrm{C}\mathrm{a}\mathrm{C}\mathrm{l}}_2$-type (Ct) structure appears at lower pressures than in the anhydrous system. Infrared spectroscopy identified strong OH modes from the dense silica samples. Both previous experiments and our density functional theory calculations support up to 0.48 hydrogen atoms per formula unit of (${\mathrm{S}\mathrm{i}}_{1-x}{\mathrm{H}}_{4x}$)${\mathrm{O}}_2\hspace{0.17em}\left(x=0.12\right)$. At pressures above 60 GPa, ${\mathrm{H}}_2$O further changes the structural behavior of silica, stabilizing a niccolite-type structure, which is unquenchable. From unit-cell volume and phase equilibrium considerations, we infer that the niccolite-type phase may contain H with an amount at least comparable with or higher than that of the Ct phase. Our results suggest that the phases containing both hydrogen and lithophile elements could be the dominant materials in the interiors of water-rich planets. Even for fully layered cases, the large mutual solubility could make the boundary between rock and ice layers fuzzy. Therefore, the physical properties of the new phases that we report here would be important for understanding dynamics, geochemical cycle, and dynamo generation in water-rich planets.

The discovery of exoplanets with diverse sizes and compositions calls for a major revision of the theories of planets (1). Such an effort requires knowledge of the properties of a wide range of materials over an extreme range of pressure–temperature–composition $\left(P-T-X\right)$ conditions beyond those expected for the Earth. This highlights the importance of understanding the fundamental building blocks of planets spanning a range of conditions much broader than considered to date.

Along with gases (hydrogen and helium) and metals (iron metal and alloys), rocks (silicates, oxides, and even carbides) and ices (water, methane, and ammonia) are the main building materials of planets. Although silicates and water can react and form hydrous silicates at the surface of planets, it has been assumed that their mutual solubility is limited at the elevated $P-T$ conditions of the planetary interiors. Therefore, due to their large density difference, they would form separate layers. For example, standard models for the internal structures of Uranus and Neptune, water-rich planets in our solar system, have assumed separate layers of ice and rock (2). However, in order to explain the low luminosity of Uranus, recent models included a compositional gradient in the thick ice layer (3, 4). Although rock-forming heavy elements were assumed for the compositional gradient and therefore, the properties of rock were used as a component for a mechanical mixture, the exact state of matter under such ${\mathrm{H}}_2$O-rich high $P-T$ conditions remains unknown. Can ice and rock react with each other under such conditions? If such reactions occur, how much of the deep rocky layer can be hydrated, and what components in the rocky layer and how much of them can be dissolved into the ice layer? Understanding such high-pressure processes has become even more important as a significant population of exoplanets has very thick layers of ices (5, 6) (e.g., waterworlds and sub-Neptunes). Even multiples of waterworld planets have been proposed for a single planetary system, TRAPPIST-1 (7).

${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ and ${\mathrm{H}}_2$O have been extensively studied individually at high $P-T$ as archetypal materials for rocks and ices, respectively. Although a significant amount of ${\mathrm{H}}_2$O (up to $\sim 3.2$ wt %) has been documented in pure stishovite (Stv) below 10 GPa (8–10), the behavior of the ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$–${\mathrm{H}}_2$O system is unknown at higher pressures, including above the stability field of Stv. The importance of studying ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ + ${\mathrm{H}}_2$O reactions can be further emphasized by the striking fact that many dense hydrosilicate and hydroxide phases discovered at high pressures have crystal structures also found in the high-pressure phase diagram of ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$. For example, H-${\mathrm{M}\mathrm{g}\mathrm{S}\mathrm{i}\mathrm{O}}_2$ (OH)₂ (or phase H), $\delta$-AlOOH, and $ϵ$-FeOOH (11–13) are based on a ${\mathrm{C}\mathrm{a}\mathrm{C}\mathrm{l}}_2$-type (Ct) structure, which can also be found at pressures above 50 to 80 GPa in ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ (14, 15). Another example is pyrite-type FeOOH, which is stable at pressures above 80 GPa (16, 17). In ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$, the pyrite-type structure is stable above 268 GPa (18). The stability of the pyrite-type structure was also predicted for AlOOH (19). Here, we report a significant solubility of ${\mathrm{H}}_2$O in dense ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ polymorphs at pressures greater than 24 GPa. We also found that the ${\mathrm{H}}_2$O incorporation in the crystal structure of ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ alters its phase behavior at high $P-T$. We will discuss the implications of these findings for the internal structures of water-rich planets.

To investigate the solubility of ${\mathrm{H}}_2$O in dense polymorphs of ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$, we conducted experiments in the laser-heated diamond anvil cell (LHDAC) (Methods and SI Appendix, Table S1). At 45 GPa and 1740 K, we observed the formation of a pure phase with a Ct structure after 33 min of heating of a hydrous silica gel (hGel) starting material in a neon (Ne) medium (Fig. 1A; Methods discusses different starting materials and other experimental details). In anhydrous ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$, the Ct phase appears only above 70 GPa at the same temperature (14), suggesting that ${\mathrm{H}}_2$O reduces the Stv-to-Ct transition pressure by at least 20 GPa.

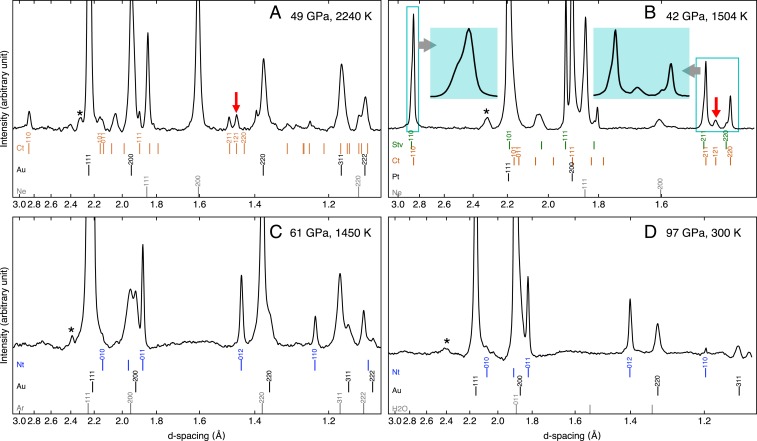
Fig. 1.

XRD patterns of hydrous silica polymorphs at high pressures. (A) Ct phase, (B) Stv + Ct phases, and (C and D) Nt phase. The ticks at the bottom of the diffraction patterns show the expected peak positions of Stv (green), Ct (orange), Nt (blue), pressure standard (black), and pressure medium (gray). B, Insets in light blue show two key areas for phase identification. The red arrows in A and B highlight the diagnostic 121 line of the Ct phase. The Miller indices are shown for the lines with more than 10% intensities. The backgrounds of the patterns are subtracted. The wavelength of the X-ray beam is 0.3344 Å except for in B, where 0.4066 Å was used. The pressures and temperatures presented here are for individual diffraction patterns, while the values shown in SI Appendix, Table S1 are averages over heating cycles. *These peaks are from laser mirrors.

Among the new peaks and peak splitting, we observed that, for orthorhombic Ct phase (SI Appendix, section 1), the most notable diffraction feature is the 121 line (red arrow in Fig. 1A). In anhydrous Ct, the $121_{\mathrm{C}\mathrm{t}}$ line appears as a shoulder of the $211_{\mathrm{S}\mathrm{t}\mathrm{v}}$ line at 63 GPa (the subscript after the Miller index distinguishes phases). In hydrothermally synthesized Ct, we found that the line appears approximately halfway between the $211_{\mathrm{S}\mathrm{t}\mathrm{v}}$ and $220_{\mathrm{S}\mathrm{t}\mathrm{v}}$ lines, being clearly resolved without any peak overlaps with the Stv lines. Such a large separation of the 121 line leads to significantly larger axial ratios of the hydrothermally synthesized Ct at lower pressures compared with those of anhydrous Ct, resembling the axial ratios expected at much higher pressures in the anhydrous system (Fig. 2A and SI Appendix, Table S2). For example, the $c/b$ ratio of hydrothermally synthesized Ct at 45 GPa is comparable with that of anhydrous Ct at $\sim$100 GPa.

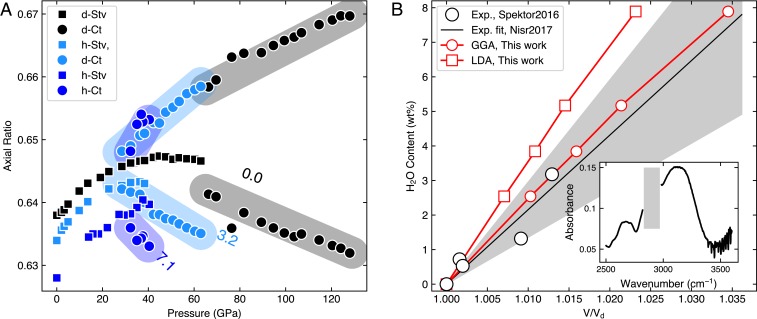
Fig. 2.

Effects of ${\mathrm{H}}_2$O incorporation on the Ct phase. (A) The axial ratios of Stv (squares) and Ct (circles) measured during decompression. The greater and smaller values for Ct are $c/a$ and $c/b$, respectively. The numbers are the weight percentage of ${\mathrm{H}}_2$O contained in dense silica polymorphs: 0% from ref. 20 and 3.2% from ref. 10. (B) Relationship between unit-cell volume expansion $\left(V/V_d\right)$ ($V_d$ is the unit-cell volume of dStv) and ${\mathrm{H}}_2$O content constructed from TGA and IR measurements (9, 21) (black circles). The gray area indicates $2\sigma$ uncertainties in the line fit of the data. We also include our DFT calculations (red symbols) for comparison. Inset shows the IR-active OH vibrational modes detected from a sample recovered from 45 GPa and 1740 K (the C–H peaks from diamond anvils and IR optics were masked with the gray rectangle). Some of the peak fitting results for A are presented in SI Appendix, Table S4. LDA, local density approximation. GGA, generalized gradient approximation.

During decompression of the sample, diffraction patterns showed that Ct converts to Stv near 1 GPa. At 1 bar, only a few Ct peaks remained in the diffraction pattern as weak features. The unit-cell volume fit to Stv was much larger (3.2%) than that of anhydrous stishovite (dStv) at 1 bar. Former studies have shown that the unit-cell volume of Stv linearly increases with the amount of structurally incorporated ${\mathrm{H}}_2$O up to 2.3% (8, 9). The infrared (IR) spectrum that we obtained from the recovered sample from pure Ct showed clear OH vibrational modes (Fig. 2B), providing direct evidence for the structural incorporation of OH in the sample (SI Appendix, section 2). Together, these observations support significantly enhanced solubility of ${\mathrm{H}}_2$O in the Ct phase compared with Stv.

In a heating run of a dStv starting material immersed in an ${\mathrm{H}}_2$O medium at 51 GPa and 2086 K, we observed progressive conversion of Stv to Ct, although we could not heat long enough for a complete transformation. IR of the recovered sample showed weaker but clear OH vibrational modes (SI Appendix, Fig. S1). In anhydrous ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ at high temperatures and 50 GPa, Stv is stable instead of Ct (14). The outcome of this heating run is significant because it shows that the hydration of Stv through a phase transition to Ct occurs stably by progressive hydration at this $P-T$ condition.

In other heating runs at pressures between 42 and 56 GPa, we observed both Stv and Ct (Fig. 1B). These heating runs were, however, conducted for shorter durations and therefore, could represent an incomplete hydration leading to an incomplete transformation from Stv to Ct. In these runs, the Ct lines gained intensity with time, while those of Stv decreased, further supporting the argument. Alternatively, some of these runs could have sampled an Stv + Ct mixed phase in the ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$–${\mathrm{H}}_2$O phase diagram, although the runs with free ${\mathrm{H}}_2$O as a medium could have reached saturation to a single phase with maximum ${\mathrm{H}}_2$O content if the reaction time was sufficient enough. In anhydrous ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$, the Stv-to-Ct transition is displacive and therefore, does not exhibit a mixed-phase region (22). However, structurally incorporated ${\mathrm{H}}_2$O can lead to a compositional gap between Stv and Ct because composition is an extensive quantity (23). In our lowest-pressure diamond anvil cell (DAC) run at 24 GPa, the diffraction lines of Stv appeared first from an anhydrous glass + ${\mathrm{H}}_2$O starting mixture at the beginning of the laser heating. With further heating, some Ct lines appeared in the diffraction patterns (Fig. 1B, Insets). In the recovered sample, we found two Stv phases with different unit-cell volumes (therefore, different ${\mathrm{H}}_2$O contents). We were also able to quench two-phase assemblages from 48 GPa. The observation supports a mixed phase region for Stv + Ct in the ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$–${\mathrm{H}}_2$O system.

We successfully quenched all of the samples with the Ct phase to 1 bar and found that they consistently revert back to Stv on decompression. The unit-cell volumes of the samples recovered to 1 bar (in Stv) were systematically greater than that of dStv by up to 3.9% (Fig. 2B). We also found a strong negative correlation between the unit-cell volume expansion and the $c/a$ ratio measured at 1 bar for the recovered samples in Stv (SI Appendix, Fig. S3). ${\mathrm{H}}_2$O incorporation increased the $a$ axis, while the $c$ axis remained almost unaffected, thereby decreasing the $c/a$ ratio. This trend has also been found for hydrous Stv samples at lower pressures (8). The strong correlation between the structural parameters observed from the recovered samples (SI Appendix, Fig. S3) indicates that 1) OH is incorporated as a structural component in the Ct phase and that 2) the substitution mechanism remains likely the same between 24 and 56 GPa.

Through direct measurements of ${\mathrm{H}}_2$O contents for the large quantity of the hydrous Stv samples synthesized in multianvil press, former studies (8, 9, 21) have found a linear relationship between ${\mathrm{H}}_2$O content and volume expansion, providing a way to estimate the ${\mathrm{H}}_2$O content from the measured unit-cell volume (SI Appendix, section 3). We obtained the unit-cell volumes of all of the recovered samples from Rietveld refinements. As shown in SI Appendix, Fig. S2, it is already clear from the raw diffraction patterns that the Stv peaks of the samples recovered from hydrothermal synthesis of Ct are systematically shifted to higher $d$ spacings from those expected for dStv. Combining the calibration in Fig. 2B and the measured unit-cell volume expansions, we found 0.4 to 8.4 wt % ${\mathrm{H}}_2$O in the recovered samples.

In order to further examine the relationship between the ${\mathrm{H}}_2$O content and the unit-cell volume expansion, we conducted density functional theory (DFT) calculations (Methods and SI Appendix, section 4) for a total of six different crystal structure models with ${\mathrm{H}}_2$O contents of 0 to 7.89 wt %. Despite some limitations in the calculated models and the temperature differences (experimental data at 300 K and DFT data at 0 K without zero-point motion), the volume expansion caused by ${\mathrm{H}}_2$O predicted by our DFT calculations agrees very well with our experimental results (Fig. 2B). We extrapolated the ${\mathrm{H}}_2$O and unit-cell volume expansion relationship on the recovered Stv for evaluating the ${\mathrm{H}}_2$O content of the high-pressure Ct phase. At the moment the method is the only plausible way, because the pressure stability of Ct is too high for the existing high-pressure apparatus to produce sufficient quantities of samples for the ${\mathrm{H}}_2$O content characterization through thermogravimetric analysis (TGA). IR of the LHDAC samples for the quantification also has a few significant uncertainty sources (SI Appendix, section 5).

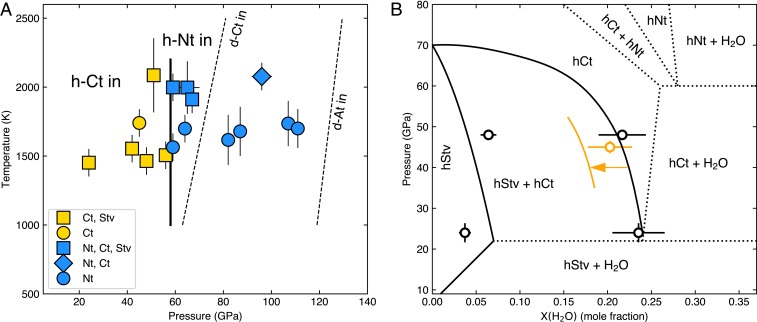
The inferred ${\mathrm{H}}_2$O contents for our samples allowed us to further investigate the ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$–${\mathrm{H}}_2$O phase relations, although the data points are limited, and the partial reactions and ambiguities in the bulk ${\mathrm{H}}_2$O content at the laser spot make detailed constructions difficult (SI Appendix, section 6). In two of the recovered samples, X-ray diffraction (XRD) identified two Stv phases with different unit-cell parameters. In situ diffraction patterns showed that both Stv and Ct were present during laser heating at high pressure. Therefore, one of the Stv phases in the quenched sample should be the conversion product of the Ct phase during decompression. Because pure Ct can contain a much larger amount of ${\mathrm{H}}_2$O than Stv as discussed above (SI Appendix, Table S1), the Stv phases with larger unit-cell volumes are likely converted from Ct during decompression. Based on these observational constraints, we constructed a provisional binary $P-X\left({\mathrm{S}\mathrm{i}\mathrm{O}}_2\right)$ phase diagram at 1,400 to 1,500 K in Fig. 3B, where a large mixed-phase region of Stv + Ct is expected to be found.

Fig. 3.

Conditions for observations of different hydrous silica phases. (A) Pressure–temperature conditions for the observations of different phases. The error bars are the $1\sigma$ estimated uncertainties. The vertical lines show the pressures where new polymorphs begin to appear. The phase boundaries in the anhydrous ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ system (thin dashed lines) are shown for comparison (14, 15). (B) A provisional phase diagram of ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$–${\mathrm{H}}_2$O at 1400 to 1500 K (SI Appendix, section 6 has details). Although temperature is different, we also considered a data point with pure Ct from LHDAC (orange circle, $\sim$1700 K). The data point provides insights on temperature-dependent changes of the phase boundaries. d, anhydrous; h, hydrous.

At 59 GPa and 1564 K, the diffraction patterns became remarkably simpler (Fig. 1C). For example, the most intense peak, 110, of Stv and Ct and some diagnostic Ct peaks, such as 211 and 220, were systematically absent. The observed peaks were well indexed with a hexagonal niccolite-type (Nt) structure. In three separate experiments performed between 59 and 67 GPa at higher temperatures, we found the Nt and Ct phases together (with possibly weak Stv peaks), indicating that these conditions may be close to the Ct-to-Nt phase boundary. An extra silica peak, 111, persisted in some of these runs and may correspond to either some remaining Stv or a second Ct phase with less incorporated ${\mathrm{H}}_2$O. At 65 GPa and 1997 K, we observed both Stv and Ct peaks at the beginning of the laser heating. The Nt peaks appeared and intensified with further heating, suggesting that the Nt phase is stable at these $P$–$T$ conditions (SI Appendix, Fig. S4).

At 64 to 111 GPa and 1600 to 1700 K, pure Nt phase formed within 0 to 2 min of heating in an ${\mathrm{H}}_2$O medium and remained without the appearance of other silica polymorphs for up to 33 min of heating (Fig. 1D). The observation suggests that the reaction kinetics of Nt formation are more favorable and also indicates that Nt is the solid phase present at saturation in the ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$–${\mathrm{H}}_2$O system above 59 GPa (Fig. 3B).

The Nt phase has been previously reported in some high-pressure experiments on silica (24–26). In earlier experiments, the phase was found in recovered samples from 20 to 40 GPa at unknown temperatures. In more controlled experiments, Nt was synthesized at 30 to 60 GPa but only in the narrow range of 1000 to 1300 K for a heating duration less than 10 min (26). At higher temperatures, it transformed to either Stv or Ct. In our experiments, the Nt phase was stable for a longer heating duration (33 min), at higher temperatures (1500 to 2000 K), for a wider pressure range (59 to 111 GPa), and most importantly, in the presence of ${\mathrm{H}}_2$O. The previous study that observed a disordered Nt phase did not document the ${\mathrm{H}}_2$O content of the starting materials. It is possible that some ${\mathrm{H}}_2$O was present to stabilize that phase or that the Nt phase can occur metastably in anhydrous ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ under restricted conditions. For example, in an experiment for a starting material setup with a restricted amount of ${\mathrm{H}}_2$O (a hydrous gel starting material without an ${\mathrm{H}}_2$O medium) at 96 GPa and 2077 K, we observed peaks from both Ct and Nt for 15 min of heating. The observation of the Ct phase in this run is likely associated with the lack of ${\mathrm{H}}_2$O medium (no thermal insulation) and therefore, insufficient amount of ${\mathrm{H}}_2$O.

Like the Ct phase, the Nt phase is not recoverable. Many samples lose crystallinity at pressures below 1 GPa, but in one case, an Nt sample, synthesized at 107 GPa and 1736 K, was successfully decompressed, and the diffraction patterns were measured to 1.3 GPa. The molar volume of the Nt phase measured at 1.3 GPa was 3.9% greater than those of dStv at 1 bar. However, at pressures above $\sim$60 GPa, the molar volume of Nt was systematically smaller than those of dStv and Ct. Compared with the volume extrapolated from the equation of state of Ct with 3.2% ${\mathrm{H}}_2$O (10), the volume of the Nt phase is also systematically smaller. From the fitting of the decompression data to the Birch–Murnaghan equation (SI Appendix, section 7 and Table S3), we found a bulk modulus of 239 $\pm$ 6 GPa, which is 30 to 40% smaller than that of dStv and Ct (310 and 334 GPa, respectively) (20). In view of previous observations that ${\mathrm{H}}_2$O can increase the molar volume but decrease the bulk modulus in the ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ phases (10), the observations of the large molar volume and the reduced bulk modulus found in Nt are consistent with a significant ${\mathrm{H}}_2$O solubility. The measured volumes of the Nt phase at 70 to 95 GPa are greater than those extrapolated from the stable pressures of the $\alpha$-${\mathrm{P}\mathrm{b}\mathrm{O}}_2$-type (At) phase reported in anhydrous ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ at pressures above 130 GPa, which can be interpreted as the volume expansion induced by ${\mathrm{H}}_2$O incorporation. Interestingly, because of the lower bulk modulus, the volume of Nt approaches that of the anhydrous At phase with compression (SI Appendix, Fig. S5).

Although the extrapolation is indirect, we can estimate the ${\mathrm{H}}_2$O content from the measured volume at 1.3 GPa. Compared with the reported unit-cell parameters of the Nt phase at 1 bar in earlier experiments and assuming that the phase is an anhydrous form, the molar volume of our Nt phase at 1.3 GPa is 3.5% greater. In comparison with anhydrous At (15), the molar volume of the Nt phase at 1.3 GPa is 5.5% greater. Assuming the same degree of volume expansion induced by ${\mathrm{H}}_2$O incorporation between Nt and Ct, we obtained 7.6 to 11.6 wt % ${\mathrm{H}}_2$O in the Nt phase depending on the synthesis of $P$–$T$ conditions of the sample. However, the relative amount of incorporation is likely not the same because of the difference in the crystal structure. Nevertheless, the estimates are consistent with an amount of ${\mathrm{H}}_2$O at least similar to what we found in the Ct phase, supporting the idea that the solubility of ${\mathrm{H}}_2$O in silica polymorphs remains significant at higher pressures. Additionally, the appearance of Nt instead of Ct at ${\mathrm{H}}_2$O saturation above 56 GPa may also indicate a higher ${\mathrm{H}}_2$O content than in the Ct phase, which is still stable under these conditions for the ${\mathrm{H}}_2$O-undersaturated system.

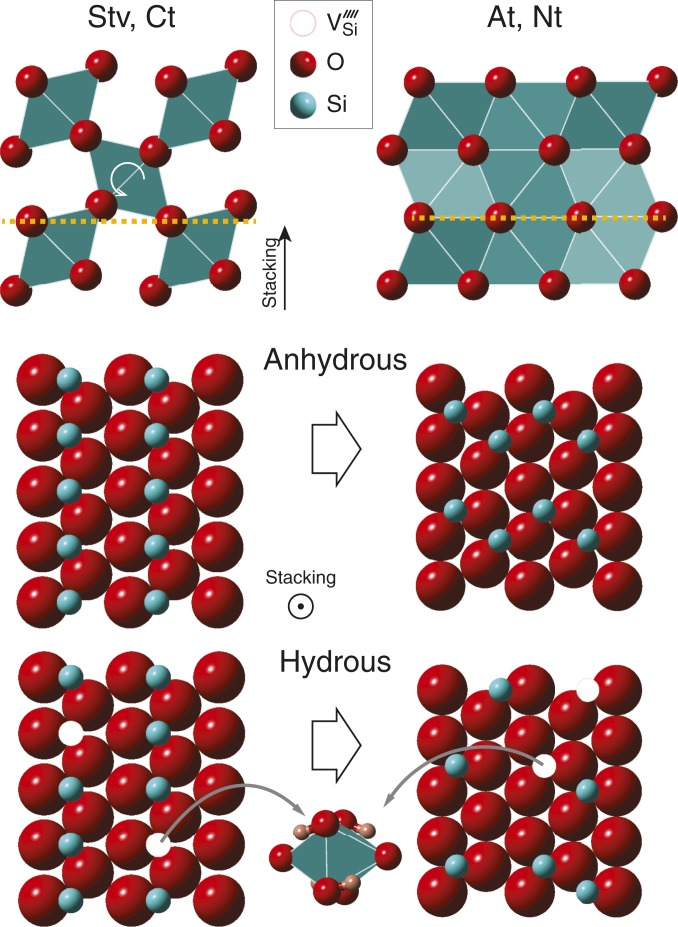
Our study showed that the large amount of ${\mathrm{H}}_2$O incorporated into the crystal structure of dense silica increases the orthorhombic distortion of the Ct phase and alters the sequence of high-pressure phase transitions, resulting in the stabilization of Nt, which is not stable in anhydrous ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$. The oxygen sublattice of the rutile-type Stv is an 11-coordinated sphere packing, consisting of puckered O layers (27) (Fig. 4). In anhydrous ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ through a sequence of phase transitions Stv $\to$ Ct $\to$ At with an increase in pressure, the oxygen layers become planar hexagonal nets (therefore, 12-coordinated sphere packing). The oxygen layer is not completely planar in Ct, but in its stability field, the oxygen atoms gradually move toward the hexagonal close packed (hcp)-layer positions through the rotation of the ${\mathrm{S}\mathrm{i}\mathrm{O}}_6$ octahedra. Such structural evolution in the Ct stability field manifests in the diverging trends between the $c/a$ and $c/b$ ratios with compression (10), which ultimately leads to the phase transition to At with the flat O layers in anhydrous ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ (Fig. 4). The alternation of empty and Si-filled octahedral sites in Stv and Ct also plays an important role for the puckered O layers in those structures. In At, however, the zigzag distribution of the Si atoms prevents such uneven charge distribution, allowing a planar O distribution.

Fig. 4.

Effect of ${\mathrm{H}}_2$O on the crystal structure of dense silica polymorphs. Top shows changes from the puckered to the flat O layers during the phase transition from Stv/Ct to At/Nt as viewed perpendicular to the stacking direction of the O layers. The orange dashed line is a guide for the eye, and the white arrow highlights the rotation of the ${\mathrm{S}\mathrm{i}\mathrm{O}}_6$ octahedra with compression. Middle and Bottom show the changes in the arrangement of the Si atoms during the phase transition for anhydrous and hydrous silica, respectively. In hydrous silica, the direct substitution of ${\mathrm{S}\mathrm{i}}^{4+}$ for 4${\mathrm{H}}^{+}$ (white circles in Bottom and an octahedron at Bottom Center) can result in the disordering of Si in the octahedral sites, stabilizing Nt instead of At.

In the hydrous Ct phase, we found similar but more rapid divergence of the $c/a$ and $c/b$ ratios (Fig. 2A). For less hydrated Ct, the same trend was found but at systematically higher pressure than the more hydrated Ct, suggesting that H substitution promotes the flattening of the O layer at lower pressures. However, the hydrous Ct phase transforms to an Nt structure instead of the At phase. In an Nt structure, anion spheres can arrange in hcp similar to At. An important difference is that in Nt the Si atoms occupy the octahedral site randomly, leading to a more uniform charge distribution than what is found in Stv and Ct. In hydrous dense silica, Spektor et al. (8) suggested that H atoms enter the crystal structure through direct substitution (${\mathrm{S}\mathrm{i}}^{4+}\hspace{0.17em}\to$ 4${\mathrm{H}}^{+}$) in which they form bonds with four O atoms around an Si defect site, therefore (${\mathrm{S}\mathrm{i}}_{1-x}{\mathrm{H}}_{4x}$)${\mathrm{O}}_2$ (Fig. 4). Based on this mechanism, we estimated up to $x\simeq 0.12$ for the Ct and also likely Nt phases from experimental data and DFT calculations. Such a large amount of H would be sufficient to induce or promote a random distribution of Si atoms in silica, changing the transition paths. In this scenario, the solubility of ${\mathrm{H}}_2$O leads to different Si atom distribution motifs, leading to a different phase (Nt) in order to achieve the same structural evolution via planarization of the O layers. In this context, ${\mathrm{H}}_2$O dramatically reduces the transition pressure to flat O layers to 60 from 130 GPa.

The large amount of ${\mathrm{H}}_2$O found in the Ct phase in Al-free silica is also in line with the recent findings of hydrous phases in the same type of structure, such as $\delta$-AlOOH, $ϵ$-FeOOH, and H-${\mathrm{M}\mathrm{g}\mathrm{S}\mathrm{i}\mathrm{O}}_2$ (OH)₂ (or phase H) (11, 13, 17), in that the Ct structure may provide a favorable environment for H₂O solubility. In those hydrous phases, a pyrite-type structure has been suggested as a possible higher-pressure phase of Ct (17, 19). However, in SiO₂, the Nt phase becomes stable at higher pressures despite the fact that anhydrous silica has a stability field for the pyrite-type structure at those pressures (18). The difference is likely related to the crystallographic sites that hydrogen can occupy. In the hydroxide phases, hydrogen atoms occupy empty octahedral sites in Ct, and there is one H atom per empty octahedron. For pure silica, Spektor et al. (8) proposed a direct substitution of 4${\mathrm{H}}^{+}$ for a ${\mathrm{S}\mathrm{i}}^{4+}$ from spectroscopy data (Fig. 4). As discussed above, direct substitution is more compatible with the Nt phase because the H atoms create Si defects and assist the disordering of Si necessary for the Nt structure to stabilize. However, we do not exclude the possibility of a stable pyrite-type structure in hydrous silica at even higher pressures.

Standard models have assumed separate layers of ice and rock in water-rich planets, such as the ice giants in our solar system (Uranus and Neptune), sub-Neptune exoplanets, and waterworld exoplanets. According to our result, the enhanced solubility of ${\mathrm{H}}_2$O in silica can open up the possibility of a “fuzzy” boundary between the ice layer and the rocky layer. A range of potentially water-rich exoplanets may have this fuzzy boundary between ice and rock or even a “diluted” rocky layer. The pressure ranges estimated for the ice–rock interface are $\sim$25 GPa for TRAPPIST-1c and -1f (28) and $\sim$120 GPa for GJ1214b (29, 30), which are close the pressure range of our experiments. Therefore, it is of particular interest to include the phase behaviors found in this study in the future structural and dynamic models of these exoplanets.

If the interior of a water-rich planet is not well differentiated as some models have invoked for Uranus (3, 4), mutual solubility of water and silica can even open up a possibility for a single high metallicity layer where ${\mathrm{H}}_2$O ice at shallower depths undergoes a gradual change to hydrous silica at greater depths, assuming increasing mutual solubility of ${\mathrm{H}}_2$O and ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ with pressure. Accordingly, we propose that the Uranus models should incorporate the effects of significant mutual solubility between ${\mathrm{H}}_2$O and ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ that we report here.

In order to further develop our understanding on the mineralogy of water-rich planets, it is important to consider other major lithophile elements, such as Mg. Some exoplanet hosting stars have sufficiently low Mg/Si ratios, and therefore, water-rich planets around those stars could have rocks with sufficient ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ to form free silica phases (31). In this case, our study reported here on the ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$–${\mathrm{H}}_2$O system would have direct implications.

If Mg/Si ratio is higher than one, ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ can react with MgO and form Mg silicates, such as ${\mathrm{M}\mathrm{g}\mathrm{S}\mathrm{i}\mathrm{O}}_3$, at lower pressures. Computational studies have suggested possible breakdown of Mg-silicate phases, which can produce silica as a free phase at pressures over 1 TPa (32–34). Pressure for the breakdown is sensitive to free energy difference between Mg silicates and their breakdown products, ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$. We showed that a large amount of ${\mathrm{H}}_2$O can dissolve in the crystal structure of ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ and change the stable crystal structure of ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$. Therefore, under ${\mathrm{H}}_2$O-saturated conditions of water-rich planets, hydrated dense silica would be the energetically more favored form, and therefore, the breakdown and formation of free silica could occur at much lower pressures.

It is also important to consider chemical differentiation in water-rich planets. The differentiation might have occurred when the planets were young and therefore, hot. In such conditions, both silicates and ${\mathrm{H}}_2$O would be molten. Studies have suggested that silicate melt and ${\mathrm{H}}_2$O fluid could be miscible at high pressures (35). With cooling, heavy ions, such as Mg and Si, would be incorporated into precipitating crystalline phases possibly together with H. However, we do not have sufficient data to model whether these ions would distribute homogeneously throughout different depths or differentiate into different depth ranges in water-rich planets. If the latter is the case because of pressure-dependent changes in the solubilities of different cations in fluid (36), such compositional gradients could make particular depths range favorable for the stabilization of dense hydrated silica.

The sequence of phase transitions that we found above could provide important insight for future investigations on chemically more complicated systems for water-rich planets. So far, dense hydrous phases stable at high $P-T$, such as FeOOH, AlOOH, and ${\mathrm{M}\mathrm{g}\mathrm{S}\mathrm{i}\mathrm{O}}_2$(OH)₂ (11–13, 17), appear to imitate the high-pressure behaviors of silica. In the dense silica polymorphs with sixfold coordinated Si (therefore, ${\mathrm{S}\mathrm{i}\mathrm{O}}_6$ octahedra), the edge shared oxygen atoms bond to H (8). Although bridgmanite with all O atoms in corner sharing appears to store very little OH (37), the postperovskite (ppv) phase has the edge shared O atoms similar to dense silica polymorphs. Therefore, it is possible that Si⁴⁺ → 4H⁺ substitution is important in ppv similar to dense silica polymorphs. Although a first principles study found higher H partitioning into ppv over bridgmanite through Al involved substitution (38), to our knowledge, the direct substitution has not been explored for ppv.

In summary, our study reveals that hydration of silicates is important to consider for the interiors of water-rich planets. For example, hydration effects can alter the mass–radius relations of water-rich planets, which are particularly important for estimating compositions of exoplanets from astrophysical measurements of mass and size. In current mass–radius relation models, separate ice and rocky layers are assumed, and equations of state of dry silicates are used (39). As shown in this study, ice and silicates can exhibit significant mutual solubility at high pressure, thereby dramatically altering the equations of state for the Si–O–H bearing phases formed in the geological context of waterworlds. It has been believed that the phase changes in H₂O play an important role for the observed magnetic fields of Uranus and Neptune (40). If a significant amount of silicate is dissolved in the ${\mathrm{H}}_2$O layer, the properties of the ice layer could be altered. Therefore, future studies should investigate the related physical properties of dense hydrated silica phases, such as conductivity. If the solubility of ${\mathrm{H}}_2$O in ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ gradually changes with pressure, materials transported by convection would undergo mixing and demixing at different depths in water-rich planets, affecting the geochemical cycle.

The large ${\mathrm{H}}_2$O storage in dense silica also has implications for the deep ${\mathrm{H}}_2$O cycle of much drier rocky planets, such as Earth. From the observed low solubility of ${\mathrm{H}}_2$O in bridgmanite and ferropericlase, the ${\mathrm{H}}_2$O storage capacity of the lower mantle has been believed to be extremely low (37, 41, 42). Although silica would not be stable in the MgO-rich pyrolitic lower mantle, studies have shown that silica is one of the major phases in subducting oceanic crust (43, 44). These chemical heterogeneities are expected to persist for geological timescale in the lower mantle without much chemical reaction because of extremely slow chemical diffusion in the region (45). This argument is supported by observations of some deep diamonds containing dense silica polymorphs (46). Owing to its high temperature stability over a wide pressure range (from the mantle transition zone to the base of the mantle) (Fig. 3A), the silica polymorphs (Ct and Nt) that we found should play a major role in the circulation of ${\mathrm{H}}_2$O in the lower mantle. Such storage in the deeply subducted materials may explain the greater amount of ${\mathrm{H}}_2$O detected in ocean island basalts (1,000 ppm), which are believed to originate from the deep lower mantle, than in midocean ridge basalt (500 ppm), which are from the upper mantle (41).

Methods

Sample Preparation.

Three different types of starting materials were prepared for the high-pressure experiments: hGel (Sigma; purity $\ge$99.0%), anhydrous silica glass (dGla; Alfa; purity $\ge$99.5%), and dStv (SI Appendix, Table S1). The hGel starting material contains $\sim 8$ to 9 wt % ${\mathrm{H}}_2$O according to TGA performed at Arizona State University (ASU). The dStv phase was synthesized from amorphous silica, SPEX, with a purity of $\ge$99.9% at 10 GPa and 1473 K for 1 h in a 14/8 assembly in a multianvil press at ASU (47).

Preparation for LHDAC Experiments.

Powdered forms of the starting materials were mixed separately with either 12 wt % platinum (Pt) or gold (Au) powder, which was used as both an internal pressure calibrant (48) and a laser absorber. The powder mixtures were cold pressed into thin foils of approximately $60\times 60$ $\mathrm{\mu }{\mathrm{m}}^2$ in size and $10\hspace{0.17em}\mathrm{\mu }$m in thickness in a DAC with 500-$\mathrm{\mu }$m culet anvils. The foils were then loaded in a DAC with 150-, 200-, or 400-$\mathrm{\mu }$m diamonds culets diameter in a 80-, 100-, or 260-$\mathrm{\mu }$m-diameter hole drilled in a rhenium gasket. As a pressure-transmitting medium, we loaded ${\mathrm{H}}_2$O for the dGla and dStv starting materials. For the hGel starting material, Ne or argon was loaded as a medium for thermal insulation and homogeneity in stress. In two runs, ${\mathrm{H}}_2$O was loaded with the hGel starting material. For ${\mathrm{H}}_2$O loading, we injected a drop of deionized filtered water (Sper scientific) with a small syringe to the sample chamber. The DAC was closed immediately to reach a pressure of 5 to 6 GPa. The Ne loading was conducted in the gas-loading system at the GeoSoilEnviroConsortium for Advanced Radiation Sources (GSECARS) (49). Argon was loaded cryogenically at ASU.

Synchrotron Experiments.

We conducted LHDAC experiments combined with in situ XRD at the 13-IDD beamline of GSECARS (50) and the beamline 16-IDB of the High Pressure Collaborative Access Team (HPCAT) sectors (51) at the Advanced Photon Source. Angle-dispersive XRD patterns were measured with a monochromatic X-ray beam with a wavelength of 0.3344 Å at GSECARS and 0.4066 and 0.3544 Å at HPCAT. Diffraction images were measured on a MarCCD or Mar345 detector before, during, and after each heating cycle. We also measured diffraction patterns for the samples during decompression and for the recovered samples at 1 bar. Samples synthesized in a multianvil press were measured with both synchrotron and laboratory X-ray instruments. For in situ heating, we aligned two near-IR laser beams coaxially with the X-ray beam. The laser beams were focused on the samples in the DAC. We heated four to seven different spots on each sample, and each spot was heated for 5 to 33 min. The temperature was estimated by fitting the measured thermal radiation spectra to the Planck equation for both sides of the samples in LHDAC.

XRD Analysis.

We integrated all of the diffraction images to 1D diffraction patterns in the DIOPTAS software (52). We corrected for detector tilts and sample-to-detector distances ($\sim 200$ or $\sim 250$ mm) using the calibration measurements from ${\mathrm{L}\mathrm{a}\mathrm{B}}_6$ or ${\mathrm{C}\mathrm{e}\mathrm{O}}_2$ diffraction standards. We obtained the peak positions by fitting each diffraction peak with a pseudo-Voigt profile function in the Peakpo software (53). With Peakpo, we also conducted phase identification. From the measured unit-cell volumes of Au or Pt, we calculated the pressures for each diffraction pattern combined with their equations of state (48).

Rietveld Refinements.

Rietveld refinements were conducted in the general structure analysis program package, GSAS (54). We refined scale factors first and then, the lattice parameters, the peak profile shape function, and the spherical harmonic terms for preferred orientations. After reaching a good visual fit, we refined all of the parameters together or consecutive different combination of parameters in case the fit diverges to further reduce the fit residue. After background subtraction, the residual $\left(R_{\mathrm{w}\mathrm{p}-\mathrm{b}\mathrm{k}\mathrm{n}\mathrm{d}}\right)$ of all our refined patterns ranges between 1 and 7%.

IR Spectroscopy Measurements.

We conducted IR spectroscopy measurements on the recovered samples at room temperature and 1 bar at the Infrared Laboratory of the National Synchrotron Light Source II (NSLS) at Brookhaven National Laboratory and at beamline 1.4.3 of the Advanced Light Source (ALS). At NSLS, all IR spectra were collected using a Bruker Vertex 80v FTIR spectrometer under vacuum and a dry nitrogen-purged Hyperion 2000 IR microscope equipped with a liquid nitrogen-cooled midband MCT detector to minimize the impact of water vapor absorption in the O–H stretching vibrational region. A tungsten source and a ${\mathrm{C}\mathrm{a}\mathrm{F}}_2$ beam splitter were employed to achieve a maximized spatial resolution. The aperture size was set from $15\times 15$ to $30\times 30$ $\mathrm{\mu }{\mathrm{m}}^2$ depending on the sample sizes. We applied 1,024 scans and 4-${\mathrm{c}\mathrm{m}}^{-1}$ spectral resolution to all spectra. At ALS, a bend magnet synchrotron radiation was directed to an FTIR spectrometer (Nicolet Magna 760) with a KBr/Ge beamsplitter. The synchrotron light was focused through the DACs with a custom horizontal microscope consisting of two Schwarzschild objectives to achieve a diffraction-limited spot size and detected with an external MCT detector (Infrared Associates; FTIR-22-0.10). For the 1-bar measurements, the DACs were opened to avoid strong fringes due to the reflections between the two diamond culet surfaces. The quenched samples from the laser heating were kept on one anvil. Enough empty space (diamond only) was available to obtain reference spectrum for each measurement.

First Principles Calculations.

We conducted the calculations using the GPAW code (55) with both generalized gradient approximations (GGAs) and local density approximation for the exchange correlation potentials. For GGA, we used Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional (56). For the projected augmented wave (57) method adopted here, a plane-wave cutoff of 1,100 eV was sufficient to converge the unit-cell electronic energy to the millielectronvolt level and reduce the residual atomic forces to 0.02 eV/Å. We obtained the crystal structure model of Ct by adopting the unit-cell volume value from Stv at 1 bar and the unit-cell parameter ratios from those at 140 GPa (20). We constructed two groups of models: Ct8 ($2\times 2\times 2$ supercell, a total of 48 to 54 atoms) and Ct12 ($2\times 2\times 3$ supercell, a total of 72 to 78 atoms). A total of six different models were calculated: dCt8 and dCt12 (no H atoms), hCt8-4H and hCt12-4H (one Si defect or 4H in the supercells; 3.84 and 2.54 wt % ${\mathrm{H}}_2$O, respectively), and hCt8-8H and hCt12-8H (two Si defects or 8H in the supercells; 7.89 and 5.17 wt% ${\mathrm{H}}_2$O, respectively). We used Monkhorst–Pack sampling (58): a total of 16 points $\left(2\times 2\times 4\right)$ for the Ct8 cells and 8 points $\left(2\times 2\times 2\right)$ for the Ct12 cells. For the starting crystal structure, we adopted the H coordination presented in Spektor et al. (8). For the H-bearing structures, H atom positions were also varied together with all other atoms during simulations. We conducted simultaneous optimization for the atomic positions and lattice constants using the Broyden–Fletcher–Goldfarb–Shanno algorithm in the Atomic Simulation Environment (59) at 1 bar and in the static lattice approximation (e.g., 0 K without zero-point motion). In the models with two defects, we arranged them at the maximum possible distances from each other.

Data Availability.

The authors declare that all relevant data supporting this study are available within the paper and SI Appendix or available on request from S.-H.S.