Metrics that matter for assessing the ocean biological carbon pump

Abstract

The biological carbon pump (BCP) comprises wide-ranging processes that set carbon supply, consumption, and storage in the oceans’ interior. It is becoming increasingly evident that small changes in the efficiency of the BCP can significantly alter ocean carbon sequestration and, thus, atmospheric CO₂ and climate, as well as the functioning of midwater ecosystems. Earth system models, including those used by the United Nation’s Intergovernmental Panel on Climate Change, most often assess POC (particulate organic carbon) flux into the ocean interior at a fixed reference depth. The extrapolation of these fluxes to other depths, which defines the BCP efficiencies, is often executed using an idealized and empirically based flux-vs.-depth relationship, often referred to as the “Martin curve.” We use a new compilation of POC fluxes in the upper ocean to reveal very different patterns in BCP efficiencies depending upon whether the fluxes are assessed at a fixed reference depth or relative to the depth of the sunlit euphotic zone (Ez). We find that the fixed-depth approach underestimates BCP efficiencies when the Ez is shallow, and vice versa. This adjustment alters regional assessments of BCP efficiencies as well as global carbon budgets and the interpretation of prior BCP studies. With several international studies recently underway to study the ocean BCP, there are new and unique opportunities to improve our understanding of the mechanistic controls on BCP efficiencies. However, we will only be able to compare results between studies if we use a common set of Ez-based metrics.

Marine ecosystems are of fundamental importance in their capacity to influence the transformation, fate, and storage of carbon and associated elements in Earth’s biosphere. In particular, ocean biota export particles through the ocean’s biological carbon pump (BCP), which refers to the combined processes that transfer organic carbon that is biologically produced in the surface ocean to depth (e.g., ref. 1). While there are several modes for transporting organic carbon to depth, including gravitational settling, physical injection pumps, and biologically mediated vertical fluxes (2), we expressly consider in this paper sinking particles which are the largest component of the BCP. We focus our attention on the transfer of C out of the sunlit euphotic zone (Ez) and through the upper twilight zone (TZ = depths below Ez down to 500 m) where the attenuation of particulate organic carbon (POC) flux is largest and differs the most between oceanic provinces (3). We separate the BCP efficiency into two components. The first is the relative strength of the BCP, that is, the magnitude of POC flux out of the surface ocean, and the second is its transfer efficiency, that is, the fraction of sinking POC that is transported to depth (see SI Appendix, Table S1 for definitions of terms).

The flux of sinking particles out of the surface ocean and its attenuation with depth is most often quantified in field observations by a fit to POC sinking flux data as introduced by Martin et al. (4):

$$F_z=F_{100}{\left(\frac{z}{100}\right)}^{-b}.$$ [1]

This “Martin curve” was derived from a selected set of open ocean stations in the Pacific measuring POC flux where F_z is the sinking flux of POC at depth z measured using sediment traps and F₁₀₀ is the trap flux at a fixed 100-m reference depth. An exponent “b” of 0.86 captured the average attenuation of POC flux, with approximately a 90% decline in POC flux between 100 m and 1,000 m in this dataset.

As noted by Cael and Bisson (5), numerous POC flux-vs.-depth parameterizations are possible that are statistically indistinguishable from the Martin curve, while having very different implications for flux attenuation and the mechanisms governing the BCP. Importantly, since the Martin curve is not mechanistically based, this relationship does not allow for projected alterations of BCP efficiencies as ecosystems change in response to altered climate or other forcings (6). At this time of their 1987 publication, Martin et al. (4) emphasized that this equation was used as a statistical expedient and it was not based on a priori physics. Critically, the Martin curve is based on a power law with a fixed shallow reference depth, and thus the flux curve pivots around this point. As a result, the interpolated fluxes are sensitive to the availability of sufficient vertically resolved data just below the fixed reference depth needed to quantify the b value, and such resolution is rare in most sediment trap studies (7, 8).

We take a different approach here. We assess BCP efficiencies relative to the spatially and seasonally varying depth of light penetration and new particle production, that is, the depth of the Ez (3). To do this, we compiled a set of comparable POC flux observations that span a range of high and low BCP efficiencies, as well as shallow and deep Ezs (from 30 to 175 m). We also selected studies where depth-integrated NPP (net primary production) data are available. POC fluxes in our compilation are determined either with thorium-234, a naturally occurring tracer of POC flux, or by flux measurement with shallow drifting sediment traps that directly collect particles settling out of surface waters.

We focus our attention on a variable Ez-based reference depth since it is only within the sunlit Ez where inorganic C is fixed into organic matter (OM) via photosynthesis, thus creating a pool of de novo particulate and dissolved OM. We ignore chemotrophic production of POC, which is a smaller relative term in the upper ocean. We define an Ez depth based upon chlorophyll fluorescence, or the depth below which few viable chlorophyll pigments are detected. This depth is similar to a relative light depth of 0.1% PAR (photosynthetically available radiation). This Ez_0.1 depth has been observed to coincide with the depth where net particle export decreases, based upon ²³⁴Th results [e.g., Maiti et al. (9)]. This Ez-based assessment allows us to compare the same flux data evaluated at the base of the Ez compared to using a fixed depth. To do this, we need to consider how to select the Ez depth (underwater irradiance measurements or chlorophyll distributions) and recognize the importance of having datasets with high vertical resolution around the Ez. For example, Olli (8) recommends deploying sediment traps at at least six depths, starting in the vicinity of the depth of the Ez. While our emphasis is on sinking particle fluxes out of the Ez and their attenuation in the upper TZ, we briefly consider how the criteria to determine reference depths would differ for particle injection pumps and biologically enhanced transport by vertical migrators (SI Appendix). In the final section, the influence on our understanding of regional BCP efficiencies for sinking particles is discussed in context of global estimates of C export and we reconsider the conclusions of several prior studies in context of a variable Ez.

Fixed Depth Compared to Ez Depth-Based Metrics for BCP Efficiencies

The use of the Martin curve implicitly assumes a relationship between flux and flux attenuation with depth and enables the intercomparison of BCP efficiencies among sites. The Martin curve (Eq. 1) requires a fixed reference depth for a POC flux, which is commonly based upon the shallowest sampling depth measured by sediment traps. The main issue with this approach is that the depth of OM production is constrained by the depth of the Ez, which can vary from less than 20 m to almost 200 m (SI Appendix, Fig. S1; see Choosing a Biogeochemically Relevant Reference Depth). This Ez depth will depend upon the criteria used to define Ez and will vary both regionally and seasonally. So, a fixed-depth comparison does not assess BCP efficiencies relative to the layer where the OM is produced and the sharp gradients in POC flux that are often just below the Ez (9). The extent of this vertical mismatch becomes apparent when comparing BCP efficiencies when the Ez differs significantly between sites, and yet flux is measured at the same fixed reference depth.

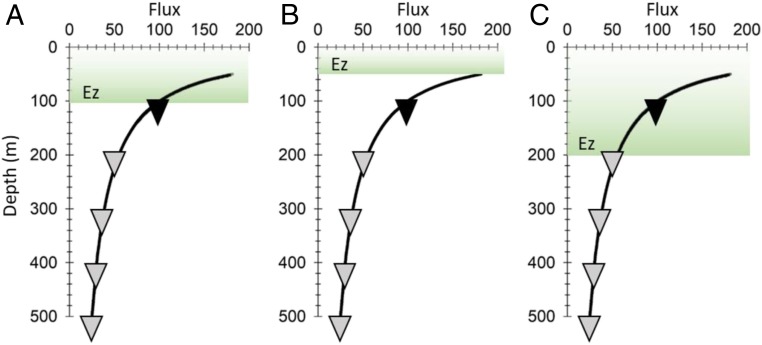
For example, POC fluxes are measured ideally at the base of the Ez and the BCP efficiencies are determined relative to that boundary (Fig. 1A). However, traps are most often deployed at the same fixed depth, so if a trap was deployed at 100 m whereas the depth of the Ez was 50 m, you would underestimate the in situ BCP efficiency (Fig. 1B), and vice versa, for deeper Ezs (Fig. 1C). A simple sensitivity analysis reveals that the 100-m export ratio (i.e., POC flux at 100 m/NPP) would be 45 to 65% of the value derived from the base of the Ez (here, 50 m), calculated for bs ranging from 0.6 to 1.2 (SI Appendix, Fig. S2A). With a deeper Ez of 200 m, the export ratio using the measured flux at 100 m would be 1.5 to 2.3 higher than an Ez-based assessment given this same range of bs. When assessing POC flux attenuation below the Ez, the BCP transfer efficiencies (POC flux 100 m below reference depth/flux at reference depth) would be 25 to 30% lower and 50% higher for a 50-m and 200-m Ez, respectively, assuming POC flux was assessed at a fixed 100-m reference depth (SI Appendix, Fig. S2B).

Fig. 1.

Conceptual diagram showing consequences of a changing Ez depth when using the Martin curve and fixed sampling depths shown by inverted triangles that represent sediment traps with reference flux measured at 100 m (black inverted triangle). In this example, the flux at 100 m is 100 (unitless) and flux attenuation vs. depth is identical in each panel. (A) Ideal case where Ez = 100 m and the first flux measurement is also at 100 m. (B) Same flux profile, but Ez = 50 m, in which case using the measured flux at 100 m the apparent export efficiency and flux attenuation would be underestimated at 100 m, relative to actual values at Ez. (C) Same flux profile with Ez = 200 m, in which case using the measured flux at 100 m the apparent export efficiency and attenuation would be overestimated.

Using a compilation of POC flux observations that span a range of high and low BCP efficiencies, as well as shallow and deep Ezs (from 30 to 175 m in this dataset; SI Appendix, Table S2), we can illustrate the effect of using an Ez-based reference depth relative to a fixed depth assessment of BCP efficiencies. To do this, we present a subset of studies with high vertical flux resolution (more than seven depths) and, in most cases, with several flux assessments in a given season/site to avoid aliasing by small-scale spatial variability. We begin with the already well-documented flux dataset in Buesseler and Boyd (3), where all POC fluxes were derived using the naturally occurring radionuclide ²³⁴Th as a particle flux tracer (10, 11). We have supplemented this ²³⁴Th dataset to expand the range of sites and oceanic conditions, and hence provide a wider range of Ez depths and BCP characteristics (SI Appendix, Table S2).

The same type of C flux assessments can be made with sediment traps; however, traps are rarely deployed at sufficient enough vertical depth resolution to accurately define the flux gradient around the base of the Ez. Three trap studies in contrasting settings are presented here that have sufficiently high vertical depth resolution to calculate export at varying depths around Ez. These include a high export site in the Barents Sea with 14 traps in the upper 200 m (12), a study off the northwestern (NW) Spanish coast with 8 depths in the upper 200 m (13), and a study from the North Pacific subtropical gyre, with 12 trap depths in the upper 500 m (14).

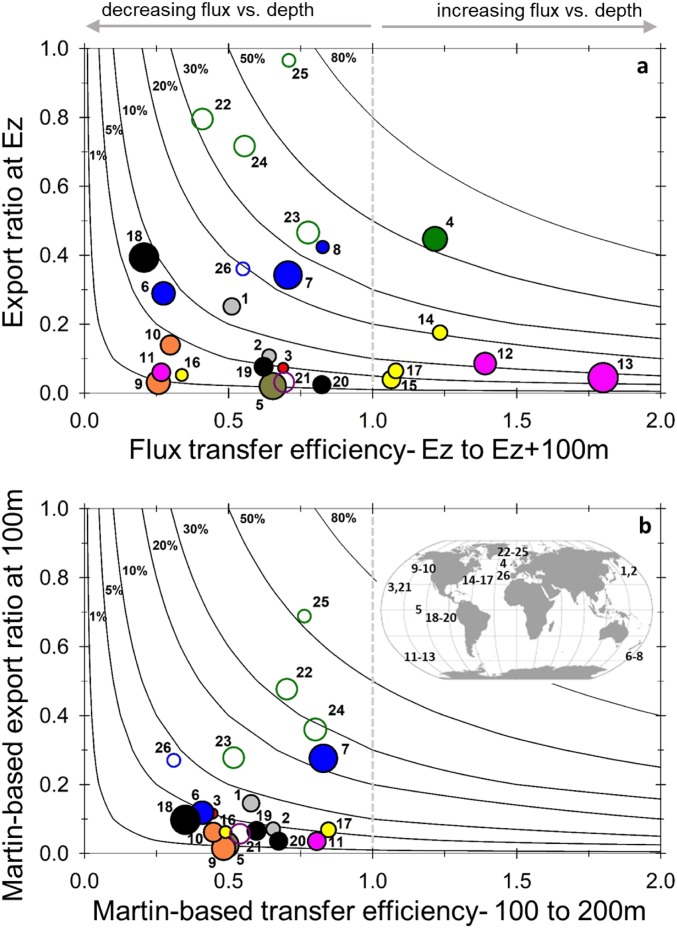
As in Buesseler and Boyd (3) we parameterize the relative strength of the biological pump using the Ez-ratio (= POC flux at the base of Ez/NPP). In this Ez framework, the shallow fluxes are assessed at depths ranging from 30 to 175 m. The total range here in Ez-ratios is from 0.02 to 0.96 (SI Appendix, Table S2), indicating that as little as 2% of the NPP is exiting the Ez (oligotrophic gyres), to sites and times with more than half to 96% of the NPP being exported (Barents Sea).

We then calculate the transfer efficiency which is a measure of POC flux that is not attenuated within the upper TZ, parameterized here as T₁₀₀ (= POC flux 100 m below Ez/flux at Ez). In this data compilation we are assessing flux attenuation to depths ranging from 130 to 275 m. A T₁₀₀ = 1 would indicate no POC flux attenuation between the base of the Ez and 100 m below, whereas a T₁₀₀ = 0 would indicate 100% remineralization of sinking POC. Most of the data are between a T₁₀₀ of 0.3 and 0.8, indicating an attenuation in POC flux between 70% and 20% in the 100-m stratum below the Ez (Fig. 2A). In this dataset, six of the studies showed an increase in POC flux below Ez, in which case T₁₀₀ will exceed 1.0 (up to 1.8).

Fig. 2.

Export ratio vs. transfer efficiencies. (A) Upper plot calculates export ratio (Ez-ratio) from POC flux at base of Ez/NPP (y axis) and transfer efficiency (T₁₀₀) from the ratio of flux 100 m below Ez/flux at Ez (x axis). Note a transfer efficiency >1 indicates a flux increase with depth. Lines of constant BPC efficiencies (flux 100 m below Ez/NPP; 1 to 80%) are also shown. (B) Same plot and POC flux data, but using a Martin curve to calculate export ratios and flux transfer efficiencies relative to a 100-m fixed reference depth. See SI Appendix, Table S2 for study site details and ID numbers. In both panels, filled circles are POC fluxes derived from ²³⁴Th, open circles are from sediment traps, color indicates a single study, and the area of the circle is proportional to NPP. The map inset is provided in B to show nominal study locations.

In Fig. 2A, we also plot the lines of constant BCP efficiency for the deeper reference depth 100 m below Ez (F_Ez+100/NPP). The data range from 1% and 70% when assessed at this deeper depth (curved lines, Fig. 2). Note that a low BCP efficiency can result from either low export out of the Ez and/or rapid attenuation below this depth. The only way to achieve a high BCP efficiency is to have both a high Ez-ratio and a high transfer efficiency below.

These Ez-based metrics reveal the locations and seasons with the strongest and weakest BCP efficiencies (Fig. 2A). At sites with T₁₀₀ < 1.0 (flux is decreasing with depth), the Barents Sea is conspicuous with the highest BCP efficiencies (ID nos. 22 through 25, SI Appendix, Table S2). The weakest BCP efficiencies are associated with HNLC (high-nutrient low-chlorophyll) waters in the northeastern Pacific (ID nos. 9 and 10) and the Southern Ocean polar frontal zone (SoFEX site prior to Fe addition; ID no. 11). Additionally, low BCP efficiencies are found in subtropical waters such as in the North Pacific (ID no. 3), at an equatorial upwelling region (ID no. 5), and offshore and in the gyre of the equatorial South Pacific (ID nos. 18 and 19). Several of the sites where the flux increases with depth, T₁₀₀ > 1, are associated with transient events, such as the northeastern Atlantic bloom (ID no. 4) or the HNLC Southern Ocean waters after a purposefully stimulated bloom using mesoscale Fe addition (ID nos. 12 and 13). Three of the North Atlantic subtropical gyre sites also exhibited a modest increase in flux vs. depth (ID nos. 14, 15, and 17).

The key message from the compilation is that a very different view of the relative BCP efficiencies is evident if the Martin curve is used to calculate b values and F₁₀₀. Using the Martin curve, we can calculate b to assess the ratios of POC flux at 100 m to NPP and the transfer efficiency below (flux 200 m/flux 100 m; Fig. 2B). In contrast to the Ez-normalized metrics, using the Martin curve results in on average much lower Ez-ratios, and an increase in transfer efficiencies, along with a reduced range of Ez-ratio and T₁₀₀ variability between sites. Not only are the BCP efficiencies lower and less variable when using the fixed reference depth approach, the interpretation of which site has a higher or lower BCP efficiency can change. For example, based upon the Martin curve, the NW Pacific site had a higher transfer efficiency (T₁₀₀ = 0.58 to 0.66) relative to the North Pacific subtropical gyre (T₁₀₀ = 0.44; compare sites ID nos. 1 and 2 vs. ID no. 3 in Fig. 2B). However, if we consider that the Ez in the NW Pacific was 50 m and normalize export ratios to this shallower depth, the two sites are reversed with respect to the trends in their BCP efficiencies (Fig. 2A vs. 2B), with the NW Pacific now having lower transfer efficiencies (lower T₁₀₀). In addition, those studies with an increase in flux with depth cannot be fit by a Martin curve, which excludes 6 of the 26 cases studies from this intercomparison. Whether this flux increase represents a transient feature due to a surface particle flux that is rapidly decreasing over time, or an indication of active transport by diel vertical migration, or lateral inputs creating a local POC flux maximum is discussed further in SI Appendix.

It is important to emphasize that the differences between Fig. 2 A and B have nothing to do with the choice of data; the same POC flux data are used. However, our view of the strength and transfer efficiency of the BCP would diverge if we use different metrics to define the BCP efficiencies. We contend and discuss further below that an Ez-based metric is better suited to capturing distinctive regional biogeochemical characteristics of the BCP, especially when considering processes that control BCP efficiencies just below the sunlit Ez and throughout the upper TZ.

Choosing a Biogeochemically Relevant Reference Depth

Before we further consider the influence of using an Ez-based metric to define the BCP efficiencies, we need to consider how best to choose a biogeochemically relevant, light-based reference depth below which little or no photosynthetic de novo production of OM can occur. Primary production is commonly measured in the water column to a relative light level of 1% PAR. This Ez_1.0 depth varies regionally and seasonally in the ocean primarily as a function of biotic and abiotic particle abundances, with a strong regional bias of shallower Ezs at higher latitudes (SI Appendix, Fig. S1A). PAR is readily measured using in situ sensors and PAR profiles can also be derived as well from surface chlorophyll [from measurement or remote sensing (15, 16)]. However, PAR is zero during nighttime casts and relative Ez depths vary with short-term meteorological events, such as cloud cover. In addition, absolute photon fluxes, not relative PAR depths, are the physical driver of photoautotrophic production (e.g., refs. 17 and 18).

In order to systematically define this layer of POC production that fuels the downward particle flux, Owens et al. (19) defined the “primary production zone” (PPZ) as the depth at which the signal from in-situ fluorescence sensors dropped to 10% of the maximum above that depth (after correction for sensor background signal). This “fluoro-cline” delineates between surface waters where chlorophyll pigments are present, indicating a “fresh” source of OM, and deeper layers where there is insufficient light to maintain chlorophyll stocks. This definition allows for rapid identification of the PPZ reference depth on any cast with standard CTD sensors. Owens (20) found in a study of POC flux in the western Antarctic Peninsula that the mean light level at the PPZ was 0.3% and 0.6% PAR during summer and autumn sampling, respectively. This approximates to the community compensation depth that Marra et al. (21) showed to be several meters to tens of meters deeper than 1% PAR (Ez_1.0), closer to 0.1% PAR (Ez_0.1). Globally, the Ez_0.1 depth also has large regional differences, with deeper values exceeding 150 m in the oligotrophic gyres (SI Appendix, Fig. S2B; note these PAR boundaries are satellite- and model-derived). If the key question here is what controls the export rate of sinking particles out of the productive layer and its attenuation below, we contend that this deeper Ez_0.1 or PPZ depth needs to be considered in order to define a boundary below which there are few viable phytoplankton and remineralization processes will lead to POC flux attenuation.

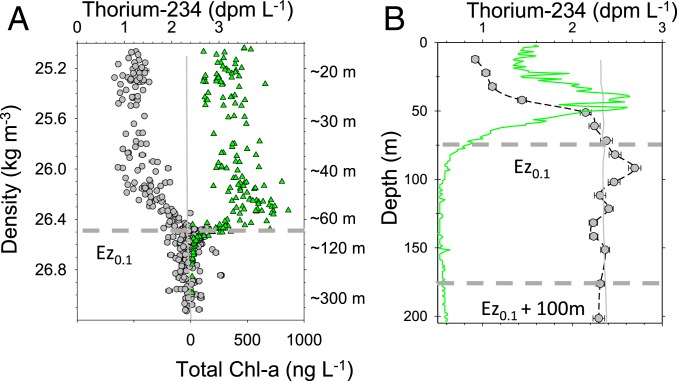
The robustness of the PPZ for demarcating the layer of particle production from attenuation below is also supported by vertical profiles of ²³⁴Th, where a deficit of ²³⁴Th relative to its parent ²³⁸U (²³⁴Th < ²³⁸U) indicates net particle export, and a ²³⁴Th excess (²³⁴Th > ²³⁸U) indicates remineralization of sinking particles by physical or biological processes. The overlap between the zone of ²³⁴Th deficit and the surface layer with chlorophyll pigments can readily be seen in higher-vertical-resolution ²³⁴Th datasets such as presented in Fig. 3A. Indeed, this ²³⁴Th equilibrium depth has been used by Puigcorbé et al. (22) and Lemaitre et al. (23) as their particle export reference depth, rather than a PAR- or a chlorophyll-based boundary. The ²³⁴Th excess immediately below Ez_0.1 is most conspicuous with high-vertical-resolution ²³⁴Th data, such as the example from a 17-depth profile of ²³⁴Th and fluorescence in the NW Pacific (Fig. 3B). A layer of ²³⁴Th excess, indicating enhanced POC remineralization, is now being detected more commonly in both high- and low-flux settings as vertical sampling resolution for ²³⁴Th increases (e.g., ref. 9). One explanation for this feature is that just below the Ez the sinking particles are the most energy-rich (14), yet low light levels limit predation on zooplankton consumers, allowing for intense zooplankton grazing and fragmentation of sinking POC. The location of this narrow layer of rapid remineralization is also consistent with optical techniques which show that at depths immediately below the Ez there is an active layer of particle consumption, where zooplankton “gatekeepers” play an important role in fluxes to the TZ [e.g., Jackson and Checkley (24)].

Fig. 3.

(A) ²³⁴Th (gray circles; upper x axis), ²³⁸U (vertical gray line same scale as ²³⁴Th), and chlorophyll-a concentrations (green triangles; lower x axis offset) vs. density (left y axis). Data taken from the VERTIGO NW Pacific site and redrawn from Buesseler et al. (62). (B) Single high-resolution ²³⁴Th profile (gray circles), ²³⁸U (vertical gray line), and chlorophyll fluorescence profile (green line, relative sensor scale). Horizontal dashed lines show Ez reference depths. Modified from Maiti et al. (9).

These observations do not preclude small vertical offsets between the depth of PPZ, ²³⁴Th, and Ez_0.1, but generally all three covary and respond to the same regional and seasonal changes in light which set the depth stratum for photosynthesis. Such vertical offsets are possible since these features respond on different time scales. The shortest time scales are associated with the rapid changes in light intensity (for PAR), increasing to the multiple day lifetime of chlorophyll pigments (used to define the PPZ), to the longer residence time of ²³⁴Th (approximately a few days to a couple of weeks; refs. 25 and 26). So, the PPZ should be seen as a multiday average boundary for de novo OM production that is readily measured on a single cast and an improvement over using a fixed depth when comparing BCP efficiencies across sites and seasons.

The examples discussed above of differing BCP efficiencies are all at sites that have mixed layers (ML) shallower than the PPZ, a common feature in much of the ocean, at least during the phytoplankton growth season. However, if the ML is deeper than the PPZ, suspended and sinking particles will be physically mixed below the Ez to varying degrees. This has consequences for sampling the gravitational flux of sinking particles. For example, at the Bermuda Atlantic time-series site (BATS), sediment trap samples are considered nonquantitative if they are deployed within the ML, which can occur during the winter months (27, 28). Of course, if the line of inquiry is related to C sequestration in the deep ocean, then a reference depth that is the maximum depth of the winter ML is appropriate. Studies by Antia et al. (29) (using traps) and Palevsky and Doney (30) (with a global ocean model) consider the influence of varying the depth of winter mixing on zonal global patterns of deep BCP efficiencies. To compare upper ocean BCP efficiencies we recommend using a reference depth that is either the PPZ or ML, whichever is deeper, and note this in the discussion thereof.

Impact of Using an Ez-Based Metric on BCP Efficiencies

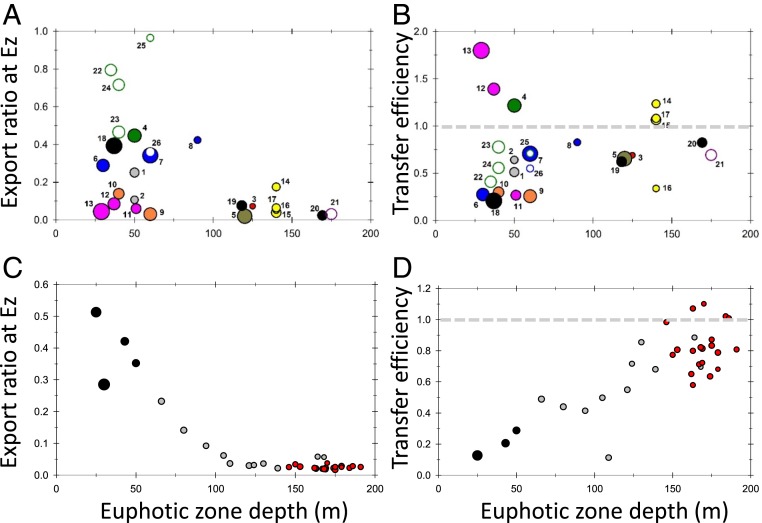
We find that when Ez depths are deep (>100 m), the Ez-ratios are always low (5% on average; Fig. 4A). In contrast, both high and low Ez-ratios can be found when Ez depths are shallow. This trend is even more conspicuous when results within the time span of an individual study are compared. Instead of averaging the results in Black et al. (31) for several stations from the shelf, offshore and gyre regions off Peru as in Fig. 4 A and B (ID nos. 18 through 20), we examine the individual station by station results along that transect in Fig. 4 C and D. This analysis reveals a more systematic trend, showing high Ez-ratios only in the shelf waters off Peru where Ez < 50 m, decreasing systematically as Ez depths increase offshore and where we find relatively constant Ez-ratios around 0.05 as individual Ez depths as deep as 195 m are found (Fig. 4C; Ez determined by PPZ in this study).

Fig. 4.

Plots of Ez-ratio and T₁₀₀ vs. the depth of the Ez. (A) Ez-ratio vs. Ez depth in the same studies and IDs as in Fig. 2 and SI Appendix, Table S2. (B) T₁₀₀ vs. Ez depth for same dataset. The coloring and size of the circle is proportional to NPP as in Fig. 2. (C) Ez-ratio vs. Ez depth for individual stations along the Equatorial Pacific Zonal Transect as in ref. 31. (D) T₁₀₀ vs. Ez depth for same data as in C. In C and D, black circles indicate shelf stations, gray indicates offshore, and red indicates gyre. The averages of these three zones are provided in SI Appendix, Table S2 (ID nos. 18 through 20) and shown in A and B.

We observe more scatter and no clear relationship across all studies between T₁₀₀ and Ez depths (Fig. 4B), even if we only look at the T₁₀₀ values <1.0. However, looking again only at Black et al. (31), T₁₀₀ increases more systematically with deeper Ezs (Fig. 4D). In this transect off Peru, one factor that may influence POC flux attenuation is the low O₂ concentrations in waters that are shallower closer to the coast, either by limiting the depth of zooplankton vertical migration (32) and/or by geochemical processes that take place at this oxic/anoxic boundary. On the shelf, the shallow depth of the Ez (25 to 50 m) corresponds to the upper boundary of the oxygen-deficient zone (<1 µM O₂). We find on the shelf both high downward export from the Ez and rapid flux attention in the first 100 m below Ez (a low T₁₀₀). As that oxygen-deficient zone boundary deepens offshore and into the gyre, the depth of the Ez deepens and along with it the fluxes out of the Ez and POC flux attenuation both decrease.

While Black et al. (31) report greater flux attenuation near shore, Pavia et al. (33) reported the highest attenuation rates in the gyre along the same transect. What differs is that the latter POC fluxes were determined by the longer-lived thorium-230 isotope (half-life = 75,400 y) and thus represent a longer integration time. Of more influence on the outcome, perhaps, is that they used a Martin curve to quantify flux attenuation. Their Martin curves were a best fit to three variables: b, the reference depth, and flux at that depth. In this manner, their reference depth averaged 60 m, which is 100 m shallower than in Black et al. (31) (median Ez = 160 m for offshore and gyre locations). The Pavia et al. (33) scenario is similar to the conditions depicted in Fig. 1C, in which case a Martin curve would overestimate flux attenuation compared to a deeper, Ez-based metric. In essence, Pavia et al. (33) are fitting attenuation in the shallower part of the POC flux curve, and thus reaching the opposite conclusion regarding flux attenuation trends.

We suspect that trends in BCP efficiencies and Ez are clearer in a comparative sense within any single study, such as in Black et al. (31), because a sole NPP method was used (here modeled NPP from MODIS satellite data), and also a common and highly resolved POC flux approach (²³⁴Th for POC flux and POC/Th at 8 to 12 depths), along with a single protocol to define the Ez boundary (PPZ method). In our larger compilation in Fig. 4 A and B, studies are included where the NPP is model derived and others where it is determined from incubations with ¹⁴C. In some of these studies Ez is determined by 1 or 0.1% PAR, or the PPZ criteria (SI Appendix, Table S2). Even when POC flux is determined by the ²³⁴Th approach, different analytical methods and vertical resolution have been used to quantify ²³⁴Th activities and the POC/Th ratios needed to derive POC fluxes, as well as different methods to quantify POC/Th ratios (traps and filtered particle methods). While none of these factors ought to introduce large biases, the combination of slightly higher/lower POC flux, NPP, and deeper/shallower reference Ez depth will contribute scatter to results such as plotted in Fig. 4 A and B. Also, as shown by Estapa et al. (34), we may need to compare multiple stations to relate export to production, since submesoscale processes can decouple production and export on smaller, kilometer scales (35). Here, the number of sites that are averaged in Fig. 4 A and B ranges from 1 to 20 (see numbers of stations in SI Appendix, Table S2). Thus, in some cases we are comparing several POC flux curves that would average out submesoscale variability, as opposed to single stations that are more prone to a spatial decoupling in export, which may conceal these relationships.

In this paper we do not attempt to resolve which mechanisms are the most important in setting BCP efficiencies but note that it will be impossible to address this issue unless we adjust the BCP flux metrics to the depth of the Ez in a systematic way. It is interesting, perhaps, that we observe as much variability in T₁₀₀ as for Ez-ratios across all sites (Fig. 2A), but in some settings short-term variability in T₁₀₀ can be greater than variability in Ez-ratios. This can be seen, for example, in the sediment trap data at the BATS, where POC fluxes are consistently low, but the gradient in flux vs. depth varies greatly from month to month (e.g., ref. 27). We calculate from BATS trap data low Ez-ratios (0.06 ± 0.04) and a T₁₅₀ ranging from 0.2 to 1.4 (SI Appendix, Fig. S3). In the same Sargasso Sea area, using daily resolved optical flux proxies, variability in both the magnitude of flux attenuation and events with an increasing flux vs. depth are found (36). Thus, changes in export properties are happening on small spatial and temporal scales, reflecting variability in the biological and physical mechanisms that drive the sinking flux of POC and its attenuation with depth, and these processes should not be considered invariant.

Why Does an Ez-Based Reference Depth Matter?

The often-stated goal of studies into BCP efficiencies is to resolve the mechanisms that control the transfer of OM to depth (37). No single mechanism has been found to control BCP efficiencies, although considerable effort has focused on the potential relationships between POC flux and NPP (38, 39), food web controls (40, 41), ballast (42, 43), oxygen (44, 45), temperature (46–48), and variable sinking and degradation rates (49–51). However, if we want to quantify the mechanism(s) that lead to differences in the BCP efficiencies, we need to start by normalizing POC flux to the depth where it is produced and below which only particle flux attenuation occurs. This is the case not just for POC fluxes but also would apply to vertical profiles of suspended POC which also decrease with depth. For example, an Ez framework was needed to gain insights into BCP efficiencies from POC concentrations measured via filtration [e.g., Lam et al. (52)]. However, to link POC concentration profiles to POC flux we would need estimates of local particle sinking rates and a better understanding of the mass balance between fluxes and stocks and how these vary over time.

We contend that comparisons between sites based on a fixed reference depth, such as the Martin approach, can lead to a misunderstanding of the controlling mechanisms on BCP efficiency. For example, in a synthesis of regional export ratios, the VERTIGO “b” results (ID’s nos. 1 through 3) were used to support the suggestion that temperature is a controlling variable on POC flux attenuation, with lower attenuation (lower bs) in colder waters such as the NW Pacific site (48). As shown here, when renormalized to the shallower Ez, the flux attenuation is actually larger at this colder NW Pacific site than when we used a fixed depth (ID nos. 1 and 2). Therefore, this site no longer fits the same temperature trends as put forth in Marsay et al. (48), and vice versa for their warmer subtropical site (ID no. 3).

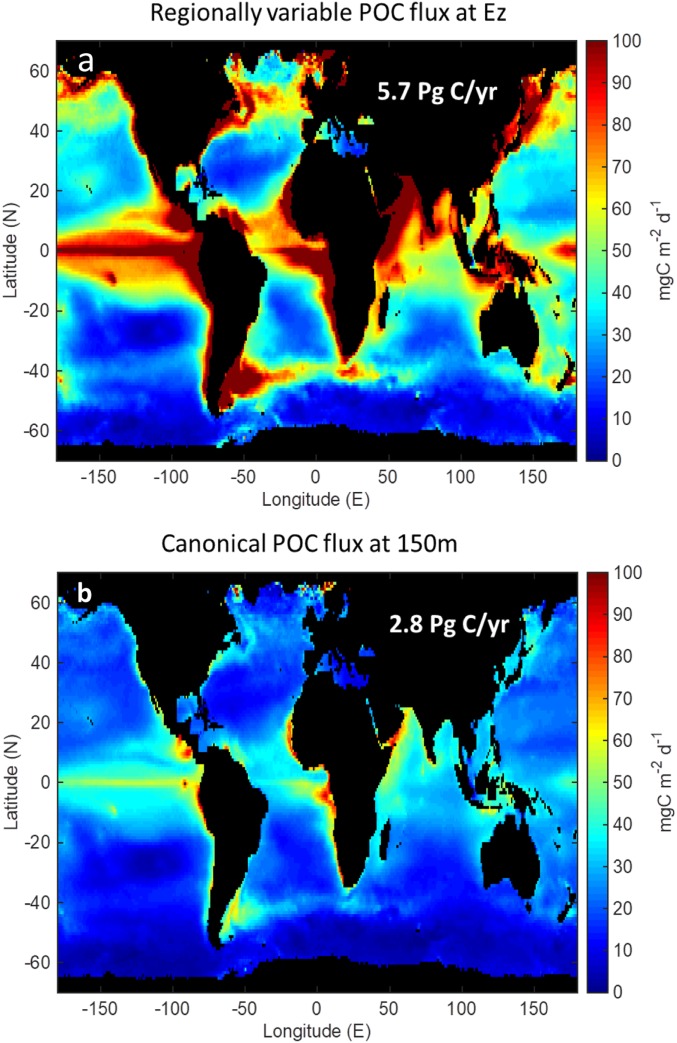
Another reason to use a common Ez metric is that considerable attention is being given to the role of the BCP in the global C cycle and its impact on current and future climate. Many global biogeochemical models assess export at fixed reference depths (e.g., refs. 53–55) and this choice of a reference depth can be significant. Siegel et al. (56) used remote sensing data and a simple food web model to globally assess BCP efficiencies considering an Ez-based reference depth. Their prediction of global C export from the Ez (Ez_1.0) is 5.7 Pg C⋅y⁻¹, with large regional variability, including higher Ez-ratios at high latitudes (Fig. 5A), a finding consistent with this compilation here. If their same model with a fixed b and export depth of 150 m is used, global fluxes decrease by twofold (2.8 Pg C⋅y⁻¹) and the regional gradients in Ez-ratio largely disappear (Fig. 5B). Given that much of the world’s oceans have shallow Ezs, any assessment that does not consider an Ez-normalized framework will always produce lower average POC fluxes and export ratios, particularly at higher latitudes.

Fig. 5.

(A) Results of a global diagnostic model for the annual mean POC export flux at the depth of the Ez [TotEZ in Siegel et al. (56)] where the Ez depth is defined as the depth of 1% PAR [following Morel et al. (16)]. (B) For the same model, the distribution of the POC export flux at 150 m using the canonical Martin curve to project the TotEZ values to 150 m assuming a global fixed b value of 0.86.

Several studies are attempting to quantify the variability in BCP efficiencies across the global ocean and explore the reasons for regional differences in POC flux vs. depth. For example, estimates of shallow POC flux from ²³⁴Th at 100 m and deep traps at 2,000 m are compared to derive the export ratios and transfer efficiencies at these two fixed reference depths (57). The conclusion of their study is that high latitudes have higher export ratios at 100-m depth than low latitudes, and that high latitudes have lower transfer efficiencies. Lutz et al. (58, 59) also used fixed depths for their consideration of global BCP efficiencies and seasonality. If one considers that the high latitudes more commonly have shallower Ezs than 100 m (SI Appendix, Fig. S1), then all of the fixed-depth assessments would be systematically biased between high- and low-latitude regions. Using an Ez-normalized boundary would result in higher export ratios and lower transfer efficiencies at high latitudes and a higher total POC export globally than when quantified with their fixed reference depths (Fig. 5).

Moving Forward with Metrics That Matter

The ocean is characterized by pronounced variations in depths of the distinct strata where particles are produced and consumed. Examination of BCP datasets across contrasting settings reveals very different BCP efficiencies when assessed at a fixed depth compared with consideration of the varying depths of particle production in the sunlit Ez waters. The fixed-depth approach underestimates BCP efficiencies when the Ez is shallow and overestimates it when the Ez is deeper. Since shallower Ezs are more common in higher latitudes and upwelling regions, and deeper Ezs are more common in the low-latitude gyres, there are regional biases when determining global C export based upon at the depth of Ez, relative to a fixed depth of 150 m (Fig. 5). Importantly for C sequestration and climate, the impact on global carbon budgets is also large, with export being a factor of 2 higher for an Ez-normalized C flux, compared with using the canonical fixed 150-m depth flux assessment.

The ocean’s TZ is considered by many to be an unchanging region of the ocean where OM, produced during photosynthesis in the Ez, is passively sinking as “marine snow” through this layer, in a defined and constant manner. To quote Rachel Carson, this is the most “stupendous snowfall on earth” (60). We know that marine snow is a key food source for biota in the TZ, whose activities determine the amount of POC that can escape and be sequestered in the deep ocean on time scales long enough to matter for climate. On average 90% of the snowfall, however, does not reach depths greater than 1,000 m, since it is the food source that is consumed by almost all biota that live below the sunlit surface ocean. However, variability around this average is large on regional, local, and seasonal scales (Fig. 2A), driven both by processes that control the strength of the BCP out of the Ez and processes that impact the transfer efficiency of sinking POC through the TZ.

Future BCP studies need to more carefully and systematically track the variable depth of sinking POC production, which can be approximated using the PPZ, 0.1% PAR, or ²³⁴Th, and apply this Ez depth to define the local BCP efficiencies. This Ez boundary is most readily approximated using fluorescence sensors common on most conductivity, temperature, and depth/Rosette water samplers, as well as globally using autonomous profiling floats (61). Finally, whether using the ²³⁴Th approach or sediment traps, highly vertically resolved flux profiles are needed to capture the steep POC flux gradients immediately below the Ez (8, 9). Ultimately, the flux of carbon and its attenuation with depth sets up the vertical gradient in ocean dissolved C, and hence the extent of ocean–atmosphere CO₂ exchange, thus impacting climate. Understanding BCP efficiencies and mechanisms is important, as these processes will impact how Earth will respond to increasing atmospheric CO₂. Projecting future climate is arguably the scientific question of our era, because all of humanity will be affected.

Data Availability.

All data compiled here are in SI Appendix, Table S2 and references therein.