Development and Refinement of Patient-Reported Outcome Measures for Hearing: A Brief Introduction to Nonparametric Item Response Theory

Abstract

Purpose

The purpose of this report was to demonstrate the value of incorporating nonparametric item response theory in the development and refinement of patient- reported outcome measures for hearing.

Conclusions

Nonparametric item response theory can be useful in the development and refinement of patient-reported outcome measures for hearing. These methods are particularly useful as an alternative to exploratory factor analysis to determine the number of underlying abilities or traits represented by a scale when the items have ordered-categorical responses.

Patient-reported outcomes (PROs) are commonly used in many disciplines, including audiology, to capture a patient's perspective about their condition. This type of outcome where the quality of interest cannot be directly observed is known as a latent variable. The development of PRO measures (PROMs), which are used to indirectly measure latent variables, requires psychometric evaluation of the items considered for inclusion. Most of the currently used hearing-related PROMs were developed using traditional psychometric analysis or classical test theory (CTT); however, more appropriate modern psychometric approaches known collectively as item response theory (IRT) have been recently used in the development and reevaluation of hearing-related PROMs (Boeschen Hospers et al., 2016; Chenault, Berger, Kremer, & Anteunis, 2013; Demorest, Wark, & Erdman, 2011; Heffernan, Maidment, Barry, & Ferguson, 2019; Jessen, Ho, Corrales, Yueh, & Shin, 2018; Mokkink, Knol, van Nispen, & Kramer, 2010). Each of the previously referenced examples of psychometric evaluation used parametric IRT models (i.e., Rasch and graded response models), but a class of more flexible, nonparametric IRT models exists, which can be particularly useful in scale development. This brief report serves as an introduction to Mokken scale analysis (MSA), a nonparametric approach to IRT, and how it can be used to determine the number of underlying abilities represented in a PROM (Mokken, 1971).

Dimensionality

One of the first steps in psychometric analysis is to determine the dimensionality, or the number of (sub)scales that are represented by the items considered for inclusion in an instrument. Some scales are designed as unidimensional instruments that only measure one underlying attribute, whereas others are designed to be multidimensional, such as the Hearing Handicap Inventory for the Elderly and the Hearing Handicap Inventory for Adults (HHIE/A), with two reported subscales measuring emotional response and social/situational problems due to hearing impairment (Newman, Weinstein, Jacobson, & Hug, 1990; Ventry & Weinstein, 1982). Factor analysis, which is based on CTT, is widely used to explore and test hypotheses about the dimensionality of items (Probst, 2003; van der Eijk & Rose, 2015). If there is a strong theoretical basis for the grouping of items, confirmatory factor analysis is often used to evaluate the validity of the hypothesized dimensions. If the dimensions are yet to be established, exploratory factor analysis is used.

Despite the widespread use of factor analytic methods to explore and test hypotheses about the dimensionality of items from PROMs, a key assumption required for this type of analysis is often violated. Specifically, an assumption of factor analysis is the interval-level measurement of the items, that is, the distance between values is meaningful (e.g., on the Fahrenheit scale, the distance from 30° to 40° is the same as the distance from 60° to 70°). However, PROMs are often composed of ordered-categorical items (e.g., the HHIE/A: “no,” “sometimes,” “yes”) for which the distance between the values is unknown. Violation of the assumption of interval-level measurement can result in overdimensionalizing where too many “important” factors are incorrectly identified (van der Eijk & Rose, 2015).

In contrast to CTT, IRT models are designed to analyze ordered-categorical responses, such as those used in the HHIE/A. In addition, IRT models, which can be used in conjunction with CTT, are able to overcome some of the important limitations of analyses based on CTT alone (for a discussion of these limitations, see Heffernan et al., 2019). Mokken models are one type of nonparametric IRT models that relax some strong statistical assumptions of the more commonly used parametric IRT models (Stochl, Jones, & Croudace, 2012). MSA can be used to build unidimensional scales and to assess how well items adhere to the common assumptions of IRT models. The next section gives an overview of MSA and how it can be used as an alternative to factor analysis to better explore dimensionality.

MSA

MSA includes tools for assessing and building scales from items considered for inclusion in an instrument. The specific MSA tools highlighted in this report are those used to explore dimensionality. Before discussing these tools, the Mokken models are introduced.

Mokken Models

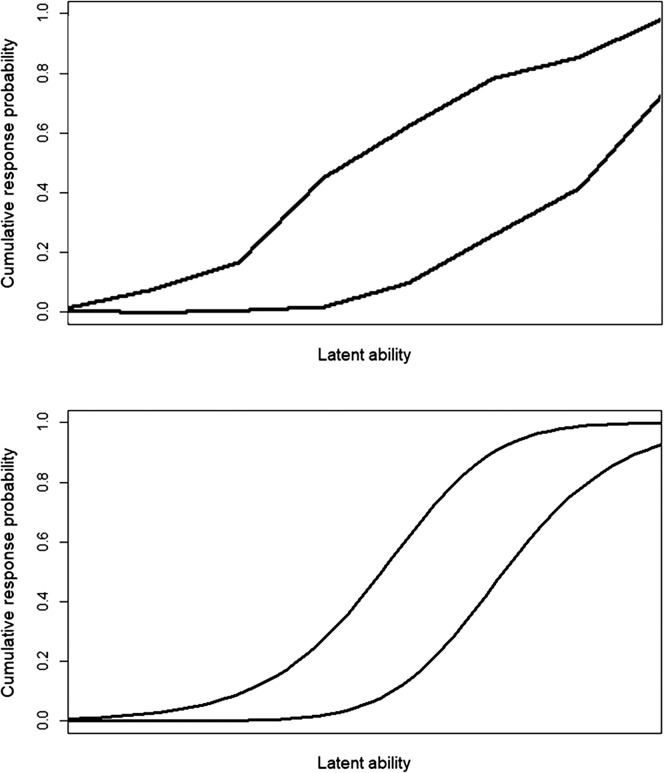
Consider an item i with three response categories (such as “no,” “sometimes,” and “yes”), and let X_i be the score on item i with values x_i = 0, 1, 2. In IRT models, the “item step response function” gives the probability of obtaining an item score of at least x_i for a person with a given level of the latent variable (e.g., hearing handicap).Unlike parametric IRT models, Mokken models do not make any strict assumptions about the shape of the response probabilities. In parametric models, such as the Rasch model, items could potentially be discarded because the shape of their item step response function does not fit the assumed form,which is usually S-shaped (logistic, for example; Stochl et al., 2012; Wright & Masters, 1982). As displayed in Figure 1, rather than assuming a shape, Mokken models only require that the item step response function be monotonically nondecreasing (always increasing or remaining constant), potentially resulting in more items being retained in the scale.

Figure 1.

Examples of item step response functions for an item with three response categories from nonparametric (top) and parametric (bottom) item response models.

Two models were originally introduced by Mokken (1971) for dichotomous items (items with two response categories), the monotone homogeneity model (MHM) and the double monotonicity model. These models were later extended for polytomous items, or items with more than two response categories (such as the HHIE/A; Molenaar, 1997). The Mokken models, as well as many other IRT models, share three assumptions: unidimensionality, monotonicity, and local independence. Unidimensionality means all of the items of a scale measure the same latent variable. The latent variable could be an ability or some other quality (i.e., self-perceived hearing handicap). Monotonicity means that a person with more of the ability or quality measured by the latent variable is more likely to respond to an item in a way that is representative of having a higher level of the latent variable (e.g., a person with more self-perceived hearing handicap is more likely to answer positively to an item measuring hearing handicap than another person with less handicap). Local independence means that holding the level of the latent variable constant, the items are uncorrelated (i.e., the responses to two items on a hearing handicap scale should not be related once handicap level is taken into consideration; Nguyen, Han, Kim, & Chan, 2014).

The three assumptions of the MHM are also shared with many of the commonly used parametric models (including the Rasch and graded response models), making the investigation of the MHM a useful step in fitting parametric IRT models. Notably, when all three of the assumptions of the MHM are met (unidimensionality, monotonicity, and local independence), the ordering of people by their total observed score is justified, with respect to the intended latent variable (i.e., people with higher total scores on a hearing handicap scale have higher levels of the latent variable of hearing handicap; Sijtsma & Verweij, 1992; van der Ark & Bergsma, 2010).

A recent expert tutorial (Sijtsma & van der Ark, 2017) details 10 steps for conducting MSA (readers interested in employing MSA should read this excellent tutorial). After examination of issues with the data (negatively worded items, missingness, and outliers), the first step in scale identification is to explore the items for dimensionality using item selection. Item selection in MSA focuses on the relationship between items and how well the items contribute to the ordering of people with respect to the latent variable. One of the tools in MSA is an automated item selection procedure (AISP). The AISP partitions items to form unidimensional scales using item scalability coefficients, which indicate how well each item helps order subjects by total score on a scale. This procedure can be used to assess whether a number of items measure the same latent variable and how well they discriminate between different values of the latent variable. Items are selected to form unidimensional scales where items are added one by one until no more items discriminate well enough for inclusion on the first scale. If items are leftover, the procedure will check for a second unidimensional subscale (and so on). Weakly discriminating items are rejected and are not included in any scale.

Because the AISP selects items in a bottom-up stepwise method, it is possible that items that initially satisfied the conditions for scaling could potentially no longer satisfy the conditions after more items are included on the final scale. The recently developed genetic algorithm addresses this issue and improves the AISP by checking all possible sets of the items (Straat, van der Ark, & Sijtsma, 2013). The AISP or genetic algorithm can be used to explore dimensionality of items in the user-friendly “mokken” library in the statistical package R (van der Ark, 2012). If the goal is to use the total score of the items, the other two assumptions of monotonicity and local independence can also be assessed using this package (for details of the assessment of these assumptions, see the tutorial by Sijtsma & van der Ark, 2017).

Conclusions

Dimensionality assessment of dichotomous or polytomous items based on factor analysis can lead to overdimensionalization because interval-level measurement is assumed. MSA includes tools that can be used to explore dimensionality, which were designed to analyze ordered-categorical responses. In the development of new PROMs for hearing, these tools can be useful to determine dimensionality of candidate items. Additionally, it may be worthwhile to use these tools to reevaluate commonly used PROMs for hearing that were developed decades ago when tools for psychometric analysis were less readily accessible. The results could be used to provide justification for the use of the total score of the instrument or to explore dimensionality if previous statistical justification was lacking. We explored the dimensionality of the HHIE/A using MSA, and the results are reported separately (Cassarly, Matthews, Simpson, & Dubno, 2019). Briefly, the results suggest that the original subscales designed to assess emotional response and social/situational problems due to hearing impairment are not truly distinct. Instead, results from this nonparametric approach indicate that the HHIE/A items form strong scales that measure self-perceived hearing handicap on a single dimension.

Funding Statement

This research was supported (in part) by National Institute on Deafness and Other Communication Disorders Grant P50 DC000422 (awarded to Judy R. Dubno) and by the South Carolina Clinical and Translational Research Institute, with an academic home at the Medical University of South Carolina, National Center for Advancing Translational Science Clinical and Translational Science Award Grant UL1 TR001450 (awarded to Kathleen T. Brady). This work was conducted in a facility constructed with support from Research Facilities Improvement Program Grant C06 RR14516 (awarded to John R. Raymond) from the National Center for Research Resources.