Resolving absolute depth in circular-ranging optical coherence tomography by using a degenerate frequency comb

Abstract

In Fourier-domain optical coherence tomography, an interference signal is generated that spans an RF bandwidth proportional to the product of three parameters: the imaging range, the imaging speed, and the inverse of the axial resolution. Circular-ranging optical coherence tomography (CR-OCT)architectures were introduced to ease long-range imaging by decoupling the imaging range from the signal RF bandwidth. As a consequence, present CR-OCT systems resolve the relative, but not the absolute, depth location of the scatterers. We introduce here a modified implementation of CR-OCT that uses a degenerate frequency comb source that allows recovery of absolute depth information while only minimally impacting the previously described RF bandwidth compression benefits of CR. We show that this degenerate frequency comb can be created by relatively simple modifications to existing frequency comb source designs, and we present absolute ranging capabilities through imaging studies and simulations.

In Fourier-domain optical coherence tomography, an acquisition system with a finite electronic bandwidth is used to capture the generated optical signals. In applications that require long depth ranges relative to the 1–2 mm imaging depth of optical coherence tomography OCT into most samples, a large portion of the acquired signal bandwidth is dedicated to the measurement of the signal-void regions that are located prior to the sample surface or past the deepest imageable depth. Circular-ranging-OCT captures these signals with higher data efficiency by overlapping equally spaced depth points into a single measurement depth [1,2]. This is done in the optical domain such that the electronic acquisition can operate at a reduced bandwidth and with less noise. As such, CR-OCT decouples the imaging range and acquisition bandwidth, making simultaneous high-speed and long-range imaging more practical.

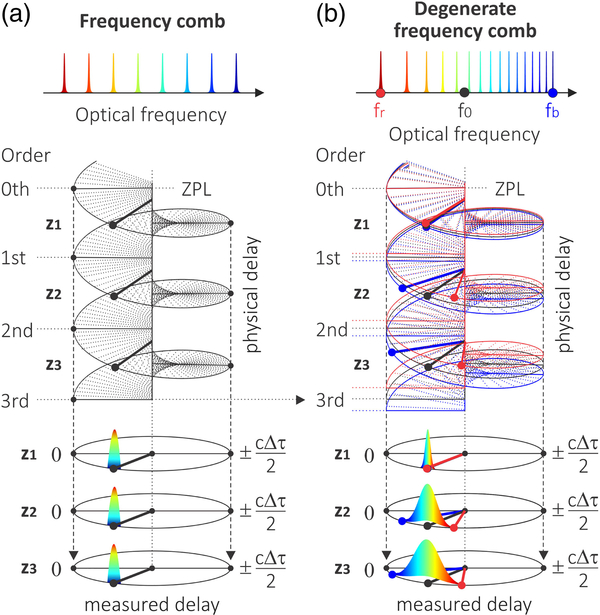
The CR-OCT technique is illustrated in Fig. 1(a), demonstrating the circular mapping of a physical delay coordinate (z axis) into a measured circular delay coordinate (x y plane). Note that each measured delay is a superposition of a set of equally spaced physical delays. This spacing is termed the circular delay range. Importantly, it can be appreciated from this illustration that a distribution of reflected signals only spanning a delay range that is less than the circular delay range can be resolved in the measured/circular delay space without overlapping artifacts. As shown in prior works, a frequency comb source, in combination with complex (in-phase and quadrature) detection of interference fringes, leads to circular-ranging [3,4], and the circular delay range is proportional to the inverse of the free spectral range (FSR) of the frequency comb source, Δτ = 1/(2fsr) [2]. For convenience, a corresponding circular depth range can be defined as the product of the circular delay range and the speed of light in the imaged material. We note that the term delay in this Letter is always defined in relation to the reference arm delay.

Fig. 1.

Comparison of the mapping between physical and measured CR-OCT using (a) a frequency comb source and (b) a degenerate (chirped) frequency comb source. ZPL, zero pathlength.

One consequence of the circular mapping shown in Fig. 1(a) is that the absolute delay of the sample is not measured. In this Letter, we present a method for resolving absolute delay in CR-OCT. Absolute ranging is achieved by adopting a degenerate frequency comb, i.e., a frequency comb with unequally spaced optical frequency lines. We specifically demonstrate that a chirped-frequency degenerate comb source allows measurement of absolute position while maintaining a high compression factor (the core motivation underlying CR-OCT). Further, we demonstrate that it is straightforward to modify existing CR-OCT sources to generate the degenerate comb output.

As a starting point, it is instructive to consider a simple approach [5] to resolving the absolute delay in a CR-OCT system. Here we consider a first measurement using a first frequency comb source with a given FSR, fsr ₁. A given signal can then be localized in a delay subject to an unknown integer number of cycles (termed order) of the corresponding circular delay range, Δτ₁ = 1/(2fsr₁). If a second measurement of the same sample is acquired with a different FSR, fsr₂, the signal may appear at a different circular delay, depending on its absolute position. Thus, by measuring the relationship between the measured circular delay using each of fsr₁ and fsr₂, it is possible to retrieve the integer order parameter in each of the measurements and, thereby, the absolute delay. This can be analogized to the measurement of the elapsed time of an event using a stopwatch with a seconds hand, but no minutes hand. A single stopwatch cannot distinguish between, for example, an elapsed time of 17 s and 1 m 17 s. By adding a second stopwatch that runs faster than the original stopwatch by a known amount, the difference between the seconds-hand measurements of the two watches can now be used to calculate the minutes (that is, order).

While straight forward to understand, the dual-FSR approach has a few disadvantages. First, it is not obvious how to generate two frequency combs with distinct FSRs without significantly complicating the overall source module. Secondly, two A-lines are required to add the absolute depth measurement, which doubles the number of measurements and decreases the efficiency/compression advantage of the CR approach.

In this Letter, we demonstrate an implementation based on similar principles, but with a simpler source implementation and minimally reduced compression penalty. Rather than using two distinct FSRs, we use a frequency comb with a continuously chirped FSR, i.e., degenerate frequency comb. The principle of this approach is similar to that of the dual FSR; the variation in FSR across the optical frequency provides clocks with varying speeds that can be used to decipher the absolute delay. However, the information is now contained within a single depth measurement (A-line). Additionally, the chirped FSR can be created by simply using a dispersive Fabry–Perot etalon within the laser source, fsr(ω)= c/(2n_g (ω)l), where ω is the angular optical frequency, n_g is the group refractive index of the etalon, l is the etalon thickness, and c the speed of light. Figure 1 compares the absolute-to-measured delay mapping of the proposed approach [Fig. 1(b)] relative to a conventional single FSR CR-OCT approach [Fig. 1(a)]. By using a degenerate frequency comb, the spiral mapping of the physical delay to measured delay becomes dependent on the optical frequency and, thus, yields a chirp shown in illustration for three discrete optical frequencies and three delays in Fig. 1(b). The dispersion in the spectrally resolved circular delays (now dependent on optical frequency) is used to calculate the absolute delay. Then, with knowledge of the absolute delay of the scattering signals, it is possible to dechirp the measured fringe such that an image resolve across absolute delay and with transform-limited axial resolution can be generated.

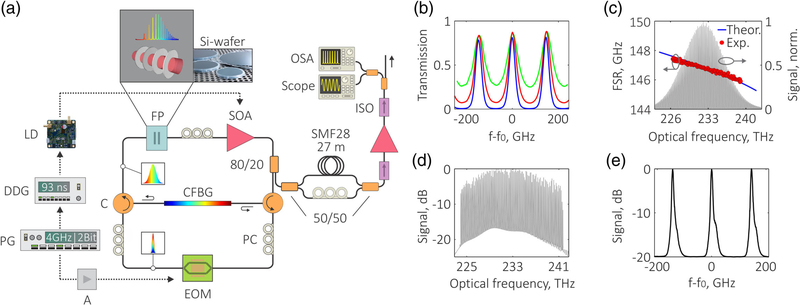
We implemented a CR-OCT system using a degenerate frequency comb by placing a dispersive Fabry–Perot etalon within a previously described [4] stretched-pulse active mode-locked (SPML) laser architecture at 1.29 μm (Fig. 2). The degenerate frequency comb SPML had a repetition rate of 7.6 MHz at 76% duty cycle. Silicon (Si)-wafers providing a group velocity dispersion of approximately 1750 ps²/km at 1.3 μm were used as etalons. The 280 μm thick wafer offered a FSR of 146.7 GHz at the center optical frequency, providing a circular depth range of approximately 1 mm in air. The single-pass transmission and frequency-dependent FSR is shown in Figs. 2(b) and 2(c). The spectrum at the laser output and a magnified plot of three comb lines is shown in Figs. 2(d) and 2(e). The coherence length of the source was measured to be approximately 2 cm (two-sided, double-pass FWHM around zero pathlength in air). This source, in combination with a simple interferometer and acquisition system, provided measured fringe signals. Quadrature detection of the fringe signals was implemented using a LiNbO₃ phase modulator in the reference arm [4].

Fig. 2.

(a) Experimental CR-OCT setup showing the SPML laser with a degenerate frequency comb output. The Fresnel reflection of the Si-etalon produced a finesse of 2.1 per etalon and a combined finesse of 5.1 after four etalons. LD, laser diode driver; DDG, digital delay generator; PG, pattern generator; A, amplifier; EOM, electro-optical modulator; PC, polarization controller; CFBG, chirped fiber Bragg grating; SOA, semiconductor optical amplifier; FP, Fabry–Perot etalon spectral filter; OSA, optical spectrum analyzer; ISO, optical isolator. Si-wafer photograph included with permission from WaferPro. (b) Measured etalon transmission at 1290 nm (232.5 THz) for 1 (green line), 2 (red line), and 4 (blue line) Si-wafer in series. (c) Etalon FSR across the spectrum. The red points show the experimental data, and the blue line shows the theoretical curve. A single-pass ASE spectrum is shown in black. (d) Spectrum at the SPML output. (e) Magnified plot of three comb lines at the SPML output.

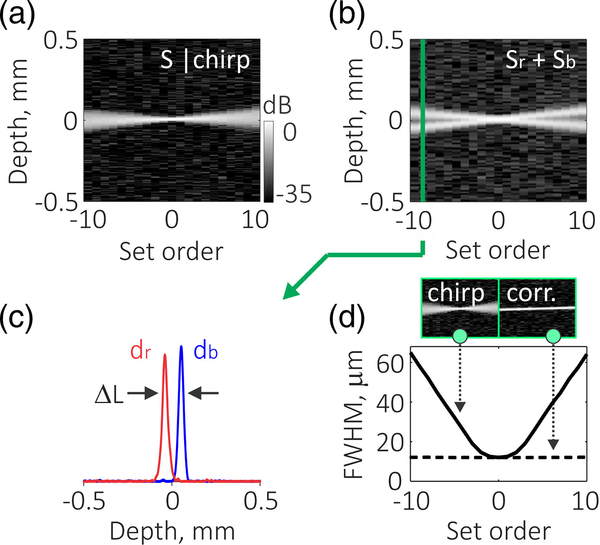
We built a numerical forward model of CR-OCT fringe signals generated from the aforementioned system, i.e., with the same optical source properties and interferometer design. Using this model, we constructed and validated a processing pipeline to extract absolute depth information from mirror fringe signals. As a starting point, we present in Fig. 3(a) the simulated PSFs for a mirror signal generated by processing the degenerate frequency comb signals using conventional CR-OCT approaches. Here a mirror located at the same circular depth (0 mm), but at different orders of the circular depth range (where the circular depth range, is defined by the mean FSR of the degenerate frequency comb). Here we can see the expected chirp (blurring) of the PSF due to the use of the degenerate frequency comb. Next, we implemented a dual-band processing approach that analyzed detected fringes separately in blue and red spectral bands, centered at 1265 nm (237.2 THz) and 1315 nm (228.1 THz), respectively. The difference in the mean FSR within each band was approximately Δ= 1.3 GHz, with fsr_r > fsr_b (Δτ_r < Δτ_b). The simulated PSFs for the same mirror positions are plotted in Fig. 3(b). Here we can resolve the overall chirp of Fig. 3(a) into two PSFs that are walking off from each other. With the measured depth shift, ΔL, between the blue- and red-band PSFs [Fig. 3(c)], the order parameter, k, is calculated by

$$\mathrm{\Delta }L(k)=\frac{kc}{2}\left(\frac{1}{fs{r}_b}-\frac{1}{fs{r}_r}\right),$$ (1)

where fsr_b,r is the mean FSR across the blue and red band, respectively.

Fig. 3.

Numerical simulation of CR depth signals using a degenerate frequency comb and dispersive Si-etalon. (a) Simulated mirror signals for various set orders for a degenerate frequency comb spectrum centered at 1290 nm with a 100 nm bandwidth. (b) Superimposed mirror signals from the blue band (S_b, centered at 1265 nm) and red band (centered at 1315 nm, S_r) as a function of the set order. (c) CR A-line showing the blue- and red-band PSFs and their walk-off at the −9th set order. (d) Extracted PSF width before and after correcting for the degenerate frequency comb chirp using the recovered order parameter and D = 0.54 × 10⁻³ ps².

Next, we developed a technique to eliminate the chirp (axial blurring) resulting from the use of the degenerate frequency comb [see Fig. 3(a)]. A corrected fringe signal, s ′(ω_i), is calculated by multiplying the measured complex fringe, s (ω_i), and a correction vector given by exp (i Dk(ω − ω₀)²), where k is the integer depth order parameter [Fig. 4(d)]. The parameter D is given by the properties of the degenerate frequency comb as

$$D=-{\frac{1}{2fs{r}^2\left({\omega }_o\right)}\frac{dfsr(\omega )}{d\omega }|}_{\omega ={\omega }_o},$$ (2)

the derivation of which is beyond the scope of this Letter.

Fig. 4.

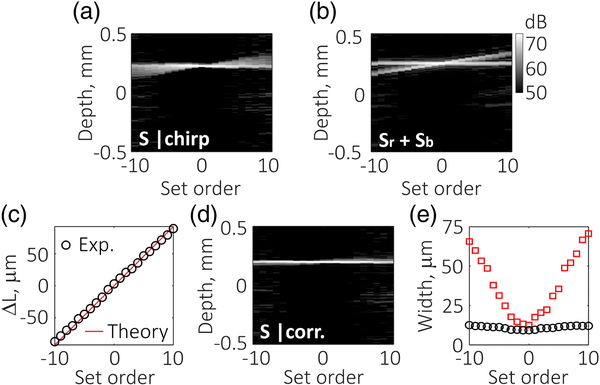
Experimental PSF results using a degenerate frequency comb. (a) PSF calculated from the full spectrum. (b) Superimposed PSFs from the blue and red sub-bands. The tilt seen in (a) and (b) was due to the A-line depth alignment in post-processing. (c) Extracted PSF shift. (d) PSF as in (a) after dechirping using the calculated order and D = 0.54 × 10⁻³ ps². (e) Measured PSF widths before (red squares) and after dechirping (black circles) as a function of the set order.

This processing pipeline was then applied to experimental data. Figure 4 shows PSF measurements at a circular depth of approximately 250 μm using the degenerate frequency comb for order parameters ranging between ±10 acquired analogously to the simulated data in Fig. 3. Figures 4(a) and 4(b) shows the PSFs when using the full and red/blue spectral bands, respectively. Note that the PSF placement at different orders was imprecise due to asymmetric chirping. For better illustration, neighboring PSFs were manually aligned in post-processing, which had no effect on the measurements. The PSF walk-off was extracted by A-line cross-correlation [Fig. 4(c)]. We note that, in practice, wrapping of the PSF walk-off can occur at the circular depth range boundaries. To obtain the true PSF shift in such a scenario, boundary conditions must consider the measured shift, ΔL′, as well as the blue-band circular depth range (because fsr_r > fsr_b), ΔL = ΔL′ ± cΔτ_b. We confirmed that the order calculated from the measured PSF shift matched the set order for each measurement (set order from −10 to 10). Using this resolved order parameter, we corrected the broadening of the full spectral data as described by Eq. (1) and generated a dechirped PSF [Fig. 4(d)]. The recovered PSF width before and after correction is presented in Fig. 4(e). Due to PSF asymmetry, we here show the root-mean-square width $\delta z_{\text{rms}}={\left(\sum \left({\left(z-z_0\right)}^{2}S\right)/\sum S\right)}^{1/2}$, where z is depth, z₀ is the PSF center depth, and S is the signal amplitude.

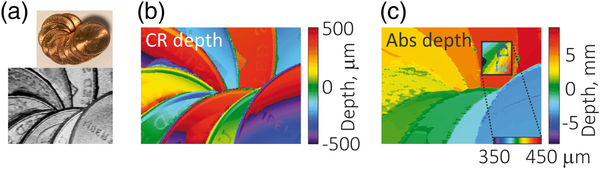
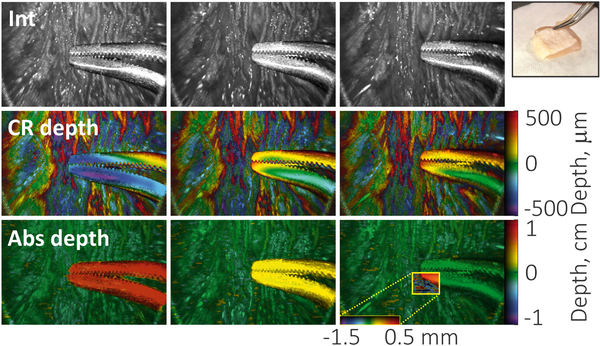
To test the reconstruction of absolute depth information from a sample, we imaged a stack of 9 U.S. pennies (Fig. 5). Circularly wrapped and absolute topographic images are shown in Figs. 5(b) and Fig. 5(c), respectively. Note that the absolute image spans a much larger depth range, but retains the same height resolution (given by the axial resolution) as the conventional circularly wrapped image depth range. The errors in the measured height are believed to originate from a low measurement signal-to-noise ratio (SNR). In a second experiment, the technique was used to provide feedback on the absolute positioning of a surgical instrument relative to a tissue surface (Fig. 6). The absolute topographic images (bottom row), but not the circularly wrapped conventional CR topographic images (middle row), allow the proximity of the instrument to the tissue to be measured. This absolute depth mapping technique could enable high depth perception in real time to visualize complex organs within a surgical field during a procedure.

Fig. 5.

Absolute height topographical imaging of a stack of U.S. pennies using the proposed CR-OCT system. (a) Photograph and intensity depth projection. (b) Circular depth map. (c) Reconstructed absolute depth.

Fig. 6.

Resolving absolute position of a surgical instrument using the proposed CR-OCT system. Surgical forceps were positioned above a tissue (chicken skin) sample. The images depict en face intensity projections (top row), circular depth maps (middle row), and recovered absolute depth maps (bottom row).

Finally, we briefly comment on the magnitude of etalon dispersion required to perform absolute ranging. Again returning to the dual-FSR technique as a simplified example, we can estimate the minimum FSR difference, Δ_min, required to generate a detectable shift by setting ΔL = δz for k = 1 in Eq. (1), where δz is the transform-limited axial resolution of each measurement, yielding

$${\mathrm{\Delta }}_{\min }=\frac{2\delta z{\overline{fsr}}^2}{2\delta z\overline{fsr}+c},$$ (3)

where $\overline{fsr}$ is the mean FSR between the measurements. Applying this to the degenerate frequency comb technique presented in this Letter, we can set $\overline{fsr}=(fs{r}_b+fs{r}_r)/2$ and δz equal to the transform-limited axial resolution of each sub-band. To estimate a maximum differential FSR, Δ_max, we note that the shift, ΔL, induced by a sample located in the largest order a system is designed to measure accurately, k_max, should not exceed half of the circular delay range, yielding

$${\mathrm{\Delta }}_{\max }<\frac{\overline{fsr}}{1+2k_{\max }},$$ (4)

where k_max = l_c /(2ΔL_k=₁), with l_c being the coherence length and ΔL_k=₁ being ΔL for k = 1, i.e., the difference in the circular depth range. We note that this limit can be overcome in the degenerate frequency comb method by shifting the spectral windows closer to the center frequency and, thereby, reducing the differential FSR between the measurements.

This Letter describes and validates numerically and experimentally that a degenerate frequency comb constructed from a dispersive Fabry–Perot etalon can be used to recover absolute delay positions without significantly affecting measurement compression. This Letter focuses on the principles and first-order implementations and, as such, has a few limitations. First, uncoated Si-etalons (Si-wafer) were used and, due to a resulting low finesse, multiple etalons were cascaded. A custom-designed coated Si (or other dispersive material) etalon providing higher finesse values would improve system performance, including coherence length and measurement SNR. The processing approach used simple red/blue sub-band analysis and PSF shift measurements based on the cross-correlation of dominant signals, i.e., sample surface. Once the order is obtained via this method, depth-resolved images comparable to those that would be acquired using non-degenerate CR-OCT methods can be obtained. It is likely that processing can be enhanced to better utilize the continuous chirping that occurs through the spectral band. Related to this, the construction of absolute delay resolving algorithms that impose a minimal processing (and sampling) penalty over conventional CR-OCT is critical and the subject of ongoing studies.