A Coupled Mass Transport and Deformation Theory of Multi-constituent Tumor Growth

Abstract

We develop a general class of thermodynamically consistent, continuum models based on mixture theory with phase effects that describe the behavior of a mass of multiple interacting constituents. The constituents consist of solid species undergoing large elastic deformations and compressible viscous fluids. The fundamental building blocks framing the mixture theories consist of the mass balance law of diffusing species and microscopic (cellular scale) and macroscopic (tissue scale) force balances, as well as energy balance and the entropy production inequality derived from the first and second laws of thermodynamics. A general phase-field framework is developed by closing the system through postulating constitutive equations (i.e., specific forms of free energy and rate of dissipation potentials) to depict the growth of tumors in a microenvironment. A notable feature of this theory is that it contains a unified continuum mechanics framework for addressing the interactions of multiple species evolving in both space and time and involved in biological growth of soft tissues (e.g., tumor cells and nutrients). The formulation also accounts for the regulating roles of the mechanical deformation on the growth of tumors, through a physically and mathematically consistent coupled diffusion and deformation framework. A new algorithm for numerical approximation of the proposed model using mixed finite elements is presented. The results of numerical experiments indicate that the proposed theory captures critical features of avascular tumor growth in the various microenvironment of living tissue, in agreement with the experimental studies in the literature.

1. Introduction

There is a vast and growing literature on mathematical and computational models of the physical and biological processes involved in the initiation, development, and growth of cancer [2, 12, 61, 80, 121, 131, 137, 149, 167]. Most tumor models can be categorized as either a discrete cell-based model, or a continuum model. The continuum approach considers the average of the global cell population behavior [35, 96, 120, 160, 164], while discrete approaches track and update individual cell dynamics using a prescribed set of biophysical rules [19, 82, 135, 154]. Due to the rapid increase in the computational cost of discrete methods with the number of cells modeled, continuum methods are often favored for providing predictions in in vivo systems for events at experimentally observable spatial and temporal scales.

Fundamental theoretical challenges in the continuum modeling of tumor growth arise in describing the associations between gain and loss of mass and stresses induced by cancer cell proliferation and apoptosis, as well as the effect of a nonuniform microenvironment. Extensive efforts over the last two decades have resulted in various theoretical approaches [4, 46, 76, 106, 121, 165, 166]. Although these previous efforts address several open issues in understanding, simulating, and predicting tumor growth, the development of a unified mathematical framework for modeling the growth process is still a central challenge in biomechanics [4].

Several continuum theories are based on the abstraction of a homogenized, single-constituent tumor [137, 165]. These purely mechanical models implicitly assume sources of mass supply to drive the growth of the tumor. Although these methods can yield self-consistent frameworks, they are incapable of accounting for important biophysical phenomena encountered in tumor progression including, for example, nutrient delivery by the surrounding tissues and consumption by tumor cells. A more realistic representation of a tumor growing in a microenvironment can be achieved through a framework based on continuum theories of mixtures [24, 38, 120, 132] which naturally incorporate various solid and fluid constituents involved in the underlying biophysical phenomena. Mixture theory has been the focus of much research in mechanics for many years [23] as a basis for treating the behavior of porous media involving two or more interacting bodies. In mixture models of tumor growth, the governing equations consist of mass and momentum balance equations for each species, interphase mass, and momentum exchange, along with appropriate constitutive equations. Recently, multiphase mixture models have been developed to address heterogeneities in cell-phenotypes and the mechanical response of tumor phases (see, e.g., [8, 25, 28, 48, 49, 57, 111, 116, 139]). Phase-field models provide a general approach to modeling multiphase materials [22, 100], in which the interface between phases is handled automatically as a feature of the solution and represents boundary layers between phases. In general, such models are obtained by incorporating gradients of the order parameters, such as the concentrations of various constituents, in the free energy functionals of a multiphase material to approximate surface energies at interfaces. The most common model of this type is the Cahn-Hilliard model of binary phase separation [29] in which the free energy contains gradients in concentrations multiplied by parameters which characterize the thickness of the smoothed interfaces between the phases. Phase field models have provided important frameworks for characterizing microstructural evolution at the mesoscale [155], solidification [22], grain growth [112], dislocation dynamics [169], and self-assembly of block copolymers [32] among others. Recently, phase-field models have been applied to simulate tumor growth and decline [35, 96, 120, 164]. A multi-species framework allows for characterizing the interaction between (for example) the necrotic, apoptotic, quiescent, and proliferative cells present in solid, avascular tumors.

In addition to the underlying mathematical framework, another challenge in developing tumor growth models is simulating the mechanical cues to tumor cells alongside the biological and chemical factors. Experimental studies indicate that the mechanical stresses of the solid phase of a tumor play a vital role in the expansion, invasion, and metastasis of tumors [26, 78, 79, 91, 109, 147, 157]. These macroscopic stresses arise due to heterogeneous tumor growth as well as the effect of surrounding tissue confinement. While the generation of residual stresses from heterogeneous growth is significant in normal tissues such as arteries and mucosa [92, 93, 144, 150], the external stresses on tumors produced by the surrounding tissues can be more prominent than those incurred by the heterogeneous growth [4, 7]. The mechanical stresses moderate the development of solid tumors by compressing both the tumor and the associated vasculature. These effects result in lowering the proliferation rate and stimulating apoptosis of the cancer cells, as well as enhancing the invasiveness and metastatic potential of a tumor [72, 79, 113]. However, these mechano-chemo-biological mechanisms, which are determined by cell-cell and cell-microenvironment interactions, have not been adequately addressed by current theoretical continuum models [4, 46]. The majority of the previous investigations on modeling growth-induced stresses rely on phenomenological evolution equations of the growth-associated strains. Such assumptions result in models that fail to address the effect of microscale evolutions on the macroscopic stress and strain, and they are inadequate to characterize the mechanical aspects of the biological growth [4].

To overcome the above-mentioned modeling challenges, we develop a general class of thermodynamically consistent continuum models, based on mixture theory with diffuse interface effects, that describes the biomechanical behavior of a mass of N interacting constituents. M of these N constituents are solid species undergoing finite strain elastic deformation and growth, and NM can be compressible, Newtonian viscous fluids. A general phase-field framework is developed by considering the free energy and rate of dissipation potential as primary potentials and thermodynamic forces are derived considering the processes leading to energy storage and dissipation. The constitutive relations are deduced from specific forms of the Helmholtz free energy and rate of dissipation to simulate major features of avascular tumor growth in a microenvironment. Special attention is given to the mechanical cues detected by tumor cells and their effects on tumor progression. In this regard, a fully coupled deformation and mass transfer model is developed through physically and mathematically consistent construction. The proposed mathematical model is numerically solved using mixed finite elements, and several numerical experiments are conducted considering a system consists of four interacting constituents: tumor cells, healthy cells, nutrient-rich and nutrient-poor extracellular water. The numerical experiments indicate that the general diffusion-deformation framework proposed in this work enables simulating the significant mechano-chemo-biological features of avascular tumor growth in the various microenvironment of living tissue, in agreement with the experimental studies in the literature. In particular, the proposed model accounts for the growth of the proliferating tumor cells due to nutrient consumption, the directional movement of tumor cells towards the nutrient supply, and the surface tension stress due to cell-cell adhesion at the interface of tumor and healthy cells constituents. More importantly, this work enables simulating the significant inhibitory effect of the confinement induced by the surrounding tissues on the avascular tumor growth, using a new evolution equation of the growth deformation gradient derived from the mass transfer relations.

The rest of this contribution is organized as follows. Section 2 presents the theoretical development of the phase-field mixture theory, providing a framework for the proposed four-constituent tumor growth model, which is described in section 3. The results of numerical experiments designed to demonstrate the qualitative model prediction are described in section 4. The Discussion and Conclusions are given in section 5.

2. Theoretical Framework: Coupled Mass Transport and Deformation of Multi-species Mixtures

Our theoretical framework of tumor growth model is founded in the continuum theory of mixtures, advanced by Truesdell [151], Truesdell and Toupin [153], Bowen [23, 24], and Eringen and Ingram [42, 77]. Parallel developments of theories of porous media share many aspects of mixture theory for two- or three-phase materials, as can be seen in works such as those by de Boer [37, 38] among many others. The development of diffuse-interface models based on mixture theory involves an additional level of complexity due to the dynamical effects associated with changes in the volume fractions of the constituents [120, 132]. We follow the basic hypotheses of Truesdell and Noll [152] in developing a physically meaningful continuum theory. In this regard, the general theory governing a continuum mixture of N constituents is developed based on the balance laws for mass, momentum, and energy as well as the inequality for entropy production. These laws are the fundamental building blocks on which to frame theories of material behavior. Then a general phase-field version is developed by closing the system with constitutive equations. In this regard, the free energy and rate of dissipation potential are considered as primary potentials, and thermodynamic forces are derived considering the processes leading to energy storage and dissipation.

2.1. A Continuum Theory of Mixture

In continuum mechanics, a body $\mathcal{B}$ is viewed as a set of material points that occupy subsets of Euclidean space as the motion of the body carries it through various configurations. It is a convention to choose one such region as a reference and refer to it as the reference configuration of $\mathcal{B}$. The material points of the body are identified with their positions X. The underlying assumption of mixture theory is that a material body $\mathcal{B}$ consists of N constituent species that occupy a common part of physical space at the same time. The body undergoes a motion which maps the reference configuration $\mathcal{B}$ onto a current configuration ${\mathcal{B}}_t$, with the spatial position of material points at time t, given by $\mathbf{x}=\mathcal{X}(\mathbf{X},t)$. In an N-species mixture the motion is defined by

$$\mathbf{x}={\mathcal{X}}_{\alpha }({\mathbf{X}}_{\alpha },t),$$ (1)

where α = 1, 2, ⋯ , N and X_α is the position of the material points of the α-th constituent in its reference configuration. The deformation gradient is defined by

$${\mathbf{F}}_{\alpha }≔\frac{\partial {\mathcal{X}}_{\alpha }}{\partial {\mathbf{X}}_{\alpha }}.$$ (2)

Each spatial position x is occupied by N different constituents, and each constituent has a mass density, ${\widehat{\rho }}_{\alpha }(\mathbf{x},t)$, representing the mass of the α-th constituent per unit volume of the mixture at time t. The mass density of the mixture at a point (x, t) is defined as¹,

$$\rho (\mathbf{x},t)=\sum _{\alpha }{\widehat{\rho }}_{\alpha }(\mathbf{x},t),$$ (3)

and the (partial) density, ρ_α, is

$${\widehat{\rho }}_{\alpha }(\mathbf{x},t)={\rho }_{\alpha }(\mathbf{x},t){\varphi }_{\alpha }(\mathbf{x},t),$$ (4)

representing the mass of α-th constituent per unit volume of the constituent. The mass concentration and volume fraction of the α-th constituent are defined respectively by,

$$c_{\alpha }(\mathbf{x},t)=\frac{{\widehat{\rho }}_{\alpha }(\mathbf{x},t)}{\rho (\mathbf{x},t)},{\varphi }_{\alpha }(\mathbf{x},t)=\frac{d{v}_{\alpha }}{dv},$$ (5)

where dv is a differential volume containing the point x, and dv_α is the proportion of volume occupied by constituent α. From (5) clearly,

$$\sum _{\alpha }{c}_{\alpha }=1,\sum _{\alpha }{\varphi }_{\alpha }=1.$$ (6)

In addition, the velocity of each constituent and the mixture velocity are defined as,

$${\mathbf{v}}_{\alpha }(\mathbf{x},t)=\frac{\partial {\mathcal{X}}_{\alpha }({\mathbf{X}}_{\alpha },t)}{\partial t},\mathbf{v}=\frac{1}{\rho }\sum _{\alpha }{\rho }_{\alpha }{\varphi }_{\alpha }{\mathbf{v}}_{\alpha }.$$ (7)

The diffusion velocity for the α-th constituent is also defined by

$${\mathbf{p}}_{\alpha }={\mathbf{v}}_{\alpha }-\mathbf{v},\text{with}\sum _{\alpha }{\rho }_{\alpha }{\varphi }_{\alpha }{\mathbf{p}}_{\alpha }=0.$$ (8)

The velocity gradient of each constituent, L_α = ∇ · v_α, can be split into symmetric, D_α, and skew-symmetric, W_α, parts in which,

$${\mathbf{D}}_{\alpha }=\frac{1}{2}(\nabla {\mathbf{v}}_{\alpha }+\nabla {\mathbf{v}}_{\alpha }^T),{\mathbf{W}}_{\alpha }=\frac{1}{2}(\nabla {\mathbf{v}}_{\alpha }-\nabla {\mathbf{v}}_{\alpha }^T).$$ (9)

Finally, the link between Lagrangian and Eulerian descriptions in time derivatives can be made according to

$$\frac{d^{\alpha }\varphi }{dt}=\frac{\partial \varphi }{\partial t}+{\mathbf{v}}_{\alpha }\cdot \nabla \varphi ,$$ (10)

where d^αϕ/dt is the material time-derivative related to the motion of each constituent and ϕ is any differentiable function of x and t.

Each of the N species must satisfy its own balance laws consistent with the presence of interaction among constituents. The balance laws govern the behavior of a general mixture that must hold for all α, 1 ≤ α ≤ N, are presented in the next sections.

2.2. Macroscopic and Microscopic Force Balances

Let ${\mathcal{R}}_t$ denote an arbitrary spatial region convecting within the body $\mathcal{B}$ at time t. The basic balance laws for linear and angular momentum assert that the net force and momentum on ${\mathcal{R}}_t$ are balanced by temporal changes in the linear and angular momentum of ${\mathcal{R}}_t$. In this regard, the balance of linear momentum for α-constituent in the mixture requires,

$$\frac{d^{\alpha }}{dt}{\int }_{{\mathcal{R}}_t}{\rho }_{\alpha }{\varphi }_{\alpha }{\mathbf{v}}_{\alpha }\mathrm{d}V={\int }_{\partial {\mathcal{R}}_t}{\mathbf{T}}_{\alpha }.\mathbf{n}\mathrm{d}A+{\int }_{{\mathcal{R}}_t}({\rho }_{\alpha }{\varphi }_{\alpha }{\mathbf{b}}_{\alpha })\mathrm{d}V,$$ (11)

where T_α is the partial Cauchy stress tensor, b_α is the body force per unit mass, n(x, t) denotes the outward unit normal field on the boundary $\partial {\mathcal{R}}_t$, and dA and dV are differential surface and volume elements of $\partial {\mathcal{R}}_t$. Using the divergence theorem, and taking into account that (11) must hold for all spatial regions, leads to the macroforce balance,

$$\frac{d^{\alpha }{\rho }_{\alpha }{\varphi }_{\alpha }{\mathbf{v}}_{\alpha }}{dt}=\nabla \cdot {\mathbf{T}}_{\alpha }+{\rho }_{\alpha }{\varphi }_{\alpha }{\mathbf{b}}_{\alpha }.$$ (12)

In the case of nonpolar materials (neglecting, e.g., electromagnetic effects and micro-moments), the balance of angular momentum results in the relation,

$${\mathbf{T}}_{\alpha }={\mathbf{T}}_{\alpha }^T$$ (13)

so the partial Cauchy stress is symmetric.

To describe the phase dynamics in the mixture (following the arguments of [62]), in addition to local force balances, we postulate the existence of a set of microscopic forces that accompany the evolution of each order parameter (i.e., the volume fraction in the present formulation). These thermodynamical forces are termed “microscopic” because they are involved with phenomena that occur at a scale (e.g., cell level) smaller than macroscopic interactions (e.g., tissue level). The notion of microscopic forces has been successfully applied to to develop generalized frameworks such as strain gradient-plasticity theories [64, 158], generalized heat transfer [44], micromorphic approaches [16, 45], and mixture theories of porous media [59, 126].

The (micro-)kinematics of phase, ϕ_α, such as the phase separation and mixing of different components, is associated with three microforces per unit volume, including the internal microforce π_α and the external microforce τ_α that are associated with volume fraction² and the thermodynamic stress conjugate to the gradient of species volume fractions ξ_α that represents a flux through the boundary $\partial {\mathcal{R}}_t$. These nonlocal forces are balanced through the following relation,

$${\int }_{\partial {\mathcal{R}}_t}{\xi }_{\alpha }.\mathbf{n}\mathrm{d}A+{\int }_{{\mathcal{R}}_t}{\pi }_{\alpha }\mathrm{d}V+{\int }_{{\mathcal{R}}_t}{\pi }_{\alpha }\mathrm{d}V=0.$$ (14)

Making use of the divergence theorem and the fact that ${\mathcal{R}}_t$ is arbitrary leads to the following species microforce balance,

$$\nabla \cdot {\xi }_{\alpha }+{\pi }_{\alpha }+{\tau }_{\alpha }=0.$$ (15)

The additional balance law (15) arises due to considering the volume fraction of each constituent as an independent kinematical quantity in the mixture theory. This force balance is essential in the theory of phase-field mixtures to account for the dynamical effects associated with changes in the volume fractions of the constituents, although it does not ordinarily arise in mixture theories. The general formulation described in this section leads to biological interpretations of microforces in tumor growth phenomena described in section 2.6³ (See Appendix A for an alternative approach to determine the associated balance of macroscopic and microscopic forces using the principle of virtual power.)

2.3. Diffusing Species Mass Balance

The net mass of the diffusing species in the spatial region ${\mathcal{R}}_t$ is represented by ${\int }_{{\mathcal{R}}_t}{\rho }_{\alpha }{\varphi }_{\alpha }\mathrm{d}V$. The species transport to ${\mathcal{R}}_t$ can be characterized by the rate at which the species is transported to ${\mathcal{R}}_t$ by diffusion across $\partial {\mathcal{R}}_t$ as well as the rate of transport to ${\mathcal{R}}_t$ by constituents external to the body. In this regard, species mass balance requires that,

$$\frac{d^{\alpha }}{dt}{\int }_{{\mathcal{R}}_t}{\rho }_{\alpha }{\varphi }_{\alpha }\mathrm{d}V=-{\int }_{\partial {\mathcal{R}}_t}{\mathbf{J}}_{\alpha }.\mathbf{n}\mathrm{d}A+{\int }_{{\mathcal{R}}_t}{S}_{\alpha }\mathrm{d}V,$$ (16)

where J_α is the mass flux and S_α is external species mass supplied (a source term). Thus, (16) suggests that the mass-rate-of-change of the α-th component must balance with the net rate of generation of the α-th component in ${\mathcal{R}}_t$. Using the Reynolds’ transport relation along with the divergence theorem, the local species mass balance is [43]

$$\frac{\partial {\rho }_{\alpha }{\varphi }_{\alpha }}{\partial t}+\nabla \cdot ({\rho }_{\alpha }{\varphi }_{\alpha }{\mathbf{v}}_{\alpha })=S_{\alpha }-\nabla \cdot {\mathbf{J}}_{\alpha }.$$ (17)

The right-hand side of (17) is called the mass growth rate of the αth component [23].

2.4. Force and Mass Balance for the Mixture

The balance equations for the mixture, governing the motion of a single body, should follow the individual species balance equation summing over all constituents. Thus the continuum balance laws of the full mixture can be written as,

$$\rho \frac{d\mathbf{v}}{dt}=\nabla \cdot \mathbf{T}+\mathbf{b},$$ (18)

$$\nabla \cdot \xi +\pi +\tau =0,$$ (19)

$$\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \mathbf{v})=0,$$ (20)

subject to the following constraints,

$$\begin{gathered} \mathbf{b}=\frac{1}{\rho }\sum _{\alpha }{\rho }_{\alpha }{\varphi }_{\alpha }{\mathbf{b}}_{\alpha }, \\ \sum _{\alpha }{S}_{\alpha }=\sum _{\alpha }\nabla \cdot {\mathbf{J}}_{\alpha }, \\ \xi =\sum _{\alpha }{\xi }_{\alpha }, \\ \pi =\sum _{\alpha }{\pi }_{\alpha }, \\ \tau =\sum _{\alpha }{\tau }_{\alpha } \\ \mathbf{T}=\sum _{\alpha }{\mathbf{T}}_{\alpha }-{\rho }_{\alpha }{\varphi }_{\alpha }{\mathbf{p}}_{\alpha }\otimes {\mathbf{p}}_{\alpha }. \end{gathered}$$ (21)

In the above relations, ρ, T, b, and v are the mass density, Cauchy stress, body force per unit mass, and velocity of the mixture, respectively.

2.5. Thermodynamics Derivation

2.5.1. The First Law: Balance of Energy

The first law of thermodynamics represents a balance between the internal energy of ${\mathcal{R}}_t$, the rate at which power is expended on ${\mathcal{R}}_t$, and the energy carried into ${\mathcal{R}}_t$ by species transport. In the present formulation, we consider isothermal processes (i.e., the heating $d\mathcal{Q}∕dt\approx 0$) and assume that the kinetic energy is negligible. Defining the net internal energy of mixture as $\mathcal{E}={\int }_{{\mathcal{R}}_t}\rho \epsilon \mathrm{d}V$, with ε being the specific internal energy, the first law of thermodynamics is written as

$$\frac{d}{dt}\mathcal{E}={\mathcal{P}}_{\text{ext}}+\mathcal{M},$$ (22)

where ${\mathcal{P}}_{\text{ext}}$ is the external power. In addition to the classical terms of macroscopic forces, we consider non-classical terms contributing to the energy balance. This includes power expenditures of the microforces in ${\mathcal{P}}_{\text{ext}}$ along with energy flux due to the species diffusion (i.e., fluxes and sources). In (22), $\mathcal{M}$ is the (free-)energy carried into ${\mathcal{R}}_t$ by mass (species) transport (see, e.g., [62, 66, 98]). As J_α and S_α carry with them a flux and supply of energy, respectively, characterized by the chemical potential μ_α, we write

$$\mathcal{M}=\sum _{\alpha }\left(-{\int }_{\partial {\mathcal{R}}_t}{\mu }_{\alpha }{\mathbf{J}}_{\alpha }\cdot \mathbf{n}\mathrm{d}A+{\int }_{{\mathcal{R}}_t}{\mu }_{\alpha }{S}_{\alpha }\mathrm{d}V\right).$$ (23)

The chemical potential μ_α of species α is a quantity defined as the rate of change of free energy with respect to the change in the particle number of the species that are added or removed from the thermodynamic system. The magnitude of the chemical potential is independent of the size of the system, but it does include phenomena affecting diffusion; e.g., the strain energy gradient, electric field, and temperature gradient. Thus, in (23), μ_α characterizes the flux and supply of energy to the system and needs to be considered in the energy balance relation.

From the mass balance relation (16), along with the divergence theorem,

$$\begin{gathered} {\int }_{\partial {\mathcal{R}}_t}{\mu }_{\alpha }{\mathbf{J}}_{\alpha }.\mathbf{n}\mathrm{d}A={\int }_{{\mathcal{R}}_t}({\mu }_{\alpha }\nabla \cdot {\mathbf{J}}_{\alpha }\cdot \nabla {\mu }_{\alpha })\mathrm{d}V \\ =-\left({\mu }_{\alpha }\frac{d^{\alpha }{\rho }_{\alpha }{\varphi }_{\alpha }}{dt}-{\mathbf{J}}_{\alpha }\cdot \nabla {\mu }_{\alpha }-{\mu }_{\alpha }{S}_{\alpha }\right)\mathrm{d}V, \end{gathered}$$

one can write,

$$\mathcal{M}=\sum _{\alpha }{\int }_{{\mathcal{R}}_t}\left({\mu }_{\alpha }\frac{d^{\alpha }{\rho }_{\alpha }{\varphi }_{\alpha }}{dt}-{\mathbf{J}}_{\alpha }\cdot \nabla {\mu }_{\alpha }\right)\mathrm{d}V.$$

Consequently, (22) can be written as,

$$\begin{gathered} \frac{d}{dt}{\int }_{{\mathcal{R}}_t}\rho \epsilon \mathrm{d}V≔\sum _{\alpha }{\int }_{{\mathcal{R}}_t}\left({\mathbf{T}}_{\alpha }:{\mathbf{L}}_{\alpha }+{\tau }_{\alpha }\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}\right)\mathrm{d}V+\sum _{\alpha }{\int }_{\partial {\mathcal{R}}_t}({\xi }_{\alpha }\cdot \mathbf{n})\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}\mathrm{d}A \\ +\sum _{\alpha }{\int }_{{\mathcal{R}}_t}\left({\mu }_{\alpha }\frac{d^{\alpha }{\rho }_{\alpha }{\varphi }_{\alpha }}{dt}-{\mathbf{J}}_{\alpha }\cdot \nabla {\mu }_{\alpha }\right)\mathrm{d}V. \end{gathered}$$ (24)

From the symmetry of the Cauchy stress in (13), the term T_α : L_α can be replaced by T_α : D_α. Moreover, applying the divergence theorem again yields,

$${\int }_{\partial {\mathcal{R}}_t}({\xi }_{\alpha }\cdot \mathbf{n})\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}dA={\int }_{{\mathcal{R}}_t}{\xi }_{\alpha }\nabla \left(\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}\right)dV+{\int }_{{\mathcal{R}}_t}(\nabla \cdot {\xi }_{\alpha })\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}dV,$$

along with

$$\nabla \cdot {\xi }_{\alpha }\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}+{\tau }_{\alpha }\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}=-{\tau }_{\alpha }\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}.$$

Following (15), the relation for the local energy balance is derived as,

$$\begin{gathered} \rho \frac{d\epsilon }{dt}=\sum _{\alpha }\left({\mathbf{T}}_{\alpha }:{\mathbf{D}}_{\alpha }-{\pi }_{\alpha }\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}+{\xi }_{\alpha }\cdot \nabla \left(\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}\right)\right) \\ +\sum _{\alpha }\left({\mu }_{\alpha }\frac{d^{\alpha }{\rho }_{\alpha }{\varphi }_{\alpha }}{dt}-{\mathbf{J}}_{\alpha }\cdot \nabla {\mu }_{\alpha }\right). \end{gathered}$$ (25)

It is worth mentioning that both b_α and π_α are internal forces in ${\mathcal{R}}_t$ at the macroscopic and microscopic length scales respectively. While b_α and π_α exist in the force balances (12) and (15), they are not present in the working terms of the energy equation(24). Moreover, the balance equation (22) for the mixture is transferred into individual constituents, in which the local and global balances are related according to

$$\rho \frac{d\epsilon }{dt}=\sum _{\alpha }{\rho }_{\alpha }{\varphi }_{\alpha }\frac{d^{\alpha }{\epsilon }_{\alpha }}{dt}.$$ (26)

2.5.2. The Second Law: Entropy Production Inequality

The second law of thermodynamics (entropy principle) is used here for imposing restrictions on constitutive equations. In mixture theory, while the implementation of such constraints for every individual species is possible and restrictive, its satisfaction for all constituents is a necessary and sufficient condition for the presence of dissipative processes within the mixture [37, 38]. It should also be noted that the entropy inequality has to be manipulated to include fundamental and special physical properties of the system under study. Depending on the behavior of the body, the supplementary constraints might be taken into consideration at the local (constituent) level and/or applied globally to the full mixture⁴. Moreover, this inequality is a necessary constraint on constitutive equations. There is not a unique way to fulfill this inequality, and many choices that satisfy the inequality may lead to simulations that do not accurately reflect the physical phenomena.

The entropy production inequality requires that the free energy increases at a rate not greater than the rate at which work is performed. The net entropy production per unit time, is given by

$$\mathcal{N}=\frac{d}{dt}{\int }_{{\mathcal{R}}_t}\eta dV\ge 0,$$ (27)

where η is the specific entropy of the mixture and (27) is often referred to as the Clausius-Duhem inequality [69, 70]. The entropy density of the mixture can be written as a sum of the specific entropy of individual constituents as

$$\rho \eta =\sum _{\alpha }{\rho }_{\alpha }{\varphi }_{\alpha }{\eta }_{\alpha }.$$ (28)

We continue with the derivation of the Clausius-Duhem inequality by defining the Helmholtz (specific) free-energy of the mixture as,

$$\psi (\mathbf{x},t)=\epsilon (\mathbf{x},t)-\theta (\mathbf{x},t)\eta (\mathbf{x},t).$$ (29)

The free-energy per unit volume is,

$$\Psi (\mathbf{x},t)=\rho \psi (\mathbf{x},t),$$ (30)

with the free energy for every individual species (e.g., [120]) given as,

$${\Psi }_{\alpha }={\rho }_{\alpha }{\varphi }_{\alpha }{\psi }_{\alpha }.$$

Taking the time derivative of free-energy and substituting (25) into (29) along with (30), yields the local free-energy imbalance for fixed temperature θ = θ₀⁵,

$$\begin{gathered} -\frac{d\Psi }{dt}+\sum _{\alpha }\left({\mathbf{T}}_{\alpha }:{\mathbf{D}}_{\alpha }-{\tau }_{\alpha }\frac{d^{\varphi }{\varphi }_{\alpha }}{dt}+{\xi }_{\alpha }\cdot \nabla \left(\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}\right)\right) \\ +\sum _{\alpha }\left({\mu }_{\alpha }\frac{d^{\alpha }{\rho }_{\alpha }{\varphi }_{\alpha }}{dt}-{\mathbf{J}}_{\alpha }\cdot \nabla {\mu }_{\alpha }\right)\ge 0. \end{gathered}$$ (31)

The invariance properties discussed in [43] lead to all quantities in (31) being invariant under a change in frame.

The force balance equations (12) and (15), mass balance (17), along with first and second laws of thermodynamics (25) and (31) describe balance laws for a constituent α in a mixture of N constituents. The requirements that these balance laws must be consistent with those for the mixture as a whole imposes constraints depicted in (21). This system is closed by adding suitable constitutive equations and describing the physical and biological processes that might take place in the mixture.

2.6. Coleman-Noll Procedure

The balance laws for mass and momentum as well as the first and second laws of thermodynamics are presumed to hold for all bodies. It is necessary to prescribe constitutive equations for a particular material, and the processes that bodies comprised of the given material may undergo. Within rational continuum mechanics, the Coleman-Noll procedure [34] is established to derive requirements for constitutive equations. According to Ziegler [172], continuum mechanics allows one to establish constitutive relations, deduced from free energy and dissipation functions characterizing reversible and irreversible processes, respectively. This leads to the decomposition of the thermodynamic conjugate forces into energetic and dissipative counterparts. The energetic forces are entirely determined by the specific free energy while the dissipative forces are determined from the dissipative function [170, 171]. Guided by the inequality in (31), it is assumed that the Cauchy stress tensor for each species admits the decomposition into energetic and dissipative components,

$${\mathbf{T}}_{\alpha }={\mathbf{T}}_{\alpha }^{en}+{\mathbf{T}}_{\alpha }^{dis},$$ (32)

while other thermodynamical conjugate forces are identified as completely energetic or dissipative in nature. This choice is made based upon our current knowledge about the physical and biological events that contribute to the tumor growth process. In general, other conjugate forces can be decomposed as in (32) where additional phenomena are identified that contribute to energy storage and dissipation⁶.

To derive the relation between thermodynamic forces. The Helmholtz free energy, Ψ, and dissipative potentials, $\mathcal{D}$, we initially consider a general form of free energy considering the contribution of μ and ∇μ, and assuming a system far from equilibrium (μ is not given).⁷,

$$\begin{gathered} \Psi =\Psi ({\mathbf{F}}_1,\cdots ,{\mathbf{F}}_N,{\rho }_1,\cdots ,{\rho }_N,{\varphi }_1,\cdots ,{\varphi }_N, \\ \nabla {\varphi }_1,\cdots ,\nabla {\varphi }_N,{\mu }_1,\cdots ,{\mu }_N,\nabla {\mu }_1,\cdots ,\nabla {\mu }_N). \end{gathered}$$ (33)

The time derivation of Ψ (using the chain rule) results in,

$$\begin{gathered} \frac{d\Psi }{dt}=\sum _{\alpha }(\frac{\partial \Psi }{\partial ({\mathbf{C}}_{\alpha },{\mathbf{F}}_{\alpha })}:{\mathbf{D}}_{\alpha }+\frac{\partial \Psi }{\partial {\rho }_{\alpha }}\frac{d^{\alpha }{\rho }_{\alpha }}{dt}+\frac{\partial \Psi }{\partial {\varphi }_{\alpha }}\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}+\frac{\partial \Psi }{\partial (\nabla {\varphi }_{\alpha })}\frac{d^{\alpha }(\nabla {\varphi }_{\alpha })}{dt}\phantom{)} \\ +\phantom{(}\frac{\partial \Psi }{\partial {\mu }_{\alpha }}\frac{d^{\alpha }{\mu }_{\alpha }}{dt}+\frac{\partial \Psi }{\partial (\nabla {\mu }_{\alpha })}\frac{d^{\alpha }(\nabla {\mu }_{\alpha })}{dt}), \end{gathered}$$ (34)

Where

$$\frac{\partial \Psi }{\partial ({\mathbf{C}}_{\alpha },{\mathbf{F}}_{\alpha })}:{\mathbf{D}}_{\alpha }=\{\begin{array}{cc}2{\mathbf{F}}_{\alpha }^T\frac{\partial \Psi }{\partial {\mathbf{C}}_{\alpha }}{\mathbf{F}}_{\alpha }:{\mathbf{D}}_{\alpha },\hfill & 1<\alpha \le M,\hfill \\ \hfill & \hfill \\ \frac{\partial \Psi }{\partial {\mathbf{F}}_{\alpha }}{\mathbf{F}}_{\alpha }^T:{\mathbf{D}}_{\alpha },\hfill & M<\alpha \le N.\hfill \end{array}\phantom{\}}$$ (35)

Making use of the gradient of material time derivatives,

$$\nabla \left(\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}\right)=\frac{d^{\alpha }}{dt}(\nabla {\varphi }_{\alpha })+\nabla \cdot {\mathbf{v}}_{\alpha }\cdot \nabla {\varphi }_{\alpha },$$

along with substituting (34) into the free energy imbalance (31) and grouping terms together, we find the following inequality

$$\begin{gathered} \sum _{\alpha }\{\left({\mathbf{T}}_{\alpha }^{en}-\frac{\partial \Psi }{\partial ({\mathbf{C}}_{\alpha },{\mathbf{F}}_{\alpha })}+{\xi }_{\alpha }\otimes \nabla {\varphi }_{\alpha }\right):{\mathbf{D}}_{\alpha }+\left(-{\pi }_{\alpha }+{\rho }_{\alpha }{\mu }_{\alpha }-\frac{\partial \Psi }{\partial {\varphi }_{\alpha }}\right)\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}\phantom{\}} \\ +\left({\xi }_{\alpha }-\frac{\partial \Psi }{\partial (\nabla {\varphi }_{\alpha })}\right)\frac{d^{\alpha }(\nabla {\varphi }_{\alpha })}{dt}-\frac{\partial \Psi }{\partial {\mu }_{\alpha }}\frac{\partial {\mu }_{\alpha }}{dt}-\frac{\partial \Psi }{\partial (\nabla {\mu }_{\alpha })}\frac{d^{\alpha }(\nabla {\mu }_{\alpha })}{dt}+{\mu }_{\alpha }{\rho }_{\alpha }\frac{\partial \Psi }{\partial {\rho }_{\alpha }}\frac{d^{\alpha }{\rho }_{\alpha }}{dt} \\ +\phantom{\{}{\mathbf{T}}_{\alpha }^{dis}:{\mathbf{D}}_{\alpha }-\nabla {\mu }_{\alpha }\cdot {\mathbf{J}}_{\alpha }\}\ge 0. \end{gathered}$$ (36)

The classical Coleman-Noll argument asserts that, in order that the inequality (36) hold, the coefficient of quantities such as D_α, d^αϕ_α/dt, etc. must vanish as these terms can assume arbitrary large negative values. Thus, the fact that the time derivatives of the variables are arbitrary, results in the following choices being sufficient to ensure the free energy inequality,

$${\xi }_{\alpha }=\frac{\partial \Psi }{\partial (\nabla {\varphi }_{\alpha })},$$ (37)

$${\mathbf{T}}_{\alpha }^{en}=\frac{\partial \Psi }{\partial ({\mathbf{C}}_{\alpha },{\mathbf{F}}_{\alpha })}-{\xi }_{\alpha }\otimes \nabla {\varphi }_{\alpha },$$ (38)

$${\pi }_{\alpha }={\rho }_{\alpha }{\mu }_{\alpha }-\frac{\partial \Psi }{\partial {\varphi }_{\alpha }}.$$ (39)

The above relations defines the energetic part of the thermodynamic forces. Using the microforce balance (15), one can derive a relation for the chemical potential such as

$${\rho }_{\alpha }{\mu }_{\alpha }=\frac{\partial \Psi }{\partial {\varphi }_{\alpha }}-\nabla \cdot {\xi }_{\alpha }-{\tau }_{\alpha }$$ (40)

which can be simplified further by replacing ξ_α from (37).

By a similar Coleman-Noll argument we have,

$$\frac{\partial \Psi }{\partial {\rho }_{\alpha }}=0,\frac{\partial \Psi }{\partial {\mu }_{\alpha }}=0,\frac{\partial \Psi }{\partial (\nabla {\mu }_{\alpha })}=0,$$ (41)

suggesting that the thermodynamic process is admissible if and only if the Helmholtz free energy density is independent of ρ_α, μ_α and ∇μ_α. Thus, the free energy takes a simpler form⁸,

$$\Psi =\Psi ({\mathbf{F}}_1,\cdots ,{\mathbf{F}}_N,{\varphi }_1,\cdots ,{\varphi }_N,\nabla {\varphi }_1,\cdots ,\nabla {\varphi }_N).$$ (42)

Not all power expended on a spatial region can be transformed into changes in the free energy, and part of the power goes into dissipation. Thus, the remaining terms in the inequality (36), after considering (37)-(39), are the rate of dissipation potential,

$$\mathcal{D}=\sum _{\alpha }\left\{{\mathbf{T}}_{\alpha }^{dis}:{\mathbf{D}}_{\alpha }-\nabla {\mu }_{\alpha }\cdot {\mathbf{J}}_{\alpha }\right\}\ge 0.$$

The definition of the dissipative thermodynamic forces can then be obtained from the complementary part of dissipation potential as,

$${\mathbf{T}}_{\alpha }^{dis}=\frac{\partial \mathcal{D}}{\partial {\mathbf{D}}_{\alpha }},$$ (43)

$${\mathbf{J}}_{\alpha }=\frac{\partial \mathcal{D}}{\partial \nabla {\mu }_{\alpha }},$$ (44)

Where

$$\mathcal{D}=\mathcal{D}({\mathbf{D}}_1,\cdots ,{\mathbf{D}}_N,{\varphi }_1,\cdots ,{\varphi }_N,\nabla {\varphi }_1,\cdots ,\nabla {\varphi }_N,\nabla {\mu }_1,\cdots ,\nabla {\mu }_N).$$ (45)

2.7. Constitutive Relations for the Admissible Potentials

The continuum theory presented here attempts to provide a general framework for addressing many of the complex biological phenomena that take place in cancer. This consists of multiple interactions among various constituents. In this regard, it is considered that the N-species mixture consists of M solid constituents undergoing both hyper-elastic deformation and biological growth and N − M viscous compressible fluid constituents. The constitutive relations are defined by proposing two primary potentials, Helmholtz free energy, and the rate of dissipation.

2.7.1. Helmholtz Free Energy

We postulate the following general definition of the free energy of the mixture,

$$\Psi ={\Psi }^{\text{els}}+{\Psi }^{\text{chm}}+{\Psi }^{\text{int}}+{\Psi }^{\text{taxis}},$$ (46)

where Ψ^els denotes elastic energy for solid species and Ψ^chm and Ψ^int represents (bio-)chemical energy and interface counterparts, respectively, normally employed in phase-field models. The free energy functional also includes the energy due to taxis-inducing chemical and molecular species, Ψ^taxis; see, e.g., [1, 35, 96].

Hereafter, we assume the fluid constituents of the mixture are compressible, thus

$$\frac{\partial {\Psi }^{\text{els}}}{\partial {\mathbf{F}}_{\alpha }}{\mathbf{F}}_{\alpha }^T=-p_{\alpha }\mathbf{I},M<\alpha \le N,$$

where p_α is the classical equilibrium pressure,

$$-p_{\alpha }={\widehat{\rho }}_{\alpha }^2\frac{\partial {\psi }_{\alpha }}{\partial {\widehat{\rho }}_{\alpha }},M<\alpha \le N,$$ (47)

where ${\widehat{\rho }}_t$ is the mass density of constituent (4), and the thermodynamic pressure is represented as the derivative of free energy per unit mass for each fluid constituent. Moreover, the solid species are considered to be isotropic hyperelastic. In a hyperelastic body, the Piola-Kirchhoff stress is the derivative of a scalar function W called strain energy density. Therefore, the second Piola-Kirchhoff stress is given by,

$${\mathbf{S}}_{\alpha }=\text{det}{\mathbf{F}}_{\alpha }{\mathbf{F}}_{\alpha }^{-1}{\mathbf{T}}_{\alpha }{\mathbf{F}}_{\alpha }^{-T}=\frac{\partial W_{\alpha }}{\partial {\mathbf{C}}_{\alpha }},1<\alpha \le M,$$ (48)

where ${\mathbf{C}}_{\alpha }={\mathbf{F}}_{\alpha }^T{\mathbf{F}}_{\alpha }$ is the right Cauchy-Green deformation tensor and W_α = W_α(C_α, ϕ_α) represents the strain energy function for the α-th solid constituent⁹. The strain energy density and elastic free energy are related through the mass density of a constituent in the reference configuration, $W_{\alpha }={\rho }_{\alpha }^0{\varphi }_{\alpha }^0{\psi }_{\alpha }^{\text{els}}$.

An important class of diffuse-interface or phase-field models of Cahn-Hilliard type are characterized by a Helmholtz free energy that consists of a double-well potential function for Ψ^chm = Ψ^chm (ϕ₁, ⋯ , ϕ_N) called a “coarse-grain” free energy, and an interfacial energy of the form,

$${\Psi }^{\text{int}}={\Psi }^{\text{int}}(\nabla {\varphi }_1,\cdots ,\nabla {\varphi }_N)=\sum _{\alpha }\frac{{ϵ}_{\alpha }}{2}\mid \nabla {\varphi }_{\alpha }{\mid }^2,$$ (49)

where ϵ_α (sometime referred to as the Landau-Ginzburg constants) characterizes the interface thickness. The interfacial energy (49) models longer-range interactions among the components by representing the effects of large gradients in concentrations that occur at interface regions between different constituents.

Following [35, 164], the effect of energy due to taxis-inducing chemical and molecular species is included in the free energy by,

$${\Psi }^{\text{taxis}}=({\varphi }_1,\cdots ,{\varphi }_N)=\sum _{\alpha }{\varphi }_{\alpha }\sum _{\beta =1}^L{\eta }_{\alpha \beta }{c}_{\beta },$$ (50)

where c_β, 1 ≤ β ≤ L, are the concentrations of chemical factors that may induce taxis (e.g., various sources of nutrient) and η_αβ is the taxis coefficient. In particular, (50) accounts for the reaction between concentrations of various vital nutrients in the mixture (such as oxygen or glucose) and the constituent α. This relation enables describing complex invasive behavior of a tumor observed in in vivo. Here, taxis refers to directional migration toward particular chemical or molecular species (i.e., chemotaxis) gradients or toward adhesion site gradients (i.e., haptotaxis). In a chemotaxis scenario, cells migrate in the direction of increased nutrient concentration [71]. The movement of the nutrient towards the tumor can be seen as active transport of the nutrient [54]. Garcke et al [54] studied the effects of chemotaxis and active transport on the tumor growth. Through numerical experiments, they verified the jump on the nutrient concentration at the tumor interface due to active transport. In vascular models of tumor growth (e.g., [9, 96]), the chemotactic term accounts for the endothelial cells moving up the concentration gradient of vascular endothelial growth factor (VEGF). VEGF is a pro-angiogenic factor released by tumor cells in an effort to recruit new vasculature to support further tumor growth [128].

2.7.2. Rate of Dissipation Potential

As discussed in section 2.6, energetic-dissipative decomposition of the thermodynamic conjugate forces results in the development of an energy dissipation rate. Here the dissipation energy potential can be considered as the summation of dissipations due to viscosity ${\mathcal{D}}^{\text{vis}}$ and diffusion ${\mathcal{D}}^{\text{diff}}$,

$$\mathcal{D}={\mathcal{D}}^{\text{vis}}+{\mathcal{D}}^{\text{diff}}\ge 0.$$

For hyperelastic solid constituents,

$${\mathcal{D}}^{\text{vis}}({\mathbf{D}}_1,\cdots ,{\mathbf{D}}_M,{\varphi }_1,\cdots ,{\varphi }_M)=0,$$

where D_α is defined in (9) and we assume the internal viscosity of fluid species can be described by a dissipation potential as a general isotropic, second-order tensor function of deformation rate,

$${\mathcal{D}}^{\text{vis}}({\mathbf{D}}_{M+1},\cdots ,{\mathbf{D}}_N,{\varphi }_{M+1},\cdots ,{\varphi }_N)=\sum _{\alpha }\frac{1}{2}{A}_{\alpha }\mid {\mathbf{D}}_{\alpha }{\mid }^2,M<\alpha \le N,$$ (51)

where A_α(ϕ_α) is the shear viscosity of fluid species. The above relation results in a dissipative counterpart of the Cauchy stress,

$${\mathbf{T}}_{\alpha }^{dis}=A_{\alpha }{\mathbf{D}}_{\alpha },M<\alpha \le N.$$ (52)

Cahn-Hilliard type equations are considered in this formulation for characterizing the energy dissipation due to diffusion,

$${\mathcal{D}}^{\text{diff}}({\mathbf{D}}_1,\cdots ,{\mathbf{D}}_N,{\varphi }_1,\cdots ,{\varphi }_N,{\mu }_1,\cdots ,{\mu }_N)=\sum _{\alpha }\nabla {\mu }_{\alpha }\cdot {\mathbf{M}}_{\alpha }\cdot \nabla {\mu }_{\alpha }$$ (53)

where μ_α is the chemical potential and M_α = M_α(C_α, ϕ_α) is the positive semi-definite mobility tensor. Using the frame-indifference principle discussed in [43], it can be shown that M_α is symmetric and invariant under a change in frame.

2.7.3. Energetic and Dissipative Forces

From the functional forms of Ψ and $\mathcal{D}$, one can derive relations for the thermodynamic forces. From (37), the energetic micro-stress ξ_α has the form

$${\xi }_{\alpha }={ϵ}_{\alpha }\nabla {\varphi }_{\alpha }.$$ (54)

Using (38) and (43), the Cauchy stress for solid and fluid constituents can be derived as

$${\mathbf{T}}_{\alpha }={\mathbf{T}}_{\alpha }^{en}+{\mathbf{T}}_{\alpha }^{dis}=\{\begin{array}{cc}\frac{2}{\text{det}{\mathbf{F}}_{\alpha }}{\mathbf{F}}_{\alpha }{\mathbf{S}}_{\alpha }{\mathbf{F}}_{\alpha }^T-{ϵ}_{\alpha }\nabla {\varphi }_{\alpha }\otimes \nabla {\varphi }_{\alpha }\hfill & ,1<\alpha \le M\hfill \\ \hfill & \hfill \\ p_{\alpha }\mathbf{I}+A_{\alpha }{\mathbf{D}}_{\alpha }-{ϵ}_{\alpha }\nabla {\varphi }_{\alpha }\otimes \nabla {\varphi }_{\alpha }\hfill & ,M<\alpha \le N\hfill \end{array}\phantom{\}}$$ (55)

The ξ_α enters in species microforce balance (recall (14) and (15)) as a flux and divergence term. This suggests that ξ_α is an stress-type quantity and associated with the interaction forces at the interface of the constituents. From (54), one can argue that the microstress ξ_α accounts for cell adhesion due to volume fraction changes at the interface of each constituent. In contrary to (for example) the chemotaxis phenomenon which can be addressed with a local model, cell adhesion is intrinsically a non-local process [141]. The nonlocality arises because the cellular adhesion forms a biological interaction between cells and their surroundings such that cells contribute adhesion molecules at its position as well as its neighboring region [27]. Following a phase-field approach and acknowledging the existence of microscopic force balances, results in automatic incorporation of cell adhesion in the current model, a phenomenon that is challenging to address using local continuum models [15, 141]. The term ϵ_α is the interaction parameter and represents the thickness of the interface (i.e., how sharp is the interface between the phases). In biological processes involved in tumor growth, this term is directly related to the cell-cell adhesion [36, 104]. Sharp interfaces (i.e., ϵ_α close to zero with α indicating tumor constituent) can model cells with high adhesion such as epithelial tumors [156] and increasing the value of interface thickness enables mimicking the behavior of cells with low adhesion and higher motility as glioblastoma and stromal cells [84, 104, 133]. This relation suggests that stronger cell-cell adhesion results in sharper interfaces and more compact morphology. The first term in the Cauchy stress of solid constituents in (55) reflects the hyperelastic deformation with growth. However, the microforce balance of (15) results in another term in the Cauchy stress; i.e., ϵ_α∇ϕ_α ⊗ ∇ϕ_α. In biological processes, this term mimics surface tension-like cell-adhesion forces in the Cauchy stress and exists in the absence of elastic deformation (see [43] for the evolution of this counterpart of the Cauchy stress).

Another dissipative thermodynamic force is the mass flux that can be derived from (44) and (53) as,

$${\mathbf{J}}_{\alpha }=-{\mathbf{M}}_{\alpha }\cdot \nabla {\mu }_{\alpha }.$$ (56)

Assuming (56) holds, the equation describing the evolution of species content (recall (17)) becomes,

$$\frac{\partial {\rho }_{\alpha }{\varphi }_{\alpha }}{\partial t}+\nabla \cdot ({\rho }_{\alpha }{\varphi }_{\alpha }{\mathbf{v}}_{\alpha })=S_{\alpha }-\nabla \cdot ({\mathbf{M}}_{\alpha }\cdot \nabla {\mu }_{\alpha }).$$ (57)

Making use of (39), the chemical potential can be derived as,

$${\rho }_{\alpha }{\mu }_{\alpha }=\frac{\partial {\Psi }^{\text{els}}}{\partial {\varphi }_{\alpha }}+\frac{\partial {\Psi }^{\text{chm}}}{\partial {\varphi }_{\alpha }}+\sum _{\beta =1}^L{\eta }_{\alpha \beta }{c}_{\beta }-{ϵ}_{\alpha }\Delta {\varphi }_{\alpha }-{\tau }_{\alpha },$$ (58)

where Δ denotes the spatial Laplacian operator (i.e., Δ = ∇ · ∇). Relation (58) indicates the dependency of μ_α on volume fractions¹⁰.

Equation (57) represents a system of N fourth-order, parabolic partial differential equations of the Cahn-Hilliard type. These equations along with the macro-force balance (12), together with the appropriate boundary and initial conditions, characterize a general coupled phase-field and elastic deformation, continuum mixture model of a complex media consisting of multiple solid and fluid species. The constituents can be compressible, the fluid species are Newtonian, the solid constituents are isotropic hyperelastic, and the effects of diffusion of chemical or biological constituents due to chemo- or bio-taxis as well as surface effects due to gradients in concentrations are included.

To apply such general models in a meaningful manner to simulate tumor growth, several specific details are needed. These include specific forms of the constitutive equations for each constituent along with the inclusion of growth effects due to mass exchange and deformation. These are discussed in detail in the next section.

3. A Four-Constituent Phase-Field Model of Tumor Growth

In this section, the general multi-species theory described in section 2 is adapted to simulate the significant features of the growth of tumors in a microenvironment. We derive a coupled formulation for diffusion and large elastic deformation of avascular tumor based on a hybrid 10-constituent phase-field model proposed by Lima et al. [94, 96]. The tumor volume fraction ϕ_T accounts for proliferative, hypoxic, and necrotic cells and ϕ_σ indicates the nutrient volume fraction so-called nutrient-rich extracellular water according to [35]. In particular, we consider a mixture consists of four constituents by considering two complementary species, ϕ_C, and ϕ_σ0. ϕ_C represents the normal (healthy) cells, and it is complimentary to tumor volume fraction ϕ_T, while ϕ_σ0 is the complimentary constituent to the nutrient volume fraction, hereon called nutrient-poor extracellular water. Then the saturation condition of the mixture ϕ_T + ϕ_C + ϕ_σ + ϕ_σ0, is enforced by rescaling the volume fractions. The solid, s = ϕ_T + ϕ_C, and fluid, w = ϕ_σ + ϕ_σ0 are assumed to vary from 0 to 1 depending on a constant C by defining s = C and w = 1 − C. This rescaling normalizes the values of ϕ_T and ϕ_σ to take on values between 0 and 1 and the volume fraction of the healthy computed as ϕ_C = 1 − ϕ_T.

The tumor cells (proliferative, hypoxic, and necrotic) have similar adhesive properties and they prefer to adhere to one another [35, 97], causing a segregation from healthy cells. This behavior of separation among phases, typical of binary Cahn-Hilliard systems, is modeled by a double-well potential and a capillary interfacial energy. The presence of a nutrient-rich volume fraction in the mixture contributes to an increase of the system energy through a quadratic term and interacts chemotactically with tumor cells, yielding a directional movement towards the nutrient supply [96, 164]. These assumptions yield the following chemical and interface components of the Helmholtz free energy of the system:

$${\Psi }^{\text{chm}}({\varphi }_T,{\varphi }_{\sigma })=\kappa {\varphi }_T^2(1-{\varphi }_T{)}^2+\frac{1}{2{\delta }_{\sigma }}{\varphi }_{\sigma }^2,$$ (59)

$${\Psi }^{\text{int}}(\nabla {\varphi }_T,\nabla {\varphi }_{\sigma })=\frac{{ϵ}_T^2}{2}\mid \nabla {\varphi }_T{\mid }^2,$$ (60)

where the coefficient κ > 0 in the quadratic double-well function is an energy scale giving rise to a well-delineated phase separation of the tumor and the host tissues. In (59), δ_σ is a coefficient that controls the increase of energy due to nutrient volume fraction. The interfacial surface energy due to spatial gradient of the tumor volume fraction is defined through an interaction length parameter ϵ_T. In particular, ϵ_T controls the interface among tumor cells and other constituents. The effect of energy due to taxis-inducing chemical and molecular species is addressed through,

$${\Psi }^{\text{taxis}}({\varphi }_T,{\varphi }_{\sigma })=-{\chi }_0{\varphi }_T{\varphi }_{\sigma },$$ (61)

where χ₀ > 0 is a constant governing the relative strength of the interaction between tumor cells and nutrient.

We take into account a Cahn-Hilliard type energy dissipation due to diffusion, such as

$${\mathcal{D}}^{\text{diff}}=\nabla {\mu }_T\cdot {\mathbf{M}}_T\cdot \nabla {\mu }_T+\nabla {\mu }_{\sigma }\cdot {\mathbf{M}}_{\sigma }\cdot \nabla {\mu }_{\sigma }.$$ (62)

The coupling effect of deformation on the tumor mass transfer results in the dependency of tumor mobility and mass exchange to a measure of deformation. Modeling this dependency is discussed in the following section. Finally, the energy dissipation due to viscosity is considered to be,

$${\mathcal{D}}^{\text{vis}}=\frac{1}{2}{A}_{\sigma }\mid {\mathbf{D}}_{\sigma }{\mid }^2,$$ (63)

where A_σ is extracellular water viscosity coefficient [132].

3.1. Kinematics of Hyperelastic, Growing Solid Tumor

The mechanical stresses of a solid tumor have fundamental implications for both its growth [72] and response to treatment [160]. For example, it has been shown that compression of cancer cells reduces their proliferation rate, induces apoptosis, and enhances their invasive and metastatic potential. Thus, tumors that manifest higher stress levels may have lower growth rates and a higher tendency to metastasize [26, 30, 40, 78, 79, 85, 91, 157]. Moreover, the force applied by the surrounding tissue during the growth of a tumor can alter both tumor expansion and shape [72, 74, 159, 160, 162]. Here we consider two mechanisms participating in the mechanical behavior of a tumor: the externally applied stress due to mechanical interactions among the solid components of the growing tumor and the surrounding tissue, and the growth-induced stress due to proliferating cancer cells

We consider the kinematics of growth such that the total deformation gradient result from a geometrically necessary elastic deformation associated with mass growth, along with a deformation due to an externally applied stress. Consequently, the deformation gradient of the tumor, F_T, accepts the following decomposition (see, e.g., [57]),

$${\mathbf{F}}_T={\mathbf{F}}_T^S{\mathbf{F}}_T^G,$$ (64)

where ${\mathbf{F}}_T^G$ is the growth deformation gradient tensor, that acting alone leads to incompatible deformation [144] leading to residual stresses developments. ${\mathbf{F}}_T^S$ is the elastic component of the deformation gradient tensor that accounts for the elastic deformation required to ensure compatibility (resulting in the internal growth-induced stress) as well as the deformation due to external stress such as surrounding tissue confinements [57]. The multiplicative decomposition (64) is based on introducing an intermediate unstressed configuration by elastic distressing of the current configuration ${\mathcal{B}}_t$ to zero stress. Assuming the elasticity parameters are independent of tumor volume fraction, one can write

$$\frac{\partial {\Psi }^{\text{els}}}{\partial {\mathbf{F}}_T}=\frac{\partial {\Psi }^{\text{els}}}{\partial {\mathbf{F}}_T^S}:\frac{\partial {\mathbf{F}}_T^S}{\partial {\mathbf{F}}_T},$$ (65)

where

$$\frac{\partial {\mathbf{F}}_T^S}{\partial {\mathbf{F}}_T}=\frac{\partial {\mathbf{F}}_T({\mathbf{F}}^G{)}^{-1}}{\partial {\mathbf{F}}_T}=\mathbf{I}\otimes ({\mathbf{F}}^G{)}^{-1}.$$ (66)

We consider a compressible Neo-Hookean material for the tumor material¹¹ that is a commonly used constitutive model for the elastic response of soft tissue [53, 105, 157]. The strain energy function is,

$$W=\frac{G_T}{2}\left((J_T^S{)}^{-\frac{2}{3}}{I}_{C_1}^S-3\right)+\frac{K_T}{2}(J_T^S-1{)}^2,$$ (67)

where G_T and K_T are shear and bulk modulus, respectively, and $I_{C1}^S$ is the first invariant of the right Cauchy-Green deformation tensor defined as,

$$I_{C_1}^S=\text{tr}({\mathbf{C}}_T^S),$$ (68)

where ${\mathbf{C}}_T^S=({\mathbf{F}}_T^S{)}^T{\mathbf{F}}_T^S$. In (67), $J_T^S$ is a volume change measure,

$$J_T^S=\sqrt{\text{det}({\mathbf{C}}_T^S)}=\text{det}({\mathbf{F}}_T^S).$$ (69)

From (55) and the specific form of strain energy (67), a relation for the Cauchy stress is obtained as,

$${\mathbf{T}}_T=\left(\frac{G_T}{J_T^{S^{5∕3}}}\left({\mathbf{B}}_T^S-\frac{1}{3}tr({\mathbf{B}}_T^S)\mathbf{I}\right)+K_T(J_T^S-1)\mathbf{I}\right)({\mathbf{F}}_T^G{)}^{-T}-{ϵ}_T\nabla {\varphi }_T\otimes \nabla {\varphi }_T,$$ (70)

where ${\mathbf{B}}_T^S={\mathbf{F}}_T^S({\mathbf{F}}_T^S{)}^T$ is the left Cauchy-Green deformation tensor. The following relations can be also derived for the components of (70),

$$J_T^S=\frac{1}{\text{det}({\mathbf{F}}_T^G)}{J}_T,$$ (71)

$${\mathbf{B}}_T^S={\mathbf{B}}_T({\mathbf{F}}_T^G{)}^{-1}({\mathbf{F}}_T^G{)}^{-T},$$ (72)

$$\text{det}({\mathbf{B}}_T^S)=\text{det}({\mathbf{B}}_T)\cdot \text{det}\left(({\mathbf{F}}_T^G{)}^{-1}({\mathbf{F}}_T^G{)}^{-T}\right).$$ (73)

The remaining derivation related to Ψ^els is to evaluate the effect of deformation on the chemical potential (58). Taking into account that F^G can be a function of volume fraction, one can write,

$$\frac{\partial {\Psi }^{\text{els}}}{\partial \varphi }=\frac{\partial {\Psi }^{\text{els}}}{\partial {\mathbf{F}}_T}:\frac{\partial {\mathbf{F}}_T}{\partial {\mathbf{F}}_T^G}:\frac{\partial {\mathbf{F}}_T^G}{\partial \varphi }$$ (74)

where

$$\frac{\partial {\mathbf{F}}_T}{\partial {\mathbf{F}}_T^G}={\mathbf{F}}_T^S\otimes \mathbf{I}.$$ (75)

Skalak et al [142, 143] cast the kinematics of growth into the mathematical theory of finite strain continuum mechanics through the notion of “volumetric growth”. However, considering the kinematic effect of growth alone, where material is added to or lost from the body, might lead to incompatible adjacent neighborhoods of the body in Euclidean space and F^G cannot then be expressed as the gradient of a vector field¹². In (64) both F^G and F^S are incompatible, but their multiplicative decomposition is compatible by construction. This multiplicative framework has been widely employed to model certain features of biological growth (e.g., [5, 6, 60, 102, 150, 166]). Nevertheless, some investigators, (e.g., [18, 76]), argued against such a decomposition based on the mass gain or loss during growth. They pointed out that if the mapping between configurations is defined only by the deformation, in the case of biological growth, the notion of a fixed reference configuration vanishes. Such a fundamental deficiency is valid for the theories of growth that consider tissue as a single-constituent solid continuum. However, the growth models based on mixture theory, where different species can possess different natural configurations, removes the challenge encountered in identifying reference configurations for the growing tissue [4].

3.2. Constitutive Relations for Deformation Feedback on Diffusion

Prior to presenting an evolution relation for the growth tensor, we first postulate the way deformation is coupled to the diffusion equation. To account for the restriction of tumor expansion produced by the surrounding tissues, one might consider the dependency of diffusion on deformation [55]. Such hypothesis testing using in vivo data is shown to significantly improve the predictability of computational models [74, 97, 160, 161] in addressing the experimental observations. Most of the previous models considered the dependency of the mobility tensor (i.e., the diffusion coefficient in reaction-diffusion models) to a stress quantity. However, the principle of material frame-indifference [43] shows that the mass flux can be a function of the right Cauchy-Green deformation tensor or its invariants, volume fraction, and gradient of chemical potential, such as

$${\mathbf{J}}_T={\mathbf{J}}_T({\mathbf{C}}_T,{\varphi }_T,\nabla {\mu }_T).$$ (76)

Thus, from (56) along with considering the dependency of the tumor mobility tensor on the volume fraction [94, 96], we postulate the following form describing tumor mobility, M_T = M_TI¹³,

$$M_T={\lambda }_T^{\text{mob}}{\varphi }_T^2(1-{\varphi }_T{)}^2.$$ (77)

The double-well functional form of the dependency to the volume fraction in (77) assumes that the pure phases (i.e., just tumor (ϕ_T = 1) or healthy cells (ϕ_T = 0)) do not diffuse. This functional ensures the mobility is always positive and avoids possible inconsistency in the phase field model [41, 71]¹⁴. Moreover, the inhibitory effect of the surrounding tissue on tumor growth is mimicked by an exponential decay, such as

$${\lambda }_T^{\text{mob}}={\alpha }_T^{\text{mob}}\text{exp}(-{\gamma }_T^{\text{mob}}{J}_T),$$ (78)

where ${\alpha }_T^{\text{mob}}$ and ${\gamma }_T^{\text{mob}}$ are constants and $J_T=\sqrt{\text{det}({\mathbf{C}}_T)}$ is a measure of volume change.

We postulate that the following source terms govern the tumor mass exchange term

$$S_T={\lambda }_T^{\text{pa}}{\varphi }_T(1-{\varphi }_T){\varphi }_{\sigma }.$$ (79)

The relation for the tumor source term addresses the biophysical processes including (i) continuous growth of the proliferating tumor cells when consuming nutrient and (ii) the tumor volume fraction levels off when reaching the volume fraction of 1. The constant rate of the cellular mitosis minus apoptosis is indicated by ${\lambda }_T^{\text{pa}}$, characterizing the growth in the solid phase. We thus assume that growth evolution in the mass balance, as the process of mass addition and loss, is directly related to both the tumor and nutrient-rich extracellular water volume fractions. Moreover, a relation for ${\lambda }_T^{\text{pa}}$ is proposed to account for the mechanical effects of decreasing the rate of tumor cell proliferation with increasing the surrounding tissue stress, such as

$${\lambda }_T^{\text{pa}}={\alpha }_T^{\text{pa}}\text{exp}(-{\gamma }_T^{\text{pa}}{J}_T),$$ (80)

where ${\alpha }_T^{\text{pa}}$ and ${\gamma }_T^{\text{pa}}$ are constants controlling decay of the growth stretch with increasing tumor volume. The further dependency of ${\lambda }_T^{\text{pa}}$ addresses the increase in proliferation rate in the area with high tumor cell density. The relation between proliferation rate and cell density is shown in a recent investigation using in vitro measurements [95].

The mobility tensor for nutrient rich water is assumed uniform throughout the domain, given as

$${\mathbf{M}}_{\sigma }=M_{\sigma }\mathbf{I},$$ (81)

where M_σ is a constant describing the nutrient mobility. The nutrient concentration decreases, as it is consumed by the tumor cells, at a rate λ_σ. Here, we neglect the natural decay and healthy cell consumption of nutrient, as we consider that the healthy cells are in homeostasis. With these assumptions, the nutrient source term is given as

$$S_{\sigma }=-{\lambda }_{\sigma }{\varphi }_T{\varphi }_{\sigma },$$ (82)

where λ_σ is a constant.

In the current formulation, the feedback of deformation on the tumor mobility and source term is considered through a function of volume change. Even in the absence of other biological and chemical effects, there is no general agreement in the literature on whether growth processes relate best to stress or strain [4]. Here we argue that the stress is an unobservable quantity and does not directly appear in observational data to support or contradict any particular hypothesis with respect to an explicit form of the stress tensor. Thus, in the relations of tumor mobility (78), tumor mass exchange (80), and (consequently) the evolution equation of the growth stretch ratio (85), we consider a representative measure of the tumor deformation J_T, which correlates an increase or decrease in the tumor volume with the increase or decrease of the surrounding tissue induced stress to the solid tumor. While the mathematical arguments for the proposed mechanical feedback on the tumor mobility and source term are intuitive, more physics-based constitutive relation is needed based on the underlying mechanisms of such complex bio-physical phenomena from cellular and sub-cellular investigations.

3.3. Constitutive Relation for Growth Tensor

The continuum mechanics treatment of growth introduces ${\mathbf{F}}_T^G$ as a new unknown that is neither governed by a new balance law nor can be found based on thermodynamic arguments. Thus, a constitutive relation must be postulated for the evolution law of growth in relation to physical, biological, and chemical effects. Proposing an evolution relation for growth can follow two general approaches. Motivated from engineering materials modeling, micromechanically-based evolution equations might be considered for growing tissue. However, this approach encounters additional challenges in describing biological growth due to the requirement of in vivo characterization of living tissue and strong dependency of the growth law on the type of tissue under consideration. Additionally, micro-mechanical based models might lead to a large number of model parameters and challenges the predictive capability of the model due to the lack of experimental observations to calibrate and validate the model. Another approach consists of hypothesizing phenomenological laws based on experimental observations. Such models result in the development of theories that can be effectively informed by specific experiments from which model parameters can be evaluated¹⁵. Since a primary goal of the current formulation is to develop a tumor model that can ultimately be informed by experimental data of tumor evolution, we follow the latter approach.

Tumor growth is taken to be anisotropic and the growth component of the deformation gradient (growth tensor) is given by

$${\mathbf{F}}_T^G={\Lambda }_T^G\Omega ,$$ (83)

where ${\Lambda }_T^G$ is the growth stretch ratio (${\Lambda }_T^G$ > 1 indicates growth and ${\Lambda }_T^G$ < 1 represents resorption) and

$$\Omega =\left[\begin{array}{ccc}\hfill {\omega }_1\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill {\omega }_2\hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill {\omega }_3\hfill \end{array}\right],{\omega }_1^2+{\omega }_2^2+{\omega }_3^2=1$$ (84)

is the anisotropy tensor, with ω₁, ω₂, and ω₃ being anisotropic growth multipliers [10, 11, 13, 14] and isotropic growth (see, e.g., [147, 166]) corresponds to Ω = I. Such anisotropic growth allows preferential expansion of tumors in the direction of low stress and enables stress-relaxation even in the absence of viscose dissipation, a phenomenon that is observed experimentally (see, e.g., [72]).

If the mass balance equation is not included in the formulation, the evolution of the growth stretch ratio ¹⁶ can be related to the induced pressure expressed in terms of the trace of the second Piola-Kirchhoff stress [102, 150], von Mises stress [146, 147], or the Mandel stress [73]. However, a more realistic representation of the biophysical process of a growing tumor in a heterogeneous microenvironment must account for both diffusion and deformation. In a coupled diffusion and deformation setting, the growth stretch ratio ${\Lambda }_T^G$ and creation or degradation rate of the solid tumor constituent through mass transfer must be explicitly related to one another. We have derived a relation among the growth tensor evolution and the mass exchange terms in Appendix B. According to (108), and considering a domain $\Omega \in {\mathbb{R}}^d(d=1,2,3)$, an evolution equation for the growth stretch ratio can be written as,

$$\frac{1}{{\Lambda }_T^G}\frac{\partial {\Lambda }_T^G}{\partial t}=\frac{1}{d}(S_T-\nabla \cdot ({\mathbf{M}}_T\cdot \nabla {\mu }_T)).$$ (85)

As opposed to the phenomenological evolution equations of growth stretch (e.g., [125, 146, 147, 157]), the relation (85) is derived based on physically and mathematically consistent framework (inline with [7, 116]) without the requirement of introducing additional model parameters.

3.4. Summary of Governing Equations

Using the macro-force balance (12) and neglecting the body forces, the governing equation for deformation of tumor and nutrient rich water reduces to,

$$\frac{\partial {\rho }_T{\varphi }_T{\mathbf{v}}_T}{\partial t}+\nabla \cdot ({\rho }_T{\varphi }_T{\mathbf{v}}_T\otimes {\mathbf{v}}_T)=\nabla \cdot {\mathbf{T}}_T,$$ (86)

$$\frac{\partial {\rho }_{\sigma }{\varphi }_{\sigma }{\mathbf{v}}_{\sigma }}{\partial t}+\nabla \cdot ({\rho }_{\sigma }{\varphi }_{\sigma }{\mathbf{v}}_{\sigma }\otimes {\mathbf{v}}_{\sigma })=\nabla \cdot {\mathbf{T}}_{\sigma },$$ (87)

where

$$\begin{gathered} {\mathbf{T}}_T=\frac{1}{{\Lambda }_T^G}\left(\frac{G_T}{J_T^{S^{5∕3}}}\left({\mathbf{B}}_T^S-\frac{1}{3}tr({\mathbf{B}}_T^S)\mathbf{I}\right)+K_T(J_T^S-)\mathbf{I}\right){\Omega }^{-1} \\ -{ϵ}_T\nabla {\varphi }_T\otimes \nabla {\varphi }_T, \end{gathered}$$ (88)

$${\mathbf{T}}_{\sigma }=-p_{\sigma }{\varphi }_{\sigma }\mathbf{I}+\frac{1}{2}{A}_{\sigma }(\nabla {\mathbf{v}}_{\sigma }+\nabla {\mathbf{v}}_{\sigma }^T).$$ (89)

The species mass balance relations (17) for two constituents are,

$$\frac{\partial {\rho }_T{\varphi }_T}{\partial t}+\nabla \cdot ({\rho }_T{\varphi }_T{\mathbf{v}}_T)=S_T-\nabla \cdot ({\mathbf{M}}_T\cdot \nabla {\mu }_T),$$ (90)

$$\frac{\partial {\rho }_{\sigma }{\varphi }_{\sigma }}{\partial t}+\nabla \cdot ({\rho }_{\sigma }{\varphi }_{\sigma }{\mathbf{v}}_{\sigma })=S_{\sigma }-\nabla \cdot ({\mathbf{M}}_{\sigma }\cdot \nabla {\mu }_{\sigma }),$$ (91)

where S_T and S_σ are defined in (79) and (82), M_σ is defined in (81), the form of M_T is presented in (77). Neglecting the external microforce, the chemical potentials are defined as:

$$\begin{gathered} {\rho }_T{\mu }_T=2\kappa {\varphi }_T(2{\varphi }_T^2-3{\varphi }_T+1)-{\chi }_0{\varphi }_{\sigma }-{ϵ}_T^2\Delta {\varphi }_T \\ +\frac{J_T}{{\Lambda }_T^G}\frac{\partial {\Lambda }_T^G}{\partial {\varphi }_T}({\mathbf{T}}_T+{ϵ}_T\nabla {\varphi }_T\otimes \nabla {\varphi }_T):\mathbf{I}, \end{gathered}$$ (92)

$${\rho }_{\sigma }{\mu }_{\sigma }=2\frac{1}{{\delta }_{\sigma }}{\varphi }_{\sigma }-{\chi }_0{\varphi }_T.$$ (93)

Differential equations (86), (87), (90), and (91), characterize the coupled diffusion and hyperelastic deformation of tumor growth. Additionally, Ambrosi and Mollica [6] argue that in the case of biological tissues, the characteristic velocities are so small that the process can be conveniently modeled as quasi-static. Assuming the velocities of tumor and nutrient rich extra cellular water are negligible (v_T ≈ 0 and v_σ ≈ 0) and considering isotropic growth (${\mathbf{F}}_T^G={\Lambda }_T^G\mathbf{I}$), the following (simplified) system of partial differential equation for mass balance and deformation equations is obtained,

$$\phantom{\{}\begin{array}{c}\frac{\partial {\varphi }_T}{\partial t}=S_T-\nabla \cdot (M_T\nabla {\mu }_T),\hfill \\ {\mu }_T=2\kappa {\varphi }_T(2{\varphi }_T^2-3{\varphi }_T+1)-{\chi }_0{\varphi }_{\sigma }-{ϵ}_T^2\Delta {\varphi }_T\hfill \\ +\frac{J_T}{{\Lambda }_T^G}\frac{\partial {\Lambda }_T^G}{\partial {\varphi }_T}{\mathbf{T}}_T:\mathbf{I},\hfill \\ \frac{\partial {\varphi }_{\sigma }}{\partial t}=S_{\sigma }-\nabla \cdot (M_{\sigma }\nabla {\mu }_{\sigma }),\hfill \\ {\mu }_{\sigma }=2\frac{1}{{\delta }_{\sigma }}{\varphi }_{\sigma }-{\chi }_0{\varphi }_T,\hfill \\ \nabla \cdot {\mathbf{T}}_T=0.\hfill \end{array}\}$$ (94)

In the above relations, it is also assumed that the mass density of the tumor and nutrient are constant, thus ρ_T and ρ_σ do not appear in mass balances. For the numerical experiments, the governing equations of the four-species mixture models in (94) are numerically approximated using finite elements formulation by developing a new solution algorithm (see Appendix C).

4. Numerical Results

In this section, the results of numerical experiments are discussed to investigate the main features of the proposed model. The numerical analyses are conducted on a tumor growing on the domain Ω = [−1, 1]² with an ellipsoidal shaped initial tumor subdomain in the center of Ω,

$$\left\{(x,y):\frac{x^2}{0.8}+\frac{y^2}{1.1}\le {0.2}^2\right\}.$$ (95)

In all numerical experiments, a regular triangular mesh with 6400 elements and Δt = 0.05 selected to ensure spatial and temporal accuracy. The parameter values used in the numerical experiments are shown in Table 1. We present the simulation results of four different cases. In one set of numerical experiments, the initial nutrient volume fraction is taken to be uniform, while in the other set a nutrient gradient is initially prescribed. For each initial nutrient scenario, the effect of mechanical stress feedback on tumor growth is investigated by considering two cases: unconfined growth representing freely growing tumor without the effects of the surrounding tissue characterized by ${\gamma }_T^{pa}={\gamma }_T^m=0$, and confined growth indicating the inhibitory effect of the externally applied stress on the growing tumor by assigning ${\gamma }_T^{pa}={\gamma }_T^m=1$. The motivation for choosing these cases is in vitro data obtained from multicellular tumor spheroid experiments [3, 30, 72, 127, 163], in which the tumor cells are cultured in a matrix (polymeric gel). Such in vitro models mimic the confinement induced by the tumor environment (surrounding tissues) and enable systematic investigation of the externally applied stresses on tumor growth. These studies show that the mechanical properties of the surrounding matrix have a significant influence on the proliferation and migration of tumor cells [3, 30, 127, 163]. We aim to investigate the capability of the developed mixture model by simulating the underlying phenomena observed in these experiments through the mechanical stress feedback on the development of the tumor.

Table 1:

Set of parameters used in the numerical experiments.

Parameter	Value	Meaning
χ0	0.15	chemotactic parameter
ϵT	0.01	interfacial strength among tumor cells and other species
κ	0.025	energy scale of the chemical free energy of tumor cells
δσ	0.01	energy scale of the chemical free energy of nutrient
λσ	10	coefficient of nutrient consumption by tumor cells
KT	5.83	Bulk modulus of tumor
GT	1.25	Shear modulus of tumor
Mσ	1	nutrient mobility
Aσ	0	viscosity coefficient of nutrient
${\alpha }_T^{pa}$	1.0	constant rate of the tumor cell mitosis minus the apoptosis
${\alpha }_T^m$	2.5	tumor cell mobility
${\gamma }_T^{pa}$	0 or 1	coefficient that controls the stress feedback on tumor mass change
${\gamma }_T^m$	0 or 1	coefficient that controls the stress feedback on tumor mobility

4.1. Uniform Initial Nutrient Volume Fraction

The first set of the numerical experiments are conducted by assigning a spatially uniform nutrient distribution (ϕ_σ=0.5) as the initial condition and imposing no flux boundary conditions of Neumann type on ϕ_T, μ_T, and μ_σ and Dirichlet conditions on ϕ_σ and displacement u_T:

$$\phantom{\{}\begin{array}{c}\nabla {\varphi }_T\cdot \mathbf{n}=0,\nabla {\mu }_T\cdot \mathbf{n}=0\hfill \\ {\varphi }_{\sigma }=0.5,{\mathbf{u}}_T=0\hfill \end{array}\}\text{on}\Gamma$$

where Γ is the Lipschitz boundary of Ω and n is a unit exterior normal vector on Γ. The snapshots of the tumor and nutrient volume fractions for the confined (panels A-F) and unconfined (panels G-L) tumor growth are shown in Figure 1. In both cases, the tumor volume fraction uniformly increases over time while the nutrient is consumed in the center of the tumor. However, including the effect of mechanical feedback of the surrounding tissue on tumor development in the confined case, results in reducing the growth rate leading to 70.82% smaller tumor area¹⁷ at the final simulation time t=12.5. These results are in agreement with the in vitro models of tumor cells growth within a polymer gel, in which increasing the gel stiffness inhibits tumor growth by reducing tumor cell proliferation and inducing apoptosis [30, 72, 87].

Figure 1:

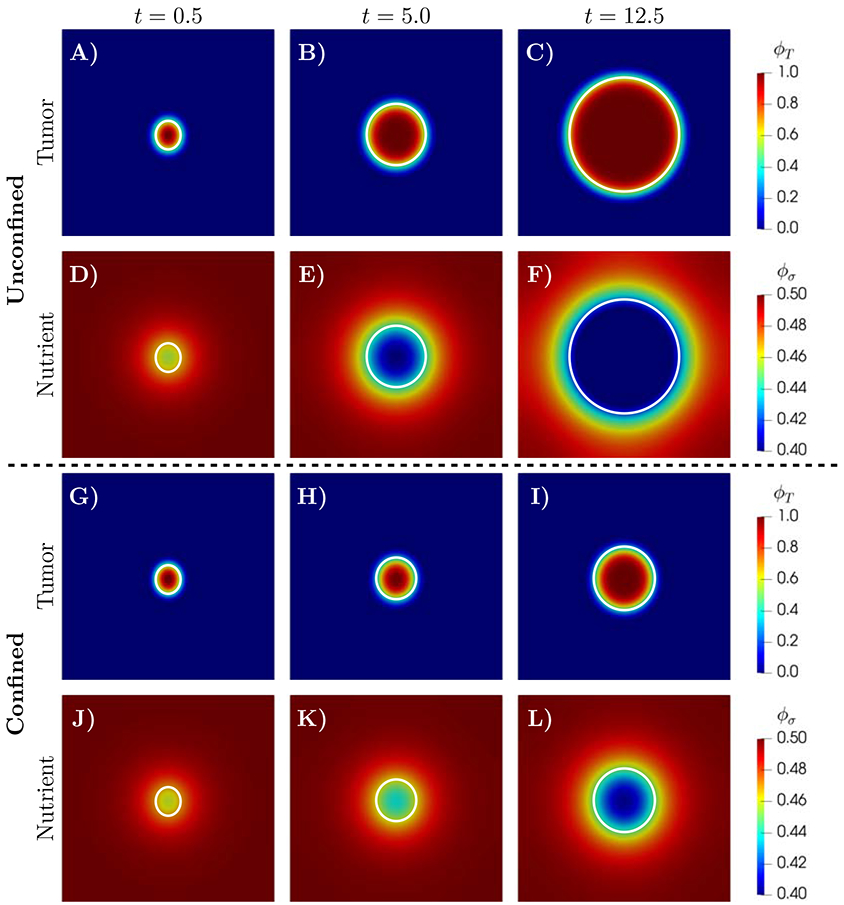
Simulation results for unconfined (A-F, ${\gamma }_T^{pa}={\gamma }_T^m=0.0$) and confined (G-L, ${\gamma }_T^{pa}={\gamma }_T^m=1.0$) tumor growth with a uniform nutrient initial condition. The time evolution of tumor volume fraction, ϕ_T, and nutrient volume fraction, ϕ_σ, are shown at t=0.5, 5.0 and 12.5. In both scenarios, as the tumor grows, the nutrient is consumed. However, the mechanical feedback in the confined scenario results in a 70.82% smaller tumor size at t=12.5. The white line marks the tumor boundary.

It is important to note that the proposed theory couples two mechanisms of tumor growth governed by the source term S_T in the diffusion equation of tumor (79), and the growth stretch ratio ${\Lambda }_T^G$ that evolves according to (85). In a finite element simulation, the former mechanism corresponds to occupying more elements with the tumor volume fractions, while the latter growth mechanism results in the tumor elements stretch. Both mechanisms affect the rate of increase in tumor area and are controlled by the term ${\lambda }_T^{pa}$ according to (80). Thus, the postulated exponential decay with the model parameters ${\gamma }_T^{pa}$ and ${\alpha }_T^{pa}$ represents the property of the tumors surrounding environment that regulates the externally applied stress. For instance, higher values of the model parameter ${\gamma }_T^{pa}$ lowers the rate of tumor area expansion with time by simulating stronger confinement induced by the surrounding tumor environment.

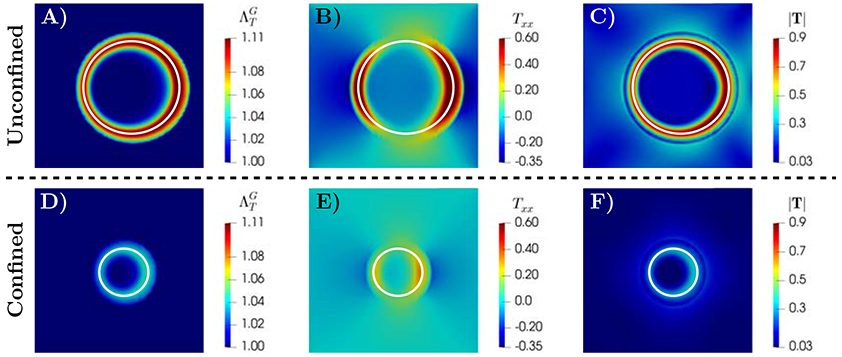
Figure 2 presents the spatial distributions of the growth stretch ratio ${\Lambda }_T^G$ (panels A and D), the normal component of the Cauchy stress along x-axis T_xx (panels B and E), and the magnitude of the Cauchy stress tensor ∣T∣ in the tumor and surrounding host tissue (panels C and F) for unconfined (top row) and confined scenarios (bottom row), respectively. The spatial profiles of the tumor growth stretch ratio¹⁸ in these figures show a higher growth rate in the periphery of the tumor (a ring close to the interface of tumor and surrounding tissues) with 10.97% higher ${\Lambda }_T^G$ in periphery compared to tumor interior at t=12.5. This response can be explained by the spatial distribution of nutrients and its evolution throughout tumor development. As observed in experiments [30, 147], during the avascular stage of tumor growth, the supply of nutrients from the environment is transported to the tumor interior via diffusion. This process leads to a gradient of nutrient concentration, and an associated gradient in growth rate, from the periphery to the interior of the tumor. The simulation results of nutrient volume fraction (Figure 1) and the growth stretch ratio (Figure 2) indicate that the proposed model is able to capture this physical process. Aligned with simulations from multiscale agent-based models [103, 121, 135], the formation of a ring in the ${\Lambda }_T^G$ profile that varies radially in space suggests that the periphery contains the proliferative tumor cells while the quiescent and necrotic cells are in the tumor interior, depending on the nutrient availability. Figure 3 shows the time evolution of tumor area normalized by the domain area. For these plot, a larger domain size Ω = [−2.5, 2.5]² is employed to allow larger tumor size. The results of unconfined growth indicate that after the initial period of monotonic growth the rate of increase in tumor area reduces with time. Such responses suggest that the avascular tumor may not always grow indefinitely even in the absence of external confinement [6, 7, 165, 166]. Such a decrease in the growth rate can occur when the rate of tumor growth overcomes the nutrient transport characterized by M_σ, known as diffusion-limitation in avascular tumor growth [109, 111, 117]. This phenomenon leads to an avascular tumor reaching a steady-state size, which corresponds to a balance between proliferation and apoptosis and agrees with both in vivo and in vitro experiments [3, 72, 88, 108, 110, 148]. In principle, the non-uniform distribution of nutrients leads to heterogeneous growth, and hence, the generation of residual stress retained inside the tumor that inhibits tumor cell proliferation [4, 17, 46, 147]. However, it is shown that the stress field generated in unconfined growth does not considerably impact the size of the tumor, compared to the surrounding tissue confinement [7, 78].

Figure 2:

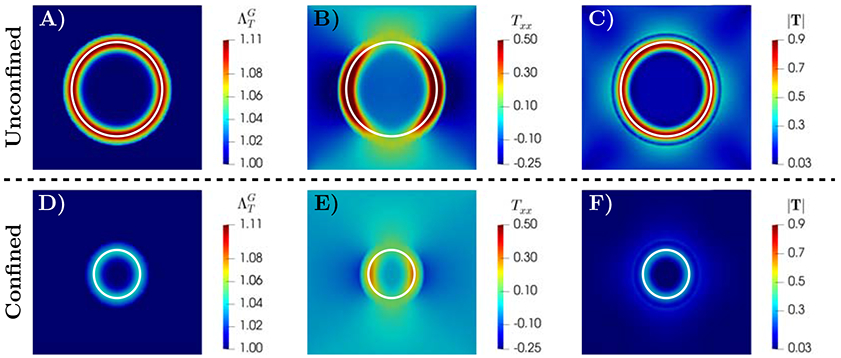
Simulation results for unconfined (A-C, ${\gamma }_T^{pa}={\gamma }_T^m=0.0$) and confined (D-F, ${\gamma }_T^{pa}={\gamma }_T^m=1.0$) tumor growth with a uniform nutrient initial condition. The spatial distributions at t=12.5 are shown for: A and D) growth stretch ratio ${\Lambda }_T^G$, B and E) a component of Cauchy stress T_xx, and C and F) magnitude of Cauchy stress ∣T∣. In both scenarios, the growth rate is higher at the periphery of the tumor compared to tumor interior (with the ratios of 1.12 for unconfined and 1.045 for the confined scenarios), indicating the presence of proliferative tumor cells. The white line marks the tumor boundary.

Figure 3:

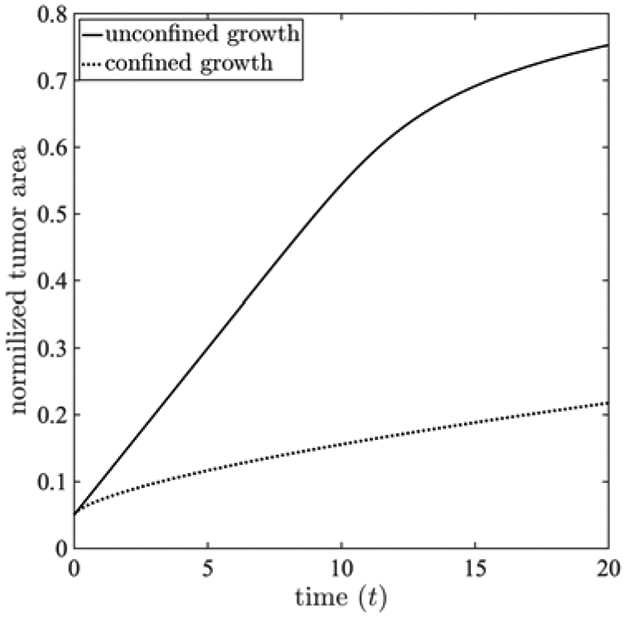
The time evolution of normalized tumor area by the domain area for unconfined (${\gamma }_T^{pa}={\gamma }_T^m=0.0$) and confined (${\gamma }_T^{pa}={\gamma }_T^m=1.0$) tumor growth with a uniform nutrient initial condition. The mechanical feedback on cell migrations and proliferation in the confined scenario results in a lower tumor growth rate. The unconfined scenario shows an eventual reduction in tumor growth rate due to diffusion-limited supply of nutrients. For these results, a larger simulation domain Ω = [−2.5, 2.5]² is used.

The Cauchy stress profiles in Figure 2 (panels C and F) indicate that, in both confined and unconfined scenarios, the stress magnitude is higher in the tumor periphery compared to the interior of the tumor. The ratios of the average ∣T∣ in the periphery to interior regions are approximately 9.1 for the unconfined and 15.5 for the confined cases at the final time t=12.5. The simulation results of T_xx show that in the radial direction (along y-axis) the stress within tumor interior area is compressive (negative sign) and they diminish radially in space at the interface of the tumor with the surrounding tissue. However, the stress in the circumferential direction (T_xx along the x-axis) is compressive and spatially uniform within the tumor interior, and it turns to tensile (positive sign) at the periphery. Such stress developments are also important in the vascular stage of tumor growth in which the compressive stress in the tumor interior can collapse blood vessels. Additionally, competition among compressive and tensile stresses at the interface of the tumor and normal tissue may result in deformation of peritumoral vessels [124, 147].

Comparing the growth stretch ratio and the Cauchy stress developments in confined and unconfined growth scenarios (Figure 2, panels A and D) shows the remarkable regulatory effect of the externally applied stress. Such stress induced by the surrounding tissue on tumor cell proliferation suppresses the growth rate and reduces the stress development in the solid tumor. The formation of a highly proliferative ring in the ${\Lambda }_T^G$ profile and the effect of surrounding tissue confining stress applied on tumor shown in Figure 2 are in agreement with experimental observations [3, 30, 113, 114] and analytical studies under fully symmetric spherical growth assumption [7, 46, 78, 138, 140, 165]. The physical phenomena captured by the proposed model, naturally arise from the phase development of the tumor and mathematical consistency among the growth tensor and mass exchange, without any ad hoc introduction of these processes. Additionally, the current phase-field mixture model accounts for the surface tension-like force (due to cell-cell adhesion) at the interface of the tumor and healthy constituents. Such microscopic force is controlled by the interface thickness parameter ϵ_T, and promotes the higher compressive stress in the tumor periphery (see [43] for numerical results of the evolution of adhesion force). In this regard, the proposed theory accounts for the nonlocal cell adhesion effect on the solid tumor stress and enables capturing the responses of high adhesion (e.g., epithelial tumors [156]) and low adhesion and higher motility cells (e.g., glioblastoma and stromal tumors [84, 104, 133]).

4.2. Spatially Varying Initial Nutrient Volume Fraction

In the second set of the numerical experiments, we investigate the role of the chemotactic term on the evolution of the tumor growth. In this case, we considered the following boundary condition at the top and bottom boundaries of the domain, Γ_tb,

$$\phantom{\{}\begin{array}{c}\nabla {\varphi }_T\cdot \mathbf{n}=0,\nabla {\mu }_T\cdot \mathbf{n}=0\hfill \\ \nabla {\varphi }_{\sigma }\cdot \mathbf{n}=0,{\mathbf{u}}_T=0\hfill \end{array}\}\text{on}{\Gamma }_{\text{tb}}.$$

However, on the left and right boundaries Γ_lr, Dirichlet boundary conditions are imposed on ϕ_σ to create a nutrient gradient along x direction,

$$\phantom{\{}\begin{array}{c}\nabla {\varphi }_T\cdot \mathbf{n}=0,\nabla {\mu }_T\cdot \mathbf{n}=0\hfill \\ {\varphi }_{\sigma }=0.1\text{and}0.9,{\mathbf{u}}_T=0\hfill \end{array}\}\text{on}{\Gamma }_{\text{lr}},$$

with nutrient volume fraction of ϕ_σ=0.1 at the left boundary, and ϕ_σ=0.9 at the right boundary. With these boundary conditions, the scenario mimics the effects of a nutrient source (for example a blood vessel) on the right side of the tumor.

Figure 4 shows snapshots of tumor and nutrient volume fractions, at t = 0.5, 5.0, 12.5. According to (61), the nutrient acts as a chemoattractant in the proposed model; that is, the diffusion of the tumor volume fraction is strengthened by nutrient gradients. As a result of this effect, in both the confined and unconfined cases, the tumor grows towards the direction of higher nutrient concertation (right boundary) [49, 54, 96]. Over time, the chemotactic effect results in a non-symmetric shape of the tumor in which the right interface between the tumor and healthy cells has approximately 60% higher thickness. Higher thickness of the tumor interface captures the increase of the tumor proliferation at the higher nutrient environment. These figures indicate that the proposed mixture theory can characterize the development of heterogeneous morphology and invasive patterns as observed in both in vivo and in vitro experiments [52, 129, 162, 168]. Similar to the uniform initial nutrient scenario, the inhibitory effect of the surrounding tissue stress on tumor development in the confined case (Figure 4, bottom two rows) reduces the growth rate leading to 71.04% reduction in tumor area at the final time t=12.5. Additional numerical experiments show that the intensity of tumor cells migration towards nutrient sources is proportional to the value of the chemotactic parameter χ₀.

Figure 4:

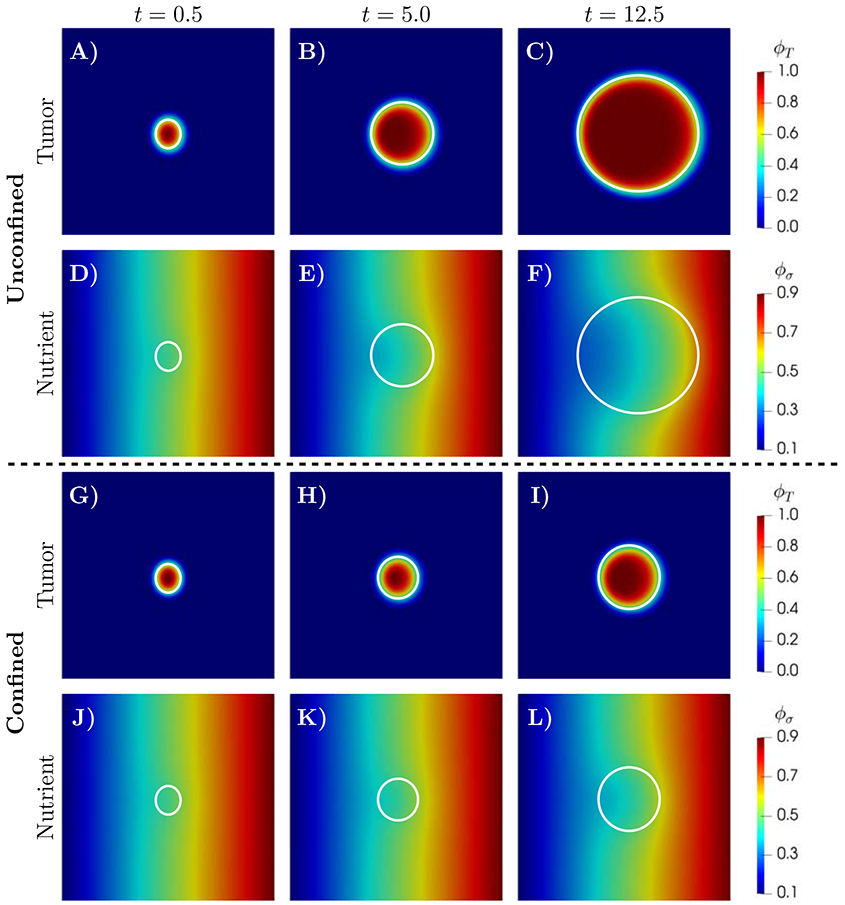
Simulation results for unconfined (A-F, ${\gamma }_T^{pa}={\gamma }_T^m=0.0$) and confined (G-I, ${\gamma }_T^{pa}={\gamma }_T^m=1.0$) tumor growth with a spatially varying nutrient initial condition. The time evolution of the tumor and nutrient volume fractions, ϕ_T and ϕ_σ, respectively, are show at t=0.5, 5.0 and 12.5. In both scenarios, the tumor grows toward the higher nutrient concentration. However, the mechanical feedback in the confined scenario, results in 71.04% smaller tumor size at t=12.5. The white line marks the tumor boundary.

The spatial distributions of the ${\Lambda }_T^G$, T_xx, and ∣T∣, for the spatially varying nutrient scenario, is shown in Figure 5. As expected, the proliferative tumor cells tend to concentrate on the higher nutrient area, leading to approximately 45% thicker proliferation ring with 2.75% higher value of growth stretch ratio on the right side compared to the left side of the simulated tumor periphery at t=12.5. In these figures, the compressive Cauchy stress in the tumor interior remains the same compared to the uniform nutrient scenario. However, 41.3% higher tensile circumferential stress in the tumor periphery region is observed in the right side of the tumor. Additionally, in the confined case (Figure 5, panels D, E, and F), the tumor cell proliferation is suppressed in the direction of higher mechanical stress, in agreement with experimental observations [30].

Figure 5:

Simulation results for unconfined (A-C, ${\gamma }_T^{pa}={\gamma }_T^m=0.0$) and confined (D-F, ${\gamma }_T^{pa}={\gamma }_T^m=1.0$) tumor growth with spatially varying nutrient initial condition. The spatial distributions at t = 12.5 are show for: A and D) growth stretch ratio ${\Lambda }_T^G$, B and E) a component of Cauchy stress T_xx, and C and F) magnitude of Cauchy stress ∣T∣. In both scenarios, the growth rate is higher (2.75% in unconfined and 1.05% in the confined cases) on the right side of the tumor, which is closer to the higher concentration of nutrients. The white line marks the tumor boundary.

5. Discussion

We have developed a general mixture theory for mass transfer of multiple constituents to address the key mechano-chemo-biological mechanisms involved in avascular tumor growth at the tissue scale, while accounting for certain phenomena at the cellular scale. The local species mass balance relations result in a system of fourth-order parabolic partial differential equations of the Cahn-Hilliard type to be solved together with the deformation differential equations incurred by the macro-force balances. These equations, along with appropriate boundary and initial conditions, characterize a general, coupled phase-field and hyper-elastic deformation, continuum mixture model of a complex media consisting of multiple solid and fluid species. The constituents can be compressible, the fluid species are Newtonian, the solid constituents are isotropic hyperelastic, and the effects of diffusion of chemical or biological constituents due to chemo- or bio-taxis, as well as surface effects due to cell adhesions, are considered. We then specialized the general framework to describe the response of a mixture consisting of four constituent volume fractions: tumor cells, nutrient-rich extracellular water, nutrient-poor extracellular water, and healthy cells. We were particularly interested in modeling biological and chemical factors, as well as the mechanical cues to tumor cells and their link with tissue level tumor progression. In addition to mass transfer, the growth effects and its interaction with the deformation are included in this model through the decomposition of the tumor deformation gradient into elastic and growth components. To fully characterize the biological growth in relation to mechanical, biological, and chemical effects, constitutive relations were postulated for the tumor growth while accounting for the deformation feedback on the mass transfer processes. In particular, we proposed phenomenological constitutive models accounting for the mechanical effect of decreasing the rate of tumor cell proliferation with increasing tumor volume. In this regard, the mobility tensor and mass exchange source term in the diffusion equations of the tumor species is considered as a decay function of the tumor of volume change indicating the increase/decrease of induced pressure from surrounding tissues. Both the diffusion source term and the growth deformation gradient tensors characterize the cancer cell proliferation and apoptosis. As a result of this physical feature, an evolution equation is derived for the growth part of the deformation gradient as a function of mass exchange terms. The differential equation relating the growth stretch ratio and the mass growth rate ensure the mathematical consistency of the tumor growth model.

Numerical experiments are conducted by means of the finite element solution of the model. The computational results on the spatio-temporal evolution of simulated tumors reveal a number of important capabilities of the proposed theory in capturing key features of avascular tumor growth. In particular, it is demonstrated that the directional movement of tumor cells towards the nutrient supply, due to the chemotactic effect, results in asymmetric morphology of the tumors from the initially symmetric shape. It is also shown that stress in the tumor interior is compressive while the stress is tensile at the interface of the tumor and surrounding tissue. Additionally, the evolution of the growth deformation gradient indicates a higher growth rate in the periphery region of the tumor compared to the tumor interior. The evolutions of the stress and growth stretch ratio denote the inhibitory effect of the externally applied stress induced by the surrounding tissue on tumor cell proliferation. Accordingly, the proposed model is capable of describing the critical mechano-chemo-biological features of avascular tumor growth in the various microenvironment of living tissue, in agreement with the experimental studies in the literature [3, 30, 72, 87, 88, 148].

The proposed theoretical framework of tumor growth is built on the previous diffusion-based models of tumor growth in the microenvironment, e.g., [6, 35, 57, 76, 102, 120, 160], as well as purely mechanical models simulating the effect of macroscopic mechanical stress on the tumor cell proliferation, e.g., [10, 46, 92, 125, 143, 147, 165, 166], in the literature. The current contribution advances the previous efforts by developing a fully coupled deformation and mass transfer model, based on phase-field mixture theory, to address the fundamental governing equations of biological growth. In this regard, the proposed model provides a unified mathematical framework for simulating major biophysical phenomena encountered in tumor progression, in a thermodynamically consistent fashion. Several important physical processes captured by the proposed model naturally arise from the mathematical derivations, without any ad hoc introduction of these processes. For example, following a phase-field approach and recognizing the existence of microscopic force balances in the current theory, results in the incorporation of the stress developments due to tumor cell adhesion at the interface of tumor and surrounding phases. Additionally, the formation of the proliferative ring in the periphery region of a tumor inherently arises from the consistency of the evolution equation of the growth deformation gradient with the nutrient driven biological growth characterized by the mass transfer.

Although the proposed model addresses critical mechanisms in tumor development including the coupling of stress and growth, future investigations are required to overcome the limitations of the constitutive models. While the mathematical arguments for the mechanical feedback on tumor development are intuitive, the proposed constitutive relation is a starting point for describing complex biological events involved in biological growth. Perhaps, identification of appropriate evolution equations for the growing mass is one of the most challenging problems in biomechanics and mechanobiology. The postulated constitutive relations for the inhibitory effect of mechanical stress on tumor cell proliferation, as a function of a deformation measure, needs to be examined and enhanced with clear biomechanical interpretations as underlying mechanisms of this phenomena that are merging from cellular and sub-cellular investigations. Furthermore, considering that the tumor growth is both organ and patient-specific, future insights from both theory and experiment are needed to validate and refine the constitutive models proposed in this contribution. Further areas to be explored are assessing the predictive capabilities of the proposed model concerning the in vivo measurements of cancer development as well as investigating the influence of organ confinement on tumor growth [101]. Additionally, extending the computational implementation to isolate mechanical interactions among cancer cells and the environment enables studying a range of phenomena observed in in vitro tumor spheroids under stress [72, 108, 110]. Important avascular tumor responses to be investigated using this model include the non-sphericity of tumor morphology growing in stiffer mechanical environment [109], as well as stress-driven cell migration, proliferation, and death [30, 46].

6. Conclusions

We have developed a general thermodynamically consistent theory, based on multispecies phase-field methods to address the multiphysics and multiscale mechanisms involved in tumor growth in a heterogeneous microenvironment. The proposed theory provides a unified mathematical framework for developing high-fidelity tumor growth models by considering, for example, the interactions among various tumor constituents, angiogenesis phenomena, and the effect of different therapeutic strategies.

Appendices

A. Deriving Force Balances From The Principles of Virtual Power

An alternative approach to determine the associated balance of macroscopic and microscopic forces is to use the principle of virtual power; see, e.g., [58, 63]. The main feature of this classical principle is a physical structure involving thermodynamic conjugate forces through the manner in which they expend power. This allows one to use the virtual-power principle to determine local and nonlocal force balances when the forms of the balances are not known a priori and provide a foundation to build more general theories; see, e.g., [44, 64, 65, 158].

The form of the power expenditure is determined by the terms contributing to the energy sources and postulated in the first and second laws of thermodynamics. In this regard, the internal virtual power is expressed in terms of the energy contribution in ${\mathcal{R}}_t$ such as

$${\mathcal{P}}_{\text{int}}=\sum _{\alpha }{\int }_{{\mathcal{R}}_t}\left({\mathbf{T}}_{\alpha }:{\mathbf{D}}_{\alpha }-{\pi }_{\alpha }\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}+{\xi }_{\alpha }\cdot \nabla \left(\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}\right)\right)dV.$$ (96)

The internal power is balanced by the power expended by traction t_α on the surface $\partial {\mathcal{R}}_t$ and body force b_α acting within the body to account for the inertia,

$${\mathcal{P}}_{\text{ext}}=\sum _{\alpha }\left\{{\int }_{\partial {\mathcal{R}}_t}{\mathbf{t}}_{\alpha }\cdot {\mathbf{v}}_{\alpha }dA+{\int }_{{\mathcal{R}}_t}({\rho }_{\alpha }{\varphi }_{\alpha }{\mathbf{b}}_{\alpha }\cdot {\mathbf{v}}_{\alpha }-{\tau }_{\alpha }\frac{d^{\alpha }{\varphi }_{\alpha }}{dt})dV+{\int }_{\partial {\mathcal{R}}_t}{m}_{\alpha }\frac{d^{\alpha }{\varphi }_{\alpha }}{dt}dA\right\}.$$ (97)

To account for the microscopic boundary conditions that arise from the volume fraction gradients, it is further assumed here that the external power is affected by the micro traction m_α that is a force conjugate to the time change of volume fractions on constituent interfaces [68, 120]. If we define virtual velocity to be (${\tilde{\mathbf{v}}}_{\alpha }$, $d^{\alpha }{\tilde{\varphi }}_{\alpha }∕dt$) and write (96) and (97) for the corresponding internal and external expenditures of virtual power, then the principle of virtual power is the requirement that the virtual power balance ${\mathcal{P}}_{\text{int}}={\mathcal{P}}_{\text{ext}}$ be satisfied for any subregion ${\mathcal{R}}_t$ of the deformed body and any virtual velocity $\mathcal{V}$. Using the divergence theorem,

$$\begin{gathered} {\int }_{{\mathcal{R}}_t}{\mathbf{T}}_{\alpha }:{\tilde{\mathbf{L}}}_{\alpha }dV={\int }_{\partial {\mathcal{R}}_t}({\mathbf{T}}_{\alpha }\mathbf{n}){\tilde{\mathbf{v}}}_{\alpha }dA-{\int }_{{\mathcal{R}}_t}(\nabla \cdot {\mathbf{T}}_{\alpha }){\tilde{\mathbf{v}}}_{\alpha }dV, \\ {\int }_{{\mathcal{R}}_t}{\xi }_{\alpha }\cdot \nabla \left(\frac{d^{\alpha }{\tilde{\varphi }}_{\alpha }}{dt}\right)dV={\int }_{\partial {\mathcal{R}}_t}({\xi }_{\alpha }\cdot \mathbf{n})\frac{d^{\alpha }{\tilde{\varphi }}_{\alpha }}{dt}dA-{\int }_{{\mathcal{R}}_t}(\nabla \cdot {\xi }_{\alpha })\frac{d^{\alpha }{\tilde{\varphi }}_{\alpha }}{dt}dV, \end{gathered}$$

and substituting into (96), along with equating the external power to the internal power (${\mathcal{P}}_{\text{int}}={\mathcal{P}}_{\text{ext}}$), results in,

$$\begin{gathered} \sum _{\alpha }\{{\int }_{\partial {\mathcal{R}}_t}({\mathbf{T}}_{\alpha }\mathbf{n}-{\mathbf{t}}_{\alpha }){\tilde{\mathbf{v}}}_{\alpha }dA+{\int }_{{\mathcal{R}}_t}(-\nabla \cdot {\mathbf{T}}_{\alpha }-{\rho }_{\alpha }{\varphi }_{\alpha }{\mathbf{b}}_{\alpha }){\tilde{\mathbf{v}}}_{\alpha }dV+\phantom{\}} \\ \phantom{\{}{\int }_{{\mathcal{R}}_t}(-{\pi }_{\alpha }-{\tau }_{\alpha }-\nabla \cdot {\xi }_{\alpha })\frac{d^{\alpha }{\tilde{\varphi }}_{\alpha }}{dt}dV+{\int }_{\partial {\mathcal{R}}_t}({\xi }_{\alpha }\cdot \mathbf{n}-m_{\alpha })\frac{d^{\alpha }{\tilde{\varphi }}_{\alpha }}{dt}\}dA=0. \end{gathered}$$ (98)

Since ${\mathcal{R}}_t$ and virtual velocities are arbitrary, the microscopic and macroscopic force balances and traction conditions follow form (98),

$$\text{macroforce balance}:\nabla \cdot {\mathbf{T}}_{\alpha }+{\rho }_{\alpha }{\varphi }_{\alpha }{\mathbf{b}}_{\alpha }=0,$$ (99)

$$\text{microforce balance}:{\pi }_{\alpha }+{\tau }_{\alpha }+\nabla \cdot {\xi }_{\alpha }=0,$$ (100)

$$\text{macrotraction condition}:{\mathbf{t}}_{\alpha }={\mathbf{T}}_{\alpha }\mathbf{n},$$ (101)

$$\text{microtraction condition}:m_{\alpha }={\xi }_{\alpha }\cdot \mathbf{n}.$$ (102)

As indicated previously, the microforces π_α, τ_α, and ξ_α are generalized forces that arise due to nonlocality encountered in the evolution of phase boundaries [68, 83]¹⁹. In the context of biological events responsible for the growth of a tumor, these terms represent the power expended by the interaction and adhesion between cell concentrations due to rates of change of each volume fraction on the surface of the full mixture [35, 164].

The relations (99) - (102) demonstrate the consequence of the principle of virtual power. This shows that after postulating the proper form of energy balance law, the virtual power balance encapsulates the local force balance (12) as well as additional balance laws representing the events in smaller scales (15). In particular, without assuming a priori that the force and momentum balance laws are satisfied, they are derivable from another hypothesis; i.e., the principle of virtual power. Requiring the internal power ${\mathcal{P}}_{\text{int}}$ to be frame-indifferent, eliminates the need to impose a balance of angular moments.

B. Growth Tensor and Mass Exchange Rate

The fundamental governing equation of biological growth, as the process of mass addition and loss, is the mass balance written in terms of the order parameter, i.e., volume fraction in the current formulation. This diffusion equation is necessary to address the physical phenomena involved in macroscopic growth. In the case of coupled diffusion-deformation formulation, an evolution equation of the growth tensor must be consistent with the growth characterization through the mass transfer equation (i.e., mass supply and flux). Here we derive a relation between growth tensor ${\mathbf{F}}_T^G$ and mass exchange rate under the isotropic growth assumption²⁰,

$${\mathbf{F}}_T^G={\Lambda }_T^G\mathbf{I}.$$ (103)

Considering a two phase mixture with volume v in which a solid phase (tumor) undergoes pure growth process ${\mathbf{F}}_T^S=0$. In this case, the volume occupied by tumor constituent increases from initial value $v_T^0=v_T$(t₀) to a volume v_T(t) in time t. The volume change due to this growth process is,

$$J_T^G=\frac{d{v}_T}{d{v}_T^0}.$$ (104)

Following (103), the change in the tumor volume can be also represent as,

$$J_T^G=\text{det}({\mathbf{F}}_T^G)=({\Lambda }_T^G{)}^3.$$ (105)

Equating above relations along with the definition of tumor volume fraction (5), results in following relation consistent with the formulation developed by Garikipati et al [56, 57, 116],

$${\Lambda }_T^G={\left(\frac{{\rho }_T{\varphi }_T}{{\rho }_T^0{\varphi }_T^0}\right)}^{1∕3},$$ (106)

where ${\varphi }_T^0={\varphi }_T$(t₀) and ${\rho }_T^0={\rho }_T$(t₀).

Additionally, the tumor mass balance under quasi-static assumption is

$$\frac{\partial {\rho }_T{\varphi }_T}{\partial t}=S_T-\nabla \cdot ({\mathbf{M}}_T\cdot \nabla {\mu }_T).$$ (107)

Substituting ρ_Tϕ_T from (106) into above relation, one can find an evolution equation for growth stretch ratio as,

$${\rho }_T^0{\varphi }_T^0\frac{\partial ({\Lambda }_T^G{)}^3}{\partial t}={\rho }_T{\varphi }_T(S_T-\nabla \cdot ({\mathbf{M}}_T\cdot \nabla {\mu }_T)).$$ (108)

The above equation provides a consistent framework to determine the growth tensor evolution equation from functional forms of S_T and M_T postulated based upon biophysical phenomena. A similar relation is presented by Ambrosi and Mollica using a consistent mathematical derivations based on the natural configuration argument and Lagrangian form of the mass balance(for more details see [6, 7]).

C. Finite Element Formulation

C.1. Semi-implicit Time-discretization Scheme

Because of both the bilaplacian operator and the nonlinearity of the Cahn-Hilliard-type tumor diffusion equations the development of stable time-discretization scheme is a non trivial challenge. For the proposed model, we make use of a first-order accurate unconditional energy-stable scheme for gradient-flow systems based on the splitting of the non-mechanical part of the Helmholtz free energy,

$$\Psi =\frac{{ϵ}_T^2}{2}\mid \nabla {\varphi }_T{\mid }^2+\kappa {\varphi }_T^2(1-{\varphi }_T{)}^2+\frac{1}{2{\delta }_{\sigma }}{\varphi }_{\sigma }^2-{\chi }_0{\varphi }_T{\varphi }_{\sigma }$$ (109)

into a convex (contractive) and concave (expansive) part,

$$\Psi ={\Psi }_c+{\Psi }_e.$$ (110)

The idea of the energy splitting scheme is to treat the contracting, more stable, part implicitly and the expanding part explicitly. Following [71, 96], one can write the following split of the free energy,

$${\Psi }_c=\frac{3}{2}\kappa {\varphi }_T^2+\frac{{ϵ}_T^2}{2}\mid \nabla {\varphi }_T{\mid }^2-{\chi }_0{\varphi }_T{\varphi }_{\sigma },$$ (111)

$$-{\Psi }_e=\kappa ({\varphi }_T^4-2{\varphi }_T^3-\frac{1}{2}{\varphi }_T^2).$$ (112)

Thus, dividing the time domain into n time step of size Δt = t_n+1 − t_n, the time stepping scheme in the tumor chemical potential can be represented as,

$$\begin{gathered} {\mu }_{T_{n+1}}=\frac{\partial {\Psi }_c({\varphi }_{T_{n+1}})}{\partial {\varphi }_T}-\frac{\partial {\Psi }_e({\varphi }_{T_n})}{\partial {\varphi }_T}, \\ =3\kappa {\varphi }_{T_{n+1}}-{\chi }_0{\varphi }_{{\sigma }_{n+1}}-{ϵ}_T^2\Delta {\varphi }_{T_{n+1}}-\kappa (4{\varphi }_{T_n}^3-6{\varphi }_{T_n}^2-{\varphi }_{T_n}) \end{gathered}$$ (113)

C.2. Finite Element Solution of the Nonlinear System

The finite element solution for the coupled nonlinear system of equations (94) is obtained by uncoupling the equation according to Algorithm 1. Newton’s method is employed to solve each set of equations. To define the finite element space relevant to (94), we consider homogeneous Neumann boundary conditions for all variables. Let $\mathcal{V}$ being a Hilbert space consisting of functions of time with values in H¹(Ω). We define the finite-dimensional spaces ${\mathcal{V}}^h$ by,

$${\mathcal{V}}^h=\{v^h\in H^1(\Omega ):v^h{\mid }_{\tau }=\widehat{v}\circ F_{\tau },\widehat{v}\in Q_1,\tau \in {\mathcal{T}}^h\},$$ (114)

where ${\mathcal{T}}^h$ is a quasi-uniform family of triangulations of Ω, F_τ is an affine map from the master element $\widehat{\tau }$ to τ, and Q₁ is the tensor product of polynomials of degree 1. Let (·, ·) denote the L²(Ω)-inner product with $(u,v)={\int }_{\Omega }uvdx$ (see [119] for details).

The weak formulation for the nutrient diffusion considering v_σ as test function is given by

$$\begin{gathered} \text{Find}{\varphi }_{{\sigma }_{n+1}}\in {\mathcal{V}}^h,\forall v_{\sigma }\in {\mathcal{V}}^h: \\ ({\varphi }_{{\sigma }_{n+1}}-{\varphi }_{{\sigma }_n},v_{\sigma })-\Delta t(S_{\sigma }({\varphi }_{T_n},{\varphi }_{{\sigma }_{n+1}}),v_{\sigma }) \\ -\Delta t(M_{\sigma }\nabla {\mu }_{\sigma }({\varphi }_{T_n},{\varphi }_{{\sigma }_{n+1}}),\nabla v_{\sigma })=0. \end{gathered}$$ (115)

We consider a mixed variational formulation of Cahn-Hilliard equation of tumor diffusion involving both ϕ_T and μ_T as separate unknowns. Applying the semi-implicit time-stepping scheme, the weak formulation for the tumor diffusion, considering v_T and q_T as test functions, is defined as

$$\begin{gathered} \text{Find}({\varphi }_{T_{n+1}},{\mu }_{n+1})\in {\mathcal{V}}^h\times {\mathcal{V}}^h,\forall v_T,w_T\in {\mathcal{V}}^h: \\ ({\varphi }_{T_{n+1}}-{\varphi }_{T_n},v_T)-\Delta t(S_T({\varphi }_{T_{n+1}},{\varphi }_{{\sigma }_{n+1}},J_{T_n}),v_T) \\ -\Delta t(M_T({\varphi }_{T_{n+1}},J_{T_n})\nabla {\mu }_{T_{n+1}},\nabla v_T)=0, \end{gathered}$$ (116)

$$\begin{gathered} ({\mu }_{T_{n+1}},w_T)+\Delta t(3\kappa {\varphi }_{T_{n+1}}-{\chi }_0{\varphi }_{{\sigma }_{n+1}}-{ϵ}_T^2\Delta {\varphi }_{T_{n+1}},w_T) \\ -\Delta t(\kappa (4{\varphi }_{T_n}^3-6{\varphi }_{T_n}^2-{\varphi }_{T_n}),w_T) \\ +\frac{J_{T_n}^S}{d}({\Lambda }_T^G{)}_n^3\Delta t({\mathbf{T}}_{T_n},w_T)=0. \end{gathered}$$ (117)

Having ϕ_Tn+1, the growth stretch ratio can be updated using the discretized evolution equation (85), as

$$\begin{gathered} \text{Find}({\Lambda }_T^G{)}_{n+1}\in {\mathcal{V}}^h: \\ ({\Lambda }_T^G{)}_{n+1}=({\Lambda }_T^G{)}_n+\frac{1}{d}({\Lambda }_T^G{)}_n[{\varphi }_{T_{n+1}}-{\varphi }_{T_n}]. \end{gathered}$$ (118)

Finally, the weak formulation for the tumor deformation considering v_u as test function is given by

$$\begin{gathered} \text{Find}{\mathbf{u}}_{n+1}\in ({\mathcal{V}}^h{)}^d,\forall {\mathit{v}}_u\in ({\mathcal{V}}^h{)}^d: \\ ({\mathbf{T}}_T({\mathbf{u}}_{T_{n+1}},{\varphi }_{T_{n+1}}),\nabla {\mathit{v}}_u)=0. \end{gathered}$$ (119)

Algorithm 1 summarizes the solution procedure using Newton iteration to solve the weak formulations.

Algorithm 1: Algorithm to solve the decoupled system of equations governing the four species tumor model.

$$\begin{gathered} \begin{array}{cc}\hfill & \\ \mathrm{Input}:{\varphi }_T,{\mu }_T,{\varphi }_{{\sigma }_0},({\Lambda }_T^G{)}_0,{\mathbf{u}}_0\hfill \\ \hfill & \\ \mathrm{Output}:{\varphi }_{T_n},{\mu }_{T_n},{\varphi }_{{\sigma }_n},({\Lambda }_T^G{)}_n,{\mathbf{u}}_n\hfill \\ \hfill & 1\mathbf{begin}\hfill \\ \hfill & \begin{array}{c}2\hfill \\ 3\hfill \\ 4\hfill \\ 5\hfill \\ 6\hfill \\ 7\hfill \\ 8\hfill \\ 9\hfill \end{array}\mid \begin{array}{c}n\leftarrow 0\hfill \\ \mathbf{repeat}\hfill \\ \\ \mid \begin{array}{c} \\ \text{Solve}{\varphi }_{{\sigma }_{n+1}}\text{from (115) given}{\varphi }_{T_n},{\varphi }_{{\sigma }_n}\hfill \\ \\ \text{Solve}{\varphi }_{T_{n+1}}\text{and}{\mu }_{T_{n+1}}\text{from (116) given}{\varphi }_{T_n},{\varphi }_{{\sigma }_{n+1}},{\mathbf{u}}_n,({\Lambda }_T^G{)}_n\hfill \\ \\ \text{Update}({\Lambda }_T^G{)}_{n+1}\text{form}(118)\text{given}{\varphi }_{T_n},{\varphi }_{T_{n+1}},({\Lambda }_T^G{)}_n\hfill \\ \\ \text{Solve}{\mathbf{u}}^{n+1}\text{from}(119)\text{given}({\Lambda }_T^G{)}_{n+1},{\mathbf{u}}_n\hfill \\ \\ n\leftarrow n+1\hfill \end{array}\phantom{\mid }\hfill \\ \mathbf{until}\underset{¯}{n\Delta t>T_{\max }}\hfill \end{array}\phantom{\mid }\hfill \end{array} \end{gathered}$$