Phenomics-based quantification of CRISPR-induced mosaicism in zebrafish

SUMMARY

Genetic mosaicism can manifest as spatially variable phenotypes that vary from site-to-site within an organism. Here, we use imaging-based phenomics to quantitate phenotypes at many sites within the axial skeleton of CRISPR-edited G0 zebrafish. Through characterization of loss-of-function cell clusters in the developing skeleton, we identify a distinctive size distribution shown to arise from clonal fragmentation and merger events. We quantitate the phenotypic mosaicism produced by somatic mutations of two genes, plod2 and bmpla, implicated in human Osteogenesis Imperfecta. Comparison of somatic, CRISPR-generated G0 mutants to homozygous germline mutants reveal phenotypic convergence, suggesting that CRISPR screens of G0 animals can faithfully recapitulate the biology of inbred disease models. We describe statistical frameworks for phenomic analysis of spatial phenotypic variation present in somatic G0 mutants. In total, this study defines an approach for decoding spatially variable phenotypes generated during CRISPR-based screens.

Graphical Abstract

eTOC Blurb:

Genetic mosaicism manifests as spatially variable phenotypes, whose detection and interpretation remains challenging. Watson et al. identify biological factors influencing phenotypic patterns in the skeletons of CRISPR-edited mosaic zebrafish, and establish methods for their detection using large-scale phenotyping.

INTRODUCTION

Phenomics is the utilization of large-scale phenotyping to systematically infer genotype to phenotype relationships (Houle et al., 2010). As such, phenotypic profiling at a large number of anatomical sites can advance our understanding of biology that involves relationships between phenotypes across the whole organism (Hur et al., 2017). One example of such biology is genetic mosaicism: the presence of cells with multiple distinct genotypes constituting the organism on the whole. Mosaicism can arise naturally through errors in DNA replication, or intentionally through genetic manipulation. This genetic heterogeneity results in a hallmark of mosaicism—site-to-site phenotypic variability—which makes identifying gene-to-phenotype relationships challenging. In animal models, somatic mutations form the basis for rapid-throughput G0 screens, prototypes for which are rapidly increasing following the advent of CRISPR (Clustered- Regularly Interspaced Short Palindromic Repeats)-based gene editing (Cong et al., 2013; Jinek et al., 2012). In humans, chromosomal mosaicism in embryos is quite common (McCoy, 2017; Vanneste et al., 2009), its role in disease may be prevalent and underappreciated (Gottlieb et al., 2010; Iourov et al., 2010), and at the most fundamental level, it is suggested that every complex, multi-cellular organism is likely to harbor at least some somatic mosaicism (Campbell et al., 2015; Forsberg et al., 2017). In the context of disease, mosaic phenotypic patterns can inform the timing of mutagenesis, which may help predict the likelihood of mutations in germ cells that can be passed on to progeny (Campbell et al., 2015). Phenotypic profiling at a number of anatomical sites may help decode somatic mutant phenotypes, which are important in both experimental and clinical settings.

Extracting biological information from somatic mutant phenotypes remains challenging for several reasons. One source of difficulty is our lack of understanding of quantitative phenotypic variation arising from mosaicism, and how best to analyze it. For spatially distributed organs (e.g., bone, skin, nerves, blood vessels), mosaicism can manifest as relatively uniform phenotypes reminiscent of a generalized condition, or alternating patterns of affected and unaffected body segments (Bernards and Gusella, 1994). Much of our knowledge of the phenotypic consequences of mosaicism has been derived from easily observable traits where spatial variations are readily discernible (Biesecker and Spinner, 2013). As such, our ability to discern phenotypic manifestations of mosaicism for complex traits remains relatively limited (Biesecker and Spinner, 2013). Large-scale phenotyping workflows have mostly been defined in germline mutants (Gistelinck et al., 2018; Hur et al., 2017; Thyme et al., 2019) or animals subjected to systemic drug exposure (Pardo-Martin et al., 2013). Different analytical methods may be needed for somatic mutants, where the specific set of altered measures, acquired from different anatomical locations, may be different from animal-to-animal.

Another source of difficulty is our limited understanding of biological factors that influence phenotypic expressivity in mosaic individuals. It is broadly accepted that spatial phenotypic patterns are dependent on the proliferation of mutant cells and their translocation to different sites. Lineage tracing of clonal populations from embryonic to adult zebrafish has provided a wealth of knowledge on clonal abundance in a variety of tissues, and suggests that, in most cases, a few clonal progenitors account for a majority of cells comprising the resulting tissue type (McKenna et al., 2016). Yet, how these clones distribute spatially within and across tissues remains unknown, and is a critical piece of information needed to interpret somatic mutant phenotypes.

A prime instance of experimental biology which necessitates decoding somatic mutant phenotypes is in a rapid-throughput genetic screen. Several prototypes for rapid CRISPR-based reverse genetic screens have been developed in which phenotyping is performed directly in G0 founders (Shah et al., 2015; Wu et al., 2018). This increases throughput by alleviating the time and resources needed to breed mutant alleles to homozygosity. Such approaches may also be useful for animal models that require longer durations to reach sexual maturity or have long gestational intervals, making breeding to homozygosity impractical. However, creating equivalent loss-of-function on an organism-wide scale (i.e. every individual cell) is challenging. When complexed with a targeting guide RNA (gRNA), the bacterial Cas9 enzyme will create a double strand break at a genome-specific location determined by complementary sequence in the gRNA. Errors in endogenous repair leads to insertions and deletions (indels) at the cut site, and potential loss of gene product function. Yet, when administered a single gRNA, 1/3 of indels are expected to be in-frame. Thus, less than half ([2/3]²=4/9) of cells are expected to have bi-allelic out-of-frame mutations, even with peak editing efficiency (Shah et al., 2015). While the use of multiple gRNAs to redundantly target the same gene can increase the proportion of bi-allelic out-of-frame mutations, this may also increase toxicity, and variable penetrance of null phenotypes is still prevalent (Wu et al., 2018). Microhomology-mediated end joining (MMEJ) is a promising direction to enrich somatic mutations for a predictable out-of-frame allele (Ata et al., 2018). However, imperfect editing efficiencies and some degree of mutated allelic mosaicism are still expected following MMEJ. These problems are confounded when multiple genes are knocked down; for example, when studying epistatic interactions of genes that are tightly linked, or knockdown of clusters of genes with functional redundancy (Sanjana, 2017; Shah et al., 2015; Shalem et al., 2014). Yet, mutation efficiency often decreases with the number genes that are multiplexed, due to a reduction in Cas9:gRNAs per gene. Due to the lower fidelity in detecting somatic mutant phenotypes, prototypical screens have mostly focused on severely dysmorphic phenotypes (Wu et al., 2018), or phenotypes whose spatial variations are easily observable (Shah et al., 2015).

In this study, our aims were threefold: to 1) characterize how CRISPR-induced mutations distribute-within individual bones, and groups of bones-in the skeletons of G0 zebrafish, and to better understand the etiology of such mosaic patterns; 2) assess how such mosaic patterns are phenotypically manifested by characterizing somatic mutant phenotypes for plod2 and bmpla; and 3) identify statistical methods effective at discerning somatic mutant phenotypes. Our studies identify strategies for decoding spatially variable phenotypes, i.e. those that have the potential for high site-to-site variability within a single organ system, in G0 zebrafish. When paired with CRISPR- based screens, these methods can identify genes contributing to skeletal disease.

RESULTS

CRISPR-based gene editing results in clusters of cells with loss-of-function

Our first aim was to characterize how CRISPR-induced mutations distribute in the skeletons of G0 zebrafish, and to better understand the etiology of such mosaic patterns. To examine this, sp7:EGFP (DeLaurier et al., 2010) embryos were injected with Cas9:gRNA ribonucleoprotein complexes (RNPs) targeting the fluorescent transgene. This enabled loss-of-function mutations in EGFP to be visualized as loss-of- fluorescence (LOF) in sp7+ (osterix+) osteoblasts. Injected fish were examined for functional EGFP loss at 10-12dpf, a stage when the larvae are still transparent and most skeletal elements have formed. Regions of LOF were observed in virtually all formed skeletal elements (Figure 1A). This included bones of the craniofacial skeleton, median fin rays, hypurals, and the spine. While penetrance of LOF was high, expressivity was variable in regard to which bony elements in each animal exhibited fluorescence loss, as well as the size and number of such regions within each bony element. Quantification of mean centrum fluorescence in sp7:EGFP somatic mutants revealed that, when averaged across the sample, fluorescence was uniformly decreased across the spine (Figure 1B). However, we observed jagged traces in some individual mutants, demonstrating variability in LOF within individuals (Figure 1C). As expected, centra in adult sp7:EGFP somatic mutants were well-mineralized and did not exhibit gross defects (Figure S1), indicating that LOF was attributable to loss of the transgene and not to loss of osteoblasts.

Figure 1. A common distribution underlies loss-of-function cluster size in bones of distinct developmental lineages, and in animals with different mutation efficiencies.

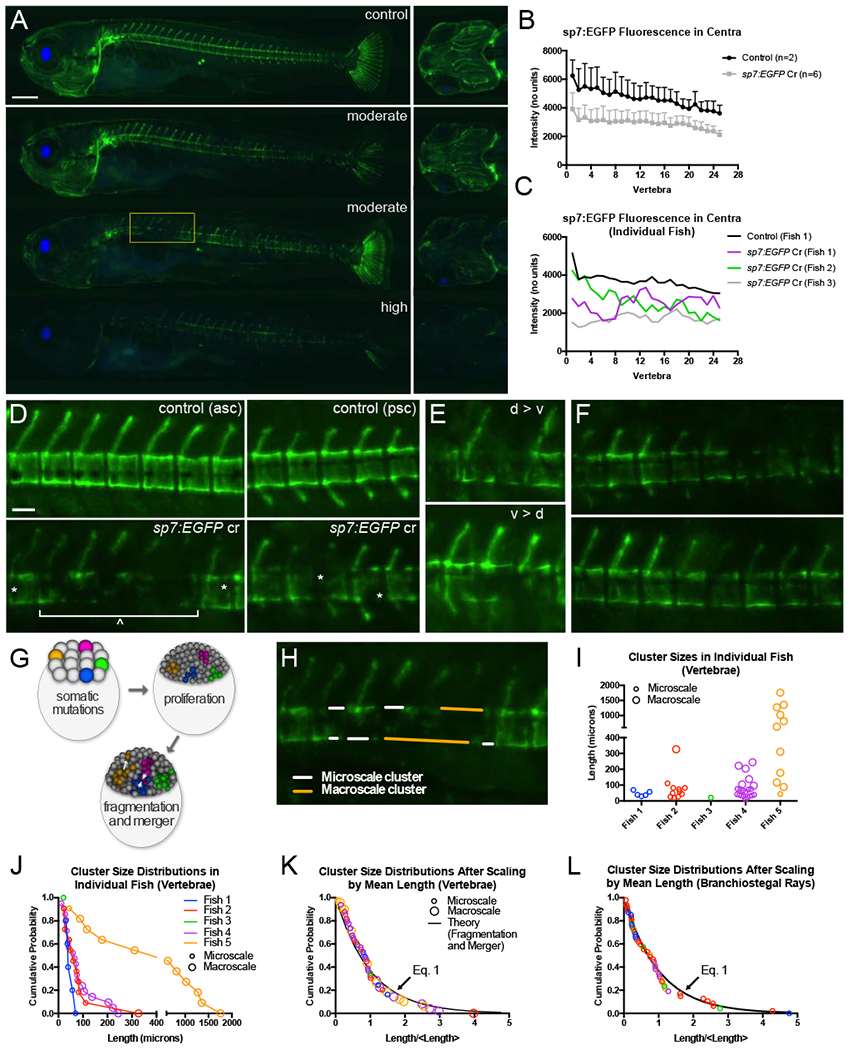
(A) Larval sp7:EGFP transgenic fish show relatively uniform EGFP expression in the skeleton of control fish (top). Somatic mutants with either moderate (middle) or high (bottom) loss-of-fluorescence (LOF) display a wide and varied range of LOF clusters, including in the craniofacial skeleton, the axial skeleton, and in the caudal fin rays. Fish shown are 10 dpf clutchmates. Scale bar, 500 μm. (B) Somatic mutants have a mean reduction in sp7:EGFP fluorescence in the developing axial skeleton of 10dpf zebrafish compared to non-injected clutchmates (controls). (C) Traces of fluorescence intensity for each developing centrum along the spine for individual somatic mutants (purple, green and gray lines) show jagged topology, indicating clusters of loss of transgene expression compared to control (black line) and averaged expression (panel B). (D) Loss-of-fluorescence occurs on both the ^Amacroscale (spanning multiple vertebral bodies) and the *microscale (contained within a vertebral body) compared to controls. Note the distinction between opacity due to developing pigmentation in the controls (top) compared to loss-of-fluorescence in somatic mutants (bottom). asc, anterior spinal column; psc, posterior spinal column. (E) On multiple instances, loss-of-fluorescence in somatic mutants was stratified along the dorso-ventral axis of the centrum, with loss occurring preferentially on the dorsal side (top) or ventral side (bottom). (F) EGFP expression on the dorsal side of the centrum in somatic mutants often corresponded to expression in the neural arch and spine. Scale bar for (D-F) = 100 μm. (G) Schematic demonstrating clonal fragmentation and merger events. (H) Example tracing of microscale (white) and macroscale (orange) LOF clusters on dorsal and ventral centrum surfaces. (I) Cluster sizes in vertebrae of individual fish. Note the differences in the number and sizes of clusters, indicative of differences in functional loss in each fish. (J) Vertebral cluster size distributions in individual fish, using data from panel I. (K) Vertebral cluster size distributions in individual fish, when normalized by the mean length in each fish. Color mapping is same as for panels I and J. The data collapse onto a common distribution, which overlaps with Eq. 1. See Figure S2 for distributions of only micro- or macroscale clusters. (L) Cluster size distributions for LOF clusters in the branchiostegal rays. Color mapping is same as for panels I and J.

LOF regions are composed of clusters of cells with loss-of-function mutations: cells comprising each cluster represent a single clone, or multiple clones that merged at an earlier point in development (we are unable to distinguish these two possibilities). Within individual vertebrae, we often observed multiple, contiguous centra with complete or partial LOF, and which were flanked by at least one centra with no LOF. This resulted in two distinguishable types of cell clusters: “microscale” clusters confined within single vertebrae, and “macroscale” clusters spanning contiguous vertebrae (Figure 1D). Inspection at higher magnification revealed that some centra exhibited LOF in ventral, but not dorsal, regions (or vice versa). This dorso-ventral stratification could at times be seen across contiguous centra (Figure 1E), potentially due to these bodies’ shared clonal partners. In the neural arches, LOF often appeared to be associated with LOF in the centrum of the same vertebral body (Figure 1F). Because many bones retained partial or complete expression of the transgene, this suggested that individual bony elements are not explicitly derived from single clonal populations, and cannot be evaluated as independent functional or non-functional units.

A common distribution underlies the sizes of loss-of-function clusters in bones of distinct developmental lineages, and in animals with different mutation efficiencies

We next sought to understand the etiology of such mosaic patterns. While some aspects of patterns of fluorescence loss appeared to be non-random, patterns from fish- to-fish were unpredictable, suggesting that stochastic forces were an important etiological factor. Models of clonal population dynamics in fluorescence-based cell lineage tracing studies have demonstrated that while different factors can contribute to cluster size distributions during tissue growth, over time, contributions from random clonal merger and fragmentation (Figure 1G) become dominant over those from cell behaviors specified by developmental programs (e.g., cell division or loss) (Rulands et al., 2018). As a consequence, cluster size distributions across diverse developmental processes often exhibit the same characteristic distribution once cluster sizes in each individual are normalized by the average cluster size in that individual (Rulands et al., 2018). This distribution has the form:

$$y=e^{(-x/<x>)}$$ (Eq 1)

where x is cluster size, and <x> is the mean of x (Rulands et al., 2018).

Fluorescently-labeled cell clusters in lineage tracing studies and LOF cell clusters in somatic mutants share commonalities in their physical origins (postzygotic mutations) and interpretation (clusters may be comprised of a single clonal population, or multiple clones that merged earlier in development). As such, we hypothesized that LOF clusters in somatic animals would also exhibit universality in their size distributions described by Eq 1. To test this, we manually traced regions of LOF on the dorsal and ventral aspects in the centra in each animal (Figure 1H). Individual fish exhibited variable numbers and sizes of LOF clusters (Figure 1I), as well as different compositions of microscale versus macroscale clusters. This variability manifested as distinct distributions of cluster sizes in each fish (Figure 1J). However, when normalized by average cluster size in each animal, the cluster size distributions collapsed to the distribution in Eq 1 for both microscale and macroscale clusters (Figure 1K). When microscale and macroscale clusters were analyzed separately, the curve fit was noticeably weaker (Figure S2A,B), presumably from incomplete sampling of cluster sizes. Note that results in Figure 1K were obtained by manual tracing of LOF regions. Similar results were obtained when regions were traced by a different individual (Figure S2C), suggesting that results were not strongly sensitive to individual differences in thresholding.

We hypothesized that this distribution would also describe LOF cluster sizes in bones of a different developmental lineage. We quantified LOF cluster size distributions within the branchiostegal rays of the craniofacial skeleton, which unlike the somite- derived vertebral column, derives from neural crest (Kague et al., 2012). Consistent with our hypothesis, a similar data collapse was observed (Figure 1L). These studies demonstrate that loss-of-function cluster sizes in bones of distinct developmental lineages, and in animals with different loss-of-function efficiencies, can be described by a single distribution (Eq 1); the origin of which derives from numerical convergence behaviors associated with clonal fragmentation and merger events.

Quantifying the mosaic phenotypes associated with loss-of-function mutants in two models of Osteogenesis Imperfecta

In humans, mutations in PLOD2 and BMP1 are associated with Osteogenesis Imperfecta (OI). The enzyme encoded by PLOD2, lysyl hydroxylase 2, localizes to the endoplasmic reticulum, and catalyzes lysine residue hydroxylation in fibrillar collagen telopeptides (Gistelinck et al., 2016). BMP1 is a secreted enzyme that functions in the cleavage of C-propeptides from procollagen precursors (Muir et al., 2014). We and others previously showed that zebrafish germline loss-of-function mutants for plod2 and bmpla exhibit severe skeletal abnormalities as adults, reminiscent of OI phenotypes (Asharani et al., 2012; Charles et al., 2017; Gistelinck et al., 2016; Hur et al., 2017).

Somatic mutants for plod2 and bmpla were generated by injection of RNP complexes into embryos, and a subset of larvae were individually screened for indels at 12 dpf. Sanger sequencing and TIDE analysis (Brinkman et al., 2018) estimated mutation efficiencies of 82.7-88.1% and 71.0-87.5% for plod2 and bmpla, respectively. At 90 dpf, somatic mutants for both genes exhibited clear skeletal abnormalities similar to their adult germline mutant counterparts (Figure S3A,B). Somatic mutants for plod2 exhibited severe vertebral malformations including compression of the vertebrae along the anteroposterior axis, kyphosis, and increased bone formation. Somatic mutants for bmpla exhibited increased vertebral radiopacity and bone thickening. Standard length (S.L.) was significantly reduced compared to sham controls for both plod2 (Figure S3C; n=11/group) and bmpla (Figure S3D; n=10 controls, n=14 bmpla somatic mutants). The presence of adult phenotypes adds to recent reports (D’Agati et al., 2017; Wu et al., 2018) examining the durability of crispant zebrafish phenotypes through the larval-to- adult transition.

Variability in phenotypic expressivity across animals was clearly evident. For plod2, such variability was perceptible by the number of dysmorphic vertebrae in each animal; in the 24 anterior-most precaudal and caudal vertebrae, plod2 somatic mutants exhibited 12 [6-20] (median [range]) obviously thick or malformed vertebrae per fish. Further, 100% (11 out of 11) of animals were penetrant, as all individuals exhibited at least one severely malformed vertebra per animal. For bmpla somatic mutants, many animals exhibited a qualitative increase in vertebral radiopacity along the spine, which was variable among individuals, ranging from mild to severe. Variability in phenotypic expressivity within each animal was also evident in some cases. Certain plod2 somatic mutants exhibited “patchy” expressivity characterized by contiguous spans of dysmorphic vertebrae surrounded by vertebrae that appeared qualitatively normal. In plod2 germline mutants, vertebrae are uniformly dysmorphic (Gistelinck et al., 2016), suggesting that patchy expressivity is not an inherent property of plod2 loss in adult fish. In contrast, for bmpla somatic mutants, intra-animal variability in phenotypic expressivity was less obvious; while radiopacity and thickening was variable from fish-to-fish, within each animal, these characteristics appeared relatively uniform.

We hypothesized that while plod2 and bmpla somatic mutants exhibit inter- and intra-animal variability, the traits affected in somatic mutants might be indicative of those affected in germline mutants when averaged across a large sample. Our rationale was partly based on loss-of-fluorescence in sp7:EGFP somatic mutants, which, as described earlier, were highly variable in each individual, yet when averaged across the group, resulted in a uniform decrease in fluorescence across the spine (see Figure 1B,C).

To test our hypothesis, we performed microCT-based spinal phenomics (Hur et al., 2017). We previously developed a microCT-based workflow and segmentation software, FishCuT, which enables rapid quantification of 100s of measures in the axial skeleton of adult zebrafish (Gistelinck et al., 2018; Hur et al., 2017, 2018). In this workflow, 25 different quantities are computed for each vertebra (Hur et al., 2017); see STAR Methods for description. Once calculated, these quantities are plotted as a function of vertebra number along the axial skeleton for each fish; we have termed such entities “vertebral traces”. For each combination of outcome/element, a standard score is computed and these data are arranged into matrix constructs that we have termed “skeletal barcodes”. In our studies, 16 vertebrae (16*25=400 measures/animal) in 52 animals were analyzed, resulting in 52*400=20,800 data points that provided a comprehensive characterization of bone morphology and microarchitecture across the majority of the axial skeleton for our zebrafish cohort. To facilitate comparisons with prior studies (Hur et al., 2017), we present data on ten combinatorial quantities (the nine possible combinations of 3 vertebral elements (centrum, Cent; neural arch, Neur; and haemal arch, Haem) x 3 characteristics (tissue mineral density, TMD; thickness, Th; and volume, Vol) plus centrum length (Cent.Le) in the 16 anterior-most vertebrae in the main text, and have included all 25 quantities in the supplemental material.

We assessed which FishCuT measures exhibited differences in the global test. Analysis for plod2 somatic mutants (n=11 fish/group) indicated significant differences in Cent.TMD (p=0.000005), Haem.TMD (p=0.00008), Neur.TMD (p=0.00005), Cent.Vol, (p=0.004), Cent.Th (p=0.04), Cent.Le (p=0.00009), and Neur.Th (p=0.00007) (Figure 2A–L). Somatic mutants for bmpla (n=15 fish/group) exhibited significant differences in Cent.TMD (p=0.000004), Haem.TMD (p=0.00002), Neur.TMD (p=0.00005), Cent.Vol (p=0.004), Cent.Th (p=0.02), Cent.Le (p=0.01), and Haem.Th (p=0.008) (Figure 2A’–L’). Data for all 25 combinatorial measures for plod2 and bmpla are provided in Figure S4 and Figure S5, respectively. For both plod2 and bmpla, most significantly different features were associated with vertebral traces that were elevated or depressed across all vertebrae; an exception was neural arch thickness in plod2 somatic mutants, which was lower in anterior vertebrae, but higher in posterior vertebrae. Notably, for plod2 somatic mutants, mean vertebral traces appeared smooth—despite intra-individual variability in phenotypic expressivity in some measures (Figure S6A; compare with bmpla somatic mutants, Figure S6B)—due to averaging across the sample.

Figure 2. FishCuT analysis of somatic mutants.

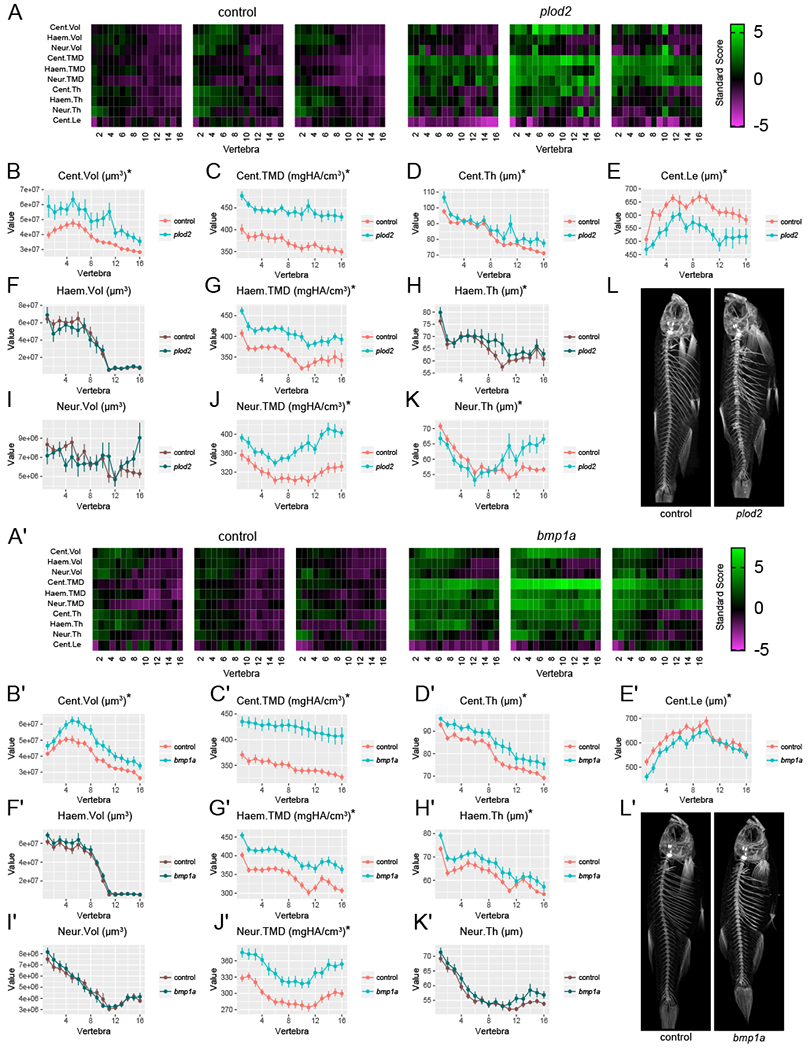
(A,A’) Skeletal barcodes visually depict individual phenomes for control and plod2 (A) or bmpla (A’) somatic mutant fish (3 fish/group shown). See STAR Methods for barcode quantification. (B-K,B’-K’) Phenotypic features, indicated by the graph title (with units for y-axis), are plotted as a function of vertebra along the axial skeleton. Plots associated with p<0.05 in the global test are in a lighter coloring scheme and are indicated by an asterisk (mean ± SE, see text for p-values). For plod2 (B-K) n=11/group, and for bmpla (B’-K’) n=15/group. Data for all 25 combinatorial measures are presented in Figure S4 and S5. Cent, centrum; Haem, haemal arch, Neur, neural arch; Vol, volume; TMD, tissue mineral density; Th, thickness; Le, length. (L,L’) Representative maximum intensity projections of microCT scans for plod2 (L) and bmpla (L’) somatic mutant fish and controls.

Individual cells in the G0, somatic mutant zebrafish generated for both genes have a wide-ranging spectrum of allelic variation, conferring different levels of functional loss for plod2 or bmpla between chromosomes, cells, tissues and individuals. In contrast, germline mutants for each gene have a single, stably inherited loss-of-function allele for which they were bred to homozygosity. As such, we wanted to assess the extent to which somatic mutants for plod2 and bmpla could act as faithful models of their germline mutant counterparts. For these analyses, we compared global test results to measurements and FishCuT outputs for plod2 and bmpla germline mutants (n=3 for both germline groups) previously generated in (Hur et al., 2017) (Figure 3). Characteristic effect sizes in plod2 and bmpla somatic mutants were, on average, 25.6% and 24.4%, respectively, of those in their germline mutant counterparts (plod2 somatic: 0.95; plod2 germline: 3.71; bmpla somatic: 0.80; bmpla germline: 3.23).

Figure 3. Correspondence between somatic and germline mutant phenotypes for plod2 and bmp1a.

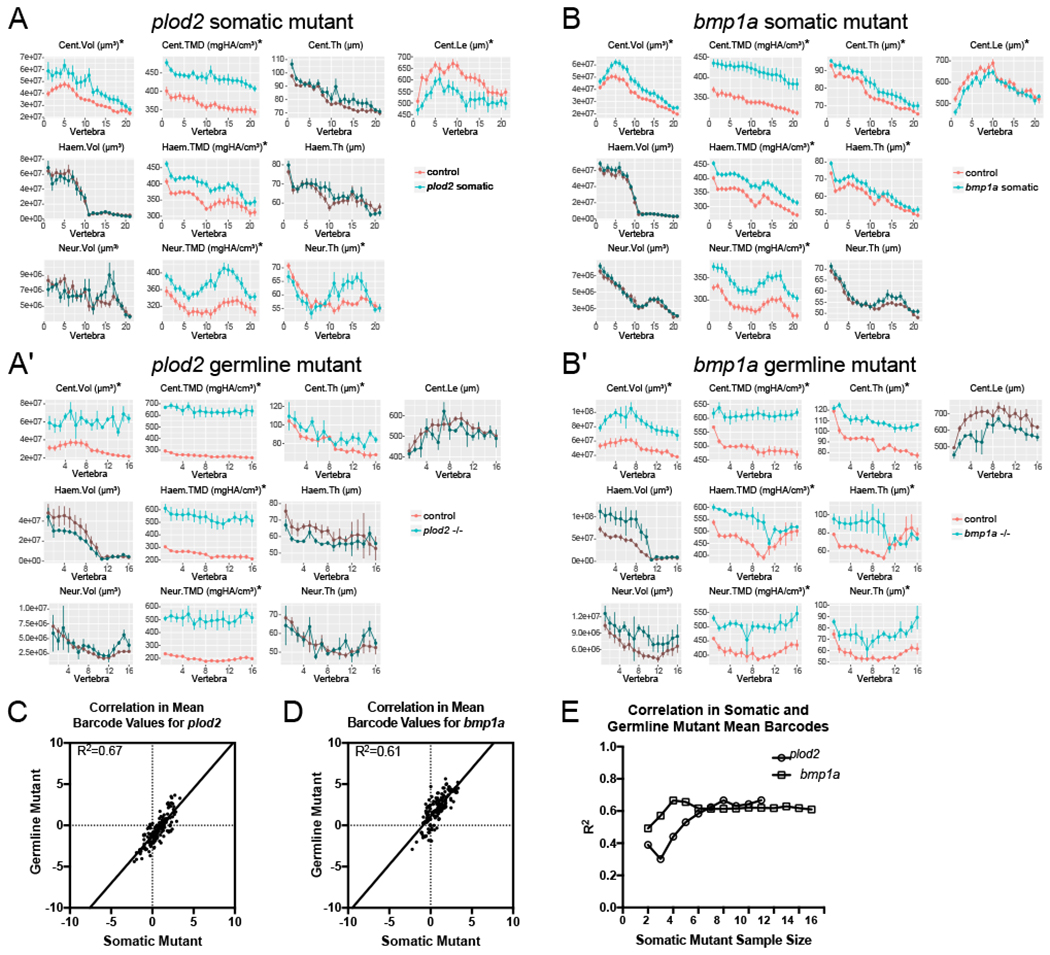
Phenotypic features are plotted as a function of vertebra (mean ± SE). Plots associated with p<0.05 in the global test are in a lighter coloring scheme (see text for p-values) and indicated by an asterisk. (A-A’) Comparison of plod2 somatic (A) and germline (A’) mutants. Data in (A’) were subjected to allometric normalization, due to the severe reduction in body length in plod2 germline mutants. (B-B’) Comparison of bmpla somatic (B) and germline (B’) mutants. A majority of statistically different traits in germline mutants for both genes are also affected in somatic mutants. For A’ and B’, n=3/group. Cent, centrum; Haem, haemal arch; Neur, neural arch; Vol, volume; TMD, tissue mineral density; Th, thickness; Le, length. (C-D) Correlations between mean somatic mutant barcodes for entire plod2 (C, n= 11) and bmpla (D, n=15) cohorts, plotted against respective mean germline mutant barcodes (n=3/group). (E) Correlation in mean somatic and germline mutant barcodes as a function of somatic mutant barcode sample size. As sample size (the number of barcodes included in the analysis) increases, phenome-wide correlation increases in an asymptotic manner.

Since the reduced standard length in plod2 somatic mutants was more muted compared to plod2 germline mutants (~4x less), we compared somatic mutant results to plod2 germline mutant phenotypes that had been subjected to allometric normalization. We previously showed that by transforming WT sibling data to a virtual phenome (scaled to the mean standard length of age-matched mutants) allometric models enable length- matched comparisons from an age-matched control group (Hur et al., 2017). Across the 10 primary measures, somatic mutants for plod2 exhibited significant differences for 80% (4 out of 5) of the measures significantly altered in plod2 germline mutants (Figure 3A,A’). Moreover, 60% (3 out of 5) of the combinatorial measures not significantly different in plod2 germline mutants were also not different in plod2 somatic mutants. Correspondence of affected traits was noticeably lower when plod2 somatic mutants were compared to plod2 germline mutants that had not been allometrically normalized (3 of 6 corresponding measures with statistical significance, 50%; and 1 of 4 corresponding measures without statistical significance, 25%). Comparisons of results to the other 15 measures in FishCuT were not possible because allometric models have yet to be developed for them.

We also observed similarity in affected traits in bmpla somatic and germline mutants (Figure 3B,B’). Specifically, across the 10 primary measures, bmpla somatic mutants exhibited significant differences for 86% (6 out of 7) of the measures significantly different in bmpla germline mutants. Further, 67% (2 out of 3) of the measures not significantly different in bmpla germline mutants were also not significantly different in bmpla somatic mutants. Correspondence was not improved when comparing bmpla somatic mutants to bmpla germline mutants that had been subjected to allometric normalization.

As an alternate method to assess similarity in somatic and germline mutant phenotypes, we computed correlations in mean barcode values in each group (Figure 3C,D). We chose to perform correlations on barcode values because 1) germline mutants were larger than their somatic mutant counterparts (mean (SD); 23.67 (1.01) mm vs 27.90 (0.72) mm for plod2 somatic and germline controls, respectively; 23.11 (0.89) mm vs 25.77 (1.19) mm for bmpla somatic and germline controls, respectively), and 2) barcode values are computed by normalizing to controls, facilitating comparisons across different cohorts in which there are differences in body size. We computed R² values of 0.67 and 0.61 for plod2 and bmpla, respectively. Correlations between mean skeletal barcodes for germline (always n=3) and somatic mutants generally improved as the number of somatic barcodes included in the analysis increased (Figure 3E). Note that for Figure 3, because all p-values were calculated based on comparisons of mutants to their clutchmate controls, this also accounts for differences between control groups. Despite their greater inter- and intra-animal variability, these data indicate that somatic mutants can predict germline mutant phenotypes with high fidelity if averaged across a sufficiently large sample.

The global test and Moran’s I are effective at discerning somatic mutant phenotypes

The third aim of this study was to identify statistical methods effective at discerning somatic mutant phenotypes, which are distinct from germline mutant phenotypes in regard to their inter- and intra-animal variability. Previously, we showed that the global test (Goeman et al., 2004), a multivariate statistical test designed for data sets in which many features have been measured for the same subjects, was effective in detecting differences in collections of vertebral traces in germline mutants (Hur et al., 2017). Statistical power in multivariate tests is dependent on underlying distributions— e.g., whether there are small changes in a large number of measures, or large changes in a few measures. In somatic mutants, only a subset of vertebra may be affected, and these vertebrae can be different from animal-to-animal. Thus, the performance of the global test in discriminating somatic mutant populations, and how it compares to univariate approaches, is unknown. We tested the hypothesis that assessing vertebral patterns with the global test would provide greater sensitivity in distinguishing somatic mutants with variable phenotypic expressivity compared to (a) Mann-Whitney (M.-W.) of individual vertebrae, and (b) M.-W. tests of quantities averaged across all vertebrae. We chose the M.-W. test as a reference univariate test because, like the global test, the M.- W. test is non-parametric.

To test this, we performed Monte Carlo simulations (see STAR Methods). The universal scaling distribution defined in sp7:EGFP somatic mutants (Eq 1) was used to simulate different patterns of mosaicism and levels of phenotypic variability (1,000 simulations per analysis). For microscale loss-of-function clusters (Figure 4A), analyzing vertebrae 1:16 using the global test resulted in up to a 1.41-fold increase in sensitivity (fraction of times in which p<0.05 when comparing simulated mutant fish to WT fish) compared to using the M.-W. test using vertebra 2, and a 1.15-fold increase compared to the M.-W. test using quantities averaged across vertebrae 1:16 (Figure 4A’). Differences in testing procedure were dependent on how loss-of-function regions were spatially clustered. For instance, for macroscale loss-of-function clusters (Figure 4B), analyzing Cent.Vol in vertebrae 1:16 with the global test conferred up to a 3.65- and 1.21-fold increase in sensitivity compared to analyzing vertebra 2 and the mean of vertebrae 1:16 with the M.-W. test, respectively (Figure 4B’); noticeably higher compared to simulations using microscale clusters. We found that the relative benefits of the global test, compared to the univariate tests, became heightened as mutants become increasingly mosaic (i.e., less similar to germline mutants). Specifically, the sensitivity of the global test increased relative to the other tests with decreased values of lambda, the model parameter which parameterizes intra-animal variation (Figure 4C).

Figure 4. Analyses of vertebral patterns using the global test and Moran’s I are useful in discriminating somatic mutant phenotypes.

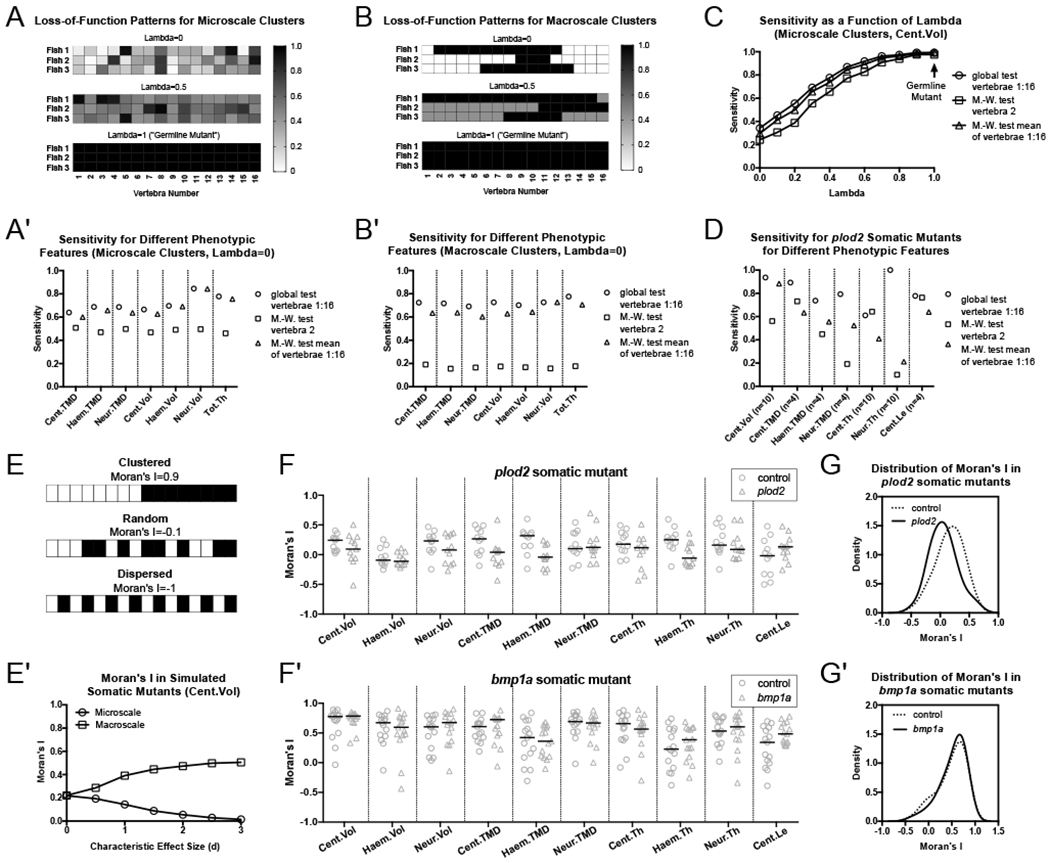
(A-C) Monte Carlo simulations of somatic vertebral patterns were analyzed for sensitivity in detecting differences in phenotypic measures. Representative mosaic patterns are shown for simulations of microscale (A) and macroscale (B) loss-of-function clusters. Values indicate extent of gene loss. Sensitivity of the global test is higher compared to univariate approaches for simulated mutants with microscale (A’) or macroscale (B’) loss-of-function clusters. (C) Sensitivity of the global test in detecting changes in centrum volume compared to univariate approaches for simulated mutants with microscale loss-of-function clusters and different degrees of intra-animal variability (parameterized by lambda). Improvement of the global test over univariate tests is heightened as mosaicism increases (i.e., as lambda goes to zero). (D) Bootstrap analysis using experimentally-derived data from plod2 somatic mutants. The global test out-performs M.-W. tests for 6 of the 7 statistically significant phenotypic measures detected for plod2 somatic mutants and is nearly as sensitive for the final measure. For details on bootstrap analysis, (e.g. use of n) see STAR Methods. (E) Schematic of Moran’s I for different simulated patterns of mosaicism. (E’) Moran’s I changes with characteristic effect size, d. Simulated microscale loss-of-function clusters decrease Moran’s I, whereas simulated macroscale clusters increase it. (F,F’) Moran’s I quantified for each of the 10 primary combinatorial measures in plod2 (F) and bmpla (F’) somatic mutants. (G,G’) Combined distributions of all quantities calculated for Moran’s I shown in panels F and F’. Moran’s I for plod2 mutants (G) shows a shift towards a random distribution compared to controls, while that of bmpla mutants (G’) does not.

Simulated mutants generally underestimate phenotypic variability in the real world, as the characteristic effect size is assumed to be identical across all vertebrae. Thus, we examined the performance of the global test with experimental phenotypic data. We performed non-parametric simulations using experimental data derived from plod2 somatic mutants (Figure 4D). Generally, sensitivity differences between the global test and univariate tests were exacerbated when analyzing experimentally-derived phenotypes from plod2 somatic mutants compared to simulated mutant phenotypes. This was particularly evident when examining sensitivity differences between the global test and the M.-W. test using averaged quantities, which were somewhat modest using simulated mutant phenotypes (1.15-1.21 fold increase in sensitivity), but more pronounced using experimentally-derived phenotypes from plod2 somatic mutants. For instance, across the seven measures in Figure 4D, the global test resulted in, on average, a 1.82-fold increase in sensitivity compared to the M.-W. test using averaged quantities. Taken together, our studies show that the global test is an effective test for detecting differences in collections of spatially varying phenotypes in somatic mutants. Further, they provide evidence that spinal phenomics increases sensitivity, with similar specificity, in discriminating somatic mutant populations, compared to analyzing single readouts.

Next, we explored statistical methods to discern the extent to which phenotypic expressivity in somatic mutants tended to be uniformly or focally dispersed throughout the skeleton, as such spatial phenotypic variation has the potential to encode biological information. For instance, phenotypic variability resembling a dosage curve has been previously hypothesized to occur when mutating a gene encoding a secreted factor, with different numbers of cells carrying the relevant mutation (Teboul et al., 2017). On the other hand, for genes that function cell-autonomously, phenotypic expressivity may be less uniform, and more closely resemble patterns of mosaicism at the cellular level. However, consensus approaches to discern spatial variability within phenomic data are lacking.

We explored the utility of Moran’s I, a measure of global spatial autocorrelation commonly employed for geostatistical analysis, for this purpose. Moran’s I usually ranges from approximately −1 to 1, and can be interpreted as the extent to which values are spatially clustered (positive), dispersed (negative), or random (zero) (Figure 4E). In Monte Carlo simulations, we found that microscale clusters resulted in Moran’s I tending to decrease, whereas macroscale clusters resulted in Moran’s I tending to increase (Figure 4E’).

We computed Moran’s I for 10 combinatorial measures in plod2 (Figure 4F) and bmpla (Figure 4F’) somatic mutants. When the distribution of Moran’s I was calculated across all 10 combinatorial measures, there was a marked shift in the center of the distribution toward I=0 for plod2 somatic mutants compared to controls (Figure 4G). In contrast, no obvious shift in distribution center was observed for Moran’s I in somatic mutants for bmpla (Figure 4G’). The global test revealed a significant difference (p=0.008) in the values of Moran’s I in plod2 somatic mutants compared to controls, but no significant difference (p=0.53) in bmpla somatic mutants compared to controls. Note that distributions for plod2 and bmpla control groups also appeared different, presumably due to normal clutch-to-clutch variability. Finally, we used Moran’s I to examine spatial variability of loss-of-fluorescence in sp7:EGFP somatic mutant larvae (Figure S6C). Somatic sp7:EGFP mutants exhibited increased Moran’s I, with the M.-W. test revealing a statistical (p=0.0480) difference between groups. Thus, while the patchy phenotypic expressivity in plod2 somatic mutants superficially resembles mosaicism in sp7:EGFP somatic mutants, we found differences in the specific nature of spatial variation in each group.

DISCUSSION

This study demonstrates how somatic mutations distribute in CRISPR-edited G0 zebrafish, how this mosaicism phenotypically manifests in the skeleton, and how to statistically discern such phenotypes within phenomic datasets.

We found that Eq 1 described loss-of-function cluster sizes in the skeletal tissues studied. Because this relation arises via contributions from clonal fragmentation and merger events rather than cell fates specified by developmental programs, the data collapse in our study is unlikely to be unique to skeletal tissues, as clonal fragmentation and merger events initiate early in the developing embryo (Rulands et al., 2018). In lineage tracing studies, Eq 1 has been found to fit clonal cluster size distributions in diverse contexts (e.g. development of zebrafish heart, mouse liver, and mouse pancreas) but not when clonal fragmentation and merger events are actively suppressed (e.g., mouse acinar cells) (Rulands et al., 2018). We expect similar conditionality to apply in regard to CRISPR-induced somatic mutations.

While our studies implicate clonal fragmentation and merger as an influential factor in mosaic pattern development, they do not imply that developmental programs are unimportant. In zebrafish, the centrum first ossifies through direct mineralization of the notochord sheath, which is then encased by intramembranous bone produced by somite-derived osteoblasts (Fleming et al., 2004). In the intervertebral growth center (IGC) model (Inohaya et al., 2007), osteoblasts on adjacent centra, as well as the arches they flank, are all descendants of the same intervertebral cells. The IGC model predicts that loss-of-fluorescence should be related in the centra of adjacent vertebra, as well as in the neural arches and centra of the same vertebral bodies—events we observed in individuals. In this context, developmental programs and clonal fragmentation and merger events may work in concert to influence mosaic patterns; while the latter primarily contributes to size distributions in loss-of-function clusters, both contribute to spatial distributions.

A general relationship describing loss-of-function cluster sizes in somatic animals may facilitate the detection and interpretation of spatially varying phenotypes commonly observed in G0 screens. In our own studies, Eq 1 enabled us to accurately model mosaicism in computer simulations and to make predictions on their phenotypic effects. These simulations enabled us to rigorously test the performance of the global test and univariate tests in discriminating somatic mutant populations, as well as estimate statistical power. They also enabled us to simulate how different patterns of mosaicism influence Moran’s I, and in turn, whether the nature of spatial phenotypic variation in plod2 and bmpla somatic mutants (as characterized by Moran’s I) could be traced to the pattern of LOF in sp7:EGFP fish during early development. Eq 1 may also be useful in analyzing non-skeletal tissues and in instances where estimates of cluster size distributions are needed, such as in therapeutic applications of CRISPR editing.

Lastly, we identify statistical methods to discern variable phenotypes in somatic mutants. In addition to finding that Moran’s I was useful to quantify spatial phenotypic variation, we also found that the global test was effective in discriminating collections of spatially variable phenotypes. The increased sensitivity of analyzing vertebral patterns with the global test, relative to univariate approaches, underscores the potential for phenomics to improve G0 screen productivity, and facilitates the study of genetic variants of smaller effect sizes. Notably, the global test can be used for multivariate phenotypes where spatial relationships are not specified (e.g., a panel of measures taken at the same anatomical site), and thus may be broadly useful for detecting differences in groups of measures between different populations.

STAR METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Claire Watson (cwalk1@uw.edu).

This study did not generate any new unique reagents.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Zebrafish rearing

All studies were performed on an approved protocol in accordance with the University of Washington Institutional Animal Care and Use Committee (IACUC). Embryos were spawned in group breeding tanks, and all fish were housed in plastic tanks on a commercial recirculating aquaculture system. Animals were kept on a 14:10 hour light:dark cycle in a facility maintained at 28^oC. Studies were conducted in mixed sex animals from either the wild-type AB strain or the transgenic sp7:EGFP (DeLaurier et al., 2010) background. Stocks of both strains were obtained from the Zebrafish International Resource Center (ZIRC, http://zebrafish.org). The AB and sp7:EGFP embryos used in this study were 1 and 3 generations removed from imported ZIRC stocks, respectively.

As we wanted to determine the feasibility of detecting subtle changes in the zebrafish skeleton, particular care was invested in maintaining genetic and environmental consistency between somatic mutants and their respective controls. Injected embryos and respective controls were progeny of the same breeding, and all embryos were collected prior to allocating into separate dishes for CRISPR-RNP or sham injections. Embryos used for injections for plod2 and bmpla cohorts did, however, come from different AB breeders (which were original ZIRC imports), possibly accounting for some of the clutch-to-clutch variability noted in the study. (Of note, the wild-type AB line at ZIRC is intentionally bred to maintain some genetic diversity and robustness.) After injection (with either a gene-specific guide RNA or sham for controls) embryos were maintained in separate dishes until transferring into polyculture media at 5 dpf. Initial polyculture media was prepared in bulk for all larvae (so rotifer density was equivalent between groups), and subsequently divided into tanks for each experimental group at a volume of 20 mL/fish. Initial polyculture tanks contained no more than 40 fish. Fish were counted daily, and rotifer supplements were added daily on a per fish basis to equalize feed content/fish. At 12 dpf fish were transferred to our recirculating system where they were kept in adjacent 2.8L tanks. At this stage, tank populations for fish used in this study were as follows: plod2 somatic (29 fish), plod2 sham controls (31 fish), bmpla somatic (two tanks, 29 and 30 fish), bmpla sham controls (29 fish). All fish were fed the GEMMA Micro diet (Skretting) daily, on a per fish basis, according to the schedule provided in Table S1 to maintain consistency in growth within an experimental cohort (e.g. plod2 somatic mutants and sham controls). At 30 dpf, fish densities were equalized between mutant and control tanks for each experimental cohort to account for differences in survival during the larval to juvenile transition. Equal housing densities were maintained until 90 dpf, when zebrafish were euthanized by immersion in ice water and either immediately scanned, or stored frozen at −20°C.

CRISPR-induced generation of somatic mutants

CRISPR mutagenesis was performed using the Alt-R^™ CRISPR-Cas9 System from Integrated DNA Technologies (IDT). Target sequences were identified using the web-based tool, CHOPCHOP (Labun et al., 2016; Montague et al., 2014), were designed using the GRCz10 reference genome (http://www.ensembl.org) and are as follows (PAM sequence in lowercase letters): GATGGCCGCGTCGATTCTGGagg for sp7, GACCAGGATGGGCACCACCCcgg for EGFP, AAGTATCCGTCTGTACGCAGtgg for plod2, and ATACGTGGGCCGCAGAGGAGggg for bmp1a. CRISPR-Cas9 crRNAs (gene-specific) and tracrRNAs (generic) were chemically synthesized and ordered from IDT. For each gene, gRNAs were generated by mixing the crRNA and tracrRNA in a 1:1 ratio, diluting to 20 μM in nuclease-free duplex buffer (IDT), incubating at 95^oC for 5 minutes and cooling on ice. Cas9 protein (20 μM, NEB) was mixed in a 1:1 ratio with the gRNA complex and incubated for 5-10 minutes at room temperate to produce the Cas9:gRNA RNP complex at a final concentration of 10 μM. Sham complexes were injected into clutchmates as controls, these contained Cas9:tracrRNA at final concentration of 10 μM. RNPs were loaded into pre-pulled microcapillary needles (Tritech Research), calibrated, and 2 nL RNP complexes were injected into the yolk of 1- to 4-cell stage embryos.

METHOD DETAILS

Sequencing and mutation efficiency analysis

Between 24 and 96 hpf, a few embryos from each injection group were pooled, DNA extracted, Sanger sequenced (GenScript), and screened for mutagenesis efficiency using the TIDE webtool (Brinkman et al., 2014). Individual animals were also screened for mutagenesis using whole larvae at 12 dpf to predict mutation efficiencies using the TIDE webtool, and to check for clonal fitness effects. These data are reported as intra-animal efficiencies in the main text. Furthermore, without exception for bmpla and plod2, indel efficiencies were limited by the R² value in the TIDE analysis, suggesting that these may represent the lower boundary of CRISPR-induced indels for all samples and/or target sites.

MicroCT scanning

MicroCT scanning was performed using a vivaCT40 (Scanco Medical, Switzerland). Scans with 21 pm isotropic voxel resolution were acquired using the following settings: 55kVp, 145mA, 1024 samples, 500proj/180 ° 200 ms integration time. DICOM files of individual fish were generated using Scanco software, and analyzed using FishCuT software (Hur et al., 2017, 2018). Two fish were scanned simultaneously in each acquisition. Preserved tissue from plod2 and bmpla germline mutants were used for analysis in this study; a description of these lines is described in (Hur et al., 2017).

Fluorescent imaging

Between 10-12dpf, zebrafish of the transgenic sp7:EGFP (DeLaurier et al., 2010) background were anesthetized in MS-222 and mounted into borosilicate glass capillaries using 0.75% low melt-agarose (Bio-Rad) diluted in system water containing 0.01% MS- 222. Capillaries were set on a custom 3-D printed holder to aid manipulation and rapid orientation of the specimen. Dual-channel (GFP, excitation 450-490, emission 500-550; DAPI, excitation 335-383, emission 420-470) images were collected on a high-content fluorescent microscopy system (Zeiss Axio Imager M2, constant exposure settings for all experiments) using a 2.5x objective (EC Plan-Neofluar 2.5x/0.075). For each fish, a composite image stack (usually 3/1 images in the x/y directions; and optimized to 3070 pm slice intervals in the z direction across the entire region of interest, usually about 9 slices; all at 2.58 pm/pixel) was acquired in mediolateral and anteroposterior views. Maximum intensity projections were generated from image stacks in Fiji (Schindelin et al., 2012) for analysis.

Monte Carlo simulations

We previously characterized multivariate distributions for select FishCuT measures that exhibit evidence of multivariate normality (Hur et al., 2017). Using parameter estimates previously derived for such measures, we constructed wild-type and mutant distributions using methods described in Supplemental Information. Mutant phenotypic distributions were parameterized by several variables: d (characteristic effect size), λ (extent of intra-animal variation in phenotypic expressivity; 1=0 is most variable, λ=1 is least variable), and p_i (a ‘loss-of-function vector’ whose values range from 0 to 1, and which encodes the spatial pattern of loss-of-function in each vertebra). We examined two classes of loss-of-function vectors. The first class, p_i^microscale, simulated phenotypes arising from microscale loss-of-function clusters. The second class, p_i^macroscale, simulated macroscale loss-of-function clusters. When λ=1, mutant distributions were identical for both microscale and macroscale clusters; because loss-of-function was uniform in this case, we refer to simulated mutants with λ=1 as “germline mutants”. For simulations, unless otherwise noted, we assumed a characteristic effect size of d=2, and a sample size of n=10, or a characteristic effect size of d=2.5, and a sample size of n=15. Similar methods were used for Monte Carlo simulations for Moran’s I.

We previously characterized multivariate distributions for select FishCuT measures that exhibit evidence of multivariate normality (Hur et al., 2017). Using parameter estimates previously derived for such measures, we constructed two distributions. The wild-type (WT) distribution, y_i^WT, consisted of a multivariate normal distribution using means μ_i^WT (which denotes the mean value in vertebra i in WT fish) and covariances ∏_ij^WT (which denotes the covariance between vertebra i and vertebra j in WT fish) (Hur et al., 2017). The mutant distribution was computed as

$${{\mathrm{y}}_{\mathrm{i}}}^{\text{mutant}}={{\mathrm{y}}_{\mathrm{i}}}^{\mathrm{WT}}+{\mathrm{d}}^{\ast }{{\sigma }_{\mathrm{i}}}^{\mathrm{WT}}[(1-\lambda ){\mathrm{p}}_{\mathrm{i}}+\lambda ]$$ Eq 2

where d is the characteristic effect size (Hur et al., 2017), σ_i^WT is the standard deviation in vertebra i in WT fish, λ is a parameter controlling intra-animal variability in loss-of-function that ranges from zero to one, and p_i is a vector of values ranging from zero to one. When λ=0, Eq 2 simplifies to y_i^mutant = y_i^WT + d*σ_i^WT*p_i. Here, it can be seen that phenotypic severity varies from vertebra-to-vertebra, depending on values of p_i. We termed p_i the ‘loss-of-function vector’ because it encodes the degree of phenotypic severity in each vertebra.

We constructed two classes of loss-of-function vectors. The first class, p_i^microscale, simulated phenotypes arising from microscale loss-of-function clusters. In this case, values of p_i^microscale were drawn from the distribution of Eq 1, assuming <x>=0.5 vertebrae. The second class, p_i^macroscale, simulated macroscale loss-of-function clusters. Here, each mutant possessed a single macroscale loss-of-function cluster whose size was drawn from the distribution of Eq 1. For this, we assumed <x>=8 vertebrae, representing a moderately variable phenotype where half of the vertebrae, on average, are affected. For this class, p_i was specified as a binary vector, with the center of the macroscale cluster drawn from a uniform distribution. In both cases, gene action was assumed to be cell autonomous, in that phenotypic severity in each vertebra was proportional to the extent of loss-of-function within it. Note that when λ=1, Eq 2 simplifies to y_i^mutant = y_i^WT + d*σ_i^WT, and is identical for both microscale and macroscale clusters. For simulations, unless otherwise noted, we assumed a characteristic effect size of d=2, and a sample size of n=10, or a characteristic effect size of d=2.5, and a sample size of n=15. All Monte Carlo simulations were performed in R (Team, 2015). For all simulations, specificity (1 - the fraction of times in which p<0.05 when comparing WT to WT fish) ranged between 0.94-0.97, closely bracketing the expected value of 0.95.

For simulations in Figure 4D, we used FishCuT data from the plod2 somatic mutant and sibling controls to perform bootstrap simulations in which control and somatic mutant phenotypic profiles were randomly sampled (with replacement) to form groups of biological replicates. After these groups of phenotypic profiles were formed, testing procedures proceeded identically to those in our other Monte Carlo analyses (1,000 simulations per analysis). For initial simulations, n=10 was chosen. For traits with larger effect sizes in the plod2 experimental cohort, n=10 resulted in saturation (i.e. sensitivity=1 for all tests). In these instances, sample size was modified to n=4.

Moran’s I

Similar methods to those above were used for Monte Carlo simulations for Moran’s I. Moran’s I was computed using the Moran.I function in the ape package in R (Team, 2015). The following weight matrix Wij was used:

Wij = 1 if abs(i-j)=1, else

Wij = 0

where i and j denote the i^th and j^th vertebra. We computed Moran’s I for each vertebral trace as I(d_i), where d_i = [y_i−μ_i^WT]/σ_i^WT, and y_i is a vertebral trace drawn from the distribution of Eq 2.

QUANTIFICATION AND STATISTICAL ANALYSIS

Fluorescent cluster analysis

Max intensity projected images of each sp7:EGFP somatic mutant larvae were analyzed for microscale and macroscale clusters by tracing loss-of-fluorescence regions along both the dorsal and ventral sides of the developing notochord in Fiji (Schindelin et al., 2012). Loss-of-fluorescence was subjective to user interpretation, but can be generally defined as a region with no detectable fluorescence above background, and/or markedly reduced signal compared to adjacent bony structures. Multiple users quantified loss-of-fluorescence in the centra, to account for individual differences in thresholding, and generated comparable datasets (Figure 1K and Figure S2C). A similar approach was used in the quantification of loss-of-fluorescence clusters in the craniofacial skeleton.

Of note, grouped breeding of this line yields ~95% positive “glower” fish (when screened at 24hpf) suggesting breeders and G0 crispants from this line are comprised of at least 50% of fish homozygous for the transgene. Notably, Eq 1 is expected to hold for clones representing mono- or multi-allelic loss, and thus our use of animals with mixed transgenic zygosities is not expected to influence our results. G0 crispants used for assessment of clonal dynamics were excluded if no distinct fluorescence could be detected above background during imaging. No attempt was made to quantify relative levels of fluorescence between fish.

MicroCT image analysis

MicroCT scanned images of each fish were converted to DICOM files and analyzed using FishCuT software, the following description of which is adapted from (Hur et al., 2017). FishCuT analysis proceeds in 6 stages:

1. Preprocessing: Images were rotated along the anteroposterior axis to orient specimens in an upright position.

2. Thresholding: Thresholds for each animal were calculated using a semi-automatic approach. To filter out background, an ROI was drawn from a maximum intensity projection to outlining the entire fish. Values outside the ROI were set to 0, and the threshold was calculated using the IsoData algorithm in Fiji (Schindelin et al., 2012).

3. Vertebral segmentation: Planes of separation between vertebra were defined by drawing a ‘separation line’ between each pair of centra. The software sets voxels within a plane defined by the separation line as 0, connected components are computed, and connected component labels are tallied for each of the two volumes separated by the plane. If the connected components with the plurality of votes in the two regions are distinct, the algorithm stops; otherwise, the separation line is extended, and the process repeated until all vertebrae are segmented. In cases where two distinct vertebrae were not automatically segmented by FishCuT software after this step (usually when severe vertebral malformations cause a fusion of relevant bones), the manual cutting tool was used to sever connections between skeletal elements.

4. Vertebral assignment: Vertebrae 1:16 were assigned by manually clicking on each vertebra, resulting in a color-coded map of connected components for each vertebra.

5. Intra-vertebral segmentation: Neural arches, centra, and haemal arches were segmented for each vertebrae by FishCut. Segmentations were verified from a color- coded output and manually adjusted as necessary.

6. Calculation of measures: FishCuT software computed the following measures as herein described. Local thickness is computed using the Local Thickness plugin (Dougherty and Kunzelmann, 2007) in Fiji (Schindelin et al., 2012). Volume and surface area were computed using the nnz and bwperim functions in MATLAB. TMD was computed using the following relationship: mgHA/cm3 = (x/4096)*slope + intercept, where x = the pixel intensity in the DICOM image, and the values for slope (281.706) and intercept (−195.402) were acquired during scanner calibration. Centrum length is calculated as the distance between planes separating adjacent vertebral bodies. Variation (indicated as “.sd”) was computed for measures dependent on mean values within a skeletal element and were calculated as the standard deviation in either voxel TMD (TMD.sd) or local thickness (Th.sd).

Thus, the following key describes the 25 combinatorial measures quantified for each vertebrae: centrum surface area (Cent.SA), centrum thickness (Cent.Th), variation in centrum thickness (Cent.Th.sd), centrum tissue mineral density (Cent.TMD), variation in centrum tissue mineral density (Cent.TMD.sd), centrum length (Cent.Le), haemal arch surface area (Haem.SA), haemal arch thickness (Haem.Th), variation in haemal arch thickness (Haem.Th.sd), haemal arch tissue mineral density (Haem.TMD), variation in haemal arch tissue mineral density (Haem.TMD.sd), neural arch surface area (Neur.SA), neural arch thickness (Neur.Th), variation in neural arch thickness (Neur.Th.sd), neural arch tissue mineral density (Neur.TMD), variation in neural arch tissue mineral density (Neur.TMD.sd), vertebral surface area (Vert.SA), vertebral thickness (Vert.Th), variation in vertebral thickness (Vert.Th.sd), vertebral tissue mineral density (Vert.TMD), and variation in vertebral tissue mineral density (Vert.TMD.sd). Vertebral measures (Vert) represent the total vertebral body, with all three elements (centrum, haemal arch, neural arch) combined.

Standard scores were computed to generate skeletal barcodes, and were defined as the difference between the value of the feature in the individual fish and the mean value of the feature across all vertebrae in the control population, divided by the standard deviation of the feature across all vertebrae in the control population. Thus, a single barcode represents the spectrum of values for each feature for an individual fish, compared to the entire control population for that fish. Mean barcodes were computed as the average value for each feature among two or more skeletal barcodes. Correlations of values in mean barcodes were plotted and R² values computed in Prism software (GraphPad).

Statistical approach

For mutant fish with a known axial skeletal phenotype (bmpla and plod2 somatic mutants), results are reported from a single experiment; for characterization of mosaicism in sp7:EGFP fish, results are reported from two experiments. Each biological replicate represents one technical replicate. Empirical data are shown as either distributions of individual measurements, or are reported as mean ± SEM. Group sizes (n) are reported in the Figure panels themselves or in respective legends. Mild and extreme outliers were identified only for descriptive purposes; all data were included in statistical analyses. All statistical analyses were performed in R (Team, 2015), with the following exceptions; R² values of mean barcode correlations, and Mann-Whitney test of somatic standard lengths; which were performed in GraphPad Prism. In general, the Mann-Whitney test was used for univariate analyses between two groups. Dysmorphic phenotypes were analyzed using a test for equal proportions.

Multivariate analysis using the global test was performed using the globaltest package (Goeman et al., 2004). p<0.05 was considered statistically significant in all cases. To reduce Type I error, we minimized the number of hypotheses tested per mutant. We did this in two ways. First, we focused on 10 out of 25 combinatorial measures, selected based on our previous studies of plod2 and bmpla germline mutants. Second, rather than performing univariate tests on each measure at each location, we performed global tests using spinal patterns of each measure. This reduced the number of hypotheses tested per mutant from 160 (16 vertebrae x 10 measures = 160 measures total) to 10 total. Reported p-values for these 10 measures are uncorrected. This is consistent with common practice when reporting a similar number of microCT measures in the literature, where a minimal set of 8 measures (4 for cortical, and 4 for trabecular) are recommended for murine bone (Bouxsein et al., 2010).

DATA AND CODE AVAILABILITY

All datasets generated and analyzed during this study are included in the manuscript.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Bacterial and Virus Strains
Biological Samples
Chemicals, Peptides, and Recombinant Proteins
20 uM Cas9-NLS	NEB	Cat #: M0646T
Alt-R CRISPR-Cas9 tracrRNA	IDT	Cat #: 1072532
Nuclease-Free Duplex Buffer	IDT	Cat # 11-01-03-01
Phenol Red	Sigma-Aldrich	Cat #: P0290
MS-222	Sigma-Aldrich	Cat #: E10521
Low-melt agarose	Bio-Rad	Cat #: 161-3111
Critical Commercial Assays
GeneJET Gel Extraction Kit	Thermo Scientific	Cat #: K0691
Deposited Data
Experimental Models: Cell Lines
Experimental Models: Organisms/Strains
Zebrafish: AB	ZIRC	ZFIN ID: ZDB-GENO-960809-7
Zebrafish: Tg(sp7:EGFP)b1212	ZIRC	ZFIN ID: ZDB-ALT-100402-1
Oligonucleotides
Protospacer sequence for crRNA design: plod2, AAGTATCCGTCTGTACGCAG	IDT	Alt-R® CRISPR-Cas9 crRNA, 2 nmol, custom design
Protospacer sequence for crRNA design: bmp1a, ATACGTGGGCCGCAGAGGAG	IDT	Alt-R® CRISPR-Cas9 crRNA, 2 nmol, custom design
Protospacer sequence for crRNA design: sp7:EGFP, GATGGCCGCGTCGATTCTGG	IDT	Alt-R® CRISPR-Cas9 crRNA, 2 nmol, custom design
sp7 F: ACCCCAAGAATCAAACCCCA sp7 R: AGTTAACATGCAGTAATCATCGCA	Sigma-Aldrich	Custom oligo
plod2 F: ACTGGAAAGCAGTGGACAGG plod2 R: AGGGTTGAAGACGGGGTAGA	Sigma-Aldrich	Custom oligo
bmp1a F: AGTTGGACGATATTTACCCTGGT bmp1a R: CGCACCCCCAGAGAAAACC	Sigma-Aldrich	Custom oligo
Recombinant DNA
Software and Algorithms
Fiji	Schindelin et al., 2012	https://imagej.net/Fiji
Prism 6 and 7	GraphPad	https://www.graphpad.com/
R	R Core Team, 2016	https://www.R-project.org/
FishCuT	Hur et al., 2017	https://github.com/elifesciences-publications/FishCuT
MATLAB	MathWorks	https://www.mathworks.com/products/matlab.html
Other

Highlights:

• #1Clonal clusters arising from CRISPR editing follow a universal size distribution
• #2Distinct phenotypic patterns arise from mosaic gene loss
• #3Large-scale phenotyping heightens sensitivity in detecting somatic mutant populations