scBatch: batch-effect correction of RNA-seq data through sample distance matrix adjustment

Abstract

Motivation

Batch effect is a frequent challenge in deep sequencing data analysis that can lead to misleading conclusions. Existing methods do not correct batch effects satisfactorily, especially with single-cell RNA sequencing (RNA-seq) data.

Results

We present scBatch, a numerical algorithm for batch-effect correction on bulk and single-cell RNA-seq data with emphasis on improving both clustering and gene differential expression analysis. scBatch is not restricted by assumptions on the mechanism of batch-effect generation. As shown in simulations and real data analyses, scBatch outperforms benchmark batch-effect correction methods.

Availability and implementation

The R package is available at github.com/tengfei-emory/scBatch. The code to generate results and figures in this article is available at github.com/tengfei-emory/scBatch-paper-scripts.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

In the recent decade, RNA sequencing (RNA-seq) has become a major tool for transcriptomics. Due to the limitation of sequencing technology and sample preparations, technical variations exist among reads from different batches of experiments, such as varying sequencing depth and amplification bias (Hicks et al., 2018; Tung et al., 2017). These unwanted technical variations, or batch effects, affect both mean and variance of the distribution of gene expression in count matrices obtained from different experiment batches, which eventually leads to misleading scientific findings in downstream data analysis (Hicks et al., 2018). Typically, batch effects can alter the sample patterns, causing false interpretations about cell lineage and heterogeneity. If the goal is to detect differential expression (DE) genes, the analysis can suffer loss of statistical power and/or bias. In a broader sense, a number of factors can be considered as batches, including different laboratories, different sample preparation batches, different sequencing batches, or even different subjects, as single cells collected from different subjects can exhibit different characteristics based on different sample handling and the subjects’ personal genetic background and exposures.

While the severity of batch effects varies in different datasets, batch-effect corrections were shown to be effective in general. For instance, batch-effect correction on the ENCODE human and mouse tissues bulk RNA-seq data (Lin et al., 2014), where the batch effects were intense, obtained largely different and more sensible tissue clustering results compared to before correction (Gilad and Mizrahi-Man, 2015). In other datasets, batch effects are often more subtle. In such cases, although the true biological pattern is maintained to some extent, weak to moderate batch effects can still be observed. Hicks et al. (2018) discussed the coexistence of biological signal and technical variation, which may still compromise the downstream analysis. The correction of the batch effects can yield better clustering results (Fei et al., 2018) on data with weak to moderate batch effects that were unobvious from dimension reduction plots (Muraro et al., 2016; Usoskin et al., 2015). These previous efforts argue for the inclusion of batch-effect corrections as a routine procedure in data preparation.

Since the microarray era, efforts have been made to correct batch effects. One prevalent strategy for batch-effect correction is to establish linear models of gene expression with biological groups (e.g. disease and control groups, cell types) and confounding effects (e.g. batch labels, patient IDs) as covariates. Johnson et al. (2007) proposed an empirical Bayes algorithm, ComBat, to normalize the data by removing additive and multiplicative batch effects. As a widely applied tool for DE gene analysis, package limma also incorporates batch-effect removal into its linear model framework (Ritchie et al., 2015). Recently, an improved version of ComBat, ComBat-seq, was developed to correct batch effects in RNA-seq data by negative binomial regression (Zhang et al., 2020). Researchers also utilized the technology of control probes in microarray (Yang, 2006) and spike-in genes in RNA-seq (Jiang et al., 2011) to find and correct unknown batch effects in mircoarray (Gagnon-Bartsch and Speed, 2012) and RNA-seq data (Leek, 2014; Risso et al., 2014). The family of linear model-based methods, however, requires the knowledge of biological groups for each observation, which is hardly feasible, if not impossible, in single-cell RNA-seq (scRNA-seq) data due to the high heterogeneity of cells (Luo and Wei, 2019).

The aforementioned limitation of linear models motivated the recent development of alternative batch-effect correction methods for scRNA-seq data. Kiselev et al. (2017) introduced the consensus clustering method SC3 to conduct clustering analysis based on multiple distance metrics; Shaham et al. (2017) applied deep-learning technique in the software BatchEffectRemoval; Chen and Zhou (2017) proposed a linear model-based method, scPLS, that utilizes control-gene information and is insensitive to the influence from unknown biological groups; we developed a robust non-parametric approach, named QuantNorm, to correct sample distance matrix by quantile normalization (Fei et al., 2018); Haghverdi et al. (2018) utilized the mutual nearest neighbor (MNN) relationships among samples from different batches to establish the MNN correction scheme. As observed from the results in Kiselev et al. (2017), Fei et al. (2018) and Haghverdi et al. (2018), the recently developed methods improved clustering and dimension reduction performances, compared to linear model-based approaches.

While there is a rich set of choices of batch-effect correction methods, we still notice space for improvement. The scPLS method (Chen and Zhou, 2017) requires the presence of spike-in genes, which is not applicable to all datasets; SC3 (Kiselev et al., 2017) and QuantNorm (Fei et al., 2018) only return distance matrices, thus not supporting downstream DE analysis; MNN (Haghverdi et al., 2018) assumes that the direction of batch effects being orthogonal to the direction of biological differences, which may be strong if the batch effects involve not only shifting and rescaling but also rotating. In addition, DE detection appears not to be the emphasis of recent methods evaluation. Chen and Zhou (2017), Kiselev et al. (2017) and Fei et al. (2018) only evaluated the clustering performances. Although Haghverdi et al. (2018) conducted DE tests, the user manual (https://bioconductor.org/packages/3.8/workflows/vignettes/simpleSingle

Cell/inst/doc/work-5-mnn.html) of the corresponding bioconductor function, mnnCorrect, recommends not using the corrected count matrix for DE analysis with considerations on manipulated data scales and altered mean-variance relationship.

Motivated by the challenges faced in batch-effect correction, in this study, we develop a new method, scBatch, to utilize the corrected sample distance matrix to further correct the count matrix. Specifically, we seek a linear transformation to the count matrix, such that the Pearson correlation matrix of the transformed matrix approximates the corrected correlation matrix obtained from QuantNorm. QuantNorm is a non-parametric method that can adjust for non-linear batch effects in the sample patterns, which is feasible as the sample distance matrix is limited in size. However pursuing non-linear transformation in the original count matrix makes the search space too large, which can cause spurious solutions. Thus, in this work, we seek a linear transformation to the original count matrix, with the goal of approximating the non-linear correction in the sample distance matrix while keeping the method robust. For this purpose, we propose a random block coordinate descent algorithm to conduct linear transformation on the p (genes) $\times n$ (samples) count matrix. The resulting corrected count matrix inherits the advantages of QuantNorm, such as enhanced clustering results and decreased outlier influence on sample pattern. Simulation studies demonstrate that in terms of DE gene detection, our method corrects the count matrix better compared to multiple batch correct or normalization schemes, with consistently higher adjusted Rand index (ARI) and relatively better area under the receiver operating characteristic curve (AUC) and area under the precision-recall curve (PR-AUC). In real data analyses, the proposed method also shows strong performances in clustering and DE detection in a bulk RNA-seq dataset (Lin et al., 2014) and three scRNA-seq datasets (Kim et al., 2015; Usoskin et al., 2015; Xin et al., 2016).

2 Materials and methods

The scBatch method considers a study design scenario where the cell type or disease status composition is not severely confounded with batch, i.e. different cell subtypes or disease status are roughly evenly distributed among the batches. This balanced study design scheme has been recommended (Hicks et al., 2018) and widely adopted because it helps to avoid bias caused by confounding with batch. Under this assumption, although the batch effect may interrupt the overall data pattern, the data pattern within each batch should share similar characteristics, including similar quantile distributions in different batch blocks in the sample distance matrix. The above study design assumption has been justified in our previous study (Fei et al., 2018), which demonstrated solid-clustering performances of QuantNorm on two scRNA-seq datasets (Muraro et al., 2016; Usoskin et al., 2015) with relatively balanced study design. It is worth noting that there is a reasonable variation of the batch-level cell type proportion in the two tested datasets, further justifying the robustness of QuantNorm correction.

Figure 1 summarizes the workflow of scBatch. Given a count matrix X and its Pearson correlation matrix, we first utilize QuantNorm to obtain the corrected sample Pearson correlation matrix D. Then, X and D are input to the proposed algorithm to seek the weight matrix W, such that the Pearson correlation matrix of the linear transformation X × W approximates D. After the algorithm converges, the linear-transformed count matrix $Y=X\times W$ is output as the corrected count matrix that inherits the corrected sample pattern in D. Note that, the resulting linear transformation indeed approximates a non-linear correction of sample pattern. Although more complex models can be used to achieve non-linear transformation, we believe linear transformation can avoid over-correction while still achieving good results.

Fig. 1.

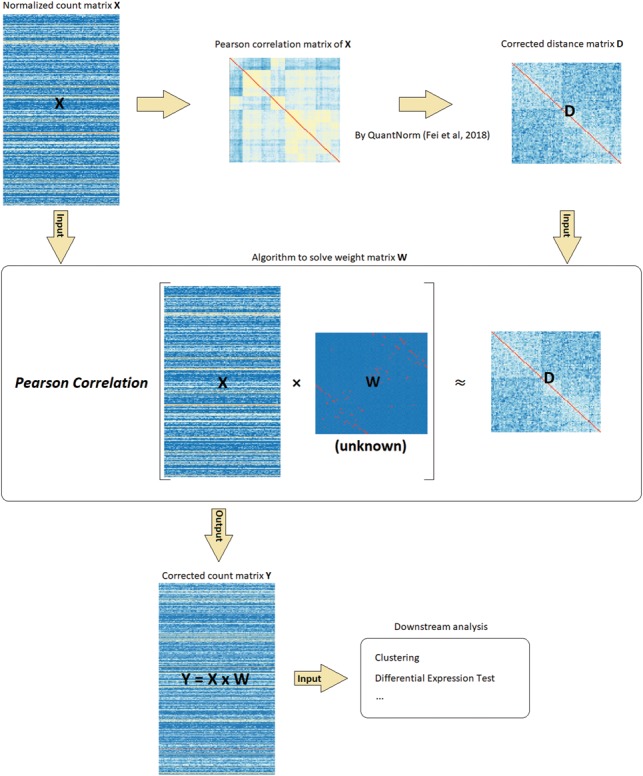
Overview of scBatch workflow. For the preprocessed count matrix X, the Pearson correlation matrix is corrected by QuantNorm to obtain a reference sample distance matrix D. Then the main algorithm is utilized to search for the weight matrix W to achieve the objective that the Pearson correlation of X × W is close to D. The corrected count matrix $Y=X\times W$ inherits the sample pattern information from D, which can be used for downstream analyses

2.1 Main algorithm

Problem setup. The count matrix $X_{p\times n}$ with p genes and n cells, in which the n cells fall into multiple batches, is subject to batch effects. Based on the Pearson correlation matrix of X, a corrected n × n correlation matrix D with improved sample similarities is obtained using the distance matrix correction algorithm QuantNorm (Fei et al., 2018). Given D, the objective is to solve for an optimal n × n weight matrix W such that the Pearson correlation of the linear-transformed count matrix Y = XW approximates the sample pattern in D. The transformed count matrix Y can then be used in downstream analyses. We note that similar to other methods, the resulting matrix may no longer be composed of non-negative integers.

Least squares loss function. In order to solve W, we propose to minimize the following least squares loss function:

$$L(W)=\frac{1}{2}\left|\right|D_Y-D|{|}_F^2=\frac{1}{2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n|}}{D}_Y{}_{ij}-D_{ij}{|}^2,$$ (1)

where D_Y is the Pearson correlation matrix of Y, $\left|\right|·|{|}_F$ is the Frobenius norm and A_ij denotes the (i, j) entry of matrix A. Thus, the optimized weight matrix W_opt satisfies $W_{\mathit{opt}}={\text{argmin}}_{W}L(W)$ and the corrected count matrix is Y_opt = XW_opt.

Gradient of the loss function. By chain rule, the gradient of the loss function L(W) is:

$$\frac{\partial }{\partial W}L(W)={(\frac{\partial }{\partial W}{D}_Y)}^T(D_Y-D).$$

By definition, the i, j entry of D_Y satisfies:

$${\left\{D_Y\right\}}_{ij}=\frac{{(X{W}_i)}^T{(I_p-\frac{1}{p}{1}_p{1}_p^T)}^{2}X{W}_j}{{\prod }_{k\in \{i,j\}}\sqrt{{(X{W}_k)}^T{(I_p-\frac{1}{p}{1}_p{1}_p^T)}^{2}X{W}_k}},$$

where W_i is the ith column of W, I_p is the p × p identity matrix and $1_p$ is the $p\times 1$ vector with all entries =1. As can be observed, $\frac{\partial }{\partial W}{D}_Y$ is a fourth-rank tensor in n-dimensional space. Thus, the gradient of the loss function L(Y), which is the product of $\frac{\partial }{\partial W}{D}_Y$ and the n × n matrix $(D_Y-D)$, is also a n × n matrix.

Although the scale of computation appears large, we derived an equivalent but more economic approach to compute the gradient in practice. Since ${\left\{D_Y\right\}}_{ij}$ involves only two columns from W, the tensor $\frac{\partial }{\partial W}{D}_Y$ is sparse so that all its entries can be saved in a third-rank tensor in n-dimensional space. Let A_k denotes the kth column of matrix A. Considering the gradient performance and practical computing, moreover, we further decompose the calculation into column-wise gradients $\frac{\partial }{\partial W_k}{D}_Y,k=1,\dots ,n$, which are n × n matrices. Using column-wise gradients as the unit, both coordinate gradient descent (Wright, 2015) and standard gradient descent can be easily implemented.

Denote $C=X^T{(I_p-\frac{1}{p}{1}_p{1}_p^T)}^{2}X$. By some algebra, the column-wise gradient $\frac{\partial }{\partial W_k}L(W)$ satisfies:

$$\begin{array}{l}\frac{\partial }{\partial W_k}L(W)={(\frac{\partial }{\partial W_k}{D}_Y)}^T\{D_Y{}_k-D_k\}\\ +\text{trace}[{(\frac{\partial }{\partial W_k}{D}_Y)}^T\{D_Y-D\}]e_k,\end{array}$$

where ${\mathbf{e}}_{\mathit{k}}$ is a $n\times 1$ vector in which the k entry is equal to 1 and others are equal to 0, and

$$\begin{array}{c}\frac{\partial }{\partial W_k}{D}_Y=[\frac{CW}{{(W_k^{T}C{W}_k)}^{1/2}}-\frac{C{W}_k{(W^{T}C{W}_k)}^T}{{(W_k^{T}C{W}_k)}^{3/2}}]\\ \odot [{\{1_n\otimes \text{diag}{(W^{T}CW)}^{°1/2}\}}^{°-1}],\end{array}$$

where $\odot ,°$, respectively, represents Hadamard (elementwise) product and power, and ⊗ represents outer product.

Algorithm 1.

Random block coordinate descent algorithm.

 Input: raw count matrix $X\in {\mathbb{R}}^{p\times n}$, reference distance matrix $D\in {\mathbb{R}}^{n\times n}$, initial weight matrix $W\in {\mathbb{R}}^{n\times n}$, group number $m\in [1,n]$, step size $ϵ\in {\mathbb{R}}^{+}$, tolerance $\mathit{tol}\in (0,ϵ)$, function L returning loss function and column-wise gradients.

  $[p,n]$ = dim(X)

 while $ϵ>\mathit{tol}$ do

  group = sample(1: m, size=n, replace=T)

  for i = 1, 2,…, max(group) do

   $W_0=W$

    $\mathit{idx}=\mathit{group}==i$

    $L,dL=L(W,\mathit{idx})$

    $W=W-ϵ.\times dL$

    $L_{\mathit{new}}=L(W)$

   if $L_{\mathit{new}}\ge L$ then

    $ϵ=0.5ϵ$

     W = W₀

   else

    $ϵ=1.5ϵ$

   end if

  end for

 end while

  Y = X × W

 Output: Y.

Random block coordinate descent algorithm. We adapt a flexible gradient descent algorithm (Algorithm 1). In each iteration, the algorithm first randomly partitions n subjects into m groups. Then, gradient descent is sequentially conducted from group 1 to group m to update the group-specific columns in W. That is, the subjects are randomly partitioned in m group blocks in each iteration to improve the robustness of gradient descent. Note the number of groups m can be customized as any integer from 1 to sample size n. When m = 1, the algorithm is equivalent to the traditional gradient descent algorithm; when m = n, the algorithm is equivalent to the coordinate descent algorithm (Wright, 2015). The flexibility alleviated both the long running time of coordinate gradient descent algorithm (Wright, 2015) and the excessive use of memory of gradient descent algorithm. In order to dynamically adjust the learning rate, we utilized Armijo line search (Armijo, 1966). The algorithm is stopped when the step size decreases below a threshold tol, indicating the approximation of a local minimum. We then applied batch-wise standardization after obtaining the corrected count matrix. The algorithm is implemented by RcppArmadillo (Eddelbuettel and Sanderson, 2014) in R package scBatch, which is available at https://github.com/tengfei-emory/scBatch.

2.2 Simulation design

We applied Bioconductor package PROPER (Wu et al., 2015) for simulation. In each dataset, gene expression counts for 20 000 genes were generated for six cell types in three batches. Specifically, three cell type pairs with randomly generated DE genes were generated to obtain the six cell types, where the proportion of DE gene is fixed as 0.05. The randomly generated DE genes for the three pairs were later used as gold standard to evaluate the performances of DE gene detection. In order to make the characteristics of cell proportions of simulated data close to a real scRNA-seq data, we varied the cell type proportions across the batches. Specifically, we first generated batches with systematic cell proportion differences, using six cell types with the proportion of 1:3:1:1:1:6, 3:10:3:4:3:13 and 6:17:7:8:6:28, respectively, for the three batches. Then, for every batch, we randomly drew cells based on the proportions, such that random variation in cell sampling also factor into the data. As a result, the cell proportions vary across different batches.

To generate batch effects, we considered two aspects. First, the log-scaled baseline gene expression level (lexp) for each gene was perturbed in each batch by a random uniformly distributed variable. Second, the log-scaled over-dispersion parameter (lOD) for each gene varied in each batch. This way, the batch effects were gene-specific, a more realistic and more challenging scenario than the naive batch effects having the same effect for all genes.

We considered three sample size configurations (270 cells, 540 cells and 1080 cells). For batch-effect parameter configurations, lexp was perturbed by a Uniform(−3,3) random variable for each gene in batch 2 and batch 3; lOD was increased by a Uniform(0,0.5) random variable for batch 1 and 2, and was increased by a Uniform(4,5) random variable for batch 3. As a control group, we also simulated datasets without batch effects by keeping lexp and lOD identical among the three batches, for the three sample size configurations. For batch-effect data or control data, we simulated 50 datasets in each sample size and conducted batch-effect correction by various methods, including scBatch, MNN [Haghverdi et al. (2018), function mnnCorrect in package batchelor], linear model-based methods ComBat (Johnson et al., 2007), ComBat-seq (Zhang et al., 2020) and limma [Ritchie et al. (2015), function removeBatchEffect], and naive dataset normalization or standardization scheme included in packages scater [McCarthy et al. (2017), function normalize] and batchelor [Haghverdi et al. (2018), function rescaleBatches], which is similar to ScaleData in package Seurat (Satija et al., 2015). For MNN, default hyperparameters were used. For scBatch, the hyperparameter m was chosen to be 1.

2.3 Datasets, preprocessing and correction

Mouse embryonic stem cells (mESCs) data. The data were generated by Kim et al. (2015). The raw data are available in the ArrayExpress database with accession number E-MTAB-2600. We utilized a processed dataset from the public data repository of Hemberg Group (https://hemberg-lab.github.io/scRNA.seq.datasets/). The batch labels were requested from the authors conducting the experiment. The two batches of 469 mESCs cultured in three different conditions were used in batch correction and analysis. All 38 616 genes, including 92 External RNA Controls Consortium (ERCC) spike-in genes were included.

Mouse neuron data. The data were generated by Usoskin et al. (2015). The raw data can be obtained from the NCBI Gene Expression Omnibus (GEO) with accession number GSE59739. We also obtained the data from the same public repository (https://hemberg-lab.github.io/scRNA.seq.datasets/), where normalization, outlier exclusion and log transformation were conducted to obtain a dataset with 622 cells and 25 334 genes. We further removed two batches with too few samples. The final data used for batch correction consisted of 610 cells and 25 334 genes.

Human pancreas data. The data were generated by Xin et al. (2016). The raw data are available at the NCBI GEO with accession number GSE81608. The data used for analysis were also obtained from Hemberg Group’s repository (https://hemberg-lab.github.io/scRNA.seq.datasets/). We used the same gene filter mentioned in Xin et al. (2016) and retained genes with RPKM counts >100 in no <10 samples. Only cells from healthy donors were selected in batch correction and downstream analysis. The processed data contained 651 cells and 6797 genes.

For each dataset, we conducted corrections using the six batch-effect correction methods used in simulation study. For data with ERCC spike-in genes, we also used scPLS (Chen and Zhou, 2017), which utilizes spike-in genes information. For ComBat-seq, we used raw count matrix as input to ensure its assumption of negative binomial distribution was met.

2.4 Analysis and performance evaluation scheme

DE analysis. We applied Seurat (Satija et al., 2015) to conduct DE gene tests and adjusted the P-values by Benjamini and Hochberg approach (Benjamini and Hochberg, 1995). In simulation studies, we base on the gold standard to directly calculate AUC and PR-AUC to compare DE detection results. In addition, numbers of discovered true DE genes at false discovery rate (FDR) 0.2, denoted by NDE(0.2), were reported. For real data, comparisons were made for genes with adjusted P-values $<{10}^{-6}$ and log fold-changes >2 to check the agreements among different count matrices. Functional analysis of the DE gene lists are conducted using the GOstats package (Falcon and Gentleman, 2007), which conducts tests of over-representation of gene sets using hypergeometric test.

Clustering analysis. We repeatedly conducted 50 k-means clustering on the Pearson correlation matrix of the corrected count matrix to obtain cell clusters, where k was determined by the number of cell types reported by the raw data. Then, we utilized ARI (Hubert and Arabie, 1985) to evaluate the agreement between the cell type labels and the k-means cluster labels. The ARI index equals 1 if the clustering result perfectly matches the cell labels, while the index values around zero under random assignment. Finally, the average ARI for the 50 k-means clustering results were reported.

Batch correction evaluation. For real datasets, we conducted k-nearest-neighbor batch-effect test (kBET) (Büttner et al., 2019) to evaluate whether cells from different batches were well-mixed after correction. For the human pancreas dataset GSE81608, we further applied a batch-correction evaluation framework (B-CeF) (Somekh et al., 2019) to examine the preservation of biological signal in the form of gene–gene association. Specifically, we obtained the gold-standard gene network for human pancreas from GIANT database (Greene et al., 2015) (giant.princeton.edu/download/) and evaluated whether the corrected count matrix may recover the gold-standard associations.

Dimension reduction. For real datasets, we applied t-distributed stochastic neighbor embedding (t-SNE) (Maaten and Hinton, 2008), uniform manifold approximation and projection (UMAP) (Becht et al., 2019) and principal component analysis (PCA) (Wold et al., 1987) for dimension reduction. We used default parameters for the three dimension reduction tools. The first two dimension-reduced components were plotted to display the sample pattern after batch correction.

3 Results

3.1 Simulation study

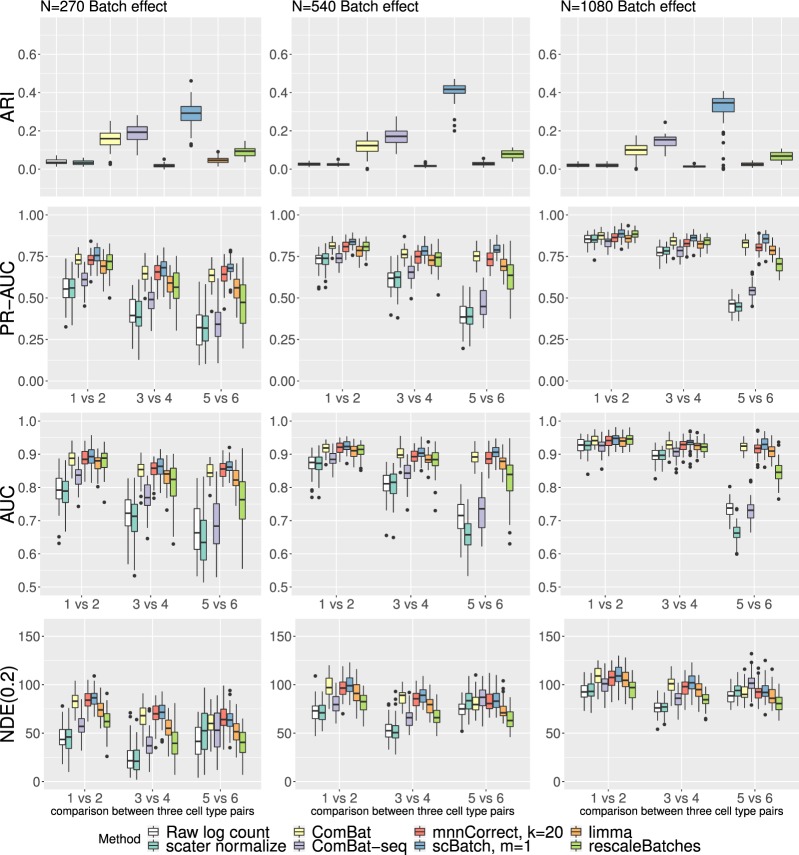
Figure 2 and Supplementary Figure S1 generated by ggplot2 (Wickham, 2016) displays the simulation results for the three sample size configurations under batch effect (Fig. 2) or control settings (Supplementary Fig. S1). As observed in Supplementary Figure S1, when there were no batch effects, the clustering and DE detection performances were similar for all methods with slightly better performances as the sample size increased. Compared to the control setting without batch effects, both clustering and DE detection performances were adversely affected when batch effects were present (Fig. 2).

Fig. 2.

Boxplots of metrics evaluating batch-effect correction methods in the 50 simulations with gene-specific batch-effects, under different configurations of sample size. PR-AUC, AUC and NDE(0.2) were calculated based on adjusted P-values from Seurat DE tests

When there was batch effect, scBatch showed strong performance under different sample size settings. As indicated by the consistently higher ARI index, scBatch inherited good clustering performances from the distance matrix obtained by QuantNorm. In addition, scBatch achieved better median PR-AUC, AUC and NDE(0.2) in most pairwise DE comparisons. Furthermore, DE detection performances improved as sample size increased (Fig. 2). Generally for all methods, when the sample sizes were small (3 versus 4), or the ratio between the cell counts of the two groups under comparison were large (5 versus 6), the ARI, PR-AUC and AUC results tended to be slightly worse. When there was no batch effect, scBatch yielded slightly better ARI results but slightly worse PR-AUC results compared to the raw data and other methods (Supplementary Fig. S1). This indicates a small amount of artifact introduced when scBatch tries to force the distance between samples to follow the same distribution within every batch and between batches. In real data, usually the batch effects are relatively strong. In the next sections, we examine the methods’ performance on real datasets.

3.2 scRNA-seq datasets

Under the assumption of scBatch algorithm, the correction can be reliably applied for batches with similar cell type compositions. This assumption is particularly suitable for the investigation of cell heterogeneity from a certain tissue. In practice, however, the assumption of balanced cell distribution may not be satisfied. In our real data analysis, we compared batch-effect correction of various methods on three scRNA-seq datasets with increasing complication of cell distributions among batches (Kim et al., 2015; Usoskin et al., 2015; Xin et al., 2016). The performances on the three datasets revealed the robustness of scBatch: the method not only obtained better sample patterns, but also retained important information in marker genes.

3.2.1 mESC dataset E-MTAB-2600

The mESCs data were generated by Kim et al. (2015). The mESCs were cultured in three different conditions, namely serum/leukemia inhibitory factor (LIF), 2i/LIF (2i) and alternative 2i/LIF (a2i). The batch labels were requested from the authors and the culture condition labels are available with the raw data. As shown in Supplementary Table S1, the mESCs with the three culture conditions are balancedly distributed in the two batches. In addition, the high-rejection rate of kBET test (Supplementary Fig. S2) indicates reasonable batch effects in the raw data.

Batch-effect corrections were conducted by ComBat, ComBat-seq, MNN, scBatch, limma, rescaleBatches and scPLS. For ComBat-seq, we conducted correction with raw count matrix and then normalized it by scater (McCarthy et al., 2017). For the other methods, batch-effect correction was conducted after scater normalization. As shown in Supplementary Figure S2, all seven correction schemes achieved a lower kBET rejection rates compared to the raw data, for neighborhoods of k = 20 cells. We further conducted t-SNE (Fig. 3A), UMAP (Supplementary Fig. S3) and PCA (Supplementary Fig. S4) dimension reduction and the average ARI based on repeated k-means clustering. As the t-SNE plots indicate, most correction schemes managed to group cells of the same type together. MNN yielded a pattern with some residual batch effects. With limma and rescaleBatches, we can still observe several cells with lif (orange) condition mixed in the tail of 2i and a2i clusters. In contrast, ComBat, scBatch and scPLS produced a relatively more separated pattern for the three groups.

Fig. 3.

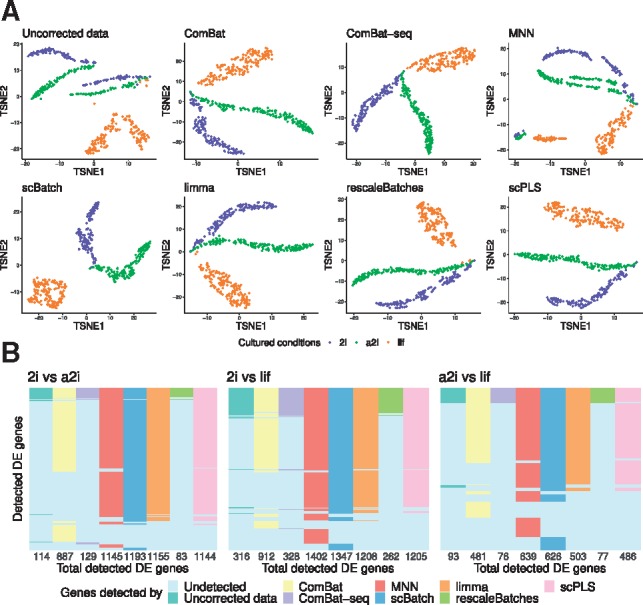
Analysis results for the mESCs data: (A) t-SNE plots of the sample patterns from uncorrected data (normalized raw count data), ComBat-corrected data, MNN-corrected data, scBatch-corrected data, limma-corrected data, rescaleBatches-corrected data and scPLS-corrected data, colored by different cultured conditions; (B) comparison of the significant genes from pairwise differential-gene tests by Seurat (Satija et al., 2015) with adjusted P-values $<{10}^{-6}$ and log fold-changes >2

The 2D pattern alone does not reflect the cell type separation in the high-dimensional space. We guaged the separation using the average ARI indices from k-means clustering. The ARI further indicated that scBatch ($\overline{\text{ARI}}=0.55$) obtained better sample separation than uncorrected data ($\overline{\text{ARI}}=0.15$), ComBat ($\overline{\text{ARI}}=0.26$), ComBat-seq ($\overline{\text{ARI}}=0.30$), MNN ($\overline{\text{ARI}}=0.10$), limma ($\overline{\text{ARI}}=0.21$), scPLS ($\overline{\text{ARI}}=0.24$) and rescaleBatches ($\overline{\text{ARI}}=0.243$).

DE gene detection was then conducted between the pairs of culture conditions. Figure 3B shows the comparison of DE genes detected by the data corrected by different methods. As observed, the uncorrected data, rescaledBatches and ComBat-seq detected least DE genes that largely overlap, while the other methods obtained mostly overlapped DE gene sets, with ComBat disagreeing with the other three methods to some extent. The functional analyses by GOstats (Falcon and Gentleman, 2007) of the selected genes showed similar results between scBatch, MNN and limma (full list: Supplementary File S2; top 5 GO terms after manual removal of highly overlapping terms: Supplementary File S3). For example, in the comparison between a2i/LIF versus serum/LIF, scBatch, MNN and limma all selected ‘positive regulation of Notch signaling pathway’ as one of the top biological processes, while ComBat selected less genes from this pathway and did not select it as one of the major biological processes. Given the inhibitor used in this study, GSK3β, is an established regulator of the Notch signaling pathway (Zheng and Conner, 2018), we expected the pathway to be one of the most significantly changed pathways between the two culture conditions. Overall, the methods agree reasonably well with each other. This can probably be explained by the well-balanced study design and relatively straightforward pattern of batch effects. In the next two real data examples, we attempted to correct more challenging batch effects with less balanced study design.

3.2.2 Mouse neuron dataset GSE59739

The mouse neuron scRNA-seq data were generated by Usoskin et al. (2015). Cell labels determined by marker genes were provided in the data. We based our analyses on the given cell labels to investigate the differences of four main subtypes of cells, namely non-peptidergic nociceptors, tyrosine hydroxylase containing, neurofilament containing and peptidergic nociceptors.

The source of batch effects came from different libraries, as confirmed by kBET test with high-rejection rates (Supplementary Fig. S5). In addition, Supplementary Table S2 shows that the different libraries contain the four cell types with varied proportions. Therefore, the cell distribution is slightly imbalanced. As observed in the 2D t-SNE plot (Fig. 4A, top-left panel), although the uncorrected data maintained part of the clusters of the four cells, there are still splitting of a single cell type, and mixture of cell types.

Fig. 4.

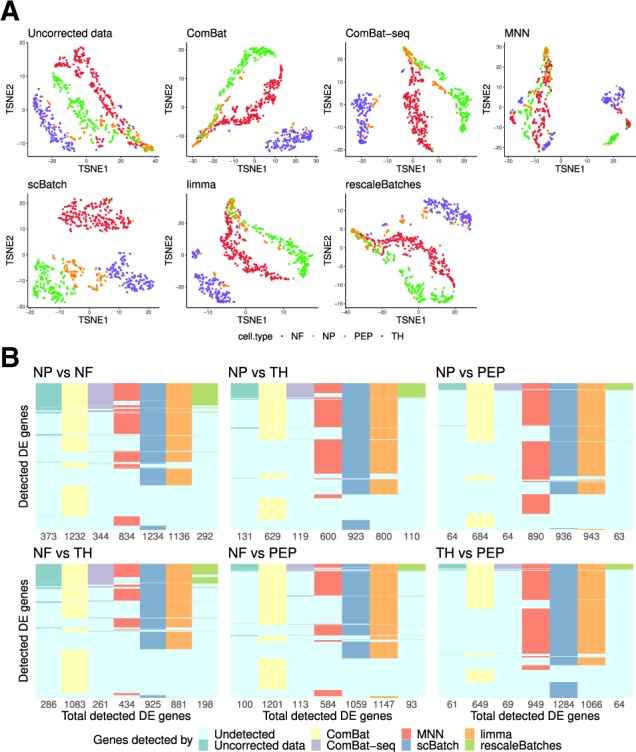
Analysis results for the mouse neuron data: (A) t-SNE plots of the sample patterns from uncorrected data (normalized raw count data), ComBat-corrected data, MNN-corrected data, scBatch-corrected data, limma-corrected data and rescaleBatches-corrected data, colored by cell types; (B) comparison of the significant genes from pairwise differential-gene tests by Seurat (Satija et al., 2015) with adjusted P-values $<{10}^{-6}$ and log fold-changes >2

Regarding the libraries as batches, we conducted batch-effect correction using ComBat, ComBat-seq, MNN, scBatch, limma and rescaleBatches. Note that, for ComBat-seq, the raw count matrix was corrected then normalized, while for the other methods the normalized count matrix was corrected. As shown in Supplementary Figure S5, scBatch correction achieved the lowest average kBET rejection rate, indicating that the batches are better mixed at any neighborhoods of k = 20 cells.

In order to evaluate the clustering performance, we utilized t-SNE (Fig. 4A), UMAP (Supplementary Fig. S6), PCA (Supplementary Fig. S7) dimension reduction and the average ARI based on multiple k-means clustering results. As the t-SNE plots display, scBatch (bottom left) obtained a clearer sample pattern which distinguished the four subtypes better. The ARI indices based on k-means clustering results also demonstrated that scBatch ($\overline{\text{ARI}}=0.64$) outperformed uncorrected data ($\overline{\text{ARI}}=0.09$), ComBat ($\overline{\text{ARI}}=0.11$), ComBat-seq ($\overline{\text{ARI}}=0.08$), MNN ($\overline{\text{ARI}}=0.15$), limma ($\overline{\text{ARI}}=0.13$) and rescaleBatches ($\overline{\text{ARI}}=0.09$) by a large margin. To further investigate whether corrected count matrices kept crucial marker information, we plot the marker gene expression levels in the t-SNE plots for the four cell subtypes, displayed in Supplementary Figure S8. It can be observed that scBatch correction inherited the marker information from the uncorrected data with large contrast, while the other approaches did not maintain as strong contrast in the marker genes.

Due to its ability to restore better sample patterns and maintain important marker contrasts, scBatch also showed good performance in DE gene detection. We conducted DE gene detection between all cell type pairs. Figure 4B shows the comparison of DE genes detected from the different count matrices. Similar to the results for the mESCs data, for most pairs of cell types, the DE gene set detected by scBatch covered the DE gene set obtained by other methods, except for ComBat and MNN. This indicates that more underlying information masked by batch effects may be revealed by scBatch.

In most of the comparisons, scBatch and ComBat both covered the genes detected by uncorrected data, rescaleBatches and ComBat-seq. At the same time, MNN showed smaller agreement with raw data, rescaleBatches and ComBat-seq. ScBatch also mostly covered the genes detected by limma. With regard to biological interpretations, the methods MNN, scBatch, comBat and limma mostly pointed to similar top pathways that were biologically quite plausible, indicating the biological signal was very strong in this dataset (full list: Supplementary File S4; top five GO terms after manual removal of highly overlapping terms: Supplementary File S5).

3.2.3 Human pancreas data GSE81608

We analyzed another scRNA-seq data of human pancreas cells (Xin et al., 2016). The dataset consists of cells from healthy controls and patients with type II diabetes.

Here, we focused on healthy control cells to investigate the cell heterogeneity. The data were collected from 12 donors. We first examined whether the data show any subject effects. There are four dominating endocrine cell types—alpha cells that produce glucagon, beta cells that produce insulin and amylin, delta cells that produce somatostatin and gamma cells that produce pancreatic polypeptide. By observing the t-SNE and UMAP plots (Supplementary Fig. S9), we found that the sample patterns were confounded with donor IDs. Specifically, cells from the same donor tend to form their own clusters. Therefore, the data are subject to confounding subject effects, which affect downstream data analysis in similar ways as batch effects and can be corrected by batch correction approaches. In other words, the donor IDs were treated as batches in this analysis. Furthermore, the distribution of cell types between the donor IDs, or batches, vary substantially (Supplementary Table S3). The proportion of alpha cells ranged from 16.7% to 74.6% among the batches. The proportion of beta cells ranged from 14.0% to 54.2%. Given that gamma and delta cells account for small proportions in the pancreas islet, they were not present in some of the batches. The range for delta cell was from 0% to 8.3%; the range for gamma cell was from 0% to 20.0%. These variations made the data more challenging than the mESCs data and the mouse neuron data. In specific, since delta or gamma cells can be missing in some batches, it is not reasonable to assume a good mixture of batches for delta or gamma cells after correction. Thus, the kBET rejection rates may not be a representative metric for batch-effect correction under the imbalanced nature of the dataset.

We applied similar analysis procedure used for the mouse neuron data. As expected, the kBET rejection rates (Supplementary Fig. S10) for scBatch remains high due to the imbalanced cell distribution among batches, while comBat, limma and rescaleBathes achieved lower rejection rates. However, the sample pattern reflected by the t-SNE and UMAP plots (Fig. 5A and Supplementary Fig. S11) indicated a better clustering pattern for scBatch, especially for delta (yellow points) and gamma (pink points) cells. In K-means clustering results, scBatch achieved highest average ARI (0.60), compared to uncorrected data (0.42), ComBat (0.44), ComBat-seq (0.43), MNN (0.07), limma (0.48) and rescaleBatches (0.17). The marker gene expressions on t-SNE plots (Supplementary Fig. S13) similarly demonstrated that scBatch was able to maintain marker gene information from the original data. Combining the kBET results, dimension reduction plots and clustering performances, we found that the kBET results may not be associated with better dimension reduction or clustering performances for this specific dataset with very imbalanced study design.

Fig. 5.

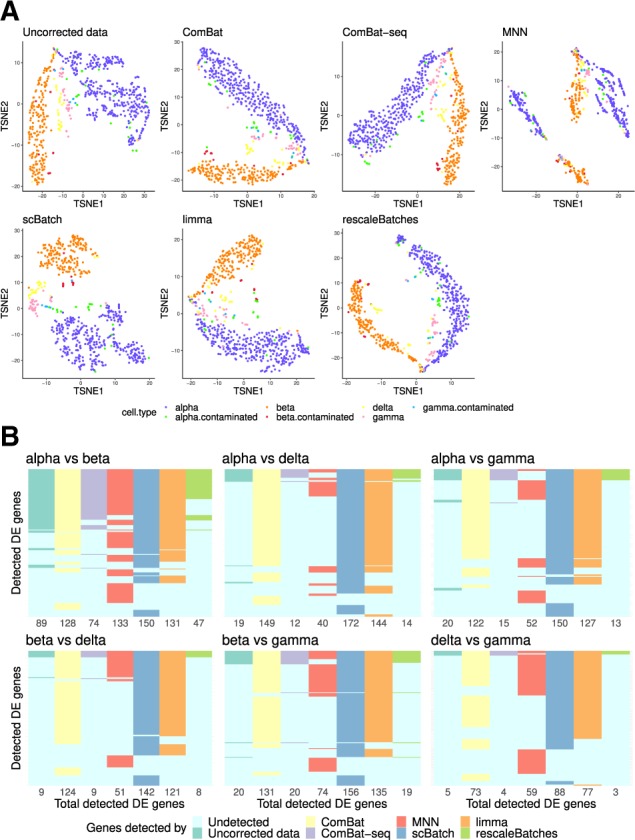
Analysis results for the human pancreas data: (A) t-SNE plots of the sample patterns from uncorrected data (normalized raw count data), ComBat-corrected data, MNN-corrected data, scBatch-corrected data, limma-corrected data and rescaleBatches-corrected data, colored by cell types; (B) comparison of the significant genes from pairwise differential-gene tests by Seurat (Satija et al., 2015) with adjusted P-values $<{10}^{-6}$ and log fold-changes >2

Figure 5B displays the comparison of significant DE genes. Similar to the results for the two mouse datasets, uncorrected data and rescaleBatches detected least DE genes. Apart from MNN, high degrees of agreement were observed among other methods, where scBatch was able to detect the most DE genes in all six pairs. In addition, scBatch also achieved highest AUC in the B-CeF evaluation (Supplementary Fig. S14). However, the AUCs for all count matrices were lower than 0.6. This is expected given tissue-specific gene–gene associations were used as gold standard. Currently, no good data source is available for cell type-specific gene–gene associations.

We again used GOstats to analyze the over-representation of gene ontology biological processes by the selected genes (Falcon and Gentleman, 2007). We took the DE genes between delta and gamma cells as an example, as it showed the largest difference between MNN and the other methods. Delta cells secrete somatostatin, the growth hormone-inhibiting hormone; gamma cells secrete pancreatic polypeptide that regulates pancreatic secretion activities. At the P-value threshold of 0.005, MNN yielded six significant biological processes, while the other correction methods each yielded more than 20. In addition, given the biological functions of the two cell types, various hormone metabolism and hormone response processes were repeatedly found by ComBat, ComBat-seq, scBatch, limma and rescaleBatches. But they were not selected by MNN (full list: Supplementary File S6; top 5 GO terms after manual removal of highly overlapping terms: Supplementary File S7).

Overall, in all three datasets we analyzed, scBatch tended to yield the clearest cell type patterns, and select the most number of DE genes. In each dataset, there were one or two methods that tended to select somewhat different DE genes compared with the other methods. ScBatch stayed in the majority in every dataset, which suggested its robustness.

4 Discussion

Batch effects are frequently encountered in omics data analysis, thus a crucial issue to address before downstream analysis that leads to scientific discoveries. In this article, we introduced a novel method for batch-effect correction. We have shown that the proposed method, scBatch, can obtain better clustering pattern, maintain crucial marker information and detect more DE genes.

The proposed method assumes roughly balanced sample population among batches. The assumption is reasonable (Hicks et al., 2018), and the method appeared to be robust when the assumption is mildly violated, as demonstrated in the analysis for human pancreas data (Xin et al., 2016). It is worth noting, however, that the balanced study design may be unrealistic due to logistical limitations (Bacher and Kendziorski, 2016) and batches and biological factors are commonly confounded (Stegle et al., 2015). In addition, although we did not consider utilizing information from spike-in genes, the performance of our method was comparable to the approaches designed for control-gene scenario, such as scPLS (Chen and Zhou, 2017). In fact, the clustering performance of scBatch outperforms control-gene-based method for the mESCs data (Kim et al., 2015). Furthermore, since our method is based on non-parametric distance matrix correction, it can handle data with different characteristics. We show in Supplementary Section S3 and Figure S15 that our method achieved good performance on a bulk RNA-seq dataset. Nevertheless, when the study design is extremely imbalanced, such as for a dataset with cells from different developmental stages distributed in separate batches, we do not recommend using our method.

Another popular analysis objective for scRNA-seq data is to combine datasets from several platforms. Haghverdi et al. (2018) provided a benchmark example on combining four human pancreas datasets (Grün et al., 2016; Lawlor et al., 2017; Muraro et al., 2016; Segerstolpe et al., 2016) from SMART-seq2 (Picelli et al., 2013) and CEL-seq/CEL-seq2 (Hashimshony et al., 2012) protocols. We managed to reproduce the results for MNN, ComBat and limma, and applied scBatch to correct the batch effect among the four datasets. As shown in Supplementary Section S4 and Figure S16, scBatch still achieved the highest ARI compared to other benchmark methods. The sample patterns obtained by scBatch, ComBat and limma, however, still clearly showed residual batch influences. Although MNN obtained larger clusters that appeared to mix batches better and restore the patterns for the seven cell types, each cluster actually consisted of a mixture of cell types. From the above observations, the batch correction across sequencing platforms appears unsatisfactory for every tested correction scheme. In fact, our previous article (Fei et al., 2018) demonstrated that one of the four human pancreas datasets (Muraro et al., 2016) has batch effect within the dataset. It might be a better practice to correct within-dataset batch effect before considering cross-dataset batch effect. Despite the difficulty, scBatch still retrieved better sample pattern in terms of ARI, showing promising signs in applying non-parametric distance matrix correction on similar tasks involving multiple datasets. We plan to study hierarchical batch-effect correction, first within study, and then between study, in our future work.

Computation is another practical concern for the application of scBatch. As discussed in Section 2.1, the memory use is excessive when computing the gradient of the loss function without random blocks, while more random blocks reduce the memory use at costs of longer running time to convergence. According to the supplementary simulation results (Supplementary Section S5 and Fig. S17), for datasets with relatively small sample size, full gradient descent without random blocks, i.e. m = 1, is the best practice. If the computational cost of full gradient descent is unaffordable, utilizing random blocks, i.e. m > 1, can be used to achieve similar clustering and DE detection performance. In addition, Supplementary Figure S18 indicates reasonable stability of clustering and DE detection performance of the random block approach. In terms of running speed, scBatch requires more computation time to reach optimal results compared to most existing approaches. Moreover, as shown in Supplementary Figure S19, the scBatch running time increases faster than a linear growth rate as the sample size increases. Moreover, for a fixed sample size, the time to convergence for scBatch also varied. The varied running time was determined by the complication of batch effects, which decided the similarity between uncorrected sample pattern and the corrected referencing sample pattern. Although slower than other alternatives, the running speed of scBatch is within acceptable range. For a few hundred cells, the computing time was in the range of minutes. For large studies with over 1000 cells, the computing can take hours.

There is still large room to improve the proposed method. First, we only adopted the simplest linear transformation of raw count matrix in this article, while a non-linear transformation may better depict the sample pattern in the corrected distance matrix. Secondly, the metrics of distance can also affect the correction. We used the Pearson correlation matrix because it was easy to interpret and convenient for gradient computation, while other distance metrics, such as Spearman correlation may bring other insights to the data pattern. Thus, a more universal numerical gradient descent algorithm may be applied to adapt to different types of distance matrices. Furthermore, the current implementation of algorithm can be potentially improved and accelerated by utilizing graphic processing units computing, which is already available under R software framework (Determan, 2019; Rupp et al., 2016).