Experimentally-Driven Protein Structure Modeling

Abstract

Revolutions in natural and exact sciences started at the dawn of last century have led to the explosion of theoretical, experimental, and computational approaches to determine structures of molecules, complexes, as well as their rich conformational dynamics. Since different experimental methods produce information that is attributed to specific time and length scales, corresponding computational methods have to be tailored to these scales and experiments. These methods can be then combined and integrated in scales, hence producing a fuller picture of molecular structure and motion from the “puzzle pieces” offered by various experiments. Here, we describe a number of computational approaches to utilize experimental data to glance into structure of proteins and understand their dynamics. We will also discuss the limitations and the resolution of the constraints-based modeling approaches.

Graphical Abstract

Introduction

The past century has been transformational for many scientific disciplines. Some of the most prominent revolutions happened in biology: the field transformed from the descriptive and cataloging field to a mechanistic one, whereby we have started to understand the molecular origins, processes, and mechanisms responsible for life of species. We dove deeper into molecular and atomic scale of these processes and learned how atomic constellations of biological molecules result in interactions between these molecules, resulting in higher-order physiological phenotypes. Not only we started to understand molecular mechanisms underlying physiological processes, but also learned how to rationally manipulate biological systems using genetic tools, molecular engineering, and drug discovery.

Molecular architecture and atomic structure have become central to biology. Recognizing the impact of structural biology, many nations contributed to Structural Genomics Initiative. The USA National Institutes of General Medical Sciences have sponsored one of the most successful programs, Protein Structure Initiative (PSI) [1], that resulted in significant expansion of coverage of protein fold space. This initiative has resulted in determination of nearly 7,000 protein structures including many unique folds. PSI has also promoted innovations in molecular structure determination methods and technologies [2].

Technological developments have been central to structural biology revolution. These developments can be stratified in to three categories: experimental, computational, and hybrid, in which sparse experimental, knowledge-based, and/or evolutionary information is used to determine protein structure. Next, we outline the strengths and limitations of these approaches, challenges, and strategies to tackle modern day problems of protein structure determination.

High-resolution experimental approaches

The solution of the first X-ray crystallographic structure of the protein myoglobin by Sir John Kendrew in 1958 [3] opened the flood gates of molecular structural revolution. Technological and scientific advances, that included the development of the nuclear magnetic resonance (NMR) techniques [4,5], negative staining and cryo-electron microscopy (cryo-EM) [6–8], computational and theoretical approaches [9–34], resulted in exponential explosion of the number of determined protein structures (Figure 1). In turn, newly discovered structures empowered scientists with unprecedented abilities to (i) establish structure-functional relationships in molecules, which resulted in a new field of molecular biology [35], (ii) discover new drugs based on small molecule-receptor structures, which resulted in the field of molecular pharmacology [36,37], (iii) design new proteins, which resulted in the field of computational protein design [38,39]. The structural revolution has had a profound impact on our society and we continue to benefit from the expanding field of structural biology.

Figure 1.

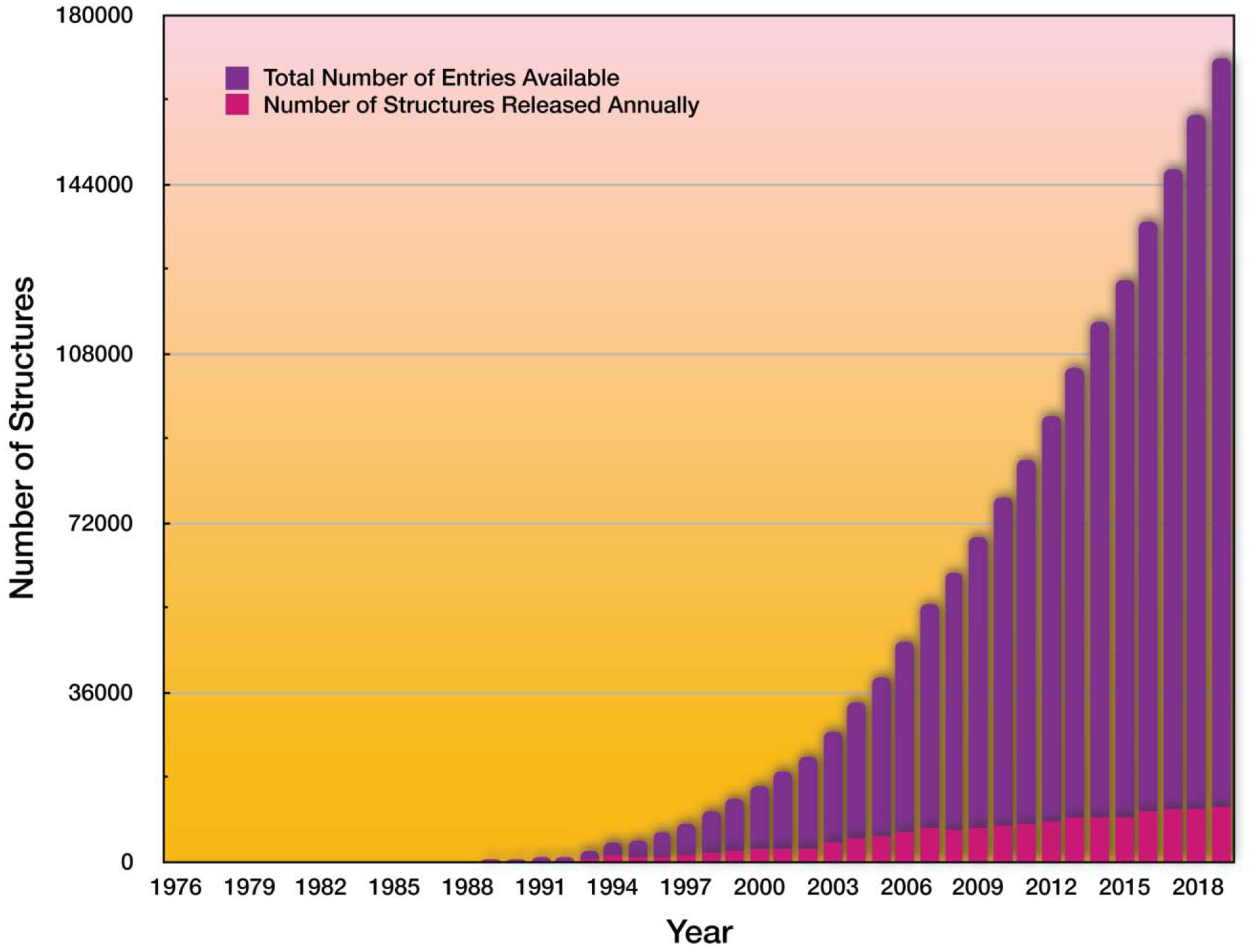
Exponential knowledge growth of structures of biological molecules (mostly proteins) over the past 40 years.

Initial growth in determined protein structures has been due to advances in X-ray crystallography, however, the introduction of NMR for protein structure determination by Kurth Wüthrich [40–42] and others altered the landscape of molecular structure determination. Although one of the principal limitations of NMR has been the size of the molecule, a number of innovative techniques pushed the boundaries of molecular weight limit on studied proteins (Table 1). This technique offers a critical advantage with respect to crystallography, namely the ability to witness conformations of proteins, that float freely in, albeit crowded, solutions.

Table 1.

Advantages and limiations of experimental structure determination techniques.

Technique	Advantages	Limitations
X-ray crystallography	Large proteins and complexes High resolution structures	Requires high protein concentration Possible crystallographic artifacts: packing, non-native conformatins Ad hoc detemination of crystalizing conditions for the target protein Limited to stable proteins Molecular motion is challenging to obtain
NMR	Multiple complementary techniques for structure determination: two (and higher)-dimensional NMR, residual dipolar coupling, hydrogen-deuterium exchange, paramagnetic relaxation enhancements Ability to quantify dynamics and witness large-scale conformational dynamics of proteins	Requires high protein concentration Atominc assignment may present challenges
CryoEM	Large structures Ability to witness many conformational states Fairly rapid workflow	Small proteins still present a challenge

Technological innovations, as well as innovations in computer algorithms have led to breakthrough advances in cryo-EM technology and the rise of new era in structural biology. The number of protein structures solved using cryo-EM has been growing, including especially challenging transmembrane proteins and whole viruses [43]. According to estimates [44], we have not reached the theoretical limits of what is possible with cryo-EM, and the emerging field of cryo-electron tomography. Cryo-EM field promises to revolutionize molecular structure determination.

Computational modeling

Molecular modeling has been playing a critical role in structural determination. It is hard to imagine any structural biology experiment that would not rely on computational assistance in data processing and reconstruction. Molecular modeling has been used in molecular reconstruction of crystallographic data using molecular replacement, structural refinement, as well as building ensembles of molecular conformations using NMR data.

Ever increasing computational power enabled significant advances in molecular modeling. Initial success in structure prediction has come from phenomenological modeling, whereby known structural information was used to reconstruct previously unknown molecules. “Threading” [45] was one of the original dominant approaches for structure modeling that has been relying on a critical observation that if two proteins share sequence similarity, their structures are also similar (homologous) [46–50]. Thus, the first step in threading is identification of homologous proteins (with known structures) to a given target protein. In the second step, all the sequence information is stripped from the identified homologous proteins and only backbone trace remains. In the third step, the sequence of the target protein is “threaded” through the backbone trace of the homologous proteins. Upon resolution of clashes and further structural optimization (energy minimization), the final energy of the threaded sequence, E, is evaluated and compared to that of the average of a randomly reshuffled sequences, $\overline{E}$ (to maintain amino acid composition). Based on this comparison one can build a distribution of Z-scores ($Z=\frac{E-\overline{E}}{{\sigma }_E}$, where σ_E is the standard deviation of the distribution). The probability, p, of finding a particular structure with a given Z-score can be obtained by integrating the tail of the normal distribution of Z-scores (due to the central limit theorem). This approach proved to be powerful [51–53], but limiting to closely related homologs. More distant homologous proteins featured backbone rearrangements. Since the threading score is susceptible to backbone variations, the threading procedure results in less accurate results for more distant homologs.

The next revolution in protein structure prediction has come from the fragment-based modeling, [54,55] whereby known protein structures are deconstructed into fragments of several amino acids. The library of fragments is then used to assemble the structures of an unknown target protein by matching corresponding sequence fragments of the target protein to that of a fragment from the library. This approach has proved to not only accurately predict protein structure, but enabled successful and robust protein design protocol, implemented in RosettaDesign [56]. Nonetheless, even this approach reached the limit of prediction accuracy as it is evidenced from the adaption of new approaches in the field of protein structure prediction.

The next breakthrough in computational structure determination was based on observation that if two amino acids in proteins form stabilizing interaction, then substitution of one would impact the other amino acid [57,58]. Based on this observation then, we can relate the strength of covariation of amino acids at various positions in the course of evolution with the chances that these residues interact in 3D space. Several methods have been developed to extract the potential interactions between positions along the chain using such direct coupling analysis [59–62], or DCA. As the result protein structure prediction reached new highs in the Critical Assessment of Structure Prediction (CASP) [63] competitions. The most recent breakthrough in computational structure prediction has come from the implementation of machine learning approaches [64–66]. Combination of the computational approaches has had a profound impact on structural biology.

Challenges

Despite these paramount advances in experimental and computational approaches, we are still facing some of the critical challenges in our understanding of molecular structure and dynamics. These challenges are typically associated with the complexity of characterization of intrinsic molecular dynamics and capturing conformational states of interest. Some examples of such obstacles include: (i) characterization of disordered proteins [67–72], (ii) identifying rare conformations [63–65], (iii) witnessing templating conformational conversions [73–76] (key steps in protein aggregation), (iv) determining structures of molecular complexes, especially featuring interactions with disordered conformations [77–81], and (v) ligand-induced conformational disorder-order transitions [82–88]. All of these obstacles induce heterogeneity in samples, making structural determination extremely challenging.

The thread among above challenges is the characterization of disorder. Unlike structural determination of proteins that populate most of their life time in the near-native conformations, disordered proteins lack well-defined states and, instead, feature some persistent structural elements in otherwise diverse conformational ensemble. In this regard, the meaning of structural characterization is shifted from the concept of “one protein – one structure” to identifying persistent elements of conformational ensembles.

Problem formulation

How can we characterize these ensembles of disordered proteins? To understand how to characterize the ensembles, we look into the physical properties of heterogeneous proteins. Unlike random homopolymers, heteropolymers feature non-equal interactions between distinct regions of the polymers. According to Boltzmann distribution, the probability, p(Γ), of observing a particular conformation, Γ, is $p(\Gamma )~exp\left(-\frac{E(\Gamma )}{k_{B}T}\right)$, where E is the energy of this conformation, k_B is the Boltzmann constant and T is the temperature. Thus, heteropolymeric segments that feature preferable interactions are more likely to appear in proximity within each other as such conformations feature lower energies than those that do not have strongly interacting segments in proximity. These more favorably interacting segments in proteins determine their conformational landscape. In structurally ordered proteins the attraction between interacting segments (ΔH) compete against conformational entropy (ΔS) to converge on a well-defined near-native structural ensemble, with stability ΔG = ΔH – TΔS < 0. In natively disordered proteins, there is little distinction between any sub-states and the unfolded states, i.e. ΔS ≈ 0. We can deconstruct contribution to ΔH = ΔH_sis + ΔH_wis, where ΔH_sis is the enthalpic contribution of the strongly interacting segments, and ΔH_wis is that of the contribution of the weakly interacting segments. The probability to observe conformations with the strongly interacting segments present, considering that the weakly interacting segments have minimal energy contribution (ΔH_wis ≈ 0), would be $p_i(\Gamma )~exp\left(\frac{-\Delta H_{sis}(\Gamma )+T\Delta S}{k_{B}T}\right)$, which is much larger than that when these strongly interacting segments do not interact, $p_0(\Gamma )~exp\left(\frac{-\Delta H_{wis}(\Gamma )+T\Delta S}{k_{B}T}\right):p_i(\Gamma )>p_0(\Gamma )$. Hence, in heteropolymers, one expects dynamic persistence of strongly interacting structural segments. Even in folded proteins, local unfolding around strongly interacting structural segments determine the dynamics of proteins and their aggregation morphologies [89].

Although strongly interacting segments shape protein conformational states, their characterization is not trivial as these conformational ensembles can be complex and context/condition-dependent. For example, there can be multiple competing conformations resulting in a given conformational ensemble. To better understand the problem, it is worth consider various evolutionary scenarios for appearance of natively disordered proteins.

There are several scenarios how proteins evolve to be disordered or feature some level of disorder (Figure 2). In one scenario, a stable protein loses its structure in the course of evolution. For example, partial loss of a function due to the stability loss of a given protein can be compensated to preserve fitness of the organism by having a compensation in a different protein with a similar function. Hence, the stability of the protein does not have to be maintained for organismal fitness. Yet unless a protein performs some function in cells, its expression becomes an energetic burden. Hence, proteins that lose their stability in the course of evolution either maintain its function, although at a lower level, or acquire new function(s). Not all mutations that result in disordered but functional protein are fixed. Thermodynamically stable proteins pack their hydrophobic cores on the inside and expose hydrophilic patches on the outside. When such proteins are unfolded, unfolded protein response (UPR) is initiated: these proteins are recognized by chaperones by binding to exposed hydrophobic patches. These chaperones either assist refolding of the misfolded protein or target it to proteasomal degradation. Hence, natively disordered proteins also evolve to evade UPR.

Figure 2. Two evolutionary scenarios resulting in functional yet intrinsically disordered protein.

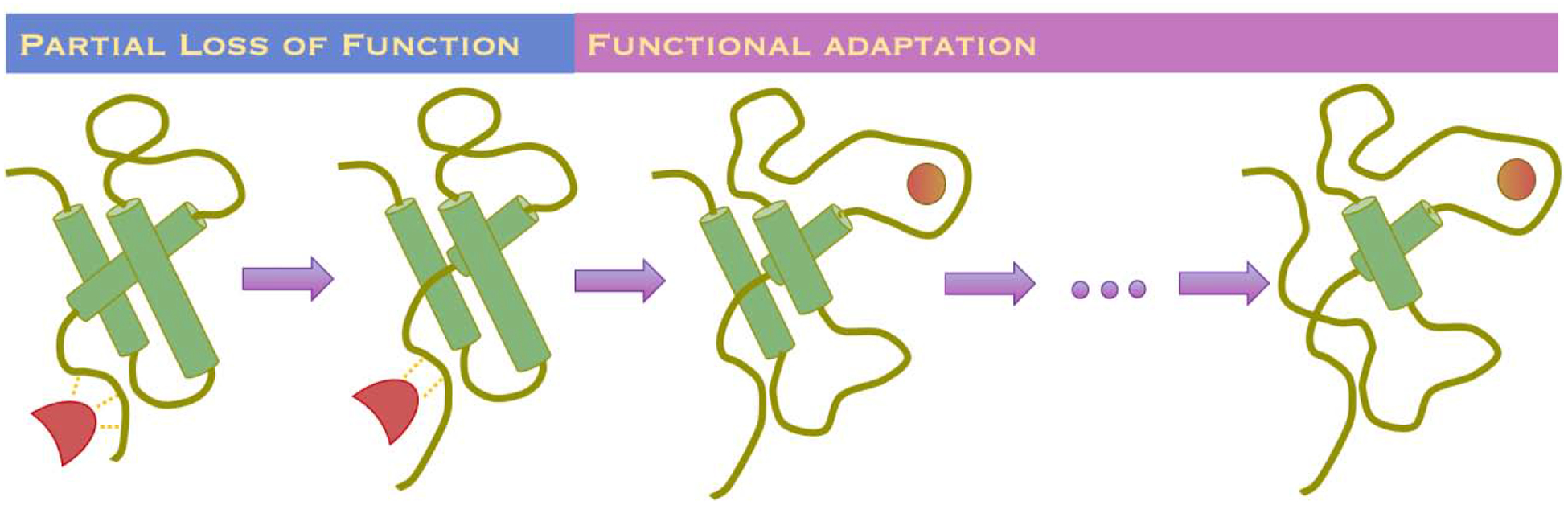
In one scenario, a partial loss of function can be compensated by the increased functionality of orthologous genes or reduced need of a given functionality in evolved environments. In another scenario, a given scaffold can be adapted to carry a distinct function that require less ordering of the protein.

Another scenario for evolution of the natively disordered proteins may come from functional adaptation of a given protein. In the course of evolution, a protein may adapt a new function, and likely a new functional conformational ensemble. In this case, these two (original and acquired) functional ensembles compete with each other, making the protein de facto disordered, although it persistently populates these two functional states.

Although other scenarios for evolution are likely, the keys differentiating these scenarios are the number of dominant structural conformations and the kinetics of interconversion between them. Hence, to characterize the conformational states of the natively disordered proteins, one needs to generate these ensembles and, then, identify their chemical and biological properties, as well as the rates of conversions between states.

Molecular dynamics (MD) computer simulations allow generation of hypothetical ensembles of protein conformations. Upon sufficient sampling, MD simulations faithfully reproduce physical properties of natively disordered proteins [90]. However, sufficient sampling can be challenging with the traditional MD [91–100]. To circumvent this challenge, several approaches have been developed. One class of approaches is based on innovative strategies for sampling states, that include replica exchange (REX) [101,102] and accelerated MD (aMD) [103]. Another class of sampling enhancement approaches comes from parallelization, utilization of graphical processor units (GPUs) [104–107], and custom processor architectures, e.g. Anton [108]. Faster algorithms for simulations, such as Monte Carlo and discrete molecular dynamics (DMD) [109–113] offer increase in raw speed of simulations. These algorithms can often be combined with different sampling strategies, and hardware acceleration.

Even with software and/or hardware acceleration, the sampling maybe insufficient due to the size of the system. Furthermore, imperfections of the force fields may bias the conformational ensembles. A number of strategies have been developed to circumvent these challenges with the premise of restricting the search space by utilizing prior knowledge, such as evolutionary data, experiments, and literature. In all of these cases the restriction of the search space impacts the entropy and reduces the free energy barrier that separates low energy conformational state(s) from the random coil states. Next, we will describe several such strategies.

Fitting the experimental collective observables

Various experiments offer different types of observables. In case when experiments report on collective variables, $S_{exp}^i$, for a given observable i, a method to restrict computational sampling of molecular conformations is to impose constraints on the difference between computational, $S_{\mathit{\text{comp}}}^i$, and experimental values of the collective observables by minimizing their ${\chi }^2\left({\overrightarrow{S}}_{\mathit{\text{comp}}},{\overrightarrow{S}}_{exp}\right)$ values:

$$\{\begin{array}{c}{\chi }^2\left({\overrightarrow{S}}_{\mathit{\text{comp}}},{\overrightarrow{S}}_{exp}\right)=\frac{1}{n}\sum _{i=1}^n{\left(S_{\mathit{\text{comp}}}^i-S_{exp}^i\right)}^2\\ {\chi }_{min}^2=mi{n}_{{\overrightarrow{S}}_{\mathit{\text{comp}}}}{\chi }^2\left({\overrightarrow{S}}_{\mathit{\text{comp}}},{\overrightarrow{S}}_{exp}\right)\end{array}$$ (1)

The solution of these equations guarantees an optimal ensemble that satisfies experimental data and the level of agreement between thus computationally-constructed and experimental conformational ensembles is characterized by the value of ${\chi }_{min}^2$.

This approach has been extensively used in protein folding community to build protein folding-unfolding transition state ensembles by using as the collective variables ϕ-values, which is an approximate measure of a particular residue, i, contribution to the transitional state ensemble [114–121]: Sⁱ = ϕ_i. Mapping transition state ensembles by fitting of the experimental ϕ-values allowed the determination of the structural properties of some of the kinetically most evasive states.

Sample and select

If sampling of conformational states is not an obstacle, an alternative strategy, named “sample and select”, is based on the generation of the naïve (without experimental biases) conformational ensembles in MD simulations, and selection of conformations from the obtained ensembles that satisfy experimental data using Equation (1). This approach has been developed by Chen et al. [122], for utilizing NMR residual dipolar coupling (RDC) data as the bias to obtain conformational ensembles consistent with the RDCs. It has also been utilized by other groups for interpreting NMR data of RNA and DNA molecules [123–125].

Pairwise constraints-based modeling

Various experiments, such as amino-acid cross linking, FRET, and NMR, and evolutionary inference studies [57–62] often report on pairwise proximity of residues. Pairwise proximity data can be readily incorporated into the physical force field, H_phys,

$$H=H_{\mathit{\text{phys}}}+\lambda H_{\mathit{\text{constr}}},$$ (2)

where

$$H_{\mathit{\text{constr}}}={\sum }_{{(i,j)}_{\mathit{\text{constr}}}}{U}_{ij}(r),$$ (3)

(i, j)_constr are pairs of constrained residues, and λ < 1 is a weight coefficient for the constraints’ potential. The form of potentials, U_ij(r), can be chosen as spring (quadratic) potential, if it is used in traditional MD engine, or square wells, if used in DMD (Figure 3). The middle of the well, r_ij, corresponds to the average distance expected between residues i and j, and the width, σ_ij, corresponds to the expected variation of distances between these residues.

Figure 3. Implementations of constrains in the force field.

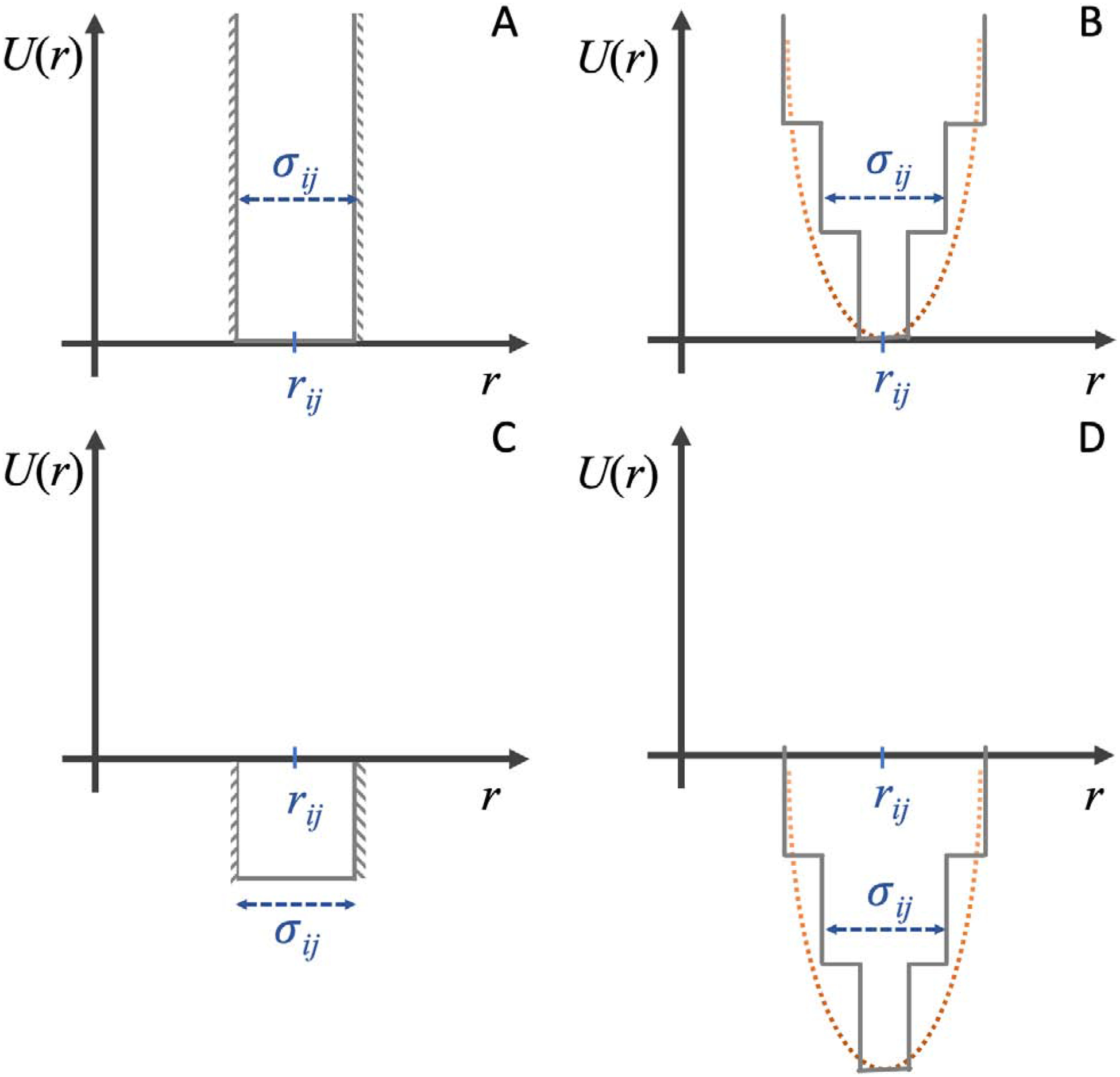
(A) Restrictive constraints enforce residues within a given range. (B) Hookean spring potential is a “softer” analog of potential (A). This potential can be approximated by square-well potential function to enable its implementation in DMD. (C) Biasing constraints make it more favorable for residues to be within a certain range. This potential allows constraints to not be satisfied, which is an important property when constraints, representing distinct states, are in conflict with each other. (D) Hybrid constraints potential between that of (B) and (C).

An important experimental limitation that needs to be considered is that some of the pairwise proximity data set may conflict within itself. The solution to this limitation is described in the Ensemble deconstruction and Conflicting and “dirty” constraints sections below.

The utilization of the pairwise proximity information offers a rapid construction of protein conformations that are consistent with this information [126]. Satisfying each constraint reduces entropy of protein by ΔS ~ ln|i – j| [127], thus driving the conformational ensemble towards the states that satisfy constraints and minimize the free energy of the system.

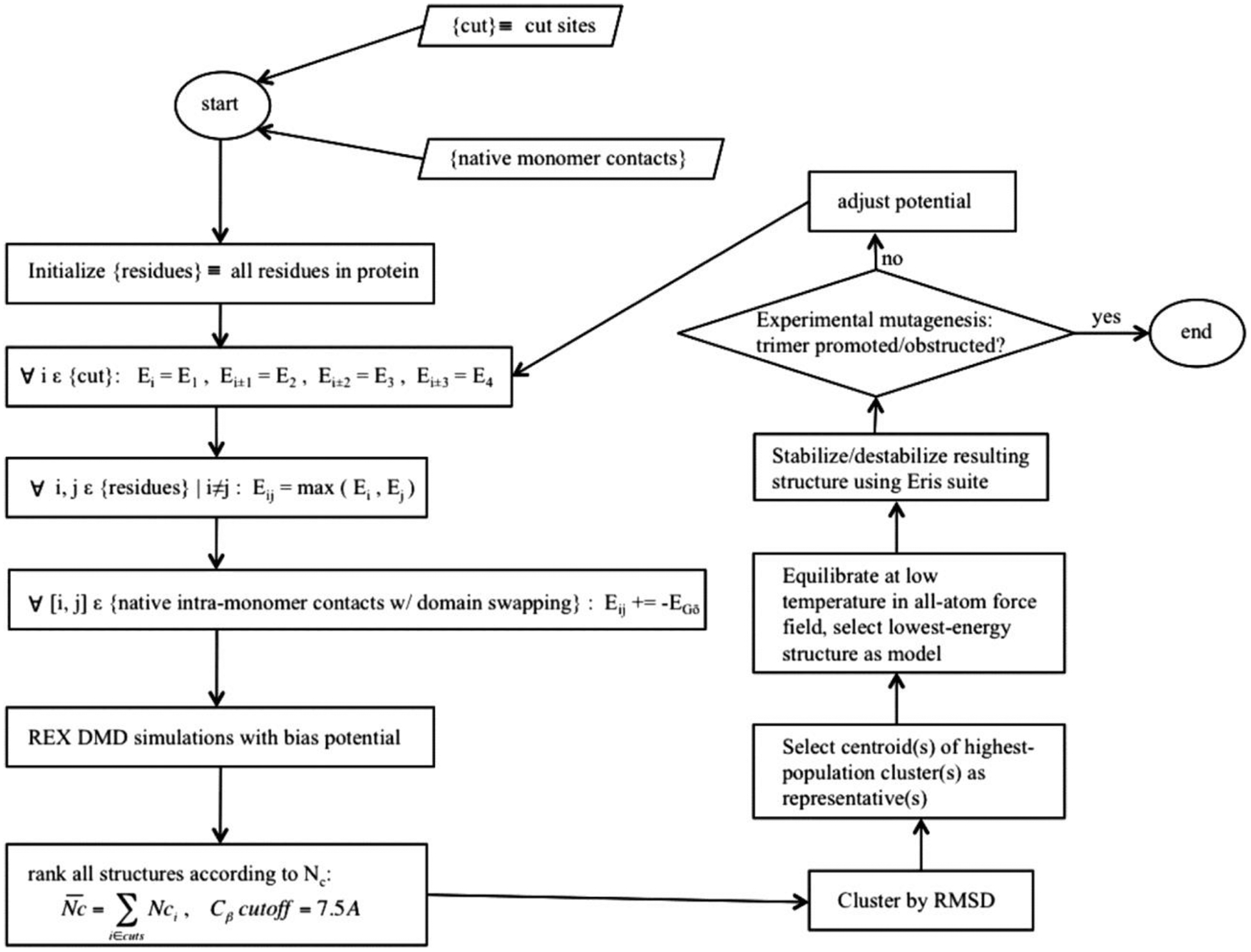
A number of groups develop methodologies for incorporating cross-linking and co-evolutionary constraints [128–130]. Borchers and Dokholyan laboratories developed cross-linking driven DMD engine that streamlines utilization of chemical cross-linking information in DMD simulation [72,131] (Figure 4). This approach has been successfully applied to a number of proteins [131,132], including intrinsically disordered proteins (IDP) [133–135] α-synuclein [72] and tau [71] proteins.

Figure 4. The workflow for CL-DMD protein structure prediction [117].

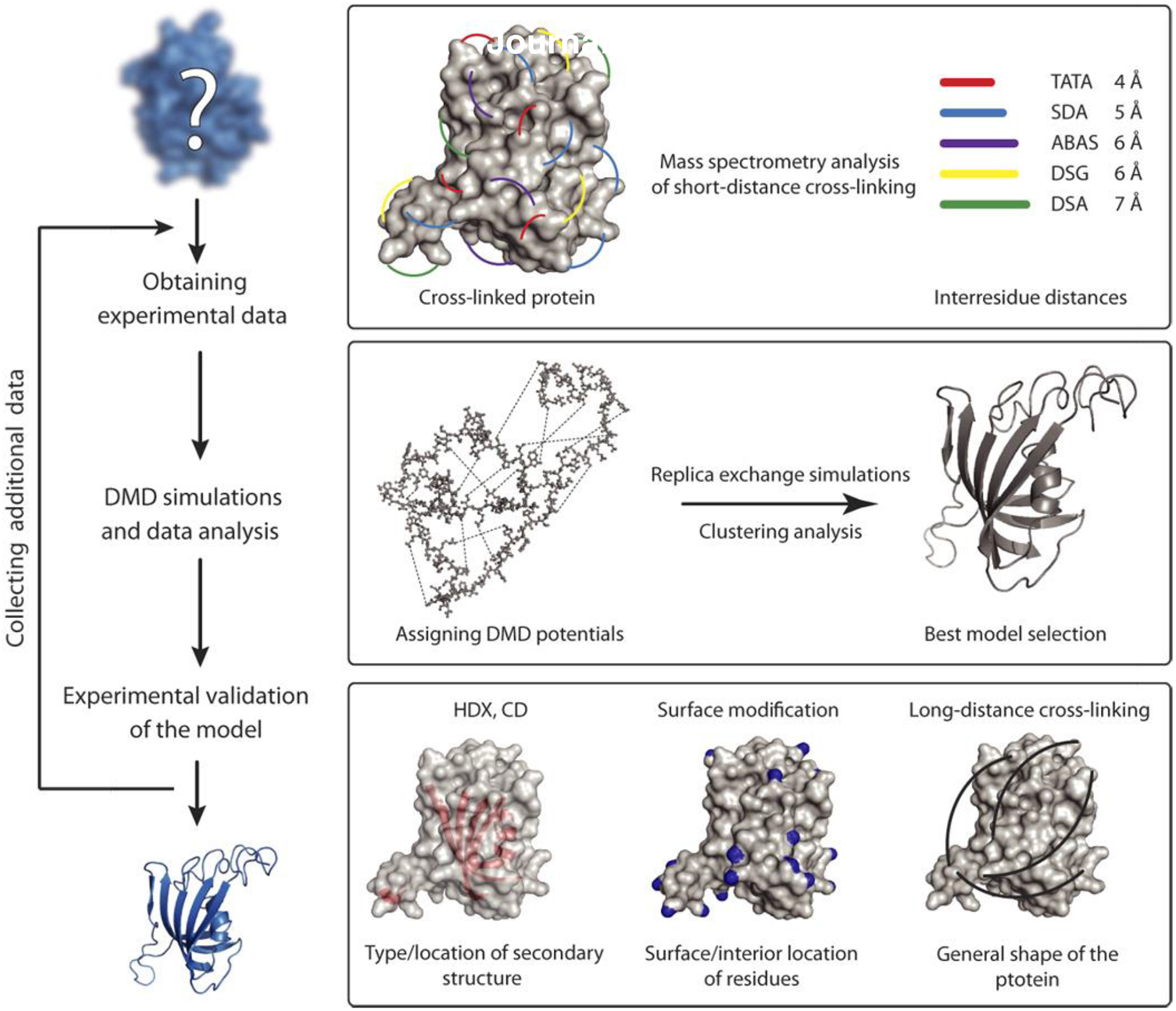
Copyright (2017) Science.

Shape constraint-based modeling

Shape of the protein can be determined using several approaches, such as small angle X-ray scattering (SAXS), atomic force microscopy (AFM), and negative staining EM. Shape can be also used as constraints for building a structure. Many packages utilizing SAXS data build molecular shapes by filling in spheres into the volume and optimizing the shape of the volume until significant match between experimental and computational intensities of scattered X-ray [136–140].

Alternative approaches may include: (i) fitting the shape density profiles to computationally-derived ones by using χ² minimization, similar to Equation (1); (ii) determining shape fingerprints, such as Zernike functions, and matching experimentally derived ones to those coming from known structures [141,142]; (iii) using simulations with biasing potential towards a particular shape. While the last approach has not been implemented for ab initio structure prediction, Dokholyan laboratory uses this approach routinely to bias simulations using experimental constraints [79].

Surface exposure-based modeling

Measuring exposure of various amino acids to solvent can be readily achieved in biochemical and biophysical experiments. Next, we describe several techniques used to perform protein surface mapping.

In a limited proteolysis approach a protein is subject to proteases for a period of time sufficient for a single cut to occur. The conditions are controlled by the buffer and the reaction is rapidly quenched at the time point where we expect a single proteolytic event. This approach requires calibration of protease reaction kinetics through a set of time course experiments. Single cuts are most likely to occur on the surface of a thermodynamically-stable proteins, while cleavable sites are buried in the protein cores. The cleavage sites are readily detectable using mass spectrometry (MS).

In these experiments, thermodynamic stability of a protein determines how noisy is the data. For a two-state protein the ratio of folded versus unfolded state is determined by the equilibrium constant $K_F=\raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$u$}\right.$, where f and u are fraction of folded and unfolded states correspondingly. If K_F ≫ 1, then proteolytic cleavage occurs predominantly in the folded state. In contrast, when K_F~1, cleavage of the unfolded conformations contributes to the signal, thereby mixing folding and unfolding states. Even for marginally stable proteins, limited proteolysis can be a viable approach to determine structures of protein native folded states, although in this case, quantitative MS should be used to determine contribution of each states and deconvolute them using Ensemble deconstruction technique described below.

An important benefit of the proteolysis is that some of the proteases are specific to a particular amino acid sequence epitope. If these proteases do not cleave a protein in a particular specific to these proteases’ sites, this negative information can also be used as a constraint in simulations.

An approach to utilize surface exposure data in simulations was proposed by Proctor et al. [143], who developed a modified Gō potential [144,145] to perform DMD simulations. Gō force field biases the protein towards the native state by assigning attractive or repulsive potential to pairs of residues that are proximal or distal in the native state [67,146,147]. In this approach, experimental data was used as a biasing potential to a native Gō potential [110,144,145], i.e.

$$\text{H}=-{ϵ}_0{\sum }_{i<j}{\Delta }_{ij}{\delta }_{ij}+\lambda {\sum }_{l\in \mathit{\text{cuts}}}{\sum }_{k<l}{\text{E}}_{cut}(j,k),$$ (4)

where the first term is the Gō potential and the second term is the biasing term that is attractive for all potential cut sites that are not cut in experiments, i.e. they are protected, and is repulsive for the potential cut sites that were cut in experiments [143]. Using this potential, Proctor et al, was able to propose a model of a transient trimeric intermediate of superoxide dismutase 1 (SOD1) that appears on its aggregation pathway and has relevance to amyotrophic lateral sclerosis (ALS), discussed below.

Hydrogen-deuterium exchange (HDX) experiments utilize the propensity for amide hydrogens to be replaced by deuteriums when protein is immersed into the heavy water. The exchange rates can be measured by NMR (quantitatively) in the EX2 limit (in which conformational changes occur at faster than the exchange between hydrogen and deuterium) [148] and MS. In the EX2 regime, satisfied for most stable proteins, the protection factor of a given residue, P_f, is a ration of the intrinsic k_rc and an experimentally measured k_ex exchange rates, $P_f=\raisebox{1ex}{$k_{rc}$}\!\left/ \!\raisebox{-1ex}{$k_{ex}$}\right.$. Protection factors are related to residues (k) contributions to the free energy differences between open and closed states:

$$\Delta G_{HDX}={\sum }_k\Delta G_{HDX}(k)=-RT{\sum }_k\text{ ln }{P}_f(k).$$ (5)

There are two approaches to reconstruct protein conformational ensembles using protection factors: one was developed by Vendruscolo et al. [149], and one developed in Dokholyan laboratory [148]. Vendruscolo et al. proposed to minimize the difference between the protection factors determined from the simulated conformational ensembles and experimental ones, in essence, similar to Equation (1). Dokholyan laboratory used protection factors to design a force field that would guide rapid DMD simulations towards ensembles consistent with the observed protection factors. The latter approach is agnostic about physical force field since we generate ensembles based on the force field derived directly from the experiments.

Chemical modifications mapping is another approach to utilize residue reactivity to reagents present in solutions. The modifications of residues exposed to the solvent that reacted with the reagents, can be detected using MS or chemical/physical sensors, such as fluorescent reporter binding at the modification site[150]. The approach to model molecular structure based on chemical modification is conceptually similar to the approaches used for HDX or limited proteolysis-based structure modeling.

Ensemble deconstruction

All described methods result in conformational ensembles, Γ, that are consistent with various experimental data. These ensembles contain information about (meta)stable states, some of them are rare. To uncover these states, clustering of protein conformations is performed based on the pairwise root-mean square distance (RMSD) between all conformations. The clustering procedure partitions the conformational ensemble into states, Γ_k, whose population is the weight of the cluster, w_k:

$$\Gamma ~{\cup }_{k=1}^{N_{cl}}{\Gamma }_k,$$ (6)

where N_cl is the number of obtained clusters. In essence, these clusters represent conformational landscape of a protein [151,152] and the logarithm of weights is related to the free energy of these states:

$$F_k=-k_{B}T\text{ log }{w}_k,$$ (7)

Where k_B is the Boltzman constant and T is the temperature.

Depending on the algorithm, the clustering may depend on one or more free parameter that, in most cases, is/are chosen ad hoc. This threshold or cutoff parameter defines the number of clusters N_cl that one expects to obtain, which requires intuition about the properties of system under consideration. One algorithm, where there is no arbitrary cutoff parameter is based on the physical assumption of criticality, i.e. the partitioning of the protein conformational space is a critical phenomenon. In such case, the number of clusters in clustering critically depends on the order parameter, which is the cutoff. The critical point of this transition is at the midpoint of quazi-first order or second-order phase transition. In the first order phase transition critical points separates two discontinuous phases, and the transition is discontinuous. However, due to the finite size of the system, the boundary conditions do not allow discontinuity and the dependence of N_cl as a function of the cutoff is typically a sharp sigmoidal curve (Figure 6). In the second-order phase transition, N_cl depends on the cutoff also as a sigmoidal curve, although this curve is typically less sharp at the transition point than that in the quasi-first order transition. The advantage of this clustering approach is that it does not require subjective intuition about the number of states in the system. Criticality-based clustering was implemented by Dokholyan et al. [153] to uncover the intrinsic evolutionary relationship between structures of unrelated proteins.

Figure 6. The dependence of the size of the largest cluster on the cutoff parameter, p, is a sigmoidal curve.

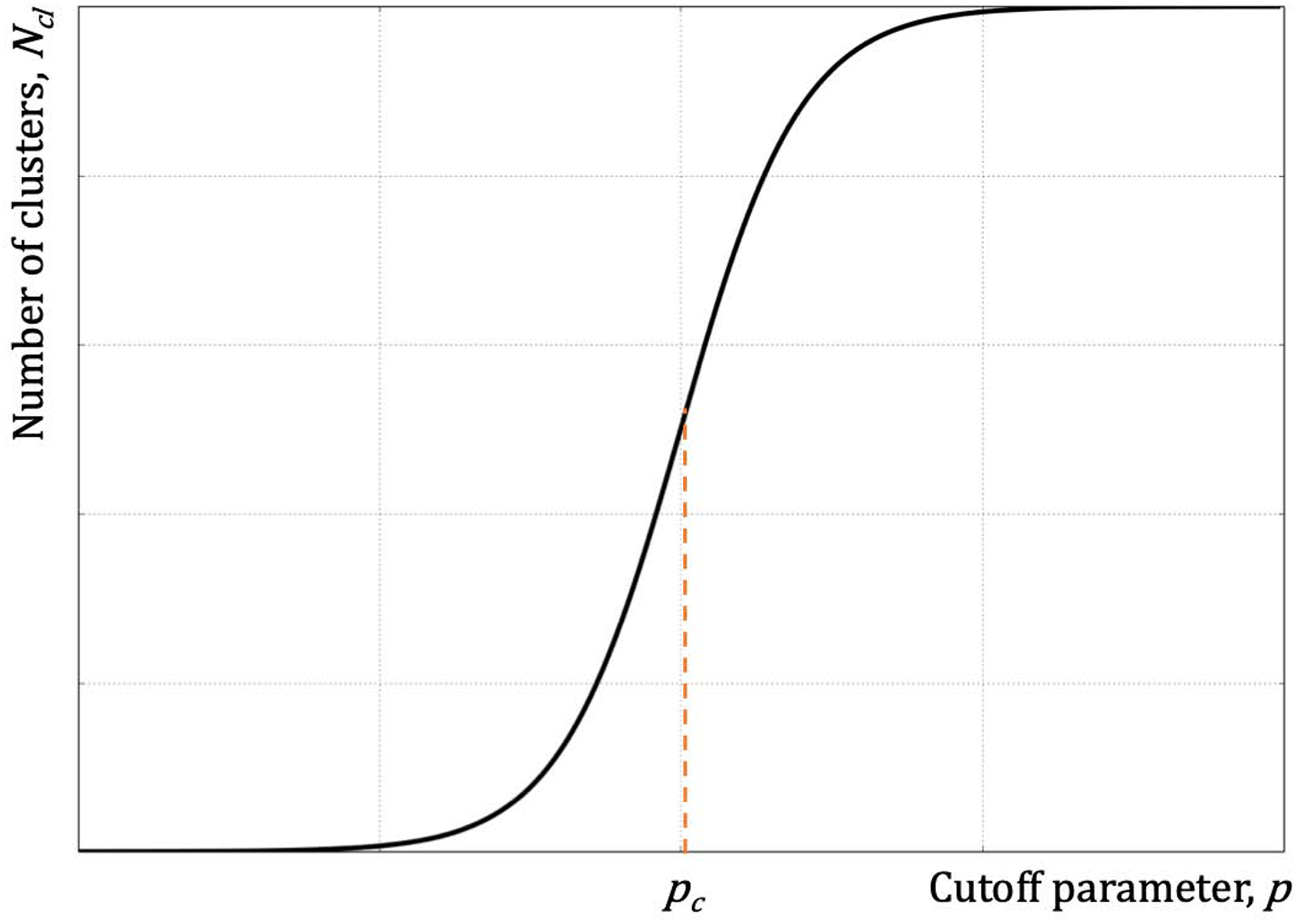
The midpoint of the transition, p_c, denotes the critical regime with the appearance of clusters of all sizes with one maintaining the majority of the elements.

Conflicting and “dirty” constraints

Experimental measurements come with errors stemming from (i) the instrumental inaccuracies, (ii) incorrect interpretation/assignment of measured values (wrong assignment), and, (iii) when dealing with molecular conformations, measurements of variables, that due to insufficient instrumental resolution, effectively represent an average between distinct states (insufficient resolution). Next, we will address methods for mitigating these errors in computational modeling using experimental constraints using protocols established over years in Dokholyan’s laboratory using DMD simulations [110–112,146,147,154–158], although these protocols can be implemented in other simulation packages.

(i) Mitigating instrumental inaccuracies. A hallmark feature of the DMD simulations is the force field that is represented by square-well potentials. In essence, the force field itself can be thought of a set of pairwise constraints between different atom types, U^Medusa(r), (in all atom force field, e.g. Medusa) [159]. Integration of experimental pairwise constraints is then just an addition of the square well potentials, $U_i^{\mathit{\text{cons}}}$, to the main force field with the width, δ, of the square well corresponding to the instrumental variability of the signal (Figure 3).

$$U(r)=U^{\mathit{\text{medusa}}}(r)+w{\sum }_i{U}_i^{\mathit{\text{cons}}}(r),$$ (8)

where w is the relative weight of the constraints and

$$U_i^{\mathit{\text{cons}}}(r)=\{\begin{array}{c}-{\epsilon }_i,d_i-{\delta }_i/2<r<d_i+{\delta }_i/2\\ 0,\mathit{\text{otherwise}}\end{array}.$$ (9)

The depth of the square well, ε, is set to contribute comparatively with other terms of the force field. For simplicity, all the well depth parameters ε_i can be set to a single value ε, unless there is evidence for other experimental biases. The distances d_i between atoms or amino acids are derived from the experimental constraints.

How to choose the weight, w, in DMD simulation? The answer to this question is in the physical properties of a protein. The energy function Eq. (8) defines the folding temperature, hence, the weight is chosen in such a way that the melting temperature of the protein agrees with the experimental value. Hence, the weight should be adjusted in such a way that (a) the constraints terms ${\sum }_i{U}_i^{\mathit{\text{cons}}}(r)$ do not overpower the physical terms U^Medusa(r), i.e. both terms are of the same order of magnitude, and (b) the folding transition temperature matches experimental values. Alternatively, weight w can be chosen by minimizing the square difference of observable parameters measured in simulations and experiments, and identifying the value of w_min, where this difference is minimal.

(ii) Wrong assignments may appear due to human or algorithmic errors in assigning the experimental data to a particular atom/residue(s).

(iii) Insufficient resolution. Lack of experimental resolution may result in overlap/averaging between two or more distinct states and measured value corresponds to a non-physical conformation. For example, if the time scale resolution of experiments is longer than the life time of a protein in either of two states, the measured variable will represent an average between these two states, which may not have any physical meaning (Figure 7).

Figure 7. Superposition of two distinct physical states may have no real physical manifestation.

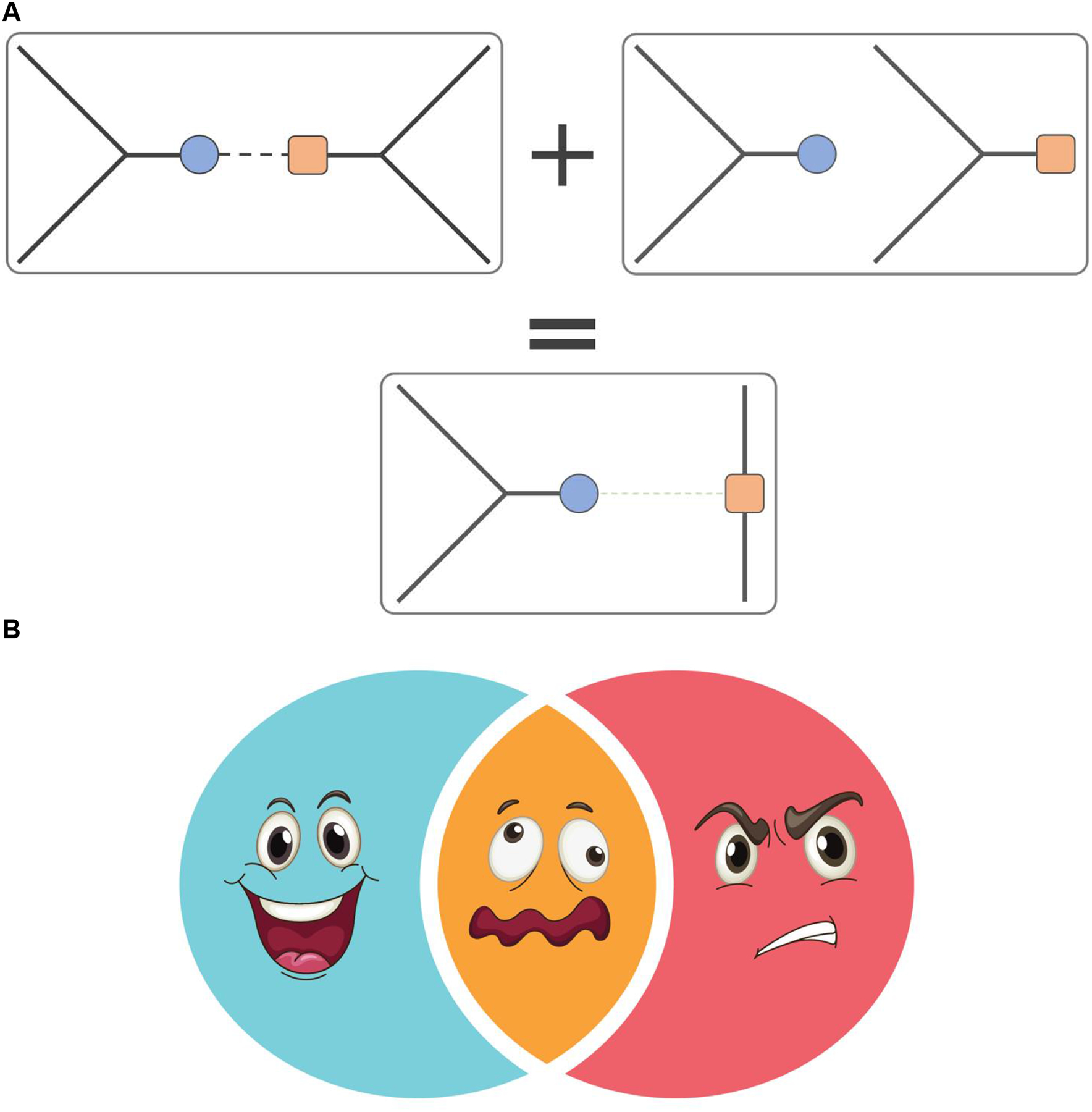
(A) In this example, the peptide bond of the average state is non-physical (bottom) upon averaging structures of two physical states of the ensemble (top). (B) Superposition of happy and angry faces does not result in a neutral one, but rather in not a face.

Both errors (ii) and (iii) are automatically mitigated by the sufficient sampling and the sufficient amount of properly assigned constraints. Clustering typically separates conformational states. Constraints stemming from both wrong assignments and the insufficient resolution would form substates distinguishable from other states because non-physical constraints effectively frustrations in the free energy landscape of proteins [160–162]. These frustrations can be mitigated by extensive sampling that overcomes artificial free energy barriers introduced by these constraints. Thus, identified conformational states can either be physical or artificial. Even if the incorrect experimental constraints dominate the system, a small number of correct constraints may be sufficient to “pull down” physical states [163].

How to distinguish physical states? Any computational study results in a model, and, as such, this model requires validation. Hence, a critical step in any modeling studies is a forward validation step, whereby based on the developed model, one predicts previously-unknown properties of the system. With the advent of protein design, this approach presents a viable and potent tool to perform forward validation of the model protein. For example, in order to determine transient oligomeric states of SOD1, Proctor et al. [143] implemented surface exposure-based modeling by performing limited proteolysis of the isolated oligomers SOD1 and identifying the proteolytic sites using MS. Identified cut sites shape a map of solvent accessibility, which can be used to build model structures of oligomers. For forward validation, Proctor et al. designed mutations that stabilize and destabilize the oligomers, which indeed had corresponding effects in both biochemical and cellular assays.

Additional consideration to keep in mind when applying constraints is that molecular kinetics may play role in how imposed constraints are satisfied, i.e. even if all constraints are representing a single state, the order of the constraints’ satisfaction may have a detrimental impact on whether the molecule can reach the target state. Hence, the constraints should be “soft” enough to allow them to form and break easily, if the kinetics of folding prevents satisfaction of all constraints (Figure 3CD).

Ensemble completeness

How can we make sure that the computational sampling is sufficient? The real answer is never. Ultra-rare state may never be sampled in simulations. Perhaps the most pragmatic question is: when do we know that we have achieved sufficient enough conformational sampling to address particular biological questions? One approach to address this question, is to compare the properties of measured in simulation observables ω derived from trajectories spanning time t and 2t. Indistinguishability of these observables, ω(t) ≈ ω(2t), indicates a plausible convergence of the simulation and an adequate sampling. If these observables vary significantly, ω(t) ≠ ω(2t), then further simulation time doubling is performed until convergence.

Integrated modeling

Complex problems often require complex solutions. Building structural models of multifaceted molecules and molecular complexes may require multiple diverse orthogonal and nonorthogonal experimental interrogations of these molecules. In this complex system, integrating developed algorithms to incorporate different types of constraints offers a direct approach for building structural models. Perhaps one of the most striking examples of integrated model building was developed by Sali laboratory [164], where they were able to build one of the largest complexes in living cells, 50 MDa nuclear pore complex (NPC), which comprises of 456 proteins [165]. Alber et al. integrated a number of different experiments, ranging from crystallography, NMR, cryo-EM, affinity purification and computational modeling to reconstruct NPC [166]. Sali laboratory offers imp package for integrated modeling [137].

Multiscale modeling

Computational or experimental approaches offer only a limited view of the biological processes in living cells, which can span a broad range of time and length scales. For example, studies of electron transport require understanding quantum processes, conformational dynamics, and protein-protein interactions. Over the past two decades many multiscale modeling approaches have been developed that allow spanning sufficiently broad range of the life of a single biological molecule. Many laboratories are moving towards developing multiscale modeling for whole cell simulations. The pioneering work from Schulten’s laboratory [167] demonstrated the feasibility of such approaches. Conceptually, the multiscale modeling workflow consists of approaches that span overlapping but distinct time and length scale regions. These approaches must agree in the overlap regions, and these regions tend to be particularly challenging [158] to model due to inherently different methods used in these approaches. Nobel Prize in Chemistry 2013 (The Nobel Prize in Chemistry 2013. NobelPrize.org) was awarded to Michael Levitt, Ariel Warshell, and Martin Karplus for the development of multiscale approaches in computational chemistry. Since their original pioneering works, a number of computational approaches have been developed to span scales relevant to life of biological molecules [26,168]. Constraintsbased modeling can be incorporated into multiscale modeling workflow at any scale, barring in mind effects those constraints may have on the boundary regions between different scales.

Resolution of computational models

The resolution of structural model is a critical parameter in experimental structure determination, as it allows one to understand the level of “trust” of the determined atomic positions. Likewise, the resolution of computational model is as critical. One approach to evaluate the resolution of a structural model that is used in Dokholyan laboratory is to relate uncertainty in atomic positions from the fluctuations of the molecular structure within a low free energy basin, i.e. resolution of the model is approximated by the root mean square fluctuations over the ensemble of conformations. We perform simulated annealing simulations [169,170], whereby the system gradually is brought to a free energy basin with satisfied experimental constraints. At this point, the root mean square fluctuations of the conformational ensemble determines allowed space for our system, thereby determining the resolution of the structural model. This approached was proposed by Chen et al. [171], and Dokholyan laboratory has used it for internal evaluation of structural models. For example, in attempt to understand the molecular etiology of cystic fibrosis, we build a structural model of the cystic fibrosis transmembrane conductance regulator (CFTR), which revealed that the most common mutation ΔF508 occurs at the interface between the surface of the nucleotide-binding domain 1 (NBD1) and a cytoplasmic loop (CL4) in the C-terminal membrane-spanning domain (MSD2) [172]. We further validated the model by performing cross-linking experiments, which tested the proximity of residues predicted by our structural model. The experiments indeed validated our model. To determine the accuracy of CFTR in the NBD1-CL4 interface, we performed simulations with the constrains imposed by the linkers and, using a protocol described above, determined that our resolution is approximately 3 Å (unpublished). This approach can be broadly utilized for estimating resolutions of structural models based on experimental constraints.

Future challenges

Approaches to model protein structure are becoming increasingly complex and are being integrated into multi-step workflows. Each of the approaches has limitations and the integration often requires explicitly taking those limitations in the consideration. The advantage of these modeling workflows is that they offer one stop solution for building molecular structures. The drawback is that these modeled structures are taking without further validation. Constructions of CFTR [172,173] ryanodine receptor (RyR) [174–177], and the dynein [178,179] models have been particularly challenging because direct modeling workflows failed and we had to resort to manual molecular structure reconstruction. Understanding limitations of each of the step in the modeling workflow and forward validation of computational models in experiments are critical to validity of the molecular models.

The advent of machine learning techniques offers new horizons in our ability not only to build structural models, but also to select models most likely to be resembling “real” proteins. The advantage of the machine learning approaches is in establishing connections in data, otherwise “invisible” to rational thought processes. The disadvantage in such approaches is our inability to gauge whether the constructed structural models are appropriate and truthful representations of the targets. Thus, forward experimental validations of structural models built using machine learning approaches are essential to the validity of molecular models.

Figure 5. The workflow for structural modeling of protein complexes using information derived from proteolytic cleavage of these complexes [143].

Copyright (2016) National Academy of Sciences.

Significance.

Experimentally-driven computational structure modeling and determination is a rapidly evolving alternative to traditional approaches for molecular structure determination. These new hybrid experimental-computational approaches are proving to be a powerful microscope to glance into the structural features of intrinsically or partially disordered proteins, dynamics of molecules and complexes. In this review, we describe various approaches in the field of experimentally-driven computational structure modeling.