Portable system for Time-Domain Diffuse Correlation Spectroscopy

Abstract

We introduce a portable system for clinical studies based on Time-Domain Diffuse Correlation Spectroscopy (TD-DCS). After evaluating different lasers and detectors, the final system is based on a pulsed laser with about 550 picosecond (ps) pulse width and a coherence length of 38 mm, and two types of single-photon avalanche diodes (SPAD). The higher efficiency of the red-enhanced SPAD maximizes detection of the collected light, increasing the signal-to-noise ratio, while the better timing response of the CMOS SPAD optimizes the selection of late photons and increases spatial resolution. We discuss component selection and performance, and we present a full characterization of the system, measurement stability, a phantom-based validation study, and preliminary in-vivo results collect from the forearms and the foreheads of four healthy subjects. With this system we are able to resolve blood flow changes 1 cm below the skin surface with improved depth sensitivity and spatial resolution with respect to continuous wave DCS.

I. INTRODUCTION

REGULATED cerebral blood flow (CBF) warrants adequate delivery of oxygen and glucose to the brain, ensuring cerebral structural integrity and neuronal function. However, impaired cerebral autoregulation in patients suffering from conditions such as shock, stroke, cerebral edema, traumatic brain injury, or those under anesthesia or mechanical ventilation, can cause CBF dysregulation. While CBF management is essential in neuro-intensive critical care, none of the currently available bedside monitors provides a convenient, continuous and reliable measure of CBF ¹.

Near-infrared spectroscopy (NIRS) is non-invasive and uses continuous measurement of the attenuation of light propagating through the cerebral cortex and estimates cerebral blood volume (CBV) and cerebral hemoglobin oxygenation (SO₂). However, neither SO₂ nor CBV are good surrogates of CBF. Hemoglobin oxygenation depends on both perfusion and consumption, and cannot disentangle changes in flow and oxygen metabolism ^2,3. The use of CBV as a surrogate of CBF is based on the Grubb relationship ⁴, which fails during fast dynamic changes ⁵, with disease ^6,7 or altered physiology ^8,9. NIRS can also estimate CBF from manipulations of expired oxygen ¹⁰ or boluses of injected dyes like indocyanine green ¹¹, but these methods are more invasive and cannot provide continuous monitoring.

Diffuse Correlation Spectroscopy (DCS) is a direct way to optically measure microvascular blood flow ^12,13 by using a coherent, near-infrared light source and measuring the speckle interference pattern caused by light scattering events within the tissue. Dynamic scattering of the light by moving red blood cells causes the speckle pattern to fluctuate at a rate proportional to flow rate. These fluctuations are typically detected up to 3 cm away from the source and are quantified by computing the temporal intensity autocorrelation curve of a single speckle lobe^13,14. Typically, the semi-infinite medium solution to the correlation diffusion equation assuming a diffusive motion model is fitted to the decay of the autocorrelation curve to obtain an index of blood flow (BF_i) in units of cm²/s. Although the units of BF_i are not the conventional ml/min/100g, it has been shown to be reliably proportional to absolute flow, as demonstrated by validation studies against “gold standard” measurements, such as arterial spin-labeled MRI ^15–17, fluorescent microspheres ¹⁸, bolus tracking time-domain NIRS ¹⁹, and phase-encoded velocity mapping MRI ²⁰. DCS is mostly sensitive to blood flow in the capillaries and small vessels ²¹, potentially making it a better measure of tissue perfusion than methods such as ultrasound, which measure blood velocity in large supply vessels.

We recently proposed a novel technique called time-domain diffuse correlation spectroscopy (TD-DCS) ^[22], that aims at merging DCS with time-resolved reflectance spectroscopy (TRS) ^23–25. A long-coherence length, pulsed laser introduces light into a sample, and the back-scattered light is collected by single-photon sensitive detectors to acquire the temporal point spread function (TPSF) through the measurement of photon time-of-flight (ToF). The TPSF is the convolution of the impulse response function of the sample with the instrument one ^[26]. Each detector event is time-tagged to record the absolute arrival time of the photons, which allows for calculating the temporal autocorrelation function for DCS. Thus, with TD-DCS it is possible to use TD-NIRS analysis for recovering the tissue optical properties and DCS processing to measure BF_i. Furthermore, the time-resolved detected photon selection provides discrimination between short and long photon path lengths, allowing processing of only late photons that have travelled deeper into the tissue, therefore increasing sensitivity to the brain. This discrimination can be performed at much shorter source-detector separation than the ~3 cm separations commonly used with NIRS ^[27], maintaining depth sensitivity while increasing the signal-to-noise ratio, increasing the spatial resolution, and making the optical probe more compact.

Despite the challenges posed by this technology, TD-DCS is being quickly adopted, and a few systems have been proposed. One group has described a system comprising a custom-made Ti:Sapphire laser operated in the active mode-locked regime at 785 nm and a SPAD detector collecting light 12 mm away from the source ^[28]. The bulky and complex laser used in this system is not suitable for a compact bedside device. Another group has recently presented a TD-DCS system based on a commercial laser module and photomultiplier detectors ^[29], which, similar to our initial work ^[22], only provides sub-optimal performances due to the short coherence length of the laser.

In the last two years, we have worked on determining the optimal commercially available components for a compact TD-DCS system suitable for human subject measurements and built the first portable prototype. The system employs a half-nanosecond pulsed laser and four single-photon avalanche diodes (SPADs) detectors to acquire data from multiple source-detector separations simultaneously. The system includes a custom-made FPGA-based correlator board able to simultaneously measure the ToF of individual photons (micro-time) and the absolute photon arrival times (macro-time). From these, a software routine generates an autocorrelation function at selected time delays. In this paper, we present the comparison between four laser sources and two SPAD detectors, and identify the best components for a portable TD-DCS approach. Finally, we present the device characterization and validation measurements on tissue-like phantoms and in-vivo healthy adult subjects.

II. METHODS

Our novel TD-DCS system is an improved version of the one described in Ref. ²². We have optimized several components to increase the device performance and fit the device into a portable cart.

A. Laser selection

One of the main challenges is the selection of the laser source. TRS works best with the narrowest laser pulses possible, to get a precise impulse response of the sample. DCS, in contrast, requires a long coherence length, and the maximum coherence length for a pulsed laser is limited by the temporal width of the pulse itself. Therefore, a compromise between long coherence length and narrow temporal pulse width is required to simultaneously recover the TPSF curve and to perform the autocorrelation function of the selected photons. In addition, the pulse width and shape affect the pathlength distribution of the photons sampled at a specific time ^[30]. Figure 1a shows a graphic representation of the pathlength distribution of the light collected at a single sampling time for two finite Gaussian-shaped pulses striking a sample. By computing the TPSF as the convolution of the impulse response function of the sample (i.e., sample response function - SRF) with the impulse response function of the instrument (i.e., instrument response function - IRF) ^[26], we sum the contribution of all the possible pathlengths. At a given time t_s (sampling time), the detected photons include a pathlength distribution defined by the area below the product between the SRF and the IRF flipped and centered on the selected time. As the width of the laser pulse increases, the pathlength distribution becomes broader, indicating the inclusion of photons with different pathlengths which interrogated different volumes of the sample. The broad pathlength distribution complicates estimation of the blood flow index by mixing photons arriving at different times ^[30]. We evaluated four lasers with different full-width-half-maximum (FWHM) pulse widths ranging from 70 ps to 600 ps to individuate the best compromise between narrower IRF, and therefore pathlength distribution, and longer coherence length. The first laser is a custom DBR pulsed laser (PH852DBR, by Photodigm Inc.) used in Ref. ^[22]. The other three lasers are Picoquant GmbH products: the CPDL-S-760 and two from the VisIR family (VisIR-765-HP “STED”, called here VISIR-500 and VisIR-765, called here VISIR-70). A specification comparison is shown in Table I.

Fig. 1.

Example of pathlength distributions (dashed areas) of the photons at a sampling time of 1.5 ns. The optical properties used for the sample response function (SRF) are μ_a = 0.05 and μ_s’ = 10 cm⁻¹. (a) Two Gaussian IRFs with 100 ps and 500 ps FWHM, centered on t_s, and the corresponding pathlength distributions. (b) 500 ps Gaussian IRF with the addition of diffusion tails representative of two different detectors and the corresponding pathlength distributions. The IRFs are flipped so that the total delay (sum of the ToF and emission time relative to IRF peak) equals t_s to for the photons in the distribution. Note that the longer tail causes increased contribution of photons with short ToF to the pathlength distribution at t_s.

TABLE I.

Lasers Specifications

Laser name	λ (nm)	Pulse width (ps)	Frequency (MHz)	Average output power (mW)
DBR	850	125	150	≤ 1
CPDL	767	120	≤ 40	∼ 2.5
VISIR-70	767	70	≤ 80	≤ 100
VISIR-500	767	550	≤ 80	≤ 1500

B. Detector selection

Another challenge is the selection of the proper detector. State-of-the art DCS systems are based on single photon counting modules (SPCM) (by Excelitas Technologies Corp.) due to their high photon detection efficiency (PDE), which can reach more than 60% in the 750–850 nm range. Unfortunately, the nearly 300 ps FWHM timing uncertainty of the detected photons makes them unsuitable for properly recovering the TPSF. There are other detector solutions with excellent timing jitter performance, but most have peak efficiency around 400–500 nm and less than 10 % PDE in the NIR range of interest ^[31]-[34]. There are a few detectors with both good timing jitter (100 ps FWHM) and good PDE in the near-infrared (>35 %) ^[35], but they suffer from the contribution of a long diffusion tail ^[36]. Fig. 1b shows the effect on the pathlength distribution of two exponential decays, emulating detector diffusion tails, added to a 500 ps FWHM Gaussian IRF. The longer the tail decay, the greater the contribution of photons that have traveled a shorter path (shorter ToF), resulting in a reduced depth sensitivity at late sampling times. We evaluated two detector modules from Micro-Photon Devices Srl. The first detector (MPD-RE), based on a custom technology SPAD ^[35], has 40% PDE at 767 nm, about a 100 ps FWHM timing jitter and a long 900 ps diffusion tail exponential decay. The second detector (MPD-FG) ^[32], based on a CMOS SPAD ^[33], has 60 ps FWHM timing jitter, 60 ps diffusion tail decay, but only 5% PDE at 767 nm. The comparison aims to evaluate the trade-off between the high efficiency needed to minimize the acquisition time vs. the length of the diffusion tail needed to be kept shorter to maximize depth sensitivity. The dark count rate (DCR) of the two detectors are about 900 (MPD-RE) and 250 cps (MPD-FG). In TD-DCS the detector noise has less impact than CW-DCS because of the selection of the photons in a specific gate leads to the collection of a fraction (gate width over laser repetition rate) of the DCR. In our case, the equivalent DCR per gate is lower than 5 cps.

C. Portable TD-DCS system setup

Fig. 2a shows a schematic diagram of the portable TD-DCS system. The laser (the VisIR-500 was chosen due to its longer coherence length, see results) is coupled to an FC connector, and the maximum output power is limited to below 50 mW for safety reasons. A multimode fiber optical splitter is used to deliver 99% of the light to the target medium. For the measurements reported here, two co-located single-mode fibers (780-HP by Nufern) are used to collect light at a 1 cm distance from the source, and a third single-mode fiber collects light at a 2 cm distance from the source. The system uses four SPAD detectors: three MPD-RE and one MPD-FG. Two of the MPD-RE modules are used to detect the light at 1 and 2 cm and compare results at different source-detector separations, and one is used to collect the IRF from the attenuated 1% output of the laser and to continuously assess laser stability. The MPD-FG SPAD also collects the light at 1 cm separation, and is used to evaluate the trade-off between the diffusion tail decay and PDE at the shorter distance.

Fig. 2.

Block diagram of the system setup, where three MPD-RE detectors are used to measure the IRF and the light collected at 1 and 2 cm away from the source. A MPD-FG module collects the light at a 1 cm separation from the source. For the laser source, we chose the Vis-IR 500 because of the longer coherence length. A correlator board acquires the ToF measured by TDC-cards and pairs this information with the absolute arrival time of the photon, then transfers the data to a PC via USB 3.0. (b) A photo of the system, showing an enlarged view of the optical probe (the probe has also a 15 mm separation, not used in this work).

The detector’s outputs are routed to four time-to-digital converter (TDC) cards ^[37] to measure the photon ToF with 10 ps resolution and a timing jitter of less than 50 ps FWHM. The detector signals are also sent to the four-channel FPGA to tag each detection event with the result of the TDC card as well as the value of a 150 MHz clock reference so that each photon from all four channels has a record of both the micro-time (from the TDC card) and the macro-time (from the 150 MHz clock) of its detection. All results are transferred to the PC through a USB 3.0 interface.

A clock synthesis and distribution board is used to control the laser repetition rate, based on a low-jitter programmable clock oscillator (Si514 family, by Silicon Laboratories Inc.). A multi-output clock distribution circuit (AD9512, by Analog Devices Inc.) creates the laser trigger and the TDC-card signals for the ToF measurement. A programmable delay line (NB6L295, by ON Semiconductor) is used to synchronize the two copies of the clock signal.

The portable TD-DCS system is approved by theInstitutional Review Board (IRB) for Partners Healthcare, the Partners Human Research Committee (PHRC), to be used on human subjects. All the components are secured inside a 61×46×122 cm³ enclosure on a wheeled cart, as shown in Fig. 2b. In the front of the cart, there is a door to access the laser hardware controls and the fiber connectors for the optical probe. The optical fiber probe is ultra-light, low-profile and flexible to easily fit on the head. To minimize the probe profile, we used optical prisms placed inside an elastomeric 3D printed probe. A 60° holographic diffuser between the source fiber and a 1.5 mm prism, expands the source light beam to greater than 1 mm in diameter, allowing us to use up to 26 mW at 766 nm while remaining within the ANSI cutaneous Maximum Permissible Exposure (MPE) to laser radiation, as specified in the ANSI Standard Z136.1–1993 Table. The light is then collected by four 4 μm single-modefibers, to allow detection of single speckles, at 1 and 2 cm from the source. The first 10 cm of the fibers are protected only by a thin black plastic coating (125 μm diameter) to maximize flexibility and minimize weight. Then the fibers are bundled inside a protective jacket that facilitates handling and safeguards them from possible damage. The fiber bundle exits via a port in the rear panel, together with the power cord and four BNC cables used as auxiliary channels to record trigger signals or synchronization signals from other devices. On the rear panel, there are two AC-powered fans to cool the electronics. Power is provided through an Uninterruptible Power Manager (by Powervar) to both filter the AC supply voltage and prevent unexpected shut downs. There is a safety shutoff switch on the right side of the cart to shut down the laser in case of emergency.

D. Laser repetition rate considerations

For TD-DCS, the repetition rate of the laser (f_L) and the clock frequency used by the correlator board to measure the macro-time (f_S) must be chosen to ensure a constant probability of detecting a photon within each macro-time period of the f_S to avoid causing artifacts in the autocorrelation function. In continuous wave (CW)-DCS this is guaranteed by a stable, constant light intensity within 1/f_S, while TD-DCS requires having the same integer number (n) of laser pulses for each f_S period (f_L = n f_S). This can be done by setting f_L to an integer multiple of f_S and synchronizing the laser frequency to the correlator board clock. In our case, since f_S (150 MHz) is larger than f_L (max laser repetition rate 80 MHz) we performed resampling correction by setting f_L to 12.5 MHz so that f_s is an integer multiple of f_L, and then, to restore the f_L = f_S relationship, we resampled each macro-time with 1/f_L time-resolution. In cases where it is not possible to have f_s and f_L integer multiples of each other, one can use jitter correction to artificially compensate for the non-uniformity of the light within each sampling period by adding a random jitter value from 0 to 1/f_L to each absolute arrival time to destroy correlated structure on the timescale of the jitter (the artifacts are most prominent at the early, narrow time-lag bins). Fig. 3 shows an example of an intensity temporal autocorrelation function (g₂), where f_S is an integer multiple of f_L and either resampling or jitter correction is independently applied to remove the pattern introduced by the light non-uniformity within the sampling periods. The oscillations in the blue curve scale down every time the correlator algorithm doubles the bin size, and disappears when every bin contains the same number of laser pulses; in this case above 20 μs. The two correction algorithms have equivalent performance, and either one is able to remove the artificial pattern in the g₂ providing a clean curve.

Fig. 3.

Autocorrelation functions (g₂) of the CW equivalent photons (i.e. using the whole TPSF) when using a 12.5 MHz laser repetition rate (fL), 150 MHz correlator sampling frequency (fS), and 1 cm source-detector separation. For these measurements, we used a silicone oil liquid phantom with a very slow decay (in the 100 μs to 1 ms range) to achieve a constant pattern in the μs range and better visualize the oscillations. The g₂ curve computed without any correction shows oscillations which are due to the fact f_L is not equal to nor an integer multiple of f_S. By applying either a jitter or a resampling correction the oscillations are completely removed.

E. Phantom measurements

We validated the TD-DCS portable system with measurements using two tissue-like liquid phantoms, each with a different viscosity. The aqueous phantom uses a mixture of 1600 ml water, 50 ml of 20% Intralipid suspension (by Fresenius Kabi) and 4 ml of 0.4% diluted black India ink to achieve a reduced scattering coefficient (μ_s’) of 6.5 cm⁻¹ and an absorption coefficient (μ_a) of 0.05 cm⁻¹ at 767 nm. The second is a silicone oil phantom, much more viscous than water, with white pigment to match the scattering of the Intralipid-based phantom and μ_a = 0.04 cm⁻¹. The silicone oil phantom provides a slow decay of the autocorrelation function (between 10⁻⁴ and 10⁻³ seconds), and is used to evaluate the g₂ curves and estimate the laser coherence properties of the different lasers, while the Intralipid-based phantom provides a faster decay.

The two phantoms were also combined to perform a two-layer phantom experiment. The silicone oil floats on water, so it is possible to have a layer of silicone oil floating on top of the Intralipid. The goal of this experiment is to evaluate the ability of TD-DCS to distinguish the superficial and deeper layer BF_i by selecting photons with different ToF, and to compare it to CW-DCS. We started by measuring the silicone oil and Intralipid-based phantoms alone for reference, and then we repeated the measurements on the lower Intralipid layer with a top layer of silicone oil of thickness varying from 5 to 20 mm at 5 mm steps. For each step, we acquired data for 10 minutes to collect about 10 million photons at late gates with a 2 cm source-detector separation. The more viscous silicone on top of the more fluid intralipid layer is meant to mimic the superficial vs. deep layers in vivo, for example in the context of brain or muscle measurements.

In a second liquid phantom-based experiment, called the flow experiment, we used a 2-mm diameter Teflon transparent tube with a very thin wall immersed 10 mm deep into an Intralipid-based phantom prepared according to the recipe described above. The tube was connected to a syringe filled with the same Intralipid solution and an automated pump that was used to provide a constant axial velocity of 2 mm/s inside the tube. The goal of this experiment was to evaluate both the depth sensitivity and the spatial resolution of TD-DCS by comparing results with or without flow in the tube, and by scanning the optical probe across the tube. For the scan, we assigned x = 0 to the tube under the source and thus the tube under the MPD-FG detector was located at x = 10 mm. We started at x = −10 mm and moved to x = 30 mm in 5 mm step increments. At each position, we acquired data for 5 minutes, both with and without flow in the tube.

F. Human subject measurements

To show feasibility in humans, we performed experiments in four adult volunteers by measuring blood flow in the forearm muscle and in the forehead. The study protocol was reviewed and approved by the Institutional Review Board (IRB) for Partners Healthcare and the Partners Human Research Committee (PHRC). The study method was designed and carried out in accordance with PHRC requirements and the regulations that govern human subject research. The first experiment, called the forearm cuff occlusion experiment, consisted of monitoring the blood flow on the forearm before, during, and after 30 seconds(s) of arterial occlusion. The TD-DCS fiber optic probe was secured to the forearm of the subject and data was acquired for 30 s of baseline, 30 s of occlusion created by applying a cuff pressure of 180 mmHg to the upper arm, and 60 s of recovery after the cuff was relaxed. We repeated the protocol twice for each subject, and we acquired the pressure trace through an analog input channel of the system. During occlusion, blood flow is stopped everywhere in the forearm and we expect to see changes at both the early and late gates. The goal of these measurements is to demonstrate the ability of the system to acquire dynamic BF_i changes in-vivo. The second experiment, called the forehead pressure experiment, consisted of monitoring blood flow while changing the pressure applied to the skin under the optical probe. The optical probe was secured on the forehead of the subject with an elastic bandage and we applied a light pressure by hand on the probe for 30 s, every 2 minutes. This perturbation changes the blood flow through the skin outside the skull without changing the blood flow in the brain ^[38], therefore, we expect to measure larger changes in the blood flow at early gates (scalp) than at late gates.

G. Data analysis

For both phantom and human experiments, we present TD-DCS BF_i results at two gates: from 240 to 120 ps before the TPSF peak, called early photons (EP) and from 360 to 720 ps after the TPSF peak, called late photons (LP). Since there is plenty of signal for the EP gate, we chose a narrower gate width of 120 ps to maximize the coherence factor beta (beta = g₂(τ=0)-1) ^[30]. On the other hand, to increase SNR for the LP gate, we chose a wider gate width of 360 ps, with a tradeoff between increasing the number of detected photons and decreasing beta. The center-to-center distance between the two gates is about 700 ps, resulting in an average pathlength difference of about 14 cm. Only for the two-layer experiment we present additional results by using very-late and ultra-late photons (VLP and ULP, respectively 720 to 1080 ps and 1.08 to 1.44 ns after the TPSF peak), resulting in an average pathlength difference, with respect to the EP, of about 21 and 28 cm.

For the phantom experiments, in addition to TD-DCS, we also performed measurements with a CW-DCS device. This custom-built CW-DCS device has four photon-counting detectors (SPCM-850–14-FC, SPCM-NIR series by Excelitas Technologies) and a long coherence length laser at 767 nm (PH767DBR, by Photodigm Inc.). The CW-DCS measurements were performed simultaneously with TD-DCS, keeping the two optical probes far enough from each other to avoid optical cross-talk. For the CW-DCS measurements, we used source detector separations of 1, 2, and 3 cm. The TD-DCS blood flow fitting was performed offline using MATLAB®, and takes into account the finite coherence length of the laser, the pathlength distribution due to the gate width, and the finite IRF. Equations and details of this analytical model are reported in Ref. ^[30].

III. RESULTS

A. Laser comparison

During development of the portable TD-DCS system we first evaluated the performance of four commercially available lasers. The DBR and CPDL-S lasers are more compact and less expensive than the VisIR lasers, but they provide less than 1 mW average output power at the probe, resulting in a count rate lower than 50 kcps at a 1 cm source-detector separation. Photon selection within a specific narrow gate further reduces the amount of detected signal, resulting in longer acquisition times to achieve sufficient SNR for these detectors. The high output power of the two VISIR lasers considerably reduces acquisition time. They provide 30 times more signal than the DBR and CPDL-S lasers while still complying with ANSI standards for skin exposure. The IRF of the four lasers are measured with the MPD-FG and are shown in Fig. 4a. After removing the jitter contribution ³⁹ of both the TDC-card and the MPD-RE detector, we estimated the widths to be respectively, 64, 122, 124 and 574 ps FWHM for the VISIR-70, CPDL-S, custom DBR, and VISIR-500 lasers.

Fig. 4.

Pulse width comparison (a) and g₂ comparison (b) of the four lasers tested. The g₂s are evaluated on a silicone oil liquid phantom at 1 cm source-detector separation, while selecting the photons in a gate of 60 ps centered at the TPSF peak. For narrower laser pulses, the g₂ are much lower because of the shorter coherence length.

While narrow pulses are preferable for time resolved systems, a narrower pulse means a lower coherence length, which for DCS means a g₂ curve closer to the noise floor. In fact, the maximum amplitude of g₂ depends on the coherence length of the laser, with beta ranging from 0 for incoherent light to 0.5 for unpolarized light with coherence length longer than the longest photon path through the illuminated media. We compared the g₂ and beta of the four lasers, using measurements on the silicone oil phantom at a fixed narrow gate (60 ps) centered on the peak of the TPSF (Fig. 4b). To achieve a similar noise level, the VISIR lasers’ results are based on 10 seconds of data, while the CPDL-S and the DBR results are based on 300 seconds of data. As expected, the lowest beta (0.05) corresponded to the narrowest pulse of the VISIR-70 and both the DBR and the CPDL lasers, with about 120 ps width, reach a slightly higher beta of 0.1. The highest beta of 0.43 is provided by the VISIR-500, which is very close to the 0.5 maximum value for unpolarized light.

To evaluate the coherence length of this laser, we measured the dependence of beta on gate width. We collected a 300 s measurement and, for each gate, we computed a g₂ curve every 3 s. In Fig. 5, we show the beta value (as average and standard deviation of the 100 g₂s) when increasing the width of the gate from 10 to 500 ps in 10 ps steps, with the gates centered on the TPSF peak. The beta decays when increasing the gate width, and the decay trend depends on the coherence length of the laser ³⁰. Fig. 5 shows a decay slope change at ~180 ps, so we estimate the laser coherence length to be L_C ≃ 180 ps × c/n ≃ 38 mm, where c is the speed of the light and n (=1.4) is the refractive index of the phantom. We performed the same measurements with the other lasers, using gate widths from 10 to 100 ps in 10 ps steps, but we were unable to find a constant beta, suggesting that the coherence length of these three pulsed lasers is less than 5 mm.

Fig. 5.

Beta measured at different gates centered on the TPSF peak. We changed the gate width from 10 to 500 ps (roughly the FWHM of the VisIR-500 laser). The beta drop changes slope around 180 ps, that corresponds to the coherence length of the laser (~40 mm).

Despite the very wide pulse, non-transform limited coherence length, non-Gaussian shape, and pre-peaks of the VisIR-500, we chose this laser for our TD-DCS system due to the higher beta and higher output power compared to the other three commercially available solutions.

B. Detector comparison

To assess detector performance for TD-DCS, we first compared the IRF of the VISIR-500 as acquired with two detectors. As shown in Fig. 6, the MPD-FG (green IRF) measures an IRF with a fast extinction ratio, dropping by almost 30 dB in less than 1 ns. In contrast, the MPD-RE (blue IRF) presents an extinction time of more than 5 ns. The diffusion tail of the MPD-RE is also affected by the laser pulse width. When measuring the IRF of the VisIR-70 (red IRF) with the MPD-RE detector the IRF drops by 30 dB in about 3 ns. Fitting the exponential decay tails of the two IRFs (dashed magenta line) reveals that both lines have similar decay slopes, suggesting that the mechanism of the decay is the same. Unfortunately, the starting point of the tail is higher with wider laser pulses, causing longer decay at critical time delays.

Fig. 6.

IRF comparison using the two detectors. The MPD-FG IRF (green) has a fast extinction time of 585 ps to drop two orders of magnitude, while the MPD-RE IRF (blue) takes about 2.28 ns. A measurement of the VISIR-70 and VISIR-500 lasers (blue vs red curve) both acquired with the MPD-RE shows the effect of the source width on the long diffusion tail. For an increased pulse width, the diffusion tail contribution starts higher (at −13 dB instead of −18 dB).

While the good temporal response of the MPD-FG is preferable to better discriminate late from early photons (Fig. 1b), the problem with these detectors is their low efficiency at 767 nm. The MPD-FG efficiency is about 5 % at 767 nm, some 8 times lower than the efficiency of the MPD-RE (about 40% at 767 nm). As a result, with the MPD-RE we can acquire faster and at larger source-detector separations. For our system testing, we decided to use both detectors, positioning the MPD-FG at 1 cm from the source and two MPD-RE detectors at 1 cm and 2 cm from the source.

C. System stability

The stability of the system was evaluated by monitoring the intensity, peak position, and pulse width of the IRF (acquired with the last MDP-RE detector, after the splitter and the attenuator, as shown in Fig. 2a) over a long acquisition time. The acquisition started as soon the system was turned on, while keeping the laser off. After about 2 minutes the VIsIR-500 laser was turned on, and data was collected for about 140 min. Fig. 7 shows the results, where the light intensity is plotted as the count rate of the SPAD (black line), normalized to the average intensity of the last one hour data.

Fig. 7.

Normalized count rate (black, left y-axis), IRF peak position (blue, right y-axis), and IRF FWHM (green, right y-axis) for a long acquisition time. The system stabilizes after about 25 minutes of warm-up time.

Within the first 25 minutes there is an overshoot of less than 20% with about 10% fluctuation. After this warm-up time, the count rate becomes stable with fluctuations less than 1%. Similar results are found for the peak position (blue line with y-axis on the right), which shows a slight shift of about 20 ps during the warm-up time, after which it stabilizes to around 510 ps with a ± 10 ps uncertainty due to the quantization error of the TDC (10 ps resolution). Finally, after the warm-up time, the IRF FWHM (green line with y-axis on the right) settles to 574 ps with a deviation below 10 ps.

D. Two-layer experiment

The two-layer experiment aims to test the improvement in depth sensitivity of the portable TD-DCS by selecting late photons. For this, we present a comparison of autocorrelation curves computed using early photon (EP) and late photon (LP), selected from the early and late gates mentioned previously.

Figure 8a–i shows the position of the two gates on the TPSF (a, d, and g), and the respective autocorrelation functions for all the homogeneous and layered phantoms for the MPD-FG detector at 1 cm separation, and for the two MPD-RE detectors at 1 and 2 cm separation (top to bottom). Due to the similar optical properties of Intralipid and silicone oil, the TPSF of all phantoms only differ at very late times.

Fig. 8.

Results of the two-layer experiment. On the TD-DCS side, the g2 of the early (EP, 240 to 120 ps before the TPSF peak) and late (LP, 360 to 720 ps after the TPSF peak) photons show a large decay time difference between the Intralipid (IL) and the silicone oil (SO) phantoms, while the normalized TPSFs show minor differences due to the small difference in optical properties. For all detectors, the g₂ of the 20 mm top-layer is close to the silicone oil one. When selecting the late photons, the g₂ of the 0.5 and 1 cm top-layer phantoms show a decay closer to the Intralipid. On the CW-DCS side, the difference in the g₂ decay between intralipid and silicone oil is evident at all source-detector separation. For the two-layer phantoms, the g₂ show a decay closer to the one of the bottom layer whenthe top layer is thin and the source-detector separation is larger.

Despite the noise, the difference on the TPSFs at 1 cm separation is more evident for the MPD-FG (a) than the MPD-RE because of the contribution of early photons to the MPD-RE tail. At 2 cm separation, the early photons’ contribution is lower and the difference between the phantoms is visible in the TPSFs with the MPD-RE (g). For the g₂ curves, the silicone oil (dark blue) has a much slower decay time with respect to the Intralipid (black) homogeneous phantom.

By adding a layer of silicone oil on top of the Intralipid-based phantom, the autocorrelation curves are closer to the g₂ of silicone oil or Intralipid depending on the top layer thickness, gate time, and detector. Specifically, for early photons and 1 cm separation (panels b and e) only the g₂ of the 5-mm top-layer phantom shows some sensitivity to the Intralipid (bottom layer). Sensitivity to the bottom layer increases with source-detector separation, as shown by the 2 cm results (panel h) where the g₂ of the 5-mm top-layer phantom is closer to the Intralipid g₂, and the g₂ of the 10-mm top-layer phantom presents a faster decay than the g₂ of silicone oil.

When selecting late photons, the decay of the g₂ of all the two-layer phantoms shows some sensitivity to the bottom layer, even if limited to the 20 mm top-layer phantom. By selecting a later gate than the one chosen here, it would be possible to further improve sensitivity to the bottom layer, but the lower number of photons at these gates would require a much longer integration time.

Figure 8j–l shows the results of the CW-DCS measurement on the same set of phantoms at 1, 2 and 3 cm source-detector separations.

To better quantify the differences between TD-DCS EP and LP and CW DCS we computed the BF_i for each g₂ and normalized results between the minimum BF_i of the silicon oil (min = 0) and the maximum BF_i of the Intralipid (max = 100). Figure 9 shows the normalized BF_i versus layer thickness, where the LP of TD-DCS at 2 cm separation (solid black line) has highest sensitivity to the bottom layer. TD-DCS LP at 1 cm (solid blue and brown lines) is comparable to CW-DCS at 2 cm (solid magenta line), suggesting that the late 1 cm separation measurement travel to a similar depth as the bulk of the photons for 2 cm separation. The MPD-RE and MPD-FG detectors presented minor differences due to the different detectors tails. TD-DCS EP at 2 cm (dashed black line) has the same sensitivity to CW-DCS at 1 cm (solid green line).

Fig. 9.

Comparison of the normalized BF_i at different thickness between TD- and CW-DCS. TD-DCS with LP at 2 cm separation shows the maximum sensitivity to depth, while LP results at 1 cm are comparable to CW-DCS at 2 cm. The sensitivity is good up to 15 mm layer thickness, and becomes poor at 20 mm.

Figure 10 shows the sensitivity achievable by pushing the selection of the photons to later gates (very-late and ultra-late photons, VLP and ULP). When selecting ULP both the MPD-FG at 1 cm (Fig. 10a) and the MPD-RE at 2 cm (Fig. 10c) measure about 20% of the bottom layer BF_i at 15 mm top layer thickness. In this case, the 2 cm separation doesn’t have a better sensitivity due to the effect of the MPD-RE detector tail, despite being a limited effect at such separation thanks to the TPSF (Fig. 8g) which has a slower decay than at 1 cm (Fig. 8a and d). In fact, for the MPD-RE at 1 cm the ULP gate is clearly at the beginning of the tail decay in Fig. 8d because not only do the VLP and ULP sensitivity profiles (Fig. 10b) fail to increase, their sensitivity also decreases even when the top layer is thin. The error bars in Fig. 10 show how the SNR is limited for the later gates.

Fig. 10.

Comparison of the normalized BF_i (average and standard deviation obtained by splitting the measurement in 60 parts of 10 s each) at different thickness between the MPD-FG (a) and the MPD-RE (b) detectors at 1 cm and the MPD-RE at 2 cm (c) separation when pushing the selection of photons to late gates, up to 1 ns after the TPSF peak. The sensitivity of the MPD-FG increases while the MPD-RE at 1 cm starts losing sensitivity at thin layer due to increasing contribution of the diffusion tail. The MPD-RE at 2 cm is less penalized by the detection tail thanks to the slower decay of the TPSF at larger source-detector separation, but the sensitivity at very-late and ultra-late gates (VLP and ULP) is not improved as in the MPD-FG detector.

Looking back at Fig. 8 we note it provides an additional performance comparison between the MPD-FG and the MPD-RE detectors. The lower efficiency of the MPD-FG detector affects both the TPSF and the autocorrelation curves. The noise floor in the TPSF is higher for the MPD-FG (a) than the MPD-RE (d) at 1 cm, and the g₂ curves at both EP and LP gates are noisier for the MPD-FG detector. On the other hand, the longer diffusion tail of the MPD-RE results in a bigger drop in the beta value for the g₂ at late photons (f and i) with respect to the MPD-FG (c).

E. Flow experiment

To further evaluate the depth sensitivity and spatial resolution of our TD-DCS prototype, we measured a flow phantom consisting of a 2 mm diameter tube submerged 10 mm below the surface of an Intralipid-based solution. Figure 11 shows the relative BF_i ratio between the BF_i measured when the Intralipid is flowing vs. when it is static, measured with the TD-DCS and CW-DCS systems scanning the optical probes across the tube.

Fig. 11.

Results of the flow experiment when the source-detector separation is 1 cm (a) and 2 and 3 cm (b). The highest contrast is achieved when the tube is centered between source and detector: x = 5 mm (a), x = 10 mm (b) and x = 15 mm (b, orange curve). At 1 cm source-detector separation, the flow is not detected by the early photons (EP), while the maximum flow contrast is obtainable when selecting the late photons (LP) and using the short tail detector (MPD-FG, brown line). Similar results are obtained at 2 cm source-detection separation. CW-DCS at 3 cm (orange) provides lower contrast and spatial resolution than LP TD-DCS.

For the detectors at 1 cm separation from the source (Fig. 11a) x = 5 mm corresponds to the tube being centered between source and detector. The tube is most visible and the relative BF_i is the highest at that location. The tube is not resolved by the EP (dashed curves). The BFi contrast is 23 ± 3% for CW-DCS, while the contrast for the LP gate is higher, 32 ± 16% for the MPD-RE and 67 ± 22% for the MPD-FG detectors. By pushing to the VLP gate of the MPD-FG, the contrast reaches 182 ± 91%, very noisy due to the low number of photons in this late gate. For a source detector separation of 2 cm (Fig. 11b) x = 10 mm corresponds to the tube centered between source and detector and the measured flow is again highest there. Also, in this case the contrast is higher for the TD-DCS LP than for CW-DCS at the same separation.

The contrast for the 2 cm TD-DCS LP is 102 ± 35%, that is higher than the maximum contrast for CW-DCS at 3 cm (peak contrast is 84 ± 44%) at x = 15 mm. The LP MPD-FG at 1 cm show equivalent contrast to the CW-DCS at 3 cm, but much better lateral resolution. The FWHM of the relative BF_i linear scan is about 10 mm, as opposed to 18 mm for the MPD-RE at 2 cm, or 26 mm for the CW-DCS at 3 cm.

F. Forearm cuff occlusion experiment

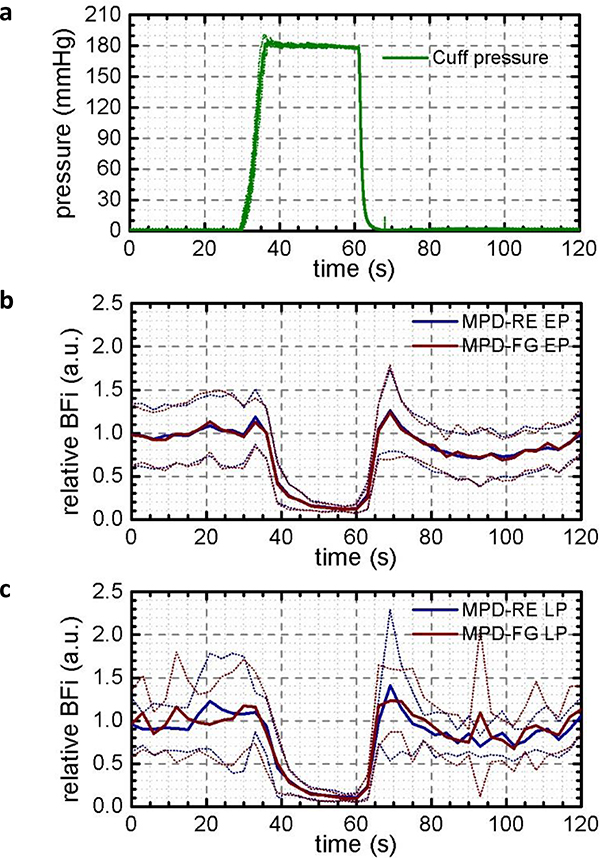
We validated the portable TD-DCS system on four healthy adult subjects. We attached the TD-DCS probe to the forearm. Ischemia measurements were performed by placing the cuff on the upper arm and inflating it to a pressure of 180 mmHg to block both arterial and venous blood flow for 30 seconds, then deflating it to restore normal circulation.

We computed a BF_i value every 3 s as a trade-off between a sufficiently long averaging time to maximize the SNR and a sufficiently short one to get the flow dynamics. Despite the 3 s integration, for data at 2 cm this did not provide sufficient SNR, and is not shown.

In Fig. 12, we report the results as the average of all eight measurements with two repetitions for each of the four subjects. Fig. 12a shows the average cuff pressure across all measurements and the variability across subjects calculated as the mean and standard deviation of the cuff pressure. The application of the pressure is very repeatable (pressure error < ±2 mmHg), with a variation lower than ±1 s in duration.

Fig. 12.

Results of the cuff occlusion experiment. Cuff pressure shown in panel (a), blood flow index when selecting early photons (b) and late photons (c) at 1 cm source-detector separation. In both cases, and with both detectors, we see BF_i drop to almost zero during ischemia. At late gates, the higher efficiency of the MPD-RE (blue curve) results in less noise than the MPD-FG (brown curve). The bold lines are means and faint lines the standard deviations of eight trials in total.

In response to pressure-induced ischemia, the relative, averaged BF_i among the eight measurements (solid line) drops almost to 0, for both the early (Fig. 12b) and the late (Fig. 12c) photons. There is no difference in the drop with the two gates because the pressure in the cuff stops the blood flow in the whole forearm. The dotted lines in the plot represent the variability of the relative BF_i. The distance between the upper and the lower line is due to the different BF_i of the subjects, while the ripple is due to the noise. In fact, for both EP and LP the amplitude of the variability is the same, while the LP results are noisier because of the lower number of photons in the late gate. The blood flow differs from subject to subject by about ±30%. The noise is about 10% for the EP of both detectors, 15% for the MPD-RE LP, and almost 20% for the MPD-FG LP.

G. Forehead pressure experiment

The second human subject experiment consisted of applying light manual pressure to the optical probe when placed on the forehead. The pressure expels some blood from the skin beneath the probe pad, reducing the skin blood flow in the area below the optical probe^[38]. Since no pressure reaches the brain, cerebral blood flow is unaffected.

In this case, we compared the average blood flow the 30 s before and the 30 s during the application of pressure, for both early and late photons, as shown in Fig. 13. As expected, when selecting the early photons, both detectors show a blood flow drop of more than 30%. For the LP gate, the MPD-FG shows a 7% reduction, while the MPD-RE shows a 22% reduction. This confirms the limited performances of the MPD-RE due to the diffusion tail already seen in the phantom experiments. The lower detection efficiency of the MPD-FG SPAD reduces the SNR and results in larger error bars in the BF_i results.

Fig. 13.

Relative BF_i changes at 1 cm source-detector separation using the MPD-RE (blue) and the MPD-FG (brown) before and during the application of light manual pressure on the optical probe placed on the forehead. By using the early photons, the BF_i drops by 31% after applying the pressure, as expected. By using the late photons, the MPD-FG shows a small drop of 7%, while the MPD-RE shows a drop of 22% due to the tail contribution.

IV. DISCUSSION AND CONCLUSION

We presented the first portable TD-DCS system with the goal of measuring cerebral blood flow at different depths by selecting photons with different ToF. The system is the culmination of extensive research into commercial and/or custom components able to fit into a compact device and that are available at modest cost.

A major challenge is the availability of a compact pulsed laser with a coherence length of 5 cm or more and a pulse width shorter than 500 ps. Theoretically, the maximum coherence length is limited only by the pulse width. For example, a transform-limited coherence length of 5 cm would correspond to a Gaussian laser pulse width of about 250 ps at 767 nm. Long coherence length is not typically demanded of pulsed lasers, hence the limited commercial availability. All the lasers we tested showed a coherence length 3–4 times lower than the transform limit. The VisIR-500, the laser selected for the presented system, has a coherence length of 3.8 cm, which is close to our target of 5 cm. But it is not an optimal solution for TD-DCS measurements because the spectral content of the 570 ps of the pulses generated by the VisIR-500 can be accommodated by a shorter, 180 ps pulse width. This results in three drawbacks: 1) The beta drops with larger gates and later times, adding noise in the computation of the BF_i for late photons. 2) The IRF is broader than necessary, making the computation of the optical properties less accurate when using TRS processing, and most importantly, 3) mixing early and late photons at the selected sampling time reduces depth sensitivity. To overcome the limitation of a short coherence length, the use of a custom-made active mode-locked Ti:Sapphire laser has been proposed ^[28].While this would provide superior performance, this system would be bulky and complex, resulting in a laser system not well-suited for a compact, bedside device. We believe that a better choice would be to develop a custom transform-limited laser with a FWHM width of about 200–300 ps.

Another important consideration on the laser choice is output power. Because of the low duty-cycle, a solid-state laser without amplification cannot provide sufficient power for single speckle detection. We believe that the VISIR-500 laser used in this paper represents a good trade-off between cost, complexity and output power.

On the detector side, there are several options available to perform TD-DCS measurements, and SPADs with good timing jitter have been developed and are being used for time-domain NIRS ^{[27], 40}. One major difference between TD-NIRS and TD-DCS requirements involves light detection probability. TD-NIRS can compensate for the low detector efficiency at NIRS wavelengths by collecting light from a larger active area. TD-DCS requires a small collection area to detect the intensity fluctuation of a single speckle lobe. Therefore, detector efficiency plays a key role for TD-DCS. Silicon detectors can only achieve high responsivity in the near-infrared by using a thick active region, which unfortunately reduces their timing performance.

We compared two detectors: one with optimized timing performance but low efficiency (MPD-FG) and one with optimized efficiency but a long diffusion tail in the timing response (MPD-RE). Even if the higher efficiency of the MPD-RE allows us to compute BF_i every few seconds with limited noise, the long tail mixes the pathlength contribution of photons, resulting in lower depth sensitivity. To improve the current system, we need a better compromise between timing response and detection efficiency than is currently available. For now, we can improve either one by reducing laser pulse width to enhance spatial resolution or adding parallel channels to collect more light and improve SNR.

We optimized the system by using custom electronics to optimize TPSF alignment in the detection window, minimize the package size and allow real-time pre-processing in the FGPA. The raw data were post-processed to allow flexibility in the selection of the gates, but the system is capable of real-time computation of autocorrelation functions.

Our characterization of the portable TD-DCS shows it is capable of measuring blood flow at different depths, both in phantom-based experiments and in-vivo measurements. The liquid phantom experiments allowed us to compare the performance of the TD-DCS system against a state-of-the-art CW-DCS system, as summarized in Table II. The two-layer phantom experiment demonstrated that the TD-DCS with 1 cm source-detector separation has similar sensitivity to the flow in a lower layer (covered by a 15 mm top layer) as the CW-DCS at 2 cm and slightly less than CW-DCS at 3 cm. By selecting photon at later gates (ULP), TD-DCS at 1 cm source-detection separation overtook the sensitivity of the CW-DCS at 3 cm, but only using the MPD-FG detector thanks to its very fast diffusion tail. Unfortunately the low efficiency of the detector didn’t allow for enough signal at the ULP in the in vivo measurement, because of the low SNR achievable with a limited acquisition time of 3 seconds per BF_i point. The flow experiment demonstrated a depth and spatial sensitivity at 1 cm source detector separation superior to CW-DCS at 2 and 3 cm separation.

TABLE II.

Performance comparison between TD-DCS (using MPD-FG detector) and CW-DCS

	TD-DCS EP	TD-DCS LP	TD-DCS VLP	CW-DCS at 1 cm	CW-DCS at 3 cm
Sensitivity to a 1 cm layer (%)	∼0	9.8 ± 0.5	29 ± 3	3 ± 0.1	15± 2
Sensitivity to a 1.5 cm layer (%)	∼0	1.6 ± 0.5	9 ± 3	0.8 ± 0.1	5.2 ± 2
Sensitivity to a 1 cm tube (%)	<2	67± 22	182 ± 91	23 ± 3	84 ± 44
Spatial resolution (mm)	-	∼10	∼10	∼10	∼26

The in vivo cuff occlusion measurement demonstrated the ability of the portable TD-DCS system to compute BF_i every 3 seconds, providing the ability to monitor dynamic changes in blood flow. Pressure modulation of the probe on the forehead shows the importance of using detectors with a clean timing response to distinguish between BF_i in the scalp and the brain.

Future improvements in detectors will allow selection of later gates and will further improve depth sensitivity. Narrower pulse width lasers, which are less penalized from the detector diffusion tails and optimized coherence length, will allow shorter source-detector separations, further improving spatial resolution.

In conclusion, we presented a portable TD-DCS system suitable for measurements in human subjects, which is able to distinguish between superficial and deeper blood flow by measuring the photon arrival times. We reported the performance of the system both in phantom-based and in-vivo experiments. The overall performance of the system is limited by the coherence length of the pulsed laser and the trade-off between efficiency and timing response of the detectors. Nonetheless, we were able to measure BF_i at 0.3–0.5 Hz, and resolve blood flow changes 1 cm below the skin surface with improved spatial resolution with respect to CW-DCS.