Abstract
There is extensive evidence that functional organization of the human brain varies dynamically as the brain switches between task demands, or cognitive states. This functional organization also varies across subjects, even when engaged in similar tasks. To date, the functional network organization of the brain has been considered static. In this work we use fMRI data obtained across multiple cognitive states (task-evoked and rest conditions) and across multiple subjects, to measure state- and subject-specific functional network parcellation (the assignment of nodes to networks). Our parcellation approach provides a measure of how node-to-network assignment (NNA) changes across states and across subjects. We demonstrate that the brain’s functional networks are not spatially fixed, but that many nodes change their network membership as a function of cognitive state. Such reconfigurations are highly robust and reliable to the extent that they can be used to predict cognitive state with up to 97% accuracy. Our findings suggest that if functional networks are to be defined via functional clustering of nodes, then it is essential to consider that such definitions may be fluid and cognitive-state dependent.
Graphical Abstract
1. Introduction
The human brain is organized into functional networks that reflect the coordinated effort of individual subunits (or nodes) to execute specific functions (Finn et al., 2015; Power et al., 2011; Smith et al., 2009; Thomas Yeo et al., 2011). Previous studies have identified 5–20 networks during the resting-state that putatively represent the “intrinsic” functional organization of the brain (Meunier et al., 2009; Power et al., 2011; Smith et al., 2012; Thomas Yeo et al., 2011). These functional networks have been associated with a wide range of cognitive tasks (Dosenbach et al., 2007; Grayson et al., 2014; Laird et al., 2011) and alterations in the spatial organization of these networks have been linked to clinical disorders (Greicius et al., 2004; Stern et al., 2012; van Eimeren et al., 2009). Increasingly, there is evidence that the functional organization of the brain is fluid and reconfigures with task demands or specific cognitive states (Cole et al., 2014; Krienen et al., 2014; Mennes et al., 2012). Understanding network reconfiguration across different task states is a key step towards understanding the functional organization of the brain.
Recent studies have made significant progress in defining state-evoked changes in functional connectivity elicited by task performance (Cole et al., 2010; Cole et al., 2014; Cole et al., 2016; Cole et al., 2013; Davison et al., 2015; Di et al., 2013; Krienen et al., 2014; Shine et al., 2016; Telesford et al., 2016). However, none of these studies explicitly examined the possibility that the spatial topography of functional networks reconfigures, with most studies explicitly assuming that the networks remain spatially unchanged across tasks (Cole et al., 2014; Cole et al., 2016; Gratton et al., 2018; Telesford et al., 2016). Such analyses have been primarily restricted to investigating differences in connectivity between functional networks, and not whether nodes reconfigure into different groups across tasks. Changes in functional network topography, are in fact driven by changes in functional connectivity across different tasks. Another line of research takes a more abstract perspective by computing global network measures (such as modularity and participation coefficient) and comparing these measures across different states (Bassett et al., 2011; Cohen and D’Esposito, 2016; Di et al., 2013; Kinnison et al., 2012; Mohr et al., 2016; Shine et al., 2016). While such approaches address the modular reconfiguration of the brain as a whole, they do not quantify how or whether node network memberships change across states. Such studies also typically define a new set of networks (ranging between 3 to 7) for every state, whose correspondence to the putative resting-state networks is unclear (Bassett et al., 2011; Di et al., 2013; Kinnison et al., 2012; Mattar et al., 2015a). Finally, many studies do not directly examine cross-subject variations in network reorganization (Krienen et al., 2014), or consider cross-subject and cross-state changes as similar notions for defining reorganization (Mattar et al., 2015b). However, the functional organization of the brain varies significantly across subjects, yielding large individual differences in functional network definitions (Gordon et al., 2017a; Gordon et al., 2017b). In this work, we account for both cross-subject and cross-state variability in functional network organization demonstrating the dynamic flexibility of this organization.
A new approach is introduced to dynamically map node membership in functional networks across task-evoked and resting states, and across individuals. We apply our recently developed exemplar-based parcellation method (Salehi et al., 2018) to assign a set of pre-defined nodes to individualized, state-specific functional networks, while preserving precise network correspondences across subjects and states. We demonstrate that resting-state networks reconfigure as nodes change their allegiance in specific manners according to the task condition or cognitive state. We demonstrate that the observed state-evoked reconfiguration of functional networks is reliable, through the use of a cross-validated predictive model that decodes the cognitive state of unseen subjects based on their node-to-network assignments (NNA). Elucidating functional network configurations across a number of tasks reveals three classes of nodes based on the stability of these node-to-network assignments: 1) steady nodes that exhibit the same network assignment across states and subjects; 2) flexible nodes that change their network assignment across states, but are consistent across subjects, and 3) transient nodes that change their network assignment across both subjects and states. To give behavioral context for these node classes, we use a large-scale meta-analysis of task activation studies from BrainMap to assign behavioral domains and paradigm classes to each node. Together, our findings provide a comprehensive view of how large-scale functional networks (as putatively defined during resting-state) are modulated by task.
2. Materials and Methods
2.1. Participants and processing
Functional MRI data from the Human Connectome Project (HCP) (Van Essen et al., 2013) were analyzed. We limited the analysis to 718 subjects for which data were available for all nine functional conditions (hereafter, “states”): MOTOR, GAMBLING, WORKING MEMORY (WM), EMOTIONAL, LANGUAGE, RELATIONAL, SOCIAL, REST1, and REST2. For details of scan parameters, see (Uğurbil et al., 2013) and (Smith et al., 2013). Starting with the minimally preprocessed HCP data (Glasser et al., 2013), further preprocessing steps were performed using BioImage Suite (Joshi et al., 2011) and included regressing 12 motion parameters (Movement_Regressors_dt.txt), regressing the mean time courses of the white matter and cerebro-spinal fluid as well as the global signal, removing the linear trend, and low pass filtering (as previously described in (Finn et al., 2015)).
2.2. Functional distance and functional connectivity matrices
Functional matrices were assessed using a functional brain atlas (Shen et al., 2013) consisting of 268 nodes covering the whole brain; this atlas was defined using resting-state data from a separate population of healthy subjects (Finn et al., 2015). For every subject in each functional condition, time courses for the two functional runs with opposing phase-encoding directions (left-right, “LR”, and right-left, “RL”) were concatenated and further used to generate a ground set V consisting of N = 268 vectors in T-dimensional space, where T indicates the length of scan session. To construct the parcellations, we first normalized all the data points to a unit norm sphere centered at origin. We then calculated the pairwise squared Euclidean distances between the data points, yielding a distance matrix of size 268 × 268 for each subject and each state. We also constructed functional connectivity matrices to visualize the brain connectivity patterns in different states. To this end, the Pearson correlation coefficients between the time courses of each possible pair of nodes were calculated and normalized using Fisher’s z-transformation. Each element of the functional connectivity matrix represents a functional connection, or edge, between two nodes.
2.3. Individualized and state-specific functional network parcellation
We used exemplar-based parcellation (Salehi et al., 2018) to assign nodes into functional networks in an individualized manner for each state and subject, such that every subject acquired an individualized node-to-network assignment (NNA) for each state. This parcellation method provides an approach to summarize data by introducing a set of K exemplars that best represents the full data.
We followed the same methodology explained in (Salehi et al., 2018), by attempting to find K exemplar labels S = {e1, e2, … , eK} with ei ∈ {1, … , N = 268} , whose corresponding exemplar vectors for each individual j in each state n, i.e., maximizes a desired utility function, as follows:
| (1) |
where S is the exemplar label set and Sm,j is the set including the corresponding exemplar vectors in subject j ∈ {1, … , J = 718} at state m ∈ {1, … , M = 9}. Here, ƒ m,j: 2Vm,j → ℝ is the utility function of subject j at state m. This utility function is derived from the following loss function L(S), which measures how much information we lose if we summarize the entire ground set to the exemplar set S by representing each data point with its closest exemplar:
| (2) |
where Vm,j is the ground set of size 268 and dimension T for subject j at state m,and vm,j ∈ Sm,j ⊆ Vm,j is the node exemplar vector corresponding to the exemplar label e ∈ S.
While minimization of (2) subject to the cardinality constraint would output the desired exemplar set, this minimization is NP-hard. We transform this minimization into maximization of a monotone, non-negative, submodular function (see (Fujishige, 2005) for a formal definition and for properties of submodular functions) by introducing an auxiliary exemplar, v0, as follows (Krause and Gomes, 2010):
| (3) |
Maximization of (3) subject to the cardinality constraint is tractable using general greedy algorithm, which is known to provide an efficient 1–1/e ≈ 0.63 approximation to the optimal solution (Nemhauser et al., 1978). The auxiliary exemplar can be an arbitrary vector whose distance to every data point is greater than the pair-wise distances between data points. Here we used v0 = [3,0, … ,0] as the auxiliary exemplar and employed an accelerated version of the greedy algorithm, known as Lazy Greedy (Minoux, 1978).
After K exemplar labels were identified, the corresponding exemplar vectors in every subject and state were used to parcellate the brain. We assigned each node n in subject j and state m (i.e. vector ) to the closest exemplar (which represents the corresponding community or network), i.e.:
| (4) |
Thus, the brain was parcellated into K networks each represented by an exemplar.
To generate the state-specific population-level parcellations, we employed the winner takes all algorithm over all subjects in each state. That is, region n was assigned to network k at state n if the majority of subjects in that state voted for this assignment. As the number of networks (K) is an arbitrary parameter, we repeated the analysis for K = 2 − 50 networks. Results presented in the main text are for K = 12 networks, as it was the minimum number of networks after which the assignments stabilized with significantly less changes in the NNAs (see Supplementary Materials, Figure S3).
2.4. Functional network reconfigurations across states
We quantified the state-evoked functional network reconfigurations by computing the pair-wise Hamming distances (Hamming, 1950) between every pair of state-specific population-level parcellation vectors. This resulted in a distance matrix D9×9 , where every element dm1, dm2 represents the number of nodes that changed their assignment from state m1 to state m2 . To quantify each individual network reconfigurations, we considered REST1 as the benchmark for comparison. For every network k, we computed the normalized Hamming distance between the NNA vector limited to the nodes that are assigned to network k during REST1, and the vector containing the same nodes’ network assignment during every other state.
2.5. Decoding cognitive states by node-to-network assignments (NNA) as features
To demonstrate that the state-evoked reconfigurations are robust across subjects and specific to each state, we built a cross-validated predictive model that decodes the cognitive state of each individual brain based solely on the NNAs. We employed two separate predictive pipelines: in the first pipeline, we employed a two-class (binary) classification on every pair of states. For every pair of state m1 and m2, we combined the corresponding populations resulting in a data set with 718 × 2 subejcts. In this case, the chance accuracy was equal to 50%. In the second pipeline, we employed an eight-class classification over the entire data set (excluding REST2). REST2 was excluded to eliminate the reduncdancy of resting-state session and balance the probability space evenly across sessions. For both pipelines, we developed a predictive model using gradient boosting machine [GBM (Friedman, 2001)] with 100 estimators (or decision trees) and 0.05 learning rate. We randomly divided the entire population into a training set and a testing set. We calculated exemplars using the training set and used those to parcellate the entire population. Next, we trained a GBM on the NNAs of the training set and predicted the state for the unseen subjects in the testing set. To evaluate the significance of the results, we employed non-parametric permutation test: we randomly permuted the output vector (here the cognitive states) 1000 times and each time ran the permuted values through the same predictive pipeline and calculated the accuracy.
Note that we restricted the exemplar identification to the training set to assure the independency of the training and the testing set throughout the pipeline. However, we repeated the entire analysis using the initial parcellation schemes in a 10-fold cross-validated setting (Figure S4). The predictive pipeline was implemented using Python’s Scikit-learn library (Pedregosa et al., 2011).
2.6. Classifying nodes based on NNA reconfigurations
To quantify the state-evoked functional network reconfigurations, we employed a statistical ensemble analysis. For every state, we randomly divided the entire population into two equal-size sets, and employed the population-level parcellation on each set independently using the winner-takes-all strategy over the corresponding subjects. We repeated this 50 times, to derive a distribution of 100 state-specific population-level parcellations. Using this distribution, we quantified which nodes changed their NNAs across states and subjects. To this end, we calculated the entropy (a metric of uncertainty from information theory (Borda, 2011)) of the NNA histograms. We used two measures of entropy: 1) Entropycross–subject to measure the variation across multiple groups of subjects within the same state (see Eq. 5–6), and 2) Entropycross–state to measure the variation across multiple states for the same group of subjects (see Eq. 7–8). A high entropy in either of these measures means high variation in NNAs.
| (5) |
| (6) |
| (7) |
| (8) |
where 1 represents the indicator function:
| (9) |
Here, Prcross–state(pi,m ∈ k) indicates the probability of node p in iteration i ∈ {1, … ,100} and state m ∈ {1, … , M} to be assigned to network k ∈ {1, … , K}, averaged over all states. Similarly, Prcross–subj(pi,m ∈ k) indicates this probability averaged over all iterations. In this regard, every node falls into a two-dimensional space with cross-state and cross-subject entropies as its axes. We then grouped the nodes into three entropy classes, based on their position in this space: 1) steady nodes, those with zero cross-state and cross-subject entropies, 2) flexible nodes, those with positive (non-zero) cross-state entropies, and relatively low cross-subject entropies, and 3) transient nodes, regions with positive cross-state entropies and relatively high cross-subject entropies. To define a threshold to separate low and high cross-subject entropies, we took the average of this measure after excluding steady nodes ( = 29.47). Eq. 10 formally defines the three entropy classes:
| (10) |
where E stands for Entropy.
We also performed a subject-based entropy analysis, where instead of performing a statistical ensemble analysis to create a pool of 100 population-level parcellations, we considered every single individual-level parcellation, resulting in a pool of size 718 (and thus replaced 100 with 718 in the equations above.) The subsequent analyses are based on the population-based entropies, and the subject-based entropies are included in the Supplementary Materials (Figure S5).
2.7. Functional characterization of entropy classes
To provide behavioral context for these entropy classes, we conducted a meta-analysis using the behavioral domains and paradigm classes reported in the BrainMap Functional Database (Fox and Lancaster, 2002). We examined the association between BrainMap’s 55 behavioral domains and 108 paradigm classes (reflecting 10,467 task-activation experiments from 27,820 subjects) within the node entropy classes (steady, flexible, and transient), both at the node-level (with 268 nodes) and at the network-level (with 12 networks). The details are referenced in Supplementary Materials.
2.8. Graph visualization of the functional network reconfiguration across states
To provide a complementary analysis on how different functional networks interact with each other, we employed a graph visualization approach. While the delineation of functional networks represents the integration and segregation of different regions, functional connectivity analysis—using graph visualization—provides additional information on connections both within- and between-networks. This analysis further differentiates the notion of community and connection, as motivated by previous studies (Bassett et al., 2015; Mattar et al., 2015b). To this end, we constructed a population-level connectivity matrix for each state by taking the average of the individualized connectivity matrices. For the purpose of visualization, we summarized the average matrix to the top 10% edges and removed all self-loops. The resulting matrix for each functional condition was visualized as a graph using R package networkd3 [https://CRAN.R-project.org/package=networkD3]. These force-directed graphs aim to visually organize networks such that the energy of the graph as a whole is minimized. This is accomplished by assigning both repulsive and attractive forces to each pair of nodes such that the nodes with stronger interconnections are displayed closer to each other and the ones with weaker connections are shown as more distant.
2.9. Effects of head motion on the state-evoked functional network reconfigurations
Head motion is a known confound of connectivity analyses (Van Dijk et al., 2012). We ruled out the possibility that the network differences are derived by systematic differences in head motion across functional conditions. We employed a pairwise Wilcoxon signed-rank test on the mean frame-to-frame displacement (Movement_RelativeRMS.txt) across functional conditions and corrected for multiple comparisons using Bonferroni correction (see Figure S9).
3. Results
3.1. Functional network reconfigurations across states
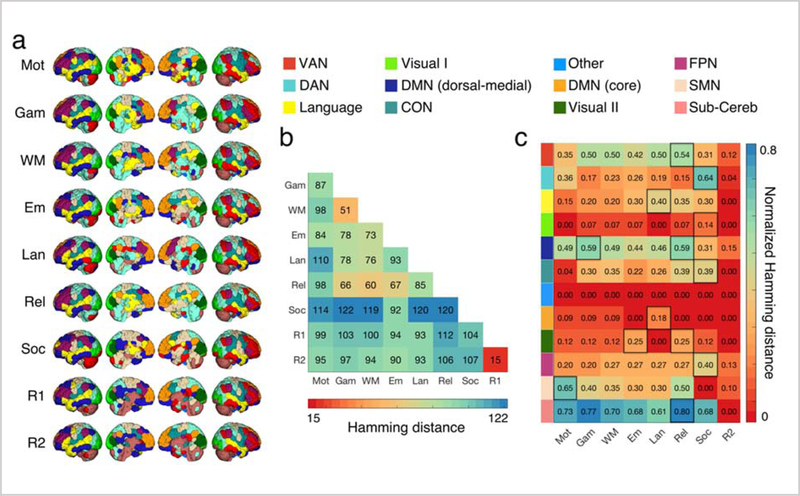
Figure 1a displays state-specific population-level functional networks for 12 networks (K = 12) across nine functional conditions. While the overall functional network structure remained largely intact, specific nodes changed their network assignment in different task states. For example, the posterior areas of the caudate nucleus were associated with the ventral attention network during rest, but their network assignments changed to the language or the sensorimotor network during task performance (Figure 1a). To quantify functional network reconfiguration across states, we calculated the Hamming distance (Hamming, 1950)—or the number of nodes that change their NNAs—for each pair of states (Figure 1b).
Figure 1. Functional network reconfigurations across states.
a) Each row shows a state-specific population-level parcellation, calculated using the winner-takes-all strategy for each functional condition (Mot: MOTOR, Gam: GAMBLING, WM: WORKING MEMORY, Em: EMOTION, Lan: LANGUAGE, Rel: RELATIONAL, Soc: SOCIAL, R1: REST1, and R2: REST2). b) Hamming distance between every pair of state-specific population-level parcellation schemes is visualized. Hamming distance is calculated as the number of different NNAs between the two states, with values ranging from 0 (perfect matching) to the number of nodes (here, 268). As expected, the two resting states have the most similar parcellations (15/268 = 5.6% different NNAs). SOCIAL and GAMBLING are the least similar parcellations (122/268 = 45/5% different NNAs). SOCIAL task is the most distinct with 41.9% (=112.25/268) different NNAs on average. c) The ratio of the nodes that changed their NNAs from REST1 to every other state is calculated for every network separately. For every network, the state during which the maximum reconfiguration is observed is highlighted in black. VAN: ventral attention network, DAN: dorsal attention network, Visual I: primary visual, DMN: default mode network, CON: cingulo-opercular network, Visual II: secondary visual, FPN: frontoparietal network, SMN: sensorimotor network, Sub-Cereb: subcortical/cerebellum. See Figure S1 for a probabilistic illustration of these network definitions.
The two resting-states (REST1 and REST2) had the most similar functional organization with only a 5.6% (15/268) difference in their NNAs. In contrast, the smallest reconfiguration between any pair of states was over three times larger: WM and GAMBLING, 19% (51/268). GAMBLING and SOCIAL demonstrated the highest level of network reconfiguration (45.5% difference). SOCIAL was the most distinct with 41.9% network reconfiguration on average.
To quantify the level of state-evoked reconfiguration for each functional network we computed the ratio of the nodes that change their network assignments from REST1 to every other state (Figure 1c). Among all eight states, REST2 exhibited the maximum similarity to REST1, with 7 of 12 networks exhibiting no reconfiguration. Networks including subcortical/cerebellum nodes exhibited the maximum reconfiguration, while the visual networks (visual I and II), and the default mode network (core) exhibited the least reconfiguration from REST1 to all other states. The sensorimotor network displayed the maximum reconfiguration during MOTOR task, and the language network displayed the maximum reconfiguration during LANGUAGE task. Similarly, a majority of the higher-order association networks—including the frontoparietal network, the dorsal attention network, and the cingulo-opercular network—showed maximum reconfiguration during the SOCIAL cognition task (Figure 1a). These observations suggest that the task relevant nodes regroup into specific networks in order to execute a particular task. These fuzzy functional network profiles are displayed in detail in Figure S1.
3.2. Node-to-network assignments (NNA) decode cognitive states
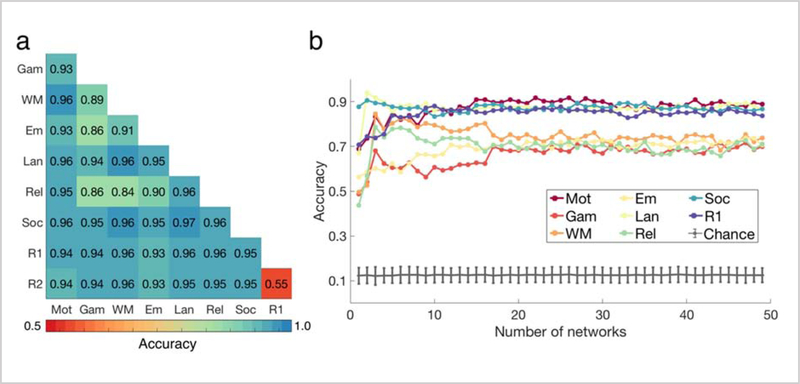
Figure 2 illustrates the accuracy of the predictive models that predict the cognitive state of unseen subjects, based on their NNAs. For the two-class (binary) classification (Figure 2a), the random accuracy was 50%. The minimum prediction accuracy was associated with the REST1-REST2 pair (accuracy=55%) consistent with the fact that these two runs reflect similar cognitive states. We successfully decoded all other pairs of states with accuracies considerably higher than random, with minimum, maximum, and average accuracy of 84%, 97%, and 94%, averaged over all K s from 2–50 (Figure 2a). Similarly, the 8-class classification accuracies were also significantly higher than random with minimum, maximum, and average accuracy of 66%, 87%, and 78%, averaged over all numbers of networks: Ks from 2–50 (Figure 2b). That we could significantly predict cognitive state based solely on NNAs suggest that functional networks reorganize due to changes in state in a robust, reliable, and predictive manner across subjects.
Figure 2. Decoding cognitive states by node-to-network assignments (NNA) as features.
The subject pool was split into training and testing sets of equal-size. The exemplars (nodes with fixed NNAs both across states and subjects, representing each network) were computed using the training set and were used to parcellate the entire population. A GBM was trained on the training set using the NNA vectors as features. It was then used to predict the cognitive state of the novel subjects in the test set. a) The binary classification accuracies averaged over number of networks ranging from 2 to 50 are displayed. b) The 8-class classification accuracies are displayed for all number of networks (K = 2 − 50). The gray error bars represent the chance accuracy, computed as the mean and standard deviation of 1000 permutations. For Ks larger than 17 the accuracies tend to stabilize with marginal variation. As expected, the minimum accuracies are observed for K = 2, since the entire vector only consists of two numbers: 1 or 2, depending on whether the node is assigned to network #1 or network #2. GAMBLING, RELATIONAL, EMOTION, and WM display lower prediction accuracies than MOTOR, SOCIAL, LANGUAGE, and REST. See Figure S4 for a 10-fold cross-validated predictive model with parcellation schemes derived from the entire population (not just the training set as shown above).
We also ruled out the possibility that the state-specific functional network reconfigurations are derived by the differences in the number of time points across different task conditions. To this end, we trimmed all functional runs to equal the length of the shortest task, (SOCIAL 176 time points), and repeated the analysis by generating the individualized and state-specific functional networks and re-running the steps in the predictive model. Similar functional network reconfigurations and prediction accuracies were observed (Figure S10), suggesting that the differences in network configurations across states are not driven by differences in the amount of data, but reflect the underlying cognitive state.
3.3. Classifying nodes based on NNA reconfigurations
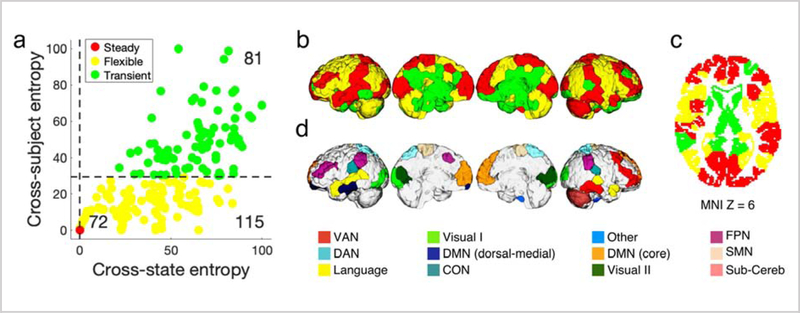
We next quantified the cross-state and cross-subject entropies for every node in the brain (Figure 3a). We observed that the two entropies were significantly correlated with each other (r=0.78, p<1×10−16), suggesting that the nodes with high cross-subject variation also tend to have high cross-state variance.
Figure 3. Classifying nodes based on NNA reconfigurations.
a) For every node, we calculated two measures of variability: the NNA entropy across states (Entropycross-state) and the NNA entropy across subjects (Entropycross-subject). The two measures are significantly correlated (r=0.78, p<1×10−10). We grouped nodes into three entropy classes based on their position in the 2-dimensional entropy space: stable nodes (red, n=72/268); flexible nodes (yellow, n=115/268); and transient nodes (green, n=81/268). b) The three entropy classes are visualized on the brain. The steady class includes areas in superior frontal cortex, a large portion of the temporal and occipital lobe. The flexible class revolves around higher-order association areas including a large portion of the frontal and parietal lobes. The transient class is mainly localized in the subcortex and cingulate cortex. Also see Figure S5 for a more detailed illustration of these entropy measures, and Figure S6 for visualization of these flexibility classes as a continuum. c) The three entropy classes projected on the axial plane. d) Functional network assignments for the steady nodes, which are fixed across all functional conditions.
Next, we used the two entropy measures to categorize nodes into three entropy classes: 1) steady nodes, those with consistent cross-state and cross-subject NNAs (displayed as red); 2) flexible nodes, those with flexible cross-state NNAs but consistent cross-subject NNAs (displayed as yellow); and 3) transient nodes, those with flexible cross-state and cross-subject NNAs (displayed as green). Figure 3b illustrates the localization of these entropy classes on the brain. We observed that steady nodes were mainly located in the superior frontal cortex, dorsolateral prefrontal cortex (dlPFC), precuneus, post-central gyrus, superior and middle temporal gyrus, and the occipital lobe. Flexible regions were located mainly in the inferior frontal gyrus, pre-central gyrus, anterior cingulate cortex, posterior parietal cortex, inferior parietal lobule, and cerebellum (Figure 3b). Finally, transient nodes were located mainly in subcortical areas such as the hippocampus/parahippocampus, thalamus, and caudate. Figure 3c illustrates NNAs for the steady nodes.
The current classification assigns nodes into discrete flexibility classes, which is suitable for visualization purposes. Figure S6 provides an illustration of these flexibility classes as a continuum, and Figure S5 visualizes the cross-state and cross-subject entropy values for all nodes using both population-based and subject-based analyses (see Methods for details).
3.4. Localization of the node entropy classes in functional networks
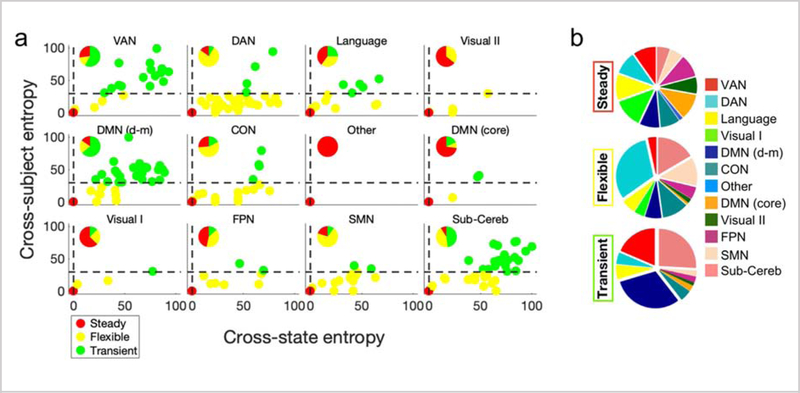
We next investigated the association between the three node entropy classes and our functional networks (Figure 4). We observed that all networks—excluding the visual I network—contained nodes of each class. However, the distribution of the three entropy classes differed considerably across networks (Figure 4a). For example, the dorsal attention network (76.6%), the cingulo-opercular network (56.5%), and the sensorimotor network (70.0%) had the majority of flexible nodes; the ventral attention network (57.7%), and the dorsal-medial portion of the default mode network (64.1%) had the most transient nodes; and the visual I network (62.5%), visual II network (64.3%), and the core portion of the default mode network (72.7%) contained most of the steady nodes. Finally, we observed that all functional networks contributed evenly to the steady class, but did not contribute evenly to the flexible or transient classes (Figure 4b). For example, the dorsal attention network contributed the most to the flexible class, while the dorsal-medial portion of the default mode network and the subcortical/cerebellum contributed the most to the transient class. This suggests that individual functional networks have varying levels of stability, as defined by NNA entropy across task states and subjects.
Figure 4. Localization of the node entropy classes in functional networks.
a) The Entropycross-state versus Entropycross-subject diagram is displayed for the nodes within each network. The withinnetwork distribution of the entropy classes is further demonstrated. Primary and secondary visual networks and the core portion of default network are mainly comprised of steady nodes. The DAN, CON, and SMN mainly include flexible regions, and the VAN, dorsal-medial DMN and subcortical/cerebellum networks are mainly comprised of transient regions. The FPN has a large portion of both steady and flexible regions, the subcortical/cerebellum network has a large portion of both flexible and transient nodes, and the Language network has close to an even distribution of all three entropy classes. b) The distribution of functional networks within each entropy class is visualized. While the contribution of functional networks to the steady class is evenly distributed across all networks, the DAN, CON, SMN, and subcortical/cerebellum have the largest contribution to the flexible class, and the VAN, dorsal-medial DMN, and subcortical/cerebellum have the largest contribution to the transient class. DMN (d-m): DMN (dorsal-medial)
3.5. Functional characterization of entropy classes
Next, we demonstrate that these entropy classes are functionally meaningful divisions. To this end, we provide evidence for the distinct functionality of these entropy classes.
3.5.1. Flexible nodes inform state-decoding
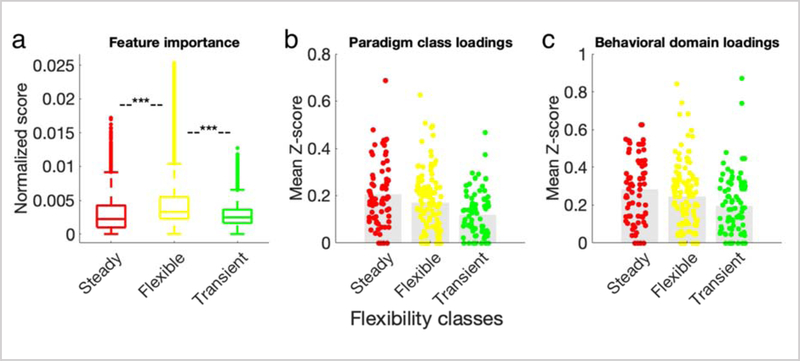
We hypothesized that nodes in the flexible entropy class should have the highest predictive power for decoding states. We support this hypothesis with two lines of logic: first, because flexible nodes change their functional network organization according to task state, how the NNA reconfigures should therefore reflect the underlying state; second, because flexible nodes have consistent NNAs across subjects, they should generalize across novel subjects. To test our hypothesis, we computed how important each NNA feature was in the employed predictive pipeline. Node importance (i.e. “feature importance”) was calculated by the GBM classifier as the number of times that each node was used to make a key decision that improved the classifier’s performance measure (Friedman, 2001). We examined the distribution of the importance scores within each node entropy class. Consistent with our hypothesis, the flexible regions had the largest importance scores on average (Figure 5a; two-tailed t-test Bonferroni corrected for multiple comparisons, t(flexible, steady)=26.8, p<3×10−16, t(flexible, transient)=30.4, p<3×10−17, t(steady, transient)=0.34, p<0.79). That the task state can be decoded based on the NNA of the brain’s flexible nodes suggests that these nodes are strongly modulated by the task demands such that the behavior of flexible nodes forms a robust and reliable signature of task state.
Figure 5. Functional characterization of entropy classes.
a) The distribution of the feature (node) importance in predicting states is displayed across the three entropy classes. The flexible class contains the most important nodes for state decoding. Two-tailed t-test between every pair of steady, flexible, and transient class was performed and Bonferroni corrected for multiple comparisons, *** p<1×10−16. b) The distribution of paradigm classes across entropy classes is displayed. Steady nodes have higher values of significant paradigm class loadings than either flexible (t=1.7, p<0.09) or transient nodes (t=4.6, p<8×10−6). c) The distribution of behavioral domains across entropy classes is displayed. Steady nodes have higher values of significant behavioral domain than either flexible (t=1.5, p<0.15) or transient nodes (t=3.3, p<0.001). Analyses in (b) and (c) represent node-level analyses of BrainMap Functional Database’s experimental meta-data representing 55 behavioral domains and 108 paradigm classes. Profiles were computed within each node as the forward inference likelihood z-scores, thresholded at z>1.96, and summed over all behavioral domains or paradigm classes. Colored circles represent the 268 nodes, colored according to their entropy classes. See Figure S7 for network-level functional relevance.
3.5.2. Steady nodes display the strongest behavioral associations
Similarly, we investigated the behavioral profiles of different entropy classes. We hypothesized that “steady” nodes should be more strongly associated with specific behavioral domains or paradigm classes. This is because steady nodes are less likely to “switch” association with task state and subjects, and therefore are more likely to be consistently reported among a significant number of task-based fMRI and PET experiments in BrainMap database, indicating a more specific brain-behavior association. We observed that indeed, there was a trend for steady nodes to have stronger behavioral domain and paradigm class loadings than either flexible or transient nodes (One-tailed t-test Bonferroni corrected for multiple comparisons, behavioral domain: t(steady, flexible)=1.5, p<0.15, t(steady, transient)=3.3, p<0.001; paradigm class: t(steady, flexible)=1.7, p<0.09, t(steady, transient)=4.6, p<8×10−6; Figure 5b, c). The same trend was observed at the network-level (Figure S7). A breakdown of each node’s behavioral domains and paradigm class association is referenced in Table S1. This further suggests that entropy classes provide information that is relevant to how the brain executes its functional repertoire, as defined by behavioral domains and paradigm classes.
3.6. Graph visualization of the functional network reconfiguration across states
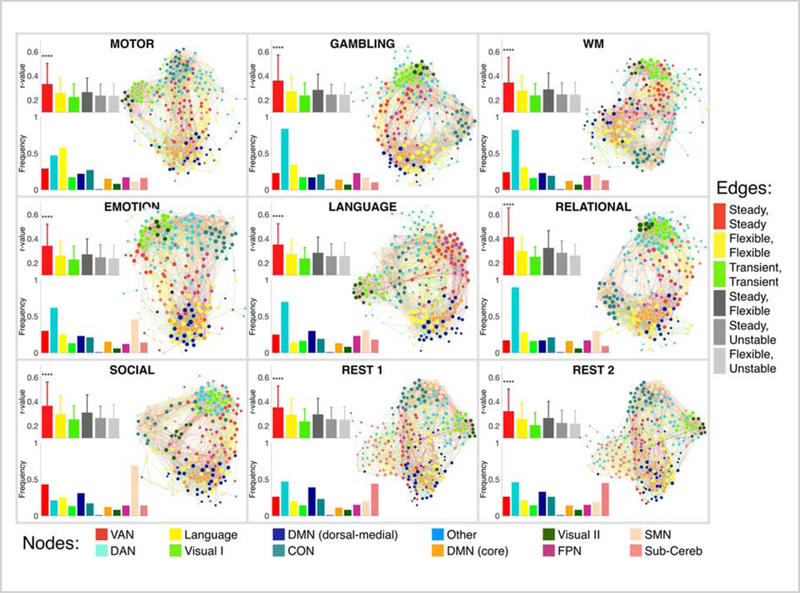
Finally, we evaluated the functional connectivity changes associated with changes in state, for comparison with studies that investigate connectivity changes as a proxy for functional network reorganization. Figure 6 (the right side of each panel) visualizes the connectivity matrices as force-directed graphs with nodes colored according to the functional network to which they belong and edges colored according to the entropy class of their two end points. Node size is proportional to the graph theory measure degree. We observed that nodes from different but related networks were integrated for all states. For instance, the core and dorsal-medial portions of the default mode network as well as the visual I and visual II networks showed strong integration with each other (Figure 6). However, the magnitude of this integration differed across different states. For example, while the visual I and visual II networks displayed strong integration across all states, the functional connectivity between them was weaker during the Social task. Finally, networks changed their segregation and integration patterns as a function of state. For instance, the dorsal attention network differed considerably across states, with higher segregation during the task states and higher integration during the rest states. Conversely, the subcortical/cerebellum and SMN presented higher segregation during the rest state and higher integration during the task states.
Figure 6. Graph visualization of the functional connectivity reconfiguration across states.
Each panel corresponds to one functional condition. For each functional condition, three diagrams are displayed. The right diagram is the force-directed graph visualization of the functional connectivity matrix, thresholded to retain the top 10% of the edges, and averaged over all subjects. Nodes are colored according to their population-level network assignments (see the bottom legend bar), and are sized proportional to their degree values (that is, the sum of edge weights connected to the node). Edges are colored according to the entropy class of their two end points (see the right legend bar), for example the connections between two steady nodes are colored red, connections between a steady node and a flexible node are colored light gray, and so on. The graphs are structured such that nodes with stronger connections are spatially closer to each other. As expected, nodes within the same network are clustered spatially close to each other. Further, nodes from different but related networks are also spatially integrated (for example, the core and dorsal-medial portions of DMN, or primary and secondary visual networks are integrated). However, there is a difference in the integration and segregation level of different functional networks across different task states. The bottom left diagram within each panel represents the frequency of the nodes assigned to each functional network. The top left diagram within each panel represents the strength of different types of connections. Error bars represent the standard deviation across connections. The connections within steady nodes are significantly stronger than the rest of the connections. These steady nodes form a strong core organization in the brain with large interconnections, similar to the “rich club” pattern (see Figure S8).
We next quantified the reorganization of functional networks across states (Figure 6; the bar plots on the bottom-left of each panel). The distribution of functional networks changed considerably across states, with more uniform distribution during rest than task. In this sense, the dorsal attention network was the largest network (with the maximum number of nodes) during GAMBLING, WM, EMOTION, LANGUAGE, and RELATIONAL states. The subcortical/cerebellum was considerably larger during rest than task, suggesting that nodes in the subcortical/cerebellum network tend to integrate with other networks during the execution of a task, while displaying segregated behavior during rest (consistent with our observation from the graph). The sensorimotor network lost the maximum number of nodes during the MOTOR task, while the language network lost the maximum number of nodes during the LANGUAGE task. While this observation may seem contradictory to the demands of the tasks, it could be an indication that these networks tend to integrate most with other networks when the task strongly engages them, potentially facilitating the information flow across networks (Cole et al., 2016; Ito et al., 2017). This is also consistent with our earlier finding (Figure 1c) that these networks displayed the maximum reconfiguration in changing to these tasks.
To investigate the role of entropy classes in the context of functional connectivity, we quantified the connectivity (i.e. edge strength) between nodes from the same or different entropy classes (Figure 6; the error bars on the top-left of each panel): steady-steady edges (colored as red), steady-flexible edges (colored as dark gray), steady-transient edges (colored as gray), flexible-flexible edges (colored as yellow), flexible-transient edges (colored as light gray), and transient-transient edges (colored as green). We observed that the edge strength between steady nodes was significantly stronger than the edge strength between other node classes (p<2×10−16, Bonferroni corrected for multiple comparisons). Among edges between nodes of the same class, edges between steady nodes were significantly stronger than the edges between flexible nodes (p<2×10−16, Bonferroni corrected for multiple comparisons) and edges between flexible nodes were significantly stronger than edges between transient nodes (p<1×10−2, Bonferroni corrected for multiple comparisons). Among edges between nodes of differing class, the edges between steady and flexible nodes were the strongest (p<2×10−2, Bonferroni corrected for multiple comparisons). Edges associated with transient nodes had the lowest strength.
4. Discussion
In this work, we studied individualized and state-specific functional network reconfigurations evoked by different task and rest states. Our findings highlight that the brain’s functional network organization is not fixed, but rather, that networks reconfigure as a function of cognitive state. We showed that this holds true across different task states and across individuals. We measured functional network reconfiguration as node-to-network assignments (NNA) and demonstrated that a novel subject’s current state could be predicted with 66–97% accuracy based on NNA alone (Figure 2). This finding demonstrates that functional networks reconfigure in a meaningful and reproducible manner across cognitive states. This also highlights the robustness of state-evoked functional network reconfigurations across subjects. Further, we showed that nodes group into three entropy classes based on their NNAs across states and subjects (Figure 3). Steady nodes exhibit consistent NNAs across both states and subjects and are primarily located in visual and medial cortical regions. Flexible nodes change their network assignments according to state in a consistent manner across subjects and are primarily located in higher order cognitive regions. Transient nodes exhibit variable network assignments across both states and subjects and are primarily located in the sub-cortex and cerebellum; regions known to have lower reliability in functional connectivity studies (Noble et al., 2017). A direct assessment of reliability however, showed that there are no significant differences in reliability values across the three flexibility classes (Supplementary Materials, Figure S11).
Despite these trends of anatomical locations of nodal classes, all functional networks contain some nodes from each class. We further demonstrated the functional relevance of these nodal classes: flexible nodes contribute the most to models predicting cognitive state and steady nodes display the largest behavioral loadings based on a large-scale meta-analysis of task activation studies (Figure 5 and Figure S7). Together, these results take connectivity changes as a function of task a step further and demonstrate that nodes regroup into specific functional networks associated with specific tasks, with the networks including or dropping nodes according to the demands of a particular task state. In a recent work, Bijsterbosch et al. have shown that cross-subject changes in spatial configuration of functional regions can be interpreted as changes in functional connectivity (Bijsterbosch et al., 2018). Similarly, the observed cross-state changes in functional network definitions are likely to be interpreted as changes in node-to-node connectivity across states. As such, the state-evoked reconfigurations need to be considered when interpreting changes in connectivity or any graph theory measures across states.
4.1. Functional network organization is state-dependent
Our results suggest that a similar core functional network structure is observed across many different cognitive states, but that nodes can be added to or subtracted from these functional networks as a function of the specific state. These results suggest flexible functional network definitions as a function of the cognitive state. Furthermore, our BrainMap meta-analysis shows that nearly all nodes were significantly associated with multiple paradigm classes, supporting the flexibility of nodes in executing functions. Altogether, our results suggest that the node-to-network assignments are inherently probabilistic as the functional organization of the brain is constantly reconfiguring with task (Figure 1 and Figure S1).
Numerous previous studies have focused on fixed networks in various ways, typically by using coordinates from previous resting-state studies (Cassady et al., 2019; Cole et al., 2014; Cole et al., 2016; Gratton et al., 2018; McMenamin et al., 2014; Mohr et al., 2016; Satterthwaite et al., 2015; Schultz and Cole, 2016; Telesford et al., 2016). Several studies, for example (Cole et al., 2013; Zanto and Gazzaley, 2013), have examined a single network, the frontoparietal network, and measured changes within this network as a function of task-state. While such an approach can be justified, it potentially misses additional information that could be gleaned in considering how the network itself reconfigures. The sensorimotor network also has been studied as an implicitly defined fixed functional network (Cassady et al., 2019; Power et al., 2011). While it is true that there is a core structural network, the findings presented here illustrate that node participation in the sensorimotor network is highly variable across states (Figure 4a), revealing substantial state-evoked reconfigurations that have not been previously characterized. Perhaps as one would expect, the largest reconfiguration of the sensorimotor network occurs when subjects are executing the motor task (Figure 1c). The sensorimotor network had the lowest portion of transient regions, suggesting the low cross-subject variability, consistent with previous observations (Finn et al., 2015; Mueller et al., 2013).
In addition, our results also replicate previously observed network reconfigurations. Consistent with Andrews‐Hanna et al. (Andrews‐Hanna et al., 2014), we highlight that there is a core sub-system of the default mode network (including medial superior frontal gyrus) and dorsal-medial and medial-temporal sub-systems of the default mode network (including ventral medial prefrontal cortex (vmPFC), inferior temporal gyrus and temporal pole). Our results extend this characterization by suggesting that the two sub-systems of the default mode network display distinct reconfiguration properties, with the core subsystem remaining unchanged across states, and the dorsal-medial subsystem reconfiguring flexibly across states and subjects (Zhang et al., 2016). Highlighting the complex role of the default mode network in both tasks and rest, our observations indicate that the default mode network nodes change their network membership from the default mode network to other higher-order association networks (such as the frontoparietal network and the cingulo-opercular network). Overall, these observations support the notion that all functional networks reorganize in a task specific manner
4.2. Functional networks contain steady, flexible, and transient nodes
Our findings reveal that all functional networks contain a combination of steady, flexible, and transient nodes (Figure 4a). This suggests that functional networks consist of a core set of steady nodes that then recruit or dismiss flexible and transient nodes according to the task demands. This result suggests that within each network there are specialized regions associated with distinct functionalities, altering both intra-network communication and inter-network integration. These functionalities are corroborated by the theory of “local” versus “distributed” neural communication (Cole et al., 2016; Ito et al., 2017), where transitions across states require the segregated processing units (distinct functional networks) to integrate information through flexibly changing network assignments.
The contribution to the steady nodes was evenly distributed across all networks (Figure 4b), indicating all networks retained some core functional network configuration. The majority of steady nodes were located in regions previously been implicated as part of the “rich club”, a common organization in complex systems where important (or “rich”) nodes connect preferentially to other important nodes (Grayson et al., 2014; Park and Friston, 2013; Van Den Heuvel and Sporns, 2011) (see Supplementary Materials, Figure S8). Additionally, we observed strong functional connectivity between nodes in the steady class (Figure 6, the top left error bars) in a similar vein to the connections between rich club nodes. These observations were consistent across all nine states (Figure S8), implying that the “rich club” organization of the brain is independent of task-state. This also mirrors a core-periphery structure in the brain with core nodes strongly and mutually interconnected and periphery nodes sparsely connected to each other and to the core nodes (Bassett et al., 2013; Fedorenko and Thompson-Schill, 2014; Park and Friston, 2013).
In contrast, the distribution of flexible nodes varies across networks, suggesting that some networks reconfigure more with cognitive state changes than others (Figure 4b). For example, the DAN, CON, and FPN had a larger proportion of flexible nodes (Figure 4a, b). Previous studies report that these networks rapidly update their connectivity patterns according to the task context (Anderson et al., 2013; Cole et al., 2013; Crossley et al., 2013; Krienen et al., 2014; Mennes et al., 2012), facilitating the information flow across networks (Cole et al., 2016; Ito et al., 2017). The large number of nodes that change their network assignments to the DAN, CON, and FPN may underlie these previously observed changes in connectivity patterns. Our results are also consistent with the role of these networks as functional hubs (Cole et al., 2013; Power et al., 2013) and their strong out-of-network connections (Ito et al., 2017).
Finally, the majority of the transient nodes were assigned to the subcortical/cerebellum, dorsal-medial subsystem of the default mode network, and the ventral attention network (Figure 4a, b). These nodes, mainly located in heteromodal association and limbic cortex, actively change their network assignment across both subjects and states. High cross-subject variability in these regions has been previously reported (Mueller et al., 2013; Zhang et al., 2016), and linked to differences in intelligence (Li et al., 2009), attention (Cohen et al., 2015; Rosenberg et al., 2016), and personality traits (Adelstein et al., 2011). This suggests that these regions promote a more personalized reconfiguration in the brain to adapt to the task at hand. Future work could explore the extent to which differences in the functional network reconfiguration in these regions could be indicative of, or be inferred from, the individual differences in task performance.
4.3. Functional network configuration predicts state
Individual cognitive states can be predicted from node-to-network assignments, suggesting that the state-specific information of functional network organization is sufficiently robust and reliable to form a signature for a given state. Prior work on task decoding has typically employed binarized classification of tasks. The pair-wise accuracies (binarized classification) achieved here (ranging from 84% to 97% with average of 94%; Figure 2a) were significantly higher than those previously reported (Cole et al., 2011; Heinzle et al., 2012; Woolgar et al., 2011). Our accuracies for the 8-class classification (ranging from 66% to 87% with average of 78%; Figure 2b) were also higher than the accuracies reported in the literature, even for easier decoding problems such as classification with lower number of classes (Cole et al., 2013) or within-subject classification paradigms (Haxby et al., 2014). Nevertheless, the main focus of the predictive analysis was to demonstrate that state-evoked demands lead to different functional network reconfigurations, and functional connectivity studies should consider these reconfigurations when studying within- and between-network connectivity patterns. In fact, even though the node-to-network assignment vector (of length 268) contains only integer values (i.e., 1, …, K for K networks), this minimal information was sufficient to predict the cognitive state (task) of novel subjects. This highlights the reliability of these state-specific reconfigurations of the brain’s large-scale functional network organization.
4.4. Individualized functional networks are needed
In addition, our results highlight the need for individualized approaches to systems neuroscience and medicine (Perez Velazquez, 2017; Satterthwaite and Davatzikos, 2015) by demonstrating that node-to-network assignments contain large individual variations across states (i.e. our transient node class). Previous work has shown promise in defining functional network boundaries at the individual level (Braga and Buckner, 2017; Braga et al., 2019; Gordon et al., 2017b; Kong et al., 2018; Laumann et al., 2015; Wang et al., 2015). Individualized functional networks are shown to be highly reliable (Laumann et al., 2015), closely correspond with task activations (Gordon et al., 2017b), and behaviorally meaningful (Kong et al., 2018). Our work builds on this literature and extends it by highlighting that even within an individual the functional networks reliably reconfigure as a function of cognitive state. Such state-specific individualized networks could provide input for real-time fMRI neurofeedback paradigms (Emmert et al., 2016; Hartwell et al., 2016; Koizumi et al., 2017), and brain stimulation therapies (Fitzgerald, 2011; Plow et al., 2016), focusing on the disruption of functional networks at the single subject level. The conventional approach of defining fixed functional networks via population-level resting-state parcellations may limit the efficacy of such treatments. State-specific individualized networks also may provide higher specificity when considered as predictive features in machine learning algorithms (Bzdok and Meyer-Lindenberg, 2017; Vu et al., 2018).
In a recent work, Gratton et al. have studied the magnitude of functional network variability across subjects, tasks, and sessions (Gratton et al., 2018). Their study of brain reconfiguration was restricted to changes in functional connectivity matrices as a whole (i.e., correlation of the vectorized connectivity matrices) with the core finding that connectivity matrices are remarkably stable. Our work differs in that we study the large-scale functional network reconfigurations by probing the changes in node-to-network assignments across subjects and states. These two divergent but complementary views shed light on different aspects of the brain dynamics. While their analysis has shown that functional connections are largely stable with subtle cross-state changes (in terms of correlating vectorized matrices), here we demonstrate that about 73% (i.e., 196 out of 268) of the nodes actually change their network assignment as a function of state. In addition, their observations of functional connectivity matrices indicate that the state-evoked modulations are largely individual-specific (i.e., the consistent state-specific changes are subtle), whereas we demonstrate that state-specific changes in NNAs are sufficiently robust and reliable across subjects to predict the cognitive state. Combined, these observations suggest that while gross matrix level connectivity patterns change only minimally with state (Gratton et al., 2018) consistent with earlier functional fingerprinting findings across state (Finn et al, 2015), individual node to network assignments are flexible, allowing the brain to reconfigure its functional organization as the task demands change. Such reconfigurations are easily measured and change in a significant and meaningful manner.
4.5. Further considerations
Although cognitive-state dependent functional network reconfigurations were investigated here, we did not investigate the temporal dynamics within a given task. This was partly because the length of the sessions in HCP data vary (Uğurbil et al., 2013; Van Essen et al., 2013) and because of methodological concerns surrounding dynamic brain-state definitions, that is, we currently lack a strict way of identifying and validating within-task cognitive states which are consistent across all subjects. However, it is likely that the same reconfiguration is observed dynamically, on a moment-to-moment basis within each condition, specifically for the HCP tasks, which were designed to tap different cognitive processes even within a single task run (Barch et al., 2013). Future work could extend this framework to study the within session dynamics of functional network reconfiguration.
We employed a functional atlas consisting of 268 nodes, generated from an independent group of healthy subjects (Finn et al., 2015; Shen et al., 2013). This atlas has proven to be reproducible and reliable (Shen et al., 2013), beneficial in understanding cross-subject variability, and useful for developing predictive models of behavior (Finn et al., 2015; Rosenberg et al., 2013; Rosenberg et al., 2017; Shen et al., 2017). Given this past performance, this 268-node atlas represents a reasonable way to operationalize the brain’s sub-units in network analyses. However, this atlas was defined at the group-level and therefore might not account for the individual variability in node definitions. To verify that the observed functional network reconfigurations are not confounded by the group-defined nodes, we repeated our analyses, using individualized node atlases as our starting point (see Supplementary Materials). Similar results were obtained (Figure S12), suggesting that the state-evoked functional network reconfigurations are not derived by the incongruency of signals within a node, but are robust observations of brain function. We would anticipate similar results with other atlases of a similar scale.
Just as the core functional connectivity patterns across the whole-brain are stable, underlying these functional patterns is a relatively fixed structural connectivity infrastructure (fixed on the time-scale of an fMRI study). That is, the changing functional patterns on a moment to moment or task to task basis, are not due to structural changes. While there is a large literature where investigators have performed network analysis on structurally defined networks these two approaches are not mutually exclusive and this flexible functional organization is acknowledged to sit on top of a fixed brain infrastructure.
Moving forward it will be important to relate state-evoked functional network reorganization with individual differences in behavior and/or clinical measures. Future work could quantify the extent to which subjects with similar node to network reconfiguration patterns are also similar in state, behavioral, or clinical measures; potentially grouping homogeneous subjects based on their NNA phenotypes. This methodology could be particularly compelling when applied to subjects with different clinical, neurodevelopmental, and aging categories.
5. Conclusion
We showed that the functional network organization of the brain is not fixed, but rather that functional networks reconfigure dynamically, in predictable ways, as a function of cognitive state. Future work should consider state-evoked reconfigurations when studying changes in connectivity across different task-states. Such an approach will hopefully allow us to begin to relate individual differences in functional network reconfiguration to individual differences in behavior or clinical symptoms.
Supplementary Material
Acknowledgments
Data were provided by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Uǧurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University. This work was supported by NIH Grants R01 MH111424, T32 MH019961, R25 MH071584 and DARPA Young Faculty Award (D16AP00046).
Footnotes
Code availability
The 268-node functional parcellation is available online on the BioImage Suite NITRC page (https://www.nitrc.org/frs/?group_id=51). MATLAB, R (for graph visualization), and Python (for predictive modeling) scripts were written to perform the analyses described; these code are available on GitHub at https://github.com/YaleMRRC/Network-Parcellation-Tasks.git. The graph visualization is released separately under the terms of GNU General Public License and can be found here: https://github.com/YaleMRRC/Network-Visualization.git.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Reference
- Adelstein JS, Shehzad Z, Mennes M, DeYoung CG, Zuo X-N, Kelly C, Margulies DS, Bloomfield A, Gray JR, Castellanos FX, 2011. Personality is reflected in the brain’s intrinsic functional architecture. PloS one 6, e27633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson ML, Kinnison J, Pessoa L, 2013. Describing functional diversity of brain regions and brain networks. Neuroimage 73, 50–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews‐Hanna JR, Smallwood J, Spreng RN, 2014. The default network and self‐ generated thought: component processes, dynamic control, and clinical relevance. Annals of the New York Academy of Sciences 1316, 29–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barch DM, Burgess GC, Harms MP, Petersen SE, Schlaggar BL, Corbetta M, Glasser MF, Curtiss S, Dixit S, Feldt C, 2013. Function in the human connectome: task-fMRI and individual differences in behavior. Neuroimage 80, 169–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Wymbs NF, Porter MA, Mucha PJ, Carlson JM, Grafton ST, 2011. Dynamic reconfiguration of human brain networks during learning. Proceedings of the National Academy of Sciences 108, 7641–7646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Wymbs NF, Rombach MP, Porter MA, Mucha PJ, Grafton ST, 2013. Task-based core-periphery organization of human brain dynamics. PLoS computational biology 9, e1003171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Yang M, Wymbs NF, Grafton ST, 2015. Learning-induced autonomy of sensorimotor systems. Nature neuroscience 18, 744–751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bijsterbosch JD, Woolrich MW, Glasser MF, Robinson EC, Beckmann CF, Van Essen DC, Harrison SJ, Smith SM, 2018. The relationship between spatial configuration and functional connectivity of brain regions. Elife 7, e32992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borda M, 2011. Fundamentals in information theory and coding. Springer Science & Business Media. [Google Scholar]
- Braga RM, Buckner RL, 2017. Parallel interdigitated distributed networks within the individual estimated by intrinsic functional connectivity. Neuron 95, 457–471. e455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braga RM, Van Dijk KR, Polimeni JR, Eldaief MC, Buckner RL, 2019. Parallel distributed networks resolved at high resolution reveal close juxtaposition of distinct regions. Journal of Neurophysiology. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bzdok D, Meyer-Lindenberg A, 2017. Machine learning for precision psychiatry: Opportunites and challenges. Biological Psychiatry: Cognitive Neuroscience and Neuroimaging. [DOI] [PubMed] [Google Scholar]
- Cassady K, Gagnon H, Lalwani P, Simmonite M, Foerster B, Park D, Peltier SJ, Petrou M, Taylor SF, Weissman DH, 2019. Sensorimotor network segregation declines with age and is linked to GABA and to sensorimotor performance. NeuroImage 186, 234–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen JD, Lee RF, Norman KA, Turk-Browne NB, 2015. Closed-loop training of attention with real-time brain imaging. Nature neuroscience 18, 470–475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen JR, D’Esposito M, 2016. The segregation and integration of distinct brain networks and their relationship to cognition. Journal of Neuroscience 36, 12083–12094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Bagic A, Kass R, Schneider W, 2010. Prefrontal dynamics underlying rapid instructed task learning reverse with practice. The Journal of Neuroscience 30, 14245–14254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Bassett DS, Power JD, Braver TS, Petersen SE, 2014. Intrinsic and task-evoked network architectures of the human brain. Neuron 83, 238–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Etzel JA, Zacks JM, Schneider W, Braver TS, 2011. Rapid transfer of abstract rules to novel contexts in human lateral prefrontal cortex. Frontiers in human neuroscience 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Ito T, Bassett DS, Schultz DH, 2016. Activity flow over resting-state networks shapes cognitive task activations. Nature neuroscience 19, 1718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Reynolds JR, Power JD, Repovs G, Anticevic A, Braver TS, 2013. Multi-task connectivity reveals flexible hubs for adaptive task control. Nature neuroscience 16, 1348–1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossley NA, Mechelli A, Vértes PE, Winton-Brown TT, Patel AX, Ginestet CE, McGuire P, Bullmore ET, 2013. Cognitive relevance of the community structure of the human brain functional coactivation network. Proceedings of the National Academy of Sciences 110, 11583–11588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison EN, Schlesinger KJ, Bassett DS, Lynall M-E, Miller MB, Grafton ST, Carlson JM, 2015. Brain network adaptability across task states. PLoS Comput Biol 11, e1004029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di X, Gohel S, Kim EH, Biswal BB, 2013. Task vs. rest—different network configurations between the coactivation and the resting-state brain networks. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosenbach NU, Fair DA, Miezin FM, Cohen AL, Wenger KK, Dosenbach RA, Fox MD, Snyder AZ, Vincent JL, Raichle ME, 2007. Distinct brain networks for adaptive and stable task control in humans. Proceedings of the National Academy of Sciences 104, 11073–11078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emmert K, Kopel R, Sulzer J, Brühl AB, Berman BD, Linden DE, Horovitz SG, Breimhorst M, Caria A, Frank S, 2016. Meta-analysis of real-time fMRI neurofeedback studies using individual participant data: How is brain regulation mediated? NeuroImage 124, 806–812. [DOI] [PubMed] [Google Scholar]
- Fedorenko E, Thompson-Schill SL, 2014. Reworking the language network. Trends in cognitive sciences 18, 120–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finn ES, Shen X, Scheinost D, Rosenberg MD, Huang J, Chun MM, Papademetris X, Constable RT, 2015. Functional connectome fingerprinting: identifying individuals using patterns of brain connectivity. Nature neuroscience. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitzgerald PB, 2011. The emerging use of brain stimulation treatments for psychiatric disorders. Australian & New Zealand Journal of Psychiatry 45, 923–938. [DOI] [PubMed] [Google Scholar]
- Fox PT, Lancaster JL, 2002. Mapping context and content: the BrainMap model. Nature Reviews Neuroscience 3, 319. [DOI] [PubMed] [Google Scholar]
- Friedman JH, 2001. Greedy function approximation: a gradient boosting machine. Annals of statistics, 1189–1232. [Google Scholar]
- Fujishige S, 2005. Submodular functions and optimization. Elsevier. [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, 2013. The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon EM, Laumann TO, Adeyemo B, Petersen SE, 2017a. Individual variability of the system-level organization of the human brain. Cerebral cortex 27, 386–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon EM, Laumann TO, Gilmore AW, Newbold DJ, Greene DJ, Berg JJ, Ortega M, Hoyt-Drazen C, Gratton C, Sun H, 2017b. Precision functional mapping of individual human brains. Neuron 95, 791–807. e797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gratton C, Laumann TO, Nielsen AN, Greene DJ, Gordon EM, Gilmore AW, Nelson SM, Coalson RS, Snyder AZ, Schlaggar BL, 2018. Functional brain networks are dominated by stable group and individual factors, not cognitive or daily variation. Neuron 98, 439–452. e435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grayson DS, Ray S, Carpenter S, Iyer S, Dias TGC, Stevens C, Nigg JT, Fair DA, 2014. Structural and functional rich club organization of the brain in children and adults. PloS one 9, e88297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Srivastava G, Reiss AL, Menon V, 2004. Default-mode network activity distinguishes Alzheimer’s disease from healthy aging: evidence from functional MRI. Proceedings of the National Academy of Sciences of the United States of America 101, 4637–4642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamming R, 1950. Error detecting and error correcting codes. Bell System Technical Journal 29, 147–160. [Google Scholar]
- Hartwell KJ, Hanlon CA, Li X, Borckardt JJ, Canterberry M, Prisciandaro JJ, Moran-Santa Maria MM, LeMatty T, George MS, Brady KT, 2016. Individualized real-time fMRI neurofeedback to attenuate craving in nicotine-dependent smokers. Journal of psychiatry & neuroscience: JPN 41, 48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haxby JV, Connolly AC, Guntupalli JS, 2014. Decoding neural representational spaces using multivariate pattern analysis. Annual review of neuroscience 37, 435–456. [DOI] [PubMed] [Google Scholar]
- Heinzle J, Wenzel MA, Haynes J-D, 2012. Visuomotor functional network topology predicts upcoming tasks. Journal of Neuroscience 32, 9960–9968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito T, Kulkarni KR, Schultz DH, Mill RD, Chen RH, Solomyak LI, Cole MW, 2017. Cognitive task information is transferred between brain regions via resting-state network topology. bioRxiv, 101782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi A, Scheinost D, Okuda H, Belhachemi D, Murphy I, Staib LH, Papademetris X, 2011. Unified framework for development, deployment and robust testing of neuroimaging algorithms. Neuroinformatics 9, 69–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinnison J, Padmala S, Choi J-M, Pessoa L, 2012. Network analysis reveals increased integration during emotional and motivational processing. Journal of Neuroscience 32, 8361–8372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koizumi A, Amano K, Cortese A, Shibata K, Yoshida W, Seymour B, Kawato M, Lau H, 2017. Fear reduction without fear through reinforcement of neural activity that bypasses conscious exposure. Nature human behaviour 1, 0006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong R, Li J, Orban C, Sabuncu MR, Liu H, Schaefer A, Sun N, Zuo X-N, Holmes AJ, Eickhoff SB, 2018. Spatial topography of individual-specific cortical networks predicts human cognition, personality, and emotion. Cerebral cortex 1, 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krause A, Gomes RG, 2010. Budgeted nonparametric learning from data streams. Proceedings of the 27th International Conference on Machine Learning (ICML-10), pp. 391–398. [Google Scholar]
- Krienen FM, Yeo BT, Buckner RL, 2014. Reconfigurable task-dependent functional coupling modes cluster around a core functional architecture. Phil. Trans. R. Soc. B 369, 20130526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird AR, Fox PM, Eickhoff SB, Turner JA, Ray KL, McKay DR, Glahn DC, Beckmann CF, Smith SM, Fox PT, 2011. Behavioral interpretations of intrinsic connectivity networks. Journal of cognitive neuroscience 23, 4022–4037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laumann TO, Gordon EM, Adeyemo B, Snyder AZ, Joo SJ, Chen M-Y, Gilmore AW, McDermott KB, Nelson SM, Dosenbach NU, 2015. Functional system and areal organization of a highly sampled individual human brain. Neuron 87, 657–670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Liu Y, Li J, Qin W, Li K, Yu C, Jiang T, 2009. Brain anatomical network and intelligence. PLoS computational biology 5, e1000395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattar MG, Cole MW, Thompson-Schill SL, Bassett DS, 2015a. A functional cartography of cognitive systems. PLoS Comput Biol 11, e1004533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattar MG, Cole MW, Thompson-Schill SL, Bassett DS, 2015b. A functional cartography of cognitive systems. PLoS computational biology 11, e1004533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMenamin BW, Langeslag SJ, Sirbu M, Padmala S, Pessoa L, 2014. Network organization unfolds over time during periods of anxious anticipation. Journal of Neuroscience 34, 11261–11273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mennes M, Kelly C, Colcombe S, Castellanos FX, Milham MP, 2012. The extrinsic and intrinsic functional architectures of the human brain are not equivalent. Cerebral cortex 23, 223–229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meunier D, Lambiotte R, Fornito A, Ersche K, Bullmore ET, 2009. Hierarchical modularity in human brain functional networks. Frontiers in neuroinformatics 3, 37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minoux M, 1978. Accelerated greedy algorithms for maximizing submodular set functions Optimization Techniques. Springer, pp. 234–243. [Google Scholar]
- Mohr H, Wolfensteller U, Betzel RF, Mišić B, Sporns O, Richiardi J, Ruge H, 2016. Integration and segregation of large-scale brain networks during short-term task automatization. Nature communications 7, 13217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mueller S, Wang D, Fox MD, Yeo BT, Sepulcre J, Sabuncu MR, Shafee R, Lu J, Liu H, 2013. Individual variability in functional connectivity architecture of the human brain. Neuron 77, 586–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nemhauser GL, Wolsey LA, Fisher ML, 1978. An analysis of approximations for maximizing submodular set functions—I. Mathematical Programming 14, 265–294. [Google Scholar]
- Noble S, Spann MN, Tokoglu F, Shen X, Constable RT, Scheinost D, 2017. Influences on the test–retest reliability of functional connectivity MRI and its relationship with behavioral utility. Cerebral cortex 27, 5415–5429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park H-J, Friston K, 2013. Structural and functional brain networks: from connections to cognition. Science 342, 1238411. [DOI] [PubMed] [Google Scholar]
- Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, 2011. Scikit-learn: Machine learning in Python. Journal of machine learning research 12, 2825–2830. [Google Scholar]
- Perez Velazquez JL, 2017. Dynamiceuticals: The Next Stage in Personalized Medicine. Frontiers in neuroscience 11, 329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plow E, Sankarasubramanian V, Cunningham D, Potter-Baker K, Varnerin N, Cohen L, Sterr A, Conforto A, Machado A, 2016. Models to tailor brain stimulation therapies in stroke. Neural Plasticity 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Cohen AL, Nelson SM, Wig GS, Barnes KA, Church JA, Vogel AC, Laumann TO, Miezin FM, Schlaggar BL, Petersen SE, 2011. Functional network organization of the human brain. Neuron 72, 665–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Schlaggar BL, Lessov-Schlaggar CN, Petersen SE, 2013. Evidence for hubs in human functional brain networks. Neuron 79, 798–813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg M, Noonan S, DeGutis J, Esterman M, 2013. Sustaining visual attention in the face of distraction: A novel gradual-onset continuous performance task. Attention, Perception, & Psychophysics 75, 426–439. [DOI] [PubMed] [Google Scholar]
- Rosenberg MD, Finn ES, Scheinost D, Papademetris X, Shen X, Constable RT, Chun MM, 2016. A neuromarker of sustained attention from whole-brain functional connectivity. Nature neuroscience 19, 165–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg MD, Hsu W-T, Scheinost D, Constable RT, Chun MM, 2017. Connectome-based models predict separable components of attention in novel individuals. The Journal of Cognitive Neuroscience, Submitted. [DOI] [PubMed] [Google Scholar]
- Salehi M, Karbasi A, Shen X, Scheinost D, Constable RT, 2018. An exemplar-based approach to individualized parcellation reveals the need for sex specific functional networks. NeuroImage 170, 54–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Davatzikos C, 2015. Towards an individualized delineation of functional neuroanatomy. Neuron 87, 471–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Wolf DH, Roalf DR, Ruparel K, Erus G, Vandekar S, Gennatas ED, Elliott MA, Smith A, Hakonarson H, 2015. Linked sex differences in cognition and functional connectivity in youth. Cerebral cortex 25, 2383–2394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz DH, Cole MW, 2016. Higher Intelligence Is Associated with Less Task-Related Brain Network Reconfiguration. The Journal of Neuroscience 36, 8551–8561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X, Finn ES, Scheinost D, Rosenberg MD, Chun MM, Papademetris X, Constable RT, 2017. Using connectome-based predictive modeling to predict individual behavior from brain connectivity. nature protocols 12, 506–518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X, Tokoglu F, Papademetris X, Constable RT, 2013. Groupwise whole-brain parcellation from resting-state fMRI data for network node identification. NeuroImage 82, 403–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shine JM, Bissett PG, Bell PT, Koyejo O, Balsters JH, Gorgolewski KJ, Moodie CA, Poldrack RA, 2016. The dynamics of functional brain networks: integrated network states during cognitive task performance. Neuron 92, 544–554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Beckmann CF, Andersson J, Auerbach EJ, Bijsterbosch J, Douaud G, Duff E, Feinberg DA, Griffanti L, Harms MP, 2013. Resting-state fMRI in the human connectome project. NeuroImage 80, 144–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Fox PT, Miller KL, Glahn DC, Fox PM, Mackay CE, Filippini N, Watkins KE, Toro R, Laird AR, 2009. Correspondence of the brain’s functional architecture during activation and rest. Proceedings of the National Academy of Sciences 106, 13040–13045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Moeller S, Xu J, Auerbach EJ, Woolrich MW, Beckmann CF, Jenkinson M, Andersson J, Glasser MF, 2012. Temporally-independent functional modes of spontaneous brain activity. Proceedings of the National Academy of Sciences 109, 3131–3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern ER, Fitzgerald KD, Welsh RC, Abelson JL, Taylor SF, 2012. Resting-state functional connectivity between fronto-parietal and default mode networks in obsessive-compulsive disorder. PloS one 7, e36356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Telesford QK, Lynall M-E, Vettel J, Miller MB, Grafton ST, Bassett DS, 2016. Detection of functional brain network reconfiguration during task-driven cognitive states. NeuroImage 142, 198–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas Yeo BT, Krienen FM, Sepulcre J, Sabuncu MR, Lashkari D, Hollinshead M, Roffman JL, Smoller JW, Zöllei L, Polimeni JR, Fischl B, Liu H, Buckner RL, 2011. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. Journal of Neurophysiology 106, 1125–1165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uğurbil K, Xu J, Auerbach EJ, Moeller S, Vu AT, Duarte-Carvajalino JM, Lenglet C, Wu X, Schmitter S, Van de Moortele PF, 2013. Pushing spatial and temporal resolution for functional and diffusion MRI in the Human Connectome Project. NeuroImage 80, 80–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Den Heuvel MP, Sporns O, 2011. Rich-club organization of the human connectome. Journal of Neuroscience 31, 15775–15786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dijk KR, Sabuncu MR, Buckner RL, 2012. The influence of head motion on intrinsic functional connectivity MRI. NeuroImage 59, 431–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Eimeren T, Monchi O, Ballanger B, Strafella AP, 2009. Dysfunction of the default mode network in Parkinson disease: a functional magnetic resonance imaging study. Archives of neurology 66, 877–883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, Consortium W-MH, 2013. The WU-Minn human connectome project: an overview. NeuroImage 80, 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vu M-AT, Adalı T, Ba D, Buzsáki G, Carlson D, Heller K, Liston C, Rudin C, Sohal VS, Widge AS, 2018. A Shared Vision for Machine Learning in Neuroscience. Journal of Neuroscience 38, 1601–1607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang D, Buckner RL, Fox MD, Holt DJ, Holmes AJ, Stoecklein S, Langs G, Pan R, Qian T, Li K, 2015. Parcellating cortical functional networks in individuals. Nature neuroscience 18, 1853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolgar A, Thompson R, Bor D, Duncan J, 2011. Multi-voxel coding of stimuli, rules, and responses in human frontoparietal cortex. Neuroimage 56, 744–752. [DOI] [PubMed] [Google Scholar]
- Zanto TP, Gazzaley A, 2013. Fronto-parietal network: flexible hub of cognitive control. Trends in cognitive sciences 17, 602–603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Cheng W, Liu Z, Zhang K, Lei X, Yao Y, Becker B, Liu Y, Kendrick KM, Lu G, 2016. Neural, electrophysiological and anatomical basis of brain-network variability and its characteristic changes in mental disorders. Brain 139, 2307–2321. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.