Beyond Beer's Law: Why the Index of Refraction Depends (Almost) Linearly on Concentration

Abstract

Beer's empiric law states that absorbance is linearly proportional to the concentration. Based on electromagnetic theory, an approximately linear dependence can only be confirmed for comparably weak oscillators. For stronger oscillators the proportionality constant, the molar attenuation coefficient, is modulated by the inverse index of refraction, which is itself a function of concentration. For comparably weak oscillators, the index of refraction function depends, like absorbance, linearly on concentration. For stronger oscillators, this linearity is lost, except at wavenumbers considerably lower than the oscillator position. In these transparency regions, linearity between the change of the index of refraction and concentration is preserved to a high degree. This can be shown with help of the Kramers–Kronig relations which connect the integrated absorbance to the index of refraction change at lower wavenumbers than the corresponding band. This finding builds the foundation not only for refractive index sensing, but also for new interferometric approaches in IR spectroscopy, which allow measuring the complex index of refraction function.

Linear or not? Like the absorbance, the change of the index of refraction at a particular spectral point can depend linearly on concentration for low oscillator strength or concentration.

The exact origin of the form of Beer's law, as we employ it nowadays1, 2

$${\displaystyle A\left(\tilde{v}\right)=ϵ{}^{*}\left(\tilde{v}\right)·c·d}$$ (1)

wherein $ϵ{}^{*}\left(\tilde{v}\right)$ is the molar attenuation coefficient, c the concentration and d the sample thickness, remains unclear. It seems that it was not employed in this form before about 1900, as it was not discussed nor provided in this form in Kayser's handbook of spectroscopy,3 which was the reference work at this time. When Max Planck derived his particular kind of dispersion theory and employed it to compare the results with Beer's law in 1903,4 he was most probably unaware of Equation (1), otherwise he probably would have derived it from dispersion theory. Recently, this derivation was carried out, first from dispersion theory5 and, subsequently, from simple electromagnetic theory.6 One of the main results of the derivation is that the molar attenuation coefficient is inversely proportional to the index of refraction, which is itself a function of concentration. Concerning the nature of this dependence, as was already stated in Ref. [5], a law comparable to Beer's law, but for the index of refraction function, can be derived. In ref.5 the nature of this dependence was not investigated in detail. As we will show in the following, the use of the index of refraction variation instead of the absorbance to investigate concentration may have several advantages.

To derive the concentration dependence of the complex index of refraction, it is possible to start from simple electromagnetic theory. Accordingly, the macroscopic polarization $\overrightarrow{P}$ is related to the dipole moment $\overrightarrow{p}$ induced in an atom or a molecule by the following relation:

$${\displaystyle \overrightarrow{P}=N·\overrightarrow{p}}$$ (2)

Here, N is the number of dipole moments per unit volume (which is equal to the molar concentration multiplied by Avogadro's constant, N=N_A⋅c). Inherent to Equation (2) is the assumption that there are no interactions between the microscopic dipoles, i. e. there are no chemical interactions. On the other hand, macroscopically, for scalar media, the polarization is related to an applied electric field $\overrightarrow{E}$ [Eq. (3)]:

$${\displaystyle \overrightarrow{P}={ϵ}_0({ϵ}_r-1)\overrightarrow{E}={ϵ}_0\chi \overrightarrow{E}}$$ (3)

wherein ${ϵ}_r$ is the relative dielectric function, $\chi$ the electric susceptibility and ${ϵ}_0$ the vacuum permittivity. The use of a scalar dielectric function implies that the polarization is always co‐oriented to the electric field and that the material is isotropic and homogenous in relation to the resolution limit of light. Using the relation between electric susceptibility and polarizability $\alpha$ , $\chi =N·\alpha /{ϵ}_0$ , and assuming additionally that there are no local field effects, we find that [Eq. (4)]:

$${\displaystyle \chi =c\frac{N_A·\alpha }{{ϵ}_0}}$$ (4)

A similar equation relates in Raman spectroscopy the Raman tensor and the change of polarizability of a molecule or a unit cell during a vibration. In contrast to Raman spectroscopy, however, in UV‐Vis and IR‐spectroscopy we have to invoke Maxwell's wave equations to understand the changes of the intensity due to absorption. Assuming that our medium is not only scalar but perfectly homogenous (in particular nearfield interactions/electromagnetic coupling are excluded7), then the simple and well‐known relation ${ϵ}_r={\widehat{n}}^2$ follows,8 wherein $\widehat{n}$ is the complex index of refraction. Accordingly, it follows:

$${\displaystyle \widehat{n}=n+ik=\sqrt{1+\chi }=\sqrt{1+c\frac{N_A·\alpha }{{ϵ}_0}}}$$ (5)

Focusing on the (real) index of refraction n and assuming that the electric susceptibility $\chi \ll 1$ , so that $\sqrt{1+\chi }\approx 1+\chi /2$ , we find:

$${\displaystyle n\left(\tilde{v}\right)=1+c\frac{N_A·{\alpha }^{\text{'}}\left(\tilde{v}\right)}{2{ϵ}_0}}$$ (6)

Here, ${\alpha }^{\text{'}}\left(\tilde{v}\right)$ is the real and wavenumber dependent part of the polarizability. Therefore, as long as the electric susceptibility is small, a linear relation between the change of the index of refraction and the concentration can be expected (note that this result is, not by accident, similar to the one which is obtained from the Lorentz‐Lorenz equation for a diluted gas!9).

What if the condition $\chi \ll 1$ does not hold? For the index of absorption, it was found that Beer's law is no longer valid for individual spectral points. This finding is closely connected to the properties of the Lorentz‐oscillator and the difference between it and a Lorentz‐profile.10 The latter is derived from the Lorentz‐oscillator by the same assumption that simplifies Equation (5) to Equation (6). If Lorentz‐profiles really would be able to resemble the bands of the absorption index function, the bands would be always symmetric around the band positions independent of oscillator strength. This would guarantee that absorbance increases linearly with concentration. In contrast, this is not generally the case if Lorentz‐oscillators are assumed. For higher oscillator strength, the peak maxima of absorbance bands described by Lorentz‐oscillators blueshift relative to the oscillator position (Figure 1, lower panel). This blueshift and the corresponding loss of mirror symmetry is due to the fact that the imaginary part of the dielectric function has to be divided by the non‐symmetric index of refraction function to obtain the index of absorption (cf. Figure 1).

Figure 1.

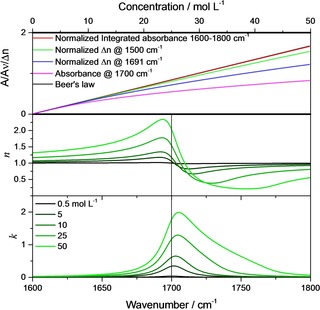
Upper panel: Beer's law (black line) compared with concentration dependence of the normalized integrated absorbance (from 1600–1800 cm⁻¹, red line), the normalized change of the index of refraction at 1500 cm⁻¹ (green line), the normalized change of the index of refraction at 1693 cm⁻¹ (blue line), and the absorbance at the oscillator position (1700 cm⁻¹, pink line). Center panel: Index of refraction function. Lower panel: Index of absorption function for different concentrations of 0.5, 5, 10, 25 and 50 mol L⁻¹ (S*²=4900 L/(mol cm²), ${\tilde{v}}_0=$ 1700 cm⁻¹ γ=20 cm⁻¹).

Still, even in this case, there is a quantity that is preserved and remains linear to the concentration, which is the integral molar absorbance:11

$${\displaystyle \underset{0}{\overset{\infty }{\int }}\tilde{v}k\left(\tilde{v}\right)d\tilde{v}=\frac{\pi }{4}{S}^2=\frac{\pi }{4}c·S{{}^{*}}^2}$$ (7)

This integral molar absorbance is equal to the square of the oscillator strength S ² or the molar oscillator strength S*² times the concentration. Equation (7) is one of the so‐called Kramers–Kronig sum rules. Classically, the oscillator strength was introduced by dispersion relations, the most prominent of which is the classical damped harmonic oscillator model for which the relative dielectric function is a sum of contributions from each of the oscillators. It is defined via $S^2=q^{2}N/\left(\mu {ϵ}_0\right)$ , where q is the (partial) charge and μ the reduced mass of the vibrating atoms. If, for simplicity, we keep assuming only a single oscillator, the relative dielectric function is given by [Eq. (8)]:

$${\displaystyle {ϵ}_r\left(\tilde{v}\right)=1+c\frac{S{{}^{*}}^2}{{\tilde{v}}_0^2-{\tilde{v}}^2-i\tilde{v}y}}$$ (8)

For wavenumbers clearly below the resonance in the range where the imaginary part of the relative dielectric function ${ϵ}_r^{\text{'}\text{'}}\left(\tilde{v}\right)\approx 0$ , the damping term $i\tilde{v}y$ is negligible and, since the wavenumber is lower than the resonance wavenumber ${\tilde{v}}_0$ , ${\tilde{v}}_0^2\gg {\tilde{v}}^2$ .

Therefore:

$${\displaystyle {ϵ}_r\left(\tilde{v}\right)\approx 1+c\frac{S{{}^{*}}^2}{{\tilde{v}}_0^2}}$$ (9)

Usually, $S{{}^{*}}^2\ll {\tilde{v}}_0^2$ , so that even for large molar concentrations, $cS{{}^{*}}^2/{\tilde{v}}_0^2\ll 1$ in Equation (9). Accordingly, even for stronger oscillators ($\sqrt{cS{}^{*}2}>200{\mathrm{cm}}^{-1}$ ),

$${\displaystyle n\left(\tilde{v}\right)\approx 1+c\frac{S{{}^{*}}^2}{2{\tilde{v}}_0^2}}$$ (10)

and the increase of the index of refraction due to absorption as implied by Equation (7) can be understood as being conform to the Kramers‐Kronig relations (unfortunately a direct prove/derivation seems to be not possible)11. In other words, the increase of the index of refraction is proportional to the integral absorbance. Nevertheless, the former may be easier to determine experimentally, at least for strong oscillators, since in case of the latter the determination of the baseline may cause ambiguities.

Note that for real materials we usually have contributions from oscillators at higher wavenumbers (both in the infrared as well as in the UV‐Vis spectral region), the effects of which can be captured by replacing unity in Equation (10) by $n_{\infty }$ :

$${\displaystyle n\left(\tilde{v}\right)=n_{\infty }+c\frac{S{{}^{*}}^2}{2{\tilde{v}}_0^2}}$$ (11)

$n_{\infty }$ is the approximately constant index of refraction in the transparency region between the infrared and the UV/VIS spectral region. It is connected to the dielectric background ${ϵ}_{\infty }$ via ${ϵ}_{\infty }=n_{\infty }^2$ .

If we have a mixture or a solution, for which the solvent is non‐absorbing in the spectral region we are interested in, the solvent might change $n_{\infty }$ , the oscillator strength and even the oscillator position by chemical interactions, but the linear change of the index of refraction should be preserved to a good approximation.9

Before we apply the relations on a real system, we first illustrate them employing a model system consisting of one Lorentz‐oscillator with S*²=4900 L / (mol cm²), ${\tilde{v}}_0=$ 1700 cm⁻¹, γ=20 cm⁻¹ and c=50 mol L⁻¹ for the neat substance. For this system, for concentrations c <1 mol L⁻¹ the index of refraction $n\left(\tilde{v}\right)$ stays close to unity (not shown). Therefore, the shape of the absorption index band is approximately symmetric like the one for the imaginary part of the relative dielectric function (cf. lower panel of Figure 2 with upper panel). As soon as the concentration increases, $n\left(\tilde{v}\right)$ begins to significantly differ from unity in the vicinity of the absorption band, as illustrated in Figure 1 center panel, while ${ϵ}_r^{\text{'}\text{'}}\left(\tilde{v}\right)$ always stays symmetric (Figure 1, upper panel).

Figure 2.

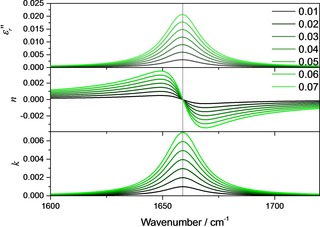
Imaginary part of the relative dielectric function (upper panel), the index of refraction function (center panel, displayed is actually $n-n_{\infty }$ ) and the index of absorption function (lower panel) for different concentrations between 0.01–0.07 mol L⁻¹ (S*²=9801 L/(mol cm²), ${\tilde{v}}_0=$ 1659 cm⁻¹ γ=20 cm⁻¹).

As a consequence, the absorbance band begins to blue‐shift with increasing concentration and to show a large tail towards higher wavenumbers. Accordingly, if we monitor the changes of the absorbance at the oscillator position, i. e. at 1700 cm⁻¹, we see in Figure 1, upper panel, that for c>2 mol L⁻¹ the absorbance increase noticeably deviates from linearity. On the other hand, the integrated band intensity is, according to Equation (7), a preserved quantity. Even when the integration is carried out only from 1600–1800 cm⁻¹, the increase of the integrated absorbance stays, as already mentioned, to a very large degree approximately linear. In practice, however, integrating the bands may be problematic, since the result is strongly depending on the choice of the baseline. This is where quantitative optical spectroscopy could greatly benefit from determining the increase of the index of refraction instead (or additionally), since this approach is essentially baseline‐independent. Concerning this approach, we compare the increase of the index of refraction at its maximum for the sample with the lowest concentration (c=0.5 mol L⁻¹, 1691 cm⁻¹).

As can be seen in Figure 1, upper panel, this clearly extends the range of linearity compared to the case where the pointwise validity of Beer's law is assumed (orange line in Figure 1, upper panel). A further extension of this range is possible, when instead of the maximum of the index of refraction function a preferably strong red‐shifted wavenumber is chosen, like, as in Figure 1, upper panel, 1500 cm⁻¹. As Equation (10) predicts, the change of the index of refraction at this wavenumber is mostly a linear function of the concentration, albeit in a smaller concentration range than the integrated absorbance. This linear change has been confirmed numerous times experimentally and builds the foundation for the determination of concentrations by refractive index sensing and well‐established methods like, e. g., sugar concentration determination by refractometer.12

For comparably weak oscillators, like most vibrations in organic and biological materials, linearity based on Equation (6) could be assumed over the whole concentration range. From Figure 1, upper panel, we see that linearity holds to about c ≈8 mol L⁻¹ (comparison of black and pink curve, absorbance value at 1700 cm⁻¹). This would be synonymous with $\sqrt{cS{{}^{*}}^2}=S=200{\mathrm{cm}}^{-1}$ , which is approximately the oscillator strength of a pure organic or biological material comparable intense C=O vibration, which can be found usually in the range of 1650–1750 cm⁻¹. This limiting value of the oscillator strengths also agrees with the limits of applicability of the Lorentz‐profile, which is based on the same approximation that leads to Beer's law, and the need for a Lorentz‐oscillator instead as shown in Ref. [10].

To prove this assumption and to show that Equation (6) is indeed applicable, we used a quantum cascade laser‐based Mach‐Zehnder interferometer which allows to determine absorption and dispersion spectra in the mid‐infrared region.13, 14 With this instrument, we determined the index of refraction variation of solutions of ϵ‐caprolactam in chloroform in the region between 1580 and 1730 cm⁻¹, which are due to the C=O vibration located at 1659 cm⁻¹, in dependence of the concentration. For the used concentration range (10–70 mmol L⁻¹) comparably small changes of Δn with the wavenumber are expected, and a pointwise linear dependence of Δn could be safely assumed. To test this hypothesis, and to illustrate the evaluation of the index of refraction variation with concentration, we assumed a second model oscillator located at 1659 cm⁻¹. The further parameters of this oscillator are given by S*²=9801 L / (mol cm²), γ=20 cm⁻¹ and c=9 mol L⁻¹, which is approximately the concentration of neat ϵ‐caprolactam. The corresponding imaginary part of the dielectric function, the index of refraction function and the index of absorption function are displayed in Figure 2.

In this concentration range, the oscillator parameters lead to a symmetric shape of the band in the index of absorption function. Correspondingly, the index of refraction function shows a point where $n-n_{\infty }=0$ independent of concentration, which is (almost) located at the oscillator position. At wavenumbers in the vicinity of this point, it seems that the index of refraction changes linearly with wavenumber. This is illustrated in the upper panel of Figure 3. Indeed, linear fits confirm linear variations of Δn with concentration in the range ±2 cm⁻¹ around the inflection point (≈1700 cm⁻¹). Δn, on the other hand, changes linearly with the wavenumber in the same range with R²=0.99986. Accordingly, not only $n-n_{\infty }$ , but also its derivative with respect to wavenumber should be linearly depending on the concentration. That the slope of Δn around the inclination/the oscillator position is indeed also a linear function of the concentration is demonstrated in the lower part of Figure 3. This means that at the location of the largest changes, several experimental points can be averaged, which is the preferred strategy given that the changes of the index of refraction are overall quite small. The selection of appropriate points depends ultimately on spectral resolution and the damping constant. The latter is to a good approximation the full width at half height (FWHH). The wavenumbers of the points at half height are for comparable weak oscillators the positions of the maximum and the minimum of the index of refraction. To stay in the linear regime, it is advisable not to take points which are further away than ±1/6−1/8 FWHH from the inflection point as a rule of thumb.

Figure 3.

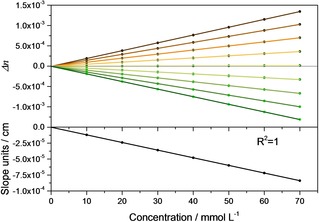
Upper panel: Δn as a function of concentration for the inflexion point (near zero line) and the points within ±2 cm⁻¹ (one point per 0.5 cm⁻¹, lines above the zero line refer to lower wavenumbers). Lower panel: Change of the inclination around the inflexion point as a function of concentration.

The theoretical considerations above are fully consistent with experimental data. Figure 4 shows the experimentally obtained index of refraction functions for solutions of ϵ‐caprolactam in chloroform around the C=O vibration located at 1659 cm⁻¹ (for experimental details cf. the supporting information). Obviously, as already discussed, around the point of inflection located at the oscillator position the index of refraction changes approximately linearly and the inclination changes with the concentration (See inset in Figure 4, lower panel.) Conform to theory, this change of the inclination with concentration is linear.

Figure 4.

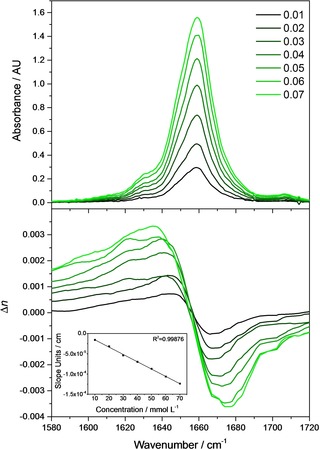
Experimentally recorded absorbance (upper panel) and index of refraction (lower panel) spectra of ϵ‐caprolactam at different concentrations. Inset shows the change of the inclination around the inflexion point as a function of concentration.

In summary, we have extended the theoretical derivation of the concentration dependence of the absorbance (“Beer's law”) to include the concentration dependence of the index of refraction function. For not too strong oscillators in combination with not too high concentrations, the changes of the index of refraction function are linearly related to concentration. This was demonstrated by experimental results.

Experimental Section

The experimental section and details about data analysis are provided in the Supporting Information.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

T. G. Mayerhöfer, A. Dabrowska, A. Schwaighofer, B. Lendl, J. Popp, ChemPhysChem 2020, 21, 707.