Premature Deaths, Statistical Lives, and Years of Life Lost: Identification, Quantification, and Valuation of Mortality Risks

Abstract

Mortality effects of exposure to air pollution and other environmental hazards are often described by the estimated number of “premature” or “attributable” deaths and the economic value of a reduction in exposure as the product of an estimate of “statistical lives saved” and a “value per statistical life.” These terms can be misleading because the number of deaths advanced by exposure cannot be determined from mortality data alone, whether from epidemiology or randomized trials (it is not statistically identified). The fraction of deaths “attributed” to exposure is conventionally derived as the hazard fraction (R – 1)/R, where R is the relative risk of mortality between high and low exposure levels. The fraction of deaths advanced by exposure (the “etiologic” fraction) can be substantially larger or smaller: it can be as large as one and as small as 1/e (≈0.37) times the hazard fraction (if the association is causal and zero otherwise). Recent literature reveals misunderstanding about these concepts. Total life years lost in a population due to exposure can be estimated but cannot be disaggregated by age or cause of death. Economic valuation of a change in exposure‐related mortality risk to a population is not affected by inability to know the fraction of deaths that are etiologic. When individuals facing larger or smaller changes in mortality risk cannot be identified, the mean change in population hazard is sufficient for valuation; otherwise, the economic value can depend on the distribution of risk reductions.

1. INTRODUCTION

Health effects of environmental exposures are quantified for use in impact studies and environmental burden of disease (EBD) studies. Impact studies evaluate the effects on health of government regulations and other policies to reduce exposures, such as requiring emission‐control equipment or imposing fees on emissions. The estimated health effects are often used as inputs to a benefit‐cost analysis that quantifies the positive and negative effects of the policy in monetary terms to help determine whether it is on balance desirable. EBD studies evaluate the harms to health from exposure compared with some counterfactual situation, to provide perspective on the importance of different exposures and the possible benefits of reducing them.

Both impact and EBD studies present results described using terms such as “premature deaths” and “statistical lives saved.” The economic value of reducing mortality risk is calculated using the concept of “value per statistical life.” The literature suggests there is much confusion about how these and similar terms are defined and what can be known about the mortality effects of environmental exposures.

In particular, the number or fraction of deaths among individuals exposed to some hazard that occur earlier than they would have if the individuals had not been exposed (“etiologic deaths”) cannot be determined from mortality data alone, whether from epidemiological studies or randomized controlled trials. The problem is that etiologic deaths are not statistically identified: the time at which an exposed individual dies can be observed, but the time at which she would have died had she not been exposed is counterfactual and cannot be observed. From mortality data alone, one cannot distinguish between situations in which a few people die much earlier than they would have if unexposed and situations in which many people die a little earlier than they would have if unexposed.

The fraction of deaths in an exposed population that are etiologic can be bounded but the bounds are much farther apart than the ends of typical confidence or uncertainty intervals presented in the literature. The total number of life years lost due to exposure is statistically identified but cannot be disaggregated into life years lost conditional on death at specified ages or from specified diseases, as these quantities are not statistically identified. Nevertheless, uncertainty about the fraction of deaths that are etiologic and the number of life years lost conditional on death at a specified age does not affect the economic value of reducing exposure as conventionally defined, because the economic value depends on the change in mortality risk, which is identified.

In Section 1.1, we describe some of the problems with how mortality risks are described in the literature that motivate this article. The terms we discuss are defined in Table I.

Table I.

Summary of Concepts

Concept	Definition	Comments
Relative risk	R = (hazard in exposed population)/(hazard in unexposed population)	R is usually > 1 and is often assumed to be independent of age (“constant proportional hazard”)
Hazard fraction	(R – 1)/R, based on relative risk R	If R is age‐dependent, so is the hazard fraction. Often called “attributable fraction” or “population attributable fraction”
Attributable fraction	Fraction of deaths in the exposed population attributed to exposure, equal to the hazard fraction
Etiologic fraction	Fraction of deaths in the exposed population caused by exposure (i.e., that occur earlier than if these individuals were never exposed), under the assumption that exposure is never protective	Cannot be identified from mortality data. Lower bound depends on R: (R‐1)/R R/(R‐1) (assuming R > 1 and independent of age) and upper bound equals 1 (assuming R > 1)
Attributable deaths (in a specified time period)	Expected number of deaths in the exposed population that would not have occurred in the period if the hazard during only that period was equal to the hazard in the unexposed population	Calculated as (deaths in exposed population during period) × (hazard fraction). Always > 0, if R > 1. Equals decrease in deaths in exposed population if suddenly unexposed and hazard depends only on current exposure. Cannot be meaningfully summed over periods
Statistical lives saved (in a specified time period)	Expected reduction in the number of deaths in the period for a specified population and reduction in hazard. Can be <0, if hazard is increased	Equal to the sum over individuals of the reductions in individuals’ hazards in the period. If the hazard in the exposed population is instantaneously reduced to the hazard in the unexposed population, statistical lives saved = attributable deaths for that instant
Excess deaths	Expected steady‐state difference in number of deaths between the exposed and unexposed populations, that is, the number of deaths that would not have occurred absent exposure	The sum of excess deaths across all ages is zero. Excess deaths are typically > 0 for younger ages and < 0 for older ages. Excess deaths at age t < attributable deaths at age t (if exposure reduces chance of surviving to t)
Etiologic deaths	Number of deaths in the exposed population that occur earlier than if these individuals were never exposed. Number of deaths caused by exposure, under the assumption that exposure is never protective	Cannot be identified from mortality data. Etiologic deaths at age t ≥ minimum of excess deaths at age t and zero and ≤ all deaths in exposed population at age t. Lower bound depends on R but is no smaller than 1/e (≈ 0.37) times attributable deaths (assuming R > 1 and independent of age); upper bound is all deaths in exposed population (assuming R > 1)
Premature deaths	No technical definition	Seems to imply etiologic deaths, often used to describe attributable deaths
Expected years of life lost (YLL) among the exposed	Sum over age of (exposed deaths) × (residual life expectancy in exposed population)	Can be calculated in total and identified by covariates like age or cause of death
Expected years of life lost (YLL) due to exposure	Difference between life expectancy for unexposed and exposed populations. Equal to and often calculated as sum over age of attributable deaths × residual life expectancy if unexposed	Can be identified from mortality data for entire population but not for subpopulations defined by age of death or cause (disease)
Expected years lived with disability (YLD) due to exposure	YLD among the exposed that are attributed to exposure. YLD among the exposed are a function of prevalence and/or incidence of sequelae and disability weights	Calculated as YLD among the exposed × hazard fraction. Assumes elimination of all disability among individuals affected by exposure if exposure is reduced, that is, assumes no disability among these individuals even if they would suffer the disease absent exposure. Potentially biased estimate of YLD due to exposure = YLD among the exposed – YLD among the exposed had exposure been absent
Expected disability adjusted life years (DALYs) due to exposure	DALYs among the exposed that are attributed to exposure. DALYs among the exposed = YLL among the exposed + YLD among the exposed	DALYs due to exposure by age of death or cause (disease) cannot be identified from epidemiological data (see YLL due to exposure). Are potentially biased (see YLD due to exposure)
Value per statistical life (VSL)	Individual‐specific rate of substitution between wealth and infinitesimal change in survival probability for a specified (short) period.	Monetary value to an individual of an increase in period survival probability ≈ VSL × (probability change). VSL may depend on wealth, age, life expectancy, health, and other factors. The approximation is good for monetary values that are small compared with the individual's wealth.
Value per statistical life year (VSLY)	Individual‐specific rate of substitution between wealth and infinitesimal change in life expectancy.	Monetary value to an individual of an increase in life expectancy ≈ VSLY × (change in life expectancy). VSLY depends on the same factors as VSL. VSLY need not be the same for all changes to the hazard function yielding the same increase in life expectancy. Similar to VSL, the approximation is best for monetary values that are small compared with wealth.

In Section 1.2, we present a simple example that illustrates our key points: the fraction of deaths in an exposed population that are etiologic cannot be determined from mortality data alone nor can the life years lost to fatality at specified ages or from specified causes. In contrast, total life years lost in the exposed population and the economic value of reducing exposure‐related mortality risk can be determined. The economic value of reducing exposure‐related mortality risk is unaffected by uncertainty about the fraction of deaths that are etiologic, though it could be affected by knowledge of how the fatality risk differs among identifiable individuals. Readers who are not interested in the technical details may wish to read only the introduction (Section 1) and conclusions (Section 4).

In Sections 2 and 3, we describe in principle what aspects of the mortality effects of environmental exposures can be estimated using mortality data (in Section 2) and how the effects on mortality are valued using economics (in Section 3). We focus on concepts and statistical identifiability rather than questions of sample size, data quality, and empirical methods that affect the precision with which quantities can be estimated. These sections present the basic concepts and equations underlying quantification and valuation of exposure‐related mortality and can serve as an introduction to these topics. Conclusions and implications are in Section 4.

For concreteness, we focus our discussion on the mortality effects of (fine particulate) air pollution. But our analysis is more general and is applicable to other cases in which one cannot determine whether a specific death was the result of exposure to a particular hazard. As noted, our discussion is not limited to epidemiological studies; the same issues arise in randomized controlled trials. The critical issue is that the age at which an individual dies is observable but the (counterfactual) age at which she would have died had her exposure been different is not.

1.1. Terminology Commonly Used in the Literature

EBD and impact studies that quantify the harms to human health from air pollution or other exposures, or the health benefits of reducing exposure, often use wording such as “premature deaths” (Anenberg et al., 2017; Landrigan et al., 2018), “excess deaths” (Burnett et al., 2018), “attributable deaths” (Cohen et al., 2017), “deaths attributable to AAP [ambient air pollution]” (World Health Organization, 2016), “PM_2.5‐related premature mortality” (Wang et al., 2017), and “premature mortality attributable to air pollution” (Lelieveld, Evans, Fnais, Giannadaki, & Pozzer, 2015). These terms are often used interchangeably and in a causal sense: for example, Cohen et al. (2017) described numbers of deaths “attributed” to exposure as numbers of deaths “caused” by exposure; Anenberg, Miller, Henze, and Minjares (2019) used “premature deaths” in the same sense as “attributable deaths” and described emissions as “responsible” for pollutant‐attributable deaths; Burnett et al. (2018) equated “excess” and “avoided” deaths. Goodkind, Tessum, Coggins, Hill, and Marshall (2019) concluded that “anthropogenic PM2.5 was responsible for 107,000 premature deaths in 2011, at a cost to society of $886 billion.”

The estimates of “premature,” “excess,” or “attributable” deaths in these articles are computed as products of mortality counts and hazard fractions (Environmental Protection Agency, 1996; GBD 2017 Risk Factors Collaborators, 2018; Lim et al., 2012). Some articles (Cohen et al., 2017; Landrigan et al., 2018; World Health Organization, 2016) also present results in terms of disability‐adjusted life years (DALYs), calculated as the sum of years of life lost to death and years lived with disability (GBD 2017 Risk Factors Collaborators, 2018; Murray, 1994; Prüss‐Üstün, Mathers, Corvalán, & Woodward, 2003; World Health Organization, 2016).

These terms can be misleading. It is not possible based on current science to know the number of etiologic deaths, that is, the number of individuals who die earlier than they would have because of air pollution or other exposures lacking a distinctive relationship between exposure and disease. As is well known (Rothman, Greenland, & Lash, 2008), epidemiology can identify associations between exposure and mortality, but determining whether an exposure causes mortality requires other forms of reasoning and evidence, for example, to rule out the possibility that both exposure and mortality are caused by some other (confounding) factor. Well‐conducted randomized controlled trials have the advantage that the estimated association between exposure and mortality is statistically unbiased, that is, the expected association between exposure and any possible confounding factor is zero. Moreover, the probability of drawing a random sample having any specified degree of association between exposure and possible confounders declines toward zero as the sample size increases (Greenland, 1990).

The question of causality is not the focus of this article; from this point onward, we assume that any observed relationship between exposure and mortality is causal. The limitations we describe apply even in an ideal situation of true causal effects and epidemiological studies or randomized controlled trials free of bias and random error. If the association between exposure and mortality is not causal, then tautologically no deaths are caused by exposure.

The standard calculation used to quantify the mortality effects of exposure estimates the number of “deaths attributable to exposure” (or “attributable deaths”), which is the difference between the number of deaths expected to occur in an exposed population (during a defined period) and the number that would be expected to occur in that population if mortality risk in the period was the same as in an unexposed population. Attributable deaths are calculated as the product of total deaths in the exposed population and the hazard fraction. The number of etiologic deaths can be smaller or much larger than the number of attributable deaths. Attributable deaths can also differ from “excess deaths,” which is the difference between the steady‐state numbers of deaths that occur in a period if the population has been continuously exposed and the number that would occur if the population was never exposed.

In contrast to etiologic deaths, the total number of life years lost in the exposed population is statistically identified and can be estimated using mortality data. However, for the same reason that the number of etiologic deaths is not identifiable, the life years lost due to exposure among individuals who die at specified ages or from specified causes (which are used to calculate DALYs) are not identified and cannot be known using only mortality information. Similarly, estimates of the monetary value of a change in mortality risk based on the change in life expectancy (e.g., using a constant “value per statistical life year” [VSLY]) can be calculated at the population level but cannot be disaggregated to categories such as deaths at specific ages or from specific diseases.

1.2. A Tale of Two Cities

Suppose there are two cities that are identical, except in air pollution and mortality. In one (Clearville), the air is clean and one‐quarter of the population dies at ages 70, 80, 90, and 100 years; in the other (Smokeville), the air is polluted and one‐quarter of the population dies at ages 60, 70, 80, and 90 years. Assume that individuals live their entire lives in their city of birth, that the difference in mortality is caused by air pollution, and that if pollution in Smokeville were eliminated the mortality rates would instantaneously become identical to those in Clearville. Consider two questions:

1. What fraction of the deaths in Smokeville is etiologic, that is, occur earlier than they would have if there were no pollution? Equivalently, what fraction of the people in Smokeville would live longer if pollution were eliminated?

2. What is the economic value of eliminating the mortality risk due to air pollution in Smokeville? Does it depend on the answer to question 1?

The fraction of deaths that is etiologic is not statistically identified using mortality data. It could be one, if all deaths are advanced by 10 years. It could be one‐quarter, if people who would die at 100 absent air pollution die at 60 in its presence and no one else is affected. It can be any number between these extremes; for example, if some people are of type A (who die 10 years earlier if exposed to air pollution) and the remainder are of type B (who are unaffected, except the quarter who would live to 100 in the absence of air pollution die at 60 in its presence).

Figure 1 illustrates the probability distributions for age of death in Smokeville and Clearville for three possible fractions of deaths that are etiologic. Panel A shows the distribution in Smokeville, where the colors characterize people who die at each age. In Panel B, each individual's age of death in Clearville is 10 years older than in Smokeville. In Panel C, individuals who die at 60 in Smokeville would die at 100 in Clearville, and all other individuals die at the same age in Clearville as in Smokeville. Panel D presents the case in which the fraction of deaths at each age that is etiologic equals the fraction that is attributable to air pollution (as described in Section 2). In this case, all the people who die at 60 would have lived longer in Clearville: some would have lived to 70, some to 80, some to 90, and some to 100. The fractions of people who die at ages 70, 80, and 90 who would have lived longer in Clearville are one‐quarter, one‐third, and one‐half, respectively.

Figure 1.

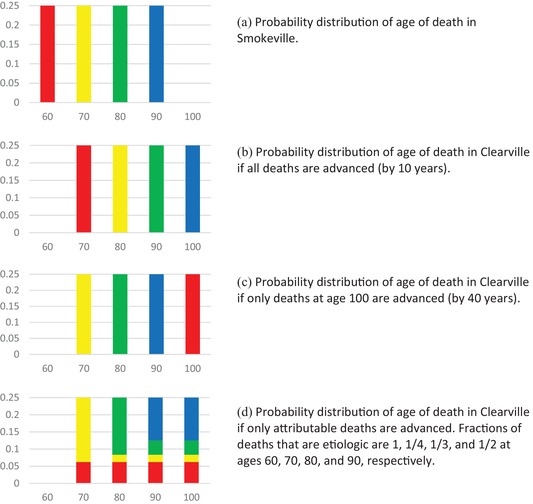
Probability distribution of age of death showing alternative possible fractions of deaths advanced by age. Colors correspond to age at which individual would die in Smokeville.

Although the probability distribution of age at death is the same in panels B, C, and D, the fractions of people whose age at death in Smokeville is less than their age at death in Clearville equals 1, 0.25, and 0.52 in Panels B, C, and D, respectively. Knowing only the probability distributions of age at death does not allow one to distinguish between these three situations (or many others that could be constructed).

Some important concepts are statistically identified and can be estimated using mortality data for the two cities. The excess deaths by age (the difference between the expected number of deaths by age in Smokeville and Clearville) is identified; as a fraction of each birth cohort it is one‐quarter at 60, minus one‐quarter at 100, and zero at all other ages. The number of life years lost due to exposure is also identified: it is 10 per capita. However, the number of life years lost due to exposure and conditional on death at a particular age is not identified: for deaths at 60, it is between 10 and 40; for deaths at 70, 80, and 90 it is between 0 and 30, 20, and 10, respectively. Similarly, the number of life years lost due to exposure and conditional on cause of death is not identified. Assume that some of the deaths at age 60 are caused by heart attack and that all the deaths at older ages are from other causes. Then, the life years lost due to exposure and conditional on death from heart attack is between 10 and 40.

The economic value of reducing mortality risk in Smokeville by eliminating air pollution is equal to the sum over the population of each individual's value of her risk reduction. For an individual of age a < 60, the value is equal to the expected present value of the risk reductions at future ages,

$$V=\sum _{t=60}^{90}v\left(t\right)r\left(t\right)S\left(t\right){\rho }^{t-a},$$ (1)

where V is her total monetary value, v(t) is her average value per unit risk reduction of reducing her hazard at age t by r(t), S(t) is her probability of surviving to t, and ρ is her discount factor (equal to 1/[1 + her discount rate]). If there is no additional information about the age at which each individual will die, the value V does not depend on the etiologic fraction: whatever its value, each individual substitutes a lottery with equal chances of dying at ages 70, 80, 90, or 100 for a lottery with equal chances of dying at ages 60, 70, 80, or 90.

To confirm that the value of eliminating exposure‐related mortality risk is independent of the etiologic fraction, assume that an individual's total value depends on whether she is of type A or B defined above; the values V^A and V^B are the results of Equation (1) conditional on being of each type.

The elements of Equation (1) are presented in Table II. Conditional on being of type A, eliminating pollution eliminates the mortality hazard at ages 60, 70, 80, and 90. The individual will benefit from exactly one of these (though which one is unknown) and the total value is the sum of the four terms, each weighted by its probability. Conditional on being of type B, eliminating pollution eliminates the mortality hazard at age 60 and the total value is the value of this change multiplied by the probability the individual would die at 60. Note that the value of reducing risk at each age depends on type. For type A, v^A(t) is the value of delaying death from t to t + 10; for type B, v^B(t) is the value of delaying death from t to t + 40. But ${\mathrm{v}}^{\mathrm{B}}(60){\rho }^{60-a}={\sum }_{t=60}^{90}{\mathrm{v}}^{\mathrm{A}}(t){\rho }^{t-a}$ because both sides of this equation are the value at age a of delaying death from 60 to 100. Hence, the value of eliminating exposure‐related mortality risk is the same for types A and B; knowledge of the individual's type has no effect on her value.

Table II.

Value of Risk Reduction in Smokeville

		Type A			Type B
t	S(t)	h(t)	r(t)	Value	h(t)	r(t)	Value
60	1	1/4	1/4	$v^{\mathrm{A}}(60)·1/4·1·{\rho }^{(60-\mathrm{a})}$	1/4	1/4	$v^{\mathrm{B}}(60)·1/4·1·{\rho }^{(60-\mathrm{a})}$
70	3/4	1/3	1/3	$v^{\mathrm{A}}(70)·1/3·3/4·{\rho }^{(70-\mathrm{a})}$	0	0	0
80	1/2	1/2	1/2	$v^{\mathrm{A}}(80)·1/2·1/2·{\rho }^{(80-\mathrm{a})}$	0	0	0
90	1/4	1	1	$v^{\mathrm{A}}(90)·1·1/4·{\rho }^{(90-\mathrm{a})}$	0	0	0
100	0	0	0	0	1	0	0
Total				$V^A=1/4{\sum }_{t=60}^{90}{v}^A(t){\rho }^{t-a}$			$V^B=1/4v^B(60){\rho }^{60-a}$

Knowledge about an individual's type could affect valuation if the age at which she would die in Smokeville is known. If she would die at 70, 80, or 90 in Smokeville, the value of eliminating exposure is zero if she is of type B and is positive if of type A. If she would die at 60 in Smokeville, the value of eliminating exposure is greater if she is of type B rather than type A.

The following sections generalize the results of this example, describe the calculation of attributable deaths, and provide additional details. To summarize, the difference in the probability of death by age between populations that differ in exposure is identified and can be estimated, as can the total life years lost due to exposure. However, the fraction of deaths that occur earlier in the exposed population and the life years lost conditional on age or cause of death and due to exposure are not identified; their values differ between alternative models of the relationship between exposure and mortality that cannot be distinguished using only mortality data. These problems affect conventional estimates of the burden of disease but not of the economic value of a change in exposure, as valuation depends only on changes in individuals’ risks. Knowledge of the etiologic fraction does not change the economic value, unless there is also information about how an individual's risk of death at each age differs from the population average risk.

2. EPIDEMIOLOGY: ESTIMATING MORTALITY EFFECTS

Epidemiological studies collect data that can be used to estimate population‐level mortality‐hazard functions and survival functions for different exposures. For example, studies of the effects of fine‐particulate air pollution on mortality compare mortality rates between populations living in different locations (long‐term cohort studies, e.g., Dockery et al., 1993; Hoek et al., 2013) or within the same population at different times (time‐series studies, e.g., Atkinson, Kang, Anderson, Mills, & Walton, 2014; Dominici, McDermott, Daniels, Zeger, & Samet, 2005, and intervention studies, e.g., Pope, Schwartz, & Ransom, 1992, 2007). Hazard and survival functions may be estimated for subpopulations defined by individuals’ age, sex, ethnicity, smoking status, and other observable factors within the limits of epidemiology (e.g., sample size, difficulties in measuring individual characteristics, inability to control for unobserved individual characteristics, uncertainty about appropriate functional form such as constant proportional hazard).

For simplicity, we assume stable populations. A population is stable if the birth rate (number of births per year) is constant, all birth cohorts face the same hazard function, and steady state has been reached. Given these assumptions, the age distribution of a population in every calendar year coincides with the survival function of the birth cohorts. We will make use of this correspondence in the following, often implicitly. Thus, our results apply to EBD population studies (that assume stable populations) as well as to epidemiological cohort studies.

Assume there are two exposure levels of interest, “high” and “low” (we will sometimes describe individuals exposed to these levels over their lifetimes as “exposed” and “unexposed,” respectively). We assume there are no other differences between the populations that affect mortality. Consider the hazard functions for total mortality (i.e., for all causes of death) corresponding to these two exposure levels for a birth cohort (or a subcohort defined by observable characteristics). The hazards are functions of individual age t (t = 0 at birth). Let h ₀(t) and h ₁(t) be the hazard functions corresponding to low and high exposure over a lifetime, respectively. Then, for j = 0, 1, the corresponding survival curves are

$$S_j\left(t\right)=\exp \left(-\underset{0}{\overset{t}{\int }}{h}_j\left(\tau \right)d\tau \right),$$ (2)

and the marginal probability distributions for age at death are

$$f_j\left(t\right)=h_j\left(t\right)S_j\left(t\right)=-\frac{d}{dt}{S}_j\left(t\right).$$ (3)

For stable populations, the age distribution of the population is also described by Equations (2) and (3). To simplify notation, let population be measured as a proportion of the birth cohort, so annual births and (at steady state) annual deaths equal one.

If exposure increases mortality risk at all ages (i.e., h ₁(t) > h ₀(t) for all t > 0), then the number of people of any age t > 0 is larger in the unexposed population (S ₀(t) > S ₁(t)). Figure 2 provides an illustration of these functions where h ₁(t) is the hazard function for US males (the exposed population) and h ₀(t) = (2/3) h ₁(t) is the hazard function for the unexposed population (the factor 2/3 is chosen for illustration and does not represent typical hazard ratios found in environmental studies). In the figure, h ₁(t) > h ₀(t) and, hence, S ₁ (t) < S ₀(t) for all t > 0.

Figure 2.

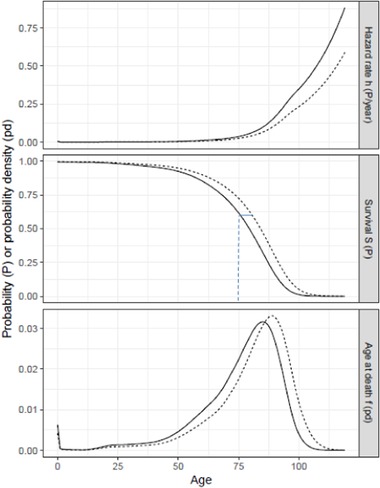
Annual hazard, survival, and marginal distribution of deaths by age. Exposed (h ₁, solid curves) are for US males (2014 period lifetable http://www.ssa.gov/oact/STATS/table4c6.html). Unexposed (h ₀, dashed curves) are for annual hazard = (2/3) annual hazard if exposed. The short horizontal line segment in the middle panel is the years of life lost by individuals dying at age 75 when all deaths are etiologic, that is, S ₀ ⁻¹[S ₁(75)] – 75 in expression (7).

The standard calculation of attributable deaths at age t, D(t), is

$$D\left(t\right)=\frac{R\left(t\right)-1}{R\left(t\right)}{f}_1\left(t\right),$$ (4)

where f ₁(t) is the total number of deaths at age t in the exposed population, [R(t) – 1]/R(t) is the hazard fraction, and R(t) = h ₁(t)/h ₀(t) is the relative risk or rate ratio, which is typically treated as constant across t (the proportional hazard assumption).

Substituting for R(t) and f ₁(t), Equation (4) can be expressed as

$$D\left(t\right)=\left[h_1\left(t\right)-h_0\left(t\right)\right]S_1\left(t\right).$$ (5)

At age t, attributable deaths D(t) is the difference between observed deaths in the exposed population h ₁(t) S ₁(t) and expected deaths in that population in the absence of exposure h ₀(t) S ₁(t). It describes the result of a hypothetical and extreme situation: the instantaneous reduction in the expected number of deaths occurring in a population with age distribution S ₁(t) when exposure is suddenly eliminated, if the effects of exposure on mortality depend on current but not on past exposure (no latency or cessation lag).

An alternative measure of the mortality effect of exposure is the “excess” deaths at t, which is the expected steady‐state difference in the number of deaths by age between exposed and unexposed populations,

$$\begin{array}{ccc}\mathrm{\Delta }\left(t\right)& =& f_1\left(t\right)-f_0\left(t\right)=h_1\left(t\right)S_1\left(t\right)-h_0\left(t\right)S_0\left(t\right)\\ & =& \left[h_1\left(t\right)-h_0\left(t\right)\right]S_1\left(t\right)+h_0\left(t\right)\left[S_1\left(t\right)-S_0\left(t\right)\right]\\ & =& D\left(t\right)-h_0\left(t\right)\left[S_0\left(t\right)-S_1\left(t\right)\right].\end{array}$$ (6)

Excess deaths Δ(t) equals attributable deaths D(t) minus a term that accounts for the difference in the population at risk, which depends on previous exposure. The standard calculation of attributable deaths D(t) from (5) overestimates the number of excess deaths Δ(t) that could be delayed by a permanent reduction in exposure at every age t for which S ₀(t) > S ₁(t) and h ₀(t) > 0. Unless exposure decreases hazard at some ages, Equation (5) overestimates the steady‐state reduction in deaths at all ages > 0. The second term in Equation (6) is the additional number of deaths at age t > 0 that would have occurred in the absence of exposure, equal to the increase in the population surviving to age t multiplied by the hazard if unexposed. Hence, the number of deaths attributable to exposure does not correspond to the number of excess deaths due to exposure except in special situations (e.g., for a rare disease, h ₀(t) ≈ 0, or one that has negligible effect on mortality, S ₁(t) ≈ S ₀(t)). Moreover, attributable deaths in different periods cannot be meaningfully summed, since these depend on the exposed population living in each period.

The total number of deaths that occur in a year is the integral of f_j(t) over all ages and the difference in total annual deaths between exposed and unexposed populations is the integral of Δ(t) over all ages. In steady state, total deaths equal total births and the difference in total annual deaths is zero. However, the age distribution of deaths is different: for any age t, the total number of deaths occurring at ages younger [older] than t is smaller [larger] in the unexposed than in the exposed population (on the assumption that S ₀(t) – S ₁(t) > 0 for all t > 0).

For the case illustrated in Figure 2, as shown in the bottom panel, fewer [more] deaths occur in the unexposed than in the exposed population at every age younger [older] than 86 years. In contrast, attributable deaths D(t) is strictly greater than zero for all t > 0, because the instantaneous hazard is larger for the exposed than the unexposed population (h ₁(t) > h ₀(t)) and some members of the exposed population are living at all ages shown in the figure (S ₁ (t) > 0).

The hazard functions h_j(t) and, hence, the survival functions S_j(t) and hazard fraction [R(t) – 1]/R(t)] can be estimated under “essentially the same conditions often cited for general study validity,” that is, absence of confounding, misclassification, and differential censoring (Robins & Greenland, 1989a). From these, the expected number of deaths that would occur at each age given continuous high or low exposure can be estimated. However, these estimates are not sufficient to determine how many individuals would die earlier if exposed rather than unexposed, how much earlier each would die, or how much longer each exposed individual would have lived if unexposed. While the marginal distributions of deaths by age in the exposed and unexposed birth cohorts are observable, mortality data provide no information about the joint distribution of the ages at which an individual would die conditional on high or low exposure (one is observable, the other is counterfactual). As illustrated in Section 1.2 and Figure 1, many patterns of association between the age of death conditional on exposure to high and to low air pollution are consistent with the two marginal distributions. Recognition of this point is not new; Tsiatis (1975) proved that any set of marginal probability distributions for age at death conditional on alternative exposure levels is consistent with an infinity of joint distributions across exposure levels, and hence estimates of concepts that depend on the joint distribution require additional information. Rabl (2003) provided an excellent graphical illustration of why the number of deaths that are advanced and the extent to which each is advanced cannot be identified from epidemiological data. Athey and Imbens (2006) discuss these identification problems in the econometrics literature and show that, when outcomes are discrete, the counterfactual distribution of outcomes may not be identified but can be bounded.

The inability to identify the joint distribution of the ages at which an individual would die if she was exposed or unexposed can be illustrated using Figure 2. Consider the probability distributions for age at death in the bottom panel. To transform the probability distribution if exposed f ₁(t) to the distribution if unexposed f ₀(t), one can imagine shifting a small amount of probability of death at a specific age t′ to some older age t″. This corresponds to shifting the age at death for some individual from t′ to t″. The effect will be to decrease the value of f ₁(t′) and increase the value of f ₁(t″). One can continue in this way to shift probability density to the right (increasing individuals’ ages of death) until the modified version of f ₁(t) falls to the level of f ₀(t) for all ages where f ₁(t) > f ₀(t) (i.e., all ages less than 86 years) and rises to the level of f ₀(t) for all ages where f ₁(t) < f ₀(t) (i.e., all ages older than 86 years). The number of different possibilities for shifting probability from one age to another to achieve this transformation is infinite; Figure 1 illustrates three possibilities for the example described in Section 1.2. Hence, the set of joint distributions associating age at death if exposed and if unexposed that are consistent with the marginal probability distributions is infinite (Tsiatis, 1975).

Equivalently, one can think of representing the relationship between individuals’ ages of death if exposed and unexposed by shifting the survival curve in the middle panel from S ₁(t) to S ₀(t). Any shift of probability density from a younger (t′) to an older age at death (t″) in the density function f ₁(t) has two effects on the survival curve S ₁(t). First, it shifts the point (t′, S ₁(t′)) to the right (to t′′) and down (to S ₁(t′′)). The downward shift is because the affected individual moves from dying before to dying after all those who die between ages t′ and t′′. Second, all the points on S ₁(t) for values of t between t′ and t′′ shift up (because these individuals are moved from dying after to dying before the affected individual). One can continue shifting the survival curve S ₁(t) in this way until it corresponds to the survival curve if unexposed S ₀(t). Again, there is an infinite set of these small probability shifts that transform the survival function if exposed to the survival function if unexposed.

2.1. Bounds on the Etiologic Fraction

In this section, we investigate what can be inferred about etiologic deaths from mortality data. We change our focus from the exposed and unexposed populations to the birth cohorts that generate the populations. As noted above, the exposed and unexposed birth cohorts have the same survival functions as the exposed and unexposed populations.

Robins and Greenland (1989a) derive bounds on the “etiologic fraction,” defined as the fraction of deaths occurring in the exposed birth cohorts that occur earlier than they would have if unexposed (equivalently, the probability that a death randomly drawn from all exposed deaths was advanced by exposure). If S ₀(t) > S ₁(t) for all t > 0, the upper bound on the etiologic fraction is 1. This occurs when exposure shifts all deaths earlier in time. On the stronger and common “constant proportional hazard” assumption (R(t) = R > 1 is constant across t), the lower bound on the etiologic fraction is (R − 1)/R^{R /( R ‐1)}. This value is smaller than the hazard fraction (R – 1)/R.

The hazard fraction and the lower bound depend on the value of R. In the limit as R decreases toward 1, the hazard fraction and the lower bound decrease toward 0 and the ratio of the lower bound to the hazard fraction decreases toward its limiting value 1/e (≈ 0.37). As R increases toward infinity, the hazard fraction, the lower bound, and the ratio of the lower bound to the hazard fraction all increase toward the limiting value 1. The ratio of the upper bound to the hazard fraction, R/(R – 1), also depends on R. In the limit as R increases to infinity, this ratio decreases toward its limiting value, 1. But as R decreases toward 1, the ratio of the upper bound to the hazard fraction increases without limit; for R = 1.01, the ratio is approximately 100. Hence, the bounds on the ratio of the etiologic fraction to the hazard fraction are asymmetric; the number of etiologic deaths cannot be smaller than about 37% of the total number of attributable deaths (i.e., of the sum over all ages of D(t)), but it can be much larger than the number of attributable deaths when R is close to 1).

The maximum number of etiologic deaths at age t equals the total number of deaths at age t, f ₁(t). This occurs when all deaths are advanced by exposure. The minimum number can be derived using the number of excess deaths at age t, Δ(t) = f ₁(t) – f ₀(t). If Δ(t) ≤ 0, it is possible that none of the deaths at t are caused by exposure and so the minimum number of etiologic deaths at t is zero. If Δ(t) > 0, at minimum these excess deaths must have been caused by exposure. Combining these results, the minimum number of etiologic deaths at t is max (0, Δ(t)). Assuming constant proportional hazard with R > 1, the integral of max (0, Δ(t)) over t leads to the lower bound described above. Robins and Greenland (1989a) showed that the range defined by these upper and lower bounds cannot be narrowed using only mortality data. There always exist consistent causal models that generate the lower and upper bounds of the etiologic fraction.

Under the assumption that exposure never increases the chance of survival (i.e., that S ₁(t) < S ₀(t) for all t > 0), then Δ(t) must be less than zero for very old ages. Clearly, if some members of the unexposed population live to be older than anyone in the exposed population, excess deaths will be less than zero when these individuals die. At ages for which excess deaths are less than or equal to zero, the lower bound on the fraction of deaths that are etiologic is zero; it is possible that none of the deaths at these ages are caused by exposure. An alternative (and often more plausible) explanation for excess deaths being less than zero at very old ages is that, although some of the deaths at every age are caused by exposure, the number of people surviving to very old ages is larger when exposure is low; for these ages, both the total number of deaths and the number due to exposure are larger when exposure is low rather than high.

As noted before, these results about identifiability and bounds on numbers of etiologic deaths apply to populations and EBD studies as well as to cohorts. For cases of interest, the difference between the numbers of etiologic and attributable deaths can be quite large. We illustrate with a few recent examples from the literature.

Lelieveld et al. (2015) calculated that “outdoor air pollution, mostly by PM_2.5, leads to 3.3 (95% confidence interval 1.61–4.81) million premature deaths per year worldwide.” For values of R typical of the parts of the world that dominate global air‐pollution‐impact estimates, for example, 1.2 for ischemic heart disease (Lelieveld et al., 2015), the hazard fraction equals 0.17. The lower and upper bounds on the etiologic fraction are 0.067 and 1. Hence, the number of premature deaths due to exposure could be between 0.4 and six times as large as the reported value. This possible bias is large compared with the reported confidence interval (1.61/3.3 = 0.5, 4.81/3.3 = 1.5). As noted by Lelieveld et al., the reported confidence interval reflects imprecision in the estimation of R, which is distinct from the inability to identify the etiologic fraction, even if R is known precisely.

In a project to develop concentration‐response functions for the health risks of air pollution in Europe, Héroux et al. (2015) reported R = 1.064 per 10 µg/m³ PM_2.5 (annual mean) for all‐cause natural mortality, ages 30 years and older. The bounds on the etiologic fraction are 0.023 and 1, whereas the hazard fraction is 0.060. The corresponding bounds on the ratio of the etiologic to the hazard fraction are approximately 0.4 and 17. In their reply to a letter to the editor, the authors acknowledged the difference between the hazard and etiologic fractions and cited passages from HRAPIE (2013) and COMEAP (2010) that describe the difference qualitatively (Héroux et al., 2017).

Jonson et al. (2017) estimated the number of premature deaths in Europe that may be attributed to excess NO_x emissions from diesel cars. They estimated that diesel cars contribute 0.19 µg/m³ to ambient PM_2.5, and used a relative risk to concentration slope of 1.062 per 10 µg/m³ for all‐cause natural mortality in the adult population (HRAPIE, 2013). A 50% reduction in diesel‐car contribution to PM_2.5 (0.095 µg/m³) implies the relative risk R = 1 + (1.062 – 1) 0.095/10 = 1.00059 and the hazard fraction (R – 1)/R = 0.00059. The lower and upper bounds on the etiologic fraction are 0.00022 and 1, less than 0.4 and almost 1700 times as large as the hazard fraction, respectively.

With biological or other nonepidemiological information about the relationship between exposure and mortality, the bounds may be narrowed. Robins and Greenland (1989a) note that the hypothesis that the etiologic fraction equals its upper bound (all deaths are advanced by exposure) is implausible when there are multiple causes of mortality and some are unaffected by exposure. Even when (as is common) air‐pollution studies limit their outcomes to nonaccidental mortality or to cardiovascular mortality, the existence of additional pathways that are not affected by air‐pollution exposure seems evident; hence, the possibility that the etiologic fraction equals one is implausible.

Robins and Greenland (1989a) also suggest the lower bound is implausible as it assumes all exposure‐related deaths occur as early as possible and before the number of deaths in the exposed population falls to the number in the unexposed population (ie, before f ₁(t) ≤ f ₀(t); they assume h ₁(t) > h ₀(t) for all t). However, they present an example of a mechanism that generates an etiologic fraction equal to the theoretical minimum (see their appendix I). The lower bound (R – 1)/R^{R /( R −1)} is the result of following the cohort forever (evaluating the integral on their p. 851 over t from 0 to infinity), which may differ from the value calculated over reasonable spans. To investigate the effect of restricting the integration to realistic follow‐up periods (50 years, from age 30 to 80) for small values of the hazard ratio relevant to air pollution (R = 1.1, HRAPIE 2013), we use the baseline hazard h ₀ = 0.05/year suggested by Robins and Greenland (1989a). The fraction of deaths that are attributable (the hazard fraction) = 0.09. The fraction that are etiologic calculated using the integral is 0.037, close to the lower bound (R − 1)/R^{R /( R ‐1)} = 0.035. Using short follow‐up periods (10 and 20 years), the result is 0.070 and 0.053. Hence, the value of the integral exceeds the lower bound but can approach it even if realistic values are chosen for the integration span.

When the population is heterogeneous (so that an individual's hazard may differ from the population hazard), Robins and Greenland (1989b) show that the etiologic fraction equals the hazard fraction [R(t) – 1]/R(t) when individual increases in hazard h _{1 i}(t) – h _{0 i}(t) are distributed independently of individual baseline hazards h _{0 i}(t) (where i indexes individuals). Sufficient conditions for such independence are (a) when the increase is additive to the baseline or (b) when there is no heterogeneity in the baseline hazard. If the population is well‐ordered by hazard, the hazard fraction is a lower bound on the etiologic fraction if the effect of exposure is superadditive to baseline (people at higher baseline risk face a larger increase in risk) and is an upper bound if the effect is subadditive. Note that none of the conditions required for these results (well‐ordered by hazard, additivity, superadditivity, and subadditivity) can be tested using epidemiological data (Robins & Greenland, 1989b); any claim that one or another is satisfied must be supported by other sources of information.

2.2. Life Years Lost

The inability to statistically identify the number of etiologic deaths has implications for estimating the number of years of life lost and DALYs caused by air pollution and other exposures. The expected number of years of life lost due to exposure in the population (YLL) is the steady‐state reduction in life expectancy, that is, the difference between the areas under the two survival curves,

$$YLL=\underset{0}{\overset{\infty }{\int }}{S}_0\left(t\right)dt-\underset{0}{\overset{\infty }{\int }}{S}_1\left(t\right)dt.$$ (7)

Because the two survival curves are identified, YLL due to exposure can be estimated using mortality data. However, because the number of etiologic deaths at age t is not identified, years of life lost due to exposure and conditional on death at age t, YLL(t), cannot be estimated. As noted by Robins and Greenland (1991), YLL can be expressed alternatively as a function of total or of attributable deaths by age. Using total deaths, YLL can be expressed as

$$YLL=\underset{0}{\overset{\infty }{\int }}{f}_1\left(t\right)\left\{S_0^{-1}\left[S_1\left(t\right)\right]-t\right\}dt,$$ (8)

where f ₁(t) is the number of exposed deaths at age t and the expression in curly brackets is the horizontal distance between the survival curves at S ₁(t) (illustrated for t = 75 years by the short horizontal line segment in the middle panel of Figure 2). This horizontal distance corresponds to the years of life lost by people dying at age t if all exposed deaths are etiologic and the population is well‐ordered by hazard (i.e., the order in which people die if all are exposed is the same as the order in which they would die if all are unexposed). Alternatively, using attributable deaths YLL can be expressed as

$$YLL=\underset{0}{\overset{\infty }{\int }}D\left(t\right)\left[\frac{1}{S_0\left(t\right)}\underset{t}{\overset{\infty }{\int }}{S}_0\left(u\right)du\right]dt,$$ (9)

where D(t) is the number of attributable deaths at age t and the term in square brackets is life expectancy at age t in the unexposed population. Expression (9) corresponds to the situation in which etiologic deaths are equal to attributable deaths and hazard depends only on current exposure. In this case, if exposure were suddenly eliminated, individual life expectancy at every age would immediately increase to its value for an unexposed individual of that age.

Because total exposed deaths at age t (f ₁(t)) and attributable deaths at age t (D(t)) are not equal but expressions (8) and (9) yield the same total YLL, the formulas for years of life lost at age t embedded in the two expressions cannot be equal. This illustrates the fact that YLL(t) is not identified by mortality data. Returning to the example in Section 1.2, although exposure reduces life expectancy at birth by 10 years, mortality data do not allow one to determine which of many possible relationships between age at death if exposed or unexposed is accurate. These include the possibilities that: (a) people who die at 60 if exposed would have lived 40 years longer if unexposed and no one else is affected; (b) everyone dies 10 years earlier if exposed than unexposed (as modeled by Equation (8) and illustrated by panel B of Figure 1); and (c) etiologic deaths are equal to attributable deaths D(t), that is, the fractions of the exposed population whose deaths are advanced by air pollution are 1/4, 1/16, 1/12, and 1/8, and YLL(t) are 25, 20, 15, and 10, at ages 60, 70, 80, and 90, respectively (as modeled by Equation (9) and illustrated by panel D of Figure 1).

DALYs are defined as the sum of two components: years of life lost due to mortality and years lived with disability (GBD 2017 Risk Factors Collaborators 2018; Prüss‐Üstün et al., 2003; World Health Organization, 2016). The standard calculation of years of life lost due to exposure multiplies estimates of attributable deaths at each age D(t) by age‐specific reference life expectancies (Equation (9)). This total is correct for the population but cannot be disaggregated by age or cause of death. Estimates of years lived with disability (YLD), the other component of DALYs, are subject to a similar identification problem. These are based on estimates of the attributable cases of disease at each age, which are not necessarily equal to the etiologic cases. As noted by Murray, Ezzati, Lopez, Rodgers, and Vander Hoorn (2003, p. 12 of 20), “if the outcome variable used in causal attribution of disease and mortality to a risk factor only involves counting of adverse events (such as disease incidence or death), it is not possible to characterize those cases whose occurrence would have been delayed in the absence of the risk factor.”

3. ECONOMICS: VALUING MORTALITY EFFECTS

The monetary value to a population of a reduction in mortality risk (as defined for benefit‐cost analysis) does not depend on the number of etiologic deaths. The monetary value is defined as the sum over the affected population of each person's private value for her risk reduction. For a small change in current mortality risk (over a short period), an individual's private value is approximately equal to the product of the change in risk and her marginal rate of substitution between wealth and mortality risk in that period, often called her “value per statistical life” (VSL). An individual's VSL depends on her preferences and circumstances. As illustrated in Figure 3, it can be represented as the slope of her indifference curve between wealth and probability of surviving the current period at her current wealth and survival probability. VSL may also depend, inter alia, on the individual's age, life expectancy, and anticipated future health, income, and expenses.

Figure 3.

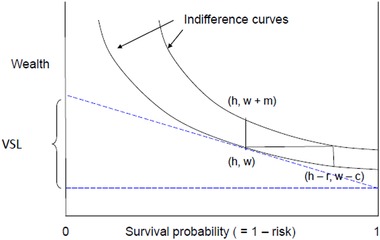
VSL is the slope of the individual's indifference curve at current wealth w and survival probability 1 – h. The value of a reduction in risk from h to h – r can be measured as compensating variation c or equivalent variation m. For r ≈ 0, c ≈ m ≈ r • VSL (for clarity, the value of r in the figure is much larger than is usually relevant).

The term “value per statistical life” is often misinterpreted as the monetary value assigned to an individual's life, or the amount an individual would pay to avoid, or perhaps accept as compensation for, immediate death (Cameron, 2010). Although estimates of VSL are used to calculate the monetary value to a population of a change in mortality risk, the VSL that is used is conceived as an average of the individual rates of substitution in the affected population. As illustrated by Figure 3, VSL is a slope conventionally measured in units of dollars (or other currency) per unit change in survival probability (i.e., from 0 to 1). Equivalently, it can be measured in units of dollars per “micromort” (a survival‐probability increment of 10⁻⁶; Howard, 1984), dollars per “standardized mortality unit” (a survival‐probability increment of 10⁻⁴; Jamison et al., 2013), or other units.

For a small increase in current survival probability at age t, the individual's monetary value is approximately equal to v_i(t) r_i(t), where v_i(t) is her VSL and r_i(t) is the increase in survival probability; if mortality risk depends only on current exposure, r_i(t) = h _{1 i}(t) – h _{0 i}(t) (i indexes individuals). The total value V to a population of N individuals of a reduction in their current hazards is

$$V=\sum _{i=1}^N{v}_i{r}_i$$ (10)

(to simplify notation, the dependence on age is suppressed). The population value is often approximated as

$$V\approx \overline{v}\sum _{i=1}^N{r}_i,$$ (11)

where $\overline{v}$ is the mean of v_i and the sum of risk reductions is the decrease in the expected number of deaths occurring in the period, often called the number of “statistical lives saved” or “premature fatalities averted.” The number of statistical lives saved (or lost) depends on the population and the change in hazard; for example, when the hazard depends on current but not on past exposure and a population with age distribution S ₁(t) is suddenly unexposed, the instantaneous number of lives saved is the sum over all ages of attributable deaths D(t) (Equation (5)).

The approximation (11) is exact if v_i and r_i are uncorrelated in the population. One case in which they are not is when the change in hazard is correlated with wealth (e.g., because the geographic patterns of a change in air pollution and in wealth are similar). As described below, VSL is positively correlated with wealth.

The value to an individual at age t of a small continuing perturbation to her mortality hazard (e.g., due to a permanent change in air pollution) can be represented as the expected present value of the associated stream of risk reductions,

$$V_i=\underset{\tau =t}{\overset{\infty }{\int }}{v}_i\left(\tau \right)r_i\left(\tau \right){\sigma }_i\left(\tau \right)e^{-\rho \left(\tau -t\right)}d\tau ,$$ (12)

where v_i(τ) is her VSL and r_i(τ) is the reduction in hazard at age τ, σ_i(τ) is her probability of survival to τ conditional on being alive at age t, and ρ is the rate at which she discounts future monetary flows (e.g., the interest rate on savings). VSL v_i(t) may depend on age t and on the survival function σ_i(t), which itself depends on her new hazard function, h _1i(t) – r_i(t). Future VSL may also depend on the conditions under which the individual can save or borrow money (and hence reallocate her consumption of market goods and services over time). The value to a population is the sum over individuals of the private values V_i, which depend on the individuals’ time paths of VSL and of hazard reductions.

The economic model underlying VSL assumes an individual seeks to maximize her expected utility, which depends on her mortality hazard h in the current period and her wealth w,

$$EU=\left(1-h\right)u_a\left(w\right)+h{u}_d\left(w\right),$$ (13)

where u_a(w) and u_d(w) are her utility conditional on surviving and not surviving the period, respectively (Drèze, 1962; Jones‐Lee, 1974; Weinstein, Shepard, & Pliskin, 1980). The function u_d(w) is often described as a bequest function: it represents the utility the individual gains from knowing her wealth will benefit her heirs or others after her death. The function u_a(w) is the individual's expected utility conditional on surviving the current period and depends inter alia on her future income, expenses, and risks to life, health, and wealth (Eeckhoudt & Hammitt, 2001).

The individual's marginal rate of substitution of wealth for a reduction in current hazard holding expected utility constant is derived by totally differentiating Equation (13), yielding

$$\begin{array}{c}\hfill \mathrm{VSL}=\frac{\mathrm{dw}}{\mathrm{dh}}=\frac{u_a\left(w\right)-u_d\left(w\right)}{\left(\mathit{1}-h\right){u^{\prime }}_a\left(w\right)+h{u^{\prime }}_d\left(w\right)}=\frac{\mathrm{\Delta }U\left(w\right)}{{\mathrm{EU}}^{\prime }\left(w\right)},\end{array}$$ (14)

where the prime (′) denotes first derivative with respect to w. The numerator of Equation (14) equals the gain in utility from surviving the period rather than dying and the denominator represents the expected marginal utility of wealth (i.e., the utility forgone by spending a small amount to increase survival probability, which cannot be spent on other goods and services). It is conventional and reasonable to assume that u_a(w) > u_d(w) (survival is preferred to death), u_a′(w) > u_d′(w) ≥ 0 (the marginal utility of wealth is strictly larger conditional on survival than on death and the marginal utility of a bequest is nonnegative), and u_a′′(w) ≤ 0 and u_d′′(w) ≤ 0 (the two utility functions for wealth are weakly concave, which implies the individual is averse to financial risk; ′′ denotes second derivative with respect to w). Under these conditions, VSL is strictly greater than zero and is increasing in w and in h, which implies the indifference curves are downward sloping and convex, as illustrated in Figure 3.

The economic value of a small decrease in mortality risk is well‐approximated by the product of the individual's VSL and reduction in current hazard, v_i r_i. For larger risk reductions, the value depends on the concept of economic valuation that is adopted, compensating or equivalent surplus. Compensating surplus is the amount by which the individual's wealth would have to be reduced so that she is equally well off with the risk reduction and smaller wealth as she would be without the change (the reduction in wealth compensates for the risk reduction, leaving her no better off). Equivalent surplus is the amount by which her wealth would need to be increased so that she is equally well off with her initial hazard and the increased wealth, or with the reduction in hazard and initial wealth (the increase in wealth has the equivalent effect on her wellbeing as the risk reduction). For any reduction in current hazard, the compensating surplus is less than or equal to the equivalent surplus. Moreover, compensating surplus is a concave function of risk reduction (it increases at a decreasing rate) and equivalent surplus is a convex function (it increases at an increasing rate), which implies the two values diverge as the hazard reduction increases.

The magnitude of the difference between the economic value and the approximation vr can be evaluated using Equation (14) supplemented by empirical estimates of the sensitivity of VSL to wealth (Alolayan, Evans, & Hammitt, 2017; Hammitt, Geng, Guo, & Nielsen, 2019). The compensating surplus c for a reduction in hazard r equals the product of r and a VSL that is between the initial VSL (at wealth w and hazard h) and the smaller VSL at hazard h – r and wealth w – c (illustrated in Figure 3). The effect of the change in hazard on VSL can be derived from Equation (14); holding wealth constant, the ratio of VSL with hazard h to VSL with hazard h – r is bounded above by $\frac{1-(h-r)}{1-h}=1+\frac{r}{1-h}$. When h is much smaller than one, this ratio is close to one (r cannot exceed h). The effect of the reduction in wealth after paying c, holding risk constant, depends on the magnitude of c relative to wealth and on the sensitivity of VSL to wealth, generally measured by the wealth or income elasticity. Theory provides little guidance about the magnitude of the income elasticity; most empirical estimates are on the order of one, with some estimates as high as two or three (Hammitt & Robinson, 2011; Hammitt et al., 2019; Masterman & Viscusi, 2018; Viscusi & Masterman, 2017). For the United States, typical estimates of VSL are roughly $9 million and annual household income averages roughly $60,000 (Robinson & Hammitt, 2016). This implies the value of a risk reduction of 1/10,000 is less than $900 or 1.5% of income. Compared with VSL at the initial point, VSL at the smaller income would be 1.5% smaller with an income elasticity of 1 and 4.4 percent smaller with an income elasticity of 3 (i.e., VSL after paying $900 would be $8.6 million = $9 million [1 – 0.015]³). Combining the effects of changes in risk and income implies the value of the risk reduction of 1/10,000 is between $900 and $860. The equivalent surplus m for a reduction in hazard r equals the product of r and a VSL that is bounded by the initial VSL (at wealth w and hazard h) and the larger VSL with hazard h and wealth w + m. For a risk reduction of 1/10,000 and an income elasticity of 3, VSL after an increase in wealth equal to m = $900 is about $9.4 million (= $9 million [1 + 0.015]³); hence, the equivalent surplus for a risk reduction of 1/10,000 is between $900 and about $940. For larger risk reductions, the difference between the equivalent and compensating surpluses can be arbitrarily large; compensating surplus is bounded by ability to pay (i.e., by wealth or income) but equivalent surplus can increase without limit (Hanemann, 1991).

As suggested by the notation v_i(t), an individual's VSL may depend on age. Yet it is common practice in applications to use the same value for all ages, in part because the evidence on how VSL varies with age is weak. The effect of age on VSL in the theoretical model is ambiguous: an increase in life expectancy conditional on surviving the current period (negatively associated with age) presumably increases the utility of survival u_a(w), which increases the numerator in Equation (14). But it may also increase the opportunity cost of spending u_a′(w), hence, increasing the denominator and making the effect on the ratio indeterminate. To illustrate, an individual who must support herself from a fixed quantity of wealth must husband her resources carefully (and has a high opportunity cost of spending) if her life expectancy is long but may spend profligately (with low opportunity cost) if it is short. Empirical estimates of how VSL varies with age conflict. There is some evidence that VSL rises then falls with age, but estimates of the amplitude of the change, the age at which VSL peaks, and the rates at which it rises and falls differ substantially among studies (Aldy & Viscusi, 2008; Krupnick, 2007).

3.1. Valuing Life Years Lost

An alternative to the conventional approach to valuing mortality risk using VSL is to value the corresponding change in life expectancy using the concept of “value per statistical life year” (VSLY), defined as the marginal rate of substitution between wealth and life expectancy. Any change to an individual's hazard function implies a unique change to her life expectancy. Hence, the value V_i of a continuing perturbation r(τ) to her mortality hazard described in Equation (12) can be characterized as the product of a VSLY and the corresponding increase in life expectancy (which depends on the initial hazard function and the perturbation; Hammitt, 2007). A special case of Equation (12) is an instantaneous decrease r in mortality hazard h(t) for a short duration δ, which increases life expectancy by the product of the increase in probability of surviving beyond age t and life expectancy at age t, that is, by $r\delta \frac{{\int }_t^{\infty }S(\tau )d\tau }{S(t)}$. The value of this risk reduction can be described as the product of VSL and the risk reduction rδ, or as the product of VSLY and the gain in life expectancy. As described above, the appropriate VSL depends on the individual's age, hazard function, and other characteristics; hence, the appropriate VSLY depends on the same characteristics. VSLY also depends on the specific perturbation of the hazard function; many different perturbations can yield the same increase in life expectancy (e.g., a small hazard reduction over a long period and a larger hazard reduction over a shorter period) and the values of these perturbations to an individual need not be the same. If VSLY for an individual is independent of age, VSL must be proportional to age‐specific life expectancy, which is generally decreasing with age. The common finding that VSL rises then falls with age implies VSLY must increase with age over some period, after which it may remain constant, increase, or decrease depending on how rapidly VSL decreases with age. For example, Aldy and Viscusi (2008) estimate that VSLY increases from age 18 to 54 then decreases to age 62 (cohort‐adjusted VSLY as illustrated in their Figure 2).

Both the population change in hazard function and in life expectancy are identified in epidemiological studies; hence valuation using VSL or VSLY are both feasible. The inability to identify etiologic deaths does not preclude economic valuation, which is based on the monetary value of a reduction in hazard. Given uncertainty about how VSL and VSLY vary with age, life expectancy, and other factors, valuation in practice applies a constant VSL to all risk reductions or a constant VSLY to all life‐expectancy gains. Which of these approaches better approximates the true value (e.g., Equation (12)) is unknown and merits investigation.

3.2. Valuation and Identification of Individual Risks

An individual's valuation for a reduction in exposure‐related mortality risk depends on her hazard function and the change to her hazard due to the change in exposure. Neither her baseline hazard nor the change can be observed. Absent additional information, an individual may perceive the change to her hazard as a random draw from the population distribution of changes in individual hazards with mean equal to the change in the population hazard; in this case, the change in population hazard is sufficient for valuation. An individual with information about her exposure, health, or other factors might perceive her change in hazard to be larger or smaller than the population average, but an analyst will typically not have access to such information and cannot do better than to estimate the individual's risk reduction as equal to the population average (in some circumstances, such as when the change in hazard differs with spatial patterns of air pollution, it may be possible to estimate the correlation with individuals’ wealth or other characteristics and hence part of the correlation with VSL).

Even if it were known whether exposure advances everyone's death by a small amount or advances the deaths of a few people by a larger amount and has no effect on other people's mortality, valuation would not be affected unless individuals had information about how their own changes in hazard differ from the population average. More‐refined information about an individual's prospects can affect her valuation. In the extreme case where there is a subset of the population who know their lives would be extended by a reduction in exposure and a complementary subset who know their lifespans would be unaffected, those in the first subset would value a reduction in exposure and those in the second subset would not (setting aside altruism or other ways in which their wellbeing may depend on others’ survival). Whether the population value of a change in exposure is larger or smaller when the subpopulations can be identified depends on the sensitivity of individuals’ values to the magnitude of the change in hazard and on the direction of the change. Hammitt and Treich (2007) show that the economic value to a population of a reduction in the population hazard is larger when the individuals whose risk reductions differ from the average cannot be identified; when individuals are identified, the increase in value of those whose risk reductions are larger than average is insufficient to offset the decrease in value of those whose risk reductions are smaller. In contrast, the total amount a population would demand as compensation for an increase in the population hazard is larger when the subsets who face larger and smaller changes than average are identified. If the risk changes to all individuals are small, individual valuations are well‐approximated by the product of individual VSL and risk reduction and so whether individuals facing different risk changes are identified and whether the value is for a risk reduction or risk increase should have little effect on the population value.

4. CONCLUSION

Table I summarizes some of the key concepts related to quantifying mortality and economic valuation we have addressed. Our analysis yields several conclusions:

Mortality data, whether from epidemiological studies or randomized controlled trials, can be used to estimate marginal probability distributions such as population hazard and survival functions. Hence, concepts that can be calculated from differences in marginal distributions (e.g., attributable deaths, excess deaths, years of life lost due to exposure) can be estimated. Concepts that depend on the joint distribution of age at death under different exposures, such as etiologic deaths and years of life lost due to exposure and conditional on age or cause of death, cannot be estimated because they are not statistically identified.

The result that the etiologic fraction is not statistically identified should not be equated with the fact that epidemiological studies cannot identify individuals or groups of individuals who die (or develop a disease) because of exposure. It is stronger: one cannot even determine the number of such individuals.

If attributable deaths are reported, authors should take care to prevent readers from confusing this statistic with a count of the number of deaths caused by exposure. Numbers of deaths “attributable to exposure” are the result of an attribution algorithm; they are not equivalent to and should not be interpreted as “numbers of deaths caused by exposure.” As stated by the Committee on the Medical Effects of Air Pollutants (COMEAP, 2010), “attributable deaths are not an estimate of the number of individuals in whose earlier death air pollution has played some part” (p. 61). “It is not plausible to think of the figure of ‘attributable’ deaths as enumerating an actual group of individuals … the group is in reality a fiction, and … the number of people in whose deaths air pollution has played a part might be much larger …. We therefore also consider it inappropriate to use the term ‘premature’ deaths to express the outcome of the burden calculation” (p. 71).

When evaluating the EBD, total life years lost in a population due to exposure can be estimated but cannot be disaggregated into categories defined by age at death or cause (e.g., disease). EBD studies typically disaggregate life years lost assuming the fractions of deaths by age or cause that are due to exposure are equal to the hazard fractions. The fraction of deaths that are advanced because of exposure (the etiologic fraction) can be smaller or much larger than the hazard fraction; it can be as large as one and as small as about 37% of the hazard fraction. These results are conditional on the existence of a causal relationship between exposure and mortality: if exposure does not cause (advance) mortality, the etiologic fraction is zero by definition. Estimates of the number of cases of disease caused by exposure, used to calculate years lived with disability, are subject to the same identification problem. EBD studies typically assume the fraction of cases of a disease that are due to exposure is equal to the hazard fraction, but the etiologic fraction can be smaller or much larger. In contrast, total or average life years lost due to exposure in the population is a useful measure of burden; it is identified and can be calculated from mortality data. Life years lost in the population is not sufficient for monetary valuation, however, because an individual's VSLY may depend on her age, hazard function, and aspects of the change in her hazard in addition to the increase in life expectancy.

As explained by Greenland (2015, p. 160), the article that introduced the term “etiologic fraction” (Miettinen, 1974) produced confusion by equating etiologic, excess, and attributable cases (though without using the latter term). Although Miettinen‘s conceptual misunderstandings were later clarified (Greenland & Robins, 1988), the three terms are still often equated, at least implicitly, as illustrated by quotations from recent literature in Section 1.1.

The monetary value of a reduction in exposure‐related mortality risk, as defined for benefit‐cost analysis, can be estimated using the marginal distributions that are identified using mortality data. The monetary value for a population is the sum of individuals’ values, which depend only on the difference between individuals’ mortality hazard functions if exposed or unexposed; the probability distribution of the difference in age of death between exposure conditions is irrelevant. Inability to know the fraction of deaths that are etiologic does not invalidate conventional estimates of the monetary value of a change in exposure‐related population mortality hazard (e.g., due to a change in air pollution). But the common practice of describing the sum of the reductions in individuals’ hazards as “statistical lives saved” can lead to misinterpretation.

Economic values are always conditional on information; if all that is known for an individual is that her change in hazard can be viewed as a random draw from the population distribution of individuals’ changes in hazard, then the relevant measure for valuation is the mean change in population hazard. If more information about the changes in individuals’ mortality hazards is available, it can affect their valuations and hence the total population value (though the effect on the population value will be small if individuals’ changes in risk are small). Such information can also reduce uncertainty about how many deaths are etiologic.

Because any change to an individual's hazard function implies a unique change to her life expectancy, the individual's monetary value can be expressed as the product of a VSLY and change in life expectancy. VSLY is individual‐specific and may depend on the change in hazard. An individual may have preferences among alternative changes to her hazard function that yield the same increase in life expectancy (e.g., a small risk reduction over many years or a larger risk reduction over a few years); if so, her VSLYs for these changes would differ.

The conventional approach to describing the effects of a change in exposure by the number of “lives saved” or “premature deaths averted” and the economic value of that change as the product of lives saved and value per statistical life is misleading: the number of “lives saved” cannot generally be determined and the value per statistical life is not the economic value of saving a life. We suggest that communication and understanding may be enhanced by describing the mortality effects and the economic value of a change in exposure in terms of the reductions in individuals’ mortality risks and the individuals’ values of those changes. For example, rather than describing the mortality effects of eliminating air pollution on the 200 million US residents aged 30 and older as preventing 100,000 premature deaths per year with a total annual value of $1 trillion, we suggest describing them as decreasing annual mortality risk by an average of 5/10,000 (increasing life expectancy by about four months) with an average annual individual value of $5,000.

The confusion induced by equating premature, etiologic, excess, and attributable deaths is not a trivial semantic issue. Two decades ago, Greenland (1999, subtitle) characterized the issue as “a methodologic error that has become a social problem.”

Appendix 1.

1.1.

The limiting values of the ratio of the lower bound to the hazard fraction as R approaches 1 and infinity can be derived as follows. The hazard fraction $HF=\frac{R-1}{R}$ and the lower bound $LB=\frac{R-1}{R^{\frac{R}{R-1}}}$. The ratio $\frac{HF}{LB}=\frac{R-1}{R}\frac{R^{\frac{R}{R-1}}}{R-1}=R^{\frac{R}{R-1}-1}=R^{\frac{1}{R-1}}$ and the logarithm of the ratio $\ln (\frac{HF}{LB})=\frac{\ln (R)}{R-1}$. By l'Hôpital's rule, $\underset{R\to 1}{\lim }[\ln (\frac{HF}{LB})]=\underset{R\to 1}{\lim }\frac{\frac{d}{dR}\ln (R)}{\frac{d}{dR}R-1}=\underset{R\to 1}{\lim }\frac{\frac{1}{R}}{1}=1$. Hence, $\underset{R\to 1}{\lim }[\frac{HF}{LB}]=\exp (1)=e$ and the limiting value of LB/HF as R → 1 = 1/e.

To determine the limiting value of the ratio of the lower bound to the hazard fraction as R approaches infinity, change the limiting value of R in the expression using l'Hôpital's rule above to obtain $\underset{R\to \infty }{\lim }[\ln (\frac{HF}{LB})]=\underset{R\to \infty }{\lim }\frac{\frac{1}{R}}{1}=0$. Hence, $\underset{R\to \infty }{\lim }[\frac{HF}{LB}]=\exp (0)=1$ and the limiting value of LB/HF as R → ∞ = 1.