Abstract
The physics-based molecular force field (PMFF) was developed by integrating a set of potential energy functions in which each term in an intermolecular potential energy function is derived based on experimental values, such as the dipole moments, lattice energy, proton transfer energy, and X-ray crystal structures. The term, “physics-based,” is used to emphasize the idea that the experimental observables that are considered to be the most relevant to each term are used for the parameterization rather than parameterizing all observables together against the target value. PMFF uses MM3 intramolecular potential energy terms to describe intramolecular interactions and includes an implicit solvation model specifically developed for the PMFF. We evaluated the PMFF in three ways. We concluded that the PMFF provides reliable information based on the structure in a biological system and interprets the biological phenomena accurately by providing more accurate evidence of the biological phenomena.
Keywords: force field, molecular docking, solvation free energy
1. Introduction
Because the biological activities of biomolecules depend on their molecular structures, it is necessary to obtain the correct three-dimensional structure of the target biomolecule to describe its physical, chemical, and biological properties. Over the past several decades, the three-dimensional structures of many biomolecules, such as protein, DNA, RNA, and their complexes, have been identified through X-ray or NMR experiments, and their number is growing rapidly. As the number of biomolecular structures and the demand for computational structural biology increase, particularly in the field of drug discovery, it is necessary to describe and predict the function of biomolecules using computational methods, such as a molecular docking simulation and molecular dynamics simulation.
The computational methods for biomolecules are composed of two main parts: a simulation algorithm that can accurately simulate natural phenomena or processes, and energy calculation methods for the system to be investigated. The energy calculation method can be roughly divided into two classes: a quantum-mechanics based molecular orbital (MO) calculation and a molecular-mechanics based empirical potential energy function called a force field. Although MO calculation methods provide more accurate results for the structure and intermolecular interactions of the target molecules, a high computational cost hinders their application to large systems, such as biomolecules. The time required for a Hartree–Fock calculation, which is a representative MO calculation, increases by approximately n4 where n corresponds to the number of basis functions. However, the time required in a force field is proportional to slightly more than m4 where m corresponds to the number of atoms. Therefore, a force field is more proper for application to large biomolecules and is frequently considered to be used to study not only the static but also dynamic properties of biomolecules.
A force field consists of equations and parameters that define the potential energy surface of a molecule. The potential energy used in a force field is composed of intramolecular and intermolecular energy components. In general, the parameters are not transferable from one force field to another because they are correlated within the force field. The reliability of the force field was dependent on several factors, such as mathematical equations for each component, the optimum set of parameters, and molecules included in the parameterization process.
Several force fields that are broadly used include the Empirical Conformational Energy Program for Peptides (ECEPP)1–5, a Molecular Mechanics (MM) force field6–8, Chemistry at Harvard Molecular Mechanics (CHARMM)9–17, Assisted Model Building with Energy Refinement (AMBER)18–23, Merck Molecular Force Field (MMFF)24–28, Consistent Valence Force Field (CVFF)29, and Optimized Potentials for Liquid Simulations (OPLS)30–32. ECEPP was developed to calculate the interatomic interactions between amino acid residues to delineate the conformational energy of polypeptides and proteins.5 ECEPP consists of electrostatic, nonbonded, hydrogen bond, and torsional terms in its potential energy function (PEF). This energy configuration is advantageous in a Monte Carlo simulation focused on the torsional space but disadvantageous in a molecular dynamics simulation owing to the absence of a PEF to describe the bond stretching and angle bending in molecular dynamics. MM3, the third version of MM, was developed with accurate intramolecular potential functions to allow a precise energy difference in the conformational change of small molecules to be calculated. In particular, the MM3 electrostatic potential energy is calculated by charge distribution represented by a set of bond dipoles. For electrostatic potential energy calculation, MM3 introduced the charge-charge and charge-dipole interactions together. CHARMM is extensively used to simulate the properties of proteins, nucleic acids, lipids, and carbohydrates. To use for drug-like molecules, CHARMM General Force Field (CGenFF)10 was developed in 2009. CGenFF newly introduced the potential parameters for the atom types appeared in hetero cyclic scaffolds and the atoms those attached to the hetero-cyclic scaffold. Therefore, CGenFF is better suited for drug design studies than original CHARMM. AMBER is mainly focused on biomolecules such as proteins and nucleic acid. Charges, called an electrostatic potential (ESP) charge, fit the quantum electrostatic potential energy from a quantum chemistry calculation at the HF 6–31G* level. The van der Waals parameters were derived from amide crystal data by Lifson’s group33, 34 and from liquid-state simulations calculated by Jorgensen35. Force constants, bond lengths, and bond angles were derived from the crystal structure and adapted to match the normal mode frequencies for peptide fragments. MMFF was developed for pharmaceutical applications, and calculates not only in the gas phase but also in the condensed phase.24 The potential parameters of MMFF were obtained by using the energy and electrostatic properties as constraints, and the reliability of the parameters was verified by comparing with experimental data. The type of data used to develop the MMFF is a receptor-ligand interaction involving proteins and nucleic acids as a receptor and a large assortment of chemical structures and ligands. The CVFF is focused on the simulation of organic, polymeric, and biopolymeric systems, as well as the modeling of vibrational spectroscopic properties. The CVFF parameters are derived from the energy and its first and second derivatives with respect to the coordinates of the amino acids, water, and a variety of other functional groups. OPLS consists of intramolecular PEFs in AMBER and intermolecular PEFs developed by Jorgensen’s group. This force field is focused on the modeling of a liquid-phase system whereas the other force fields are focused on the gas phase system. To represent a liquid system accurately, the training set used in the OPLS parameterization consists of liquid phase data instead of gas-phase data and molecular structures are calculated through a Monte Carlo simulation to represent a liquid. Each force field has a slightly different functional form, parameters, and experimental dataset used during the parametrization process to serve the developer’s purpose. Because no force fields are quite applicable to all cases, most are still used in different places to meet different needs.
Owing to the aqueous environment in a biological system, it is important to include a reliable solvation model that describes solute-solvent and solvent-solvent interactions directly and a solute-solute interaction indirectly. In addition, it is ideal to have a solvation model that harmonizes well with other intermolecular energy components. In the case of CHARMM, AMBER, and OPLS, their parameters were optimized for the TIP3P water model, an explicit solvation model.30 Since in explicit solvation models, the positions and interactions of the atoms of the water molecules are explicitly treated, the number of the atoms in a simulation biological system is considerably large, and the simulation takes an extremely long time to obtain reasonable results. To overcome these limitations, many implicit models36–40 have been developed. In implicit models, some of the force field parameters were modified in order to include the influence of the interaction between biological molecules and water.
Herein, we introduce a new type of force field called a physics-based molecular force field (PMFF) that consists of MM3 intramolecular potential energy functions, a newly developed intermolecular energy component comparable to an MM3 force field, and an implicit solvation model. The solvation model was developed based on the parameters used in intermolecular interactions of this force field for harmonization between the solvation model and other intermolecular energy components. Because the solvation model is an implicit model, it requires a lower computational cost than other explicit solvation models. We call this new force field a physics-based molecular force field to emphasize that all parameters in each term in the intermolecular potential energy functions are derived based on experimental values, such as dipole moments, lattice energy, proton transfer energy, and X-ray crystal structures and it calculates reliable energy with fewer parameters using physics-based theory. Details are well described in Section 2.2.
The reliability and suitability among the energy components in a PMFF were examined using the conformer energy difference of certain organic compounds, a molecular docking simulation, and the octanol-water partition coefficient of the peptides.
2. Method
A force field calculates the potential energy, VTotal, by summing the intra- and inter-molecular potential energies and the solvation free energy as follows:
| (1) |
where VIntra and VInter represent the intra- and inter-molecular potential energy, respectively, and Vsolv represents the solvation-free energy of a system.
It was assumed that the intra-atomic potential functions are not significantly affected by the inter-atomic interactions, and thus we considered the potential parameters of stretching, bending, and torsional motions to be usable as is without any modifications even if the chemical environments, mainly through space interactions, change. Based on this assumption, a PMFF potential set introduced in the MM3 intramolecular PEF for VIntra; an intermolecular PEF, that is, VInter; and a solvation-free energy, that is, Vsolv, calculation model was newly developed.
2.1. Intramolecular Potential Energy Function
The MM3 intramolecular potential function parameter set was introduced for the intramolecular potential energy calculation of the PMFF set because the MM3 calculates the intramolecular potential energy in the most precise manner through an introduction of an energy term accounting for couplings between internal coordinates6. The MM3 intramolecular potential function parameter set is described as follows:
| (2) |
where VIntra is the intramolecular potential energy, Vstretch is the bond stretch potential energy, Vbend is the angle bending potential energy, VTorsion is the torsional potential energy, VCross is the energy of the cross terms among the intra coordinates, Vintra–electrostatic is the intramolecular electrostatic potential energy, and Vintra-vdW is the intramolecular van der Waals (vdW) potential energy. The role of the cross term is to act as a coupling effect between two components of the intramolecular potential energy and thus to represent the molecular structure more accurately. The cross term is described as follows:
| (3) |
where VStretch-Bend is the stretch-bending potential energy, VStretch–Torsion is the stretch-torsion potential energy, and VBend–Bend is the bending-bending potential energy. An atom set related to more than 1-4 topological distances was calculated using Vintra–electrostatic and Vintra–vdW. The function form for Vintra–electrostatic and Vintra–vdW is the same as intermolecular electrostatic and vdW PEF and a detailed description is given in the following section.
2.2. Intermolecular Potential Energy Function
The intermolecular PEFs of a PMFF can be described as follows:
| (4) |
where VInter is the intermolecular potential energy, VElectrostatic is the electrostatic potential energy, Vpol is the polarization potential energy, VvdW is the vdW potential energy, and VH–Bond is the potential energy of a hydrogen bond (HB).
The sequential process of the intermolecular PEF parameter set development is illustrated in Figure 1. The potential parameters of the components of eq 4 were determined based on a modified partial equalization of an orbital electronegativity (m-PEOE)41–45 model determined through experimental dipole and quadrupole moments and the quantum mechanical electrostatic potential energy. An electrostatic PEF is calculated using the effective net atomic charges on the atoms in the molecule or molecules. The other potential parameters are determined sequentially and self-consistently. vdW PEF is calculated using the dispersion parameters determined using the Slater–Kirkwood formula46 and charge dependence of the effective atomic polarizability (CDEAP) model47, as well as the repulsion parameters determined based on the X-ray structures of molecular crystals, the experimental lattice energy, and proton transfer enthalpy.48 A hydrogen bond PEF is calculated using parameters determined by the gas phase HB dimer energy and structure, X-ray crystal structure of organic hydrogen bond molecules, and the quantum mechanical potential surface of the HB dimer.49 Finally, the solvation-free energy function is calculated using a parameter determined through the experimental solvation-free energy of organic molecules as well as the peptides and various chemical properties.50, 51
Figure 1.
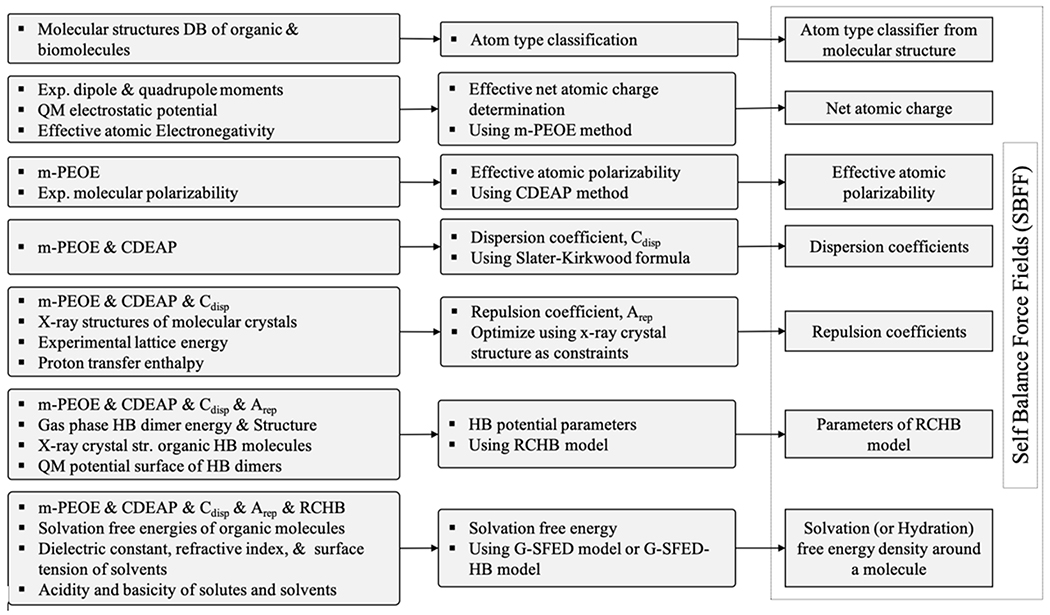
Sequential process of the intermolecular potential energy function set development in PMFF. The components of intermolecular potential energy function set were dependent on other components of the intermolecular potential energy function. Effective atomic polarizability is dependent on the net atomic charge. The nonbonding potential energy function is developed by parameters determined by atomic partial charge and atomic polarizability. The hydrogen bond potential energy function is developed by parameter determined by net atomic charge and nonbonding parameters. The solvation free energy function is developed by parameters determined by net atomic charge, atomic polarizability, nonbonding parameter, and hydrogen bond parameter.
Because each intermolecular PEF in the PMFF is dependent on the other PEFs, the error is distributed evenly among the potential energy components, and trying to obtain the potential parameters results in a good balance among the components through the procedure we introduced for the parameter calculation and optimization in VInter. When developing the repulsion parameter used in vdW PEF, the X-ray crystal structure was optimized using electrostatic PEF. The parameters used in HB PEF were determined using electrostatic and vdW PEF. Therefore, intermolecular PEFs are harmonized. The potential set developed this time do not included Vpol because calculation cost is expensive.
2.2.1. Effective Atomic Charge Calculation
In the PMFF, an atom-centered effective atomic point charge was used for the electrostatic potential energy calculation, and the effective atomic charges were calculated using a modified-PEOE (m-PEOE) method41–45. The electron flow between covalently bonded atoms A and B is calculated based on the electronegativity difference between atoms A and B. Because the electron flow between covalently bonded atoms depends on the difference in the electronegativity of the atomic orbitals that participate in the chemical bond, a number of damping factors describing the different possible bond types in a biomolecule were introduced. The bond types and damping factors41–45 are summarized in Table 1. With the m-PEOE method, the electron flow between the covalently bonded atoms A and B is calculated as follows: 41–45
| (5) |
where is the amount of electron flow between atoms A and B at the n-th iteration, and are the electronegativity of atoms A and B at the (n-1)th iteration, χA+ is the electronegativity of the positive ions of atom A, and fAB is the damping factor of bond type A-B. The electronegativity of atom A at the nth iteration, , was recalculated as follows:
| (6) |
where ai and bi are m-PEOE coefficients (Table 2), and is the net atomic charge of atom A at the nth iteration, which is calculated as
| (7) |
where is the net atomic charge on atom A after the n-th iteration, and is the initial net atomic charge at atom A. The final atomic partial charges were obtained after the net atomic charges are converged through the iterative procedure.
Table 1.
The classification of damping factor values according to bond type used in equation 5.41–45 Damping factor was defined by type of chemical bond to show nature of the electron distribution in different chemical bond.
| Damping factor | Parameter value | Bond Type |
|---|---|---|
| f1 | 0.482 | H-sp3 |
| f2 | 0.569 | H-sp2 |
| f3 | 0.501 | sp3-sp3 |
| f4 | 0.530 | sp3-sp2 |
| f5 | 0.972 | sp2-sp2 |
| f6 | 0.467 | N+-H(N) |
| f7 | 0.703 | N+-Calpha or N+-C(N+) |
| f8 | 0.466 | O-C(O−) |
| f9 | 0.683 | C(O−)-Calpha |
| f10 | 0.805 | C(O−)-C(CO2−) |
| f11 | 0.441 | Aromatic-Aromatic(Not H) |
| f12 | 0.549 | Aromatic-H |
| f13 | 0.664 | Aromatic-not Aromatic |
| f14 | 0.699 | X-C, X-N, X-O, K-C, K-N, K-O, nitro O-N (only neutal) |
| f15 | 0.731 | X-C, X-N, X-O (only charged) |
| f16 | 0.501 | Si-H |
| f17 | 0.457 | Si-sp3 |
| f18 | 0.990 | sp-sp |
| f19 | 0.980 | sp-sp2 |
| f20 | 0.554 | sp-sp3 |
| f21 | 0.210 | sp-H |
Table 2.
The electronegativity parameter set according to atom type used in equation 7 and 8.41–45 ai and bi are m-PEOE coefficient. is initial atomic partial charge.
| Atom | Atom type | ai | bi | |
|---|---|---|---|---|
| C | Csp2 | 9.795 | 25.195 | 0.00 |
| C | Car | 9.288 | 7.919 | 0.00 |
| C | Csp3 | 7.967 | 4.862 | 0.00 |
| C | C=O | 8.218 | 8.288 | 0.00 |
| C | Csp3-P5 or S6 | 12.397 | 6.667 | 0.00 |
| C | Csp3-Si | 7.767 | 12.429 | 0.00 |
| C | Csp | 10.000 | 5.000 | 0.00 |
| C | Csp3-S4 | 9.292 | 3.764 | 0.00 |
| C | C-N+ | 8.660 | 6.893 | 0.35 |
| C | CO2− | 5.159 | 3.005 | 0.20 |
| C | Cα | 7.772 | 2.008 | 0.35 |
| C | Csp3-P5− or S6− | 14.384 | 7.411 | 0.20 |
| H | H atom | 7.711 | 31.958 | 0.00 |
| H | Har | 7.428 | 6.722 | 0.00 |
| H | H-Si | 9.097 | 3.727 | 0.00 |
| H | H-Csp | 7.780 | 20.000 | 0.00 |
| H | H-N+ | 7.067 | 8.445 | 0.35 |
| H | H-Cα | 9.024 | 9.962 | 0.05 |
| H | H-CO2− | 7.963 | 19.067 | 0.10 |
| O | Oar | 10.896 | 11.136 | 0.00 |
| O | Osp2 | 14.284 | 13.857 | 0.00 |
| O | Osp3 | 12.941 | 12.808 | 0.00 |
| O | Osp3-P5 or S6 | 13.685 | 12.446 | 0.00 |
| O | Osp2=P5 or S6 | 15.409 | 12.341 | 0.00 |
| O | Osp3-Si | 7.767 | 12.429 | 0.00 |
| O | Osp2=S4 | 14.495 | 13.039 | 0.00 |
| O | Osp3-S4 | 13.062 | 10.860 | 0.00 |
| O | O=C-O− | 14.664 | 9.324 | −0.60 |
| O | O-sp3-P5 or S6 | 17.692 | 6.478 | −0.60 |
| O | O—N+=O | 16.263 | 13.130 | 0.00 |
| N | Nar2 | 15.130 | 3.155 | 0.00 |
| N | Nar3 | 12.941 | 3.240 | 0.00 |
| N | N−= | 15.478 | 11.914 | 0.00 |
| N | Nsp3 | 12.184 | 13.538 | 0.00 |
| N | Nsp3-P5 or S6 | 14.385 | 8.896 | 0.00 |
| N | Nsp2 | 11.700 | 31.000 | 0.00 |
| N | Nsp | 15.500 | 12.500 | 0.00 |
| N | Nsp3-S4 | 12.792 | 5.295 | 0.00 |
| N | N+sp3 | 15.722 | 14.277 | −0.40 |
| N | N+sp3-P5 or S6 | 14.615 | 2.975 | −0.40 |
| N | N+O2− | 7.967 | 15.621 | 0.00 |
| S | Sar | 9.340 | 12.157 | 0.00 |
| S | Ssp3 | 10.435 | 5.126 | 0.00 |
| S | S6 | 4.861 | 2.920 | 0.00 |
| S | Ssp2 | 12.892 | 18.852 | 0.00 |
| S | S4 | 8.599 | 5.952 | 0.00 |
| S | S6− | 3.329 | 8.156 | 1.60 |
| P | Psp3 | 11.133 | 17.700 | 0.00 |
| P | P5 | 4.664 | 2.951 | 0.00 |
| P | P5− | 2.972 | 6.209 | 1.40 |
| Si | Si | 4.402 | 7.703 | 0.00 |
| Cl | Cl | 11.861 | 13.647 | 0.00 |
| Br | Br | 11.649 | 13.388 | 0.00 |
| I | I | 11.375 | 17.898 | 0.00 |
2.2.2. Calculation of Effective Atomic Polarizabilities in a Molecule
The effective atomic polarizability concept is useful for calculating the molecular polarizability from the effective atomic polarizabilities using the additivity approximation, allowing the polarization stabilization energy under an atom-atom pair potential approximation, as well as the dispersion interaction coefficients, to be calculated. The optimum effective atomic polarizabilities of the atoms in different hybrid states were determined by Miller and Savchik52 and Kang and Jhon53. No et al. developed an effective atomic polarizability calculation method by considering the chemical environments of the atoms in a molecule, namely, the CDEAP model47. With the CDEAP model, the effective atomic polarizability is described as a linear function of the net atomic charge as follows:
| (8) |
where is the atomic polarizability at atom A, is the atomic polarizability at a zero effective net atomic charge of atom A, and dqA is the net atomic charge calculated using m-PEOE at the formal charged atom A. The CDEAP parameters, and aA, are described in Table 3.
Table 3.
The effective atomic polarization parameter set according to atom type used in equation 8.47 is atomic polarizability at zero formal charged atom i. ai is ratio by atomic partial charge.
| Atom | Atom type | ai | |
|---|---|---|---|
| C | Csp2(ethylene) | 1.5160 | 0.5680 |
| C | Csp2(aromatic) | 1.4500 | 0.7630 |
| C | Csp2(carbonyl) | 1.2530 | 0.8620 |
| C | Csp3 | 1.0310 | 0.5900 |
| C | Csp | 1.4900 | 1.1000 |
| H | Hsp3 | 0.3960 | 0.2190 |
| H | Hsp2(aromatic) | 0.2980 | 0.4040 |
| O | Osp2 | 0.7200 | 0.3470 |
| O | Osp3 | 0.6230 | 0.2810 |
| N | Nsp2(aromatic,pyrrole) | 0.8710 | 0.4240 |
| N | Nsp2(aromatic,pyridine) | 0.6560 | 0.4360 |
| N | Nsp2(amide) | 0.8210 | 0.4220 |
| N | Nsp3 | 0.9660 | 0.4370 |
| N | Nsp | 0.9800 | 0.3100 |
| N | −N=N- | 0.8210 | 0.4220 |
| S | Ssp3(−S-) | 2.6880 | 1.3190 |
| S | S0 | 4.3200 | 1.9954 |
| S | S6 | 5.1520 | −1.7304 |
| P | P5 | 11.1010 | −7.0057 |
| F | F | 0.2260 | 0.1440 |
| Cl | Cl | 2.1800 | 1.0890 |
| Br | Br | 3.1140 | 1.4020 |
| I | I | 5.1660 | 2.5730 |
2.2.3. van der Waals Potential Energy Function
For a nonbonding potential energy calculation48, a Lennard–Jones potential function was introduced:
| (9a) |
| (9b) |
where rij is the distance between atoms i and j, and Aij, Cij, εij, and σij are Lennard–Jones potential parameters between atoms i and j. These parameters for a hetero atomic pair were obtained using the following combination rule:54
| (10a) |
| (10b) |
The Lennard–Jones potential parameters, εii and σii, are summarized in Table 4.
Table 4.
The classification of Lennard-Jones potential parameter set according to atom type used in equation 9a.48 εii is the depth of the potential well. σii is the finite distance at which the inter-particle potential is zero.
| Atom type | Description | εii(kcal/mol) | σii(Å) |
|---|---|---|---|
| H1 | Aliphatic hydrogen | 0.031 | 2.628 |
| H2 | H bonded to amide | 0.094 | 2.076 |
| H3 | H bonded to aromatic system | 0.011 | 2.815 |
| H4 | Hydroxyl hydrogen | 0.031 | 2.628 |
| C1 | Aliphatic carbon | 0.042 | 3.697 |
| C2 | Aromatic carbon | 0.096 | 3.555 |
| C3 | Carbon in carboxylic group | 0.139 | 3.074 |
| C4 | Carbon in amide | 0.157 | 3.011 |
| C5 | Carbon in Carboxylate ion | 0.088 | 2.931 |
| N1 | Aromatic nitrogen with 3 bonds | 0.235 | 2.833 |
| N2 | Aromatic nitrogen with 2 bonds | 0.105 | 3.118 |
| N3 | Nitrogen in amide or amine | 0.157 | 3.011 |
| N4 | Nitrogen in ammonium ion | 0.388 | 2.682 |
| O1 | Oxygen in carboxylic or amide group | 0.226 | 2.717 |
| O2 | sp3 oxygen | 0.200 | 2.655 |
| O3 | Oxygen in carboxylate ion | 0.181 | 2.922 |
| S1 | Sulfur | 0.480 | 3.554 |
| P1 | Phosphorus | 0.220 | 3.800 |
| F1 | Fluorine | 0.069 | 3.458 |
| Cl1 | Chlorine | 0.069 | 3.970 |
| Br1 | Bromine | 0.100 | 4.260 |
2.2.4. Angle-Dependent HB Potential Energy Function
A simple hydrogen bond model was proposed by No et al.,49 where the 1-3 atomic pairs in a hydrogen-bonded system proved to be the most important terms in the description of the angular dependence of the hydrogen bond potential surfaces. To describe the angle dependency of such a surface, an interatomic distance set (rHA, rXA, rBH, and rXB), described in Figure 2b, was introduced instead of the internal coordinate set, which has been widely used, as indicated in Figure 2a, for describing the angle dependency of a hydrogen bond. The hydrogen bond potential function of the PMFF is approximated using the 1-6-12 type function as follows:
| (11) |
where VH–Bond, , and are the total hydrogen bond potential energy, and the electrostatic and vdW potential energies in the hydrogen bond, respectively, and rk describes the distance between atom pairs, namely, rHA, rXA, rBH, and rXB. A vdW potential function in a hydrogen bond potential function is the same as in a previous vdW potential function.
| (12) |
where Bk, Dk, εk, and σk are Lennard–Jones parameters in one of the atomic pairs participating in the hydrogen bond. To represent the unique property of a hydrogen bond interaction, a repulsive core is applied, which was represented by a 6-12 type function. The radius of the repulsive cores (Figure 2c) is defined based on the distance of a 1-3 interaction when the hydrogen bond interaction is the most stable. If the distance in a 1-3 interaction is shorter than the repulsive core radius defined, the hydrogen bond becomes unstable, and the energy is increased. The atom types and parameters are described in Table 5. In this study, the parameters for alcohol in carboxylic acid, and the nitrogen and hydrogen in amide, were used to calculate the normal alcohol and amine type owing to the high structural similarity between them.
Figure 2.
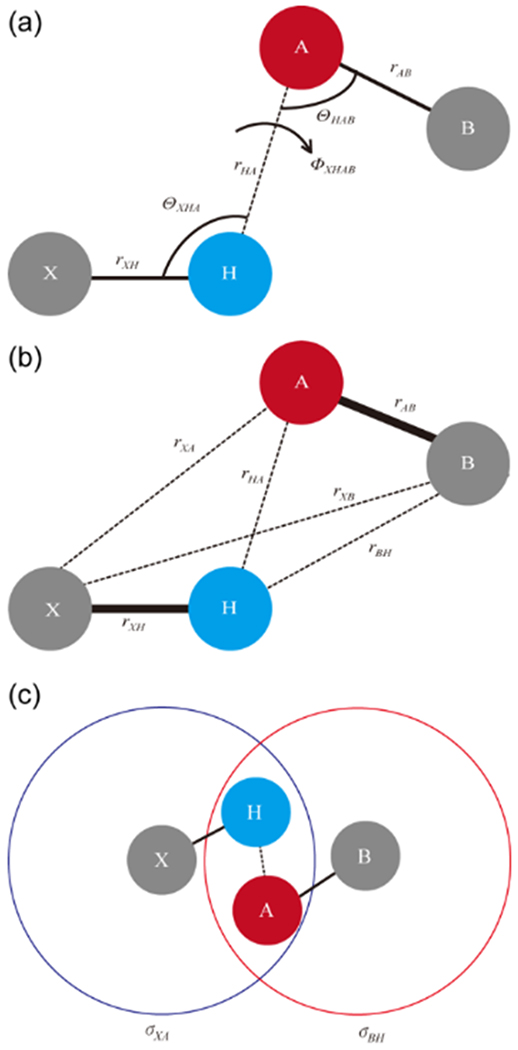
(a) Hydrogen bond coordinate system, rHA, θXHA, θHAB, and ϕXHAB, which is usually used to describe the hydrogen bond system (b) Coordinate system, rHA, rXA, rBH, and rXB, which is introduced in our model for describing the hydrogen bond (c) Repulsive cores, σXA and σBH of the 1-3 atomic pairs for the X-H⋯A=B hydrogen bond system
Table 5.
The classification of hydrogen bond parameter set according to the atom type used in 12.49
| (a) Hydrogen bond atom type | |
|---|---|
| Atom type | Description |
| H1 | amide hydrogen |
| H2 | hydrogen in CO2H |
| H3 | bonded to N+ |
| C1 | carbonyl carbon in carboxylic group |
| C2 | carbonyl carbon in amide |
| C3 | carbonyl carbon in carboxylate ion |
| N1 | nitrogen in amide |
| N2 | nitrogen in ammonium ion |
| O1 | carbonyl oxygen in carboxylic group |
| O2 | carbonyl oxygen in amide |
| O3 | sp3 oxygen in CO2H |
| O4 | carbonyl oxygen in carboxylate ion |
| (b) Hydrogen bond parameters | |||
|---|---|---|---|
| Conformations | Interaction atomic pairs | ε(kcal/mol) | σ(Å) |
| Amide – Amide | H1 ⋯ O2 | 2.325 | 1.604 |
| N1 ⋯ O2 | 0.043 | 3.651 | |
| H1 ⋯ C2 | 0.013 | 3.609 | |
| Carboxyl Acid – Carboxyl Acid (open-chain) | H2 ⋯ O1 | 2.764 | 1.722 |
| O3 ⋯ O1 | 0.052 | 3.399 | |
| H2 ⋯ C1 | 0.014 | 3.570 | |
| Carboxyl Acid – Carboxyl Acid (cyclic) | H2 ⋯ O1 | 4.186 | 1.515 |
| O3 ⋯ O1 | 0.141 | 2.878 | |
| H2 ⋯ C1 | 0.017 | 3.483 | |
| Amide – Carboxyl Acid dimer 1 | H2 ⋯ O2 | 3.519 | 1.732 |
| O3 ⋯ O2 | 0.061 | 3.309 | |
| H2 ⋯ C2 | 0.015 | 3.558 | |
| Amide – Carboxyl Acid dimer 2 | H1 ⋯ O1 | 2.790 | 1.437 |
| N1 ⋯ O1 | 0.032 | 3.843 | |
| H1 ⋯ C1 | 0.015 | 3.545 | |
| Ammonuim ion – Carboxylate ion | H3 ⋯ O5 | 4.211 | 1.648 |
| N2 ⋯ O5 | 0.072 | 3.476 | |
| H3 ⋯ C3 | 0.029 | 2.987 | |
2.3. Solvation-Free Energy Calculation Model and Generalized Solvation Free Energy Density (GSFED) Model
The PMFF has a solvation-free energy model, namely, GSFED50, 51, which is well balanced with other potential energy functions. Solvation-free energy, ΔGsolv, in the GSFED model is described using five experimental values as follows:
| (13a) |
| (13b) |
where S and NA represent the number of surface fragments on the cavity surface and atoms of the solute, rik represents the distance between the ith atom and the kth surface fragment, A and B represent the HB acidity and basicity of the hydrogen bonded molecules, respectively, θ is the HB angle described in Figure 3, ri0 is the equilibrium distance of the particular HB donor or acceptor atom i, and are the effective HB acidity and basicity of atom i, respectively, is the number of surface grid points of atom i that are within the surface designed by the HB angle θ, and εm and ηm are the dielectric constant and refractive index of the solvent, respectively. The net atomic charge, qi, and effective atomic polarizability, αi, of the ith atom of the solute is calculated using m-PEOE and CDEAP. The cavity surface is represented by the sum of the solvent accessible surface of each atom. Each solvent accessible surface of an atom is described using the sum of the van der Waals radius and the effective solvent shell thickness. The solvent parameters used in GSFED and GSFED-HB, Cj, are described in Table 6. The coefficients of the HB acidity and basicity are described in Table 7.
Figure 3.
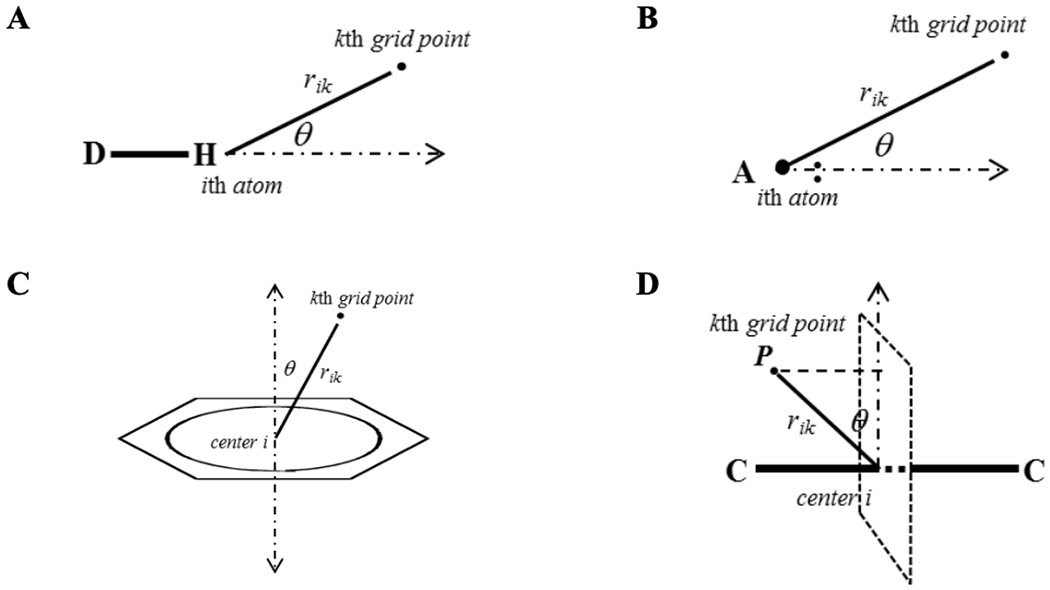
Description of angle θ and distance r used in the GSFED-HB model. (A) hydrogen bond donor (B) hydrogen bond acceptor (C) aromatic groups as hydrogen bond acceptor, and (D) alkene and alkyne functional groups as hydrogen bond acceptor
Table 6.
The generalized solvation free energy density model parameter used in equation 13.50, 51 The parameters have units that enable the product of the basis function and the coefficient to be expressed in kcal/mol.
| Parameter | GSFED | GSFED-HB | Parameter | GSFED | GSFED-HB |
|---|---|---|---|---|---|
| C1,0 | −1.76E-03 | −4.41E-04 | C4,0 | 6.72 | 1.68 |
| C1,1 | −1.37E-01 | −3.43E-02 | C4,1 | −8.99 | −2.25 |
| C2,0 | −2.89E-03 | −7.23E-04 | C5 | −7.53 | −7.53 |
| C2,1 | −1.84E-01 | −4.59E-02 | C6 | −4.35 | −4.35 |
| C3,0 | −2.16E-01 | −5.40E-02 | C7 | 7.12E-05 | 1.78E-05 |
| C3,1 | 2.64E-01 | 6.61E-02 | C8 | −2.66E-01 | −2.66E-01 |
Table 7.
The classification of hydrogen bond potential energy function parameter set used in equation 13a.51 r0 is the equilibrium distance of the particular HB donor or acceptor atom i. θ is angle described by Figure 3. If θ is bigger than the parameter, HB acdity or basicity is zero. N0 is the maximum number of surface grid point of the atom that are within the range of the HB angle θ used in equation 13a.
| (a) Parameters for hydrogen bond acidity | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Type | α* | r0(Å) | θ < | N0 | Type | α* | r0(Å) | θ < | N0 | |
| Csp-H | 0.354 | 2.100 | 60 | 338 | H2N-H | 0.369 | 1.950 | 90 | 491 | |
| RO-H | 2.434 | 1.804 | 90 | 457 | Car-N-H | 0.481 | 2.100 | 90 | 377 | |
| c-O-H | 1.491 | 1.804 | 90 | 339 | RCONH-H | 1.350 | 2.016 | 90 | 451 | |
| HO-H | 3.039 | 1.880 | 90 | 577 | RCONR-H | 1.006 | 1.988 | 90 | 317 | |
| CarO-H | 3.893 | 1.724 | 90 | 390 | HCONH-H | 1.454 | 2.016 | 90 | 470 | |
| RCOO-H | 6.595 | 1.629 | 90 | 438 | HCONR-H | 1.614 | 1.988 | 90 | 417 | |
| HCOO-H | 8.129 | 1.629 | 90 | 439 | Nar-H | 1.356 | 1.988 | 30 | 88 | |
| RHN-H | 0.309 | 2.120 | 90 | 419 | SO2NH-H | 2.606 | 1.710 | 90 | 380 | |
| R2N-H | 0.284 | 2.140 | 90 | 359 | SO2NR-H | 1.013 | 1.710 | 90 | 306 | |
| CONR-H | 0.543 | 1.988 | 30 | 88 | ||||||
| (b) Parameters for hydrogen bond basicity | ||||||||||
| Type | β* | r0(Å) | θ < | N0 | Type | β* | r0(Å) | θ < | N0 | |
| −Csp2 | 0.066 | 3.570 | 30 | 1039 | −NH2 | 1.397 | 2.840 | 60 | 404 | |
| c-Csp2 | 0.085 | 3.570 | 30 | 657 | −NRH | 1.283 | 2.890 | 60 | 318 | |
| −Car | 0.076 | 3.400 | - | - | NR3 | 1.260 | 2.900 | 60 | 233 | |
| Csp3-Car | 0.306 | 3.400 | - | - | NH3 | 1.215 | 2.840 | 60 | 484 | |
| −Csp | 0.080 | 3.350 | 30 | 1102 | N/O-Car | 0.793 | 3.400 | - | - | |
| Csp3-F | 0.006 | 3.070 | 90 | 844 | RCO-NH2 | 0.874 | 2.840 | 90 | 856 | |
| Csp3-Cl | 0.070 | 3.196 | 90 | 971 | RCO-NHR | 1.378 | 2.840 | 90 | 745 | |
| Csp3-Br | 0.283 | 3.470 | 90 | 1081 | RCO-NR2 | 1.674 | 2.840 | 90 | 741 | |
| Csp3-I | 0.640 | 3.610 | 90 | 1081 | HCO-NH2 | 1.108 | 2.840 | 90 | 869 | |
| RC(=O)-OH | 0.143 | 2.940 | 60 | 779 | HCO-NHR | 0.891 | 2.840 | 90 | 766 | |
| RC(=O)-OR | 0.257 | 2.940 | 60 | 523 | HCO-NR2 | 1.454 | 2.840 | 90 | 766 | |
| Car-F | 0.080 | 3.070 | 90 | 915 | RC≡N | 1.391 | 2.940 | 60 | 1272 | |
| Car-Cl | 0.028 | 3.196 | 90 | 1021 | Csp3-NO-O | 0.342 | 3.040 | 90 | 843 | |
| Car-Br | 0.032 | 3.470 | 90 | 1100 | Car-NO-O | 0.205 | 3.040 | 90 | 767 | |
| Car-I | 0.020 | 3.610 | 90 | 1086 | Nar | 0.337 | 2.950 | 30 | 130 | |
| R-OH | 0.931 | 2.931 | 60 | 751 | Nar-H/R | 0.577 | 2.905 | 40 | - | |
| c-OH | 0.100 | 2.831 | 60 | 624 | −SH | 0.482 | 3.310 | 60 | 1162 | |
| H2O | 0.605 | 2.852 | 60 | 852 | R2S | 0.514 | 3.530 | 60 | 1130 | |
| Car-OH | 0.163 | 2.890 | 60 | 688 | RSSR | 0.252 | 3.530 | 60 | 984 | |
| R2O | 0.760 | 2.910 | 60 | 618 | RSO2-NHR | 1.547 | 2.854 | 90 | 872 | |
| R2C=O | 1.184 | 2.840 | 90 | 833 | RSO2-NHR | 0.250 | 2.840 | 60 | 355 | |
| RCHO | 0.846 | 2.840 | 90 | 854 | RSO2-NR2 | 0.205 | 2.854 | 90 | 745 | |
| c-C=O | 1.072 | 2.840 | 90 | 845 | RSO2-NR2 | 1.886 | 2.890 | 60 | 224 | |
| HC(OR)=O | 0.462 | 2.840 | 90 | 741 | c-R2O | 0.319 | 2.910 | 60 | 155 | |
| RC(OR)=O | 0.842 | 2.840 | 90 | 733 | aromatic ring | - | 3.400 | 40 | 667 | |
| RC(=O)-OH | 0.792 | 2.840 | 90 | 866 | Oar | 0.059 | 2.910 | 30 | 117 | |
| HC(=O)-OH | 0.070 | 2.840 | 90 | 876 | Sar | 0.041 | 3.530 | 30 | 118 | |
| CONR2 | 0.007 | 2.840 | 90 | 849 | ||||||
2.4. Software Implementation
To examine the suitability, reliability, and accuracy of the PMFF using a structural optimization and docking simulation by integrating all components of the PMFF, we developed a program using JAVA and the Chemistry Development Kit (CDK)55. The parameters used in MM3 intramolecular PEFs were taken from the internal parameter set file in Maestro56. For the structural optimization and docking simulation, the direction of the vector searched in the geometric parameter space was calculated using the steepest descent method57, and the size of the vector was determined using the golden section search method58.
The intermolecular potential energy is dependent on the distance and slowly converges to zero at long distances. The cutoff distance in the intermolecular PEFs was introduced into the calculation to describe these phenomena and reduce the computation time. In addition, a smooth function was introduced to maintain the continuous derivative of the PEFs, which is described as
| (14) |
where dmin and dmax are the minimum and maximum cutoff distances, and d is the distance between two atoms. When the value of d is between the minimum and maximum cutoff distance, the potential energy is calculated based on the product of the smooth function and intermolecular PEF. In this validation, dmin was determined based on 6Å in an electrostatic PEF and 4Å in a hydrogen bond and nonbonding PEF, and dmax was determined based on 12Å in an electrostatic PEF and 6Å in a hydrogen bond and nonbonding PEF.
2.5. Calculation of Conformer Energy Difference for Small Molecules
MM3 force fields were developed for the accurate conformational analysis of small organic molecules. Since the MM3 was introduced to calculate the intra potential energy portion of the PMFF, it is necessary to ensure that the PMFF maintains the accuracy in conformational analysis of organic molecules at the similar accuracy level of the MM3, even though intramolecular electrostatic and vdW PEF were incorporated in intramolecular PEF set of MM3.
To confirm this hypothesis, structures of 17 molecules were collected from Pubchem59 and are listed in Table 8. The of the 17 molecules was determined by a gas phase determination of activation enthalpy or potential energy difference60 or solution measurements of free energy of activation60.-Since the values of the 17 molecules are not enough to check whether both MM3 and PMFF gave similar levels of accuracy in conformational analysis, 133 organic ligands from the X-ray crystal structures of ligand-protein complexes were further selected from the Protein Data Bank (PDB)61 (Table S1), and then their were calculated with an ab initio molecular orbital (MO) calculation method. The 133 compounds have molecular weight of less than 400 and the number of rotatable bonds is one or two to avoid too much conformers. Also 133 compounds were selected in order to have maximum structural variance in the principle component space that was constructed with molecular geometrical descriptors. The counter conformers of the 133 ligands were generated by considering axial and equatorial or by considering a torsional energy barrier. The minimum energy structures, which should correspond to a local minimum, of the 300 conformers, 34 from the gas-phase experiments and 266 from ligand-protein complexes, were obtained using ab initio MO calculation with a HF/6-31G** basis set. Since the number of experimentally obtained energy differences between the conformers of the molecules that are the analogues of proteins is limited, the authors could have collected only gas-phase experimental data of 17 molecules. The values of the 133 organic compounds were calculated using the conformer energy difference of the pair conformers using density functional theory (DFT) with B3LYP/6-31G** in Gaussian09. The 266 minimum energy conformer structures were used as the initial structure for the geometry optimization with MM3 and PMFF. Since the steepest descent algorithm keeps the local minimum, the structural change is not great. When the root-mean-square distance (RMSD) is smaller than 10−4Å/atom then the geometry optimization stops. Since both and were obtained at the gas phase, the dielectric constant was set to 1 for the MM3 and PMFF calculations. The MM3 conformer energy difference, corresponds to the energy difference between the minimum energy conformers calculated with MM3. The , the conformational energy difference calculated with PMFF, was calculated in the same way as the . The ΔEconf values obtained with experiments, MM3, and PMFF are summarized in Table 8. The values of the 133 compounds are summarized in Table S2 together with and .
Table 8.
Conformer energy difference (Kcal/mol) compared between MM3 and PMFF.
| Moleculea | b | MM3c | PMFF | ||
|---|---|---|---|---|---|
| 2,3-Dimethylbutane (a-g) |
−0.05 | −0.03 | 0.02 | 1.47 | 1.52 |
| Butane (a-g) |
−0.97 | −0.55 | 0.42 | −0.84 | 0.13 |
| Cyclohexanamine (ax-eq) |
1.49 | 2.63 | 1.14 | 2.31 | 0.82 |
| Methoxyethane (a-g) |
−1.50 | −1.76 | 0.26 | −2.50 | 1.00 |
| Ethanol (a-g) |
−0.70 | −0.72 | 0.02 | −1.01 | 0.31 |
| Propanol (a-g) |
−0.30 | −0.62 | 0.32 | −0.04 | 0.26 |
| Methyl acetate (cis-trans) |
−8.00 | −6.90 | 1.10 | −9.70 | 1.70 |
| 1,3,5-Trineopentylbenezene (allsyn-twosyn) |
−1.04 | 0.36 | 1.40 | −0.01 | 1.03 |
| 2-Methoxyoxane (ax-eq) |
−1.00 | −1.48 | 0.48 | −2.15 | 1.15 |
| 2-Methylpiperidine (ax-eq) |
2.50 | 2.58 | 0.08 | 2.86 | 0.36 |
| 3-Methylpiperidine (ax-eq) |
1.60 | 1.44 | 0.16 | 1.74 | 0.14 |
| 4-Methylpiperidine (ax-eq) |
1.93 | 1.66 | 0.27 | 2.03 | 0.10 |
| cis-1,3-Dimethylcyclohexane (ax,ax-eq,eq) |
5.50 | 5.74 | 0.24 | 5.56 | 0.06 |
| Methylcyclohexane (ax-eq) |
1.75 | 1.66 | 0.09 | 1.89 | 0.14 |
| N,N-Dimethylcyclohexanamine (ax-eq) |
1.31 | 0.96 | 0.35 | 0.90 | 0.41 |
| N-Methylpiperidine (ax-eq) |
3.20 | 2.63 | 0.57 | 3.26 | 0.06 |
| trans-1,2-Dimethylcyclohexane (ax,ax-eq,eq) |
2.58 | 2.31 | 0.27 | 2.38 | 0.20 |
| Average | 0.46 | 0.56 | |||
| Standard Deviation | 0.43 | 0.54 | |||
a: Anti, g: Gauche, ax: Axial, eq: Equatorial
Experimental conformer energy taken from ref 60
Version of MM3 is made in 2006 with 1.6
2.6. Molecular Docking Simulation
In docking simulation, even if the target protein is assumed rigid and the energy minimum structure is obtained with the ligand’s translational and rotational motion and its internal degrees of freedom, it is very difficult to find the global minimum of the PES of the complex structure due to the multiple minima problem. Thus, in this docking simulation, it is assumed that the structure of the ligand in the complex will be similar to the ligand’s stable conformers. The suitability of the PMFF for protein-ligand interaction studies can be determined by the agreement between the X-ray structure of the protein-ligand complex and the PMFF global minimum energy structure of the complex. However, due to the multiple minima problem, it is very difficult to obtain the global energy minimum of a protein-ligand complex using any kind of computer simulation. To overcome this problem, a multi-step docking algorithm, PMFF-MDA (PMFF multi-step docking algorithm), was devised and the minimum energy structures of the protein-ligand complex were calculated and compared with the X-ray structure of the complex. The designed algorithm can be divided into two blocks each consisting of a few steps. The algorithm is explained in Figure 4.
Figure 4.
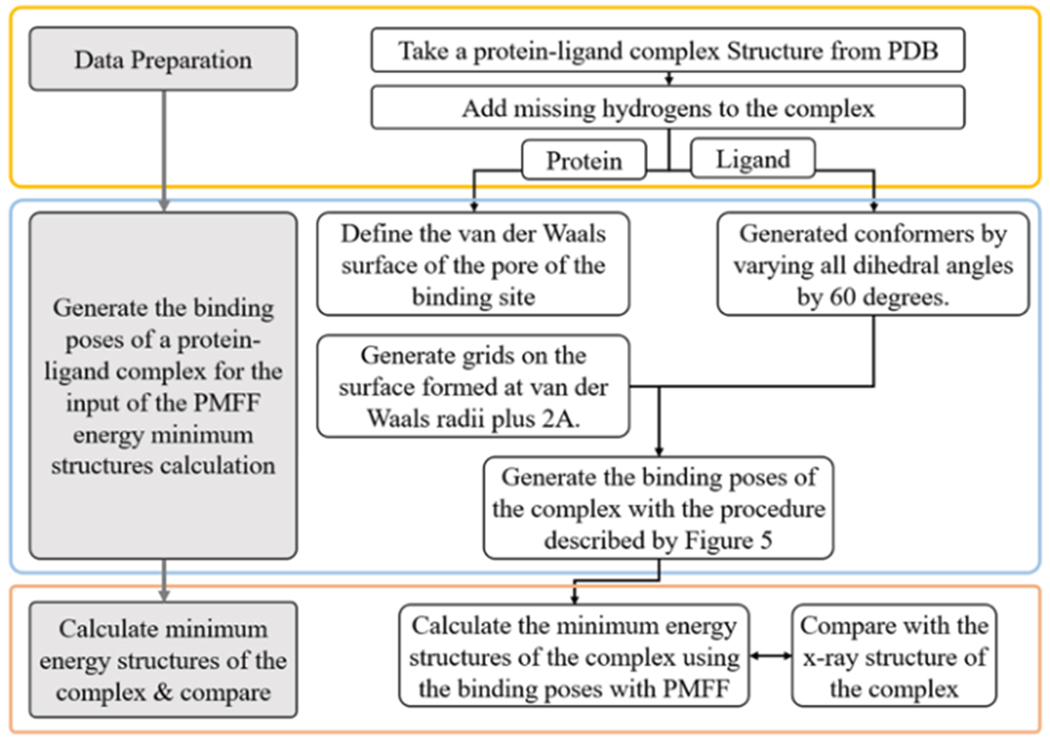
Flow diagram of the molecular docking simulation algorithm devised in this work. The procedure of the generation of the binding poses is described in Figure 5.
To determine how well the PMFF-MDA and Glide programs predict the experimentally obtained protein-ligand complex structure, 214 protein-ligand complex structures, a test set used in the development of the Glide program, were collected from PDB. Then, the missing hydrogens of the complexes were added using Maestro56. In order to explore the high dimensional potential energy surface of protein-ligand interaction, various conformers of the ligand were used as the initial structure of the docking simulation. To generate ligand conformers, the rotatable bonds in the ligand were identified using a SMART62 key and then rotated at an interval of 60°, with the number of the generated conformers denoted as M. When the energy of the generated conformer is greater or less than 1kcal compared to the energy of the ligand structure of the complex, the confirmer was removed from the ligand structure pool for the initial structures of docking simulations.
The docking procedure of the PMFF-MDA is described in Figure 5. It was assumed that the distance at which the atoms of a ligand reach maximum interaction with a protein is 2 Å plus the van der Waals surface of the protein, Interaction Surface (IS). (A) Based on the assumption, IS was generated and grid points were generated on the IS with an interval 0.1 Å. Then, the grid points were indexed as PI,J, which is the Jth point of the Ith amino acid in the binding pocket. (B) The atoms in the ligand are numbered k, and the atom-type of the m-PEOE, l,was assigned where the kth atom with the lth atom type is donated as lk, as shown in Table b-1. Then, the atom type, l, of the ligand’s atoms was collected, and each atom, k, was assigned to one of the atom types, (l1,l2,…,ln), as shown in Table b-1, [(1:1,5), (2:2,3,4), (3:6), (4:7), (5:8), (6:9)]. (C) The interaction energy at all the grid points, PI,Js, was calculated with all kinds of atom types (l1, l2,…,ln) {E(PI,J,lm), for all I & J,m = 1,n}. (D) For every atom-type l, the top-N was selected; here, as an example where N=3, energetically stable grid points were selected, three from {E(PI,J,lm)} for each l, {E(PI1,J1,lm), E(PI2,J2,lm)}, E(PI3,J3,lm)}, as described in Table d-1. (E) All the energetically favorable binding modes of each conformer (M conformers) were generated through the following procedure. (i) All the possible combinations of the three atom types from the n atom-types were generated, (lm1, lm2, lm3), with nC3 combinations (ii) For each atom-type lm in the combination, (lm1, lm2, lm3) three grid points were assigned in step (D), {(PI1,J1,lm1), (PI2,J2,lm2), (PI3,J3,lm3)} then all the possible grid point combinations of the of each atom-type combination became 27. For example, one of the 27 combination is {(lm1,lm2,lm3), (PI1,J1,lm1), (PI2,J2,lm2), (PI3,J3,lm3)}, and this combination index means PI1,J1 grid from atom type lm1, PI2,J2 grid from atom-type lm1, PI2,J2, and PI3,J3 grid from atom-type lm3. (iii) The atom-type index is replaced with the atomic index of the ligand. Since more than one atom of the ligand was assigned to one atom type, a large number of the combinations were generated as, {(klm1,klm2,klm3), (PI1,J1,lm1), (PI2,J2,lm2), (PI3,J3,lm3)}, which is described in the last column of Table e-1. (F) By minimizing the following function,
| (15) |
the triangles, (klm1, klm2, klm3) and {(PI1,J1,lm1), (PI2,J2,lm2), (PI3,J3,lm3)} have the maximum overlap. Since the protein structure was fixed during docking simulation, only the translation and orientation of the triangle of (klm1, klm2, klm3) is changed during the D2 minimization. Using (klm1, klm2, klm3), the geometry of the ligand can be generated. The total potential energy about generated geometries of protein-ligand was calculated by PMFF and used in docking score. The performance of the docking simulation was evaluated with the RMSD between the X-ray structure and generated binding pose of the ligand. The RMSD was calculated only with heavy atomic positions. The top-ranked pose and closest pose, described in Table 10, were defined to be the binding pose having the lowest total potential energy and RMSD among generated geometries of the protein-ligand complex.
Figure 5.
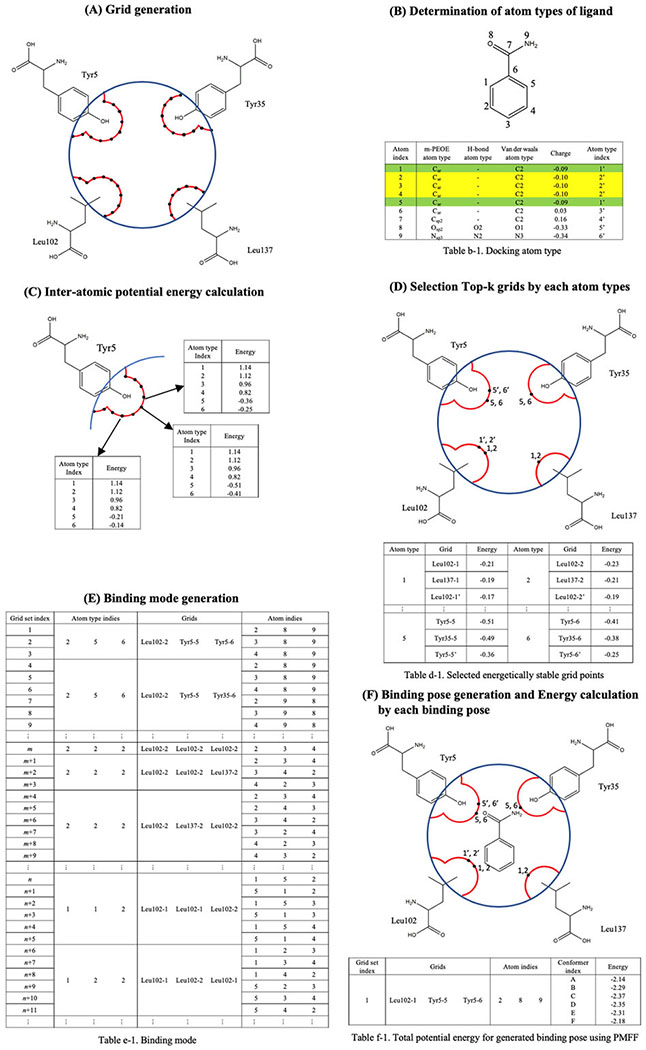
Description of protocol of binding pose generation. (a) Grids are generated. Red lines describe atomic surface. Blue lines describe user-selected pore of binding sites. Black circles describe grids. (b) Docking atom types for each atom of ligands are determined by atomic partial charge and atom types used in m-PEOE, HB, and vdW PEFs. (c) Inter-atomic potential energy is calculated when atom defined docking atom type is located on the grid. (d) Top-k grids for each docking atom type are selected in order of low inter-atomic potential energy. (e) Grid sets to generate binding poses using an alignment algorithm are generated by combination of the Top-N grids and the docking atom types. (f) Binding pose is generated to align between grids and ligand atoms about all structures of conformers, and binding affinity about generated binding poses are calculated using PMFF.
Table 10.
The RMSD (Å) for Glide and PMFF for members of Glide test set. Top-ranked pose was determined by minimum intermolecular potential energy. Closest pose was determined by minimum RMSD.
| PDB ID | Ligand Atoms | Rot. bonds | Glide | PMFF | ||
|---|---|---|---|---|---|---|
| Top-Ranked pose | Closest pose | Top-Ranked pose | Closest pose | |||
| 121P | 46 | 8 | 1.57 | 0.71 | 2.94 | 2.18 |
| 1AAQ | 91 | 21 | 1.30 | 1.23 | 1.49 | 1.20 |
| 1ABE | 20 | 0 | 0.17 | 0.17 | 1.51 | 0.90 |
| 1ABF | 23 | 0 | 0.20 | 0.06 | 1.62 | 1.37 |
| 1ACJ | 29 | 0 | 0.28 | 0.14 | 2.36 | 1.78 |
| 1ACM | 22 | 7 | 0.29 | 0.24 | 2.01 | 1.73 |
| 1ACP | 16 | 4 | 1.02 | 0.51 | 1.89 | 1.26 |
| 1ADD | 33 | 2 | 0.53 | 0.42 | 2.33 | 1.66 |
| 1ADF | 68 | 11 | 11.25 | 2.29 | 3.22 | 2.15 |
| 1AHA | 15 | 0 | 0.11 | 0.07 | 1.75 | 1.70 |
| 1AKE | 83 | 16 | 3.35 | 2.06 | 3.84 | 3.71 |
| 1APB | 23 | 0 | 0.18 | 0.06 | 0.82 | 0.81 |
| 1APT | 84 | 21 | 0.58 | 0.58 | 3.17 | 2.66 |
| 1APU | 81 | 19 | 1.18 | 0.68 | 3.00 | 1.35 |
| 1APV | 80 | 18 | 1.47 | 1.47 | 0.60 | 0.60 |
| 1APW | 79 | 18 | 0.42 | 0.42 | 2.80 | 2.37 |
| 1ATL | 47 | 10 | 0.94 | 0.94 | 2.99 | 2.71 |
| 1AVD | 31 | 5 | 0.52 | 0.27 | 1.48 | 0.91 |
| 1B6K | 103 | 13 | 2.04 | 1.68 | 1.07 | 0.98 |
| 1B6L | 82 | 8 | 1.06 | 1.06 | 2.92 | 0.92 |
| 1B6M | 92 | 12 | 1.40 | 1.09 | 0.73 | 0.65 |
| 1BAP | 20 | 0 | 0.23 | 0.19 | 1.68 | 1.12 |
| 1BBP | 77 | 11 | 4.96 | 1.72 | 1.66 | 1.05 |
| 1BKM | 77 | 19 | 2.24 | 1.16 | 2.83 | 2.70 |
| 1BRA | 18 | 1 | 0.36 | 0.26 | 1.95 | 1.68 |
| 1BYB | 87 | 10 | 10.49 | 1.66 | 0.77 | 0.77 |
| 1C3I | 63 | 14 | 0.69 | 0.69 | 0.73 | 0.73 |
| 1C5P | 18 | 1 | 0.21 | 0.15 | 1.74 | 1.51 |
| 1C83 | 24 | 4 | 0.13 | 0.12 | 2.63 | 1.73 |
| 1C84 | 26 | 4 | 0.24 | 0.21 | 2.32 | 1.79 |
| 1C86 | 25 | 4 | 0.20 | 0.15 | 2.28 | 1.09 |
| 1C87 | 25 | 4 | 0.24 | 0.20 | 2.35 | 0.90 |
| 1C88 | 27 | 4 | 0.23 | 0.22 | 2.43 | 2.35 |
| 1C8K | 49 | 2 | 5.42 | 0.68 | 2.66 | 1.18 |
| 1CBS | 49 | 5 | 1.96 | 0.45 | 3.19 | 1.51 |
| 1CBX | 25 | 5 | 0.36 | 0.32 | 2.23 | 1.56 |
| 1CDE | 54 | 10 | 1.29 | 0.94 | 2.72 | 2.45 |
| 1CDG | 45 | 4 | 3.98 | 3.71 | 1.98 | 1.43 |
| 1COM | 28 | 4 | 3.64 | 2.83 | 1.99 | 1.37 |
| 1COY | 49 | 0 | 0.28 | 0.14 | 2.34 | 1.26 |
| 1CTR | 53 | 5 | 3.56 | 2.31 | 2.04 | 1.64 |
| 1CTT | 30 | 2 | 4.93 | 1.86 | 2.05 | 1.91 |
| 1D3D | 75 | 9 | 3.25 | 1.50 | 3.15 | 1.13 |
| 1D3P | 78 | 11 | 2.37 | 1.15 | 3.05 | 1.29 |
| 1DBB | 55 | 1 | 0.41 | 0.22 | 2.48 | 1.89 |
| 1DBJ | 51 | 0 | 0.20 | 0.18 | 0.61 | 0.51 |
| 1DBK | 49 | 0 | 0.47 | 0.41 | 2.40 | 1.73 |
| 1DBM | 66 | 6 | 1.97 | 0.48 | 2.69 | 2.22 |
| 1DDS | 53 | 10 | 1.91 | 1.91 | 2.20 | 0.85 |
| 1DHF | 49 | 10 | 6.48 | 3.58 | 2.34 | 1.04 |
| 1DID | 25 | 2 | 3.82 | 1.19 | 2.09 | 1.41 |
| 1DIE | 25 | 1 | 0.79 | 0.43 | 1.55 | 0.79 |
| 1DIH | 74 | 13 | 4.17 | 2.53 | 3.03 | 2.36 |
| 1DM2 | 29 | 0 | 0.67 | 0.52 | 2.05 | 1.54 |
| 1DOG | 25 | 1 | 3.74 | 0.28 | 1.61 | 1.45 |
| 1DR1 | 28 | 2 | 1.47 | 0.18 | 2.36 | 1.72 |
| 1DWB | 18 | 1 | 0.25 | 0.23 | 2.26 | 1.73 |
| 1E5I | 14 | 4 | 0.19 | 0.16 | 1.15 | 1.11 |
| 1EAP | 43 | 11 | 2.32 | 0.63 | 2.69 | 2.12 |
| 1EJN | 53 | 6 | 0.70 | 0.70 | 3.32 | 2.37 |
| 1ELA | 64 | 13 | 1.60 | 0.97 | 2.24 | 1.76 |
| 1ELB | 69 | 16 | 4.40 | 1.42 | 2.22 | 1.97 |
| 1ELC | 70 | 16 | 8.22 | 4.36 | 2.64 | 2.54 |
| 1ELD | 52 | 12 | 4.40 | 1.42 | 2.89 | 2.12 |
| 1ELE | 48 | 11 | 2.52 | 1.97 | 2.52 | 2.41 |
| 1EPB | 49 | 5 | 1.78 | 0.60 | 0.87 | 0.85 |
| 1EZQ | 66 | 11 | 1.66 | 1.10 | 3.07 | 1.81 |
| 1F0U | 66 | 11 | 1.59 | 1.16 | 3.12 | 3.12 |
| 1FEN | 50 | 4 | 0.66 | 0.66 | 1.35 | 1.05 |
| 1FH8 | 37 | 2 | 0.15 | 0.15 | 2.52 | 0.92 |
| 1FHD | 39 | 2 | 6.28 | 1.73 | 2.52 | 1.50 |
| 1FJS | 60 | 9 | 8.49 | 2.62 | 2.82 | 2.54 |
| 1FKG | 68 | 11 | 1.25 | 1.07 | 2.97 | 2.58 |
| 1FKI | 70 | 0 | 1.92 | 1.48 | 2.55 | 1.16 |
| 1FRP | 30 | 6 | 0.27 | 0.27 | 2.44 | 1.37 |
| 1GHB | 31 | 7 | 1.89 | 0.64 | 2.16 | 1.80 |
| 1GLQ | 51 | 15 | 0.29 | 0.29 | 2.72 | 1.13 |
| 1HBV | 95 | 17 | 3.05 | 3.05 | 3.17 | 0.79 |
| 1HDC | 89 | 6 | 0.58 | 0.37 | 1.64 | 1.43 |
| 1HGG | 81 | 12 | 2.10 | 0.64 | 1.13 | 1.12 |
| 1HGH | 42 | 7 | 0.28 | 0.28 | 1.82 | 1.16 |
| 1HGI | 47 | 9 | 0.28 | 0.28 | 2.48 | 1.55 |
| 1HGJ | 44 | 7 | 0.18 | 0.16 | 2.11 | 1.79 |
| 1HIH | 92 | 19 | 1.34 | 1.28 | 2.98 | 1.23 |
| 1HPS | 93 | 19 | 11.85 | 2.33 | 0.80 | 0.80 |
| 1HPX | 87 | 18 | 9.82 | 2.54 | 3.08 | 2.11 |
| 1HRI | 42 | 9 | 1.59 | 1.51 | 0.94 | 0.91 |
| 1HSG | 92 | 14 | 0.32 | 0.30 | 3.18 | 3.15 |
| 1HSL | 20 | 3 | 1.31 | 0.28 | 2.06 | 1.05 |
| 1HTF | 79 | 15 | 2.99 | 2.02 | 2.30 | 2.01 |
| 1HTI | 14 | 3 | 4.40 | 0.38 | 1.88 | 1.55 |
| 1HVR | 84 | 8 | 1.50 | 0.83 | 0.66 | 0.66 |
| 1HYT | 25 | 5 | 0.28 | 0.28 | 2.26 | 0.91 |
| 1IDA | 104 | 18 | 11.88 | 0.82 | 3.25 | 1.03 |
| 1IGJ | 81 | 3 | 1.30 | 0.67 | 2.84 | 2.62 |
| 1IMB | 27 | 2 | 0.89 | 0.73 | 2.47 | 1.99 |
| 1IVB | 25 | 4 | 4.97 | 0.45 | 2.27 | 1.90 |
| 1IVC | 24 | 3 | 1.94 | 1.52 | 2.29 | 1.69 |
| 1IVD | 24 | 4 | 0.72 | 0.66 | 1.98 | 1.33 |
| 1IVE | 24 | 3 | 2.61 | 0.89 | 2.24 | 2.02 |
| 1IVF | 36 | 6 | 0.53 | 0.50 | 2.40 | 1.45 |
| 1LAH | 22 | 4 | 0.13 | 0.13 | 1.97 | 1.30 |
| 1LCP | 23 | 3 | 1.98 | 1.48 | 1.72 | 1.26 |
| 1LDM | 8 | 1 | 0.30 | 0.30 | 1.65 | 1.43 |
| 1LMO | 57 | 8 | 0.93 | 0.42 | 2.74 | 2.12 |
| 1LNA | 41 | 9 | 0.95 | 0.70 | 2.49 | 1.61 |
| 1LST | 25 | 5 | 0.14 | 0.14 | 2.10 | 1.05 |
| 1MBI | 9 | 0 | 1.68 | 0.22 | 1.92 | 1.85 |
| 1MCR | 38 | 7 | 4.33 | 2.26 | 1.79 | 1.18 |
| 1MDR | 21 | 2 | 0.52 | 0.46 | 1.61 | 1.33 |
| 1MFE | 64 | 6 | 6.22 | 0.77 | 2.25 | 0.59 |
| 1MLD | 18 | 5 | 0.32 | 0.15 | 1.73 | 1.36 |
| 1MRG | 15 | 0 | 0.30 | 0.22 | 2.04 | 1.78 |
| 1MRK | 32 | 2 | 1.20 | 0.58 | 2.25 | 1.71 |
| 1MUP | 22 | 2 | 4.37 | 1.99 | 1.28 | 1.04 |
| 1NIS | 18 | 5 | 0.97 | 0.94 | 2.06 | 0.83 |
| 1NNB | 36 | 6 | 0.55 | 0.25 | 2.17 | 1.34 |
| 1NSC | 39 | 6 | 1.21 | 1.19 | 2.56 | 1.58 |
| 1NSD | 36 | 6 | 0.27 | 0.22 | 2.49 | 1.58 |
| 1ODW | 84 | 20 | 2.81 | 1.04 | 2.98 | 0.85 |
| 1PBD | 16 | 1 | 0.21 | 0.15 | 2.04 | 1.64 |
| 1PGP | 27 | 7 | 1.88 | 1.20 | 2.04 | 2.04 |
| 1PHA | 44 | 8 | 0.69 | 0.60 | 2.02 | 1.59 |
| 1PHD | 19 | 1 | 1.22 | 0.85 | 2.03 | 0.99 |
| 1PHF | 19 | 1 | 1.14 | 0.56 | 2.16 | 1.33 |
| 1PHG | 31 | 3 | 4.32 | 1.42 | 2.07 | 1.47 |
| 1PPI | 111 | 12 | 6.24 | 1.97 | 3.20 | 1.63 |
| 1PPK | 80 | 19 | 0.45 | 0.41 | 3.04 | 2.76 |
| 1PPL | 91 | 21 | 2.82 | 1.95 | 3.42 | 0.72 |
| 1PPM | 81 | 20 | 0.62 | 0.62 | 3.44 | 3.33 |
| 1PRO | 80 | 10 | 1.46 | 1.46 | 0.89 | 0.89 |
| 1RBP | 51 | 5 | 0.96 | 0.87 | 1.30 | 1.30 |
| 1RDS | 63 | 8 | 3.75 | 0.82 | 0.60 | 0.60 |
| 1RHL | 37 | 4 | 0.93 | 0.42 | 1.92 | 1.50 |
| 1RLS | 37 | 4 | 2.69 | 0.51 | 2.40 | 1.40 |
| 1RNE | 114 | 24 | 10.08 | 3.51 | 1.25 | 1.04 |
| 1RNT | 36 | 4 | 0.72 | 0.53 | 2.43 | 2.05 |
| 1ROB | 33 | 4 | 1.85 | 1.12 | 1.99 | 1.83 |
| 1SBG | 81 | 16 | 0.74 | 0.67 | 1.09 | 0.95 |
| 1SLT | 51 | 6 | 0.51 | 0.24 | 1.10 | 1.10 |
| 1SNC | 37 | 6 | 1.91 | 0.97 | 2.63 | 2.17 |
| 1STP | 31 | 5 | 0.59 | 0.33 | 2.39 | 1.79 |
| 1TDB | 33 | 4 | 1.46 | 0.99 | 2.62 | 1.50 |
| 1THY | 32 | 4 | 2.31 | 1.65 | 2.54 | 1.38 |
| 1TMN | 67 | 14 | 2.80 | 0.81 | 2.75 | 2.56 |
| 1TNG | 24 | 1 | 0.19 | 0.09 | 0.91 | 0.91 |
| 1TNH | 18 | 1 | 0.33 | 0.12 | 1.91 | 1.49 |
| 1TNI | 27 | 4 | 2.18 | 0.59 | 1.60 | 1.17 |
| 1TNJ | 21 | 2 | 0.35 | 0.24 | 1.99 | 1.28 |
| 1TNK | 24 | 3 | 0.87 | 0.69 | 1.71 | 0.91 |
| 1TNL | 22 | 1 | 0.23 | 0.11 | 1.85 | 1.16 |
| 1TPP | 27 | 4 | 1.12 | 0.39 | 2.25 | 2.01 |
| 1TYL | 20 | 2 | 1.06 | 0.41 | 1.66 | 1.14 |
| 1UKZ | 35 | 4 | 0.37 | 0.35 | 2.36 | 1.21 |
| 1ULB | 16 | 0 | 0.28 | 0.25 | 2.11 | 1.34 |
| 1WAP | 27 | 3 | 0.12 | 0.06 | 2.03 | 1.33 |
| 1XID | 20 | 2 | 4.30 | 1.14 | 2.00 | 1.87 |
| 1XIE | 23 | 1 | 3.86 | 0.22 | 1.91 | 1.00 |
| 2ADA | 33 | 2 | 0.53 | 0.37 | 2.34 | 2.10 |
| 2AK3 | 35 | 4 | 0.71 | 0.70 | 2.73 | 1.41 |
| 2CGR | 49 | 8 | 0.38 | 0.35 | 3.00 | 2.15 |
| 2CHT | 28 | 2 | 0.42 | 0.19 | 2.00 | 1.54 |
| 2CMD | 18 | 5 | 0.65 | 0.27 | 2.06 | 1.67 |
| 2CPP | 27 | 0 | 0.17 | 0.09 | 1.73 | 0.97 |
| 2CTC | 21 | 3 | 1.61 | 0.48 | 1.22 | 0.80 |
| 2DBL | 67 | 6 | 0.69 | 0.67 | 2.91 | 1.63 |
| 2GBP | 24 | 1 | 0.15 | 0.11 | 1.02 | 0.79 |
| 2IFB | 49 | 14 | 1.36 | 0.87 | 2.11 | 1.40 |
| 2LGS | 18 | 4 | 7.55 | 0.33 | 2.34 | 1.82 |
| 2MCP | 24 | 4 | 1.30 | 0.81 | 1.88 | 1.17 |
| 2PHH | 15 | 1 | 0.38 | 0.28 | 1.96 | 1.70 |
| 2PK4 | 22 | 5 | 0.86 | 0.58 | 1.41 | 1.21 |
| 2PLV | 59 | 15 | 1.88 | 0.77 | 2.59 | 2.59 |
| 2R04 | 51 | 10 | 0.80 | 0.64 | 3.35 | 1.34 |
| 2R07 | 45 | 8 | 0.48 | 0.48 | 2.43 | 2.05 |
| 2SIM | 36 | 6 | 0.92 | 0.30 | 2.28 | 1.66 |
| 2TPI | 38 | 7 | 0.49 | 0.48 | 1.13 | 1.13 |
| 2UPJ | 81 | 15 | 3.65 | 2.85 | 1.58 | 1.17 |
| 2XIS | 22 | 4 | 0.85 | 0.37 | 2.03 | 1.22 |
| 2YPI | 11 | 3 | 0.31 | 0.20 | 1.98 | 1.42 |
| 3CLA | 32 | 7 | 8.51 | 3.46 | 1.84 | 1.10 |
| 3CPA | 30 | 6 | 2.40 | 0.66 | 1.01 | 0.77 |
| 3DFR | 53 | 10 | 0.87 | 0.38 | 0.95 | 0.95 |
| 3HVT | 34 | 1 | 0.77 | 0.62 | 1.25 | 1.15 |
| 3MTH | 19 | 2 | 5.48 | 0.21 | 2.28 | 1.71 |
| 3PTB | 18 | 1 | 0.27 | 0.20 | 1.91 | 1.78 |
| 3TPI | 38 | 7 | 0.49 | 0.23 | 1.83 | 1.54 |
| 4AAH | 27 | 3 | 0.30 | 0.14 | 2.19 | 1.34 |
| 4CTS | 11 | 3 | 0.44 | 0.19 | 2.18 | 1.71 |
| 4DFR | 53 | 10 | 1.12 | 0.92 | 2.09 | 1.04 |
| 4FAB | 35 | 2 | 4.50 | 0.69 | 2.20 | 1.97 |
| 4FBP | 35 | 4 | 0.56 | 0.56 | 2.51 | 1.90 |
| 4FXN | 50 | 7 | 0.44 | 0.44 | 2.41 | 1.04 |
| 4HMG | 39 | 6 | 0.78 | 0.72 | 1.86 | 1.80 |
| 4PHV | 88 | 14 | 0.38 | 0.38 | 0.79 | 0.65 |
| 4TIM | 16 | 4 | 1.32 | 0.97 | 2.03 | 1.25 |
| 4TPI | 35 | 6 | 0.51 | 0.23 | 1.99 | 0.92 |
| 4TS1 | 24 | 3 | 0.85 | 0.57 | 2.56 | 1.85 |
| 5ABP | 24 | 1 | 0.21 | 0.10 | 1.51 | 1.41 |
| 5CPP | 25 | 0 | 0.59 | 0.10 | 1.55 | 1.21 |
| 5CTS | 11 | 3 | 0.28 | 0.17 | 1.62 | 1.18 |
| 5P2P | 69 | 21 | 1.82 | 1.34 | 3.10 | 2.53 |
| 6ABP | 20 | 0 | 0.40 | 0.14 | 1.99 | 1.06 |
| 6CPA | 58 | 14 | 4.58 | 1.37 | 2.90 | 2.77 |
| 6RNT | 35 | 4 | 2.22 | 2.22 | 2.69 | 1.84 |
| 6TIM | 17 | 4 | 1.73 | 0.25 | 2.28 | 2.02 |
| 6TMN | 63 | 16 | 2.66 | 1.26 | 2.95 | 2.75 |
| 7ABP | 23 | 0 | 0.20 | 0.06 | 0.83 | 0.83 |
| 7CPA | 74 | 17 | 4.14 | 2.41 | 2.99 | 2.64 |
| 7CPP | 18 | 0 | 0.61 | 0.61 | 1.69 | 0.96 |
| 8ABP | 24 | 1 | 0.22 | 0.13 | 1.00 | 1.00 |
| 8ATC | 23 | 7 | 0.37 | 0.34 | 2.17 | 1.70 |
| 8GCH | 44 | 9 | 0.30 | 0.30 | 2.16 | 1.77 |
| 9ABP | 24 | 1 | 0.15 | 0.13 | 1.37 | 1.31 |
| Average | 1.86 | 0.82 | 2.12 | 1.52 | ||
| Standard deviation | 2.31 | 0.79 | 0.67 | 0.58 | ||
3. Result and Discussion
3.1. Calculation of Conformer Energy Difference for Small Molecules
To examine the suitability of the intramolecular potential energy function, the conformer energy difference was calculated using MM3 and PMFF for 17 organic compounds (Table 8) and 133 organic compounds (Table S1), and the difference in conformer energy was compared between MM3 and the PMFF. According to this measure, the m-PEOE charge model is suitable for use with the intramolecular potential energy. The average absolute error between the experiment and prediction was 0.46±0.43 kcal/mol in MM3 and 0.56±0.54 kcal/mol in the PMFF, and that between the quantum mechanical data and prediction was 1.93±1.73 kcal/mol in MM3 and 1.70±1.36 kcal/mol in the PMFF.
The reason for the suitability and accuracy is that the m-PEOE charge model was developed to be focused on the dipole and quadrupole moment data. In general, an accurate dipole or quadrupole moment calculation depends on an accurate molecular structure and atomic partial charge. If the types of atoms or chemical bonds are the same but the surrounding atoms and chemical bonds are different, the atomic partial charge will be slightly different, which affects the charge distribution of the molecule. The m-PEOE charge model can explain the charge distribution of the molecule according to the chemical bond and atom type; therefore, it can examine not only the interactions between the two target systems using the intermolecular potential energy but also the molecular stability using the intramolecular potential energy.
3.2. Molecular Docking Simulation
If the intermolecular PEFs express the energy-stable protein-ligand complex structure well, the structure calculated using a docking simulation is the same as the experimental crystal structure, and the RMSD, which expresses the difference between two structures, is zero.
First, to evaluate the accuracy of the initial binding pose determination, the geometries of co-crystallized ligands were reproduced through a docking simulation taken from a set of 214 PDB complexes. The RMSD between the experimental crystal structure and the reproduced structure was compared between Glide and the PMFF. The scoring function in Glide, which is used to evaluate the similarity with the experimental structure, consists of a weighted potential energy function in the OPLS. In the PMFF, the scoring function was replaced with the potential energy for each complex. Table 9 describes the distribution of the rotatable bond and the number of conformers for 214 ligands. A rotatable bond for a ligand was distributed from zero to 24. The number of conformers for a ligand was distributed from 1 to 36982. The average RMSD for the top-ranked pose was smaller in the ligand with a greater number of rotatable bonds. Because the conformer, whose absolute potential energy difference between the generated conformer and the experimental structure is lower than 1.00 kcal/mol, was removed in the PMFF, the number of conformers was not related to the number of rotatable bonds. The average RMSD for the top-ranked pose increases with the number of conformers. Table 10 describes the docking simulation results for the 214 PDB complexes. The average of the RMSD for the top-ranked binding pose was 1.86±2.31 Å in Glide and 2.12±0.67 Å in the PMFF. The average of the RMSD for the closest binding pose for a co-crystallized ligand in each complex was 0.82±0.79 Å in Glide and 1.53±0.58 Å in the PMFF.
Table 9.
Distribution of number of rotatable bonds and conformers for molecular docking simulation on 214 PDB complexes.
| Distribution of number of rotatable bonds | |||
|---|---|---|---|
| No. of rotatable bonds | No. of cases | Average RMSD Top-ranked pose (Å) |
|
| Glide | PMFF | ||
| 0-3 | 73 | 1.28 | 1.90 |
| 4-7 | 70 | 1.40 | 2.11 |
| 8- | 70 | 2.91 | 1.71 |
| Distribution of number of conformers | |||
| No. of conformer | No. of cases | Average RMSD Top-ranked pose (Å) |
|
| Glide | PMFF | ||
| 1 | 90 | 1.70 | 1.99 |
| 2-50 | 94 | 1.76 | 2.11 |
| 51- | 30 | 2.67 | 2.54 |
The performance of the docking simulation was described based on the performance of the scoring function and the binding pose search algorithm. The scoring function is considered more accurate because the RMSD for a top-ranked binding pose is small. In addition, the binding pose search algorithm is considered more accurate because the RMSD for the closest binding pose for an X-ray structure is also small. To evaluate the performance of a force field, not only the performance of the scoring function but also the difference in RMSD between the top-ranked and closest binding pose is important. Although the average RMSD for the top-ranked binding pose in the PMFF is bigger than that in Glide, the average difference in RMSD between the top-ranked and closest binding poses in the PMFF was smaller than that in Glide. The standard deviation of the RMSD is related to the generality of the potential energy function. The standard deviation of the RMSD in the PMFF is not only smaller than that of Glide but is also less than 1 Å. The results for Glide show 16 PDB complexes with the RMSD for a top-ranked binding pose of greater than 5Å. According to these results, if an accurate binding pose can be generated in a binding pose search algorithm, the calculated binding poses are accurately evaluated by the scoring function used in the PMFF and have greater reliability. Therefore, the PMFF can be expressed well in a biological system.
A comparison of computation time between Glide and our algorithm is shown in Table S1. The calculation time for our algorithm is longer than the calculation time for Glide because our algorithm was dependent on the number of conformers of ligand. If the algorithm of determination of the rotatable bond is more efficient, such as not including hydrogen in methyl group, calculation time will be reduced.
3.3. Verification of the Combination between PMFF and GSFED Models
To confirm the suitability of the combination of the PMFF and GSFED models50, preliminary studies using the water-octanol partition coefficients of various peptide lengths and 193 natural peptides were performed to calculate and compare with the experiment data. The structures of the peptides were calculated using the PMFF, and the majority of parameters used in GSFED, shown in eq 13, are from the PMFF. The mean absolute error and root mean square error for neutral peptides were 1.615 log units and 2.140 in SM5.42R and 0.322 log units and 1.468 in GSFED. Therefore, the combination between PMFF and GSFED models is well described for a biological system.
4. Conclusions
This paper describes a continuous 25 year effort to develop a force field for the simulation of protein and biological molecules. The force field is the result of tremendous effort of many different people and a long period of time. As the term physics-based molecular force field suggests, the force field is well balanced for representing inter- and intra-interactions as well as the solvation effect. The performance of the PMFF was validated by comparing the difference in conformer energy, applying a docking simulation on 214 PDB complexes, and calculating the octanol-water partition coefficient for neutral peptides. The test results prove that the PMFF predicts the molecular structure more reliably and interprets the biological phenomena extremely accurately. It is therefore suitable for describing biological phenomena.
A PMFF-based graphic user interface program for molecular structure optimization, a single point energy calculation, solvation-free energy calculation, and molecular docking simulation is available on GitHub (github.com/PMFF/GUI).
Supplementary Material
ACKNOWLEDGMENT
This study was supported by BMDRC. Kyoung Tai No thanks Harold A. Scheraga for waiting 25 years for this study. We thank Late Dr. Mu Shik Jhon for many helpful discussions. H.A.S. thanks the National Institutes of Health (GM-14312) for the support.
Footnotes
ASSOCIATED CONTENT
Supporting Information. Calculation time of molecular docking simulation for 5 protein-ligand complexes using Glide and PMFF; Distribution of the 133 organic molecules in the principle component space; Conformer energy difference (Kcal/mol) calculated with DFT B3LYP/6–31G**, MM3, and PMFF
The authors declare no competing financial interest.
REFERENCES
- 1.Momany FA; McGuire RF; Burgess AW; Scheraga HA, Energy parameters in polypeptides. VII. Geometric parameters, partial atomic charges, nonbonded interactions, hydrogen bond interactions, and intrinsic torsional potentials for the naturally occurring amino acids. J. Phys. Chem 1975, 79, 2361–2381. [Google Scholar]
- 2.Nemethy G; Pottle MS; Scheraga HA, Energy parameters in polypeptides. 9. Updating of geometrical parameters, nonbonded interactions, and hydrogen bond interactions for the naturally occurring amino acids. J. Phys. Chem 1983, 87, 1883–1887. [Google Scholar]
- 3.Sippl MJ; Nemethy G; Scheraga HA, Intermolecular potentials from crystal data. 6. Determination of empirical potentials for O-H…O=C hydrogen bonds from packing configurations. J. Phys. Chem 1984, 88, 6231–6233. [Google Scholar]
- 4.Nemethy G; Gibson KD; Palmer KA; Yoon CN; Paterlini G; Zagari A; Rumsey S; Scheraga HA, Energy parameters in polypeptides. 10. Improved geometrical parameters and nonbonded interactions for use in the ECEPP/3 algorithm, with application to proline-containing peptides. J. Phys. Chem 1992, 96, 6472–6484. [Google Scholar]
- 5.Arnautova YA; Jagielska A; Scheraga HA, A New Force Field (ECEPP-05) for peptides, Proteins, and Organic Molecules. J. Phys. Chem 2006, 110, 5025–5044. [DOI] [PubMed] [Google Scholar]
- 6.Allinger NL; Yuh YH; Lii JH, Molecular mechanics. The MM3 force field for hydrocarbons. 1. Journal of the American Chemical Society 1989, 111, 8551–8566. [Google Scholar]
- 7.Lii JH; Allinger NL, Molecular mechanics. The MM3 force field for hydrocarbons. 2. Vibrational frequencies and thermodynamics. Journal of the American Chemical Society 1989, 111, 8566–8575. [Google Scholar]
- 8.Lii JH; Allinger NL, Molecular mechanics. The MM3 force field for hydrocarbons. 3. The van der Waals’ potentials and crystal data for aliphatic and aromatic hydrocarbons. Journal of the American Chemical Society 1989, 111, 8576–8582. [Google Scholar]
- 9.Brooks BR; Bruccoleri RE; Olafson BD; States DJ; Swaminathan S; Karplus M, CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem 1983, 4, 187–217. [Google Scholar]
- 10.Vanommeslaeghe K; Hatcher E; Acharya C; Kundu S; Zhong S; Shim J; Darian E; Guvench O; Lopes P; Vorobyov I; Mackerell AD Jr., CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J Comput Chem 2010, 31, 671–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Brooks BR; Brooks CL III; Mackerell AD Jr.; Nilsson L; Petrella RJ; Roux B; Won Y; Archontis G; Bartels C; Boresch S; Caflisch A; Caves L; Cui Q; Dinner AR; Feig M; Fischer S; Gao J; Hodoscek M; Im W; Kuczera K; Lazaridis T; Ma J; Ovchinnikov V; Paci E; Pastor RW; Post CB; Pu JZ; Schaefer M; Tidor B; Venable RM; Woodcock HL; Wu X; Yang W; York DM; Karplus M, CHARMM: The biomolecular simulation program. Journal of Computational Chemistry 2009, 30, 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pastor RW; MacKerell AD, Development of the CHARMM Force Field for Lipids. The Journal of Physical Chemistry Letters 2011, 2, 1526–1532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vanommeslaeghe K; MacKerell AD, Automation of the CHARMM General Force Field (CGenFF) I: Bond Perception and Atom Typing. Journal of Chemical Information and Modeling 2012, 52, 3144–3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Vanommeslaeghe K; Raman EP; MacKerell AD, Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges. Journal of Chemical Information and Modeling 2012, 52, 3155–3168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Patel S; Brooks CL III, CHARMM fluctuating charge force field for proteins: I parameterization and application to bulk organic liquid simulations. Journal of Computational Chemistry 2004, 25, 1–16. [DOI] [PubMed] [Google Scholar]
- 16.Patel S; Mackerell AD Jr.; Brooks CL III, CHARMM fluctuating charge force field for proteins: II Protein/solvent properties from molecular dynamics simulations using a nonadditive electrostatic model. Journal of Computational Chemistry 2004, 25, 1504–1514. [DOI] [PubMed] [Google Scholar]
- 17.Guvench O; Hatcher E; Venable RM; Pastor RW; MacKerell AD, CHARMM Additive All-Atom Force Field for Glycosidic Linkages between Hexopyranoses. Journal of Chemical Theory and Computation 2009, 5, 2353–2370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Weiner SJ; Kollman PA; Case DA; Singh UC; Ghio C; Alagona G; Profeta S; Weiner P, A new force field for molecular mechanical simulation of nucleic acids and proteins. Journal of the American Chemical Society 1984, 106, 765–784. [Google Scholar]
- 19.Cornell WD; Cieplak P; Bayly CI; Gould IR; Merz KM; Ferguson DM; Spellmeyer DC; Fox T; Caldwell JW; Kollman PA, A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Moleculs. J. Am. Chem. Soc 1995, 117, 5179–5197. [Google Scholar]
- 20.Wang J; Wolf RM; Caldwell JW; Kollman PA; Case DA, Development and testing of a general amber force field. Journal of Computational Chemistry 2004, 25, 1157–1174. [DOI] [PubMed] [Google Scholar]
- 21.Homeyer N; Horn AHC; Lanig H; Sticht H, AMBER force-field parameters for phosphorylated amino acids in different protonation states: phosphoserine, phosphothreonine, phosphotyrosine, and phosphohistidine. Journal of Molecular Modeling 2006, 12, 281–289. [DOI] [PubMed] [Google Scholar]
- 22.Peters MB; Yang Y; Wang B; Füsti-Molnár L; Weaver MN; Merz KM, Structural Survey of Zinc-Containing Proteins and Development of the Zinc AMBER Force Field (ZAFF). Journal of Chemical Theory and Computation 2010, 6, 2935–2947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dickson CJ; Rosso L; Betz RM; Walker RC; Gould IR, GAFFlipid: a General Amber Force Field for the accurate molecular dynamics simulation of phospholipid. Soft Matter 2012, 8, 9617–9627. [Google Scholar]
- 24.Halgren TA, Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94. Journal of Computational Chemistry 1996, 17, 490–519. [Google Scholar]
- 25.Halgren TA, Merck molecular force field. II. MMFF94 van der Waals and electrostatic parameters for intermolecular interactions. Journal of Computational Chemistry 1996, 17, 520–552. [Google Scholar]
- 26.Halgren TA, Merck molecular force field. III. Molecular geometries and vibrational frequencies for MMFF94. Journal of Computational Chemistry 1996, 17, 553–586. [Google Scholar]
- 27.Halgren TA; Nachbar RB, Merck molecular force field. IV. conformational energies and geometries for MMFF94. Journal of Computational Chemistry 1996, 17, 587–615. [Google Scholar]
- 28.Halgren TA, Merck molecular force field. V. Extension of MMFF94 using experimental data, additional computational data, and empirical rules. Journal of Computational Chemistry 1996, 17, 616–641. [Google Scholar]
- 29.Maple JR; Dinur U; Hagler AT, Derivation of force fields for molecular mechanics and dynamics from ab initio energy surfaces. Proceedings of the National Academy of Sciences 1988, 85, 5350–5354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Jorgensen WL; Tirado-Rives J, The OPLS Potential Functions for Proteins. Energy Minimizations for Crystals of Cyclic Peptides and Crambin. J. Am. Chem. Soc 1988, 110, 1657–1666. [DOI] [PubMed] [Google Scholar]
- 31.Harder E; Damm W; Maple J; Wu C; Reboul M; Xiang JY; Wang L; Lupyan D; Dahlgren MK; Knight JL; Kaus JW; Cerutti DS; Krilov G; Jorgensen WL; Abel R; Friesner RA, OPLS3: A Force Field Providing Broad Coverage of Drug-like Small Molecules and Proteins. Journal of Chemical Theory and Computation 2016, 12, 281–296. [DOI] [PubMed] [Google Scholar]
- 32.Damm W; Frontera A; Tirado–Rives J; Jorgensen WL, OPLS all-atom force field for carbohydrates. Journal of Computational Chemistry 1997, 18, 1955–1970. [Google Scholar]
- 33.Hagler AT; Huler E; Lifson S, Energy functions for peptides and proteins. I. Derivation of a consistent force field including the hydrogen bond from amide crystals. J. Am. Chem. Soc 1974, 96, 5319–5327. [DOI] [PubMed] [Google Scholar]
- 34.Hagler AT; Lifson S, Energy functions for peptides and proteins. II. Amide hydrogen bond and calculation of amide crystal properties. J. Am. Chem. Soc 1974, 96, 5327–5335. [DOI] [PubMed] [Google Scholar]
- 35.Jorgensen WL, Transferable Intermolecular Potential Functions for Water, Alcohols, and Ethers. Application to Liquid Water. J. Am. Chem. Soc 1981, 103, 335–340. [Google Scholar]
- 36.Klamt A, Conductor-like Screening Model for Real Solvents: A New Approach to the Quantitative Calculation of Solvation Phenomena. The Journal of Physical Chemistry 1995, 99, 2224–2235. [Google Scholar]
- 37.Klamt A; Schüürmann G, COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. Journal of the Chemical Society, Perkin Transactions 2 1993, 799–805. [Google Scholar]
- 38.Giesen DJ; Gu MZ; Cramer CJ; Truhlar DG, A Universal Organic Solvation Model. The Journal of Organic Chemistry 2000, 65, 5886–5886. [DOI] [PubMed] [Google Scholar]
- 39.Li J; Zhu T; Hawkins GD; Winget P; Liotard DA; Cramer CJ; Truhlar DG, Extension of the platform of applicability of the SM5.42R universal solvation model. Theoretical Chemistry Accounts 1999, 103, 9–63. [Google Scholar]
- 40.Cramer CJ; Truhlar DG, A Universal Approach to Solvation Modeling. Accounts of Chemical Research 2008, 41, 760–768. [DOI] [PubMed] [Google Scholar]
- 41.No KT; Grant JA; Scheraga HA, Determination of net atomic charges using a modified partial equalization of orbital electronegativity method. 1. Application to neutral molecules as models for polypeptides. The Journal of Physical Chemistry 1990, 94, 4732–4739. [Google Scholar]
- 42.No KT; Grant JA; Jhon MS; Scheraga HA, Determination of net atomic charges using a modified partial equalization of orbital electronegativity method. 2. Application to ionic and aromatic molecules as models for polypeptides. The Journal of Physical Chemistry 1990, 94, 4740–4746. [Google Scholar]
- 43.Park JM; No KT; Jhon MS; Scheraga HA, Determination of net atomic charges using a modified partial equalization of orbital electronegativity method. III: application to halogenated and aromatic molecules. J. Comput. Chem 1993, 14, 1482–1490. [Google Scholar]
- 44.Park JM; Kwon OY; No KT; Jhon MS; Scheraga HA, Determination of net atomic charges using a modified partial equalization of orbital electronegativity method. IV. Application to hypervalent sulfur- and phosphorus-containing molecules. Journal of Computational Chemistry 1995, 16, 1011–1026. [Google Scholar]
- 45.Suk JE; No KT, Determination of net atomic charges using a modified partial equalization of orbital electronegativity method. V. Application to silicon-containing organic molecules and zeolites. Bull. Korean. Chem. Soc 1995, 16, 915–923. [Google Scholar]
- 46.Scott RA; Scheraga HA, Conformational Analysis of Macromolecules. III. Helical Structures of Polyglycine and Poly‐L‐Alanine. The Journal of Chemical Physics 1966, 45, 2091–2101. [Google Scholar]
- 47.No KT; Cho KH; Jhon MS; Scheraga HA, An empirical method to calculate average molecular polarizabilities from the dependence of effective atomic polarizabilities on net atomic charge. Journal of the American Chemical Society 1993, 115, 2005–2014. [Google Scholar]
- 48.No KT; Kwon OY; Kim SY; Cho KH; Yoon CN; Kang YK; Gibson KD; Jhon MS; Scheraga HA, Determination of Nonbonded Potential Parameters for Peptides. The Journal of Physical Chemistry 1995, 99, 13019–13027. [Google Scholar]
- 49.No KT; Kwon OY; Kim SY; Jhon MS; Scheraga HA, A Simple Functional Representation of Angular-Dependent Hydrogen-Bonded Systems. 1. Amide, Carboxylic Acid, and Amide-Carboxylic Acid Pairs. The Journal of Physical Chemistry 1995, 99, 3478–3486. [Google Scholar]
- 50.Lee SH; Cho K-H; Kang Y-M; Scheraga HA; No KT, A generalized G-SFED continuum solvation free energy calculation model. Proceedings of the National Academy of Sciences 2013, 110, E662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ma S; Hwang SB; Lee SH; William E. Acree J; No KT, Incorporation of Hydrogen Bond Angle Dependency into the Generalized Solvation Free Energy Density Model. J. Chem. Inf. Model 2018, 58, 761–772. [DOI] [PubMed] [Google Scholar]
- 52.Miller KJ; Savchik JA, A new empirical method to calculate average molecular polarizabilities. Journal of the American Chemical Society 1979, 101, 7206–7213. [Google Scholar]
- 53.Kang YK; Jhon MS, Additivity of atomic static polarizabilities and dispersion coefficients. Theoretica chimica acta 1982, 61, 41–48. [Google Scholar]
- 54.Israelachvili J In Intermolecular and Surface Forces; Academic Press: New York, 1991; Chapter 11. [Google Scholar]
- 55.Steinbeck C; Han YQ; Kuhn S; Horlacher O; Luttmann E; Willighagen E, The Chemistry Development Kit (CDK): An open-source Java library for chemo- and bioinformatics. Journal of Chemical Information and Computer Sciences 2003, 43, 493–500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Schrödinger Release 2018-3: Maestro, Schrödinger, LLC, New York, NY, 2018. [Google Scholar]
- 57.Goldstein AA, Cauchy’s method of minimization. Numerische Mathematik 1962, 4, 146–150. [Google Scholar]
- 58.Kiefer J, Sequential minimax search for a maximum. Proceedings of the American Mathematical Society 1953, 4, 502–506. [Google Scholar]
- 59.Kim S; Thiessen PA; Bolton EE; Chen J; Fu G; Gindulyte A; Han L; He J; He S; Shoemaker BA; Wang J; Yu B; Zhang J; Bryant SH, PubChem Substance and Compound databases. Nucleic Acids Research 2016, 44, D1202–D1213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Gundertofte K; Liljefors T; Norrby P.-o.; Pettersson I, A comparison of conformational energies calculated by several molecular mechanics methods. Journal of Computational Chemistry 1996, 17, 429–449. [Google Scholar]
- 61.Berman HM; Westbrook J; Feng Z; Gilliland G; Bhat TN; Weissig H; Shindyalov IN; Bourne PE, The Protein Data Bank. Nucleic Acids Research 2000, 28, 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Daylight 4. SMART-a language for describing molecular patterns. http://www.daylight.com/dayhtml/doc/theory/theory.smarts.html
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


