Epidemic spreading in random rectangular networks

Abstract

The use of network theory to model disease propagation on populations introduces important elements of reality to the classical epidemiological models. The use of random geometric graphs (RGGs) is one of such network models that allows for the consideration of spatial properties on disease propagation. In certain real-world scenarios—like in the analysis of a disease propagating through plants—the shape of the plots and fields where the host of the disease is located may play a fundamental role in the propagation dynamics. Here we consider a generalization of the RGG to account for the variation of the shape of the plots or fields where the hosts of a disease are allocated. We consider a disease propagation taking place on the nodes of a random rectangular graph and we consider a lower bound for the epidemic threshold of a susceptible-infected-susceptible model or a susceptible-infected-recovered model on these networks. Using extensive numerical simulations and based on our analytical results we conclude that (ceteris paribus) the elongation of the plot or field in which the nodes are distributed makes the network more resilient to the propagation of a disease due to the fact that the epidemic threshold increases with the elongation of the rectangle. These results agree with accumulated empirical evidence and simulation results about the propagation of diseases on plants in plots or fields of the same area and different shapes.

I. INTRODUCTION

The study of epidemiological models on networks is one of the areas that has observed a major development in the application of network theory to real-world problems [1]. The discovery of the fact that networks with fat-tailed degree distributions do not display an epidemic threshold in the asymptotic limit is a relevant example of how the connectivity pattern of interacting agents can dramatically change the course of an epidemic [2,3]. The use of network theory in epidemiological models provides a way to incorporate the individual-level heterogeneity necessary for the mechanistic understanding of the spread of infectious disease. These characteristics are very attractive for the application of network epidemiological models in ecology on the different spatial and temporal scales.

Although there have been many successful applications of network theory to human and animal epidemiology, the situation is a little less developed for epidemics on plants. Ten years ago Jeger et al. [4] recognized the relatively low use of network theory for studying plant diseases. Since then, more theoretical developments have been presented in the literature. These models include the important description of the geometric constraints in which the pathogen is spreading as well as stochasticity and several sources of heterogeneity in the transmission of infection [5–8].

In order to consider spatial effects in the transmission of diseases it is possible to consider spatial networks that treat interactions as a continuous variable that decays with increasing distance or by distributing randomly and independently a set of vertices on the Euclidean plane to represent the relative spatial location of individual hosts or habitat patches. The second kind of model is based on random geometric graphs (RGGs) [9–12], in which each node is randomly assigned geometric coordinates and then two nodes are connected if the (Euclidean) distance between them is smaller than or equal to a certain threshold $r$. Random geometric graphs have found applications to model populations which are geographically constrained in a certain region [13–18], which offer many valuable features over other types of random graphs [19,20]. Brooks et al. [21] have used RGGs to model the interactions between the anther smut fungus and fire pink using temporal data that spans 7 years of field studies. They have concluded that the use of spatially explicit network models can yield important insights into how heterogeneous structure promotes the persistence of species in natural landscapes.

When studying the propagation of diseases in plants there is an important factor that needs to be taken into account. It is obvious that plants are not as mobile as humans and animals; thus they reach lower levels of mixing in a given population due to mobility. The immediate consequence of this lack of mobility is the fact that the shape of the plot or field in which the plants are distributed may significantly affect disease dynamics. In fact, there is both empirical and theoretical evidence that supports this hypothesis [22–30]. In general, it has been suggested that square plots and fields favored higher spreading of plant diseases than elongated ones of the same area [22–25]. We should make here some remarks about the shape of plots in different scenarios. First, we should mention the experimental plots for different crops. In those cases, the size and shape of the plots are controlled typically to estimate crop yields. Thus, they are typically of almost perfect square or rectangular shapes (see, for instance, Ref. [24]). The second scenario is when crops are cultivated in country fields. In these cases the sizes and shapes of the fields depends on the geographical conditions of the region. However, in general these fields can be grossly approximated as rectanglelike or squarelike on the basis that they are more or less elongated. Such shapes are also thought to facilitate the mechanized work on the fields more than irregular shapes. Finally, there is a third scenario in which plants are growing naturally in a given environment. In these cases it is obvious that the distribution could be quite irregular and acquiring many different shapes. However, when studying the influence of the shape of these natural fields on the propagation of an epidemic it is typical to approximate their shapes to rectangular or square ones, as it is well illustrated for the case study of the spatial and spatiotemporal pattern analysis of coconut lethal yellowing in Mozambique [26].

It is important to remark that the area of the field also plays a fundamental role, with larger plots and fields favoring more the spreading of diseases [27,29,30]. Also, the orientation of elongated fields may affect the disease propagation with orientations perpendicular to prevalent winds suppressing epidemic progression [23,25]. All in all, for plots and fields of the same area and orientation there is empirical and theoretical evidence that elongated shapes decrease the impact of epidemics on plant populations. It is worth noting that the theoretical models [28–30] used in the previously mentioned studies do not use network theory as a tool for the study of epidemic spreading.

In this work we consider a generalization of the RGG known as the random rectangular graph (RRG) model which has been recently introduced [31]. In this case, the nodes are uniformly and independently distributed on a unit rectangle of given side lengths. Thus, we simulate plots and fields of the same size in which we can analyze the effect of elongation on epidemic spreading on plants. When both sides are of the same length we recover the RGG which accounts for squared shapes. It is worth mentioning that previous models have considered the variation of the shape for the region where the nodes are distributed in the RGG. In some of these works more general boundaries, such as right prisms and fractal regions have been considered in particular for analyzing the connectivity of the resulting RGGs [32–34]. In this work we consider a susceptible-infected-susceptible (SIS) model on the RRGs to describe the propagation of a disease on a plant population on a field of varied rectangular shapes. We obtain analytical and simulation results that support the empirical observations and theoretical evidence about the fact that (ceteris paribus) elongated plots and fields decrease significantly the propagation of diseases on plants. In particular, our results show that the epidemic threshold is significantly displaced to the right with the elongation of the rectangle, which indicates that the number of infected plants necessary to produce an epidemic grows with the rectangle elongation. Finally, we stress that in classical, noninteracting systems—either homogeneous or heterogeneous—the resemblance of SIS and susceptible-infected-recovered (SIR) epidemiological models translates into a strong mathematical symmetry between them that leads to identical expressions for the epidemic thresholds under mean-field approaches (i.e., when neglecting the effects of dynamical correlations). We therefore anticipate that our results will be also valid in a SIR framework, which as a matter of fact could be more relevant for plant diseases.

II. RANDOM RECTANGULAR GRAPHS

Here we consider a population, e.g., plants, represented by the nodes of a graph for which the edges represent the interaction between the individuals in the population. Then, our representation consists of simple graphs $G=(V,E)$ defined by a set of $n$ nodes $V$ and a set of $m$ edges $E=\left\{\right(u,v\left)\right|u,v\in V\}$ between the nodes. These graphs are unweighted and undirected, with no self-loops (edges from a node to itself) and no multiple edges. The matrix $A=\left(A_{ij}\right)$, called the adjacency matrix of the graph, has the following entries:

$$A_{ij}=\left\{\begin{array}{cc}1\hfill & \text{if}(i,j)\in E,\hfill \\ 0\hfill & \text{otherwise,}\hfill \end{array}\right.\forall i,j\in V.$$

Once the structure of a network is defined, the adjacency matrix is not changed during the process of disease propagation to be modeled on the nodes and edges of that network. That is, the network topology is static and not changing with time. The degree $k_i$ of the node $i$ is the number of edges incident to it, equivalently $k_i={\sum }_j{A}_{ij}$. Let $G=(V,E)$ be a simple connected graph and let ${\lambda }_1>{\lambda }_2\ge \cdots \ge {\lambda }_n$ be the eigenvalues of its adjacency matrix. The eigenvalue ${\lambda }_1$ is known as the principal eigenvalue of the adjacency matrix, also as the Perron-Frobenius eigenvalue. Below we show that ${\lambda }_1$ is key to determining the conditions of invasion.

When modeling epidemic disease propagation on plants, Brooks et al. [21] have considered the plants as the nodes of an RGG, in which the $n$ nodes are points uniformly and independently distributed in the unit square ${[0,1]}^2$ [9]. Then, two points are connected by an edge if their Euclidean distance is at most $r$, which is a given fixed number known as the connection radius. This connection radius indicates the maximum distance at which a disease can be transmitted from one plant to its nearest neighbors (see Ref. [21]).

Here we use an extension of the RGG to consider a rectangle, $[0,a]\times [0,b]$, where $a,b\in \mathbb{R}$ and $a\ge b$. Due to the accumulated evidence that reveals the importance of the plot or field size on disease propagation, we keep the area of the rectangle fixed in order to analyze only the influence of the rectangle elongation on the disease spreading. Consequently, we consider unit rectangles of the form $\left[0,a\right]\times \left[0,a^{-1}\right]$. The rest of the construction of an RRG is similar to that of an RGG. That is, we distribute uniformly and independently $n$ points in the unit rectangle $[0,a]\times [0,a^{-1}]$ and then connect two points by an edge if their Euclidean distance is at most $r$. Obviously, when $a=1$ the rectangle $[0,a]\times [0,a^{-1}]$ is simply the unit square ${[0,1]}^2$, which means that the $RRG$ becomes the classical $RGG$ [31].

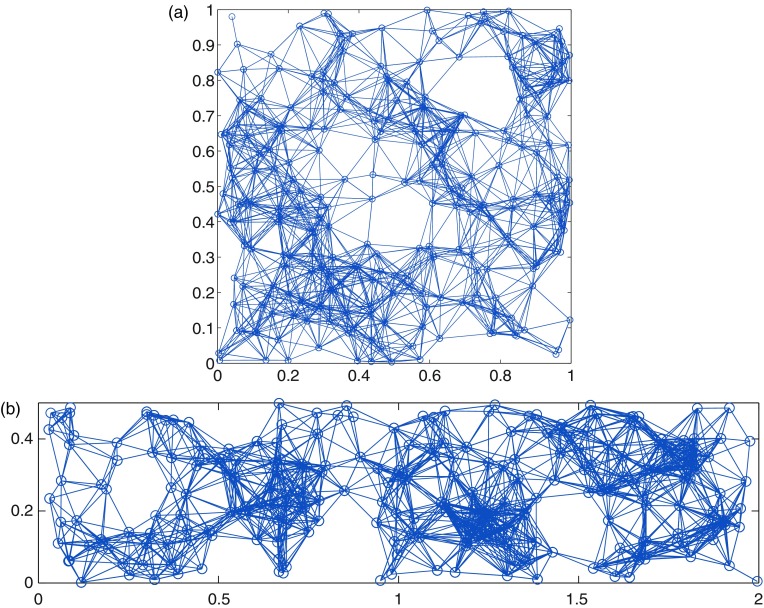
In Fig. 1 we illustrate two RRGs with different values of the rectangle side length $a$ and the same number of nodes and edges. In the first case when $a=1$ the graph corresponds to the classical random geometric graph in which the nodes are embedded into a unit square. The second case corresponds to $a=2$ and it represents a slightly elongated rectangle.

FIG. 1.

Illustration of an RRG created with 250 nodes embedded into a unit square, with $a=1$ (a), and a unit rectangle, with $a=2$ (b). In both cases the nodes are connected if they are at a Euclidean distance smaller than or equal to $r=0.15$.

A. About the connectivity of RRGs

An important question when studying RGGs in general is related to the connectivity of the resulting graphs. That is, for which values of the connection radius is an RGG with $n$ nodes connected with high probability? In the case of the square, Penrose [35] proved that for the two-dimensional case

$$\underset{n\to \infty }{lim}P[\overline{k}-logn\le \alpha ]=exp[-exp(-\alpha )],$$ (1)

where $P\left[\cdots \right]$ represents the probability that $\left[\cdots \right]$ takes place and $\overline{k}$ is the average degree.

This means that for $\alpha \to +\infty$ the RGG is almost surely connected when $n\to \infty$ and almost surely disconnected when $\alpha \to -\infty$.

In the case of the RRG where the value of $\overline{k}$ depends on the relation between the two sides of the rectangle we can write Eq. (1) for the unit rectangle as [31]

$$\underset{n\to \infty }{lim}P[(n-1)f-logn\le \alpha ]=exp[-exp(-\alpha )],$$ (2)

where $f$ is given by

$$\begin{array}{c}\hfill f=\left\{\begin{array}{cc}\hfill 0\le r\le a^{-1},& \hfill \pi r^2-\frac{4}{3}(a+a^{-1})r^3+\frac{1}{2}{r}^4,\\ \hfill a^{-1}\le r\le a,& \hfill -\frac{4}{3}a{r}^3-r^2{a}^{-2}+\frac{1}{6}{a}^{-4}+\left(\frac{4}{3}{r}^2+\frac{2}{3}{a}^{-2}\right)\sqrt{a^2{r}^2-1}\\ & \hfill +2r^{2}arcsin\left(\frac{1}{ar}\right),\\ \hfill a\le r\le \sqrt{a^2+a^{-2}},& \hfill -r^2(a^2+a^{-2})+\frac{1}{6}(a^4+a^{-4})-\frac{1}{2}{r}^4\\ & \hfill +\left(\frac{4}{3}{r}^2{a}^{-1}+\frac{2}{3}a\right)\sqrt{r^2-a^2}+\left(\frac{4}{3}{r}^2+\frac{2}{3}{a}^{-2}\right)\sqrt{a^2{r}^2-1}\\ & \hfill -2r^2\left[arccos\left(\frac{1}{ar}\right)-arcsin\left(\frac{a}{r}\right)\right].\end{array}\right.\end{array}$$ (3)

The significance of the function $f$ is clearer when we consider [31] that the expected average degree in an RRG is given by

$$\overline{k}=(n-1)f.$$ (4)

Because the parameter $\alpha$ is unknown and it depends on the specific RRG considered, we have obtained a lower bound for $exp\left[-exp\left(-\alpha \right)\right]$ using (2)

$$exp(-exp\{-[(n-1)f-logn\left]\right\})\le exp[-exp(-\alpha \left)\right].$$ (5)

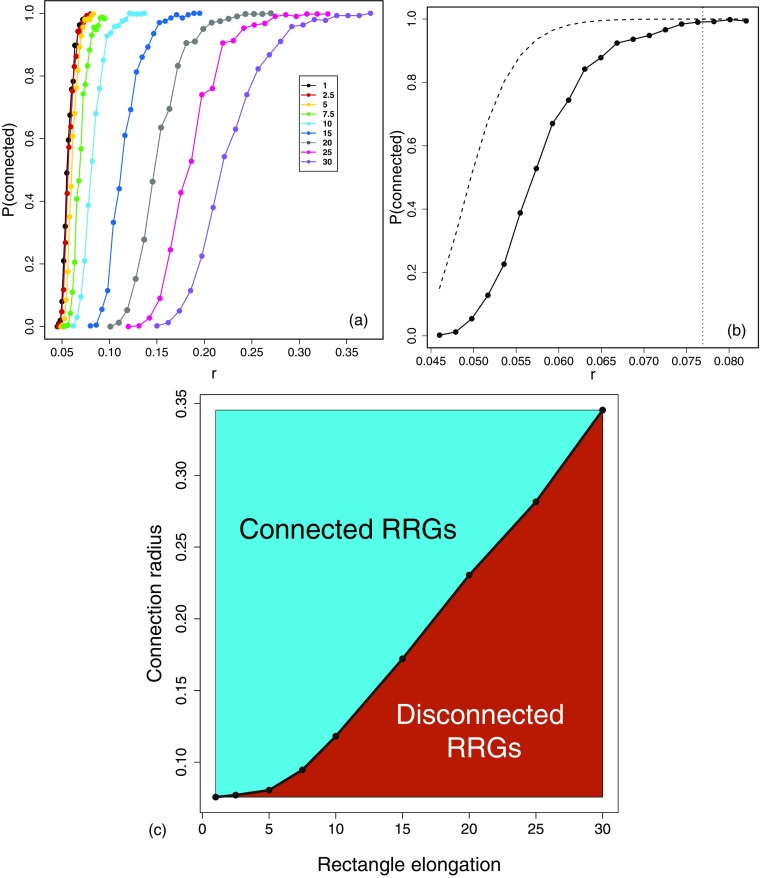
In Fig. 2(a) we illustrate the variation of the connectivity of RRGs with the change of the connection radius for different values of the rectangle elongation obtained by computational realizations of the RRGs. As can be seen the probability that the RRG is connected changes as a sigmoid function with the increase of the connection radius in a similar way as in the case of the RGGs. However, as the elongation of the rectangle increases (increase of $a$) it is more difficult for the graph to be connected, and the critical radius guaranteeing that the graph is connected increases significantly with $a$. In Fig. 2(b) we illustrate the way in which we determine these critical radii. For a given value of $a$ we find the minimum value of $r$ for which $P\left(\mathrm{connected}\right)=1$. Although we use in all cases the values obtained from the simulations, we can see that the theoretical bound for $P\left(\mathrm{connected}\right)$ (5) produces very similar results.

FIG. 2.

(a) Change of the connectivity of RRGs with the change of the connection radius for different values of the rectangle elongation. (b) Illustration of the way in which the critical radius for an RRG is obtained. Also the upper bound (5) (red dotted line) is illustrated. (c) Plot of the connection radius versus the rectangle elongation for the RRGs. The line dividing the two regions represents the critical values of the radius and elongation. All RRGs studied here have $n=1000$ nodes and all the calculations are the result of averaging 20 random realizations of the RRG with the given parameters.

We then plot the values of the connectivity radius versus the elongation of the rectangles [see Fig. 2(c)]. The curve joining the points of this plot makes a separation between the RRGs which are connected (upper triangular part) from those which are disconnected (lower triangular part). That is, the curve represents the critical radii versus critical elongation, and it gives the critical region indicating the connectivity of the RRGs. It can be read in two different ways. You can fix a value of $a$ and then determine which is the critical radius for which the network will be disconnected. For instance, for a rectangle with longer side $a=15$ it is necessary to use a radius larger than 0.17 to make the RRGs connected. More interesting for this work is the other way around. That is, we have a fixed radius of connection, which may represent the radius of spreading of a disease among plants. Then, you can find what elongation of the rectangle disconnects the network. For instance, if the connection radius is fixed to $r=0.35$ every RRG is connected for $a<30$. Then, we emphasize here that we always work in the region of connected RRGs in this work. That is, any analysis carried out in this paper is based on graphs for which the connectivity of the graph is 100% guaranteed as we work in the upper triangular part of this plot. In addition, we check computationally that every RRG generated in this work is connected.

III. EPIDEMICS ON NETWORKS

The spreading of an infectious disease on networks can be modeled representing individuals as nodes and the contacts between them as edges. In this context individuals are categorized in different compartments according to their health state [36]: susceptible (S) for individuals that can be infected by the disease, infected (I) for infectious individuals that can spread the pathogen, or recovered (R) for individuals that have already passed the disease and are immune to it.

Two fundamental models for disease spreading are the so-called SIS and SIR models [36,37]. The SIS model is intended to model recurrent diseases that do not provide immunity, i.e., most sexually transmitted diseases, where individuals can get the infection multiple times during their lifetime. Instead, in the SIR model, once an individual gets cured of the disease she enters the recovered compartment and cannot be infected again, that is, she acquires immunity. Both SIS and SIR dynamics are governed by two parameters, namely, the per contact infection rate $\beta$ and the recovery rate $\mu$. Let, $s_i$, $x_i$, and $r_i$ be the probabilities that the node $i$ is susceptible, infected, or has recovered from infection, respectively. The equations governing a SIS process are the following:

$$\begin{array}{cc}\hfill {\dot{s}}_i& =-\beta s_i\sum _j{A}_{ij}{x}_j+\mu x_i,\hfill \end{array}$$ (6)

$$\begin{array}{cc}\hfill {\dot{x}}_i& =\beta s_i\sum _j{A}_{ij}{x}_j-\mu x_i,\hfill \end{array}$$ (7)

while those governing a SIR one are

$$\begin{array}{cc}\hfill {\dot{s}}_i& =-\beta s_i\sum _j{A}_{ij}{x}_j,\hfill \end{array}$$ (8)

$$\begin{array}{cc}\hfill {\dot{x}}_i& =\beta s_i\sum _j{A}_{ij}{x}_j-\mu x_i,\hfill \end{array}$$ (9)

$$\begin{array}{cc}\hfill {\dot{r}}_i& =\mu x_i.\hfill \end{array}$$ (10)

In these models, $\beta$ represents the rate for a susceptible individual to catch the disease once in contact with an infected one through a link of the network, whereas the recovery rate $\mu$ characterizes the rate at which an infected individual recovers from the disease. Note that the spreading of the disease depends on the network of contacts (an isolated individual cannot catch the disease), while the recovery phase is independent of the substrate network (an isolated infected individual will recover after some time).

The ratio $\beta /\mu$ drives the spreading of the disease. Depending on its infectious power two distinct phases are possible: an absorbing one where the spreading is not efficient enough to reach a large fraction of the system and the disease is absorbed and an active phase where the epidemic reaches a macroscopic fraction of the network. The transition from the absorbing to the active phase strictly resembles a nonequilibrium second-order phase transition in statistical physics [38,39]. The critical value of this transition ${\left(\frac{\beta }{\mu }\right)}_c=\tau$ is defined as the epidemic threshold. This term is also known as the basic reproduction number and it represents a threshold in the sense that when $\tau <1$ the infection dies out and if $\tau >1$ the disease becomes an epidemic. In those cases where $\tau =1$, the disease remains in the population becoming endemic. The value of this threshold strongly depends on the topology of the network. In particular, for a given graph $G=\left(V,E\right)$, it has been shown that [40–42]

$$\tau =\frac{1}{{\lambda }_1\left(G\right)},$$ (11)

where ${\lambda }_1\left(G\right)$ is the largest eigenvalue of the adjacency matrix of the network. In the case of RGGs, Preciado and Jadbabaie [43] have made an exhaustive spectral analysis of virus spreading using the spectral moments of the adjacency matrix. They have found that for the RGG in a $d$-dimensional cube, the spectral radius is bounded as ${\lambda }_1\left(G\right)<c_{d}n{r}^d$, where $c_d$ is a constant characteristic of the RGG in the $d$-dimensional cube. In two-dimensional space this means that ${\lambda }_1\left(G\right)<c_{2}n{r}^2$. Then, because in these graphs the average degree is $n{r}^2$, the previous expression basically tells us that the spectral radius is bounded by the average degree of the RGG.

IV. EPIDEMIC THRESHOLD IN RRGS

In this section we concentrate more on the phenomenology of the process than on deriving analytical results about the dependence of the epidemic threshold with the topological parameters of the RRGs. Thus, we obtain some sort of mean-field approach that captures the behavior of the disease parameters with the topological ones. We start by considering the following well-known bounds for the largest eigenvalue of the adjacency matrix of a simple graph ${\lambda }_1\left(G\right)={\lambda }_1$,

$$\overline{k}\le {\lambda }_1\le k_{\max },$$ (12)

where $k_{\max }$ and $\overline{k}$ are the maximum and the average degree, respectively. Then, it is straightforward to realize that

$$\tau \ge \frac{1}{\overline{k}}.$$ (13)

Then, by substituting Eq. (4) in Eq. (13) we have the following bound for the epidemic threshold of an RRG:

$$\tau \ge \frac{1}{\left(n-1\right)f}.$$ (14)

This result generalizes the one obtained by Preciado and Jadbabaie [43] for the RGG to the case where we have a rectangle of any elongation and where we consider explicitly the border effects of the rectangle (respectively, the square in RGG).

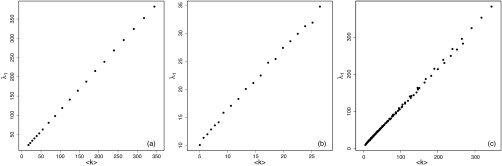
Let us now consider what happens to the epidemic threshold when we elongate the rectangle without disconnecting the RRG. That is, what is the behavior of the epidemic threshold when $a\to a_c$. In the following we prove that, when $a\to a_c$, $f$ decreases. Consequently, the spectral radius of the adjacency matrix ${\lambda }_1$ also decreases when $a\to a_c$, which implies that the epidemic threshold grows monotonically. Our strategy here is to prove that the increase of the rectangle elongation produces a decay of the average degree of the RRGs. Strictly speaking, proving that the average degree decreases with the elongation of the rectangle is not proof that the spectral radius also decreases. Although such proof is analytically possible, it is out of our intention of working more on the phenomenology of the process in this work. However, it is possible to indirectly infer such a relation between the elongation and the spectral radius as follows. First, it is well known in spectral graph theory that the average degree is a tight bound to the spectral radius of graphs in general. In particular, we are interested here in showing whether the average degree and the spectral radius of RRGs show the same behavior when the rectangle is elongated. In Fig. 3 we illustrate the plot of the spectral radius versus the average degree for RRGs with $a=1$ [panel (a)], $a=30$ [panel (b)], and $a=1$, 2.5, 5, 7.7, 15, 20, 25, and 30 [panel (c)] for different values of the connection radius. As can be seen in all cases, and particularly in the last one, the trends of the spectral radius and the average degree are exactly the same and indeed they are very highly linearly correlated. Thus, our conclusion here is that proving that the average degree has a certain behavior when the rectangle is elongated can be directly extrapolated to the behavior of the spectral radius with the elongation of the rectangle.

FIG. 3.

Scatter plots of the spectral radius versus the average degree for RRGs with $a=1$ (a), $a=30$ (b) and $a=1,2.5,5,7.7,15,20,25,30$ (c) for different values of the connection radius.

Then, in order to prove this result we first consider what happens to the function $f$ when $a\to a_c$. Let $0<r\le a^{-1}$. Then, the first derivative of $f_1=f\left(0\le r\le a^{-1}\right)$ is given by

$$\frac{\partial f_1}{\partial a}=-\frac{4}{3}{r}^3(1-a^{-2}),$$ (15)

and since

$$(1-a^{-2})\ge 0,$$

this is bounded by

$$\frac{\partial f_1}{\partial a}\le 0.$$

Let $a^{-1}\le r\le a$. Then, the first derivative of $f_2=f\left(a^{-1}\le r\le a\right)$ is given by

$$\begin{array}{ccc}\hfill \frac{\partial f_2}{\partial a}& =& \frac{-4r^3}{3}+\frac{2r^2}{a^3}-\frac{2}{3a^5}+\frac{4(a^4{r}^4-2a^2{r}^2+1)}{3a^3\sqrt{a^2{r}^2-1}},\hfill \end{array}$$ (16)

which is bounded as

$$\frac{\partial f_2}{\partial a}\le h<0,$$ (17)

where

$$\begin{array}{ccc}\hfill h& =& \underset{r\to a}{lim}\frac{\partial f_2}{\partial a}=\frac{2}{a}-\frac{4a^3}{3}-\frac{2}{3a^3}+\frac{4(a^8-2a^4+1)}{3a^3\sqrt{a^4-1}}.\hfill \end{array}$$ (18)

Let $a\le r\le \sqrt{a^2+a^{-2}}$. Then, the first derivative of $f_3=f\left(a\le r\le \sqrt{a^2+a^{-2}}\right)$ is given by

$$\begin{array}{ccc}\hfill \frac{\partial f_3}{\partial a}& =& 2r^2\left(\frac{1}{a^3}-a\right)+\frac{2}{3}\left(a^3-\frac{1}{a^5}\right)+\frac{4(a^4{r}^4-2a^2{r}^2+1)}{3a^3\sqrt{a^2{r}^2-1}}\hfill \\ & & -\frac{4(a^4-2a^2{r}^2+r^4)}{3a^2\sqrt{r^2-a^2}},\hfill \end{array}$$ (19)

which is bounded as

$$\frac{\partial f_2}{\partial a}\le g<0,$$ (20)

where

$$\begin{array}{ccc}\hfill g& =& \underset{r\to t}{lim}\frac{\partial f_3}{\partial a}=0,\hfill \end{array}$$ (21)

and $t=\sqrt{a^2+a^{-2}}$. Then, because all the derivatives are negative, we have proven the result. Strictly speaking the fact that $1/\left(n-1\right)f$ increases with increasing $a$ does not necessarily imply that $\tau$ will exhibit a similar trend for every $a$. However, as we see in the next section there is a very good linear correlation between the values of $\tau$ obtained from the simulations and the lower bound $1/\left(n-1\right)f$, which indicates that both quantities follow the same trend and consequently that the previous assertion relating the behavior of the epidemic threshold when $a\to a_c$ is general. We discuss this in more detail in the next section.

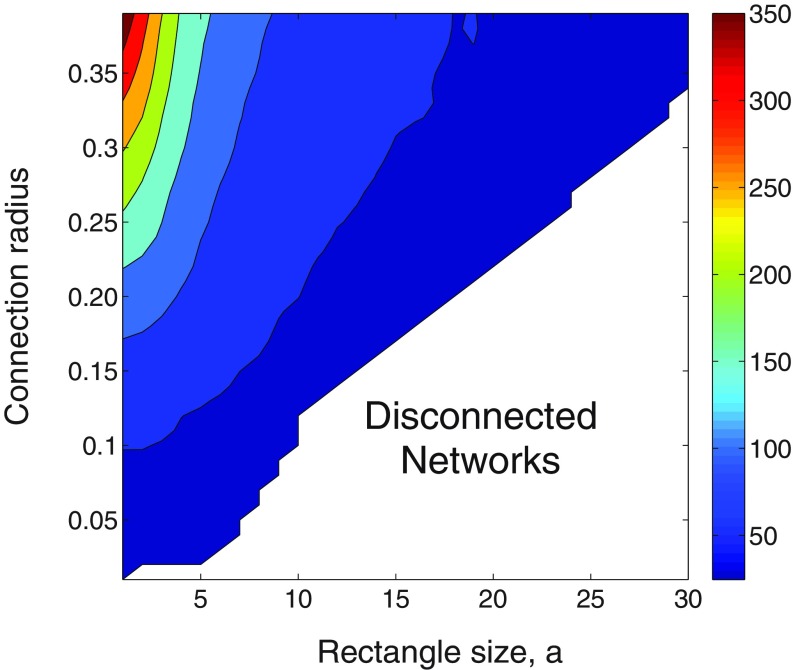
In Fig. 4 we illustrate the plot of the spectral radius of the adjacency matrix of RRGs as a function of both the rectangle size length $a$ and the connection radius $r$. As expected the lower triangular part of the plot corresponds to the disconnected RRGs, which are never used in this work. However, in the upper triangular part of the plot we observe a large variation of the spectral radius ${\lambda }_1$ of an RRG with both parameters of the model. For a fixed connection radius the values of ${\lambda }_1$ decay with the elongation of the rectangle as expected from the previous analytical results. Notice that ${\lambda }_1$ can change as much as from 380 to 35 for a constant radius $r=0.4$ when changing the rectangle size from $a=1$ to $a=30$. This, of course, is the main cause of the change of the epidemic threshold predicted by the bound (13) obtained at the beginning of this section.

FIG. 4.

Values of the spectral radius ${\lambda }_1$ of the adjacency matrix of RRGs with $n=1000$ nodes as a function of the rectangle size length $a$ and the connection radius $r$. The bottom-right part of the plot corresponds to networks which are created with a radius below the critical radius, $r<r_c$ [see plot (c) in Fig. 2], and consequently are disconnected. All the calculations are the result of averaging 20 random generations of the RRG with the given parameters.

V. EPIDEMICS IN RRGs: SIMULATIONS

In this section we conduct extensive numerical simulations of the SIS dynamics for different values of the elongation $a$ and a fixed radius $r$ with the goal of checking the goodness of the bound defined in Eq. (13) and to illustrate how the elongation of the rectangle in the RRG model changes the epidemic dynamics. In the simulations we start seeding the infection in a small fraction, ${\rho }_0=0.01$, of the nodes and let the SIS dynamics evolve for $5\times {10}^4$ time steps. At this point, we let the simulations run for an additional ${10}^3$ time steps and calculate the fraction of infected nodes $\rho$ as the average of $\rho \left(t\right)$ over this period. For each selection of the parameters we performed 250 independent runs with different initial conditions. The final value of $\rho$ is obtained as the average over all the runs.

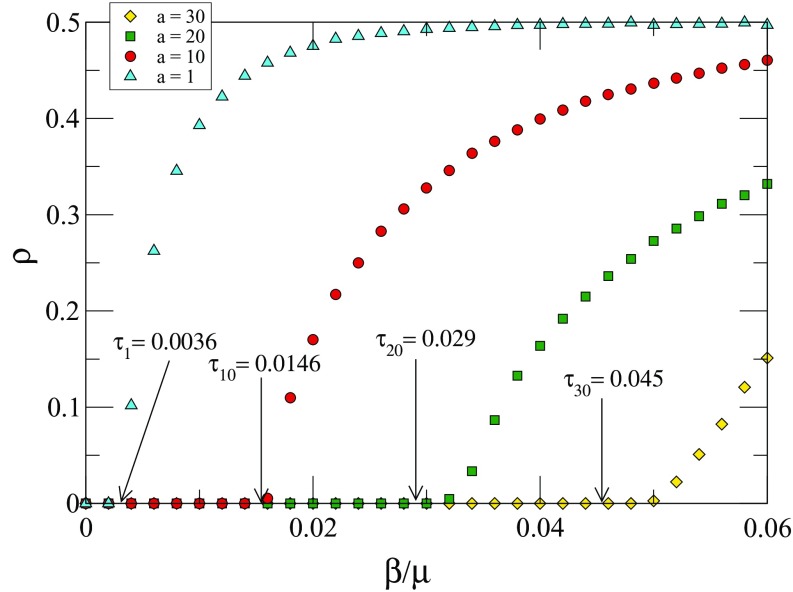
Figure 5 shows the fraction of infected nodes in the stationary state against the infection rate $\beta$ for different values of $a=1$, 10, 20, and 30. The values shown by arrows are the analytical ones obtained using Eq. (14).

FIG. 5.

(a) Fraction of infected nodes at the stationary state $\rho$ as a function of the infection rate $\beta$ for different values of $a=1$, 10, 20, and 30. $a=1$ represents the first case ($0\le r\le a^{-1}$) of Eq. (3) while $a=10$, 20, and 30 fall in the second case ($a^{-1}\le r\le a$). Other parameters are $n={10}^3$ nodes, $r=0.35$, and $\mu =1.0$. Each point is an average over 250 independent runs. The values shown by arrows are the analytical ones obtained using Eq. (14).

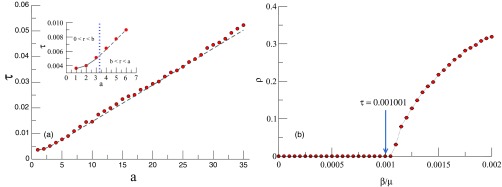
To have a more detailed picture of the behavior of the epidemic threshold, in Fig. 6(a) we compare the theoretical bound with the epidemic threshold obtained via the numerical simulations. As we have stressed in the previous section this comparison is very important for understanding whether the epidemic threshold and the bound $1/\left(n-1\right)f$ follow the same trend with the elongation of the rectangle. Our comparison covers two of the three cases of Eq. (3): $0\le r\le a^{-1}$ and $a^{-1}\le r\le a$, respectively. As can be seen in this figure the lower bound (14) is very tight, and more importantly the bound and the “observed” epidemic threshold display the same behavior when the rectangle elongation changes. Indeed, our analysis of the difference between the observed value of the epidemic threshold and the lower bound obtained by Eq. (13) shows that for all the RRGs having $1\le a\le 35$ such relative difference is 2.93% and in no case it is larger than 10%. Also we observe no trend in the relative difference related to the elongation of the rectangle. That is, the relative difference is neither increasing nor decreasing with the elongation of the rectangle.

FIG. 6.

(a) Comparison between the theoretical bound and the epidemic threshold obtained via numerical simulations. Lines represent the theoretical prediction of Eq. (13) while points represent the numerical threshold. The inset shows a zoom for the first case of Eq. (3), $0\le r\le a^{-1}$, (solid line) and the second case, $a^{-1}\le r\le a$ (dashed line). Other parameters are $n={10}^3$ nodes, $r=0.35$, and $\mu =1.0$. Each point is average over 250 independent runs. (b) Fraction of infected nodes at the steady state $\rho$ as a function of the infection rate $\beta$ for $a\le r\le \sqrt{a^2+a^{-2}}$. In the simulations $a=3$ and $r=3.01$. Other parameters are $n={10}^3$ nodes and $\mu =1.0$. Each point is average over 250 independent runs.

Finally, in Fig. 6(b) we also tested the third case of Eq. (3), $a\le r\le \sqrt{a^2+a^{-2}}$ for $a=3$ and $r=3.01$. In all cases, as expected, the theoretical and the simulation results show that the increase of the elongation of the rectangle produces an increase of the epidemic threshold. In other words, the elongation of the rectangle retards the disease progression through the nodes embedded in the rectangle.

In the case of disease propagating on plants, these results—both analytical and simulations—coincide with the field observations and simulations using stochastic models [22–30] which suggest that square plots and fields favored higher spreading of plant diseases than elongated ones of the same area [22–25].

Our analytical and simulation results point to the fact that, under the same conditions, the propagation of an epidemic on a rectangular plot or field is much harder than on a square one because a larger number of infected individuals is needed for the disease to become epidemic. Here we have kept the size of the plot or field constant by considering unit rectangles in our analysis. However, it is important to consider that other factors, such as the orientation of the plot or field, play fundamental roles in the propagation of a disease on plants. For instance, if the rectangular plots are placed perpendicular to the direction of the prevalent winds the disease will not propagate as a consequence of this factor.

VI. CONCLUSIONS

We have studied the propagation of diseases on a recently proposed RRG model, deriving analytically a lower bound of the epidemic threshold for a SIS or SIR model running on these networks. This model is appropriate for the simulation of disease spreading on plants allocated on plots and field of varied shapes. RRGs account for the spatial distribution of nodes allowing the variation of the shape of the unit square commonly used in RGGs. We have shown here by using analytical results and extensive numerical simulations of the SIS dynamics for different values of the elongation $a$ and a fixed radius $r$ that the elongation of the plots or fields in which the nodes (plants) are distributed makes the network more resilient to the propagation of epidemics. This is due to the fact that the epidemic threshold increases with the elongation of the rectangle. These results agree with a large accumulation of empirical evidence about the role of elongation of plots and fields on the propagation of diseases on plants. This model represents a new way to analyze disease propagation on plants or similar scenarios, by combining the heterogeneities introduced at individual levels by networks with the influence produced by the shape variation of the plots and fields where the plants are growing.