Abstract
We investigate three aspects of the importance of nodes with respect to susceptible-infectious-removed (SIR) disease dynamics: influence maximization (the expected outbreak size given a set of seed nodes), the effect of vaccination (how much deleting nodes would reduce the expected outbreak size), and sentinel surveillance (how early an outbreak could be detected with sensors at a set of nodes). We calculate the exact expressions of these quantities, as functions of the SIR parameters, for all connected graphs of three to seven nodes. We obtain the smallest graphs where the optimal node sets are not overlapping. We find that (i) node separation is more important than centrality for more than one active node, (ii) vaccination and influence maximization are the most different aspects of importance, and (iii) the three aspects are more similar when the infection rate is low.
I. INTRODUCTION
One of the central questions in theoretical epidemiology [1–3] is how to identify individuals that are important for an infection to spread [4,5]. What “important” means depends on the particular scenario—what kind of disease spreads and what can be done about it. In the literature, three major aspects of importance have been discussed. First, influence maximization is aimed at identifying the nodes that, if they are sources of the outbreak, would maximize the expected outbreak size (the number of nodes infected at least once) [6,7]. Second, vaccination is aimed at finding the nodes that, if vaccinated (or, in practice, deleted from the network), would reduce the expected outbreak size the most [5]. Third, sentinel surveillance is aimed at finding the nodes that are likely to get infected early [8,9]. These three notions of importance do not necessarily yield the same answer as to which node is most important. In this work, we investigate how the ranking of important nodes for these three aspects differs and why (see Fig. 1).
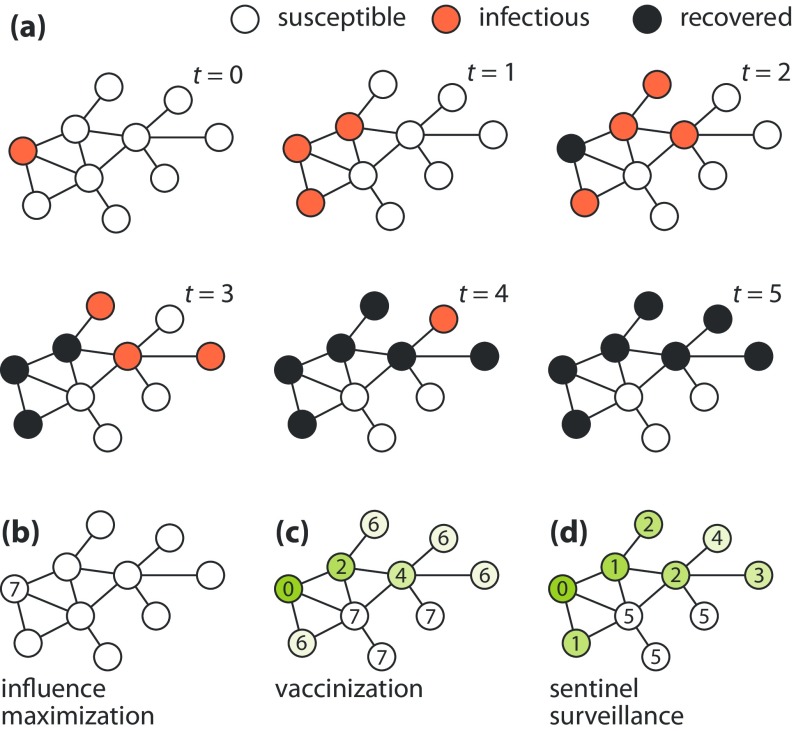
FIG. 1.
Illustration of the three different notions of importance we explore in this work. Panel (a) shows an example of an SIR outbreak in a seven-node network. Panels (b)–(d) show how this outbreak influences maximization (a), vaccination (b), and sentinel surveillance, respectively. The idea of influence maximization (b) is that a node is important if the outbreak originating at it is expected to be large. The idea of vaccination (c) is that a node is important if removing it would reduce significantly the average outbreak size. The idea of sentinel surveillance (d) is that a node is important if a sensor on it would detect the outbreak early. The shades of the nodes in (c) and (d) are proportional to their contribution. In a stochastic simulation, one would average the values over many runs and, for (c) and (d), many seeds of the outbreak. In this work, however, rather than running simulations, we calculate the exact expectation values of these quantities.
In this paper, we evaluate the three aspects of importance with respect to the susceptible-infectious-removed (SIR) disease-spreading model [1–3,10] on small connected graphs (all connected graphs from three up to seven nodes). The main reason we restrict ourselves to small graphs is that it allows us to use symbolic algebra, and thus exact calculations [11]. In this way we can discover, e.g., the smallest graph where the three aspects of importance disagree about which node is most important; cf. Ref. [12]. We argue that graphs of seven nodes are still large enough to illustrate the effects of distance.
Nevertheless, large networks are important to study. A possible future extension of this work will be to address the relationship between the three importance measures for larger networks. In the related Ref. [13], the difference between influence maximization and vaccination problems on (some rather large) empirical networks is studied. The authors compare the top results of heuristic algorithms to identify influential single nodes, whereas in this paper we will consider the influence of all nodes, and also all sets of two and three nodes. (The terminology of Ref. [13] is a bit different from ours—they call important nodes for vaccination “blockers” and important nodes for influence maximization “spreaders”.)
We will proceed by discussing our setup in greater detail: our implementation of the SIR model, how to analyze the three aspects of importance, network centrality measures that we need for our analysis, and our results, including the smallest networks where different nodes come out as most important.
II. PRELIMINARIES
In this section, we provide the background to our analysis. The basis of our analysis is graphs consisting of nodes and links .
A. Importance
As mentioned earlier, there are three ways to think of importance in theoretical infectious disease epidemiology. Influence maximization was first studied in computer science with viral marketing in mind [6,7]. As was mentioned, a node is important for influence maximization if it is a seed of an infection that could cause a large outbreak. For epidemiological applications, therefore, it might be interesting if one could immunize people against a disease before an outbreak happens. We will simply measure the expected outbreak size (the expected number of nodes to catch the disease), with as the set of source nodes, and we will rank the set of nodes according to their .
For vaccination, we will use the average outbreak size from one random seed node to estimate the importance of a node [1,2,14,15]. One could rephrase it as a cost problem [16]. We assume the vaccinees are deleted from the network before the outbreak starts. The node with the smallest is the one that is most important for the vaccination problem.
Sentinel surveillance assumes a response after the outbreak already started (compared to influence maximization and vaccination, where the action affecting the nodes in question is assumed to take place before the outbreak happens). A node is important for sentinel surveillance if it gets infected early so that the health authorities can activate their countermeasures. This is usually determined by the lead time—the expected difference between the time a sentinel node gets infected, or the outbreaks dies out, and the infection time of any node in the graph [8]. We will instead measure the average discovery time time from the beginning of the infection until a node gets infected or the outbreak dies [9]. The node with the smallest discovery time is then considered most important for sentinel surveillance. If the purpose of the surveillance is just to discover the outbreak—not to rid the population of the disease as early as possible—one could measure conditioned on the outbreak reaching a sentinel before it dies out. We will briefly discuss such a conditioned and refer to it as .
For all of the three problems mentioned above, one can consider sets of nodes rather than individuals. There can be more than one source (for influence maximization), vaccinee, or sentinel. We will, in general, call these sets active nodes and denote their number as . We will try to find the optimal sets of active nodes (and call them optimal nodes). Note that this is not the same as ranking the nodes in order of importance and taking the most important ones—such a “greedy” approach can in many cases fail [7,15].
Note that for vaccination and sentinel surveillance, we use one source node of the infection. This is the standard approach in infectious disease epidemiology simply because most outbreaks are thought to start with one person [3,17].
B. SIR model
We will use the constant infection and recovery-rate version of the SIR model [17]. In this formulation, if a susceptible node is connected to an infectious node , then becomes infected at a rate . Infected nodes recover at a rate . Without loss of generality, we can set (equivalently, this means we are measuring time in units of ). Let be a configuration (i.e., a specification of the state—S, I, or R—of every node), is the number of links between S and I nodes, and is the number of infected nodes. Then, the rate of events (either infections or recoveries) is , which gives the expected duration of as
| (1) |
Proceeding in the spirit of the Gillespie algorithm, the probability of the next event being an infection event is , and the probability of a recovery event is [2,18].
C. Exact calculations of and
Exactly calculating the outbreak size and time to discovery or extinction is, in principle, straightforward. Consider the change from configuration into by an infection event (changing node from susceptible to infectious). This can happen in ways, where is the number of links between and an infectious node. Thus the probability for the transition from to is . The probability that the next event will be a recovery event is simply . To compute the probability of a chain of events, one simply multiplies these probabilities over all transitions. To compute the expected time for a chain of events, one sums the for all configurations of the chain.
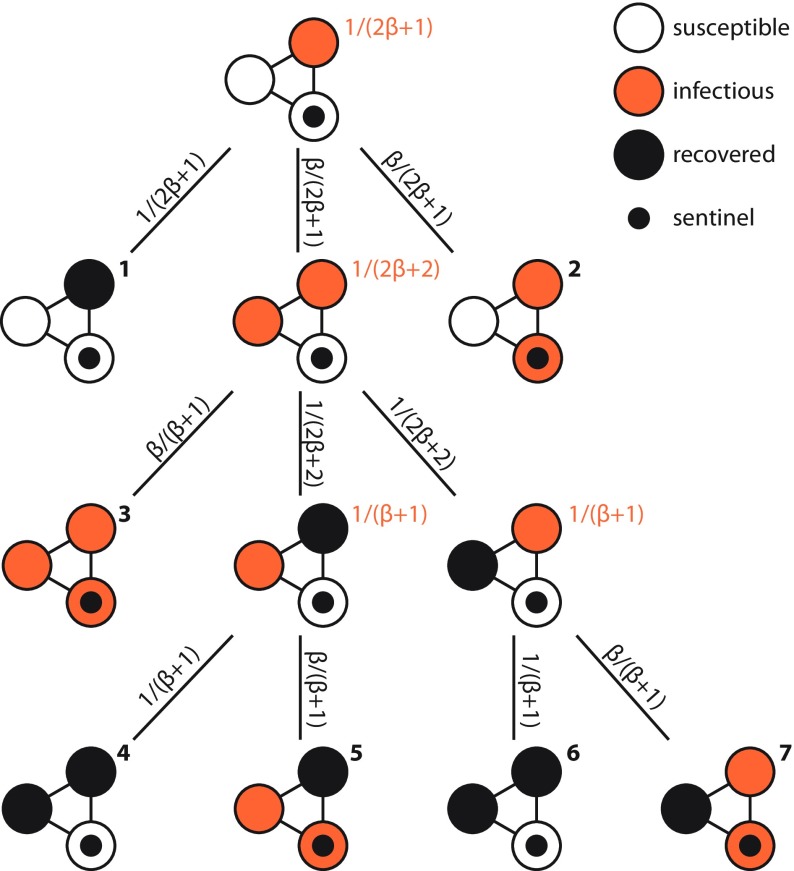
We will illustrate the description above with an example. See Fig. 2. The probability of the outbreak chain 7 is (multiply the probabilities of the transitions)
| (2) |
The expected duration of the infection chain is
| (3) |
giving a contribution
| (4) |
of chain 7 to . Then these contributions need to be summed up for all chains, and averaged over all starting configurations. For the example in Fig. 2, this gives
| (5) |
The expressions of and are fractions of polynomials. For the largest networks we study (seven nodes), these polynomials can be of order up to 43 with up to 54-digit integer coefficients.
FIG. 2.
Illustration of how to calculate the expected time to discovery or extinction in a small network with one sentinel. The probabilities of transitions are marked on the links (with black text). The expected time to stay in a configuration is next to the configurations (in orange). The final states (where there are either no infectious nodes or a sentinel is infected) are enumerated by boldface numbers.
Calculating for the influence maximization or vaccination problems follows the same path as the calculation above. The difference is that instead of multiplying by the expected time of a chain, one would multiply by the number of recovered nodes in that branch. Furthermore, there are no sentinels to stop outbreaks, so trees (like Fig. 2) become larger.
In practice, our approach to analyzing network epidemiological models is time-consuming. The major bottleneck is the polynomial algebra (to be precise, calculating the greatest common divisor needed to reduce the fractions of polynomials to their canonical form). Because of this, we could not handle networks of more than seven nodes. The code was implemented in both Python (with the SymPy library [19]) and C with the FLINT library [20]. It also uses the subgraph isomorphism algorithm VF2 [21] as implemented in the igraph C library [22]. Our code is available at http://github.com/pholme/exact-importance, which also includes code to calculate (mentioned above but not investigated in the paper).
D. Centrality measures
To better understand how the network structure determines what nodes are most important, we measure the average values of static importance predictors. In general, there are many ways to be the central means for a node—is it a node often passed by things traveling over the network, or is it a node for which short paths exist to other nodes? Different rationales give different measures. These are typically positively correlated, but they do not rank the nodes in the exact same way, and thus they can complement each other [23]. We focus on three measures: degree, closeness centrality, and vitality.
Degree centrality is simply the number of neighbors of a node. If a node has twice the neighbors of another, it has twice as many nodes to which to spread an infection. This makes it more important for influence maximization and vaccination. It also has twice as many nodes from which to get the infections, which contributes to its importance for vaccination and sentinel surveillance. On the other hand, degree is not a global quantity—it could happen that the neighbors of a high-degree node are so peripheral that a disease could easily die out there. The simplest way of modifying the degree to become a global measure is to operationalize the idea that a node is central if it is the neighbor of many central nodes. With the simplest possible assumptions, this reasoning leads to eigenvector centrality, i.e., the centrality of node can be estimated as the entry of the leading eigenvector of the adjacency matrix [10]. For the small graphs that we consider, however, the eigenvector centrality is so strongly correlated with degree (intuitively so, because “everything is local” in a very small graph) that it makes little sense to include it in the analysis.
Many centrality measures are based on the shortest paths. Perhaps the simplest of these measures is closeness centrality—using the idea that a node is central if it is on average close to other nodes [10,23]. This leads to a measure of the centrality of as the reciprocal distance to all other nodes in the network:
| (6) |
The main problem, in general, with closeness centrality may be that it is ill-defined on disconnected graphs. In our work, however, we consider only connected graphs.
We chose the third centrality measure—vitality—with the vaccination problem in mind. Vitality is, in general, a class of measures that estimate node centrality based on its impact on the network if it is deleted [23]. In our work, we let vitality denote the particular metric
| (7) |
where is the number of nodes in the largest component of . This measure is thus in the interval , and it increases with 's ability, if removed, to fragment the network. Since vaccination is, in practice, like removing nodes from the network, we expect to identify important nodes for close to 1. For large graphs, we expect to be very close to 1, so we only recommend it for small graphs such as the ones we used here. Another popular centrality measure—betweenness centrality (roughly how many shortest paths there are in the network that passes a node) [10]—is very strongly correlated with vitality for our set of small graphs, and it is thus omitted from the analysis.
E. Small distinct graphs
In our work, we systematically evaluate small distinct (nonisomorphic) connected graphs. We use all such graphs with . There are two such graphs with , six with , 20 with , 112 with , and 853 with . To generate these, we use the program geng [24].
III. RESULTS
In our analysis, we will focus on when and why the three cases of node importance rank nodes differently. We will start with some extreme examples, and continue with general properties of all small graphs.
A. Special cases
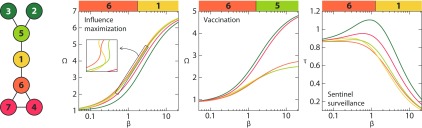
Inspired by Ref. [12], we will start with a special example (Fig. 3). This is the smallest graph where the most important single node () is different for influence maximization, vaccination, and sentinel surveillance. For , node 6 is the most important node for influence maximization, 5 is most important for vaccination, and 1 is most important for sentinel surveillance. For small values, 6 is most important for all three aspects of importance. In this region, the outbreaks die out easily. The fact that 5 and 6 have a larger degree than the others is, of course, helpful for an outbreak to take hold in the population. Node 6 is slightly more important as a seed node since the extra link in its neighborhood helps the outbreak to persist longer [there are the and infection paths that, although unlikely, do not exist for diseases starting at 5]. This reasoning also explains why 6 is most important for vaccination. For sentinel surveillance and for low enough , the outbreak would typically end by the outbreak becoming extinct rather than hitting a sentinel. Thus, for low , when an outbreak has the highest chance of surviving if it starts at 6, then putting in a sentinel is good because an outbreak is either instantly discovered or will likely soon be extinct. With a conditional discovery time , the curves are strictly decreasing (since the early die-off is omitted), so 1 is the most important node for all .
FIG. 3.
A small graph with special properties. It is the smallest graph where the three aspects of importance all have distinct nodes as the most important. For in the interval , 6 is the most important node for influence maximization, 5 for vaccination, and 1 for sentinel surveillance. The curves are color-coded according to the graph to the left (with one curve and color per automorphic equivalence class). The inset in panel (a) shows a zoomed and rotated view of some of the crossings of the curves (one of them being the point where node 1 takes over from node 6 as the most important).
For larger , node 1 becomes, relatively speaking, more important for influence maximization and sentinel surveillance. This is the most central node in aspects other than degree. For vaccination, however, node 5 is most important as it fragments the network most [the vitality is the same for both nodes , but the size of the second biggest component is larger if 1 is deleted]. So since 1 becomes more important than 6 at a larger value for influence maximization compared with sentinel surveillance, there is an interval of beta where the network of Fig. 3 has three distinct most important nodes for the three aspects of importance that we investigate.
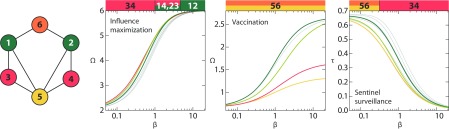
For two active nodes (), the smallest network with no overlap between the optimal node sets is actually smaller than for . This network, displayed in Fig. 4, has six nodes and eight links. Note that is the smallest number of nodes to make three distinct sets of two nodes, so in that sense the example seems more extreme than the counterpart, Fig. 3.
FIG. 4.
A special graph for two active nodes. To the left, the colors highlight the automorphic equivalence classes. For , are the most important source nodes (influence maximization), are the most important for vaccination, and finally are the most important for sentinel surveillance. The color bars indicate the most important node-pairs as a function of , and the curves are showing the dependence of the objective quantities and . The four node combinations that are optimal at some value for some scenario are highlighted; the others are gray.
For large values, 1 and 2 are the most important nodes for influence maximization, 5 and 6 are most important for vaccination, and 3 and 4 are most important for sentinel surveillance. 5 and 6 are the nodes that, if deleted, break the network into the smallest components, which explains why they are most important for vaccination (at least for large ). In addition to 5 and 6, 1 and 2 are the only pair of nodes whose neighborhoods contain all other nodes. Nodes 1 and 2 both have degree 3, as opposed to 5 and 6, which have degrees 4 and 2, respectively. It is not clear whether that makes 1 and 2 better than 5 and 6 for influence maximization, or why. Similarly, it is hard to understand why 3 and 4 are the best nodes for sentinel surveillance. The neighborhoods of these nodes do not even contain the entire graph.
We can see that the optimal sets of nodes in Fig. 4 do not have links within themselves. This seems natural for most networks and all three notions of importance. This means that as grows, the distance between the optimal nodes will be larger than 1. This is an observation we will make more quantitatively in the next section. Another such observation is that for small , the optimal nodes for the three importance aspects are overlapping. In this parameter region, most outbreaks die out before they reach a sentinel. If the outbreak starts at a high-degree node in a highly connected neighborhood, there is a larger chance for it to survive. For all three importance aspects, it is important to have active nodes where an outbreak would be likely to survive. Still, as evident from Fig. 4, there are examples where the optimal nodes are not overlapping.
B. dependence
We will now move to a more statistical evaluation of all graphs with 3–7 nodes. We will present average quantities over all these graphs as functions of . Other summary statistics, including grouping the graphs according to size, give the same conclusions.
Let be the optimal sets for a given network, , and importance classes and . The first quantity we look at is the pairwise overlap of sets of optimal nodes as measured by the Jaccard overlap,
| (8) |
where
| (9) |
For example, in Fig. 4 at , we have
| (10a) |
| (10b) |
| (10c) |
where is influence maximization and represents sentinel surveillance, giving
| (11) |
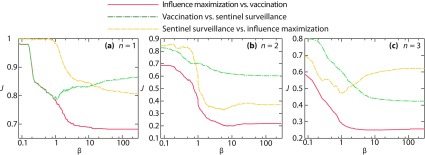
As seen in Fig. 5, for , the overlap between the optimal nodes for vaccination and sentinel surveillance has a minimum as a function of . The same is true for sentinel surveillance versus influence maximization when . It is hard to say why, beyond that, for individual graphs the curves can of course be nonmonotonous as different aspects of the graph structure determine the role of the nodes. We note that (for a different spreading model and much larger networks), Ref. [13] finds the Jaccard similarity between influence maximization and vaccination to have a minimum as a function of .
FIG. 5.
The average pairwise Jaccard overlap between the sets of the most influential nodes for the three different aspects of importance. Panels (a), (b), and (c) show the overlap for one, two, and three active nodes, respectively. For larger than shown, the curves are constant.
C. Structural predictors
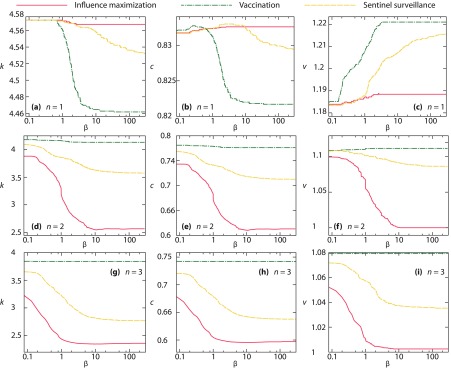
Next, we investigate the structural properties of the most influential nodes and how they depend on . In Fig. 6, we plot the degree, closeness centrality, and vitality as a function of for all aspects of importance and . We start by examining the case ; see Figs. 6(a), 6(b), and 6(c). The first thing to notice is the general impression that centralities of the optimal nodes decrease with . The only case with an opposite trend is vitality [Fig. 6(c)], where the curves are increasing monotonically. If we first focus on the case with one active node, this could be understood as the ability of nodes to (if removed) fragment the network. This ability is captured by vitality and becomes more important as increases.
FIG. 6.
Average centrality values for the different aspects of centrality and the different numbers of active nodes. Panels (a), (d), and (g) show the average degree; panels (b), (e), and (h) show closeness centrality; and panels (c), (f) and (i) show curves for vitality. Panels (a), (b), and (c) show results for ; (d), (e), and (f) for ; and (g), (h), and (i) for .
Continuing the analysis for , when is low the most important thing is for the outbreak to persist in the population. If an active node has a high degree, it is likely to be the source of a large outbreak, meaning it is important for influence maximization (which was also concluded by Ref. [13]). If a high-degree node is deleted, it would remove many links that could spread the disease and thus be important for vaccination [25]. It would also be important not to put a sentinel on a low-degree node for sentinel surveillance and low as diseases reaching low-degree nodes would likely die out. So panels Figs. 6(a) and 6(c) can be understood as a shift from nodes of high degree to nodes of high vitality. Closeness centrality—seen in Fig. 6(b)—is harder to explain. Values of increase with for influence maximization but decrease for vaccination. One way of understanding this is from the observation that vitality is most important for vaccination [as evident from Fig. 6(c)], and degree is most important for influence maximization [as seen in Fig. 6(a)]. The results of Fig. 6(b) then suggest that the high vitality nodes optimizing the solution of the vaccination problem have a lower closeness centrality. Indeed, for many of the graphs we study, the highest vitality node has many degree-1 neighbors—cf. node 5 in Fig. 3—which does not necessarily contribute to the closeness centrality. For influence maximization, it seems that the optimal nodes are central in the closeness sense—the closer to average the seed node is to the rest of the network, the higher is the chance for the outbreak to reach the entire network.
For and 3, the picture is somewhat different than for . In these cases, all centrality measures are decreasing monotonically. The order of importance measures are all the same, with vaccination having the largest values, and influence maximization the smallest. It is no longer the case for vaccination that the optimizing nodes have high vitality and low closeness centrality (as it was for ). Indeed, for the vaccination case, the optimal nodes are usually independent of , which is why the curves for vaccination in Figs. 3(d)–3(i) are almost straight. Naively, one would think that some centrality measure needs to increase with . However, as we will argue further below, the optimal nodes would usually not be close to each other. One could think of each node being responsible for (and centrally situated within) a region of the network, and that that tendency is so strong that it overrides all simple centrality measures. On the other hand, there are group centrality measures that could perhaps increase with [26] (that could be a theme for another paper).
D. Distance between optimal nodes
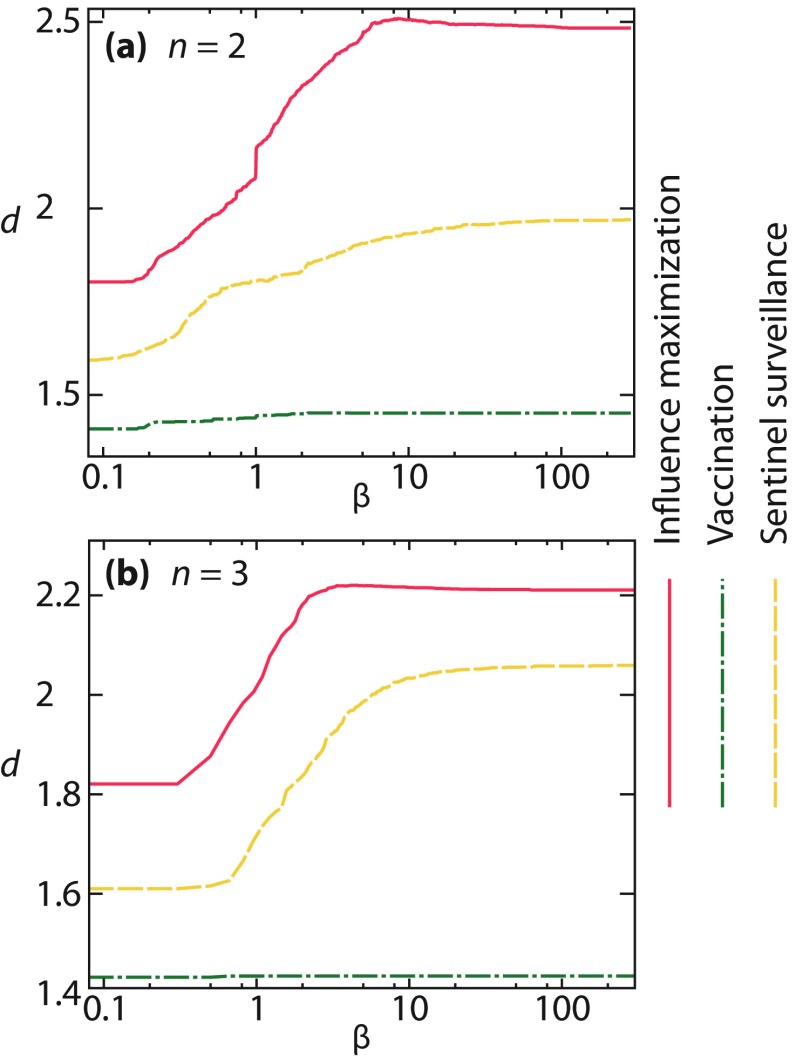
The fact that all the curves of Figs. 6(d)–6(i) are nonincreasing could be explained by the fact that the separation of the optimal nodes increases with . In Fig. 7, we try to make this argument more quantitative by measuring the average (shortest path) distance between the optimal nodes. In the limit of small , these values come rather close to its minimum of 1, but as increases, so does . Essentially, the pattern from Fig. 7 is the reverse of Figs. 6(d)–6(i)—the vaccination curve is almost constant, sentinel surveillance increases moderately, but influence maximization increases much more.
FIG. 7.
The average distance between optimal nodes when the number of active nodes is (a) and 3 (b).
A larger separation gives the sentinels the ability on average to be closer to outbreaks anywhere in the network, while for influence maximization a larger separation means that there are more susceptible-infectious links (fewer infectious-infectious links) in the incipient outbreak. For vaccination there is no such positive effect of a larger separation that we can think of, which is a part of the explanation as to why the optimal sets are relatively independent of for . The rest of the explanation, i.e., why the trends for are so much weaker when , is not clear to us, and it is something we will investigate further in the future.
IV. DISCUSSION
We investigated the average properties of the optimal nodes for all our graphs. We found that the overlap between the optimal nodes of the different importance aspects are largest for small . In the small- region, a high degree seems most important for all importance aspects. For larger nodes, it becomes more important for them to be positioned such that they would fragment the network if they were removed, particularly for the vaccination problem (slightly less for the sentinel surveillance problem, and much less for influence max- imization). On the other hand, when the number of active nodes increases, it becomes important for the nodes to be spread out—the average distance between them increases. This effect is large for influence maximization, intermediate for sentinel surveillance, and very small for vaccination. The small effect for vaccination can be understood since all that matters is to fragment the network, and for that purpose the vaccine does not necessarily have to be distant.
Most of the behavior discussed above seems quite natural. For small , the dominant aspect of the dynamics is how fast an outbreak will die out. For large , the outbreak will almost certainly reach all nodes. For vaccination and sentinel surveillance, this leads to a question of deleting nodes that would break the network into the smallest components. (In the former case, this is trivial since the size of the outbreak is almost surely the size of the connected component to which the seed node belongs. In the latter, we conclude this from the monotonically increasing vitality).
As an extension, it would be interesting to confirm this work in larger networks using stochastic simulations. This would not allow for the discoveries of special graphs such as those in Figs. 3 and 4, but it could reinforce the connection between the different notions of centrality. We believe that many of our conclusions hold for larger networks, an indication being that our results are consistent with the results of Ref. [13] (comparing the vaccination and influence maximization for in large empirical networks).
ACKNOWLEDGMENTS
We thank Petteri Kaski, Nelly Litvak, and Naoki Masuda for helpful comments.
REFERENCES
- [1].I. Z. Kiss, J. C. Miller, and P. L. Simon, Mathematics of Epidemics on Networks (Springer, Heidelberg, 2017). [Google Scholar]
- [2].R. Pastor-Satorras, C. Castellano, P. Van Mieghem, and A. Vespignani, Rev. Mod. Phys. 87, 925 (2015). 10.1103/RevModPhys.87.925 [DOI] [Google Scholar]
- [3].H. W. Hethcote, SIAM Rev. 42, 599 (2000). 10.1137/S0036144500371907 [DOI] [Google Scholar]
- [4].L. Lü, D. Chen, X.-L. Ren, Q.-M. Zhang, Y.-C. Zhang, and T. Zhou, Phys. Rep. 650, 1 (2016). 10.1016/j.physrep.2016.06.007 [DOI] [Google Scholar]
- [5].Z. Wang, C. T. Bauch, S. Bhattacharyya, A. d'Onofrio, P. Manfredi, M. Perc, N. Perra, M. Salathé, and D. Zhao, Phys. Rep. 664, 1 (2016). 10.1016/j.physrep.2016.10.006 [DOI] [Google Scholar]
- [6].J. Sun and J. Tang, A Survey of Models and Algorithms for Social Influence Analysis (Springer, Boston, 2011), pp. 177–214. [Google Scholar]
- [7].D. Kempe, J. Kleinberg, and É. Tardos, in Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (ACM, Washington, DC, 2003), pp. 137–146. [Google Scholar]
- [8].N. A. Christakis and J. H. Fowler, PLoS One 5, e12948 (2010). 10.1371/journal.pone.0012948 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].P. Bajardi, A. Barrat, L. Savini, and V. Colizza, J. R. Soc. Interface 9, 2814 (2012). 10.1098/rsif.2012.0289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].M. E. J. Newman, Networks: An Introduction (Oxford University Press, Oxford, UK, 2010). [Google Scholar]
- [11].N. Masuda, J. Theor. Biol. 258, 323 (2009). 10.1016/j.jtbi.2009.01.025 [DOI] [PubMed] [Google Scholar]
- [12].U. Brandes and J. Hildenbrand, Network Sci. 2, 416 (2014). 10.1017/nws.2014.25 [DOI] [Google Scholar]
- [13].F. Radicchi and C. Castellano, Phys. Rev. E 95, 012318 (2017). 10.1103/PhysRevE.95.012318 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].T. Britton, S. Janson, and A. Martin-Löf, Adv. Appl. Probab. 39, 922 (2007). 10.1017/S0001867800002172 [DOI] [Google Scholar]
- [15].J. Gu, S. Lee, J. Saramäki, and P. Holme, Europhys. Lett. 118, 68002 (2017). 10.1209/0295-5075/118/68002 [DOI] [Google Scholar]
- [16].P. Holme and N. Litvak, PLOS Comp. Biol. 13, e1005696 (2017). 10.1371/journal.pcbi.1005696 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].P. Holme, J. Logist. Eng. Univ. 30, 1 (2014). 10.3969/j.issn.1672-7843.2014.03.001 [DOI] [Google Scholar]
- [18].R. Huerta and L. S. Tsimring, Phys. Rev. E 66, 056115 (2002). 10.1103/PhysRevE.66.056115 [DOI] [PubMed] [Google Scholar]
- [19].A. Meurer, C. P. Smith, M. Paprocki, O. Čertík, S. B. Kirpichev, M. Rocklin, A. Kumar, S. Ivanov, J. K. Moore, S. Singhet al. , PeerJ Comput. Sci. 3, e103 (2017). 10.7717/peerj-cs.103 [DOI] [Google Scholar]
- [20].W. B. Hart, in Proceedings of the Third International Congress on Mathematical Software (Springer-Verlag, Berlin, 2010), ICMS'10, pp. 88–91. [Google Scholar]
- [21].L. P. Cordella, P. Foggia, C. Sansone, and M. Vento, in 3rd IAPR-TC15 Workshop on Graph-based Representations in Pattern Recognition (Springer, Berlin, 2001), pp. 149–159. [Google Scholar]
- [22].G. Csárdi and T. Nepusz, InterJournal Complex Systems 1695 (2006). [Google Scholar]
- [23].D. Koschützki, K. Lehmann, L. Peeters, S. Richter, D. Tenfelde-Podehl, and O. Zlotowski, in Network Analysis: Methodological Foundations (Springer, Berlin, 2005), pp. 16–61. [Google Scholar]
- [24].B. D. McKay and A. Piperno, J. Symbol. Computat. 60, 94 (2014). 10.1016/j.jsc.2013.09.003 [DOI] [Google Scholar]
- [25].R. Pastor-Satorras and A. Vespignani, Phys. Rev. E 65, 036104 (2002). 10.1103/PhysRevE.65.036104 [DOI] [PubMed] [Google Scholar]
- [26].M. G. Everett and S. P. Borgatti, J. Math. Sociol. 23, 181 (1999). 10.1080/0022250X.1999.9990219 [DOI] [Google Scholar]