Abstract
Several recent studies have tackled the issue of optimal network immunization by providing efficient criteria to identify key nodes to be removed in order to break apart a network, thus preventing the occurrence of extensive epidemic outbreaks. Yet, although the efficiency of those criteria has been demonstrated also in empirical networks, preventive immunization is rarely applied to real-world scenarios, where the usual approach is the a posteriori attempt to contain epidemic outbreaks using quarantine measures. Here we compare the efficiency of prevention with that of quarantine in terms of the tradeoff between the number of removed and saved nodes on both synthetic and empirical topologies. We show how, consistent with common sense, but contrary to common practice, in many cases preventing is better than curing: depending on network structure, rescuing an infected network by quarantine could become inefficient soon after the first infection.
I. INTRODUCTION
Networks provide a convenient framework for investigating epidemics, with nodes corresponding to potential hosts of the infectious agent, and links between nodes indicating potential routes for the spread of the infection [1]. Much effort has been spent on elaborating efficient procedures to immunize a network [2–4]. A novel and effective approach has been recently proposed [5], based on the concept of optimal percolation. The idea is that, in order to confine the infection and avoid large outbreaks, one must delete, in the contact network, the minimal number of nodes sufficient to break the system into small, isolated fragments, with no giant component.
Although interesting from a theoretical perspective, the idea of preventively reducing the risk of epidemics by removing nodes from a network can sometimes be impractical. For example, the modification of a transportation network [6] has deep economic and societal implications, apart from the obvious technical difficulties. In other scenarios, ethical aspects add to the implementation challenges. For example, it would be very controversial to designate specific individuals in the population for mandatory vaccination. Similarly, in a spatial network [7] that maps infection pathways for agricultural pests, it would be very difficult to require costly preventive actions from some farmers only, especially in the case of a purely hypothetical threat [8].
In addition, different kinds of threat would modify the underlying network, hence calling for different immunization strategies, not only in terms of how to immunize a node but also in terms of the identity of nodes to be immunized. Considering the last example, a network of infection pathways for an agricultural pest can be generated by connecting all pairs of crops within a certain threshold distance, representing how far a pathogen can spread from one crop to another in a single step [8]. This distance, however, depends on several aspects related to the pathogen's features (such as the flight distance of its vectors), so that the same crops in a given region may be arranged in a particular network topology for a certain disease, and in a very different one for another. In turn, this would lead to the identification of different sets of critical nodes.
The discovery of a serious disease in the first phases of its spread often leaves no other choice than to sacrifice individual interests in the hope of preventing an outbreak with a coordinated action. From a theoretical perspective, the simple removal of infected nodes is a straightforward, trivial solution to the problem of stopping an epidemic. However, in real-world scenarios, due to infection latency (the interval between the time a host becomes infectious and the time it shows signs of disease), it is common practice to try to isolate the infected nodes from the rest of the network by also taking action on the surrounding nodes. For example, in the case of the spread of disease in plants, it is usual procedure to eliminate all the susceptible hosts close to an infected one [8,9]. Similarly, in the case of human diseases, a typical intervention is the quarantine of asymptomatic individuals that have had contacts with infected nodes (see, for example, [10]).
Some recent studies have investigated various aspects related to the efficiency of different quarantine strategies. Nian and Wang [11] considered “high-risk” immunization (more properly, quarantine) of susceptible neighbors of infected individuals, occurring with a probability , and they found that increasing reduces the epidemic threshold of the susceptible-infected-removed-susceptible (SIRS) dynamics. Hasegawa and Nemoto [12] studied numerically and analytically a similar strategy for susceptible-infected-removed (SIR) dynamics, finding it more efficient at suppressing epidemics than random or acquaintance immunization. Pereira and Young [13] investigated, for susceptible-infected-susceptible (SIS) dynamics, the effect of the time period between the infection of an individual and its isolation.
Apart from the difficulties that may arise in the practical implementation of the two approaches (i.e., preventive immunization versus quarantine), a crucial question to be answered is as follows: Under which circumstances is a preventive immunization strategy preferable to a post-outbreak (quarantine) intervention? To avoid confusion (the same terms are often used with different meanings in the literature), let us specify that with quarantine we intend the post-outbreak removal of nodes that have been in contact with infectious individuals. Immunization is instead the pre-outbreak removal of nodes based on some a priori prevention strategy.
In this paper, we analyze the question by comparing the fraction of nodes saved using preventive immunization against the fraction of nodes that can be saved if quarantine is implemented at different times after the beginning of the outbreak. We mainly focus on the conservative concept of “complete” quarantine, i.e., we assume that the quarantine strategy is implemented by removing all susceptible neighbors of infected nodes. Moreover, we assume that outbreak detection is immediate and perfect: we always know which nodes are infectious. In reality, early outbreak detection is a nontrivial problem for which clever strategies can be devised [14].
We assess whether and when preventing an outbreak by immunization is a preferable strategy (in terms of saving more individuals) to attempting to rescue an infected network by quarantine. We consider a very simple theoretical framework (in terms of epidemic dynamics, network topologies, and assumptions about the cost of immunization, quarantine, or being hit by the infection) with the aim of grasping the main features of the problem. In contrast to previous approaches, the preventive immunization strategy considered here is based on the recently introduced concept of optimal percolation.
The overall resulting message of our study is that quarantine may be a viable alternative only if enacted immediately after the start of the outbreak. If the implementation is not prompt enough, then quarantine becomes highly inefficient, as it stops the epidemic at the price of removing many more nodes than those that would have been removed by preventive immunization. In some cases, it may even be more convenient to let the disease propagate freely rather than applying a quarantine measure. These conclusions hold very strongly for networks possessing the small-world property (i.e., having a small diameter). They hold in a weaker form for networks with a large diameter (such as planar graphs): in that case, the number of infected nodes grows more slowly, and, as a consequence, quarantine remains convenient for longer times.
The “complete” quarantine makes sense in many real-world scenarios where the topology of the contact pattern is not known. This applies, for example, to the case of quarantining people who have come into contact with a dangerous pathogen: although they clearly belong to some sort of social network, its structure would be, in most cases, elusive. Nevertheless, when the contact pattern is known, it is possible to devise a more refined quarantine strategy, which removes a node only if this saves on average more than one other node. We investigate this aspect by introducing an improved quarantine strategy that takes into account the average effect, on the epidemic process, of whether or not a node is quarantined. We show that the set of nodes that should be quarantined to halt an epidemic can be significantly smaller than the set of healthy neighbors surrounding infected nodes. Nevertheless, even this improved quarantine strategy is not more efficient than preventive immunization.
The structure of the paper is the following. In Sec. II we define the epidemic dynamics considered, the synthetic topologies of the underlying interaction pattern, and we give details on the different approaches to be compared. We then compare the quarantine strategy with two alternative courses of action: no intervention (Sec. III) and preventive immunization (Sec. IV). Section V reports the same type of analysis for two real-world topologies. The next section is devoted to the presentation and performance evaluation of the improved quarantine strategy. The final section contains some concluding remarks, and an outlook about future work.
II. EPIDEMIC MODEL AND COUNTERMEASURES
We consider the independent cascade model, a parallel implementation of the SIR dynamics, the simplest model for the spreading of a pathogen conferring permanent immunity [15]. Each individual sits on a node of a network and can be in one of three states: susceptible (S), infected (I), or removed (R). The total number of individuals is . At a given time step, a list of infected nodes is created and each node in the list tries to infect each of his or her susceptible neighbors: each attempt is successful with probability . After all the nodes in the list have been considered, they all recover (i.e., with probability 1) switching to state R. Time is increased by 1 and the next iteration begins with the compilation of the list of newly infected nodes: is the only parameter of the dynamics. In the initial configuration, a single randomly selected node is infected, all others being susceptible. In a finite system, the dynamics unavoidably reach a final absorbing configuration with no infective nodes: all individuals are either untouched by the epidemic (in state S) or are recovered (state R) after having been infected. The fraction of recovered nodes in the final state plays the role of the order parameter: for small values of the epidemic reaches only a small number of individuals around the initial seed ( is close to 0 for large systems); for large instead an extensive set of individuals is reached by the infection, so that is finite in large systems. The two regimes are separated by a critical value (the epidemic threshold ) distinguishing for between extensive spreading for and small-scale local spreading for . We consider two classes of synthetic networks representing the static contact pattern among individuals. On the one hand, there are low-diameter networks (i.e., having the small-world property), represented by Erdös-Rényi graphs or by scale-free networks with degree distribution with and , built using the uncorrelated configuration model [16]. The network size is in all cases . The average degree is, unless specified otherwise, ( for the scale-free network). The epidemic threshold is, with very good approximation, [17]. On the other hand, we also consider another type of network, which does not possess the small-world property: a random geometric graph, built in the two-dimensional square of unit size by connecting nodes at Euclidean distance smaller than (). In this topology, the diameter grows asymptotically as a power of the number of nodes [18], as in a regular lattice.
Most of our work concerns a comparison between a preventive immunization protocol and a quarantine strategy implemented only after the outbreak has started.
The preventive immunization is based on the concept of optimal percolation proposed by Morone and Makse [5].1 Extensive epidemic outbreaks in a network are possible only if a giant component (i.e., a cluster of connected nodes covering a finite fraction of the structure) is present. Otherwise, only small outbreaks can occur even for extremely infective pathogens (). Therefore, by removing a number of nodes sufficient to dismantle the giant component, it is possible to prevent large outbreaks. By means of different strategies [5,20–22], it is possible to reduce this number to values close to the theoretical minimum, thus providing an optimal preventive immunization. If the removal of a fraction of nodes destroys the giant component, one can consider that a fraction of nodes is effectively saved from infection. In Appendix A, we provide details on how is determined in our study.
The alternative strategy to contain the epidemic and save individuals is quarantine, which is intended here as the removal at a given time step of all susceptible neighbors of all infected nodes. This procedure leads to the immediate end of the epidemic, leaving a fraction of the nodes saved, i.e., not reached by the contagion. In practice, it is possible to calculate the fraction for each time step as the epidemic unfolds by simply counting the number of susceptible nodes that are not direct neighbors of infected nodes.
In the following, we compare the fraction of nodes saved by quarantine with the fraction of those saved by optimal percolation or not reached by the epidemic in the absence of any intervention. The underlying assumption is that immunizing a node or quarantining it has the same cost of the node being infected. This might be an appropriate scenario for, say, an incurable deadly tree disease, for which immunization or quarantine both imply the physical felling of the tree. In other cases in which the cost of the different actions is not the same, the analysis is more complicated, and beyond the scope of this paper.
III. COMPARISON BETWEEN QUARANTINE AND NO INTERVENTION
The first question we address is whether a quarantine strategy is any better than doing nothing. The answer to this question is not completely trivial: for small values of the spreading probability , the epidemic soon becomes extinct spontaneously, touching a very limited number of individuals; a quarantine intervention in such a case implies the removal of more individuals than those likely to be reached by the epidemic. For larger values of it is a matter of timeliness: if the intervention is quick enough, quarantine may be useful; otherwise, it is more costly than allowing the epidemic to spontaneously evolve and disappear.
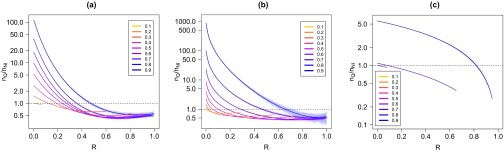
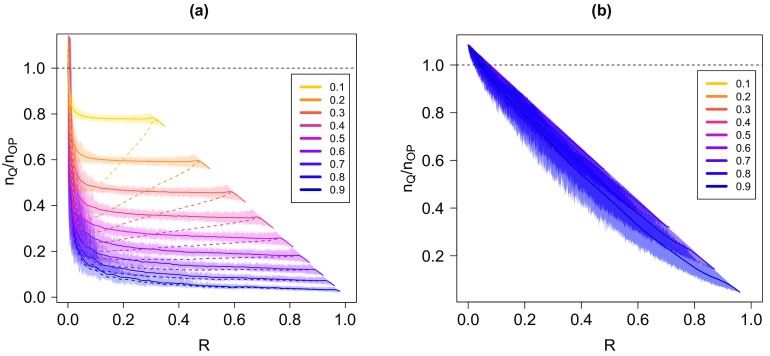
This is confirmed in Fig. 1, where we plot the ratio between the fraction of nodes saved by the quarantine strategy and the fraction of nodes that are not reached by the infection in the absence of any intervention. Unsurprisingly, it turns out that for up to the epidemic threshold, quarantine is never convenient: it removes more individuals than those that would be hit by the freely evolving epidemics. For larger values of , quarantining may be very useful, but only if promptly implemented: for example, for an Erdös-Rényi graph and , the implementation of quarantine actually saves more individuals than those that would have survived with no intervention only if applied as long as . For a scale-free network, the effect is even more noticeable. A different scenario applies instead for the random geometric graph. In that case, above the threshold (which is of the order of 0.8) the ratio remains very large up to values of close to 1: quarantine is more convenient than no intervention practically at any time during the epidemic.
FIG. 1.
(a) Ratio between the fraction of nodes saved by quarantine and the fraction of nodes not reached by the infection in the absence of any intervention as a function of the fraction of nodes recovered at the time the quarantine is implemented. The network is an Erdös-Rényi graph with nodes. The curves are for growing values (bottom to top) of the spreading probability . The dashed line indicates when the ratio is 1, i.e., the value discriminating between convenient quarantine (ratio and inconvenient quarantine (ratio . (b) The same plot for a scale-free network with . (c) The same plot for a random geometric graph. For this figure (and in all the others) we performed 10 000 realizations of the process. Solid lines are average values computed over 100 intervals (of width 0.01), while the shaded areas around them are the variations between the minimum and the maximum in 1000 intervals.
IV. COMPARISON BETWEEN QUARANTINE AND PREVENTIVE IMMUNIZATION
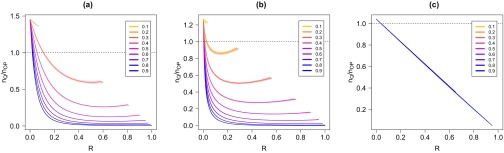
We now evaluate the efficiency of a quarantine procedure compared to that of a preventive immunization strategy based on optimal percolation. In practice, the latter is implemented by removing a fraction of the nodes, breaking the network into small clusters so that any outbreak cannot grow large (see Appendix A for details). In particular, we compare the global fraction of nodes saved by applying the preventive immunization strategy with the fraction saved by applying the quarantine strategy. Also in this case, the efficiency of quarantine depends on its timeliness, i.e., on the value of at the time it is applied. Figure 2 shows that, for the two small-world networks, decays very rapidly below : unless applied in the very early stages of the epidemic, quarantine is less efficient than preventive immunization. The only exception to this rule occurs for small values of : in such cases, the epidemic spontaneously becomes extinct after relatively short times, so that preventive immunization is never more efficient. Again, the effect is more dramatic when the topology is scale-free: quarantine becomes highly inconvenient as soon as only a few percent of the population have been hit by the epidemics. For the random geometric graph, the effect is once again considerably milder. The ratio decays linearly with with the same slope for any value of . Hence the initial window for an efficient quarantine intervention has the same width independent from .
FIG. 2.
(a) Ratio between the fraction of nodes saved by quarantine and the fraction of nodes saved by preventive immunization as a function of the fraction of nodes in state R when quarantine is applied. The network is an Erdös-Rényi graph with nodes. The curves are for growing values (top to bottom) of the spreading probability . The dashed line indicates when the ratio is 1, i.e., the value discriminating between convenient quarantine (ratio ) and inconvenient quarantine (ratio ). (b) The same plot for a scale-free network with . (c) The same plot for a random geometric graph.
A qualitative understanding of the phenomenology is straightforward. Starting from the initial seed, at time the epidemics reaches nodes at distance from the seed. In a network with small-world property, the number of these nodes grows exponentially, approximately as . In a few steps the whole population is reached and hence the application of quarantine is highly ineffective, apart from the very first moments of the spreading process. In a planar network instead, the same quantity grows much more slowly (quadratically) in time. Hence quarantine remains effective up to considerably longer times.
It is possible to analytically estimate, in both scenarios, the value after which the quarantine strategy becomes less efficient than preventive immunization.
For the random regular network, given the quasiplanar structure, the set of removed nodes forms approximately a circle around the seed, its radius growing over time. Infected nodes form a ring sitting at the boundary of the circle, and nodes to be quarantined form another ring surrounding the first. For this reason, the fraction of infected nodes is proportional to , and the same is true for the fraction of nodes to be quarantined. As soon as the number of removed nodes is of the order of a few dozen, and can be neglected with respect to . Hence the fraction of saved nodes is
| (1) |
This formula fully explains the linear behavior and the lack of dependence on observed in Fig. 2(c). The value after which quarantine is inefficient is .
The derivation of the same relation for locally small-world (locally treelike) networks is more involved. A calculation based on the heterogeneous mean-field (HMF) approximation for SIR dynamics is presented in Appendix B, yielding
| (2) |
where
| (3) |
By equating this expression to , we obtain
| (4) |
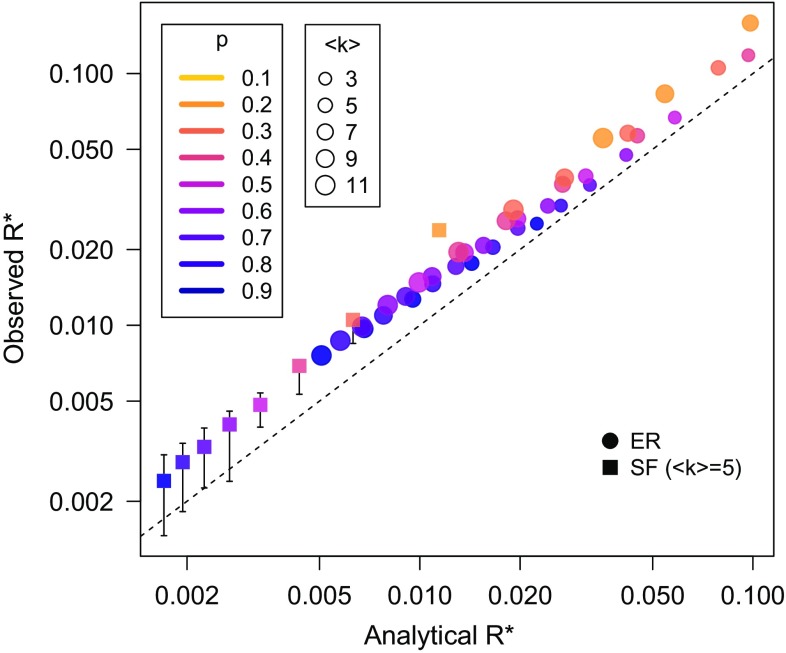
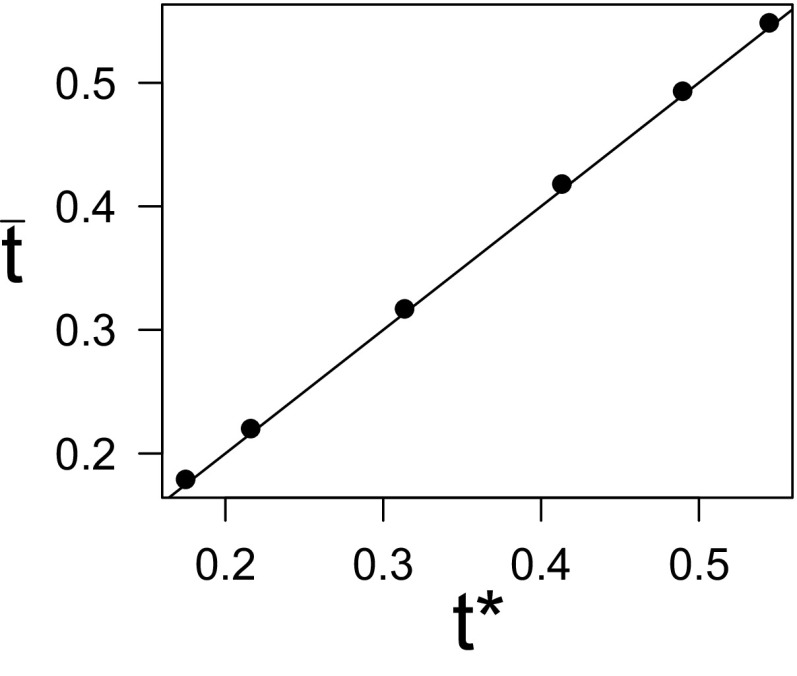
In Fig. 3, we compare this analytical prediction with the results obtained from numerical simulations on both ER and scale-free networks. The agreement is satisfactory, also considering the known discrepancies between HMF theory for SIR and simulation results [1,23]. We note that the value of is reduced as the average degree of homogeneous networks is increased or as the network becomes more heterogeneous.
FIG. 3.
Comparison between analytical predictions [Eq. (4)] and simulation results for the fraction of recovered nodes after which quarantine becomes less convenient than preventive immunization. The dashed line indicates perfect equality. Simulations are performed on Erdös-Rényi (ER) networks with various values of the average degree and on a scale-free (SF) network. Error bars are not shown when smaller than symbols size. System size is .
In Fig. 2, preventive immunization is implemented by optimal percolation, i.e., by removing the minimum number of nodes sufficient to destroy the giant component of the network, thus precluding the possibility of endemic outbreaks, even in the extreme hypothesis that the transmission probability is . If one has information about the actual value of , it is possible to use it in the preventive immunization strategy. In that case, one can compare with the average fraction of nodes saved, given that the spreading probability is . Clearly, [with . See Appendix A for details about the calculation of . The ratio of the fractions of saved nodes with the two strategies (“informed” preventive immunization versus quarantine) is displayed in Fig. 4. In this scenario, where is known a priori, the observed patterns are very similar to those observed assuming ; the higher convenience of preventive immunization is just slightly more pronounced. Moreover, one must consider that is only the average fraction of saved individuals. Depending on the specific realization of the epidemic process, the actual value can be larger but also smaller. Only the immunization assuming is guaranteed to save a fraction of the nodes. Since the patterns observed assuming (Fig. 2) are very similar to those observed for known a priori (Fig. 4), i.e., the “informed” (and hence partial) immunization does not, on average, lead to the saving of a much larger number nodes than those saved by the optimal percolation, the latter should be, in general, preferred.
FIG. 4.
Ratio between the fraction of nodes saved by quarantine and the fraction of nodes saved by “informed” preventive immunization (i.e., with known a priori) as a function of the fraction of nodes removed when quarantine is applied. The network is an Erdös-Rényi graph with nodes. The curves are for growing values (top to bottom) of the spreading probability .
V. ON REAL-WORLD TOPOLOGIES
In this section, we check whether the same phenomenology observed in synthetic networks also occurs in real-world topologies, where correlations, clustering, and mesoscopic structures add complexity to the picture. We consider an instance of a small-world network with small diameter, an undirected version of the World airline Network (WAN) [24]. The number of nodes is , the average degree , and the diameter is 12. We also consider the U.S. power-grid network [25], a quasiplanar graph with large diameter (46), nodes, and .
We show the comparison between the quarantine strategy and preventive immunization in Fig. 5.
FIG. 5.
Ratio between the fraction of nodes saved by quarantine and the fraction of nodes saved by preventive immunization as a function of the fraction of nodes removed. The topology is (a) WAN and (b) U.S. power grid. In the WAN topology (a) we report both the results of the simulations implementing either the complete quarantine (dashed lines) or the improved one (solid lines). The curves are for growing values (top to bottom) of the spreading probability .
The figure confirms the same qualitative behavior observed in synthetic networks. For small-world networks, quarantine becomes, almost immediately after the beginning of the outbreak, a less efficient strategy than preventive immunization. For all the considered values of , the observed values are (i.e., nodes), close to the analytical estimates ( nodes). In the case of the quasiplanar network instead, the dependence of on is almost linear and as a consequence there is a finite (yet small) range of values for which quarantine is more efficient than preventive immunization. Also, the comparison of quarantine with nonintervention (not shown) confirms the qualitative behavior observed in synthetic networks.
VI. IMPROVED QUARANTINE STRATEGY
In the previous sections, we have seen that a post-outbreak quarantine strategy is almost always less convenient (in terms of saved individuals) than optimal preventive immunization. So far, however, we have considered a crude quarantine strategy consisting in the removal of all susceptible neighbors of infected individuals. This approach makes sense in many real-world situations, where the complete topology of the network is not known a priori. For example, it is reasonable to quarantine all people who have been exposed to a dangerous pathogen because, in most cases, the structure of the social network to which they belong is not well known. However, in other situations in which the topology is available, complete quarantine may not be the best strategy compared to a more parsimonious approach aimed at avoiding the removal of a particular node unless it brings benefit to other nodes. A trivial example of such a situation is that of a healthy node completely surrounded by infected neighbors. Removing the healthy node from the network will not affect the probability of infection of other uninfected nodes. Thus, rather than removing it from the network, it would be more reasonable to leave it untouched, hoping it remains uninfected.
General criteria for the identification of nodes that are not to be quarantined may, however, be less self-evident. We consider a simple one, based on the evaluation of , i.e., the number of nodes that will be, on average, reached by the infection if the candidate for quarantine is left untouched. If this number is smaller than 1, quarantining would lead to a reduction in the number of saved individuals: hence it is more convenient not to quarantine it.
For the independent cascade model with transmission probability on a tree structure, the average number of nodes that will be infected if a node candidate to be quarantined is not removed is
| (5) |
Here is the probability that actually becomes infected, is the number of nodes at exactly steps from , and is the path length from to the farthest uninfected node. If , then should be quarantined. Otherwise, leaving untouched would result, on average, in less than one node being infected. Hence, a higher number of saved nodes is obtained if is not quarantined. On a network that is not a tree, Eq. (5) is no longer exact. However, one can use it as an approximation, provided that is computed after the exclusion from the network of all other nodes candidate for quarantine, as well as the exclusion of all removed () nodes. Moreover, we can replace the first factor with the probability that the infection is transmitted to by one of its infected neighbors.
As in the case of the “informed” preventive immunization, with will provide information on the average expected effect of not quarantining a node, i.e., it will not exclude the possibility that a much larger number of nodes than the expected value is actually reached by the infection. Conservatively setting allows for the identification of the trivial cases of nodes surrounded by infected nodes only.
Another limitation of this simple approach is that in nontree networks there will generally be an overlap among sets of nodes protected by different nodes. Especially for high values of , there could be situations in which a high number of nodes are simultaneously protecting a small number of healthy nodes. In such cases, will likely be greater than 1 for most of the candidates , but quarantining all of them will save a small number of nodes at the expense of removing many. Avoiding the quarantine of all the nodes that protect the same (small) set of healthy nodes could be the most efficient strategy. A very simple procedure for taking this into account is implemented by excluding from the network all infected and removed nodes, and then counting the expected number of nodes that will be infected (i.e., the sum of their values) in any network component. If that sum plus the number of healthy nodes in the component is smaller than the total number of nodes in the component, no nodes in the component should be quarantined.
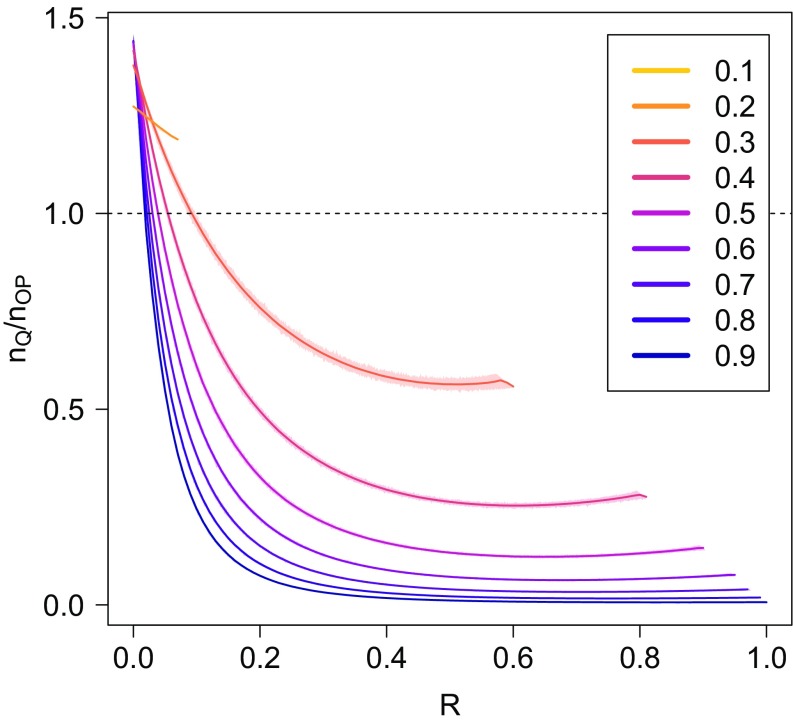
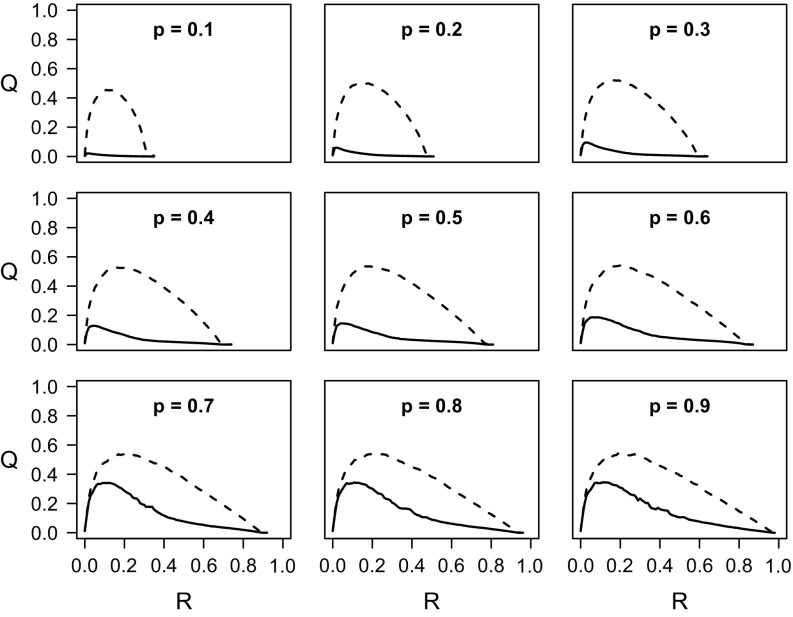
We tested the combination of these criteria on the WAN topology. In Fig. 6 we show how the method substantially reduces the number of nodes to be quarantined. In Fig. 5 we show that, although it translates into a net improvement in the average fraction of nodes saved by the quarantine, this does not affect our main conclusion: preventive immunization is still much more efficient than quarantine shortly after the first infection.
FIG. 6.
Comparison of the number of nodes to be quarantined as a function of in the case of complete quarantine (dashed lines) or improved quarantine (solid lines). Different panels refer to different values of the spreading probability . The topology is the WAN.
VII. CONCLUSIONS
In this paper, we have compared the efficiency of quarantine protocols with respect to optimal prevention strategies in terms of the number of individuals that remain unaffected by the spread of the epidemic. We find that preventing is almost always better than curing, unless the quarantine approach is applied in the very early stages of the spreading process. The time window for quarantine to be convenient is extremely short for topologies with small diameter (possessing the small-world property) and is further reduced if the average degree is increased or the degree distribution is broader. If quarantine is applied too late, it may even become more costly than leaving the contagion to evolve freely until its spontaneous disappearance. Quarantine performs better in networks with large diameter such as planar graphs and the like. In such a case, the number of infected nodes does not grow exponentially with time, and this makes the quarantine strategy relatively efficient for longer intervals.
These results provide a basic understanding of the salient features of the problem. A number of limitations must, however, be clearly spelled out.
First, there are many epidemics where the infection can be transmitted from one individual to another, even before symptoms permitting the identification of infection show up. For example, in the case of vector-borne diseases, a newly infected host may become able to transmit the disease to a vector before the signs of the disease become detectable. In such a situation, limiting the attention to the nearest-neighboring nodes may not be enough to ensure that the spread is stopped.
Second, the identification of the optimal percolating set requires full knowledge of the contact network. If the topology is not completely known, it is impossible to immunize optimally; conversely, quarantine is possible, as it requires only local information. On the other hand, if the quarantine is applied too late, it might be not only less efficient than prevention, but also too resource-demanding, as it requires the simultaneous treatment of an exponentially large number of individuals.
Finally, it will be interesting to remove the assumption that the costs of being infected, immunized, or quarantined are the same. More realistic scenarios, in which these costs differ (and may even depend on the infection stage), may give rise to a rich and interesting phenomenology.
ACKNOWLEDGMENTS
The views expressed are purely those of the authors and may not under any circumstance be regarded as stating an official position of the European Commission.
APPENDIX A: IMMUNIZATION STRATEGY BASED ON OPTIMAL PERCOLATION
The preventive immunization strategy is based on the concept of optimal percolation, i.e., the identification of the smallest possible set of nodes such that their removal splits the whole topology into a set of mutually disconnected clusters of nonextensive size. If nodes belonging to this optimal set are removed, it is physically impossible for any outbreak to reach a finite fraction of the network, so no global epidemic is possible. To implement this approach, we use the procedure described by Morone and Makse [5]. We remove sequentially one by one all nodes in the network based on their collective influence, which is recalculated at each step (using a radius of 3, that is, considering in the computation all nodes within three steps from the target node).
At any step we take note of the number of nodes still in the network () and of the size () of each connected network component (). In the case of an epidemic starting from a random node in the network at step , the probability that a component is infected is equal to . If the seed belongs to , the number of nodes saved will be equal to . Thus, after removing nodes, the expected number of saved nodes is
| (A1) |
will in general be low at the beginning of the immunization, when the size of the largest connected component is still very large. Then, it will increase until it reaches a maximum, representative of the best tradeoff between the number of nodes removed and the level of immunization reached. After that optimal point, additional node removals will not lead to an overall reduction of network component size (so that will decrease approaching 0).
We assume the number corresponding to the maximum value of is the number of nodes sacrificed by a preventive immunization approach. Figure 7 shows that this value almost perfectly matches the value calculated via the usual criterion as the number of nodes to be removed such that the largest connected cluster remaining is smaller than [21].
FIG. 7.
Scatter plot of vs for ER graphs with various and scale-free with and () showing that the two quantities are almost identical. The solid line indicates perfect equality.
This indicates that plays the role of susceptibility for the optimal percolation transition.
The procedure just described guarantees that, after removing nodes, no outbreak can reach endemic proportions, even in the worst case, . If the spreading probability is smaller than 1, however, the fraction of saved nodes will be on average larger than . To determine this quantity, the procedure is the following. At step (i.e., after nodes have been removed based on their collective influence), some SIR simulations are performed and the average number of saved nodes is computed. This quantity tends to grow with due to the immunization, but for larger values it decreases because of the node removal. The value of corresponding to the maximum sets the optimal value used in Fig. 4.
APPENDIX B: ANALYTICAL EVALUATION OF
In this appendix, we present the details of the derivation of Eq. (2) based on the heterogeneous mean-field (HMF) theory for SIR [26]. Alternative approaches based on message-passing [27] or branching processes [28] would be possible.
We define as , and , respectively, the density of nodes of degree that are in state S, I, and R, respectively, at time . The total fraction of nodes in state S is (analogous formulas hold for the other states). For simplicity, we omit the explicit indication of the time dependence when not needed. For continuous dynamics [defined by the parameters (rate of spontaneous recovery) and (rate of infection through an edge connecting a node in state I with a node in state S)], the evolution of the densities is, within the HMF approximation, given by
| (B1) |
| (B2) |
| (B3) |
where
| (B4) |
is the probability that an edge points to an infected vertex and is capable of transmitting the disease. By rescaling the time unit, it is possible to set with no loss of generality. The form of the equations guarantees the conservation of the total probability . The initial condition with a single infected node implies , and .
Multiplying the equation for by and summing over , we obtain
| (B5) |
For sufficiently short times, one can assume , so that
| (B6) |
The temporal scale
| (B7) |
governs the exponential growth (or decay) of , depending on whether is larger or smaller than the threshold .
By integrating Eq. (B6) and inserting the result into the equation for , we get
| (B8) |
which can be integrated yielding
| (B9) |
where .
By integrating the equation for [Eq. (B3)], we obtain
| (B10) |
so .
The quarantine procedure consists in removing from the system all infected nodes and all their susceptible neighbors. For infected nodes of degree , this means removing nodes; the factor accounts for the fact that one neighbor of an infected node is the node that transmitted the infection to it, therefore it cannot be susceptible. Hence the global fraction of nodes that are left after the quarantine procedure is
| (B11) |
The last term on the right-hand side in Eq. (B11) can be rewritten, by considering the temporal evolution of [Eq. (B9)], as
| (B12) |
which, inserted into Eq. (B11) and using , yields the expression for the total fraction of nodes saved by a quarantine applied when the number of recovered nodes is :
| (B13) |
It is important to note that this expression holds for short times and on locally treelike networks [otherwise the expression for the number of neighbors of nodes of degree to be quarantined is overestimated].
To compare with simulation results performed using the independent cascade model, we notice that HMF theory provides an epidemic threshold that is only approximate for continuous-time SIR but is exact for the ICM [1]. Exploiting this correspondence, we assume the validity of Eq. (B13) for ICM dynamics, provided is replaced with the probability in Eq. (B7) for .
Footnotes
Notice that, despite the formulation of the original paper, optimal percolation is a strategy for minimizing (not for maximizing) spreading in a network [19].
REFERENCES
- [1].R. Pastor-Satorras, C. Castellano, P. Van Mieghem, and A. Vespignani, Rev. Mod. Phys. 87, 925 (2015). 10.1103/RevModPhys.87.925 [DOI] [Google Scholar]
- [2].R. Pastor-Satorras and A. Vespignani, Phys. Rev. E 65, 036104 (2002). 10.1103/PhysRevE.65.036104 [DOI] [PubMed] [Google Scholar]
- [3].R. Cohen, S. Havlin, and D. ben-Avraham, Phys. Rev. Lett. 91, 247901 (2003). 10.1103/PhysRevLett.91.247901 [DOI] [PubMed] [Google Scholar]
- [4].Y. Chen, G. Paul, S. Havlin, F. Liljeros, and H. E. Stanley, Phys. Rev. Lett. 101, 058701 (2008). 10.1103/PhysRevLett.101.058701 [DOI] [PubMed] [Google Scholar]
- [5].F. Morone and H. A. Makse, Nature (London) 524, 65 (2015). 10.1038/nature14604 [DOI] [PubMed] [Google Scholar]
- [6].A. Tatem, D. Rogers, and S. Hay, in Global Mapping of Infectious Diseases: Methods, Examples and Emerging Applications, Advances in Parasitology Vol. 62, edited by A. G. Simon I. Hay and D. J. Rogers (Academic Press, London, 2006), pp. 293–343. [DOI] [PubMed] [Google Scholar]
- [7].M. Barthélemy, Phys. Rep. 499, 1 (2011). 10.1016/j.physrep.2010.11.002 [DOI] [Google Scholar]
- [8].G. Strona, C. J. Carstens, and P. S. A. Beck, Sci. Rep. 7, 71 (2017). 10.1038/s41598-017-00077-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].J. M. Rodrigues, in Pine Wilt Disease: A Worldwide Threat to Forest Ecosystems (Springer, Dordrecht, Netherlands, 2008), pp. 5–14. [Google Scholar]
- [10].M. Lipsitch, T. Cohen, B. Cooper, J. M. Robins, S. Ma, L. James, G. Gopalakrishna, S. K. Chew, C. C. Tan, M. H. Samore, D. Fisman, and M. Murray, Science 300, 1966 (2003). 10.1126/science.1086616 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].F. Nian and X. Wang, J. Theor. Biol. 264, 77 (2010). 10.1016/j.jtbi.2010.01.007 [DOI] [PubMed] [Google Scholar]
- [12].T. Hasegawa and K. Nemoto, Phys. Rev. E 96, 022311 (2017). 10.1103/PhysRevE.96.022311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].T. Pereira and L.-S. Young, Phys. Rev. E 92, 022822 (2015). 10.1103/PhysRevE.92.022822 [DOI] [PubMed] [Google Scholar]
- [14].S. Eubank, H. Guclu, V. Kumar, M. Marathe, A. Srinivasan, Z. Toroczkai, and N. Wang, Nature (London) 429, 180 (2004). 10.1038/nature02541 [DOI] [PubMed] [Google Scholar]
- [15].W. Chen, L. V. S. Lakshmanan, and C. Castillo, Information and Influence Propagation in Social Networks (Morgan & Claypool, 2013). [Google Scholar]
- [16].M. Catanzaro, M. Boguñá, and R. Pastor-Satorras, Phys. Rev. E 71, 027103 (2005). 10.1103/PhysRevE.71.027103 [DOI] [PubMed] [Google Scholar]
- [17].S. N. Dorogovtsev, A. V. Goltsev, and J. F. F. Mendes, Rev. Mod. Phys. 80, 1275 (2008). 10.1103/RevModPhys.80.1275 [DOI] [Google Scholar]
- [18].R. B. Ellis, J. L. Martin, and C. Yan, Algorithmica 47, 421 (2007). 10.1007/s00453-006-0172-y [DOI] [Google Scholar]
- [19].F. Radicchi and C. Castellano, Phys. Rev. E 95, 012318 (2017). 10.1103/PhysRevE.95.012318 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].A. Braunstein, L. Dall'Asta, G. Semerjian, and L. Zdeborová, Proc. Natl. Acad. Sci. (U.S.A.) 113, 12368 (2016). 10.1073/pnas.1605083113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].P. Clusella, P. Grassberger, F. J. Pérez-Reche, and A. Politi, Phys. Rev. Lett. 117, 208301 (2016). 10.1103/PhysRevLett.117.208301 [DOI] [PubMed] [Google Scholar]
- [22].L. Zdeborová, P. Zhang, and H.-J. Zhou, Sci. Rep. 6, 37954 (2016). 10.1038/srep37954 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].C. Castellano and R. Pastor-Satorras, Eur. Phys. J. B 89, 243 (2016). 10.1140/epjb/e2016-60953-5 [DOI] [Google Scholar]
- [24].http://openflights.org/, accessed: 2016-04-15.
- [25].D. J. Watts and S. H. Strogatz, Nature (London) 393, 440 (1998). 10.1038/30918 [DOI] [PubMed] [Google Scholar]
- [26].M. Boguñá, R. Pastor-Satorras, and A. Vespignani, in Statistical Mechanics of Complex Networks, Lecture Notes in Physics Vol. 625, edited by R. Pastor-Satorras, J. M. Rubí, and A. Diaz-Guilera (Springer Verlag, Berlin, 2003), pp. 127–147. [Google Scholar]
- [27].T. Rogers, Europhys. Lett. 109, 28005 (2015). 10.1209/0295-5075/109/28005 [DOI] [Google Scholar]
- [28].J. P. Gleeson, K. P. O'Sullivan, R. A. Baños, and Y. Moreno, Phys. Rev. X 6, 021019 (2016). 10.1103/PhysRevX.6.021019 [DOI] [Google Scholar]