Robustness and fragility of the susceptible-infected-susceptible epidemic models on complex networks

Abstract

We analyze two alterations of the standard susceptible-infected-susceptible (SIS) dynamics that preserve the central properties of spontaneous healing and infection capacity of a vertex increasing unlimitedly with its degree. All models have the same epidemic thresholds in mean-field theories but depending on the network properties, simulations yield a dual scenario, in which the epidemic thresholds of the modified SIS models can be either dramatically altered or remain unchanged in comparison with the standard dynamics. For uncorrelated synthetic networks having a power-law degree distribution with exponent $\gamma <5/2$, the SIS dynamics are robust exhibiting essentially the same outcomes for all investigated models. A threshold in better agreement with the heterogeneous rather than quenched mean-field theory is observed in the modified dynamics for exponent $\gamma >5/2$. Differences are more remarkable for $\gamma >3$, where a finite threshold is found in the modified models in contrast with the vanishing threshold of the original one. This duality is elucidated in terms of epidemic lifespan on star graphs. We verify that the activation of the modified SIS models is triggered in the innermost component of the network given by a $k$-core decomposition for $\gamma <3$ while it happens only for $\gamma <5/2$ in the standard model. For $\gamma >3$, the activation in the modified dynamics is collective involving essentially the whole network while it is triggered by hubs in the standard SIS. The duality also appears in the finite-size scaling of the critical quantities where mean-field behaviors are observed for the modified but not for the original dynamics. Our results feed the discussions about the most proper conceptions of epidemic models to describe real systems and the choices of the most suitable theoretical approaches to deal with these models.

I. INTRODUCTION

Network science has been marked by its interdisciplinary nature since its consolidation as a new branch [1,2], especially the investigation of dynamical processes on networked substrates [3]. Epidemic spreading, one of the most prominent and widely investigated issues, is usually investigated by means of stochastic agent-based models [4]. Despite several advances in the understanding of epidemic models on networks [4–11], it remains target of recent intensive investigations [12–19].

One of the most basic but still not fully understood epidemic processes on networks is the susceptible-infected-susceptible (SIS) model [4], which consists of agents lying on the vertices of a network which can be infected or susceptible. Infected individuals become spontaneously healed (susceptible) with rate $\mu$ and transmit the disease to their susceptible contacts with rate $\lambda$. In principle, the SIS dynamics can exhibit a phase transition between a disease-free (absorbing) state and an active stationary phase, in which the epidemics persists in an endemic state. The transition occurs at an epidemic threshold ${\lambda }_c$. However, for uncorrelated random networks with a power-law degree distribution $P\left(k\right)\sim k^{-\gamma }$, it was rigorously proved [5] and later put in sound physical grounds [11] that the absorbing phase is unstable in the thermodynamic limit implying that the epidemic threshold is formally zero.

Considering that both real and computationally generated networks are finite, the finite-size dependence of the epidemic variables is a fundamental issue. Analytically, it is frequently accessed by mean-field approximations that take into account the network heterogeneity but truncate at some level the dynamical correlations [8]. Two classes of mean-field theories are mostly used. The degree-based theory [20,21], termed as heterogeneous mean-field (HMF) [1,3], is a coarse-grained mixing approach, in which the vertex degree is the relevant quantity. This method is closely related to the annealed network regime where the connections are rewired in time scales much shorter than those of the dynamical processes taking place on the top of the network [4,22]. The individual-based theory [23–25], termed quenched mean-field (QMF) [7], considers the network structure without mixing using its adjacency matrix [1]. These theories predict equivalent epidemic thresholds of the SIS dynamics on uncorrelated random networks with power-law degree distribution of exponent $2<\gamma <5/2$ but are sharply conflicting for $\gamma >3$ [7], for which HMF predicts finite thresholds whereas QMF vanishing ones as $N\to \infty$. The latter is asymptotically in agreement with the exact results [5,6] and supported by stochastic simulations [11,26,27]. For $5/2<\gamma <3$, both theories state a null threshold as $N\to \infty$, but the way that the asymptotic value is approached and, thus, the effective finite-size thresholds are different. Improvements of these theories including dynamical correlations by means of pairwise approximations [8] do not change the foregoing scenarios [16,27,28].

Recently, a criterion formerly conceived for SIS model [11] was applied to determine the nature of epidemic thresholds of generic processes on networks with power-law degree distributions [12]. The criterion involves the recovering time ${\tau }_k$ of an epidemics on a star graph, consisting of a central vertex connected to $k$ leaves of degree 1 that mimics the hubs of a network, and the time ${\tau }^{\text{(inf)}}$ that the hubs take to mutually transmit the infection to each other. If ${\tau }_k\gg {\tau }^{\text{(inf)}}$, hubs remain active for times sufficiently long to infect each other and the epidemics is triggered by the mutual activation of hubs, leading to a vanishing threshold in the thermodynamic limit. If ${\tau }_k\lesssim {\tau }^{\text{(inf)}}$, the mutual reinfection is knocked out and the transition to an endemic phase can only take place collectively involving a finite fraction of the network and happens at a finite threshold. In Ref. [12], this criterion notably predicted that waning immunity [29], in which infected individuals are temporarily immunized before to become susceptible, leads to a finite threshold for $\gamma >3$ which disagrees with the prediction of QMF approximation, but in agreement with extensive numerical simulations.

A fundamental question naturally arises. How robust is the hub mutual activation mechanism of the standard SIS dynamics? In the present work, we tackle this problem comparing slightly modified versions of the standard SIS model, preserving the spontaneous healing and infection capacity increasing proportionally to the vertex degree. All modified and original models have the same thresholds in both HMF and QMF theories. However, the criterion of mutual reinfection time of hubs [11,12] predicts a finite threshold in the thermodynamic limit for the modified models in uncorrelated networks [30] with $\gamma >3$, in contrast with the standard SIS. Stochastic simulations [31] on large networks corroborate this prediction. For $5/2<\gamma <3$, we observed that the modified dynamics present a vanishing threshold in better agreement with HMF than QMF. For $2<\gamma <5/2$, the SIS infection mechanism is robust and all models have essentially the same epidemic threshold. This duality is explained in terms of epidemic activation mechanisms [9,12,32].

Our results gathered with previous reports of Ref. [12], in which waning immunity can drastically change the threshold behavior, lead to the following take-home messages. First, the metastable, localized, and active states of the standard SIS dynamics necessary to sustain the endemic activity for any infection rate for $\gamma >3$ are not universal and their realizations in real epidemic processes may be unrealistic. Second, for the widely more frequent case of networks with $2<\gamma <3$, the null threshold is a robust feature, obtained irrespectively of the existence of locally self-activated star subgraphs. In such an absence, epidemics is triggered in the innermost, densely connected component of the network given by a $k$-core decomposition [33], while for the original SIS model it happens only for $2<\gamma <5/2$ [32]. Last but not least, the HMF theory [3,4,20], which has been frequently pretermitted due to its failure in capturing the asymptotically null epidemic threshold of the standard SIS for $\gamma >3$ [7,23,24], is more accurate than the QMF theory for the present modified SIS models and also in other models as contact processes [28] and SIRS [12]. The origins of this worse performance of the QMF theory is discussed in our conclusions.

The remaining of the paper is organized as follows. Section II describes the investigated models, and their mean-field theories are discussed in Sec. III. Epidemic thresholds obtained in numerical simulations are presented and compared with mean-field theories in Sec. IV. The finite-size scaling of the critical quantities are provided in Sec. V. We draw our concluding remarks and prospects in Sec. VI. Appendices A, B, and C complement the paper with analytical and numerical details.

II. EPIDEMIC MODELS

We investigate three epidemic dynamics where each vertex of the network can be either infected or susceptible. The infected ones are spontaneously healed with rate $\mu$ in all models. In the standard SIS, hereafter called $\mathrm{SIS}\text{-}\mathcal{S}$, an infected vertex infects each susceptible nearest-neighbor with rate $\lambda$. In the $\mathrm{SIS}\text{-}\mathcal{T}$ model, infection is a threshold process where susceptible vertices are infected with rate $\lambda$ if they have at least one infected nearest-neighbor.¹ Finally, $\mathrm{SIS}\text{-}\mathcal{A}$ is a modification of the contact process [35] where the infected vertices simultaneously infect all susceptible neighbors with rate $\lambda$. The symbols $\mathcal{S}$, $\mathcal{T}$, and $\mathcal{A}$ make reference to standard, threshold, and all in the model definitions. The models rules and some details of their computer implementations described in Appendix A are summarized in Table I.

TABLE I.

Epidemic model definitions and some computer implementation details of the Gillespie algorithm (GA) presented in Appendix A. Symbols: $N_{\inf }$ is the number of infected vertices; $N_{\mathrm{SI}}$ is number of susceptible vertices with at least one infected nearest neighbor; $N_{\mathrm{e}}$ is the number of edges emanating from infected vertices; and $u$ is random variable uniformly distributed in the interval (0,1).

$\mathrm{SIS}\text{-}\mathcal{T}$ (threshold) [36,37]	$\mathrm{SIS}\text{-}\mathcal{A}$ (all) [38,39]	$\mathrm{SIS}\text{-}\mathcal{S}$ (standard) [4]
Infected vertices are	Infected vertices are	Infected vertices are
spontaneously healed	spontaneously healed	spontaneously healed
with rate $\mu$	with rate $\mu$	with rate $\mu$
Susceptible vertices become	Infected vertices infect	Infected vertices
infected with rate $\lambda$	at once all susceptible	independently infect
if they have at least one	neighbors with	each susceptible neighbor
infected neighbor	rate $\lambda$	with rate $\lambda$
GA infection probability	GA infection probability	GA infection probability
$q={\displaystyle \frac{\lambda N_{\mathrm{SI}}}{\mu N_{\inf }+\lambda N_{\mathrm{SI}}}}$	$q={\displaystyle \frac{\lambda }{\mu +\lambda }}$	$q={\displaystyle \frac{\lambda N_{\mathrm{e}}}{\mu N_{\inf }+\lambda N_{\mathrm{e}}}}$
GA time step	GA time step	GA time step
$\tau ={\displaystyle \frac{-ln\left(u\right)}{\mu N_{\inf }+\lambda N_{\mathrm{SI}}}}$	$\tau ={\displaystyle \frac{-ln\left(u\right)}{(\mu +\lambda )N_{\inf }}}$	$\tau ={\displaystyle \frac{-ln\left(u\right)}{\mu N_{\inf }+\lambda N_{\mathrm{e}}}}$

The modified dynamics preserve two central features of the standard SIS model: spontaneous healing and infection capacity of a vertex increasing proportionally to its degree. All models have their counterparts in regular lattices with a fixed coordination number $k$: $\mathrm{SIS}\text{-}\mathcal{S}$ can be mapped in the contact process (CP) [35,40], in which infected vertices transmit to a nearest-neighbor chosen at random with rate ${\lambda }_{\text{CP}}$ and heals spontaneously, using ${\lambda }_{\text{SIS}}={\lambda }_{\text{CP}}/k$. $\mathrm{SIS}\text{-}\mathcal{A}$ was investigated in Refs. [38,39] while $\mathrm{SIS}\text{-}\mathcal{T}$ was investigated in Refs. [36,37]. In lattices, all models belong to the directed percolation universality class [35].

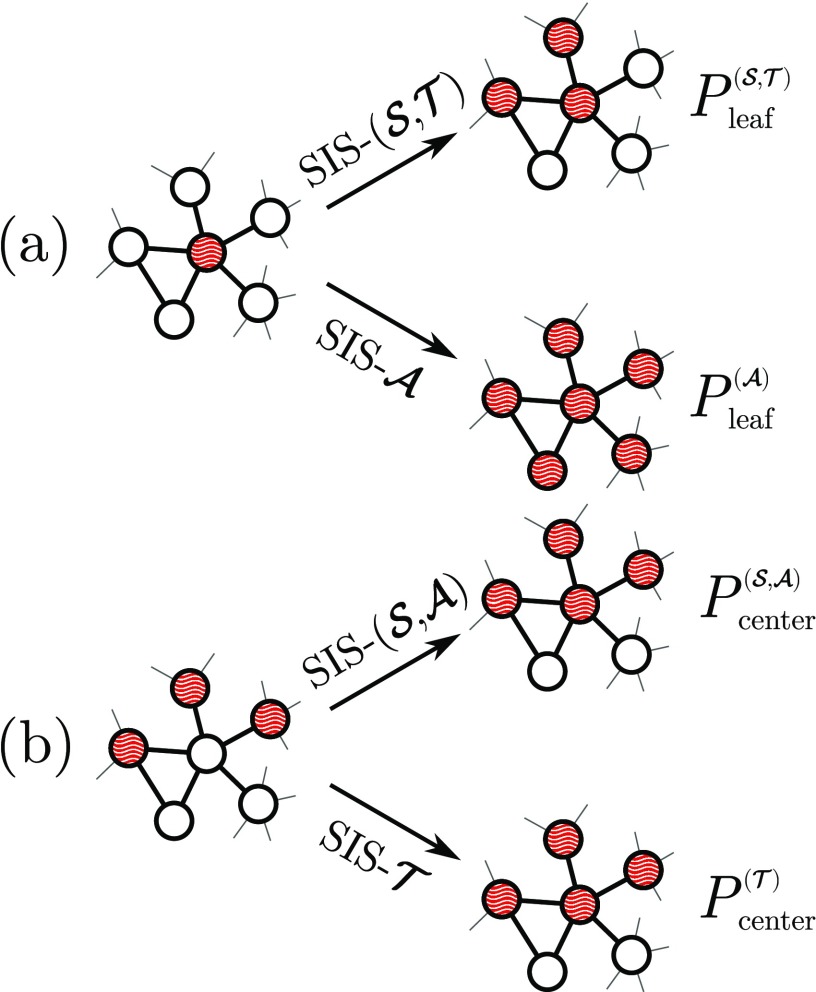
Figure 1 shows two important situations where the modified models differ from the standard SIS. Consider an infinitesimal time interval $\mathrm{\Delta }t$ and an infected vertex (the center) surrounded by $k$ susceptible neighbors (leaves); see Fig. 1(a). The probability that $s$ leaves are infected by the center for both $\mathrm{SIS}\text{-}\mathcal{S}$ and $\mathrm{SIS}\text{-}\mathcal{T}$ is

$$P_{\text{leaf}}^{(\mathcal{S},\mathcal{T})}\left(s\right)=\left(\genfrac{}{}{0pt}{}{k}{s}\right){\left(\lambda \mathrm{\Delta }t\right)}^s{(1-\lambda \mathrm{\Delta }t)}^{k-s},$$ (1)

while for $\mathrm{SIS}\text{-}\mathcal{A}$ it is

$$P_{\text{leaf}}^{\left(\mathcal{A}\right)}\left(s\right)=\lambda \mathrm{\Delta }t{\delta }_{s,k},$$ (2)

where ${\delta }_{s,k}$ is the Kronecker $\delta$ symbol. Note that both expressions produce the same mean number of infected leaves $\langle s\rangle =\lambda k\mathrm{\Delta }t$. Now, the probability that a susceptible center surrounded by $s>0$ infected leaves, Fig. 1(b), is infected is given by

$$P_{\text{center}}^{(\mathcal{S},\mathcal{A})}\left(s\right)=1-{(1-\lambda \mathrm{\Delta }t)}^s\approx \lambda s\mathrm{\Delta }t$$ (3)

for $\mathrm{SIS}\text{-}\mathcal{S}$ and $\mathrm{SIS}\text{-}\mathcal{A}$, while for $\mathrm{SIS}\text{-}\mathcal{T}$ it becomes

$$P_{\text{center}}^{\left(\mathcal{T}\right)}=\lambda \mathrm{\Delta }t.$$ (4)

So, while the infection of leaves by the center in $\mathrm{SIS}\text{-}\mathcal{S}$ is equivalent to $\mathrm{SIS}\text{-}\mathcal{T}$, the infection of the center by leaves in $\mathrm{SIS}\text{-}\mathcal{S}$ is equivalent to $\mathrm{SIS}\text{-}\mathcal{A}$.

FIG. 1.

Some infection processes in the SIS models. (a) An infected vertex (center) with many susceptible neighbors (leaves). (b) A susceptible center with infected leaves. Transition probabilities are defined in Eqs. (1)–(4).

The simulations of these models were performed using the algorithms described in Appendix A, which include phantom processes [31] in the statistically exact Gillespie algorithm (GA) [41] for the simulations of general Markovian stochastic processes. Some important implementation details are highlighted in Table I. The equivalence between optimized prescriptions and the original GA as well as their computational performances for several models, including $\mathrm{SIS}\text{-}\mathcal{S}$, can be found in Ref. [31]. The implementations of $\mathrm{SIS}\text{-}\mathcal{T}$ and $\mathcal{A}$ can be derived in an analogous way.

III. MEAN FIELD ANALYSIS

The HMF theory consists in dynamical equations for the probability ${\rho }_k$ that a vertex of degree $k$ is infected and disregards the stochasticity of the process. The probability that a neighbor of a vertex of degree $k$ is infected reads as [34] ${\mathrm{\Theta }}_k={\sum }_{k^{\prime }}P\left(k^{\prime }\right|k){\rho }_{k^{\prime }}$ where $P\left(k^{\prime }\right|k)$ is the probability that a neighbor of a vertex with degree $k$ has degree $k^{\prime }$. So, ${\rho }_k$ evolves as

$$\frac{d{\rho }_k}{dt}=-\mu {\rho }_k+\lambda (1-{\rho }_k){\mathrm{\Psi }}_k\left({\mathrm{\Theta }}_k\right),$$ (5)

where ${\mathrm{\Psi }}_k\left({\mathrm{\Theta }}_k\right)=k{\mathrm{\Theta }}_k$ for $\mathrm{SIS}\text{-}\mathcal{S}$ and $\mathrm{SIS}\text{-}\mathcal{A}$, and ${\mathrm{\Psi }}_k\left({\mathrm{\Theta }}_k\right)=1-{(1-{\mathrm{\Theta }}_k)}^k$ for $\mathrm{SIS}\text{-}\mathcal{T}$. The QMF theory consists of dynamical equations for the probability ${\rho }_i$ that a vertex $i$ is infected and reads as

$$\frac{d{\rho }_i}{dt}=-\mu {\rho }_i+\lambda (1-{\rho }_i){\mathrm{\Psi }}_i,$$ (6)

where ${\mathrm{\Psi }}_i={\sum }_j{A}_{ij}{\rho }_j$ for $\mathrm{SIS}\text{-}\mathcal{S}$ and $\mathrm{SIS}\text{-}\mathcal{A}$, and

$${\mathrm{\Psi }}_i=1-\prod _{j|A_{ij}=1}(1-{\rho }_j)$$

for $\mathrm{SIS}\text{-}\mathcal{T}$, in which and the adjacency matrix is given by $A_{ij}=1$ if $i$ and $j$ are connected and $A_{ij}=0$ otherwise. The multiple simultaneous infections in $\mathrm{SIS}\text{-}\mathcal{A}$ do not play a role in these one-vertex mean-field theories since there are no multiple connections. It is worth mentioning that the HMF theory of $\mathrm{SIS}\text{-}\mathcal{T}$ for uncorrelated networks with $P\left(k^{\prime }\right|k)=k^{\prime }P\left(k^{\prime }\right)/\langle k\rangle$ [42] was recently investigated [43].

The mean-field epidemic thresholds can be obtained with the stability analysis and linearization of Eqs. (5) and (6) around the fixed points ${\rho }_k=0$ or ${\rho }_i=0$, respectively. The linearized equations are the same for the three models

$$\frac{d{\rho }_k}{dt}=-\mu {\rho }_k+\lambda \sum _{k^{\prime }}{C}_{k{k}^{\prime }}{\rho }_{k^{\prime }}$$ (7)

and

$$\frac{d{\rho }_i}{dt}=-\mu {\rho }_i+\lambda \sum _j{A}_{ij}{\rho }_j,$$ (8)

where $C_{k^{\prime }k}=kP\left(k^{\prime }\right|k)$. The HMF and QMF thresholds are obtained when the largest eigenvalue of the respective Jacobians $J_{k{k}^{\prime }}^{\text{HMF}}=-\mu {\delta }_{k{k}^{\prime }}+\lambda C_{k{k}^{\prime }}$ and $J_{ij}^{\text{QMF}}=-\mu {\delta }_{ij}+\lambda A_{ij}$ are zero. For the HMF theory, it is given by [44]

$${\lambda }_c^{\text{HMF}}=\frac{1}{{\mathrm{{\rm Y}}}_{\text{max}}},$$ (9)

where ${\mathrm{{\rm Y}}}_{\text{max}}$ is the largest eigenvalue of $C_{k^{\prime }k}$. For uncorrelated networks we obtain

$${\lambda }_c^{\text{HMF}}=\frac{\langle k\rangle }{\langle k^2\rangle },$$ (10)

where $\langle k^s\rangle ={\sum }_k{k}^{s}P\left(k\right)$. For the QMF theory, we obtain [7]

$${\lambda }_c^{\text{QMF}}=\frac{1}{{\mathrm{\Lambda }}_{\text{max}}},$$ (11)

where ${\mathrm{\Lambda }}_{\text{max}}$ is the largest eigenvalue of the adjacency matrix $A_{ij}$.

The HMF theory on uncorrelated networks was compared with the numerical simulations on annealed networks (see Appendix A), for which this theory exactly predicts the threshold and average density of infected vertices in the thermodynamic limit [22,45]. Simulations with absorbing states near the transition need special techniques [31]. We use here the standard quasistationary (QS) method described in Ref. [46], in which the averaging is constrained to the active states and converges to the actual stationary phase in the thermodynamic limit. The threshold in finite networks can be estimated using the principal peak of the dynamical susceptibility $\chi$ defined in the QS state as [26]

$$\chi =N\frac{\langle {\rho }^2\rangle -{\langle \rho \rangle }^2}{\langle \rho \rangle }.$$ (12)

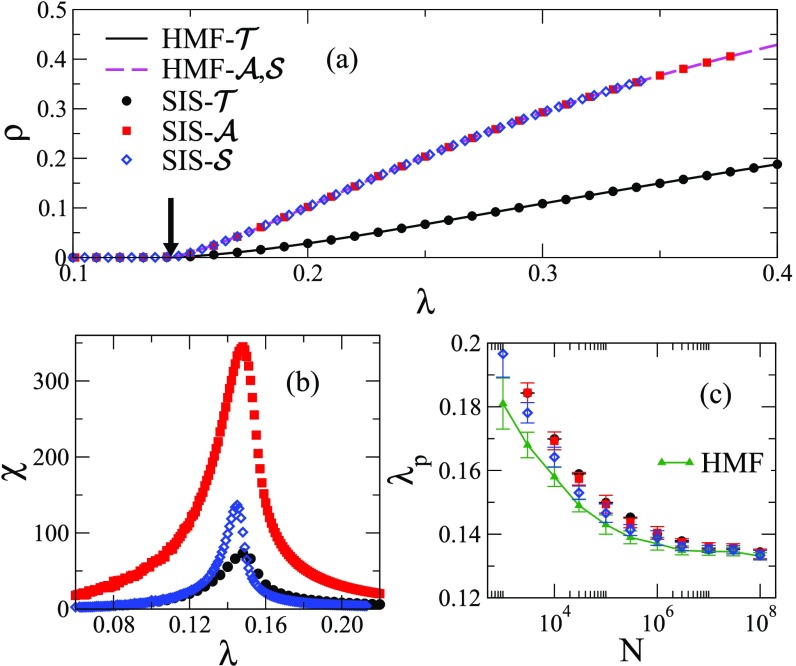
Figures 2(a) and 2(c) confirm the agreement between simulations on annealed networks and HMF theory for the stationary densities and the thresholds, respectively, in all investigated models. However, the fluctuations of the order parameter are different as shown by the susceptibility curves in Fig. 2(b). See also Sec. V.

FIG. 2.

Comparison of HMF theory and simulations on annealed networks with $N={10}^5$ vertices, degree distribution $P\left(k\right)\sim k^{-3.5}$, minimal degree $k_{\text{min}}=3$, and upper cutoff $k_{\text{c}}=\sqrt{N}$. (a) QS density and (b) susceptibility versus infection rate curves are shown. Lines in (a) are numerical solutions of Eq. (5) in the stationary regime and the arrow indicates the HMF epidemic threshold ${\lambda }_c^{\text{HMF}}=\langle k\rangle /\langle k^2\rangle$. (c) Finite-size dependence of the threshold estimated via susceptibility and HMF theory. The curves correspond to averages over 10 independent network realizations.

IV. SIS MODELS ON SYNTHETIC QUENCHED NETWORKS

A. Epidemic thresholds

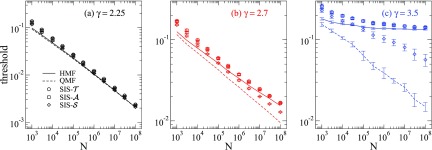
We investigate networks having power-law degree distribution $P\left(k\right)\sim k^{-\gamma }$, generated with the uncorrelated configuration model (UCM) [30] with minimal vertex degree $k_{\text{min}}=3$ and structural upper cutoff $k_{\text{c}}=\sqrt{N}$, granting the absence of degree correlations [47] permitting, therefore, comparison with the HMF epidemic threshold given by Eq. (10). The thresholds obtained in simulations are compared with HMF and QMF theories in Fig. 3.

FIG. 3.

Epidemic thresholds for SIS models on UCM networks with $k_{\text{min}}=3$, $k_{\text{c}}=\sqrt{N}$, and different degree exponents (a) $\gamma =2.25$, (b) 2.7, and (c) 3.5. Solid and dashed lines correspond to HMF and QMF theories, respectively. Curves are averages over 10 network realizations. Negligible error bars in mean-field theories are not shown.

For $\gamma <5/2$, here represented by $\gamma =2.25$ in Fig. 3(a), all models have approximately the same threshold well described by both HMF and QMF theories, which have already been reported for $\mathrm{SIS}\text{-}\mathcal{S}$ [26].

For $5/2<\gamma <3$, represented by $\gamma =2.7$ in Fig. 3(b), $\mathrm{SIS}\text{-}\mathcal{T}$ and $\mathrm{SIS}\text{-}\mathcal{A}$ have essentially the same threshold whose scaling is very well fitted by the HMF theory and deviates from QMF. The threshold of the standard $\mathrm{SIS}\text{-}\mathcal{S}$ vanishes with a scaling deviating from both HMF and QMF scalings. A good agreement between the threshold of the standard SIS for $\gamma =2.7$ can be recovered with the pairwise QMF theory of Ref. [27] but not with the pairwise HMF theory of Refs. [16,28]; see Appendix B.

The results for modified SIS models are markedly contrasting with the standard one² for $\gamma >3$, represented by $\gamma =3.5$ in Fig. 3(c). The modified $\mathrm{SIS}\text{-}\mathcal{T}$ and $\mathcal{A}$ dynamics present a finite threshold in very satisfactory accordance with HMF theory and contrasting with the original $\mathrm{SIS}\text{-}\mathcal{S}$ that presents the well-known threshold approaching zero as the size increases. Note, however, that the thresholds of $\mathrm{SIS}\text{-}\mathcal{S}$ have a scaling incompatible with QMF for the investigated size range that cannot be reckoned by neither pairwise QMF [27] or HMF [16,28] theories (see Appendix B). The latter still predicts a finite threshold, inconsistent with simulations and the rigorous results [5] for $\mathrm{SIS}\text{-}\mathcal{S}$.

B. Activation mechanisms for $\gamma >3$

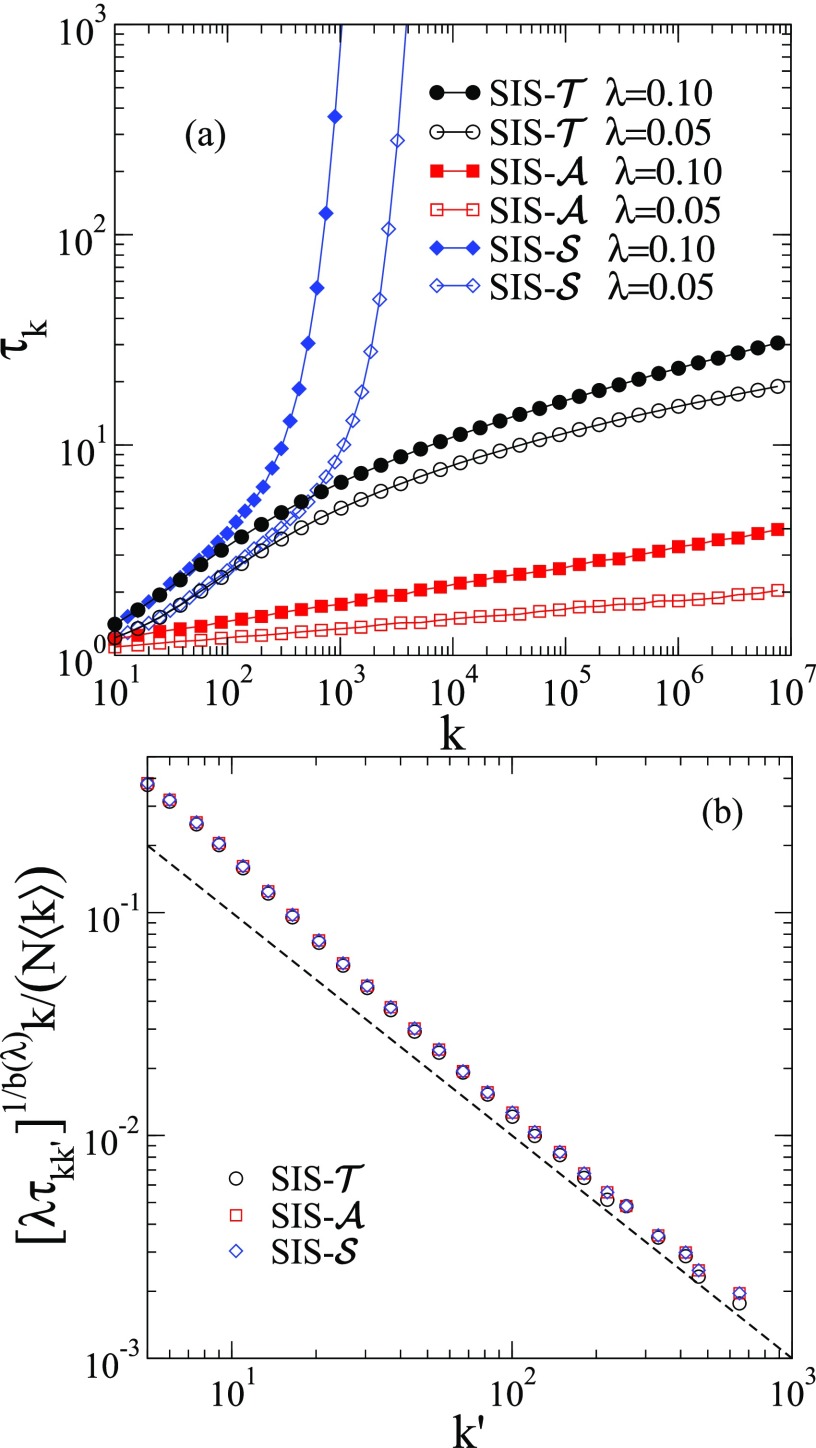
To clarify the antagonistic results for $\gamma >3$, we consider the recovering time of the epidemics on star graphs for small values of $\lambda$. Figure 4(a) shows the epidemic lifespan for the distinct SIS models as a function of the star graph size. For standard $\mathrm{SIS}\text{-}\mathcal{S}$, we see an exponential growth predicted by the approximated discrete time dynamics of Ref. [11] (also Ref. [12]) given by ${\tau }_k^{\left(\mathcal{S}\right)}\approx \frac{2}{\mu }exp\left[k{(\lambda /\mu )}^2\right]$; see Appendix C. However, $\mathrm{SIS}\text{-}\mathcal{T}$ and $\mathrm{SIS}\text{-}\mathcal{A}$ present epidemic lifespans increasing very slowly with graph size, consistent with a logarithmic growth. Applying the discrete time approach, a finite lifespan is obtained for $\mathrm{SIS}\text{-}\mathcal{A}$ and, after some refinement of the theory, a logarithmic increase is found for $\mathrm{SIS}\text{-}\mathcal{T}$; see Appendix C for details. Indeed, the activities in $\mathrm{SIS}\text{-}\mathcal{A}$ are more correlated, and this has a significant effect on the probability of hub activation.

FIG. 4.

(a) Activity lifespan for epidemic processes on star graphs. The initial condition is the center infected and all leaves susceptible. The number of runs varies from ${10}^3$ to ${10}^5$, the larger number the smaller $\lambda$. (b) Mutual reinfection of hubs scaled according to Eq. (13). The degree exponent is $\gamma =3.5$, the size is $N={10}^6$ and infection rate is $\lambda =0.05$. The vertex that is kept infected has degree $k=50$. The dashed line is the prediction of the right-hand side of Eq. (13).

An upper bound for the long-range infection times of hubs of degrees $k$ and $k^{\prime }$, denoted by ${\tau }_{k{k}^{\prime }}^{\text{(inf)}}$, for uncorrelated networks can be obtained following the same steps of Ref. [11] (also Ref. [12]). The result is the same for all investigated SIS models and given by

$${\tau }_{k{k}^{\prime }}^{\text{(inf)}}\le {\tau }_{k{k}^{\prime }}=\frac{1}{\lambda }{\left[\frac{N\langle k\rangle }{k{k}^{\prime }}\right]}^{b\left(\lambda \right)},$$ (13)

where $b\left(\lambda \right)=ln(1+\mu /\lambda )/ln\kappa$ and $\kappa =\langle k^2\rangle /\langle k\rangle$. Even being rigorously an upper bound, the right-hand side of Eq. (13) works very accurately for $\lambda \ll \mu$ and $\gamma >3$ such that we can adopt ${\tau }_{k{k}^{\prime }}^{\text{(inf)}}\approx {\tau }_{k{k}^{\prime }}$ as done for $\mathrm{SIS}\text{-}\mathcal{S}$ [11] and other epidemic models [12]. This agreement is confirmed in Fig. 4(b) for $\gamma =3.5$. The simulation is run keeping one single vertex of degree $k$ always infected (never heals) and computing the time for the infection to reach for the first time each vertex of the network, limited to a maximal time $t_{\text{max}}={10}^{10}$. Vertices that were not reached are not included in the averages but they represent a tiny fraction.

With the approximation given by the right-hand side of Eq. (13), we have that ${\tau }_{k{k}^{\prime }}^{\text{(inf)}}\gtrsim {\tau }_{k_{\text{max}},k_{\text{max}}}^{\text{(inf)}}$, where $k_{\text{max}}$ is the largest degree of the network that scales as $\langle k_{\text{max}}\rangle \sim N^{1/(\gamma -1)}$ for UCM networks with $\gamma >3$ [47]. Also, we have that $b\left(\lambda \right)$ is finite since $\kappa$ converges to a constant as $N\to \infty$ for $\gamma >3$, providing an algebraic increase of ${\tau }_{k{k}^{\prime }}^{\text{(inf)}}$ with $N$. The condition ${\tau }^{\text{(inf)}}\gg {\tau }_k^{(\mathcal{T},\mathcal{A})}$ is obeyed such that epidemics in the modified SIS models cannot be activated by hubs when $\lambda \ll \mu$ and a collective phase transition at finite threshold is expected [12] in contrast with ${\tau }^{\text{(inf)}}\ll {\tau }_k^{\left(\mathcal{S}\right)}$ of the standard SIS, in which the hub activation mechanism is at work and the threshold is null in the thermodynamic limit.

C. Activation mechanisms for $2<\gamma <3$

For $\gamma <3$, the hubs are sufficiently close [48] to infect each other even if their activity lifespans are not too large (exponential) and the threshold goes to zero for all models as $N\to \infty$. However, there exists a difference in the threshold scaling for $\gamma =2.7$ but does not for $\gamma =2.25$. It has been claimed [9] that the most effective spreaders in an epidemic processes lie in a subset containing the innermost core of the networks identified by the maximal index of the $k$-core decomposition³ [22,33]. For $\mathrm{SIS}\text{-}\mathcal{S}$, this mechanism is claimed to hold for uncorrelated networks with $\gamma <5/2$ but the case $5/2<\gamma <3$ has activation ruled by the hubs [32]. Since hubs cannot be activated in isolation for arbitrarily small $\lambda$ in $\mathrm{SIS}\text{-}\mathcal{A}$ and $\mathrm{SIS}\text{-}\mathcal{T}$, we propose that the epidemic threshold should be ruled by the subgraph identified by the maximal $k$-core for the whole range of scale-free networks with $2<\gamma <3$.

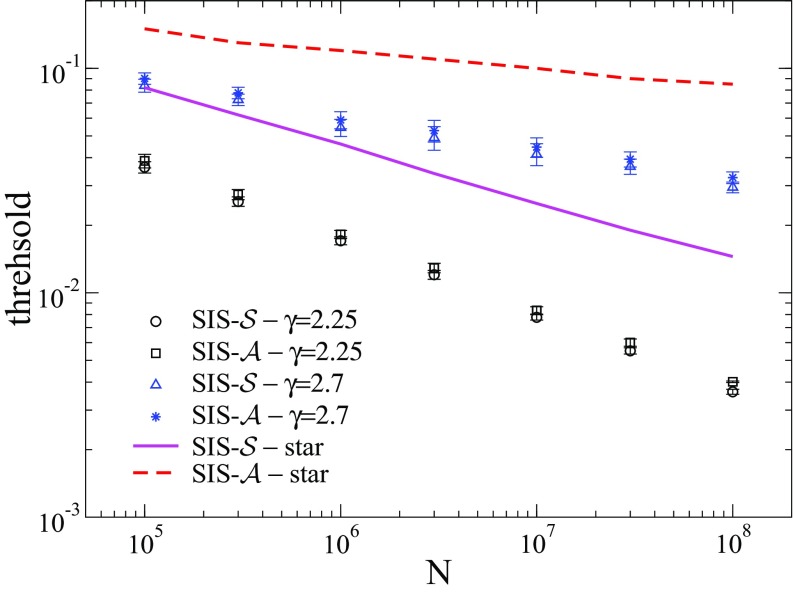
To check this conjecture we ran SIS models on subgraphs containing only the vertices belonging to either the maximum $k$-core or the star graph centered on the most connected vertex of the network with degree $k_{\text{max}}\approx \sqrt{N}$. Figure 5(a) shows that the $\mathrm{SIS}\text{-}\mathcal{S}$ and $\mathrm{SIS}\text{-}\mathcal{A}$ essentially have the same activation threshold for the maximal $k$-core for both values of $\gamma =2.25$ and 2.7 while the activation of the stars centered on the most connected vertex happens in very different thresholds for these models. The same analysis holds in the not shown data for $\mathrm{SIS}\text{-}\mathcal{T}$. Therefore, the following framework can be drawn. For $\gamma =2.25$, the $k$-core is activated first than hubs and the epidemic activation is triggered in the maximal $k$-core for all models. For $\gamma =2.7$, the hubs are activated firstly for $\mathrm{SIS}\text{-}\mathcal{S}$ while $k$-core is activated firstly in the other models such that the epidemic activation is due to hubs for the standard model and still $k$-core for the modified dynamics.

FIG. 5.

Epidemic thresholds for $\mathrm{SIS}\text{-}\mathcal{S}$ and $\mathrm{SIS}\text{-}\mathcal{A}$ running on the maximum $k$-core subgraph of networks with degree exponents $\gamma =2.25$ and 2.7. The simulation results on star graphs with $k_{\text{max}}\approx \sqrt{N}$ leaves are also presented. The averages were done over 10 networks realizations.

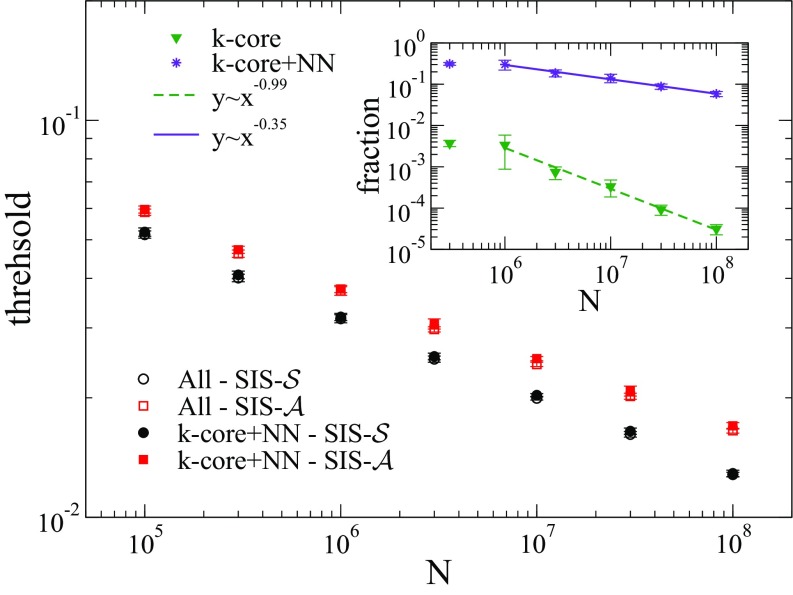
For $\gamma =2.7$, the effective epidemic thresholds for the entire networks are smaller than those calculated using only the maximal $k$-core or star centered on the largest hub even with these subgraphs being associated with the activation of the epidemics. We performed simulations in a subgraph with the maximal $k$-core plus their nearest-neighbors, which still represents a subextensive fraction of the network as shown in the inset of Fig. 6. The epidemic thresholds in this subset are essentially the same as those of the whole network for all models, as shown in Fig. 6 for $\mathrm{SIS}\text{-}\mathcal{A}$ and $\mathrm{SIS}\text{-}\mathcal{S}$. The trimming of edges reduces the epidemic activity in the subset containing only the maximal $k$-core while the $k$-core mediates the mutual interactions among hubs in the activation driven by them. We see that a large fraction of the network is redundant for the epidemic threshold independently if hub ($\mathrm{SIS}\text{-}\mathcal{S}$) or $k$-core activation ($\mathrm{SIS}\text{-}\mathcal{A}$ and $\mathcal{T}$) is at work. In both cases, the relevant region to reproduce the numerical threshold includes the maximal $k$-core plus its nearest neighbors.

FIG. 6.

Epidemic thresholds for $\mathrm{SIS}\text{-}\mathcal{S}$ and $\mathrm{SIS}\text{-}\mathcal{A}$ running on a subgraph with the maximum $k$-core plus the nearest-neighbor (NN) vertices of a UCM network with $\gamma =2.7$. Inset shows the fraction of the network that belongs to the maximal $k$-core including or not its NNs. Lines are power-law regressions.

Returning to the case $\gamma >3$, UCM networks do not present a $k$-core structure in the sense that the decomposition provides a single component containing the whole network [33]. So, since hubs cannot sustain activity for $\lambda \ll \mu$, the phase transition happens collectively, involving a finite fraction of the network at a finite threshold [12].

V. FINITE-SIZE SCALING OF CRITICAL QUANTITIES

The transition between endemic and disease-free phases can be suited as an absorbing state phase transition [35,49]. The finite-size scaling (FSS) at the critical point (or epidemic threshold) is fundamental for the characterization of the transition and its critical exponents [35,49]. Several studies concerned with the universality of the phase transition of the contact process [35] on complex networks have been performed both numerically and analytically [28,45,50–56]. For $\mathrm{SIS}\text{-}\mathcal{S}$, numerical analyses have been done [26,46]. A basic approach is to fit the critical QS density and susceptibility to power-laws in the forms

$$\rho \sim N^{-\nu }$$ (14)

and

$$\chi \sim N^{\varphi },$$ (15)

where $\nu$ and $\varphi$ are the critical exponents related to FSS.

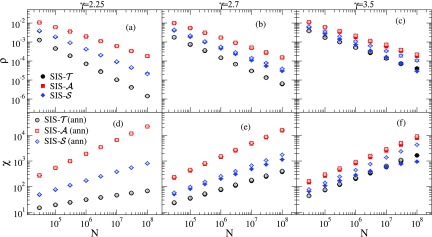
We considered simulations on annealed networks with same degree distributions as the quenched ones to represent the mean-field counterpart; see Appendix A for algorithms. Figure 7 presents the FSS of $\rho$ and $\chi$ at the effective, size-dependent epidemic threshold of the three SIS models on both UCM and annealed networks. For $\gamma =3.5$, we used a hard cutoff $k_c\sim N^{1/\gamma }$ that prevents outliers in the degree distribution and multiple peaks in the susceptibility curves of quenched networks [13,26] making, thus, the determination of the transition point much more accurate; see Refs. [13,31] for further discussion. For $\gamma <3$ the structural cutoff $k_c=\sqrt{N}$ was used. The FSS exponents obtained by simple power-law regressions for $N\ge {10}^6$ are shown in Table II. Uncertainties were calculated using different fit regions aiming at establishing equivalences or discrepancies between annealed and quenched simulations rather than accurate estimates of the asymptotic exponents.

FIG. 7.

Finite-size scaling of the critical QS quantities for SIS models on UCM networks with different degree exponents. The QS densities of infected vertices are shown in (a)–(c) while the QS susceptibilities are shown in (d)–(f). The data correspond to averages over 10 network realizations and error bars are smaller than symbols.

TABLE II.

Critical exponents of the FSS for the SIS models on UCM ($\nu$ and $\varphi$) and annealed (${\nu }_{\text{ann}}$ and ${\varphi }_{\text{ann}}$) networks. Exponents for $\mathrm{SIS}\text{-}\mathcal{S}$ with $\gamma =3.5$ are missing due to the smearing of the transition.

	$\gamma =2.25$		$\gamma =2.7$		$\gamma =3.5$
Model	$\nu$	${\nu }_{\text{ann}}$	$\nu$	${\nu }_{\text{ann}}$	$\nu$	${\nu }_{\text{ann}}$
$\mathcal{T}$	0.845(6)	0.84(2)	0.697(4)	0.692(6)	0.55(1)	0.555(3)
$\mathcal{A}$	0.519(9)	0.517(4)	0.52(1)	0.515(9)	0.499(6)	0.49(3)
$\mathcal{S}$	0.63(2)	0.655(2)	0.60(2)	0.57(1)	–	0.506(7)
	$\varphi$	${\varphi }_{\text{ann}}$	$\varphi$	${\varphi }_{\text{ann}}$	$\varphi$	${\varphi }_{\text{ann}}$
$\mathcal{T}$	0.167(2)	0.169(1)	0.353(1)	0.352(1)	0.458(1)	0.467(3)
$\mathcal{A}$	0.530(2)	0.528(2)	0.514(1)	0.513(1)	0.494(1)	0.497(1)
$\mathcal{S}$	0.329(5)	0.329(4)	0.372(1)	0.421(1)	–	0.496(1)

The FSS of the critical quantities provides a scenario in consonance with that observed for the thresholds. The FSS of both $\mathrm{SIS}\text{-}\mathcal{T}$ and $\mathcal{A}$ are in full agreement with the annealed simulations showing their mean-field behaviors for all values of $\gamma$ investigated. Moreover, the agreement between quenched and annealed networks is also found for $\mathrm{SIS}\text{-}\mathcal{S}$ for $\gamma <5/2$. For $\gamma >5/2$, the dichotomy with respect to $\mathrm{SIS}\text{-}\mathcal{S}$ is again present. A significant difference in the scaling happens for $\gamma =2.7$ and a sharp difference is obtained for $\gamma =3.5$. In the latter, we can see a susceptibility of the $\mathrm{SIS}\text{-}\mathcal{S}$ bending downwardly for the quenched network, which has been associated to a smearing of the phase transition [57], while in the annealed network a power-law typical of an ordinary critical phase transition is seen. No sign of smearing is observed for $\mathrm{SIS}\text{-}\mathcal{T}$ and $\mathcal{A}$.

The FSS provides different exponents for distinct models. So, despite being described by the same mean-field equations, the role played by stochastic fluctuations depends on the model. Further analytical studies are required to clarify the distinction among the exponents.

VI. DISCUSSION

Conception of theoretical frameworks for epidemic processes frequently passes over the model's fine-tuning due to the belief that universality takes over and all central features, related to the leading properties and symmetries of a system, will be obtained irrespective of the specific details. However, this does not seem to be always the case when the substrate carrying out the process is a complex network. The standard SIS model, called $\mathrm{SIS}\text{-}\mathcal{S}$ in this work, is an example that behaves very differently from most of other related processes. For example, while many fundamental models on random networks with a power-law degree distribution (susceptible infected recovered (SIR) model [58], Ising model [59,60], synchronization [61], etc.) have a finite order parameter for any value of the control parameter only for degree exponent $\gamma <3$ [3], this happens for any value of $\gamma$ in $\mathrm{SIS}\text{-}\mathcal{S}$ [5,7]. A dichotomy also appears in the two basic mean-field theories for $\mathrm{SIS}\text{-}\mathcal{S}$, namely, QMF and HMF, which predict different outcomes for the epidemic threshold for $\gamma >5/2$ [7,26], being only QMF in agreement with the asymptotically null threshold for $\gamma >3$.

One could naturally wonder if these peculiar characteristics of $\mathrm{SIS}\text{-}\mathcal{S}$ are universal features observed in many other processes. We investigated two slightly different versions of the standard SIS, termed $\mathrm{SIS}\text{-}\mathcal{A}$ and $\mathrm{SIS}\text{-}\mathcal{T}$, in which the spontaneous healing and the unlimited infection capacity of a vertex are preserved. These alternative models present exactly the same thresholds of the $\mathrm{SIS}\text{-}\mathcal{S}$ in both QMF and HMF theories. Stochastic simulations on uncorrelated synthetic networks, however, show a dual scenario where the three models have essentially the same vanishing thresholds for $\gamma <5/2$ but disparate results are found for $\gamma >5/2$. In particular, a finite threshold is observed for $\gamma >3$ in both modified models, in contrast with the asymptotically null threshold of the standard case. This same framework was observed for SIRS model in Ref. [12], in which an individual acquires temporary immunity when the agents cannot neither transmit infection nor be infected. The dissonance is explained in terms of self-sustained, long-lived activation of hubs for any finite value of $\lambda$ [11] that holds for $\mathrm{SIS}\text{-}\mathcal{S}$ but does not for the other models. The epidemic lifespan of hubs with the modified dynamics increases slowly (algebraically or logarithmically) with the hub degree in contrast with the exponential increase of the standard case. The last one permits the long-range mutual activation or reactivation of hubs [11,12].

We also analyzed the activation mechanisms of the epidemic phase on uncorrelated networks. While the activation for $\mathrm{SIS}\text{-}\mathcal{S}$ occurs in the innermost, densely connected core of the network, determined by the largest index of a $k$-core decomposition, for $\gamma <5/2$ and in hubs for $\gamma >5/2$ [32], this happens for the whole range of scale-free networks with $2<\gamma <3$ for $\mathrm{SIS}\text{-}\mathcal{A}$ and $\mathrm{SIS}\text{-}\mathcal{T}$. Absence of a $k$-core organization [33] and a short-lived activity in star subgraphs as $\lambda \to 0$ for $\gamma >3$ suggests that the activation of the epidemic phase in the modified SIS models is collective, involving essentially the whole network [12], and occurs at a finite threshold.

The aforementioned dichotomy is also observed in the finite-size scaling of the quasistationary density and susceptibility computed at the epidemic threshold. Agreements between simulations on quenched and annealed versions of the investigated networks are observed for $\mathrm{SIS}\text{-}\mathcal{A}$ and $\mathrm{SIS}\text{-}\mathcal{T}$ irrespective of the degree exponent. In turn, they deviate in the hub activated regime with $\gamma >5/2$ in $\mathrm{SIS}\text{-}\mathcal{S}$, being more marked for $\gamma >3$ where the transition observed for quenched networks seems to be smeared [57], in contrast with a regular critical transition in the annealed case.

Here, we also comment the nature of the epidemic activation in processes with spontaneous healing with uniform rates and a bounded infection produced by a vertex, differing from the three SIS models investigated here and from SIRS [12]. In these bounded infection models, the epidemic lifespan on stars is finite for any value of the infection rate [12] and the epidemics can be activated only collectively in a finite threshold for any value of $\gamma$, as observed in simulations of the contact process on quenched networks [50,52,54], for example. Table III summarizes the activation mechanism of the different epidemic models investigated or discussed in the present work.

TABLE III.

Activation mechanisms for different epidemic models presenting active steady states on uncorrelated networks with degree distribution $P\left(k\right)\sim k^{-\gamma }$.

Model	$2<\gamma <5/2$	$5/2<\gamma <3$	$\gamma >3$
$\mathrm{SIS}\text{-}\mathcal{S}$	Max $k$-core	Hub	Hub
$\mathrm{SIS}\text{-}\mathcal{T}$	Max $k$-core	Max $k$-core	Collective
$\mathrm{SIS}\text{-}\mathcal{A}$	Max $k$-core	Max $k$-core	Collective
SIRS	Max $k$-core	Max $k$-core	Collective
CP	Collective	Collective	Collective

An interesting point observed in our analysis is that the HMF theory was more accurate than QMF theory in all investigated cases, except for $\mathrm{SIS}\text{-}\mathcal{S}$. Dynamical correlations are neglected in both approaches assuming that the states of interacting vertices, in case of QMF, or interacting compartments, in the case of HMF, are independent. This approximation becomes more problematic for QMF since we explicitly reckon the interactions with the actual nearest-neighbors of each vertex and assume that their states are independent. The leading approximation in HMF is to assume that the probability to be infected depends only on the vertex degree, neglecting the local structure of the network. As an effect, HMF theory may not be able to capture localized activity due to specific motifs as those observed for star subgraphs in the $\mathrm{SIS}\text{-}\mathcal{S}$ model. Finally, QMF theory is not a genuine mean-field approach since it does not present mixing of vertices while HMF does through the degree compartmentalization. Our results thus reinforces the belief that mean-field approaches with heterogeneous mixing are suitable approximations for most dynamical processes on networks with a small-world property, in which the average distance between vertices increases logarithmically with the system size [1].

Our results gathered with previous reports raise an important question on the modeling of epidemic processes on networks. Once details may matter, which would be the actual mechanisms used in models that correspond to real epidemics and which would be the best approaches to analytically investigate real epidemic processes? The summary presented in Table III suggests that the hub activation mechanism, intensively investigated recently [5,7,11–13,15,17,62,63], seems to be more a peculiarity than a rule in epidemic spreading. We expect that our results will guide the analysis of other classes of the dynamical process on networks such as the complex contagion models [64–67] where activation requires more than one interaction to be effected.

APPENDIX A: COMPUTER IMPLEMENTATIONS OF THE EPIDEMIC MODELS

To build the computer implementations, all involved rates are reckoned using statistically exact prescriptions based on the Gillespie algorithms [41]. We consider phantom processes that do nothing but counting for time increments. These ideas are detailed in Ref. [31]. Below we present recipes for the models investigated in the present work.

1. $\mathrm{SIS}\text{-}\mathcal{S}$

The $\mathrm{SIS}\text{-}\mathcal{S}$ dynamics in a network of size $N$ with infection and healing rates $\lambda$ and $\mu$ can be efficiently simulated as follows. A list with all infected vertices, their number $N_{\inf }$, and the number of edges $N_{\mathrm{e}}$ emanating from them are recorded and constantly updated. Each time step involves the following procedures. (i) With probability

$$p=\frac{\mu N_{\inf }}{\mu N_{\inf }+\lambda N_{\mathrm{e}}},$$ (A1)

an infected vertex is selected with equal chance and healed. (ii) With complementary probability $1-p$, an infected vertex is selected with probability proportional to its degree. A neighbor of the selected vertex is chosen with equal chance and, if susceptible, is infected. Otherwise, no change of state is implemented (it is a phantom process). (iii) The time is incremented by

$$\tau =\frac{-ln\left(u\right)}{\mu N_{\inf }+\lambda N_{\mathrm{e}}},$$ (A2)

where $u$ is a pseudorandom number uniformly distributed in the interval (0,1) and the simulation runs to the next step.

2. $\mathrm{SIS}\text{-}\mathcal{A}$

This model implementation is very similar to the contact process [35]. A list with the infected vertices and their number $N_{\inf }$ is built and constantly updated. At each time step, the rules are the following. (i) With probability

$$p=\frac{\mu }{\mu +\lambda },$$ (A3)

an infected vertex is randomly chosen and healed. (ii) With complementary probability $1-p$, all susceptible neighbors of a randomly chosen infected vertex are infected at once. (iii) The time is incremented by

$$\tau =\frac{-ln\left(u\right)}{(\mu +\lambda )N_{\inf }}.$$ (A4)

3. $\mathrm{SIS}\text{-}\mathcal{T}$

As in $\mathrm{SIS}\text{-}\mathcal{S}$ and $\mathcal{A}$, a list containing the infected vertices and their number $N_{\inf }$ is built and constantly updated. We have also to maintain an auxiliary list including the number of infected neighbors $n_i$ of each vertex $i$ and the total number of susceptible vertices $N_{\mathrm{SI}}$ that have at least one infected neighbor. At each time step, the rules are the following. (i) With probability

$$p=\frac{\mu N_{\inf }}{\mu N_{\inf }+\lambda N_{\mathrm{SI}}},$$ (A5)

an infected vertex is selected with equal chance and healed. With complementary probability $1-p$, an infected vertex is selected with probability proportional to its degree and one of its neighbors is randomly chosen. If the selected neighbor $i$ is susceptible it is accepted and infected with probability $1/n_i$. The procedure of choosing a susceptible vertex is repeated until one of them is found. The time is incremented by

$$\tau =\frac{-ln\left(u\right)}{\mu N_{\inf }+\lambda N_{\mathrm{SI}}}.$$ (A6)

4. Simulation on uncorrelated annealed networks

On uncorrelated annealed networks, the unique difference in $\mathrm{SIS}\text{-}\mathcal{S}$ and $\mathrm{SIS}\text{-}\mathcal{A}$ with respect to the quenched case is that the choice of the neighbors to be infected is done by selecting any vertex of the network with probability proportional to its degree.

For $\mathrm{SIS}\text{-}\mathcal{T}$, however, the algorithm becomes trickier and, consequently, very slow. The probability that a susceptible vertex $j$ becomes infected is given by

$$P_j=1-{(1-\mathrm{\Theta })}^{k_j},$$ (A7)

where $k_j$ is the degree of vertex $j$ and $\mathrm{\Theta }=N_{\mathrm{e}}/\left(N\langle k\rangle \right)$ is the probability that a randomly selected neighbor (at the other side of the edge) is infected in the annealed network. Let us define a total rate that one tries to infect a susceptible vertex as $L=\lambda (N-N_{\inf })$, which is larger than the real one since only the susceptible vertices that have at least one infected neighbor can actually be infected and this happens with probability $P_j<1$. The total rate that a vertex is healed is $M=\mu N_{\inf }$. The algorithm becomes the following. (i) An infected vertex is randomly chosen and healed with probability $p=M/(L+M)$. (ii) With probability $1-p$, a susceptible vertex is randomly chosen and infected with probability $P_j$. (iii) The time is incremented by $\tau =-ln\left(u\right)/(L+M)$.

The exactness of these algorithms is confirmed in Fig. 2 where simulations on annealed networks are compared with the integration of the HMF equations.

APPENDIX B: PAIRWISE APPROXIMATIONS FOR $\mathrm{SIS}\text{-}\mathcal{S}$

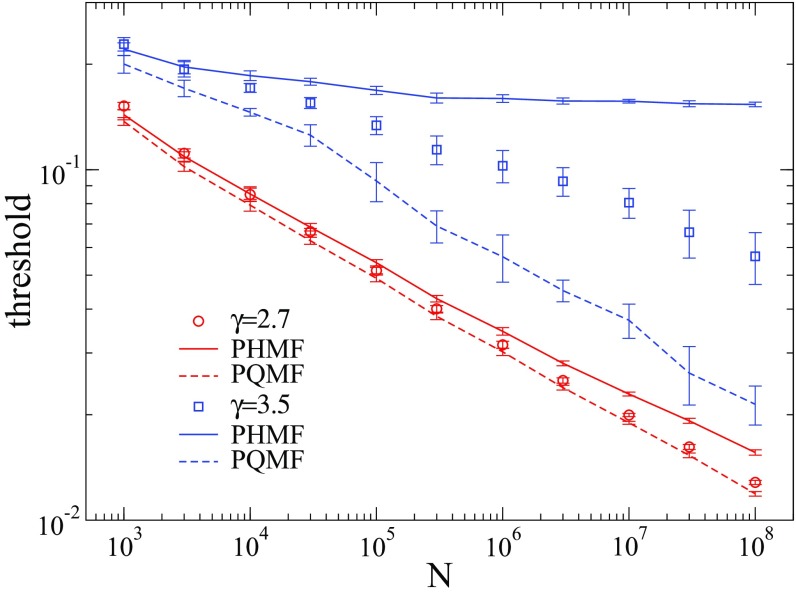
The pairwise heterogeneous mean-field (PHMF) approximation for $\mathrm{SIS}\text{-}\mathcal{S}$ with $\mu =1$ on uncorrelated networks provides a threshold [28]

$${\lambda }_c^{\text{PHMF}}=\frac{\langle k\rangle }{\langle k^2\rangle -\langle k\rangle }.$$ (B1)

The threshold of the pairwise quenched mean-field approximation (PQMF) is obtained when the largest eigenvalue of the matrix [27],

$$L_{ij}=-\left(1+\frac{{\lambda }^2{k}_i}{2\lambda +2}\right){\delta }_{ij}+\frac{\lambda (2+\lambda )}{2\lambda +2}{A}_{ij},$$ (B2)

is null. Figure 8 shows the thresholds of the pairwise theories computed for UCM networks.

FIG. 8.

Comparison of pairwise approximations with simulations (symbols) for epidemic thresholds of the $\mathrm{SIS}\text{-}\mathcal{S}$ on UCM networks, given by Eqs. (B1) and (B2). Data correspond to averages over 10 network samples.

APPENDIX C: APPROXIMATED EXPRESSIONS FOR EPIDEMIC LIFESPAN ON STAR GRAPHS

To obtain approximated expressions for the lifespan of the SIS epidemic processes ($\mathcal{S}$, $\mathcal{A}$, and $\mathcal{T}$) on a star graph with $k$ leaves, we consider the following discrete time dynamics based in Ref. [12]:

(i) At time $t=0$, the center is infected and all leaves are susceptible.

(ii) At a time $t=t_1$, the center is healed and $n$ leaves are simultaneously infected with probability $P_1\left(n\right|k)$.

(iii) At time $t=t_1+t_2$, the center is reinfected and all leaves become simultaneously susceptible. This occurs with probability $P_2\left(n\right)$.

The probability that the dynamics survives after this sequence is

$$Q=\sum _{n=1}^k{P}_2\left(n\right)P_1\left(n\right|k),$$ (C1)

and the probability that the dynamics ends up at the $s\mathrm{th}$ step is $Q^{s-1}(1-Q)$. So, the average number of steps is

$$\langle s\rangle =\sum _{s=0}^{\infty }s{Q}^{s-1}(1-Q)=\frac{1}{1-Q}.$$ (C2)

Next, we define the times $t_i$ and probabilities $P_i$ ($i=1,2$) for each model.

The steps for standard SIS [11,12] are reproduced here as a guide to the other models. We chose $t_1=t_2=1/\mu$, which is the average time that a vertex takes to be healed. The probability that the center infects a leaf before healing is $p=\lambda /(\mu +\lambda )$ [11], which is the same for all leaves. So, the probability that $n$ leaves were infected at time $t_1$ becomes

$$P_1\left(n\right|k)=\left(\genfrac{}{}{0pt}{}{k}{n}\right)p^n{(1-p)}^{k-n}.$$ (C3)

The probability that at least one leaf reinfects the center before healing at time $t_2$ is

$$P_2\left(n\right)=1-{(1-p)}^n.$$ (C4)

Plugging Eqs. (C3) and (C4) into (C1), we obtain

$$Q=1-{(1-p^2)}^k\approx 1-exp(-k{\lambda }^2/{\mu }^2),$$ (C5)

where the approximation holds for the regime $\lambda \ll \mu$, in which we are interested in. Now, substituting Eq. (C5) into Eq. (C2), we obtain

$${\tau }_k^{\mathcal{S}}=(t_1+t_2)\langle s\rangle \approx \frac{2}{\mu }exp\left(\frac{{\lambda }^2}{{\mu }^2}k\right).$$ (C6)

The prediction is an exponential increase with the star size.

For $\mathrm{SIS}\text{-}\mathcal{A}$, since all leaves are simultaneously infected before healing with probability $p=\lambda /(\mu +\lambda )$ we have that $P_1\left(n\right|k)=p{\delta }_{n,k}$ and the other variables are assumed to be the same. So, we have $Q=p[1-{(1-p)}^k]$, which leads to $\langle s\rangle \approx 1$ and the epidemic lifespan

$${\tau }_k^{\mathcal{A}}=(t_1+t_2)\langle s\rangle \approx \frac{2}{\mu }$$ (C7)

for $\lambda \ll \mu$. The prediction is a finite lifespan.

For $\mathrm{SIS}\text{-}\mathcal{T}$ we have the same expression of $\mathrm{SIS}\text{-}\mathcal{S}$ for $P_1\left(n\right|k)$ while the probability that center is reinfected is simply $P_2\left(n\right)=p$, irrespective of $n$. So, $\langle s\rangle \approx 1$ as in $\mathrm{SIS}\text{-}\mathcal{A}$. However, since infection rate of the center is independent of how many infected leaves are present, we must use the average time for all leaves to be healed instead of the average time for a single leaf to be healed. Considering the healing processes of each leaf as being an independent Poisson process and neglecting the possibility of reinfections of leaves during this process, the average time for $n$ leaves to be healed is

$$t_2^{\left(n\right)}={\int }_0^{\infty }t\left[n{(1-e^{-\mu t})}^{n-1}{e}^{-\mu t}\right]\mu dt\approx \frac{0.92}{\mu }lnn.$$ (C8)

The term between brackets is the probability that one single leaf is infected at time $t$, $\mu dt$ is the probability that it heals at time $t$, and the saddle point approximation was used to compute the integral assuming $n\gg 1$. So, replacing $n$ by the average number of infected leaves in part (ii), $\langle n\rangle =pk$, to estimate $t_2=\langle t_2^{\left(n\right)}\rangle \approx t_2^{(\langle n\rangle )}$, we obtain

$${\tau }_k^{\mathcal{T}}\approx \frac{1+0.92ln\left(pk\right)}{\mu }\simeq \frac{0.92}{\mu }lnk$$ (C9)

for $\lambda \ll \mu$. The prediction is a logarithmic increase with the star size.