Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Mar 18;124(14):8047–8054. doi: 10.1021/acs.jpcc.0c02287

Trapping and Detrapping in Colloidal Perovskite Nanoplatelets: Elucidation and Prevention of Nonradiative Processes through Chemical Treatment

Sander J W Vonk ‡, Magnus B Fridriksson †, Stijn O M Hinterding ‡, Mark J J Mangnus ‡, Thomas P van Swieten ‡, Ferdinand C Grozema †, Freddy T Rabouw ‡,*, Ward van der Stam †,*
PMCID: PMC7217613  PMID: 32421082

Abstract

graphic file with name jp0c02287_0007.jpg

Metal-halide perovskite nanocrystals show promise as the future active material in photovoltaics, lighting, and other optoelectronic applications. The appeal of these materials is largely due to the robustness of the optoelectronic properties to structural defects. The photoluminescence quantum yield (PLQY) of most types of perovskite nanocrystals is nevertheless below unity, evidencing the existence of nonradiative charge-carrier decay channels. In this work, we experimentally elucidate the nonradiative pathways in CsPbBr3 nanoplatelets, before and after chemical treatment with PbBr2 that improves the PLQY. A combination of picosecond streak camera and nanosecond time-correlated single-photon counting measurements is used to probe the excited-state dynamics over 6 orders of magnitude in time. We find that up to 40% of the nanoplatelets from a synthesis batch are entirely nonfluorescent and cannot be turned fluorescent through chemical treatment. The other nanoplatelets show fluorescence, but charge-carrier trapping leads to losses that are prevented by chemical treatment. Interestingly, even without chemical treatment, some losses due to trapping are mitigated because trapped carriers spontaneously detrap on nanosecond-to-microsecond timescales. Our analysis shows that multiple nonradiative pathways are active in perovskite nanoplatelets, which are affected differently by chemical treatment with PbBr2. More generally, our work highlights that in-depth studies using a combination of techniques are necessary to understand nonradiative pathways in fluorescent nanocrystals. Such understanding is essential to optimize synthesis and treatment procedures.

Introduction

Research and development of lead-halide perovskite nanocrystals (NCs) has almost reached the same maturity as more conventional II–VI and III–V semiconductor nanomaterials, offering exciting properties such as narrow emission linewidths, fast excited-state decay, and high material gain.1,2 Furthermore, synthesis protocols for high-quality perovskite NCs of various compositions and shapes have been developed over the past five years.3−12 While the fluorescence of the conventional II–VI and III–V semiconductor NCs is strongly quenched unless their surface is covered with a wide-band gap shell material, it is different for perovskite NCs.4,13−16 The optical properties of perovskite NCs are less sensitive to (surface) defects than their II–VI and III–V counterparts because the localized electronic states due to defects often lie outside the band gap.17,18 Even simple synthesis procedures for single-component perovskite NCs, without shell, yield fluorescence with a photoluminescence quantum yield (PLQY) as high as a few tens of percent.4,5 Nevertheless, better synthesis methods,11 ligand-exchange procedures,17 and other postsynthesis chemical treatments18 continue to be discovered that lead to even higher PLQY values. Clearly, structural imperfections in the interior of perovskite NCs or on their surface deteriorate the PLQY by opening nonradiative decay channels, but they can be removed or prevented if the right chemical methods are used. Unity PLQYs have been achieved for some compositions and shapes of perovskite NCs, but not yet for many others.19−21 The success of synthesis and treatment procedures in preventing nonradiative losses is usually evaluated in terms of the PLQY and excited-state decay dynamics of the resulting NCs. These parameters serve as a feedback to optimize the chemical methods. However, batches of NCs are typically heterogeneous with strong interparticle-property variations. This complicates the ability of the community to identify the nonradiative loss pathways in an ensemble of NCs and, consequently, to evaluate and optimize the chemical procedures used.

In this work, we unravel the nonradiative processes in CsPbBr3 nanoplatelets (NPLs), before and after chemical treatment with PbBr2 that improves the PLQY. We analyze the excited-state dynamics over 6 orders of magnitude in time using a combination of integrating-sphere PLQY measurements, streak camera experiments, and time-correlated single-photon counting (TCSPC). We find that trapping of charge carriers occurs over a wide range of timescales, from subpicosecond to nanoseconds.18 While some trapped charge carriers recombine nonradiatively, another part is detrapped on longer timescales and contributes to the delayed emission of photons up to several hundred nanoseconds after photoexcitation. Chemical treatment of the CsPbBr3 NPLs with PbBr2 removes the picosecond-to-nanosecond trapping pathways, resulting in an increase of the PLQY. However, our combination of spectroscopic techniques reveals the presence of a “dark fraction” of entirely nonfluorescent NPLs that cannot be healed by chemical treatment with PbBr2. Our results show that multiple nonradiative processes are operative in an ensemble of CsPbBr3 NPLs, each with a distinct signature in the excited-state dynamics and with a distinct response to chemical surface treatment with PbBr2. More broadly, our analysis method provides a framework to identify the effect of a chemical treatment on the nonradiative pathways in fluorescent nanomaterials.

Results and Discussion

CsPbBr3 NPL Synthesis and Characterization before and after PbBr2 Treatment

Colloidal CsPbBr3 NPLs of two thicknesses (4 and 6 monolayers, ML) were prepared following the procedure of Bohn et al.18 Sharp features are observed in the photoluminescence (PL) spectra, indicating controlled NPL thicknesses (Figure 1a). Surface treatment with a PbBr2 precursor solution was performed on the NPLs,18,22 which resulted in an enhancement of the PLQY (Figure 1b). Transmission electron microscopy (TEM) confirms the platelet shape of our NCs (Figure 1c,d). The variations in the side length, which were also observed by Bohn et al.,18 have limited effect on the emission wavelength because this is determined by the thickness of the NPLs. X-ray diffraction confirms the CsPbBr3 perovskite crystal structure of our NPLs (Supporting Information, Figure S1). In total, four NPL samples were prepared and studied in this work: 4ML, 4ML-treated, 6ML, and 6ML-treated CsPbBr3 NPLs. The main text will focus mainly on the data obtained for the 4ML and 4ML-treated NPLs. All measurements in the article were conducted one day after the synthesis, so that the picosecond-to-nanosecond excited-state dynamics and the PLQY could be directly combined and compared without complications due to slow degradation over the timescale of days to weeks.

Figure 1.

Figure 1

Open in a new tab

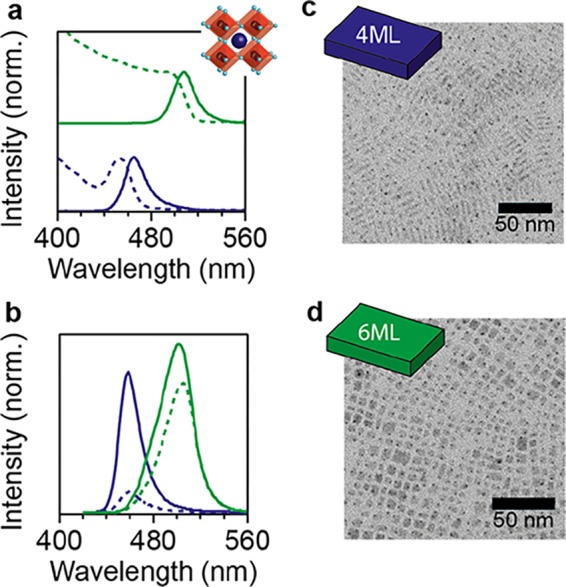
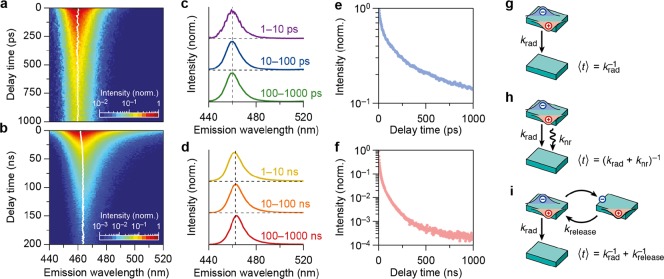
Optical and structural characterization of CsPbBr3 NPLs. (a) Steady-state absorption (dashed lines) and PL (solid lines) spectra of CsPbBr3 NPLs with a thickness of 4ML (dark blue) and 6ML (green). The inset shows the perovskite crystal structure (blue sphere; Cs+, black sphere; Pb2+, light blue sphere; Br–). (b) PL spectra normalized to the PLQY before (dashed lines, 4ML 10.2%, 6ML 50.8%) and after PbBr2 treatment (solid lines, 4ML 44.2%; 6ML 68.8%). TEM images of (c) 4ML thick and (d) 6ML thick CsPbBr3 NPLs. PL decay measurements on picosecond, nanosecond, and microsecond timescales.

We studied the excite-state dynamics of the NPLs using picosecond streak camera (Figure 2a) and nanosecond TCSPC measurements (Figure 2b). By measuring the excited-state decay with TCSPC as a function of the photon energy using a monochromator, we obtain a two-dimensional map of the excited-state dynamics vs. energy, that is, time-resolved emission spectra (TRES). Using both techniques—streak camera and TRES—we are able to resolve the spectral position, linewidth, and intensity over a wide range of delay times (Figure 2a,b). We keep the laser excitation fluence low (estimated to yield an average of 0.03 excitons per NPL per pulse for the streak camera measurement; see the Supporting Information) to minimize the creation of multiexcitons and the influence of Auger recombination on the decay dynamics.

Figure 2.

Figure 2

Open in a new tab

Picosecond streak camera measurements and TCSPC on 4-monolayer CsPbBr3 NPLs. (a) Streak camera image measured over the first 1000 ps and (b) time-resolved emission spectrum measured over the first 200 ns after photoexcitation for untreated 4ML CsPbBr3 NPLs. Spectral slices measured with (c) streak camera and (d) TCSPC show that the spectral position [white line in panels (a,b)] and the width remain nearly constant over the entire time range. The constant 2 nm shift of the peak position between the two different measurements is due to calibration differences between the TCSPC and the streak camera setup. The PL decay traces obtained by (e) streak camera (from 0 to 1000 ps) and (f) TCSPC (from 0 to 1000 ns) measurements, showing a multiexponential decay. Schematic representation of the radiative and nonradiative processes that typically occur in nanomaterials: (g) radiative recombination, where an excitation is directly followed by a photon emission, (h) nonradiative recombination, which results in energy losses and shortens the timescale of the photon emission, and (i) temporary storage of charge carriers and subsequent release leads to delayed emission of photons.

The peak emission energy and linewidth remain nearly constant over the entire experimental time range (Figure 2c,d). This indicates that radiative recombination of the photogenerated charge carriers occurs always from the same exciton state irrespective of the timescale. Because of the subpicosecond cooling time of hot charge carriers,23 this must be the lowest-energy exciton state, whose energy is dependent on the thickness of the NPLs through quantum confinement effects (Figure 1). We ascribe the small (∼3 nm) shift of the emission peak over the first 20 ns to a slight inhomogeneous broadening and a wavelength-dependent density of optical states.24

Although the narrow linewidth in the TRES measurements (Figure 2b) indicates radiative recombination from identical 4ML NPLs, the PL decay curves (Figure 2e,f) show multiexponential excited-state dynamics. This suggests a variation in nonradiative processes within the subpopulations of NPLs in the sample. As reported previously,18,22,25,26 and as we investigate in more detail below, the radiative decay rate krad of the lowest-energy exciton state in perovskite NCs is on the order of krad = 0.1–1 ns–1.18 Based on this rate, we expect an average delay time of ⟨t⟩ = krad–1 = 1–10 ns (Figure 2g) if no other recombination pathways are active. However, the PL decay curve measured here clearly contains significantly faster (Figure 2e) as well as slower (Figure 2f) decay components. The decay components that are faster than the radiative rate can be ascribed to nonradiative trapping processes from imperfect NPLs in the sample, which are in competition with radiative recombination. Nonradiative trapping at rate knr shortens the timescale of the emission (Figure 2h) to ⟨t⟩ = (krad + knr)−1. If the charge carriers recombine nonradiatively after trapping, this lowers the PLQY. The decay components that are slower than the radiative rate can also be due to nonradiative processes. Trapping of a charge carrier, followed by detrapping at rate krelease and radiative recombination at rate krad will increase the timescale of the emission to ⟨t⟩ = krad + krelease–1 (Figure 2i, see the Supporting Information for the derivation). However, because this sequence of processes yields a photon eventually, it does not affect the PLQY. This photon emission following trapping and detrapping is often referred to as delayed emission and has been shown to influence the PL dynamics in perovskite NCs26−28 as well as other materials.29−31 Below, we will study both nonradiative processes (trapping/nonradiative recombination and trapping/detrapping) and characterize the influence of the PbBr2 surface treatment on these nonradiative processes.

Stitching of the PL Decay Curves and Modeling of the Nonradiative Processes

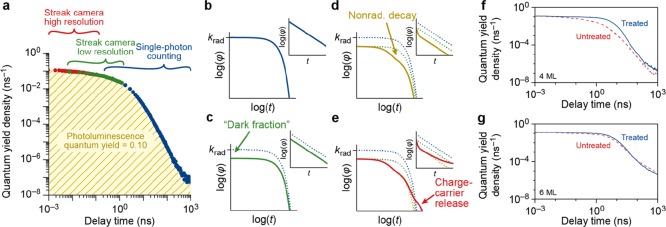
In Figure 3a we combine the streak camera and TCSPC measurements over 6 orders of magnitude in time by stitching them together. This procedure is detailed in the Supporting Information. In addition to the PL decay trace, the PLQY measured with an integrating sphere also contains information about nonradiative processes. We combine the information from all measurements by defining the “quantum yield density” φ(t), which is obtained by normalizing the stitched PL decay data such that the total area (the time-integrated quantum yield density) equals the PLQY:

graphic file with name jp0c02287_m001.jpg 1

Figure 3.

Figure 3

Open in a new tab

Stitching of the streak camera and TCSPC measurements. (a) Example of the combination of high- and low-resolution streak camera measurements with TCSPC measurements for a sample of untreated 4ML NPLs in order to obtain a PL decay trace over 6 orders of magnitude in time. The area under the PL decay curve is normalized to the PLQY of 10.2%, yielding what we define as the quantum yield density φ(t). (b) Model of the PL decay trace on a double logarithmic scale (and semi logarithmic inset) in case all generated charge carriers recombine radiatively (PLQY = 100%). (c) Model of the PL decay trace, in case a fraction of the NPLs is dark, resulting in a decrease of the amplitude because the extremely fast dynamics of the dark fraction is masked by the instrument response function. (d) Model of the PL decay trace, but in addition to the model in (c), part of the bright fraction NPLs exhibit nonradiative recombination that is in competition with radiative recombination. (e) Model of the PL decay trace, but in addition to the model in (d), delayed photons are taken into account, that is radiative recombination of charge carriers after the temporary storage in a nonemissive state. (f) Experimental PL decay traces for untreated (dashed line) and PbBr2 treated (full line) 4ML CsPbBr3 NPLs. (g) Same, but for 6ML CsPbBr3 NPLs.

The quantum yield density has units of inverse time and represents the photon emission probability per unit delay time per absorption event from the ensemble of NPLs. The quantum yield density plot contains information about the fast trapping—even those processes that are faster than the instrument response of our streak camera—as well as the slow detrapping processes.

Figure 3b–e illustrates how we quantify different nonradiative processes by analyzing the quantum yield density plot φ(t), under the assumption that all NPLs have the same intrinsic radiative decay rate krad. In the simplest scenario (Figure 3b, blue), radiative recombination of the exciton is the only decay pathway and no competing nonradiative processes in any of the NPLs in the ensemble are present. In this case, the PLQY would be unity, and the quantum yield density would follow single-exponential decay, i.e. φ(t) = krad e–kradt.

In practice, batches of NCs typically contain a “dark fraction”,32 that is, some NCs do not emit any photons upon photoexcitation and are therefore not directly observable in spectroscopic measurements.32−34 This dark fraction of entirely nonfluorescent NPLs that we identify below is qualitatively different from the “dark NPLs” with weak and fast fluorescence that Bohn et al. discuss.18 The presence of a truly dark fraction has a large influence on the quantitative analysis of the decay processes.35 Photogenerated excitons in these dark NPLs are quenched by ultrafast nonradiative charge carrier recombination, which may even outcompete the thermalization rate to the band edge. This subpopulation is invisible in the PL decay traces but does show up in the PLQY measurements. The Supporting Information Figure S3 discusses the concept of a dark fraction in more detail and provides an analysis strategy to identify if a dark fraction is present in an NC sample. Figure 3c (green) shows the quantum yield density for the scenario that a fraction 1 – f of NPLs is dark, while the other NPLs (bright fraction f) exhibit exclusively radiative decay, which follows φ(t) = fkrad e–kradt. From the amplitude φ(0) = fkrad of the quantum yield density plot, we can thus estimate the bright fraction within the NPL ensemble

graphic file with name jp0c02287_m002.jpg 2

Figure 3d,e shows the additional features that may appear in the quantum yield density plots if a fraction of NPLs in the sample exhibit trapping of charge carriers, which can lead to nonradiative recombination (Figure 3d, yellow), or detrapping and the subsequent delayed emission of photons on longer timescales (Figure 3e, red). These processes introduce additional components in the quantum yield density plots that are faster (nonradiative recombination) or slower (delayed emission) than the radiative recombination, respectively (see Figure 2g–i).

Figure 3f shows the experimental quantum yield density plot φ(t) of the untreated and treated 4ML NPL samples, and Figure 3g for the untreated and treated 6ML NPL samples. We see that the untreated and treated samples have very similar amplitudes φ(0), indicating that the treatment with PbBr2 does not affect the dark fraction of NPLs (see model in Figure 3c). In addition, we observe that the treatment process makes the decay dynamics on the picosecond-to-nanosecond timescales (<10 ns) slower. This is consistent with a suppression of nonradiative trapping pathways in imperfect NPLs by the PbBr2 treatment. Finally, we observe additional slow (>50 ns) multiexponential components in the quantum yield density φ(t) for all samples associated with delayed emission of photons following trapping and detrapping (Figure 2i). Interestingly, the contribution of the delayed emission events to the total amount of emitted photons changes with treatment. From these measurements, we conclude that the PbBr2 treatment procedure affects the nonradiative processes contributing to nonradiative recombination in the bright fraction of NPLs, as well as those contributing to the delayed emission, whereas the dark fraction is unaffected by the treatment.

Identifying Radiative and Nonradiative Processes in CsPbBr3 NPL Ensembles

For a more quantitative analysis of the nonradiative processes in our NPL samples, we have to determine the radiative decay rates krad. For example, the value of krad is necessary for the quantitative identification of the dark fraction (eq 2) and the distinction between charge-carrier trapping followed by nonradiative recombination (Figure 3d) or delayed emission (Figure 3e).

We measured the excited-state decay of three independently synthesized samples of 4ML NPL with slightly different PLQY (see Figure 4a). The fitted lifetime of the excited state is constant (blue line) indicating that the synthesis procedure gives synthesis-to-synthesis variations in the dark fraction. An alternative explanation—where the PLQY changes because of a variation in the nonradiative rates—would result in a positive slope of the lifetime of the excited state versus the PLQY (red dashed line, see the Supporting Information for details), which does not follow the data. From this, we conclude that the slowest decay dynamics of the treated NPLs on the 1–10 ns timescale are predominantly due to krad. From the measurements on the treated samples, we extract krad = 1/(5.6 ns) for the 4ML NPLs and krad = 1/(5.7 ns) for the 6ML NPLs. This is approximately a factor of 2 faster than the radiative rate estimated by Bohn et al.18 because we take into account that the dark fraction of NPLs is the cause for most of the losses in the ensemble, while most fluorescent NPLs show purely radiative decay.35 The absolute values for krad for the two samples are determined by the electronic structure of the NPLs, including the thermal occupation of various exciton fine structure states36 and photonic effects, including a shape-dependent local field factor.1 To further confirm that the ns component in the PL decay dynamics is due to radiative decay, we measured the excited-state decay using TCSPC on 6ML NPLs in different photonic environments by changing the solvent (see Figure 4b). We observed that the lifetime of the excited state became shorter when increasing the refractive index from n = 1.374 [hexane, dark yellow, krad = 1/(6.8 ns)] to n = 1.63 [CS2, red, krad = 1/(5.2 ns)]. This is consistent with a change in the radiative rate of the NPLs due to an increase of the local density of optical states.

Figure 4.

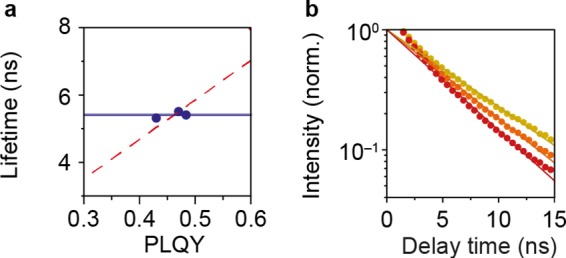
Figure 4

Open in a new tab

Determination of the radiative decay rate. (a) Lifetime vs. PLQY for three independently synthesized treated 4ML NPL samples. The lifetime of the excited state is approximately constant krad = 1/(5.6 ns), independent of the PLQY, indicating variations in the dark fraction from sample to sample (blue line). The red dashed line shows the expected trend if the nonunity PLQY were due to nonradiative decay in each NPL (rather than a dark and bright fraction), with sample-to-sample variations in the PLQY due to sample-to-sample variations in knr. (b) Decay curve for treated 6ML NPLs of one synthesis batch dispersed in hexane (n = 1.375, dark yellow), toluene (n = 1.5, orange), and CS2 (n = 1.63, red). The lifetime of the excited state decreases for increasing refractive index n showing that the total decay rate is dominated by radiative processes.

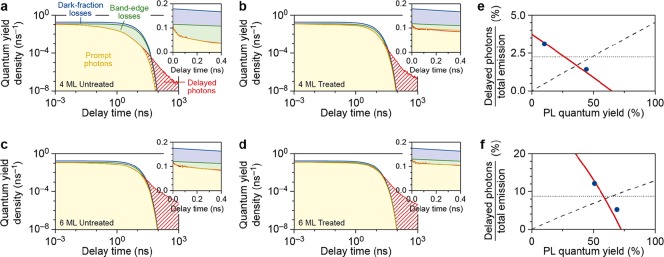
Using these values for krad and the concepts explained in Figure 3b–e, we identify and quantify the different nonradiative processes at play in the sample of untreated 4ML NPLs in Figure 5a. The red line is the experimental quantum yield density plot φ(t) obtained after stitching of the PL streak camera and TCSPC measurements. The yellow line is a multiexponential fit (to account for variations of nonradiative trapping rates between subpopulations of NPLs) to the first 20 ns of which the slowest fit component is fixed to krad. This captures the excited-state dynamics due to picosecond-to-nanosecond charge-carrier trapping from the band-edge exciton state (see Figure 3d) but excludes the delayed emission on timescales longer than 1/krad (see Figure 3e). The blue line (Figure 3b) is the hypothetical quantum yield density assuming a unity PLQY sample, that is, no dark fraction decaying with the radiative rate krad. The green line (Figure 3c) shows the calculated quantum yield density we would measure if the bright fraction f suffered no band-edge losses, in which case the excited-state dynamics would follow a single-exponential decay with the radiative rate krad.

Figure 5.

Figure 5

Open in a new tab

Identifying the radiative and nonradiative processes from the PL decay traces. (a–d) Stitched experimental PL decay traces (solid red line) and the comparison to the model distinguishing the contribution of prompt photons (yellow-shaded area), band-edge losses (green-shaded area), the dark fraction (blue-shaded area), and delayed PL (red-shaded area) for (a) untreated and (b) PbBr2-treated 4ML CsPbBr3 NPLs, and (c) untreated and (d) PbBr2-treated 6ML CsPbBr3 NPLs. The insets show a zoom of the first 400 ps. (e,f) Plots of the percentage of delayed photons with respect to the total number of emitted photons versus the PLQY, before and after treatment for (e) 4ML NPLs and (f) 6ML NPLs, and the comparison to the different possible models for temporary trapping and how it is affected by chemical treatment (see the Supporting Information for details): hot-exciton trapping with a constant rate (dotted lines), band-edge exciton trapping with a constant rate (dashed line), and band-edge exciton trapping with a rate that changes to the same extent as the nonradiative recombination rate (red solid line).

By integrating the appropriate areas between the curves in Figure 5a, we estimate the probabilities of different decay pathways in our NPL ensemble and thus the influence of the various nonradiative processes. Because the quantum yield density is normalized to the PLQY (eq 1), integration immediately yields the probabilities of decay pathways per photon absorption event. Specifically, in this way, we obtain the probability of prompt photon emission (yellow-shaded area), band-edge losses due to charge-carrier trapping (green-shaded area), and losses due to the dark fraction of NPLs (blue-shaded area). In addition, the red-shaded area represents the delayed emission on timescales exceeding prompt emission. Figure 5b–d shows the same plots and analysis for the treated 4ML NPLs (Figure 5b), the untreated 6ML NPLs (Figure 5c), and the treated 6ML NPLs (Figure 5d).

From these plots, it becomes clear that in a fraction of NPLs charge carriers are “lost” by trapping on the subpicosecond timescale (blue-shaded area) and/or picosecond-to-nanosecond (green-shaded area) timescale. The delayed emission (red-shaded areas in Figure 5a–d) is due to the detrapping of charge carriers and the subsequent photon emission on long timescales compared to the prompt emission. To determine the timescales of temporary trapping and how the treatment affects it, we plot the contribution of the delayed emission to the total emission, against the ensemble PLQY in Figure 5e (4ML NPLs) and Figure 5f (6ML NPLs).

As can be seen in Figure 5e,f, the delayed-emission fraction (contribution of the delayed emission to the integrated quantum yield density) decreases as the PLQY increases by PbBr2 treatment. From this analysis, we have to conclude that surface treatment not only suppresses nonradiative recombination pathways for the bright NPLs, but also has a profound influence on temporary charge carrier trapping and detrapping. There are three possible scenarios that we consider for the effect of treatment on the rates of nonradiative processes in our NPLs (detailed explanation in the Supporting Information). If only the nonradiative recombination rate knr is suppressed by the chemical treatment, we can calculate the delayed-emission fraction as a function of the PLQY, assuming trapping from (1) a hot exciton state (Figure 5e,f dotted line) or (2) a band-edge exciton state (Figure 5e,f dashed line). Neither scenario reproduces the measurements of the delayed-emission fraction before and after treatment. However, if we assume that the treatment suppresses (3) nonradiative recombination knr as well as temporary trapping ktrap from the band-edge exciton to the same extent, that is, both rates are reduced by the same factor, we can reproduce the delayed-emission fraction dependence on the PLQY before and after treatment for both NPL samples (Figure 5 e,f red lines).

We conclude from this analysis that trapping from the band-edge exciton state is the dominant mechanism contributing to delayed emission in perovskite NPLs. Additionally, we identified that the process leading to nonradiative recombination (i.e., trapping followed by recombination) and temporary trapping (i.e., trapping followed by detrapping) is affected to the same extent by chemical treatment with PbBr2. This might indicate that the defects that are responsible for these two processes have the same chemical nature. As charge-carrier trapping on these defects can be reversible (giving rise to delayed emission), the defect probably acts as a “shallow trap state”, that is, close in energy to the conduction- or valence-band edge. Indeed, undercoordinated Pb may lead to such shallow trap states, whose density is expected to decrease by chemical treatment of the NPLs with excess PbBr2.13

Quantifying the contribution of Nonradiative and Radiative Processes

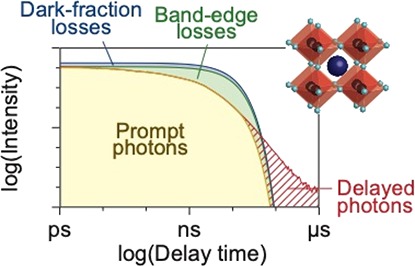
Figure 6a schematically summarizes the various excited-state decay pathways of an ensemble of perovskite NPLs that we studied with our combined PL decay and PLQY measurements. After excitation from the ground state (0) to a hot-carrier state (1), some NPLs in the ensemble decay nonradiatively on subpicosecond timescales leading to dark-fraction losses (blue). In the other subpopulation of NPLs, charge carriers quickly thermalize to form a band-edge exciton (2). From this lowest-energy exciton state, there is a probability to recombine radiatively, yielding prompt photons (yellow). Alternatively, in imperfect subpopulations of NPLs, radiative recombination can be in competition with nonradiative trapping from the lowest-energy exciton state followed by nonradiative recombination, leading to band-edge losses (green). Some of these trapping events from the lowest-energy exciton state do not result in nonradiative recombination, but instead the trapped charge (3) is detrapped after some time. After detrapping and restoration of the lowest-energy exciton, radiative recombination can occur contributing to delayed emission of photons (red).

Figure 6.

Figure 6

Open in a new tab

Models for radiative and nonradiative processes in CsPbBr3 NPLs (a) Schematic summary of the radiative and nonradiative processes at play in subpopulations of an ensemble of CsPbBr3 NPLs. After photoexcitation from the ground state (0) to the excited state (1), hot charge carriers are initially generated. In some NPLs—the dark fraction—nonradiative recombination is so fast that it outcompetes thermalization to the band-edge exciton state. The hot charge carriers can also cool to the band edge (2), from which there is a probability to recombine radiatively (prompt emission of photons) or get trapped (band-edge losses). Some NPLs trap charge carriers temporarily (3), that is, they are subsequently detrapped and eventually recombine from the lowest-energy exciton state (delayed photons). (b) The contributions of radiative recombination (prompt photons, yellow area), band-edge losses (green area), and dark-fraction losses (blue area) of our four samples of NPLs. The red-shaded area denotes band-edge trapping that is followed by detrapping and delayed emission. Comparing the untreated and treated samples, it is evident that chemical treatment with PbBr2 suppresses band-edge trapping while the dark-fraction is hardly influenced.

We plot the contributions of the different decay pathways for the different batches (4ML and 6ML), as shown in Figure 6b. The contributions of dark-fraction losses (blue), band-edge losses (green), and prompt photon emission (yellow) add up to 100%, but the numbers are rounded to the nearest 1%. The emission of delayed photons (red) compensates for a part of the band-edge losses. Clearly, the main effect of PbBr2 treatment is the enhancement of the prompt emission (yellow) and suppression of band-edge trapping (green), while the dark fraction remains similar. Therefore, to approach unity PLQY values for CsPbBr3 perovskite NPLs, an alternative postsynthetic chemical treatment that can heal the dark fraction is necessary.

The effect of PbBr2 treatment on the absolute delayed-emission intensity is nontrivial: the delayed-emission intensity increases for the 4ML NPLs, but decreases for the 6ML NPLs. This can be understood by considering that delayed emission follows a multistep pathway: (i) a charge carrier is first trapped from the band-edge exciton state, (ii) released, and then (iii) recombines radiatively. On the one hand, treatment suppresses nonradiative recombination of the band-edge exciton, so that steps (i) and (iii) become more efficient and delayed emission thus more likely. On the other hand, treatment also suppresses trapping of carriers into temporary traps, as shown in Figure 5e,f, thus making the delayed emission less likely. This balance between competing effects is well captured by the model shown in Figure 5e,f (see also the Supporting Information Figure S4). This model shows that while the delayed-emission fraction of the total emission always decreases with treatment (Figure 5e,f), the absolute intensity of delayed emission may or may not increase if the NPLs become significantly brighter overall (Figure 6b).

We showed with our analysis method that the PLQY is increased because of reduced band-edge losses. However, the treatment procedure still does not yield CsPbBr3 NPLs with unity PLQY. Our results indicate that the defect chemistry of perovskite nanomaterials is complex, and the main factor that needs to be tackled in order to reach unity PLQY values for this interesting class of materials is the dark fraction of NPLs within the ensemble. Future research into the atomic-scale structural details25,37 of treated and untreated NPLs may shed further light on the microscopic nature of the defects responsible for the various distinct nonradiative pathways. Our approach of combining picosecond streak camera and TCSPC measurements provides a platform to disentangle and understand radiative and nonradiative processes in luminescent materials, which serves as an input for the rational design of highly emissive nanomaterials with unity PLQY.

Conclusions

We have elucidated the nonradiative processes in CsPbBr3 NPLs by probing the excited-state dynamics with a combination of PL streak camera and TCSPC measurements. This combination of spectroscopic techniques allowed us to probe the excited-state dynamics of CsPbBr3 NPLs over 6 orders of magnitude in time. We have found that chemical treatment with PbBr2 suppresses the nonradiative processes associated with charge-carrier trapping from the lowest-energy exciton state and therefore enhances the prompt emission. The dark fraction of NPLs—the nonemissive subpopulation of nanocrystals within the ensemble—is unaffected by the chemical treatment with PbBr2. Furthermore, we find that the contribution of delayed emission due to trapping–detrapping events to the total emission decreases upon surface treatment. This is consistent with a reduction of band-edge trapping and nonradiative recombination. We have identified charge-carrier trapping processes that limit the PLQY (nonradiative recombination) and those that do not (delayed emission). Furthermore, using the definition of quantum yield density provides a framework to test and optimize the synthesis procedures or postsynthetic chemical treatments on a variety of fluorescent nanocrystals.

Acknowledgments

W.v.d.S., M.B.F., and F.C.G. acknowledge the ERC Grant ICONICAL for funding. F.T.R. is supported by the NWO Veni grant number 722.017.002. S.J.W.V. and F.T.R. acknowledge the NWO (OCENW.KLEIN.008) for funding. S.O.M.H., M.J.J.M., T.P.v.S., and F.T.R. acknowledge support from The Netherlands Center for Multiscale Catalytic Energy Conversion (MCEC), an NWO Gravitation program funded by the Ministry of Education, Culture and Science of the government of The Netherlands. The authors thank Wiel Evers (TU Delft) for assistance with the TEM measurements and Jos Thieme (TU Delft) for assistance with the PL streak camera measurements.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.0c02287.

  • Figures showing X-ray diffraction; decay curve stitching procedure; identification of the dark fraction; delayed emission models; and derivation timescale between trapping and photon emission (PDF)

Author Present Address

§ Inorganic Chemistry and Catalysis, Debye Institute for Nanomaterials Science, Utrecht University, Utrecht, The Netherlands.

Author Contributions

S.J.W.V. and M.B.F. contributed equally to this work. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

jp0c02287_si_001.pdf (438.4KB, pdf)

References

  1. Becker M. A.; Vaxenburg R.; Nedelcu G.; Sercel P. C.; Shabaev A.; Mehl M. J.; Michopoulos J. G.; Lambrakos S. G.; Bernstein N.; Lyons J. L.; et al. Bright Triplet Excitons in Caesium Lead Halide Perovskites. Nature 2018, 553, 189–193. 10.1038/nature25147. [DOI] [PubMed] [Google Scholar]
  2. Utzat H.; Sun W.; Kaplan A. E. K.; Krieg F.; Ginterseder M.; Spokoyny B.; Klein N. D.; Shulenberger K. E.; Perkinson C. F.; Kovalenko M. V.; et al. Coherent Single-Photon Emission from Colloidal Lead Halide Perovskite Quantum Dots. Science 2019, 363, 1068–1072. 10.1126/science.aau7392. [DOI] [PubMed] [Google Scholar]
  3. Bodnarchuk M. I.; Boehme S. C.; Ten Brinck S.; Bernasconi C.; Shynkarenko Y.; Krieg F.; Widmer R.; Aeschlimann B.; Günther D.; Kovalenko M. V.; et al. Rationalizing and Controlling the Surface Structure and Electronic Passivation of Cesium Lead Halide Nanocrystals. ACS Energy Lett 2019, 4, 63–74. 10.1021/acsenergylett.8b01669. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Kovalenko M. V.; Protesescu L.; Bodnarchuk M. I. Properties and Potential Optoelectronic Applications of Lead Halide Perovskite Nanocrystals. Science 2017, 358, 745–750. 10.1126/science.aam7093. [DOI] [PubMed] [Google Scholar]
  5. Protesescu L.; Yakunin S.; Bodnarchuk M. I.; Krieg F.; Caputo R.; Hendon C. H.; Yang R. X.; Walsh A.; Kovalenko M. V. Nanocrystals of Cesium Lead Halide Perovskites (CsPbX3, X = Cl, Br, and I): Novel Optoelectronic Materials Showing Bright Emission with Wide Color Gamut. Nano Lett. 2015, 15, 3692–3696. 10.1021/nl5048779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Akkerman Q. A.; Rainò G.; Kovalenko M. V.; Manna L. Genesis, Challenges and Opportunities for Colloidal Lead Halide Perovskite Nanocrystals. Nat. Mater. 2018, 17, 394–405. 10.1038/s41563-018-0018-4. [DOI] [PubMed] [Google Scholar]
  7. Swarnkar A.; Ravi V. K.; Nag A. Beyond Colloidal Cesium Lead Halide Perovskite Nanocrystals: Analogous Metal Halides and Doping. ACS Energy Lett. 2017, 2, 1089–1098. 10.1021/acsenergylett.7b00191. [DOI] [Google Scholar]
  8. Koscher B. A.; Bronstein N. D.; Olshansky J. H.; Bekenstein Y.; Alivisatos A. P. Surface- vs Diffusion-Limited Mechanisms of Anion Exchange in CsPbBr3 Nanocrystal Cubes Revealed through Kinetic Studies. J. Am. Chem. Soc. 2016, 138, 12065–12068. 10.1021/jacs.6b08178. [DOI] [PubMed] [Google Scholar]
  9. Yu Y.; Zhang D.; Kisielowski C.; Dou L.; Kornienko N.; Bekenstein Y.; Wong A. B.; Alivisatos A. P.; Yang P. Atomic Resolution Imaging of Halide Perovskites. Nano Lett. 2016, 16, 7530–7535. 10.1021/acs.nanolett.6b03331. [DOI] [PubMed] [Google Scholar]
  10. Creutz S. E.; Crites E. N.; De Siena M. C.; Gamelin D. R. Anion Exchange in Cesium Lead Halide Perovskite Nanocrystals and Thin Films Using Trimethylsilyl Halide Reagents. Chem. Mater. 2018, 30, 4887–4891. 10.1021/acs.chemmater.8b02100. [DOI] [Google Scholar]
  11. Tong Y.; Bladt E.; Aygüler M. F.; Manzi A.; Milowska K. Z.; Hintermayr V. A.; Docampo P.; Bals S.; Urban A. S.; Polavarapu L.; et al. Highly Luminescent Cesium Lead Halide Perovskite Nanocrystals with Tunable Composition and Thickness by Ultrasonication. Angew. Chem., Int. Ed. 2016, 55, 13887–13892. 10.1002/anie.201605909. [DOI] [PubMed] [Google Scholar]
  12. Nedelcu G.; Protesescu L.; Yakunin S.; Bodnarchuk M. I.; Grotevent M. J.; Kovalenko M. V. Fast Anion-Exchange in Highly Luminescent Nanocrystals of Cesium Lead Halide Perovskites (CsPbX3, X = Cl, Br, I). Nano Lett. 2015, 15, 5635–5640. 10.1021/acs.nanolett.5b02404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Brandt R. E.; Poindexter J. R.; Gorai P.; Kurchin R. C.; Hoye R. L. Z.; Nienhaus L.; Wilson M. W. B.; Polizzotti J. A.; Sereika R.; Žaltauskas R.; et al. Searching for ″Defect-Tolerant″ Photovoltaic Materials: Combined Theoretical and Experimental Screening. Chem. Mater. 2017, 29, 4667–4674. 10.1021/acs.chemmater.6b05496. [DOI] [Google Scholar]
  14. Houtepen A. J.; Hens Z.; Owen J. S.; Infante I. On the Origin of Surface Traps in Colloidal II-VI Semiconductor Nanocrystals. Chem. Mater. 2017, 29, 752–761. 10.1021/acs.chemmater.6b04648. [DOI] [Google Scholar]
  15. Kirkwood N.; Monchen J. O. V.; Crisp R. W.; Grimaldi G.; Bergstein H. A. C.; du Fossé I.; van der Stam W.; Infante I.; Houtepen A. J. Finding and Fixing Traps in II-VI and III-V Colloidal Quantum Dots: The Importance of Z-Type Ligand Passivation. J. Am. Chem. Soc. 2018, 140, 15712–15723. 10.1021/jacs.8b07783. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. van der Stam W.; du Fossé I.; Grimaldi G.; Monchen J. O. V.; Kirkwood N.; Houtepen A. J. Spectroelectrochemical Signatures of Surface Trap Passivation on CdTe Nanocrystals. Chem. Mater. 2018, 30, 8052–8061. 10.1021/acs.chemmater.8b03893. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Krieg F.; Ochsenbein S. T.; Yakunin S.; Ten Brinck S.; Aellen P.; Süess A.; Clerc B.; Guggisberg D.; Nazarenko O.; Shynkarenko Y.; et al. Colloidal CsPbX3 (X = Cl, Br, I) Nanocrystals 2.0: Zwitterionic Capping Ligands for Improved Durability and Stability. ACS Energy Lett. 2018, 3, 641–646. 10.1021/acsenergylett.8b00035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Bohn B. J.; Tong Y.; Gramlich M.; Lai M. L.; Döblinger M.; Wang K.; Hoye R. L. Z.; Müller-Buschbaum P.; Stranks S. D.; Urban A. S.; et al. Boosting Tunable Blue Luminescence of Halide Perovskite Nanoplatelets through Postsynthetic Surface Trap Repair. Nano Lett. 2018, 18, 5231–5238. 10.1021/acs.nanolett.8b02190. [DOI] [PubMed] [Google Scholar]
  19. Liu F.; Zhang Y.; Ding C.; Kobayashi S.; Izuishi T.; Nakazawa N.; Toyoda T.; Ohta T.; Hayase S.; Minemoto T.; et al. Highly Luminescent Phase-Stable CsPbI3 Perovskite Quantum Dots Achieving Near 100% Absolute Photoluminescence Quantum Yield. ACS Nano 2017, 11, 10373–10383. 10.1021/acsnano.7b05442. [DOI] [PubMed] [Google Scholar]
  20. Dutta A.; Behera R. K.; Pal P.; Baitalik S.; Pradhan N. Near-Unity Photoluminescence Quantum Efficiency for All CsPbX3 (X=Cl, Br, and I) Perovskite Nanocrystals: A Generic Synthesis Approach. Angew. Chem., Int. Ed. 2019, 58, 5552–5556. [DOI] [PubMed] [Google Scholar]
  21. Pradhan N. Journey of Making Cesium Lead Halide Perovskite Nanocrystals: What’s Next. J. Phys. Chem. Lett. 2019, 10, 5847–5855. 10.1021/acs.jpclett.9b02412. [DOI] [PubMed] [Google Scholar]
  22. Wang Y.; Zhi M.; Chang Y.-Q.; Zhang J.-P.; Chan Y. Stable, Ultralow Threshold Amplified Spontaneous Emission from CsPbBr3 Nanoparticles Exhibiting Trion Gain. Nano Lett. 2018, 18, 4976–4984. 10.1021/acs.nanolett.8b01817. [DOI] [PubMed] [Google Scholar]
  23. Vale B. R. C.; Socie E.; Burgos-Caminal A.; Bettini J.; Schiavon M. A.; Moser J.-E. Exciton, Biexciton, and Hot Exciton Dynamics in CsPbBr3 Colloidal Nanoplatelets. J. Phys. Chem. Lett. 2020, 11, 387–394. 10.1021/acs.jpclett.9b03282. [DOI] [PubMed] [Google Scholar]
  24. Henderson B.; Imbusch G. F.. Optical Spectroscopy of Inorganic Solids; Clarendon Press: Oxford, 1989. [Google Scholar]
  25. van der Stam W.; Geuchies J. J.; Altantzis T.; Van Den Bos K. H. W.; Meeldijk J. D.; Van Aert S.; Bals S.; Vanmaekelbergh D.; de Mello Donega C. Highly Emissive Divalent-Ion-Doped Colloidal CsPb1-xMxBr3 Perovskite Nanocrystals through Cation Exchange. J. Am. Chem. Soc. 2017, 139, 4087–4097. 10.1021/jacs.6b13079. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Wang Y.; Zhi M.; Chan Y. Delayed Exciton Formation Involving Energetically Shallow Trap States in Colloidal CsPbBr3 Quantum Dots. J. Phys. Chem. C 2017, 121, 28498–28505. 10.1021/acs.jpcc.7b09040. [DOI] [Google Scholar]
  27. Rainò G.; Becker M. A.; Bodnarchuk M. I.; Mahrt R. F.; Kovalenko M. V.; Stöferle T. Superfluorescence from Lead Halide Perovskite Quantum Dot Superlattices. Nature 2018, 563, 671–675. 10.1038/s41586-018-0683-0. [DOI] [PubMed] [Google Scholar]
  28. Chirvony V. S.; González-Carrero S.; Suárez I.; Galian R. E.; Sessolo M.; Bolink H. J.; Martínez-Pastor J. P.; Pérez-Prieto J. Delayed Luminescence in Lead Halide Perovskite Nanocrystals. J. Phys. Chem. C 2017, 121, 13381–13390. 10.1021/acs.jpcc.7b03771. [DOI] [Google Scholar]
  29. Whitham P. J.; Knowles K. E.; Reid P. J.; Gamelin D. R. Photoluminescence Blinking and Reversible Electron Trapping in Copper-Doped CdSe Nanocrystals. Nano Lett. 2015, 15, 4045–4051. 10.1021/acs.nanolett.5b01046. [DOI] [PubMed] [Google Scholar]
  30. Marchioro A.; Whitham P. J.; Nelson H. D.; De Siena M. C.; Knowles K. E.; Polinger V. Z.; Reid P. J.; Gamelin D. R. Strong Dependence of Quantum-Dot Delayed Luminescence on Excitation Pulse Width. J. Phys. Chem. Lett. 2017, 8, 3997–4003. 10.1021/acs.jpclett.7b01426. [DOI] [PubMed] [Google Scholar]
  31. Rabouw F. T.; Kamp M.; Van Dijk-Moes R. J. A.; Gamelin D. R.; Koenderink A. F.; Meijerink A.; Vanmaekelbergh D. Delayed Exciton Emission and Its Relation to Blinking in CdSe Quantum Dots. Nano Lett. 2015, 15, 7718–7725. 10.1021/acs.nanolett.5b03818. [DOI] [PubMed] [Google Scholar]
  32. Durisic N.; Godin A. G.; Walters D.; Grütter P.; Wiseman P. W.; Heyes C. D. Probing the ″Dark″ Fraction of Core-Shell Quantum Dots by Ensemble and Single Particle pH-Dependent Spectroscopy. ACS Nano 2011, 5, 9062–9073. 10.1021/nn203272p. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Hinsch A.; Lohmann S.-H.; Strelow C.; Kipp T.; Würth C.; Geißler D.; Kornowski A.; Wolter C.; Weller H.; Resch-Genger U.; et al. Fluorescence Quantum Yield and Single-Particle Emission of CdSe Dot/CdS Rod Nanocrystals. J. Phys. Chem. C 2019, 123, 24338–24346. 10.1021/acs.jpcc.9b07957. [DOI] [Google Scholar]
  34. Ebenstein Y.; Mokari T.; Banin U. Fluorescence Quantum Yield of CdSe/ZnS Nanocrystals Investigated by Correlated Atomic-Force and Single-Particle Fluorescence Microscopy. Appl. Phys. Lett. 2002, 80, 4033–4035. 10.1063/1.1482785. [DOI] [Google Scholar]
  35. Würth C.; Geißler D.; Behnke T.; Kaiser M.; Resch-Genger U. Critical Review of the Determination of Photoluminescence Quantum Yields of Luminescent Reporters. Anal. Bioanal. Chem. 2015, 407, 59–78. 10.1007/s00216-014-8130-z. [DOI] [PubMed] [Google Scholar]
  36. Fu M.; Tamarat P.; Trebbia J. B.; Bodnarchuk M. I.; Kovalenko M. V.; Even J.; Lounis B. Unraveling Exciton–Phonon Coupling in Individual FAPbI3 Nanocrystals Emitting near-Infrared Single Photons. Nat. Commun. 2018, 9, 1–10. 10.1038/s41467-018-05876-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Orfield N. J.; McBride J. R.; Keene J. D.; Davis L. M.; Rosenthal S. J. Correlation of Atomic Structure and Photoluminescence of the Same Quantum Dot: Pinpointing Surface and Internal Defects That Inhibit Photoluminescence. ACS Nano 2015, 9, 831–839. 10.1021/nn506420w. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp0c02287_si_001.pdf (438.4KB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES