Highlights
-
•
NMF-based method to identify abnormal connectivity patterns of ASD brains.
-
•
ASD children were characterized by interhemispheric under-connectivity.
-
•
Long-range connections modulated by slower rhythm; local-range by faster frequency.
-
•
Alpha-band interhemispheric pattern play pivotal role in ASD neurodevelopment.
Keywords: Resting-state EEG, Autism and early childhood development, Network decomposition, Non-negative matrix factorization, Abnormal connectivity patterns
Abstract
Autism spectrum disorder (ASD) is associated with altered patterns of over- and under-connectivity of neural circuits. Age-related changes in neural connectivities remain unclear for autistic children as compared with normal children. In this study, a parts-based network-decomposition technique, known as non-negative matrix factorization (NMF), was applied to identify a set of possible abnormal connectivity patterns in brains affected by ASD, using resting-state electroencephalographic (EEG) data. Age-related changes in connectivities in both inter- and intra-hemispheric areas were studied in a total of 256 children (3–6 years old), both with and without ASD. The findings included the following: (1) the brains of children affected by ASD were characterized by a general trend toward long-range under-connectivity, particularly in interhemispheric connections, combined with short-range over-connectivity; (2) long-range connections were often associated with slower rhythms (δ and θ), whereas synchronization of short-range networks tended to be associated with faster frequencies (α and β); and (3) the α-band specific patterns of interhemispheric connections in ASD could be the most prominent during early childhood neurodevelopment. Therefore, NMF would be useful for further exploring the early childhood developmental functional connectivity of children aged 3–6 with ASD as well as with typical development. Additionally, long-range interhemispheric alterations in connectivity may represent a potential biomarker for the identification of ASD.
1. Introduction
Autism spectrum disorder (ASD) is a complex neurodevelopmental disorder that is characterized by repetitive behaviors, restricted interests, and impairments in social interaction and communication (Keown et al., 2017). Evidence that ASD could be a result of altered patterns of neural connectivity is growing (Geschwind and Levitt, 2007; O'Reilly et al., 2017; Minshew and Keller, 2010). The developmental–disconnection model of ASD indicates that changes in functional connectivity in individuals with ASD follow a pattern of short-range over-connectivity (Belmonte et al., 2004) and long-range under-connectivity (Geschwind and Levitt, 2007) or even global under-connectivity (Hughes, 2007; Just et al., 2004). Recent findings, however, emphasize a mixture of hypo- and hyper-connectivity (Kana et al., 2014). This abnormal connection pattern may then reflect inadequacy in the fine-tuning of networks during development in ASD, which is a process that is typically characterized by increased integration within local networks and increased segregation across separate networks (Bos et al., 2014). However, several findings remain unreplicated, and conclusions regarding the nature of altered patterns of connectivity in ASD have been divergent.
A substantial body of research has partially addressed questions regarding brain connectivity in ASD, including approaches that have investigated structural connectivity by diffusion imaging (Anagnostou and Taylor, 2011; Müller, 2014) and correlated activity by functional magnetic resonance imaging (fMRI) (Thai et al., 2009; Uddin et al., 2013). Specifically, fMRI studies have identified atypicalities in functional-connectivity patterns in individuals with ASD (Hahamy et al., 2015), which include reductions in various functional connections (Belmonte et al., 2004; Just et al., 2004), particularly in interhemispheric connections (Hahamy et al., 2015; Dinstein et al., 2011; Di Martino et al., 2014). Moreover, fMRI studies have reflected a shift in the understanding of the biological basis and cognitive deficits of ASD toward the patterns of functional connectivity between areas of the so-called default mode network (DMN), which are neural networks that are activated at rest (Raichle, 2009).
Brain connectivity can also be evaluated by multiple electroencephalography (EEG) signals. According to its high temporal resolution and direct relationship with neuronal potential activity, EEG-connectivity analyses can provide abundant information about the dynamic activation and deactivation of functional networks (O'Reilly et al., 2017). Recently, aberrant gamma activity has been reported in autistic children, which has been interpreted as the supporting hypothesis of aberrant brain connectivity (Brown et al., 2005). EEG coherence has been directly used as a measure of connectivity in several EEG studies, and the reports support the evidence of both under- and over-connectivity in different frequency bands in ASD populations (Murias et al., 2007). However, a more complete understanding of the patterns of connectivity in ASD remains lacking. Thus, our goal in this study is to identify connectivity patterns and effective brain connectivity in ASD, with a focus on factors impacting over- versus under-connectivity during the early stage of neurodevelopment (ages: 3–6 years old).
Given the complexities and conflict in the ASD literature, data-driven techniques provide exploratory approaches that are appropriate for identifying connectivity patterns, even in the absence of strong directional assumptions (Keown et al., 2017). To address these conflicting reports, a data-driven approach that can extract the parts of functional brain networks that encode resting states associated with altered patterns of connectivity—and track their expression over time—is required. Such a capability would improve our understanding of those patterns of brain networks that are significant for different groups of ASDs and how these patterns change over time.
In this work, we identified four frequency-band-specific (δ, θ, α, and β bands) patterns of functional brain networks associated with autistic resting states using an unsupervised machine-learning technique known as non-negative matrix factorization (NMF) (Lee and Seung, 1999). In recent years, this new tool has been applied to identify time-varying functional connectivity patterns in the brain (Marimpis et al., 2016). Intuitively, NMF decomposes functional brain networks into the following: (1) a set of subnetworks (patterns) overlapping in space and time and (2) corresponding coefficient time series that quantify the contribution of each subnetwork (pattern) at each time point (Chai et al., 2017; Khambhati et al., 2017, 2018a,b). One possible definition for an EEG subnetwork—and the one that we use in this study—is that it reflects the pattern of connectivity. This computational tool allows us to track how groups of networks interacting across brain areas are dynamically expressed during rest states. As compared to hard-partitioning schemes, the advantage of this method is that it provides information about brain-network dynamics in a continuous, overlapping manner in space and time rather than in discrete partitions. Furthermore, owing to the parts-based nature of the technique, we obtained subnetworks that resembled the localized features of large-scale brain networks rather than generalized patterns of the overall network (Lee and Seung, 1999; Chai et al., 2017). Based on prior work suggesting distance-dependent organization of brain networks into local, function-specific interactions (characteristic of clusters and modules (Rubinov and Sporns, 2010; Telesford et al., 2011)), we hypothesize that subgraphs are selectively sensitive to functional interactions over different distances. Specifically, we applied this technique to a control group of early childhood neurodevelopmental autistic and age-matched children to address the following hypotheses: the first hypothesis considered autism to be characterized by long-range under-connectivity (particularly in interhemispheric connections) potentially combined with short-range over-connectivity, reflecting atypical development of functional networks. The second hypothesis is that we would find differences between groups (i.e., between autistic and control children) in these canonical patterns of functional connectivity. The third hypothesis is that there would be an age-related trend in the measured patterns of connectivity, potentially owing to slight differences in early childhood developmental trajectories between autistic and control children.
2. Methods and materials
2.1. Participants
In this study, we collected EEG data from 256 children, including 115 children with ASD (age range 3–6 years old, mean age: 4.7 years, SD: 1.53 years) and 141 age-matched typically developing (TD) controls (age range: 3–6 years old, mean age: 4.85 years, SD: 1.47 years). All children in the ASD group were recruited because they had a prior diagnosis of ASD, according to the Diagnostic and Statistical Manual of Mental Disorders, Fifth Edition (DSM-V) (Association, 2013). The research protocol was approved by the ethics committee of Beijing Normal University. Informed consent was obtained from all parents before the start of the experiment. All protocols of this study conform to the Declaration of Helsinki guidelines.
2.2. EEG collection and preprocessing
The EEG was continuously recorded from a 128-channel EEG system (Electrical Geodesics Inc., Eugene, OR). Scalp impedance was checked online via the Use Net Station (EGI, Inc.) and was maintained below 50kΩ. EEG data were referenced online to Cz and digitized at a sampling rate of 1,000 Hz. Open-eyes resting-state EEGs were recorded for at least 5 min. Children were instructed to sit comfortably and relax during the recording and were usually accompanied by their caregiver in a quiet room.
The resting-state EEG data were preprocessed offline using EEGLAB, v14.0.0b (Delorme and Makeig, 2004) and MATLAB 2017b (Mathworks, Inc., USA). According to the 10-10 standard international system, the same 62 electrodes were selected from the 128 channels of the Geodesic Sensor Net (GSN) for all participants to ensure the broadest spatial coverage of the whole brain (frontal, central, temporal, and occipital). The data were re-referenced to a common average reference and down-sampled to 512 Hz. A notch filter centered at 50 Hz was applied to minimize line-noise artifacts, and the data were then band-pass filtered (0.5–45 Hz). Independent component analysis (ICA) was performed on cleaned data using FastICA (Rogasch et al., 2014) to decompose 62 spatiotemporal features of the EEG-independent components (EEG ICs), and then the corresponding blink/oculomotor, muscle, or transient electrode artifacts were subtracted from the data via visual inspection in terms of channel-based scalp topography measures and power spectral density (PSD) measures (median, variance, and kurtosis). To ensure the quality of the resting-state data, the middle portion of the EEG data (of 2 min duration) was used for subsequent analysis, as it was less noisy than the entire time series. The EEG data were then cut into 30 non-overlapping segments of 4 s each.
2.3. Time-varying network construction
After preprocessing the rest-state EEG data for each participant, we obtained a 120-s time series from each electrode and divided it into 30 non-overlapping 4-s windows. Thereafter, we examined the time-varying brain functional connectivity, for which the connectivity between all pairs of brain regions (i.e., channels or electrodes) was required to be estimated as a function of time and frequency using the sliding-window technique (Cai et al., 2018). For each time window, we measured functional connectivity between each pair of brain regions based on the imaginary part of wavelet coherency within four frequency bands: δ (2–4 Hz), θ (4–8 Hz), α (8–13 Hz), and β (13–30 Hz).
In this study, we only analyzed connectivity at the sensor level owing to the lack of MRI data. Certain known limitations exist to scalp-level analysis of functional networks (Colclough et al., 2016; Brookes et al., 2014): (i) the locations of EEG channels are not related directly to the location of the underlying sources and (ii) spurious estimates of functional connectivity can possibly occur between channels owing to the effects of field spread and volume conduction. To overcome the problems of sensor-level connectivity, Stam et al. (2007) and Nolte et al. (2004) came up with two methods—the phase lag index (PLI) and the imaginary part of coherency, respectively. These methods discard zero-lag connectivity and are, therefore, insensitive to volume conduction. In this study, we adopted the imaginary part of coherency (Nolte et al., 2004; Helfrich et al., 2016) based on wavelet transforms. The main steps are detailed below.
Let xt and yt denote two stationary multivariate time series. The continuous wavelet transforms, denoted as Xω and Yω, are defined as
| (1) |
| (2) |
where b is a time index and a denotes the wavelet scale. The function ψ0 is chosen to be the complex Morlet wavelet:
| (3) |
where the parameter ω0 governs the relative time and frequency resolution.
We assume throughout that Xω and Yω each have zero mean. Let
| (4) |
| (5) |
| (6) |
denote complex-valued covariance matrices, where the superscript‘*’denotes vector/matrix transposition and complex conjugation. These matrices correspond to the wavelet cross-spectral density matrices.
Subsequently, we use the imaginary part of the covariance matrices to calculate general lagged coherence, proposed by Nolte et al. (2004), with the zero-lag effect removed:
| (7) |
where syyw and sxxw denote pure real variances and syxw denotes the complex-valued covariance, with the real and imaginary parts denoted as Re(syxw) and Im(syxw), respectively.
For each participant, coherence values were stored in an N × N × T connectivity tensor A, where N = 62 channels and T = 30 time windows. Thereafter, these tensors were converted into matrices (vectorizing the upper diagonal of each N × N connectivity matrix of a time window). For real data with multiple participants, we built the matrix V by concatenating the columns from all participants (from all conditions) together to form a single time-varying network configuration matrix V. This matrix V had dimensions where S = 115 + 141 = 256 participants. These pooled neural data, which facilitated network sharing by all participants could be identified (Fig. 1A−E illustrates these matrices). In our weighted-network analysis, we retained and analyzed all possible connection weights between nodes without applying any threshold. This matrix was then used as input to the NMF algorithm and for subsequent processing (Fig. 1E, F).
Fig. 1.
Flowchart of data processing. (A–B) In all, 128 channels of resting-state EEG signals were recorded, of which 62 channels were chosen and 120-s time series were extracted and divided into 30 non-overlapping 4-s time windows. (C) We computed wavelet coherence between each pair of channels in each time window. (D) Next, we unfolded matrices for each time window into column vectors and concatenated time windows from all participants. We then applied nonnegative matrix factorization (NMF) algorithm, which decomposes concatenated matrix into matrix W of subnetworks (E) and matrix H of time-dependent coefficients (F) that quantify activation of each subnetwork in each time window. (G–I) NMF-based subnetwork detection requires optimizing three parameters—number of subnetworks, k; temporal sparsity of subnetwork expression, β; and regularization of subnetwork-edge weights, α. Kernel-density estimate of each bivariate distribution is represented by contour plot, where darker shades of blue indicate higher probability mass of random-sampling distribution. The best parameter is average parameter value that produces a cross-validation error at bottom of sample distribution and is indicated by green dashed line. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
2.4. Decomposing dynamic network into network patterns
To identify network patterns, we applied an unsupervised machine-learning algorithm, NMF (Lee and Seung, 1999), to the constructed time-varying network (Fig. 1D). This technique allowed us to pursue a near-decomposition of the whole network into topological subnetworks and the corresponding dynamically temporal coefficients (Fig. 1E, F). Each pattern is an additive component of the original network, weighted by its associated time-varying expression coefficient, and represents a pattern of functional interactions between brain regions. The NMF-based connectivity pattern learning paradigm is a basis decomposition of a collection of dynamic networks that separates co-varying network edges into subnetworks, or basis functions, with associated temporal coefficients, or basis weights. Unlike other graph clustering approaches that seek a hard partition of nodes and edges into clusters (Mucha et al., 2010; Bassett et al., 2013), the temporal variability coefficients provide a soft partition of the network edges, such that the original functional network of any time window can be reconstructed through a linear combination of all of the connectivity patterns weighted by their associated temporal variability coefficients in that time window (Leonardi et al., 2013; Leonardi et al., 2014). This computation implies that at a specific time window, connectivity patterns with a high temporal variability coefficient contribute their pattern of functional interactions more than subgraphs with a low temporal variability coefficient (Khambhati et al., 2018a).
Mathematically, NMF is a multivariate-decomposition technique that approximates a data matrix V (here, of size E × M) as the product of two non-negative matrices W and H. Next, we solved the matrix-factorization problem V ≈ WH, W ≥ 0, H ≥ 0 by optimizing the following cost function:
| (8) |
where k is the number of patterns to decompose, β is a penalty weight that enforces sparsity on the temporal variability coefficients, and α is a regularization parameter that provides an upper bound on the connection strengths within the patterns (Kim and Park, 2011). To solve the NMF equation, we performed 100 iterations using alternating non-negative least squares with the block-pivoting method to quickly and efficiently decompose the original matrices (Kim et al., 2014). We initialized W and H with non-negative weights drawn from a uniform-random distribution on the interval [0, 1].
To select the parameters k, β, and α, we used a random-sampling scheme, demonstrating effective optimization of high-dimensional parameter spaces (Khambhati et al., 2018a; Bergstra and Bengio, 2012), where we re-ran the NMF algorithm for 1000 parameter sets, where k was randomly selected from 2 to 20, β was randomly selected from 0.01 to 1, and α was randomly selected from 0.01 to 1 (Fig. 2). We evaluated subnetwork-learning performance based on a fivefold cross-validation scheme. Iteratively, four folds were used to extract subnetworks and the one fold left out was used to calculate the cross-validation error (). The optimal parameter set yielded subnetworks that minimized the cross-validation error and reliably spanned the observed network topology space (Khambhati et al., 2018a). Based on these criteria, we chose an optimal parameter set (, ,) that yielded a low residual error according to our scheme (Fig. 1G−I).
Fig. 2.
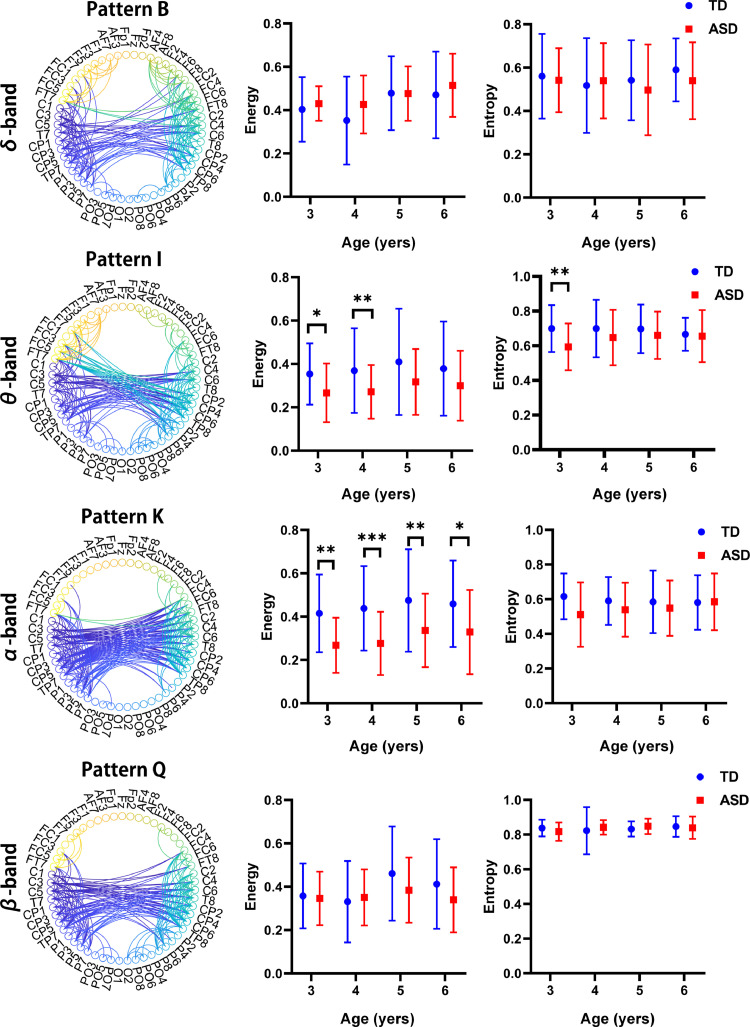
Age-related differences in patterns of homotopic−interhemispheric connections. Among the 23 patterns of networks, four patterns were highlighted as examples of age-related variation in network connectivity. For visualization, the thresholds of the subnetwork maps were set at the 90th percentile, and the connections are depicted in a circular format. Significant differences for each age group in terms of the energy (middle panel) and temporal variability (denoted by entropy; right panel) of the four patterns as well as statistical analysis of the two groups without considering age factors (inset) were observed. Only significant group effects are marked. * indicates the network pairs with significant connectivity differences between groups (*, **, and *** indicate p < 0.05, p < 0.01, and p < 0.001, respectively).
Owing to the non-deterministic nature of this approach, we integrated patterns estimates over multiple runs of the algorithm using consensus clustering—a general method of testing robustness and stability of clusters over several runs of one or more non-deterministic clustering algorithms (Monti et al., 2003). Our adapted consensus clustering procedure involved the following steps: (i) run the NMF approach R times on each network configuration matrix, (ii) concatenate the subnetwork matrix W across R runs into an aggregate matrix with dimensions (iii) apply NMF to the aggregate matrix to determine a final set of subnetworks Wconsensus and the dynamic coefficient Hconsensus. In this study, we set R = 100.
As a sanity check, we compared our NMF-based results of decomposing the α-band network with the classic and sparse NMF schemes (Lee and Seung, 1999; Berry et al., 2007; Hoyer, 2004), which in theory should provide very similar results. The results of this comparison are displayed in Figure S2. Overall, the three NMF derivative approaches yield very similar patterns. We evaluated their performance based on a fivefold cross-validation scheme. The classification module classified the feature vector, i.e., extracted six network components energy, using the support vector machine (SVM) classifier to identify the children with ASD (ASD vs TD). The classification accuracies of our NMF-based, original NMF, and sparse NMF approaches are 72.5%, 70.1%, and 70.25%, respectively. The results reflect that the proposed NMF-based approach performs better than the original and sparse NMF approaches.
2.5. Test-retest reliability of connectivity patterns
It is essential to consider the reproducibility of patterns measured using NMF. To quantify the reproducibility of the connectivity patterns, we measured the extent to which the pattern of the subgraph edge weights measured in one dataset predicts the pattern of the subgraph edge weights measured in a second dataset. Specifically, we first applied NMF using the optimal parameter set to two different datasets ( and ), resulting in two subnetwork matrices (W1 and W2). It is noted that the connectivity patterns along the columns of W1 may not necessarily be ordered similarly to the subgraphs along the columns of W2 because of the stochastic nature of the NMF algorithms. To reorder the connectivity patterns from the second dataset such that they correspond to the same order as the patterns from the first dataset, we sought a mapping Xij of the subnetwork to the subnetwork , where X is a Boolean matrix that prescribes whether the ith subnetwork from the first dataset is uniquely assigned to the jth subnetwork from the second dataset. The cost Ci, j associated with assigning to is equal to . To determine a unique X, we minimized the cost function using the Hungarian algorithm (Kuhn, 1955). After calculating an optimal assignment between the connectivity patterns of the two datasets, we measured the similarity in the pattern of the edge weights between the assigned subnetwork pairs (i, j) by calculating the Pearson correlation coefficient (Khambhati et al., 2018a, b). This approach would enable us to assess the reproducibility of each individual subnetwork based on the magnitude of the Pearson correlation similarity measure relative to that expected by chance (Khambhati et al., 2018a).
2.6. Statistics
To track the time-varying changes in the expression or activation of the subnetworks, we first calculated the signal energy of the time-dependent coefficients for each subnetwork and child. Signal energy is defined as , where Hn is the activation coefficient in time window and L is the length of the signal for a participant (Chai et al., 2017). Second, to quantify the dynamic switching behavior of the network component expression, we calculate the signal entropy of the activation coefficient time series to characterize temporal variability. The signal entropy is defined as where P(xi) is a probability mass function on the activation coefficient computed using the histogram-based entropy estimator (Nelson et al., 2010).
To facilitate between-subject comparisons, we standardized the energy and entropy values for each subnetwork—we computed the means of the time-dependent coefficients for each participant and each network component and then divided all time-dependent coefficients for each subject and each subnetwork by their respective means. A two-way analysis of variance (ANOVA) was performed to evaluate the energy and entropy values in different bands, including the factor groups (ASD, TD) and age (3–6 years), using Bonferroni's post-hoc test for multiple comparisons between groups. The α-level of the significance was set at 0.05. Furthermore, the Pearson correlation was calculated between the energy (or entropy) values and age (3–6 years) to explore the trajectory of brain development in early childhood. Only significant group effects are reported. All statistical analyses and graphical representations were produced using GraphPad Prism 7.0 Software. Data are expressed as mean ± standard error unless otherwise specified.
3. Results
3.1. Extract patterns of connectivity from the resting-state EEG via NMF
To identify the patterns of resting-state connectivity network, we first measured the resting-state EEG from a group of 115 children with ASD and 141 age-matched typically developing controls (TD; Fig. 1A). In particular, we selected 62 sensors of interest to ensure the maximum spatial coverage of the frontal, central, temporal, and occipital regions (Fig. 1B). We then constructed time-varying brain networks for each participant, in which network nodes represented brain regions and network edges between the nodes represented the wavelet-based coherence coefficient among the regional EEG time series (Fig. 1C). Specifically, we computed a 62 × 62 adjacency matrix for each participant within each EEG time window (corresponding to a 120-s time series that was divided into 30 non-overlapping 4-s time windows) for four specific-frequency bands (δ, θ, α, and β). This process resulted in 30 window-level adjacency matrices per participant. Finally, we aggregated all functional brain networks into a network-configuration matrix (Fig. 1D) with a size of 1891 × 7680. The first dimension of size 1891 corresponded to all unique, pairwise edges between the 62 channels; the second dimension of size 7680 corresponded to all combinations of the 30 repeated time windows and 256 participants.
To uncover the patterns of connectivity and their dynamic expressions from group-level brain networks, we applied the NMF technique to the network-constructed configuration matrix. This technique enabled us to pursue a parts-based decomposition of network edges into additive functional subnetworks (i.e., patterns; Fig. 1E) with accompanying expression coefficients over time and over subjects (Fig. 1F) (Chai et al., 2017; Khambhati et al., 2018a). Each subnetwork was composed of a 62 × 62 adjacency matrix, and the expression coefficients of each subnetwork were composed of a vector of length 7680. Thus, the subnetworks comprised the topological components of the functional brain network, and the temporal coefficients quantified their connection strengths and dynamic expressions over time.
A critical step in using NMF is the optimization of model parameters that identify a robust set of connectivity patterns. We apply a random sampling scheme to characterize the rich parameter space of the number of subnetworks k, temporal sparsity of subnetwork expression β, and regularization of subnetwork-edge weights α across the time-varying networks of all participants to ensure the generalizability of patterns without overfitting the model to the constructed configuration matrix. In this paper, we only present the optimization results of the α-band connectivity (Fig. 1G−I).
By designing a fivefold, leave-one-fold-out cross-validation scheme, we measured the relationship between the fivefold cross-validation error and each parameter k, α, and β (Fig. 1G−I). We observed a weak relationship between the cross-validation error and temporal sparsity (Pearson r = −0.15, p = 0.15). We also observe a significant increase in cross-validation error as the subnetwork regularization parameter (Pearson r = 0.36, p < 0.001). Similarly, we observe a significant positive relationship between the cross-validation error and number of subnetworks (Pearson r = 0.66, p < 1).
Collectively, these results suggest a potential strategy for choosing parameters that achieve a balance between the spatial and temporal generalizability and specificity of the subgraphs. Therefore, we averaged the randomly sampled parameters associated with the lowest 25% cross-validation error and found the optimal number of subnetworks to be six, the temporal sparsity to be 0.65, and the regularization of the subnetwork edge weights to be 0.45 (Fig. 1G−I). Thus, we performed parameter optimization on four frequency-band-specific connectivity−configuration matrices (Table 1). The results presented a near-linear increase in the number of patterns with increasing bandwidth from the δ to β bands. These results can be explained by the fact that a wider bandwidth yields a greater capacity to hold information and, thus, results in a larger number of patterns. To summarize, 23 patterns of connectivity were identified in the autistic group-level EEG data over four frequency-band-specific connectivity patterns (patterns A–D for δ connectivity, patterns E–I for θ connectivity, patterns J–O for α connectivity, patterns P–W for β connectivity). We then visualized the resulting adjacency matrices as circular-ring graphs (Figure S1). The pairwise correlation matrix between the spatial topology of network components identified with NMF in four specific frequency bands is displayed in Figure S3. Overall, the four frequency-band-specific network components are similar. The α-band-specific network components were topologically more similar than the other frequency-based counterparts. The autocorrelation of spatial topology is on the diagonal.
Table 1.
Result of parameter optimization on four frequency-band-specific connectivity−configuration matrices.
| Frequency band | δ | θ | α | β |
|---|---|---|---|---|
| (2–4 Hz) | (4–8 Hz) | (8–13 Hz) | (13–30 Hz) | |
| k | 4 | 5 | 6 | 8 |
| α | 0.82 | 0.84 | 0.65 | 0.62 |
| β | 0.42 | 0.5 | 0.45 | 0.42 |
Next, we considered the time-varying expression of patterns across individuals. To measure how strongly a pattern was expressed over time windows, we computed the energy of pattern expression for the temporal coefficients of each pattern for each participant. Similarly, to measure how transiently the pattern was expressed, we also computed the temporal variability of pattern expression using a histogram estimator. We then statistically compared the energy and temporal variability of pattern expression between the group of 114 autism children and the group of 141 typically developing children (Table S1). The development trajectory of all connectivity patterns was evaluated in Table S2.
3.2. Homotopic interhemispheric patterns
We first analyzed the homotopic interhemispheric-connection patterns, as they offered a relatively simple yet robust subset of brain connectivity. The homotopic interhemispheric pattern is defined as interhemispheric connectivity between homologous areas. Interhemispheric connections were apparent between the bilateral temporal lobes across four frequency bands (Fig. 2). We observed that in the α-band connectivity pattern (pattern K), the energy at different ages displayed a significant decreasing trend in the ASD group compared to the TD group (see Table S1), indicating an under-connectivity in the homotopic interhemispheric-connection patterns in ASD. In the θ-band connectivity pattern (pattern I), the energy was significantly lower in the ASD group compared to the TD group at the ages of 3 (p < 0.05) and 4 (p < 0.05). However, in the δ- and β-band connectivity patterns (patterns B and Q), we found no significant differences in energy between the groups (ASD vs TD) across all ages. We then considered the time-varying expression of subnetworks—or subnetwork dynamics—across individuals. In the four frequency-band connectivity patterns, a slightly decreasing trend of temporal variability was observed in the ASD group, but this did not reach statistical significance. The results suggest that the α rhythms are preferentially associated with the interaction processes involving homotopic interhemispheric connections.
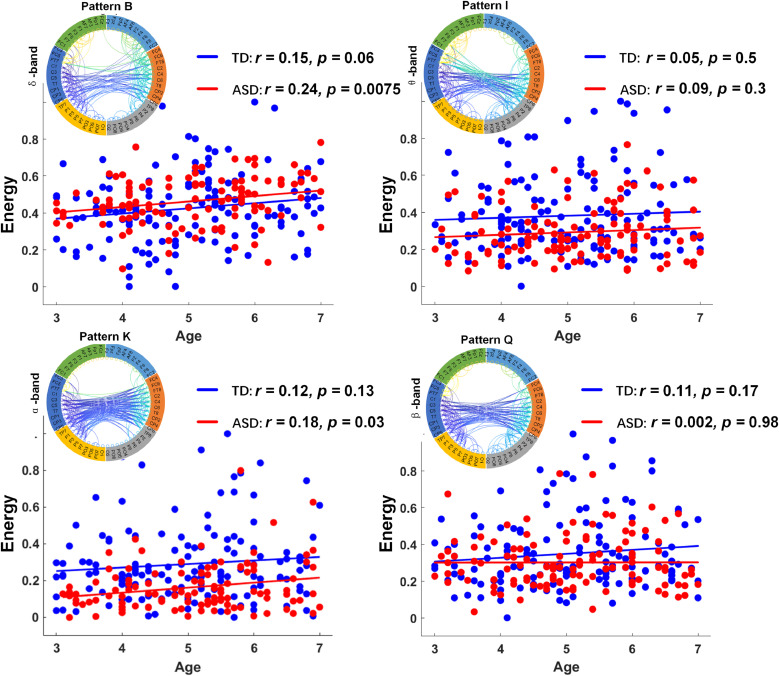
Fig. 3 illustrates group differences between ASD and TD children in subnetwork energy in different age groups, demonstrating differences in early childhood developmental trajectories of interhemispheric connectivity. In Fig. 3, the homotopic interhemispheric pattern of the ASD group displays a significant trend of increasing network energy with age in the δ band (pattern B; r = 0.24, p = 0.0075) and α band (pattern K; r = 0.18, p = 0.03), whereas the trends were not found to be significant in the TD group (pattern B; r = 0.15, p = 0.06; pattern K; r = 0.12, p = 0.13). In the θ-band-based pattern I and β-band-based pattern Q, the TD group illustrated a weak correlation between subnetwork energy and age (pattern I; r = 0.05, p = 0.5; pattern Q; r = 0.11, p = 0.17); a similar trend was observed in the ASD group.
Fig. 3.
Development of homotopic interhemispheric subnetwork properties of ASD group (red) and TD group (blue) at each frequency band. Scatter plot depicting correlation between age and network energy in each frequency band. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Taken together, the control group exhibited a faster rate of incremental increases in interhemispheric connectivity during early childhood development compared to that of the ASD group. Particularly, the α-band connectivity exhibited the largest developmental significant difference in terms of long-range interhemispheric connections; ASD-related abnormalities in the α band have been reported fairly consistently and, thus, may represent a biomarker of ASD (Han et al., 2017). Interesting relationships might be hypothesized linking this potential initial under-connectivity with the early abnormal development of the brain in ASD individuals.
3.3. Heterotopic interhemispheric and intrahemispheric patterns
The heterotopic interhemispheric connection was considered as a characteristic distortion of idiosyncratic connectivity. To address this question, we compared heterotopic interhemispheric-connectivity patterns and intrahemispheric-connectivity patterns of autistic and control children across four frequency bands (Fig. 4). The heterotopic interhemispheric pattern is defined as interhemispheric connectivity between heterogeneous areas. Extending our findings of idiosyncratic connectivity, the ASD group demonstrated a consistent reduction in long-range heterotopic interhemispheric-connectivity patterns in comparison to that of the control groups (e.g., patterns A, C, E, N, and U). In δ-band connectivity patterns (pattern A), the energy was significantly lower in ASD group compared to that in the TD group at ages of 3, 4, and 5, whereas the δ-band connectivity pattern C displayed no significant difference between the groups. Similarly, in the θ-band connectivity pattern E, the energy illustrated a significant decreasing trend in the ASD group compared to the TD group. The same phenomenon was evident in terms of the connectivity within the bilateral short-range hemispheric patterns (e.g., patterns L and O). These qualitative assessments of patterns of connectivity reveal a generally heterotopic bilateral and lateralized organization across hemispheres. These results indicate that ASD is characterized by heterotopic interhemispheric patterns.
Fig. 4.
Age-related differences in patterns of heterotopic−interhemispheric connections. The following seven patterns were highlighted as examples of age-related variation in the heterotopic−interhemispheric network across four frequency-band-specific connectivities—patterns A and C for δ-band connectivity; pattern E for θ-band connectivity; patterns L, N, and O for α-band connectivity; and pattern U for β-band connectivity. Significant differences for each age group in terms of the energy (middle panel) and entropy (right panel) of the four patterns as well as statistical analysis of the two groups without considering age factors (inset) were observed. * indicates network pairs with significantly different connections between groups (*, **, and *** indicate p < 0.05, p < 0.01, and p < 0.001, respectively).
In addition to the significant difference in connection strength, we also observed a significant difference between the groups in terms of the temporal variability (denoted by the entropy value) of the patterns A, C, E, and U, which represent lateralized long-range interhemispheric connections. Specifically, temporal variability was higher in the control group, suggesting that there was a higher tendency for these patterns to change over time in the controls compared to that in ASD children. Conversely, the patterns of α-band connectivity—including the short-range, within-frontal lobe (pattern L), within-occipital lobe (pattern O), and prefrontal−occipital junction in both hemispheres (pattern N)—were not significantly different between the two groups and were less prone to change.
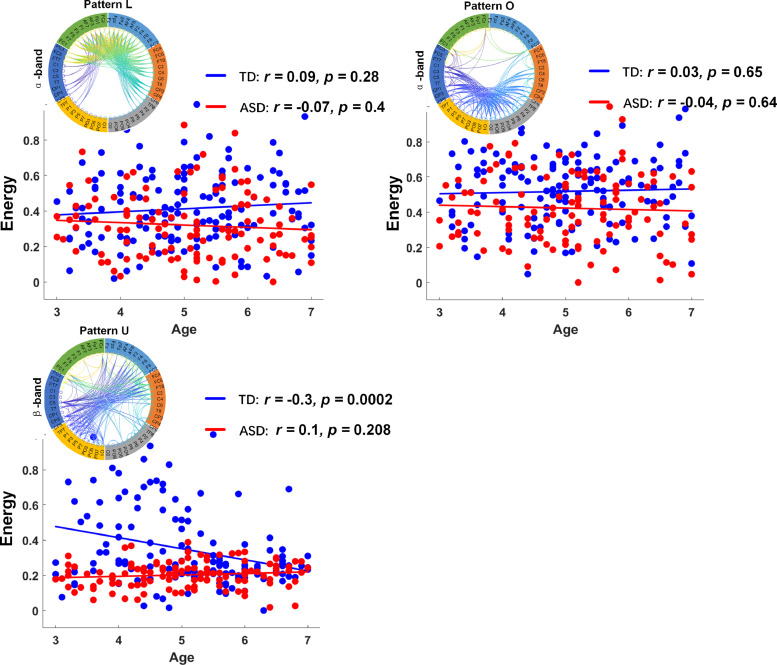
Fig. 5 depicts group differences between ASD and TD children in subnetwork energy at different ages. Pattern L comprised relatively dense connectivity, including both short-range, within-frontal-lobe and longer, between-frontal-lobe connections. The strength of pattern L followed a weak increasing trend with age in the TD group (r = 0.09, p = 0.28). However, the ASD group reflected an opposite trend with respect to age in the α band (r = −0.07, p = 0.4). Similar trends in connectivity were seen for the pattern O, which comprised relatively dense connectivity that included both short-range, within-occipital-lobe and longer, between-occipital-lobe connections. The strength of pattern O followed a weak increasing trend with age in the TD group (r = 0.03, p = 0.65), whereas the opposite trend was observed in the ASD group (r = −0.04, p = 0.64). Interestingly, the variance in pattern U in the ASD group appears to be nearly zero (approximately 0.1); meanwhile, there was a significance difference (p < 0.001) in variance between groups (ASD vs TD). A significant decreasing trend was observed for the TD group (r = −0.04, p = 0.64). Pattern U appears to be an early brain development network pattern sensitive to typically developing children, which may be useful for tracking development trajectory.
Fig. 5.
Development of heterotopic interhemispheric and intrahemispheric patterns of ASD group (red) and TD group (blue). Scatter plot illustrating correlation between age and network energy. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
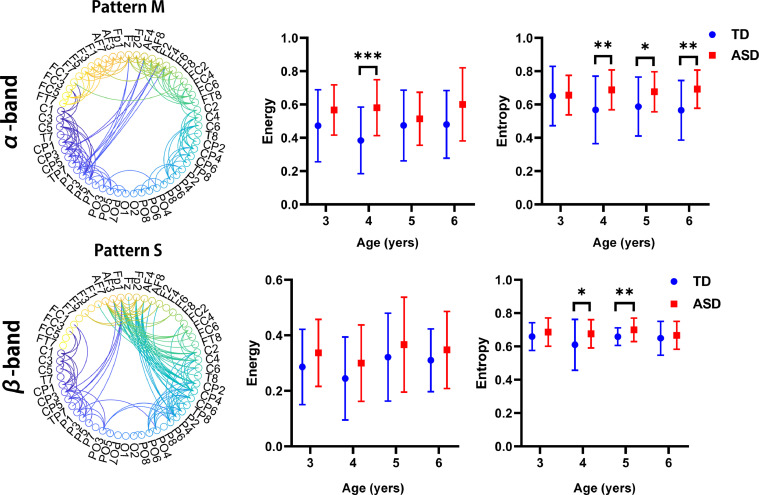
3.4. Generalization of short-range connectivity patterns
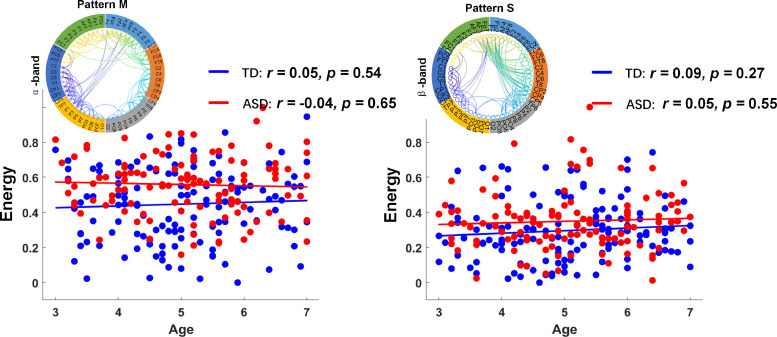
Thus far, we have established that the interhemispheric-connectivity patterns were more under-connected in the ASD group compared to those of the control group. However, it is also possible that there were common patterns of short-range connectivity in ASD groups across the four frequency bands of connectivity. Indeed, the patterns of over-connectivity within the ASD group have been identified in α-band and β-band connectivities (Fig. 6; patterns M and S). These maturational patterns appeared to differ in the ASD group from lower frequencies (δ and θ bands) to higher frequencies (α and β bands), as the short-range over-connectivity patterns were only observed in higher frequency bands (α and β bands). An interesting relationship may be hypothesized, linking this potential initial over-connectivity with the early overdevelopment of the brain in ASD (Courchesne et al., 2011, 2007) and the early maturation of white-matter tracts previously reported in young children with ASD (Bashat et al., 2007; Weinstein et al., 2011; Billeci et al., 2012). Some recent evidence suggests that seemingly divergent under- and over-connectivity findings in ASD may be reconciled in a model of reductions, both in network integration (under-connectivity within neurotypical networks) and in network differentiation or segregation (over-connectivity with atypical regions outside neurotypical networks) (O'Reilly et al., 2017).
Fig. 6.
Age-related differences in generalized patterns of localized connections. Following two patterns are highlighted as examples of age-related variation in localized network across four frequency-specific bands of connectivity: pattern M for α-band connectivity and pattern S for β-band connectivity. Significant differences for each age group in terms of the energy (middle panel) and entropy (right panel) of the four patterns as well as statistical analysis of the two groups without considering age factors (inset) were observed. * indicates network pairs with significantly different connections between groups (*, **, and *** indicate p < 0.05, p < 0.01, and p < 0.001, respectively).
Fig. 7 depicts a linear correlation of network energy with age in patterns M and S. We did not observe a clear developmental trajectory in patterns M and S. Specifically, the TD group illustrated a slight increasing trend of energy with age in pattern M (r = 0.05, p = 0.54), whereas the opposite trend was observed in the ASD group (r = −0.04, p = 0.65).
Fig. 7.
Development of local connectivity patterns of ASD group (red) and TD group (blue). Scatter plot depicting correlation between age and network energy. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
4. Discussion
Using novel dynamic machine-learning techniques that decompose matrices into time-varying subnetworks, we studied how dynamic patterns altered and evolved with early childhood development in a group of 115 children with ASD and 141 age-matched typically developing controls. Considerable changes occurred in the patterns of functional brain networks during an early stage of neurodevelopment. We demonstrated that the homotopic interhemispheric patterns of resting-state connectivity in the ASD participants were significantly decreased relative to those in the control children. Moreover, we compared heterotopic interhemispheric-connectivity patterns as well as within-hemisphere connectivity patterns of the autistic and control participants. The ASD group demonstrated a consistent reduction in long-range connectivity in comparison to that of the control group in terms of heterotopic interhemispheric-connectivity patterns. Finally, we observed a pattern of over-connectivity in the ASD group in terms of α-band and β-band connectivities.
4.1. Functional connectivity via resting-state EEG
Resting-state brain networks have revealed architectures closely related to underlying anatomical connections (Deco and Corbetta, 2011). The notion of globally coordinated and dynamically competing resting-state networks directly motivates studies that can identify overlapping cognitive systems and explain and predict their dynamics (Chai et al., 2017).
Previous work in spatially and temporally overlapping community detection has uncovered cohesive structures in resting-state brain networks (Fortunato, 2010). In the present study, we employed an NMF approach, which identifies the subnetworks of a brain network that dynamically vary across participants and across time, to obtain the connectivity for each subject in each time window as a nonnegative combination of basis subnetworks (Chai et al., 2017; Eavani et al., 2013). NMF offers prominent advantages over other dynamic graph-modeling approaches. First, the non-negativity constraint means that subnetworks can be interpreted as additive components, which together form the original network. Second, NMF does not make any explicit assumptions (including orthogonality or independence) with respect to the resulting subnetworks, which provides extra flexibility in extracting network components that may correspond to brain processes that overlap spatially (Khambhati et al., 2018c). Third, compared with the hard-partitioning of nodes into discrete modules in dynamic-community detection, NMF pursues a soft-partitioning of the network and allows one to track how functionally interacting brain areas can be dynamically expressed in a continuous and overlapping manner (Khambhati et al., 2018a).
Thus, from the perspective of network-based encoding of the ASD-related networks, we observed salient connectivity patterns in resting-state EEG data acquired from a group of 115 children with ASD and 141 age-matched typically developing controls.
4.2. Abnormal connectivity patterns in ASD
Our study revealed that the ASD group was characterized by short-range over-connectivity and long-range under-connectivity, particularly in interhemispheric connections. Both aberrant intrahemispheric and interhemispheric connectivity was observed, with a general trend toward under-connectivity, but with probable local short-range over-connectivity as well. Long-range under-connectivity was observed in lower frequency bands, which we hypothesized to be preferentially involved in long-range integrative networks (Figs. 2 and 4), whereas a stronger tendency for over-connectivity was observed (see Fig. 6) in higher frequency bands (hypothesized to be generally associated with more localized processes).
Our present finding regarding the frequency-band-based modulation of over- versus under-connectivity is consistent with that of slower oscillators involving more neurons in larger volumes (Von Stein and Sarnthein, 2000). Indeed, coordination of faster frequency required lager axons for any particular distance between two regions. Based on this fact, sharing a short range of high-frequency-band activity is more efficient for bias connectivity, whereas long-range interactions are required for lower frequency bands. Several studies have recently reported that high EEG frequencies are preferentially associated with more localized neural activity, whereas slower rhythms (δ, θ) are preferentially associated with more widespread integrative cross-region interaction processes that involve long-range connections. The synchronization of short-range cortical networks tend to be associated with higher frequencies (α, β) (Uhlhaas and Singer, 2010; Von Stein et al., 2000). These recent findings are consistent with our present results.
4.3. Neurodevelopmental changes in salient connectivity patterns
Considerable changes in the patterns of functional brain networks occur throughout neurodevelopment. The modularity of brain structures evolve with age, as does inter-regional connectivity (Meunier et al., 2009). Several studies (Teipel et al., 2009) have reported a correlation between EEG α-band coherence and the structural integrity of white matter and the fact that the connections among resting-state networks strengthen with age (Betzel et al., 2014). Consistent with these findings, we observed age-related differences in the strength and flexibility of the α-band patterns between autistic and control children. Specifically, the α-band patterns of interhemispheric homotopic long-range connections (pattern K) displayed the largest developmental differences. Interesting relationships may be hypothesized between the α-band interhemispheric long-range connections and neurodevelopment to link this pattern with ASD-related idiosyncratic early childhood development markers.
Group differences were observed in the developmental trajectories of specific brain connectivity patterns. With respect to the brain connectivity pattern that may display the largest developmental differences, our findings demonstrated that interhemispheric connectivity patterns are particularly vulnerable to ASD. In general, our findings demonstrated an age-dependent ASD connectivity pattern with interhemispheric long-range under-connectivity and local short-range over-connectivity. This observation is supported by findings from several past studies—a delay in the onset of axonal remodeling could drive brain overgrowth; thus, short-distance connections are favored over long-distance connections via typical developmental mechanisms (Lewis et al., 2013; Lewis and Elman, 2008).
4.4. Limitations
The present work had some limitations. First, we analyzed only sensor-level signals, which suffer from the effects of spatial leakage. In addition, the estimation of connectivity between sensors may be difficult to interpret, which prompted us to adopt source-level connectivity with the NMF algorithm. There are several advantages of source space projection in connectivity assessment (Schoffelen and Gross, 2009). First, the results can be overlaid directly onto structural brain images, enabling direct interpretation with respect to underlying anatomy. Second, source localization (via adaptive techniques such as beamforming) reduces artifacts in M/EEG data, indicating that the signal-to-noise ratio (SNR) of projected data is higher than the SNR of raw data in channel space (Lai et al., 2018). This suggests to us that the combination of source-level connectivity and NMF could be complementary and provides a tool for analyses of cortical communication patterns from the EEG.
Moreover, the ICA-based artifact-rejection technique that we used may have distorted the network topology we obtained. ICA is widely regarded as a robust and powerful method for artifact removal from EEG data and has recently received increasing attention (Castellanos and Makarov, 2006; Zafar et al., 2019). However, during subtraction (ICA is a linear operation applied to all sensors) of an artifactual waveform from segments of artifactual data, several challenges are encountered: (a) it is unclear what part of the artifactual waveform is artifact and what part is signal, (b) ICA does not completely remove the entire signal from any channel, even if the entire signal was artifactual, (c) ICA contaminates other channels with the artifactual component, and (d) ICA applies the same transformation throughout the recording and, therefore, mixes the non-artifactual time segments using the same spatial coefficients computed for that component. Therefore, ICA should only be applied to artifacts such as eyeblink, muscle, and cardiac rhythms that persist throughout the recording. Future studies should elucidate the effects of ICA artifact rejection on subsequent connectivity and network analyses.
5. Conclusions
We applied a novel extracting-dynamic-network framework for uncovering a set of interpretable patterns that highlighted significant group-level differences between ASD and control children. Our results support the framework that ASD is characterized by a general trend toward a long-range under-connectivity of lower band frequencies, particularly for interhemispheric connections, combined with short-range over-connectivity. These results provide a context for more clearly understanding how early childhood developmental factors induce ASD-related abnormalities in brain connectivity throughout early childhood development.
Few studies have investigated individual variability within ASD and neurodevelopmental status. Hence, future studies must pay more attention to individually distinct (idiosyncratic) distortions in participants with ASD. Further, the EEG analyses of ASD individuals typically involve the computation of spectral power over predefined frequency bands (i.e., 2–4 Hz for θ, 4–8 Hz for δ, 8–13 Hz for α, and 13–30 Hz for β bands). In fact, these frequency bands change over time and among participants, particularly in children. In future work, individual frequency bands must be considered. Moreover, our NMF approach may provide invaluable insights on a variety of other neurodevelopmental disorders such as schizophrenia and attention-deficit hyperactivity disorder.
CRediT authorship contribution statement
Tianyi Zhou: Conceptualization, Methodology, Software, Writing - original draft. Jiannan Kang: Data curation. Fengyu Cong: Methodology. Dr. Xiaoli Li: Supervision, Writing - review & editing.
Declaration of Competing Interest
The authors state that they have no conflict of interest.
Acknowledgements
The authors are extremely thankful to the anonymous reviewers for their helpful suggestions for improving the manuscript and to Zheng Li for language editing. This research was supported by grants from the National Natural Science Foundation of China (grant no. 61761166003) and the National Key R&D Program of China (grant no. 2016YFC1306203).
Footnotes
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.nicl.2020.102251.
Appendix. Supplementary materials
References
- Anagnostou E., Taylor M.J. Review of neuroimaging in autism spectrum disorders: what have we learned and where we go from here. Mol. Autism. 2011;2:4. doi: 10.1186/2040-2392-2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Association A.P. American Psychiatric Pub; 2013. Diagnostic and Statistical Manual of Mental Disorders (DSM-5®) [DOI] [PubMed] [Google Scholar]
- Bashat D.B., Kronfeld-Duenias V., Zachor D.A., Ekstein P.M., Hendler T., Tarrasch R. Accelerated maturation of white matter in young children with autism: a high b value DWI study. Neuroimage. 2007;37:40–47. doi: 10.1016/j.neuroimage.2007.04.060. [DOI] [PubMed] [Google Scholar]
- Bassett D.S., Porter M.A., Wymbs N.F., Grafton S.T., Carlson J.M., Mucha P.J. Robust detection of dynamic community structure in networks. Chaos. 2013;23 doi: 10.1063/1.4790830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belmonte M.K., Allen G., Beckel-Mitchener A., Boulanger L.M., Carper R.A., Webb S.J. Autism and abnormal development of brain connectivity. J. Neurosci. 2004;24:9228–9231. doi: 10.1523/JNEUROSCI.3340-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergstra J., Bengio Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012;13:281–305. [Google Scholar]
- Berry M.W., Browne M., Langville A.N., Pauca V.P., Plemmons R.J. Algorithms and applications for approximate nonnegative matrix factorization. Comput. Stat. Data Anal. 2007;52:155–173. [Google Scholar]
- Betzel R.F., Byrge L., He Y., Goñi J., Zuo X.-N., Sporns O. Changes in structural and functional connectivity among resting-state networks across the human lifespan. Neuroimage. 2014;102:345–357. doi: 10.1016/j.neuroimage.2014.07.067. [DOI] [PubMed] [Google Scholar]
- Billeci L., Calderoni S., Tosetti M., Catani M., Muratori F. White matter connectivity in children with autism spectrum disorders: a tract-based spatial statistics study. BMC Neurol. 2012;12:148. doi: 10.1186/1471-2377-12-148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bos D.J., van Raalten T.R., Oranje B., Smits A.R., Kobussen N.A., van Belle J. Developmental differences in higher-order resting-state networks in Autism Spectrum Disorder. NeuroImage. 2014;4:820–827. doi: 10.1016/j.nicl.2014.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brookes M.J., O'Neill G.C., Hall E.L., Woolrich M.W., Baker A., Corner S.P. Measuring temporal, spectral and spatial changes in electrophysiological brain network connectivity. Neuroimage. 2014;91:282–299. doi: 10.1016/j.neuroimage.2013.12.066. [DOI] [PubMed] [Google Scholar]
- Brown C., Gruber T., Boucher J., Rippon G., Brock J. Gamma abnormalities during perception of illusory figures in autism. Cortex. 2005;41:364–376. doi: 10.1016/s0010-9452(08)70273-9. [DOI] [PubMed] [Google Scholar]
- B. Cai, G. Zhang, A. Zhang, J. M. Stephen, T. W. Wilson, V. D. Calhoun, et al., "Capturing dynamic connectivity from resting state fMRI using time-varying graphical lasso," IEEE Trans. Biomed. Eng., 2018. [DOI] [PMC free article] [PubMed]
- Castellanos N.P., Makarov V.A. Recovering EEG brain signals: artifact suppression with wavelet enhanced independent component analysis. J. Neurosci. Methods. 2006;158:300–312. doi: 10.1016/j.jneumeth.2006.05.033. [DOI] [PubMed] [Google Scholar]
- Chai L.R., Khambhati A.N., Ciric R., Moore T.M., Gur R.C., Gur R.E. Evolution of brain network dynamics in neurodevelopment. Netw. Neurosci. 2017;1:14–30. doi: 10.1162/NETN_a_00001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colclough G.L., Woolrich M.W., Tewarie P., Brookes M.J., Quinn A.J., Smith S.M. How reliable are MEG resting-state connectivity metrics? Neuroimage. 2016;138:284–293. doi: 10.1016/j.neuroimage.2016.05.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Courchesne E., Campbell K., Solso S. Brain growth across the life span in autism: age-specific changes in anatomical pathology. Brain Res. 2011;1380:138–145. doi: 10.1016/j.brainres.2010.09.101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Courchesne E., Pierce K., Schumann C.M., Redcay E., Buckwalter J.A., Kennedy D.P. Mapping early brain development in autism. Neuron. 2007;56:399–413. doi: 10.1016/j.neuron.2007.10.016. [DOI] [PubMed] [Google Scholar]
- Deco G., Corbetta M. The dynamical balance of the brain at rest. Neuroscientist. 2011;17:107–123. doi: 10.1177/1073858409354384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delorme A., Makeig S. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods. 2004;134:9–21. doi: 10.1016/j.jneumeth.2003.10.009. 2004/03/15/ [DOI] [PubMed] [Google Scholar]
- Di Martino A., Yan C.-G., Li Q., Denio E., Castellanos F.X., Alaerts K. The autism brain imaging data exchange: towards a large-scale evaluation of the intrinsic brain architecture in autism. Mol. Psychiatry. 2014;19:659. doi: 10.1038/mp.2013.78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dinstein I., Pierce K., Eyler L., Solso S., Malach R., Behrmann M. Disrupted neural synchronization in toddlers with autism. Neuron. 2011;70:1218–1225. doi: 10.1016/j.neuron.2011.04.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- H. Eavani, T. D. Satterthwaite, R. E. Gur, R. C. Gur, and C. Davatzikos, "Identifying patterns in temporal variation of functional connectivity using resting state FMRI," in 2013 IEEE 10th International Symposium on Biomedical Imaging, 2013, pp. 1086-1089. [DOI] [PMC free article] [PubMed]
- Fortunato S. Community detection in graphs. Phys. Rep. 2010;486:75–174. [Google Scholar]
- Geschwind D.H., Levitt P. Autism spectrum disorders: developmental disconnection syndromes. Curr. Opin. Neurobiol. 2007;17:103–111. doi: 10.1016/j.conb.2007.01.009. 2007/02/01/ [DOI] [PubMed] [Google Scholar]
- Hahamy A., Behrmann M., Malach R. The idiosyncratic brain: distortion of spontaneous connectivity patterns in autism spectrum disorder. Nat. Neurosci. 2015;18:302. doi: 10.1038/nn.3919. [DOI] [PubMed] [Google Scholar]
- Han J., Zeng K., Kang J., Tong Z., Cai E., Chen H. Development of brain network in children with autism from early childhood to late childhood. Neuroscience. 2017;367:134–146. doi: 10.1016/j.neuroscience.2017.10.015. [DOI] [PubMed] [Google Scholar]
- Helfrich R.F., Knepper H., Nolte G., Sengelmann M., König P., Schneider T.R. Spectral fingerprints of large‐scale cortical dynamics during ambiguous motion perception. Hum. Brain Mapp. 2016;37:4099–4111. doi: 10.1002/hbm.23298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoyer P.O. Non-negative matrix factorization with sparseness constraints. J. Mach. Learn. Res. 2004;5:1457–1469. [Google Scholar]
- Hughes J.R. Autism: the first firm finding= underconnectivity? Epilepsy Behav. 2007;11:20–24. doi: 10.1016/j.yebeh.2007.03.010. [DOI] [PubMed] [Google Scholar]
- Just M.A., Cherkassky V.L., Keller T.A., Minshew N.J. Cortical activation and synchronization during sentence comprehension in high-functioning autism: evidence of underconnectivity. Brain. 2004;127:1811–1821. doi: 10.1093/brain/awh199. [DOI] [PubMed] [Google Scholar]
- Kana R.K., Uddin L.Q., Kenet T., Chugani D., Müller R.-A. Brain connectivity in autism. Front. Hum. Neurosci. 2014;8:349. doi: 10.3389/fnhum.2014.00349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keown C.L., Datko M.C., Chen C.P., Maximo J.O., Jahedi A., Müller R.-A. Network organization is globally atypical in autism: a graph theory study of intrinsic functional connectivity. Biol. Psychiatry. 2017;2:66–75. doi: 10.1016/j.bpsc.2016.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khambhati A.N., Bassett D.S., Oommen B.S., Chen S.H., Lucas T.H., Davis K.A. Recurring functional interactions predict network architecture of interictal and ictal states in neocortical epilepsy. eNeuro. 2017;4 doi: 10.1523/ENEURO.0091-16.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- A. N. Khambhati, A. E. Kahn, J. Costantini, Y. Ezzyat, E. A. Solomon, R. E. Gross, et al., "Predictive control of electrophysiological network architecture using direct, single-node neurostimulation in humans," bioRxiv, 2018. [DOI] [PMC free article] [PubMed]
- Khambhati A.N., Mattar M.G., Wymbs N.F., Grafton S.T., Bassett D.S. Beyond modularity: fine-scale mechanisms and rules for brain network reconfiguration. NeuroImage. 2018;166:385–399. doi: 10.1016/j.neuroimage.2017.11.015. [DOI] [PubMed] [Google Scholar]
- Khambhati A.N., Medaglia J.D., Karuza E.A., Thompson-Schill S.L., Bassett D.S. Subgraphs of functional brain networks identify dynamical constraints of cognitive control. PLoS Comput. Biol. 2018;14 doi: 10.1371/journal.pcbi.1006234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khambhati A.N., Sizemore A.E., Betzel R.F., Bassett D.S. Modeling and interpreting mesoscale network dynamics. NeuroImage. 2018;180:337–349. doi: 10.1016/j.neuroimage.2017.06.029. 2018/10/15/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J., He Y., Park H. Algorithms for nonnegative matrix and tensor factorizations: a unified view based on block coordinate descent framework. J. Glob. Optim. 2014;58:285–319. [Google Scholar]
- Kim J., Park H. Fast nonnegative matrix factorization: an active-set-like method and comparisons. SIAM J. Sci. Comput. 2011;33:3261–3281. [Google Scholar]
- Kuhn H.W. The Hungarian method for the assignment problem. Naval Res. Logist. Q. 1955;2:83–97. [Google Scholar]
- Lai M., Demuru M., Hillebrand A., Fraschini M. A comparison between scalp-and source-reconstructed EEG networks. Sci. Rep. 2018;8:1–8. doi: 10.1038/s41598-018-30869-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee D.D., Seung H.S. Learning the parts of objects by non-negative matrix factorization. Nature. 1999;401:788. doi: 10.1038/44565. [DOI] [PubMed] [Google Scholar]
- Leonardi N., Richiardi J., Gschwind M., Simioni S., Annoni J.-M., Schluep M. Principal components of functional connectivity: a new approach to study dynamic brain connectivity during rest. NeuroImage. 2013;83:937–950. doi: 10.1016/j.neuroimage.2013.07.019. [DOI] [PubMed] [Google Scholar]
- Leonardi N., Shirer W.R., Greicius M.D., Van De Ville D. Disentangling dynamic networks: separated and joint expressions of functional connectivity patterns in time. Hum. Brain Mapp. 2014;35:5984–5995. doi: 10.1002/hbm.22599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis J.D., Elman J.L. Growth‐related neural reorganization and the autism phenotype: a test of the hypothesis that altered brain growth leads to altered connectivity. Dev. Sci. 2008;11:135–155. doi: 10.1111/j.1467-7687.2007.00634.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis J.D., Theilmann R.J., Fonov V., Bellec P., Lincoln A., Evans A.C. Callosal fiber length and interhemispheric connectivity in adults with autism: brain overgrowth and underconnectivity. Hum. Brain Mapp. 2013;34:1685–1695. doi: 10.1002/hbm.22018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marimpis A.D., Dimitriadis S.I., Adamos D.A., Laskaris N.A. NNMF connectivity microstates: a new approach to represent the dynamic brain coordination. Front. Neuroinf. 2016;10 [Google Scholar]
- Meunier D., Achard S., Morcom A., Bullmore E. Age-related changes in modular organization of human brain functional networks. Neuroimage. 2009;44:715–723. doi: 10.1016/j.neuroimage.2008.09.062. [DOI] [PubMed] [Google Scholar]
- Minshew N.J., Keller T.A. The nature of brain dysfunction in autism: functional brain imaging studies. Curr. Opin. Neurol. 2010;23:124–130. doi: 10.1097/WCO.0b013e32833782d4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monti S., Tamayo P., Mesirov J., Golub T. Consensus clustering: a resampling-based method for class discovery and visualization of gene expression microarray data. Mach. Learn. 2003;52:91–118. [Google Scholar]
- Mucha P.J., Richardson T., Macon K., Porter M.A., Onnela J.-P. Community structure in time-dependent, multiscale, and multiplex networks. Science. 2010;328:876–878. doi: 10.1126/science.1184819. [DOI] [PubMed] [Google Scholar]
- Müller R.-A. Comprehensive Guide to Autism. 2014. Anatomical and functional connectivity in autism spectrum disorders; pp. 49–75. [Google Scholar]
- Murias M., Webb S.J., Greenson J., Dawson G. Resting state cortical connectivity reflected in EEG coherence in individuals with autism. Biol. Psychiatry. 2007;62:270–273. doi: 10.1016/j.biopsych.2006.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson S.M., Cohen A.L., Power J.D., Wig G.S., Miezin F.M., Wheeler M.E. A parcellation scheme for human left lateral parietal cortex. Neuron. 2010;67:156–170. doi: 10.1016/j.neuron.2010.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nolte G., Bai O., Wheaton L., Mari Z., Vorbach S., Hallett M. Identifying true brain interaction from EEG data using the imaginary part of coherency. Clin. Neurophysiol. 2004;115:2292–2307. doi: 10.1016/j.clinph.2004.04.029. [DOI] [PubMed] [Google Scholar]
- O'Reilly C., Lewis J.D., Elsabbagh M. Is functional brain connectivity atypical in autism? A systematic review of EEG and MEG studies. PLoS ONE. 2017;12 doi: 10.1371/journal.pone.0175870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raichle M.E. A paradigm shift in functional brain imaging. J. Neurosci. 2009;29:12729–12734. doi: 10.1523/JNEUROSCI.4366-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogasch N.C., Thomson R.H., Farzan F., Fitzgibbon B.M., Bailey N.W., Hernandez-Pavon J.C. Removing artefacts from TMS-EEG recordings using independent component analysis: importance for assessing prefrontal and motor cortex network properties. Neuroimage. 2014;101:425–439. doi: 10.1016/j.neuroimage.2014.07.037. [DOI] [PubMed] [Google Scholar]
- Rubinov M., Sporns O. Complex network measures of brain connectivity: uses and interpretations. Neuroimage. 2010;52:1059–1069. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
- Schoffelen J.M., Gross J. Source connectivity analysis with MEG and EEG. Hum. Brain Mapp. 2009;30:1857–1865. doi: 10.1002/hbm.20745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stam C.J., Nolte G., Daffertshofer A. Phase lag index: assessment of functional connectivity from multi channel EEG and MEG with diminished bias from common sources. Hum. Brain Mapp. 2007;28:1178–1193. doi: 10.1002/hbm.20346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teipel S.J., Pogarell O., Meindl T., Dietrich O., Sydykova D., Hunklinger U. Regional networks underlying interhemispheric connectivity: an EEG and DTI study in healthy ageing and amnestic mild cognitive impairment. Hum. Brain Mapp. 2009;30:2098–2119. doi: 10.1002/hbm.20652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Telesford Q.K., Simpson S.L., Burdette J.H., Hayasaka S., Laurienti P.J. The brain as a complex system: using network science as a tool for understanding the brain. Brain Connect. 2011;1:295–308. doi: 10.1089/brain.2011.0055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thai N.J., Longe O., Rippon G. Disconnected brains: what is the role of fMRI in connectivity research? Int. J. Psychophysiol. 2009;73:27–32. doi: 10.1016/j.ijpsycho.2008.12.015. [DOI] [PubMed] [Google Scholar]
- Uddin L.Q., Supekar K., Lynch C.J., Khouzam A., Phillips J., Feinstein C. Salience network–based classification and prediction of symptom severity in children with autism. JAMA Psychiatry. 2013;70:869–879. doi: 10.1001/jamapsychiatry.2013.104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uhlhaas P.J., Singer W. Abnormal neural oscillations and synchrony in schizophrenia. Nat. Rev. Neurosci. 2010;11:100. doi: 10.1038/nrn2774. [DOI] [PubMed] [Google Scholar]
- Von Stein A., Chiang C., König P. Top-down processing mediated by interareal synchronization. Proc. Natl. Acad. Sci. 2000;97:14748–14753. doi: 10.1073/pnas.97.26.14748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Von Stein A., Sarnthein J. Different frequencies for different scales of cortical integration: from local gamma to long range alpha/theta synchronization. Int. J. Psychophysiol. 2000;38:301–313. doi: 10.1016/s0167-8760(00)00172-0. [DOI] [PubMed] [Google Scholar]
- Weinstein M., Ben‐Sira L., Levy Y., Zachor D.A., Itzhak E.B., Artzi M. Abnormal white matter integrity in young children with autism. Hum. Brain Mapp. 2011;32:534–543. doi: 10.1002/hbm.21042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zafar R., Qayyum A., Mumtaz W. Automatic eye blink artifact removal for EEG based on a sparse coding technique for assessing major mental disorders. J. Integr. Neurosci. 2019;18:217–229. doi: 10.31083/j.jin.2019.03.164. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.