Altered topological blueprint of trabecular bone associates with skeletal pathology in humans

Abstract

Bone is a hierarchically organized biological material, and its strength is usually attributed to overt factors such as mass, density, and composition. Here we investigate a covert factor – the topological blueprint, or the network organization pattern of trabecular bone. This generally conserved metric of an edge-and-node simplified presentation of trabecular bone relates to the average coordination/valence of nodes and the equiangular 3D offset of trabeculae emanating from these nodes. We compare the topological blueprint of trabecular bone in presumably normal, fractured osteoporotic, and osteoarthritic samples (all from human femoral head, cross-sectional study). We show that bone topology is altered similarly in both fragility fracture and in joint degeneration. Decoupled from the morphological descriptors, the topological blueprint subjected to simulated loading associates with an abnormal distribution of strain, local stress concentrations and lower resistance to the standardized load in pathological samples, in comparison with normal samples. These topological effects show no correlation with classic morphological descriptors of trabecular bone. The negative effect of the altered topological blueprint may, or may not, be partly compensated for by the morphological parameters. Thus, naturally occurring optimization of trabecular topology, or a lack thereof in skeletal disease, might be an additional, previously unaccounted for, contributor to the biomechanical performance of bone, and might be considered as a factor in the life-long pathophysiological trajectory of common bone ailments.

Highlights

• •Mechanical performance of the skeleton results from many factors and their interplay.
• •Topological blueprint as a basic trabecular design plan is an understudied factor.
• •Topological blueprint deviation undermines mechanical properties of trabecular bone.
• •Higher bone mass or thicker trabeculae do not compensate for deviant topology.

1. Introduction

The primary function of the skeleton is to facilitate locomotion. Naturally, all bones of the skeleton must be strong for their mechanical performance, and lightweight for low metabolic cost. The optimal mechanical performance of bone results from an interplay among several factors: i) the physiology of the musculoskeletal system as a whole (body posture and tone, balance, agility, muscular strength, power and endurance) (Hsu et al., 2014; Wainwright et al., 2005), ii) the net bone mass that depends on body size and anatomic constitution (Seeman, 2008), iii) the quality of the material (bone composition that depends on metabolism and includes for example organic-inorganic ratio, hydration, crosslinking) (Reznikov et al., 2016a; Creecy et al., 2020; Ganeko et al., 2015; Bala and Seeman, 2015), and iv) the 3D architecture (spatial distribution of osseous tissue within a bone) (Currey, 2001; Reznikov et al., 2016b). Various combinations of these factors may amplify or counterbalance their individual effects (Ferretti et al., 2003; Vale et al., 2013). An excellent review on the interplay of the independent determinants of bone quality was published by Fonseca et al.(Fonseca et al., 2014).

The 3D architecture, and principally the type of bone tissue – compact or trabecular – reflects the specific biomechanical demands imposed on it (Seeman, 2008). Compact bone predominantly comprises the hollow tubular shafts of the long bones. From a materials science perspective, a hollow tube geometry with a maximized second moment of area for a given net mass of material is the most advantageous geometry to withstand bending (Currey, 2003) and, accordingly, this suggests that the shafts of long bones perform as rigid levers perfectly adapted to bending (Seeman, 2008), and not merely to compression in the direction of gravity. Although trabecular bone is composed of the same lamellar tissue as compact bone (Reznikov et al., 2015), and the same principle of having the highest strength at the lowest metabolic cost applies to it, the architecture of trabecular bone is adapted for a different purpose (Fig. 1A), as described below. The three-dimensional trabecular network is located primarily at the anatomical sites where movement is possible, such as in the joints, or in the vertebral column. Trabecular bone at these sites is subjected to multidirectional loading, consistent with the range of movement. As well, the thickness of the compact shell that encloses trabecular bone tissue in the epiphyses of long bones, in carpal, tarsal bones or vertebral bodies, is normally only about several hundreds of micrometers, thus being comparable in thickness to individual trabecular struts and plates. It therefore seems reasonable to state that trabecular bone borders against soft tissue (cartilage in the joints or intervertebral disks in the spine) and therefore must fulfil the function of impact damping (Seeman, 2008). Thus, in trabecular bone, the ability to accommodate maximal stresses without dramatic deformation (as occurs in the compact bone of long bone shafts) is sacrificed in favor of the ability to accommodate maximal strains without fracture. In comparison to compact bone, trabecular bone must cope not only with various magnitudes of forces, but also with various orientations of forces, while at the same time maintaining appropriately lower stiffness and higher impact-damping properties.

Fig. 1.

Architecture of trabecular bone. A) Compact (grey) and trabecular (blue) bone in a human proximal femur. A virtual section through the femoral head illustrates that the compact shell is nearly as thin as a single trabecula, and another section through the shaft shows compact bone tissue and a hollow tube geometry. Such a different architecture is indicative of different biomechanical roles for compact and trabecular bone. B and C show thicker and thinner trabeculae, respectively (purposefully generated by manual thresholding). D is the topological blueprint that describes the spatial relationship of the interconnected trabeculae in both B and C, and this normally ensures the inherent multidirectional resilience of trabecular bone tissue.

1.1. Morphological and topological functional adaptation of trabecular bone

The optimization of trabecular bone architecture begins as early as during fetal development and continues as life-long functional adaptation. This process is driven by cell-mediated remodeling that affects quality, quantity and 3D distribution of bone material. Local variation of stresses exerted on bone tissue brings about morphological differences in volume fraction, trabecular thickness, trabecular separation, and trabecular anisotropy (Odgaard, 1997; Bouxsein et al., 2010; Morgan et al., 2003; Gibson and Ashby, 2001). This morphological variation reflects a long-term record of bone loading history and its biomechanical environment (Reznikov et al., 2017).

Besides the morphological optimization, trabecular bone undergoes a more fundamental and less apparent process of topological optimization. During fetal development, bone tissue forms in excess. As a part of normal growth and development, overproduced bone soon undergoes constructive regression and refinement, and many redundant elements are eliminated (Ryan and Krovitz, 2006; Acquaah et al., 2015). Eventually, constructive regression establishes a fundamental topological blueprint for trabecular bone. A topological blueprint, or bauplan (from German, Bau – “building, structure” and Plan – “plan, layout”), stands for the basic 3D organizational pattern that allows for various morphological modifications of the elements, and yet remains generally unchanged. For example, here described for bone, a topological blueprint does not account for size and shape of its elements, or the scale of their assembly, but rather it accounts for their spatial relationship to each other (Fig. 1B–D). To state this another way, the trabecular bone topological blueprint is an edge-and-node (also called graph) characteristic assembly of framework elements that ensures multidirectional load buttressing coupled with biomechanically appropriate resilience. The multidirectional resilience is achieved by i) equiangular offset of edges emanating from a node, and by ii) necessary and sufficient coordination of nodes. Below we elaborate on this mathematical concept in its biological context.

To analyze trabecular bone topology, each trabecula can be digitally skeletonized to a one-pixel-thick line coinciding with the centroid of the original 3D trabecula. This line is called an edge in conventional topology nomenclature. In the case of plate-shaped trabeculae, the longest dimension is selected as the orientation of the centroid. These edges connect at nodes and form a skeleton (called a graph in topological nomenclature). A skeleton, or graph, can be presented either visually as a 3D meshwork of interconnected edges, or as a list of all the edges with their 3 coordinates of the origin and 3 coordinates of the end. The edges sharing a set of 3 coordinates form a node, the valence, or coordination of which equals the number of the emanating edges. The nodes can be classified depending on their coordination as 3-neighbor (3-N), 4-neighbor (4-N), 5-neighbor (5-N) nodes, and so on. In a typical graph of trabecular bone, the abundances of nodes having a valence of 3, 4, 5 or more, decay exponentially. A trabecular bone graph is thus a decentralized, nonhierarchical, sparsely connected network since the connections of low coordination dominate (Fig. 1). The prevalence of low valence nodes apparently makes the network robust against random impacts, as opposed to hierarchical networks where destruction of the hub would result in disintegration of the whole. Finally, in a node of a given coordination/valence, the connected edges are maximally offset from each other, spanning maximal 3D volume with that number of connected elements (approaching 120° for triple nodes, 109.5° for quadruple nodes, and so on) (Reznikov et al., 2016b).

In previous work we demonstrated that the topological blueprint of healthy trabecular bone is highly conserved among various anatomical sites, among different individuals, and even among different species (Reznikov et al., 2016b; Reznikov et al., 2017; Ben Zvi et al., 2017). The established topological blueprint can accommodate different trabecular morphologies (e.g. thick vs. thin elements, rods vs. plates, anisotropy, stress trajectories) and shows little variation (Reznikov et al., 2016b; Reznikov et al., 2017; Ben Zvi et al., 2017), all the while adequately serving its mechanical purpose. However, the reasons for how and why trabecular bone fails (Gupta and Zioupos, 2008) are often convoluted: is it an outcome of merely a strong impact, or the decreasing net bone mass, deteriorating material properties, or altered topological blueprint (or a combination thereof)? Here, in a cross-sectional study, we test the hypothesis that an altered topological blueprint is associated with pathological conditions like joint degeneration in osteoarthritis and fragility fracture in osteoporosis. To address this hypothesis, we have compared the topological blueprints of healthy, osteoporotic and osteoarthritic human trabecular bone samples, and we assessed the effect of topological parameters on mechanical behavior using in silico testing. This assessment of the virtual, abstract structure is devoid of morphological descriptors such as trabecular size, shape and net bone mass. This abstract numerical analysis allowed decoupling of topology from the morphological descriptors. This analysis differs from previously published studies that correlate bone mechanical behavior with trabecular morphometrics (Odgaard, 1997; Wolff, 1892; Keaveny et al., 2001; Maquer et al., 2015; Ciarelli et al., 2000; Mosekilde et al., 2000) but not with its topology alone.

2. Materials and methods

2.1. Sample collection and processing

Sample collection was conducted in compliance with ethical guidelines, and IRB approval was granted for the study from both University Hospital of Malaga and McGill University. In total, 75 pathological samples were collected as “surgical waste” from elective arthroplasties conducted at the Regional University Hospital of Malaga, Spain, in 2013–2014 from patients that sustained an osteoporotic fragility fracture (OP, 31 cases, with none involving the femoral head), and from those that suffered osteoarthritic joint degeneration (OA, 44 cases). The samples were fixed in normal formalin at room temperature and scanned using a Nikon Metrology μCT XT H 225ST scanner (95 kV, 70 μA, 1600 projections, voxel size 35 μm, 16 bit grey scale). Following image reconstruction (Dragonfly™, Object Research Systems, Montréal, QC, Canada), 1 OP sample was excluded from further analysis because its size was <1 cm³, and 5 OA samples were excluded because of the presence of massive cystic lesions that did not allow digital isolation of a 1 cm³ cubic specimen for analysis. Of the remaining 39 OA samples, 19 also contained cystic lesions, but it was nonetheless possible to exclude the cysts (as well as other visible defects) from the region of interest for analysis, (Fig. 3A). The selected 69 (39 OA, 30 OP) pathological samples were compared to normal proximal femora obtained from the Maude Abbott Medical Museum, Faculty of Medicine, McGill University (Montréal, Quebec, Canada). The presumably normal samples were selected based on the criteria of having completely fused epiphyses (i.e., being adult), having the diameter of the femoral head equal to or exceeding 50 mm (i.e., being male and/or large body size donors) and not having any visible lesions on either the proximal or distal articulating surfaces of the femur, e.g., no osteophytes or eburnations (Molnar et al., 2011). For these aforementioned reasons, although we had no documented information about the health status of the individuals from this museum, we nevertheless refer to these as the morphologically normal samples. These ten normal femurs were scanned and reconstructed using the same methodology and cropped to generate 1 cm³ cubic-shaped samples originating from the same location within the femoral head as the pathological samples (Fig. 2). Although ethnic and race differences in bone mineral density and fracture propensity have been reported, these differences mostly account for the gross anthropometric descriptors (body size, limb length, bone shaft cross-section geometry) and life style, and pertain to the ageing and morbidity trajectories rather than to the intrinsic differences in the trabecular architecture (Nam et al., 2010; Marshall et al., 2008; Danielson et al., 2013).

Fig. 3.

Non-metric findings in proximal femur, selected examples. (A) Subchondral cysts (also called geodes, asterisks) were found in 50% of the joint degeneration OA samples. (B) In pathological OP samples, unremodeled residues of the fused growth plate (also known as the metaphyseal “scar”, arrowheads) can be observed even in the case of elderly donors. All samples presented are 15 mm in diameter.

Fig. 2.

Bone sample harvesting and digital processing for analysis. (A) Sample locations within a normal proximal femur. In each full proximal femur scan, a reference sample was digitally cropped from the femoral head as approximately shown by the purple cylinder. (B) Pathological samples of about 15 mm in diameter were harvested from the femoral head during elective total hip arthroplasty, and they were individually scanned by μCT. The sample preparation for FEA is shown in (C), and includes cropping to the uniform cubic size, replacement of each trabecula by a centroid (skeletonization), and replacement of each centroid by a straight edge (3D graph). FEA simulation of compressive loading of the topological blueprint is shown in (D): every element (topological edge) is a discretized beam with 4 segments. Local stress is color-coded in each segmented beam.

All normal and pathological samples were segmented using Otsu thresholding (Otsu, 1979), and analyzed morphometrically to obtain bone volume fraction, trabecular thickness, trabecular separation, connectivity density per unit of volume and mean intercept length (MIL) anisotropy (Dragonfly™). Trabecular thickness and trabecular separation were measured in 3D by locally inscribing a sphere of the maximal radius into the foreground (trabecular thickness) and background (trabecular separation) structures in 3D binary images. Trabecular aspect ratio is the trabecular length divided by its thickness. As the parameter of slenderness of individual trabeculae, it is an indirect derivative of the combination between trabecular separation and trabecular thickness. Broad separation combined with greater thickness, or narrow separation combined with lower thickness, may produce similar aspect ratios, or slenderness, of trabeculae. The mean intercept length was calculated in 3D as a fabric tensor of mean distances between the background-foreground interfaces measured for 5000 orientations (minimal number of iterations 100, maximal number of iterations 2000). The binary 3D images were then skeletonized and reduced to 3D edge-and-node networks, or graphs (Dragonfly™), for calculating the mean trabecular length, and for the topological analysis followed by Finite Element Analysis (FEA). The topological analysis using Dragonfly™ was generally identical to our previously published Matlab routine (Reznikov et al., 2016b). As an improvement of the original routine, every entry in such an array also had an assigned scalar value of the local thickness. The local thickness value was computed by inscribing a sphere of maximal radius into the foreground element (bone). This scalar local thickness was used for the local pruning threshold. For example, if an edge, one end of which was not connected to other edges, was shorter than the sum of the radii of the spheres inscribed into the nodes of its origin and terminus, such an edge was deleted. If the edge length of dead end was larger than the sum of the radii of the origin and terminus, it was kept intact. In the original Matlab script, the mean trabecular thickness was used as a pruning threshold, instead of the local node thickness. Alternatively, smoothing of the binarized image of the bone sample prior to skeletonization could be used instead of local thickness-based pruning. In that scenario, the smoothing kernel should be experimentally adjusted to the pixel size. As opposed to the earlier Matlab routine, no merging of close nodes was conducted. Thus, the results were slightly different from the previous studies in a sense that the proportion of simpler nodes was even more pronounced. The method of topological analysis has been validated (Felder and Doube, 2018) for various μCT resolutions, and it was found to yield consistent results on the coordination number (valence) of nodes as long as average trabecular thickness exceeded a voxel size by a factor 3–6.

Since the size of the groups was the maximal attainable size (this is a common limitation in the studies of cadaveric material), and because in both pathological groups the measured values had a broad scatter, nonparametric Kruskal-Wallis test and Mann-Whitney tests (asymptotic significance p value <0.05) were conducted in order to ascertain better robustness without assuming the normality of the distributions. For each parameter, we report 3 comparisons (normal-OP, normal-OA, and OA-OA).

2.2. Finite element mechanical simulation of skeletonized specimens

Table 1 describes the output parameters measured in FEA of bone graph samples.

Table 1.

FEA output parameters and their interpretation.

Parameter	Definition	Significance in FEA of this study
Apparent modulus	Modulus of elasticity – ratio of stress to strain – of the entire structure. Depends on the geometry and microstructure of an inhomogeneous specimen. Apparent modulus is usually lower (less stiff, more compliant) than material (true) modulus	When input material parameters and strain are the same, a higher apparent modulus indicates that the structure is more rigid because of the way its elements are assembled in 3D
Von Mises stress, maximal within element and averaged over sample	An approach to combine all values of stress (which is a tensor) into a single measure. In the von Mises stress formula, the non-axial stress components such as bending, shear and torsion are factored by 6 [35]. This indicates that for most materials yield/failure conditions will be met sooner if the proportion of non-axial stress is higher	When averaged over all the elements in the structure and normalized by apparent modulus, this parameter characterizes local deformations experienced by individual elements
Von Mises stress, SD		Higher SD indicates that load redistribution is non-uniform and stress concentrations are present
Shear and stretch %	The edges experience a combination of axial (stretch: favorable) and lateral (non-axial, including bending, shear and torsion: detrimental) local loads to which they react correspondingly by axial and lateral deformations. Numerical predominance of either axial or lateral deformations was used to classify the elements into being stretch or shear-dominated	Stretch-dominated structures are generally more robust and stable than shear-dominated structures at a given mass and load. The % value indicates where a structure is positioned on the spectrum between pure stretch and pure shear

SD: standard deviation.

Finite element analysis (FEA) of bone samples was conducted by coupling MATLAB (Release 2017b, The MathWorks, Inc., Natick, Massachusetts, USA) with Abaqus (Version 6.11, Dassault Systems Simulia Corporation, Johnston, RI, USA). Graph information from skeletonized bone specimens was provided as CSV files that were imported into MATLAB for preprocessing (indexation of edges, removing duplicate nodes and edges, and discretization of edges into smaller finite elements) where an Abaqus input file containing the node coordinates, node connectivity and boundary conditions was prepared and then submitted to Abaqus solver. Although topological blueprints – graphs – are inherently devoid of size, shape and material properties of the edges, these properties were uniformly assigned in order to embody in 3D the one-dimensional edges of the in silico model for the purpose of simulated loading. The edges of the graphs were rendered as Timoshenko beam elements that account for transverse shear behavior, with a length-to-cross-sectional-radius ratio of 8:1 (Liu et al., 2017). Each Timoshenko beam was discretized into 4 segments, and the beam cross-section was rendered circular. Of note, using uniform beams is applicable only for simulated loading of the truss-like topological blueprints, and would be inappropriate for modeling the effect of bone morphological parameters (for which 3D brick or tetrahedral elements would best be used). The elastic modulus of each beam was set at 13 GPa (based on experimentally documented ultrasonic and nanoindentation measurements of bone) with a Poisson's ratio of 0.3 (Ashman and Rho, 1988; Zysset et al., 1999). All FE simulations of topological blueprint behavior were conducted under unidirectional loading and linear elastic analysis. Compressive loading was applied until 0.7% compression of the sample to remain below the yield compressive strain of human bone material (Kopperdahl and Keaveny, 1998). While the top 20% of all the nodes comprising the cubic sample were displaced in compression, the bottom 20% of the nodes were fixed in the compression direction (along the z-axis only, which was aligned with the anatomical longitudinal axis). The output parameters of interest were the apparent elastic modulus (i.e., the modulus of the entire cubic sample), average von Mises stress among all the elements within a sample, maximal von Mises stress per sample, and percentage of shear-dominated and stretch-dominated elements. The apparent elastic modulus was calculated by dividing the sum of reaction forces at fixed nodes by cross-sectional area of the cubic sample perpendicular to the compression z-axis and by the sample's net compressive strain E = (∑F) / (A * ε). While the net compressive strain was identical for all the samples, the local deformation of individual interconnected beams might vary due to variations in the topological blueprints of the different bone samples. Therefore, the average von Mises stress divided by apparent modulus was used as an indicator for the local strain of individual beams, assuming that the von Mises criterion to be the controlling mechanism for yielding. The maximal local von Mises stress normalized by the sample apparent modulus was used as the determinant of the local concentration of the effective strain. Furthermore, we counted an element having the lateral strain component greater than the axial strain component as a shear-dominated element. The percentage of shear-dominated elements was then obtained for every sample by dividing their number by the total number of elements in the sample.

3. Results

The inventory of the study material, including biological profile (where applicable), morphometric analysis and Finite Element Analysis (FEA) is given in Table 2. Generally, the biological profile of the donors (age, sex and body mass index) is consistent with the typical risk groups for osteoporotic (OP) fragility fracture (older, female, lighter) and for osteoarthritic (OA) hip joint degeneration (earlier onset than osteoporosis, even prevalence in both sexes, higher body mass). In addition, we noticed the presence of certain non-metric features to be different among the groups. While none of the normal samples and only one of OP samples had subchondral cysts (or geodes), half of the OA specimens had one or more subchondral cysts, that are a common occurrence in OA (Resnick et al., 1977). As well, half of the normal samples and 40% of OP samples contained a clearly visible metaphyseal line, which indicated the location of the fused growth plate (Fig. 3).

Table 2.

Sample inventory and analysis for two pathological and one control group of samples. In the morphometric analysis and FEA columns, the mean value is given and the standard deviation is indicated in parentheses. The groups were cross-compared using Kruskal-Wallis non-parametric analysis of variance (SPSS Statistics) and Mann-Whitney for 3 pairs of groups. Statistically significant differences between the groups are labeled here by the symbols ^#, * or ^ø; p < 0.05 (Mann-Whitney test, two groups labeled with the same symbol are significantly different).

	Parameter	Normal	Osteoarthritis (OA)	Osteoporosis (OP)
Biological profile	Number; F:M	10	39; 18:21	30; 21:9
	Age	Adult	64.0* (±10.3)	78.8* (±10)
	BMI	n/a	28.3 (±3.8)	25.9 (±3.7)
Morphometric analysis of full volumes	BV/TV	0.30* (±0.04)	0.28# (±0.07)	0.24*# (±0.05)
	MIL	0.63* (±0.05)	0.61# (±0.1)	0.67*# (±0.07)
	Tb Th, mm	0.25*# (±0.03)	0.23* (±0.04)	0.22# (±0.03)
	Tb length, mm	0.5 (±0.02)	0.41 (±0.04)	0.44 (±0.04)
	Tb aspect ratio	2.01 (±0.23)	1.86 (±0.28)	1.99 (±0.2)
	Tb Sep, mm	0.68 (±0.04)	0.66* (±0.14)	0.77* (±0.17)
	Connectivity, mm−3	4.7* (±0.6)	7.0*# (±3.5)	5.0# (±2.3)
FEA of topological blueprints	Apparent modulus	31.8*# (±4.8)	15.6* (±6.3)	19.6# (±8.1)
	Maximal local strain	8.6*# (±1.3)	16.0* (±4.8)	14.9# (±5.5)
	Shear-dominated elements, %	69.2*# (±2.3)	73.8* (±3.1)	71.9# (±2.8)
Non-metric features	Subchondral cyst	0	19/39	1/30
	Growth plate residue	5/10	3/39	12/30

BMI, body mass index; BV/TV, bone volume fraction; MIL, mean intercept length anisotropy; Tb Th, trabecular thickness; Tb Sep, trabecular separation. The exact biological profile was not available for the normal group donors.

The morphometric parameters of the bone samples are presented in Table 2. Primarily, the morphometric parameters in both OP and OA groups were highly heterogeneous. Out of 7 morphometric descriptors compared among the 3 groups (21 pairs), only nine pairs demonstrated a statistically significant difference. Bone volume fraction was higher in normal bone than in OP bone, and it was also higher in OA than in OP bone. Mean intercept length (MIL) anisotropy was higher in OP than in either normal or OA bone. Among the other morphometric parameters, normal bone had higher trabecular thickness than both OA and OP bone, and there was no significant difference in trabecular thickness between OA and OP groups. The OP group had higher trabecular separation than the OA group. OA bone had the highest connectivity density per unit volume than either normal or OP groups. No difference was registered in trabecular length or trabecular aspect ratio for either pair of groups. Of note, no statistically significant difference was found between OP and normal bone in terms of connectivity density and trabecular separation.

Fig. 4 shows the topological parameters of the samples. Node abundances are plotted against node valence for all samples analyzed in the study forming overlapping graphs that resemble exponential decay curves. It is important to note that the ratio of nodes with 3, 4, 5 and 6 connected edges is scale-independent (as are all topological characteristics), and this ratio cannot be substituted by connectivity density per unit volume. For example, the absolute number of the nodes of a certain type within a standardized sample volume varies as much as 4-fold (within the normal bone group) and up to 7-fold (within either OA or OP groups). Presentation of the node type abundances as percentage of the total number of nodes allows comparison of different individuals and groups. The mean coordination number was calculated for the analyzed nodes with coordination number 3, 4, 5, and 6, multiplied by their abundance as a fraction of unity (for example, in the OA group the mean coordination number equals 3.206 = 3 × 0.819 + 4 × 0.149 + 5 × 0.027 + 6 × 0.004). The difference was statistically significant for all the node abundances and node mean coordination number in normal/OP and normal/OA pairs, but not in the OP/OA pair.

Fig. 4.

Topological parameters of normal and abnormal samples. Abundance of nodes with a different valence (number of connected edges) in normal and pathological samples. Samples from the donors with bone diseases, OA and OP, demonstrate slightly (but significantly) higher abundance of low-valence nodes and lower abundance of high-valence nodes. Mean abundances of nodes are indicated as black bars with the corresponding node abundance indicated in %. Mean coordination number was calculated as a sum of node coordination numbers factored by their abundance as a fraction of the unity.

While the morphological parameters being inconclusively distinct among the 3 pairs of groups (Table 2, Fig. 5A–C), the results from simulated loading of the topological blueprints (i.e., of the abstract, digital rendering of trabecular bone as graph, devoid of the morphological information) demonstrated a distinction between the normal and pathological groups (Fig. 5D–F) but no distinction between OA and OP. Following FEA of the sample 3D topological blueprint under uniaxial compression, both pathological OA and OP sample groups were statistically more compliant (p < 0.0005), had higher von Mises stress values than normal samples (p < 0.0005), and had a higher proportion of shear-dominated elements within a sample (p < 0.002). Statistically significant differences with the normal group were observed despite the broad scatter of values in the pathological groups, as can be seen in Fig. 5D–F. Interestingly, the simulated apparent modulus of the topological blueprints of the pathological samples OA and OP (not the physical apparent modulus of the respective samples) did not show correlation with bone volume fraction (Fig. 5G). Two important morphometric parameters such as volume fraction and trabecular thickness correlated strongly only in the normal group (Fig. 5H). Connectivity density and trabecular thickness showed low correlation (Fig. 5I), and other correlations among morphological parameters (not shown) were equally unremarkable.

Fig. 5.

Morphometric parameters, FEA of the mechanical behavior of the topological networks and correlation plots between selected parameters. The first row A-C shows dispersed morphometric descriptors in both pathological groups and somewhat more clustered values in the normal group. Brackets indicate statistically significant difference. The second row compares simulated mechanical performance of the topological blueprints (D-F). Here, despite the scatter of values in both pathological groups, both OA and OP groups are significantly different from the normal group. Because the topological models exist only in silico, the absolute values of the apparent moduli and strain directly reflect the assumed input parameters (elastic modulus, Poisson's ratio, element cross-section of the FEA model), and are therefore not given in numbers. The third row G-I shows selected correlation plots; correlation coefficient R² is given in the legends. Note that simulated apparent modulus of the graphs does not depend on volume fraction because the latter is inherently excluded from the FEA test (G). Among the morphological parameters (H and I), no correlation or trend could be identified except for the volume fraction versus trabecular thickness in the normal group, green markers (H).

The difference in the mechanical behavior of the topological frameworks between normal and pathological samples that could not be explained by changes in isolated morphometric descriptors, at the same time could be explained by the subtle but significant difference in the topological blueprint, such as the relative proportion of the nodes of low valence (Fig. 4B, C). Interestingly, neither topological blueprint parameters nor simulated loading of the virtual topological blueprint could distinguish between OP and OA groups (although clinically, OP samples all had a mechanical failure, and none of the OA samples had a fracture).

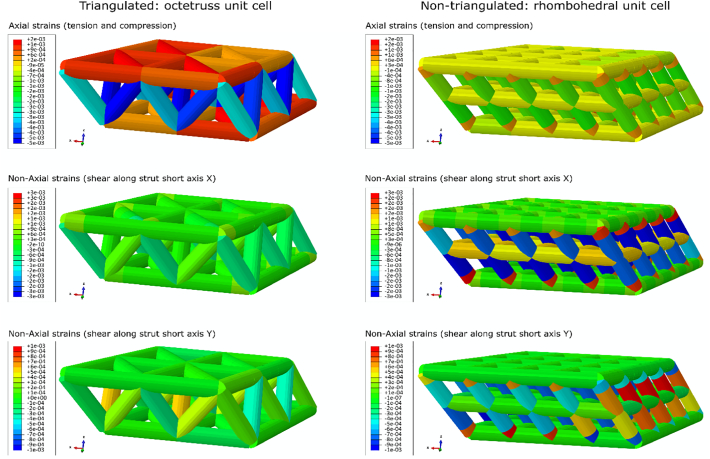
As a post hoc test complementary to our data, we have designed two virtual 3D truss structures of the same size and volume fraction; one structure is based on the octetruss (18) unit cell (an octetruss contains one octahedron and two tetrahedrons, and it is triangulated), and the other structure is based on the rhombohedral unit cell, which is a particular case of a parallelepiped and is not triangulated (Fig. 6). While the volume fraction and size of the phantoms were controlled, their topological blueprints were different. The triangulated octetruss-based phantom had a higher coordination number of the nodes (average 5.8), and the nontriangulated rhombohedral phantom contained nodes with a lower coordination number (average 4.5) even though the total number of connections per unit volume is four times higher in the rhombohedral phantom. Note here that the phantoms do not represent normal and pathological bone respectively – the difference between the normal and pathological bone samples is very subtle from the perspective of engineering design (compare the average coordination numbers in the range of 3.195–3.265 in bone with 4.5 and 5.8 in the phantoms), and the phantoms served merely an illustrative purpose. Both structures were loaded in simulated compression, as it was performed for the bone samples in this study. During identical compressive loading experiments, the octetruss-based structure demonstrates solely axial loading of its elements and negligible shear and bending stresses (stretch-dominated structure), whereas the rhombohedron-based structure responds to overall compression by shear-dominated deformation and relatively low axial loading of its elements (Table 3).

Fig. 6.

FEA illustrating the effect of a stable and unstable elementary structural motif on mechanical behavior of the phantom. The octetruss-based triangulated phantom (left panels) is stable because triangulation results in axial loading (top) and allows minimization of shear and bending stresses in the elements (middle and bottom). Non-triangulated rhombohedron-based phantom (right panels) is unstable and shear-dominated under compressive loading. Middle and bottom right panels illustrate that the non-triangulated phantom has local shear strains near the nodes that are likely to result in failure of the structure despite it having a higher connectivity density and equal volume fraction.

Table 3.

Results of FEA compressive testing of triangulated (octetruss-based) and non-triangulated (rhombohedron-based) phantoms (n = 1). Test conditions, assumed material modulus and Poisson's ratio are the same as in the FEA of bone under compression.

Parameter	Octetruss	Rhombohedral
Apparent strain (%)	0.7	0.7
Element cross-section diameter (mm)	0.25	0.2
Number of nodes	18	75
Number of elements	53	170
Average element length (mm)	1	0.5
Structure volume (mm3)	5.77	5.77
Structure volume fraction	0.45	0.45
Mean coordination number	5.8	4.5
Apparent modulus (MPa)	948	260
Average von Mises stress ± SD (MPa)	36.10 (±28.45)	23.41 (±23.54)
Local max von Mises stress (MPa)	87.40	73.43
Normalized local strain (max stress/app modulus)	0.092	0.283
Axial strain (%)	100	0.6
Lateral strain (%)	0	99.4

4. Discussion

This study used an approach that allows decoupling of trabecular bone morphology from its topology in terms of their respective effects on mechanical performance and the presence (or absence) of clinical pathological conditions. Evaluation of the topology is only possible by simulation, because direct conventional mechanical testing inherently assesses the combined effect of both morphology and topology. The results of this study reveal an association between the altered topological properties of trabecular bone and the presence of clinically apparent pathological conditions.

4.1. Similar underlying topological motif in two distinct diseases

Although both OA and OP are both associated with ageing, the populations affected by these diseases do not quite overlap. Moreover, primary OA and OA accompanied by OP show distinct local histological features and apparently follow different pathophysiological trajectories (Chu et al., 2019; Perilli et al., 2007). Comparison of morphometric descriptors of OA bone as volume fraction or trabecular thickness in isolation produces an inconclusive picture that suggests that the underlying pathophysiological mechanism is a collective effect of aberrant remodeling and suboptimal mechanical behavior (Keaveny et al., 2001; Chu et al., 2019; Li and Aspden, 1997a; Li and Aspden, 1997b) rather than a linear change in one or another parameter. Moreover, analysis of local trabecular morphology (also known as single trabecula analysis) indicates that the impaired biomechanical behavior of trabecular bone – a cumulative phenomenon at the tissue scale – is an immediate upstream contributor to joint degeneration (Chen et al., 2018; Guo and Kim, 2002). Although alterations in individual, isolated morphological parameters such as volume fraction, trabecular thickness, anisotropy, or connectivity density undoubtedly affect the mechanical performance of trabecular bone (Keaveny et al., 2001; Ciarelli et al., 2000; Goulet et al., 1994), these isolated changes may ameliorate, aggravate or neutralize each other (see the lack of correlation in Fig. 5H and I). It is the unique combination of multiple structural factors that eventually defines the character of biomechanical incompetency (e.g., too stiff, too compliant, too anisotropic) and ultimately results in the deterioration of skeletal health. Such equifinality makes it difficult to assign the correct weight to each of multiple contributors.

While the lower resistance to simulated loading at the topological level was somewhat expected for the OP samples as they indeed sustained fracture, the lower resistance to simulated loading of the OA samples (that did not have fractures) was unexpected and intriguing to us. One explanation for this phenomenon could possibly be the advanced age of the individuals in both OA and OP groups. However, since it is uncertain that the normal group was of a younger age, another feasible explanation could be the presence of clinically manifest skeletal pathology in both OA and OP groups. Like for the normal bone samples, for the OA group there was no prior history of mechanical failure. However, when the morphological parameters were excluded from comparison, the behavior of the topological blueprints under simulated loading revealed nearly identical results for both the OP (that had a history of fracture) and OA samples (that did not have a prior history of fracture). The disadvantageous mechanical behavior of the topological blueprints can be summarized as having lower stiffness (lower apparent modulus) and uneven distribution of local stresses. The common feature of the OA and OP samples was that they were all indeed surgically removed as dysfunctional tissue, whether fractured or otherwise degenerated. The observation of simulated inferior mechanical behavior in both OA and OP samples at the level of their topological frameworks might therefore provide new insight into the etiology of these most common bone ailments.

4.2. Shear force and biological materials

About a century ago, D'Arcy Thompson stated that most natural materials self-align with principal tension and compression forces to evade shear, where he remarked not only upon remodeling bone trabeculae, but also upon grass bending in the wind, or aligned filaments in a rope (“a hank of tow”) (Thompson, 1942). In these examples he gave, all the elements that are oblique with respect to the acting force will be either re-aligned or eliminated. This indeed is an accurate illustration of one design principle found in Nature – that all materials are stronger in axial loading than they are in shear, and therefore are preferentially used in compression and tension, within stretch-dominated structures. However, in cases where the direction of loading inherently varies, a way to evade shear stresses lies in using stable triangulated shapes, as is observed in plants, corals, diatoms and spider webs (Thompson, 1942), or in engineered structures such as electricity pylons, construction cranes and truss bridges (Hibbeler, 2004). In 3D, triangulated rigid shapes like tetrahedrons and octahedrons redistribute all loads axially, while inherently unstable shapes like parallelepipeds (“non-triangulated”) deform primarily in shear and bending (Fig. 6). As illustrated using triangulated and non-triangulated phantoms, the octetruss-based phantom is more stable, and the parallelepiped-based phantom resists compressive loading less effectively (apparent modulus nearly ×4 lower) and has regions of potentially detrimental shear stress concentration. Although the phantoms presented in this simulation are extreme cases of stable and unstable design, they exemplify trabecular bone topological blueprint behavior. A higher proportion of low coordination nodes indicates that the network is less rigid (less triangulated), which also explains the calculated lower axial:non-axial strain ratio in the pathological OA and OP samples.

When a truss-based structure is subjected to compression, the individual elements, which collectively resist deformation, react to loading in a mixed mode of varying proportions of axial and non-axial strains. Following the notion of stable (triangulated, axially loaded) and unstable (bend- and shear-dominated) structural motifs, a poor topological framework (dominated by non-axial strains) may result in a structural failure at a given load, unless the poor topology is masked by morphological parameters. The ultimate magnitude of the load that leads to a failure depends on the morphometric features, such as the thickness of elements, or the scale of the network. Our simulation results show that both pathological groups have a higher proportion of local non-axial strains, and that explains the lower apparent modulus of the topological models – when the geometry of the elements is taken out of consideration (and before it does, or does not, compensate for the low apparent modulus of the topological framework). Previous simulation studies have shown that the loss of trabecular elements, i.e., a topological alteration, has a more detrimental effect on the mechanical performance than the loss of net mass and thickness of the elements (Guo and Kim, 2002; Deshpande et al., 2001).

Even when the effect of disadvantageous topological blueprint is masked by having larger size of the elements in the structure, the shear- and bend- domination may result in cumulative damage. The presence of higher shear forces in an unstable topological framework (even without causing fracture) might trigger adverse bone cell reactions that result in certain clinical manifestations. Here, notably, none of the OA specimens had a history of mechanical failure, yet in more than half of the pathologic OA specimens we found large cystic lesions (geodes). These samples did not fail or fracture because they have a higher volume fraction and thicker trabeculae, but according to the FEA, the redistribution of stresses in OA samples was as poor as in those of all the OP samples that did fracture. There is a potential association between the shear-dominated loading and the occurrence of cystic lesions in subchondral trabecular bone. In vitro studies using bone cell culture indicated that shear stress triggers the production of prostaglandin E2 (PGE2) in a linear manner (Kreke et al., 2008), and that PGE2 in turn is a principal mediator of inflammation in diseases such as OA and rheumatoid arthritis (Park et al., 2006). Thus, it is possible that the high incidence of the cystic lesions in the OA samples (Resnick et al., 1977) might be related to abnormal distribution of loads and the effects of shear stress. Fig. 2 A illustrates typical cystic lesions that we observed.

4.3. Non-metric features of pathological samples

Bone is built and maintained by cells, which are responsive to mechanical signals (Chen et al., 2010; Klein-Nulend et al., 2005). Thus, the large-scale anatomical and architectural effects of bone tissue adaptation to its mechanical environment are primarily slow and cumulative – years and decades of consistent and recurrent mechanical stimulation are required to leave behind a structural imprint in skeletal architecture, whereas transient loads do not leave detectable traces (Reznikov et al., 2017; Ruff, 1987; Kivell, 2016). Secondarily, the acquisition of functional adaptation is not linear, with strenuous mechanical stimuli occurring early in life induce more detectable bone specialization for a particular type of loading (Warden et al., 2014; Bass et al., 2009), in comparison to loading occurring later in life when skeletal maturation is complete (Ruff et al., 2006). In this context, in the absence of sufficiently strenuous mechanical stimulation, the slowing down of the acquisition of structural change in trabecular bone (Christen et al., 2014) can also be viewed as a subtype of functional adaptation. In the present study, 40% of OP samples demonstrated clearly visible vestiges of the fused growth plate, which in the cases of octogenarian or nonagenarian individuals (Fig. 2B) is indicative of an extremely slow bone turnover and a negligible accrual of adaptive change. Indeed, reasonably stimulated trabecular bone turnover would be expected to eliminate the traces of the so called “metaphyseal scar” during the adult life course. Since Nature is frugal with energy expenditure, and since no biological material is built or retained unless its existence is justified by function, it is tempting to suggest that life-long relative disuse/underuse of the skeleton (manifested as diminished bone remodeling) may result to some extent in osteoporotic bone fragility. An age-controlled study comparing the presence of the growth plate vestiges in the proximal femur of normal and osteoporotic individuals would be an interesting endeavor to test this conjecture. The occurrence of the metaphyseal scar in older individuals as a proxy for slow bone remodeling would then show whether or not insufficient mechanical stimulation leads to gradual simplification of trabecular bone topology, which in turn undermines the stability of the 3D trabecular assembly – regardless of bone mass – in withstanding random impacts.

Besides possibly being of more advanced age, it is somewhat unclear at present why the altered topologies (lower coordination number, less contribution of axial loading) are similar between the OP and OA groups. While the trabecular bone “disuse” scenario in OP seems to be feasible considering the biological and demographic profile of OP patients, multiple questions remain about how and why topological alteration occurs in the OA population. One explanation is that OA is a chronic condition that typically persists for years by the time clinical manifestations justify a total hip arthroplasty. Many years of pain and limited mobility may trigger a secondary disuse effect, such that the observed topological simplification and advanced joint degeneration are not linked by causality, but rather are independent outcomes of another shared cause. Another possible fit of the “disuse” hypothesis is that it pertains not only to the magnitude of loading, but rather to the variation and range of the directions of loading. Modern lifestyle is characterized by stereotypical, habitual loading (Bacon, 1990) which is not necessarily of low magnitude, especially in the cases of overweight individuals, but most likely is of limited range as a result of lower maneuverability in comparison to what Nature's “design” of joints allows for. On the other hand, hip OA is a multifactorial disease that can also be triggered by occupational injury or trauma, and other factors cannot be unequivocally narrowed down to a certain mode of joint use. Therefore, further natural history studies of OA are required, possibly involving long-term observation of individuals at risk, and using non-invasive 3D imaging. Fortunately, contemporary imaging technologies, such as high-resolution MRI or CT, have reached a level of quality that makes possible non-invasive assessment of natural history (West et al., 2018; Manske et al., 2015; Krug et al., 2010; Baum et al., 2013).

4.4. Limitations and future perspectives

The most fundamental limitation of this work was, as is often the case with cadaveric studies, the restricted availability of normal human material and the lack of demographic information about the normal subjects. Despite having a body of evidence that trabecular topology is highly conserved among anatomical sites, individuals, or even species (Reznikov et al., 2016b; Reznikov et al., 2017; Ben Zvi et al., 2017), we cannot completely rule out gradual age-related changes of node coordination in the 3D trabecular framework. Moreover, if such changes do indeed accumulate with time, it is yet obscure as to whether they are compatible with healthy ageing, or perhaps contribute to the development and clinical manifestation of age-associated musculo-skeletal diseases. A controlled natural history study using a robust age series of specimens from a well-characterized modern skeletal collection would be an ideal endeavor to validate or disprove this premise.

The topological analysis of trabecular bone from different anatomic locations – e.g. appendicular versus axial – will be instructive as to whether the generally preserved topological blueprint responds to long-term local stimuli, or whether it reflects the general biomechanical environment and musculoskeletal physiological status of an individual. Such a study would provide insights into the mechanisms of bone functional adaptation, and it may also generate an early diagnostic/prognostic tool for OP and OA. Another venue for trabecular bone topology research will be the comparison of the topological blueprint in embryonic and juvenile bone versus that of mature bone. Moreover, having learned about the role of topological blueprints in the mechanical properties of morphologically comparable structures, it might inspire novel engineering design forms for lightweight and resilient structures that might even outperform bone in terms of topological optimization.

5. Conclusions

In the present study on the role of trabecular bone topology in determining mechanical properties, both OA and OP pathological samples demonstrated an extremely broad scatter and inhomogeneity in the mechanical-testing simulation results, whereas normal sample results where highly similar and clustered close to one another. This implies that topology alone – the robust and conserved blueprint of trabecular bone – does not necessarily by itself foretell particular clinical outcomes such as a fragility fracture or the degeneration of a joint. Other factors, such as bone composition, net mass, or even musculoskeletal coordination may accelerate or preclude biomechanical failure. On the other hand, to function well, the net amount and the 3D distribution of bone, together with the quality of the bone material itself, all must be optimal. A failure in just one of multiple factors may result in bone disease, degeneration or traumatic failure. For the optimal performance of the whole, each and every possible deficiency should be averted. As Leo Tolstoy wrote, “happy families are all alike, every unhappy family is unhappy in its own way”. Apparently, the same notion pertains not only to social dynamics but also to human physiology and to bone structure-function relationships.

Transparency document

Transparency document.

CRediT authorship contribution statement

Natalie Reznikov: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing - original draft, Writing - review & editing. Ammar A. Alsheghri: Formal analysis, Investigation, Methodology, Software, Validation, Writing - original draft, Writing - review & editing. Nicolas Piché: Funding acquisition, Methodology, Project administration, Resources, Software, Supervision, Writing - review & editing. Mathieu Gendron: Formal analysis, Methodology, Validation, Writing - review & editing. Catherine Desrosiers: Formal analysis, Methodology, Validation, Writing - review & editing. Ievgeniia Morozova: Data curation, Visualization, Writing - review & editing. Juan Manuel Sanchez Siles: Data curation, Resources, Writing - review & editing. David Gonzalez-Quevedo: Data curation, Resources, Writing - review & editing. Iskandar Tamimi: Data curation, Resources, Writing - review & editing. Jun Song: Funding acquisition, Methodology, Project administration, Resources, Software, Supervision, Writing - review & editing. Faleh Tamimi: Funding acquisition, Investigation, Project administration, Resources, Supervision, Writing - review & editing.

Declaration of competing interest

Authors have no conflicts of interest to disclose.