Abstract
We present an Algorithm to understand Inter-pixel similarity, which shall be observed in images with the help of a data structure Full Binary Tree. The Full Binary Tree has certain properties like every node must have 2 children or none. Based on this property of Binary Tree, the method of Sliced Binary Pattern is proposed. The inter-pixel similarity may be observed by converting any pixel information of an image within a block of size 3 × 3 to its binarized form, as the pixel information, whose similarity with neighboring pixel cannot be exploited, when it is in decimal form. Thus, we convert all pixel information within a block of size 3 × 3 to its binarized form then we compare the binary pattern of a central pixel with its 8-nearest neighbors. If there is a binary pattern match between central pixel and its 8-nearest neighbors of a block, we assign weights to it, where the weights are determined by the position of match that exist between central pixel and 8-other neighboring pixels of an image. This process helps in determining the inter-pixel similarity of 8-nearest neighbors with respect to central pixel of a block. Every block of 3 × 3 pixels is processed with this strategy to obtain the similarity between patterns in an image. The erected Weighted Full Binary Tree-Sliced Binary Pattern analyzes an image in RGB-Dimensions based on patterns of Inter-Pixel Similarity by tracing the similarity path. The proposed RGB-D texture based inter-pixel similarity addresses the verification of facial similarity. Further, the proposed WFBT-SBP has yielded a good classification accuracy of 77.4%, 77.3%, 77.98%, and 77.94% over a relations of F–S, F-D, M-S, M-D of KinfaceW-I and 76.89%, 76.72%, 77.01%, 76.99% over a relations of F–S, F-D, M-S, and M-D of KinfaceW-II respectively.
Keywords: Computer science, Sliced binary pattern, Representation learning, Feature extraction, Classification
Computer Science; Sliced Binary Pattern; Representation Learning; feature extraction; classification.
1. Introduction
Texture is a method of describing an image for the analysis of challenging problems of computer vision, where the objects of an image are understood by analyzing the texture information of pixels of an image. It has been a problem of interest to address some of the challenging issues of face kinship verification [1, 2, 3] face detection, face spoofing detection etc. Even though, many of the recently proposed research works [4, 5, 6], on texture based method have been proposed and have shown their significant contribution towards determining the facial kinship verification using the texture descriptors, still there is a need of a robust descriptor, which can address the similar kind of texture based methods [7, 8, 9], in computer vision.
In this paper, we present a novel RGB-D weighted texture descriptor based on Full Binary Tree. Proposed RGB-D weighted Full Binary Tree - Sliced Binary Pattern texture based method shall be used in various applications like kinship verification, face detection, face spoofing detection etc. The use of one such application pertaining to the proposed method is shown in Figure 1. Given an input image to the proposed system, the processing of certain tasks like tracing of similarity path to identify the inter-pixel similarity, assigning weights to the traced similarity path are made to extract suitable texture information from an image and produces a RGB-D texture description of an input image.
Figure 1.
Represents the dataset KinfaceW consisting of father-daughter, father-son, mother-daughter and mother-son described by WFBT-SBP has been shown, (a) represents the proposed RGB-D texture WFBT-SBP descriptor on dataset KinfaceW on single face (b) represents one of the described face of KinfaceW.
The local binary pattern [4, 10, 11, 12] considers a window of varying sizes like 3 × 3, 5 × 5 and so on. While describing the features of an image with a window of 3 × 3. SBP does the task of considering the central pixel with respect to 8-nearest neighbors represented by decimal values. If the value of central pixel is greater than individual 8-nearest neighbors, then a value 1 is assigned to the respective positions of 8-nearest neighbors otherwise 0 is assigned, this does not exploits the hidden information of an image completely. Thus, inspired by the findings of LBP [13, 14, 15], we proposed a novel approach to exploit all hidden information at each and every individual 8-nearest neighbor by converting decimal values of nearest neighbors along with central pixel to binary form, in-turn the weights are assigned to the traced similarity path of central pixel with respect to the individual 8-nearest neighbors. This process of converting the decimal notations of every pixel to binary notation and assigning weights to the traced similarity path exploits the completely hidden information of an image and described it well. The proposed method has focused on a window of 3 × 3, which shall be extended to 5 × 5 as well to achieve good accuracy and performance in terms of exploiting information of an image.1
The proposed work makes the following contributions:
-
1)
We exploited the hidden information of an input image by tracing the similarity path of inter-pixels within a window of 3 × 3 and assigning the weights to computed results of central pixels with respect nearest neighbors of a window of 3 × 3. Thus, we made a contribution of finding the similarity between pixel locations of an input image.
-
2)
We have designed an architecture, which overcomes the performance of [6,16,17], in terms of identifying the facial kinship among father-daughter, father-son, mother-daughter and mother-son relationship images of a dataset KinfaceW.
This paper has been organized into different sections like section 2 describes the works related to our proposed method. Section 3, presents a novel texture descriptor. Section 4 presents the implementation details of the proposed RGB-D weighted Full Binary Tree-Sliced Binary Pattern method, Sections 5 gives the insight of the proposed method on dataset KinfaceW in comparison with other contemporary methods. Finally section 6 concludes the proposed method with few contributions.
2. Related work
Inspired by the findings of [1, 5, 9, 18, 19, 20] the property of LBP has been incorporated with a data structure Full Binary Tree to obtain the texture analysis of an image. In fact, the property of SBP does not provide much detailed information of an image, but the details of LBP incorporated with FBT yields sufficient information of an image. The research work of MS Guzel [21] also shown its importance of identifying the features from an image. Since the system needs an efficient features descriptors to recognize an objects of an image, the MS Guzel [21] has given an incite of how well the features extractions are helpful in recognizing an objects of an image.
The research work of Goshtasby A.A [22]. provides details as to how the image registration is to be done by measuring the image descriptions. Further, Image descriptions are needed to determine the correspondence between control points in source and target images (two images). Once control points are detected, the windows centered at them are selected that helps in verifying the correspondence between the two images. If images have rotation and scaling differences, the systems with scaling and rotation invariant features descriptors helps to recognize an image. The proposed method has performed the task of invariant features of images, while recognizing the similarity and dissimilarity of an image.
2.1. Texture
Texture based methods and its importance in facial feature analysis was first introduced in 1990 [19, 23, 24] for addressing the problems of image and computer vision applications. In fact many of the recent facial analysis problems addressed in most recent approaches [25, 26, 27], there are still many challenges to be met in the applications of texture based facial analysis. Since the inception of LBP into the applications of facial analysis, many variants [28, 29, 30, 31] of features have been proposed. However, there are many challenges and comparison of accuracy and performance between texture [28,32, 33] texture based methods represents the information of facial representation and PCA for dimensionality reduction. Many of the recently proposed [18, 34, 35, 36] works focuses and relies on texture based methodologies as well as deep learning based on datasets Related Families in the Wild (RFIW) [7, 14, 31, 37] for analyzing the facial information of an image. There are numerous methods exist [17, 38, 39, 40, 41, 42, 43] for discriminant analysis of texture information of an image, but the proposed WFBT-SBP has shown significant information of an image in terms of texture analysis. Further, the proposed methods can be used in applications like detection of faces and verification of kinships among faces its importance is addressed by various other methods [16, 17, 25, 44] for face recognition with dimensionality reduction. Jiwen Lu at. al [38] have used LBP, LE, SIFT, TPLBP as a measure of image descriptors to assess the kinship verification in their NRML and MNRML methods. Hence, the proposed method has been assessed and experiments have been conducted to measure the efficacy of proposed WFBT-SBP with respect to other existing facial image descriptors.
3. Proposed method
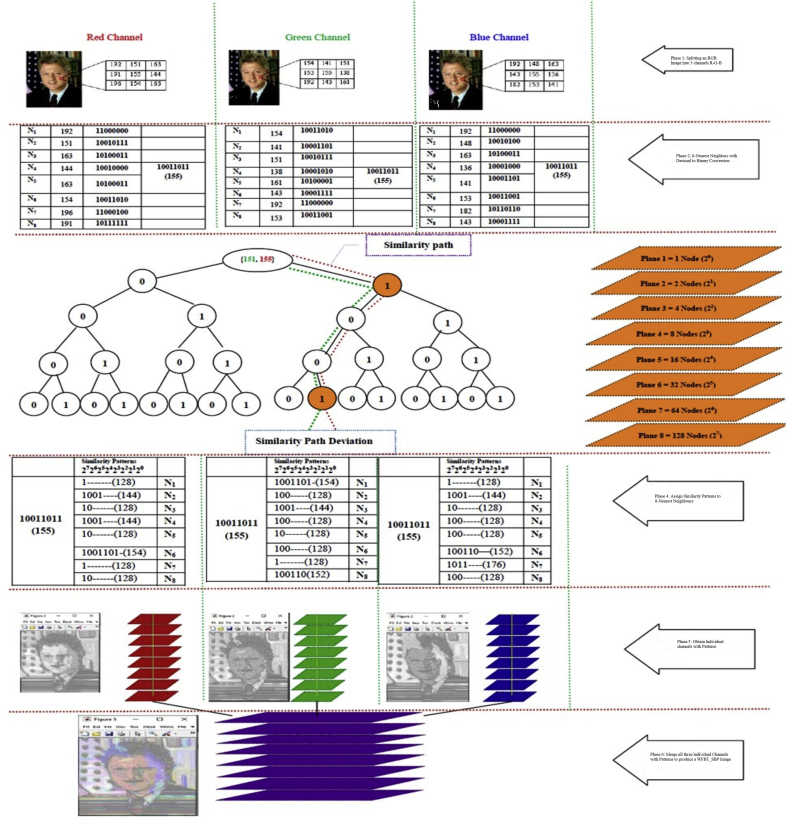
The texture characteristics of neighboring pixels with central pixel in a window while determining LBP patterns has inspired to propose a new variant of LBP called Weighted Full Binary Tree - Sliced Binary Pattern (WFBT-SBP), the method WFBT-SBP Algorithm has been designed to understand the similarity characteristics of neighboring pixels with respect to central pixel in a window of size 3 × 3. The proposed RGB-D FBT-SBP Texture descriptor has been presented in Figure 2. Consisting of different stages like separating an RGB into 3 different channels Red, Green, Blue in phase 1, Decimal to Binary pattern conversion in phase 2, tracing the similarity path in phase 3, determination of weights of the similarity patterns in phase 4, combining the matched patterns of different channels to form a RGB-D texture descriptor in phase 5.
Figure 2.
Overall architecture of a proposed WFBT-SBP is shown above.
3.1. WFBT-SBP
Texture descriptor based method has been proposed by associating weights of Full Binary Tree with Sliced Binary Pattern to analyze the texture information of an image. The technique Weighted Full Binary Tree-Sliced Binary Pattern (WFBT-SBP) has been designed to extract more finely textured details of an image. So that the patterns of an image can be very well understood.
The problem of facial similarity measurement has been addressed by formulating the problem as follows.
-
1)Neighborhood Similarity
-
•The similarities between neighboring pixels are measured by considering the binary representation of 8- neighbours with the central pixels within a window of 3 × 3. The neighborhood similarity can be understood from levels of bit plane represented by the represented by the neighboring pixel values with respect to the central pixel of a window of size 3 × 3. Further, the similarity between two neighboring elements are represented in the form of decimal notation is not suitable for calculating the similarity. Therefore, the pixel information of 8 neighboring elements of a window is converted to binary representation of neighboring elements to get the exact similarity values of 8 neighboring elements with respect to central pixel of a window 3 × 3. Binary representation: The purpose of converting neighboring pixel values to binary form is to analyze and understand the similarity between 2 patterns, which is very convenient, when the neighboring pixel values are represented in the form of binary form than decimal form of neighboring elements. The Binary representation plays quite a good role, while understanding the texture details of an image. As we are mainly focused on extracting the fine texture details of an image, we require an appropriate mechanism to understand the vital features of an image.
-
•Conversion from Binary to Decimal form: The matching 1's along with weights assigned (2n) in similarity patterns are added together to get the similarity value (decimal value) between two patterns. The center of a pixel window with its 8-nearest neighboring patterns are compared and matched from MSB to LSB. This process is most essentially needed to understand the similarity between central and neighboring pixels in a window.
-
•Assign Weights to similarity pattern: The weights are assigned to the binary similarity pattern consisting of 0's and 1's. If MSB to LSB of binary form is same between two patterns, then we consider the bit position, where 1's are matching in similarity pattern. The 1's are identified by scanning the entire bit pattern from left to right (MSB to LSB) and compared with neighboring pattern. So as to make convenient to understand the features and assign appropriate weights to the pattern
-
•Average of similarity patterns of 8 neighbors: The similarity patterns obtained along similarity path are considered for calculating similarity patterns of 8-nearest neighbors. Further, the averages of similarity values of 8 neighborhood elements are considered to determine the similarity value of a central pixel of a window of size 3 × 3.
-
•
An Image I, whose texture features can be assessed by using (1).
| (1) |
Eq. (1) has a term R, G, B representing the different components of an image. R indicates the red component, G indicates the Green component, and B indicates the Blue component. Further, Eq. (1) has been split into eq. (2), eq. (3), and Eq. (4).
| (2) |
| (3) |
| (4) |
where Ri indicates the Red component of an image I, Gi refers to the Green component of an image I and Bi represents a Blue component of an Image I. Further, Xj,k indicates the inter-pixel values of a Red component, Yj,k refers to the inter-pixel values of a green component and Zj,k represents inter-pixel values of blue component of an image.
| (5) |
| (6) |
| (7) |
The above (5), (6) and (7) does the task of converting any pixel value of decimal form to binary form; as such it is more helpful in analyzing the inter-pixel similarity. Further, the converted binary patterns of image pixels are exposed to the data structure Full Binary Tree. The (5), (6), (7) is repeated for other two components of an image like Green and Blue to obtain Yj,k and Zj,k. Xj,k, Yj,k and Zj,k represents the 3-color (RGB) components of an image. After converting the pixel values lying within a window of size 3 × 3 from decimal values to their corresponding binary values.
-
2)
Construction of RGB-D texture Full Binary Tree - Sliced Binary Pattern
We consider a data structure Full Binary Tree, where every node represents the pixel locations of a window. The central pixel (x,y) of a window 3 × 3 represents the root of a Full Binary Tree and the other 8 nearest neighbors, whose pixel locations addressed with (-x,-y) represents left sub tree of level 1 and (x,-y) represents the right child of a root node.
The Full Binary Tree is a data structure adopted to understand the shared similarity patterns of two neighboring pixels within a window of size 3 × 3. Figure 3 indicates the comparison of pixels using Full Binary Tree with weights. Further, the proposed method has achieved a good benchmark results with the help of Weighted Full Binary Tree (WFBT) and the Sliced Binary Pattern (SBP) of an image. Both WFBT and the concept of a window adopted in SBP have been incorporated to understand the similarity patterns between two facial images and hence, the proposed method has been named as WFBT-SBP.
Figure 3.
Comparison of pixels along with Weighted Full Binary Tree-Sliced Binary Pattern. (a) presents the first neighbor with relation of (-1,-1) of central pixel, (b) indicates the second neighbor with (0,-1) relation.(c) provides a relationship of (1,-1), (d) designates a relationship of (1,0), (e) gives a relationship of (1,1), (f) provides a relationship of (0,1), (g) indicates the relationship of (-1,1) and finally (h) presents the relationship of (-1,0) with reference to central pixels withn a window of size 3 × 3.
The Similarity path can be traced by considering the left sub tree as 0 and right sub tree as 1. This process is repeated until the similarity binary pattern matches between central pixel value and the nearest 8 neighboring pixel values of an image. The binary pattern matching has been achieved between central pixel and 8-nearest neighboring elements of a window can be visualized from (8) as shown below.
| (8) |
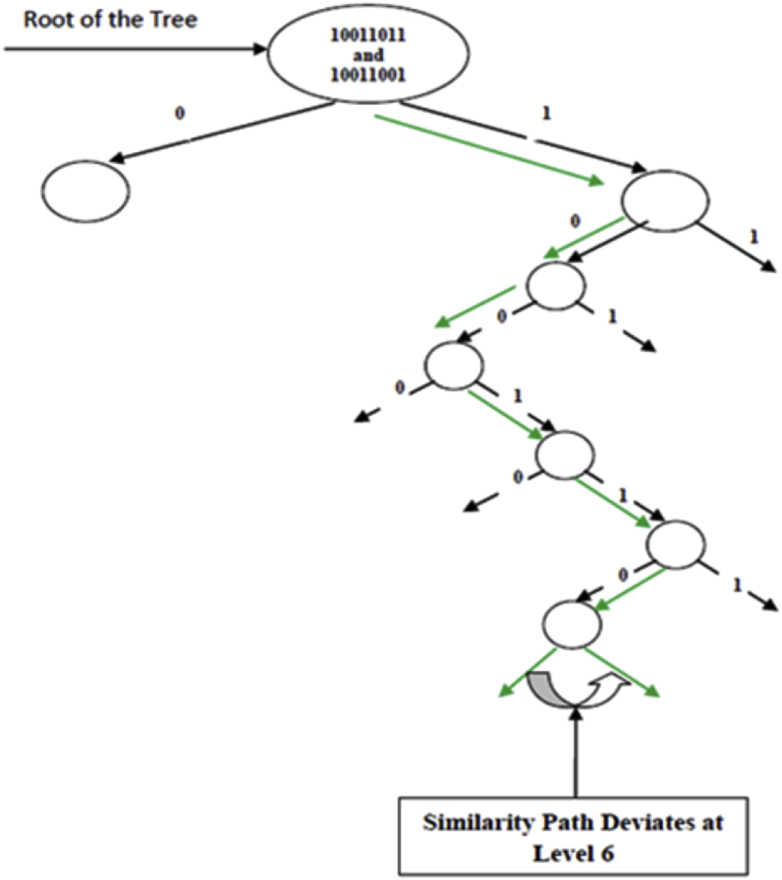
where, represents the binary pattern of block q with pixel locations within a window of size 3 × 3. The indices (i,j) represents the 8-nearest neighbors and central pixel of a block q. Consists of 8 bit values, where each bit position indicates a level of a Full Binary Tree. First bit of pattern represents level 1 of a Full Binary Tree and subsequent bit values indicates subsequent levels of a Full Binary Tree. The Pattern 1 is 01010111 is indicated in Figure 2, and Pattern 2 is 01111101 also indicated in Figure 2. It is clear from Figure 2 that the similarity pattern matches between central pixel and third 8-nearest neighboring pattern matches till level 2 of full binary tree then the pattern mismatch occurs after level 2 of a full binary tree. The below Figure 4 represents the general structure of a Full Binary Tree corresponding to the central pixel and one of the 8-nearest neighbors of SBP.
Figure 4.
Similarity path traversed to assign the weights to determine the WFBT-SBP of every pixels of an image.
When a pattern match occurs, Figure 5. Indicates how the weights are assigned at an appropriate level when pattern match occurs and assignment of weights are stopped when a pattern match breaks at level 2. If a pattern match occurs at level 1 a weight of 21 is assigned similarly if a pattern match occurs till level 6, we keep assigning the weights to the matched pattern at the respective level till level 6 that is 26. Finally all weights whose pattern matches are summed up to obtain a calculated WFBT-SBP value of first among 8-neighboring pixel locations of an image. This process is repeated for all 8-nearest neighboring elements of a window, which results in a respective matched decimal pattern. This process of shared inter-pixel similarity estimates the similarity pattern of one pixel values with respect to its neighboring pixel values of an image. This also describes the texture patterns of any image. Comparison of results of accuracy with reference to images of a dataset are shown in Figure 8. Further, Figure 8 indicates the results of accuracy of Father-Son (F-S) relations on KinfaceW-I dataset. (see Figures. 6, 7, 8).
| (9) |
| (10) |
| (11) |
| (12) |
Figure 5.
Construction of weighted Full Binary Tree to learn the pixel similarity.
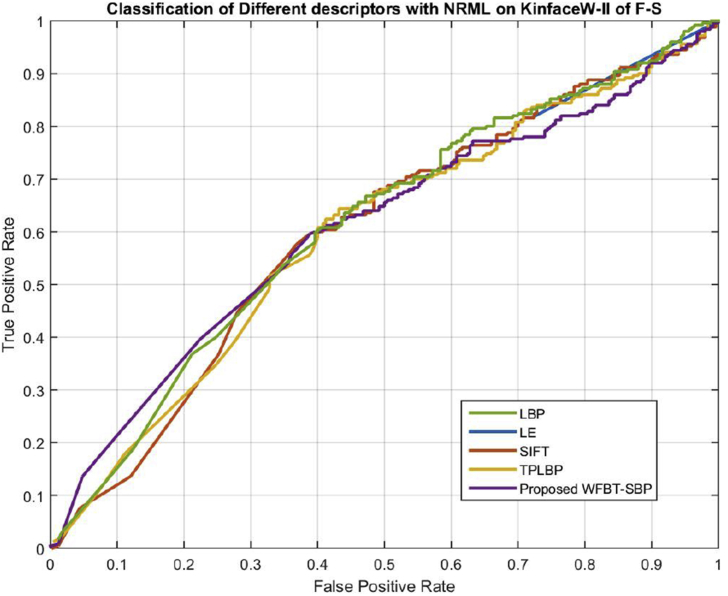
Figure 8.
Proposed WFBT-SBP and other methods on a dataset KinfaceW-I using NRML + WFBT-SBP in relations with F–S.
Figure 6.
Results of accuracies of proposed WFBT-SBP on a dataset KinfaceW-I with respect to the relations F–S, F-D, M-S, and M-D using NRML and MNRML.
Figure 7.
Results of accuracies of proposed WFBT-SBP on a dataset KinfaceW-I with respect to the relations F–S, F-D, M-S, and M-D of KinfaceW-II.
4. Training WFBT-SBP
The proposed weighted full binary tree-sliced binary pattern has been implemented with certain principles like Conversion to binary from decimal forms of nearest neighbors, Assign weights to traced similarity path, average of similarity patterns obtained from the traced similarity path. Figure 24 corresponds to results of KinfaceW-I and KinfaceW-II represented by a proposed WFBT-SBP descriptor.
Figure 24.
Output of the Proposed WFBT-SBP on datasets Kinface-W consisting of Father-Daughter in row 1 and row 2 respectively, Father-Son in row 3 and row 4 respectively, Mother-Son in row 5 and row 6 respectively and Mother-Daughter relationship of images in row 7 and row 8 respectively.
4.1. Proposed WFBT-SBP RGB-D texture descriptor algorithm
Algorithm 1
Proposed WFBT-SBP RGB-D Texture Descriptor
Algorithm 1: Proposed WFBT-SBP RGB-D Texture Descriptor
Input: The set of images of dataset Description: The images are processed with WFBT-SBP Algorithm to obtain the texture descriptors of images of dataset. Step 1: Split RGB image into different components like Red, Green and Blue. Solve 1.1: Solve (1) Step 2: Initialization Step 3: Conversion from decimal values to binarized values of R, G, B Step 3.1: Solve (5) to obtain X Step 3.2: Solve (6) to obtain B. Step 3.3: Solve (7) to get Xj,k. Step 3.4: Repeat 2.1 to 2.3 to convert decimal to binary Step 4: [If there is a pattern match, assign weights and summate the matched patterns] Step 4.1: Solve (8) to compare patterns of central pixel with 8-nearest neighbors. for q = 1: n
End
EndStep 5: Obtain WFBT-SBP in the form of Xj,k Step 6: Repeat Step 3 to 5 for Green component to obtain. Step 7: Repeat Step 3 to 5 for Blue component to obtain Zj,k. Step 8: Combine the result of Step 5, Step 6 and Step 7. Output: Weighted FBT-SBP of an image. Algorithm: The proposed WFBT-SBP has been incorporated to achieve solution to the problem of texture analysis.
5. Proposed texture descriptor.WFBT-SBP on dataset KinfaceW
The WFBT-SBP can be used in various applications like sex determination of a child based on comparing the facial features of a child with respect to that of their parents or gender recognition. Another application, where the proposed method has been applied and the result of improvement would have obtained on the dataset KinfaceW-I and KinfaceW-II by using our proposed method Full Binary Tree-Sliced Binary Pattern (WFBT-SBP). The applications on which the proposed method has been assessed has been listed below.
-
1)
Proposed WFBT-SBP over a benchmark dataset KinfaceW-I and KinfaceW-II
The proposed Weighted Full Binary Tree-Sliced Binary Pattern descriptor has been assessed over other datasets like KinfaceW-I and KinfaceW-II. The descriptor WFBT-SBP has shown significant improvement over other descriptors on the same dataset KinfaceW consisting of KinfaceW-I and KinfaceW-II.
The below Figure 9 shows the accuracy of the proposed method over a dataset KinfaceW-I consisting of images of Father, Daughter, Mother, Son relations. The proposed method has outperformed the state of the art method of Lu.et.al of 2014.
Figure 9.
Proposed WFBT-SBP and other methods on a dataset KinfaceW-I using NRML + WFBT-SBP with respect to the relations F-D.
The proposed WFBT-SBP has shown a significant improvement over a benchmark dataset KinfaceW consisting of KinfaceW-I and KinfaceW-II. Verification accuracy of proposed WFBT-SBP has yielded an accuracy of 77.4, 77.33, 77.98 and 77.94 over a relation of F–S, F-D, M-S, and M-D of KinfaceW-I dataset. The results of accuracy shall be seen in Figure 9.
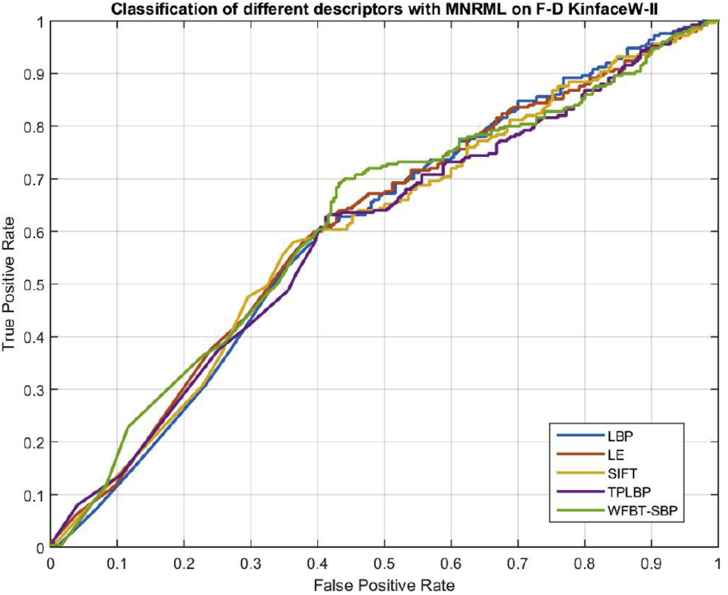
The proposed WFBT-SBP has shown a significant improvement over a benchmark dataset KinfaceW consisting of KinfaceW-I and KinfaceW-II. Verification accuracy of proposed WFBT-SBP has yielded an accuracy of 76.89, 76.72, 77.01 and 76.99 over a relation of F–S, F-D, M-S, and M-D of KinfaceW-II dataset. The results of accuracy shall be seen in Figure 10. Figure 11, Figure 12, Figure 13, Figure 14 corresponds to results of KinfaceW-I, Figure 15, Figure 16, Figure 17, Figure 18 corresponds to results of KinfaceW-II with comparison of different descriptors. Figure 19, Figure 20, Figure 21, Figure 22 corresponds to results of KinfaceW-I, Figure 23 corresponds to results of KinfaceW-II with comparison of different descriptors.
Figure 10.
Proposed WFBT-SBP and other methods on a dataset KinfaceW-I using NRML + WFBT-SBP with respect to the relations M-S.
Figure 11.
Proposed WFBT-SBP and other methods on a dataset KinfaceW-I using NRML + WFBT-SBP with respect to the relations M-D.
Figure 12.
Proposed WFBT-SBP and other methods on a dataset KinfaceW-II using NRML + WFBT-SBP with respect to the relations F–S.
Figure 13.
Proposed WFBT-SBP and other methods on a dataset KinfaceW-II using NRML + WFBT-SBP with respect to the relations F-D.
Figure 14.
Proposed WFBT-SBP and other methods on a dataset KinfaceW-II using NRML + WFBT-SBP with respect to the relations M-D.
Figure 15.
Proposed WFBT-SBP and other methods on a dataset KinfaceW-II using NRML + WFBT-SBP with respect to the relations M-S.
Figure 16.
Results of accuracies of proposed WFBT-SBP and other contemporary methods on a dataset KinfaceW-I with respect to the relations F–S of MNRML.
Figure 17.
Proposed WFBT-SBP and other contemporary methods on a dataset KinfaceW-I with respect to the relations F-D of MNRML.
Figure 18.
Results of accuracies of proposed WFBT-SBP and other contemporary methods on a dataset KinfaceW-I with respect to the relations M-S of MNRML.
Figure 19.
Results of accuracies of proposed WFBT-SBP and other contemporary methods on a dataset KinfaceW-I with respect to the relations M-D of MNRML.
Figure 20.
Proposed WFBT-SBP and other contemporary methods on a dataset KinfaceW-II with respect to the relations F–S of MNRML.
Figure 21.
Proposed WFBT-SBP and other contemporary methods on a dataset KinfaceW-II with respect to the relations F-D of MNRML.
Figure 22.
Proposed WFBT-SBP and other contemporary methods on a dataset KinfaceW-II with respect to the relations M-S of MNRML.
Figure 23.
Proposed WFBT-SBP and other contemporary methods on a dataset KinfaceW-II with respect to the relations M-D of MNRML.
Table 1 presents the classification accuracies of different descriptors with respect to the proposed WFBT-SBP on dataset KinfaceW-I. Similarly, Table 2 presents the classification accuracies of different descriptors with respect to the proposed WFBT-SBP on a dataset KinfaceW-II that the accuracies produced by the proposed method is better than other facial feature descriptors for all possible combination of relationships of F–S, F-D, M-S and M-D. The accuracies mentioned in Lu.et.al of 2014, that the NRML + LE (63.0%) have given boost to the performance of NRML. But the NRML + proposed WFBT-SBP has produced even better accuracies (77.6%) than using existing feature (see Tables 3, 4, 5)
Table 1.
Classification accuracy of feature representation on subsets of KinfaceW-I.
| Feature | F–S | F-D | M-S | M-D | Mean |
|---|---|---|---|---|---|
| LBP | 63.7 | 61.2 | 55.4 | 62.4 | 60.7 |
| LE | 61.1 | 58.1 | 60.9 | 70.0 | 62.5 |
| SIFT | 66.5 | 60.0 | 60.0 | 56.4 | 59.8 |
| TPLBP | 57.3 | 61.5 | 63.2 | 57.0 | 59.7 |
| WFBT-SBP | 77.40 | 77.33 | 77.98 | 77.94 | 77.66 |
Table 2.
Classification accuracy of feature representation on subsets of KinfaceW-II.
| Feature | F–S | F-D | M-S | M-D | Mean |
|---|---|---|---|---|---|
| LBP | 63.7 | 61.2 | 55.4 | 62.4 | 60.7 |
| LE | 61.1 | 58.1 | 60.9 | 70.0 | 62.5 |
| SIFT | 66.5 | 60.0 | 60.0 | 56.4 | 59.8 |
| TPLBP | 57.3 | 61.5 | 63.2 | 57.0 | 59.7 |
| WFBT-SBP | 76.89 | 76.72 | 77.01 | 76.99 | 76.90 |
Table 3.
Classification Accuracy of various texture based descriptors over a dataset KinfaceW-I.
| Method | Feature | F–S | F-D | M-S | M-D | Mean |
|---|---|---|---|---|---|---|
| CSML | LBP | 63.7 | 61.2 | 55.4 | 62.4 | 60.7 |
| LE | 61.1 | 58.1 | 60.9 | 70.0 | 62.5 | |
| SIFT | 66.5 | 60.0 | 60.0 | 56.4 | 59.8 | |
| TPLBP | 57.3 | 61.5 | 63.2 | 57.0 | 59.7 | |
| NCA | LBP | 61.7 | 62.2 | 56.4 | 62.4 | 60.7 |
| LE | 62.1 | 57.1 | 61.9 | 69.0 | 62.3 | |
| SIFT | 67.5 | 61.0 | 61.0 | 57.4 | 60.8 | |
| TPLBP | 56.3 | 60.5 | 62.2 | 56.0 | 58.7 | |
| LMNN | LBP | 62.7 | 63.2 | 57.4 | 63.4 | 61.7 |
| LE | 63.1 | 58.1 | 62.9 | 70.0 | 63.3 | |
| SIFT | 69.5 | 63.0 | 63.0 | 59.4 | 62.8 | |
| TPLBP | 57.3 | 61.5 | 63.2 | 57.0 | 59.7 | |
| NRML | LBP | 62.7 | 60.2 | 54.4 | 61.4 | 59.7 |
| LE | 66.1 | 59.1 | 58.9 | 68.0 | 63.0 | |
| SIFT | 65.5 | 59.0 | 55.5 | 55.4 | 58.8 | |
| TPLBP | 56.3 | 60.5 | 56.0 | 62.2 | 58.7 | |
| NRML + Proposed WFBT-SBP | WFBT-SBP | 77.40 | 77.33 | 77.98 | 77.94 | 77.66 |
Table 4.
Classification Accuracy of various texture based descriptors over a dataset KinfaceW-II.
| Method | Feature | F–S | F-D | M-S | M-D | Mean |
|---|---|---|---|---|---|---|
| CSML | LBP | 63.7 | 61.2 | 55.4 | 62.4 | 60.7 |
| LE | 61.1 | 58.1 | 60.9 | 70.0 | 62.5 | |
| SIFT | 66.5 | 60.0 | 60.0 | 56.4 | 59.8 | |
| TPLBP | 57.3 | 61.5 | 63.2 | 57.0 | 59.7 | |
| NCA | LBP | 61.7 | 62.2 | 56.4 | 62.4 | 60.7 |
| LE | 62.1 | 57.1 | 61.9 | 69.0 | 62.3 | |
| SIFT | 67.5 | 61.0 | 61.0 | 57.4 | 60.8 | |
| TPLBP | 56.3 | 60.5 | 62.2 | 56.0 | 58.7 | |
| LMNN | LBP | 62.7 | 63.2 | 57.4 | 63.4 | 61.7 |
| LE | 63.1 | 58.1 | 62.9 | 70.0 | 63.3 | |
| SIFT | 69.5 | 63.0 | 63.0 | 59.4 | 62.8 | |
| TPLBP | 57.3 | 61.5 | 63.2 | 57.0 | 59.7 | |
| NRML | LBP | 62.7 | 60.2 | 54.4 | 61.4 | 59.7 |
| LE | 66.1 | 59.1 | 58.9 | 68.0 | 63.0 | |
| SIFT | 65.5 | 59.0 | 55.5 | 55.4 | 58.8 | |
| TPLBP | 56.3 | 60.5 | 56.0 | 62.2 | 58.7 | |
| NRML + Proposed WFBT-SBP | WFBT-SBP | 77.40 | 77.33 | 77.98 | 77.94 | 77.66 |
Table 5.
Representation of Different methods and authors of various descriptors on different benchmark datasets.
| Method | Dataset | Authors | Feature | F–S | F-D | M-S | M-D | GF-GD | GF-GS | GM-GS | GM-GD | B–B | B–S | Sibs-Sibs | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CSML | Cornell Kinface | Mattie Peitikainen | LBP | 66.0 | 65.5 | 64.8 | 65.0 | - | - | - | - | - | - | - | 65.3 |
| Robert K Mc Connell | LE | 71.8 | 68.1 | 73.8 | 74.0 | - | - | - | - | - | - | - | 71.9 | ||
| David Lowe | SIFT | 62.0 | 58.9 | 56.8 | 57.4 | - | - | - | - | - | - | - | 58.8 | ||
| Mattie Peitikainen | TPLBP | 66.4 | 62.6 | 62.8 | 64.9 | - | - | - | - | - | - | - | 64.2 | ||
| NCA | UB Kinface | Mattie Paitikainen | LBP | 67.0 | 66.5 | 65.8 | 66.0 | - | - | - | - | - | - | - | 66.3 |
| Robert K. McConnell | LE | 73.8 | 70.1 | 74.8 | 75.0 | - | - | - | - | - | - | - | 73.5 | ||
| David Lowe | SIFT | 63.0 | 59.9 | 58.8 | 59.4 | - | - | - | - | - | - | - | 60.4 | ||
| Mattie Paitikainen | TPLBP | 67.4 | 63.6 | 63.8 | 66.9 | - | - | - | - | - | - | - | 66.5 | ||
| LMNN | UB Kinface | Mattie Paitikainen | LBP | 68.0 | 68.5 | 68.8 | 67.4 | - | - | - | - | - | - | - | 68.2 |
| Robert K. McConnell | LE | 74.8 | 71.1 | 75.8 | 76.0 | - | - | - | - | - | - | - | 74.5 | ||
| David Lowe | SIFT | 65.0 | 57.9 | 58.8 | 59.4 | - | - | - | - | - | - | - | 60.4 | ||
| Mattie Paitikainen | TPLBP | 68.4 | 65.6 | 65.8 | 67.9 | - | - | - | - | - | - | - | 68.1 | ||
| NRML, MNRML | KinfaceW-I | Mattie Paitikainen | LBP | 64.8 | 69.5 | 69.8 | 69.0 | - | - | - | - | - | - | - | 69.5 |
| Robert K. McConnell | LE | 69.8 | 73.1 | 76.8 | 77.0 | - | - | - | - | - | - | - | 75.7 | ||
| David Lowe | SIFT | 60.0 | 60.9 | 60.8 | 61.4 | - | - | - | - | - | - | - | 62.8 | ||
| KinfaceW-II | Mattie Paitikainen | TPLBP | 64.4 | 67.6 | 67.8 | 69.9 | - | - | - | - | - | - | - | 70.1 | |
| Proposed WFBT-SBP Descriptor | KinfaceW-I | Our Descriptor | WFBT-SBP | 77.4 | 77.3 | 77.9 | 77.9 | 81.3 | 81.3 | 82.4 | 82.6 | 83.2 | 81.6 | 83.2 | 80.55 |
| KinfaceW-II | Our Descriptor | WFBT-SBP | 76.8 | 76.72 | 77.0 | 76.9 | 81.4 | 84.1 | 83.2 | 83.1 | 83.9 | 88.4 | 89.6 | 81.91 | |
| TSKinface | Our Descriptor | WFBT-SBP | 78.3 | 77.9 | 78.3 | 76.8 | 80.9 | 86.2 | 83.2 | 84.2 | 83.5 | 84.3 | 83.1 | 81.51 | |
| Cornell Kinface | Our Descriptor | WFBT-SBP | 78.7 | 77.3 | 78.4 | 78.3 | 83.1 | 83.4 | 82.3 | 84.1 | 81.6 | 83.2 | 88.2 | 81.69 | |
| RFIW | Our Descriptor | WFBT-SBP | 86.4 | 82.1 | 84.3 | 82.6 | 84.6 | 83.5 | 84.2 | 84.6 | 83.4 | 83.2 | 84.6 | 83.95 |
The MATLAB Code of the proposed WFBT-SBP shall be verified to check the efficiency and improved results of RGB-D texture based method which does the task of identifying the kinship among relatives based on the texture descriptions. The experiments have been evaluated on Pentium Core I5 Fifth generation laptop without NVIDIA Graphics. The time taken to assess is comparatively more than the time consumed to run on Pentium Core I5 fifth generation computer with NVIDIA graphics card. The research experiments have been finally evaluated on a normal computer with NVIDIA graphics which is 98 % faster than the usual speed of execution. Further, the proposed WFBT-SBP has been validated with a dataset KinfaceW consisting of KinfaceW-I and KinfaceW-II, In addition to various other datasets like TSKinface, Cornell Kinface, and UBKinface. where each of these folders contain images of the father-daughter, father-son, mother-daughter and mother-son relationship of images, which has been evaluated with the proposed method WFBT-SBP and compared with other existing methods. The proposed method has been developed in MATLAB 2015.
6. Conclusion
The WFBT-SBP has shown its significant contributions towards exploiting the hidden information of describing an image and implements the approach to various applications like kinship verification over a benchmark dataset KinfaceW. It has shown its significance in improved results over other approaches by yielding very good results in comparison with contemporary approaches. The proposed method has been incorporated with a window of 3 × 3, which shall be extended to 5 × 5 and so on. The usage of WFBT-SBP will improve the results of the mentioned methods with the help of texture based WFBT-SBP descriptor. It has yielded a good classification accuracy of 77.4%, 77.3%, 77.98%, and 77.94% over a relations of F–S, F-D, M-S, M-D of KinfaceW-I and 76.89%, 76.72%, 77.01%, 76.99% over a relations of F–S, F-D, M-S, and M-D of KinfaceW-II respectively.
Declarations
Author contribution statement
Ravi Kumar Y. B: Conceived and designed the experiments; Performed the experiments; Wrote the paper.
C. K. Narayanappa: Contributed reagents, materials, analysis tools or data.
Dayananda P: Analyzed and interpreted the data.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Acknowledgements
The authors would like to thank Dhanya Nayak R, Basavaraju, Malathi K, Jyothi B, and Renuka Prasanna for their technical guidance and continuous support given in finding good results in the form of a research.
Footnotes
The authors are ready to share the code written in MATLAB 2015 for improvisation of results. Kindly send your email on ravikumarybdhanya@gmail.com mentioning your "Interested to improvise the results of WFBT-SBP Code" in your subject line.
Appendix A. Supplementary data
The following is the supplementary data related to this article:
The Blue channel of WFBT_SBP_Descriptor performs the functionality of calculating the weights of inter-pixel similarity, which is most essential for obtaining the image descriptions at Blue Channel.
The Green channel of WFBT_SBP_Descriptor performs the functionality of determining the weights of inter-pixel similarity , which is most essential for finding an image descriptions at Green Channel.
The Red channel of WFBT_SBP_Descriptor performs the functionality of determining the weights of inter-pixel similarity , which is most essential for analyzing the image at Red Channel.
The proposed method has been developed in MATLAB 2015. The Matlab code consists of a WFBT_SBP_Descriptor_RGB as a function of processing images associated with different channels of information in the form of Red Green and Blue, where information of Red is represented by Descriptor_Red as sub_function 1, information of Green is indicated by Descriptor_Green as sub_function 2, and information represented of Blue channel is represented by Descriptor_Blue as sub_function 3. Finally all three sub_functions i.e., sub_function 1, sub_function 2, sub_function 3 are merged together to obtain the Descriptions of RGB as a result of WFBT_SBP_Descriptor_RGB, which is useful for further processing of images for image analysis. examples of image analysis include, face recognition, face spoofing detection and various other related fields find the usefulness of evolved method WFBT_SBP_Descriptor_RGB and its subfunctions while describing an image.
References
- 1.Chen J., Shan S., He C., Zhao G., Pietikainen M., Chen X., Gao W. Wld: a robust local image descriptor. Trans. Pattern Anal. Mach. Intell. 2010;32(9):1705–1720. doi: 10.1109/TPAMI.2009.155. [DOI] [PubMed] [Google Scholar]
- 2.Tang X. Wang X. Random sampling for subspace face recognition. Int'l J. Computer Vision. 2006;70(1):91–104. [Google Scholar]
- 3.Bai H. Nguyen L. Cosine similarity metric learning for face verification. Proc. Asian Conf. Computer Vision. 2011:709–720. [Google Scholar]
- 4.Takala Valtteri, Ahonen Timo, Pietikainen Matti. Springer Verlag Berlin Heidelberg; 2005. Block-Based Methods for Image Retrieval Using Local Binary Patterns; pp. 882–891. 2005, SCIA 2005, LNCS 3540. [Google Scholar]
- 5.Hadid A., Zhao G., Ahonen T., Pietikainen M. World Scientific Review; 2008. Face Analysis Using Local Binary Patterns. [Google Scholar]
- 6.Li Liu(B), Paul Fieguth, Wang Xiaogang, Pietikaainen Matti, Hu Dewen. Springer international publishingAG-2016; 2016. Evaluation of LBP and Deep Texture Descriptors with a New Robustness Benchmark; pp. 69–86. ECCV 2016, Part III, LNCS 9907. [Google Scholar]
- 7.Ramanathan N., Chellappa R. Face verification across age progression. IEEE Trans. Image Process. 2006;15(11):3349–3361. doi: 10.1109/tip.2006.881993. [DOI] [PubMed] [Google Scholar]
- 8.Lu J., Tan Y.-P., Wang G. Discriminative multimanifold analysis for face recognition from a single training sample per person. IEEE Trans. Pattern Anal. Mach. Intell. 2013;1:39–51. doi: 10.1109/TPAMI.2012.70. [DOI] [PubMed] [Google Scholar]
- 9.Ling H., Soatto S., Ramanathan N., Jacobs D. Face verification across age progression using discriminative methods. IEEE Trans. Inf. Forensics Secur. 2010;5(1):82–91. [Google Scholar]
- 10.Yan S., Xu D., Yang Q., Zhang L., Tang X., Zhang H. Multilinear discriminant analysis for face recognition. IEEE Trans. Image Process. 2007;16(1):212–220. doi: 10.1109/tip.2006.884929. [DOI] [PubMed] [Google Scholar]
- 11.Xia T., Tao D., Mei T., Zhang Y. Multiview spectral embedding. IEEE Trans. Syst. Man Cybern. B Cybern. 2010;40(6):1438–1446. doi: 10.1109/TSMCB.2009.2039566. [DOI] [PubMed] [Google Scholar]
- 12.Xia S., Shao M., Luo J., Fu Y. Understanding kin relationships in a photo. IEEE Trans. Multimed. 2012;14(4):1046–1056. [Google Scholar]
- 13.Xie B., Mu Y., Tao D., Huang K. M-SNE: multiview stochastic neighbor embedding. IEEE Trans. Syst. Man Cybern. B Cybern. 2011;41(4):1088–1096. doi: 10.1109/TSMCB.2011.2106208. [DOI] [PubMed] [Google Scholar]
- 14.Lu J., Tan Y.-P., Wang G. Discriminative multi-manifold analysis for face recognition from a single training sample per person. Proc. IEEE Int'l Conf. Computer Vision. 2011:1943–1950. doi: 10.1109/TPAMI.2012.70. [DOI] [PubMed] [Google Scholar]
- 15.Lu J., Tan Y.-P. Uncorrelated discriminant nearest feature line analysis for face recognition. IEEE Signal Process. Lett. 2010;17(2):185–188. [Google Scholar]
- 16.Yang M.H. Kernel eigenfaces vs. Kernel fisherfaces: face recognition using kernel methods. Proc. IEEE Int'l Conf. Face and Gesture Recognition. 2002:215–220. [Google Scholar]
- 17.Yan S., Xu D., Zhang B., Zhang H., Yang Q., Lin S. Graph embedding and extensions: a general framework for dimensionality reduction. IEEE Trans. Pattern Anal. Mach. Intell. 2007;29(1):40–51. doi: 10.1109/TPAMI.2007.12. [DOI] [PubMed] [Google Scholar]
- 18.Antipov Grigory, Sid-Ahmed Berrani. Jean-Luc Dugelay . 2015. Minimalistic CNN-Based Ensemble Model for Gender Prediction from Face images,Elsevier, Pattern Recognition Letters; pp. 1–6. [Google Scholar]
- 19.Choi S.E., Lee Y.J., Lee S.J., Park K.R., Kim J. Age estimation using a hierarchical classifier based on global and local facial features. Pattern Recogn. 2011;44(6):1262–1281. [Google Scholar]
- 20.Zhao W., Chellappa R., Phillips P.J., Rosenfeld A. Face Recognition: A Literature Survey. ACM Computing Surv. 2003;4:399–458. [Google Scholar]
- 21.Güzel Mehmet Serdar. Performance evaluation for feature extractors on street view images. Imag. Sci. J. 2016;64(1):26–33. [Google Scholar]
- 22.Goshtasby A.A. Image Registration. Advances in Computer Vision and Pattern Recognition. Springer; London: 2012. Image descriptors. [Google Scholar]
- 23.Qin Xiaoqian, Tan Xiaoyang, Chen Songcan. Tri-Subject Kinship verification Understanding the core of a family”. IEEE Trans. Multimed. 2016:1–13. [Google Scholar]
- 24.Zhou X., Hu J., Lu Y., Shang J., Guan Y. Kinship verification from facial images under uncontrolled conditions. Proc. ACM Int'l Conf. Multimedia. 2011:953–956. [Google Scholar]
- 25.Yu W., Teng X., Liu C. Face Recognition Using Discriminant Locality Preserving Projections. Image and Vision Computing. 2006;3:239–248. [Google Scholar]
- 26.Janne Heikkila. Ojansivu Ville. 2009. Methods for Local Phase Quantization in Blur-Insensitive Image Analysis; pp. 104–111. [Google Scholar]
- 27.Ahonen Timo, Hadid Abdenour, Pietikäinen Matti. Face description with local binary patterns: application to face recognition”IEEE transactions on pattern analysis and machine intelligence. 2006;28(12) doi: 10.1109/TPAMI.2006.244. [DOI] [PubMed] [Google Scholar]
- 28.Ahonen T., Hadid A., Pietikainen M. Face description with local binary patterns: application to face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2006;28(12):2037–2041. doi: 10.1109/TPAMI.2006.244. [DOI] [PubMed] [Google Scholar]
- 29.Ahonen T. Face description with local binary patterns: application to face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2006;28(12):2037–2041. doi: 10.1109/TPAMI.2006.244. [DOI] [PubMed] [Google Scholar]
- 30.Belhumeur P.N., Hespanha J., Kriegman D.J. Eigenfaces vs. Fisherfaces: recognition using class specific linear projection. IEEE Trans. Pattern Anal. Mach. Intell. 1997;19(7):711–720. [Google Scholar]
- 31.Li B., Chellappa R. Face verification through tracking facial features. J. Opt. Soc. Am. A: 2001;18(12):2969–2981. doi: 10.1364/josaa.18.002969. [DOI] [PubMed] [Google Scholar]
- 32.Hadid Abdenour, Pietikaainen Matti, Stan Z., Li . Computer vision group; 2001. Learning Personal Specific Facial Dynamics for Face Recognition from Videos; pp. 439–446. [Google Scholar]
- 33.Li Stan Z., Chu RuFeng, Liao ShengCai, Zhang Lun. Illumination invariant face recognition using near-infrared images. IEEE Trans. Pattern Anal. Mach. Intell. 2007;29(4):627–639. doi: 10.1109/TPAMI.2007.1014. [DOI] [PubMed] [Google Scholar]
- 34.Robinson J.P., Shao M., Wu Y., Liu H., Gillis T., Fu Y. Vol. 40. 1 Nov. 2018. Visual kinship recognition of Families in the Wild; pp. 2624–2637. (IEEE Transactions on Pattern Analysis and Machine Intelligence). 11. [DOI] [PubMed] [Google Scholar]
- 35.Bordallo Lopez Miguel, Hadid Abdenour, Boutellaa Elhocine, Goncalves Jorge, Kostakos Vassilis, Hosio Simo. 2018. “Kinship Verification from Facial Images and Videos: Human versus Machine”, Machine Vision and Applications; pp. 1–18. [Google Scholar]
- 36.Kaminski G., Dridi S., Graff C., Gentaz E. Human ability to detect kinship in strangers' faces: effects of the degree of relatedness. Proc. Biol. Sci. 2009;1670:3193–3200. doi: 10.1098/rspb.2009.0677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Poggio R. Brunelli T. Face recognition: features versus templates. IEEE Trans. Pattern Anal. Mach. Intell. 2002;15(10):1042–1052. [Google Scholar]
- 38.Lu Jiwen, Zhou Xiuzhuang, Tan Yap-Pen, Shang Yuanyuan, Zhou Jie. Neighborhood repulsed metric learning for kinship verification. IEEE Trans. Pattern Anal. Mach. Intell. 2014;36(2):331–343. doi: 10.1109/TPAMI.2013.134. [DOI] [PubMed] [Google Scholar]
- 39.Zien A., Ong C. Multiclass multiple kernel learning. Proc. Int'l Conf. Machine Learning. 2007:1191–1198. [Google Scholar]
- 40.Guo G., Fu Y., Dyer C., Huang T. Image-based human age estimation by manifold learning and locally adjusted robust regression. IEEE Trans. Image Process. 2008;17(7):1178–1188. doi: 10.1109/TIP.2008.924280. [DOI] [PubMed] [Google Scholar]
- 41.Zhao G., Pietikäinen M. 1st IEEE Workshop on CVPR4HB. 2008. Principal appearance and motion from boosted spatiotemporal descriptors; pp. 1–8. [Google Scholar]
- 42.Bhatt Gaurav, PiyushJha, Raman Balasubramanian. Representation learning using Step-based deep multi- Modal auto encoders. Pattern Recogn. 2019;95:12–23. November. [Google Scholar]
- 43.Li Yi, Song Ling Xiao, Wu Xiang, he Ran, Tan Tieniu. Learning a bi-level adversarial network with global and local perception for makeup invariant face verification. Pattern Recogn. June 2019;90:99–108. [Google Scholar]
- 44.Cohen I., Sebe N., Garg A., Chen L., Huang T. Facial expression recognition from video sequences: temporal and static modeling. Comput. Vis. Image Understand. 2003;91(1):160–187. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The Blue channel of WFBT_SBP_Descriptor performs the functionality of calculating the weights of inter-pixel similarity, which is most essential for obtaining the image descriptions at Blue Channel.
The Green channel of WFBT_SBP_Descriptor performs the functionality of determining the weights of inter-pixel similarity , which is most essential for finding an image descriptions at Green Channel.
The Red channel of WFBT_SBP_Descriptor performs the functionality of determining the weights of inter-pixel similarity , which is most essential for analyzing the image at Red Channel.
The proposed method has been developed in MATLAB 2015. The Matlab code consists of a WFBT_SBP_Descriptor_RGB as a function of processing images associated with different channels of information in the form of Red Green and Blue, where information of Red is represented by Descriptor_Red as sub_function 1, information of Green is indicated by Descriptor_Green as sub_function 2, and information represented of Blue channel is represented by Descriptor_Blue as sub_function 3. Finally all three sub_functions i.e., sub_function 1, sub_function 2, sub_function 3 are merged together to obtain the Descriptions of RGB as a result of WFBT_SBP_Descriptor_RGB, which is useful for further processing of images for image analysis. examples of image analysis include, face recognition, face spoofing detection and various other related fields find the usefulness of evolved method WFBT_SBP_Descriptor_RGB and its subfunctions while describing an image.