Hole Hopping through Cytochrome P450

Abstract

High-potential iron-oxo species are intermediates in the catalytic cycles of oxygenase enzymes. They can cause heme degradation and irreversible oxidation of nearby amino acids. We have proposed that there are protective mechanisms in which hole hopping from oxidized hemes through tryptophan/tyrosine chains generates a surface-exposed amino-acid oxidant that could be rapidly disarmed by reaction with cellular reductants. In investigations of cytochrome P450_BM3, we identified Trp96 as a critical residue that could play such a protective role. This Trp is cation-π paired with Arg398 in 81% of mammalian P450s. Here we report on the effect of the Trp/Arg cation-π interaction on Trp96 formal potentials as well as on electronic coupling strengths between Trp96 and the heme both for wild type cytochrome P450 and selected mutants. Mutation of Arg398 to His, which decreases the Trp96 formal potential, increases Trp-heme electronic coupling; but, surprisingly, the rate of phototriggered electron transfer from a Ru-sensitizer (through Trp96) to the P450_BM3 heme was unaffected by the Arg398His mutation. We conclude that Trp96 has moved away from Arg398, suggesting that the protective mechanism for P450s with this Trp-Arg pair is conformationally gated.

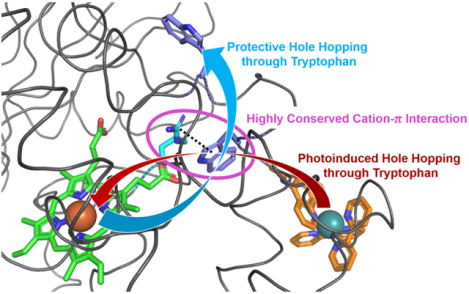
Graphical Abstract

Introduction

Cytochrome P450s, found in nearly all living systems, are monooxygenase enzymes that play critical roles in the production of hormones and the metabolism of xenobiotics.¹ The active site of P450s features a thiolate-ligated heme B capable of reacting with O₂, 2H⁺, and 2e⁻ to form a powerful oxidant, an Fe(IV)-oxo porphyrin cation radical (Por+^•) known as Compound I (Cpd I).² The ability of P450s to activate and hydroxylate strong C-H bonds with both regio- and stereospecificity has made these enzymes the poster childs of both human health and biotechnology research programs.^3–5 The catalytic mechanisms of P450s, which have been studied extensively, involve the formation of Cpd I, followed by H-atom abstraction from the substrate, forming an Fe(IV)-OH porphyrin called Compound II (Cpd II) and a substrate radical (Sub^•). The next step, a radical rebound of HO^• from Cpd II to Sub^•, affords the hydroxylated product.⁶ Although we have a good understanding of the basic steps in the catalytic cycle, we know much less about the role of conformational dynamics in substrate binding/release and control of electron flow through the enzyme, two of the factors that determine the efficiency of enzymatic function (coupled turnover).

As the functions of cytochrome P450 require the generation of a potent oxidant, Cpd I, there must be, we think, protective mechanisms against self-inflicted oxidative damage in the event of uncoupled turnover. One possible protective mechanism is based on the ejection of electron holes from Cpd I to the protein surface through redox active amino acids. Such a mechanism could be tested by variation in the local environment of individual amino acids, or by mutation of amino acids in the hole hopping chain, as these would affect the electronic coupling and reduction potentials of participating residues.

Experimental work involving LC-MS/MS analysis of cytochrome c peroxidase (Ccp1) under oxidative stress conditions, and photochemical oxidation of ruthenium (Ru)-modified P450_BM3 (Cyp102a1) monitored by transient absorption (TA) spectroscopy, have pointed to key amino acids involved in electron hole transport through these oxidative enzymes.^7–9 In a theoretical study, Beratan et al. found that electron hole transfer in P450S_SCC (Cyp11a1), P450_BM3, and Ccp1 is efficient through pathways identified in experimental work and protein structure analysis.^10,11

Work by Ener et al. involving the photooxidation of Ru-labeled P450_BM3 (RuP450_BM3) demonstrated that Trp96 is critical for hole injection from the surface photosensitizer to the heme, generating Cpd II.^7,12 The photochemical cycle, shown in Figure 1, is reversible and occurs thousands of times without enzyme degradation. Notably, the mutation of Trp96 to His precludes heme oxidation indicating that Trp96 is an essential component in the photochemical process. Moreover, Trp96 is a prime candidate for electron hole ejection in the reverse direction, from Cpd I to the enzyme surface, owing to its proximity to the heme (7.0 Å, heme edge to Trp-N).

FIGURE. 1:

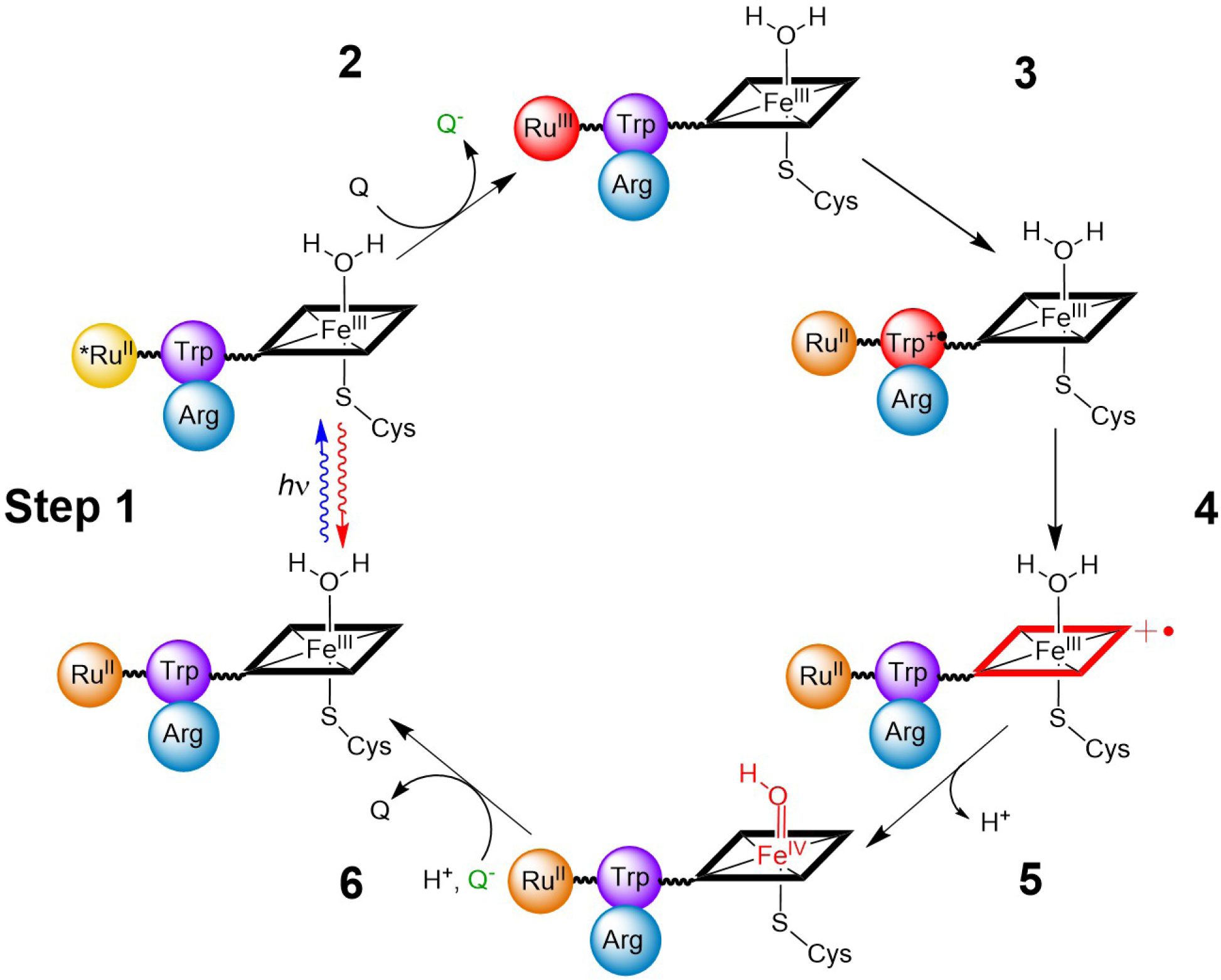
RuP450_BM3 photooxidation cycle. Species shown in red represent oxidized intermediates in the reversible cycle. As drawn, the Trp96 Arg398 cation-π interaction would be in close contact as is observed in the crystal structures PDB: 3NPL and 3R1A. The photooxidation cycle begins with a laser pulse that excites the covalently attached Ru(II)photosensitizer, Step 1. This excited species is then quenched oxidatively (Q = Quencher = [Ru(NH₃)₆]Cl₃, generating Ru(III)-photosensitizer, Step 2, and triggering the oxidation of Trp, porphyrin, and iron, forming Cpd II, Steps 3–5. The last step involves the reaction of reduced quencher (Q-) with Cpd II and returns the system to its initial state, Step 6.

In P450_BM3, Trp96 is engaged in a cation-π interaction with an arginine residue (Arg398). Polypeptide sequence alignments suggests that a Trp/Arg pair at this location is present in 81% of mammalian P450s. But, bacterial enzymes often have a histidine (His)/His motif in these positions interacting with the heme propionate. Among the many P450 enzymes having this structurally analogous tryptophan (Trp)-Arg pair, noteworthy examples are the mammalian Cyp3a4 and Cyp2b4 (P450_2b4). Cation-π contacts are generally recognized motifs that stabilize protein structures.¹³ However, there has been little discussion in the literature regarding the cation-π interaction acting as a non-covalent modulator of reduction potentials of aromatic amino acids. An electrochemical study involving a designed 3-helix bundle protein exhibited an increased reduction potential by 0.35 V vs. NHE as compared to free N-acetyl-L-tryptophanamide.¹⁴ The increased potential was attributed to a Lys-Trp cation-π interaction in the folded protein.¹⁵ Additionally, aryl-sulfur interactions have gained attention as non-covalent contacts that affect reduction potentials.^16,17 Moreover, a recent computational study suggests that a transient and flexible cation-π interaction between Tyr154 and Lys131 in the Bacteriophage-λ Exonuclease is an essential component of the catalytic cycle.¹⁸ It follows that conformational dynamics in enzymes likely cause reduction potential fluctuations in redox active amino acids. Thereby, the electron transfer pathways, which play critical roles in function and protection, are engaged and/or altered through conformational changes.

The conformational dynamics of P450 enzymes have been linked to substrate access, product exit, and the diversity of tolerated substrates. An excellent example of conformational flexibility is seen in mammalian P450_2b4;¹⁹ the open and closed conformations of this enzyme are shown in Figure 2. In the open conformation (PDB 1PO5), a large cleft is formed by movement of regions including helices F to G and B’ to C, allowing access from the enzyme surface to the heme active site. Importantly, helix C includes Trp120 (2b4 numbering), a residue analogous to Trp96 in P450_BM3. A large conformational change in helix C results in displacement of Trp120 from its cation-π contact with Arg434 (PDB 3R1A) in the closed conformation. This Trp residue is displaced by approximately 14.7 Å from the closed to the open conformations, resulting in separation of Trp120-Arg434 by 20.6 Å. Remarkably, intermediate conformations of the 2b4 enzyme have also been structurally characterized, demonstrating a dynamic C helix and multiple conformations of Trp120 (Figure 3).^19–23

FIGURE. 2:

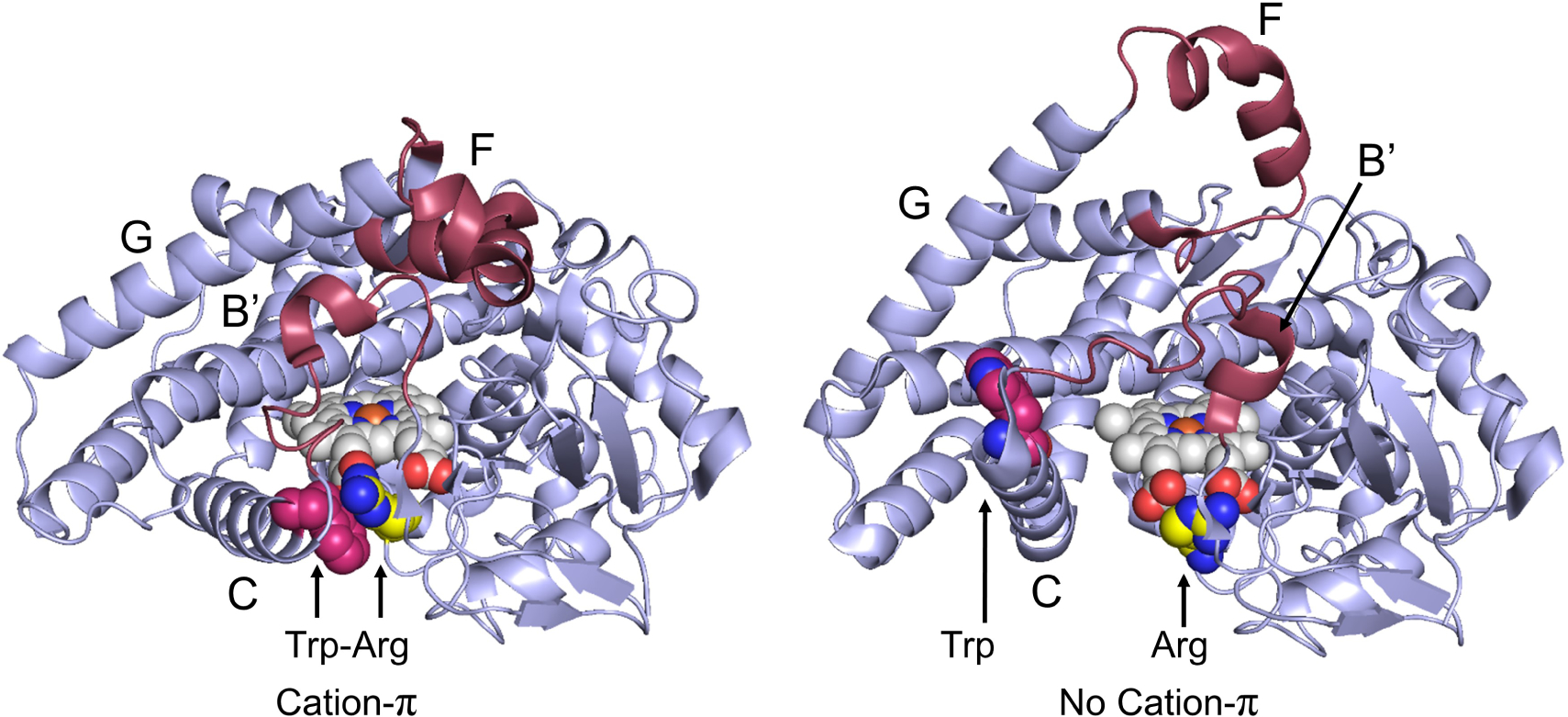
Conformational changes between the open and closed conformations of P450_2b4 from 3R1A (left) to 1PO5 (right). Region with the most change is colored maroon, heme (white and blue), Fe (orange), Arginine (yellow and blue), Tryptophan (magenta and blue). Notably, portions of the C helix containing Trp120 (Trp96 is P450_BM3 numbering) move, dramatically increasing the Trp-Arg distance. Helices with significant conformational change are labelled.

FIGURE. 3:

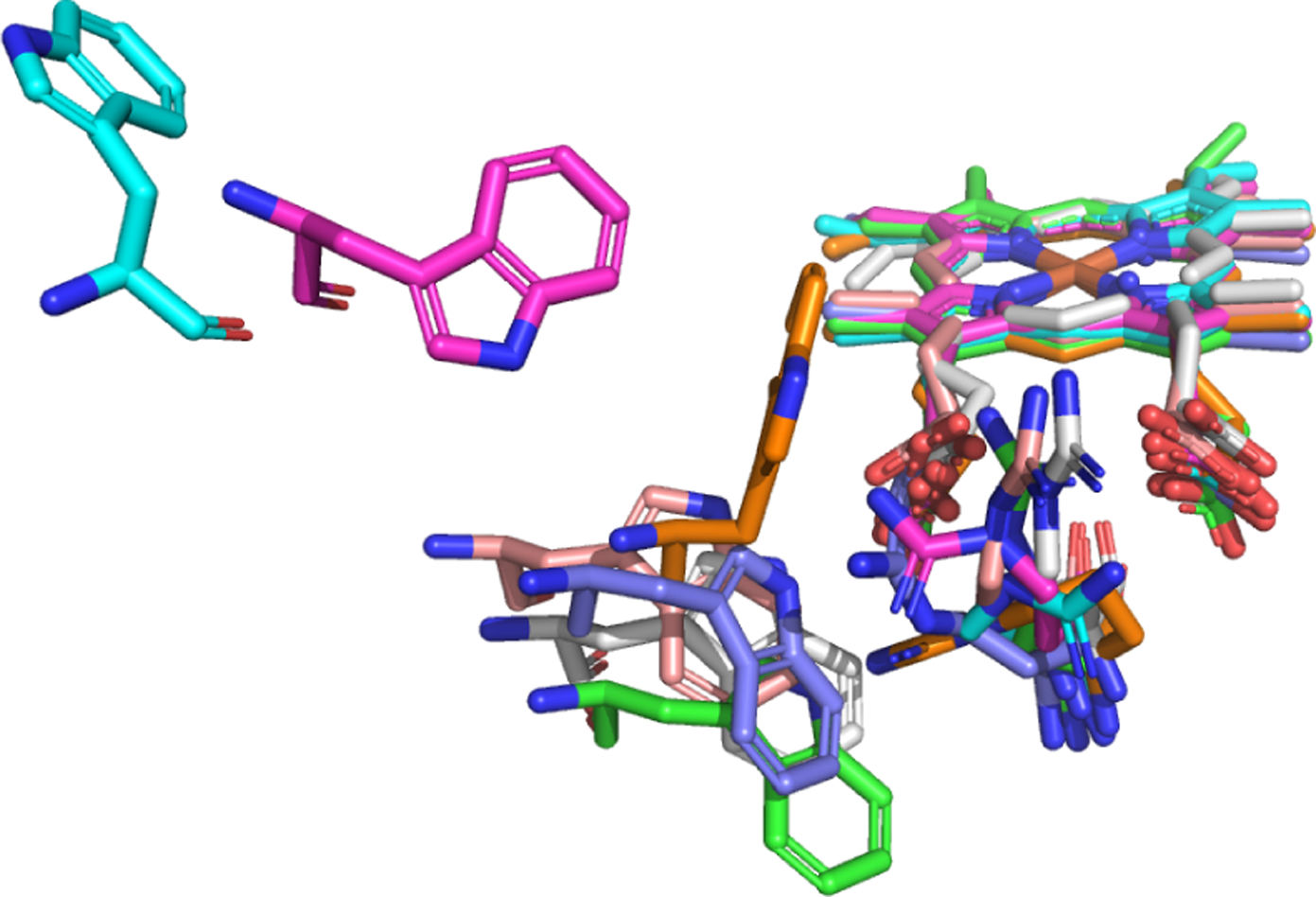
Geometry of: 1PO5 (blue), 2BDM (magenta), 3R1B (orange), 3R1A (purple), 3G5N (pink), 3G93 (white), and 1DT6 (green).

We have expanded our work to include investigations of phototriggered heme oxidation in wild-type and Arg398His RuP450_BM3. Our goal was to shed light on the role of the Trp96Arg398 pair in electron hole hopping from heme to the Ru(III) acceptor (Figure 1). Additionally, we applied a computational approach to provide metrics on the absolute reduction potential and electronic coupling elements of Trp96 in various conformational geometries and electrostatic environments. Here we report the photooxidation of wild-type P450_BM3 and its Arg398His mutant as well as calculations performed on this system and the structurally similar P450_2b4. We find that the absolute reduction potential of Trp is decreased when Arg is mutated to His. Moreover, we calculate an increase in the electronic coupling elements between Trp and heme in this mutant. Both of these findings indicate that electron transfer (ET) should be faster in both forming Cpd II and in the back reaction (Cpd II → Fe(III)) if Trp96 interacts closely with Arg398 under substrate free, solution phase conditions.

Methods

DFT Calculations

All calculations were performed using the Gaussian16 program.²⁴ We use the M06 functional, which is built for non-covalent interactions – such as the cation-π interaction between Trp and arginine (Arg).²⁵ The basis set 6–31G++(d,p) was used for calculating absolute reduction potentials. For the electronic coupling calculations, we had to use the smaller basis set 6–31G(d,p), since the extraction of electronic coupling elements rely on partitioning schemes, which become ambiguous for very large basis sets.^26–29

The protein surrounding a cluster was modeled using the polarizable continuum model (PCM) with a dielectric constant of 3.5 corresponding to the low shielding of the protein environment.^30,31 The absolute reduction potential is calculated as the energy difference between the cationic Trp^•+ and the neutral Trp:

$$\Delta E=E_{tr{p}^{•+}}-E_{trp}$$ (1)

Entropy contributions are ignored in this work.

Protein Structures

The geometries used were downloaded directly from the P450 PDB files using Pymol. Appropriate hydrogen atoms where added and removed. The heavy atoms were frozen and an optimization of the hydrogen atoms was performed. In order to study the effect of the cationic Arg in the wild types, this site was mutated to a neutral His in some structures. Mutations were performed using the Pymol software package, which suggests mutant geometries based on PDB data.³²

Electronic Coupling Elements

The electronic coupling element between donor and acceptor states is a key property for describing electron transfer. To estimate the electronic coupling, we use two simple methods from the literature. The first method, (FCD), uses a simple two state model, while the second method, (POD), is based on a block diagonalization of the Fock/Kohn-Sham matrix.

Fragment Charge Difference (FCD)

The fragment charge difference (FCD) method uses the charge difference operator to construct charge-localized orbitals.³³ So, the adiabatic molecular orbitals (MOs) are rotated into the diabatic orbitals involved in an ET reaction. Therefore, new diabatic orbitals are constructed from the two charge-localized adiabatic molecular orbitals (MOs) and then optimized for the largest charge separation, which will correspond to the diabatic orbitals for the ET reaction.³⁴ The two adiabatic MOs must be comparable to the diabatic MOs involved in the ET reaction.

The Mulliken population analysis is used to calculate the charge of the system for the adiabatic MO most similar to the isolated donor (D-MO) and the adiabatic MO most similar to the isolated acceptor MO (A-MO).³⁵ Koopmans’ theorem must be assumed to be valid when only two adiabatic MOs are used.

Furthermore, it is assumed that the ET reaction is a one-electron transfer. The electronic coupling, V_DA, between the donor and acceptor diabatic states can be calculated with the FCD method as:

$$V_{DA}=\frac{\left|\Delta q_{12}\right|\left(E_A-E_D\right)}{\sqrt{{(\Delta q(D)-\Delta q(A))}^2+4{\left(\Delta q_{12}\right)}^2}}$$ (2)

where Δq₁₂ is the transition charge difference, E_A is the Kohn-Sham MO energy for the acceptor molecular orbital (A-MO), E_D is the Kohn-Sham MO energy for the donor molecular orbital (D-MO), Δq(F) is the charge difference before and after the ET reaction at fragment F.

The charge difference at fragment F is expressed by:

$$\Delta q(F)=\sum _{k\in F}{C}_{D,k}\sum _l^M{C}_{D,l}{S}_{kl}-\sum _{k\in F}{C}_{A,k}\sum _l^M{C}_{A,l}{S}_{kl}$$ (3)

where C_D,k is the atomic orbital (AO) coefficient of orbital k for the D-MO, C_A,k is an atomic orbital (AO) coefficient for the A-MO, k ∈ F means an AO localized on Fragment F and S_kl is an element in the overlap matrix of the AO, M is the total number of basis functions (AOs) in the basis set.

The transition charge difference is expressed as:

$$\begin{gathered} \Delta q_{12}=\frac{1}{2}\left(\sum _{k\in A}{C}_{D,k}\sum _l^M{C}_{A,l}{S}_{kl}+\sum _{k\in A}{C}_{A,k}\sum _l^M{C}_{D,l}{S}_{kl}\right) \\ -\frac{1}{2}\left(\sum _{k\in D}{C}_{D,k}\sum _l^M{C}_{A,l}{S}_{kl}+\sum _{k\in A}{C}_{A,k}\sum _l^M{C}_{D,l}{S}_{kl}\right) \end{gathered}$$ (4)

Projection-Operator Diabatization (POD)

Projection-operator diabatization (POD), another simple and cost-efficient method of calculating electronic coupling elements between orbitals, was proposed by Kondov et al.³⁶ For electron hole transfer on simple organic dimer systems, it has been shown to give errors similar to constrained DFT (CDFT) (POD and CDFT couplings deviate 9.3 % and 5.3 % from the correct results of the HAB11 test set.)³⁷ In the POD method the electronic coupling element between two orbitals, ${\varphi }_i^D$ and ${\varphi }_j^A$, localized on donor and acceptor, respectively, is given by the corresponding matrix element of the Fock operator, F_ij (in the DFT formalism, the Kohn-Sham operator). The localized orbitals are then defined in terms of the Fock matrix expressed in the AO basis, F^AO. Since the AO basis functions are localized on the nuclei they can be partitioned according to donor and acceptor, respectively. The first step in the POD method is to utilize the localization of atomic orbitals to order the Fock matrix according to donor and acceptor orbitals. To work in an orthonormal basis, the AOs are Löwdin transformed and the Fock matrix in this orthonormal basis is:

$${\tilde{F}}^{AO}=S^{-1/2}{F}^{AO}{S}^{-1/2}=\left[\begin{array}{cc}{\tilde{F}}_{DD}& {\tilde{F}}_{DA}\\ {\tilde{F}}_{AD}& {\tilde{F}}_{AA}\end{array}\right]$$ (5)

where S is the overlap matrix for the AO basis. The Löwdin transformation is used since it creates the orthonormal basis closest to the original basis in a least squares sense.^38,39 The donor and acceptor orbitals are now defined as the orbitals that diagonalize the donor and acceptor block, respectively:

$${\epsilon }_i^D={\mathit{\varphi }}_{\mathit{i}}^{\mathit{D}\mathit{,}\mathit{†}}{\tilde{\mathit{F}}}_{\mathit{D}\mathit{D}}{\mathit{\varphi }}_{\mathit{i}}^{\mathit{D}}$$ (6)

$${\epsilon }_j^A={\mathit{\varphi }}_{\mathit{j}}^{\mathit{A}\mathit{,}\mathit{†}}{\tilde{\mathit{F}}}_{\mathit{A}\mathit{A}}{\mathit{\varphi }}_{\mathit{j}}^{\mathit{A}}$$ (7)

The Fock matrix can now be expressed in this localized and orthonormal basis:

$$\left[\begin{array}{cc}{\epsilon }^D& F_{loc}^{DA}\\ F_{loc}^{AD}& {\epsilon }^A\end{array}\right]$$ (8)

where ε^D and ε^A are diagonal matrices containing the donor and acceptor orbital energies respectively while the matrices on the off-diagonal, $F_{\text{loc}}^{DA}$ and $F_{\text{loc}}^{AD}$ are found as

$$F_{\text{loc}}^{DA}={\varphi }^{D,†}{\tilde{F}}_{DA}{\varphi }^A$$ (9)

$$F_{\text{loc}}^{AD}={\varphi }^{A,†}{\tilde{F}}_{AD}{\varphi }^D$$ (10)

and contain the electronic coupling elements between orbitals localized on donor and acceptor fragment, respectively.

Experimental

Protein Expression, Labeling, and Characterization

The wild type P450_BM3 heme domain was cloned into the pEt-22b(+) vector. A triple mutant protein (C62A/C156S/K97C) was prepared to remove two cysteines and introduce a new cysteine for conjugation with the photosensitizer. A quadruple mutant was prepared having the additional R398H mutation. All primers were purchased from Eurofins Genomics. In order to express the enzymes, a 25 mL stock culture of BL21(DE3) E. coli containing each mutant plasmid was grown shaken at 180 rpm overnight at 37 °C in LB broth. This stock culture was used to innoculate 2 L of TB broth in a 6 L flask and grown to an OD of 0.6 at 37 °C, shaken at 160 rpm. At this point, the cultures were charged with 0.5 mM of 5-aminolevulinic acid and 1.0 mM IPTG and the temperature was lowered to 30 °C for 16 h, shaken at 110 rpm. Cell pellets having a pink to red appearance were formed upon centrifugation (6,000 rpm, 5 min) and resuspended in 50 mM Tris-HCl, pH 8. Cell lysing was performed through sonication, on ice, in the presence of cOmplete™, Mini, EDTA-free Protease Inhibitor Cocktail (Roche). Cellular debris was removed through centrifugation (13,000 rpm, 1 h) affording a red transparent solution. The solution was purified on Ni-NTA resin and washed with 20 column volumes of 50 mM Tris-HCl containing 10 mM imidazole, pH 8. The protein was eluted with the same buffer containing 200 mM imidazole.

Imidazole was removed by repeated washing with 50 mM Tris-HCl, pH 8, buffer in 30,000 MW Amicon® Ultra-15 Centrifugal filters. Synthesis of [Ru(bpy)₂(5-iodoacetamido-1,10-phenanthroline)](PF₆)₂ was performed as previously reported.⁴⁰ Selective labeling of the triple and quadruple mutants at K97C was accomplished by mixing of 5 equivalents of photosensitizer with a 20 μM solution of protein and shaken at 100 rpm at 4 °C overnight. Excess photosensitizer was removed by centrifugal ultrafiltration and the labeled protein was concentrated and further purified by FPLC on a Mono Q anion exchange column to afford the RuP450_BM3 mutants. Labeling and sample purity were confirmed by UV-Vis and ESI-MS analysis.

Transient Absorption Measurements

Samples consisting of 10 μM RuP450_BM3 mutant and oxidative quencher (20 mM ruthenium(III)-hexaammine trichloride) were prepared in buffered solution (pH 8, 50 mM Tris-HCl). Deoxy-genation was achieved via 30 gentle pump-backfill cycles with argon while stirring. Samples were excited with 10 ns laser pulses at 460 nm, delivered by an optical parametric oscillator pumped by the third harmonic from a Spectra Physics Q-switched Nd:YAG laser. Luminescence decays were monitored at 630 nm. Single wavelength transient absorption (TA) kinetics were monitored at 390, 420, and 440 nm averaging ~500 shots per wavelength. Data from four separate timescales (2 μs, 100 μs, 10 ms, and 500 ms) were collected and spliced together to produce full kinetics traces.

Results and Discussion

As Trp96 is the critical residue identified for electron hole transfer in P450_BM3,^7,12 our theoretical work has focused on the ET reaction displayed in Figure 4. We rely on available structural data from P450_2b4 to provide geometries of the Trp, Arg, and heme.^19–23 We first examine an Arg to His mutation within Clusters A-D (Figure 5) to rationalize the effect on the absolute reduction potential of Trp. The choice of His was made to provide hydrogen-bonding (H-bonding) to the heme propionate from the D pyrrole ring, similar to that seen in bacterial P450 enzymes.^41,42 Next, we investigated how the distance of the Trp-Arg cation-π interaction, and relative geometries of Trp-Arg-heme, perturb the absolute reduction potential of Trp and electronic coupling elements of Trp-heme, respectively. In this work, we selected a series of eight crystallographic structures from P450_2b4 and P450_BM3 that contain the analogous Trp-Arg pair and encompass the open, closed, and intermediate conformations of the dynamic enzyme (Figure 3).

FIGURE. 4:

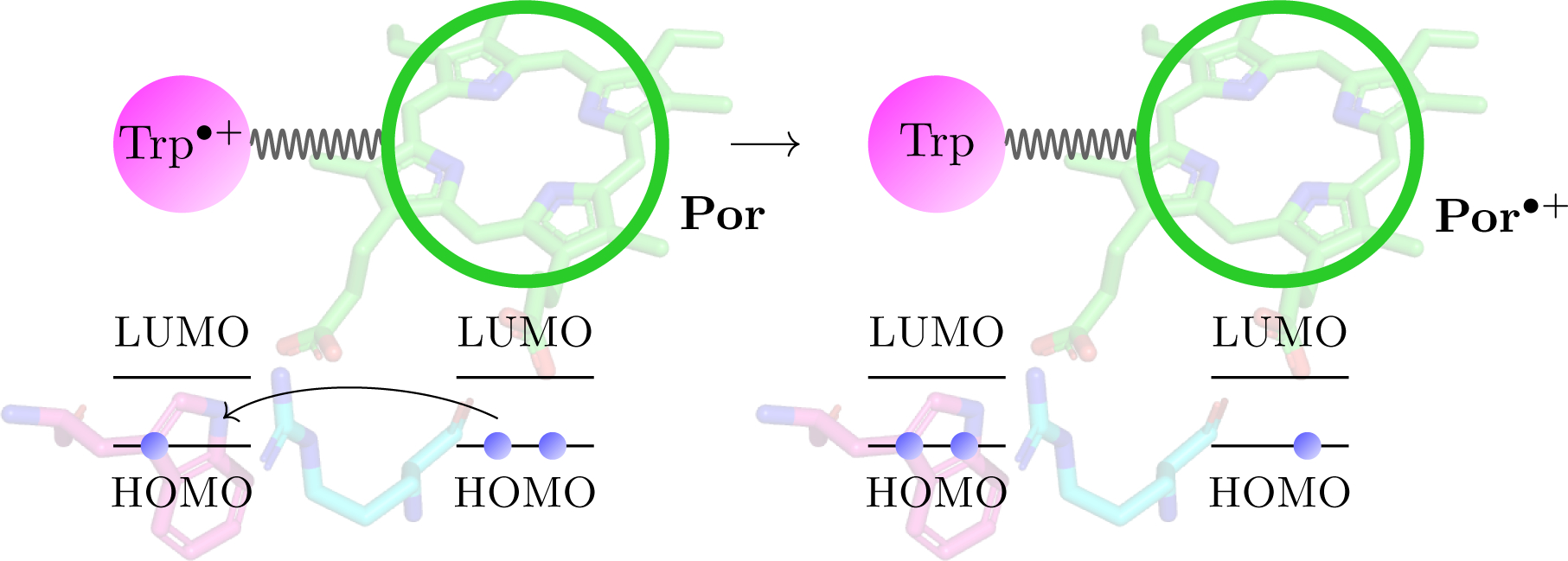
A schematic view of the electron transfer step, for which we calculate the electronic coupling elements. An electron is transferred from the porphyrin ring of the heme to the tryptophan cation, Trp^•+.

FIGURE. 5:

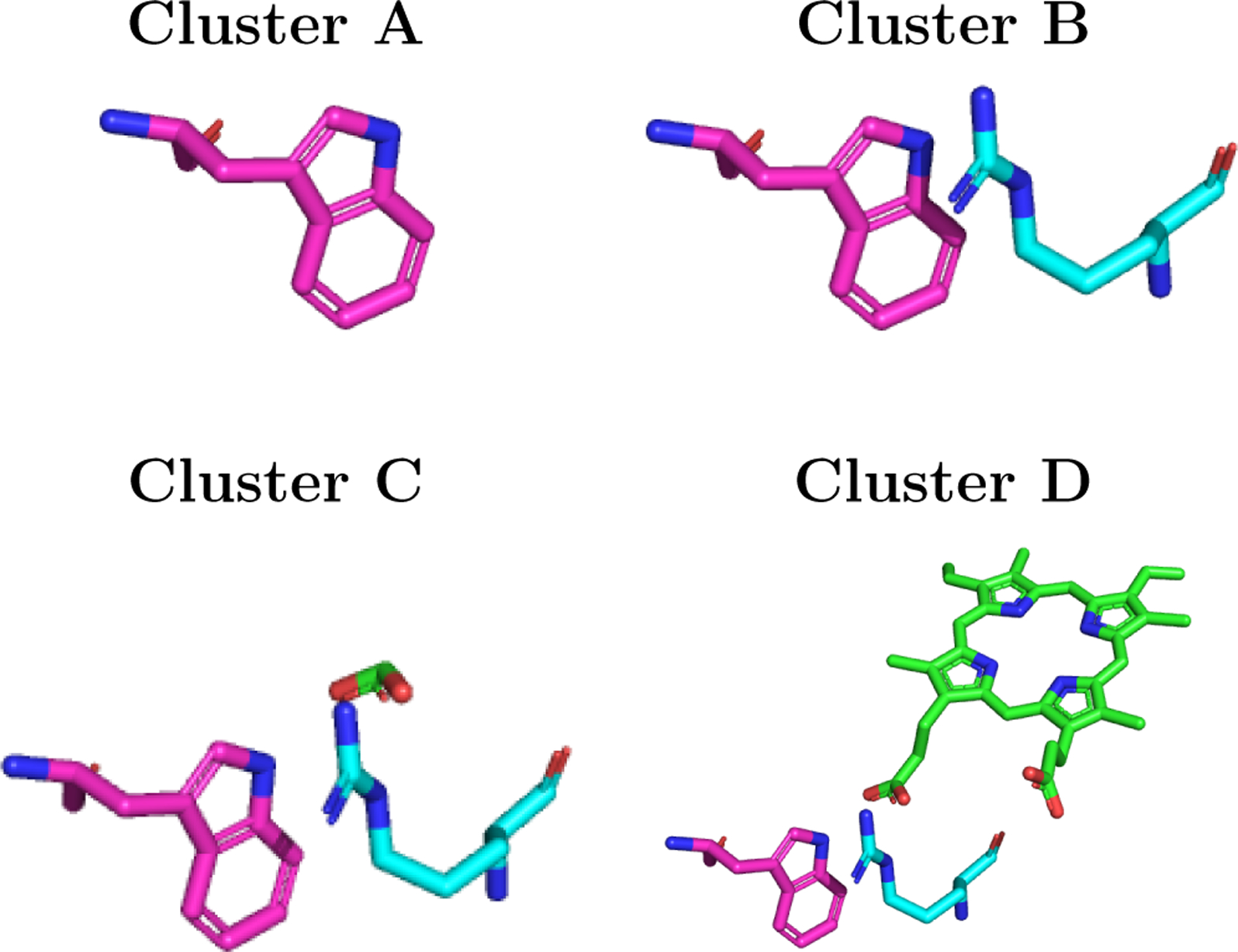
Relative orientations of Trp residues (3NPL structure): (A) single Trp; (B) Trp/Arg cluster; (C) Trp/Arg/heme-substituent (acid group) cluster; and (D) Trp/Arg/heme cluster.

Photooxidation Experiments

We investigated the effect of the Arg398His mutation by single wavelength TA spectroscopy and time-resolved luminescence decay (Figure 6). The luminescence studies show nearly identical kinetics which support similar conformations of the Ru-photosensitizer and infer structural similarity of the two mutant enzymes. Moreover, prior crystallographic characterization shows that the Ru-label does not perturb protein structure.¹² Taken together, we believe that the Arg398His mutant is structurally analogous to its non-mutant counterpart (likely due to a His-heme propionate H-bond).

FIGURE. 6:

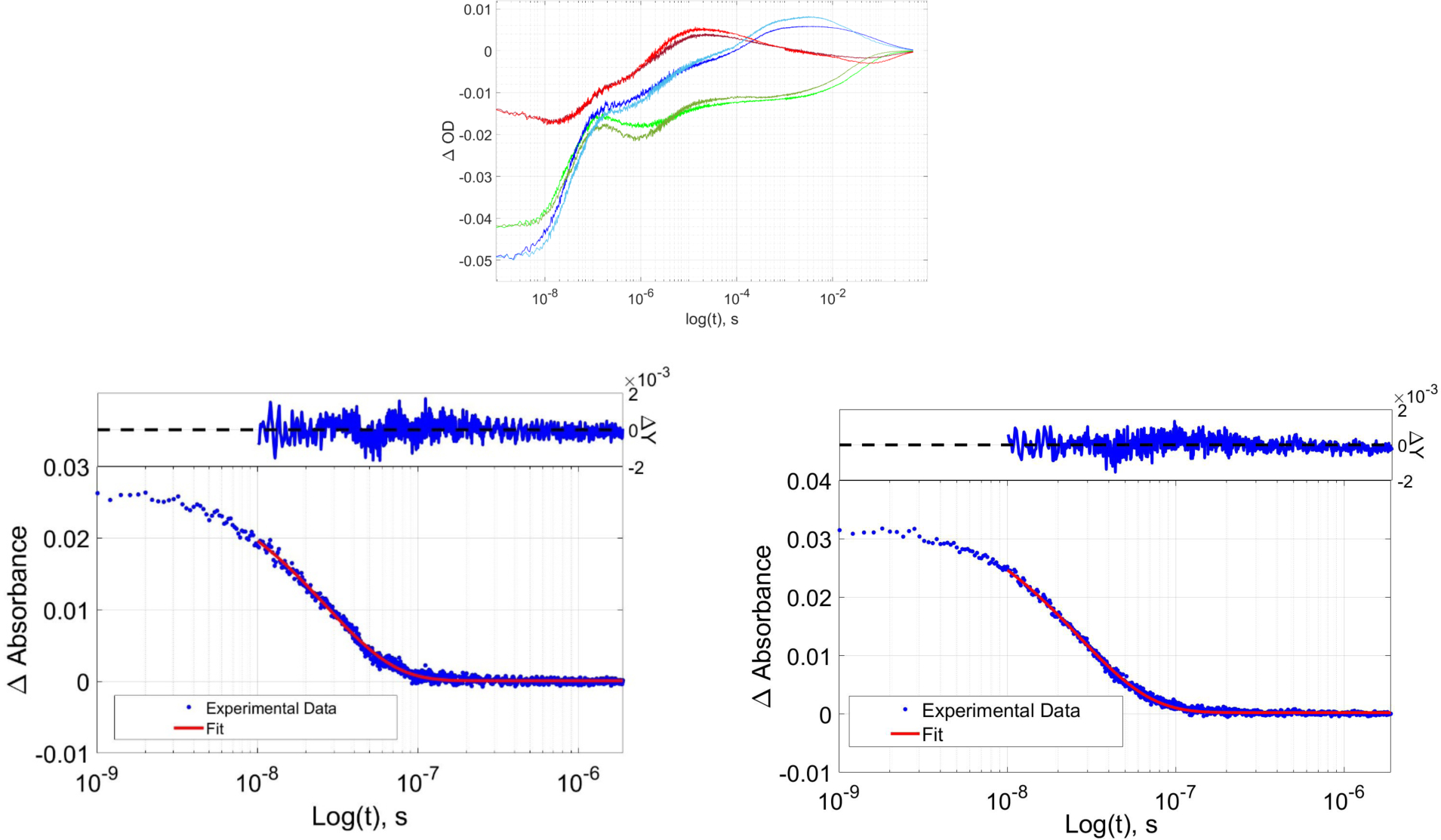
(Top) TA kinetics traces for wild type and R398H RuP450_BM3 light red (R398H, 390 nm), dark red (wt, 390 nm), light green (R398H, 420 nm), dark green (wt, 420 nm), light blue (R398H, 440 nm), dark blue (wt, 440 nm). (Bottom) wild type RuP450_BM3 luminescence decay, (left); wild type RuP450_BM3 R398H luminescence decay, (right).

We expect the Arg398His mutation, and loss of the cation-π interaction, to lower the Trp96 reduction potential. Since Trp96 is essential in the photooxidation process and likely plays a role in protective hole transport from the heme, we anticipated a change in the transient absorption profiles and globally-fit kinetics (Figure 6). Our interpretation of the molecular processes corresponding to the TA changes are the same as previously reported.^7,12 In this work, we fixed the first kinetics phase to the luminescence decay rate, furthermore, we added an additional kinetics phase in the slow time regime which afforded a slightly better global fit. Surprisingly, the single-wavelength TA traces are nearly identical in the wild type and Arg398His mutant. Global kinetics fits of each data set revealed similar kinetics for the six empirical kinetics phases (Table 1). Motivated by this intriguing result, we directed our efforts to a computational study of how conformational dynamics of the enzyme may control the reduction potential of a key Trp residue and the electronic coupling elements of the donor-acceptor pair.

Table 1:

Rate constants from multi exponential global fitting of RuP450 TA kinetics. Phase 1 corresponds to the luminscence decay rate obtained from data in Figure 6.

Kinetic Phase	Wild Type	R398H
1	3.7×107	3.8×107
2	2.9×106	1.4×106
3	2.2×105	2.0 ×105
4	3.8×103	4.2 ×103
5	4.8×101	3.6×101
6	8.4 ×100	7.5 ×100

Calculation of the Reduction Potential

In order to reduce computational time and maintain focus on the key Trp-Arg cation-π interaction, we decided to study the four molecular Clusters shown in Figure 5. DFT calculations were performed on the Clusters in a dielectric medium which mimics the shielding of the surrounding protein (for a study of the solvation method see SI). This method cuts down on the computational costs while still allowing insight into the change in absolute reduction potential and electronic coupling elements.

Initially, we sought to understand how cluster size affects the absolute reduction potential of the wild type and Arg to His mutant enzymes. To accomplish this, we selected three crystal structures: 3NPL, 3R1A, and 3R1B. This data set offers two closed conformation structures (3NPL, P450_BM3 and 3R1A, P450_2b4) in which the Trp-Arg cation-π contact is present, and an intermediate structure where the Trp-Arg cation-π contact is lost while the Trp-heme distance is shortened (3R1B, P450_2b4). The results of reduction potential as a function of Cluster size and geometry are summarized in Figure 7. For Cluster A, small variations in the reduction potential were calculated ranging from 1.06 to 1.19 V vs. NHE (SI Table 1), having good agreement with experimental values of Trp reduction potential of 1.015 eV vs. NHE in aqueous solution at pH 7.⁴³ Addition of the Arg to the Cluster shows an increase in the absolute reduction potential. We attribute this increase to a destabilization of Trp^•+ by the cationic Arg residue. The calculated reduction potentials for Cluster B are higher than expected. However, the structural similarity in 3NPL and 3R1A afforded comparable reduction potentials, and the decrease in reduction potential of 3R1B, having a longer Trp-Arg distance, are encouraging. Across Clusters B-D, the replacement of the Arg cation with a neutral His residue showed an average decrease of 0.85 V vs NHE. We believe this value to be high, but still comparable to the experimentally measured increase of 0.35 V in a lysine (Lys)-Trp cation-π interaction of a model protein.¹⁴

FIGURE. 7:

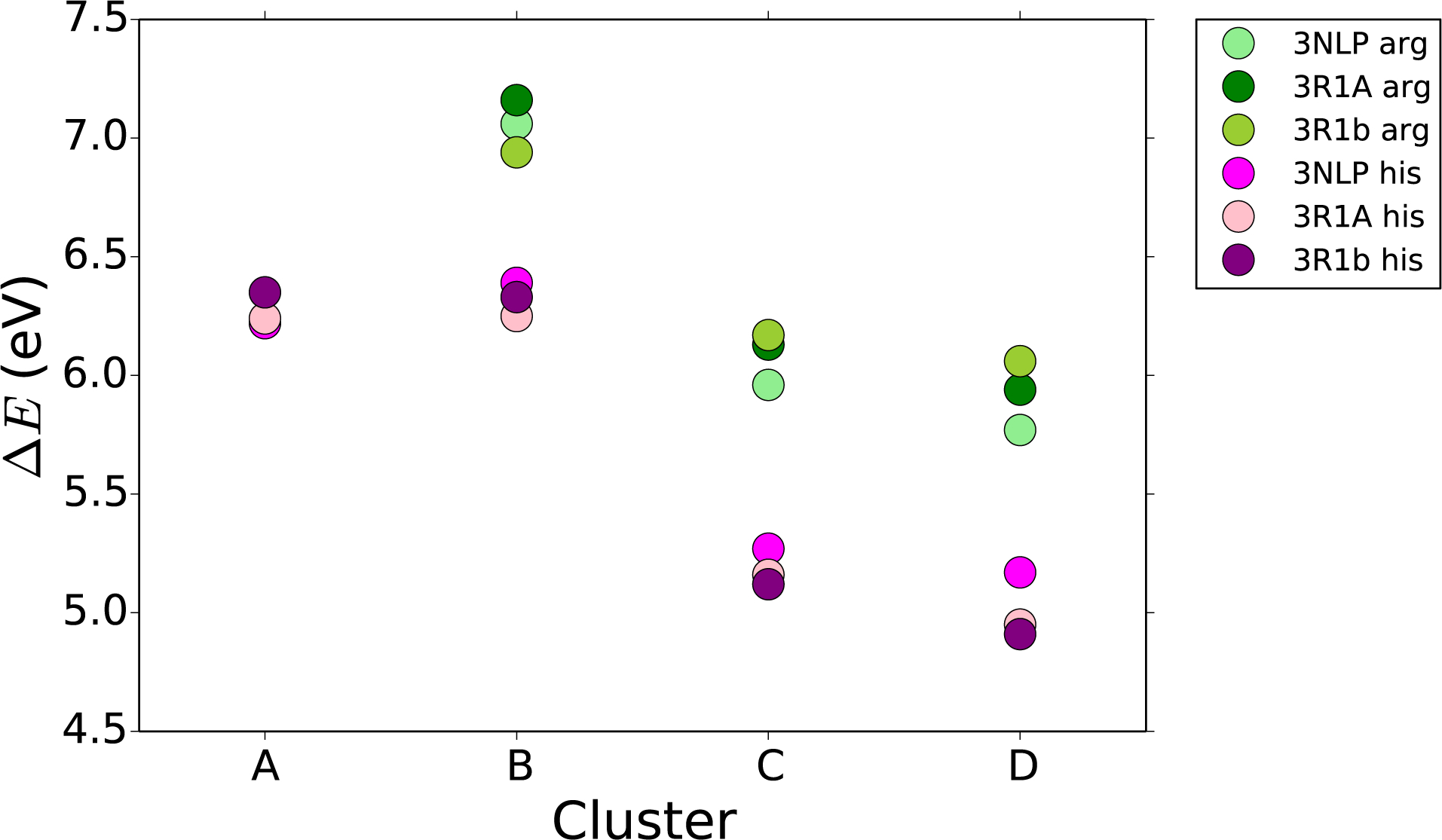
Absolute reduction potential (ΔE) (eV) of each of the four cluster sizes, shown in Figure 5, for three different geometries of P450 both the wild type (in greens) and the His mutation (in pinks). Calculations performed with the PCM solvent model.

When the anionic acid group was added to Clusters C and D, the absolute reduction potential of the entire system decreased compared to Clusters A and B, Figure 7. We attribute the energy decrease to charge balance between the cationic Arg and anionic acid group, giving an absolute reduction potential slightly smaller than for just Trp. In the His Cluster the acid group helped to stabilize the cation in Trp^•+ giving a significantly lower absolute reduction potential. The combined effects of the Arg cation and the anionic acid demonstrate the sensitivity of Trp reduction potential to the surrounding motifs. Calculated reduction potentials depend highly on the Cluster size, yet the general trends upon introduction of Arg to His mutation, and the anionic acid component were similar among all Clusters. As none of these Clusters includes the full protein, we do not expect quantitative accuracy.

There are several factors which could contribute to the rate of ET in P450. Both the barrier height for the reaction and the electronic coupling elements between Trp and heme could play a role. The barrier height is affected by the absolute reduction potential of Trp. By mutating residues and changing the electrostatic surroundings, we anticipate modulation in the Trp absolute reduction potential. In many P450 enzymes, a Trp-Arg cation-π interaction is present in close proximity to the heme, vide supra. This electrostatic interaction is expected to destabilize the one-electron oxidized Trp^•+, thereby raising the absolute reduction potential of Trp. By mutating the Arg to a neutral His, we expect the absolute reduction potential to decrease, thus decreasing the ET barrier height. In all cases where Arg/His are present we saw that cationic Arg destabilized Trp^•+ relative to the neutral His. Therefore, when Arg was mutated to His the absolute reduction potential decreased.

Calculation of Electronic Coupling Elements

We have studied the effect of mutation on the electronic coupling elements using four geometries, Table 2. The electronic coupling elements are calculated using two different methods, POD and FCD. The two methods were not in complete agreement, especially for the His mutations, owing to the choice of orbitals (see SI for more information). Generally, the wild type had smaller electronic coupling elements than the His mutants, except when the Trp-heme distance becomes large (as in the 1PO5 geometry) and then there is no electronic coupling calculated between the donor and acceptor. This result means that, when Arg is mutated to a His, the electronic coupling between Trp and heme becomes much stronger. Importantly, these results suggest that the Trp-Arg cation-π interaction makes electron transfer less favorable in two ways, first by increasing the reduction potential of Trp, and second, by decreasing the electronic electronic coupling elements between Trp and heme.

Table 2:

Electronic coupling elements (meV) between Trp and heme, calculated with both POD and FCD, in various P450 geometries which have different Trp-heme distances (Å).

Geometry	Distance (Å)	Coupling elements (meV)
		Arg		His
Cluster D	Trp-heme	POD	FCD	POD	FCD
3NPL	12.49	8.5	10.1	28	7.3
3R1A	12.50	3.7	2.7	73	33
3R1B	10.13	5.7	4.0	21	19
1PO5	21.80	0.0	0.0	0.0	0.0
3G5N	12.19	11	10
3G93	12.18	1.4	1.4
2BDM	16.32	3.6×10−6	2.2×10−4
1DT6	13.07	11	12

Enzyme Conformational Dynamics and Reduction Potential/Electronic Coupling Elements

The known structural dynamics of P450 enzymes led us to investigate more conformational geometries and their impact on reduction potential and electronic coupling elements. Specifically, we would like to know how the relative geometries between Trp-Arg and Trp-heme affect ET. Importantly, the photooxidation experiments were performed in solution at room temperature (RT). One must be cautious when applying crystal structure data to solution phenomena, however, the detailed work with P450_2b4 suggests that the extreme open conformation, 1PO5, exists in solution.¹⁹ Also, any protein mutation can cause unexpected structural changes. Notably, the luminescence decay data (Figure 6) indicate that solution structures of wild type and R398H have similar conformations (apparent in the single-exponential decay). Observation of multi-exponential decay would infer more than one conformation of the Ru-photosensitizer and therefore inconsistencies in the enzyme tertiary structure. In order to see what happens to the absolute reduction potential and the electronic coupling element when the Trp-Arg and Trp-heme distances change, we have studied computationally seven mammalian and one bacterial (3NPL) P450 conformations that have been determined by X-ray diffraction: 3G5N, 3G93, 2BDM, 3R1A, 1DT6, 3R1B, and 1PO5 (Figures 3 and 5).

Absolute Reduction Potentials

Using P450 geometries with varying Arg-Trp distances and relative orientations, we were able to study the geometric effects on the absolute reduction potential. These calculations were performed by using Clusters B-D where Arg is present. When only the Trp and Arg components are studied, Cluster B, we calculate a decrease in the absolute reduction potential as the Arg moves away from Trp. As anticipated, the further away the cationic Arg was from Trp^•+ the less it was destabilized, so the reduction potential was lowered. We can view this as a charge-charge interaction, meaning we would expect a $\frac{1}{r}$ decline, where r is the distance between Arg and Trp. We have fitted the data to a function of the form $\frac{a}{r}+b$ (seen as a pink line in Figure 8).

FIGURE. 8:

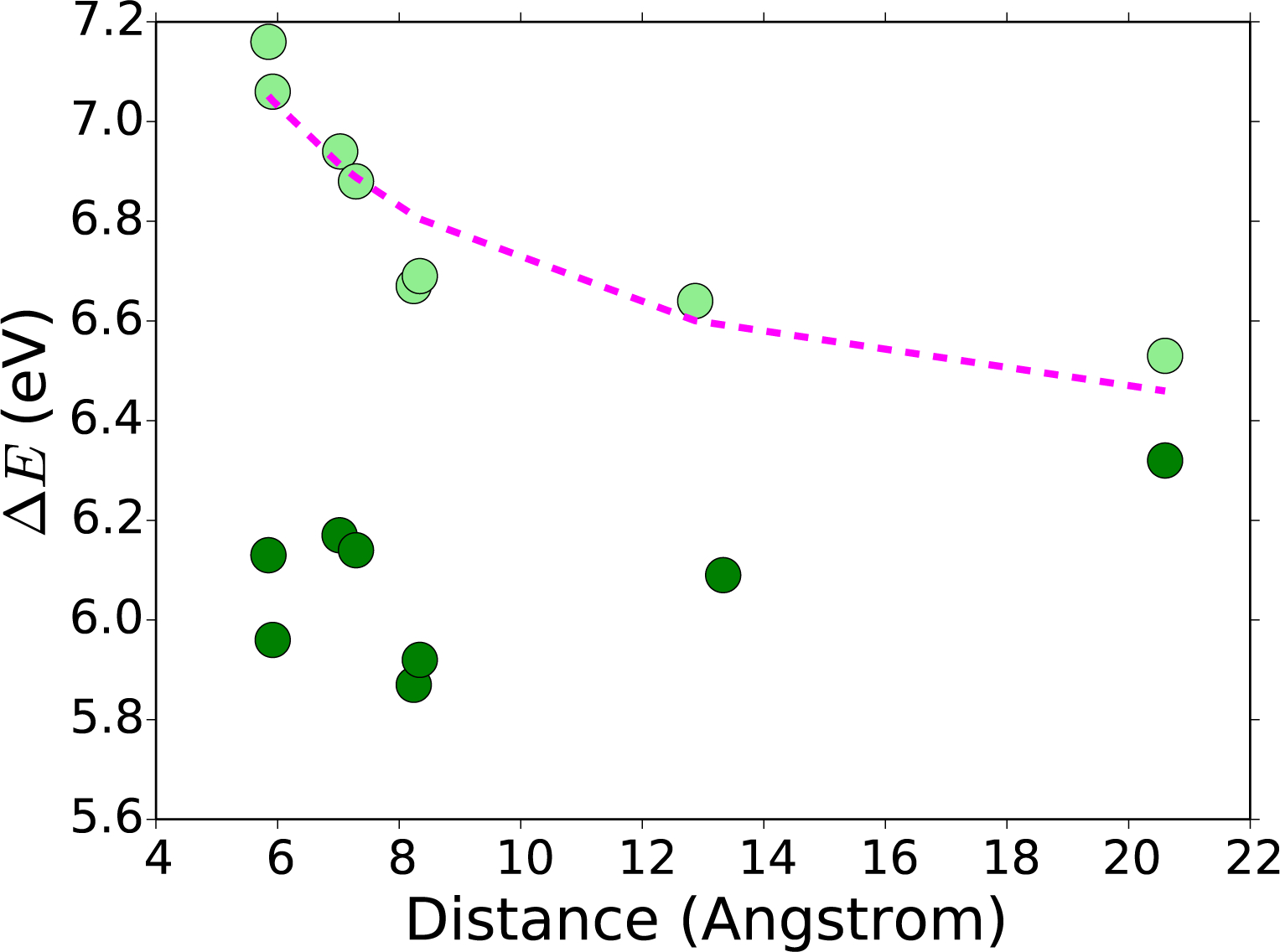
Absolute reduction potential (ΔE) (eV), of cluster B (light green), and cluster C (dark green), as shown in Figure 5. Various P450 geometries shown in relation to the Arg-Trp distance (Å). Fit of a function of the form $\frac{a}{r}+b$ to the Cluster B absolute reduction potentials (pink).

When the Cluster is expanded to include the acid group (Figure 8, Cluster C), the decrease with respect to distance disappeared (the data flattened out). In fact, the highest absolute reduction potential was found when Arg was furthest from the Trp. This finding can be understood by realizing that in 1PO5, which has the largest Trp-Arg distance, the influence of anything added near the Arg will have minimal influence on the Trp. The interaction between Trp and Arg-acid can be seen as a charge-dipole interaction, so we would expect a $\frac{1}{r^2}$ dependence. A $\frac{1}{r^2}$ dependence would be flatter than $\frac{1}{r}$ and we do see a flattening in Cluster C.

Electronic Coupling Elements

We calculated that changes in geometry and electrostatic environment have a large effect on the absolute reduction potential of Trp. Using two different methods (FCD and POD) we estimated electronic coupling parameters between Trp and heme for all the P450 geometries in Table 2. Here we did not see a strong distance to electronic coupling energy correlation when the Trp-heme distance was between 10–13 Å. Note that we are working in very small energy units, meV, which means that small differences in geometry could have a large impact on the electronic coupling elements. Within 10–13 Å the large fluctuations could be due to differences in the geometries. We have investigated some of these differences including the angle between the π-system of Trp and the cation on Arg, but have found no clear correlation. However, when they move beyond 16 Å, the electronic coupling drops to almost zero, as would be expected.

Conclusion

We have studied the absolute reduction potential of Trp and the electronic coupling elements between Trp and heme in various wild type and mutated mammalian P450s. We used simple DFT calculations on Clusters of various sizes, geometries, and mutations in order to study the qualitative trends of absolute reduction potentials and electronic coupling elements. In this work, we found that the absolute reduction potential varies as the Cluster size increases. The absolute reduction potential is decreased when the cationic Arg in the wild type P450s is mutated to a neutral His. The distance between the Trp and the Arg can tune the absolute reduction potential in smaller Clusters. However, when an anionic acid is considered, the distance dependence is no longer as pronounced.

Interestingly, ET rates are unchanged when Arg398His RuP450_BM3 is analyzed by TA spectroscopy. This experimental observation is contrary to our calculations that show that variations in both the reduction potential and electronic coupling elements predict more rapid ET. Provided that Trp96 is essential to the photooxidation process, we conclude that there must be a conformational gating of the ET reaction. It follows that Trp96 must be in an intermediate conformation, away from Arg398, where the Arg398His mutation would have little to no effect on the Trp reduction potential, but maintain solution structure similarity.

Our working hypothesis is that when substrate is bound, the enzyme is in the closed position with a cation-π interaction between Trp-Arg, thereby increasing the reduction potential of Trp and preventing this redox active amino acid from out competing substrate oxidation. When uncoupled turnover occurs, a conformational change would take place that separates the Trp-Arg pair, lowering the reduction potential to a more favorable level to facilitate ET to the heme. Distancing the Trp-Arg pair may increase electronic coupling elements, as we see in our calculations where Arg is removed, also favoring ET. Intriguingly, Arg398 is one amino acid away from the conserved Cys400 residue ligated to the heme. It is conceivable that a communication loop exists in the Cys400-Fe, Cys400-X399-Arg398, and Arg398-Trp96 network. Enzyme activity based on conformational changes caused by metal-ligand coordination are known, notably in the heme-containing guanylate cyclase.⁴⁴

Comparable open and closed dynamics have been observed in many P450s where conformational changes in the F/G helices lead to changes in active site accessibility and concomitant movement of the C-helix, where Trp96 is located.⁴⁵ Moreover, the C-helix is known to contact the P450 redox partner in P450cam (CYP101A1) and in a P450_BM3 complexed with an FMN-binding domain.^46,47 It follows that coordinated movement of the F/G/C helices may have control over key enzyme properties such as substrate access, successful redox partner binding, and possibly protective electron transfer. Here we propose that conformational dynamics in P450 enzymes having the analogous Trp-Arg pair (seen in P450_BM3 and in 81% of mammalian P450 enzymes) may control a protective ET process.