Abstract
Elevated levels of ambient air pollution has been implicated as a major risk factor for morbidities and premature mortality in India, with particularly high concentrations of particulate matter in the Indo-Gangetic plain. High resolution spatiotemporal estimates of such exposures are critical to assess health effects at an individual level. This article retrospectively assesses daily average PM2.5 exposure at 1 km × 1 km grids in Delhi, India from 2010–2016, using multiple data sources and ensemble averaging approaches. We used a multi-stage modeling exercise involving satellite data, land use variables, reanalysis based meteorological variables and population density. A calibration regression was used to model PM2.5: PM10 to counter the sparsity of ground monitoring data. The relationship between PM2.5 and its spatiotemporal predictors was modeled using six learners; generalized additive models, elastic net, support vector regressions, random forests, neural networks and extreme gradient boosting. Subsequently, these predictions were combined under a generalized additive model framework using a tensor product based spatial smoothing. Overall cross-validated prediction accuracy of the model was 80% over the study period with high spatial model accuracy and predicted annual average concentrations ranging from 87 to 138 μg/m3. Annual average root mean squared errors for the ensemble averaged predictions were in the range 39.7–62.7 μg/m3 with prediction bias ranging between 4.6–11.2 μg/m3. In addition, tree based learners such as random forests and extreme gradient boosting outperformed other algorithms. Our findings indicate important seasonal and geographical differences in particulate matter concentrations within Delhi over a significant period of time, with meteorological and land use features that discriminate most and least polluted regions. This exposure assessment can be used to estimate dose response relationships more accurately over a wide range of particulate matter concentrations.
Keywords: Particulate matter, Machine learning, Hybrid models, Pollution exposure, Satellite observations
Graphical abstract
INTRODUCTION
Air pollution is a major public health hazard in low and middle income countries, such as India, with concentrations of particulate matter (PM) far exceeding the permissible limits in regions across the country1,2. Specifically, urban centers and the Indo-Gangetic plain in India are influenced by high levels of PM3,4, with both local and global sources of emission. Numerous publications have implicated air pollution, both indoor and outdoor, as major risk factors of mortality and morbidity due to respiratory and cardiovascular causes1,5,6,7. Further, certain sections of the population, such as children, elderly and pregnant women are at a heightened risk from increasing levels of PM, thus making air pollution an area of high priority for policy changes in Delhi and India in general8,9,10. In order to better understand the impact of air pollution on both chronic and acute health effects at an individual level, it is important to accurately assess air pollution exposure.
Ambient air pollution is a complex process with multiple sources of variation across space and time. Levels of particulate matter depends on spatiotemporal variations in meteorology as well as differences in land use patterns, such as road density are spatial with slow rates of temporal change. Valid prediction models to assess ambient air pollution exposure must attempt to capture both sources of variation. In the Indian context, air pollution modeling exercises have mainly used land use regressions or remote sensing based simulations to provide predictions across space and time4,11,12. However, land use regressions capture spatial features and are not equipped to distinguish temporal variations in the data13. On the other hand, chemical transport models coupled with remote sensing observations are dependent on known chemical processes at coarse spatial resolutions, which may not capture the ground realities14. In addition, until recently, the lack of an extensive ground monitoring network and pollution data in India hindered the development of comprehensive retrospective prediction model for ambient PM concentrations.
Globally, there have been very few attempts to amalgamate data from all possible sources to predict air pollution exposure at a fine spatiotemporal resolution. In the recent years, hybrid prediction models have been developed for ambient air pollution concentrations in the New England area in United States, Mexico City, entire continental United States and Italy respectively15,16,17,18. These studies have used data derived from satellites (such as Aerosol Optical Depth (AOD) and ultraviolet absorption index), reanalysis based meteorological data and land use variables within hybrid modeling frameworks to predict levels of particulate pollution. Machine learning algorithms have been used sparsely to predict pollutant concentrations in different locations across the world and have obtained considerable prediction accuracy10,19,20. However, the application of ensemble averaging across different machine learning algorithms is under-utilized in this field. In addition, these models have been developed in regions with lower levels of particulate matter concentrations than what Delhi experiences. In the context of the Indian scenario, the existing literature does not provide any such PM2.5 prediction models for India at 1 km × 1 km resolution for a significant temporal period, that can be utilized to analyze impacts of ambient air pollution on health outcomes.
In this article, we have developed a hybrid model based on ensemble averaging for predicting daily average particulate matter (PM2.5) concentrations at a fine spatial resolution over the state of Delhi, India from 2010 to 2016. The model draws strength from a variety of predictors of ambient air pollution as well as a range of predictive algorithms. Given the high spatiotemporal resolution of the particulate matter concentrations, these estimates can be used to study both long and short term effects of ambient PM2.5 exposure on health outcomes in individuals at a neighborhood level, thus providing more accurate dose response relationships at elevated concentrations.
METHODS
Study location and summaries of pollutants:
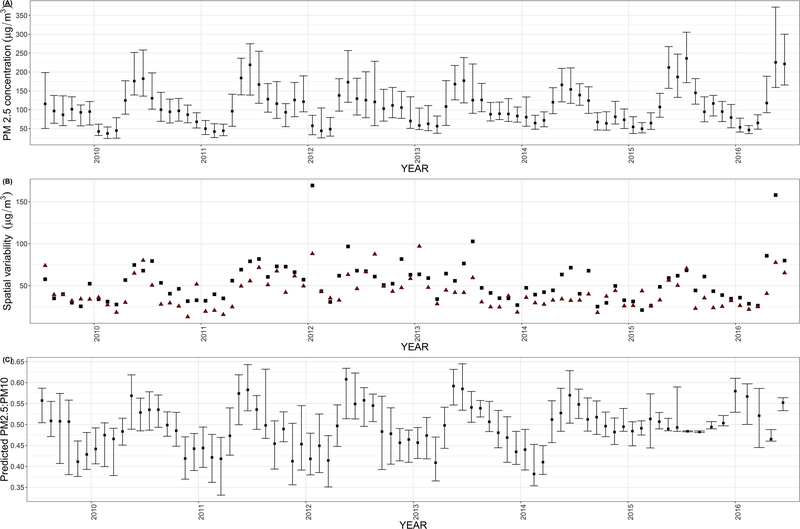
We are considering the state of Delhi with a population of 19 million for this paper. The locations of the ground monitoring stations, along with centroids for climate reanalysis data and aerosol optical depth are shown in Fig. 1A while temporal availability of PM10 and PM2.5 (measured in μg/m3) across each station are shown in Fig. 1B. Median monthly concentrations, interquartile ranges and average variability of PM2.5 at monitoring stations over time are shown in Fig 2A and Fig 2B.
Fig. 1. The study area and availability of ground monitoring data.
(A) Locations of ground monitoring stations (red triangles), reanalysis grid centroids (green dots) and satellite grid centroids (grey dots) over the National Capital Region. (B) Availability of daily PM10 and (C) daily PM2.5 concentrations at ground monitoring stations over time across the National Capital Region, after application of data cleaning filters.
Fig. 2. Observed PM2.5 concentrations and modeled ratios.
(A) Monthly median concentrations (solid black squares) and interquartile ranges (vertical lines) of PM2.5 over monitoring stations in the National Capital Region across 2010–2016. (B) Variability (standard deviations) in PM2.5 concentrations within (black squares) and between (dark red triangles) stations over months across 2010–2016. (C) Monthly median estimated ratio (solid black squares) and interquartile ranges (vertical lines) of PM2.5: PM10 over monitoring stations across 2010–2016 obtained from the calibration using a support vector regression.
Available data:
For prediction purposes, we considered the state of Delhi, which was divided into 1635 grids of area 1 sq. km. each. We predicted daily average PM2.5 concentrations in μg/m3 for each grid from January 1, 2010 to December 31, 2016. The total number of ground monitoring stations under consideration were 24, including two stations from the National Capital Region (Gurgaon and Faridabad). Data from both real time and manual monitoring stations were included in the analysis. We classified months into seasons as Winter (December, January and February), Summer (March to June), Monsoon (July, August) and Fall (September to November).
Pollutants data from monitoring stations:
Data on particulate matter were collected from 24 air pollution monitoring stations in Delhi maintained by the Central Pollution Control Board, India and Delhi Pollution Control Committee. Twelve monitoring stations provided real time monitoring data while the remaining were manual stations. To ensure quality of the pollutants data, the following data filters were applied (in order) before use in analysis:
Runs of exactly equal concentrations on consecutive days were treated as missing.
Concentrations of PM2.5 ∉ [20, 1000] and PM10 ∉ [20, 5000] were treated as missing.
All instances of PM2.5, where PM2.5 > PM10, were treated as missing.
Observations of PM2.5 ∉ [μ − 3σ, μ + 3σ] were treated as missing, where μ and σ are monthly mean and standard deviations of PM2.5 concentrations.
Meteorological data:
We used daily average global climate reanalysis data at a spatial resolution of 0.125 degrees from the European Centre for Medium-Range Weather Forecasts (ECMWF) for meteorological variables, including daily ambient and dew-point temperature, wind speed, precipitation, cloud cover, evaporation and soil temperature21. Daily boundary layer height was obtained from the same reanalysis datasets. Using inverse distance weighted interpolation, the meteorological variables were imputed over all grids for each day. We also computed daily lagged variables for temperature, relative humidity and wind speed for all grids.
Land use data:
We considered a total of 30 layers in the present study each of which represents a land use attribute, such as roads, railway tracks, stations and main terminals, bus stops and depots, interstate bus terminals, airports, metro stations, petrol and CNG pumps, traffic signals, hospitals, cremation grounds, commercial, industrial, and institutional areas, slums, malls and markets, industries, and bridges and flyovers. All attributes are stored in individual shape files implying every shape file corresponds to a single attribute layer. The shape files were obtained from maps prepared by Eicher and Open Street maps (OSMs). We checked for accuracy of the layers by overlaying them on Google Earth imageries. We identified and digitized runways and taxiways present in domestic and international terminals of Delhi airport. Information on the number of solid waste sites was obtained from Delhi municipal authorities. We employed satellite imageries to identify and digitize their locations. Information regarding location and fuel details of all major power plants in and around Delhi was obtained from the department of environment and forests, Govt of Delhi (SoE Delhi, 2010). Locations of stacks present in these power plants were aerially traced using Google Earth. Land use map of Delhi at a spatial resolution of 30m was prepared using Landsat 8 imagery (captured on 18 May 2016) in Arc GIS 10.4.1 platform. We processed the image and applied atmospheric and geo-reference corrections on the Landsat imageries to (1) remove the effects of the atmosphere on the reflectance values and (2) remove source department errors such as the curvature, and rotation of the earth (https://www.usgs.gov/landresources/nli/landsat/using-usgs-landsat-level-1-data-product). An unsupervised classification scheme was employed for classifying the image into four land use types (built-up, vegetation, water, and open spaces). The scheme generates a map by assigning each pixel of the Landsat image to a particular class based on its multispectral composition which would later be realigned to preordained classification. Information on under-construction metro stations and stretches during the study period was obtained from Delhi metro authorities and was later manually digitized. The elevation data (at 90 m resolution) of Delhi was obtained from Shuttle Radar Topography Mission Global Coverage (available at http://www.webgis.com/srtm3.html). For measures of population density, we used gridded population density from The Gridded Population of the World (GPW, version 4), provided by Center for International Earth Science Information Network (CIESIN) for India.
Satellite remote sensing data:
Daily aerosol optical depth (AOD) over one square kilometer grids, processed using the MAIAC algorithm22, were obtained from the MODIS instrument of Terra satellite. We used the measurements taken in the morning and afternoon over Delhi, for the wavelength of 470 nanometers. Data cleaning filters were employed to discard potential spurious measurements of AOD, specifically correcting for cloud masking and mask adjacency using the AOT_QA field in MAIAC data, wherein we removed observations that were categorized as cloudy pixels and those surrounded by more than eight cloudy pixels. Further we restricted AOD observations to those with uncertainty between 0 and 1 (using the data field AOT_Uncertainty within MAIAC data). To counter the sparsity of AOD observations, we calibrated the MODIS AOD observations with the Copernicus Atmosphere Monitoring Service (CAMS) reanalysis sub-daily (3hourly) surface-level Total Aerosol Optical Depth (AOD) at 469 and 550 nm data at 0.125° × 0.125° spatial resolution. A random forest model was used for this calibration while accounting for meteorology and land use variables. Monthly NDVI values were obtained at a one square kilometer spatial resolution over Delhi from MODIS instrument. Monthly data on ultraviolet absorption index (AAI) was obtained from the Ozone Monitoring Instrument (OMI) at a spatial resolution of 0.25 degrees.
We used light at night (LAN) satellite observations also as a predictor for air pollution23. The data for 2010 and 2011 were obtained from the U.S. Defense Meteorological Satellite Program’s (DMSP’s) Operational Linescan System, maintained by the National Oceanic and Atmospheric Administration’s (NOAA’s) Earth Observation Group (EOG)24. The LAN data for 2012 to 2016 were obtained from Visible Infrared Imaging Radiometer Suite (VIIRS) Day/Night Band (DNB), which is also maintained by NOOA’s EOG25. We computed z-scores to account for the difference in measurement methodologies of the two sources of light data before using them in the model. A linear mixed effects model was used to counter the sparsity of the data in the 2010–2011 time period.
Fire emissions data:
Information on fire emissions are required to account for agricultural crop residue burning and other large fires contributing to ambient air pollution26,27. We incorporated two data sources for fire; MODIS Active fire product and the Global Fire Emissions Database (GFED). MODIS Active Fire Collection 6 provided daily fire information with fire reactive power, brightness and confidence along with locations of each fire. Carbon emissions in gC/m2 were extracted from GFED-v4 with information of monthly emissions and daily fractions, which were used to obtain daily carbon emissions from fires at a spatial resolution of 0.25 degrees. We considered all recorded fires and emissions within the region bounded by 26N, 32N, 73.5E, 79.5E, which covers the states of Punjab and Haryana that are sites of most agricultural crop burning around the National Capital Region
Statistical Methodology
We implemented a multi-stage modeling approach which can be differentiated into the following major steps. Table S1 summarizes the stages of this modeling framework along with outcome, predictors and the modeling technique. Each of these major components is described in detail subsequently.
Step 1. Inverse distance weighted interpolation of meteorological variables and calibration of satellite based AOD with reanalysis based AOD.
Step 2. Calibration between PM2.5 and PM10 from ground monitoring stations to counter the sparsity of PM2.5 measurements. This provides PM2.5 observations in addition to those obtained from the ground monitoring stations.
Step 3. Using all available PM2.5 observations and predictor variables, training machine learning algorithms to predict PM2.5 based on spatiotemporal predictors
Step 4. Combining PM2.5 predictions from base learners in (3) using a generalized additive model framework with tensor product smooths over the spatial coordinates to obtain daily PM2.5 at 1km×1km grids.
Interpolation of meteorological data:
In order to obtain daily meteorological information at a 1 km × 1 km spatial resolution, we used spatial interpolation using inverse distance weighted regression on daily climate reanalysis data at 0.125 degree spatial resolution for India. Since our geographical area of interest is only the state of Delhi, we used a 0.01 degree by 0.01 degree subset grid with latitude and longitude varying between (28.125, 29.125) and (76.125, 77.125) respectively.
Calibration of PM2.5 based on PM10:
We utilized available (PM10, PM2.5) concentration pairs at the monitoring stations to predict missing PM2.5 over time using PM10 wherever available (sample size = 2846). Support vector regression models29 were used while incorporating meteorological variables (including daily temperature, relative humidity, wind speed, precipitation and their one day lags), planetary boundary layer (PBL) height, season, days involving festivals (Diwali) or major construction and land use variables such as length of roads and public transport stops within a 1 km buffer region and commercial markets within a 2 km buffer region. We used a logit transformation in order to preserve the constraints on the ratio, which can vary between 0 and 1. Predicted PM2.5 from this model were obtained for space-time combinations where PM10 was available. To adjust for prediction bias, we scaled the output using the slope between observed and predicted concentrations. These scaled predicted concentrations were used along with available PM2.5 data from monitoring stations in the subsequent modeling stages. A ten fold cross validation was conducted to measure prediction accuracy wherein the dataset was randomly split into ten folds and a 9:1 split was used to create the training and test datasets. Prediction accuracy was measured using cross-validated prediction R2 and root mean squared error (RMSE).
Modeling PM2.5 against spatiotemporal predictors using ensemble averaging:
To understand the association between daily concentrations of PM2.5 and aerosol optical depth (AOD) and other variables, we used an ensemble averaging approach using six different methodologies, while adjusting for the meteorological factors, land use variables, emission inventories and population density. The methods used were generalized additive model for big data (GAM)30, elastic net (GLMNET)31, support vector regression (SVR)29, random forests (RF)32, neural networks (NN)33 and extreme gradient boosting (XGB)34. The choice of each learner was based on the following justifications: generalized additive models are semiparametric models that control for nonlinear patterns and variability while using penalized splines for avoiding overfitting; elastic nets select a sparse model from the entire set of variables used in the prediction; support vector regressions account for complex non-linear interactions among the predictors; and tree based models such as random forests, neural networks and extreme gradient boosting are efficient at modeling non-linear relationships along with a different ensemble method for aggregating results over trees. Due to absence of previous literature on such methodologies in high concentration scenarios, we adopted an agnostic approach of implementing multiple strategies on the same data. Each of the six learners were trained on the training data with an internal tuning step (involving a ten fold cross validation) to obtain the tuning parameters for each learner. Ensemble averaged predictions were computed using a generalized additive model framework with penalized splines of each machine learning prediction serving as the independent variables., which prevents overfitting in the presence of potentially correlated predictions from different algorithms. The number of observations at each ground monitoring station within each year, used in these models are provided in Supplemental Material (Table S4).
Spatial smoothing using tensor products:
In order to spatially smooth the ensemble averaged predictions, we used tensor product smoothing over the spatial coordinates according to the following equation:
log(Pred PM(ij)) = a + te(Lat,Lon, by=log(MPMj)) + te(Lat,Lon, by=Month) + te(Lat,Lon, by=Year), where Pred PM(ij) denotes the ensemble averaged predicted PM2.5 at location i and time j, while te(Lat, Lon) denotes a tensor product smooth using penalized splines over latitude and Longitude. We fit tensor product smooths by daily average predicted PM2.5 concentrations at the monitoring locations (MPMj) as well as month and year, to allow for differential smoothing over space and time. The rationale for implementing tensor product smooths was to allow for anisotropic penalty along the two directions.
Cross-validation of predictions:
Overall assessment of prediction accuracy was carried out using 10 fold cross validation on available datasets. The complete data was divided into ten random parts with nine parts serving as the training set and the excluded part was treated as test set. These parameters were used to predict PM2.5 in the test data and prediction performance was measured using adjusted R2 from a robust linear regression between the observed and predicted PM2.5 concentrations. For spatial R2, we obtained the R2 from robust linear regressions between the observed and predicted annual averages of PM2.5 concentrations at each monitor in the cross-validated dataset. For temporal R2, we subtracted the annual average from the predicted and measured PM2.5 at each monitor, and computed the corresponding R2.
RESULTS
Calibration of PM2.5 against PM10 using support vector regression:
A support vector regression model was implemented on 2846 observations, where both PM2.5 and PM10 concentrations were available. The model accounted for variables including meteorological variables, land use and boundary layer height. The distribution (median and inter-quartile range) of the PM ratio measured at the monitoring stations were 0.462 (0.269, 0.555), 0.295 (0.26, 0.357), 0.526 (0.403, 0.634), 0.52 (0.453, 0.602), 0.463 (0.374, 0.556), 0.449 (0.339, 0.56) and 0.46 (0.366, 0.545) in the years 2010–2016 respectively. We restricted our calibration model to use values of the ratio falling between 0.2 and 0.8. The overall cross validated prediction R2 of the calibration model was 0.92, based on a repeated 10 fold cross validation with the model performance being satisfactory in all years except 2010 and 2011 (Supplemental Material, Table S2). Summaries of the predicted ratios, including median and interquartile ranges across each month from 2010 to 2016 are shown in Fig. 2C.
Modeling PM2.5 against spatiotemporal predictors using ensemble averaging:
Using the predictions from the calibration regression along with observations from ground monitoring observations, we obtained 17152 observations of PM2.5 for modeling the relationship between PM2.5 and spatiotemporal predictors. The sample size breakup across each monitoring station and year is provided in Supplemental Material (Table S3). Six different learners were implemented to model the relationship between PM2.5 and spatiotemporal predictors, which were further combined using a generalized additive model with tensor product smoothing. Overall cross-validated R2, spatial and temporal R2 for each learner and the ensemble averaged predictions are provided in Table 1A. In addition, the spatial and temporal R2 for the ensemble averaged predictions are also provided in Table 1A. Annual cross validated prediction bias and root mean squared error are provided in Table 1B. In addition, we provide the comparison of observed and predicted concentrations at each monitoring location along with measures of prediction accuracy in the Supplemental Material (Fig. S1).
Table 1. Prediction accuracy measures for ensemble averaged model.
(A) Cross-validated overall R2 for learners (generalized additive models (GAM), Elastic Net (GLMNET), Support Vector Regression (SVR), Random forests (RF), Neural Networks (NN) and Extreme gradient boosting (XGBOOST)) across years, using robust linear regression between observed and predicted daily PM2.5 concentrations. In addition, overall, spatial and temporal cross-validated R2 is reported for the ensemble averaged (EAVG) predictions. (B) Bias and root mean squared error (RMSE) in ensemble averaged predictions of PM2.5 concentrations across years and seasons. Additionally, slope of the predicted against observed concentrations according to a robust linear regression is reported.
| (A) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| YEAR | GAM | GLMNET | SVR | RF | NN | XGBOOST | EAVG | Spatial | Temporal |
| 2010 | 0.583 | 0.567 | 0.779 | 0.812 | 0.679 | 0.954 | 0.875 | 0.984 | 0.847 |
| 2011 | 0.527 | 0.478 | 0.68 | 0.748 | 0.571 | 0.769 | 0.809 | 0.934 | 0.798 |
| 2012 | 0.417 | 0.4 | 0.655 | 0.698 | 0.509 | 0.707 | 0.752 | 0.986 | 0.7 |
| 2013 | 0.675 | 0.367 | 0.648 | 0.741 | 0.569 | 0.713 | 0.755 | 0.978 | 0.671 |
| 2014 | 0.292 | 0.268 | 0.525 | 0.577 | 0.434 | 0.565 | 0.656 | 0.903 | 0.622 |
| 2015 | 0.555 | 0.505 | 0.893 | 0.798 | 0.681 | 0.826 | 0.855 | 0.994 | 0.83 |
| 2016 | 0.629 | 0.599 | 0.806 | 0.873 | 0.752 | 0.888 | 0.924 | 0.986 | 0.917 |
| (B) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Bias | RMSE | Slope | |||||||
| YEAR | Monsoon | Fall | Summer | Winter | Monsoon | Fall | Summer | Winter | |
| 2010 | 5.757 | 8.677 | 6.384 | 5.053 | 25.084 | 48.464 | 33.906 | 46.722 | 0.995 |
| 2011 | 6.031 | 8.11 | 5.692 | 14.77 | 29.132 | 49.397 | 37.321 | 65.725 | 1.071 |
| 2012 | 7.023 | 14.835 | 8.535 | 15.36 | 40.943 | 73.091 | 64.616 | 67.02 | 1.006 |
| 2013 | 2.887 | 5.676 | 8.668 | 13.086 | 51.373 | 45.912 | 58.258 | 66.364 | 0.971 |
| 2014 | 6.25 | 8.116 | 5.062 | 9.115 | 40.589 | 48.964 | 36.477 | 53.382 | 1.013 |
| 2015 | 3.437 | 3.882 | 5.929 | 4.45 | 25.064 | 46.516 | 36.568 | 56.94 | 0.953 |
| 2016 | 4.747 | 4.693 | 7.214 | 1.979 | 28.534 | 58.698 | 35.954 | 50.927 | 0.965 |
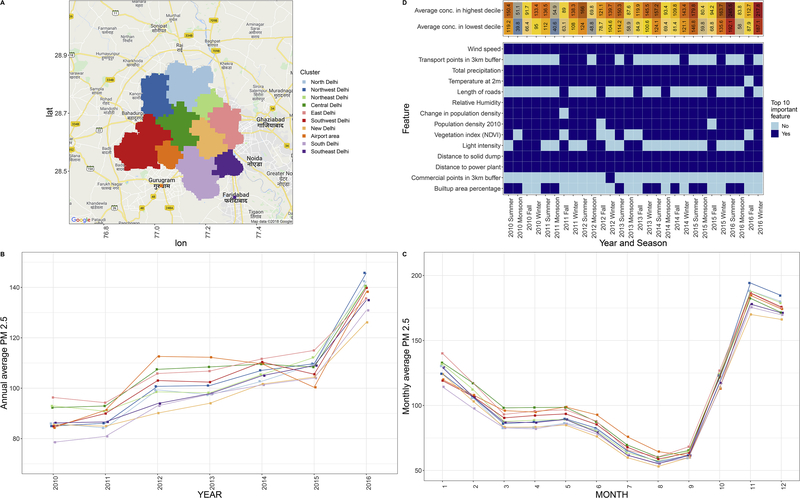
The final predictions within Delhi after tensor product smoothing under a generalized additive model framework is shown in Fig. 3, as monthly averages across the years 2010 to 2016. To understand differences between spatial regions within Delhi, we used a distance based hierarchical clustering to classify the grids in Delhi into ten clusters (Fig. 4A). Annual and monthly average PM2.5 concentrations in these clusters across the seven years is shown in Fig. 4B-4C. In addition, we identified important features that discriminate between the highest and lowest deciles of polluted grids within each season and year using random forest classifiers (Fig. 4D).
Fig. 3. Ensemble averaged predictions from 2010–2016.
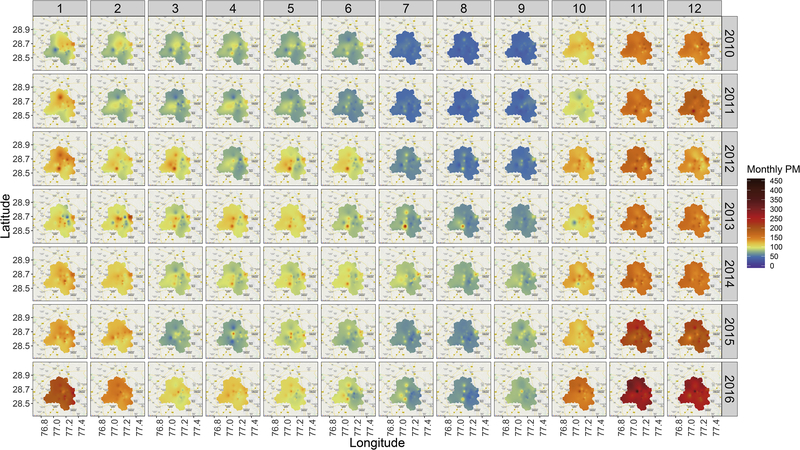
Monthly averaged predicted PM2.5 concentrations in Delhi from 2010 to 2016 using ensemble averaged predictions and tensor product based spatial smoothing.
Fig 4. Geographical differences in pollution and distinguish features.
(A) Ten spatial clusters within the state of Delhi obtained using distance based hierarchical clustering. (B) Annual average PM2.5 concentrations at the ten spatial clusters from 2010 to 2016. (C) Monthly average PM2.5 concentrations at the ten spatial clusters. Averages concentrations were computed by aggregating concentrations in all grids within particular regions across years or months. (D) Ten most important features that discriminate the grids associated with the top and bottom deciles of predicted ambient air pollution across seasons and years.
DISCUSSION
In this article, we have developed a comprehensive model for assessment of PM2.5 for the National Capital Region in India, which to our knowledge, is the first such model for predicting ambient air pollution in an Indian setting at a high spatiotemporal resolution. The major advantages of this model are two fold. Firstly, this detailed and accurate assessment of exposure would be beneficial in studying the effects of air pollution on health in epidemiological studies, specifically for cohort studies that have followed individuals to monitor health outcomes over time. Secondly, this model would serve as a template for developing nationwide prediction models for ambient PM2.5 concentrations and other pollutants.
From the calibration regression, we observed a clear seasonal pattern in the ratio of PM2.5 and PM10 with peaks during January-February and troughs at August-September over the years. The peaks may be attributed to the increased PM2.5 levels during winter from increased biomass burning and crop-residue burning coupled with meteorological conditions. In addition, there was increased variability in the predicted ratios over the years, which could be attributed to more prominent geographical differences in 2015 and 2016. The subsequent use of these modeled ratios allowed us to circumvent the use of constant ratios of PM2.5 and PM10 that do not capture the varying relationship of these pollutants with the spatiotemporal variables.
The prediction model highlights several important features of particulate matter concentrations in Delhi. Our predictions for PM2.5 concentrations showed high average levels across all years along with a temporal increase from 2010 to 2015 (except in few regions) followed by a sharp increase during 2016. The annual average predicted concentrations in the state was greater than 100 μg/m3 during the entire study period, highlighting the dire situation in the National Capital Region. The predictions also show a clear impact of the crop residue burning with increasing monthly average concentrations during October and November irrespective of the geographical location.
The high spatial variability in this small area is also notable since there is a geographical disparity in annual average concentrations putting the densely populated regions, such as East Delhi, Central Delhi and Northeast Delhi at increased risk from exposure to elevated levels of PM2.5, than regions such as North Delhi and South Delhi (Fig. 4B). We also observed the comparatively lower annual levels in the New Delhi region which might be attributed to higher vegetation cover compared to neighboring regions. The difference in annual average concentrations between the most polluted and least polluted regions ranged from 10.4 μg/m3 (in 2014) to 22.5 μg/m3 (in 2012), along with high average concentrations. This gradient in exposure would be relevant for making inferences on the dose response relationships comparing populations in these different regions.
To further investigate the features that differentiate regions with high and low ambient air pollution, we compared the grids with top and bottom deciles of the seasonal average concentrations within each year, using random forest classifiers (Fig. 4D). We observed the meteorological variables such as temperature, wind speed, relative humidity and total precipitation as being important discriminators irrespective of season and year. Among land use features, population density in 2010, change in population density from 2010 to 2015, vegetation index and distance from power plants and solid dumps are identified as important features across almost the entire period, which indicates the heavier burden of air pollution on densely populated regions close to industrial areas and garbage dumps, with lower vegetation cover. On the other hand, the percentage of builtup area determines the pollution gap mostly in the summer and monsoon seasons while length of roads is detected in fall, which may indicate the effects of local sources of pollution such as traffic or construction activities are prominent sources specific to season.
In terms of the methodologies used in the ensemble averaging approach, we observed that the predictive algorithms outperformed the generalized additive model and the elastic net procedure. This can be attributed to the ability of predictive algorithms to account for more complex interactions and non-linearity in the relationship with large number of predictors. Among machine learning algorithms, tree based models such as random forests and extreme gradient boosting outperformed other types of algorithms. Spatial R2 was high across all years for the ensemble averaged model, while temporal R2 showed a nonlinear pattern, with poor performance in the middle period. This could be attributed to higher between and within stations variability in 2012 and 2013. A high spatial R2 is particularly important in order to understand the impact of air pollution on spatially resolved health outcomes data. We also compared the performance of ensemble averaged predictions (based on six learners) to an ensemble using only the top two performers (random forests and extreme gradient boosting). We observed a marginal yet consistent increase in prediction accuracy while using the full ensemble, with larger differences in fall and winter of 2013 and 2014 (Supplemental Material, Table S6), which might indicate the need for multiple algorithms in situations with high variablity. Also we evaluated our model performance by fitting a penalized spline between the observed and predicted concentrations within each year. We observed that linearity holds across all levels of ambient concentrations (Supplemental Material, Fig. S3) except in 2014 and 2015 when the linearity fails to hold at observed concentrations beyond 200 μg/m3 and 300 μg/m3 respectively. In comparisons of cross validated R2 in days with average concentrations below and above 100, we observed better performance in days with higher concentrations, which might be caused due to the large number of such days during the year (Supplemental Material, Table S4 and S5). Given that the majority of population in Delhi is exposed to high average annual concentrations, it is important that the model performs well at high concentrations.
The Indian air pollution scenario presented unique challenges towards developing such spatiotemporal prediction models. Pollution levels and emission patterns are vastly different from developed countries with respect to spatial and temporal variability as well as average concentrations. For example, previous models for continental United States and Mexico City have reported annual average levels of 4 to 16 μg/m3 (prediction accuracy of 84%) and 19.7 to 27.2 μg/m3 (prediction accuracy of 72%) respectively (Just et al. 2015, Di et al. 2016). Models developed with data from regions with low pollution levels might not be appropriate in the Indian scenario. Similar studies from China that report overall levels of 64 to 80 μg/m3 have achieved cross-validated prediction accuracy of 54 to 64% using techniques such as geographically weighted regression and neural networks35,36.
We have demonstrated how similar methodologies, such as linear mixed effects models and neural networks performed poorly in this scenario. Further, the number of ground monitoring stations and the associated number of daily observations are small thus making the data sparse. Hence it is necessary to develop models tailored to the Indian context utilizing all relevant data sources, which could be used to better quantify exposure and also modify them to apply on other regions of the country. In addition, existing prediction models can only be used to study the associations with measures of health obtained at coarse spatial and temporal resolution, which may lead to exposure misclassification (Dey et al. 2012). For analyzing cohort based health data on individuals followed across time, spatiotemporally resolved exposures of ambient air pollution are necessary to estimate the exposure-response relationships.
The developed model has multiple novel approaches, especially in the Indian context. We have combined publicly available data from varied sources to explain the spatiotemporal nature of ambient pollution including meteorology, land use, satellite observations and geospatial information. Each type of data contributes towards explaining different features of pollution in Delhi and neighboring areas. For example, emissions from the agricultural crop residue burning in October and November exacerbates air quality in Delhi each year. Existing models for pollution in India have not incorporated these factors in a comprehensive manner, while we utilized publicly available satellite based observations to account for these factors. The novelty of the developed model, in terms of methodology, lies in the ensemble averaging approach. The high average particulate matter concentrations, spatial and temporal variability created difficulties in implementing standard statistical models such as generalized mixed effects models resulting in poor predictive performance (Table 1A). A single technique might not capture the impact of all the variables on the pollutant concentrations. To harness the advantages of different predictive algorithms, we have implemented a machine learning based approach that combines several algorithms in an ensemble averaging framework, thus improving the model performance remarkably. To summarize, we have developed a detailed prediction retrospective model of fine particulate matter for the Delhi region over 2010 to 2016 that would be utilized to study the effects of air pollution exposure on health outcomes in individuals residing in the region.
Limitations:
The prediction model developed in this article is retrospective in nature and relies on previously processed satellite observations and land use parameters. Hence we would not be able to forecast pollutant concentrations in a future time period using the current model. However, the model can be used to predict scenarios in which certain parameters are altered to compute differences in average pollutant levels between scenarios. In case of predictions over larger time periods, some of the land use variables would need to be updated since the features of the region (such as built-up area and population density) could potentially change. With updated variables, this model can be used to obtain predictions during 2000–2009 based on the satellite observations. The model for Delhi uses a large number of variables which might not be available and/or relevant for other parts of the country. In such situations, we would need to simplify the model taking into account the peculiarities of specific regions. Using the predictions from the developed model for studying effects on health would entail matching the location of households to grid cells. This might result in exposure misclassification since an individuals exposure depends on factors such as indoor air pollution and occupational exposure that are not accounted for in this prediction model. Although personal monitoring of pollution would help in reducing this error, it is expensive to carry out the exercise in a large population. However, data from individual monitoring on a group of subjects may be used to calibrate the ambient predictions to obtain individual exposure metrics in future studies.
Supplementary Material
Highlights:
Daily average PM2.5 at 1km grids over Delhi from 2010 to 2016 via a predictive model.
Utilizes multiple data types, machine learning algorithms and statistical techniques.
Resource for studying the long-and short-term effects of PM2.5 on health in India.
The model be extended to other locations as well as at the national level.
ACKNOWLEDGEMENTS
Funding: Research reported in this article was supported by the Fogarty International Center of the National Institutes of Health, National Institute of Environmental Health Sciences and National Cancer Institute, under the GeoHealth HUB research grant (Award Number U01 TW010097).
The authors acknowledge the inputs from the wider GeoHealth Hub team from Center for Chronic Disease Control, Public Health Foundation of India and Harvard School of Public Health in carrying out this work. Team members are listed below according to institution.
Center for Chronic Disease Control: Suganthi Jaganathan, Kishore K Madhipatla, Siddhartha Mandal
Public Health Foundation of India: K Srinath Reddy, D Prabhakaran, Gagandeep K Walia, Bhargav Krishna, Melina Magsumbol, Preet K Dhillon, Safraj Shahul Hameed
Harvard School of Public Health: Joel Schwartz, Richard Cash, Lindsay Jaacks, Nancy Long Sieber
Footnotes
Declaration of interests
The authors declare that they have no known competng financial interests or personal relatonships that could have appeared to influence the work reported in this paper.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- 1.Balakrishnan K, Dey S, Gupta T, Dhaliwal RS, Brauer M, Cohen AJ, Stanaway JD, Beig G, Joshi TK, Aggarwal AN, Sabde Y, Sadhu H, Frostad J, Causey K, Godwin W, Shukla DK, Kumar GA, Varghese CM, Muraleedharan P, Agrawal A, Anjana RM, Bhansali A, Bhardwaj D, Burkart K, Cercy K, Chakma JK, Chowdhury S, Christopher DJ, Dutta E, Furtado M, Ghosh S, Ghoshal AG, Glenn SD, Guleria R, Gupta R, Jeemon P, Kant R, Kant S, Kaur T, Koul PA, Krish V, Krishna B, Larson SL, Madhipatla K, Mahesh PA, Mohan V, Mukhopadhyay S, Mutreja P, Naik N, Nair S, Nguyen G, Odell CM, Pandian JD, Prabhakaran D, Prabhakaran P, Roy A, Salvi S, Sambandam S, Saraf D, Sharma M, Shrivastava A, Singh V, Tandon N, Thomas NJ, Torre A, Xavier D, Yadav G, Singh S, Shekhar C, Vos T, Dandona R, Reddy KS, Lim SS, Murray CJL, Venkatesh S, Dandona LBalakrishna K et al. 2019. The impact of air pollution on deaths, disease burden, and life expectancy across the states of India: the Global Burden of Disease Study 2017. The Lancet Planetary Health. 3, e26–e39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pant P, Guttikunda SK, Peltier RE. 2016. Exposure to particulate matter in India: A synthesis of findings and future directions. Environmental Research. 147, 480–496. [DOI] [PubMed] [Google Scholar]
- 3.Srivastava AK, Dey S, Tripathi SN. 2012. Aerosol characteristics over the Indo-Gangetic basin: Implications to regional climate. In Atmospheric Aerosols-Regional Characteristics-Chemistry and Physics. IntechOpen. [Google Scholar]
- 4.Dey S, Di Girolamo L, van Donkelaar A, Tripathi SN, Gupta T, Mohan M. 2012. Variability of outdoor fine particulate (PM2. 5) concentration in the Indian Subcontinent: A remote sensing approach. Remote Sensing of Environment, 127, 153–161. [Google Scholar]
- 5.Franklin BA, Brook R, Pope III CA. 2015. Air pollution and cardiovascular disease. Current problems in cardiology, 40(5), 207–238. [DOI] [PubMed] [Google Scholar]
- 6.Sharma AK, Baliyan P, Kumar P. 2018. Air pollution and public health: The challenges for Delhi, India. Reviews on environmental health, 33(1), 77–86. [DOI] [PubMed] [Google Scholar]
- 7.Haberzettl P, O’Toole TE, Bhatnagar A, Conklin DJ. 2016. Exposure to fine particulate air pollution causes vascular insulin resistance by inducing pulmonary oxidative stress. Environmental health perspectives, 124(12), 1830–1839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schwartz J. 2004. Air pollution and children’s health Pediatrics 113: 1037–1043. [PubMed] [Google Scholar]
- 9.Robledo CA, Mendola P, Yeung E, Männistö T, Sundaram R, Liu D, Ying Q, Sherman S, Grantz KL Robledo CA et al. 2015. Preconception and early pregnancy air pollution exposures and risk of gestational diabetes mellitus. Environmental research, 137, 316–322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Di Q, Wang Y, Zanobetti A, Wang Y, Koutrakis P, Choirat C, Dominici F, Schwartz JD Di Q et al. 2017. Air pollution and mortality in the Medicare population. New England Journal of Medicine, 376(26), 2513–2522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sanchez M, Ambros A, Milà C, Salmon M, Balakrishnan K, Sambandam S, Sreekanth V, Marshall JD, Tonne C Sanchez M et al. 2018. Development of landuse regression models for fine particles and black carbon in peri-urban South India. Science of the Total Environment, 634, 77–86. [DOI] [PubMed] [Google Scholar]
- 12.Balakrishnan K, Sambandam S, Ramaswamy P, Ghosh S, Venkatesan V, Thangavel G, Mukhopadhyay K, Johnson P, Paul S, Puttaswamy N, Dhaliwal RS, Shukla DKBalakrishnan K et al. 2015. Establishing integrated rural–urban cohorts to assess air pollution-related health effects in pregnant women, children and adults in Southern India: an overview of objectives, design and methods in the Tamil Nadu Air Pollution and Health Effects (TAPHE) study. BMJ open, 5(6), e008090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Marshall JD, Hystad P, Novotny EV, Brauer M. 2011. Challenges and Next Steps for Land-use Regression Models. Epidemiology, 22(1), S101. [Google Scholar]
- 14.Korek M, Johansson C, Svensson N, Lind T, Beelen R, Hoek G, Pershagen G, Bellander T Korek M et al. 2017. Can dispersion modeling of air pollution be improved by land-use regression? An example from Stockholm, Sweden. Journal of Exposure Science and Environmental Epidemiology, 27(6), 575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kloog I, Chudnovsky AA, Just AC, Nordio F, Koutrakis P, Coull BA, Lyapustin A, Wang Y, Schwartz JKloog I et al. 2014. A new hybrid spatio-temporal model for estimating daily multi-year PM2. 5 concentrations across northeastern USA using high resolution aerosol optical depth data. Atmospheric Environment, 95, 581590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Just AC, Wright RO, Schwartz J, Coull BA, Baccarelli AA, Tellez-Rojo MM, Moody E, Wang Y, Lyapustin A, Kloog I. Just AC et al. 2015. Using-in Mexico City. Environmental science & technology, 49(14), 85768584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Di Q, Kloog I, Koutrakis P, Lyapustin A, Wang Y, Schwartz J. Di Q et al. 2016. Assessing PM2. 5 exposures with high spatiotemporal resolution across the continental United States. Environmental science & technology, 50(9), 4712–4721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Stafoggia M, Schwartz J, Badaloni C, Bellander T, Alessandrini E, Cattani G, De’Donato F, Gaeta A, Leone G, Lyapustin A, Sorek-Hamer M, Hoogh KD, Di Q, Forastiere F, Kloog I, Stafoggia M et al. 2017. Estimation of daily PM10 concentrations in Italy (2006–2012) using finely resolved satellite data, land use variables and meteorology. Environment international, 99, 234–244. [DOI] [PubMed] [Google Scholar]
- 19.Bellinger C, Jabbar MSM, Zaïane O, Osornio-Vargas A. 2017. A systematic review of data mining and machine learning for air pollution epidemiology. BMC public health, 17(1), 907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lary DJ, Lary T, Sattler B. 2015. Using machine learning to estimate global PM2. 5 for environmental health studies. Environmental health insights, 9, EHIS15664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dee DP, Uppala SM, Simmons AJ, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda MA, Balsamo G, Bauer DP, Bechtold P, Beljaars ACM, Van-de-Berg L, Bidlot J, Bormann N, Delsol C, Dragani R, Fuentes M, Geer AJ, Haimberger L, Healy SB, Hersbach H, Hólm EV, Isaksen L, Kållberg P, Köhler M, Matricardi M, McNally AP, Monge-Sanz BM, Morcrette JJ, Park BK, Peubey, Rosnay PDe, Tavolato C, Thépaut JN, Vitart FDee DP et al. 2011. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Quarterly Journal of the royal meteorological society, 137(656), 553–597. [Google Scholar]
- 22.Lyapustin A, Wang Y, Korkin S, & Huang D. 2018. MODIS Collection 6 MAIAC algorithm. Atmospheric Measurement Techniques, 11(10). [Google Scholar]
- 23.NOAA (National Oceanic and Atmospheric Administration).2015. “Global Radiance CalibratedNight-time Lights.”Accessed November 2015http://ngdc.noaa.gov/eog/dmsp/download_radcal.html
- 24.NOAA (National Oceanic and Atmospheric Administration).2016a. “Version 4 DMSP-OLS NighttimeLights Time Series.”Accessed April 2016http://ngdc.noaa.gov/eog/gcv4_readme.txt
- 25.NOAA (National Oceanic and Atmospheric Administration).2016b. “Version 1 Nighttime VIIRS Day/Night Band Composites.”Accessed April 2016http://ngdc.noaa.gov/eog/viirs/download_monthly.html
- 26.Kaskaoutis DG, Kumar S, Sharma D, Singh RP, Kharol SK, Sharma M, Singh AK, Singh S, Singh A, Singh D. 2014. Effects of crop residue burning on aerosol properties, plume characteristics, and long-range transport over northern India. Journal of Geophysical Research: Atmospheres, 119(9), 5424–5444. [Google Scholar]
- 27.Rastogi N, Singh A, Sarin MM, Singh D. 2016. Temporal variability of primary and secondary aerosols over northern India: Impact of biomass burning emissions. Atmospheric environment, 125, 396–403. [Google Scholar]
- 28.Guttikunda SK and Calori G. 2013. A GIS based emissions inventory at 1 km×1 km spatial resolution for air pollution analysis in Delhi, India. Atmospheric Environment, 67, 101–111. [Google Scholar]
- 29.Drucker H, Burges CJ, Kaufman L, Smola AJ, Vapnik V. Support vector regression machines. InAdvances in neural information processing systems 1997. (pp. 155–161). [Google Scholar]
- 30.Hastie T, Tibshirani R. Generalized additive models: some applications. Journal of the American Statistical Association. 1987. June 1;82(398):371–86. [Google Scholar]
- 31.Zou H, Hastie T. Regularization and variable selection via the elastic net. Journal of the royal statistical society: series B (statistical methodology). 2005. April 1;67(2):301–20. [Google Scholar]
- 32.Breiman L. Random forests. Machine learning. 2001. October 1;45(1):5–32. [Google Scholar]
- 33.Haykin S. Neural networks: a comprehensive foundation. Prentice Hall PTR; 1994. October 1. [Google Scholar]
- 34.Friedman JH. Greedy function approximation: a gradient boosting machine. Annals of statistics. 2001. October 1:1189–232. [Google Scholar]
- 35.Ma Z, Hu X, Huang L, Bi J, Liu Y. 2014. Estimating ground-level PM2.5 in China using satellite remote sensing. Environmental science & technology, 48(13), 7436–7444. [DOI] [PubMed] [Google Scholar]
- 36.Ni X, Cao C, Zhou Y, Cui X, Singh RP. 2018. Spatio-Temporal Pattern Estimation of PM2. 5 in Beijing-Tianjin-Hebei Region Based on MODIS AOD and 9(3), 105. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.