Topology control of human fibroblast cells monolayer by liquid crystal elastomer

Photopatterned liquid crystal elastomer templates living tissue with predesigned alignment patterns and topological defects.

Abstract

Eukaryotic cells in living tissues form dynamic patterns with spatially varying orientational order that affects important physiological processes such as apoptosis and cell migration. The challenge is how to impart a predesigned map of orientational order onto a growing tissue. Here, we demonstrate an approach to produce cell monolayers of human dermal fibroblasts with predesigned orientational patterns and topological defects using a photoaligned liquid crystal elastomer (LCE) that swells anisotropically in an aqueous medium. The patterns inscribed into the LCE are replicated by the tissue monolayer and cause a strong spatial variation of cells phenotype, their surface density, and number density fluctuations. Unbinding dynamics of defect pairs intrinsic to active matter is suppressed by anisotropic surface anchoring allowing the estimation of the elastic characteristics of the tissues. The demonstrated patterned LCE approach has potential to control the collective behavior of cells in living tissues, cell differentiation, and tissue morphogenesis.

INTRODUCTION

Living tissues formed by cells in close contact with each other often exhibit orientational order caused by mutual alignment of anisometric cells (1–4). The direction of average orientation, the so-called director $\widehat{\mathbf{n}}$, varies in space and time, producing topological defects called disclinations (5, 6). These defects move within the tissue and play an important role in compressive-dilative stresses and processes such as extraction of dead cells (5). Finding means to design a tissue scaffold for living cells with orientational order and to control the topological type and dynamics of defects is of importance in the biomedical field and for our understanding of how living matter can be manipulated. A number of research groups demonstrated a spectacular progress in production of ordered assemblies of cells at lithographically fabricated substrates (7, 8). Ordered states have been achieved for fibroblast cells near edges of microchannels (2, 3, 9), on microgrooved substrates (8, 10, 11), and on surfaces with material stiffness gradients (12, 13). Of especial interests are substrates formed by liquid crystal elastomers (LCEs), since these materials are organic and orientationally ordered (14–18).

In this work, we present an approach to design tissues with a high degree of orientational order (up to 0.96) and a predetermined spatially varying director $\widehat{\mathbf{n}}(\mathbf{r})$ templated by the director pattern ${\widehat{\mathbf{n}}}_{\text{LCE}}(\mathbf{r})$ of LCE substrates. As building units of the templated tissue, we use human dermal fibroblast (HDF) cells. Fibroblasts are the most common mammalian connective tissue cells, usually of a flat elongated shape. They play an important role in tissue repair and restructuring, in healing of wounds, and in secretion of essential components of the extracellular matrix, such as collagen and fibronectin (19). These cells can be reprogrammed into pluripotent stem cells (20), which promises applications in diagnostics and therapy. Growth of patterned HDF tissues at the LCE substrates is completed in the following simple steps. First, before polymerization, molecular orientation of the LCE precursor is patterned by the plasmonic photoalignment (21). Second, the nanoscale molecular order is fixed by ultraviolet (UV) photopolymerization of the precursor. Third, the aqueous dispersion of the cells is deposited onto the LCE substrate. Swelling in water produces anisotropic nonflat topography of the LCE that guides the alignment of elongated HDF cells once they contact the substrate. The combined effect of seeding and cell division produces a confluent tissue with pattern of HDF cells alignment that follows the predesigned pattern of LCE director.

We demonstrate that the structured LCE imposes a marked effect on the tissues, by controlling not only the alignment pattern but also the spatial distribution of cells, their density fluctuations, and even their phenotype as evidenced by different cells’ size and aspect ratio. The patterned LCE pins the locations of topological defects in tissues through anisotropic surface interactions and limits unbinding of defect pairs. The dynamics of defects in cellular monolayer at the patterned substrates is similar to the dynamics of active nematics formed by extensile units and allows us to estimate elastic and surface anchoring parameters of the tissue. The living tissues designed in our work resemble the tissues with topological defects grown by Saw et al. (5) at template-free isotropic substrates, with that difference that the defects in the LCE-patterned tissue are of a predetermined structure and appear at predetermined locations. Since the cells’ alignment patterns, topological defects in them, and even the defect cores control many important biochemical processes at microscale, such as action potential propagation (8) and apoptosis (5), our study opens the possibility to engineer platforms for the controlled patterning of tissues and their design for specific functions.

RESULTS

The LCE substrate is supported by a glass plate. To reduce surface roughness, the glass is covered with an indium tin oxide (ITO). The next layer is a photosensitive azo dye, the in-plane alignment of which is patterned by light irradiation with spatially varying linear polarization (21). This patterned azo dye layer serves as a template for the monomer diacrylate RM257 doped with 5 weight % (wt %) of photoinitiator I651 (fig. S1). After alignment through the contact with the azo dye, the monomer is UV-irradiated to photopolymerize the LCE substrate with a predesigned ${\widehat{\mathbf{n}}}_{\text{LCE}}(\mathbf{r})$. Once the substrate is covered with an aqueous cell culture medium, the LCE swells. Within ~1 min, the LCE coating develops a nonflat profile with elongated ellipsoidal grains of an average height ~50 nm and the length up to ~30 μm (Fig. 1A and figs. S2 and S3). The typical distance between the grains is in the range 1 to 10 μm (Fig. 1A). These grains serve as a guiding rail for HDF cells (movie S1); note that their dimensions are similar to the dimensions of grooves used in conventional lithography approaches (7, 8). Other polymer coatings such as polyimide PI2555 that is often used to align liquid crystals remain flat after a contact with the cell culture medium and thus cannot serve as tissue templates.

Fig. 1. Uniform alignment of HDF cells on LCE with a uniform ${\widehat{\mathbf{n}}}_{\text{LCE}}=\text{const}$.

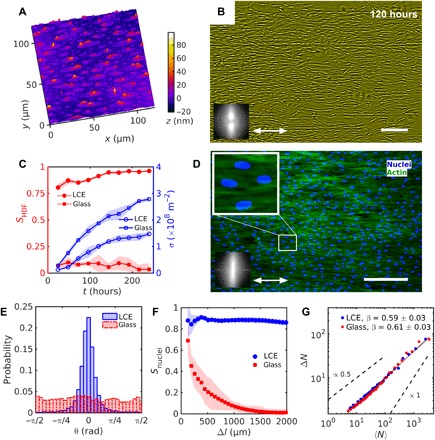
(A) Digital holographic microscopy (DHM) texture of the LCE surface after contact with the aqueous growth medium. (B) Phase contrast-microscopy (PCM) texture of HDF cells growing on LCE substrates at 120 hours after seeding. Double-headed arrow represents ${\widehat{\mathbf{n}}}_{\text{LCE}}$. (C) Evolution of the order parameter S_HDF of cells bodies (filled red symbols) and cell density σ (empty blue symbols). (D) Fluorescent microscopic textures of HDF cells on LCE; fluorescently labeled nuclei (blue) and cytoskeleton F-actin proteins (green). Magnified texture shows elongated nuclei oriented in the same direction as the cells’ bodies. Insets in (B) and (D) show fast Fourier transformation of (B) PCM and (D) fluorescent F-actin textures indicating orientational order along the uniform ${\widehat{\mathbf{n}}}_{\text{LCE}}$. (E) Distribution of nuclei orientation. (F) Dependence of the order parameter S_nuclei of nuclei on the size of a square subwindow. (G) Number density fluctuations ΔN calculated for the mean number of cell nuclei 〈N〉. Scale bars, 300 μm.

The orientational order of the elongated grains formed on a uniaxially aligned LCE, ${\widehat{\mathbf{n}}}_{\text{LCE}}=\text{const}$, is high, S_LCE = 0.95 ± 0.02, when calculated for grains of an aspect ratio (length/width) larger than 2 (see Materials and Methods). Here and in what follows, the degree of two-dimensional (2D) orientational order S and the corresponding director $\widehat{\mathbf{n}}$ of the building units of interest, such as LCE grains (S_LCE), HDF cells (S_HDF), or their elongated nuclei (S_nuclei), is calculated by using the tensor order parameter Q_ij = 2〈u_iu_j〉 − δ_ij = S(2n_in_j − δ_ij) (22), where u_i, u_j, i, j = x, y, are the components of the in-plane unit vector $\widehat{\mathbf{u}}$ that defines the long axis of an elongated unit, δ_ij is the 2 × 2 identity matrix, and 〈…〉 means averaging over all units. The maximum value of S is 1. The relatively high S_LCE is most likely associated with the strong elastic anisotropy of LCE for stretching along ${\widehat{\mathbf{n}}}_{\text{LCE}}$ and perpendicularly to ${\widehat{\mathbf{n}}}_{\text{LCE}}$ during swelling.

The HDF cells are deposited onto the LCE substrate from the aqueous cell culture. When suspended in the culture medium, the HDF cells are round. Once an HDF cell sets onto the substrate, it develops an elongated shape with the axis of elongation along ${\widehat{\mathbf{n}}}_{\text{LCE}}$. The order parameter S_HDF of HDF cells seeded on a uniaxially aligned substrate grows from 0.80 ± 0.05 to 0.96 ± 0.01 within the time interval of 24 to 168 hours after seeding, before the tissue becomes confluent (Fig. 1, B and C, and fig. S4A). To visualize the individual cells and to calculate S_HDF, we used an image intensity thresholding technique (see Materials and Methods for the details). A strong increase of S_HDF happens when the surface density of cells is in the range σ = (0.1 − 0.7)σ_c, when the cells do not contact with each other (Fig. 1C). Here, σ_c ≈ 3 × 10⁸ m⁻² is the maximum density corresponding to confluent tissue, i.e., complete coverage of the substrate by a monolayer of cells. Confluence results from the combined effect of seeding and cells division and occurs at about 240 hours after seeding.

The results on S_HDF imply that the orientational order is caused mainly by the direct interactions of each cell with the LCE substrate. In the time interval of 24 to 168 hours, the cells migrate in the plane of the substrates with the speed ~10² μm/hour (movie S1). Development of orientational order in the HDF tissues is not associated with the evolution of the grainy texture of the substrate, since the latter, after the formation period of ~1 min, does not change over at least 14 days of observations (fig. S3).

The LCE substrates align not only the bodies of HDF cells but also their elongated nuclei (Fig. 1, D and E). This feature is important since orientation and shape of the nuclei affect many cell functions, such as protein expression, motility, metabolism, phenotype, and differentiation (23). The nuclei are elongated along the same direction as the cytoskeleton (Fig. 1D) and, apparently because of that, show a high order parameter reaching S_nuclei = 0.88 ± 0.05 after 240 hours since seeding. The control ITO-glass substrates do not align cells, as there S_HDF, S_nuclei < 0.1 (Fig. 1, E and F, and fig. S4, B to D). Note here that after the cell monolayer is formed, further seeding and cell division might produce multilayered structures, but these are beyond the scope of the present study, in which the cells are fixed for fluorescent staining and analysis once the confluency is achieved.

Both aligned and unaligned assemblies of living cells exhibit high spatial fluctuations of number density (Fig. 1G), which is an attribute of out-of-equilibrium systems (24–26). In an equilibrium system, a certain area containing N objects would show fluctuations with SD ΔN proportional to N^1/2. In contrast, the aligned tissue shows ΔN that grows somewhat faster than N^1/2. To characterize the fluctuations, we followed (2, 26–28) and divided the tissue into small identical square areas and counted the number of nuclei in each of them, using fluorescent images such as the one in Fig. 1D. The calculations yield the mean number of nuclei 〈N〉 and the SD ΔN. Repeating the procedure for squares of different sizes, one obtains the dependency ΔN~〈N〉^β, with β = 0.59 ± 0.03 for the aligned tissues and a similar β = 0.61 ± 0.03 for their unaligned counterparts (Fig. 1G). Both values are close to β = 0.66 ± 0.06 measured for a misaligned array of mouse fibroblast cells (2) and higher than the equilibrium value β = 1/2.

Elongation of grains along ${\widehat{\mathbf{n}}}_{\text{LCE}}$ is caused by the anisotropy of the elastic properties of the LCE and persists when ${\widehat{\mathbf{n}}}_{\text{LCE}}$ varies in space (Fig. 2, A to C, and fig. S3). Figure 2 (B and C) clearly shows that the grains elongate along the spatially varying ${\widehat{\mathbf{n}}}_{\text{LCE}}$ even when they are very close, ~10 μm, to the cores of topological defects at which the gradients of ${\widehat{\mathbf{n}}}_{\text{LCE}}$ diverge. This wonderful feature extends the aligning ability of LCE substrates to spatially varying patterns, such as the ones with topological defects of charge m = ± 1/2, ±1,…, predesigned as

$${\widehat{\mathbf{n}}}_{\text{LCE}}=(n_x,n_y,n_z)=[\text{cos}(m\mathrm{\phi }+{\mathrm{\phi }}_0), \text{sin}(m\mathrm{\phi }+{\mathrm{\phi }}_0),0]$$ (1)

where φ = arctan (y/x) and φ₀ = const; m is a number of times the director reorients by 2π when one circumnavigates around the defect core (22). For pairs of defects of charge m₁ and m₂, separated by a distance d₀, the argument mφ in Eq. 1 is replaced by m₁ arctan [y/(x + d₀/2)] + m₂ arctan [y/(x − d₀/2)] (22) (see Supplementary Text for the explicit equations for different director patterns and fig. S5 for graphical illustration of the director field designs). The spatial variation of the LCE director ${\widehat{\mathbf{n}}}_{\text{LCE}}$ is imaged by PolScope microscopy (see Materials and Methods).

Fig. 2. Patterned alignment of HDF cells on LCE with a (−1/2,+1/2) pair of defects.

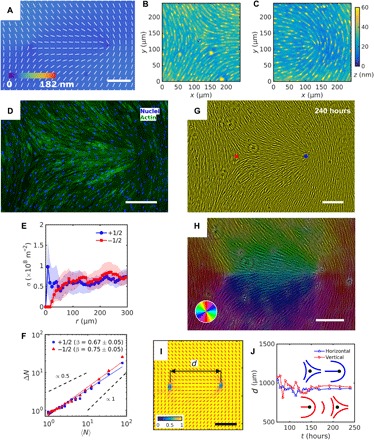
(A) PolScope texture showing ${\widehat{\mathbf{n}}}_{\text{LCE}}$ and optical retardation of LCE in contact with the cell growth medium. (B and C) DHM textures of LCE surface in contact with the cell growth medium with (B) −1/2 and (C) +1/2 defects. (D) Fluorescently stained HDF cells; 4′,6-diamidino-2-phenylindole–labeled cells nuclei (blue) and phalloidin-labeled actin cytoskeleton filaments (green). (E) The surface density of cell nuclei σ as the function of distance r from +1/2 (blue) and −1/2 (red) defect cores. (F) Large number density fluctuations ΔN of the nuclei in the vicinity of defect cores. (G) PCM images of HDF cells on LCE substrate at 240 hours after the seeding. Blue and red dots denote location of +1/2 and −1/2 defect cores, respectively, obtained from polarized optical microscopy (POM) texture of LCE. (H) Color-coded orientational field and (I) the corresponding scheme of patterned HDF tissue director ${\widehat{\mathbf{n}}}_{\text{HDF}}$ imaged with PCM. Red bars in (I) denote local orientation of cells’ long axes. (J) Separation between half-strength defects for horizontal and vertical director between them (see fig. S6). Scale bars, 300 μm.

The HDF cells self-organize into aligned assemblies that follow the preimposed director ${\widehat{\mathbf{n}}}_{\text{LCE}}(\mathbf{r})$ (Figs. 2 to 4). The orientational order of the assemblies is apolar, $\widehat{\mathbf{n}}=-\widehat{\mathbf{n}}$, as evidenced by the presence of +1/2 and −1/2 disclinations (Fig. 2). The cores of these disclinations are colocalized with the cores of disclinations in the LCE (Fig. 2, D, G, and H; figs. S5, A and B, and S6; and movie S4). The director field of cells becomes poorly defined as one approaches the defect cores (Fig. 2H) with a corresponding decrease of S_HDF (Fig. 2I), similar to the observation in (3, 6). In “wet” active nematics with momentum conservation, +1/2 and −1/2 defect pairs tend to unbind because of the high mobility of +1/2 defects (29, 30). Surface anchoring at the patterned LCE substrate prevents unbinding (Fig. 2J), thus overcoming the active and elastic forces (25). This surface anchoring prevails for relatively large separations between the defects, such as d₀ = 1 mm in Fig. 2I, but becomes comparable to elastic and active forces at shorter distances, as discussed later for the integer strength defects.

Fig. 4. Patterned alignment of HDF cells on LCE with a pair of −1 and circular +1 (bend type) defects.

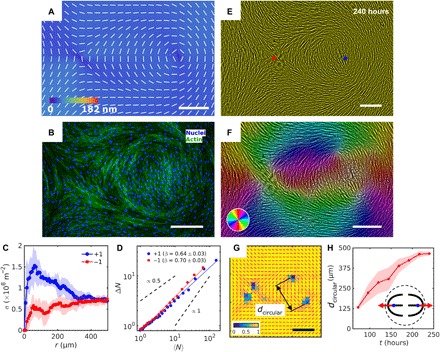
(A) PolScope image of ${\widehat{\mathbf{n}}}_{\text{LCE}}$ pattern of LCE in contact with the cell growth medium. (B) Fluorescently stained HDF cells aligned in ( − 1, + 1) circular pattern. (C) Radial dependence of the surface density of cell nuclei σ shows increase of cell density at +1 defect core. (D) Large number density fluctuations ΔN in cell nuclei calculated for increasing window size of regions with mean number of nuclei 〈N〉. −1 defects show larger slope compare to +1. (E) PCM image of HDF cells on LCE layer at 240 hours after cell seeding. Red and blue dots denote location of negative and positive sign defect cores in patterned LCE obtained from POM. (F) Color-coded orientational field and (G) of the corresponding scheme of patterned HDF tissue director ${\widehat{\mathbf{n}}}_{\text{HDF}}$ obtained from local anisotropy of the textures in (E). Red bars in (G) denote local orientation of cells’ long axes. (H) Time dependence of separation between two +1/2 defects near the +1 circular core. Scale bars, 300 μm.

The cells’ surface density σ(r) within the distance r < 60 μm from the +1/2 cores is substantially higher than near the −1/2 ones (Fig. 2E). The ±1/2 defects differ also in the characteristics of number density fluctuations. The fluctuations are stronger in the vicinity of −1/2 defects (β = 0.75 ± 0.05) as compared to +1/2 defects (β = 0.67 ± 0.05); in both cases, β is higher than the equilibrium value 1/2 (Fig. 2F). Here and in what follows, in the description of nonuniform patterns, all tissue properties, such as σ(r) and β, were determined by observing the fluorescently stained nuclei. Furthermore, β was calculated within square frames of a lateral size 800 μm, centered at the defect core.

The HDF cells alignment follows the patterned director of LCE that contains integer +1 defects of either pure splay (Fig. 3A, fig. S5C, and movie S5) or bend (Fig. 4A, fig. S5D, and movie S6). Azimuthal dependence of orientation θ of the HDF nuclei around −1 and +1 defects matches the predesigned ${\widehat{\mathbf{n}}}_{\text{LCE}}(\mathbf{r})$ (Figs. 3, B, E, and F, and 4, B, E, and F, and fig. S7) but only at some distance r > (200 to 500) μm from the preinscribed defect core in ${\widehat{\mathbf{n}}}_{\text{LCE}}$. The local cell density increases near the +1 cores (Fig. 3C). For example, at a distance 20 μm from the core, the +1 defects of a radial type show ${\mathrm{\sigma }}_{r=20 \mathrm{\mu }\mathrm{m}}^{(+1,\text{radial})}\approx 0.5\times {10}^8 {\mathrm{m}}^{-2}$, which is 1.5 times higher than the density far away from the core, at r = 300 μm, ${\mathrm{\sigma }}_{r=300 \mathrm{\mu }\mathrm{m}}^{(+1,\text{radial})}\approx 0.35\times {10}^8 {\mathrm{m}}^{-2}$ (Fig. 3C). Circular +1 defects exhibit even higher ability to concentrate cells: in Fig. 4C, ${\mathrm{\sigma }}_{r=50 \mathrm{\mu }\mathrm{m}}^{(+1,\text{circular})}\approx 1.5\times {10}^8 {\mathrm{m}}^{-2}$. In contrast, −1 defects deplete the density of the HDF cells. In Fig. 4C, ${\mathrm{\sigma }}_{r=50 \mathrm{\mu }\mathrm{m}}^{(-1,\text{circular})}\approx 0.5\times {10}^8 {\mathrm{m}}^{-2}$, which is three times lower than ${\mathrm{\sigma }}_{r=50 \mathrm{\mu }\mathrm{m}}^{(+1,\text{circular})}$ and 25 to 30% lower than the density far from the defect cores (Fig. 4C).

Fig. 3. Patterned alignment of HDF cells on LCE predesigned with a pair of −1 and radial +1 (splay type) defects.

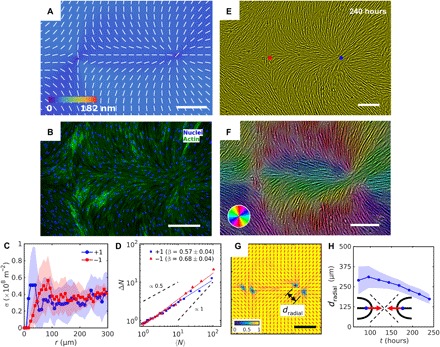
(A) PolScope image of ${\widehat{\mathbf{n}}}_{\text{LCE}}$ pattern of LCE in contact with the cell growth medium. (B) Fluorescently labeled HDF cells. (C) The surface density of cell nuclei σ as the function of distance from defect cores. (D) Large number density fluctuations ΔN with mean number of nuclei 〈N〉 showing a larger slope near −1 cores as compared to +1. (E) PCM textures of HDF cells on LCE layer at 240 hours after cell seeding. Red and blue dots denote location of −1 and +1 defects in patterned LCE obtained from crossed polarized textures. (F) Color-coded orientational field and (G) of the corresponding scheme of patterned HDF tissue director ${\widehat{\mathbf{n}}}_{\text{HDF}}$ obtained from local anisotropy of PCM texture in (E). Red bars in (G) denote local orientation of cells’ long axes. (H) Time dependence of separation between two +1/2 defects near the +1 radial core. Scale bars, 300 μm.

The LCE substrates impart a marked effect on HDF cells’ size and shapes. Since the cells are in contact with each other, the strong variations of σ’s at different LCE patterns, such as those in Fig. 4 (B, C, and E), translate into strong differences of cells’ size and shape. In Fig. 4 (B and E), the average values and their SDs, of the long (2a) and short (2b) axes of the HDF bodies approximated as ellipses, are 2〈a〉₊₁ = (68.2 ± 32.3) μm and 2〈b〉₊₁ = (26.2 ± 2.9) μm near +1 circular defect, whereas near −1 defect, the cells are significantly longer and slender, 2〈a〉₋₁ = (145.8 ± 38.6) μm and 2〈b〉₋₁ = (24.9 ± 5.1) μm. The shapes are analyzed within square frames of side length 800 μm, centered at the defect cores. The cells near the −1 defect are larger, of an average surface area 〈A〉₋₁ = 2.7 × 10³ μm² (calculated by dividing the area of 800 μm by 800 μm by the number of nuclei in it) and of a higher aspect ratio, 〈a/b〉₋₁ = 5.8 ± 2.7, as compared to their counterparts near the +1 defect, 〈A〉₊₁ = 1.8 × 10³ μm² and 〈a/b〉₊₁ = 2.6 ± 1.5 (Fig. 4, B and E, and fig. S8). These marked differences in the size and shape demonstrate that the LCE patterns influence the phenotype of HDF cells in tissues. It would be of interest to explore whether this functionality is unique to the LCEs, since Molitoris et al. (8) reported on lithographically aligned radial and circular +1 tissues but did not specified whether these patterns influenced the cells’ size or shape.

As demonstrated above in Fig. 2F, the exponent β characterizing the number density fluctuations of cells is different for the defects of charge −1/2 and +1/2. Thus, it is of interest to explore whether β depends on the particular type of deformations, splay and bend. Such a test is possible for +1 defect that can be of a splay (a radial aster) (Fig. 3D) or a bend (a circular vortex) (Fig. 4D) type. We find that the splay and bend do not produce a very strong difference in β, as β = 0.57 ± 0.04 for the radial +1 defect and β = 0.64 ± 0.03 for the circular +1 defect. In contrast, −1 defect in which splay and bend alternate produces slightly stronger fluctuations, with β = 0.68 ± 0.04 when −1 is paired with a radial +1 defect (Fig. 3D) and β = 0.70 ± 0.03 when paired with the circular +1 defect (Fig. 4D). We thus conclude that the number density fluctuations in tissues are influenced by the topological charge of the director patterns. To explore the issue in details, one would need to calculate the number fluctuations as a function of the radial distance to the defect core and the azimuthal coordinate for isolated defects of different topological charges; in these measurements, the patterned tissues should be of a much larger area than currently available.

In an equilibrium 2D nematic, the defects of an integer strength tend to split into pairs of semi-integer defects, since their elastic energy scales as ∝m² (22). Both −1 and +1 defects in the HDF tissues split into two defects of an equal semi-integer charge separated by a distance d ≈ (200 to 500) μm. Inside the region r < d, ${\widehat{\mathbf{n}}}_{\text{HDF}}$ deviates significantly from ${\widehat{\mathbf{n}}}_{\text{LCE}}(\mathbf{r})$. For the radial +1 configuration, the distance d decreases with time, as the tissue grows toward confluency, while in the circular +1 case, d increases with time (Fig. 4, F to H). These very different separation scenarios are reproducible in multiple (more than 10) samples and are reminiscent of the defect dynamics in wet active nematics with extensile units, in which the comet-like +1/2 defects move with the “head” leading the way (5, 6, 25, 31). The splitting and motion of the half-integer defects is caused by the dynamics of the cells in the tissue rather than by changes of the underlying LCE geometry: The defects in LCE show no signs of splitting beyond about 1 μm over the entire duration of the experiments (fig. S9).

DISCUSSION

The data above demonstrate that the dynamics and proliferation of defects in patterned tissues can be arrested by the surface anchoring forces. In general, topological defects in sufficiently active matter tend to unbind and disorder the system (29, 30). The prepatterned tissue demonstrates that this defect unbinding can be prevented by interactions with an anisotropic patterned substrate that establishes a finite stationary separation distance d. Consider a pair of +1/2 disclinations that split from a parent +1 disclination at the substrate patterned as a +1 radial defect, ${\widehat{\mathbf{n}}}_{\text{LCE}}=(n_r,n_{\mathrm{\phi }},n_z)=(1,0,0)$ in cylindrical coordinates. In the so-called one-constant approximation, their elastic repulsive potential is weakly dependent on d: $F_{\mathrm{E}}=-\frac{\mathrm{\pi }\mathit{Kh}}{2}\text{ln}\frac{d}{2r_{\mathrm{c}}}$, where K is the average Frank elastic modulus, h ≈ 20 μm is the thickness of the cell layer, and r_c is the size of the defect core (22). Activity, as proposed in (29, 30), contributes an additional force f_active that tends to drive +1/2 defects either toward each other (f_active < 0) in the radial geometry or away from each other (f_active > 0) in the circular geometry (Fig. 5). Since the defect splitting causes the tissue director ${\widehat{\mathbf{n}}}_{\text{HDF}}$ to differ significantly from ${\widehat{\mathbf{n}}}_{\text{LCE}}$ within an area of diameter d, the behavior of defects depends also on the surface energy penalty F_S = αWd², where α ≈ 0.2 is the numerical coefficient (see details in Materials and Methods) and W is the azimuthal surface anchoring coefficient. The stationary value of the separation distance is then defined from the balance f_active + f_elastic + f_surface = 0 of the elastic force f_elastic = − ∂F_E/∂d = πKh/(2d), surface anchoring force f_surface = − ∂F_S/∂d = − 2αWd, and active force f_active, which yields

$$d_{\mathrm{s}}=\frac{f_{\text{active}}+\sqrt{f_{\text{active}}^2+4\mathrm{\pi }\mathrm{\alpha }\mathit{hKW}}}{4\mathrm{\alpha }W}$$ (2)

Fig. 5. Schemes of defect splitting and dynamics in patterned tissue of HDF cells.

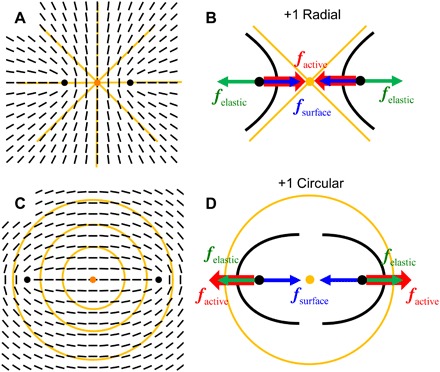
(A) A radial +1 defect in the underlying ${\widehat{\mathbf{n}}}_{\text{LCE}}$ (orange lines) and a corresponding split pair of +1/2 defects in the HDF tissue, the cells in which follow ${\widehat{\mathbf{n}}}_{\text{HDF}}$ shown as black bars. (B) Splitting of the two +1/2 defects in the radial configuration is favored by elasticity (green arrow forces) of the tissue but opposed by its surface anchoring (blue arrows) and by activity (red arrows). (C and D) Similar diagrams for a circular +1 defect; in this case, the active force assists elastic repulsion in splitting, thus producing a larger separation of the +1/2 defects.

According to Eq. 2, nonzero surface anchoring establishes a stationary finite separation of defects that is smaller in the radial geometry and larger in the circular geometry, in agreement with the experiment (Figs. 3, G and H, and 4, G and H). The difference in d_s for circular and radial geometries is caused by the opposite directionality of the active force f_active, as illustrated in Fig. 5. The experimentally determined value of this difference, Δd_s = f_active/(2αW) ≈ 350 μm, allows us to estimate f_active/W ≈ 140 μm. We also observe splitting of −1 defects. The resulting −1/2 defects can be considered in first approximation as inactive (29–31); thus, the separation distance is expected to be $d_{\mathrm{s}}=\sqrt{\mathrm{\pi }\mathit{hK}/(4\mathrm{\alpha }W)}$; in the experiment, d_s ≈ 120 μm, thus the anchoring extrapolation length of the tissue is L_anch = K/W ≈ 180 μm. Comparing this to the estimate f_active/W ≈ 140 μm, one concludes that the active force is on the order of the Frank elastic modulus of the tissue, f_active~K. Note that L_anch is comparable to the typical length of the fibroblast cell, l ≈ 100 μm, suggesting strong orientational anchoring by the LCE.

The dependence of W on system’s parameters can be estimated by considering the nonflat profile of the substrates with a typical distance between the grains being λ = 10 μm and their height u₀ = 0.1 μm (fig. S2). When a cell is aligned orthogonally to the elongated grains, it must bend around the grain. Assuming the substrate profile to be sinusoidal, u = u₀ cos (2πx/λ), the bending energy density writes $\frac{K}{2}{({\mathrm{\partial }}^{2}u/\mathrm{\partial }{x}^2)}^2$ and the surface energy per unit area as $W~4{\mathrm{\pi }}^4{\mathit{Khu}}_0^2/{\mathrm{\lambda }}^4$ (22) (see also Materials and Methods). K can be estimated using the bending modulus of fibroblast cells, $\mathrm{\kappa }=\frac{3E\mathrm{\pi }{h}^4}{64l^3}~2\times {10}^{-4} \mathrm{N}/\mathrm{m}$, where E = 10⁴ Pa (32) is the typical Young’s modulus, as K~κh~5 nN. The experimental value L_anch ≈ 180 μm then leads to W = K/L_anch~2.5 × 10⁻⁵ J/m², which is close to the theoretical expectation $W~4{\mathrm{\pi }}^4{\mathit{Khu}}_0^2/{\mathrm{\lambda }}^4~3.7\times {10}^{-5} \mathrm{J}/{\mathrm{m}}^2$.

In conclusion, we demonstrate that LCE substrates with photopatterned structure of spatially varying molecular orientation can be used to grow biological tissues with predesigned alignment of cells. Eukaryotic human tissues are designed with predetermined orientational patterns, structure, and location of topological defects in them. Besides the alignment, the substrates affect the surface density of cells, fluctuations of the number density, and the phenotype of cells as evidenced by different sizes and aspect ratios of the cells located in regions with different director deformations. In particular, higher density of cells is observed at the defect cores with positive topological charge, whereas the density is lower near the negative defects; cells are more round near positive defects and more elongated near negative defects. Anisotropic surface interactions between the tissue and the underlying LCE impose restrictions on the dynamics of topological defects in living tissues, preventing uncontrolled unbinding. The mechanism of cell alignment is rooted in swelling of the substrates upon contact with the aqueous cell culture medium; swelling produces anisotropic nonflat topography that follows the predesigned photopatterned director field of the LCE. We estimated the anchoring strength at the LCE-tissue interface and elastic modulus of the fibroblast tissue. The approach opens vast possibilities in designing biological tissues with predetermined alignment and properties of the cells, with precise location of orientational defects, which could lead to a controllable migration, differentiation, and apoptosis of cells. The proposed technique could be developed further by chemical functionalization of LCEs, by fabricating LCE substrates with dynamical topographies responsive to environmental cues, which would advance our understanding of the fundamental mechanisms underlying tissue development and regeneration. These studies are in progress.

MATERIALS AND METHODS

Substrate preparation and patterned alignment

We use ITO-coated glass slides of the rectangular shape and a size of 15 mm by 12 mm. The glass is cleaned in the ultrasonic bath of deionized water and small concentration of detergent at 65°C for 20 min. Next, we rinse the glass with deionized water and isopropanol and let it dry for 10 min, and after this, the glass is further cleaned inside the UV-ozone chamber for 15 min to remove any remaining organic contamination and improve the wettability properties. Immediately after that, the glass is spin-coated with 0.5 wt % azo dye SD-1 [synthesized following (33)] solution in dimethyl formamide, which serves as the photoaligning layer and annealed in an oven at 100 ° C for 30 min. The thickness of the azo dye layer is about 10 nm (34). For some samples, we use azo dye Brilliant Yellow (Sigma-Aldrich). Both azo dyes result in the same grain topography of LCE coatings and the same alignment quality of HDF cells. In contrast, replacement of the LCE with a polyimide PI2555 (Nissan) produced only flat topography (roughness on the order of 5 nm). We illuminate the glass with a metal-halide X-Cite 120 lamp through a linear polarizer to create uniform alignment (easy axis of alignment is perpendicular to the linear polarization of light) or through the special photomask (21), which creates high-resolution patterns of nonuniform director field. The illumination is performed for 5 min. The glass with azo dye coating is spin-coated with 6.7 wt % LC diacrylate monomer RM257 (Wilshire Technologies) and 0.35 wt % of photoinitiator I651 (Ciba Specialty Chemicals Inc.) in 93 wt % toluene and polymerize it with 365-nm UV light of a UVP-58 handheld lamp for 15 min (light intensity, 1.8 mW cm⁻²) at room temperature and ambient atmosphere. After full solvent evaporation, the concentration of photoinitiator I651 becomes 5 wt %. If the content of I651 is increased to 10 wt %, then the resulting LCE coating shows the same surface grainy topography when in contact with the cell culture medium. We calculated the thickness of the LCE layer from the average optical retardance Γ = 40 nm measured with PolScope in cells with a uniform planar director field. Since the birefringence of RM257 is about Δn ≈ 0.2 (35), the thickness of the LCE layer is Γ/Δn = 200 nm. The substrate is placed into a petri dish, additional sterilization and cleaning is done inside an UV-ozone chamber, and then the HDF cells are seeded onto the substrate and allowed to adhere, grow, and multiply on it. We also tested LCE substrates with fibronectin extracellular matrix coating (fig. S10). The fibronectin-coated substrates were prepared by immersing LCE substrates into the solution of 1 wt % fibronectin (Thermo Fisher Scientific) in deionized water and incubated for 2 hours. Fibronectin is an agent universally used for a better adhesion of HDF cells to substrates. In combination with LCE substrates, fibronectin coatings produced similar results as LCE coatings without this agent; thus, in the main text, we present the data for fibronectin-free substrates.

Cell plating

HDF cells were purchased from American Type Culture Collection (catalog no. PCS-201-010) and maintained at 37°C with 5% CO₂ and >90% humidity inside the incubator. Passages 1 to 6 are used in the experiment, and no significant difference in the behavior of different passages is recorded. Cell culture medium is composed of Dulbecco’s modified Eagle’s medium (high glucose) supplemented with 10% fetal bovine serum (FBS) (Clonetics), GlutaMAX, and penicillin/streptomycin (both from Thermo Fisher Scientific). The cells were plated at the surface density 3.3 × 10⁷ m⁻² (fixed for all experiments) onto the substrates placed in a Petri dish made of a sterilized glass [to allow for the polarized optical microscopy (POM) imaging].

Immunocytochemistry

F-actin cytoskeleton and nuclei in HDF cell cultures are immunofluorostained. Cell cultures are fixed in 4% paraformaldehyde for 20 min, permeabilized with 0.1% Triton X-100 in phosphate buffer saline (PBS) for 25 min, and nonspecific enzymatic activity was blocked with 5% FBS in PBS for 20 min. Cultures are then incubated with Alexa Fluor 488 Phalloidin (1:100 dilution, A12379, Invitrogen) for 30 min and 4′,6-diamidino-2-phenylindole (DAPI; 1:5000 dilution, D1306, Invitrogen) for 10 min.

Microscopic observation

The cells are examined under inverted phase-contrast microscopes AmScope AE2000 or Leica DH (equipped with AmScope MU-2003-BI-CK or Pixelink PL-P755CU-T cameras, pair of polarizers, and 4×/Ph0 or 10×/Ph1 objectives) without temperature and environmental control for a short period of time (not more than 5 min) every 6 or 24 hours and kept inside the incubator for rest of the time until cells reached confluency. At that point, cells’ nuclei and cytoskeleton actin filaments are stained with the fluorescent dyes (see the “Immunocytochemistry” section) and observed under the fluorescent microscope Nikon TE-2000i with sets of fluorescent cubes that allow excitation of different fluorescent dyes. The fluorescent data are recorded with an Emergent HS-20000C camera with 10× and 20× long–working distance objectives. The surface characterization is performed using atomic force microscopy (AFMWorkshop), scanning electron microscopy (Quanta 450 field emission gun environmental scanning electron microscope), and digital holographic microscopy in a reflection mode (Lyncée Tec digital holographic microscope R-1000). Imaging with the fluorescent microscope Nikon TE-2000i allows us to visualize elongated shapes of the cell nuclei and to determine S_nuclei as described below. PolScope microscopy is used for birefringent materials, such as orientationally ordered LCE, and allows one to determine the local orientation of the in-plane optic axis (which coincides with the director ${\widehat{\mathbf{n}}}_{\text{LCE}}$) and optical retardance (36). The technique is based on retardance mapping of the birefringent sample by passing a circularly polarized light through the sample and tunable liquid crystal compensator. The retardance map is reconstructed from the resulting image obtained by the microscope camera.

Image analysis

Images are processed in open-source software package Fiji/ImageJ2 (37), further analysis is performed with the custom-written code in MATLAB (MathWorks) and Mathematica (Wolfram) proprietary packages. The local cell orientation is obtained from the phase-contrast microscopy images and computed using OrientationJ Fiji/ImageJ2 plugin (38), which calculates local orientational tensor using a finite-difference intensity gradient method within the small interrogation window. The minimum window size of 20 μm was chosen to be of the order of typical isolated HDF cell width on the LCE substrates. The long-axis orientation and position of the cells’ DAPI-stained nuclei is obtained from fluorescent microscopic images. The orientation and intensity-weighted center of mass of each nucleus is calculated with Extended Particle Analyzer BioVoxxel Fiji/ImageJ2 plugin (39). Analysis of the azimuthal distribution of orientation and radial distribution of HDF cell nuclei, number density, and number density fluctuations is performed using a custom-written program in MATLAB package. Radial dependence of the surface area density σ(r) is calculated as the ratio between number of nuclei and the area of the radial annulus of width 10 μm at the given radius r from the center of defect cores in the LCE substrate.

Determination of scalar order parameters

To determine the scalar order parameter of elongated LCE grains (S_LCE), HDF cells body (S_HDF), and elongated HDF nuclei (S_nuclei), we first calculate the tensor order parameter Q_ij = 2〈u_iu_j〉 − δ_ij (22). Here, u_iu_j is the dyadic product of unit vector $\widehat{\mathbf{u}}$, with in-plane components u_i and u_j, i, j = x, y, that characterizes the orientation of axis along which an individual LCE grain, cell body, or nucleus is elongated; 〈…〉 means an averaged over all LCE grains’ (cells’ bodies or nuclei) orientations within the field of view of size w × h = 4 mm × 3 mm; δ_ij is the identity matrix. The scalar order parameter is then calculated as the maximum eigenvalue of Q_ij tensor. The distribution of local nematic order parameter in Figs. 2I, 3G, and 4G is calculated from the orientations of cells’ bodies within moving square window of the lateral size 60 μm.

Surface anchoring energy calculation

To obtain the total surface free energy of the array of HDF cells on LCE, we integrated the surface anchoring energy per unit area $\frac{W}{2}{\text{sin}}^2(\mathrm{\Delta }{\mathrm{\theta }}_{\text{HDF}})$ expressed in the Rapini-Popular form (22), where Δθ_HDF is the angle between the actual orientation of an HDF cell and the underlying director of LCE. The term sin²(Δθ_HDF) can be written as a scalar vector product $1-{({\widehat{\mathbf{n}}}_{\text{LCE}}\cdot {\widehat{\mathbf{n}}}_{\text{HDF}})}^2$ and calculated explicitly. In the polar coordinate system, within a region of radius d/2, centered at the defect

$$\begin{array}{l}{F}_{\mathrm{S}}={\displaystyle \underset{0}{\overset{2\mathrm{\pi }}{\int }}}{\displaystyle \underset{0}{\overset{d}{\int }}}\frac{W}{2}[1-{({\widehat{\mathbf{n}}}_{\text{LCE}}\cdot {\widehat{\mathbf{n}}}_{\text{HDF}})}^2]\mathit{\text{rdrd}}\mathrm{\theta }=\\ \frac{{\mathit{Wd}}^2}{32}{\displaystyle \underset{0}{\overset{2\mathrm{\pi }}{\int }}}[5-\sqrt{25-16{\text{cos}}^2\mathrm{\theta }}]d\mathrm{\theta }=\frac{{\mathit{Wd}}^2}{16}(5\mathrm{\pi }-10E(16/25))\end{array}$$

where E(m) is the complete elliptic integral of the second kind (40), which is evaluated to obtain F_S = αWd² with α = (5π − 10E(16/25))/16 ≈ 0.2.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/20/eaaz6485/DC1