Abstract
By April 7th, 2020, the Coronavirus disease 2019 (COVID-19) has infected one and a half million people worldwide, accounting for over 80 thousand of deaths in 209 countries and territories around the world. The new and fast dynamics of the pandemic are challenging the health systems of different countries. In the absence of vaccines or effective treatments, mitigation policies, such as social isolation and lock-down of cities, have been adopted, but the results vary among different countries. Some countries were able to control the disease at the moment, as is the case of South Korea. Others, like Italy, are now experiencing the peak of the pandemic. Finally, countries with emerging economies and social issues, like Brazil, are in the initial phase of the pandemic. In this work, we use mathematical models with time-dependent coefficients, techniques of inverse and forward uncertainty quantification, and sensitivity analysis to characterize essential aspects of the COVID-19 in the three countries mentioned above. The model parameters estimated for South Korea revealed effective social distancing and isolation policies, border control, and a high number in the percentage of reported cases. In contrast, underreporting of cases was estimated to be very high in Brazil and Italy. In addition, the model estimated a poor isolation policy at the moment in Brazil, with a reduction of contact around 40%, whereas Italy and South Korea estimated numbers for contact reduction are at 75% and 90%, respectively. This characterization of the COVID-19, in these different countries under different scenarios and phases of the pandemic, supports the importance of mitigation policies, such as social distancing. In addition, it raises serious concerns for socially and economically fragile countries, where underreporting poses additional challenges to the management of the COVID-19 pandemic by significantly increasing the uncertainties regarding its dynamics.
Keywords: COVID-19, Epidemiology, Mathematical modeling, Uncertainty quantification, Sensitivity analysis
1. Introduction
On December 31th, 2019, China reported an outbreak of novel pneumonia in which the causative agent was identified on January 7th as SARS-CoV-2. The new disease was called COVID-19 (short for Corona Virus Disease 2019) by the World Health Organization (WHO) [1]. One month after the first notification, WHO declared COVID-19 as a world public health emergency and on March 11th as a pandemic situation [2]. By April 7th, there were 1,418,730 people infected and 81,497 deaths in 209 countries and territories around the world and 2 international conveyances [3].
Although there are vaccine candidates for COVID-19 under exploratory or preclinical stages, they will not be available before 2021 [4]. Moreover, no antiviral has yet demonstrated efficacy and more clinical trials are necessary [5], [6], [7], [8]. Due to the lack of pharmaceutical treatments, non-pharmaceutical interventions have been proposed by many countries to deal with the pandemic, more specifically to reduce transmission and the impact on healthcare systems [9], [10], [11], [12], [13], [14], [15]. Besides, WHO has recommended massively testing of the population and due to the great demand for diagnostic tests to COVID-19 all over the world, the high demand for tests has become an issue and increases the underreporting of the cases [16].
As we write this paper, some countries managed to control the disease. Others are now experiencing the peak of the pandemic. And some countries are in the initial phase of the pandemic. South Korea had the first case entering the country on 20 January and after the initial outbreak was able to dramatically slow the spread of the disease, flattening the pandemic curve [3], [17]. Italy is one of the countries that has reported a large number of deaths related to the COVID-19 at more than 13,000. In Brazil the pandemic is in its early stages with the first case of infection reported on February 26th, 2020. One month after the first confirmed case in Brazil, 3904 cases and 114 deaths have already been registered [18].
This work proposes the use of a simple mathematical model, based on the classical SIRD model, with a reduced number of parameters, to characterize essential aspects of the COVID-19 in the three countries, Brazil, Italy, and Korea, which are examples of very different scenarios and stages of the COVID-19 pandemic. Other papers found in the literature have proposed more compartments in their models (like exposed, asymptomatic, and many others) [19], [20], [21], [22], [23], [24]. Here, we decided to keep the model as simple as possible, since adding more compartments increases the number of unknown parameters to be estimated, which in turn hinders the accurate calibration of the model. In addition, to face the fast dynamics of COVID-19 pandemic, the model includes time-dependent coefficients.
The characterization of COVID-19 in the three countries is performed using the technique of inverse uncertainty quantification (UQ). Therefore, during the calibration of the models, the coefficients are treated as unknown probability density functions (PDFs). Once estimated, the PDFs of the coefficients, their means, standard deviations (SD), and shape provide important information on model parameters that are essential in the characterization of the COVID-19 pandemic. After the inverse UQ, we observed that different PDFs of the model coefficients were needed to explain the distinct dynamics of the COVID-19 in the three countries. In summary, the methods proposed in this work assist in the development of specific models for each country and in the quantification of the level of uncertainties present in the model parameters and results.
Despite its simplicity, the proposed model incorporates new features that are important for decisions on intervention policies: parameters to characterize the reduction of contact, in response to mitigation policies, the effectiveness of border control, the percentage of positive cases that are reported, and the delay between the infection and the result of COVID-19 tests that confirm the disease.
2. Methods
2.1. Mathematical model
Several mathematical models have been proposed to represent the dynamics of populations and their interactions and forecast the dynamics of the COVID-19 pandemic [19], [20], [21], [22], [23], [24]. Most of them describe the spread of COVID-19 based on SIR (Susceptible, Infected and Recovered) or SEIR (Susceptible, Exposed, Infected, and Recovered) modifications. For example, Giordano et al. [25] extended the SIR model partitioning the population in eight stages, Prem et al. [26] used an age-structured SEIR model, and stochastic models have also been used [27].
In this work, the mathematical model proposed is a non-linear system of ordinary differential equations (ODE) [28], [29], [30], based on the classic compartmental SIRD model [31], [32], [33]. We decided to keep the model as simple as possible since adding more compartments increases the number of unknown parameters to be estimated, which in turn hinders the accurate calibration of the model. In addition, to face the fast dynamics of the COVID-19 pandemic, the model includes time-dependent coefficients. The model is described by the following equations:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where S, I, R, D, and Ir are the variables that represent the number of individuals within a population of size N that are susceptible, infected, recovered, dead, or that are reported as infected, respectively. The term denotes the rate at which a susceptible individual becomes infected; where a(t) denotes the probability of contact and b the rate of infection. The function a(t) models the non-pharmaceutical interventions adopted to contain the spread of the virus:
| (6) |
This is a simple approach that assumes the intervention for containing the spread of the virus start to be implemented at ti and at the final time it reduces the probability of contact by a factor r. The constant models the mortality rate of infected individuals, where m is the probability of death. Note that this is different to the rate of death and to the percentage of death among the reported cases of positive infection (Ir). is the number of days from infection until death, where τ 1 is the incubation time of the virus and τ 2 is the time between the first symptoms until death. Similarly, where τ 3 is the time between the first symptoms until recovery. The constant is the rate at which infected individuals recover from the virus, where τr is the number of days from infection until recovery. The function represents a positive influx of infected individuals coming from other countries, where P(t) is the number of infected individuals in the world, and was modeled as an exponential function of the form where c 0 and c 1 are coefficients determined from reported data. The parameter e models how the COVID-19 worldwide dynamics affects the country. Small values of e suggest that border controls are effective. Finally, θ represents the percentage of confirmed infected individuals that are notified or reported. Observe that is used to model the delay between the first day of infection and the notification day for the cases that are reported (Ir).
2.2. Model calibration and uncertainty quantification
The parameters related to COVID-19 dynamics are based on data reported in the available literature and reports of the epidemic in other locations experiencing more advanced stages of the spread of the disease [3], [18], [30], [34], [35], [36]. The values and ranges for the model parameters are shown in Table A.1 in the Appendix.
Table A.1.
Baseline data used for the calibration of the parameters of the proposed COVID-19 model.
| Name | Meaning (units) | Interval | Ref. |
|---|---|---|---|
| b | Transmission rate (1/day) | [35] | |
| θ | Fraction of notified cases (−) | [0,1] | – |
| r | Contact reduction (−) | [0,1] | – |
| ti | Start of intervention policy (day) | a | – |
| Δ | Duration of intervention policy (day) | [2,30] | – |
| m | Death probability (−) | [1%, 3.4%] | [47] |
| τ1 | Incubation period (day) | [2,14] | [30] |
| τ2 | Period from symptoms to death (day) | [6,22] | [3] |
| τ3 | Period from symptoms to recovery (day) | [7,17] | [3] |
| e | Border restrictions (−) | – |
The upper bound for ti is 14 days before the end of the simulation.
Model parameters were adjusted using the differential evolution (DE) optimization method implemented in the Python programming language [37], [38]. The differential evolution was used to estimate each of the parameters of the proposed mathematical model, respecting the limits established for each one of them (see Table A.1 in the Appendix). The parameter values were estimated based on official data from the epidemic reported in each country (S. Korea, Italy and Brazil), where and are the reported numbers of infected people, and the number of deaths, respectively. To this end, the following objective function was used to minimize the relative error between the data and the model:
| (7) |
where p is the set of parameters to be estimated.
Inverse UQ techniques are used to estimate the PDFs and corresponding uncertainties of the input parameters or coefficients of the model during model calibration [39]. In this work, for each parameter of the model, we estimated its PDF from the fitting procedure using the DE method. Among all candidates generated by the DE during the fitting process, we selected 15% of the individuals with the best fitness values. From these samples, the marginal distribution of each model parameter, the covariance matrix, and correlation coefficients were estimated. These data were used to perform a forward UQ analysis via the Monte Carlo method with a total of 10,000 samples using the ChaosPy library [40].
Forward UQ techniques determine how uncertainties in the input parameters of the model impact its outputs. Using the UQ technique, the model can be viewed as a mapping from input parameters treated as continuous random variables described by a probability density function to stochastic responses. One of the most used methods to perform uncertainty propagation is the Monte Carlo method, which draws samples of the input parameters and evaluates the model using them to provide statistical properties for the quantities of interest[41].
In addition, a sensitivity analysis (SA) was performed via main Sobol indices [42] using SALib [43]. These indices support the process of identifying the parameters of the model that most affect the outputs, Y, predicted by the model. The main Sobol index of the parameter pi, is the ratio between the variance of Y when only the input parameter pi is fixed and the total variance of Y when all the parameters are allowed to vary. A high value of indicates that the outputs of the models are very sensitive to pi.
3. Results and discussion
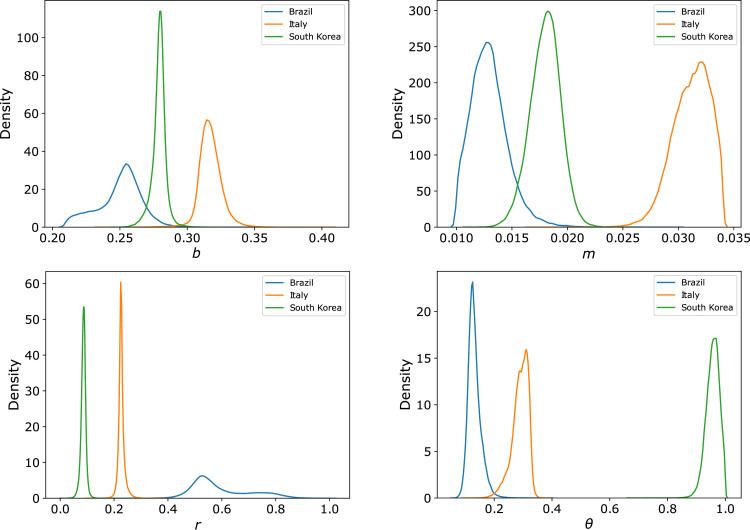
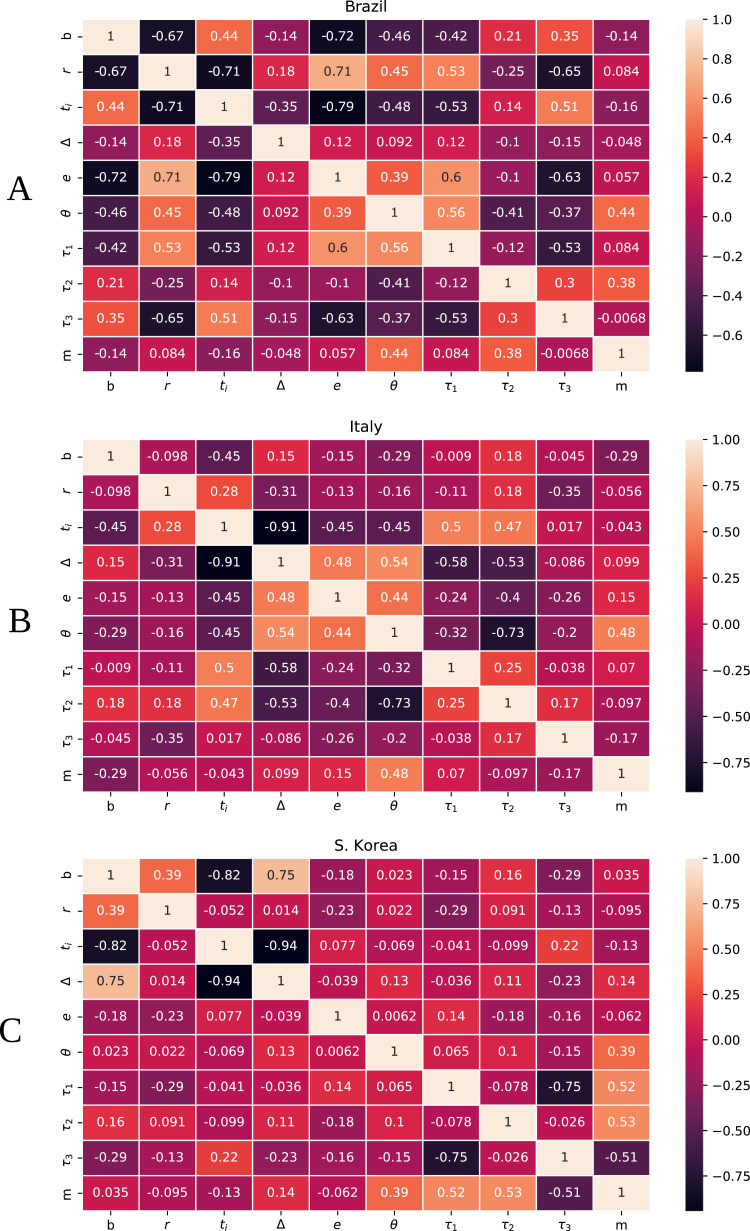
A summary of the results of the inverse UQ analysis is presented in Table A.2 in the Appendix. This table presents the mean and standard deviation (SD) of the estimated probability density functions of the parameters for the three countries. Fig. 1 presents four examples of the estimated PDFs for parameters b, m, r and θ, comparing results among the three different countries. Fig. B.3 in the Appendix also presents the Pearson’s correlation coefficients of the estimated parameters.
Table A.2.
Characterization of the COVID-19 pandemic in terms of model parameters: b is the COVID-19 transmission rate; m death probability; r contact reduction; ti start of intervention policy; Δ duration of intervention policy; τ1 incubation period; τ2 period from symptoms to death; τ3 period from symptoms to recovery; e effect of border restrictions; θ fraction of notified cases; and N the population.
| Name | Brazil |
Italy |
S. Korea |
|||
|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | |
| b | ||||||
| m | ||||||
| r | ||||||
| ti | 1.76 × 101 | 5.80 × 100 | 4.43 × 100 | 1.62 × 100 | 1.72 × 101 | 1.15 × 100 |
| Δ | 2.05 × 101 | 5.68 × 100 | 2.86 × 101 | 1.19 × 100 | 2.33 × 101 | |
| τ1 | 3.32 × 100 | 1.21 × 100 | 3.88 × 100 | 5.34 × 100 | 1.25 × 100 | |
| τ2 | 1.28 × 101 | 2.15 × 100 | 6.91 × 100 | 2.00 × 101 | 1.25 × 100 | |
| τ3 | 1.44 × 101 | 2.25 × 100 | 1.38 × 101 | 1.15 × 101 | 1.22 × 100 | |
| e | ||||||
| θ | ||||||
| N | 2.09 × 108 | – | 6.05 × 107 | – | 5.15 × 107 | – |
Fig. 1.
Probability density functions obtained for the parameters: transmission rate (b), death probability (m), contact reduction (r) and fraction of notified cases (θ) of the proposed COVID-19 model.
Fig. B.3.
Matrix of Pearson’s correlation coefficients between model parameters for (A) Brazil, (B) Italy, and (C) South Korea.
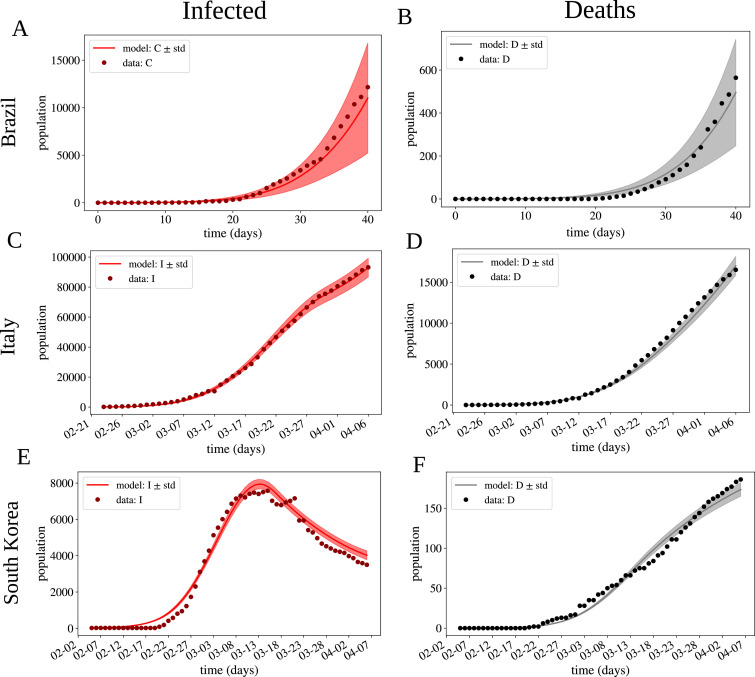
Once the PDFs of the parameters of the model have been estimated, the forward UQ analysis was performed. Fig. 2 compares the results of the fitted models to the original data for each country. For each time t, Ir(t) and D(t) are also PDFs, in response to the process of forward uncertainty quantification. It should be noted that the same model, with different parameters, was able to reproduce the very distinct scenarios of the COVID-19 pandemic in Brazil, Italy, and S. Korea. Analyzing the results of the forward UQ, we note that the uncertainties of the simulations increase in the following order, S. Korea, Italy and Brazil. This order correlates with the estimated parameter θ, that models the notification of positive cases, and with the phase of the COVID-19 pandemic in each country. Therefore, earlier phases pose more challenges and uncertainties to the modeling of the pandemic, as well as the underreporting of cases.
Fig. 2.
Simulation results for Italy, S. Korea and Brazil. (A,C,E) Number of infected people who were notified over days. (B,D,F) Number of deaths over the days. The solid lines indicate the expected value, shaded regions the ± standard deviation (SD) region, while the dots are the data from the literature [44]. Italy and S. Korea were fitted using the active case data, and Brazil the confirmed case data.
Due to the descriptive nature of the model, the analysis of the estimated parameters allows the identification of important characteristics of the phenomena. For instance, we observed that the transmission rate, b, is higher in Italy (0.37) than in S. Korea (0.28), see Fig. 1. For Brazil, the PDF of b has the highest variance, which suggests high levels of uncertainties for the estimation of this parameter in this country, at this initial stage. The percentage of mortality, m, is also higher in Italy (3.1%) than in S. Korea (1.8%). Brazil has once again a large SD, with estimated values for m between 1% and 2%. This characterization reflects the different scenarios between Italy and S. Korea. A fast spread of the virus in Italy, and a possible collapse of the health system corroborate with the highest estimated values for both b and m.
Concerning the non-pharmaceutical interventions adopted by the countries, there are also interesting differences. S. Korea has rapidly adopted an effective isolation strategy of infected individuals during the initial stage of the epidemic, followed by social distance and lock-down policies. This was well characterized by the model via the parameter r, which models the reduction of transmission. For the case of S. Korea, r was as low as 9% (which would correspond to 91% of the population respecting social distancing). For Brazil, a poor reduction of transmission was observed, with r as high as 60% (or only 40% at social isolation). And in this case, even considering the high uncertainties revealed by the large variance of this PDF, see Fig. 1, the values of r in Brazil are much higher than those of Italy, which are higher than those of S. Korea. For S. Korea, the estimated parameter e, which reflects the reduction in the influx of infected people from outside the country, was also the lowest one, near see Table A.2 in the Appendix, when compared to the values of Italy and Brazil, around . The above characterization, via parameter estimation, and comparison of distinct scenarios suggest that mitigation policies and border control are effective strategies to control the dynamics of the COVID-19 pandemic.
The parameter that models the notification of cases also varied among the different countries. The estimation of notification of infected cases in S. Korea is very high, around 95%, while in Brazil and Italy the notification is around 10% and 30%, respectively. Therefore, the number of infected cases (I) in these two countries is between 3 to 10 times the number of reported cases (Ir). These differences on percentage of notification correlates with the different dynamics observed so far in these three countries. Indeed, S. Korea has successfully tested its population and is an example of less underreported cases [45], furthermore it is also an example of a country that has decreased the infection curve [3]. This suggests that the underestimation of cases complicates the management of the pandemic, adds greater uncertainties regarding its dynamics, and poses additional challenges for controlling the pandemic.
The correlations between the estimated parameters are presented in Appendix B and Fig. B.3. In S. Korea we observe interesting negative correlations between b and Δ, the transmission rate and the time interval for the social response to mitigation policies, and ti, the start of the mitigation policies. This means that for higher transmission rates and higher delays for social response, the initial day of mitigation policies needs to be earlier. For Italy, the strong negative correlations between τ 2 and θ, and τ 1 and Δ are less intuitive. Since the mortality rate is inversely proportional to τ 2, a decrease in τ 2 increases the ratio between the number of dead and infected individuals. However, data reflects the ratio between dead and reported infected individuals. Therefore, to reestablish the fraction observed in the data, the value of θ needs to be increased. The negative correlation between τ 1 and Δ can be interpreted by the delay for reporting positive cases, . Large delays for notification (high values of τ 1) demands fast social response to the mitigation policies, i.e., small values for Δ. In Brazil, the same interpretations above for Italy explains the strong positive correlations between θ and Δ, τ 1 and ti, m and θ, and τ 1 and θ. These correlations reveal the importance of the model for the reported infected cases, Ir, which plays extremely important roles in describing the dynamics in Italy and Brazil.
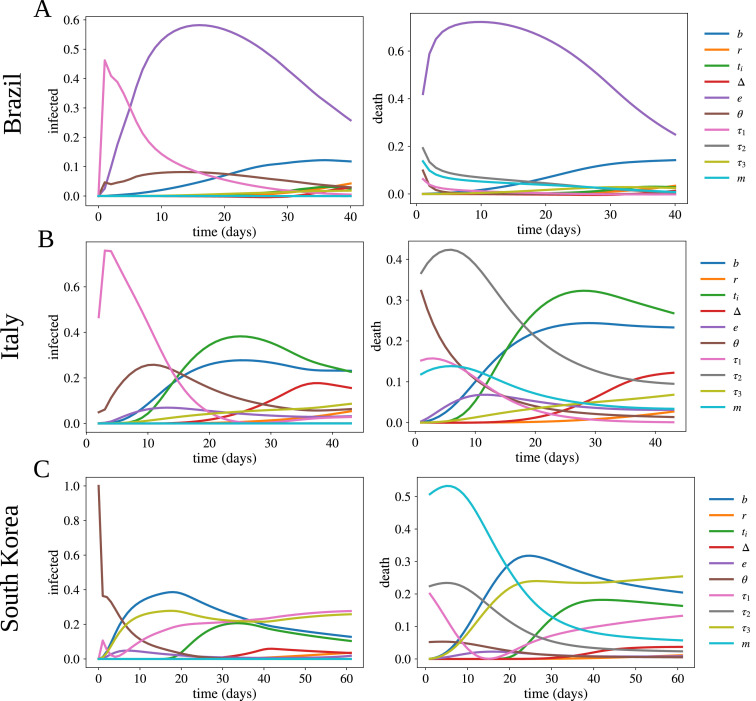
The results of the sensitivity analysis using the main Sobol indices, which represent the direct effects of an input parameter in the variance of an output quantity, are reported in Appendix C and Fig. C.4 . Among the three countries, Brazil has the largest estimated value for underreported cases (see Table A.2) and this is reflected in the sensitivity analysis, where θ plays an important role for infection in Panel C.4 A. Although Brazil has the weakest social distancing policy among these countries, the parameter for border control, e, plays an important role as revealed by the sensitivity analysis (see Panel C.4 A). Finally, for Brazil and Italy, the incubation period (τ 1) plays the main role in the initial period of the simulation, unlike S. Korea. This reflects how the reported cases are sensitive to delays for the results of the tests, in countries where underreporting is an issue.
Fig. C.4.
Main Sobol sensitivity indices for I and D, as a function of time, of the proposed model for all the cases studied here.
3.1. Limitation and future works
The mathematical model adopted highlights the importance of time-dependent parameters for the correct characterization of the fast dynamics of the COVID-19 pandemic. For simplicity, we have used only two time dependent parameters, a(t), to model the mitigation policies, and f(t) to capture the influx of infected individuals.
In this work, the contact reduction, a(t), was modeled as a linear function that decays from 1 to r. After Δ days, a(t) remains constant at r. It is a simplification, where we only consider a single intervention in terms of restriction policy. Nevertheless, this single intervention was enough to recover the very distinct dynamics observed in the three countries. Multiple phases of social distancing policies could be implemented in future works. Also, other time-dependent functions could be used for a(t), instead of a linear one, such as the exponential decay used in Fanelli and Piazza [23].
For describing the influx of infected individuals the function was adopted, where P(t) was described by an exponential: . The exponential function was chosen to simplify the implementation. This function could be easily replaced by another one with a distinct shape, such as a simple interpolation of the active cases in the world. Different from the contact reduction, a(t), the border restriction was modeled as a single time-independent parameter, e, i.e., the border restriction has an immediate impact. A time-dependent parameter for border restrictions (e(t)) may be more suitable to represent distinct scenarios and could be easily implemented in future work.
Other time-dependent parameters should be considered in the near future. For instance, with the current availability of fast kits for testing [46], the percentage of notification is likely to increase with time, θ(t). Likewise, clinical studies of new potential treatments [4], [6], [7], [8], will also affect other parameters of the model.
Finally, mathematical models have been used for both the characterization of important parameters that determine the dynamics of the COVID-19 pandemic and for forecasting and analysis of projections of different scenarios. In this work, we have focused on the fine characterization of the COVID-19 pandemic using UQ and SA methods and comparing the developed framework for the characterization of the pandemic in three different countries on very distinct stages of the pandemic. In the near future, we will extend this framework and apply it to studies that involve forecasts and projections.
4. Conclusions
A new mathematical model, based on a system of ODEs, was used to capture the dynamics of COVID-19 in countries that are at distinct stages of the pandemic: S. Korea, Italy, and Brazil. The model adopts time-dependent coefficients to follow the fast dynamics of the COVID-19 pandemics and decisions concerning mitigation policies. In addition, inverse UQ and SA were used for the proper estimation of the coefficients of the models as probability density functions, and their impact on the dynamics of the pandemic, respectively. Other novel features of the model include: (1) A variable that models the reported infected population, where θ is the percentage of reported case, and delay models the time from the day of infection to the conclusion of the test for COVID-19; (2) a model for the reduction of contact, isolation, or social distancing; and (3) a parameter that represents the effectiveness of the border control. The proposed model was used to analyze three countries at different stages of the pandemic with different intervention policies. The proposed framework helped the unique characterization of the pandemic in each country. This fine characterization of the dynamics may support authorities in important questions such as decisions on stronger or weaker social isolation, border restriction policies, as well as on the estimation of the real number of infected cases.
Forward and inverse UQ provided a rigorous analysis of the uncertainties in the parameters and the model simulation results. In addition, the computation of the correlation between the parameters of the model, together with a sensitivity analysis revealed important and unique characteristics of the dynamics of COVID-19 in the three different countries. Of notice, all the novel features of the model mentioned above played essential roles in the characterization of the pandemic.
Our results, based on data collected until April 6, suggest that the percentage of deaths among infected patients (which is different from the estimation made using the notification of infected cases) in Brazil is around 1.5% and is closer to S. Korea than to Italy, 3.1%. The notification of infected cases in S. Korea is estimated to be high, around 95%, while in Brazil and Italy, the notifications are very low, around 10% and 23%, respectively. The simulations have confirmed that S. Korea adopted very effective mitigation strategies: the virus transmission dropped to 9% of its initial value. On the other hand, Brazil only reduced their transmission rates to 60% and Italy to 23%. The number of infected people in S. Korea has been declining for almost a month. Therefore, the simulations performed in this study suggest that non-pharmaceutical interventions are decisive in fighting against the COVID-19 pandemic, and underreporting challenges the management of the pandemic by adding significant uncertainties in the characterization of the COVID-19 dynamics. The results also highlight a delicate situation for Brazil. Our estimation of the product r b, i.e., the transmission rate reduced by the mitigation policies, is 0.15, 0.07, and 0.02 for Brazil, Italy, and S. Korea, respectively. An effective transmission rate that is twice the one observed in Italy and notification of cases as low as 10% may pose additional challenges to the control of the COVID-19 pandemic in Brazil.
Data accessibility
Code to reproduce the results is available at https://github.com/FISIOCOMP-UFJF/ChaosSolitonsFractals-10-04-2020.
CRediT authorship contribution statement
Ruy Freitas Reis: Software, Methodology, Formal analysis, Writing - original draft, Writing - review & editing. Bárbara de Melo Quintela: Formal analysis, Writing - original draft, Writing - review & editing. Joventino de Oliveira Campos: Software, Formal analysis, Writing - original draft, Writing - review & editing. Johnny Moreira Gomes: Formal analysis, Writing - original draft, Writing - review & editing. Bernardo Martins Rocha: Software, Methodology, Formal analysis, Writing - original draft, Writing - review & editing. Marcelo Lobosco: Methodology, Formal analysis, Writing - original draft, Writing - review & editing. Rodrigo Weber dos Santos: Conceptualization, Methodology, Formal analysis, Writing - original draft, Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors would like to thank the researchers Guilherme Côrtes Fernandes, Thaiz Ruberti Schmal and Luis Paulo da Silva Barra for the motivating discussions that improved the quality of this work. This work was partially supported by CNPq, UFJF, and CEFET-MG.
Appendix A. Parameter estimation
For fitting the model we use the data reported in scientific literature by the Center for Systems Science and Engineering at Johns Hopkins University [36], between 01/22/2020 and 04/06/2020. Furthermore, the parameter bounds are described in Table A.1. Table A.2 shows the mean and standard deviation of all offspring solution with less than 15% of error.
Appendix B. Correlation of the parameters
The Pearson’s correlation coefficients was evaluated for all model parameters an are presented in Fig. B.3.
The correlations between the estimated parameters reveals that two significant positive correlations can be observed for S. Korea: the correlations between τ 1 and τ 2 vs. m. This is expected, since models the mortality rate of infected individuals. The observed significant negative correlations between τ 3 and m vs. τ 1 are also expected since the recovery rate . More interesting negative correlations were observed between b and δ, the transmission rate and the time interval for the social response to mitigation policies, and ti, the start of the mitigation policies. This means that for higher transmission rates and higher delays for social response, the initial day of mitigation policies needs to be earlier.
The same negative correlations between b and δ vs. ti were observed for Italy. The strong negative correlations between τ 2 and θ, and τ 1 and Δ are less intuitive. Since the mortality rate is inversely proportional to τ 2, a decrease in τ 2 increases the ratio between the number of dead and infected persons. However, data reflects the ratio between dead and reported infected individuals. Therefore, to reestablish the fraction observed in the data, the value of θ needs to be increased. The negative correlation between τ 1 and Δ can be interpreted by the delay for reporting positive cases, . Large delays for notification (high values of τ 1) demands fast social response to the mitigation policies, i.e., small values for Δ. The same interpretation explains the strong positive correlation between θ and Δ, and τ 1 and ti, see Fig. B.3 in Appendix.
Similar strong correlations described for S. Korea and Italy were observed in Brazil. In addition, strong positive correlations are present between m, and τ 1 vs. θ. The explanation for these intriguing correlations follows the one given for the correlation between τ 2 and θ for Italy. These correlations reveal the importance of the model for the reported infected cases, Ir, which plays extremely important roles in describing the dynamics in Italy and Brazil.
Appendix C. Sensitivity analysis
The results of the sensitivity analysis using the main Sobol indices, which represent the direct effects of an input parameter in the variance of an output quantity, are reported in Fig. C.4. The transmission rate (b) is a very sensitive parameter for all simulated scenarios. Among these three countries, Brazil has the largest estimated value for underreported cases (see Table A.2). This is also reflected in the sensitivity analysis, where θ plays an important role for infection (see Panel C.4 A). Although Brazil has the weakest social distancing policy among these countries, the parameter for border control, e, plays an important role as revealed by the sensitivity analysis (see Panel C.4 A). For the three countries, the mortality rate (m) and the period from the first symptoms to death (τ 2) play a key role in the entire dynamics of deaths (see death in Fig. C.4). However, for S. Korea, m decreases its sensitivity significantly along time since the number of active cases is also declining. Finally, for Brazil and Italy, the incubation period (τ 1) has played a main role in the initial period of the simulation, unlike S. Korea. This reflects how the reported cases are sensitive to delays in the results of the tests, in countries where underreporting is an issue.
References
- 1.Sohrabi C., Alsafi Z., O’Neill N., Khan M., Kerwan A., Al-Jabir A. World Health Organization declares global emergency: a review of the 2019 novel coronavirus (COVID-19) Int J Surg. 2020;76:71–76. doi: 10.1016/j.ijsu.2020.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.World Health Organization. Virtual press conference on COVID-19 - 11 March 2020. https://www.who.int/docs/default-source/coronaviruse/transcripts/who-audio-emergencies-coronavirus-press-conference-full-and-final-11mar2020.pdf; 2020a. Last accesses on March 24 of 2020.
- 3.Worldometers. COVID-19 coronavirus pandemic. 2020. Last accesses on April 7 of 2020, https://www.worldometers.info/coronavirus/..
- 4.Le T.T., Andreadakis Z., Kumar A., Romn R.G., Tollefsen S., Saville M., Mayhew S. The COVID-19 vaccine development landscape. Nature Reviews Drug Discovery. 2020 doi: 10.1038/d41573-020-00073-5. [DOI] [PubMed] [Google Scholar]; Publisher: Nature Publishing Group
- 5.Zhou Y., Hou Y., Shen J., Huang Y., Martin W., Cheng F. Network-based drug repurposing for novel coronavirus 2019-nCoV/SARS-CoV-2. Cell Discov. 2020;6(1):14. doi: 10.1038/s41421-020-0153-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dong L., Hu S., Gao J. Discovering drugs to treat coronavirus disease 2019 (COVID-19) Drug Discov Ther. 2020;14(1):58–60. doi: 10.5582/ddt.2020.01012. [DOI] [PubMed] [Google Scholar]
- 7.Baden L.R., Rubin E.J. COVID-19 – The Search for Effective Therapy. New England Journal of Medicine. 2020 doi: 10.1056/NEJMe2005477. [DOI] [PMC free article] [PubMed] [Google Scholar]; Publisher: Massachusetts Medical Society
- 8.Duan K. Effectiveness of convalescent plasma therapy in severe COVID-19 patients. Proc Natl Acad Sci. 2020 doi: 10.1073/pnas.2004168117. [DOI] [PMC free article] [PubMed] [Google Scholar]; Publisher: National Academy of Sciences Section: Biological Sciences
- 9.Ferguson N. Report. Imperial College London; 2020. Report 9: impact of non-pharmaceutical interventions (NPIs) to reduce COVID19 mortality and healthcare demand. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wilder-Smith A., Freedman D.O. Isolation, quarantine, social distancing and community containment: pivotal role for old-style public health measures in the novel coronavirus (2019-nCoV) outbreak. J Travel Med. 2020;27(2) doi: 10.1093/jtm/taaa020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wilder-Smith A., Chiew C.J., Lee V.J. Can we contain the COVID-19 outbreak with the same measures as for SARS? The Lancet Infect Dis. 2020 doi: 10.1016/S1473-3099(20)30129-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lee V.J., Chiew C.J., Khong W.X. Interrupting transmission of COVID-19: lessons from containment efforts in Singapore. J Travel Med. 2020 doi: 10.1093/jtm/taaa039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Li Q. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus–Infected Pneumonia. New England Journal of Medicine. 2020 doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]; Publisher: Massachusetts Medical Society
- 14.Heymann D.L., Shindo N. COVID-19: what is next for public health? Lancet. 2020;395(10224):542–545. doi: 10.1016/S0140-6736(20)30374-3. [DOI] [PMC free article] [PubMed] [Google Scholar]; Publisher: Elsevier
- 15.Chinazzi M., Davis J.T., Ajelli M., Gioannini C., Litvinova M., Merler S., Piontti A.P.y., Mu K., Rossi L., Sun K., Viboud C., Xiong X., Yu H., Halloran M.E., Longini I.M., Vespignani A. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science. 2020 doi: 10.1126/science.aba9757. [DOI] [PMC free article] [PubMed] [Google Scholar]; Publisher: American Association for the Advancement of Science Section: Research Article
- 16.Organization W.H.. WHO director-general’s opening remarks at the media briefing on COVID-19 - 3 March 2020. https://www.who.int/dg/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19---16-march-2020; 2020b. Last accesses on March 24 of 2020.
- 17.Lim J. Case of the index patient who caused tertiary transmission of coronavirus disease 2019 in Korea: the application of lopinavir/ritonavir for the treatment of COVID-19 pneumonia monitored by quantitative RT-PCR. J Korean Med Sci. 2020;35(6) doi: 10.3346/jkms.2020.35.e79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ministério da Saúde G.d. B.. Painel do surto de vírus COVID-19 no brasil. 2020. Last accesses on April 7 of 2020; https://covid.saude.gov.br/.
- 19.Anderson R.M., Heesterbeek H., Klinkenberg D., Hollingsworth T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet. 2020;395(10228):931–934. doi: 10.1016/S0140-6736(20)30567-5. [DOI] [PMC free article] [PubMed] [Google Scholar]; Publisher: Elsevier
- 20.Remuzzi A., Remuzzi G. COVID-19 and Italy: what next? Lancet. 2020;395(10231) doi: 10.1016/S0140-6736(20)30627-9. [DOI] [PMC free article] [PubMed] [Google Scholar]; Publisher: Elsevier
- 21.Roosa K., Lee Y., Luo R., Kirpich A., Rothenberg R., Hyman J.M., Yan P., Chowell G. Real-time forecasts of the COVID-19 epidemic in China from February 5th to February 24th, 2020. Infect Dis Model. 2020;5:256–263. doi: 10.1016/j.idm.2020.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Grasselli G., Pesenti A., Cecconi M. Critical care utilization for the COVID-19 outbreak in Lombardy, Italy: early experience and forecast during an emergency response. JAMA. 2020 doi: 10.1001/jama.2020.4031. [DOI] [PubMed] [Google Scholar]
- 23.Fanelli D., Piazza F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos Solitons Fractals. 2020;134:109761. doi: 10.1016/j.chaos.2020.109761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Roosa K., Lee Y., Luo R., Kirpich A., Rothenberg R., Hyman J.M., Yan P., Chowell G. Short-term Forecasts of the COVID-19Epidemic in Guangdong and Zhejiang, China: February 13–23, 2020. Journal of Clinical Medicine. 2020;9(2):596. doi: 10.3390/jcm9020596. [DOI] [PMC free article] [PubMed] [Google Scholar]; Number: 2 Publisher: Multidisciplinary Digital Publishing Institute
- 25.Giordano G., Blanchini F., Bruno R., Colaneri P., Di Filippo A., Di Matteo A., Colaneri M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nature Medicine. 2020:1–6. doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]; Publisher: Nature Publishing Group
- 26.Prem K., Liu Y., Russell T.W., Kucharski A.J., Eggo R.M., Davies N., Flasche S., Clifford S., Pearson C.A.B., Munday J.D., Abbott S., Gibbs H., Rosello A., Quilty B.J., Jombart T., Sun F., Diamond C., Gimma A., van Zandvoort K., Funk S., Jarvis C.I., Edmunds W.J., Bosse N.I., Hellewell J., Jit M., Klepac P. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: a modelling study. Lancet Public Health. 2020 doi: 10.1016/S2468-2667(20)30073-6. [DOI] [PMC free article] [PubMed] [Google Scholar]; Publisher: Elsevier
- 27.Kucharski A.J., Russell T.W., Diamond C., Liu Y., Edmunds J., Funk S., Eggo R.M., Sun F., Jit M., Munday J.D., Davies N., Gimma A., van Zandvoort K., Gibbs H., Hellewell J., Jarvis C.I., Clifford S., Quilty B.J., Bosse N.I., Abbott S., Klepac P., Flasche S. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect Dis. 2020;20(5):553–558. doi: 10.1016/S1473-3099(20)30144-4. [DOI] [PMC free article] [PubMed] [Google Scholar]; Publisher: Elsevier
- 28.Quintela B.M., Conway J.M., Hyman J.M., Guedj J., dos Santos R.W., Lobosco M. A new age-structured multiscale model of the hepatitis C virus life-cycle during infection and therapy with direct-acting antiviral agents. Front Microbiol. 2018;9:601. doi: 10.3389/fmicb.2018.00601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Varella V.C., Matos A.M.F., Teixeira H.C., da Conceição Oliveira Coelho A., dos Santos R.W., Lobosco M. ICCS. 2018. A stochastic model to simulate the spread of leprosy in Juiz de Fora. [DOI] [Google Scholar]
- 30.Wang H., Wang Z., Dong Y., Chang R., Xu C., Yu X. Phase-adjusted estimation of the number of coronavirus disease 2019 cases in Wuhan, China. Cell Discov. 2020;6(1):1–8. doi: 10.1038/s41421-020-0148-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kermack W.O., McKendrick A.G., Walker G.T. A contribution to the mathematical theory of epidemics. Proc R Soc Lond Ser A Contain Papers Math Phys Character. 1927;115(772):700–721. doi: 10.1098/rspa.1927.0118. [DOI] [Google Scholar]; Publisher: Royal Society
- 32.Kermack W.O., McKendrick A.G. Contributions to the mathematical theory of epidemics–I. Bull Math Biol. 1991;53(1):33–55. doi: 10.1007/BF02464423. [DOI] [PubMed] [Google Scholar]
- 33.Keeling M.J., Rohani P. Princeton University Press; 2011. Modeling infectious diseases in humans and animals. [DOI] [Google Scholar]
- 34.Fehr A.R., Perlman S. Coronaviruses: an overview of their replication and pathogenesis. Methods Mol Biol (Clifton, NJ) 2015;1282:1–23. doi: 10.1007/978-1-4939-2438-7_1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Jia J., Ding J., Liu S., Liao G., Li J., Duan B., Wang G., Zhang R. Modeling the control of COVID-19: impact of policy interventions and meteorological factors. Electron J Differ Equ. 2020;2020:1–24. [Google Scholar]
- 36.Dong E., Du H., Gardner L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect Dis. 2020 doi: 10.1016/S1473-3099(20)30120-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Oliphant T.E. Python for scientific computing. Comput Sci Eng. 2007;9(3):10–20. doi: 10.1109/MCSE.2007.58. [DOI] [Google Scholar]
- 38.Storn R., Price K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim. 1997;11(4):341–359. doi: 10.1023/A:1008202821328. [DOI] [Google Scholar]
- 39.Valdez A.R., Rocha B.M., Chapiro G., dos Santos R.W. Uncertainty quantification and sensitivity analysis for relative permeability models of two-phase flow in porous media. J Petroleum Sci Eng. 2020;192:107297. doi: 10.1016/j.petrol.2020.107297. [DOI] [Google Scholar]
- 40.Feinberg J., Langtangen H.P. Chaospy: an open source tool for designing methods of uncertainty quantification. J Comput Sci. 2015;11:46–57. doi: 10.1016/j.jocs.2015.08.008. [DOI] [Google Scholar]
- 41.Campos J.O., Sundnes J., dos Santos R.W., Rocha B.M. Effects of left ventricle wall thickness uncertainties on cardiac mechanics. Biomech Model Mechanobiol. 2019;18(5):1415–1427. doi: 10.1007/s10237-019-01153-1. [DOI] [PubMed] [Google Scholar]
- 42.Sobol I.M. Global sensitivity indices for nonlinear mathematical models and their monte carlo estimates. Math Comput Simul. 2001;55(1–3):271–280. doi: 10.1016/S0378-4754(00)00270-6. [DOI] [Google Scholar]
- 43.Herman J., Usher W. SALib: an open-source python library for sensitivity analysis. J Open Source Softw. 2017;2(9):97. doi: 10.21105/joss.00097. [DOI] [Google Scholar]
- 44.University J.H.. 2019 novel coronavirus COVID-19 (2019-nCoV) data repository by johns Hopkins university center for systems science and engineering. https://github.com/CSSEGISandData/COVID-19; 2020.
- 45.Normile D. Coronavirus cases have dropped sharply in South Korea. What’s the secret to its success? Science. 2020;17(3) doi: 10.1126/science.abb7566. [DOI] [Google Scholar]
- 46.Sheridan C. Fast, portable tests come online to curb coronavirus pandemic. Nature Biotechnology. 2020 doi: 10.1038/d41587-020-00010-2. [DOI] [PubMed] [Google Scholar]; Publisher: Nature Publishing Group
- 47.World Health Organization. WHO director-general’s opening remarks at the media briefing on COVID-19 - 3 March 2020. https://www.who.int/dg/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19---3-march-2020; 2020c. Last accesses on March 24 of 2020.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Code to reproduce the results is available at https://github.com/FISIOCOMP-UFJF/ChaosSolitonsFractals-10-04-2020.