Abstract
Multiple regression is often used to compare the importance of two or more predictors. When the predictors being compared are measured with error, the estimated coefficients can be biased and Type I error rates can be inflated. This study explores the impact of measurement error on comparing predictors when one is measured with error, followed by a simulation study to help quantify the bias and Type I error rates for common research situations. Two methods used to adjust for measurement error are demonstrated using a real data example. This study adds to the literature documenting the impact of measurement error on regression modeling, identifying issues particular to the use of multiple regression for comparing predictors, and offers recommendations for researchers conducting such studies.
Keywords: measurement error, multiple regression, predictor reliability, predictor importance
Multiple linear regression is a popular technique used in educational and psychological research. Measurement error in predictors is a well-known but often neglected problem with this technique (Pedhazur, 1997). Prior work has established that substantial bias and increased Type I error rates are expected when the included predictors are correlated and measured with moderate error (Blalock, Wells, & Carter, 1970; Brunner & Austin, 2009; O. D. Duncan, 1975; Fuller, 1987; Shear & Zumbo, 2013). While these studies make clear that measurement error in one or both predictors can bias the estimation of coefficients associated with both predictors, the focus is generally on the bias in coefficients of a key predictor, and not the predictor used for statistical control. Therefore, much of this work focuses on interpreting bias and Type I error in a single key predictor.
Multiple regression is also commonly used to compare the importance of predictors. Researchers may wish to estimate which of two or more variables is a stronger predictor of the outcome. Beyond using additional independent variables for statistical control, such analyses compare two key independent variables. When the two predictors are correlated and one or both are measured with error—a situation that is very common, if not ubiquitous in practice—the impact of measurement error becomes complex. This is particularly true when standardized regression coefficients are used to compare the predictors (Cohen, Cohen, West, & Aiken, 2003), a practice that is often used when the independent variables being compared are measured on different scales. Because two variables are being compared, the bias in each affects interpretations. As explained below, this is most egregious when one of the predictors is measured with a substantially greater level of measurement error but can affect comparisons when differences in measurement error are modest or small in certain circumstances.
The purpose of this study is to explore the impact of measurement error on the bias and Type I error rates when comparing two predictors in multiple regression. First, the knowledge of bias and Type I error rates from studies focusing on one key predictor are briefly reviewed. Then, the issues related to bias and Type I error rates when the goal is to compare multiple correlated predictors, but one is measured with error, is discussed. Throughout, a hypothetical example is used to illustrate the identified issues. Then results from a simulation experiment are presented to better quantify the impact of these issues under varying conditions. Finally, basic methods to deal with measurement error when comparing predictors in multiple regression are demonstrated with an example using real data.
This study advances the understanding of how random measurement error affects bias and Type I error rates in multiple regression in at least four ways. First, the focus is on the comparison of regression coefficients, a practice that is commonly undertaken to assess the importance of predictors. While this method has been described as one of the most difficult types of questions to answer with multiple regression (Pedhazur, 1997), it is not often addressed in the literature on measurement error. Second, the impact of measurement error on a broader range of sample sizes than in previous studies is explored. With the growing availability of large publicly available data sets, the typical sample size in multiple regression models can be expected to increase. Most simulation work on measurement error in multiple regression has limited sample size to 1,000 or less. Because sample size is closely related to Type I error rates, an understanding of the impact of measurement error on larger samples will be useful to researchers who wish to assess the impact of measurement error in predictors of large sample studies. Third, the impact of measurement error across the full spectrum of predictor reliabilities is explored. This allows a better understanding of functional form of the relation between measurement error and predictor estimation. Finally, issues related to the use of standardized coefficients in regression are raised.
Impact of Measurement Error on a Single Key Predictor
In this article, the classical additive random measurement error model (Carroll, Ruppert, Stefanski, & Crainiceanu, 2006; Lord & Novick, 1968) is assumed, which is often used in the understanding of measurement error in regression models. The classical model of random measurement error posits that an observed score for an individual is the sum of the true score for that individual, , plus measurement error :
| (1) |
and that measurement error is independent of the true score . Here, and throughout this article, capital letters are used to indicate scores measured without measurement error (e.g., ) and lowercase italicized versions of letters are used to indicate scores measured with error (e.g., ).
A hypothetical example will be used to illustrate the impact of measurement error in linear regression. Suppose a researcher is interested in quantifying the effect of entering school with higher early reading skills (e.g., letter and word identification skills) on later reading achievement scores. The researcher has access to measures of early reading skills assessed at the beginning of kindergarten and measures of reading achievement assessed at the end of eighth grade for a large nationally representative sample of U.S. students. In simple regression models with a single predictor, measurement error in the dependent variable, independent variable, or both will attenuate the estimated relation between the two variables (Fuller, 1987). The magnitude of this attenuation is directly related to the amount of measurement error. Random measurement error is quantified with the reliability coefficient (), which conceptually is the ratio of the variance of the true score () to the variance of the fallible observed score () as follows:
| (2) |
As measurement error increases, the reliability coefficient decreases. Note that in the case of simple regression, the standardized regression coefficient is identical to the zero-order correlation coefficient, which when squared, is the coefficient of determination or the . All three of these coefficients are attenuated in simple linear regression.
Even when researchers are interested in the predictive relation between a key predictor and the outcome, often one or more additional variables are included in the model as covariates. For example, suppose that the researcher in our example is interested in the magnitude of early reading skills independent of early fine motor skills, as the two are thought to be correlated and both related to later reading achievement. Early fine motor skills have been found to be predictive of later reading achievement, and it has been postulated that this relation may reflect the role of motor skills in writing, which is closely related to reading (Grissmer, Grimm, Aiyer, Murrah, & Steele, 2010; Suggate, Pufke, & Stoeger, 2018). Another proposed explanation is that fine motor skills might reflect development of higher cognitive processes involving executive functioning or visuospatial processing (Cameron et al., 2012). Therefore, the desire is to isolate the predictive relation of early reading skills to later reading achievement by including a measure of fine motor skills also measured at kindergarten entry. The following multiple regression equation represents this model:
| (3) |
where Y represents the eighth-grade reading achievement score, while and represent the reading and fine motor skills, respectively, at kindergarten entry. This model can be considered the true score model as it represents the unlikely situation where all predictors were measured without error for all members of the population. The coefficients represent the standardized relation between the respective predictor and the outcome. Of the three coefficients, is of interest, and represents the magnitude of the relation between kindergarten entry early reading skills and eighth-grade reading achievement in the population, holding constant kindergarten entry fine motor skills. Rarely do researchers have access to the entire population, and the parameters in Equation (3) are often estimated using a sample from the population represented in the following equation:
| (4) |
The convention of using Greek letters (e.g., ) to represent population parameters and Roman letters (e.g., ) to represent estimates based on samples is followed here, and throughout most of the article. The differences between the coefficients in Equation (3) and the coefficients in Equation (4) are the results of sampling variability, and the expected value of over repeated samples is the population value, . Each is therefore an unbiased estimate of the corresponding .
Equations (3) and (4) assume that all variables are measured without error. However, the assumption of no measurement error in any of the variables is not realistic in most research settings. With multiple regression using more than one predictor, measurement error in the dependent variable will also consistently lead to attenuation of estimated coefficients. Similar to simple regression, a zero-order correlation in which one or more of the variables are measured with error will also evidence attenuation. Likewise, the coefficient of determination (i.e., ) is attenuated in multiple regression. However, measurement error in one or more independent variables has a more complex impact on the partial regression coefficients. Generally, the lower the reliabilities of predictors and the higher the correlation between predictors, the greater the distortion in the estimated coefficients due to measurement error (Pedhazur, 1997). This distortion may manifest as either an upward or downward bias in the regression coefficients. Bias in regression due to measurement error affects not only those coefficients of predictors measured with error but may also affect coefficients of predictors measured without error. Therefore, Equations (3) and (4) can be modified to reflect inclusion of one or more fallible measures as follows. Equation (3) becomes
| (5) |
which would represent the situation where all members of the population were measured, but at least one of the predictors was measured with error (Shear & Zumbo, 2013; Zumbo, 2007). The difference between each in Equation (5), and each corresponding from Equation (3), reflects the bias due to measurement error. For this and the next model, the asterisk distinguishes between models including variables measured with error from those free of measurement error. A similar modification follows for Equation (4), which includes sample data. If early reading skills are measured without error while fine motor skills are measured with error, say with variable instead of , the following model is estimated instead of the model represented by Equation (4):
| (6) |
This model can be considered the observed model to reflect the more realistic situation in research settings where sample data are used and at least one variable is measured with error. The expected difference between each and the corresponding represents the bias due to measurement error in . Note, the expected values are used here to account for sampling variability that would be reflected by a coefficient estimated from a particular sample.
It is not surprising that the measurement error in would affect the estimation of the regression coefficient for this variable—that, on average, would differ from . However, it may be less apparent that, if and are correlated, measurement error in the former will also bias the estimation of the regression coefficient in the latter—on average in Equation (4) would differ from in Equation (6). The mathematical details of the bias have been thoroughly addressed (see Carroll et al., 2006; Cochran, 1970; Fuller, 1987), however researchers often overlook this bias when evaluating coefficients of predictors in multiple regression. An intuitive way to understand this bias is to consider that a proportion of the variance in the outcome attributable to the less reliably measured predictor (e.g., fine motor skills), is attributed to the more reliable predictor (e.g., early reading skills) by means of the correlation between the two. This is most clearly demonstrated when considering omitted variable bias. Omitting an important variable is a well-known problem in the literature on regression modeling and can be thought of as equivalent to including the covariate measured with zero reliability (Zinbarg, Suzuki, Uliaszek, & Lewis, 2010). For example, in the case of a simple regression of eighth-grade reading on early reading skills, the estimated coefficient is expected to be biased due to omitting fine motor skills from the model (i.e., is assumed). The primary reason for including covariates in multiple regression is to address this bias. When a measure of fine motor skills is left out of the model, the coefficient for early reading reflects both the relation between early reading and later reading as well as the shared variance between early reading and fine motor skills that is also related to the outcome. A similar bias occurs when a fallible measure of fine motor skills is included.
Efforts to quantify the bias in multiple regression due to measurement error have most often focused on the bias in one key predictor. A typical scenario in methodological studies involves a model with two predictors, with the goal being to measure the impact of measurement error in one variable on the estimation of the coefficient of the other variable, measured without error (e.g., Brunner & Austin, 2009; Shear & Zumbo, 2013). The impact of measurement error in multiple regression depends on the extent of measurement error in the predictors and is directly related to the reliability of the predictor measured with error. Returning to our example, the researcher may be interested in how measurement error in fine motor skills would impact the estimation of the relation between early reading skills and later reading achievement. Multiple studies have shown that for key predictors, if the covariate is measured with substantial error and the covariate and key predictor are correlated, the latter can be biased.
Measurement error affects not only the magnitude of the regression coefficients but also their standard errors (Carroll et al., 2006), both of which are used to test against the null hypothesis. Therefore, measurement error also affects Type I error rate. To estimate the Type I error rate due to measurement error, studies also often focus on the error rate of the key predictor. For example, simulation studies most often set the value of a population coefficient of a key predictor to the value of zero—the value assumed by the null hypothesis being evaluated—and the population value of a covariate to some positive value. Then adjustments are made to the reliability of measurements of the covariate, and the impact of this measurement error on the proportion of times the null hypothesis is erroneously rejected for the key predictor is quantified. Brunner and Austin (2009) explored the impact of measurement error in one predictor on the Type I error rate in another predictor using a simulation study. They found unacceptably high Type I error rates under conditions typical of research studies in the social sciences.
More recently, Shear and Zumbo (2013) replicated and extended prior work including Brunner and Austin (2009), by also looking at the impact of measurement error on effect size in addition to Type I error rates. They found that when the covariate and key predictor are not related, the Type I error rate is very close to the nominal .05 alpha level as expected, and is not impacted by the sample size, the level of reliability of the covariate or the of the true model. However, even with a modest correlation between the true predictors, the Type I error rate is substantially inflated. This inflation is affected by each of the other simulation parameters just mentioned. The larger the sample size the higher the Type I inflation. The less reliably the covariate is measured the greater the Type I error rate, and the larger proportion of variance () attributable to the true relation between and the outcome the greater the inflation of Type I error rates. Particularly, troubling was the finding that with moderate to large samples even traditionally acceptable reliability coefficients, typically greater than .70 for the covariate, lead to large inflation of Type I errors. Both of these studies used sample sizes of 1,000 or less in the simulations. While it is clear that the Type I error rates will be worse for larger sample sizes, it is not clear how much worse.
Impact of Measurement Error When Comparing the Importance of Predictors
Often researchers use multiple regression to compare the importance of multiple predictors. For example, educational researchers may wish to know which skills present at the beginning of school are most important in predicting children’s later achievement. The use of multiple regression for comparing the importance of predictors is fraught with problems (Pedhazur, 1997). However, this has not stopped researchers from using this procedure for such purposes. Referring to our running example, the researcher might be interested in whether early reading skills or fine motor skills are a more important predictor of later reading achievement. This may help inform which skill should be the focus of early educational intervention.
It is important to note that because the goals of studies aimed at isolating a key predictor differ from the goals of those aimed at comparing predictors, so do the hypotheses that should be tested. When the goal is to isolate a key predictor, the bias in that predictor is important, and most often researchers test the null hypothesis that the coefficient for the key predictor is zero in the population. However, when the goal is to compare two predictors, the bias in both predictors is relevant, and the appropriate null hypothesis is that the two coefficients are equal, or equivalently, that the difference between the two coefficients is zero. This is a much preferred method of testing two coefficients than to the practice of comparing their statistical significance (Gelman & Stern, 2006; Lindsay, 2015). For example, early fine motor skills may not exceed the statistical significance threshold while early reading skills do. It is possible that the two coefficients are very similar in magnitude with the former just falling short of the statistical significance threshold and the latter falling just above. As pointed out by Gelman and Stern (2006), the magnitudes of the coefficients can be quite different and the difference between the two coefficients may still not be statistically significant. Therefore, if the goal is to determine if one coefficient of a predictor is greater than the other using null hypothesis statistical testing, the appropriate statistical test is against the null that the two coefficients are equal. For linear models, such a test can be conducted using linear contrasts to generate a Wald test of the two coefficients. In this study, I use the incremental test to make such comparisons. This procedure compared a model that freely estimates the two coefficients with a model that constrains the coefficients to be equal (Fox, 2016).
Standardized Versus Unstandardized Coefficients
The test of the null hypothesis that the two coefficients are equal is often only meaningful for standardized coefficients. This is because predictors are often measured on different scales, and comparisons of the unstandardized coefficients, and the interpretation of the expected difference in the outcome for a one-unit change in the predictor, depends on this scale. If early reading skills and fine motor skills are measured on different scales, it often makes more sense to standardize the variables so that the regression coefficients are expected changes in standard deviation units. This is why most researchers focus on standardized coefficients or derivatives of the standardized coefficients when comparing predictors. Unfortunately, standardized coefficients can be problematic when one or more of the predictors are measured with error due to the inflation of the sample standard deviation compared with the population standard deviation. To understand this, consider the relation between standardized and unstandardized coefficients, which is given by the following equation:
| (7) |
where is the standardized population coefficient, and is the unstandardized coefficient. Measurement error in would lead to bias in , which would also be evident in . But because measurement error not only biases the unstandardized coefficient but also biases the sample standard deviation, the standardized coefficient is impacted by what Carroll et al. (2006) referred to as the double whammy of measurement error. The coefficient is affected by both the bias in and the bias in the sample estimate of , which in practice is used to calculate the sample-based estimates of the population parameters in Equation (7). Stated differently, measurement error leads to a bias in parameter estimates and also biases the estimates of the population sample standard deviation. Only the former impacts the point estimation of unstandardized coefficients, but both impact the standardized coefficient. Recall that in the classical measurement error model, the sample standard deviation tends to be inflated. Therefore, in situations when the predictor is measured with greater error than the outcome, the numerator of the ratio of standard deviations in Equation (7) will be larger, on average, than the true population ratio, and the standardized coefficient will therefore be biases upward.
While it is unlikely that researchers will have knowledge of the population standard deviation for predictor variables measured with error, it can be estimated and used to calculate an unbiased estimate of the population standard deviation if the reliability of the predictor is known. This can be accomplished with the following equation:
where is the sample standard deviation. This equation can be obtained by solving for the variance of in Equation (2), then taking the square root of both sides of the equation. In other words, by adjusting the sample standard deviation by multiplying it by the square root of the reliability of the predictor an unbiased estimate of the true population standard deviation is obtained. While this method will not address the total bias due to measurement error, it does adjust for the bias that results in the inflation of the sample standard deviation due to measurement error. Therefore, this adjustment is recommended when using standardized coefficients for variables measured with error and an estimate of the reliability is available.
Illustration With Hypothetical Example
To illustrate the impact of measurement error in one predictor when the goal is to compare the importance of two predictors, a hypothetical data set is used, based on the following extension of our previous example. Suppose that instead of being interested in isolating the relation of early reading skills on later reading achievement, the researcher in our example wishes to determine which of the two skills measured at kindergarten entry is the more important predictor of eighth-grade reading achievement, early reading skills or fine motor skills. Further suppose that the measurement of fine motor skills is much less developed than the established measure of early reading skills and therefore the reliability of measures on the newer variable tend to be much lower than measures of the established variable, leading to substantially greater levels of measurement error in this predictor. In other words, our researcher wishes to compare with from Equation (3) by comparing the estimates and from Equation (4). However, instead of observing directly, the researcher has obtained a fallible measure of , namely, , and therefore will be compared with , both from Equation (6).
To demonstrate the impact of measurement error on Type I error rates associated with testing the null hypothesis that the two regression coefficients are equal, further assume that the population values of the standardized coefficients are identical. The model of interest to the researcher includes three true score variables (Y, , and ) from a multivariate normal distribution that represents eighth-grade reading, early reading skills, and fine motor skills, respectively, all measured without error. To facilitate interpretation, assume that these are standardized variables, each with a mean of 0.0 and a standard deviation of 1.00, to account for possible differences of scale between original variables. Further assume that the population correlation between the two predictors, and , is 0.60, and the population correlation between each of the predictors and the outcome Y is .46, a value that would result in a model of .25 when estimating Equation (3).
While the researcher is interested in the model in Equation (3), instead of , the researcher has a fallible measure , which has been measured with a reliability of .50. Suppose our researcher has access to a nationally representative data set with 10,000 students, with measures of eighth-grade reading achievement and early reading skills measured without error, and a fallible measure of fine motor skills. So instead of estimating the model in Equation (3) the researcher estimates the model in Equation (5). Comparisons of the reliabilities of with represent extreme values of reliability in practice, and are used to emphasize the impact of measurement error on comparing regression coefficients for variables when one contains measurement error. To minimize the impact of sampling variation a very large sample size of 10,000 was used for this hypothetical example.1 Therefore, the differences due to sampling error (i.e., differences between the and coefficients, as well as the differences between the and coefficients) are negligible, and any differences can be attributed to the impacts of measurement error.
Table 1 includes the means, standard deviations, and correlations between the hypothetical variables measured without error, as well as which was measured with error. All of the means are very close to zero, even for , which is consistent with the classical measurement error model. Note that the variances of the true score variables are equal to 1.00. However, the variance of is 40% greater than , demonstrating that measurement error induces additional variance in the observed variable. Also note that the correlation between the predictors measured without error ( and ) is .60, which is the population parameter, while the correlation between and , the variable measured with error, is attenuated to .42. The correlation between both of the predictors measured without error and the outcome Y are equal to each other at .46, again as specified in the true model, while the correlations between the outcome and the predictor measured with error are different from the population value. The correlation between and Y has also been attenuated, estimated at .33. These estimates are consistent with expectations following the above discussion. Namely, when a variable is measured with error, the bivariate correlations including that variable are attenuated.
Table 1.
Means (M), Standard Deviations (SD), and Correlations of Hypothetical Data.
| M | SD | Y | X | W | |
|---|---|---|---|---|---|
| Y | −0.01 | 1.0 | |||
| X | 0.01 | 1.0 | 0.46 | ||
| W | 0.00 | 1.0 | 0.46 | 0.6 | |
| w | 0.00 | 1.4 | 0.33 | 0.42 | 0.71 |
Table 2 includes summaries of multiple regression results for two models. In the first model, the outcome Y was regressed on the versions of the predictors measured without error, and . This is the model in Equation (4), that represents use of sample data containing variables free of measurement error, but because of the very large sample size, sampling variability is minimized, and the coefficients are precise estimates of the population values represented in Equation (3). The column labeled “True model” in Table 2 illustrates that the estimated model very closely captures the population parameters just described. The coefficients for the two predictors, and , are equal in value with a magnitude of 0.29. Compare these coefficients with those in the column labeled “Observed model,” which contains the coefficients of regressing Y on and , the observed variable measured with error. Before being entered into the Observed Model, was standardized using the method recommended to adjust the biased sample standard deviation using the reliability of this predictor.2 Because these two predictor variables are correlated, and one is measured with error, both coefficients are biased. Notice that the coefficient for , the more reliable predictor, is biased upward, so that the coefficient for this variable .39 is an overestimate of the true coefficient .29, while the coefficient for the observed variable , which is the less reliable predictor, is .12, which is an underestimate of the true coefficient of .29. Also note that the multiple correlation of the observed model () is attenuated compared with that of the true model (), and the population value of .25. As noted in the previous discussion, and similar to the bivariate correlations, the multiple correlation (i.e., ) is also attenuated when variables measured with error are included in the model.
Table 2.
Impact of Measurement Error on Comparing Predictors in Hypothetical Data.
| True model | Observed model | |
|---|---|---|
| (Intercept) | −0.01 (0.01) | −0.01 (0.01) |
| X | 0.29*** (0.01) | 0.39*** (0.01) |
| W | 0.29*** (0.01) | |
| W | 0.12*** (0.01) | |
| .26 | .23 | |
| No. of observations | 10,000 | 10,000 |
p < .05. **p < .01. ***p < .001.
Compound Bias in Comparing Regression Coefficients
It is important to better understand how the change in focus from estimating bias and Type I error in a key predictor to a focus on comparing two predictors also changed the source of the bias and Type I error rates. Conceptually, bias in coefficients due to measurement error is defined as the difference between the population coefficient for from the equation including fallible measures (e.g., from Equation 5), and the true population parameter being estimated (e.g., from Equation 3). If our focus is on as the key predictor, then only the bias in is relevant, which is the difference between the population coefficient for this variable measured with error, and the population coefficient measured without error, . If we use to represent this bias, we have:
Because of the negligible sampling variability in our example, the difference between the two coefficients for from Table 2 is a precise estimate of this bias, which is 0.39 − 0.29 = 0.10. This bias represents a 30% overestimation of the population value. When the goal is not to estimate , but only to use the additional variable as a covariate, the bias in this coefficient due to measurement error is not important. However, when the focus is on comparing the two predictors, the bias in each coefficient must be considered, as each estimated coefficient is a source of bias. The bias in the coefficient for is estimated as the expected difference between the coefficient for and the coefficient for . The expected difference between , which in the current example is precisely estimated by . The negative bias indicates that the estimate using the observed variable underestimates the true population parameter for . Because the bias in the comparison of coefficients has two sources, I refer to this as compound bias. The compound bias is defined as the differences between the individual coefficient biases:
By rearranging the second term in this equation, the compound bias can be represented as the difference between the two coefficients from the model including at least one coefficient measured with error and the two coefficients from the model free from measurement error:
Importantly, in situations where the two true population coefficients are equal (i.e., ), the compound bias reduces to the difference between the coefficients from the model containing a fallible measure:
Note that the equality of and is what is assumed in the appropriate null hypothesis for comparing predictors. Because the sample-based coefficients are unbiased estimates of their population counterparts, under conditions of the null hypothesis that the two population coefficients and are equal, the expected value of the difference between the observed coefficients is an unbiased estimator of the compound bias:
where signifies expectation and here means that the compound bias in the estimation of coefficients for and is the expected difference between and over many samples. Because this condition holds for the hypothetical example, the bias in comparing the coefficients associated with the two variables and is . This difference is identical to the difference between the two coefficients in the “Observed model” column of Table 2: .
Table 2 follows the common practice of including asterisks to indicate statistically significant coefficients for the test against the null hypothesis that the population coefficients are zero. Due to the large sample size of this simulation, all coefficients are statistically significant. However, had the sample size been small, it is likely that the two coefficients in the true model would remain statistically significant, while only the coefficient for would be significant in the observed model. Only having access to the latter, a researcher may conclude that early reading skills, as measured by , are important, but early fine motor skills, as measured by , are not. But recall that these would not be the appropriate null hypotheses for comparing predictors. The appropriate statistical test when comparing two predictors is to test against the null hypothesis that the two predictors are equal. The test of the equality of the coefficients for the predictors measured without error (i.e., ) is consistent with this null hypothesis (1, 9997) = 0.09, = .766, while the same hypothesis test for the model including the predictor measured with error (i.e., ) results in a rejecting of the null hypothesis, (1, 9997) = 374.68, < .001. These two tests were computed using the incremental test to compare the model freely estimating the two coefficients to the model constraining the coefficients to be equal (Fox, 2016). Therefore, when both predictors were measured without error, there is no bias, the hypothesis test is consistent with the population parameters, and leads to the correct conclusion that the two coefficients are consistent with the null hypothesis. However, when the variable measured with error is included in the model, there is compound bias, and the null hypothesis that the two population parameters are equal is erroneously rejected, leading to a Type I error. Therefore, whether the researcher compares the magnitude of the observed model coefficients, formally tests the hypothesis that the coefficients are equal, or both, the wrong conclusion is suggested by the results of the observed model.
This example illustrates that, at least under certain circumstances, when comparing two predictors, one measured with error and when the null hypothesis for the equal coefficients for these predictors is true, the reliably measured predictor is overestimated while the less reliable predictor is underestimated. Furthermore, measurement error in a particular variable increases the variance of the observed variables and attenuates any observed correlation including this variable. Finally, under these circumstances, the Type I error rate of comparing differences in the predictors may be inflated.
Simulation Study
To understand the impact of reliability on comparison of predictors under a broader range of conditions, a Monte Carlo simulation was conducted, guided by two primary research aims. First, the impact of measurement error in one predictor on the compound bias of comparisons of two predictors was explored. Most studies of the impact of measurement error on bias in multiple regression have considered only the impact on interpretations of a single key predictor’s coefficient. With the wide-scale use of regression models to compare predictors, understanding the impact of compound bias in more than one coefficient is important. Second, the impact of measurement error on the Type I error rate for testing the null hypothesis that the predictors are equal in the population was explored. Therefore, instead of constraining the key predictor to be zero and determining what proportion of the simulations erroneously reject the null hypothesis that this key coefficient is zero, in this study the difference between the two coefficients is constrained to be zero, and the proportion of times the null hypothesis that the coefficients are equal in the population is erroneously rejected is assessed. An additional secondary aim was to estimate the impact of measurement error in large sample studies, with samples sizes considerably greater than 1,000.
Simulation Model and Conditions
A full-factorial design was used by manipulating the following factors. Sample size () was manipulated with five conditions, 50, 250, 1,000, 5,000, and 10,000. Inclusion of larger sample sizes will help researchers understand the impact of using larger data sets where at least one is measured with error. The reliability of one variable, was held constant and the reliability of the other, was manipulated to understand the impact of measurement error in one predictor on compound bias and Type I error. The reliability of () was constant at 1.00 and the reliability of () was manipulated between the values of 0.0 to 1.0 at increments of .1, resulting in 11 conditions for this factor. The correlation between the two predictors in the population () was set to five conditions: 0, .2, .5, .7, .9. The explained variance of the population () in the simulated models was manipulated using four conditions: .10, .25, .50, and .75, to reflect the broad range of models found in applied research. Note that to constrain and to be equal in the population, while allowing the population-level correlation and explained variances to vary requires that the magnitude of the population coefficients may vary across condition. While this would be problematic if the goal was to test the bias and Type I error for the null hypothesis that the coefficients are zero, it is not problematic for the current study, which is aimed at assessing the bias and Type I error rates for the null hypothesis that the difference between the coefficients is zero.
The full-factorial design resulted in 5 × 11 × 5 × 4 = 1,100 factor combinations. For each of the 1,100 combination of factors 1,000 replications were initially generated, resulting in 1,100 × 1,000 = 1.1 million simulated data sets. However, due to concerns of instability of estimates with the smaller sample size (i.e., n = 50 and n = 250), these conditions were simulated 10,000 times, resulting in 5.06 million replicated data sets. All simulations were conducted with the R statistical computing language (R Core Team, 2018), using the SimDesign package (Chalmers, 2018). Annotated computer code for the simulations as well as data sets containing the aggregated simulation results for all conditions can be found in the online Supplemental Materials. Validity of the simulation code was evaluated by using the simulation code to generate data under ideal conditions (i.e., large samples size) and evaluation of parameters estimated with variables measured with no error components. All simulation code, software version details, and random seed information is included within the online Supplemental Materials. Most simulation studies on measurement error in multiple regression restrict the manipulated reliabilities within the range of recommended reliabilities for such studies, which typically includes values greater than .50 or .70. A broader range of reliabilities were included to provide a better understanding of the functional form of the relation between measurement error and the resulting bias and Type I error rates.
Equation (3) was used as the population regression model to generate variables X and W for all simulated data sets, and the error variance of models was selected to obtain the desired population level R2 value. Then, for each data set, was generated by adding random noise to , using Equation (1), with , the measurement error term, being selected to obtain a desired level of reliability. Consistent with the assumptions of multiple regression, all variables were simulated draws from the standard multivariate normal distribution. The use of standard normal variates reflects the common practice of using standardized regression coefficients to compare predictors that are often measured on different scales. However, as discussed above, this practice introduces an additional bias due to the inflation of the sample standard deviation of the variable measured with error. As discussed in the previous section, when estimates of the reliability of the fallible measure are available, it is easy to adjust for this bias by multiplying the sample standard deviation by the square root of the estimated reliability. Because this adjustment recovers the population standard deviation well in situations where the reliability is estimated precisely, is not standardized before estimating the regression coefficients in the simulations. This decision also isolates the source of bias on the impact of measurement error in the parameter estimation, better estimating the functional form of the bias in coefficients due to measurement error. It also reduces computation time, by removing the additional computations needed to restandardize the variables across the 5 million simulations.
The two primary outcomes of interest were the observed compound bias of the two coefficients and the Type I error rates for testing the null hypothesis that the two coefficients are equal in the population. Because interest is in the compound bias for the estimates due to the focus on two predictors, the differences between the biases for each predictor were averaged as follows:
where is the number of replications in each factor combination, and was calculated as the average difference between the sample estimate and the population parameter for a given simulation factor combination.
All simulated data sets were drawn from populations where the true coefficient for and were equal. The Type I error rate was calculated as the proportion of statistical tests that falsely rejected the null hypothesis that the two coefficients were equal in the population within each combination of the study factors. The alpha level was set at .05 and the incremental test was used to compare the coefficients.
Simulation Results
Table 3 contains select tabulated results for the compound bias in comparing predictors when one is measured with errors. The cells represent the compound bias for the given condition averaged across all replications. The columns are first broken down by the correlation between the two predictors in the population (), at three levels (.0, .5, and .9). Within each of these levels, subcolumns for five levels of reliability of () are represented (i.e., .6, .7, .8, .9, 1.0). Because most researchers quantify measurement error with reliability coefficients, results are presented using reliability coefficients to make the tables and graphs more useful. Furthermore, only reliabilities typically considered acceptable are used in this table. Inspection of compound bias at other levels of reliability can be found in the online Supplemental Materials, and in Figure 1, as discussed below. The rows of Table 3 represent the four levels of population (.01, .25, .50, .75). Because the expected value of bias is not impacted by sample size as suggested by previous literature (Brunner & Austin, 2009; Shear & Zumbo, 2013) and which was confirmed in the present simulation study (see the online Supplemental Materials), the cells in Table 3 for each level of are averaged across the simulated sample sizes, as well as across replications. Compound biases greater than .10 are in bold to ease identification of excessive values.
Table 3.
Estimated Compound Bias in the Magnitude of the Difference Between Two Predictors With Measurement Error in One Predictor().
| .0 |
.5 |
.9 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| .6 | .7 | .8 | .9 | 1.0 | .6 | .7 | .8 | .9 | 1.0 | .6 | .7 | .8 | .9 | 1.0 | |
| .10 | 0.09 | 0.07 | 0.04 | 0.02 | 0.00 | 0.07 | 0.04 | 0.00 | 0.00 | ||||||
| .25 | 0.07 | 0.04 | 0.00 | 0.05 | 0.00 | 0.00 | |||||||||
| .50 | 0.05 | 0.00 | 0.08 | 0.00 | 0.00 | ||||||||||
| .75 | 0.06 | 0.00 | 0.00 | 0.00 | |||||||||||
Note. Boldfaced values indicate compound biases greater than .10 and are considered excessive values. = Correlation between and ; = Reliability of .
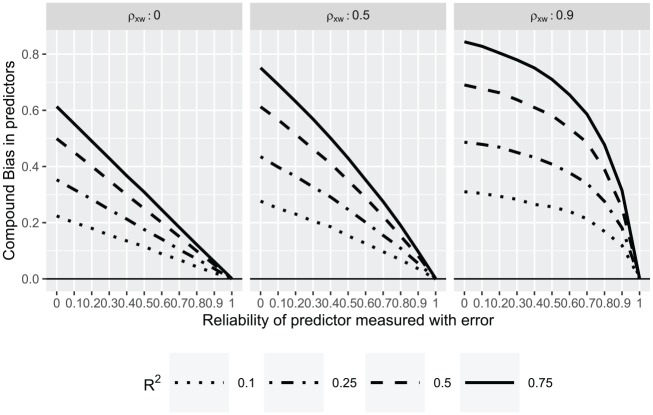
Figure 1.
The compound bias in the two predictors due to measurement error in one predictor.
Note. in all conditions and is the reliability of . is the correlation between the two predictors had they been measured without error. is the proportion of variance in the outcome explained by the two predictors if both had been measured without error.
Figure 1 contains a graphical depiction of the simulation results for compound bias given in Table 3, but includes all simulated levels of reliability for , making the full functional form of the relations between conditions apparent. Each of the graphs represents a different level of correlation between the predictors in the simulation population (e.g., 0, .5, and .9), while the curves represent the four levels of population (i.e., .10, .25, .50, and .75). For each of the graphs the x-axis indicates the level of reliability of , while the y-axis indicates the compound bias of the two predictors.
Both Table 3 and Figure 1 demonstrate that the higher the reliability of the less the compound bias in comparisons of the coefficients for and . As the reliability of approaches 1.0, the bias approaches zero. The far-right column of Table 3 indicated no bias when the reliability of both variables is 1 (e.g., measurement error is zero). Said differently, the more measurement error in , the greater the compound bias in the magnitude of the difference between these coefficients.
In addition to being impacted by the level of reliability of the compound bias is also impacted by the magnitude of the correlation between the two predictors (), and the proportion of variance explained by the two predictors (). As the magnitude of each of these factors increases, so does the compound bias. Examination of Figure 1 reveals a nonconstant relation between the reliability of , the population-level correlation between and , and the population . When the predictors are not correlated there is a linear relation between reliability of and compound bias. This is because the compound bias in this situation consists of only the bias in . The absence of a correlation between the two prevents bias in the estimation of . As the reliability of decreases the compound bias increases. The rate of increase in compound bias in relation to reliability is a function of the , which reflects the strength of the correlation between the predictors and outcome. When the predictors are correlated there is a nonlinear relation between the reliability of and compound bias. This is because the compound bias is a function of the bias in both and . This nonlinear relation appears to be quadratic in nature and most pronounced when the predictors are highly correlated (see the rightmost graph), exemplifying the impact of collinearity of regression coefficients. The compound bias is greatest when the two predictors are both highly correlated with each other and with the outcome. This suggests a strong interaction between the proportion of variance explained by the predictors and the correlation between the predictors. When the predictors are highly correlated and strongly related to the outcome, small amounts of measurement error in can have a relatively large impact on compound bias when comparing the estimated coefficients.
These results indicate substantial bias in comparisons of regression coefficients when within the range of acceptable reliabilities for variables. Note that even when the correlation between and is zero, the compound bias approaches and often exceeds .10 for reliabilities of .7, a level of reliability which many researchers would consider acceptable (Lance, Butts, & Michels, 2006). When the predictors are correlated the problem is much worse. For example, when the correlation between and is .50 and the reliability of is .70 the compound bias ranges from 0.10 to 0.27 depending on how strongly the predictors are related to the outcome (i.e., the greater the , the greater the bias). But even when the variables are weakly related to the outcome (), the compound bias reaches .10. The magnitude of the difference in reliabilities of the two predictors is clearly important, even when both reliabilities exceed what many researchers consider to be adequate levels.
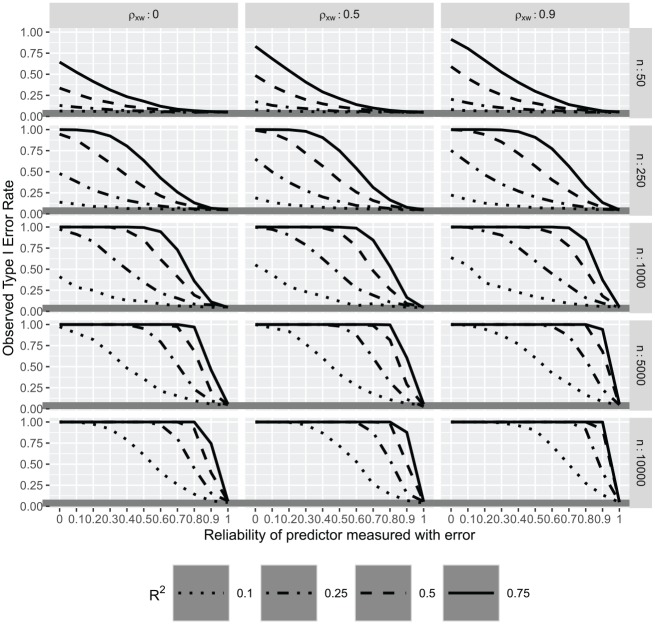
Table 4 contains select tabulated results for the Type I error rates for tests of the linear hypothesis that the two coefficients are equal when comparing predictors, one measured with error. Because sample size does impact Type I error rates, this table contains a subtable for each sample size (50, 250, 1000, 10,000) each of which is organized just as in Table 3 except that the cells contain the Type I error rates instead of compound bias. Similar to prior studies exploring Type I error rates and measurement error (e.g., Shear & Zumbo, 2013), Bradley’s (1978) criterion of .075 is used to identify excessive error rates, and such values are set in bold type in this table. Figure 2 contains a graphical depiction of select simulation results for the Type I error rates.
Table 4.
Average Estimated Type I Error Rates Testing the Equality of Coefficients When One Independent Variable Is Measured With Error ().
| .0 |
.5 |
.9 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | .6 | .7 | .8 | .9 | 1.0 | .6 | .7 | .8 | .9 | 1.0 | .6 | .7 | .8 | .9 | 1.0 | |
| 50 | .10 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.06 | 0.05 | 0.05 |
| .25 | 0.06 | 0.05 | 0.05 | 0.05 | 0.05 | 0.06 | 0.05 | 0.06 | 0.05 | 0.05 | 0.07 | 0.06 | 0.05 | 0.05 | 0.05 | |
| .50 | 0.08 | 0.07 | 0.05 | 0.06 | 0.05 | 0.09 | 0.07 | 0.06 | 0.05 | 0.05 | 0.12 | 0.09 | 0.07 | 0.06 | 0.05 | |
| .75 | 0.12 | 0.09 | 0.07 | 0.06 | 0.05 | 0.14 | 0.10 | 0.07 | 0.06 | 0.05 | 0.22 | 0.14 | 0.10 | 0.06 | 0.05 | |
| 250 | .10 | 0.06 | 0.05 | 0.05 | 0.05 | 0.05 | 0.06 | 0.06 | 0.05 | 0.05 | 0.05 | 0.07 | 0.07 | 0.05 | 0.05 | 0.05 |
| .25 | 0.09 | 0.07 | 0.06 | 0.05 | 0.05 | 0.10 | 0.08 | 0.06 | 0.05 | 0.05 | 0.15 | 0.11 | 0.08 | 0.05 | 0.05 | |
| .50 | 0.21 | 0.13 | 0.09 | 0.06 | 0.05 | 0.26 | 0.16 | 0.10 | 0.06 | 0.05 | 0.40 | 0.27 | 0.15 | 0.05 | ||
| .75 | 0.43 | 0.26 | 0.13 | 0.07 | 0.05 | 0.54 | 0.31 | 0.16 | 0.08 | 0.05 | 0.77 | 0.56 | 0.33 | 0.05 | ||
| 1,000 | .10 | 0.09 | 0.07 | 0.06 | 0.05 | 0.05 | 0.07 | 0.09 | 0.06 | 0.05 | 0.04 | 0.13 | 0.09 | 0.07 | 0.06 | 0.05 |
| .25 | 0.22 | 0.16 | 0.09 | 0.08 | 0.05 | 0.27 | 0.19 | 0.11 | 0.07 | 0.06 | 0.45 | 0.30 | 0.16 | 0.05 | ||
| .50 | 0.62 | 0.41 | 0.19 | 0.10 | 0.05 | 0.77 | 0.48 | 0.26 | 0.09 | 0.05 | 0.93 | 0.77 | 0.49 | 0.05 | ||
| .75 | 0.94 | 0.73 | 0.36 | 0.11 | 0.05 | 0.99 | 0.84 | 0.53 | 0.16 | 0.04 | 1.00 | 0.99 | 0.84 | 0.05 | ||
| 5,000 | .10 | 0.21 | 0.15 | 0.10 | 0.06 | 0.05 | 0.28 | 0.18 | 0.11 | 0.06 | 0.05 | 0.42 | 0.30 | 0.16 | 0.04 | |
| .25 | 0.79 | 0.52 | 0.23 | 0.10 | 0.05 | 0.88 | 0.60 | 0.32 | 0.11 | 0.03 | 0.98 | 0.86 | 0.58 | 0.05 | ||
| .50 | 1.00 | 0.97 | 0.68 | 0.20 | 0.05 | 1.00 | 0.99 | 0.82 | 0.29 | 0.04 | 1.00 | 1.00 | 0.99 | 0.04 | ||
| .75 | 1.00 | 1.00 | 0.97 | 0.46 | 0.06 | 1.00 | 1.00 | 1.00 | 0.60 | 0.06 | 1.00 | 1.00 | 1.00 | 0.06 | ||
| 10,000 | .10 | 0.40 | 0.26 | 0.14 | 0.06 | 0.04 | 0.53 | 0.26 | 0.14 | 0.07 | 0.04 | 0.72 | 0.50 | 0.27 | 0.05 | |
| .25 | 0.97 | 0.80 | 0.45 | 0.16 | 0.06 | 1.00 | 0.88 | 0.55 | 0.16 | 0.06 | 1.00 | 1.00 | 0.91 | 0.05 | ||
| .50 | 1.00 | 1.00 | 0.92 | 0.40 | 0.06 | 1.00 | 1.00 | 0.98 | 0.51 | 0.05 | 1.00 | 1.00 | 1.00 | 0.05 | ||
| .75 | 1.00 | 1.00 | 1.00 | 0.74 | 0.06 | 1.00 | 1.00 | 1.00 | 0.88 | 0.05 | 1.00 | 1.00 | 1.00 | 0.05 | ||
Note. Boldfaced values indicate p values greater than .075 and are considered excessive values. = Correlation between and ; = Reliability of .
Figure 2.
The probabilities of showing a significant hypothesis test that two coefficients are equal when one is measured with error.
Note. is the correlation between the two predictors had they been measured without error. is the proportion of variance in the outcome explained by the two predictors if both had been measured without error.
Similar to prior studies on the Type I error rate in a single key predictor, the results of this simulation demonstrate a stark inflation of false positives when one of the predictors is measured with error. The magnitude of this inflation is troubling. The results of the Type I error rates mirror those of the compound bias, which reflects the close relation between these two outcomes. Namely, as the reliability of approaches that of the Type I error rate approaches the nominal .05 level. Similar to the compound bias, the correlation between the two predictors and the proportion of variance explained by both impact the Type I error rate. As the correlation between predictors increases, the magnitude of the inflation of the Type I error rate increases. As the proportion of variance explained by the two predictors increases, the inflation of the Type I error increases. Unlike bias, the Type I error rate is also impacted by sample size. Consistently, the higher the sample size the greater the Type I error rates. This is because with larger samples, estimates of the standard error tend to be smaller, increasing the power of the statistical test. As the sample size increases the importance of the and the importance of the correlation between the two predictors diminishes. When sample size is 10,000, the Type I error rate is 1.00 when the reliability of the fallible measure differs from the error-free measure by at least .10, and remains unacceptably high regardless of whether the predictors are correlated and regardless of how strongly the predictors are related to the outcome. Even with no correlation between the predictors and a small proportion of the variance explained by the two predictors, the Type I error rate increases steeply as the reliability of decreases, particularly, for large samples.
The results of the simulation study demonstrate the substantial impact measurement error can have when the goal of multiple regression is to compare the importance of two predictors. The compound bias can lead to large observed standardized differences between the coefficients even when none exist in the population. Particularly with large samples, hypothesis tests of the difference between the predictors can suffer from unacceptably high Type I error rates for small levels of measurement error in one of the predictors.
Adjusting for Reliability
General strategies to minimize the impact of measurement errors in predictors include increasing the number of measures of each construct, using more reliable measures, or using latent variables (Shadish, Cook, & Campbell, 2002). However, these solutions are not always practical to researchers using existing data. Because many of the studies that use multiple regression to compare the importance of predictors use existing large nationally representative data sets, which often report reliabilities of measured variables for the samples, methods using estimates of reliabilities in adjusting for measurement error are demonstrated. Also, because there are rarely multiple measures of these variables within these data sets at a given time point, a focus on methods that can be used with a single measure of each variable were chosen. Two methods that meet these criteria are the errors-in-variables method and single-indicator structural equation modeling (SEM) with adjustment for reliabilities. The errors-in-variables method adjusts for bias by using the estimated reliabilities to alter the variance-covariance matrix for the linear model (Carroll et al., 2006; Fuller, 1987). The single-indicator SEM method models the fallible measure as a single indicator of a true score latent variable. Then the variance of the single indicator is set to be the product of the complement of the reliability of the fallible measure and its variance (e.g., ; O. D. Duncan, 1975; Kenny, 1979). The goal of this section is not to provide a comprehensive explanation of these two methods for adjusting models for measurement error, but instead the use of these methods is demonstrated. A number of software packages make available errors-in-variables regression (e.g., R, Stata) and any SEM program can be used for single-indicator SEM approach. In this demonstration, I use the error-in-variables method implemented in R using the eivtools package (Lockwood, 2018), and single-indicator SEM method using Mplus (Muthén & Muthén, 2017).3
Table 5 contains results from the true score model using variables measured without errors (“True”), and the observed model using the fallible variable (“Naive”), from Table 2. In addition, the models using the two methods for adjusting for measurement error discussed in this section are also included. Both these models use variables that are standardized adjusting for the bias in sample standard deviations using the known reliability coefficients, which must be available for the use of these methods. The third model (“Errors-in-variables”) contains a model using the eivtools package available for R. The fourth model (“SEM”) includes a single-indicator SEM model conducted in Mplus. These results recover the true population parameters quite well. Note however, that the true reliability was used here instead of an estimate of the reliability of . In real applications, the adjusted estimates will depend on the accuracy of the reliability estimates available. The regression coefficients and the model are nearly identical to the estimates in the true score model.
Table 5.
Regression Estimates for the Hypothetical Example Data Without Adjusting for Measurement Error (Naive) and With Adjustment Using the Errors-in-Variables Method and the Structural Equation Modeling (SEM) Method.
| True | Naive | Errors-in-variables | SEM | |
|---|---|---|---|---|
| (Intercept) | −0.01 (0.01) | −0.01 (0.01) | −0.01 (0.01) | −0.01 (0.01) |
| X | 0.29*** (0.01) | 0.39*** (0.01) | 0.28*** (0.01) | 0.28*** (0.01) |
| W | 0.29*** (0.01) | |||
| w | 0.12*** (0.01) | 0.30*** (0.02) | 0.30*** (0.02) | |
| R 2 | .26 | .23 | .26 | .26 |
| No. of observations | 10,000 | 10,000 | 10,000 | 10,000 |
p < .05. **p < .01. ***p < .001.
Example With Real Data
With the growing availability of data for assessing educational and psychological research questions, more and more studies will likely use multiple regression to compare the importance of predictors. For example, among educational researchers, the availability of large nationally representative longitudinal data such as the Early Childhood Longitudinal Studies allow for the comparison of various early social and psychological characteristics as predictors of children’s later academic achievement. However, these early skills are measured with varying degrees of reliability. A number of recent studies have used large nationally representative data sets to compare skills measured at kindergarten entry as predictors of later achievement (e.g., G. J. Duncan et al., 2007; Fryer & Levitt, 2004; Grissmer et al., 2010). With rare exception (e.g., G. J. Duncan et al., 2007) measurement errors in the early skills are not accounted for.
To demonstrate the use of adjustment for measurement error when comparing two predictors when one is measured with greater error, data from the kindergarten wave of the Early Childhood Longitudinal Study, Kindergarten Cohort (ECLS-K) is used to predict reading achievement at the end of eighth grade. The ECLS-K contains measures of reading skills and fine motor skills at kindergarten entry. These early skills were measured with substantially disproportionate levels of measurement error. The reported reliability is .92 for early reading, compared with .57 for early fine motor skills.
Table 6 includes the naive model in which the observed variables are used without adjustment, and the errors-in-variables model which adjusts for the estimated reliabilities. The model without adjustment for measurement error suggests that the coefficient for reading is almost twice the magnitude of fine motor skills. However, the model adjusting for measurement error suggests that the two predictors are the same in magnitude. The test of the null hypothesis that the two coefficients are equal for the naive model suggests that differences of the estimated magnitude would be extremely rare if the two coefficients were equal in the population (1, 6845) = 122.27, < .001. However, the same test on the adjusted model, suggests that the estimated differences would not be rare at all (1, 6845) = 0.02, = 0.876.
Table 6.
Simple Regressions for Fine Motor and Reading, Unadjusted Multiple Regression (Naive), and Multiple Regression Adjusting for Measurement Error (Error-in-Variables) Predicting Fifth-Grade Reading.
| Naive | Errors-in-variables | |
|---|---|---|
| (Intercept) | −0.00 (0.01) | −0.00 (0.01) |
| Reading | 0.37*** (0.01) | 0.34*** (0.02) |
| Fine motor | 0.19*** (0.01) | 0.34*** (0.02) |
| .23 | .28 | |
| No. of observation | 6,848 | 6,848 |
p < .05. **p < .01. ***p < .001.
Table 7.
Descriptive Statistics of Real Data Example.
| M | SD | Reading 8th grade | Reading K | |
|---|---|---|---|---|
| Reading 8th grade | 0 | 1.1 | ||
| Reading K | 0 | 1.0 | .43 | |
| Fine motor K | 0 | 1.3 | .34 | .31 |
Note. M = mean; SD = standard deviation.
These two analyses lead to different conclusions about the relative importance of the two predictors. Based on the naive model not adjusting for measurement error, researchers would conclude that basic reading skills are almost twice as important as early fine motor skills. A hypothesis test would lead to the rejection of the null hypothesis that the two are equal in the population and would support the conclusion that early reading skills are more important than early fine motor skills for later reading achievement. However, had the researchers adjusted for measurement error in the two predictors, a very different conclusion would be justified. As the magnitude of the adjusted model coefficients are the same, and the null hypothesis is reasonable given the hypothesis test, the adjusted results suggest that there is no evidence that one of the predictors is more important than the other. The results of using real data (Table 6) demonstrate how measurement error can lead to vastly different estimates of the importance of predictors, and how adjustment can help correct for this bias.
This real analysis example provides an opportunity to discuss limitations to the simulations conducted. First, for ease of interpretation, only two predictors were included in the simulations. Most applied studies include numerous predictors, many of which may be intercorrelated and measured with varying levels of measurement error. This will likely greatly complicate the bias and Type I error rates in the resulting models. Second, estimates of reliabilities are not always available for all covariates, and it is not clear how these may impact the comparison of key predictors. For example, in our applied example, in addition to early reading and fine motor skills, researchers may want to control for demographic variables for which reliabilities are not provided. To the extent that these are correlated with the key predictors, the inevitable measurement error will have an impact on the bias and Type I error rates related to those predictors. Future simulation studies should explore the impact of measurement errors in such variables on comparing key predictors. Third, only the impact of measurement error, and not other types of errors captured by the model residuals, was considered. The classic measurement error model, while commonly used in methodological work, may not accurately reflect situations found in real research settings. Future work should also address the additional bias incurred when standardized coefficients are used and should also explore the impact of adjustments to the sample standard deviations with estimates of reliability. Another limitation of this study was the manipulation of the reliability of only one of the two predictors being compared. An important development of the insights provided by this study will be to evaluate the comparisons of measurement error in both predictors being compared across a wide range of reliabilities to understand the impact of disproportionate measurement error. Despite these limitations, and with the increasing number of large data sets available to psychological researchers, many of which not only contain large number of participants but also often contain a wide array of variables, this study suggests that great care is needed in interpreting the results, particularly, when researchers are interested in comparing the importance of multiple predictors.
Discussion, Recommendations, and Conclusions
Multiple regression is commonly used to compare the importance of two or more predictors. Often these predictors are measured with disproportionate levels of error. Differing levels of reliability for predictors measured within samples can bias the estimation of population parameters. In this article, I demonstrated how measurement error in one predictor can substantially bias parameter estimates and inflate the Type I error rates when comparing predictors. The results are consistent with prior research focusing on the impact of measurement error on the estimation of a key predictor when a covariate is measured with error, in that they demonstrate the substantial impact measurement error can have generally in multiple regression. However, there are also issues related to bias and Type I error unique to uses of regression models to compare predictors. In this section, I summarize the problems related to measurement error when comparing predictors, emphasizing the issues unique to this situation, then offer recommendations to researchers using multiple regression for this purpose.
Problems Comparing Predictors With Measurement Error
While the results of this study are consistent with previous studies showing that measurement error can bias parameter estimates and inflate Type I error rates, these results also demonstrate problems specific to studies aimed at comparing the importance of predictors. These differences generally stem from the change in focus of the study and the related change in the hypothesis being tested. In this section, I discuss three problems with the use of multiple regression for comparing the importance of predictors when one is measured with error.
Comparisons of Uncorrelated Predictors Can Be Biased When One Is Measured With Error, Leading to Inflated Type I Error Rates
An important difference between the present results and studies of measurement error that focus on bias and Type I error rates in a key predictor involves conditions in which the two predictors are uncorrelated. When the two predictors are not correlated the measurement error in one predictor does not lead to bias in estimating the other. Therefore, studies exploring the impact of measurement error in a covariate on estimation of a key predictor have found bias only in situations when the two are correlated and have emphasized the value of modeling orthogonal predictors.
However, when comparing two predictors, as was explored in this study, resulting bias is impacted by estimates of both the predictors. Even if the two predictors are not correlated, the bias in one of the predictors may lead to considerable bias in their comparison. More problematic, this bias also leads to inflation of Type I error rates for testing the null hypothesis that the two coefficients are equal, by means of both the underestimation of the coefficients and the inflation of the standard errors of the less reliable predictor. When comparing the importance of predictors, bias and Type I error rates are problematic when these predictors are measured with disproportionate levels of measurement error, even if the predictors being compared are not correlated.
Minimal Reliabilities Are Not Sufficient to Address Measurement Error When Comparing Predictors
It is not uncommon for research articles to report reliabilities of measures, noting that all measures meet some minimal cutoff criterion. For example, Lance et al. (2006) describe how Nunnally (1978) is often misinterpreted as suggesting that reliability estimates of .70 or higher are acceptable. The results of this study suggest that this is not sufficient to address issues related to bias and Type I error when comparing predictors. For many conditions in the simulation study with reliabilities considered typical in research, bias and Type I error rates were found to be unacceptably high. This is particularly true in conditions where the two predictors are highly correlated, the multiple was relatively large, or both of these conditions are present.
Large Sample Sizes Exacerbate the Impact of Compound Bias due to Measurement Error on Type I Error Rates
This study extended previous research by including much larger samples sizes typical of the large-scale nationally representative data sets such as the ECLS-K and found that small levels of measurement error in a predictor can have a substantial impact on the conclusions drawn. While large sample sizes often help with many modeling issues, such as power, the impacts of measurement error on Type I error rates are exacerbated in larger samples. When sample sizes were large, there were many conditions in the simulation results in which the Type I error rate were unacceptable (i.e., ranged from .1 to .99) with the reliability of the less reliable predictor at .90. The results are similar to prior work showing that measurement error can lead to unacceptable levels of bias and Type I error rates.
Recommendations
A number of recommendations are provided to help researchers conduct and evaluate studies using regression models to compare the importance of predictors. First, instead of simply ensuring that predictors meet some minimum standard, it is recommended that researchers also assess the disproportionality of reliabilities of predictors being compared in a particular sample. If disproportionate levels of measurement error exist, then caution is warranted in interpreting such comparisons, and adjustments may need to be made to obtain less biased estimates and more acceptable Type I error rates. Future research should explore a wider variety of more realistic situations when both variables are measured with differing levels of reliability to give researchers a better understanding of the impact of measurement error when comparing predictors in situations when both are measured with error.
Second, when evaluating one or more studies in which the more reliably measured predictor is also more strongly correlated to the outcome than a less reliably measured predictor, researchers should suspect that the difference between the two estimated coefficients may be exaggerated. In such situations, it is possible that the more reliably measured predictor is overestimated and the less reliably measured predictor is underestimated. Third, when sample sizes are large, researchers should be very careful when interpreting differences in regression coefficients and recall that tests against the null hypothesis that the two coefficients are equal may suffer from drastic inflation of Type I error rates.
Finally, if estimates of the reliability of measures within the sample are available, using one of the available methods for adjusting for measurement error is recommended. And if standardized coefficients are being compared the variables should be standardized by adjusting the sample standard deviation using the reliability of the variables. In addition to demonstrating the problems arising from using multiple regression to compare predictors when one is measured with error, I also demonstrated that in certain situations simple adjustment methods can provide much less biased estimates with more reasonable Type I error rates. By using real data, I demonstrated how the reliabilities of the predictors can be estimated; researchers can adjust for measurement error to obtain less biased estimates.
Conclusions
Prior research has demonstrated the complication of measurement error in the bias and Type I error rates when using multiple regression to isolate the relation between a key predictor and the outcome using one or more covariates. Many of these problems also impact the use of multiple regression for comparing the relative importance of two predictors on the outcome. In both situations the greater the measurement error, the stronger the correlation between predictors, the stronger the relation between the predictors and the outcome, the greater the bias and Type I error. In both situations, the larger the sample size the greater the Type I error rate. But because the hypothesis being tested is different for these two situations, there are also some problems specific to the use of multiple regression for comparing predictors that researchers should keep in mind when designing and interpreting such studies.
A major insight provided by this study is that ensuring that the reliabilities of the predictors surpass a threshold is not sufficient to deal with the bias and Type I error rates related to measurement error when comparing two or more predictors. While large sample size helps with many analytic issues, I also demonstrated that the impact of measurement error in one predictor is much worse for large sample sizes. Additionally, I showed that in situations where the more reliable predictor is also more strongly related to the outcome, the bias when comparing predictors can be much greater than in studies focusing on a key predictor.
Related to the real data example, there is great interest in identifying new predictors of later achievement, but these candidate skills will likely continue to be measured less reliably than early reading and math skills, which are well established in the field of early education. This could lead to a systematic bias against new skills being identified as important, simply because of the relative lack of measurement work. If these candidate skills are dropped from consideration before relatively reliable measures are developed, researchers run the risk of missing important predictors of later achievement. Similar systematic biases might exist in other areas of psychological and educational fields where newer measures are being compared with highly reliable measures.
These insights highlight the importance of measure reliability for predictive modeling. A number of methods exist for adjusting for measurement error. Two were demonstrated in this article and shown to adequately deal with the bias and Type I error rates in a hypothetical example. One of these methods was also used on a real data example and demonstrated how the decision of whether to adjust for measurement error can have substantial impacts on interpretation of results. The goal of this article was to make researchers aware of the impact of measurement error on comparisons of regression coefficients and point them toward resources to help address these issues. Measurement is a critical, but often neglected, aspect in many studies. Based on the results of this study, it is recommended that researchers pay close attention to the reliabilities of predictors being compared. The methodological literature has often argued that when the goal is to compare the importance of two predictors, the appropriate statistical test is against the null hypothesis that the two coefficients are equal in the population. However, when one of the variables is measured with substantial measurement error, comparisons of coefficients may suffer from compound bias, particularly in large samples, and adjustments for the reliabilities of the measures should be considered.
Supplemental Material
This article is distributed under the terms of the Creative Commons Attribution 4.0 License (https://creativecommons.org/licenses/by/4.0/) which permits any use, reproduction and distribution of the work without further permission provided the original work is attributed as specified on the SAGE and Open Access pages (https://us.sagepub.com/en-us/nam/open-access-at-sage).
Supplemental material, relsimMerged for Compound Bias due to Measurement Error When Comparing Regression Coefficients by William M. Murrah in Educational and Psychological Measurement
Acknowledgments
I thank Erik Ruzek and two anonymous reviewers for helpful comments on this article.
R code to generate data, tables, and models for the hypothetical example are included in the online Supplemental Materials.
Note that this adjustment very closely recovers the population value of 1.00 for : 1.4 × = 0.99.
Computer code for both analyses are included in the online Supplemental Materials.
Footnotes
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
ORCID iD: William M. Murrah  https://orcid.org/0000-0001-9822-2522
https://orcid.org/0000-0001-9822-2522
Supplemental Material: Supplemental material for this article is available online.
References
- Blalock H. M., Wells C. S., Carter L. F. (1970). Statistical estimation with random measurement error. Sociological Methodology, 2, 75-103. doi: 10.2307/270784 [DOI] [Google Scholar]
- Bradley J. V. (1978). Robustness? British Journal of Mathematical and Statistical Psychology, 31, 144-152. [Google Scholar]
- Brunner J., Austin P. C. (2009). Inflation of Type I error rate in multiple regression when independent variables are measured with error. Canadian Journal of Statistics, 37, 33-46. [Google Scholar]
- Cameron C. E., Brock L. L., Murrah W. M., Bell L. H., Worzalla S. L., Grissmer D., Morrison F. J. (2012). Fine motor skills and executive function both contribute to kindergarten achievement. Child Development, 83, 1229-1244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll R. J., Ruppert D., Stefanski L. A., Crainiceanu C. M. (2006). Measurement error in nonlinear models: A modern perspective. Boca Raton, FL: CRC Press. [Google Scholar]
- Chalmers P. (2018). SimDesign: Structure for organizing Monte Carlo simulation designs. Retrieved from https://CRAN.R-project.org/package=SimDesign
- Cochran W. G. (1970). Some effects of errors of measurement on multiple correlation. Journal of the American Statistical Association, 65(329), 22-34. doi: 10.2307/2283572 [DOI] [Google Scholar]
- Cohen J., Cohen P., West S. G., Aiken L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences. Mahwah, NJ: Lawrence Erlbaum. [Google Scholar]
- Duncan G. J., Dowsett C. J., Claessens A., Magnuson K., Huston A. C., Klebanov P., . . . Japel C. (2007). School readiness and later achievement. Developmental Psychology, 43, 1428-1446. [DOI] [PubMed] [Google Scholar]
- Duncan O. D. (1975). Introduction to structural equation models. New York, NY: Academic Press. [Google Scholar]
- Fox J. (2016). Applied regression analysis and generalized linear models. Los Angeles, CA: Sage. [Google Scholar]
- Fryer R. G., Levitt S. D. (2004). Understanding the black-white test score gap in the first two years of school. Review of Economics and Statistics, 86, 447-464. [Google Scholar]
- Fuller W. A. (1987). Measurement error models (1st ed.). New York, NY: Wiley. [Google Scholar]
- Gelman A., Stern H. (2006). The difference between significant and not significant is not itself statistically significant. The American Statistician, 60, 328-331. doi: 10.1198/000313006X152649 [DOI] [Google Scholar]
- Grissmer D., Grimm K. J., Aiyer S. M., Murrah W. M., Steele J. S. (2010). Fine motor skills and early comprehension of the world: Two new school readiness indicators. Developmental Psychology, 46, 1008-1017. [DOI] [PubMed] [Google Scholar]
- Kenny D. A. (1979). Correlation and causality. New York, NY: Wiley. [Google Scholar]
- Lance C. E., Butts M. M., Michels L. C. (2006). The sources of four commonly reported cutoff criteria: What did they really say? Organizational Research Methods, 9, 202-220. [Google Scholar]
- Lindsay D. S. (2015). Replication in psychological science. Psychological Science, 26, 1827-1832. doi: 10.1177/0956797615616374 [DOI] [PubMed] [Google Scholar]
- Lockwood J. (2018). Eivtools: Measurement error modeling tools. Retrieved from https://CRAN.R-project.org/package=eivtools
- Lord F. L., Novick M. R. (1968). Statistical theories of mental test scores. Reading, MA: Addison-Wesley. [Google Scholar]
- Muthén L. K., Muthén B. O. (2017). Mplus user’s guide. Los Angeles, CA: Muthén & Muthén. [Google Scholar]
- Nunnally J. C. (1978). Psychometric theory. New York, NY: McGraw-Hill. [Google Scholar]
- Pedhazur E. J. (1997). Multiple regression in behavioral research: Explanation and prediction. New York, NY: Wadsworth. [Google Scholar]
- R Core Team. (2018). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; Retrieved from https://www.R-project.org/ [Google Scholar]
- Shadish W. R., Cook T. D., Campbell D. T. (2002). Experimental and quasi-experimental designs for generalized causal inference. Boston, MA: Houghton Mifflin. [Google Scholar]
- Shear B. R., Zumbo B. D. (2013). False positives in multiple regression: Unanticipated consequences of measurement error in the predictor variables. Educational and Psychological Measurement, 73, 733-756. [Google Scholar]
- Suggate S., Pufke E., Stoeger H. (2018). Do fine motor skills contribute to early reading development? Journal of Research in Reading, 41, 1-19. [Google Scholar]
- Zinbarg R. E., Suzuki S., Uliaszek A. A., Lewis A. R. (2010). Biased parameter estimates and inflated Type I error rates in analysis of covariance (and analysis of partial variance) arising from unreliability: Alternatives and remedial strategies; Journal of Abnormal Psychology, 119, 307-319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zumbo B. D. (2007). Validity: Foundational issues and statistical methodology. In Rao C. R., Sinharay S. (Eds.), Handbook of statistics: Vol. 26. Psychometrics (pp. 45-79). Amsterdam, Netherlands: Elsevier. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
This article is distributed under the terms of the Creative Commons Attribution 4.0 License (https://creativecommons.org/licenses/by/4.0/) which permits any use, reproduction and distribution of the work without further permission provided the original work is attributed as specified on the SAGE and Open Access pages (https://us.sagepub.com/en-us/nam/open-access-at-sage).
Supplemental material, relsimMerged for Compound Bias due to Measurement Error When Comparing Regression Coefficients by William M. Murrah in Educational and Psychological Measurement