A Model System for Photocatalysis: Ti-Doped α-Fe₂O₃(11̅02) Single-Crystalline Films

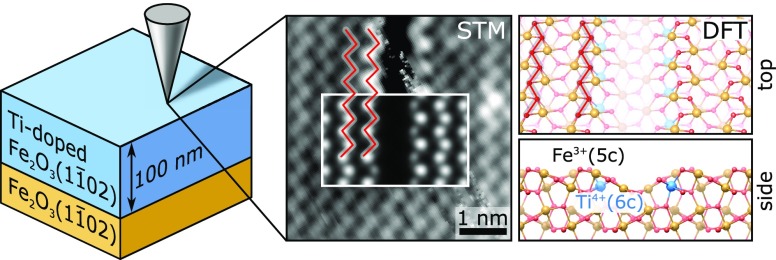
Abstract

Hematite (α-Fe₂O₃) is one of the most investigated anode materials for photoelectrochemical water splitting. Its efficiency improves by doping with Ti, but the underlying mechanisms are not understood. One hurdle is separating the influence of doping on conductivity, surface states, and morphology, which all affect performance. To address this complexity, one needs well-defined model systems. We build such a model system by growing single-crystalline, atomically flat Ti-doped α-Fe₂O₃(11̅02) films by pulsed laser deposition (PLD). We characterize their surfaces, combining in situ scanning tunneling microscopy (STM) with density functional theory (DFT), and reveal how dilute Ti impurities modify the atomic-scale structure of the surface as a function of the oxygen chemical potential and Ti content. Ti preferentially substitutes subsurface Fe and causes a local restructuring of the topmost surface layers. Based on the experimental quantification of Ti-induced surface modifications and the structural model we have established, we propose a strategy that can be used to separate the effects of Ti-induced modifications to the surface atomic and electronic structures and bulk conductivity on the reactivity of Ti-doped hematite.

1. Introduction

It has been almost half a century since sunlight was first used to produce hydrogen via photoelectrochemical water splitting.¹ Since then, generations of scientists have searched for ideal anodic materials and ways to improve their performance. Hematite (α-Fe₂O₃; for simplicity of notation, we will drop the “α” from now on) has long been a leading player in the scene. Theoretically, hematite enables a solar-to-hydrogen conversion efficiency of 15%, and with its high stability,² nontoxicity, and low cost,^3,4 it is an ideal anode material. In practice, some of its intrinsic properties severely limit performance, in particular fast charge recombination, low conductivity, and poor kinetics for water oxidation.^3,4 Lightly doping the material with Ti has proven to be a good strategy to improve the electrocatalytic performance.⁵⁻⁹ Scaling of the performance with the doping level is, however, not trivial.^7,8

To explain how Ti doping enhances the solar-to-hydrogen conversion efficiency, one first needs to understand how the dopants affect the oxygen evolution reaction (OER), a crucial reaction occurring at the surfaces of hematite photoanodes.⁴ This requires disentangling the properties of hematite that can affect the OER and are possibly doping-dependent, such as the electrical conductivity in the bulk and at the surface,⁷ the morphology and the surface crystallographic orientation,^6,8,10,11 its atomic-scale structure,^8,12,13 and the surface states that are involved in the relevant processes.¹⁴ The most commonly synthesized Ti-doped hematite electrodes do not allow this, though, because their nanostructured morphologies are neither easily controlled nor modeled.^4,8 Moreover, in nanostructured electrodes, both the morphology and the photoelectrochemical activity are affected by the doping level, e.g., via passivation of grain boundaries by the dopants.⁶ Single-crystalline samples with atomically defined surfaces are best suited for disentangling the contributions from structural, morphological, electronic, and crystallographic effects.^9,12

Well-defined epitaxial Ti-doped hematite (Ti:Fe₂O₃) films with a (0001) orientation have been successfully grown by oxygen-plasma-assisted molecular beam epitaxy (MBE)^9,15 and have provided valuable insights into the relation between Ti-induced conductivity and photoelectrochemical activity. However, so far, it has not been investigated how the atomic-scale details of the film surfaces are modified by Ti impurities and how this precisely affects the OER at hematite surfaces. This is partly due to the ongoing controversy over the atomic-scale structure of (0001)-oriented Fe₂O₃.^12,16 In this respect, the less investigated (11̅02) orientation (or “R-cut”) of hematite is a better-suited model system. Recent surface science experiments combined with density functional theory (DFT) studies^17,18 of pure (undoped) Fe₂O₃ have unveiled two relatively simple surface terminations of this facet that are stable under ultrahigh vacuum (UHV) conditions: the stoichiometric, bulk-truncated (1 × 1) (see Figure 1) and the reduced (2 × 1) surfaces. Both surface structures can be reproducibly prepared by standard sputtering–annealing cycles at appropriate oxygen chemical potentials. Their reliable experimental realization and the availability of a confirmed, atomic-scale model make Fe₂O₃(11̅02) an ideal model system to investigate how Ti impurities affect hematite surfaces.

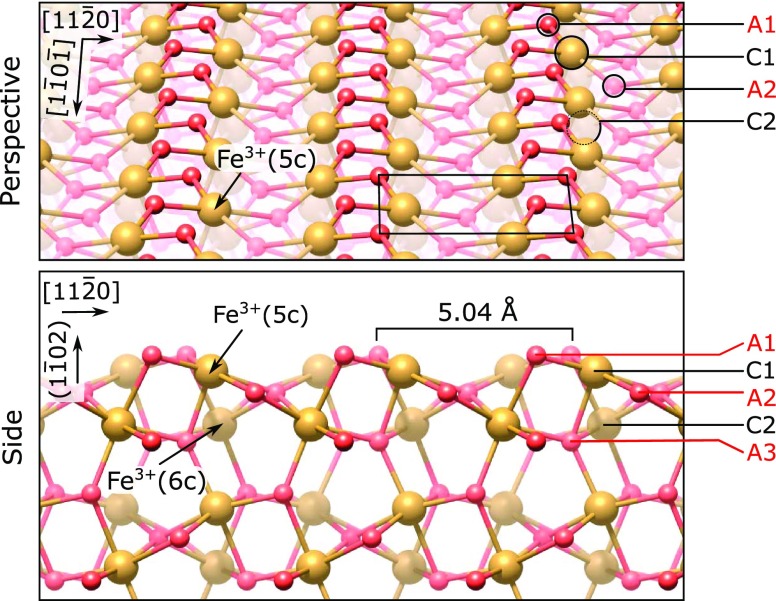
Figure 1.

Perspective (top) and side view (bottom, looking along the [1̅101] direction) of the (1 × 1) termination of the Fe₂O₃(11̅02) surface, as in ref (17). The direction perpendicular to the surface is labeled (11̅02) in round brackets because there is no integer-index vector corresponding to that direction for the (11̅02) plane. The structure is characterized by zigzag rows of oxygen (small, red spheres) and iron atoms (large, brown spheres) and has a unit cell measuring 5.04 × 5.44 Ų (black rectangle). The coordination of Fe cations is indicated in round brackets, and labels for the first few anion and cation layers are indicated on the right side.

Doping this system with Ti should enhance its conductivity,^6,7 a bonus for scanning tunneling microscopy (STM). Typically, contaminant-free, undoped Fe₂O₃(11̅02) single crystals are not conductive enough for STM unless their bulk is reduced by repeated sputtering–annealing cycles (60–100) to introduce oxygen vacancies.¹⁷ This treatment roughens the surface, though, complicating STM measurements and the interpretation of reactivity studies. Increasing the conductivity with Ti doping would cut the need for harsh sputtering treatments, thus facilitating and stimulating more surface science studies on this promising system.

We produced single-crystalline Ti:Fe₂O₃(11̅02) films by pulsed laser deposition (PLD). In previous works, we showed that metal oxide films with atomically flat surfaces suited for surface science investigations can be obtained by PLD, provided that the growth parameters are carefully optimized (e.g., one has to tune the oxygen background pressure and the substrate temperature that can affect both the growth mode and the film morphology).¹⁹⁻²¹ The introduction of a dopant such as Ti adds the challenge of controlling both the doping concentration and its distribution within the film. Doped films can be grown by PLD, either from a single, doped target or by alternating deposition from two targets. The latter approach yields high flexibility in tuning the doping level but requires a careful calibration of the deposited amounts: sticking effects, the oxygen chemical potential, and the laser fluence can all affect the species deposited by PLD.^21,22

In this work, we optimized the PLD growth conditions for well-defined, single-crystalline Ti:Fe₂O₃(11̅02) films. We tuned their doping level by alternating between Fe₃O₄ and TiO₂ targets during deposition. We observed that Ti partially segregates to the surface during growth, and we found standard sputtering–annealing treatments to be effective in removing this excess. For the doping levels explored in this work (up to 3.1 atom %), the (2 × 1) surface of undoped Fe₂O₃(11̅02) single crystals appears unmodified by the presence of Ti. On the (1 × 1) termination, line defects are formed locally, but the surface is otherwise largely undisturbed. With support from DFT, we investigated in depth how Ti affects the (1 × 1) surface over a variety of oxygen chemical potentials. Theory predicts that Ti preferentially substitutes Fe in the subsurface layer, causing the formation of the line defects observed in experiments.

The careful characterization of our Ti:Fe₂O₃(11̅02) model surfaces allows us to set the stage for future reactivity studies. We propose a strategy to disentangle the contributions of the surface atomic and electronic structures and of the bulk conductivity to the OER activity. We identify the coverage of line defects and the surface doping as suitable descriptors for the surface atomic and electronic structures, respectively, and highlight the unique dependencies of these descriptors on the oxygen chemical potential, the amount of Ti deposited after growth, and the bulk doping. One can use these quantitative relations to shed light on the mechanisms ruling the photocatalytic water-splitting activity of Fe₂O₃ model surfaces.

2. Experimental and Computational Methods

2.1. Experimental Setup

The Ti:Fe₂O₃ films were deposited in a UHV PLD chamber suited for high-temperature and high-pressure depositions (base pressure below 4 × 10^–10 mbar after bake-out).¹⁹ Substrate temperatures up to 1200 °C can be reached, and background pressures can be up to 1 mbar while monitoring the growth via reflection high-energy electron diffraction (RHEED; a doubly differentially pumped TorrRHEED gun from STAIB Instruments GmbH, 35 keV beam energy). An ultraviolet KrF excimer laser was used for growth (Coherent CompexPro 201, 248 nm, ∼20 ns pulses). During growth, the sample was heated by a collimated continuous-wave infrared laser (DILAS, 980 nm) directed on the back of the sample through a hole in the sample plate, and O₂ was dosed via a leak valve. The temperature was monitored with an Impac IGA5 pyrometer directed on the sample surface. The PLD chamber is connected via a UHV transfer chamber with a surface science system with base pressure below 5 × 10^–11 mbar. This system comprises an analysis chamber equipped with X-ray photoelectron spectroscopy (XPS; Omicron nonmonochromatic Mg/Al Kα source, SPECS Phoibos 100 analyzer), low-energy electron diffraction (LEED; Omicron SpectaLEED), and STM (SPECS Aarhus 150), as well as a preparation chamber where Ar⁺-sputtering–annealing cycles can be performed (typical parameters: 8 × 10^–6 mbar Ar, 1 keV, ∼6 μA, 12 min, plus annealing at the conditions specified in the text). Some of the films were measured in a separate, two-chamber UHV system, consisting of a preparation chamber (base pressure <1 × 10^–10 mbar) and an analysis chamber (base pressure <7 × 10^–11 mbar), equipped with a commercial LEED module (VSI), a nonmonochromatic Mg Kα X-ray source (VG), and a SPECS Phoibos 100 analyzer for XPS, as well as an Omicron μ-STM operated in constant-current mode. The preparation chamber of this second UHV setup contains an electron-beam evaporator (Omicron), which was used for deposition of Ti, and a quartz-crystal microbalance.

2.2. Substrates

Natural Fe₂O₃(11̅02) single crystals were used as substrates (SurfaceNet GmbH, 5 × 5 × 0.5 mm³, one-side polished, <0.3° miscut). To remove contamination resulting from polishing, the as-received samples were sonicated in heated neutral detergent (3% Extran MA 02, 2 × 30 min) and ultrapure water (Milli-Q, 10 min). To overcome the insulating nature of the (nominally undoped) substrate, and ensure electrical contact of the conductive film to the sample plate, Pt electrodes were deposited by magnetron sputtering on the substrate prior to the film growth (the Pt covering the front corners, sides, and a 0.5 mm-wide frame at the edge of the backside of the sample), as described elsewhere.²¹ The substrate was then mounted on an HNO₃-cleaned Nicrofer (high-temperature- and oxidation-resistant alloy) sample plate with Nicrofer clips (spot-welded onto the plate) and inserted into the UHV PLD system. Two cycles of Ar⁺ sputtering plus O₂ annealing (1 h, 1 mbar, 900 °C) were performed prior to each growth. This procedure yields contaminant-free surfaces (as judged by XPS, not shown): neither typical contaminants coming from the ex situ treatment (C, K, Na, Ca) nor foreign metals commonly present in natural hematite crystals (e.g., Mn, Cr) were observed in the survey spectra recorded with 50 eV pass energy (neither at normal nor at grazing emission). Moreover, the surfaces are atomically flat, as judged by ex situ atomic force microscopy (AFM) (Agilent 5500 ambient AFM in intermittent contact mode in air with Si tips on Si cantilevers).

2.3. Growth Parameters

The films were deposited by alternating deposition from Fe₃O₄ and TiO₂ single-crystal targets. To remove contamination from the target surfaces, they were preablated before each growth by scanning them so that the excimer laser beam hit at least 10 times each spot of the area later ablated for deposition. During preablation, the substrate was kept in a separate, interconnected UHV chamber. The substrate temperature and O₂ background pressure, as well as the doping level, were chosen to comply with three main (intertwined) constraints: (i) stabilize the oxidized hematite phase; (ii) achieve sufficient diffusion during growth to yield well-ordered, single-crystalline films; and (iii) ensure a dilute, uniform distribution of Ti dopants within the film. The hematite phase was stabilized by selecting appropriate combinations of pressure and temperature, as inferred from the phase stability diagram of iron oxides from the literature.²³ To achieve the highest possible crystallinity, we opted for temperatures enforcing a step-flow regime, i.e., above 800 °C, as judged by the real-time behavior of the intensity of the RHEED specular spot during growth. Below 750 °C, RHEED oscillations consistent with a layer-by-layer growth were observed instead. We chose a growth temperature of 850 °C to achieve a uniform distribution of the Ti dopants in the bulk of the film (more details in Section S2 of the Supporting Information). The films discussed in this paper were grown at 850 °C, 2 × 10^–2 mbar O₂, 2.0 J/cm², 5 Hz, and 60 °C/min ramp rate for heating and cooling and with no postannealing after growth. The doping levels of 0.8 and 3.1 atom % were achieved by running an automated growth recipe consisting of 120 cycles in which one (or three, for 3.1 atom %) laser pulse(s) was shot on the TiO₂ target, followed by 500 (375) laser pulses shot on the Fe₃O₄ target. The low-doped films [120 cycles of (500 + 1) laser pulses] are of 91.5 ± 7.4 nm thickness, as evaluated from stylus profilometer measurements (not shown).

2.4. XPS Analysis

The intensity of the Ti 2p peaks was evaluated in CasaXPS by normalizing their area to the O 1s peak, after subtracting the normalized intensity of the O 1s satellite (originating from the Kβ line of the Al X-ray source) superimposed to this feature. The intensity and line shape of the O 1s satellite was previously measured on an undoped Fe₂O₃(11̅02) reference sample. All XPS peak areas were evaluated after subtracting a Shirley-type background.

2.5. Definition of a Monolayer (ML)

Fe₂O₃ is composed of cation bilayers along the (11̅02) direction, where each bilayer contains four Fe atoms per (1 × 1) surface unit cell (see Figure 1). In the following, we define one monolayer (ML) as the number of Fe atoms in one cation layer per (1 × 1) surface unit cell of Fe₂O₃(11̅02), i.e., two Fe atoms per (1 × 1) surface unit cell, or 7.3 × 10¹⁴ atoms/cm². Therefore, each cation bilayer of Fe₂O₃(11̅02) contains 2 ML of Fe.

2.6. Evaluation of Trench Coverages

Trench coverages (θ) were evaluated with the image-processing software ImageJ²⁴ and correspond to the fractional amount (in monolayers) of missing Fe atoms in the topmost cation layer. The trench coverages reported were obtained by averaging the values measured on at least 10 atomically resolved 50 × 50 nm² STM images acquired at different spots on the sample. To evaluate the number of missing Fe atoms at the surface, a skeletonized mask selecting only the lattice position of surface Fe atoms was overlaid to the image (this mask was created from the maxima of the Fourier-filtered image). A threshold function was then applied to the area of the image under the mask to count the ratio of pixels of a trench with respect to the number of total pixels selected by the mask. Regions in proximity (∼2 nm) of steps were discarded from the analysis. Error bars of the coverages represent 90% confidence intervals calculated with a two-tailed Student’s t-distribution from the standard error of the mean that was obtained by statistical evaluation of the STM images. Error bars of derived quantities are calculated assuming statistical independence of the quantities involved.

2.7. Definition of Experimental Oxygen Chemical Potential

The “experimental” chemical potentials, i.e., those derived from experimental quantities, were calculated using the ideal gas relation

where p₀ = 1 × 10³ mbar; k is the Boltzmann constant; p and T are the oxygen pressure and absolute temperature used in the experiment, respectively; and μ_O2⁰(T) is the chemical potential for gaseous O₂ at pressure p₀ and temperature T as derived from the relation μ_O2(T) = H_O2(T, p₀) – H_O2(0 K, p₀) – T[S_O2(T, p₀) – S_O2(0 K, p₀)]. H_O2(T, p₀) and S_O2(T, p₀) are the enthalpy and entropy per oxygen molecule, respectively, and are derived from thermochemical tables.^25,26 “Experimental” oxygen chemical potentials are named μ_O^exp = μ_O2(T, p)/2 to distinguish them from the ones computed by DFT, μ_O, defined below.

2.8. Computational Details

All DFT calculations employed the Vienna Ab initio Simulation Package^27,28 (VASP), with the projector-augmented wave method^29,30 describing the electron–ion interactions. The Perdew, Burke, and Ernzerhof³¹ exchange–correlation functional was employed together with a Hubbard U to treat the highly correlated Fe 3d electrons.³² Consistent with previous studies,^17,33 we chose U_eff = 4.0 eV. This value has been shown to best reproduce the experimental values of the band gap and the Fe–Fe distances in the bulk of Fe₂O₃.³⁴ The same U_eff was used for the Ti dopant ions so as not to artificially bias the 3d electron occupations among different transition-metal cations.³⁵ For the best structures, calculations were also repeated with U_eff = 5.0 eV for Ti as derived from experiments and first-principles calculations,³⁵⁻³⁷ with no significant changes in the relative stabilities of the structures. The effects of the choice of U_eff on the density of states for one exemplary structure are briefly addressed in Section S5 of the Supporting Information. The plane-wave basis-set cutoff energy was set to 450 eV. Asymmetric slabs consisting of 20 atomic layers (i.e., four O–Fe–O–Fe–O units, ≈13.3 Å slab thickness) were constructed based on the previously optimized bulk structure. A vacuum gap of ≈16 Å was used to separate periodic images of the slab along the direction normal to the surface.¹⁷ Supercell sizes for testing Ti dopant positions ranged from (2 × 1) to (4 × 4), depending on the defects considered. A Γ-centered k-mesh of 4 × 8 × 1 was used for the (2 × 1) cells and adjusted according to supercell size, down to 2 × 2 × 1 for the (4 × 4) slabs. All surface models were relaxed until the residual forces acting on ions were smaller than 0.02 eV/Å. The reference energy of a free oxygen molecule in the triplet state in a 10 × 11 × 12 ų cell was calculated with the same functional and potential as for the Fe₂O₃ slabs. The chemical potential of oxygen was referenced to half of the energy of one oxygen molecule (1/2E_O2); in the following, we name this quantity μ_O^DFT. Notice that this definition does not account for entropic contributions, as common in ab initio thermodynamics.^26,38 In Section S4 of the Supporting Information, we provide estimates for the discrepancy between μ_O and μ_O^exp.

We computed the “formation energy” per Ti atom and per (1 × 1) unit cell of some surface structures with Ti substituting Fe (refer to Figure 6 and the main text) as²⁶

1

where n × m is the size of the slab in (1 × 1) unit cells; p and T are the pressure and temperature of a gas-phase O₂ reservoir, respectively; −ΔN_O and −ΔN_Fe are the number of O and Fe atoms removed from the reference structure, respectively; N_Ti is the number of Ti atoms substituting Fe; E_n×m is the DFT energy of the slab; and μ_i(p,T) is the chemical potential of Fe and O. To be more precise, eq 1 yields the differences in the grand potentials of one structure and its reference (see eq 2) at constant area and constant number of Ti atoms, assuming comparable entropic contributions. It is also related to the difference in surface energy as Δϕ_n×m = Δγ_n×mA_(1×1)/N_Ti, where A_(1×1) is the area of one (1 × 1) cell. The energy of the reference structure for an area of n × m unit cells is calculated as

2

where E_(1 × 1)Ti is the DFT energy of a (1 × 1)_Ti structure (Figure 6b), where two Ti atoms replace Fe in layer C2 in a (2 × 1) cell (hence, the factor 1/2), while E_{(1×1)undoped} is the DFT energy of a (1 × 1) cell of undoped Fe₂O₃(11̅02). In a nutshell, the reference energy in eq 2 for a given structure with a n × m size and a number of Ti atoms N_Ti is obtained by comparing to an equivalently sized slab in which the same amount of Ti is accumulated into the favored (1 × 1)_Ti structure of Figure 6b. For selected structures, we verified that eq 2 yields the same energy as explicitly relaxing these composite slabs. Notice that this choice of reference is natural for our system, as the diffusion of Ti into the bulk is inhibited at the 550 °C preparation temperature, so the number of Ti atoms in the subsurface is constant. As a consequence of this choice of reference, eq 1 does not contain the chemical potential of Ti. In other words, minimizing Δϕ yields the best structure for accommodating N_Ti atoms in the near-surface. Notice also that it is sufficient to represent Δϕ as a function of μ_O^DFT, since the chemical potentials of Fe and O are linked by the cohesive free energy of bulk hematite.²⁶

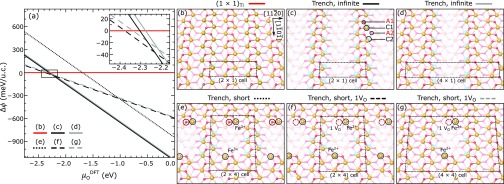
Figure 6.

Surface phase diagram and structures of Ti-doped Fe₂O₃(11̅02) as a function of μ_O^DFT. (a) Formation energies per Ti atom and per (1 × 1) unit cell of trench structures with different spacings, relative to surfaces with the same amount of Ti doping in the subsurface, but without trenches, i.e., a combination of undoped (1 × 1) and the (1 × 1)_Ti structure of panel (b) (see Section 2.8 for details). The inset shows the region around μ_O = −2.3 eV in greater detail. (b) Perspective view of the (1 × 1)_Ti structure with two Ti atoms per (2 × 1) unit cell. (c, d) Perspective views of trenches indefinitely extended along the [11̅01̅] direction, with a periodicity of two and four unit cells along the [112̅0] direction, respectively; (e–g) short trenches with and without one additional oxygen vacancy (V_O) per supercell. The dimensions of the supercells are indicated in the panels.

3. Experimental Results

3.1. UHV-Prepared PLD Films

Figure 2 compares how different bulk doping levels affect the surfaces of UHV-prepared, Fe₂O₃(11̅02) films with Ti doping levels of 0.77 ± 0.06 and 3.09 ± 0.24 atom %. The Ti concentrations are given in atomic percent of cations, such that 0.77 atom % doping corresponds to x = 0.0077 in the commonly used (Fe_1–xTi_x)₂O₃ notation. In Section S3 of the Supporting Information, we describe in detail how we estimated the doping level from an independent evaluation of the amounts of Fe and Ti deposited with each laser pulse shot on the corresponding targets. For simplicity of notation, we will often refer to these doping levels as 0.8 and 3.1 atom % or as “low” and “high”. After growth, the film surfaces were prepared following the procedures for single-crystalline, undoped Fe₂O₃(11̅02) samples.¹⁷ One can either prepare a (2 × 1) structure under reducing conditions (Ar⁺ sputtering plus UHV annealing at ≈600 °C) or a stoichiometric, bulk-terminated (1 × 1) structure (Figure 1) under slightly oxidizing conditions (Ar⁺ sputtering plus annealing at >1 × 10^–6 mbar O₂, ≈550 °C). Due to their strongly insulating nature, hematite surfaces of undoped crystals can only be imaged in STM after sufficient reduction of the bulk, commonly achieved with several (60–100) sputtering–annealing cycles.¹⁷ Remarkably, both Ti-doped films are conductive in STM at U_sample = 2 V, I_t = 0.1 nA at room temperature (RT) after a single sputtering–annealing cycle. Figure 2a₁–c₁ shows the mesoscale appearance of their surfaces after two sputtering–annealing cycles. The 50–200 nm-wide, atomically flat terraces are separated by monoatomic steps of ≈3.5 Å height. The surface quality of these Ti-doped films is significantly higher than that of the severely roughened surfaces typical of undoped crystals following the harsh sputtering treatments.

Figure 2.

UHV-prepared surfaces of differently doped Ti:Fe₂O₃(11̅02) films. (a₁–c₁) 40 × 40 nm² STM images, (a₂–c₂) 9 × 4.5 nm² STM images, and (a₃–c₃) corresponding LEED patterns. Left and middle columns: (2 × 1) and (1 × 1) terminations, respectively, obtained on the 0.8 atom % Ti-doped films with standard sputtering–annealing cycles [anneal 20 min at 600 °C, UHV for the (2 × 1), and 20 min at 550 °C, 7 × 10^–6 mbar O₂ for the (1 × 1); the corresponding experimental oxygen chemical potentials μ_O^exp are ≤−1.95 and −1.55 eV, respectively; see Section 2.7 for the definition of μ_O]. Except for the presence of dark rows (one marked by a black oval), the surfaces are very similar to those found on undoped single crystals. Right column: surface of a 3.1 atom %-doped film after preparation at slightly oxidizing conditions (550 °C, 7 × 10^–6 mbar O₂); a mostly (1 × 1) surface is obtained, with additional dark rows along the [11̅01̅] direction. The (1 × 1) periodicity is seen in the close-up STM (c₂); faint streaks corresponding to an (n × 1) periodicity are observed in LEED (c₃). Preparing the 3.1 atom %-doped film at reducing conditions results in a (2 × 1) reconstruction comparable to the one shown in the left column (not shown).

On the low-doped film, we reproduced both the (1 × 1) and the (2 × 1) surface structures known from undoped samples, as seen from the close-up STM images (Figure 2a₂,b₂) and the LEED patterns (Figure 2a₃,b₃). The (2 × 1) surface (Figure 2a₂) shows paired rows of bright protrusions running along the [11̅01̅] direction with a 10.1 Å periodicity along the [112̅0] direction, in agreement with STM images obtained on undoped samples.¹⁷ The (1 × 1) surface (Figure 2b₂) is also in line with previous experimental reports, with zigzag lines of bright protrusions (Fe atoms) along the [11̅01̅] direction, separated by ≈5.0 Å in the [112̅0] direction (also compare with the structural model of Figure 1). We note that there is no evidence for Ti impurities at the (2 × 1) surface (the observed defects are also typical for undoped single crystals). On the (1 × 1) surface, however, some new features are present in the form of dark rows oriented along the [11̅01̅] direction, as highlighted by the black oval in Figure 2b₁. Below, we argue that these defects are induced by the presence of subsurface Ti and that they form when a zigzag row of surface Fe atoms is missing. From an STM evaluation of the coverage of dark lines, we can obtain the amount of Fe atoms missing at the surface (details in Section 2.6); on the (1 × 1) surface of the 0.8 atom % film in Figure 2b₁, 2.08 ± 0.39% of Fe surface atoms are missing.

On films with a 4-times larger doping level, the same (2 × 1) reconstruction apparently unmodified by Ti can be prepared as for the 0.8 atom % film (not shown). However, some changes are observed when the surface is exposed to oxidizing conditions to achieve the (1 × 1) termination: while the mesoscale morphology is atomically flat (Figure 2c₁), more dark rows along the [11̅01̅] direction appear, suggesting a correlation between dark rows and Ti doping. Apart from the dark rows, the surface still resembles the (1 × 1) termination. The (1 × 1) periodicity is observed in the LEED pattern in Figure 2c₃ (together with a faint, streaky intensity in between the integer-order spots), and the typical zigzag lines are seen in the close-up STM images of Figure 2c₂. The coverage of dark rows now corresponds to 18.4 ± 1.1% of surface Fe sites.

We need to point out that the properties of the UHV-prepared films are somewhat different from those of the as-grown films: as we show in Section S1 of the Supporting Information, the conditions employed during growth result in a partial Ti segregation to the surface and in ill-defined, poorly ordered, Ti-rich phases. By removing the excess Ti with Ar⁺ sputtering, we can instead investigate the effect of minor doping levels on well-controlled hematite surfaces. After this first sputtering–annealing cycle, the amount of Ti at the surface remains unchanged even after tens of sputtering cycles at standard, UHV-compatible preparation conditions. This is seen in XPS (no change in the Ti 2p intensity) and in STM (unchanged coverage of dark rows at the surface), indicating a uniform doping level throughout the film. However, we observed a small increase in the Ti content at the surface after hundreds of cycles. We attribute this to the smaller sputter yield for Ti than for Fe and to the fact that Ti atoms sit in the subsurface (see Section 4).

3.2. Postgrowth Ti Deposition

To confirm that the dark rows are indeed associated with the Ti dopants, we deposited by PLD submonolayer amounts of Ti on the surface in Figure 2b, i.e., on an almost defect-free (1 × 1) surface. We also deposited Ti by MBE on an undoped Fe₂O₃(11̅02)-(1 × 1) sample. The results are shown in Figure 3a,b, respectively. Both depositions, by PLD and MBE, result in the formation of dark rows at the surface, confirming their correlation with Ti. Additionally, small and irregular islands are formed; they exhibit the same (1 × 1) surface structure with dark rows as the terrace (Figure 3d). In areas with a large number of dark rows, neighboring lines assemble to form an (n × 1) periodicity, with a local minimum spacing of n = 2 lattice units along the [112̅0] direction. This local arrangement is also reflected in the LEED pattern of Figure 3c: in between the main (1 × 1) spots, a faint horizontal streak characteristic of an (n × 1) periodicity is visible, with enhanced intensity in the region of half-integer spots. The similarity between PLD and MBE deposition allows us to exclude that the dark rows are caused by sputter-induced damage from energetic species ablated in PLD. Notice that the nominal amounts of Ti deposited by MBE for these experiments (calibrated by a quartz-crystal microbalance) and the coverage of trenches measured by STM are in agreement with the one-to-one relation between Ti coverage and trench coverage derived from our DFT model (see below).

Figure 3.

Deposition of submonolayer amounts of TiO₂ on Fe₂O₃(11̅02). (a, b) 28 × 28 nm² STM images showing the effect of submonolayer deposition of Ti on (a) a (1 × 1)-terminated 0.8 atom % Ti:Fe₂O₃(11̅02) film such as in Figure 2b and (b) on an undoped Fe₂O₃(11̅02) substrate. Similar results are achieved both by PLD [(a) 0.095 ML Ti, 550 °C, 2 × 10^–2 mbar O₂, 2 J/cm²] and by MBE [(b) 0.15 ML Ti, 500 °C, 5 × 10^–6 mbar O₂]. On the terraces, dark rows along the [11̅01̅] direction appear without significant alteration of the remaining (1 × 1)-structured areas. Additionally, small and irregular islands are formed. (c) LEED pattern corresponding to the surface in (b): an additional faint, half-integer periodicity indicates areas with dark rows in a local (2 × 1) arrangement. (d) 14.6 × 8 nm² STM image of the sample in (b), showing that the small islands appearing on the surface after deposition display the same (1 × 1) periodicity as the underlying terrace in the areas where trenches are not present.

3.3. Effect of μ_O^exp on Trench Coverages

The coverage of dark rows at the (1 × 1) surface can be controlled by varying the bulk doping, as seen in Figure 2b,c. For the low-doped film, we also observed a dependence of the coverage of dark rows on the oxygen chemical potential μ_O^exp used during annealing (Figure 4). The almost pristine (1 × 1) surface of the 0.8 atom % doped films in Figure 4a exposes more dark rows after annealing at higher μ_O (Figure 4b). Specifically, the initial 2.08 ± 0.39% coverage of dark rows, observed at 550 °C, 7 × 10^–6 mbar (μ_O^exp = −1.55 eV), changes to 4.57 ± 1.40% after 10 min at 550 °C, 3 × 10^–2 mbar (μ_O = −1.25 eV). The coverage of dark rows does not change upon further annealing at the same conditions: a coverage of 4.03 ± 0.47% was measured after 40 min. Furthermore, the process is fully reversible: the initial coverage of dark rows is recovered by annealing again for 20 min at 550 °C, 7 × 10^–6 mbar. Intriguingly, this phenomenon was not observed on the highly doped films: there, the coverage of dark rows is preserved at all O₂ pressures between 7 × 10^–9 mbar (μ_O^exp = −1.79 eV) and 3 × 10^–2 mbar (μ_O = −1.25 eV) at 550 °C.

Figure 4.

Effect of μ_O on the surface structure. The density of dark rows on the surface of a 0.8 atom %-doped Ti:Fe₂O₃(11̅02)-(1 × 1) film increases upon annealing at more oxidizing conditions: (a) annealing at 550 °C, 7 × 10^–6 mbar O₂, corresponding to μ_O^exp = −1.55 eV (see Section 2.7 for the definition of μ_O); (b) annealing at 550 °C, 3 × 10^–2 mbar O₂, corresponding to μ_O^exp = −1.25 eV. STM images are 40 × 40 nm² in size and were acquired at U_sample = +2 V, I_t = 0.2 nA.

4. Computational Results

4.1. Preferred Sites for Ti Substitution

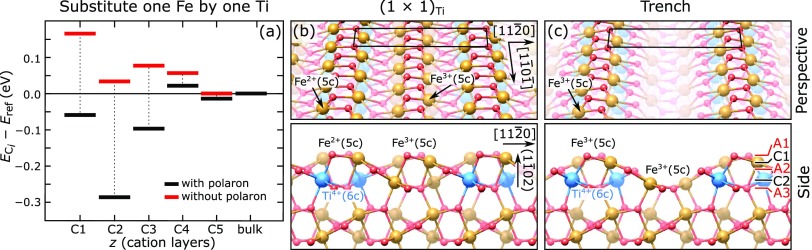
We performed DFT calculations to find a structural model for the Ti-correlated dark lines that appear on the (1 × 1) surface of our Ti:Fe₂O₃(11̅02) films. We tested different Ti concentrations based on the model for the (1 × 1) surface in Figure 1. Since previous works have demonstrated that dilute Ti impurities substitute Fe,^7,15 we first tested only Ti substitution without introducing additional defects. In a (2 × 2) supercell, we placed a single, isolated Ti atom in five different positions, one in each of the first five cation layers (for this set of calculations, we used asymmetric slabs with 30 atomic layers). The corresponding energy gains were compared to the energy gain of one Ti ion substituting Fe in a (2 × 2 × 3) bulk supercell [containing the same number of O, Fe, and Ti atoms as the (2 × 2) surface slabs; the supercell volume was fixed]. The results are shown in black in Figure 5a. Substituting one Fe atom for Ti in layers deeper than C3 is comparable to substitution in the bulk, while for layers C1, C2, and C3, there is an energy gain. Substitution in layer C2 shows the strongest energy gain (0.29 eV gain compared to substitution in the bulk and 0.23 and 0.19 eV compared to layers C1 and C3, respectively).

Figure 5.

(a) Black: calculated formation energies for substituting one Fe atom by one Ti atom in a given layer in a (2 × 2) supercell of the Fe₂O₃(11̅02)-(1 × 1) surface. For these calculations (polaron not artificially removed), the reference configuration is a bulk structure with a unit cell containing the same number of atoms as the slabs. Red: calculated formation energies for the same systems but with one electron artificially removed such that the polaron is not present. In this case, Ti substitution in layer C5 was used as a reference. (b, c) Calculated surface structures for two Ti atoms per (2 × 1) unit cell (i.e., 0.5 ML Ti). Ti is accumulated in layer C2 and preferentially orders in zigzag rows along the [11̅01̅] direction. (b) (1 × 1)_Ti structure, stable at reducing conditions: the structure of undoped (1 × 1) is retained, and surface Fe atoms above Ti have a charge state of 2+. (c) (2 × 1) trench structure, stable at oxidizing conditions: an equal number of Fe and O atoms is removed from the surface, allowing every remaining surface Fe to maintain a 3+ charge state. Atoms are labeled according to their coordination with oxygen.

During our calculations, we observed that introducing one Ti dopant always results in the formation of an electron polaron. The polaron localizes at one Fe cation, which acquires a charge state of 2+. For Ti substitution in layers C1, C2, and C3, the polaron preferentially localizes on an Fe atom in the topmost cation layer C1. Ti substitution in layers C4 and C5 causes the polaron to localize in layers C3 and C6, respectively. To address how the interaction between the dopant and the polaron affects the formation energies given in Figure 5a, we calculated the same structures with one electron artificially removed from the cell, thus removing the polaron and its interaction with the dopant.³⁹ The energy gains with respect to substitution in layer C5 are plotted in red in Figure 5a (Ti substitution in layer C5 was used as a reference in this case as this layer is sufficiently far from the surface to be considered bulklike; since the dopants have the same distances in all slabs, this choice allows us to neglect charge corrections⁴⁰ other than the jellium automatically included in the VASP code). The C2 layer is again preferred over neighboring ones, but the energy differences are less pronounced than when the polaron is present. Moreover, the substitution of isolated Ti atoms in layer C5 appears slightly more favorable than in layers closer to the surface when the polaron is removed. Therefore, we attribute most of the energy difference between C2 and the deeper layers to the dopant–polaron interaction.

4.2. Ti-Induced Surface Modifications

We also considered how two (or more) Ti atoms interact and thus preferentially arrange in the system. Rather than staying isolated, two Ti atoms in a (2 × 2) surface slab pair in the C2 layer along the [11̅01̅] direction such that they share an O-bonding partner in the A3 layer. This results in an energy gain of 0.08 eV, i.e., 0.04 eV per Ti. The best arrangement for two Ti atoms per (2 × 1) supercell (twice the amount of Ti) is shown in Figures 5b and 6b and labeled in the following as (1 × 1)_Ti. It is the most favorable arrangement of near-surface Ti, with 0.08 eV energy gain per Ti atom relative to isolated Ti in a C2 site, if one allows only cation substitutions without further modifying the composition. It consists of an infinite zigzag chain of Ti atoms in the C2 layer running along the [11̅01̅] direction, in which each Ti shares both of its O-bonding partners in layer A3 with a neighboring Ti. The top layer appears as a structurally unmodified (1 × 1). The calculated spin magnetic moments suggest that the surface Fe atoms directly above the Ti rows take on an Fe²⁺ charge state (3.5 μ_B), while all other iron atoms remain Fe³⁺ (4 μ_B).⁴¹ Further increasing the Ti concentration and substituting every Fe in layer C2 by Ti do not cause extra energy gain or energy cost.

When modifications in the composition are allowed, another structure is more favorable than the (1 × 1)_Ti surface at some values of μ_O^DFT. This is shown in Figures 5c and 6c. We call it trench reconstruction. The trenches are formed in the surface layers as a result of removing two Fe and two O atoms per (2 × 1) unit cell from the C1 and A1 layers, respectively. Because of this modification, the remaining surface Fe returns to a 3+ charge state, while Ti remains 4+ (see Figure 5c). We note that the concentration of Ti discussed here, i.e., two atoms per (2 × 1) unit cell all over the surface, is well above what is experimentally achieved with our doped films. For smaller concentrations, the trench spacing along [112̅0] can be expanded (see, for example, Figure 6d) and/or short trench structures can be constructed by breaking the periodicity along [11̅01̅]. Figure 6e–g shows a few examples (an additional oxygen atom per unit cell is missing in the structures of panels f and g).

Figure 6a shows the differences in the formation energies of these reconstructions as a function of μ_O^DFT, normalized to the supercell area and the number of Ti atoms. As detailed in Section 2.8, it plots the normalized differences Δϕ in the grand potentials of each structure and its reference, taken as a surface with the same amount of Ti doping in the subsurface but without trenches. Overall, DFT predicts the Ti-induced trench defects to be stable over a wide range of oxygen chemical potentials. The infinite trenches (solid black and gray lines, perspective views in Figure 6c,d) are more stable than the (1 × 1)-terminated surface (red line, perspective view in Figure 6b) when μ_O ≳ −2.3 eV. The spacing between the trenches does not play a major role: the black and gray lines are degenerate within the accuracy of DFT. Similarly, we observe that the spacing between the trenches along [112̅0] is irrelevant for the short trenches. As can be seen from the dotted line in Figure 6a (structure in Figure 6e), shortening the trench along [11̅01̅] results in a significant energy cost, associated with a 2-fold coordinated O atom at one end of the trench (highlighted by a red circle in Figure 6e). The short trenches can compete with the infinite ones when this 2-fold coordinated O atom is removed from the trench edge (see Figure 6f,g and the corresponding dashed lines in the phase diagram): in the μ_O^DFT region between −2.4 and −2.3 eV, the short trenches with one additional oxygen vacancy are slightly preferred. Removing this weakly bound O atom results in an overall slightly more reduced stoichiometry, with the excess charge forming one Fe²⁺ at each end of the trench defect (Figure 6f,g). One can eliminate these polarons by removing two additional FeO units at the trench ends of this structure (not shown). The formation energy of this structure is degenerate with the one of Figure 6e and, thus, unfavorable (not shown).

4.3. Experimental vs Simulated STM Images

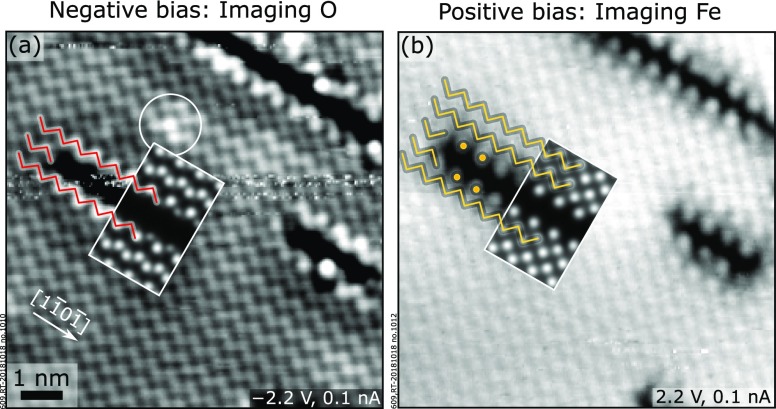
High-resolution STM images of the trench defects imaging filled and empty states are shown in Figure 7, together with the superimposed STM simulations from the model of the Ti-induced trench (Figure 6d). Both the simulated and the experimental filled-state images (negative sample bias, Figure 7a), where oxygen appears bright,¹⁷ show that the missing zigzag row of oxygen in the topmost layer (referred to as A1 in Figure 5c) appears as a dark line. The match between theory and experiment is further supported by comparing experimental and simulated empty-state images (positive sample bias, Figure 7b): at these conditions, the STM tip images the unsaturated dangling bonds of Fe, which are slightly tilted away from their topmost O neighbors.¹⁷ In the presence of a trench, two Fe zigzag rows are replaced by a dark area lined by isolated point features on both sides. The dark area relates to the missing iron atoms in the topmost layer (C1, see Figure 5c), while the isolated points are the remains of the two zigzag rows affected by the removal of Fe cations.

Figure 7.

Experimental (main panels) and simulated (insets) STM images of the Ti-modified (1 × 1) surface of Fe₂O₃(11̅02). At negative sample bias (a), the surface reconstruction appears as a missing zigzag row of O atoms in the topmost layer along the [11̅01̅] direction. At positive sample bias (b), two Fe rows are missing from the top cation layer and are imaged as a dark area surrounded on both sides by isolated point features. The experimental STM images qualitatively match with those simulated assuming the trench defect model. The STM simulations were performed at a constant height (3 Å above the surface) on a (6 × 1) supercell, with U_sample = −2 and +2 V in (a) and (b), respectively. The STM images are 9 × 9 nm².

It is worth noting that the local corrugation of the surface is not uniform (this effect is especially evident at negative bias, Figure 7a, see the white circle): atoms close to the trench appear brighter, as do some atoms within the structurally unmodified (1 × 1) areas. A modulation in the apparent height of the surface atoms is also visible in Figure 2b₂. As we discuss in Section S5, the long-range modulation of the apparent height of the surface is due to the Ti-induced modification of the density of states for surface Fe and O atoms far away from the trench itself.

5. Discussion

Consistent with previous studies on Fe₂O₃(0001),^7,15 we observe that Ti dopants in low concentration (in our case, below 3.1 atom %) do not tend to agglomerate to form titania phases in Fe₂O₃(11̅02). On the contrary, the (2 × 1) surface of slightly reduced, undoped single crystals is fully preserved, while the stoichiometric (1 × 1) surface is only slightly modified by Ti substituting Fe (leading to dark lines along the [11̅01̅] direction). In the following, we will focus on the (1 × 1) surface and the observed Ti-induced modifications.

DFT suggests that Ti preferentially occupies the first subsurface layer (C2, see Figure 5a), independent of the Ti concentration or μ_O^DFT. This allows Ti to maintain a sixfold coordination to oxygen and a charge state of 4+ (Figure 5b,c). Based on the results of Figure 5a, we attribute the preference for the C2 layer over deeper layers to the attractive interaction of the Ti-induced electron polaron (preferentially localizing on an Fe atom of layer C1) with a neighboring Ti dopant. Purely structural effects seem to play a minor role, as the energy differences between layer C2 and deeper layers are only 0.02–0.04 eV when the polaron is removed. The preference for the C2 layer over the immediate surface layer C1 is likely due to the different oxygen affinities of the cations: Ti has a higher oxygen affinity than Fe and will therefore maximize its coordination with O atoms. This is possible if Ti occupies the subsurface layer C2, while it would be fivefold coordinated if it replaced Fe in layer C1.

5.1. Structural Model of Ti-Induced Trenches

Among the structures with subsurface Ti, presented in Figures 5 and 6, we propose the Ti-induced trench structure, shown as infinitely long trenches in Figures 5c and 6c,d and as short trenches in Figure 6f,g, as the best model for the dark lines observed on the (1 × 1) surface of our UHV-prepared films (Figure 2b,c). This structure is characterized by missing rows of surface Fe and O and substitutional Ti in the subsurface. The charge of the two missing Fe³⁺O^2– units per unit cell length is compensated by replacing two subsurface Fe³⁺ atoms with Ti⁴⁺.

Several facts support this assignment. (i) First, the high-resolution STM images of the dark lines are in excellent agreement with the STM simulations of the trench structure (Figure 7). (ii) Moreover, deposition of Ti on a pristine (1 × 1) surface causes the formation of not only dark lines but also hematite islands, as seen in Figure 3. The hematite islands likely consist of oxygen from the gas phase and Fe atoms displaced as a result of both the substitutional Ti and the formation of the trenches. (iii) Finally, the predictions of the theoretical phase diagram of Figure 6 are qualitatively confirmed experimentally. On the 3.1 atom %-doped film, we observe long, at times bunched, trenches that are well modeled by the infinite trench structures of Figure 6c,d. These are predicted to be preferred at all experimentally accessible values of oxygen chemical potentials at 550 °C (this temperature was chosen because Ti diffusion is largely inhibited;⁴²⁻⁴⁴ see Section S2): at the lower limit of O₂ partial pressure of ∼1 × 10^–13 mbar and at 550 °C, μ_O^exp = −2.19 eV, which is higher than the theoretical threshold for the trench formation of μ_O = −2.3 eV. (In practice, since equilibrium at these low partial pressures will not be reached in a reasonable time, the smallest experimentally accessible value of μ_O^exp is even larger.) Consistently, the coverage of dark lines on the 3.1 atom %-doped film does not change upon annealing over the accessible range of oxygen chemical potentials. (We varied μ_O from −1.80 to −1.25 eV by annealing at 550 °C for 20 min at oxygen pressures ranging from 7 × 10^–9 to 3 × 10^–2 mbar.) On the low-doped film (0.8 atom %), the defects are shorter and sparser because of the smaller doping level, and their coverage decreases when annealing at μ_O^exp ≤ −1.55 eV (Figure 4). We interpret this transition as the evolution to the defect-free (1 × 1)_Ti surface from the trench structure. Note that the content of Ti in layer C2 stays unchanged, as suggested by the saturation of the coverage of line defects after a few minutes of annealing (Figure 4) and the fact that at the annealing temperature of 550 °C bulk diffusion of Ti is inhibited (see Section S2). Hence, the transition essentially consists of filling up the trenches by Fe and O (Fe atoms likely come from steps, as Fe diffusion in the bulk is inhibited at 550 °C,⁴²⁻⁴⁴ while O is taken from the sample or the gas phase). This behavior is qualitatively in line with the prediction of DFT that the (1 × 1)_Ti surface can be stabilized upon crossing a certain threshold of μ_O (see the inset of Figure 6a, μ_O^DFT ≤ −2.4 eV). For the smaller doping level, we refrain from quantitative comparisons between theory and experiments because (i) the smallest concentration of dopants achievable with DFT with acceptable computational efforts is significantly larger than the experimental one; (ii) kinetic limitations are not considered: these could limit the agglomeration of short trenches into infinite ones; and (iii) entropic contributions (including, e.g., mixing terms) are also not taken into account in the DFT results and could affect the relative formation energies in nontrivial ways.

While for both infinite and short trenches, a 2× periodicity in the [112̅0] direction is predicted to be degenerate with a 4× periodicity, experiments may suggest a preference for the 2×, especially in the vicinity of steps. In fact, a local (2 × 1) periodicity is observed when sufficiently large amounts of Ti (around 0.1–0.2 ML) are deposited on an Fe₂O₃(11̅02)-(1 × 1) surface, followed by oxygen annealing (see, for example, some of the islands in Figure 3). The full (2 × 1)-periodic ordering of the Ti-induced trenches was not observed on the as-grown films because the amount of near-surface Ti in our films is not sufficient to produce this superstructure. This full coverage can, however, be obtained by depositing Ti amounts around and above 0.5 ML. In Section S7, we show that the corresponding STM images are in good agreement with those simulated from the trench model with (2 × 1) periodicity. This further supports our assignment of the trench structure model for the observed defects.

5.2. Experimental Route for Mechanistic Insights into the Photocatalysis of Ti-Doped Hematite

During photocatalytic reactions, charge carriers generated by absorbed light are transferred to adsorbed molecules that react at the surface. The overall reactivity of the photocatalyst is determined by the combination of several factors: First, the efficiency of light absorption and charge migration to the surface, which are influenced by the bulk electronic structure and conductivity (e.g., critical factors are recombination centers or charge traps in the bulk). Second, the local electronic structure of the surface, which establishes how efficiently charge carriers are exchanged between the reactants and the catalyst.⁴ Finally, the specific arrangement and the coordination of the topmost atoms, defining which sites are available and preferred for adsorption, dissociation, and reaction.^2,13,45−48 Although the specific reaction pathways are defined by the electronic and geometric details of the surface, their role is often overlooked. This is partly because photoelectrochemical current–voltage measurements, commonly used to quantify the overall efficiency of a photocatalyst, lack the ability of isolating these factors. When dopants are introduced in the system and cause an increase in its photocatalytic activity, it is even harder to pinpoint the exact cause, as the foreign elements will affect all of the above ingredients.

Our Ti:Fe₂O₃(11̅02) system should be suited to address these effects one by one. The Ti dopants introduce excess electron carriers in the bulk, which affect the electrical conductivity. Ti also modifies the local surface electronic structure (Section S5): the distribution of states is altered far from the trench, and, in its proximity, a new in-gap state appears close to the valence band maximum. These may modify the adsorption energy of molecules, the localization of charge carriers, and the effectiveness of charge transfer to adsorbates. Finally, the Ti-induced modification in the surface atomic structure (trenches) makes new atoms available as possible reaction sites [Fe in layer C2, O in layer A3, not accessible on the undoped Fe₂O₃(11̅02)-(1 × 1) surface] and changes the local coordination of others (the O atoms in layer A2 at the trench edge become 3-fold coordinated). All of these effects are expected to influence reactions. In the following, we propose an experimental route to disentangle the roles of the efficiency of charge transport in the bulk and of surface electronic and atomic structures in the photocatalytic activity of our model system. To this end, for each factor, we identify suitable descriptors that can be quantified experimentally. To describe the effect of Ti on the surface atomic structure, we use the coverage of trenches θ (expressed as the fraction of surface unit cells composing trenches), which can be measured by STM or other scanning probe techniques. For quantifying the Ti-induced changes on the surface electronic structure, we define the near-surface concentration of the dopants. This quantity affects both the local density of states of Fe and O atoms potentially available as reaction sites and the availability of electrons directly accessible to adsorbed molecules. Consistent with our definition of the bulk doping in atomic percent, we define “surface” doping as c_Ti^s = n_Ti/(n_Ti + n_Fe), where n_Ti and n_Fe are the total numbers of Ti and Fe cations in layers C1 and C2. At oxidizing conditions, all available subsurface Ti atoms produce trenches with coverage θ. It can be derived that the surface doping equals c_Ti = θ/(2 – θ) at these conditions (see Section S6). Hence, the surface doping levels of the 0.8- and 3.1 atom %-doped films correspond to 2.06 ± 0.24 and 10.1 ± 0.7%, respectively (as derived from the corresponding θ values; see Section 3.1). The ratio between these surface doping levels is 4.93 ± 0.67, close to the ratio of the bulk doping levels of the two films. Note also that the surface doping levels are approximately 3 times larger than the nominal bulk doping levels. This is likely due to the strong preference of Ti to occupy the C2 layer over the neighboring ones: C2 acts as a “potential well” (Figure 5a), attracting some Ti atoms from deeper layers. Finally, one can use the bulk conductivity as a measure of the efficiency of charge separation.⁸

In Table 1, we summarize how these descriptors (columns) are affected by three independent experimental “handles” (rows), i.e., the oxygen chemical potential, the amount of Ti deposited after growth, and the bulk doping.

Table 1. Dependence of Intrinsic Properties of Ti:Fe₂O₃(11̅02) Model Surfaces on Some Experimental Parameters.

experimental parameter	trench coverage	surface doping	bulk conductivity
oxygen chemical potential, μO	f(μO)
amount of Ti deposited after growth, θTi	θTia	θTi/(2 – θTi)
bulk doping, cTib	6cTib a	3cTib/(1 – 3cTi)	f(cTib)

^aAt large enough Ti amounts and/or μ_O.

• • Oxygen Chemical Potential. As discussed above, μ_O can influence the coverage of trenches at the surface. However, the surface doping is not affected because the amount of both subsurface Ti and near-surface Fe stays unchanged when trenches are formed (recall that bulk diffusion of both Ti and Fe is inhibited at the temperatures used; see Sections 4.1 and S2). In the range of temperatures and oxygen pressures employed, the bulk conductivity is also not affected.⁴⁹

• • Amount of Ti Deposited after Growth. Deposition of controlled amounts of Ti by PLD or MBE affects the coverage of trenches θ and the surface doping but not the bulk conductivity. θ can be expressed as a function of the amount of Ti deposited in monolayers, θ_Ti. A total of 0.5 ML of Ti, i.e., one Ti atom per (1 × 1) unit cell or two Ti atoms per (2 × 1) unit cell, corresponds to the highest trench coverage of 50% (Figures 5b and 6c), i.e., two Fe atoms missing per (2 × 1) unit cell or θ = 0.5 ML. Hence, θ = θ_Ti (up to the 0.5 ML saturation coverage of trenches). The surface doping changes according to its relation with θ.

• • Bulk Doping. A change in the bulk doping, i.e., the concentration of Ti dopants in the bulk, c_Ti^b, tunes the bulk conductivity and the coverage of trenches θ: our STM evaluations reveal that θ is ≈6 times larger than the bulk doping (for low Ti concentrations, this is valid at oxidizing conditions only). The change in θ translates in a modification of the surface doping.

To gain insights into the role of dopants in reactivity, one would prepare several samples with different values of bulk doping (c_Ti^b) and evaluate how the reactivity changes with c_Ti. Most often, however, this dependence will be a combination of the three relations in the last row of Table 1, as a result of the entanglement of the factors in the top row of Table 1. With the two additional “handles” identified here (θ_Ti and μ_O), one can modify the coverage of trenches and/or surface doping of the samples by either depositing Ti after growth or using μ_O. The contributions of trenches and surface doping can then be isolated by comparing the experimental dependencies of the reactivity on θ_Ti and μ_O with the relations in Table 1. After the critical factors are identified, further atomic-scale investigations, supported by theoretical calculations based on the structural models established here, can be used to shed light on the reaction pathways and mechanisms of interest.

6. Conclusions

In our combined PLD/surface science setup, we have grown high-quality, epitaxial Ti-doped α-Fe₂O₃(11̅02) films, which are atomically flat and can be imaged with STM after standard UHV preparation. At doping levels up to at least 3.1 atom %, the native surface reconstructions of undoped Fe₂O₃ are largely preserved, except for local trench defects that are induced by the Ti dopants, for which we provide DFT-based modeling. Combining this model with experimental observations, we suggest a route to isolate the effects of the surface structure, the surface doping, and the bulk doping on the photocatalytic water-splitting performance of Ti-doped Fe₂O₃.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.chemmater.9b04908.

• Characterization of as-grown films by XPS and STM/AFM, and XPS analysis of the effect of sputtering on the Ti content (Section S1); rationale behind the choice of the deposition temperature (Section S2); determination of the bulk doping (Section S3); estimation of the discrepancy between DFT and experimental μ_O (Section S4); density of states of the trench structure (Section S5); relation between surface doping, coverage of trenches, and Ti coverage (Section S6); experimental and simulated STM images of the full-periodic (2 × 1) trench surface (Section S7); naming convention for structural files (Section S8) (PDF)

• Atomic coordinates (.cif format) for selected structures (ZIP)

The authors declare no competing financial interest.