Inferring causal gene regulatory networks from coupled single cell expression dynamics using Scribe

Summary

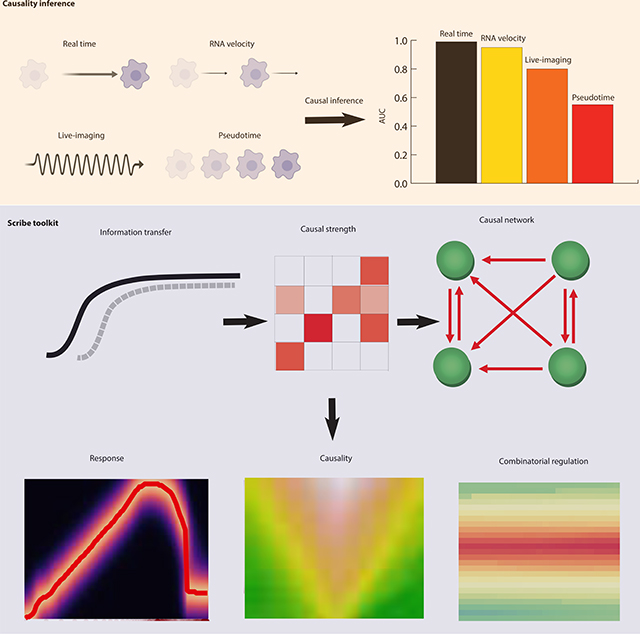
Here, we present Scribe (https://github.com/aristoteleo/Scribe-py), a toolkit for detecting and visualizing causal regulatory interactions between genes and explore the potential for single-cell experiments to power network reconstruction. Scribe employs Restricted Directed Information to determine causality by estimating the strength of information transferred from a potential regulator to its downstream target. We apply Scribe and other leading approaches for causal network reconstruction to several types of single-cell measurements and show that there is a dramatic drop in performance for “pseudotime” ordered single-cell data compared to true time series data. We demonstrate that performing causal inference requires temporal coupling between measurements. We show that methods such as “RNA velocity” restore some degree of coupling through an analysis of chromaffin cell fate commitment. These analyses highlight a shortcoming in experimental and computational methods for analyzing gene regulation at single-cell resolution and suggest ways of overcoming it.

eTOC blurb

Qiu et al present Scribe (https://github.com/aristoteleo/Scribe-py), a toolkit for detecting and visualizing causal regulatory networks between genes in diverse single cell datasets. They use Scribe to understand how casual network reconstruction depends on temporal coupling between measurements. They show that while pseudotime-ordered single-cell data fails to capture much of the information present in true temporal couplings, RNA velocity measurements restore much of this information.

Graphical Abstract

Introduction

Most biological processes, either in development or disease progression (Faith et al., 2007; Friedman et al., 2000; Langfelder and Horvath, 2008; Margolin et al., 2006; Meyer et al., 2008), are governed by complex gene regulatory networks. In the past few decades, numerous algorithms for inferring networks from observational gene expression data (Faith et al., 2007; Friedman et al., 2000; Langfelder and Horvath, 2008; Margolin et al., 2006; Meyer et al., 2008) have been developed.

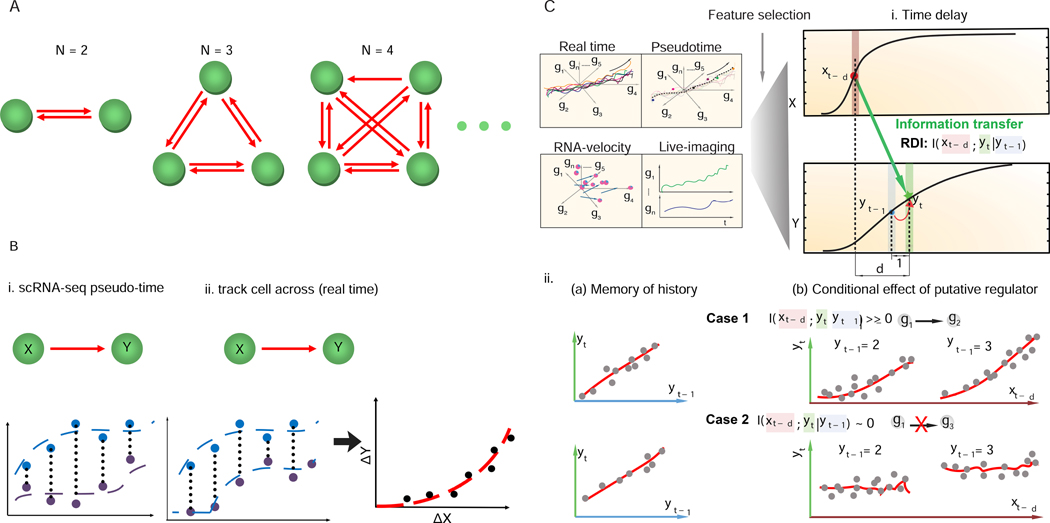
Inferring a network of regulatory interactions between genes is challenging for two main reasons. A first challenge is that adding even a handful of genes to a network inference analysis requires that an algorithm consider many additional interactions between them (Fig. 1A). Each of these potential regulatory interactions must be accepted or rejected on the basis of data. If a network that includes a particular gene regulatory interaction does not statistically “explain” the observed data substantially better than the network that excludes it, the interaction should be rejected. Deciding whether to include an interaction in a network is especially difficult because adding interactions risks overfitting to a particular dataset. Ultimately, because the number of edges explodes as the number of genes grows, so too do the algorithms demand for input data.

Figure 1: Scribe, a toolkit for inferring and visualizing causal regulations.

(A). Inferring regulatory networks from gene expression data is challenging because the number of regulatory interactions that must be evaluated grows much more quickly than the number of genes in the analysis. (B) Ordering single-cell data in “pseudotime” or tracking how fluctuations in a regulatory are followed by changes in a putative target in the same individual cells could boost power to detect causal regulatory interactions. (C) Scribe detects causality from four types of single cell measurement (“pseudotime”, “live-image”, “RNA-velocity” and “real-time”) datasets with a the metric, restricted directed information (RDI). Scribe relies on RDI (Rahimzamani and Kannan, 2016) to quantify the information transferred from the potential regulator to the target under some time delay while conditioned over its past on this pseudo-time series data. A gene often has strong memory to its intermediate previous state (Y_t−1) but RDI will only give highly positive causality score from the putative regulator to target in cases where there is still a strong relationship between the regulator’s history and the target’s present conditioned on target’s history (Case 1 vs. Case 2).

A second challenge in regulatory network inference is distinguishing upstream regulatory genes from their targets directly downstream. Most methods that aim to do so are predicated on the notion that changes in regulators should precede changes in their targets in time (Fig. 1B) (Bar-Joseph et al., 2012). Granger causality (GC) (Granger, 1969) is a statistical hypothesis test for determining whether one time series (X₁) is useful in forecasting another (X₂) which has been applied to infer biological networks (Zou and Feng, 2009). However, GC assumes a linear relationship between the regulator and the target, which is violated in many biological settings (Hill et al., 2016). Convergent Cross Mapping (CCM) (Sugihara et al., 2012), a more recent technique based on state-space reconstruction (Takens, 1981) can detect pairwise non-linear interactions. However, this method is limited to deterministic systems, and thus may be poorly suited for many cellular processes (e.g. cell differentiation), which are inherently stochastic.

Single-cell transcriptome sequencing experiments (scRNA-seq) are attractive for gene regulatory network inference for two reasons. First, scRNA-seq experiments now routinely produce thousands of independent measurements, which may open the door to sufficiently-powered inference (Liu and Trapnell, 2016). Second, algorithms that order the cells along “trajectories” that describe development or disease progress offer a tremendously high “pseudotemporal” view of gene expression kinetics (Haghverdi et al., 2016; Qiu et al., 2017a; Setty et al., 2016; Trapnell et al., 2014). The recently introduced SCENIC method (Aibar et al., 2017) combines GENIE3 (Huynh-Thu et al., 2010) with regulatory binding motif enrichment to simultaneously cluster cells and infer regulatory networks. Other studies have inferred regulatory networks from scRNA-seq data using differential equations (Matsumoto et al., 2017; Ocone et al., 2015), information measures (Chan et al., 2017), Bayesian network analysis (Sanchez-Castillo et al., 2017), boolean network methods (Hamey et al., 2017) or linear regression techniques (Huynh-Thu et al., 2010; Papili Gao et al., 2017; Wei et al., 2017). However, most methods don’t explicitly leverage time-series data to identify causal interactions, and more importantly, most fail to recover the correct network even in simple settings (Babtie et al., 2017; Fiers et al., 2018).

Here, we introduce Scribe, a scalable toolkit for inferring causal regulatory networks that relies on Restricted Directed Information (RDI) (Rahimzamani and Kannan, 2016). In contrast to GC and CCM, Scribe learns both linear and non-linear causality in deterministic and stochastic systems. It also incorporates rigorous procedures to alleviate the sampling bias and builds upon improved estimators and regularization techniques to facilitate inference of large-scale causal networks. In concordance with theory, we demonstrate that Scribe has superior performance compared to existing methods when the observations consist of true time-series data. However, current scRNA-seq protocols do not follow the same cells over time, breaking temporal coupling between measurements. We demonstrate that there is a dramatic drop in performance in causal network accuracy when the temporal coupling between measurements is lost. We then demonstrate that “RNA velocity”, a recently developed analytic technique for single-cell RNA-seq analysis, restores temporal coupling and improves causal regulatory network inference. Our results suggest that preserving this coupling should be a major objective of the next generation of single-cell measurement technologies.

Results

Previously, we proposed Restricted Directed Information (RDI) (Rahimzamani and Kannan, 2016, 2017), an information metric to accurately and efficiently quantify causality (STAR Methods). Here, we introduce Scribe, a toolkit built upon RDI, that is designed for the analysis of time-series datasets (either real time, RNA velocity, pseudotime or live-imaging datasets), and is especially tailored for single cell-RNA-seq (Supplementary Figure 1 and STAR Methods) and their visualization (Supplementary Figure 2 and STAR Methods).

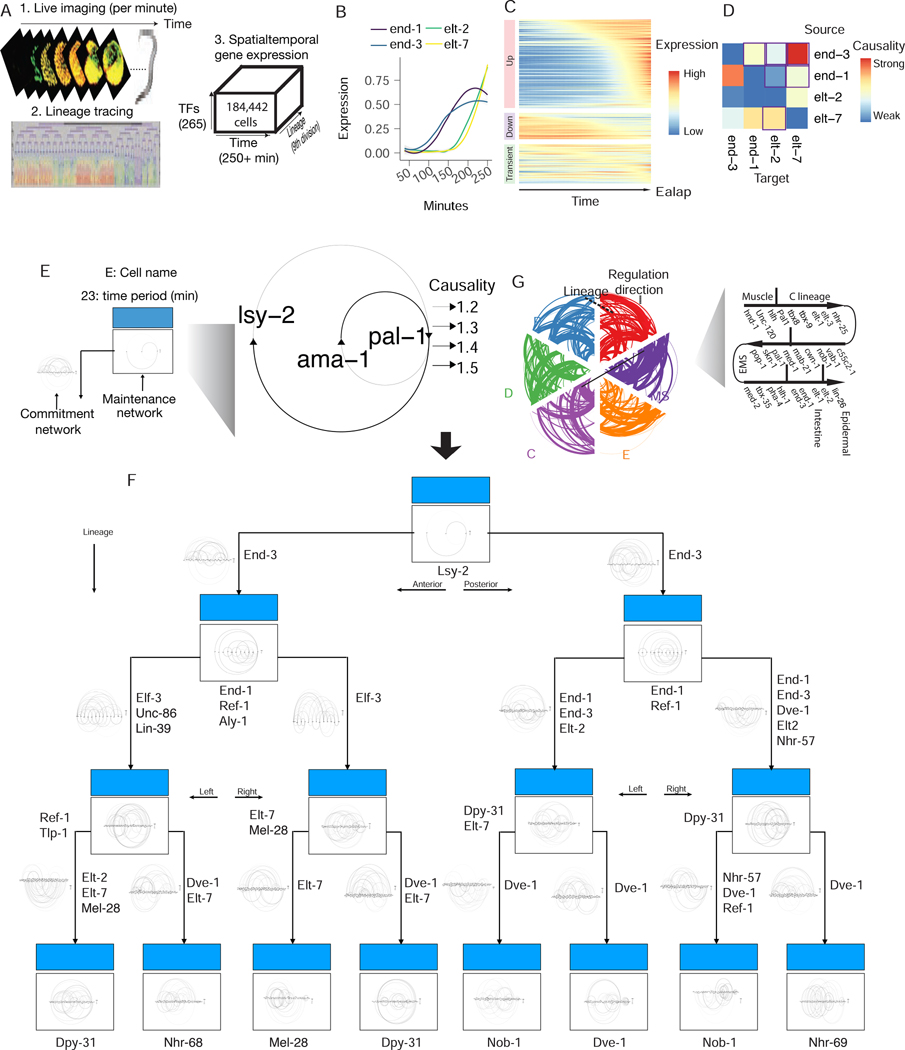
In order to assess the performance of Scribe, we examined Caenorhabditis elegans’ early embryogenesis, where live-imaging has been used to measure nearly half of all transcription factors’ protein expression dynamics in every single cell in an embryo (Murray et al., 2012). This dataset consists of 265 time series each of which tracks the expression dynamics of a transcription factor using fluorescent reporter constructs. Measurements were collected at one-minute intervals in every cell of the developing embryo for the first ~350 minutes of embryogenesis (Fig. 2A).

Fig 2: Live imaging dataset of C. elegans’ early embryogenesis captures transcription expression dynamics hierarchy.

(A) Scheme used by Murray et al for measuring transcription factors protein expression dynamics in real-time for every cell during early C. elegans embryogenesis. (B) Single cell lineage-resolved fluorescence data captures temporal dynamics of E lineage master regulators during C. elegans embryogenesis. The expression for each gene is scaled to be between 0 and 1 and then smoothed using LOESS regression, same in C. (C) Expression dynamics for 265 report TFs along the lineage leading to the Ealap cell. (D) Scribe reconstructs the causal regulatory network for the four master regulators (end-1/3, elt-2/7). Note that the outlined box corresponds to the previously known regulations. (E) A scheme for the multi-scale network for panel B. (F) An integrative multiscale model for the E lineage specification. Zoom in to see the network architecture in details. (G) Lineage (AB, P, MS, E, D, C) specific causal networks for the curated master regulators constructed with Scribe shown as a hiveplot.

We tested whether Scribe was able to learn validated genetic interactions that govern worm development. For example, it is understood that in the intestinal cell lineage Ealap the transcription factors end-1 and end-3 were upregulated prior to their targets elt-2 and elt-7 (Fig. 2B and well before most other upregulated factors in this lineage (Fig. 2C and (Wiesenfahrt et al., 2016)). We ran Scribe on these four genes to determine whether it could correctly infer the causal regulatory interactions between them. Although Scribe captured some known causal interactions among the core transcription factors that specify this lineage (Owraghi et al., 2010), it also reported both false positive and false negative interactions based on previously curated networks (Owraghi et al., 2010; Wiesenfahrt et al., 2016). For example, Scribe reports that end-1 also strongly regulates end-3 which is not supported by previous studies (Owraghi et al., 2010; Wiesenfahrt et al., 2016) (Fig. 2D). The entire Ealap lineage-specific network of C. elegans’s early embryogeneis constructed by Scribe is shown in Fig. 2E–G; zoomed-in versions of each network state is available in the Supplemental Information and Scribe’s GitHub repository. Overall, Scribe was able to accurately infer known regulatory hierarchy (Fig. 2F, (Murray et al., 2012)),

Accurate causal network inference requires temporally coupled expression data

Next, we explored Scribe’s ability to recover causal interactions using single-cell RNA-seq which in contrast to live-imaging measures many genes in each cell. We first collected publicly available datasets from several biological systems including developing airway epithelium (Treutlein et al., 2014), dendritic cell response to antigen stimulation (Shalek et al., 2014), and myelopoiesis (Olsson et al., 2016). We then pseudo-temporally ordered these cells as previously described using Monocle 2 (Qiu et al., 2017a). Next, we ran Scribe on these pseudo-time series (Fig. 3, Supplementary Figures 3) and examined the regulatory interactions reported for known transcriptional regulators of these systems. For each gene, we summed the causal interaction scores to all other genes, deriving a measure of its aggregate influence on the system. These aggregate causality scores were significantly higher for known transcriptional regulators than for genes believed to be targets by the authors of the original studies (unpaired two-sample t-test, Supplementary Figure 3).

Figure 3: Scribe recovers a core regulatory network responsible for myelopoiesis.

(A) A core network describes key regulators during the specification of monocytes and granulocytes (Olsson et al., 2016). (B) Examples of gene-target pair kinetic curves over pseudotime along the monocyte lineage. (C) Scribe infers the expected core regulatory network interactions for myelopoiesis. (D) Visualization of combinatorial gene regulation from Irf8 and Gfi1 to Zeb2 or Per3. (E) The normalized rank of lineage-specific genes’ total outgoing RDI sum. (F) Lineage-specific network of significant regulators during erythropoiesis. Edges supported by the SPRING database are colored as red lines. For panels E (F), BEAM analysis was used to identify significant branching genes associated with the four (one) lineage bifurcation events shown in the haematopoietic trajectory from ref. (Qiu et al., 2017a) based on the paul dataset (Paul et al., 2015). The top 1,000 differentially expressed genes associated with each bifurcation were chosen to build a causal network for each relevant lineage. A set of TFs relevant to specific lineages described previously is used for panel E or F. Neu: Neutrophil; Ery: Erythroid, Mk: Megakaryocyte; Mono: Monocyte; DC: Dendritic Cell; BE: Basophil / Eosinophil. (G, H) Receiver Operating Curves or ROC (G, top) and Area Under Curve or AUC (H, bottom) of the inferred causal network based on Scribe, GC and CCM, from left to right, on the Dendritic Cells (DC) dataset, the granulocyte or monocyte branch of the Olsson dataset, the erythroid branch of the Paul dataset. Four different variants of causal inference implemented in Scribe are tested: RDI ( L = 0): the default RDI method without conditioning on any other gene; RDI (L = 1): the RDI method based on conditioning on the incoming gene with highest causality score, except the current target; uRDI: the method based on the uniformization technique applied on the actual distribution in RDI; uRDI ( L = 1): the uRDI method but also with the conditioning on the incoming gene with the highest causality score, except the current target. (I) The network of the gene-set as included in the panel (panel F) retrieved from the STRING database.

We next explored whether Scribe can accurately reconstruct causal regulatory networks. Recently, Olsson and colleagues suggested a core network of transcription factors for regulating myelopoiesis (Olsson et al., 2016) by performing bulk ATAC-seq, ChIP-seq, perturbation experiments and profiling the transcriptomes of 382 cells from flow-sorted populations undergoing the transition (Fig. 3A). We used Scribe to calculate causal scores for each regulator-target pair from the Irf8 and Gfi1 master regulators of the monocyte or granulocyte lineage as identified by Olsson et al., respectively, to the other six genes in the core network, using single-cell RNA-seq data alone. We hypothesized that Scribe would return strong causal scores for the targets ascribed to each regulator but not others. We observed that expression kinetics over pseudotime correctly reflect the network architecture (Fig. 3A, B). We represent the causal network inferred by Scribe as a heatmap where each row corresponds to the causal score from the regulator to all other genes and the color corresponds to the magnitude of the causal score (Fig. 3C). Scribe assigns a high causality score for all targets of Irf8 (Gfi1, Irf5, Klf4, Per3, Zeb2) but lowest causality score to Irf8 and Ets1 which are not its direct targets. Similarly, Scribe assigns a high causality score for the majority of Gfi1’s targets (Irf8, Klf4, Per3) even though Gfi1 has low expression values (Fig. 3C). Visualization of the combinatorial regulation of Irf8 and Gfi1 to either Zeb2 or Per3, based on the Scribe visualization toolkit, captures the conflicting regulation pattern between two regulators and their two targets (Fig. 3D).

To determine Scribe’s capabilities to reconstruct transcriptome-level causal networks containing edges between transcription factors (TFs) as well as from TFs to putative downstream targets, we applied Scribe to scRNA-seq data of haematopoiesis(Paul et al., 2015). We find that the lineage-specific genes tend to have high total outgoing RDI sum among all significant transcription factors (Fig 3E). When restricting to a small subset of previously identified erythropoiesis associated TFs, we find Scribe identified several regulatory interactions, such as Gata1-Gfi1-Klf4, which are known to play an important role in myeolopoeisis (Laslo et al., 2006; Stopka et al., 2005; Tamura et al., 2015) Fig. 3F). However, in recovering known regulatory interactions in each system based on a manually curated network from the literature, Scribe only marginally outperformed GC and CCM but all three methods generally performed poorly, with no method reaching an AUC of greater than 0.7 (Fig. 3G–I).

We hypothesized that as with live imaging datasets, lack of coupling between the expression measurements in pseudo-temporally ordered single-cell RNA-seq data leads to poor accuracy during regulatory network inference. In contrast to true time series in which an individual cell is tracked and measured longitudinally, in pseudo-temporal datasets, each expression measurement comes from a different cell. Therefore, although pseudotime reveals overall trends of the gene expression dynamics, the real-time gene expression “micro-fluctuations” (fluctuations that happen within short time-scales) of a regulator to a target is not captured in pseudotime.

To test whether causal network inference requires temporal coupling between genes across measurements, we ran Scribe on simulated data based on a core network of neurogenesis (STAR Methods) collected using four strategies for obtaining longitudinal measurements from individual cells. First, we consider “real-time”, an ideal theoretical technology in which all genes are tracked in each individual cell as that cell differentiates. We therefore consider a second setting “live-imaging”, in which each cell is tracked over time but only one gene is measured. Third, we examine pseudotime, where all genes are measured only once in distinct cells that have been sampled from a population undergoing differentiation. Finally, we tested Scribe on RNA velocity data, which consists of a snapshot measurement of each cell’s current transcriptome along with a prediction of that same cell’s expression levels at a short time in the future (Supplementary Figure 4A).

Using pseudo-temporal measurements, Granger causality, convergent cross-mapping, and Scribe all performed very poorly in recovering direct, causal interactions between genes in the hypothetical network (Supplementary Figure 4B). The inability of these methods to recover regulatory interactions is unlikely to be due to the undersampling of the system, as the performance was insensitive to varying the number of cells captured in the simulated datasets (Supplementary Figure 4C, D). Performance of the three methods was only modestly better when using data captured by “live imaging.

We next evaluated two alternative modes of measuring gene expression dynamics in single cells in which fluctuations are coupled. Using conditional Restricted Directed Information, Scribe produced highly accurate reconstructions from “real-time” measurements of gene expression (AUC: 0.859 ± 0.0283), in which every gene is measured repeatedly in a set of cells as they differentiate. This demonstrates that when measurements are fully coupled across time, and fluctuations in a regulator can propagate to its targets, restricted directed information correctly reveals causal regulatory interactions. Scribe also recovered accurate networks (AUC: 0.837 ± 0.0189) with “RNA velocity” measurements (Supplementary Figure 4A). Although RNA velocity does not repeatedly measure cells, it provides a “prediction” of the future expression levels of each gene based on comparing mature to immature transcript levels, in effect introducing a form of temporal coupling to the data. These simulations show that methods for regulatory inference based on information transfer fail using data from measurement modalities in which fluctuation of a regulator’s expression across cells is “uncoupled” from fluctuations in its targets.

Causal network inference with “RNA-velocity” reveals regulatory interactions that drive chromaffin cell differentiation

We next sought to test whether Scribe could recover causal network interactions using real RNA velocity measurements. Recently, La Manno and colleagues applied RNA-velocity to study the chromaffin cell differentiation as well as their associated cell cycle dynamics (La Manno et al., 2018). We used this chromaffin dataset as a proof-of-principle for incorporating “RNA velocity” into Scribe. We first reconstructed a developmental trajectory from mature mRNA expression levels from each cell in this dataset and then applied BEAM (Qiu et al., 2017b) to identify genes that significantly bifurcate between Schwann and chromaffin cell branches (Fig. 4). These genes were enriched in processes related to neuron differentiation along the path from SCPs (Schwann Cell Progenitors) to mature chromaffin cells (Supplementary Figure 4E).

Fig 4: Causal inference in Scribe with RNA-velocity.

(A) RNA-velocity vector projected onto the first two latent dimensions. A small subset of arrows is used to visualize the velocity field of the cells. S: Sympathoblasts; C: Chromaffin. SCP: Schwann Cell Progenitor. The color of each cell corresponds to the cluster id from Fig 5B of ref. (Furlan et al., 2017). (B) A core causal network for chromaffin cell commitment inferred based on RNA-velocity. Gene set is collected from ref. (Furlan et al., 2017). CLR (context likelihood of relatedness) regularization is used to remove spurious causal edges in the network (see STAR Methods). (C) Two potential coherent FFL (feed-forward loop) motifs of chromaffin differentiation are discovered from the core network. Edge width corresponds to causal regulation strength. (D) Visualization of the six causal regulations pairs in the feedforward loops of Eya1-Phox2a-Erbb3 and Gata3-Phox2a-Notch1. (See STAR Methods for details). (E) Visualizing combinatorial regulation logic for the two feedforward loops in Panel C with Scribe. For both Panels D and E, a grid with 625 cells (25 on each dimension) is used. Similarly, expected values are scaled by the maximum to obtain a range from 0 to 1. (F) Scribe’s ability to detect causal regulatory interactions is limited by the single-cell measurement technology used. Technologies that provide measurements that are coupled across time and between genes provide more power for inference than conventional single-cell RNA-seq experiments.

We then applied Scribe to the RNA velocity measurements from the 3,665 significantly branch-dependent genes (qval < 0.01, Benjamini-Hochberg correction) (Figure 4C, Supplementary Figure 4). We first built a network between significant branching transcription factors (TFs) as well as from TFs to the significant targets in chromaffin lineage and found that only 0.75% of TFs interact with each other while 8.40% TFs regulate potential targets (causality score > 0.05) (Supplementary Figure 4E–G). We then inferred a core network between fourteen TFs believed to drive chromaffin cell differentiation (Furlan et al., 2017). Within this core network, Scribe identified two feed-forward loop (FFL) motifs (Alon, 2007): Eya1-Phox2a-Erbb3 and Gata3-Phox2a-Notch1 (Fig. 4C–E). The STRING database of genetic and molecular interactions (Szklarczyk et al., 2017) provided additional support for these regulatory motifs (Supplementary Figure 4H). From the RNA-velocity network, we also find that SCPs related TFs, such as Sh3tc2, tend to have stronger causal regulation (ranked higher in terms of hubness as shown in the arc plot) while chromaffin cell-related TFs, including Chga and Th, has much smaller causal regulations, reflecting the network captures transition from SCPs to chromaffin cells (Furlan et al., 2017).

Discussion

Despite extensive research into gene regulatory network inference over the past several decades, the fundamental source of poor performance by these methods on single-cell data remains uncertain. One possibility is that, even with the tremendous gains in the throughput achieved by the developers of single-cell RNA-seq technology over the past decade (Svensson and Vento-Tormo, 2017), these methods still haven’t been provided with sufficient data to accurately reconstruct networks. Alternatively, the basic approach of inferring genetic interactions based on statistical interactions between their measured expression levels may be fundamentally limited.

We developed Scribe, which uses recently reported advances in information theory to infer complex causal regulatory interactions between genes. Scribe employs Restricted Directed Information (RDI), overcoming limitations inherent to Granger Causality (GC) and Convergent Cross Mapping (CCM). Scribe also provides several ways to visualize causal information transfer, helping users distinguish between direct and indirect interactions and unravel combinatorial regulatory logic.

Although Scribe correctly infers causal regulatory interactions in simulated measurements that track all the genes in an individual cell over time, it performs poorly on live imaging or pseudotemporally ordered single-cell datasets. We demonstrate that poor performance is due to the loss of temporal coupling between measurements of genes that interact, in which fluctuations in the levels of a regulator propagate to measurements of its targets. This may explain poor performance by a broad class of information theoretic or statistical approaches for inferring regulatory networks from single-cell RNA-seq data. If so, then simply improving the throughput of single-cell RNA-seq protocols will not be sufficient to power inference methods. Pseudotemporally ordering single-cell RNA-seq data provides a boost to the number of genes that may be considered, and the temporal coupling provided from joint measurement via live imaging of pairs of genes could boost power further (Figure 4F).

Improvements to single-cell expression assays that produce measurements for multiple genes that are coupled across time may enable the accurate regulatory network inference possible using Scribe or similar approaches. Although methods for nondestructively tracking expression levels of many genes in single cells over time have not been described, several assays have been reported that provide snapshot estimates of both steady-state mRNA levels along with their rates of synthesis. These assays report measurements of the current and future transcriptome of individual cells, essentially providing temporal coupling over a short time horizon. For example, SLAM-seq (Herzog et al., 2017; Muhar et al., 2018) or TUC-seq (Riml et al., 2017) assay mature RNA levels and estimate the rate of their synthesis via nucleotide labeling or conversion based approaches. Importantly, single cell version of those technologies (Cao et al., 2019; Erhard et al., 2019; Hendriks et al., 2018; Qiu et al., 2019) have recently developed when this paper is under review and awaits integrating Scribe with those technologies as future investigation. Sequential multiplex RNA FISH or “Seq-FISH” (Shah et al., 2018) which probes both exons and introns of RNAs can also provide similar measurements. RNA velocity, which analyzes single-cell RNA-seq reads falling within introns and estimates both mature mRNA levels and their immature intermediates to predict the transcriptome over a short time in the future, also generates coupled measurements. Accordingly, using RNA velocity measurements greatly improves Scribe’s accuracy compared to running it on pseudo-temporal single-cell RNA-seq measurements. These assays and algorithmic improvements boost Scribe’s ability to recover causal interactions because they provide increasingly comprehensive and temporally coupled measurements across the transcriptome. Concentrating efforts to improve temporal coupling in new experimental methods should, in our view, be a priority for the field.

Single-cell RNA-seq holds great promise for powering various algorithms for network inference, but as we have shown, major obstacles remain in the way of doing so in practice. Once provided with temporally coupled measurements, Scribe accurately reconstructs networks of modest scale. As experimental and computational improvements to single-cell expression techniques couple measurements across time, we expect Scribe to be increasingly capable of dissecting the complex genetic circuits that drive development and disease.

STAR+METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Cole Trapnell (coletrap@uw.edu).

This study did not generate new materials.

METHOD DETAILS

Four possible single-cell time-series measurement modalities

Cell differentiation is an intrinsically noisy and asynchronous process. Even for the same developmental process, every cell in any given time should be regarded as a distinct sample. We consider four possible types of gene expression measurements in those single-cell samples:

1. Real-time, where we measure the gene expression for all the genes simultaneously in a single cell over time. This is the ideal situation but no existing technology can produce data like this yet.

2. “RNA-velocity” where we only capture the current state and the next state for all genes in different cells. “RNA-velocity” can be computationally inferred from single-cell RNA-seq datasets, or directly measured with Seq-FISH(Shah et al., 2018), and single-cell version of SLAM-seq (Erhard et al., 2019; Hendriks et al., 2018; Herzog et al., 2017; Muhar et al., 2018; Qiu et al., 2019), TUC-seq (Riml et al., 2017) and TimeLapse-seq (Schofield et al., 2018), among others.

3. Live-imaging datasets are those generated with multiple separate live-imagings for a single protein in a single-cell which are then aligned along the same developmental process to form a time-series for all genes.

4. Pseudo-time is where we apply a trajectory reconstruction algorithm to order the single-cell RNA-seq snapshot dataset to form a time-series.

The problem of causal regulatory network inference

In this work, we formulate the problem of causal regulatory network inference as the inference of the underlying structure of influences in a stochastic dynamical system where the time series of each gene is causally regulated by a subset of other genes. We assume that there are no unobserved confounders in order to make the problem tractable. In this setting, we can potentially infer the causal regulators based on estimating the amount of information transferred from one variable (a potential regulator) to another time-delayed response variable (a potential target). In the context of single-cell genomics (e.g. scRNA-seq, live-cell imaging), we ask how we can reconstruct a regulatory network consisting of causal regulations that accurately describe the gene expression dynamics and the associated cell fate transitions.

Causal Inference

In the setting stated above, various techniques, including Granger Causality and CCM, each associated with different assumptions have been proposed to detect the structure of the causal regulatory network. In the following, we briefly summarize these methods and introduce RDI, the method we developed and used in this study.

Granger causality

In order to determine whether one time series (X₁) is useful in forecasting another (X₂) in economics, Clive Granger first proposed Granger Causality (GC) in 1969 (Granger, 1969). According to GC, if X₁ “Granger causes” X₂, then the predictability of X₂ based on past values of X₂ and X₁ together is significantly greater than that of predicting purely based on the past values of X₂. GC in its original formulation, however, is only able to detect linear causal regulation: i.e., when the regulators regulate the target through a linear relationship.

Kernel Granger Causality

In (Marinazzo et al., 2008), a generalization of the Granger causality (kernel Granger causality or kGC) to the nonlinear case was introduced using the theory of reproducing kernel Hilbert spaces. They showed kGC outperforms linear Granger causality in the feature space of suitable kernel functions, assuming an arbitrary degree of nonlinearity. Hence choosing the proper kernel function with proper parameters is crucial for this method to perform acceptably. Furthermore, introducing kernel functions operating on the linear inner products means significantly higher computational complexity over that of naïve Granger causality.

Convergent Cross Mapping

In order to detect pairwise non-linear interactions in deterministic ecology systems, George Sugihara and colleagues proposed Convergent Cross Mapping (CCM) which is based on state-space reconstruction (Sugihara et al., 2012). One fundamental and somewhat counterintuitive idea of CCM, distinct from GC, is that it is possible to estimate X₁ from X₂, but not the other way if causation is from X₁ to X₂. CCM first constructs shadow manifolds $M_{X_2}$ and $M_{X_1}$ from lagged coordinates of the time-series X₂ and X₁. It then tests whether states in the shadow manifold $M_{X_2}$ can be used for estimating the states in $M_{X_1}$ and vice versa via mapping through nearest neighbors (cross-mapping). Another key idea of CCM is convergence which means that as the length of the time-series increases, the shadow manifolds become denser and the ellipsoid or space formed by nearest neighbors shrinks, leading to improvement of cross-map estimates. Although CCM is appealing, it cannot be generalized to stochastic systems as Takens’ theorem, the cornerstone of CCM, will break down in such scenarios (Takens, 1981). Furthermore, CCM can only infer pairwise relationships and complex multi-factorial interactions common in gene regulatory networks are not captured in CCM.

Restricted Directed Information (RDI)

As mentioned earlier, the causal inference method in Scribe is based on Restricted Directed Information (RDI). This measure determines the amount of statistical inter-dependence (or more formally the mutual information) between the past state of the regulator and current state of the target gene conditioned on the target’s immediate previous state.

Cell state transitions are controlled by hierarchical regulatory networks (Peter and Davidson, 2011). In such networks, as the expression of the regulator changes, their downstream target responds accordingly after some time delay d. A canonical measure of mutual dependence which accounts for both linear and nonlinear associations between two genes (or more generally, two random variables) X and Y, is mutual information (MI)(Cover, 2006). MI is symmetric and can quantify the “amount of information” obtained about gene X or Y, through the other gene Y or X. It essentially determines how similar the joint distribution (p_XY) of the two genes X and Y is to the products of factored marginal distribution p_Xp_Y, or formally:

$$I(X;Y)={\sum }_{x,y}{p}_{XY}(x,y)\log \frac{p_{XY}(x,y)}{p_X(x)p_Y(y)}$$

If I(X;Y) is zero, then the two genes X and Y are independent; otherwise it implies there exists some dependency between them (e.g. in the case of a regulator and its target). It is often useful to quantify the mutual dependence between two random variables (for example, regulator X and target Y) while removing the effect of a third random variable (for example another regulator Z or the history state of the target). This leads to developing of conditional mutual information, which is defined as:

$$I(X;Y|Z)={\sum }_{x,y,z}{p}_{XYZ}(x,y,z)\log \frac{p_{XY|Z}(x,y|z)}{p_{X|Z}(x|z)p_{Y|Z}(y|z)}$$

MI provides a powerful approach to quantify the symmetric interdependence between genes. However, a favorable approach would be to measure the causal score from a potential regulator to its target. We can achieve this by considering the time-series of regulators and targets (${\underset{\_}{X}}^t$, ${\underset{\_}{Y}}^t$) and quantifying the information transfer from the past state(s) of X to the current state of the variable Y denoted by Y_t.

Previously, T. Schreiber reported Directed Information (DI) as a measure for the amount of information flowing from the past state(s) of X, the regulator, to the current state of the variable Y, the target (Schreiber, 2000). DI is defined as:

$$DI(X\to Y)={\sum }_{t=1}^{T}I\left({\underset{\_}{X}}^{t-1};Y_t|{\underset{\_}{Y}}^{t-1}\right)$$

In order to remove indirect interactions, we can calculate the information transferred from the regulator to the target while conditioning on all the other genes ({X⁽ⁱ⁾, X^(j)}^C), which is,

$$DI\left(X^{(i)}\to X^{(j)}|{\left\{X^{(i)},X^{(j)}\right\}}^C\right)={\sum }_{t=1}^{T}I\left({\underset{\_}{X^{(i)}}}^{t-1};X_t^{(j)}|{\underset{\_}{X^{(j)}}}^{t-1},{\left\{{\underset{\_}{X^{(l)}}}^{t-1}\right\}}_{l\in {\left\{X^{(i)},X^{(j)}\right\}}^C}\right)$$

Furthermore, for a set of genes of interest, X⁽¹⁾, X⁽²⁾,…, X^(N) from a single-cell genomics dataset, we can infer a Directed Information graph, G_DI = (V,E) where the vertex set V corresponds to the genes X⁽¹⁾, X⁽²⁾,…, X^(N) and the edge e_ij = (X⁽ⁱ⁾, X^(j)) from gene X⁽ⁱ⁾ to exists if and only if $DI\left(X^{(i)}\to X^{(j)}|{\left\{X^{(i)},X^{(j)}\right\}}^C\right)\ne 0$ and the edge weight corresponds to the quantified DI value $DI\left(X^{(i)}\to X^{(j)}|{\left\{X^{(i)},X^{(j)}\right\}}^C\right)$.

It was shown that if a system is not purely deterministic, the directed information graph G_DI inferred from DI will correctly recover the true causal graph G_C (the network which includes all causal interactions as directed edges) (Sun et al., 2015). Although DI is able to detect both linear and non-linear causality as opposed to the linear Granger causality and is applicable to stochastic systems, it (1) can not deal with deterministic systems which may be of interest for certain scenarios and (2) poses huge computational burden because it conditions on all possible previous states of the regulator or target and (3) requires an enormous amount of data which is not affordable even with current single-cell genomic datasets.

We recently proposed a formulation of DI to alleviate those issues by employing only the immediate past of the target or regulators instead of all the past states assuming a first-order Markov system, which is generally applicable to most biological processes. In this method, the randomness is present due to the random initialization of the Markov system, hence creating a random process on which information measures are well defined. We term this method “Restricted Directed Information” (RDI) and define it as,

$$RD{I}_d(X\to Y)=I\left(X_{t-d};Y_t|Y_{t-1}\right)$$

Despite the fact that the original RDI measure is defined only for the immediate past of the regulator X, this measure can be flexibly defined for arbitrary effect delay d from X to Y as we have done here.

Conditional Restricted Directed Information (cRDI)

Similar to (Schreiber, 2000), RDI can also be extended to the case where the information transfer from X to Y is conditioned on other potential regulator(s) Z to rule out the possible indirect causal effects and confounding factors. Thus the Conditional RDI (abbreviated as cRDI) can be formulated as:

$$RD{I}_{d_1}\left(X\to Y|Z_{t-d_2}\right)=I\left(X_{t-d_1};Y_t|Y_{t-1},Z_{t-d_2}\right)$$

In (Rahimzamani, et. al, Allerton 2016), it’s shown that cRDI works in many stochastic or deterministic cases and under some mild assumptions is capable of inferring the correct regulatory network G_C. Moreover, it has shown that if the conditions are violated, no other method will be able to recover the correct network (see Section IV. in (Rahimzamani, et. al, Allerton 2016)).

In the upcoming sections we will discuss how RDI and cRDI are utilized in the Scribe toolkit.

Uniformization method for adjusting sampling bias

During our studies over the simulated benchmark data, we found that as the number of samples increases, the performance of RDI first increases and then starts to decrease. This problem was particularly acute in simulations where gene expression reached a plateau after cells committing to a cell fate. In general, while the transitional states are of higher importance in the discovery of causal interactions, oversampled equilibrium states will outnumber the transitional samples resulting in a sampling bias towards less informative equilibrium states. This phenomenon can in turn reduce the inference accuracy since RDI requires calculating conditional mutual information (I(X_t−d;Y_t|Y_t−1)) by design, which is a function of the joint distribution (p(x_t−d, y_t, y_t−1) = p(y_t|x_t−d, y_t−1)p(x_t−d, y_t−1)). That is, the distribution is influential in the RDI calculation, despite the fact that the RDI score should be fully determined only by the conditional distribution. Hence we devised a scheme to correct for sampling bias by re-weighting samples so that those from the system during transitional periods are weighted higher than cells sampled from the system at equilibrium. One may assume the input distribution is uniform and redistribute the observed samples in a more homogeneous fashion before calculating the RDI value.

This bias correction scheme, which we term Uniformized conditional mutual information (uCMI) replaces the actual distribution p(x_t−d, y_t−1) with a uniform distribution u(x_t−d, y_t−1) and then calculates the conditional mutual information for p(y_t|x_t−d, y_t−1)u(x_t−d, y_t−1). This is made possible thanks to the concept of potential Conditional Mutual Information (qCMI) (Rahimzamani and Kannan, 2017) and an estimator, in which the actual distribution p(x_t−d, y_t−1) of samples is replaced by any arbitrary distribution q(x_t−d, y_t−1) before estimating the conditional mutual information. uCMI is thus a special case of qCMI, in which the replacement distribution q(x_t−d, y_t−1) is uniform. By replacing the conditional mutual information (CMI) in RDI with uCMI, we obtain a new way of computing information transfer called uniformized Restricted Directed Information (uRDI).

The discussion above is especially relevant for single-cell genomics datasets as single cells are not homogeneously spread across many biological processes and they often will be heavily sampled from steady states while rarely from transition states. A compelling discussion of this phenomenon can be found in c.f. (Olsson et al., 2016). This imbalance of sampling confounds the performance of RDI (or other mutual information based methods) and thus leads to ignorance of rare but critical regulation that happened during transition states. We noticed that empirical methods have been reported to account for sampling biases from single-cell measures (Krishnaswamy et al., 2014). However, the uRDI method incorporated in Scribe provides a rigorous approach to replace the biased sampling distribution with a uniform distribution to quantify potential causality (how much influence a regulator can potentially exert on target without cognizance of the regulator’s distribution) and is thus arguably a superior approach to account for the sampling biases issue (Rahimzamani and Kannan, 2017).

Scribe: a toolkit for visualization and detection of complex causal regulation from single-cell genomics datasets

Although Scribe is applicable to any time-series datasets, it is specifically designed for visualizing and detecting complex gene regulation from single-cell genomics datasets (e.g. scRNA-seq). Scribe relies on (uniformized) restricted directed information to detect causality but also supports other methods, including the well-known mutual information, Granger causality and the more recent CCM. Scribe starts with time-series data, which can be based on “pseudotime-series” of a developmental trajectory reconstructed from scRNA-seq data such as those constructed using Monocle 2, live imaging data or datasets with current and predicted spliced RNA expression estimated using RNA-velocity. Scribe provides two main types of analysis:

1. Visualization and estimation of causal gene regulation;

2. Reconstruction of large-scale sparse causal regulatory networks.

Preparing pseudotime-series or RNA-velocity for scRNA-seq datasets

Scribe does not provide any built-in functionalities for pseudotime-series construction and relies on Monocle (http://cole-trapnell-lab.github.io/monocle-release/) or similar tools, such as dpt (Haghverdi et al., 2016) or wishbone(Setty et al., 2016), for reconstructing the single-cell trajectory before inferring causal networks. Scribe also doesn’t provide any built-in functionalities for RNA-velocity estimation and relies on the velocyto framework (La Manno et al., 2018) for those estimations. In relation to physical time, pseudotime has an arbitrary scale, thus Scribe doesn’t consider pseudotime value themselves instead using the ordering of each cell in pseudotime for causal network inference. Similarly, we also assume the time delays Δt used in RNA-velocity estimations are constant across cells and genes for the sake of simplicity.

Visualizing pairwise gene interaction

In order to intuitively visualize casual regulations between genes, Scribe provides different strategies to visualize the response, causality and combinatorial regulatory logic between gene pairs. The response visualization is similar to the DREVI approach as proposed by Smita Krishnaswamy, et. al(Krishnaswamy et al., 2014) with the exception that it considers time delay to visualize the expected expression of potential targets given a potential regulator’s expression after a time delay. Response visualization thus additionally aids in visualizing commonly appeared time-delayed regulations involved in cell differentiation(Alon, 2007).

One limitation of response visualization is that it ignores the effects of a gene’s previous state to the current state or memory of its history. In order to also capture this effect and thus intuitively visualize causality, Scribe is equipped with causality visualization. Essentially, this approach visualizes the causal regulation by considering the information transfer from the time-delayed potential regulator to the target’s current expression, conditioned on the target’s previous state to remove effects from auto-regulation. Causality visualization is a heatmap consisting of the expected value of the target’s current expression given the target’s immediate past expression (y-axis) and the regulator’s expression with a time lag d (x-axis). For each column, it represents the relationship for the target’s expression at the previous time point to the current state (memory of the history or “auto-regulation”) given a fixed regulator value, while for each row, the information transfer from the regulator to its targets given the previous target state.

Visualizing combinatorial gene regulation

It is of great interest to understand the combinatorial gene regulation as it often determines how cells make decisions to choose a particular cell fate or adapt to external stimuli(Ma et al., 2009). In order to visualize two-input combinatorial regulation, Scribe provides a third visualization tool. This visualization is a heatmap consisting of the expected value of the target’s current expression given knowledge of both of the regulators’ expressions with a time lag (x/y-axis). For both of the causality and the combinatorial logic visualizations, the corresponding expected value is calculated through a local average with a Gaussian kernel.

We noticed that gene regulation directly affects the rate of the target gene which then results in gene expression changes. For example, if a gene X is negatively regulated by gene Y. We may define the rate function of X as $\frac{d{X}_t}{dt}=1/\left(X_{t-1}^2+Y_{t-\mu }^2\right)$. Therefore, visualizing the expected rate of a target at its current state given knowledge of both the regulators’ expressions with a time lag (x/y-axis) allows better intuition of regulations. Although we won’t have accurate estimates of the rate of gene expression with pseudo-time series data, the RNA-velocity method can be used to obtain those estimates.

Causal network inference: an RDI-based algorithm

Causal inference in Scribe is based on RDI, which is an extension of directed information under the assumption that the underlying processes can be described by a first-order Markov model. The method we implemented basically tries to calculate the RDI value for each pair of genes (i, j) conditioned over the top L genes (default is 0 or no conditioning and 1 for cases where we used conditioning) which are candidates of being regulators of the gene j.

To reach this goal, it first calculates all the pairwise unconditioned RDI values, for all the potential delays specified by the user in vector d (by default, it is a vector including 5, 10, 20, 25). Note that for the RNA-velocity dataset, since we assume the time delays Δt for the current and predicted future RNA expression level are constant across the cell and genes, there is no need to scan for a window of potential time delays. Then for each pair (i, j), it treats the delay corresponding to the largest RDI value as the “true” delay of effect, i.e. the actual time delay by which the effect of i appears in j. Having identified the “true” delays, the method then re-calculates the pairwise RDI values for each pair of genes (i, j), this time conditioned over the top L (L can be specified by the user) genes with the highest incoming RDI values to j associated with their corresponding true delays, treating them as the potential regulators of j. The algorithm of causal inference in Scribe is as follows:

Input: gene expression time-series (either based on pseudotime-series, “RNA-velocity” or live imaging data, among others) ${\underset{\_}{X^{(i)}}}^t$ for each gene i

Output: A matrix of pairwise causality scores

Parameters: d: vector of delays, L: number of conditioning genes

Pseudocode:

1. For each pair of genes (i, j):

- For all delays δ ∈ d: Calculate RDIδ (X(i) → X(j))

- Set ${\delta }_{i,j}^{\max }:=\underset{\delta \in d}{\arg \max }RD{I}_{\delta }\left(X^{(i)}\to X^{(j)}\right)$

2. For each gene j:

- For all i: sort $RD{I}_{{\delta }_{i,j}^{\max }}\left(X^{(i)}\to X^{(j)}\right)$ values in descending order

- According to the sorting above, take the L + 1 nodes i with the highest incoming RDI values to j and store them in a set as $in{c}_j^{\max }$. Store their corresponding delays ${\delta }_{i,j}^{\max }$ in a set $d_j^{\max }$.

3. For each pair of genes (i, j):

- If $i\in in{c}_j^{\max }$, remove i from $in{c}_j^{\max }$. Otherwise, remove the node l with the lowest $RD{I}_{{\delta }_{i,j}^{\max }}\left(X^{(l)}\to X^{(j)}\right)$ from $in{c}_j^{\max }$.

4. For each pair of genes (i, j): Output $RD{I}_{{\delta }_{i,j}^{\max }}\left(X^{(i)}\to X^{(j)}|{\left\{X_{t-{\delta }_{l,j}^{\max }}^{(l)}\right\}}_{l\in in{c}_j^{\max }}\right)$

The estimation of mutual information is inspired by Kraskov’s method (Kraskov et al., 2004), which builds on counting nearest-neighbor points. In the R implementation of Scribe, nearest-neighbor points are identified with a modified RANN package.

To calculate the causal network with uRDI, we apply the same algorithm as above but simply replace RDI with uRDI. In addition to what required in RDI, uRDI also needs to estimate the actual distribution, p (x_t−d, y_t−1), which relies on kernel density estimation (KDE). We use standard Gaussian kernels from R in the Scribe package to calculate KDE.

Inferring and visualizing transcriptomic gene regulatory network

Scribe can estimate a causal network from a set of known TFs (and among the TFs) to a set of targets of interest (selected through, for example the BEAM test), or estimate the pairwise causality among all the genes in a set of genes of interest. For the first scenario, Scribe estimates causality between all pairs of TFs and the causality from each TF to each putative target; for the second scenario, Scribe estimates causality for any pair of genes in both directions. In order to retrieve significant causal edges while removing promiscuous edges and reconstruct a sparse causal regulatory network that satisfies known properties of biology networks, Scribe relies on a modified CLR regularization method (Context Likelihood of Relatedness) regularization and a directed network regularization inspired by some biological assumptions (see section Network sparsifier: CLR regularization and directed graph regularization below).

In order to facilitate the visualization of complex networks, Scribe provides a variety of approaches to visualize the RDI network either through a heatmap, a hierarchical layout, an arc diagram or a hive plot, implemented based on igraph, netbiov, ggraph, arcdiagram as well as the HiveR R packages.

We used the Kleinberg centrality to define the hubness used to order genes on the arc plot which is defined as the principal eigenvector of AA′, where A is the adjacency matrix of the graph(Kleinberg, 1999).

In addition to the core causality detection feature based on (uniformized) restricted direction information, Scribe also supports various methods for inferring the regulatory relationships including mutual information, Granger causality, and CCM implemented based on parmigene, vars, and the rEDM packages, respectively. We also provide a python package for most of the estimation methods, although without extensive support for visualization which may be supported in the future.

Parameters of RDI

Parameter	Type	Effect of tuning parameters
d	Vector of positive integers	Default: 5, 20, 40 The vector of potential delays, for which the corresponding RDI values are calculated. Setting this argument too small may limit the ability of Scribe to detect causal relationships, while setting it too large can result in the discovery of incorrect or indirect causal relationships, resulting in false delays and conditioning.
L	Non-negative Integer	Default: 0 The number of the top incoming node(s) to the target, excluding the source, over which RDI is conditioned. L = 0 corresponds to no conditioning (Plain pair-wise RDI). Any L > 0 corresponds to conditional RDI (cRDI). Conditioning over more nodes approaches the theoretical prerequisite of conditioning over all genes, excluding the source and target, needed for inferring the true causal network, however it imposes more computational burden and undesirably reduces the accuracy of the RDI estimator with fixed number of samples N, as it exponentially increases the dimension of the state space used to calculate the k-nearest neighbors.
k	Positive Integer	Default: 5 Number of the nearest neighbors in the kNN estimator for the conditional mutual information. The parameter should be set in such a way so the neighborhood captures an adequate number of samples for a good estimate of the probability corresponding to each sample.
Uniformization	Boolean	Default: False If True, uRDI instead of RDI will be used. While imposing higher computational burden over the same data than RDI, uRDI is expected to improve the causal inference in the cases with highly-biased sampling distributions.

Algorithm complexity

Algorithm	Methodology	Parameters	Worst-case Complexity N: the number of samples; d: the dimension of the X and Y manifolds (default 2); k: the number of nearest neighbors L: the number of conditioning genes I: the dimension of the features data
CCM	Determining the causality from X to Y based on how well one can reconstruct the cross-mapped estimate of X from the nearest neighbors determined on Y space	E: The number of lags embedded in the shadow manifold Tau: The time lag between each consecutive pair of time samples (default: 1)	O (2EN log N) *+ O (2(E + 1) N) ** *Complexity of kd-tree algorithm for kNN search ** Complexity of regression and weight estimation
Granger Causality	Determining the causality from X to Y based on how much the past samples of X contribute in linearly estimating the current state of Y, compared to when the Y is estimated based merely upon its own past	Maxlag: The number of lags of the past sample included in estimating the current state of Y	O (IN + 2I2 N + I3) * * The complexity of linear regression
RDI and cRDI	Determining the causality from X to Y based on the amount of mutual information between the past of X and the current state of Y conditioned over the past of (potentially) all other variables than X	k: The number of neighbors for kNN estimation of mutual information d: The lags for which the mutual information from the lagged source to the current state of target is estimated. L: The number of the conditioning nodes other than X and Y. While small L’s can result in false positives since we won’t filter out confounding and/or intermediate factors, too large L’s will result in curse of dimensionality in smaller sample set regimes and increasing the computational complexity in larger sample set regimes.	O ((d + L + 1) N log N) * + O (kN) ** *Complexity of kd-tree algorithm **Complexity of inquiry of each neighbor
uRDI and ucRDI	Same as RDI method, but including the replacement of the empirical distribution of the past samples with a uniform distribution	All Parameters from RDI plus: BW: The bandwidth of the kernel estimator	O ((d + L + 1) N log N) * + O (kN) ** + O (N3) *** *Complexity of kd-tree algorithm **Complexity of inquiry of each neighbor ***Complexity of kernel density estimation

Regularizing causal interaction networks

In theory, Scribe can remove potential indirect causal gene regulation from one gene X to another gene Y by conditioning on all other genes in the transcriptome except X. However, this requires a huge number of samples which is infeasible even with current single cell genomics techniques and is impractically slow for even modest sets of genes. Therefore, we sought alternative approaches based on statistical significance and reasonable assumptions of biology structures to remove potential indirect edges. The first method we applied is the CLR or Context Likelihood Relatedness regularization. Previously, CLR is used in conjunction with mutual information (MI). RDI (cRDI, etc) is like MI, it calculates the pairwise “causality influence score”. Simply computing MI between all pairs of genes would yield a dense network with many indirect interactions. CLR regularizes this network to enrich it for direct interactions. Just as with MI, we need some means of sparsifying the network formed by RDI links between all pairs of genes. Thus, Scribe uses a procedure for regularizing RDI networks that is analogous to the one CLR uses to regularize MI networks. It works as the following: after computing the causality score with RDI (uRDI) without conditioning between all gene-pairs, CLR calculates a normalized score based on the z-score (or 0 if the z-score is less than 0) from all the input edges to the potential target and all the output edges from the potential regulator of the gene pair. This normalized score is used as a statistical likelihood of each causal edge regarding to its network context. More formally, denoting the asymmetric matrix R corresponds to all raw causality scores calculated with Scribe, with R_ij being the causality score from gene i to gene j, we can calculate the z-score z_i based on all gene i’s output causality scores and z_i all gene j ‘s input causality scores. The normalized score of R_ij, ${\widehat{R}}_{ij}$ is defined as:

$${\widehat{R}}_{ij}=\sqrt{\max {\left(0,z_i\right)}^2+\max {\left(0,z_j\right)}^2}/2$$

The user can either use the normalized score or choose a threshold of the normalized scores and treat the edges above the threshold as significant or real regulation comparing to the background distribution of the causality scores. As discussed in the original study, CLR removes many of the false regulations in the network by eliminating “promiscuous” cases, where one regulator weakly co-varies with a large numbers of genes, or one gene weakly co-varies with many transcription factors which may arise when the assayed conditions are inadequately or unevenly sampled. We note that, however, the original CLR is only applied on a symmetric mutual information based matrix while we are dealing with an asymmetric matrix of causality scores. To avoid potential confusion, we name our modified procedure as “CLR regularization” in our text. After applying CLR, the network may be still dense and contain spurious edges. Previous studies have shown that the biological networks have some special properties distinct from those of random networks; for example, the network’s out-degree distribution is well approximated by a power law distribution where its in-degree distribution is almost an exponential distribution. Based on those assumptions, we proposed a new regularization method for a directed graph.

The goal of our method is to learn a sparse directed graph from a dense asymmetric causality network (retrieved after applying CLR regularization) satisfying two aforementioned properties. The directed graph’s structure is represented by an indicator matrix denoted by Θ ∈ {0, 1}^N×N, where θ_i,j = 1 stands for the existence of edge i to j, and 0 otherwise. Since the entries are indicators, the in-degree and out-degree of each node in the network can be easily formulated. Specifically, the out-degree of the ith node can be represented by h_out (i) = ∥θ_i∥₁ and the in-degree of the ith gene is correspondingly represented by h_in (i) = ∥θⁱ∥₁, where θ_i and θⁱ are the i th row and i th column of Θ, and ℓ₁-norm counts the number of nonzero elements since θ_i,j ∈ {0,1}. Given the asymmetric matrix of causality score R with the (i, j)-th entry as R_ij, the following optimization problem is formulated to learn the structure of the network:

$$\underset{\mathrm{\Theta }ϵ\text{A}}{\min }\left(-{\sum }_{i,j}{\theta }_{i,j}{R}_{i,j}+\alpha {\sum }_{i=1}^N\log \left({\Vert {\theta }_i\Vert }_1+\xi \right)+\lambda {\sum }_{i=1}^N{\Vert {\theta }^i\Vert }_1\right)$$

where the feasible set of the network structure is

$$\text{A}=\left\{\mathrm{\Theta }\in {\{0,1\}}^{N\times N}:{\sum }_i{\sum }_j{\theta }_{i,j}\ge B\right\}$$

The intuition of the objective function comes directly from the above three assumptions: the first term of the objective is to select the edge with large value of R_ij; the second term is the negative log likelihood of the power law distribution for the out-degree of each gene; the last term is the negative log likelihood of the exponential distribution for the in-degree of each gene. The budget parameter B is introduced to prevent trivial solution, and a small positive value ξ is used to prevent the numerical issue of log function. The parameter α is the exponent of the power law distribution and λ is the parameter of the exponential distribution.

Benchmarking Scribe with alternative algorithms on inferring causal regulatory network

We follow the same procedure as reported previously (Qiu et al., 2012) to simulate the differentiation of central nervous system (Eq. 1), except here we replace the correlated noise in the previous study with independent additive noise for the purpose of simplicity. The data generated through this simulation is regarded as “real-time” dataset.

$$\begin{gathered} {\mathit{mature}}_{\mu }=0 \\ n=4 \\ k=1 \\ a=4 \\ \eta =.25 \\ {\eta }_m=0.125 \\ {\eta }_b=0.1 \\ {a}_s=2.2 \\ {a}_e=2.2 \\ {m}_x=10 \\ \frac{dx[Pax6]}{dt}=a_s\frac{1}{1+{\eta }^n\left(x_{t-1}[Tuj1\right]+x_{t-1}[Aldh1L]+x_{t-1}^n[Olig2])x_{t-1}^n[Mature]}-k\cdot x_{t-1}[Pax6] \\ \frac{dx[Mash1]}{dt}=a\frac{x_{t-1}^n[Pax6]}{1+x_{t-1}^n[Pax6]+x_{t-1}^n[Hes5]}-k\cdot x_{t-1}[Mash1] \\ \frac{dx[Brn2]}{dt}=a\frac{x_{t-1}^n[Mash1]}{1+x_{t-1}^n[Mash1]}-k\cdot x_{t-1}[Brn2] \\ \frac{dx[Zic1]}{dt}=a\frac{x_{t-1}^n[Mash1]}{1+x_{t-1}^n[Mash1]}-k\cdot x_{t-1}[Zic1] \\ \frac{dx[Tuj1]}{dt}=a_e\frac{x_{t-1}^n[Brn2]+x_{t-1}^n[Zic1]+x_{t-1}^n[Myt1L]}{1+x_{t-1}^n[Brn2]+x_{t-1}^n[Zic1]+x_{t-1}^n[Myt1L]}-k\cdot x_{t-1}[Tuj1] \\ \frac{dx[Hes5]}{dt}=a\frac{x_{t-1}^n[Pax6]}{1+x_{t-1}^n[Pax6]+x_{t-1}^n[Mash1]}-k\cdot x_{t-1}[Hes5] \\ \frac{dx[Scl]}{dt}=a_e\frac{{\eta }^n{x}_{t-1}^n[Hes5]}{1+{\eta }^n{x}_{t-1}^n[Hes5]+x_{t-1}^n[Olig2]}-k\cdot x_{t-1}[Scl] \\ \frac{dx[Olig2]}{dt}=a_e\frac{{\eta }^n{x}_{t-1}^n[Hes5]}{1+{\eta }^n{x}_{t-1}^n[Hes5]+x_{t-1}^n[Scl]}-k\cdot x_{t-1}[Olig2] \\ \frac{dx[Stat3]}{dt}=a\frac{{\eta }^n{x}_{t-1}^n[Hes5]x_{t-1}^n[Scl]}{1+{\eta }^n{x}_{t-1}^n[Hes5]x_{t-1}^n[Scl]}-k\cdot x_{t-1}[Stat3] \\ \frac{dx[Myt1L]}{dt}=a\frac{x_{t-1}^n[Olig2]}{1+x_{t-1}^n[Olig2]}-k\cdot x_{t-1}[Myt1L] \\ \frac{dx[Aldh1L]}{dt}=a_e\frac{x_{t-1}^n[Stat3]}{1+x_{t-1}^n[Stat3]}-k\cdot x_{t-1}[Aldh1L] \\ \frac{dx[Sox8]}{dt}=a\frac{{\eta }_m^n{x}_{t-1}^n[Olig2]}{1+{\eta }_m^n{x}_{t-1}^n[Olig2]}-k\cdot x_{t-1}[Sox8] \\ \frac{dx[Mature]}{dt}=matur{e}_{\mu }\left(1-\frac{x_{t-1}[Mature]}{m_x}\right) \end{gathered}$$ Eq. 1. Ordinary differential equations for the neuron system.

For creating Supplementary Figure 1B, D, we set the time step as 0.1, samples per simulation as 100, the total number of simulations as 20. We then infer the causal network based on all the 2000 samples using CCM, GC and RDI or uRDI either without conditioning or conditioning on one gene that has the maximal input causality other than the current regulator to the target. Time delay between regulator and target used in all those algorithms is set to be 1. We compare the inferred network with the known network to calculate the AUC (area under curve). The experiment is repeated for 25 times to ensure reliable conclusions. We also increase the standard deviation of the intrinsic noise from 0 to 0.2. ROC (Receiver Operating Characteristic) curve in Supplementary Figure 1C, D is obtained similarly while setting the simulation based on a linear system where the transition matrix A is generated according to the network with non-zero coefficients randomly taken from a uniform distribution u (0.75,1.25). The A matrix is then normalized to 1.01×max{eig (A)} to avoid the divergence of the system. The intrinsic noise standard deviation (s.d) is set to be equal to 0.01. All the genes are initialized with a random value u (0.5,2). To infer the causal network, we take 100 samples per simulation and perform the simulation five times, then apply Scribe, CCM and GC on those simulated data points.

To visualize the response, causality and combinatorial regulations as in Supplementary Figure 2C–I, a single simulation leading to the neuron fate is used. To create the response and the causality visualization for the two-node motifs (Ma et al., 2009), the network motifs are firstly converted into a set of SDE functions using similar formulations as that used in the above simulation for neuronal differentiation. The expression dynamics is then simulated by setting the initial expression for both genes as 0.01 and followed based on the set of SDE equations (Supplementary Figure 2a). We used similar procedures to simulate expression of genes under combinatorial regulations with different logic gates and then create the combinatorial regulation visualizations (Supplementary Figure 2b).

To investigate the importance of temporal coupling and the number of samples on the performance of causal inference, we also simulate three other types of dataset based on the simulated “real time” dataset as following:

1. The RNA-velocity analysis framework estimates both exon and intron expression levels for each cell i or C_i. It then calculates the RNA-velocity Vⁱ(j) for each gene j in each cell i and predicts the future exon expression of E^predict after Δt = 1. Assuming the time delays from all regulators to their putative targets are the same as Δt (or 1), Scribe calculates causality from the potential regulator to the target with the conditional mutual information between the current regulator’s exon expression X_t to the predicted target exon expression Y_t+1 (or equivalently the estimated RNA velocity value V_t(Y)) conditioned on the current target exon expression Y_t or by the default formula I(X_t; Y_t+1|Y_t) (or alternatively I(X_t;V_t(Y)|Y_t)). Since X_t, Y_t+1(V_t(Y)) and Y_t are all estimated from the same cell, in theory the gene expression dynamics between X_t, Y_t+1 (V_t(Y)) and Y_t is coupled. To generate RNA-velocity simulation dataset, we randomly select one time point t for each cell and collect all genes’ current and the next time point’s expression ($X_t^{(i)}$ and $X_{t+1}^{(i)}$). RNA velocity for each cell in that time point is then simply calculated as the difference between next time point and current time point’s gene expression $(V_t\left(X^{(i)}\right)=X_{t+1}^{(i)}-X_t^{(i)})$.

2. To generate live-imaging simulation dataset, we first randomly select 13 cells where for each cell, a different gene is chosen and is followed over the entire developmental process.

3. To generate pseudotime dataset, similar to RNA-velocity, we randomly select one time point t for each cell and collect all genes’ expression at that time point. Then all data points from each cell at different time point is pooled and used as input to Monocle 2 for trajectory inference, we then set the beginning of the simulation as root state for the trajectory and order cells based on the inferred pseudotime to form a pseudotime series.

To create Supplementary Figure 4B, five replicates each with 2000 data points are used for each algorithm. For Supplementary Figure 4 C (D), the same analysis is performed but with data (replicates) downsampled to 200, 400, 600, 800, 1000, 1200, 1400, 1600, 1800 or 2000 data points (1, 5, 10, 15, 20 repeats).

Details on analyzing datasets used in this study

Benchmark Scribe with DREAM challenge datasets

In GeneNetWeaver, we looked at the DREAM3 challenge in-silico data for three networks, each of which has a size of 50. All networks were obtained from modeling network in yeast (Yeast-1, Yeast-2 or Yeast-3). For each network, GeneNewWeaver is used to simulate the time series for 10 times (i.e. we had a total of 10 runs), for a duration of 1000 time-units, and the measurement is recorded at every 10 time-units, hence 100 total time points for each run. The intrinsic noise coefficient was set to be 0.05. The measurement noise was set as the default model in microarrays which is also used in DREAM4 challenge. Each time series was then normalized after adding the noise. For each of the three networks, we conducted the inference task by running different methods over the generated time series data described above and compared the final AUC score for each network.

Inferring causal network with pseudotime ordered scRNA-seq datasets

Lung data is processed as described previously. Expression matrix is downloaded from GEO (GSE52583). After filtering, log-transformed TPM values of 183 single cells’ transcriptome are used for monocle 2 analysis. (Qiu et al., 2017a). Categorization of pneumocyte specification markers into either early and late groups used for benchmarking is based on references(Qiu et al., 2017a; Treutlein et al., 2014).

The LPS data was pre-processed as described previously. 510 cells annotated as unstimulated replicate (normal unstimulated cells were observed to have low RNA library quality), LPS stimulated cells without any perturbations, and LPS stimulated cells with Stat1 and Ifnar1 knocked out taken at each of the included time points are used. The pseudotime trajectory is reconstructed with the reversed graph embedding (Qiu et al., 2017a) on the same set of ordering genes used in this study. Only the path with wild-type cells is used for causal network inference. Regulators and targets, and the regulatory network used for benchmarking are collected from references (Amit et al., 2009) and reference (Garber et al., 2012), respectively.

Olsson data is processed as described previously. The processed FPKM values is downloaded via synapse (id syn4975060) and used for pseudotime ordering with Monocle 2. The master regulators, transcription factors and downstream targets, and the regulatory network used for benchmarking are collected from reference (Qiu et al., 2017a) and references (Su et al., 2017), respectively.

Paul data is processed as described previously. We downloaded the UMI counts data and the cell cluster annotation information for the Paul from http://compgenomics.weizmann.ac.il/tanay/?pageid=649. Only the path leading to the erythrocytic fate is used for reconstructing the causal regulatory network. The regulatory network responsible for the differentiation of erythrocyte cells used for benchmarking is collected from (Swiers et al., 2006).

Infer causal network with RNA-velocity

The data of the chromaffin cell “RNA-velocity” analysis is retrieved from (http://pklab.med.harvard.edu/velocyto/notebooks/R/chromaffin.nb.html). We use the estimated exon expression to reconstruct the trajectory for the chromaffin cell commitment. Only cells on the path from the Schwann cell progenitors to mature chromaffin cells are used to infer the casual network. Two different formulations, I(X_t;Y_t+1|Y_t), (or I(X_t;V_t(Y)|Y_t)), can be used to infer causal networks with data from RNA-velocity. In this study, we apply the first formulation.

Inferring causal network with live-image data

Lineage-resolved live-imaging data for C. elegans early embryogenesis is obtained from Waterston lab. Raw fluorescence intensity signal is directly used for causal network inference. We note two caveats in analyzing the reporter data with Scribe. First, although the promoter-fusion data sheds light on the induction kinetics of the TF of interest, once the fluorescent reporter is expressed it follows the trafficking and degradation kinetics of the histone protein, and not the TF. Second, the time series for each TF was captured in a different embryo, so this may introduce noise that obscures the regulator/target relationships between the TFs although the C. elegans development process is highly robust. Nevertheless, this data set represents an unprecedented view of TF activity at high spatiotemporal resolution during the early development of a complex organism.

DATA AND SOFTWARE AVAILABILITY

Code availability

A version of Scribe (version: 0.99) used in this study is provided as Supplementary Software. The newest Scribe implemented as an R package is available through GitHub (https://github.com/cole-trapnell-lab/Scribe), an equivalent python version is hosted at (https://github.com/aristoteleo/Scribe-py). Notebooks for usage cases of Scribe is available at https://github.com/aristoteleo/Scribe-Python-notebooks. CCM algorithm is implemented as the rccm package (https://github.com/cole-trapnell-lab/rccm) which is based on https://github.com/cjbayesian/rccm. The neurogenesis simulation is implemented as the scRNASeqSim package (https://github.com/cole-trapnell-lab/scRNASeqSim). Supplementary Software also includes a helper package containing helper functions as well as all analysis code that can be used to reproduce all figures and data in this study.

Data availability

This study did not generate new data.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
Lung dataset	(Treutlein et al., 2014)	GEO id: GSE52583
LPS dataset	(Shalek et al., 2014)	GEO id: GSE41265
MARS-seq dataset	(Paul et al., 2015)	http://compgenomics.weizmann.ac.il/tanay/?pageid=649
Olsson dataset	(Olsson et al., 2016)	synapse id syn4975060
Live imaging dataset for the C. elegans	(Murray et al., 2012)	Waterston lab
Software and Algorithms
Scribe	This paper	https://github.com/aristoteleo
rccm	Implemented based on: https://github.com/cjbayesian/rccm	https://github.com/cole-trapnell-lab/rccm
scRNASeqSim	This paper	https://github.com/cole-trapnell-lab/scRNASeqSim
Other
Supplementary software	This paper	Supplementary software

Highlights.

• Scribe detects causal regulatory networks between genes in diverse single cell datasets

• Scribe uses Restricted Directed Information to identify regulators and their targets

• Inferring causal regulatory networks requires temporal coupling between measurements

• RNA velocity outperforms pseudotime but neither perform as well as true timeseries data