Evaluation of COVID-19 epidemic outbreak caused by temporal contact-increase in South Korea

Highlights

• •Widespread COVID-19 infection occurred in South Korea after February 18 because of the mass infections in the Shincheonji Church of Jesus.
• •The mean transmission rate has increased by approximately 20 times since the mass infections from the 31 st confirmed patient occurred on February 9.
• •Voluntary prevention actions were fairly implemented, and, consequently, the effective reproduction number on February 28 has remained below unity after identifying the 31 st confirmed patient on February 18.
• •We aim for the voluntary participation by citizens in active prevention activities until vaccines or treatments are developed in the countries that are presently suffering from COVID-19.

Abstract

Objectives

On March 15, 2020, 61.3% of the confirmed cases of COVID-19 infection in South Korea are associated with the worship service that was organized on February 9 in the Shincheonji Church of Jesus in Daegu. We aim to evaluate the effects of mass infection in South Korea and assess the preventive control intervention.

Method

Using openly available data of daily cumulative confirmed cases and deaths, the basic and effective reproduction numbers was estimated using a modified susceptible–exposed–infected–recovered-type epidemic model.

Results

The basic reproduction number was estimated to be $R_0=1.77$. The effective reproduction number increased approximately 20 times after the mass infections from the 31 st patient, which was confirmed on February 9 in the Shincheonji Church of Jesus, Daegu. However, the effective reproduction number decreased to less than unity after February 28 owing to the implementation of high-level preventive control interventions in South Korea, coupled with voluntary prevention actions by citizens.

Conclusion

Preventive action and control intervention were successfully established in South Korea.

Introduction

In December 2019, people in Wuhan, China, began to contract pneumonia from an unknown cause. The condition was similar to viral pneumonia, as inferred by clinical presentation. On January 7, 2020, it was confirmed that the cause of the pneumonia was a new coronavirus. The disease was subsequently named COVID-19. COVID-19 induces symptoms that are similar to those caused by other respiratory infections, mainly affects older people with comorbidities and may result in a fatal respiratory disease (Chen et al., 2020). On January 10, 2020, Chinese authorities reported the first death due to COVID-19. After that, cases have been reported in other countries worldwide.

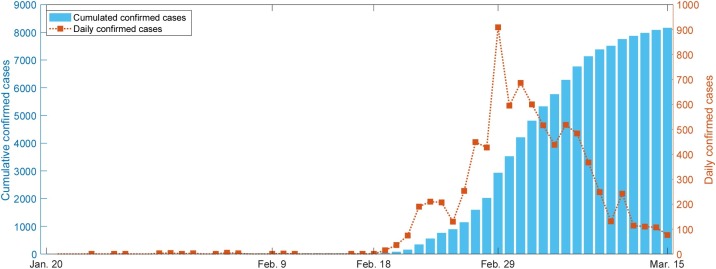
In South Korea, the first patient who had visited Wuhan was reported on January 20, 2020. Since then, 30 cases of COVID-19 were reported up to February 17. However, after the 31st case was reported in Daegu on February 18, the number of confirmed cases rapidly increased to 8,162, of which 75 had died by March 15, 2020 (see Figure 1 ) (Korean Ministry of Health and Welfare, 2020). The epidemiological investigation by the Korea Centers for Disease Control and Prevention (KCDC) revealed that the 31 st patient belonged to the Shincheonji Church of Jesus in Daegu and that she attended the church service on February 9 and 16 after she had experienced the symptoms of COVID-19 on February 7. Also, it was revealed that 5,006 confirmed cases, which accounted for 61.3% of the 8,162 confirmed cases, were associated with the church cluster in Daegu (Korean Ministry of Health and Welfare, 2020). Accordingly, KCDC guessed that on February 9, mass infections had occurred, resulting in many secondary cases, and so COVID-19 rapidly propagated in South Korea.

Figure 1.

COVID-19 outbreak size in South Korea from January 20 to March 15 versus time. The blue bar graph represents the cumulated confirmed cases and dotted line the daily confirmed cases.

As COVID-19 rapidly spread nationwide, South Koreans have actively worn masks from February 18. The Government of South Korea recognized the seriousness of the spread of COVID-19 and elevated the COVID-19 alert from level 3 to 4 (the highest level) on February 23. The government has implemented a social-distancing campaign, enhanced infection prevention and control practices in hospitals, conducted drive-through testing, and postponed the schedule of school activities. It remains committed to preventing the occurrence of COVID-19.

In this study, we constructed a mathematical model using the early data of confirmed cases that were reported from January 20 to March 15 in South Korea. Based on an epidemiological investigation, the spreading process of COVID-19 during this period is divided into three phases. We estimate the reproduction number of each phase to analyze the transmission potential and severity of COVID-19. As a result, we are able to assess the current situation of COVID-19 in South Korea.

Methods

We use a modified susceptible-exposed-infected-recovered transmission model to evaluate the COVID-19 epidemic in South Korea. Susceptible individuals $S$ enter the exposed class $E_1$ after the transmission of the virus. We consider the $n$ linear chains $E_k$, $k=\mathrm{1,2},\cdots ,n$ on the exposed class for determining a model that can be fitted to the data with limited information that the mean incubation period is $1/\epsilon ,$ fixed (Martcheva, 2015, Champredon et al., 2018). Those exposed people were infected, entered the $I$ class. The terms $Q$ and $R$ denote isolated and discharged, respectively. The term $\beta (t)$ denotes the transmission rate. The parameters $1/\eta$ and $1/\gamma$ denote the average duration from onset of symptoms to being isolated, and average duration from isolated to being discharged, respectively. The parameter $\delta$ is the case fatality rate. We have the following:

$$S^{\prime }\left(t\right)=-\beta \left(t\right)S\left(t\right)\frac{I\left(t\right)}{N-Q\left(t\right)},$$

$$E_1\left(t\right)=\beta \left(t\right)S\left(t\right)\frac{I\left(t\right)}{N-Q\left(t\right)}-n\epsilon E_1\left(t\right),$$

$$E_k^{\text{'}}\left(t\right)=n\epsilon E_{k-1}\left(t\right)-n\epsilon E_k\left(t\right),k=2,\cdots ,n,$$

$$I^{\text{'}}\left(t\right)=n\epsilon E_n\left(t\right)-\eta I\left(t\right),$$

$$Q^{\prime }\left(t\right)=\eta I\left(t\right)-\gamma Q\left(t\right),$$

$$R^{\prime }\left(t\right)=\left(1-\delta \right)\gamma Q\left(t\right).$$

To represent the temporal changes of contact, we consider the time-dependent transmission rate, $\beta (t)$. We assume the initial transmission rate to be constant, i.e., $\beta (t)={\beta }_0$ before ${t=\tau }_1$. After ${t=\tau }_1$, we assume that the transmission rate rapidly increases as $\beta (t)={\beta }_1$. After ${t=\tau }_2$, upon introducing a high level of preventive control campaigns, the transmission rate is assumed to exponentially decay at the rate $\kappa$ (Althaus, 2014). We have the following:

$$\beta \left(t\right)=\left\{\begin{array}{ll}{\beta }_0,& 0\le t<{\tau }_1\\ {\beta }_1,& {\tau }_1\le t<{\tau }_2\\ {\beta }_1\exp \left(-\kappa \left(t-{\tau }_2\right)\right),& t>{\tau }_2.\end{array}\right)$$

Notably, the above-mentioned exponential decay implies that the change rate of $\beta$, $\beta \text{'}(t)$ is proportional to $-\beta (t)$ with rate $\kappa$.

We introduce the following two key measurements that describe the infection spread: the basic reproduction number $R_0$ and the effective reproduction number $R_e$ (Jones, 2007). $R_0$ denotes the number of secondary infections generated by an infected case in wholly susceptible circumstances, and $R_e$ denotes the number of secondary infections generated in the current state of the population while implementing control interventions. A reproduction number higher than unity means continued disease transmission. However, the value lower than unity means that continuous transmission has ended, and the disease will gradually decrease and disappear. Specifically, the basic reproduction number $R_0$ in our model is simply given as follows:

$$R_0=\frac{{\beta }_{0}S\left(0\right)}{\eta N},$$

and the effective reproduction number, $R_e$, is given as follows:

$$R_e=\frac{\beta \left(t\right)S\left(t\right)}{\eta N}.$$

The total population size $N$ was assumed to be 50,000,000. We regard $N$ as a constant because the number of deaths is small, relative to the total population size. We used the method of least squares to estimate the model parameters to minimize the following sum of squared residual until the sampling time $t_T$ (Kim et al., 2020):

$$\sum _{i=1}^{t_T}{\left[\underset{0}{\overset{t_i}{\int }}\eta I\left(t\right)\text{d}t-C{Q}^{\text{Data}\left(t_i\right)}\right]}^2+\sum _{i=1}^{t_T}{\left[\underset{0}{\overset{t_i}{\int }}\delta \gamma Q\left(t\right)\text{d}t-C{D}^{\text{Data}\left(t_i\right)}\right]}^2,$$

where $C{Q}^{\text{D}\text{a}\text{t}\text{a}}(t_i)$ and $C{D}^{\text{D}\text{a}\text{t}\text{a}}(t_i)$ are cumulative data of the number of isolated and death at the $i$ th sampling time, respectively.

Results

We used the daily cumulative cases and deaths data that were publicly available from the KCDC. We studied the data recorded from January 22 to March 15. Notably, in South Korea, the first, second, and third confirmed patients were reported on January 20, 22, and 26, respectively. Because both first and second confirmed patients were immediately isolated at the airport on account of fever, we will consider the third confirmed case as the first in this study; the third confirmed patient returned to South Korea from Wuhan, China on January 22 and remained free until confirmed on January 26. Therefore, we consider January 22 as the date of initial infection $(t=0)$, and January 26 as the date of initial containment, $I(0)=1$ and $Q(4)=1$. Worship services were organized on February 9 $(t=18)$ and 16 in the Shincheonji Church of Jesus, Daegu, and the 31 st confirmed person had participated in this service, resulting in mass infection. The confirmed date of identifying for the 31 st confirmed patient is February 18 $(t=27)$. After recognizing the seriousness of this large-scale group infection, the Government of South Korea raised the COVID-19 alert level to the highest so that the preventive actions were strictly implemented. Therefore, we assume that ${\tau }_1=18$ and ${\tau }_2=27$ (days).

We made some assumptions to reduce the number of our estimated parameters for fitting the data. First, the incubation period was fixed to $1/\epsilon =5.1$ (days) as the average incubation-period estimate of the COVID-19 outbreak in Wuhan, China (Lauer et al., 2020). It was reported 66 fatal cases as of March 12, 2020, and the time taken from experiencing symptoms to confirming is about 4.5 days and the time taken from test to confirming is about 0.5 days (Jeong et al., 2020). So, we used $1/\eta =3$ (days) while assuming the presumed self-isolation to be approximately one day. The period from being isolated to discharged was taken to be 14.7 days from the data reported until March 13, 2020 from KCDC (Korean Ministry of Health and Welfare, 2020). So, we used $1/\gamma =14.7+1.5=16.2$ (days), conforming to our assumptions. Transmission rate ${\beta }_0$, ${\beta }_1$, case fatality rate $\delta$, and decay rate $\kappa$ were estimated.

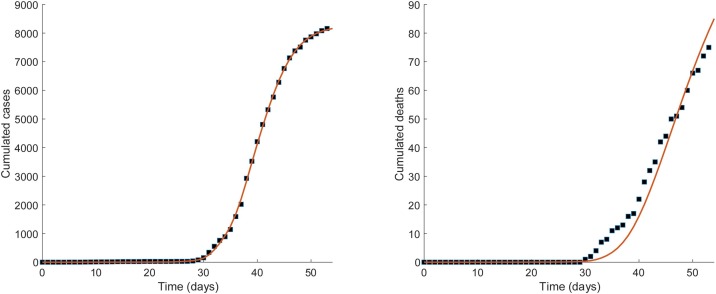
We considered 100-chain model. $n=100$ was obtained as a result of fitting with the condition $1/\epsilon =5.1$. No significant difference was found for values when $n$ is above $100$, and it did not match well for values when below $100$. In Figure 2 , we depict the result of fitting the confirmed cases and deaths data to the 100-chain model. The model fairly fits the reported data of the confirmed cases and deaths in South Korea. The estimated parameters from the model are ${\beta }_0=0.59$, ${\beta }_1=11.73$, $\kappa =0.353$, and $\delta =0.018$ and the basic reproduction number $R_0$ is 1.77 in our model analysis. It can be seen that the transmission rate on February 9 $\left(t={\tau }_1\right)$ increased by approximately 20 times of the previous day, February 8. The mean effective reproduction number, $R_e$, dropped to half on February 20, as preventive control interventions had increased after confirming the 31 st patient on February 18 $\left(t={\tau }_2\right)$. It further decreased to 1.46 and 1.02 on February 26 and February 27, respectively. Thereafter, from February 28, it has been maintained under unity.

Figure 2.

Fitting the 100-chain model to confirmed cases and deaths data. The black squared dots in both panels represent the data of the cumulative numbers of confirmed cases and deaths, respectively. The best-fit curves are shown as red solid line in both the panels. The estimated values of the parameters are β₀=0.59, β₁=11.73, κ=0.353, and δ=0.018.

Discussion

In this study, we aimed to evaluate the effects of mass infection due to temporal increases in contacts and assess the preventive control interventions using the confirmed cases and deaths data associated with COVID-19 in South Korea. The first patient was reported on January 20, 2020, but the transmission of the infection actually started from the 3rd confirmed patients from January 22 in South Korea. Since then, the COVID-19 outbreak in South Korea has resulted in 29 confirmed cases by February 18. In addition, it appeared that the outbreak was going to be controlled. It was shown that $R_0=1.77$ in our model analysis. This is slightly lower than that of Wuhan, China $(R_0=2.24–3.58)$ (Zhao et al., 2020). Personal hygiene, such as wearing masks, handwashing and disinfecting items, seems to have helped maintained this level, since the first case of outbreak in China in December 2019 was announced in South Korea. However, after the mass infection due to the 31 st confirmed patient in the Shincheonji Church of Jesus on February 9, the transmission rate of COVID-19 increased approximately 20 times. Since then, on February 18, after the confirmation of the 31 st patient, the transmission rate has halved in two days because of the high-level preventive control interventions across the nation and public volunteering. Moreover, $R_e=1.46$ on February 26, and $R_e<1$ on February 28, where 10 days after active control intervention was performed with successful analyses of prevention control. This supports previous result with the mean effective reproduction number of 1.5 on February 26 (Shim et al., 2020).

Thus far, the COVID-19 outbreak is ongoing in many countries. For example, as of March 2 2020, countries such as Italy, the United States, Spain, Germany, and France still have more than 3000 confirmed cases per day and more than 100 deaths per day. However, in South Korea, the outbreak has been reduced, as confirmed by the value of $R_e$ to less than unity within 10 days after the first mass infection was noticed. This reduction in the outbreak is attributed to the voluntary participation of the citizens in the preventive control interventions, for example, wearing masks, refraining from large outings, maintaining social distance, and banning group gatherings. Consequently, as of March 23, 2020, fewer than 100 confirmed patients per day were reported, and it seems that the outbreak is under control now. In South Korea, it is necessary for people to maintain the current momentum of preventive actions to prevent the further spread. Moreover, taking the case of South Korea as a lesson, other countries should maintain active implementation of preventive activities until vaccines or treatments are developed.

Notably, our results are preliminary. Therefore, although our study provides a result of $R_e<1$ since February 28, we are uncertain whether or not another mass infection, even with passive preventi e action, can be expected. As suggested in our study, an outbreak more severe than the current level may occur if there is another mass infection in future. Also, second big wave of outbreak may occur again caused by migrant although it seemed to have controlled as in Singapore case (A Singapore Government Agency, 2020). Even if the outbreak seems to have controlled in South Korea, reemergence might be occurred at any time when it is prevalent worldwide. Therefore, the current-level preventive control interventions and voluntary preventive actions should be continued until the disease is entirely eliminated in worldwide. Accordingly, we suggest that the government policy of “social distancing” which had been implemented in South Korea until April 5 and extended to May 5, should be maintained at some level.

Availability of data

All data are publicly available from: http://ncov.mohw.go.kr/en/.

Authors’ contribution

IHJ conceptualized the roles. IHJ and JHB designed the studies. GC, AP, JHJ, YR, SC, and IMM collected the data. SK, YDJ, and JHB analyzed the data. SK and YDJ performed the modeling, and SK illustrated the numerical simulation. All the members discussed and verified the results and wrote and revised the manuscript.

Financial support

This work was supported by the National Research Foundation of Korea (NRF) Grant funded by the Korean Government (MSIP)(NRF-2017R1A5A1015722)

Ethical approval

No ethical approval was requested.

Conflicts of interests

The authors declare that they have no competing interests.