Calibration of Blood Pressure Measurements in the Jackson Heart Study

Abstract

Background

In longitudinal research studies with follow-up examinations, the devices used to measure phenotypes may change over time. When a device change occurs, the two devices should be calibrated to each other to ensure that measurements are comparable. This paper details the Jackson Heart Study (JHS) blood pressure (BP) comparability study.

Methods

During its second clinic exam (2005–2008), the JHS switched from a random-zero sphygmomanometer (RZS) BP measurement device to an oscillometric device (OD). During this exam, BP measurements from both a RZS and an OD were taken simultaneously in 2,117 participants for the purpose of calibration. Five methods for calibrating systolic BP (SBP) and diastolic BP (DBP) were considered: ignoring the change, ordinary least squares regression, adding the average difference, Deming regression, and robust regression.

Results

Using the RZS and OD, the mean (standard deviation) SBP was 125.5 (19.2) and 126.5 (19.9), respectively, and the mean (standard deviation) DBP was 76.4 (10.6) and 74.0 (11.0), respectively. The correlation between RZS and the OD was 0.90 for SBP and 0.80 for DBP. The prevalence of high BP and hypertension and associations with albuminuria were similar when applying each of the five calibration methods. Robust regression was chosen for calibration, giving the following equations:

$${\text{SBP}}_{\text{OD}}=11.02+0.92\ast {\text{SBP}}_{\text{RZS}}$$

$${\text{DBP}}_{\text{OD}}=10.36+0.83\ast {\text{DBP}}_{\text{RZS}}$$

These equations had a higher R² statistic than using calibration equations from the Coronary Artery Risk Development in Young Adults Study and the Heinz Nixdorf Recall Study.

Conclusions

The JHS BP data has been calibrated using the above equations for use in future analyses.

In longitudinal research studies, investigators may change the devices used to measure participants’ phenotypes, including blood pressure (BP). In the 1980s and early 1990s, the random-zero sphygmomanometer (RZS) was considered an ideal device to measure BP and it was commonly used in observational research studies [1–3]. However, this type of device was found to be inaccurate, resulting in many studies transitioning to the use of an oscillometric device (OD) [4–7]. When longitudinal research studies switch devices, it is important to calibrate the BP measurements to ensure that analyses are not affected by this change.

The Jackson Heart Study (JHS), a longitudinal observational study of cardiovascular disease in African Americans, changed the device used to measure BP from a RZS to an OD during its second clinic exam, which was conducted between 2005 and 2008. A BP comparability study (BPCS) was performed to enable the calibration of BP measurements between the two devices and across exams. In this manuscript, we report the results of the JHS BPCS and the consideration of different methods for calibrating BP measurements.

Methods

The JHS was designed to identify risk factors explaining the high rate of cardiovascular disease among African Americans and to find approaches for reducing this risk. The study design, recruitment, and data collection have been described in detail previously [8, 9]. In brief, 5,306 African Americans 21 years of age and older were enrolled from the Atherosclerosis Risk in Communities (ARIC) study site in Jackson, Mississippi (30%), randomly contacted urban and rural residents from the Jackson metropolitan tri-county region (Hinds, Madison, and Rankin counties) (17%), volunteers (22%), and family members of enrolled participants (31%). To date, there have been three clinic exams that were conducted in 2000–2004, 2005–2008, and 2009–2013. The JHS protocol was approved by the institutional review boards at Jackson State University, Tougaloo College, and the University of Mississippi Medical Center. Written informed consent was provided by all participants upon enrollment and prior to each follow-up exam.

Data Collection

Information regarding age, sex, education, and antihypertensive medication use was self-reported during study interviews. Standing height in centimeters and weight in kilograms were measured and used to calculate body mass index (BMI). Fasting serum glucose was measured using a glucose oxidase method on a Vitros 950 or 250 analyzer (Ortho-Clinical Diagnostics, Raritan, NJ). Glycosylated hemoglobin A1c was measured using a high-performance liquid chromatography system (Tosoh Corporation, Tokyo, Japan). Diabetes was defined by self-report of a prior diagnosis with concurrent use of antidiabetes medication, a fasting glucose ≥126 mg/dL, or glycosylated hemoglobin A1c ≥6.5%. Urinary albumin was measured using the Dade Behring BN II nephelometer (Newark, Deleware). Urine creatinine was measured using a multi-point enzymatic spectrophotometric assay on a Vitros 950 Ortho-Clinical Diagnostics analyzer (Raritan, New Jersey). Creatinine values were calibrated to the Cleveland Clinic-equivalent Minnesota Beckman CX3 assay [10]. Urinary albumin-to-creatinine ratio (ACR) was calculated in mg/g.

Figure 1 shows the type of BP measurement device used at each of the JHS exams. A Hawksley RZS (Hawksley and Sons, Lancing, UK) was used exclusively to measure BP for participants (n=5,285) attending the first exam and attending the second exam between October 2005 and April 2007 (n=1,964). The Omron HEM-907XL (Omron Healthcare Inc., Lake Forest, Il.), an OD, was used to measure BP beginning in May 2007 (i.e., during the second exam). The BPCS (n=2,117) included participants completing the second exam between May 2007 and December 2008. Participants who completed the BPCS had their BP measured simultaneously with the Hawksley RZS and the Omron HEM-907XL OD while those who attended the second exam during this time period but did not participate in the BPCS (n=113) had their BP measured using only the OD. During the third exam, all participants had their BP measured by the OD (n=3,814).

Figure 1.

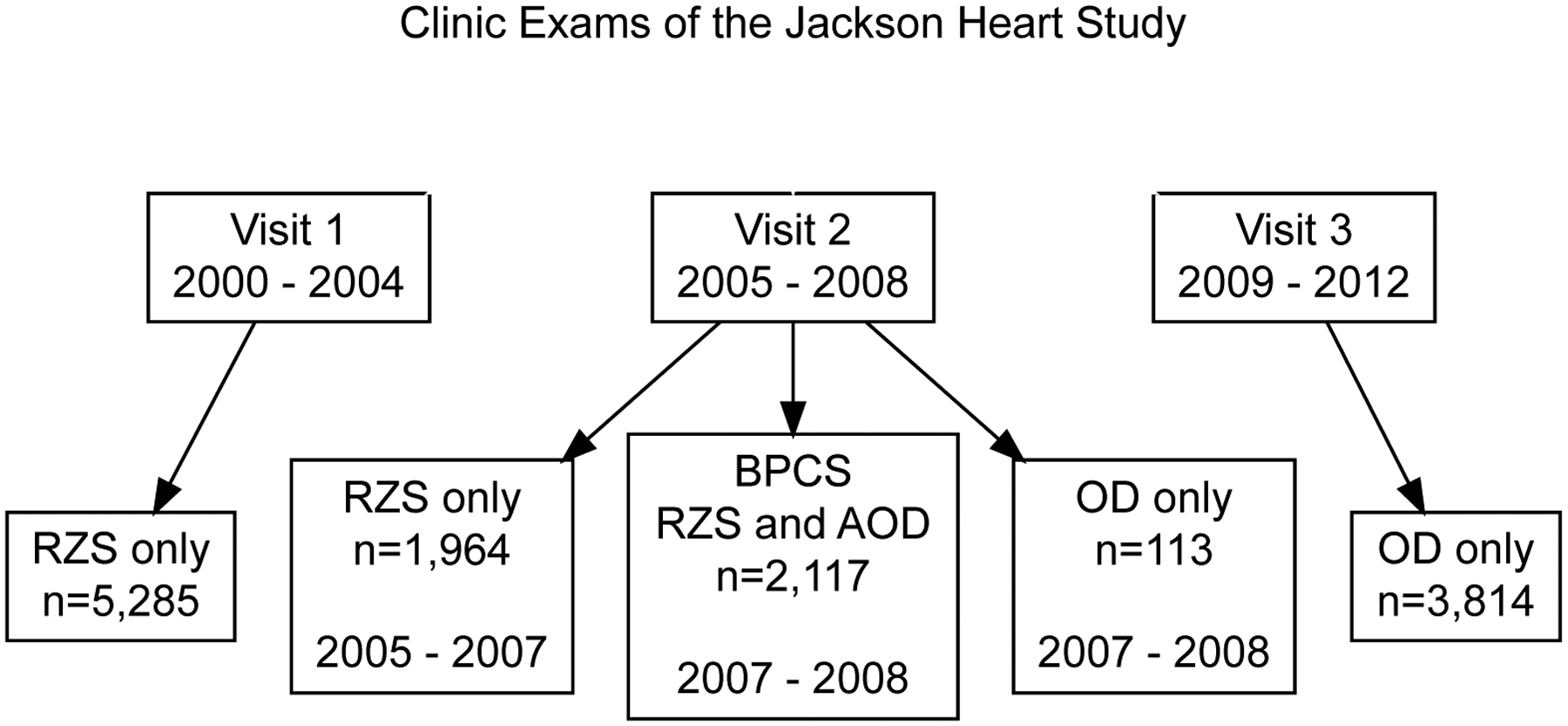
Type of device used to measure blood pressure in the Jackson Heart Study.

“RZS only” refers to participants who had their blood pressure measured using a random-zero sphygmomanometer and not the oscillometric device.

“OD only” refers to participants who had their blood pressure measured using the oscillometric device and not the random-zero sphygmomanometer.

“BPCS” refers to participants in the Blood Pressure Comparability Study who had their blood pressure measured simultaneously using a random-zero sphygmomanometer and an oscillometric device.

RZS=random-zero sphygmomanometer; OD=oscillometric device; BPCS=blood pressure comparability study

Prior to the initiation of each JHS exam, technicians were trained and certified by the clinic coordinator or a designated supervisor to conduct all study procedures including BP measurement. After initial certification, technicians were re-certified every six months. The full BPCS protocol can be viewed on the JHS website [11]. Briefly, participants’ arm circumferences were measured to determine the appropriate cuff size. An appropriately sized cuff was fitted to bare skin and the midpoint of the length of the bladder was placed over the brachial artery and the cubital fossa was at heart level. Measuring BP using the right arm was preferred, however, the left arm was used for participants who had reasons not to use their right arm (e.g., mastectomy). Prior to measuring BP, participants were seated, legs uncrossed, in a quiet room for 5 minutes. For the RZS, the first and fifth Korotkoff sounds defined SBP and DBP, respectively. High BP was defined as SBP ≥ 130 mm Hg or DBP ≥ 80 mm Hg. Hypertension was defined as self-report of a prior diagnosis, high BP at the clinic visit, or antihypertensive medication use [12].

A Y-type connector was used to connect the RZS mercury column and the OD to the BP cuff, and the OD was used to inflate and deflate the cuff; deflation occurred at approximately 2 mmHg per second, per the default factory settings. Two study technicians conducted BP readings for the BPCS using a double-headed stethoscope. One technician viewed the RZS mercury column while the other viewed the monitor of the OD. To reduce bias, the technician reading the RZS measurements could not see the OD measurements and the technician reading the OD measurements could not see the RZS measurements. Using this method, BP was measured twice, with a 30 second rest between measurements. The average of the measurements from each device was used for analysis.

Calibration Methods

The purpose of the BPCS was to allow the JHS Coordinating Center to calibrate the BP measurements of participants with only RZS readings to the OD. The following five calibration methods were assessed:

1. Ignoring the change. This method ignored that BP devices were changed (i.e., OD measurements were assumed to be equal to RZS measurements).

2. Ordinary least squares. This method created a prediction equation for the OD measurements using the RZS measurements in an ordinary least squares (OLS) regression.

3. Average difference. Instead of using regression to produce a prediction equation, all participants’ BP measurements by the OD were calibrated by adding the observed average difference between the OD and RZS measurements.

4. Deming regression. Deming regression is an error-in-variables regression method that accounts for errors in the dependent and independent variables [13]. This method created a prediction equation for the OD measurements using the RZS measurements in a Deming regression.

5. Modeling the difference between the OD and RZS as a function of RZS using robust regression. Instead of using OD measurements as the outcome, robust regression models the difference between OD and RZS measurements as the outcome as a function of the RZS measurement [14]. This modeling approach uses M-estimation via an iteratively reweighted least squares algorithm, minimizing the weight given to extreme observations [15, 16]. The resulting prediction equation was algebraically simplified so that OD measurements were being predicted by RZS measurements.

Statistical Methods

Participant characteristics and BP levels at each JHS exam, and among those who attended the second exam and completed and did not complete the BPCS, separately, were calculated as mean (standard deviation), median (25^th percentile, 75^th percentile), or n (percent), as appropriate. Among participants who completed the BPCS, locally weighted scatterplot smoothing (LOWESS) was used to visually explore the association between SBP and DBP separately, measured using RZS and OD. We also calculated Pearson’s correlation coefficients between SBP and DBP, separately, measured using RZS and OD. We further derived equations to calibrate RZS readings to the OD using the five methods outlined in the previous section.

For all analyses described below, if a participant had an OD measurement available, it was used as the BP measure for each calibration method. If a participant only had a RZS measurement available, it was calibrated to the OD measurement using each of the five calibration approaches described above. We computed the prevalence of high BP and hypertension using each of the five calibration approaches at exams 1 and 2, separately. To examine the effects of calibration on the associations of BP with other variables, we constructed models of BP with ACR as either a risk factor or outcome of interest. ACR was chosen for these analyses as it could be modeled as either a continuous or dichotomous (ACR > 30 mg/g) variable. Specifically, we conducted analyses of the associations between SBP, DBP, high BP and hypertension by each of the five calibration approaches with ACR (i.e., BP-related variables were used as independent variables and ACR was the dependent variable). In separate analyses, we investigated the association of ACR with SBP, DBP, high BP and hypertension (i.e., ACR was the independent variable and the BP-related variables were used as dependent variables) using each of the five calibration approaches. ACR, SBP and DBP were examined as continuous outcomes using linear regression. ACR > 30 mg/g, high BP, and hypertension were analyzed as binary outcomes using logistic regression. We conducted cross-sectional analyses at exam 1 and repeated measurements analyses using data from all three exams. Regression models for both cross-sectional and repeated measurement analyses included robust standard error estimates. Mixed-effects models were used for repeated measurement analyses. All regression models included adjustment for age, sex, education level (less than high school versus high school or above), diabetes, and BMI as covariates. Antihypertensive medication use was also included as a covariate in models when SBP, DBP, or high BP were either dependent or independent variables. Variables for analysis were scaled as follows: SBP was modeled per 10 mm Hg, DBP was modeled per 5 mm Hg, and continuous ACR was modeled after log₂ transformation.

Among participants in the BPCS, we calculated the prevalence of high BP and the percent agreement and R² statistic with OD-measured BP using the selected calibration approach and calibration equations from the Heinz Nixdorf Recall Study (HNRS) and the Coronary Artery Risk Development in Young Adults (CARDIA) Study [17, 18]. The calibration equations for the HNRS and CARDIA study are available in Supplemental Table 1, Supplemental Digital Content 1, http://links.lww.com/BPMJ/A93. The differences and 95% confidence interval in R² obtained from the HNRS and CARDIA calibration equations versus the JHS calibration equation was calculated using the percentile bootstrap method with 2,000 iterations.

Data management and analyses were performed using Stata version 14 [19]. Graphs were created using Stata version 14 and R 3.4.2 using the DiagrammeR package [19–21].

Results

Characteristics of the JHS participants at each study exam and those who attended exam 2 and participated and did not participate in the BPCS are presented in Table 1. Figure 2 shows a scatterplot of BP measured simultaneously by the RZS versus OD for participants who completed the BPCS. The correlation between RZS and the OD was 0.90 for SBP and 0.80 for DBP. While the majority of observations are clustered around the line of unity, differences were present for both SBP and DBP. Further, the LOWESS line for the association between the RZS and OD DBP measures was non-linear.

Table 1:

Characteristics of Jackson Heart Study participants by study exam.

Characteristic	Exam 1 (All Participants) n=5,285	Exam 2 (All Participants) n=4,194	Exam 2 (Non-BPCS Sample) n=2,077	Exam 2 (BPCS Sample) n=2,117	Exam 3 (All Participants) n=3,814
Age, years	55.3 (12.9)	60.2 (12.4)	63.5 (11.5)	56.9 (12.3)	62.5 (12.1)
Female	3,355 (63%)	2,720 (65%)	1,425 (69%)	1,295 (61%)	2,438 (64%)
High school graduate	4,197 (80%)	3,420 (82%)	1,616 (78%)	1,804 (85%)	3,169 (83%)
Body mass index, kg/m2	31.8 (7.2)	32.0 (7.1)	32.0 (7.4)	32.0 (6.8)	32.1 (7.2)
Diabetes	1,141 (22%)	1,027 (31%)	492 (41%)	535 (26%)	1,161 (31%)
ACR, mg/g	6.1 (3.9–12.6)	6.7 (4.2–14.3)	7.3 (4.5–15.9)	6.3 (4.1–13.6)	7.1 (4.5–15.4)
Antihypertensive medication	2,571 (50%)	2,635 (63%)	1,406 (68%)	1,229 (58%)	2,555 (68%)
RZS: SBP (mmHg)	127.0 (18.4)	127.5 (19.3)	129.8 (19.1)	125.5 (19.2)	--
RZS: DBP (mmHg)	78.8 (10.6)	76.9 (10.9)	77.5 (11.2)	76.4 (10.6)	--
OD: SBP (mmHg)	--	127.0 (20.2)	135.5 (22.5)	126.5 (19.9)	127.9 (18.9)
OD: DBP (mmHg)	--	73.9 (11.0)	73.2 (11.7)	74.0 (11.0)	75.0 (10.9)

Numbers in table are mean (standard deviation) or n (percent); ACR is shown as median (25^th percentile-75^th percentile).

-- Blood pressure was not measured by the oscillometric device at exam 1 and by the random-zero sphygmomanometer at exam 3.

Characteristics are restricted to participants with blood pressure measurements at the study exam.

ACR=albumin-to-creatinine ratio, BPCS=Blood Pressure Comparability Study, DBP=diastolic blood pressure, RZS=random-zero sphygmomanometer, OD=oscillometric device, SBP=systolic blood pressure

Figure 2.

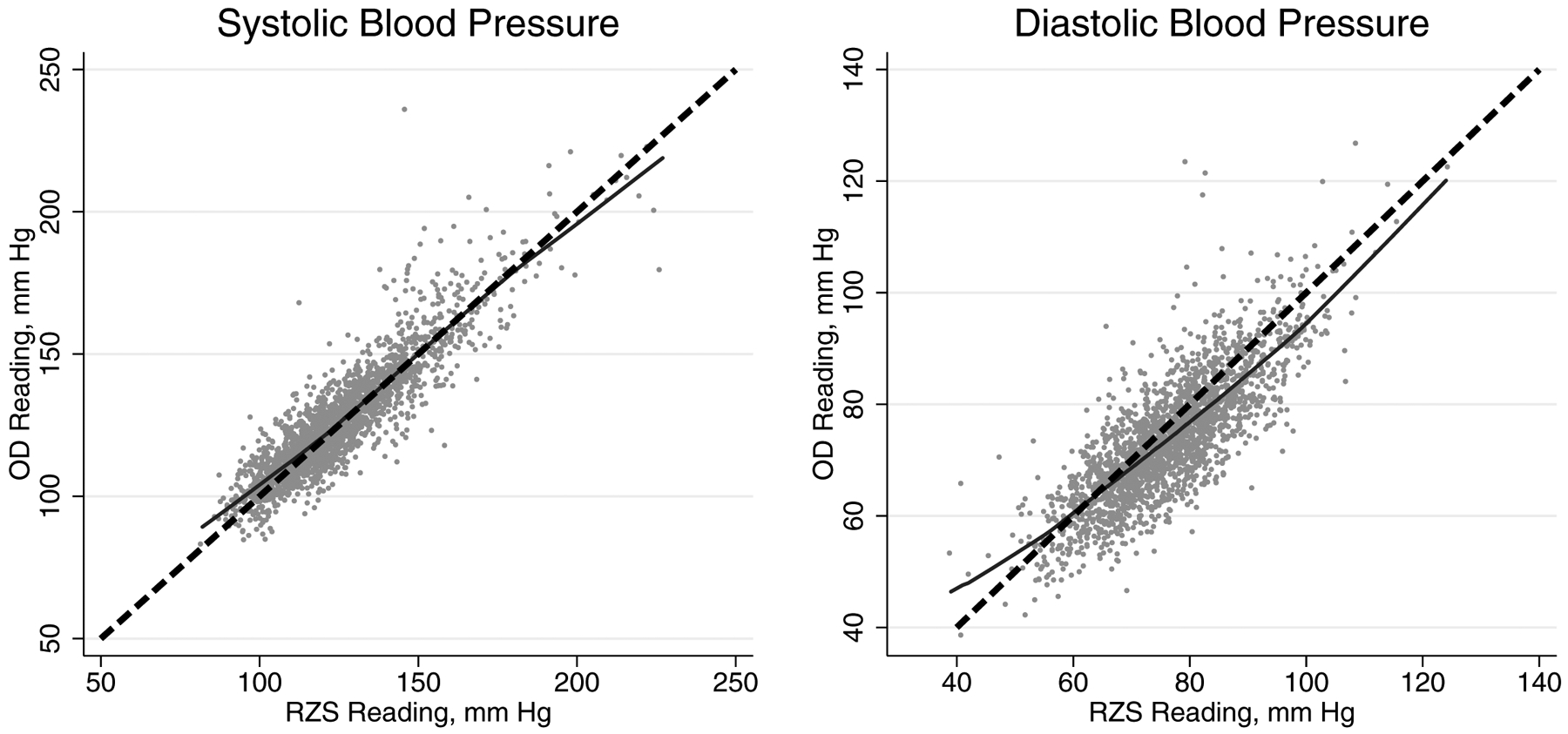
Scatterplot of random-zero phygmomanometer and oscillometric device (Omron HEM-907XL; Omron Healthcare Inc., Lake Forest, IL), systolic blood pressure (left panel) and diastolic blood pressure (right panel).

RZS=random-zero sphygmomanometer; OD=oscillometric device; mm Hg=millimeter of mercury.

The dashed line represents the line of unity (i.e., a y-intercept of 0 and a slope of 1) while the solid line represents the LOWESS line.

The five calibration equations evaluated in the BPCS are presented in Table 2. If the RZS and the OD recorded an identical BP measure for every participant, then we would expect the y-intercept to be 0 and the slope of the line to be 1. However, the intercepts of the calibration equations ranged from −4.31 to 11.02 for SBP and −6.07 to 10.40 for DBP while the slopes ranged from 0.92 to 1.04 for SBP and 0.83 to 1.05 for DBP.

Table 2:

Calibration equations for predicting systolic and diastolic blood pressure with an oscillometric device using random-zero sphygmomanometer blood pressure measurements as the independent variable.

Approach	Calibration Equations
	Systolic Blood Pressure	Diastolic Blood Pressure
Ignoring the Change	OD = RZS	OD = RZS
Ordinary Least Squares	OD = 9.81 + 0.93*RZS	OD = 10.40 + 0.83*RZS
Average Difference	OD = 1.09 +RZS	OD = −2.44 + RZS
Deming Regression	OD = −4.31 + 1.04*RZS	OD = −6.07 + 1.05*RZS
Robust Regression	OD = 11.02 + 0.92*RZS	OD = 10.36 + 0.83*RZS

RZS=random-zero sphygmomanometer, OD=oscillometric device.

Ignoring the change in BP measurement devices resulted in the highest prevalence of high BP and hypertension (Table 3). Using OLS and robust regression calibrated BP resulted in the lowest prevalence of high BP and hypertension. For the prevalence of high BP, the largest difference between calibration approaches was present at exam 1, 60.3% of participants had high BP when ignoring the change compared with 50.3% when using OLS or robust regression. The difference between calibration approaches was 3.1 percentage points or less for the prevalence of high BP at exam 2 and was 6.0 and 1.4 percentage points or less for the prevalence of hypertension at exams 1 and 2, respectively.

Table 3:

Prevalence of hypertension and high blood pressure calculated using each calibration approach.

Calibration Approach	High Blood Pressure		Hypertension
	Exam 1 (n=5,285)	Exam 2 (n=4,194)	Exam 1 (n=5,285)	Exam 2 (n=4,194)
Ignoring the Change	3,184 (60.3%)	2,213 (52.8%)	4,023 (76.1%)	3,362 (80.2%)
Ordinary Least Squares	2,660 (50.3%)	2,085 (49.7%)	3,706 (70.1%)	3,306 (78.8%)
Average Difference	2,848 (53.9%)	2,148 (51.2%)	3,807 (72.0%)	3,330 (79.4%)
Deming Regression	2,848 (53.9%)	2,148 (51.2%)	3,807 (72.0%)	3,330 (79.4%)
Robust Regression	2,660 (50.3%)	2,085 (49.7%)	3,706 (70.1%)	3,306 (78.8%)

High blood pressure was defined as systolic blood pressure ≥ 130 mm Hg and/or diastolic blood pressure ≥ 80 mm Hg.

Hypertension was defined as systolic blood pressure ≥ 130 mm Hg and/or diastolic blood pressure ≥ 80 mm Hg and/or antihypertensive medication use.

The calibration equations are provided in Table 2.

Supplemental Table 2, Supplemental Digital Content 2, http://links.lww.com/BPMJ/A94, shows the association of SBP, DBP, high BP and hypertension with the continuous outcome of log₂(ACR) in cross-sectional and repeated measurements analyses (Panels 1 and 2, respectively) and with ACR > 30 mg/g as a binary outcome in cross-sectional and repeated measurements analyses (Panels 3 and 4, respectively). For each calibration approach, the slope was within 0.04 for SBP and DBP, and within 0.18 for high BP and hypertension. Supplemental Table 3, Supplemental Digital Content 3, http://links.lww.com/BPMJ/A95, shows the association of log₂(ACR) as a continuous independent variable in cross-sectional (Panel 1) and repeated measurements (Panel 2) regression models with the separate outcomes of SBP, DBP, high BP, and hypertension. For all models, the coefficient estimates and standard errors were similar across calibration methods.

Decision by the JHS Coordinating Center

As described above, using each calibration approach resulted in similar inferences on the association of SBP, DBP, high BP and hypertension with ACR. However, because there were some noted extreme differences between the RZS and OD measures, the JHS Coordinating Center calibrated the RZS measurements using robust regression. The algebraically-simplified equations used for calibration are:

$${\text{SBP}}_{\text{OD}}=11.02+0.92\ast {\text{SBP}}_{\text{RZS}}$$

$${\text{DBP}}_{\text{OD}}=10.36+0.83\ast {\text{DBP}}_{\text{RZS}}$$

Comparison with HNRS and CARDIA calibration equations

Among participants in the BPCS, the prevalence of high BP was 45.3% using the OD-measured BP compared with 43.3%, 60.6% and 55.5% using RZS BP measurements calibrated using the robust regression, HNRS and CARDIA equations, respectively (Table 4). The overall agreement with the OD-measured BP was higher for the robust regression calibration equation when compared to BP calibrated using equations from the HNRS or CARDIA studies. Also, compared to BP calibrated using equations from the HNRS or CARDIA studies, the R² statistic for the association with OD-measured SBP and DBP were each higher for the robust regression calibration approach.

Table 4:

Comparison of uncalibrated oscillometric device measures, robust regression calibrated measures, Heinz Nixdorf Recall Study calibrated measures, and the Coronary Artery Risk Development in Young Adults Study calibrated measures among JHS participants in the blood pressure comparability study (n=2,117).

	High BP		Mean SBP	R2 SBP	Difference in R2 (95% CI)	Mean DBP	R2 DBP	Difference in R2 (95% CI)
	Prevalence	Agreement
JHS Uncalibrated OD	45.3%	-	126.5	-		74.0	-
JHS Robust Regression	43.3%	85.2%	126.1	0.802	- ref -	73.7	0.642	- ref -
HNRS	60.6%	77.9%	128.5	0.780	−0.022 (−0.030, −0.015)	79.1	0.407	−0.235 (−0.269, −0.204)
CARDIA	55.5%	80.6%	126.8	0.791	−0.011 (−0.019, −0.005)	77.4	0.506	−0.136 (−0.166, −0.111)

BP=blood pressure; SBP=systolic blood pressure; DBP=diastolic blood pressure; JHS=Jackson Heart Study; HNRS=Heinz Nixdorf Recall Study; CARDIA=Coronary Artery Risk Development in Young Adults.

High blood pressure is defined as systolic blood pressure ≥ 130 mm Hg or diastolic blood pressure ≥ 80 mm Hg.

Discussion

In the current study, we generated calibration equations to convert BP measured by a RZS to an OD for use in the JHS. The average difference between the RZS and OD was 1.09 mm Hg for SBP and −2.44 for DBP. While many participants had a small difference between RZS and OD BP measures, there were large differences in BP for some JHS participants. While these differences may reflect measurement error due to the study staff, it is also possible that they reflect methodologic differences in the RZS and OD. The associations of SBP, DBP, high BP, and hypertension with ACR was similar using each calibration approach. Robust regression was selected as the calibration approach for implementation into the JHS data because it minimized the weight given to extreme observations.

BP has been calibrated in prior longitudinal studies that changed from a RZS to an OD. In the HNRS, participants were randomized to have their BP measured by RZS or an OD followed by measurements taken with the other device approximately 40 minutes later [17]. While randomization of the ordering of devices used to measure BP is a strength of the HNRS, BP varies substantially for individuals even over a 40-minute period. Not measuring BP simultaneously using the RZS and OD may have led to increased random error when assessing the differences in BP.

The JHS followed a BP calibration protocol that was identical to the one used in the CARDIA, another National Heart Lung and Blood Institute-funded longitudinal cohort that transitioned from an RZS to an OD [18]. Despite using identical protocols to calibrate BP, the CARDIA and JHS calibration equations had different slopes and intercepts. We hypothesize that all comparability studies will result in different calibration equations as the BP distribution will not be identical for the populations under study.

The robust regression model developed in the JHS provided a more accurate estimate of BP measured by an OD when compared to applying calibration equations from the HNRS and CARDIA study. This highlights the benefit of conducting a BP measurement calibration study rather than applying externally developed calibration equations to a study cohort that is transitioning between an RZS and OD. This finding suggests that future studies should conduct their own comparability studies when transitioning between BP measurement devices.

The JHS calibrated BP levels from the RZS to the OD while CARDIA calibrated BP levels from the OD to RZS. Although the JHS calibration equations can be re-arranged to convert the OD-measured BP to RZS values, the JHS chose to calibrate BP levels from the RZS to the OD so that BP levels measured at future study exams would not require calibration. Additionally, calibrating BP to an OD may have greater applicability as these devices are increasingly being used in clinical practice.

The JHS coordinating center recommends calibrating BP to account for the transition from a RZS to an OD. Differences in the associations of SBP and DBP with ACR were small when using each calibration equation and ignoring the change in BP measurement devices. This suggests that results may not be substantially different if calibration is not performed. One reason for the consistency of results when calibration was and was not performed may be the use of a standardized protocol by trained technicians and calibrated equipment to measure BP. Prior studies have reported that BP can vary substantially due to lack of training of measurement staff or equipment that has not been calibrated [22]. A substantial proportion of participants were taking antihypertensive medication which may explain why the prevalence of hypertension was similar using each calibration approach and ignoring the change in BP measurement devices.

A major strength of the current study is the large sample size of JHS participants who completed the BPCS. JHS staff received extensive training in the measurement of BP and were re-trained every six months. Also, BP measurements were taken simultaneously rather than sequentially via a Y-type connector on the BP cuff. Further, we developed and evaluated several calibration equations using a series of cross-sectional and repeated measurements models. Despite these strengths, this study should be interpreted in the context of its potential limitations. It is unclear if the large differences in BP for some JHS participants is due to errors in the BP measurement technique or other factors. The JHS BPCS protocol used the OD to inflate and deflate the cuff and the rate of deflation may be too fast for the staff to accurately identify participants’ SBP and DBP using the RZS [11].

In conclusion, we developed equations using robust regression to calibrate SBP and DBP levels in the JHS. This calibration approach gave different results than previously published calibration equations from other studies. Therefore, we recommend that BP comparability studies be conducted by investigators when changing measurement devices rather than applying a previously published calibration equation.