Osteophyte Volume Calculation Using Dissimilarity-Excluding Procrustes Registration of Archived Bone Models from Healthy Volunteers

Abstract

Osteophytes are associated with later-stage osteoarthritis and are most commonly described using semi-quantitative radiographic grading systems. A detailed understanding of osteophyte formation is, in part, limited by the ability to quantify bone pathology. Osteophytes can be quantified relative to pre-osteoarthritic bone, or to the contralateral bone if it is healthy; however, in many cases, neither are available as references. We present a method for computing three-dimensional osteophyte models using a library of healthy control bones. An existing dataset containing the computed tomography scans of 90 patients with first carpometacarpal osteoarthritis (OA) and 46 healthy subjects was utilized. A healthy bone that best-fit each OA subject’s bone was determined using a dissimilarity-excluding Procrustes registration technique (DEP) that minimized the influence of dissimilar features (i.e., osteophytes). The osteophyte model was then computed through Boolean subtraction of the reference bone model from the OA bone model. DEP reference bones conformed significantly better to the OA bones (p < 0.0001) than by finite difference iterative closest point registration (root mean squared distances 0.33mm ± 0.05mm and 0.41mm ± 0.16mm, respectively). The effect of library size on dissimilarity measure was investigated by leave-k-out cross-validation randomly reducing k from 46 to 1. A library of n >= 31 resulted in less than 10% difference from the theoretical minimum value. The proposed method enables quantification of osteophytes when the disease-free bone or the healthy contralateral bone are not available for any three-dimensional dataset. Quantifying osteophyte formation and growth may aid in understating the associated mechanisms in osteoarthritis.

INTRODUCTION

Osteophytes are a defining pathological feature of osteoarthritis (OA).^1–3 Characterized as progressive and pathological bony projections capped in fibrocartilage,⁴ osteophytes form along joint margins and at the insertion of tendons and ligaments.^5–7 Osteophyte formation is one of the main radiographic features of OA, with increasing size and distribution reflecting the severity of disease progression.^8–11 Traditionally, osteophyte incidence, size, and location has been described qualitatively or semi-quantitatively from plain film radiographs.^9–12 Clinically, plain radiography is routinely available, however, accurately measuring osteophyte size and distribution on radiographs is challenging because they capture only two-dimensional projections and are susceptible to occlusion by overlapping bony structures. Three-dimensional datasets from magnetic resonance imaging (MRI)^13,14 and computed tomography (CT)^15,16 provide substantially more information, even when limited to semi-quantitative scoring systems.

The use of volumetric data modalities allows for the generation of three-dimensional surface models and the quantification of three-dimensional bone changes in small animal models, ^17–19 and in human patients.²⁰ In CT images, osteophytes appear contiguous with cortical bone, which makes differentiating the original or normal healthy bone from the osteophyte formations a challenge. If the bony pathology can be isolated from the bone models segmented from a CT image, a three-dimensional (3D) osteophyte model would provide a construct from which volume, surface area, proliferation patterns and exact region of occurrence can be calculated.

The conceptual basis for 3D image-based osteophyte analysis is Boolean subtraction of the healthy bone or reference bone model from the bone model that includes the pathology and osteophytes. The ideal reference bone model would be the identical healthy bone model, generated from images before the onset of pathology. In clinical studies, such images are rarely available. One potential solution is the use of the asymptomatic contralateral bone as the reference model.^19,20 To compute bony changes through Boolean subtraction, the contralateral bone is first mirrored then registered to the diseased bone using algorithms such as least squares distance iterative closest point (ICP) algorithms.²¹ One limitation of standard ICP approaches is that the entire surface is used in the registration process, thus local features associated with changes in bone shape caused by osteophytes can skew the registration of the unaffected portions of the bone models generating errors in the Boolean subtraction. An additional potential challenge with this approach is that the contralateral bone may also have bony pathology. Performing Boolean subtraction would then lead to errors in quantifying osteophyte tissue.

In this paper, we describe a method for computing osteophytes using a library of healthy controls when a disease-free bone or a healthy contralateral bone is not available for reference. We also address the limitations of standard ICP methods for registration using techniques from geometric morphometrics analysis that are designed to focus on global shape similarities while minimizing influences from localized variability.^22,23 We demonstrate our method for generating osteophyte models using the CT scans of patients with early thumb carpometacarpal (CMC) osteoarthritis. The novelty of our approach lies in its use of a library of bone models from disease-free volunteers to generate patient-specific reference bone models, and the implementation of least squares Procrustes superimposition with localized outliers (dysmorphologies) excluded,²⁴ to register bone models.

METHODS

Imaging and Bone Model Generation

The method was developed for the analysis of hand and wrist CT images of 90 (47 women, 43 men, mean age 56.7 ± 7.4 yrs.) patients diagnosed with early thumb OA (radiographic Eaton Stage 0 or 1) and 46 (25 women and 21 men, mean age 41.2 ± 17.8 yrs.) healthy volunteers (controls) who were enrolled in an IRB approved longitudinal study on the role of biomechanics in thumb CMC OA.^25–30 As part of that study, the affected hands of the patients and the dominant hands of the asymptomatic volunteers were scanned with a GE LightSpeed 16 clinical CT scanner (GE Medical Systems-America, Milwaukee, WI). However, the contralateral hands were not scanned. The images were reconstructed with a 20 cm field of view, yielding transversely isotropic 3D volume images with an in-plane resolution of 0.39 mm X 0.39 mm and a slice thickness of 0.625 mm. All images of left hands were mathematically converted to appear as right hands during segmentation.

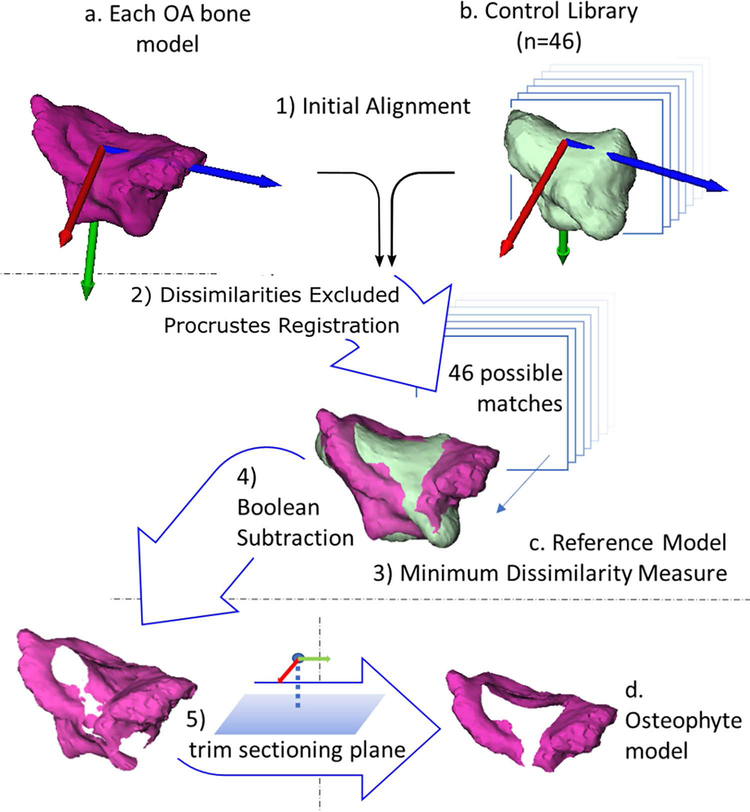
Digital bone models of the trapeziae (TPM) and first metacarpals (MC1) were generated from the CT images using commercially-available medical image processing software (Mimics v12–20, Materialise, Leuven, Belgium). Briefly, the segmentation pipeline included density-based thresholding, mask splitting to separate individual bones, and slice-by-slice manual editing to fill cavities and refine the bone boundaries to match the underlying grayscale images. Care was taken to include all exophytic mineralized tissue contiguous with the underlying bone volume (Figure 1). Once the masks were refined, 3D models of the outer cortical bone surfaces were exported as closed triangular meshes without triangle reduction and with minimal smoothing (single iteration, smoothing factor 0.030).^31–33 Articular surface-based coordinate systems (ACS) were generated for each bone model³⁴ to use as the initial seed in bone registration (Figure 2, a–b). The ACS were defined with their origins at the inflection points of the saddle-shaped articular facets of the trapeziae and first metacarpals, with positive X, Y, and Z in the volar, proximal, and radial directions, respectively (Figure 2a).

Fig. 1.

Typical segmentation of osteoarthritic bone models from computed tomography (CT) images. Axial CT images of the first metacarpal (MC1) (masked as red) and trapezium (TPM) (masked as purple). (a). Reconstructed three-dimensional (3D) bone models of the MC1 and TPM, cropped to display internal attenuation values at the corresponding CT slice (b). 3D reconstructions of the exported MC1 and TPM bone surface models (c).

Fig. 2.

Flow chart of the five main steps in generating osteophyte bone models for the trapezium. Steps for the first metacarpal were identical. 1) The articular coordinate systems of the bone models were computed (a and b) and used as an initial registration seed for all 46 control models (b) to each bone model with osteoarthritis (OA). 2) Procrustes superimposition was used to attain the final registrations. 3) The control bone with the minimum dissimilarity measure was identified as that OA model’s reference bone (c). 4) Osteophyte models were calculated by Boolean subtraction of the reference bone model from the OA model. 5) The osteophytes were then trimmed by a sectioning plane to generate the osteophyte bone model relevant to the first carpometacarpal joint (d).

Reference Bone Model Generation

Briefly, registration of all 46 control library bone models to each of the 90 trapezia and first metacarpals was performed using iterative dissimilarity-excluding Procrustes (DEP). Then, the transformed library bone model with the minimum dissimilarity measure was selected as the patient-specific reference bone model.

In more detail, the OA and control bone models were coarsely aligned by registration of their ACS (Figure 2, Step 1) and the native Matlab® Procrustes function was used to solve for the best-fit transform (procrustes.m, Mathworks, Natick, MA). The function yielded a rotation, translation, and scaling transformation, as well as a metric of fit called the dissimilarity measure. The Procrustes function requires two point clouds with one-to-one correspondence computed by the function rigidICP.m (available on Mathworks exchange).²⁴ Dense point correspondences were identified by calculating bi-directional nearest neighbors and distances (from the OA bone model to the control and from control to OA). Points were excluded if their nearest neighbor distance fell outside the 95% confidence interval of the mean, which eliminated their ability to adversely influence the overall bone model registration. The transformation output was applied to the control bone model, and the newly transformed point cloud was used as input to the next iteration of dissimilarity exclusion, point correspondence calculation, and registration. Convergence was achieved when the difference in iterative dissimilarity measures fell below 0.0001%.²⁴

The dissimilarity measure (ε), computed by Matlab’s Procrustes function is the sum of squared distances between nearest neighbor nodes of the reference bone model and the OA bone model (d), standardized by the scale of the OA point cloud, X.³⁵

$$\epsilon =d/\sum (\sum {(X-\overline{X})}^2)$$ (1)

, where $\overline{X}$ was the OA point cloud centroid. It therefore controlled for both bone size and point density. The dissimilarity measure calculations excluded focal differences in the point clouds, specifically regions of OA pathology, and therefore are interpreted as a measure of goodness-of-fit between the reference and the non-pathological features of the OA bone.

Osteophyte Model Generation

Osteophyte models for each OA bone were generated by Boolean subtraction of the reference bone model from the OA bone model (Geomagic Wrap® 2017, 3D Systems, SC, USA); (Figure 2, Step 4). For the trapezium, the osteophyte model was limited to the distal periarticular region using an automated trimming workflow, which truncated the trapezium using a sectioning plane parallel to the radial-ulnar and volar-dorsal axis of the ACS that passed through the trapezial centroid (Figure 2, Step 5). Similarly, the first metacarpal osteophyte model was trimmed with a sectioning plane parallel to the radial-ulnar and volar-dorsal axis of the first metacarpal ACS; offset from the first metacarpal ACS origin the same magnitude as the trapezium ACS origin to trapezium centroid. Since both bones have more than one articular surface, and thus the potential for multiple regions of osteophyte formation, the trimming was performed to focus the analysis on only the trapezial-first metacarpal joint. Sensitivity analysis of ACS generation has been previously reported as repeatable and robust.³⁴

Quantifying the Effect of Library Size

To evaluate the effect of the number of bone models in the control library (library size, n), we used a leave-k-out cross-validation approach, where k was iterated from 1 to n-1 and efficacy was assessed using the dissimilarity measure. For both the TPM and MC1 data, we first computed the minimum dissimilarity measure for each of the 90 OA bone models as described above. Next, a bone model was randomly excluded from the control library, the process for determining the refence bone was repeated, and the resultant dissimilarity measures were recalculated. This entire process was then repeated, incrementally excluding k+1 control models from the library at each iteration. Inspecting the plotted dissimilarity measures calculated as the library size was increased from 1 to n suggested an exponential decay trend which stabilized asymptotically as the library size approached n. Hence, the influence of library size (y) on the dissimilarity measure, y, was modeled using

$$y=\frac{a}{(n-b)+c}$$ (2)

with the coefficients,a, b and c determined using non-linear least squares fit (fit.m MATLAB®). The asymptote was calculated as the limit of the exponential decay function as n approached infinity, which represented the minimum possible dissimilarity measure. The modeled dissimilarity measures were compared as a percent difference from the asymptote for each increment of control library size.

Secondary Metric of Fit Quality

To further quantify the goodness-of-fit of the reference bone models to the OA bone models, a secondary metric was calculated that could also be calculated across registration methods for means of comparison. Root-mean-squared (RMS) distances were calculated on the result of DEP registration for each point on the reference bone model to its nearest neighbor on the OA bone model surface (dist2surf.m, iso2mesh package http://iso2mesh.sourceforge.net/). The RMS distance is a measure across the whole surface of the reference model to nearest neighbor on the OA model. As with the dissimilarity measure, portions of the OA model will not be included in the RMS (some OA model vertices will not be matched as nearest neighbors to the healthy reference). Computing the RMS for the DEP references allows the direct comparison to other registrations methods, including those which use RMS as a metric of optimization or success.

DEP Comparison to ICP

To compare DEP vs standard approaches, an alternate set of reference models was generated using the best match computed by finite difference, isometric scaling ICP registration.³⁶ The ICP reference model was selected as the control bone with the smallest nearest neighbor RMS distance to the OA bone. A two-tailed Wilcoxon matched-pairs signed rank test was performed with a significance threshold of p < 0.05 to determine if the RMS measures differed between the DEP and ICP registration methods.

Validation

To quantify the accuracy and the limitations of the method, a series of artificial osteophytes were generated by extruding the surfaces of healthy control trapezia at different locations around the CMC articular facet and by different heights, as has previously been done in animal models.³⁷ Twenty-four models were generated from four healthy bone models, with osteophyte shapes, locations and volumes representative of the range calculated from OA patients’ data.³⁸ Each simulated osteophyte model was then treated as if it was from an OA patient, and its reference model was generated with DEP. Following Boolean subtraction and trimming, the volumes of the closed surface artificial osteophyte models were computed using the divergence theorem.³⁹ Ground truth osteophyte volume was calculated as the healthy control bone volume subtracted from the whole bone volume of the newly-created artificial osteophyte model. Linear regression was used to evaluate the agreement between the ground truth and computed osteophyte volumes. In addition, a Bland-Altman analysis was used to determine if a bias existed between DEP and ground truth osteophyte volumes.

RESULTS

Representative TPM and MC1 osteophyte models superimposed on their reference models demonstrated a spectrum of osteophyte volumes and osteophyte locations on the trapezia and MC1 across the cohort of 90 OA subjects (Figure 3).

Fig. 3.

A selection of osteophyte model results. First metacarpal (top row) and trapezia (bottom row). Original bone models with osteoarthritis displayed in grey. Osteophyte models generated using dissimilarity-excluding Procrustes registration colored to reflect the distance (mm) from their surface to that of the reference bone model.

Control library size influence on dissimilarity measure

The theoretical minimal dissimilarity measure (n = ∞) for the TPM and MC1 were 2.4 × 10⁻³ and 6.6 × 10⁻⁴, respectively. The mean dissimilarity measure function for the TPM at full control library size (n = 46) was only (2.6 × 10⁻³), 6.9% greater than the theoretical minimum (Figure 4). The dissimilarity metric increased gradually with decreasing control library size, remaining within 10% until n ≤31. For the MC1, the mean dissimilarity measure at n = 46 was 6.99×10⁻⁴ (6.6% greater than the asymptote) and remained within 10% of the theoretical values until n fell below 30.

Fig. 4.

Effect of control library size on the dissimilarity measures of the reference bone models for the trapezium. Minimum dissimilarity measures for each bone model with osteoarthritis (OA) are plotted as a function of control library size (n = 1 to 46) and fit with an exponential decay function (Eq. 1). The asymptote to exponential decay function estimates the theoretical mean dissimilarity measure at n = ∞.

DEP Comparison to ICP

The RMS values calculated with the reference bone models generated by DEP were significantly less than the paired references generated by ICP (P < 0.0001) (Figure 5). The mean RMS values using DEP models were 0.34 ± 0.06 mm, while ICP had RMS mean of 0.41 ± 0.16 mm. The maximum RMS value of the 90 models was 0.48 mm using DEP and 1.3 mm using ICP; with 15% (n=14) ICP values greater than the DEP maximum RMS value. Distances calculated from reference bones to OA matches were visualized as heat maps across the bone surface, along with transparent grey surfaces of the OA bone. Particularly in OA bone models with visually advanced osteophytes, the surface of the DEP reference bones most closely aligned to the healthy regions of the OA bones (Figure 6a) than the reference model generated with ICP (Figure 6b). In our dataset, models with visually advanced osteophytes shared a pattern of formation at the radial and ulnar articular borders.³⁸

Fig. 5.

Correlation of root mean squared (RMS) values with 1:1 correspondence (dotted line). While dissimilarity-excluding Procrustes (DEP) generated reference bone RMS distances remain below 0.5mm, the bone models generated using iterative closest point (ICP) for the same matches increase to 1.3mm RMS distance. The bones with osteoarthritis that are associated with high ICP RMS values are those with visibly advanced osteophyte formation (i.e., far right in Figure 3).

Fig. 6.

An example of a representative osteoarthritic trapezium from our OA dataset. Osteophytes are depicted in transparent gray, and the heat maps depict differences between the OA and reference bone generated by dissimilarity-excluding Procrustes (DEP) (a) and by iterative closest point (ICP) (b) registrations. Visible in orange and red, the ICP reference bone has more regions of bone model surface separated by more than 0.5mm from the OA trapezium.

Validation

Simulated osteophytes ranged in volume from 0.27 mm³ to 176 mm³ (70 ± 60 mm³). Linear fit of the computed and true osteophyte volumes resulted in strong correlation (R² = 0.99), with a slope of approximately 1 (0.987) and a near zero intercept (0.31 mm³), indicating excellent agreement to the ground truth measurements (Figure 7). The Bland-Altman analysis revealed that DEP slightly undercalculated osteophyte volume with a bias of 0.59 mm³ with respect to ground truth osteophyte volume.

Fig. 7.

Results of accuracy analysis on simulated osteophyte models. Linear correlation shows high agreement of DEP calculated osteophyte volume to True osteophyte volume.

DISCUSSION

In this paper we describe a method for generating three-dimensional models of osteophytes from CT scan data when a disease-free reference bone is unavailable. The method uses dissimilarity-excluding Procrustes (DEP) registration to determine a best-fit reference bone model from a library of healthy control bone models, and then Boolean subtraction to yield a 3D osteophyte model. Novel features of this method include the use of a control library to generate comparator bones, as opposed to contralateral bones or manual segmentation, and the exclusion of local dissimilarities during bone model registration. The method was specifically developed to quantify osteophytes at the thumb carpometacarpal joint, but it could be used to analyze osteophytes in other joints or explore other types of localized differences in bone morphology.

A key assumption of this strategy for generating refence bone models was that there would be sufficient variability (and compatibility) in the shapes of a cohort of control bones to provide an acceptable fit to the non-osteophytic portions of the osteoarthritic bones. This is a reasonable assumption given the findings of Schneider et al,⁴⁰ who used digital bone models of healthy controls (the majority of which were the same as used in our method) to develop a statistical shape model of the TPM and MC1. They found that 90% of the variance in trapezia and MC1 bone shape could be described using the first seven principal components in their model. Importantly, the authors found that most of the morphological variation in the trapezia and MC1 (71%) was simply due to bone size. In addition, our validation method demonstrated that computed osteophyte measures are highly correlated with the true measures. These findings provide confidence that: (a) DEP provides reasonable fitting of the reference bone models to the osteoarthritic bone models, and (b) our reference library was large enough to capture most of the inherent (nonpathological) variability in the trapezia and MC1. Our finding that the mean dissimilarity measure decreased only incrementally once the control library size reached 31 bone models suggests that our library (n=46) was adequately large. A direction of future work may be to use methods of statistical means and shape modifying algorithms, such as coherent point drift (CPD) and statistical shape modeling (SSM) which provide a possible avenue for nearly unlimited model matches, with recent success in inflammatory arthritis.³⁸

We have confidence that our method represents accurate osteophyte models of OA bones, yet our approach only utilized the outer cortical bone surfaces. In some applications, registrations that utilize trabecular structure, if it is of high enough resolution, could potentially provide further insight into pathological changes. Lastly, the cellular structure included within the model is unknown, and to the author’s knowledge, no ground truth method of differentiating healthy tissue from osteophyte tissue exists to further validate the regions selected as osteophytes in our models.⁴¹A broad range of research areas have identified the merits of applying quantitative morphometric methods to analyze morphological variation, i.e., craniofacial disorder assessment,⁴² evolutionary biology,⁴³ and facial recognition.⁴⁴ The review by Cooper et al.²³ comprehensively lists the utility of nearly thirty quantitative techniques and stresses the benefits of adopting such techniques to research in the field of experimental embryology, including the technique used in this paper, iterative dissimilarity-excluding Procrustes superimposition (a geometric morphometric technique). While the analysis or quantification of morphological variation was not our goal, accounting for shape configurations to transform data without distortion and accounting for outliers is extremely useful in quantifying bone pathology.

An important feature of our method is the exclusion of localized dissimilarities. In shape analysis, robust techniques have been developed to overcome the fitting of two datasets that are largely similar; but where one has substantial, but localized feature differences. The possible contamination of the localized feature on registration and shape difference quantification is known as the ‘Pinocchio effect’.²² Much like Pinocchio’s nose, our bony osteophytes protrude in concentrated areas. Attempting to register a similarly shaped bone without these abnormalities to one with would largely skew alignment using conventional fitting algorithms that incorporate the entire surfaces. The use of geometric morphometric registrations that exclude dissimilar features has been shown to limit or even negate the influence of these outliers^{23,24,45–48} that are critical to studies aiming to delineate such structures as osteophytes.

Reference models computed using DEP had significantly better fits to the OA bones when comparing RMS nearest neighbor distances. RMS distance was chosen as a comparator metric because it was the ICP optimization criteria and ICP is a widely used registration algorithm. RMS as the measure for comparison of the registration techniques is a limitation of this work and expanded criteria of evaluation may be necessary. Other measures of complex 3D shape alignment, such as Hausdorff distance warrant exploration.

In this study, we used a shape-matched reference model from a library of healthy controls to generate an osteophyte model from the OA bone model. A three-dimensional osteophyte model computed from in-vivo patient CT images provides a construct from which size, shape, and location metrics could be estimated. Although this study utilized CT images of patients with thumb CMCOA, given suitable resolution, volumetric data from other imaging modalities (e.g., MRI) for other pathological bone disease could utilize this same method using a large database of other healthy bone models (e.g., carpal bones database^49,50).