Abstract
Interactions between the prefrontal cortex (PFC) and mediodorsal thalamus (MD) are critical for cognitive flexibility, yet the underlying computations are unknown. To investigate fronto-thalamic substrates of cognitive flexibility, we developed a behavioral task, where mice switched between different sets of learned cues that guided attention towards either visual or auditory targets. We found that PFC responses reflected both the individual cues and their meaning as task rules, indicating a hierarchical cue-to-rule transformation. Conversely, MD responses reflected the statistical regularity of cue presentation, and were required for switching between such experimentally-specified cueing contexts. A subset of these thalamic responses sustained context-relevant PFC representations, while another suppressed the context-irrelevant ones. Through modeling and experimental validation, we find that thalamic-mediated suppression may not only reduce PFC representational interference but could also preserve unused cortical traces for future use. Overall, our study provides a computational foundation for thalamic engagement in cognitive flexibility.
Introduction
Cognitive flexibility, the ability to mentally switch between different thoughts and action plans, is critical for survival in a rapidly changing environment1–3. This important process allows us to flexibly switch attention among competing inputs4–7. A lack of cognitive flexibility is a hallmark of many mental illnesses such as schizophrenia8,9. Furthermore, a key limiting factor to artificial general intelligence (AI) is the inability of deep learning algorithms to perform multiple tasks without interference10,11. Therefore, elucidating the circuit and computational principles underlying cognitive flexibility will have a broad multidisciplinary impact.
The prefrontal cortex (PFC) plays a central role in cognitive flexibility5,12,13, including the differential allocation of attentional resources based on learned cues14–16. Multiple recent studies have also demonstrated that PFC function is highly dependent on its interactions with the mediodorsal thalamus (MD)17–22. In particular, the MD sustains task-relevant representations in the PFC by augmenting effective connectivity between cortical neurons17. However, because previous studies did not include a controllable switching component, the role of MD-PFC interactions in cognitive flexibility remain unclear.
In this study, we examined the substrates of cognitive flexibility through a series of behavioral manipulations, temporally-precise optogenetic perturbations and multi-site multi-electrode recordings. We found that PFC responses reflected both the individual cues and their meaning as task rules, indicating a hierarchical cue-to-rule transformation in this cortical area. In contrast, MD responses reflected the statistical regularity of the cue presentation, which we refer to as the cueing context. Using causal perturbations, we found that in addition to stabilizing context-relevant representations, MD neurons also suppress context-irrelevant PFC representations. These processes impart on the PFC the flexibility to dynamically switch between different contexts with minimal interference. Altogether, our work clarifies how MD neurons regulate prefrontal representational switching and provides a computational foundation for thalamic engagement in cognitive flexibility.
Results
Prefrontal neurons display mixed selectivity during attentional switching
To examine how mouse prefrontal cortex (PFC) ensembles operate when cognitive flexibility is required, we expanded an attentional control task17,23 to incorporate a cue switching component (Fig. 1a). At the core of the task is sensory selection, where freely behaving mice select between spatially-conflicting visual and auditory targets. On each trial, a mouse selects between the two targets based on one of two 100 ms-long learned cues; a high-pass (HP) or a low-pass (LP) noise burst. These cues correspond to two rules – attend to audition and attend to vision respectively. Mice were required to hold a pseudo-randomly presented cue in mind for up to one second by maintaining snout fixation in the initiation port prior to the simultaneous presentation of the two targets. The targets corresponded to the spatial location of the reward being delivered through the right or left reward port (e.g. left LED flash on an attend to vision trial signaled a response on the left reward port). Correct performance was rewarded with 10 μL of condensed milk, while incorrect performance was punished with a timeout. Logistic regression modeling of behavior across all mice used in this study revealed that they used the cue to guide their choices (Supplementary Fig. 1a–d, see Methods).
Fig. 1.
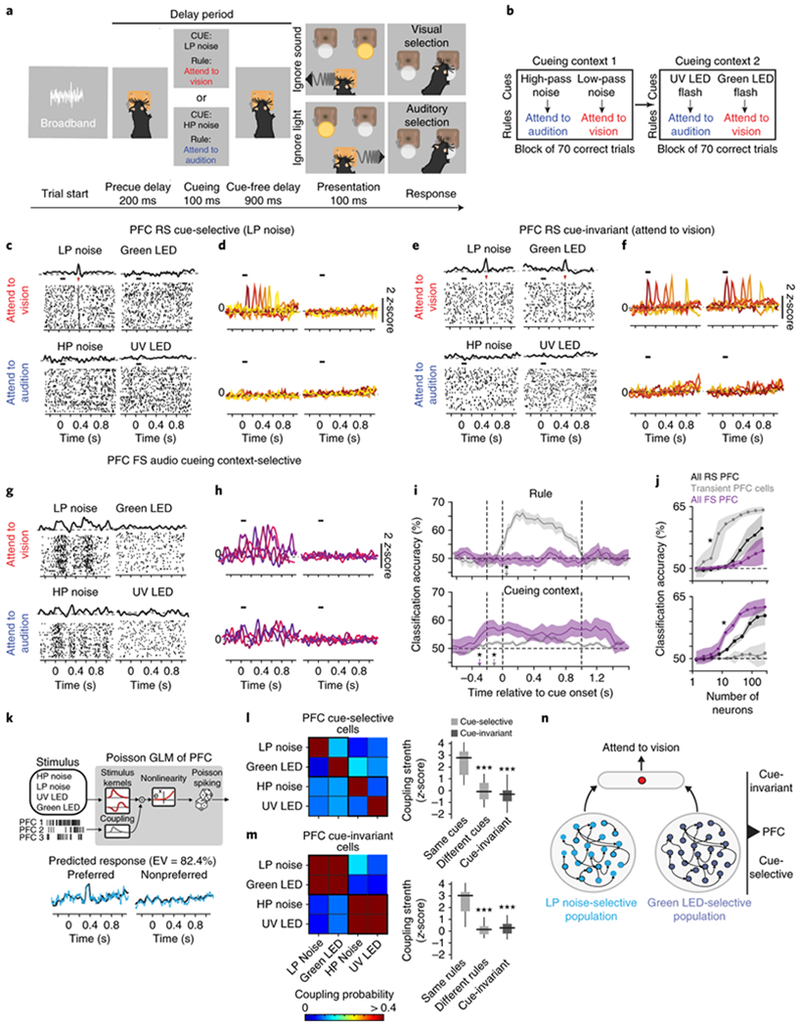
Prefrontal neurons display selectivity indicative of a hierarchical cue to rule transformation during attentional switching.
(a) Schematic of task design. (b) Mice were trained to associate four cues with two rules. These cues were presented in two blocks, each containing two cues. An animal had to achieve at least 70 correct trials in a block before moving on to the next block. For details, see Methods. (c) Example peri-stimulus time histogram (PSTH) and raster plot (number of trials vs. time) for a regular-spiking (RS) PFC neuron that is selective to a LP noise. The black bar above the raster marks the cueing period, and the red arrowhead indicates the transient increase in spiking reliability. (d) Transient responses tile the duration of the delay period. Each color is a different cue-selective neuron.(e-f) Same as (c-d) but for PFC cue-invariant cells. (g-h) Same as (c-d) but for PFC fast spiking (FS) cells. Unlike RS cells, these neurons have persistent changes in firing rate over the delay period. Representative examples in d, f and h drawn from n = 5 mice (independent samples). (i) Classification accuracy over time relative to cue onset for a decoder trained to predict either rule (top) or cue context decoding (bottom) for PFC RS and FS neuronal populations. The asterisks denote the time point at which classification accuracy is significant (i.e. p < 0.05, permutation test from n = 5 biologically-independent mice) above chance (50% classification accuracy). (j) Classification accuracy (within delay period) scales with the number of neurons. Similar to (i), the asterisk indicates the number of neurons at which classification accuracy is significantly above chance levels (p < 0.05, permutation test from n = 5 biologically-independent mice). (k) Top: Schematic of Poisson generalized linear model (GLM). Bottom: Model prediction (grey) of the PSTH (black) for one example PFC neuron. EV, explained variance. (l) Left: Heatmap showing coupling probability between the four cue-selective cell PFC cell types. Right: Box-whisker plots comparing the coupling strengths of inputs to PFC cue-selective neurons from cue-selective neurons preferring the same or different cues (light gray, p = 1.23 x 10−4) or cue-invariant neurons (dark gray, p = 0.18 x 10−4). Bonferroni-corrected Kruskal-Wallis ANOVA with post-hoc rank-sum test relative to neurons preferring the same cues (n = 5 biologically-independent mice). (m) Same as (l) but characterizing the inputs to cue-invariant PFC neurons from cue-selective neurons preferring the same or different rules (p = 1.89 x 10−6) or cue-invariant neurons (p = 1.42 x 10−6). Bonferroni-corrected Kruskal-Wallis ANOVA with post-hoc rank-sum test relative to neurons preferring the same rules (n = 5 biologically-independent mice). (n) Cartoon schematic of how cue-invariant neurons gain their selectivity by pooling from cue-selective neurons across both cueing contexts. Data is shown as mean +/− 95% confidence interval (shaded error bars). Box plots: median (line), box edges, 95% confidence interval, whiskers, range.
Once mice became proficient at using the auditory noise cues, we introduced two visual cues – an ultraviolet (UV) and green LED flash – which corresponded to the same rules (Fig. 1b). To assess how mice switched from using one cue set to another, we trained mice to perform this task in blocks (Fig. 1b). Mice had equivalent performance across both blocks regardless of their presentation order (Supplementary Fig. 1e, f), suggesting that they utilized different cue sets equivalently. Importantly, this demonstrates an ability to flexibly switch their attention when the cueing context changes.
Given the well-known role for the PFC in cognitive flexibility1,20,24,25, we asked how PFC neurons (prelimbic cortex; see Methods) engage in this task. Using unbiased trial-selection (Supplementary Fig. 1g) and spike waveform clustering analysis26–28, we classified recorded neurons into two categories: regular spiking (RS, putative excitatory) and fast spiking (FS, putative inhibitory, Supplementary Fig. 2a–d). As previously reported17, a subset of RS neurons showed a brief increase in spike-timing reliability during the delay period. We refer to these cells as transient (see Supplementary Fig. 2e–g for classification of cells). As a population, these transient cells tiled time in the delay period with distinct neurons responding at different time points (Supplementary Fig. 2h). Interestingly, these cells could be further categorized into two groups. One group responded selectively to one of the four learned cues (Fig. 1c, d, cue-selective, 233/1789, 5 mice), while another responded equivalently to two cues that had the same meaning, which may be interpreted as a single task rule (Fig. 1e, f and Supplementary Fig. 2i, cue-invariant 102/1789, 5 mice). For example, a cue-invariant PFC neuron selective to the attend-to-vision rule responds with transient elevation in spiking reliability at the same delay period time in both LP noise and Green LED trials. To our knowledge this type of cue-invariance, indicative of rule-selectivity29,30, has not been previously reported in mouse PFC.
In stark contrast to the transient RS neural responses, putative inhibitory FS neurons showed broad changes in spike rate that distinguished between the two cueing contexts but not rule meaning (Fig. 1g, h and Supplementary Fig. 2j, 418 neurons 5 mice). In fact, RS and FS populations encode distinct cognitive variables, with the rule signal being more readily decodable from RS neurons while the context signal being more readily decodable from FS neurons (Fig. 1i, j). Further analysis confirmed that RS neurons encode cues and rules through changes in spiking reliability (Supplementary Fig. 3a, b). On the other hand, FS populations encode context through broader (persistent) changes in spike rates across both the inter-trial interval and the delay period. It is important to note that, in addition to transient PFC RS cells, we observed another RS group that showed persistent spike rate changes that also correlated with context (Supplementary Fig. 3c). However, it was much harder to decode context from these cells compared to PFC FS neurons (Supplementary Fig. 3d, e).
To further test if transient PFC responses were indeed due to the sensory cue, we omitted the cue on 20% of the trials (Supplementary Fig. 4a). In addition to a decrease in behavioral performance, we observed a significant decrease in tuning strength of both PFC cue-selective and cue-invariant neurons (Supplementary Fig. 4b–d). Taken together, these results indicate that transient PFC responses are due to the learned cue, with cue-selective cells representing a physical cue and cue-invariant cells representing its meaning as a task rule.
Is it possible that the observed mixed selectivity among cue-invariant neurons reflects the differential sampling of local cue-selective neurons in a context-dependent manner? To address this question, we constructed a multi-neuronal generalized linear model (GLM, Fig. 1k) to predict the spike rate of each PFC neuron31,32. In addition to external sensory variables, our GLM model also included coupling terms to capture the dependencies between neurons (see Methods). These coupling terms were in the form of a coupling filter that allowed us to explain the effect that spiking in other simultaneously recorded neurons had on the unit being modeled. Importantly, we used a rigorous cross-validation approach to statistically evaluate the predicted coupling and to constrain the parameters of the model (see Methods). On average, the GLM was able to explain close to 75% of the response variance of both cue-selective and cue-invariant PFC neurons on each trial (Supplementary Fig. 5a–c).
By analyzing the strength of the coupling filters, we were able to make inferences about the functional connectivity between the different classes of PFC neurons. This analysis revealed that cue-selective neurons are strongly coupled among themselves only if they encode the same cue, and do not receive substantial reciprocal coupling from cue-invariant neurons (Fig. 1l). Additionally, cue-invariant neurons receive strong functional inputs from cue-selective neurons across both contexts (Fig. 1m). As such, based on this pattern of functional connectivity, we reasoned that task-relevant PFC computations are hierarchically organized, with cue-invariant neurons gaining their rule selectivity from cue-selective neurons across contexts (Fig. 1n).
Mediodorsal thalamus encodes cueing context
The mediodorsal thalamus (MD) projects extensively to the PFC has a critical role in maintaining task-relevant activity in this cortical region18,20,22,33,34. Furthermore, a recent study found that the MD might play a role in cognitive flexibility by recruiting cortical inhibitory neurons35. Given our finding that FS neurons are contextually selective (Fig. 1h, i), we next asked how MD neurons responded in our context switching task (Fig. 2a). In agreement with our previously published results17, we found that a subset of MD neurons exhibited a transient increase in spiking reliability during the delay, and distinct MD neurons tiled the delay period (Fig. 2b). Unlike PFC RS neurons, these transient MD neurons did not display cue-selective responses but had equivalent responses to both cues within the same block. Additionally, another subset of MD neuron showed the same selectivity towards the cueing context but through persistent changes in spike rate over the delay period (Figs. 2c and 2d for classification of transient and persistent MD neurons). At the population level, the cueing context was much more decodable from both persistent and transient MD neurons compared to PFC RS neurons (Fig. 2e, f). Therefore, across the PFC-MD network, MD and PFC FS neurons were the most informative of the cueing context, whereas PFC transient neurons were most informative of the rule (Fig. 2f).
Fig. 2.
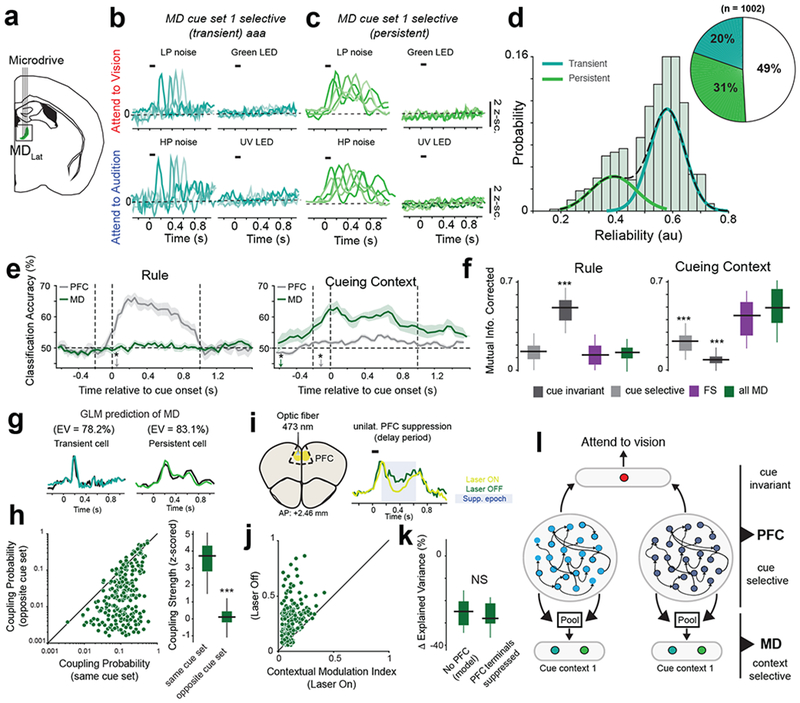
Mediodorsal thalamic responses reflect the cueing context.
(a) Schematic for MD recordings. (b-c) Example PSTHs of MD neurons with transient (b) and persistent (c) responses to both cues within the auditory cueing context. Each color indicates a distinct neuron. Representative examples drawn from n = 5 mice (independent samples). (d) Histogram of inter-trial spiking reliability scores from all task-modulated MD neurons. A gaussian mixture model (dashed lines) was used to classify cells into either persistent (low reliability) or transient (high reliability). Inset, pie chart quantifying the fraction of each MD neuron type. (e) Classification accuracy over time relative to cue onset for a decoder trained to predict either rule (top) or cue context decoding (bottom)trained to classify rule (left) and cue context (right) from PFC RS and MD populations (5 mice). The asterisks denote the time point at which classification accuracy is significant (i.e. p < 0.05, permutation test from n = 5 biologically-independent mice) above chance (50% classification accuracy). (f) Comparison of rule decoding and cueing context decoding accuracy, measured as mutual information (see Methods), between all recorded cell types. ***p < 0.001 Bonferroni-corrected Kruskal-Wallis ANOVA with post-hoc rank-sum test relative to MD neurons (n = 5 biologically-independent mice). (g) Generalized linear model (GLM) of MD neurons can accurately predict the responses of both transient (right) and persistent cells (left). EV, explained variance. Data: black, prediction: colored lines. (h) Left: Comparison of coupling probability between PFC cue-selective neurons and MD neurons within the same cue set and the opposite cue set. Right: Box-plot comparing coupling strength between MD and PFC cells selective to cues in the same cue context or the opposite context. *** p = 0.15 x 10−4 Bonferroni-corrected Kruskal-Wallis test (n = 345 MD neurons, 5 mice). (i) Left: Schematic illustrating unilateral PFC suppression. Right: Example MD neuron with suppressed firing rate following PFC suppression. Shaded blue area marks time over which the laser was turned on. (j) Comparison of contextual modulation index on Laser ON and Laser OFF trials. (k) Change in GLM prediction, measured as Δ Explained Variance, when PFC filters are excluded from the model (“No PFC”) compared to a model fit to MD responses following PFC suppression. Non-significant (NS, p = 0.42), Bonferroni-corrected Kruskal-Wallis test, n = 186 MD neurons, 3 mice. (l) Schematic of proposed PFC-MD connectivity. Data in d-h is from 5 mice, data in j,k is from 3 mice. Data is shown as mean +/− 95% confidence interval (shaded error-bars). Box plots: median (line), box edges, 95% confidence interval, whiskers, range.
Are these thalamic responses reflective of sensory input (i.e. the modality of the cues) or of something more cognitive? To answer this question, we required mice to perform the task using blocks with cues of different modalities. MD neuronal activity reflected these hetero-modal cueing blocks (Supplementary Fig. S6a–d). Furthermore, when we presented all four cues in a randomized manner, we found MD neurons that responded to all four cues, suggesting that their combination was encoded as a single context (Supplementary Fig. 6e–h). Altogether, MD activity reflects the statistical regularity of cue presentation over a multi-trial timescale, which we refer to as the cueing context (Supplementary Fig. 6i, j).
What factors could explain this contextual selectivity in the MD? We had previously shown that transient responses in the MD are dependent on PFC inputs17. Therefore, one possibility is that the MD gains contextual selectivity from PFC inputs, either from persistent RS neurons or from cue-selective ones (Supplementary Fig. 7a, b). To test these two models, we fit GLMs to MD neurons and analyzed how different PFC cell types contributed to their selectivity (Fig. 2g). PFC RS persistent cells did not contribute to spiking of either MD transient or persistent cells (Supplementary Fig. 7c–f). In contrast, more than 75% of the variance in the delay period activity of both transient and persistent MD neurons could be explained by inputs from cue-selective PFC neurons, with MD neurons more likely to receive inputs from the context-congruent cortical cue set (Fig. 2h). Also, consistent with the fact that PFC FS neurons do not project to the MD, we found that they exerted no causal influence on MD spiking, further validating the power of the GLM to infer biologically plausible circuit models (Supplementary Fig. 7c, f). Therefore, these findings suggest that MD neurons gain their contextual selectivity, at least partly, by pooling context-specific cue inputs from the PFC. MD transient cells pool from PFC cells in temporally precise manner, while MD persistent cells pool from PFC cells over a broader temporal window (Supplementary Fig. 7g, h).
To further verify these model predictions, we expressed the inhibitory channelrhodopsin, iC++, in PFC to directly inactivate its neurons or their terminals in MD [PFCMD] (Fig. 2i and Supplementary Fig. 8a–c) in a temporally precise manner. We reasoned that if MD neurons derive contextual selectivity from the PFC then suppressing PFCMD inputs should decrease its selectivity. To mitigate detrimental effect that bilateral PFC suppression as on behavior in this task 17, we suppressed the PFC unilaterally once the animal achieved stable performance in each block (Supplementary Fig. 8b, see Methods). This method allowed us to dissociate neural selectivity in the MD from changes in behavioral performance. Suppressing PFC neurons themselves or their terminals in MD diminished contextual signals in the MD (Fig. 2j and Supplementary Fig. 8d, e). Notably, removing PFC input filters in the MD GLM had a similar effect on response predictability as suppressing PFCMD terminals, providing further experimental validation of our GLM (Fig. 2k). Finally, to test the idea that PFC inputs are causally involved in generating and not just modulating contextual selectivity in the MD, we suppressed PFCMD inputs on every trial during the cueing period (Supplementary Fig. 9a). When performed unilaterally, this manipulation significantly decreased MD contextual selectivity (Supplementary Fig. 9b, c), and when performed bilaterally, it significantly impaired behavioral performance (Supplementary Fig. 9d–f).
Taken together, these results suggest that by pooling from cue-specific PFC neurons, the MD encodes the cueing context (Fig. 2l).
Encoding a cueing context is critical for behavioral performance and flexibility
Our results so far suggest that both MD and PFC FS explicitly encode cueing context, while PFC RS neurons encode other cognitive variables such as cue identity and rule. We wondered if behavioral performance benefitted from such a behavioral encoding scheme, and if so, how? We noticed that mice performed much better on sessions in which the four cues were separated into two cueing contexts compared to sessions in which the cues were equiprobable (Fig. 3a). This performance advantage occurred regardless of how cues in the block were grouped with respect to modality. Critically, although performance within either of the two blocks was higher than that when cues were fully randomized across the session, there was a clear and consistent behavioral detriment for 4–8 trials upon switching from one block to another (Fig. 3b). This decline in behavioral performance at the switch suggested that, despite previous learning, mice had to readjust to using cues in the new cueing set.
Fig. 3.
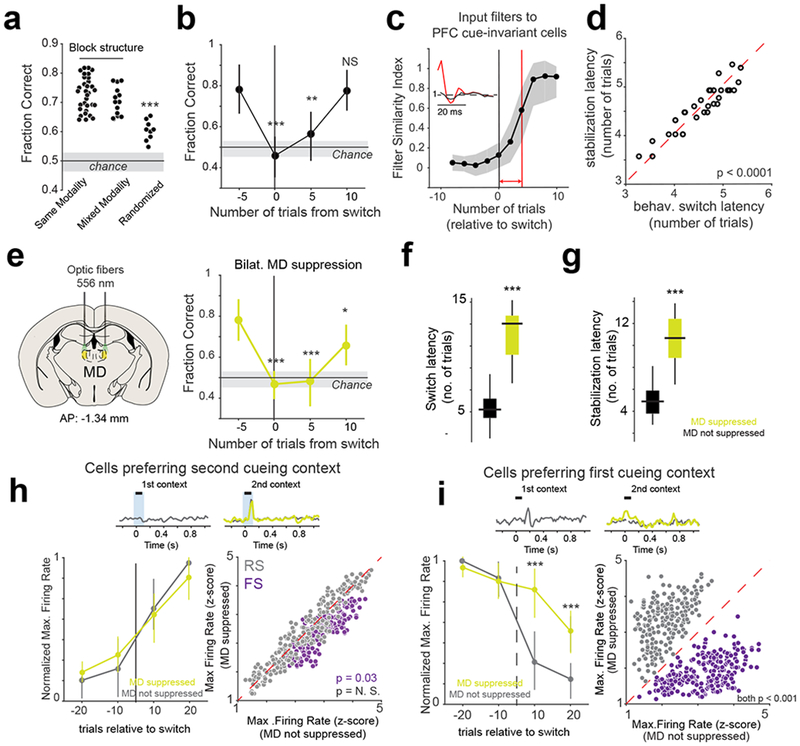
Flexible switching between contexts is associated with MD-dependent changes in PFC activity
(a) Comparison of fraction correct trials between the different task conditions. Each data point is one session per mouse from 3 mice in total. *** p = 0.023 x 10−3, Bonferroni-corrected Kruskal-Wallis ANOVA. Note, each session is treated as an independent sample. (b) Change in behavioral performance (fraction correct) relative to switch. **p < 0.01, *** p < 0.001. One-way Rank-sum test relative to 5 trials before the switch. n = 33 independent sessions from 3 mice. Data is shown as mean +/− SEM. (c) Change in filter similarity index of coupling filters from cue-selective to cue-invariant neurons in the PFC relative to switch. Insets show an example coupling filter changing between the point of switch (black) to its final stable value (red). Red line marks the filter stabilization latency. Shaded area, 95% CI. For details, see Methods. (d) Scatter plot relating behavioral (behav.) switch latency with the filter stabilization latency for inputs to cue-invariant PFC neurons. Each data point is a session (p = 0.0068 x 10−6, two-way rank-sum test, n = 33 independent sessions from 3 mice). (e) Left: Schematic illustrating bilateral MD suppression. Right: Change in behavioral performance (fraction correct) relative to switch for sessions with bilateral MD suppression. Statistics and plotting same as (b). (f-g) Box-plots comparing the effect that MD suppression has on behavioral switching latency (f, *** p = 0.78 x 10−4, Kruskal-Wallis ANOVA) and cue-invariant input filter stabilization latency (g, *** p = 0.19 x 10−4, Kruskal-Wallis ANOVA). N = 33 sessions with no suppression, 31 sessions with MD suppression from 3 mice. (h) Top: Example PSTH of a PFC neuron selective to cues in the second cueing context. Left: Time course of the change in normalized maximum firing rate (relative to stable behavior) relative to the switch. No significant difference (p = 0.92 between suppressed and non-suppressed conditions). Right: Scatter plot comparing the maximum firing rate of PFC cue selective neurons (grey) and PFC FS neurons (purple) 10 trials after switch. (i) As in (h) but showing the effect that MD suppression has on PFC cells that are selective for cues in the first cueing context. Left: *** p < 0.001, one-way rank-sum test for each time point between suppressed and non-suppressed conditions, n = 3 mice. Data is shown as mean +/− SEM. Right, p < 0.001 one-way rank-sum test for each time point between suppressed and non-suppressed conditions, n = 3 mice.
This behavioral switching dynamic was associated with several neural ones. We found that cue-selective PFC neurons showed reliable spiking earlier than cue-invariant ones upon first exposure to the new context (Supplementary Fig. 10a). This suggests that the decrease in behavioral performance at the point of context switch could be due to a remapping of inputs onto the shared cue-invariant cells. To test this hypothesis, we analyzed the temporal evolution of coupling filters from cue-selective to cue-invariant PFC cells on a trial on a trial by trial basis at the point of the switch (Supplementary Fig. 10b, see Methods). Intriguingly, the time taken for these coupling filters to stabilize followed broadly similar dynamics to that of the behavioral performance (Fig. 3c) and could explain close to 87% of the variance in the behavioral switch latency – sessions which took longer for the mouse to switch were also associated with a longer time to stabilize cue-selective inputs into cue-invariant neurons (Fig. 3d). This would be expected if PFC cue-invariance was the source of cognitive control signals (attend to vision vs. attend to audition). In contrast, although the coupling between cue-selective PFC neurons and context-selective MD neurons followed broadly similar dynamics, they were too fast to correlate with behavioral performance (Supplementary Fig. 10 c–g). Therefore, the output of the PFC cue-invariant cells, and not the MD or PFC cue-selective cells, are most likely utilized for controlling sensory selection and successful task performance.
These results also suggest that the contextual selectivity of the MD may be required for the generation of rule signals in the PFC by adjusting the functional connectivity between cue-selective and cue-invariant PFC neurons in a context specific manner. To causally test this model, we designed and executed a series of optogenetic perturbation experiments. Our previous study demonstrated that bilateral suppression of MD neurons during the duration of the delay period diminished task-relevant activity in the PFC17. In addition, in tasks lacking a delay period, MD suppression, via halorhodopsin (see Methods) during the cueing period (100 ms) had minimal effect on behavioral performance17. As such, we first asked whether cue-specific, interleaved and bilateral MD suppression had a measurable impact on behavioral performance. Interestingly, once an animal achieved stable performance within a block, such manipulation had no impact (Fig. 3e). Instead, the biggest behavioral deficit that we observed was the prolonged time taken to achieve stable performance in the new context (Fig. 3f and Supplementary Fig. 11). Consistent with the idea that MD contextual signals are relevant for establishing PFC task-relevant connectivity patterns, this MD manipulation also increased the number of trials taken to stabilize cue-invariant representations in the PFC (Fig. 3g). Notably, this laser manipulation had no unwanted effects on the MD as the same laser power and duration had no effect in mice that expressed GFP in the MD (data not shown).
MD neurons regulate PFC representational switching likely through cortical inhibition
In addition to the effects on behavioral performance and PFC representational stability, we also noted that temporally-precise MD suppression during the cueing period impacted cue-selective PFC neural spiking. Specifically, although the increase in spiking of cells preferring the second context was unaffected (Fig. 3h), we observed that cells preferring the first context continued to fire even though their sensory cue was no longer present (Fig. 3i). Suppressing MD terminals in the PFC (MDPFC) resulted in a similar ‘out-of-context’ spike rate elevation (Supplementary Fig. 12). Critically, these MD-dependent changes in PFC RS spiking activity were contrasted by changes in PFC FS firing; MD suppression attenuated the normal elevation of FS neural spiking associated with the second context (Fig. 3i). Therefore, at least a subset of MD neurons may regulate representational switching by suppressing out-of-context activity in the PFC through cortical inhibitory mechanisms.
To more directly probe this process, we turned to our multineuronal GLM to assess the impact of MD neurons on PFC targets (Fig. 4a). We found that, in contrast to cue-invariant PFC neurons (Fig. 4b), cue-selective PFC neurons received substantial MD inputs, which varied according to context (Fig. 4c). These functional inputs could be broadly segregated into two types; one predominantly inhibitory and another predominantly excitatory (Fig. 4c inset). Notably, these functional inputs originated from the two distinct MD functional subgroups; persistent MD neurons were more likely to provide inhibitory functional inputs, while transient MD neurons predominantly provided excitatory ones (Fig. 4d).
Fig. 4.
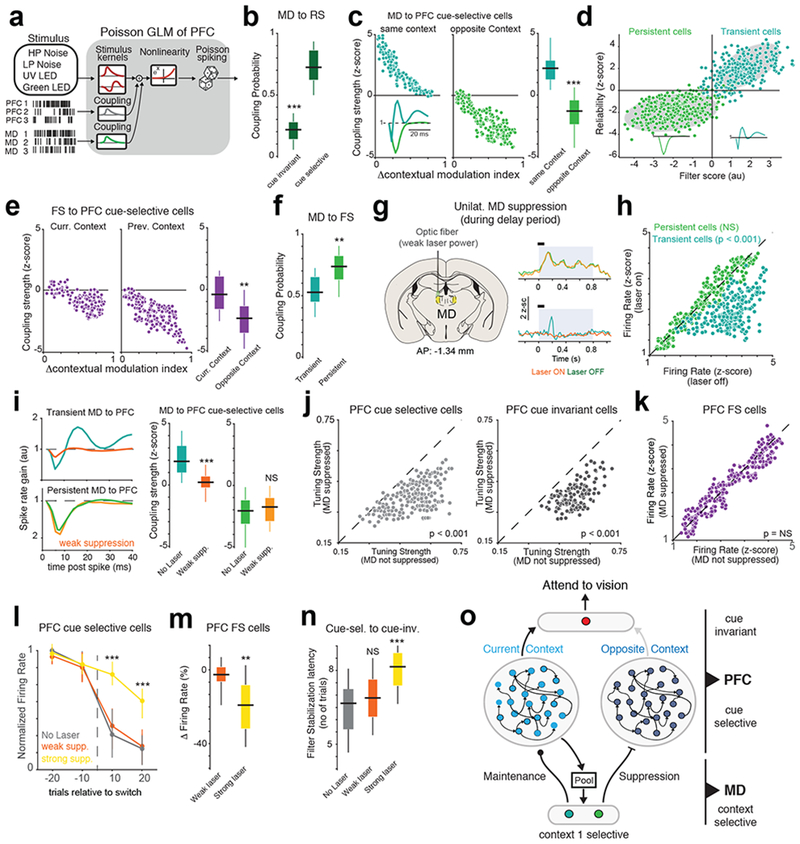
Distinct MD neurons augment and suppress context-relevant PFC representations.
(a) Schematic of Poisson GLM used to model PFC neurons including MD interactions. (b) Box-plot comparing the coupling probability between MD and PFC cue-selective (n = 230 neurons from 5 mice)) or cue-invariant neurons (n = 86 neurons from 5 mice). ***p = 0.58 x 10−5 two-way rank-sum test relative to cue-selective neurons. (c) Left: Scatter plot relating the coupling strength between MD and PFC cue-selective cell with the difference in contextual selectivity for both cells that prefer the current context or the previous context. Inset shows the two different coupling filters between MD and PFC cells. Each data point is one PFC cell from 5 mice. Right: Box-plot comparing the difference in coupling strength between MD and PFC neurons preferring the same context (n = 141 MD neurons from 5 mice) or the opposite context (n = 211 MD neurons from 5 mice). ***p = 0.89 x 10−4, two-way rank-sum test. (d) Clustering analysis relating MD-PFC coupling strength with MD spiking reliability. Each data point is one MD cell (n = 352 neurons from 5 mice). Shaded gray area is the 95% confidence interval ellipse of a Gaussian mixture model. Inset, median filter shape from each cluster. (e) Right: Scatter plot relating FS to PFC cue-selective coupling strength with difference in contextual modulation. Each data point is one PFC cell from 5 mice. Left: Box-plot comparing the difference in coupling strength between FS and PFC neurons preferring the same context (n = 141 neurons from 5 mice) or the opposite context (n = 211 neurons from 5 mice). **p = 0.31 x 10−2, two-way rank-sum test. (f) Box-plot of coupling probabilities between MD and PFC FS cells. **p = 0.78 x 10−2, two-way rank-sum test relative to transient MD neurons (n = 410 PFC FS neurons, 5 mice). (g) Left: Method for unilaterally suppressing the MD. Right: PSTHs of two example MD neurons. Persistent MD cells (top) are less affected by weak MD suppression than transient MD cells (bottom). Shaded blue area marks the duration of the laser, while the black bar marks the cueing period. (h) Scatter plot comparing the effect of weak MD suppression on the firing rates of transient (n = 260 neurons from 3 mice, p = 0.89 x 10−3) and persistent MD cells (n = 247 neurons from 3 mice, non-significant, p = 0.22, Friedman test between laser on and laser off trials. (i) Left: Example MD-PFC coupling filters with (orange) and without (green) MD suppression. Right: Box-plot comparing the effect of MD suppression on the coupling strength between transient and persistent MD cells and PFC cue selective neurons (n = 177 neurons, 3 mice). ***p = 1.02 x 10−4, NS = p = 0.12, two-way rank-sum text. (j) Scatter plot showing the change in tuning strength of cue selective (left, n = 177 neurons) and cue-invariant (right, n = 127 neurons, 3 mice) neurons caused by weak MD suppression. Friedman test between laser on and laser off trials. (k) As (j) but showing no significant effect of weak MD suppression on PFC FS neurons (264 neurons, 3 mice, p = 0.81). (l) Time course of the change in normalized maximum firing rate relative to switch of PFC cells selective for cues in the first cue set. Colors indicate various levels of MD suppression. Data shown as mean +/− SEM. N = 3 biologically-independent mice. ***p < 0.0001 one-way rank-sum test relative to no laser condition. (m) Box-plot comparing the change in firing rate of PFC FS neurons with weak and strong MD suppression (n = 264 and 212 neurons from 3 mice respectively). **p = 0.71 x 10−2 one-way Kruskal-Wallis ANOVA. (n) Box-plot comparing cue-selective to cue-invariant filter stabilization latency. No laser, n = 33 sessions, Weak laser, n = 31 sessions, Strong laser = 18 sessions from 3 mice). ***p = 0.063 x 10−4, one-way Kruskal-Wallis ANOVA with post-hoc rank-sum test. (o) Cartoon summarizing the distinct effect that MD transient and persistent cells exert on the PFC. All box plots: median (line), box edges, 95% confidence interval, whiskers, range.
Similar to MD neurons, PFC FS neurons also exerted a context-dependent inhibitory effect on cue-selective neurons, with FS neurons having a larger inhibitory effect on PFC neurons that prefer cues of the opposite context (Fig. 4e). Consistent with the idea that MD cell types may be exerting part of their effects on the PFC through local inhibitory circuits35,36, we found that MD inputs could explain more of the variance of PFC FS neuron firing than PFC cue-selective neurons (Supplementary Fig. 13a–c). MD persistent neurons were more coupled to PFC FS neurons than MD transient neurons were (Fig. 4f). Also, in contrast to FS neurons, PFC RS persistent neural responses were poorly explained by inputs from either the MD or cue-selective PFC neurons (Supplementary Fig. 13d), reinforcing the notion that they may be part of a distinct functional circuit than the one under study. Altogether, these results support a model in which the MD controls contextual switching by suppressing PFC neurons of the irrelevant context through mechanisms that involving cortical inhibition.
To further test this model causally, we needed to gain a degree of selectivity over the two identified functional MD subtypes (Fig. 4g). MD neurons in vitro have a bimodal resting membrane potential distribution37, suggesting different degrees of excitability. Because our analysis suggested that two MD populations are driven by different degrees of cortical engagement (Supplementary Fig. 7), we reasoned that this might also be due to differential excitability which may impart differential susceptible to optogenetic inhibition. Specifically, the less excitable MD population (likely transient MD cells) would require stronger or more coincident PFC inputs to fire and hence would be more susceptible to weak suppression. Conversely, persistent MD neuron may be more excitable and would require weaker and less coincident PFC inputs to fire.
By parametrically controlling laser power on an animal-by-animal basis without influencing behavior (Supplementary Fig. 14 a, b), we found that MD transient cells were far more susceptible than MD persistent cells to low levels of yellow laser power (556 nm, power at fiber tip: 0.6-1.1 mW, Fig. 4h and Supplementary Fig. 14 c, d). These laser powers did not have an appreciable effect on the spiking properties of MD persistent cells (Supplementary Fig. 14 e–g). Higher laser powers (power at fiber tip: 2.1-3.5 mW) affected both transient and persistent MD neurons (Supplementary Fig. 14h). In support of the predictions made by our GLM, selectively suppressing MD transient cells with weak laser powers selectively eliminated excitatory functional inputs to the PFC but had no impact on the inhibitory functional inputs from transient MD neurons (Fig. 4i). Suppressing MDPFC terminals had a similar effect on the PFC without affecting the firing rates of these neurons (Supplementary Fig. 14i–k). This manipulation also revealed a selective effect on the response properties of both transient PFC RS neurons subtypes (Fig. 4j and Supplementary Fig. 15a), but not PFC FS neurons (Fig. 4k). In agreement with our earlier studies17, temporally-limited MD suppression had a stronger effect on the maintenance of these peaks rather than their initiation in the PFC, confirming that the MD is not the source of PFC cue information (Supplementary Fig. 15b). Although the congruence between terminal and somatic inactivation may be surprising, the relatively large volumes of MD terminals may have larger impact on somatic excitability than what would be expected otherwise.
Consistent with the idea that persistent MD neurons provide cross-contextual PFC suppression, strong laser suppression significantly increased “out-of-context” cue-selective PFC spiking (Fig. 4l) and concomitantly decreased PFC FS neural spiking (Fig. 4m). Because of this, inputs from cue-selective PFC neurons onto cue-invariant neurons took a longer time to stabilize (Fig. 4n). Weak laser suppression, which targeted only transient cell, did not have a similar effect. Taken together, our findings strongly suggest that the MD has two distinct computational functions: (1) Transient MD cells maintain the context-relevant representation in the PFC, permitting cue information to be held in working memory; (2) Persistent MD cells suppress context-irrelevant representations in the PFC by recruiting FS neurons in a context-dependent manner (Fig. 4o).
MD-dependent suppression of context-irrelevant representations protects them for future use
Our data thus far suggest a model in which persistent MD neurons suppress PFC representations when they are no longer relevant for the current context. What computational advantage could this architecture impart? Recent theoretical work 38 has shown that a context-dependent gating mechanism, which suppresses task-irrelevant nodes in deep neural network, can increase flexibility by allowing the network to learn more tasks sequentially. We wondered whether MD-mediated inhibition could impart such a benefit onto PFC, allowing it to flexibly switch between the different cueing contexts.
To test this idea, we used a reservoir network of rate neurons as a model for PFC function39,40 and incorporated an MD-like node39 that suppressed context-irrelevant reservoir neurons (Fig. 5a). The network was trained to perform a classification task where it had to classify four cues into two rules, which was analogous to the task that mice were trained to do. Interestingly, the PFC-MD model outperformed a PFC-only model in being able to flexibly switch between cueing contexts (Fig. 5b). Without an MD, weights relevant to context 1 changed in the second context (Fig. 5c, d), which in turn increased errors when context 1 was required again. Incorporating the MD limited the spread of recurrent excitation to the context-relevant PFC neurons, making the two contextual representations practically disjoint, and disabling weight changes involving context-irrelevant neurons. Interestingly, this weight-protection benefit generalized to a much more computationally-demanding exclusive-or (XOR) classification task which is by design not linearly separable41,42 (Supplementary Fig. 16). Overall, the computational benefits imparted by an MD-like node are even more relevant in the XOR task, suggesting broad benefits of cross-contextual suppression in cognitive flexibility.
Fig 5.
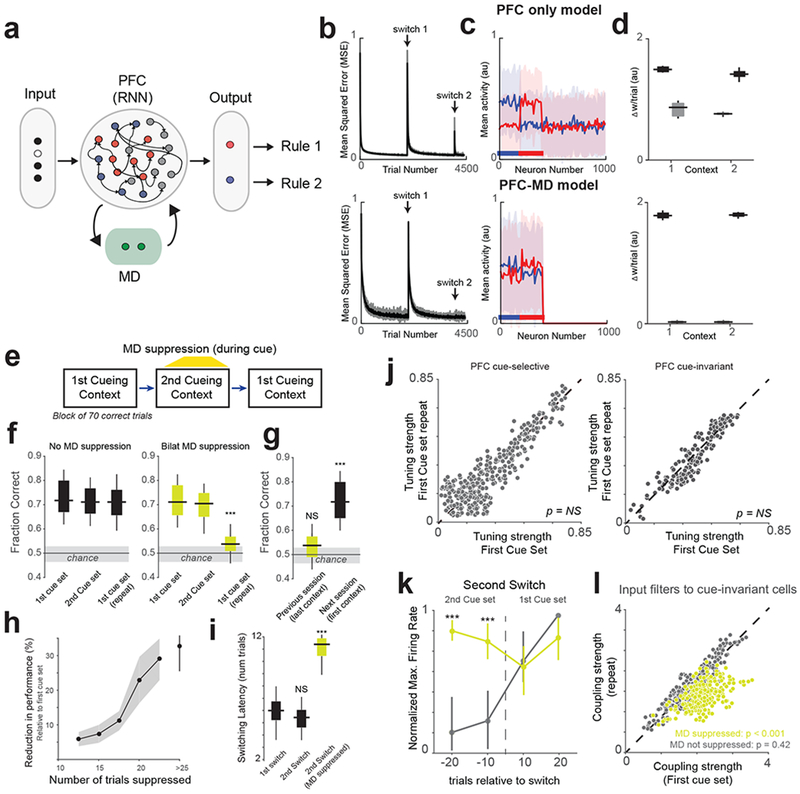
Benefit of PFC-MD over PFC-only architecture on switching contexts.
(a) Recurrent neural network (RNN) model of the PFC-MD network. The drawing depicts neural activation in a single context, with grey RNN neurons representing the currently-irrelevant context (b) The mean squared error (MSE) in decoding the desired output from the PFC over two context switches (indicated by the arrows). For details, see Methods. (c) Trial-averaged responses of 1000 neurons in the PFC to low-pass noise (blue) and high-pass noise (red). Horizontal lines below the plots indicate the sets of neurons activated by the input cues. Shaded area, SEM. (d) Trial averaged change (n = 200 trials) in connection weights per trial, from current-context neurons (black) and from other-context neurons (grey) to rule-selective output neurons during context 1 and context 2 presentation. Each box extends from lower to upper quartiles, the middle line marks the median, and the whiskers represent the range (from 10 network instances). (e) Schematic of the three-block switching paradigm that mice were required to complete. (f) Box-plots showing the effect of Bilateral (Bilat.) MD suppression in the second context on behavioral performance (fraction correct). Shaded area indicates the 95% confidence interval of chance behavioral performance derived from a probabilistic model. N = 12 independent sessions without MD suppression and 12 sessions with MD suppression from 3 mice. *** p = 0.05 x 10−4 Bonferroni-corrected rank-sum test. (g) Comparison of performance on the consecutive sessions (separated by one day). Statistical comparisons performed using one-way rank-sum test relative to chance levels. N = 10 independent sessions each. ***p = 0.08 x 10−4. (h) Relationship between the reduction in performance and the number of MD suppression trials. Data shown as mean +/− 95% confidence interval (shaded error-bar). N = 3 biologically-independent mice. (i) Bilateral MD suppression significantly increases the latency of switch back to the first context. N = 12 indepenent sessions each from 3 mice. ***p = 0.09 x 10−4, Bonferroni-corrected Kruskal-Wallis ANOVA with post-hoc rank-sum test. (j) Scatter plot relating the tuning strength of PFC cue-selective (left, n = 236 neurons) and cue-invariant (right, n = 158 neurons from 3 mice) cells in the first block with their tuning strength in the third block. NS, non-significant Friedman Test. (k) Change in normalized maximum firing rate relative to the second switch of PFC cells selective for cues in the first cue set showing an increase in maximal spiking for ‘out-of-context’ neurons when the MD is ontogenetically suppressed. N = 3 biologically-independent mice. ***p < 0.0001 one-way rank-sum test relative to no MD suppression group. Data shown as mean +/− 95% confidence interval. (l) Scatter plot of the coupling strength between first context PFC cue-selective neurons and cue-invariant ones averaged over trials 10-20 following the switch (grey dots, n = 223 neurons). Unilateral optogenetic MD suppression substantially diminishes the size of these functional connections (yellow dots, n = 150 neurons from 3 mice). P-values calculated using Friedman test between first and third cueing contexts. All box plots: median (line), box edges, 95% confidence interval, whiskers, range.
We reasoned that we could test these theoretical weight protection benefits experimentally if we employed a three-block switching paradigm (Fig. 5e, see Methods), where mice were re-exposed to the first cueing context in the third block. In this paradigm, PFC neurons selective for the first cue-set should be suppressed in the second block, but perhaps reactivated again in the third as it would be computationally efficient to simply re-engage the same functional ensemble rather than generate a new one de novo. We found that mice performed this three-block switching paradigm well, with no significant difference in performance across blocks (Fig. 5f). Interestingly, suppressing the MD bilaterally during the cueing period once behavior stabilized in the second block significantly impaired performance when the animal was re-exposed to the first block (Fig. 5f). Although performance was close to chance (as if the mouse had forgotten the first context), bilateral MD manipulations did not have any long-lasting effects as performance returned to normal the following day (Fig. 5g). This reduction in behavioral performance on re-exposure to the first block parametrically varied with the number of trials suppressed in the second block; suppressing a larger number of trials in the second block resulted in a larger behavioral deficit (Fig. 5h, inflection point, 20 trials). Interestingly, although the switching latency was marginally shorter when the animal moved from the second back to the first cueing context, MD suppression in the second block prolonged this switch (Fig. 5i and Supplementary Fig. 17). This effect is stronger than what we show in Fig. 3f, because unlike the two-block switching paradigm, mice must now reactivate representations for the first cueing context in the PFC.
To examine the neural substrates of this behavioral detriment, we again aimed at dissociating behavioral from neural manipulations and therefore employed a unilateral optogenetic suppression paradigm where we suppressed MD neurons during the cue once behavior stabilized in the second block. In sessions where no such optical manipulation was deployed, both PFC cue-selective and cue-invariant neurons were largely shared between the first cue-set and their repeat in the third block (Fig. 5j). As expected, unilateral cue-specific MD suppression resulted in out-of-context spiking of the first cue-set neurons during the second block (Fig. 5k and Supplementary Fig. 18). Although this was not associated with a delay in how these neurons were recruited in the third context, their functional inputs onto cue-invariant neurons were much weaker upon the switch (Fig. 5l). Therefore, our data suggest that in addition to suppressing context-irrelevant cortical representations such that context-relevant functional connections rapidly stabilize, such process may protect recently engaged but currently irrelevant connectivity patterns for near-future use (see Supplementary Fig. 19 for summary model).
Discussion
In this study, we expanded on a behavioral paradigm we had previously developed17,23 by nesting it in a cognitive hierarchy. Specifically, while our previous studies have explored the neural correlates of cross-modal sensory selection based on two learned cues, the current design nested the selection process within multiple cueing contexts. Importantly, these contexts were under complete experimental control and could be arbitrarily constructed on a session-by-session basis.
This allowed us to make multiple observations. First, we identified a prefrontal neural hierarchy that matches the cognitive one; neurons that reflected the meaning of the cue (the rule) derived their representations from local cue-selective inputs. Similar hierarchies are seen in sensory areas43 potentially speaking to broadly similar cortical organization principles. Notably, we found only 5% of cells in the mouse PFC to be rule selective, a contrast to higher species which have significantly larger fractions of such cells29,44. This difference may explain why mice perform worse on randomized cueing compared to primates.
Second, unlike structures like the lateral geniculate nucleus (LGN), or thalamic circuits that primarily drive excitatory responses in the cortex45, we found that the MD exerts effects on cognitive switching through local inhibitory cortical interneurons. This builds on similar recent studies22,35,36, but also provides a computational framework linking thalamic output to cortical inhibitory microcircuits. For example, transient MD neurons could recruit dis-inhibitory motifs46 to maintain activity in the PFC while persistent MD neurons could target soma-targeting interneurons36. Without further evidence however, we can only speculate that the diversity of thalamo-cortical computations may match the diversity of cortical interneurons47.
Third, the unique connectivity patterns of the lateral MD are consistent with our physiological results; convergence of individually small cortical terminal inputs onto single MD neurons20,48 may explain their lack of selectivity to categorical information that originates in cortex. Instead, our model shows that this convergence of PFC inputs may facilitate the emergence of contextual signals in the MD20. Additionally, the lack of thalamic lateral connectivity may allow MD neurons to multiplex incoming signals, a process that would be harder for cortical circuits to implement given their extensive recurrence.
Fourth, the experiments regarding multiple switches point to a variety of plasticity rules governing cortical function, as had been recently shown through recurrent neural network simulations49. Within this framework, our data suggest a unique role for the thalamus in generating contextual representations that may regulate cortical plasticity. The exact nature of cortical inhibitory neurons involved in cross-contextual suppression are still unknown at this point, and our study provides a starting point for such detailed exploration.
Lastly, it is worth mentioning that recent progress in artificial intelligence (AI) research has shown a benefit for incorporating context-specific gating mechanisms in convolutional networks on the ability to perform multiple tasks and the mitigation of ‘catastrophic forgetting’10,38. The key idea in these studies is the generation of non-overlapping task-specific representations in a context-specific manner50. We envision the MD thalamus to impart a similar computational benefit on task-specific PFC representations; rapid separation of potentially overlapping representations such that their decoding is performed more easily. Overall, our finding may not only be relevant to future research in neuroscience but may also lead to the generation of artificial networks that exhibit more stable learning and robust performance.
Methods
Mice.
All experiments were carried out under protocols approved by MIT’s Committee on Animal Care and conformed to NIH guidelines. With the exception of one mouse, who had the Sst-IRES-Cre (Jax: 013044) genotype, all mice were C57/BL6 (Taconic Biosciences). Only male mice older than 8 weeks old were used in this study. Please refer to the Life Sciences Reporting Summary for further details. Mice were housed in the vivarium on a standard 12-hour light/dark cycle and were singly housed throughout the experimental period. Experiments were performed during the light portion of the cycle.
Behavioral setup.
Behavioral training and testing took place in gridded floor-mounted, custom-built enclosures made of sheet metal covered with a thin layer of antistatic coating for electrical insulation (dimensions in cm: length, 15.2; width, 12.7; height, 24). All enclosures contained custom-designed operant ports, each of which was equipped with an IR LED/IR phototransistor pair (Digikey) for nose-poke detection. Trial initiation was achieved through an ‘initiation port’ mounted on the grid floor 6 cm away from the ‘response ports’ located at the front of the chamber. Task rule cues and auditory sweeps were presented with millisecond precision through a ceiling-mounted speaker controlled by an RX8 Multi I/O processing system (Tucker-Davis Technologies). Visual stimuli were presented by two dimmable, white-light-emitting diodes (Mouser) mounted on each side of the initiation port and controlled by an Arduino Mega microcontroller (Ivrea). Similarly, the visual cues were delivered through a pair of a wall-mounted 5 mm LEDs (UV: 320-380 nm, Green: 495-510 nm, 100 mW 25 degree viewing angle Mouser). These LEDs were bright enough to illuminate the whole arena. Two response ports were mounted at the angled front wall 7.5 cm apart, respectively. Milk reward (10 μL evaporated milk, Carnation) was delivered by a single syringe pump (New Era Pump Systems) when mice made a correct choice. Access to the response ports was restricted by vertical sliding gates which were controlled by a servo motor (Tower Hobbies). The TDT Rx8 sound production system (Tucker Davis Technologies) was triggered through MATLAB (MathWorks), interfacing with a custom-written software running on an Arduino Mega (Ivrea) for trial logic control.
Multi-electrode array construction and implantation.
Custom multi-electrode array scaffolds (drive bodies) were designed using 3D CAD software (SolidWorks) and printed in Accura 55 plastic (American Precision Prototyping) as described previously 17,23,51. Prior to implantation, each array scaffold was loaded with 12–18 independently movable micro-drives carrying 12.5-μm nichrome (California Fine Wire Company) stereotrodes or tetrodes. Electrodes were pinned to custom-designed, 96-channel electrode interface boards (EIB, Sunstone Circuits) along with a common reference wire (A-M systems). For combined optogenetic manipulations and electrophysiological recordings of the PFC, optic fibers delivering the light beam lateral (45° angled tips) were embedded adjacent to the electrodes. In the case of combined optogenetic PFC manipulations with mediodorsal recordings.
During implantation, mice were deeply anaesthetized with 1% isofluorane and mounted on a stereotaxic frame. A craniotomy was drilled centered at AP −2 mm, ML 0.6 mm for PFC recordings and at AP: 1 mm, ML 1.2 mm for mediodorsal recordings. The range of coordinates covered in our recordings for the lateral MD are: AP: −1 to −1.5 mm, ML: 0.3 to 0.8 mm relative to bregma. Similarly, for the PFC, the range of coordinates covered in our recordings are: AP: 2.1 to 2.7 mm, ML: 0.25 to 0.6 mm relative to bregma.
The dura was carefully removed, and the drive implant was lowered into the craniotomy using a stereotaxic arm until stereotrode tips touched the cortical surface. Surgilube (Savage Laboratories) was applied around electrodes to guard against fixation through dental cement. Stainless-steel screws were implanted into the skull to provide electrical and mechanical stability and the entire array was secured to the skull using dental cement.
Optogenetic Manipulation.
We utilized a dual wavelength optical silencing method to independently suppress neurons in the PFC and MD. Specifically, we virally expressed the inhibitory channelrhodopsin iC++ in the PFC (AAV-CaMKIIA-iC++-eYFP) 52, which is selective to blue-shifted wavelengths (473 nm), and expressed halorhodopsin (AAV-CaMKIIA-eNpHR3.0-eYFP) in the MD 53. Since the peak spectrum of eNpHR is red-shifted (peak ~550 nm), we could independently suppress both populations without affecting their terminals in either structures. Light was delivered to these structures using optic fibers that were part of the micro-drive (as described above). We used a 473 nm laser and a 556 nm laser (OptoEngine) to activate iC++ and eNpHR respectively.
Behavioral training.
Mice were trained to perform this task in subsequent stages. First, 10 μL of evaporated milk (reward) was delivered randomly to each reward port for shaping and reward habituation. Next, the location of the rewarded port was signaled by a white LED (same used as the visual target) in order to establish an association between the location of the visual target and the location of the reward port. Following this, mice learned the association between the auditory targets – up-sweep: 10-15 kHz and a down-sweep: 16-12 kHz – with the left and right ports respectively. An individual trial was terminated 20 s after reward collection, and a new trial became available 5 s later. As as soon as mice achieved criterion performance in this block (>60% correct), visual and auditory targets were randomly interleaved.
Second, mice learned to poke (i.e. break the IR barrier in each reward port) in order to receive reward. All other parameters remained constant. An incorrect poke had no negative consequence. By the end of this training phase, all mice collected at least 20 rewards per 30-min session.
Third, mice were trained to initiate trials. Initially, mice had to briefly (50 ms) break the infrared beam in the initiation port to trigger target stimulus presentation and render reward ports accessible. Trial rule (attend to vision or attend to audition) was indicated by 10-kHz low-pass filtered white noise (vision) or 11 kHz high-pass filtered white noise (audition) sound cues. Stimuli were presented in blocks of six trials consisting of single-modality stimulus presentation (no conflict). An incorrect response immediately rendered the response port inaccessible. Rewards were available for 15 s following correct response, followed by a 5 s inter-trial interval (ITI). Incorrect responses was punished with a time-out, which consisted of a 30 s ITI. During an ITI, mice could not initiate new trials. During this stage, the duration of the initiation time was gradually increased from 50 ms to 800 ms. Mice progressed to the next stage only when they were able to maintain snout fixation for at least 800 ms.
Fourth, conflict trials were introduced, in which auditory and visual targets were co presented indicating reward at opposing locations. Four different trial types were presented in repeating blocks: (1) three auditory-only trials; (2) three visual-only trials; (3) six conflict trials with auditory target; and (4) six conflict trials with visual target. The time that mice had to break the IR barrier in the initiation port was continuously increased over the course of this training stage (1–2 weeks) until it reached 0.5 s. At the same time, duration of the target stimuli was successively shortened to a final duration of 0.1 s. Once mice performed successfully on conflict trials, single-modality trials were removed, and block length was reduced to three trials.
Fifth, during the final stage of training, trial availability and task rule were dissociated. Broadband white noise indicated trial availability, which prompted a mouse to initiate a trial. Upon successful initiation, the white noise was immediately replaced by either low-pass or high-pass filtered noise for 0.1 s to indicate the rule. This was followed by a delay period (variable, but for most experiments it was 0.4 s) before target stimuli presentation. All block structure was removed, and trial type was randomized. Particular steps were taken throughout the training and testing periods to ensure that mice used the rules for sensory selection.
Once mice were fully familiarized with the main structure of the task and achieved consistent performance on the final stage of training, they were exposed to the visual cueing condition. After achieving 40 correct responses, mice were moved to an association block where the LEDs were paired with the congruent auditory cues (LP with Green LED and HP with UV LED). The volume of the sound decayed linearly over the course of trials, with full volume for the first 10 trials up to 1/5th of the volume for the last few trials. The sound volume was changed only after the mouse made two consecutive correct responses (an indication that the mouse understands the task). At the end of 70 trials, and depending on performance, mice were moved to the visual-only block, where no auditory cues were played. In the following session, the length of the association block was gradually reduced. Once mice were able to achieve a consistent performance of >60% on 3 consecutive sessions in the visual-only block, the association block was removed completely. At this point, mice were considered experts on the task.
Behavioral testing.
In the double block cueing paradigm, mice were required to complete 70 trials in each block. Blocks were constructed based on either cues of the same modality (HP-LP and UV-Green) or cues from both modalities (HP-Green and UV-LP). In each block, cues were drawn pseudo-randomly and the order of the blocks were randomized from session to session. Sessions in which mice did not perform >60% overall in each block were discarded and were not analyzed further.
In the randomized cueing paradigm, mice were required to complete a total of 200 trials per session. On each trial, one cue out of a possible four cues (HP, LP, UV and Green) were drawn at random. To further ensure that the cues appeared in random (i.e. without any regularity), we imposed the additional constrained that no more than three draws can be from the same modality. That is after three UV-Green draws, the next cue has to be either HP or LP. A new random seed was used each day. Mice that were previously trained on the block design took approximately a week to adjust to this new cueing condition. Although average performance was low, mice had brief periods in which their local performance was close to 80%.
In the three-block switching paradigm, mice were required to complete a total of 70 trials in the first two blocks and 90 trials in the third block. The identity of the first block (i.e. whether visual or auditory) was pseudorandomized from day-to-day. In total, we have 4 sessions per mouse (2 Auditory-Visual-Auditory, 2 Visual-Auditory-Visual) on the standard version of the task, and 4 sessions per mouse with MD suppressed in the second block. We did not notice a difference in the effect of MD suppression in the visual block compared to the auditory cueing block, and hence have pooled these sessions for analysis.
Behavioral analysis.
To quantify the behavior, we carried out regression analysis to weigh the contributions of rule and history of choice and reward on the animal’s choice on the current trial 54. To do so, we concatenated data from multiple sessions for each mouse and fit the animal’s choice with a logistic regression model of the form:
Where T is the number of trials in the past. For this model, we calculated that the model explained behavioral variance best when we included up to 10 trials in the past. In this equation S(t), F(t) ∈ [+1, −1] if a trial is a success or a failure respectively. Similarly, R(t) ∈ [+1, −1] if the rule on that trial is ‘attend-to-vision’ or ‘attend-to-audition’ respectively. This model was fit using a custom written ridge regression routine in Matlab. The hyper-parameter value for ridge regression was calculated using 5-fold cross validation.
To assess the effect that choice history had on the probability of success on the next trial, we developed a probabilistic model. Given the 2-AFC structure of our task, we assumed that on each trial, the mouse tosses a coin was a bias (q = Psuccess) that depends on the animal’s success on past trials. Therefore, the likelihood of a success given s successes and f failures in the past 10 trials is given by the binomial distribution:
Knowing that the conjugate prior of the binomial distribution is the beta distribution, we can calculate the posterior distribution using Bayes’ theorem
Using this the expected probability of success (E(q)) on the next trial is then:
All models were fit separately for each mouse (n = 5) using 1,000 runs of 5-fold cross validation. For each run, we computed the log-likelihood for the test data set for the mean value if P(Vision) or P(success). Model fit quality was assessed by computing the deviance statistic. We also used this model to assess overall behavioral performance. Trials in which behavior was close to the predicted chance levels were ignored and the overall fraction correct was computed from trials in which actual behavior deviated significantly from the model (we define these periods as “stable” behavior). As such, changes in performance accuracy reported throughout are only calculated over the period of stable behavior, and do not include switch trials.
Trial selection.
By comparing the two models – a model that includes rule-dependent components and a reward-history model – we were able to determine trials over which the animal was making either an informed choice based on the current cue or a biased choice based on history of reward. We used this to select trials. Specifically, for each trial, we computed the deviance between the full model and the history model, and selected a trial if deviance was above a threshold value that was calculated using cross validation for each session. Surprisingly, tuning peaks (described in the following section) were much more apparent in the selected trials, than in the rejected trials. Please refer to the Life Sciences Reporting Summary for further details on data omission.
Electrophysiological recordings and spike sorting.
Signals were acquired using a Neuralynx multiplexing digital recording system (Neuralynx) through a combination of 32- and 64-channel digital multiplexing headstages plugged into the 96-channel EIB of the implant. Signals from each electrode were amplified, filtered between 0.1 Hz and 9 kHz and digitized at 30 kHz. For thalamic recordings, tetrodes were lowered from the cortex into the mediodorsal thalamus over the course of 1–2 weeks where recording depths ranged from − 2.8 to − 3.2 mm DV. For PFC recordings, adjustments accounted for the change of depth of PFC across the AP axis. Thus, in anterior regions, unit recordings were obtained −1.2 to − 1.7 mm DV, whereas for more posterior recordings electrodes were lowered − 2 to − 2.4 mm DV.
Spike sorting was done automatically using MountainSort 55. Following sorting each cluster was manually inspected for quality. Only well isolated clusters with biologically plausible waveforms were selected for further analysis.
Identification of FS and RS cells.
For each spike waveform, we extracted four metrics: (1) peak-to-trough time; (2) peak-to-trough ratio; (3) spike width; (4) spike amplitude. We combined this 4-dimensional feature vector with the overall firing rate of the neuron to form a 5-dimensional feature vector for each cell. We applied k-means clustering (k++ algorithm, 1,000 runs with randomly initialized seed), and determined the optimal number of clusters using the Calinski-Harabasz criterion 56. Cluster separability was assessed statistically by calculating the ratio of between-cluster variance to within-cluster variance. For most sessions, the waveforms clustered reliably into two clusters, corresponding to FS and RS waveforms. Approximately 10% of all recorded spike waveforms could not be reliably classified into either subtype (based on 1,000 runs), and were hence not included in further analysis.
Analysis of firing rate.
For all PFC and mediodorsal neurons, changes in firing rate associated task performance were assessed using peri-stimulus time histograms (PSTHs). PSTHs were computed using a 10-ms bin width for individual neurons in each recording session4 convolved with a Gaussian kernel (25 ms full-width at half-maximum) to create a spike density function (SDF) which was then converted to a z score by subtracting the mean firing rate in the baseline (500 ms before event onset) and dividing by the variance over the same period. For comparison of overall firing rates across conditions, trial number and window size were matched between groups. Except for switching analysis, we analyzed firing rates only trials in which local performance deviated significantly from the probabilistic model (Supplementary Fig. 1).
Computing reliability and tuning strength
For each recorded neuron, we computed trial-to-trial reliability using a 150 ms sliding window. Reliability is simply the correlation in spike times between each pair-wise combination of trials, such that a neuron with perfect reliability has no spike time variation and a correlation coefficient of 1. Only neurons with responses on 15 trials or more were selected for this analysis.
To determine whether the observed level of reliability was significantly different from chance, we used a randomization test where the time period of analysis was randomly picked in the range [−2.5, 1.5], the trials randomly shuffled and the reliability score recalculated. By repeating this process 1,000 times, a null distribution of the reliability time series was constructed. A neuron was reliable if the unshuffled reliability time series exceeded the null distribution by 1.5 standard deviations (z-score > 1.5). Using this method, we were able to calculate a significant reliability trace for each neuron and for each stimulus condition.
Classification of cells into persistent and reliable.
The method described above allowed us to extract reliability scores (max in the delay period). In the PFC RS and MD populations, we noticed a bimodal distribution of reliability scores – with some neurons responding with high trial-to-trial spiking in the delay period (transient) and others responding with low reliability (persistent). To formally classify these cells, we used the expectation-maximization algorithm (python sklearn package) to fit a Gaussian mixture model to the reliability histogram. This procedure was run separately for PFC RS, FS and MD neurons. The goodness of fit of the Gaussian was assessed using the Bayes Information Criterion (BIC). Separability of the resulting gaussians was assessed by ROC analysis. PFC RS and MD populations had separable gaussians and passed the Hartigan’s dip-test for bimodality. In these populations, we classified cells as transient if they were within 95% CI of the mean of the high reliability Gaussian model. Cells were classified as persistent if they were within the 95% CI of the mean of the low reliability Gaussian model. This method allowed us to robustly classify neurons without the need to define an arbitrary threshold.
Classification of cells into cue-selective or cue-invariant.
Using the reliability time series across the delay period, we computed a cross-correlogram for all pairs of conditions (6-way comparison). Neurons with significant correlation with lags within +/− 50 ms were scored. A neuron was classified as cue-selective if it had a significant reliability event for only one out of the four stimulus conditions. A neuron was classified as mixed-selective if it had a significant reliability event for two out of the four stimulus conditions. We never found neurons in either the MD or PFC with significant reliability in more than two conditions (except for randomized cueing experiments).
To further assess the tuning strength of PFC neurons, we first sampled trials with replacement to calculate an estimate of d-prime for either cues or rules for each cell. Second, we also computed a bootstrapped value of the reliability of that cell. We defined the tuning strength as the slope of the regression line between reliability and d-prime. As such, a neuron with high reliability and high d-prime had a higher tuning strength value, indicating that this neuron was strongly selective to a cue. We used this tuning strength metric to better define cue-invariant neurons. Cue-invariant, rule-selective neurons should respond to both cues that map onto the same rule. Hence, we calculated the selectivity angle for each pair of cues corresponding to the same rule using the formula 6:
Neurons with selectivity angle of 45 degrees had the same tuning strength for both cues in the same rule and were hence classified as cue-invariant. Therefore, we used a hierarchical selection process to classify cue-invariant cells: (1) the significant reliability time series for cues 1 and 2 of rule A must be correlated within a lag of 50 ms; (2) the selectivity angle must be close to 45 degrees. Since MD and PFC FS neurons were weakly reliable, we calculated their selectivity using trial-averaged firing rates instead. In this way, MD and FS neurons were classified as context selective if (1) they had correlated responses for both cues within a context and (2) they had a within context selectivity angle was also close to 45 degrees. Each of these measures were tested for significance using a permutation test where hybrid data were created by shuffling trial labels.
Calculating contextual modulation index.
We assessed the contextual modulation index (CMI) of the trial-averaged firing rate of a neuron using the following formula:
As such, because the firing rate is non-negative, CMI ∈ [+1, −1]. To determine significance, we calculated the CMI for two hybrid spike trains created by randomly shuffling trial labels from 1,000 iterations. This created a null distribution. A cell was considered significantly contextually modulated if the unshuffled CMI was outside the 95% confidence interval of the shuffled CMI (p < 0.05, two-tailed Student’s t-test).
Decoding analysis.
Trial-by-trial classification analysis was performed using a Support Vector Machine (SVM) implemented through LIBSVM and the Matlab Neural Decoding Toolbox 57. The firing rates of neurons on each trial from the entire population (pooled across sessions) was first smoothed using a 20 ms-wide gaussian filter. The SVM classifier with a Gaussian radial basis function kernel was then trained on 60% of the data (randomly selected) while 40% of the data was used for prediction. This classifier works by first constructing an optimal hyperplane based on labelled training data and then generating predictions of the labels on testing data. Accuracy of the decoding was assessed by comparing the predicted labels to the actual labels. Classification accuracy was also quantified by computing the mutual information via the following equation:
where pij is the probability of observing label i (cue, rule or context), given that the original label is j. This classification process was repeated 1,000 times to obtain and accurately estimate the error of the classification accuracy.
To test the dependence of the number of neurons on classification, we used a Monte Carlo sampling technique (repeated 500 times) to pick n neurons (range, 1 to population size) at random from the population with replacement. The single-trial responses from these n neurons were compared to the template as described above.
Generalized linear model (GLM).
We modelled the spike trains of neurons using a generalized linear model (GLM) 31,32,58. The spike trains were discretized (Δ) into 5 ms bins. As explained elsewhere 59, the log-likelihood for a single neuron (up to an additive constant) is given by the formula:
Where φ(t) is the instantaneous spike rate (conditional intensity) of the fully coupled GLM:
In this equation, k is the weights on the stimulus covariates (akin to a receptive field); h is the postsynaptic weights that integrate the neuron’s own spiking history; c is the coupling weights (filters) on other simultaneously recorded spikes (s). In the uncoupled model, we ignored this coupling term. To avoid overfitting, regression weights were fit with a maximum a posteriori estimate with an L2 penalty. Matlab scripts used to build the GLM can be found here: https://github.com/pillowlab/neuroGLM.
These coupling filters are analogous to the positive lag of a cross-correlogram with the additional benefit of accounting for the response variance that is not already explained by the cue and other task-relevant variables. In other words, each neuron produces a coupling filter, that when convolved with the spike train of that neuron, explains part of the variance of the neuron being modeled. Mathematically, this operation can be written as:
Where m is the number of simultaneously recorded neurons and are temporal basis functions that we assumed to be nonlinearly time-scaled raised cosine functions 32. In each session, the GLM was constructed using a median of 25 PFC and 18 MD neurons with well isolated units.
To statistically validate these coupling filters, we randomized both neuronal labels and trial order, and used leave-one-neuron-out cross validation 60. This allowed us to determine the probability of a coupling being significant above chance levels. We also calculate the coupling strength as the integral (area under the curve) of each coupling filter. Because each neuron can receive many coupling filters, we used a dimensionality reduction (SVD) to determine the most common filter shapes (i.e. those that explained the largest fraction of variance). It is important to note here that we fit each GLM in an unbiased manner and determined the most significant couplings based on shuffling. In cases where we tested the effect of removing certain filters on predicting the firing rate of neurons, we first fit a model to 80% of the trials, set the necessary filter components to 0, and then used that model to predict the remaining 20% of the trials. We computed explained variance (EV) using the following formula: . We repeated this procedure 100 times. In this way, we do not bias the other terms of the model by removing terms before performing the regression.
We derived a Filter Similarity Index to determine how inputs to a neuron changed as the animal switched from one context to another. First, we used the behavioral model (see section on trial selection above) to determine trials in which choice behavior was stable in each context. Using these trials, we derived coupling filters: (1) between PFC cue selective cells, (2) from PFC cue-selective cells to MD cells, and (3) from PFC cue selective cells to PFC invariant cells. We refer to these filters as stable input filters. Next, we re-fit the GLM on a trial-to-trial basis from 10 trials before the switch to 10 trials after the switch and extracted single-trial input filters. The Filter Similarity Index is the Pearson’s correlation coefficient between the single trial coupling filter and the stable coupling filter in each context. In particular, for cells preferring the second context, we report the correlation coefficients between the single trial input filters and the stable filter in the second context. This analysis allowed us to visualize the remapping of intra-cortical and cortico-thalamic inputs as mice switched from one cueing context to another. We defined the filter stabilization latency as the trial number at which the correlation coefficient between the single trial coupling filter and the stable coupling filter in each context is significantly above chance levels.
For clustering analysis in Figure 4d, we quantified the shape of the filter using a filter score. For filters with a larger inhibitory magnitude, the filter score was the signed area under the curve of the inhibitory component. For filters with a larger excitatory magnitude, the filter score was the area under the curve of the positive component. In this way, negative filter scores correspond to MD neurons that exert an inhibitory effect on their targets, while positive filters scores correspond to MD neurons that exert an excitatory effect on their targets.
Model to explain MD responses.
We constructed a simple model to determine if, and how, MD neurons derive their contextual selectivity from PFC cue-selective neurons (Supplementary Fig. 7). To do so, we first generated a population of 1,000 Poisson spiking units with transient elevations that spanned the duration of the delay period (50 ms peak spacing). These model neurons mimicked, for example HP and LP selective neurons in the PFC, with the aim of predicting the responses of the auditory cueing context selective MD cells. For each model PFC neuron, we computed a PSTH. Each PSTH was then convolved with the PFC-MD input kernel (described above). This convolved output was then weighted and summed. We then used a least squares method to determine the best fit model that could explain the trial-averaged firing rate of either persistent or transient MD neurons. For persistent MD neurons, weights were almost uniformly distributed over all PFC inputs, suggesting that their inputs were not temporally selective. In contrast, transient MD neurons weighted inputs from co-tuned PFC neurons more strongly, suggesting that they receive temporally-selective inputs from these co-tuned cue-selective neurons.
Computational Modeling.
We use a recurrently connected reservoir of 1000 rate neurons to model the PFC. The rate of each neuron indexed by is given as a function of its input Ii as ri = tanh(Ii) if Ii > 0, and = 0 otherwise. The input consists of cue input, recurrent input and MD gating together, filtered with a decaying exponential synapse with time constant τ = 20 ms, as
cuek is a vector of length equal to the number of possible cues (corresponding to HP and LP noise, UV and green LED flash). It has entries 1 for cues that are on at the current time and 0 for those off. The input weights are set such that each cue k stimulates a set of 200 neurons, disjoint with the sets for other cues, with each weight chosen uniformly between 0.75 and 1.5. wij is set as a Gaussian-distributed variable with mean zero and standard deviation , and then the mean is subtracted across each row of the matrix. is a vector representing the activity of MD neurons with dimensionality equal to the number of contexts. We set the entry for the current context to 1 and the rest to 0. is set to −10 for those neurons that are not stimulated by cues belonging to context l, and to 0 for those that do, effectively suppressing activity of context-irrelevant neurons. μi mediates the multiplicative effect of the MD on the total recurrent input to neuron i, and is given by:
is set to 8 if neuron is one of the neurons stimulated by cues belonging to context m, else it is set to 0, effectively enhancing the recurrent input for context-relevant neurons. Note that all sums run over all the full range of the summed indices.
When simulating the PFC-only network, we set all to zero and all to 2, effectively removing all context-specific suppression and enhancement. The model included two output neurons – the first corresponding to attend to audition and the second to attend to vision, receiving input from the PFC as
with output if , and = 0 otherwise. is initialized to zero, and is plastic evolving as
where τw = 200 s, and the instantaneous error ϵn in output n is defined in terms of the target output which is cue-specific as below. Learning on the output weights is on throughout the simulations.
Each task was simulated as a run of 1000 cycles of context 1 (block 1), followed by 1000 cycles of context 2 (block 2) and then again followed by 200 cycles of context 1 (block 3). Each cycle consists of 2 trials of cue = (1,0,0,0) and cue = (0,1,0,0) during context 1, and of 2 trials of cue = (1,0,0,0) and cue = (0,1,0,0) during context 2, in random order within each cycle, for the experimental linearly separable task, representing high-pass and low-pass noise and UV and green LED flash respectively. The target output for these cues is (1,0), (0,1), (1,0), and (0,1) respectively. The two longer blocks allowed the network to learn the two contextual tasks sequentially, while the shorter third block served to test the ability of the network to recall the first context.
Similarly, for the XOR task, each cycle consists of equal to 4 trials of cue equal to (0,0,0,0), (0,1,0,0), (1,0,0,0) and (1,1,0,0) during context 1, and (0,0,0,0), (0,0,0,1), (0,0,1,0) and (0,0,1,1) during context 2, in random order. These must map to target output equal to (1,0) if only one of the cues in a context is active and to (0,1) if none or both are active.
Each trial consists of a 100 ms-long cue presentation followed by 100 ms of delay period when (0,0,0,0) is presented. The target output is maintained throughout the trial for plasticity of the output weights, and the mean squared error is computed over the full trial and across the two outputs.
Statistical Testing.
All data in this paper is pooled from 5 mice (optical perturbation 3 mice). No statistical tests were done to determine the sample size, but our sample sizes are similar to those reported in previous publications (ref 17, 23). Note, data collection and analysis were not performed blind to the conditions of the experiments.
Data were first tested for normality using the Shapiro–Wilk test. All data presented in this paper are nonnormally distributed; thus, all statistical tests were conducted using nonparametric statistics. Our experiments involved testing the influence of different conditions (cues, optical manipulations, etc.) on the same population of neurons; thus, all comparisons were performed using nonparametric repeated-measures ANOVA (Friedman test) with Bonferroni’s correction for multiple comparisons. Comparisons between independent measures was performed using the nonparametric Kruskal-Wallis ANOVA. For Bonferroni corrections, the significance value was set to 0.05. Post hoc tests were performed using the two-tailed signed-rank test (for repeated measures) or the Wilcoxon rank-sum test for independent measures. All other statistical tests that were performed are described in the text. The 95% CIs were computed by bootstrapping.
Supplementary Material
Acknowledgments
We thank Ralf D. Wimmer for help with experiments, and members of the Halassa Lab for technical assistance and discussions. We would also like to thank Wulfram Gerstner, Michale Fee, Earl Miller and Matthew Wilson for helpful discussions, and Jonathan W. Pillow and David Zlotowski for advice on the GLM model. This work was supported by grants from the National Institutes of Health, the Brain and Behavior, Klingenstein, Pew and Simons Foundations as well as the Human Frontiers Science Program to MMH, and the German Ministry of Education to AG through Raoul Memmesheimer.
Footnotes
Competing interests
Authors declare no competing interests
Code availability
All Matlab and python scripts used to analyses the data will be deposited on Github Github (https://github.com/toxine4610/ThalamusContextSwitchingCode), and (https://github.com/adityagilra/PFC_MD_weights_stability).
Data availability
All data are available from the corresponding author upon reasonable request.
References
- 1.Richter FR & Yeung N Memory and cognitive control in task switching. Psychol. Sci 23, 1256–63 (2012). [DOI] [PubMed] [Google Scholar]
- 2.Hanks TD & Summerfield C Perceptual Decision Making in Rodents, Monkeys, and Humans. Neuron 93, 15–31 (2017). [DOI] [PubMed] [Google Scholar]
- 3.Stokes MG mfl. Dynamic coding for cognitive control in prefrontal cortex. Neuron 78, 364–75 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Dias R, Robbins TW & Roberts AC Dissociation in prefrontal cortex of affective and attentional shifts. Nature 380, 69–72 (1996). [DOI] [PubMed] [Google Scholar]
- 5.Miller EK & Cohen JD An integrative theory of prefrontal cortex function. Annu. Rev. Neurosci 24, 167–202 (2001). [DOI] [PubMed] [Google Scholar]
- 6.Inagaki HK, Inagaki M, Romani S & Svoboda K Low-Dimensional and Monotonic Preparatory Activity in Mouse Anterior Lateral Motor Cortex. J. Neurosci 38, 4163–4185 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Noonan MP, Crittenden BM, Jensen O & Stokes MG Selective inhibition of distracting input. Behav. Brain Res (2017). doi: 10.1016/j.bbr.2017.10.010 [DOI] [PubMed] [Google Scholar]
- 8.Weinberger DR & Berman KF Prefrontal function in schizophrenia: confounds and controversies. Philos. Trans. R. Soc. Lond. B. Biol. Sci 351, 1495–503 (1996). [DOI] [PubMed] [Google Scholar]
- 9.Woodward ND, Karbasforoushan H & Heckers S Thalamocortical dysconnectivity in schizophrenia. Am. J. Psychiatry 169, 1092–9 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kirkpatrick J mfl. Overcoming catastrophic forgetting in neural networks. Proc. Natl. Acad. Sci. U. S. A 114, 3521–3526 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hassabis D, Kumaran D, Summerfield C & Botvinick M Neuroscience-Inspired Artificial Intelligence. Neuron 95, 245–258 (2017). [DOI] [PubMed] [Google Scholar]
- 12.Sakai K & Passingham RE Prefrontal interactions reflect future task operations. Nat. Neurosci 6, 75–81 (2003). [DOI] [PubMed] [Google Scholar]
- 13.Miller EK & Buschman TJ Cortical circuits for the control of attention. Curr. Opin. Neurobiol 23, 216–22 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Buschman TJ & Miller EK Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices. Science 315, 1860–2 (2007). [DOI] [PubMed] [Google Scholar]
- 15.Buschman TJ & Miller EK Goal-direction and top-down control. Philos. Trans. R. Soc. Lond. B. Biol. Sci 369, (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Spaak E, Watanabe K, Funahashi S & Stokes MG Stable and Dynamic Coding for Working Memory in Primate Prefrontal Cortex. J. Neurosci 37, 6503–6516 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schmitt LI mfl. Thalamic amplification of cortical connectivity sustains attentional control. Nature 545, 219–223 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bolkan SS mfl. Thalamic projections sustain prefrontal activity during working memory maintenance. Nat Neurosciadvance on, (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Parnaudeau S mfl. Mediodorsal thalamus hypofunction impairs flexible goal-directed behavior. Biol. Psychiatry 77, 445–53 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rikhye RV, Wimmer RD & Halassa MM Toward an Integrative Theory of Thalamic Function. Annu. Rev. Neurosci (2018). doi: 10.1146/annurev-neuro-080317-062144 [DOI] [PubMed] [Google Scholar]
- 21.Mitchell AS & Chakraborty S What does the mediodorsal thalamus do? Front. Syst. Neurosci 7, 37 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Marton T, Seifikar H, Luongo FJ, Lee AT & Sohal VS Roles of prefrontal cortex and mediodorsal thalamus in task engagement and behavioral flexibility. J. Neurosci (2018). doi: 10.1523/JNEUROSCI.1728-17.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wimmer RD mfl. Thalamic control of sensory selection in divided attention. Nature 526, 705–9 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Braver TS, Reynolds JR & Donaldson DI Neural mechanisms of transient and sustained cognitive control during task switching. Neuron 39, 713–26 (2003). [DOI] [PubMed] [Google Scholar]
- 25.Shipp S The brain circuitry of attention. Trends Cogn. Sci 8, 223–30 (2004). [DOI] [PubMed] [Google Scholar]
- 26.Bruno RM & Simons DJ Feedforward mechanisms of excitatory and inhibitory cortical receptive fields. J. Neurosci 22, 10966–75 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Diester I & Nieder A Complementary contributions of prefrontal neuron classes in abstract numerical categorization. J. Neurosci 28, 7737–47 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Quirk MC, Sosulski DL, Feierstein CE, Uchida N & Mainen ZF A defined network of fast-spiking interneurons in orbitofrontal cortex: responses to behavioral contingencies and ketamine administration. Front. Syst. Neurosci 3, 13 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wallis JD, Anderson KC & Miller EK Single neurons in prefrontal cortex encode abstract rules. Nature 411, 953–6 (2001). [DOI] [PubMed] [Google Scholar]
- 30.Miller EK, Freedman DJ & Wallis JD The prefrontal cortex: categories, concepts and cognition. Philos. Trans. R. Soc. Lond. B. Biol. Sci 357, 1123–36 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yates JL, Park IM, Katz LN, Pillow JW & Huk AC Functional dissection of signal and noise in MT and LIP during decision-making. Nat. Neurosci 20, 1285–1292 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Park IM, Meister MLR, Huk AC & Pillow JW Encoding and decoding in parietal cortex during sensorimotor decision-making. Nat. Neurosci 17, 1395–403 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Parnaudeau S, Bolkan SS & Kellendonk C The Mediodorsal Thalamus: An Essential Partner of the Prefrontal Cortex for Cognition. Biol. Psychiatry 83, 648–656 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mitchell AS & Chakraborty S What does the mediodorsal thalamus do? Front. Syst. Neurosci 7, 37 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ferguson BR & Gao W-J Thalamic Control of Cognition and Social Behavior Via Regulation of Gamma-Aminobutyric Acidergic Signaling and Excitation/Inhibition Balance in the Medial Prefrontal Cortex. Biol. Psychiatry 83, 657–669 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Delevich K, Tucciarone J, Huang ZJ & Li B The mediodorsal thalamus drives feedforward inhibition in the anterior cingulate cortex via parvalbumin interneurons. J. Neurosci 35, 5743–53 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kim HR, Hong SZ & Fiorillo CD T-type calcium channels cause bursts of spikes in motor but not sensory thalamic neurons during mimicry of natural patterns of synaptic input. Front. Cell. Neurosci 9, 428 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Masse NY, Grant GD & Freedman DJ Alleviating catastrophic forgetting using context-dependent gating and synaptic stabilization. (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Enel P, Procyk E, Quilodran R & Dominey PF Reservoir Computing Properties of Neural Dynamics in Prefrontal Cortex. PLoS Comput. Biol 12, e1004967 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Maass W, Natschläger T & Markram H Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comput. 14, 2531–60 (2002). [DOI] [PubMed] [Google Scholar]
- 41.Haykin S Neural Networks and Learning Machines. (2008). [Google Scholar]
- 42.Minsky M & Papert SA Perceptrons: an introduction to computational geometry. (MIT press, 2017). [Google Scholar]
- 43.Movshon JA, Thompson ID & Tolhurst DJ Spatial summation in the receptive fields of simple cells in the cat’s striate cortex. J. Physiol 283, 53–77 (1978). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Muhammad R, Wallis JD & Miller EK A comparison of abstract rules in the prefrontal cortex, premotor cortex, inferior temporal cortex, and striatum. J. Cogn. Neurosci 18, 974–89 (2006). [DOI] [PubMed] [Google Scholar]
- 45.Guillery RW & Sherman SM Thalamic relay functions and their role in corticocortical communication: generalizations from the visual system. Neuron 33, 163–75 (2002). [DOI] [PubMed] [Google Scholar]
- 46.Yang GR, Murray JD & Wang X-J A dendritic disinhibitory circuit mechanism for pathway-specific gating. Nat. Commun 7, 12815 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Tremblay R, Lee S & Rudy B GABAergic Interneurons in the Neocortex: From Cellular Properties to Circuits. Neuron 91, 260–92 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Groh A mfl. Convergence of cortical and sensory driver inputs on single thalamocortical cells. Cereb. Cortex 24, 3167–79 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Jaramillo J, Mejias JF & Wang X-J Engagement of pulvino-cortical feedforward and feedback pathways in cognitive computations. bioRxiv (2018). doi: 10.1101/322560 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Imamizu H mfl. Explicit contextual information selectively contributes to predictive switching of internal models. Exp. brain Res 181, 395–408 (2007). [DOI] [PubMed] [Google Scholar]
Methods-only references
- 51.Liang L mfl. Scalable, Lightweight, Integrated and Quick-to-Assemble (SLIQ) Hyperdrives for Functional Circuit Dissection. Front. Neural Circuits 11, 8 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Berndt A mfl. Structural foundations of optogenetics: Determinants of channelrhodopsin ion selectivity. Proc. Natl. Acad. Sci. U. S. A 113, 822–9 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Gradinaru V, Thompson KR & Deisseroth K eNpHR: a Natronomonas halorhodopsin enhanced for optogenetic applications. Brain Cell Biol. 36, 129–39 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Akrami A, Kopec CD, Diamond ME & Brody CD Posterior parietal cortex represents sensory history and mediates its effects on behaviour. Nature 554, 368–372 (2018). [DOI] [PubMed] [Google Scholar]
- 55.Chung JE mfl. A Fully Automated Approach to Spike Sorting. Neuron 95, 1381–1394.e6 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Bayati H, Davoudi H & Fatemizadeh E A heuristic method for finding the optimal number of clusters with application in medical data. Conf. Proc. … Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. IEEE Eng. Med. Biol. Soc. Annu. Conf. 2008, 4684–7 (2008). [DOI] [PubMed] [Google Scholar]
- 57.Meyers EM The neural decoding toolbox. Front. Neuroinform 7, 8 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Pillow JW mfl. Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature 454, 995–9 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Pillow JW, Paninski L, Uzzell VJ, Simoncelli EP & Chichilnisky EJ Prediction and decoding of retinal ganglion cell responses with a probabilistic spiking model. J. Neurosci 25, 11003–13 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Yu BM mfl. Gaussian-process factor analysis for low-dimensional single-trial analysis of neural population activity. J. Neurophysiol 102, 614–35 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


