Abstract
Radiotherapy is one of the most important cancer treatments, but its response varies greatly among individual patients. Therefore, the prediction of radiosensitivity, identification of potential signature genes, and inference of their regulatory networks are important for clinical and oncological reasons. Here, we proposed a novel multiple genomic fused partial least squares deep regression method to simultaneously analyze multi-genomic data. Using 60 National Cancer Institute cell lines as examples, we aimed to identify signature genes by optimizing the radiosensitivity prediction model and uncovering regulatory relationships. A total of 113 signature genes were selected from more than 20,000 genes. The root mean square error of the model was only 0.0025, which was much lower than previously published results, suggesting that our method can predict radiosensitivity with the highest accuracy. Additionally, our regulatory network analysis identified 24 highly important ‘hub’ genes. The data analysis workflow we propose provides a unified and computational framework to harness the full potential of large-scale integrated cancer genomic data for integrative signature discovery. Furthermore, the regression model, signature genes, and their regulatory network should provide a reliable quantitative reference for optimizing personalized treatment options, and may aid our understanding of cancer progress mechanisms.
Keywords: Multiple genomic data, integrated regression method, radiosensitivity, signature genes, gene regulatory network
Introduction
Radiotherapy is a major cancer treatment, but the radiosensitivity of different tumors or even the same type of tumor in different patients varies widely.1 Therefore, predicting the radiosensitivity of patients before radiation therapy, identifying underlying molecular signatures, and constructing their regulatory network have high clinical and oncological importance.
Radiosensitivity can be measured as the fraction of cells surviving a single 2 Gy dose of radiation (SF2), with high values indicating radiation resistance. While other methods are available to measure cellular radiation sensitivity in cell lines, SF2 is considered to be the gold standard and is supported by strong clinical evidence.2
Variations in mRNA expression values (GE), copy numbers, and other genomic patterns are thought to be the main underlying factors for different radiation responses. Accumulating large amounts of these data provides an effective but challenging way to predict the radiosensitivity of tumor cells.
Torres-Roca et al predicted the radiosensitivity of 35 human cell lines in a NCI-60 panel using a linear classifier of expression values of tens of genes selected by the significance analysis of microarrays (SAM) method in 2005.3 They developed a radiosensitivity index (RSI) as a biomarker of cellular radiosensitivity in 48 NCI-60 cancer cell lines in 2009. SF2 was the central criterion for both feature selection and final model training for RSI development. Ten of the selected ‘hub’ genes were then used to construct a linear prediction model of SF2.4 Additionally, Tewari et al investigated the feasibility of integrating an in vitro chemo-radiosensitivity assay with a gene microarray system,5 identifying 54 genes correlated with radiosensitivity using an integrated nearest neighbor model with Pearson correlation coefficient. Moreover, Amundson et al performed large-scale comparisons of gene expression variations in response to different doses (2, 5, and 8 Gy) of γ-ray radiation,6 and identified 22 genes that could discriminate the SF2 values of 63 cell lines (including NCI-60 and three other cell lines) between low and high groups.
Besides GE data, copy number variation (CNV) and methylation (ME) data are also related to radiosensitivity. Work by Moelans et al indicated that allelic loss and amplification at the 8p11-12 breakpoint region are associated with poor radiotherapy responses,7 while Zhu et al reported a pivotal role for DNA ME in tumor radiosensitivity.8
Unfortunately, none of the individual types of genomic data thoroughly capture the complexity of the cancer genome or precisely pinpoint the cancer-driving mechanism.9 Additionally, it has become increasingly clear that the integrative analysis of multi-omic data types can aid the search for potential “drivers” by uncovering genomic features dysregulated by multiple mechanisms.10 More importantly, true oncogenic mechanisms are more visible when combining evidence across patterns of alterations in DNA CNV, ME, GE and mutational profiles.11,12 A well-known example is the HER2 oncogene that can be activated through DNA amplification and mRNA over-expression.9 Therefore, the development of tumor molecular analysis using multiple genomic data may lead to a more comprehensive prediction of molecular signatures.
No widely accepted threshold exists between radiation-sensitive or -resistant phenotypes and SF2 values from 0 to 1. Therefore, instead of roughly dividing cell lines into different groups by subjective cutoffs of SF2 values, it may be more useful to consider a regression issue for continuous variables of SF2. To this end, we propose a novel integrated multiple genomic data regression method for SF2 prediction, focusing on identifying signature genes for functional and genetic network analysis, rather than “hotspot” or “hot-loci” from GE, CNV, and ME data.13,14
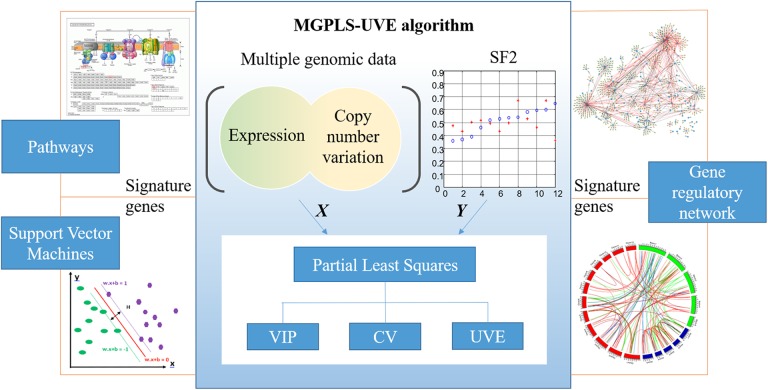
Studying the gene regulatory network (GRN) structure provides important insights into the mechanisms of complex diseases.15,16 Several studies have shown that gene expression is influenced not only by the expression of other genes but also by CNV or other biological variations.17 Therefore, it is also necessary to infer GRN using multi-genomic data. Correspondingly, the aims of this study were two-fold: 1) to identify signature genes strongly associated with radiosensitivity from fused multiple genomic data to further corroborate and expand the evidence of radiosensitivity-associated signature genes in the prediction of radioresponses; and 2) to uncover regulatory relationships among identified signatures using fused multiple genomic data, employing least absolute shrinkage and selection operator (LASSO) regression based on coordinate descent algorithms to construct GRN. Figure 1 shows the study outline.
Figure 1.
The overall structure of this paper. Based on the fact that the current standard approaches rely on separate mono-genomics data analyses followed by manual integration, multiple genomic data fused regression approach (MGPLS) is proposed to identifying signature genes. MGPLS method can analysis all data types simultaneously using a single integrated regression model as well as eliminating noise effects. VIP: variable importance on projection; CV: cross-validation; UVE: uninformative variable elimination.
Materials and Methods
Datasets
GE, CNV, and ME data of NCI-60 cell lines were downloaded from (https://discover.nci.nih.gov/cellminer/loadDownload.do). GE data were collected via five platforms (Affymetrix: HG-U95, HG-U133, HG-U133 Plus 2.0, HG Exon 1.0 ST; and Agilent: Whole Human Genome Oligo array).18 CNV data were collected via four different platforms (Agilent Human Genome CGH Microarray 44A, Nimblegen HG19 CGH 385K WG Tiling v2.0, Affymetrix GeneChip Human Mapping 500k Array Set, and Illumina Human1Mv1_C Beadchip).19 ME data were collected using the Infinium HumanMethylation450 BeadChip Kit platform. The measured SF2 values of corresponding cell lines were collected from the study of Eschrich et al4 and are listed in Table 1.
Table 1.
Measured and predicted SF2 values for NCI-60 cell lines
| Cell line | Measured SF2 | Predicted SF2(MGPLS) | Predicted SF2(SVM) | Error(MGPLS) | Error(SVM) |
|---|---|---|---|---|---|
| CNS:U251 | 0.57 | 0.568 | 0.57 | 0.002 | 0 |
| OV:OVCAR-4 | 0.29 | 0.293 | 0.291 | -0.003 | -0.001 |
| LE:CCRF-CEM | 0.185 | 0.180 | 0.186 | 0.005 | -0.001 |
| CNS:SNB-19 | 0.43 | 0.425 | 0.43 | 0.005 | 0 |
| RE:SN12C | 0.62 | 0.611 | 0.618 | 0.009 | 0.002 |
| BR:T-47D | 0.52 | 0.531 | 0.52 | -0.011 | 0 |
| RE:ACHN | 0.72 | 0.707 | 0.722 | 0.013 | -0.002 |
| LE:HL-60(TB) | 0.315 | 0.335 | 0.319 | -0.020 | -0.004 |
| ME:MALME-3M | 0.8 | 0.779 | 0.797 | 0.021 | 0.003 |
| ME:SK-MEL-5 | 0.72 | 0.697 | 0.72 | 0.023 | 0 |
| OV:OVCAR-8 | 0.6 | 0.572 | 0.597 | 0.028 | 0.003 |
| ME:UACC-257 | 0.48 | 0.510 | 0.48 | -0.030 | 0 |
| ME:SK-MEL-28 | 0.74 | 0.709 | 0.737 | 0.031 | 0.003 |
| LE:RPMI-8226 | 0.1 | 0.069 | 0.1 | 0.031 | 0 |
| PR:DU-145 | 0.52 | 0.488 | 0.52 | 0.032 | 0 |
| BR:HS 578T | 0.79 | 0.757 | 0.79 | 0.033 | 0 |
| CO:HCT-15 | 0.4 | 0.435 | 0.4 | -0.035 | 0 |
| CO:HCT-116 | 0.38 | 0.418 | 0.38 | -0.038 | 0 |
| PR:PC-3 | 0.484 | 0.445 | 0.486 | 0.039 | -0.002 |
| LC:EKVX | 0.7 | 0.660 | 0.694 | 0.040 | 0.006 |
| OV:OVCAR-5 | 0.408 | 0.452 | 0.409 | -0.044 | -0.001 |
| RE:TK-10 | 0.52 | 0.475 | 0.522 | 0.045 | -0.002 |
| LE:K-562 | 0.05 | 0.100 | 0.054 | -0.050 | -0.004 |
| OV:NCI/ADR-RES | 0.57 | 0.520 | 0.572 | 0.050 | -0.002 |
| CNS:SNB-75 | 0.55 | 0.602 | 0.55 | -0.052 | 0 |
| ME:M14 | 0.42 | 0.477 | 0.42 | -0.057 | 0 |
| ME:UACC-62 | 0.52 | 0.461 | 0.519 | 0.059 | 0.001 |
| OV:OVCAR-3 | 0.55 | 0.491 | 0.548 | 0.059 | 0.002 |
| LC:NCI-H322M | 0.65 | 0.587 | 0.65 | 0.063 | 0 |
| RE:UO-31 | 0.62 | 0.686 | 0.619 | -0.066 | 0.001 |
| CO:COLO 205 | 0.69 | 0.762 | 0.687 | -0.072 | 0.003 |
| OV:IGROV1 | 0.39 | 0.463 | 0.39 | -0.073 | 0 |
| LE:SR | 0.07 | 0.143 | 0.072 | -0.073 | -0.002 |
| CNS:SF-539 | 0.82 | 0.746 | 0.817 | 0.074 | 0.003 |
| BR:MCF7 | 0.576 | 0.500 | 0.574 | 0.076 | 0.002 |
| ME:SK-MEL-2 | 0.66 | 0.737 | 0.66 | -0.077 | 0 |
| RE:RXF 393 | 0.67 | 0.754 | 0.669 | -0.084 | 0.001 |
| LC:NCI-H522 | 0.43 | 0.344 | 0.431 | 0.086 | -0.001 |
| ME:LOX IMVI | 0.68 | 0.588 | 0.68 | 0.092 | 0 |
| LC:HOP-92 | 0.43 | 0.522 | 0.43 | -0.092 | 0 |
| CNS:SF-268 | 0.45 | 0.543 | 0.45 | -0.093 | 0 |
| ME:MDA-MB-435 | 0.1795 | 0.273 | 0.183 | -0.094 | -0.0035 |
| BR:BT-549 | 0.632 | 0.537 | 0.635 | 0.095 | -0.003 |
| ME:MDA-N | 0.45 | 0.352 | 0.449 | 0.098 | 0.001 |
| CNS:SF-295 | 0.73 | 0.631 | 0.73 | 0.099 | 0 |
| LE:MOLT-4 | 0.05 | 0.149 | 0.052 | -0.099 | -0.002 |
| RE:786-0 | 0.66 | 0.551 | 0.659 | 0.109 | 0.001 |
| LC:HOP-62 | 0.164 | 0.277 | 0.166 | -0.113 | -0.002 |
| CO:KM12 | 0.42 | 0.535 | 0.418 | -0.115 | 0.002 |
| LC:A549/ATCC | 0.61 | 0.730 | 0.61 | -0.120 | 0 |
| RE:A498 | 0.61 | 0.734 | 0.62 | -0.124 | -0.001 |
| CO:HCC-2998 | 0.44 | 0.572 | 0.439 | -0.132 | 0.001 |
| OV:SK-OV-3 | 0.9 | 0.767 | 0.894 | 0.133 | 0.006 |
| RE:CAKI-1 | 0.37 | 0.517 | 0.37 | -0.147 | 0 |
| CO:SW-620 | 0.62 | 0.473 | 0.622 | 0.147 | -0.002 |
| LC:NCI-H226 | 0.63 | 0.786 | 0.626 | -0.156 | 0.004 |
| LC:NCI-H460 | 0.84 | 0.671 | 0.835 | 0.169 | 0.005 |
| BR:MDA-MB-231 | 0.82 | 0.613 | 0.82 | 0.207 | 0 |
| CO:HT29 | 0.79 | 0.567 | 0.785 | 0.223 | 0.005 |
| LC:NCI-H23 | 0.086 | 0.315 | 0.0925 | -0.229 | -0.0065 |
* Cell lines sorted by multiple genomic data fused partial least square deep regression (MGPLS).
Data preprocessing
Before training the dataset, we performed the following preprocessing on the downloaded data:
Considering that there are only 3–4 samples per cancer type in the NCI-60 cell line panel, if the value of a gene is missing in one sample then it is absent from >25% of the samples of that cancer type. Therefore, these genes were removed from the analysis.
Common genes in all GE, CNV, and ME datasets were identified.
Because GEs and CNVs of genes that are strongly related to each other are more likely to contain less noise,19 they were selected using Pearson correlation coefficients (cutoff, 0.5).
GE, CNV, and ME data were respectively standardized with the Z-Score method for further regression analysis.
A multiple genomic data fused partial least square deep regression (MGPLS) method
Partial least squares (PLS) is a widely used algorithm for modeling relationships between sets of observed variables using latent variables. It comprises regression and classification tasks as well as dimension reducing and modeling.20 Instead of identifying hyperplanes of minimum variance between the response and independent variables, it finds a linear regression model by projecting the predicted variables (regression or classification labels) and the observed variables (fused GE, CNV, or ME values of genes in our case) to a new lower space.21 This is highly suited to the analysis of high-dimension, low-sample-size data in bioinformatics.
To integrate multiple genome data for improved regression performance, we proposed an MGPLS method:
Given the predictor matrix and the response matrix ,
| 1 |
where p = g + c + m, g is the number of variables in GE data, c is the number of variables in CNV data, and m is the number of variables in ME data.
MGPLS may be applied to cases where the aim is to describe the linear relationship between X and Y,
| 2 |
based on the basic latent variable decomposition:
| 3 |
| 4 |
where is the regression coefficient matrix, is the residual matrix, is the orthogonal latent variable (LV) matrix, and are loading matrices, and are residual matrices, and k is the number of LVs. According to the regular PLS, T is a linear transformation of X,
| 5 |
where is a matrix of weights.
From Eq.(1) and Eq.(5), it is obvious that
| 6 |
where ti is the ith LV (i.e., ith column of T), and wi is ith column of W. Hence, by the projection of the MGPLS algorithm, the p-dimensional X-space, consisting of GE, CNV, and ME, is integrated and compressed into the k-dimensional LV-space (k<<p in common cases) to remove the noise and the multi-collinearity of the raw data. This leads to a biased but lower variance estimate of the regression coefficients compared with the least squares method.22
The regression coefficient matrix B can be obtained as
| 7 |
where, in our case, SF2 is the response variable. As a result, the regression model of SF2 is a combination of GE, CNV, and ME, which means they are integrated at the raw data level. MGPLS incorporates principal component analysis and LV extraction together so that it can simultaneously analyze multiple genomic data using a single integrated regression model.
The measurement of regression/prediction performance
The root mean square error (RMSE) was used to evaluate the accuracy of the radiosensitivity prediction model:
| 9 |
where yi is the measured SF2 value of the ith cell line, is the corresponding predicted value, and n is the number of the samples. The smaller the RMSE value is, the closer the predicted values are to the real values. That is, smaller RMSE values represent a more accurate prediction model.
The identification of signature genes by optimizing SF2 regression accuracy
Because of the missing information on ME data (see Discussion), we only used GE and CNV data to complete our analysis. With integrated GE and CNV as the input matrix, real signature genes can be identified using MGPLS by optimizing the SF2 regression model. Considering the large number of variables (n=7622), two types of uninformative variable elimination (UVE) were processed iteratively to balance the calculating time and the prediction accuracy. To improve the modeling accuracy, 10 6-fold cross-validation methods were used for model training as shown in Figure 2. The details of the MGPLS-UVE algorithm and corresponding pipeline are available in the Supplementary material.
Figure 2.
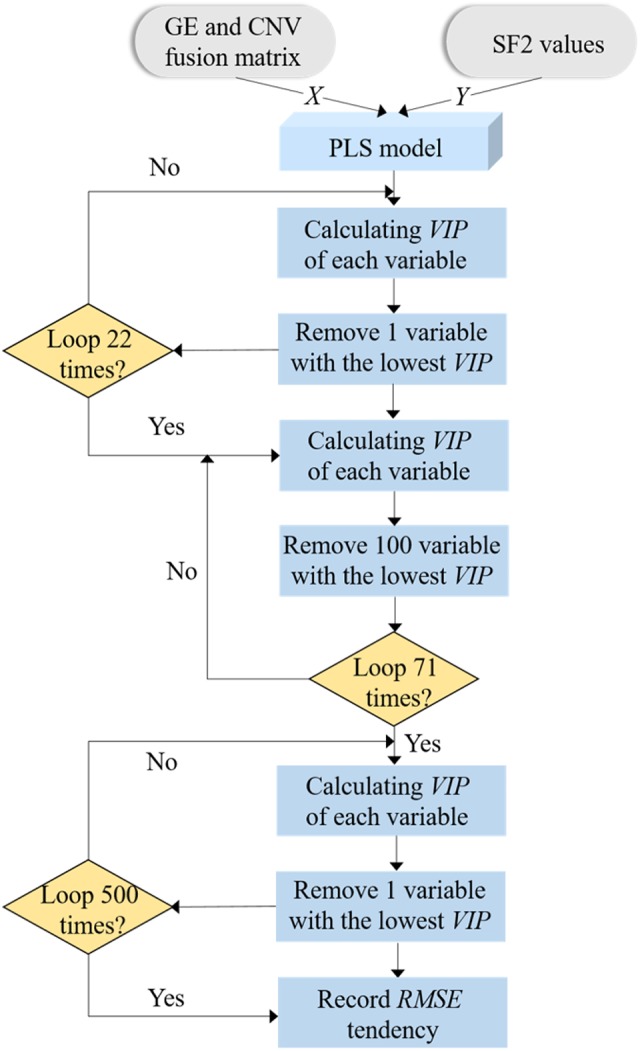
Flow chart of signature genes selection using GE and CNV data. MGPLS-UVE algorithm with 10 times of 6-fold cross-validation is employed to select the genes with the stably highest contribution to SF2 predicting model. There are 7622 variables at the beginning and 500 variables are left after MGPLS rough selection.
Support vector machine (SVM)
SVM is a supervised machine learning method used for classification and regression analysis. The key concept is to non-linearly map input vectors to a very high-dimension feature space Z, where a linear decision surface is constructed with special properties that ensure the high generalization ability of the model.23 This is usually conducted by the “kernel function” trick. The final estimated regression line (or hyperplane) can be constructed only by considering a small amount of the training data, i.e., the so-called support vectors. For the same set of data, SVM with nonlinear kernels can achieve a better fitting accuracy than linear methods such as PLS. In this study, SVM regression was implemented using a “LIBSVM” MATLAB package.24
Gene Ontology (GO) and Kyoto Encyclopedia of Genes and Genomes Pathway (KEGG) analysis
The GO knowledgebase is the largest source of information worldwide regarding gene function. It provides a comprehensive, computational model of biological systems, ranging from the molecular to the organic level, across the multiplicity of species in the tree of life.25
KEGG is a knowledgebase for the systematic analysis of gene functions at the molecular level in biological systems, from cells to organisms and ecosystems. It has been generated by genome sequencing and other high-throughput experimental technologies.26 Both GO and KEGG pathway enrichment analyses for all signature genes were performed using OmicShare tools, which is a free online platform for data analysis (www.omicshare.com/tools).
Sparse GRN inference based on the LASSO method
Let denote the matrix of GE data and denote the matrix of CNV data. If and where e i and c i are the ith row vector of matrices E and C, respectively, then the GRN is defined as follows:
| 10 |
where denote the ith row vectors of adjacency matrices and , respectively. The element represents the activation (positive) or deactivation (negative) weight of edge from jth gene to ith gene; is a model bias that can be removed by mean centered; and is a residual. Our goal is to estimate row vectors that minimize .
Eq.(10) can be rewritten in a least square minimization problem as:
| 11 |
where denotes 2 norm.
To obtain a sparse model and avoid overfitting, we added the L1 regularization term to Eq.(11) to make it a LASSO regression form as follows:
| 12 |
where s are penalty coefficients.
LASSO is a multivariate linear regression method. When there are many features and the number of samples is relatively small, LASSO can effectively avoid overfitting and obtain sparse solutions via an l 1-norm penalty.
There are two hypotheses in the model:
There is no self-regulation, i.e., the diagonal elements of the B matrix are all zero.
A gene can be directly regulated only by CNV for the gene itself not for other genes, i.e., only diagonal elements of the F matrix can be non-zero.
After obtaining adjacency matrices B and F, the genes with absolute values greater than 0.1 in B and F were selected. For a gene gi, other genes whose absolute values of regression coefficients were greater than 0.1 were selected as regulatory genes of gi. Table S1shows the steps of inferencing a spare GRN.
With the exception of KEGG and GO, all analyses were performed using MATLAB codes. The corresponding MATLAB toolkit, MGPLS-UVE, can be freely downloaded from our website https://www.clickgenome.org/papers/MGPLS.html. Further details of LASSO, GRN inference, and other methods and algorithms are included in the Supplementary materials.
Results
Identified signature genes and their SF2 prediction performance
According to the RMSE values obtained by different numbers of genes shown in Figure S1a, 113 genes corresponding to the smallest RMSE were selected as signature genes. The smallest RMSE obtained by these 113 genes means this gene set has the highest prediction performance or closest relationship to SF2. The gene names, Entrez gene IDs, and other detailed information of these 113 genes are listed in Table S2. Five (YY1AP1, INPP5A, DAP3, GON4L and JTB) of the 113 genes were highlighted because their CNV values were selected as signature variables while GE values of other genes were selected as signatures (known as CNV signatures for clarity). The other 108 genes were identified as GE signatures.
Using only the CNV values of the five CNV signatures and the GE values of the 108 GE signatures, the RMSE was optimized to 0.094 with MGPLS, a linear method. The corresponding predicted SF2s are listed in Table 1. The smallest difference between the measured and predicted SF2s of all 60 cell lines was 0.002 (CNS:U251), while the largest was 0.229 (LC:NCI-H23). The average error of the 60 cell lines was 0.075. Five cell lines (CNS:U251, OV:OVCAR-4, LE:CCRF-CEM, CNS:SNB-19, and RE:SN12C) had predicted errors <0.01 and the other 46 cell lines had predicted errors <0.1.
To improve their prediction accuracy, SVM with radial basis kernel function was explored to predict SF2 values with the CNV and GE of the 113 signature genes. The corresponding predicted SF2s are listed in Table 1. The RMSE value of the SVM prediction model was 0.0025. Twenty-two cell lines had differences between measured and predicted SF2s of 0. Only five cell lines had an absolute error >0.005 (LC:EKVX, OV:SK-OV-3, LC:NCI-H460, CO:HT29, and LC:NCI-H23).
GRN
The inference of GRN using these 113 genes was performed using the LASSO method to analyze regulatory relationships, as shown in Figure S2. Twenty-four genes with linkages >10 were selected as “hub” genes. Thus, these 24 “hub” genes can directly regulate the expression of at least 10 other genes. The GRN of the 24 “hub” genes is shown in Figure 3 and further details are listed in Table 2.
Figure 3.

Gene regulatory network among 24 “Hub” genes. The color of a gene (circle or triangle nodes) matches the color of its arrows to identify regulatory relationships between these genes more efficiently. There are two types of arrows: sharp arrows indicate the promotion of expression and blunt arrows mean the inhibition of expression. In addition, there are 12 genes (triangular nodes) whose CNV have a significant promoting effect on their respective expression process. They are SRRM1, PDCD2, RPL9, SNRPD1, ATP5A1, BLM, EWSRI, MIPEP, MCM3, MYB, CLNSIA and RPL34. it is worth noting that genes regulated by these 24 genes but not the “Hub” are not included in Figure 3.
Table 2.
Details of 24 “hub” genes
| Serial number | Gene name |
Entrez gene id | Chromosome | Cytoband | Regression coefficient |
Data type |
|---|---|---|---|---|---|---|
| 1 | ATP5A1 | 498 | 18 | 18q21 | 0.0114 | GE |
| 2 | BLM | 641 | 15 | 15q26.1 | -0.0033 | GE |
| 3 | CENPC | 1060 | 4 | 4q13.2 | -0.0009 | GE |
| 4 | CLNS1A | 1207 | 11 | 11q13.5-q14 | -0.0009 | GE |
| 5 | EWSR1 | 2130 | 22 | 22q12.2 | 0.0069 | GE |
| 6 | MCM3 | 4172 | 6 | 6p12 | 0.0007 | GE |
| 7 | MIPEP | 650794 | 13 | 13q12.11 | 0.0121 | GE |
| 8 | MYB | 4602 | 6 | 6q22-q23 | -0.0026 | GE |
| 9 | PDCD2 | 5134 | 6 | 6q27 | 0.0016 | GE |
| 10 | PRCC | 5546 | 1 | 1q21.1 | -0.0118 | GE |
| 11 | RPL9 | 6133 | 4 | 4p13 | -0.0028 | GE |
| 12 | RPL34 | 6164 | 4 | 4q25 | -0.0053 | GE |
| 13 | SMARCC1 | 6599 | 3 | 3p21.31 | -0.0110 | GE |
| 14 | SNRPD1 | 6632 | 18 | 18q11.2 | 0.0011 | GE |
| 15 | ZBTB39 | 9880 | 12 | 12q13.3 | -0.0039 | GE |
| 16 | DENND4B | 9909 | 1 | 1q21 | -0.0066 | GE |
| 17 | SRRM1 | 10250 | 1 | 1p36.11 | -0.0082 | GE |
| 18 | PAICS | 10606 | 4 | 4q12 | -0.0023 | GE |
| 19 | NISCH | 11188 | 3 | 3p21.1 | -0.0151 | GE |
| 20 | LRCH1 | 23143 | 13 | 13q14.11 | 0.0068 | GE |
| 21 | CNOT10 | 25904 | 3 | 3p22.3 | -0.0061 | GE |
| 22 | GAR1 | 54433 | 4 | 4q25 | -0.0041 | GE |
| 23 | MED28 | 80306 | 4 | 4p16 | -0.0066 | GE |
| 24 | SHPRH | 257218 | 6 | 6q24.3 | -0.0021 | GE |
Half of the 24 “hub” genes uncovered by GRN inference showed strong correlations between their own GE and CNV values (Figure 3). Corresponding Pearson correlation coefficients between GEs and CNVs are listed in Table S3, of which 12 out of 24 genes are >0.5.
Discussion
Variations in GE are thought to be the main underlying factors for different radiation responses, and several studies have attempted to correlate the relationship between radiation response and GE. Because ME and CNV are two of the main factors regulating GE, it is very important to take them into consideration.
The integration of multi-genomics data can compensate for the noise impact of mono-genomics data. This concept has been widely used in clustering and cancer subtype classification. For example, Hoadley et al27 used data on chromosome arm-level aneuploidy, DNA hypermethylation, mRNA and microRNA expression levels, and reverse-phase protein arrays to conduct comprehensive integrative molecular analyses of the Pan-Cancer Atlas to reclassify human tumors and provide future directions for exploring clinical prognosis in cancer treatment.
Additionally, because SF2 values range from 0 to 1 continuously, it is reasonable to predict the SF2 values of samples rather than to roughly classify them into sensitive or resistant groups. In this study, for the first time, we applied the concept of multi-genomic data integration analysis in regression issues using radiosensitivity prediction as an example.
In theory, all types of data can be processed simultaneously using a single integrated regression model. Indeed, ME values of more than 480,000 probes can be collected using the Illumina Infinium Human Methylation 450K BeadChip. However, available ME data for NCI-60 consists of fewer than 20,000 variables, representing the loss of 96% of useful ME information. Because raw ME data of the NCI-60 platform are missing and available preprocessed ME data are inadequate, the prediction performance is much worse with than without ME data (see Figure S1b). This was apparent from our prediction RMSE which was smaller using only GE and CNV data than using all GE, CNV, and ME data (0.094 vs. 0.170 for the linear model, respectively). Therefore, for the final SF2 prediction model, only GE and CNV data were used.
In our previous work (Zhang et al, 2014), we built a nonlinear SF2 prediction model for the NCI-60 panel using only GE data of 19,162 genes.28 The RMSE value was as low as only 0.011. To test whether multi-genomic data model could identify more essential signature genes, we herein used the same nonlinear method, SVM, to train a nonlinear SF2 model. The comparison results are summarized in Table 3. Clearly, regardless of whether a linear or nonlinear model is used, our RMSE values are notably smaller than those of Zhang et al (0.094 vs. 0.16 and 0.0025 vs. 0.011, respectively). These results indicate that our 113 signature genes are more useful at predicting radiosensitivity than the genes identified by our previous study.
Table 3.
RMSE comparison of different models.
| Linear method | Nonlinear method | ||||||
|---|---|---|---|---|---|---|---|
| Only GE | Only CNV | Multi-genomics | Only GE | Only CNV | Multi-genomics | ||
| This paper | 113 genes | 0.10 | 0.21 | 0.094 | 0.0031 | 0.015 | 0.0025 |
| 24 hub gene | 0.22 | 0.40 | 0.18 | 1.0 | |||
| Zhang et al | 0.16 | 0.011 | |||||
Previous work by Torres-Roca et al used the expression values of selected genes to predict SF2 values of NCI-60 cell lines (RMSE=0.20), then at a later date simplified this to a 10-hub-gene model to predict 12 independent cell lines (RMSE=0.38).3,4 Limited by the techniques available at the time, however, only GE data and some of the 60 cell lines were used. Additionally, two different types of cross-validations were employed to train the model. A comparison of these studies and our own would be unfair, so we instead compared the results obtained from fused multiple genomic data with those obtained from mono-genomic data. Correspondingly, RMSEs obtained using only GE or CNV values of 113 signature genes and 24 “hub” genes are shown in Table 3. The RMSE obtained using fused multiple genomic data is the smallest, indicating these data should be used to achieve the highest prediction performance or closest relationship to SF2.
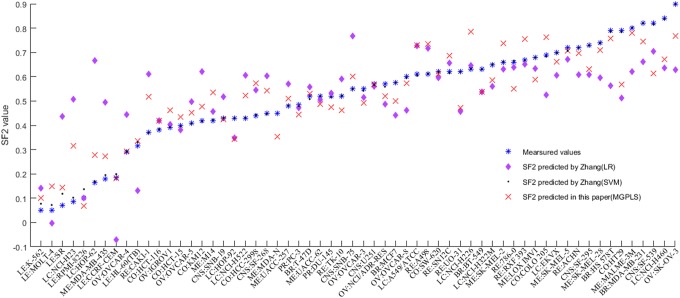
Because our data had only five CNV signatures among 113 genes, the predominance in the number of GE signatures resulted in the RMSE value of the GE-only model being just slightly worse than what was obtained using fused multiple genomic data. For the same reason, the RMSE value of the CNV-only model was much worse. The poor SF2 prediction performance of the “hub” genes is consistent with what we expected because they only number 24, which is one fifth the number of signature genes. Measured SF2 values and predicted values in different models for each cell line are shown in Figure 4.
Figure 4.
The measured and predicted SF2s of the 60 cell lines obtained using current signature genes and other published models. The measured and predicted SF2s of the 60 cell lines obtained using current signature genes and other published models.
Overfitting is almost unavoidable for cases with overwhelming high variable dimensions but small sample sizes, and our case is typical. Therefore, we attempted to overcome this in the present study as follows: 1) rather than the attempting the leave-one-out method used widely in small-sample cases, we employed 10 6-fold cross-validations in the training process; 2) we used the PLS method to reduce the original high variable dimension to a much lower LV dimension; 3) two types of UVE were processed iteratively to remove uninformative genes step by step rather than removing them in one step; and 4) we used LASSO to infer the GRN of identified signature genes because this is good at overcoming the overfitting problem in high-dimension small-sample cases.
Despite these methods, the number of samples remained extremely small compared with the number of variables, so we could not ensure that the overfitting problem was completely overcome. Therefore, molecular function analysis and pathway analysis were performed to verify the essentiality of identified signatures.
From our results, we can identify the absolute values of the regression coefficients of five CNV signatures (YY1AP1, INPP5A, DAP3, GON4L, and JTB) as the largest, suggesting that these CNV signature genes may be more useful than GE signatures in predicting radiosensitivity.
Several studies have found that some cellular functions enriched by 113 genes are closely associated with radiosensitivity29,30 or cancers such as breast cancer, lung cancer, bladder cancer, and leukemia.31-37. For example, SNX7 and PTK2 were also selected by our previous study. Gene set enrichment analysis coupled with genomic CNV assessment previously identified YY1AP1 as an oncogenic driver in hepatocellular carcinoma,38 while the fusion of EWSR1 with MYB promoted leukemia transformation by sustaining MYB expression and deregulating its target BCL2 or by fulfilling its own oncogenic potential.30,39 Additionally, BLM inactivation caused by CNV was reported to cause Bloom syndrome and increase the risk of cancer,40 while MCM3 is a potential biomarker for gastric cancer because of the strong correlation between its copy number and expression.41
According to our KEGG and GO analysis of all 113 genes shown in Figures S3 and S4, MLB, MCM3, MCM7, CDC47, POLD1, and ANAPC4 are associated with DNA replication and repair, and cell growth and death simultaneously, so they may be involved in cancer progression. Additionally, pathways involving signal transduction, focal adhesion, ErbB signaling, Wnt signaling, and vascular endothelial growth factor signaling also appear in our pathway enrichment results.
Conclusion
On the basis of the advantages of integrating multiple genomic data, we proposed a novel multiple genomic data fused partial least squares deep regression method (MGPLS), which we used to identify 113 signature genes closely related to radiosensitivity. We further inferred the GRN using GE and CNV data belonging to these signature genes. The joint regression method we propose provides a unified framework to analyze large-scale cancer genomic data. These findings provide a reliable quantitative reference for optimizing “personalized” treatment options, and might aid our understanding of cancer mechanisms.
Supplemental Material
Clean_Revised_Supplementary_material_(1) for A multiple genomic data fused SF2 prediction model, signature identification, and gene regulatory network inference for personalized radiotherapy by Qi-en He, Yi-fan Tong, Zhou Ye, Li-xia Gao, Yi-zhi Zhang, Ling Wang and Kai Song in Technology in Cancer Research & Treatment
Abbreviations
- CNV
copy number variation
- CV
cross-validation
- GE
gene expression
- GO
gene ontology
- GRN
gene regulatory network
- KEGG
Kyoto encyclopedia of genes and genomes
- LASSO
least absolute shrinkage and selection operator
- LV
latent variable
- ME
methylation
- MGPLS
multiple genomic data fused partial least square deep regression
- NCI
National Cancer Institute
- NIPALS
nonlinear iterative partial least squares
- PLS
partial least squares
- PRESS
predictive residual sum of squares
- RMSE
root mean square error
- RSS
residual sum of squares
- SAM
significance analysis of microarrays
- SF2
survival fraction at 2Gy
- SVM
support vector machine
- UVE
uninformative variable elimination
- VIP
variable importance on projection
Footnotes
Authors’ Notes: All authors specify that this manuscript has not been published in whole or in part nor is it being considered for publication elsewhere.
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This study was supported by The National Key Research and Development Program of China (2018YFC0808600).
ORCID iD: Kai Song  https://orcid.org/0000-0002-1000-852X
https://orcid.org/0000-0002-1000-852X
Supplemental Material: Supplemental material for this article is available online.
References
- 1. Tucker SL, Thames HD. The effect of patient-to-patient variability on the accuracy of predictive assays of tumor response to radiotherapy: a theoretical evaluation. Int J Radiat Oncol. 1989;17(1):145–157. [DOI] [PubMed] [Google Scholar]
- 2. West CM. Invited review: intrinsic radiosensitivity as a predictor of patient response to radiotherapy. Brit J Radiol. 1995;68(812):827–837. [DOI] [PubMed] [Google Scholar]
- 3. Torres-Roca JF, Eschrich S, Zhao H, et al. Prediction of radiation sensitivity using a gene expression classifier. Cancer Res. 2005;65(16):7169–7176. [DOI] [PubMed] [Google Scholar]
- 4. Eschrich S, Zhang H, Zhao Hy. Systems biology modeling of the radiation sensitivity network: A biomarker discovery platform. Int J Radiat Oncol. 2009;75(2):497–505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Tewari D, Monk BJ, Al-Ghazi MS, et al. Gene expression profiling of in vitro radiation resistance in cervical carcinoma: a feasibility study. Gynecol Oncol. 2005;99(1):84–91. [DOI] [PubMed] [Google Scholar]
- 6. Amundson SA, Do KT, Vinikoor LC, et al. Integrating global gene expression and radiation survival parameters across the 60 cell lines of the National Cancer Institute anticancer drug screen. Cancer Res. 2008;68(2):415–424. [DOI] [PubMed] [Google Scholar]
- 7. Moelans CB, van Maldegem CMG, van der Wall E, van Diest PJ. Copy number changes at 8p11-12 predict adverse clinical outcome and chemo- and radiotherapy response in breast cancer. Oncotarget. 2018;9(24):17078–17092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Zhu X, Wang Y, Tan L, Fu X. The pivotal role of DNA methylation in the radio-sensitivity of tumor radiotherapy. Cancer Med. 2018;7(8):3812–3819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Shen R, Mo Q, Schultz N, et al. Integrative subtype discovery in glioblastoma using iCluster. PLoS One. 2012;7(4):e35236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Chin L, Gray JW. Translating insights from the cancer genome into clinical practice. Nature. 2008;452(7187):553–563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. The Cancer Genome Atlas Research Network. Comprehensive genomic characterization defines human glioblastoma genes and core pathways. Nature. 2008;455(7216):1061–1068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. The Cancer Genome Atlas Research Network. Integrated genomic analyses of ovarian carcinoma. Nature. 2011;474(7353):609–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Henrichsen CN, Chaignat E, Reymond A. Copy number variants, diseases and gene expression. Hum Mol Genet. 2009;18(R1):R1–8. [DOI] [PubMed] [Google Scholar]
- 14. Wang S, Wang Y, Xie Y, Xiao G. A novel approach to DNA copy number data segmentation. J Bioinform Comput Biol. 2011;9(1):131–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Kim DC, Kang M, Zhang B, et al. Integration of DNA methylation, copy number variation, and gene expression for gene regulatory network inference and application to psychiatric disorders. BIBE. 2014:238–242. [Google Scholar]
- 16. Yuan L, Guo LH, Yuan CA, et al. Integration of multi-omics data for gene regulatory network inference and application to breast cancer. IEEE ACM T Comput Bi. 2018;16(3):782–791. [DOI] [PubMed] [Google Scholar]
- 17. Liu G, Xu L, Huang K. Recent advances in studying of copy number variation and gene expression. Gene Expression to Genetical Genomics. 2014;7:1–5. [Google Scholar]
- 18. Gmeiner WH, Reinhold WC, Pommier Y. Genome-wide mRNA and microRNA profiling of the NCI 60 cell-line screen and comparison of FdUMP[10] with fluorouracil, floxuridine, and topoisomerase 1 poisons. Mol Cancer Ther. 2010;9(12):3105–3114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Varma S, Pommier Y, Sunshine M, Weinstein JN, Reinhold WC. High resolution copy number variation data in the NCI-60 cancer cell lines from whole genome microarrays accessible through CellMiner. PLoS One. 2014;9(3):e92047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Tan Y, Shi L, Tong W, Hwang GT, Wang C. Multi-class tumor classification by discriminant partial least squares using microarray gene expression data and assessment of classification models. Comput Biol Chem. 2004;28(3):235–244. [DOI] [PubMed] [Google Scholar]
- 21. Wold S, Sjöström M, Eriksson L. PLS-regression: a basic tool of chemometrics. Chemometr Intell Lab. 2001;58(2):109–130. [Google Scholar]
- 22. Rosipal R, Trejo LJ. Kernel partial least squares regression in reproducing kernel Hilbert space. J Mach Learn Res. 2002;2(2):97–123. [Google Scholar]
- 23. Cortes C, Vapnik V. Support-vector networks. Mach Learn. 1995;20(3):273–297. [Google Scholar]
- 24. Chang CC, Lin CJ. LIBSVM: a library for support vector machines. ACM T Intel Syst Tec. 2007;2(3):1–27. [Google Scholar]
- 25. Ashburner M, Ball CA, Blake JA. Gene Ontology: tool for the unification of biology. Nat Genet. 2000;25(1):25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Kanehisa M, Goto S. KEGG: kyoto encyclopedia of genes and genomes. Nucleic acids research. 2000;28(1):27–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Hoadley KA, Yau C, Hinoue T, et al. Cell-of-origin patterns dominate the molecular classification of 10,000 tumors from 33 types of cancer. Cell. 2018;173(2):291–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Zhang C, Girard L, Das A, et al. Nonlinear quantitative radiation sensitivity prediction model based on NCI-60 cancer cell lines. Sci World J. 2014;2014:1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Ogawa K, Murayama S, Mori M. Predicting the tumor response to radiotherapy using microarray analysis (review). Oncol Rep. 2007;18(5):1243–1248. [PubMed] [Google Scholar]
- 30. Kim HS, Kim SC, Kim SJ. Identification of a radiosensitivity signature using integrative metaanalysis of published microarray data for NCI-60 cancer cells. BMC Genomics. 2012;13(1):348–357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Li X, Tian R, Gao H, et al. Identification of significant gene signatures and prognostic biomarkers for patients with cervical cancer by integrated bioinformatic methods. Technol Cancer Res Treat. 2018;17:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Cho JG, Lim KH, Park SG. MED28 increases the colony-forming ability of breast cancer cells by stabilizing the ZNF224 protein upon DNA damage. Oncol Lett. 2018;15(3):3147–3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Chakravarthi B, Rodriguez Pena MDC, Agarwal S, et al. A role for de novo purine metabolic enzyme PAICS in bladder cancer progression. Neoplasia. 2018;20(9):894–904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Tian Y, Tian X, Han X, et al. ABCE1 plays an essential role in lung cancer progression and metastasis. Tumour Biol. 2016;37(6):8375–8382. [DOI] [PubMed] [Google Scholar]
- 35. Shen B, Tan M, Mu X, et al. Upregulated SMYD3 promotes bladder cancer progression by targeting BCLAF1 and activating autophagy. Tumour Biol. 2016;37(6):7371–7381. [DOI] [PubMed] [Google Scholar]
- 36. Sassi A, Popielarski M, Synowiec E, Morawiec Z, Wozniak K. BLM and RAD51 genes polymorphism and susceptibility to breast cancer. Pathol Oncol Res. 2013;19(3):451–459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Barboza N, Minakhina S, Medina DJ, et al. PDCD2 functions in cancer cell proliferation and predicts relapsed leukemia. Cancer Biol Ther. 2013;14(6):546–555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Zhao X, Parpart S, Takai A, et al. Integrative genomics identifies YY1AP1 as an oncogenic driver in EpCAM+ AFP+ hepatocellular carcinoma. Oncogene. 2015;34(39):5095–5104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Pierini T, Di Giacomo D, Pierini V, et al. MYB deregulation from a EWSR1-MYB fusion at leukemic evolution of a JAK2 (V617F) positive primary myelofibrosis. Mol Cytogenet. 2016;9(1):68–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Chen W, Yuan L, Cai Y, et al. Identification of chromosomal copy number variations and novel candidate loci in hereditary nonpolyposis colorectal cancer with mismatch repair proficiency. Genomics. 2013;102(1):27–34. [DOI] [PubMed] [Google Scholar]
- 41. Cheng L, Wang P, Yang S. Identification of genes with a correlation between copy number and expression in gastric cancer. BMC Med Genomics. 2012;5(14):1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Clean_Revised_Supplementary_material_(1) for A multiple genomic data fused SF2 prediction model, signature identification, and gene regulatory network inference for personalized radiotherapy by Qi-en He, Yi-fan Tong, Zhou Ye, Li-xia Gao, Yi-zhi Zhang, Ling Wang and Kai Song in Technology in Cancer Research & Treatment