Abstract
Background
Malaria remains a public health problem in developing countries and Malawi is no different. Although there has been an improvement in reducing malaria in Malawi, it remains a problem, especially in children less than five years old. The primary objective of the study was to assess whether socio-economic, geographic and demographic factors are associated with malaria, using the generalized additive mixed model (GAMM).
Data and methodology
The study used a 2017 dataset from the Malawi Malaria Indicator Survey (MMI) with a total number of 2724 children under five years old. The study also utilized the GAMM to analyze data. The outcome was that either the child had malaria or did not, as detected using the malaria Rapid Diagnostic Test (RDT) (Ayele et al., 2014a).
Results
In this study, more than 37 % of the total number of children who were tested showed a positive malaria result. In addition, the results from this study using GAMM indicated that anaemia, mother's education level, wealth index, child's age, the altitude of the place of residence, region, place of residence, toilet facility and electricity were significantly associated with a positive malaria RDT.
Conclusion
The study revealed that socio-economic, geographical and demographic variables are the key factors in improving malaria vectors in children. Improving income levels and supporting the poorer rural community mostly from the Central Region would be a great achievement in reducing malaria vectors in Malawi. In addition, improving health care in rural areas, especially at higher altitudes, would contribute to controlling malaria and reducing anaemia.
Keywords: Malaria, Children under five years of age, GAMM, RDT, MMIS, Public heath, Infectious disease, Nutrition
Malaria; Children under five years of age; GAMM; RDT; MMIS; Public heath; Infectious disease; Nutrition
1. Introduction
Malaria is a serious disease caused by a protozoan parasite called Plasmodium species and the most dangerous is P. falciparum which occurs mainly in Africa. There are four other different parasites which are not as dangerous as P. falciparum, these being P. vivax, P. ovale, P. malariae and P. knowlesi (WHO, 2015). Plasmodium falciparum is the most prevalent parasite in Africa especially in Sub-Saharan Africa and is estimated to be the cause of 99% of malaria in 2016, while outside of Africa P. vivax is the most predominant vector (WHO, 2017).
The parasites that cause malaria are transmitted to humans through the bite of the female Anopheles mosquito and it takes 10–15 days to develop symptoms of the disease after being infected (Perkins et al., 2011). Malaria is more often transmitted during the rainy season and with higher temperatures. The disease mostly affects the poorest countries (Mhalu, 2005; Chirombo et al., 2014; Cibulskis et al., 2016). Malaria is not contagious; however, it is possible to contract the disease from another person through blood transfusions or organ transplants (WHO, 2016).
Despite the interventions and precautions taken against malaria, the disease remains a major health problem worldwide, especially in developing countries (WHO, 2016). Malaria is among the leading causes of morbidity and mortality especially in the Sub-Saharan Africa countries and the most vulnerable are pregnant women and children (WHO, 2013; Semakula et al., 2016). The global estimate of malaria cases was 237 million, 211 million and 216 million in 2010, 2015 and 2016 respectively, with Africa having the most cases each year (WHO, 2016). This shows that there has been a reduction in malaria cases generally, but with, a slight increase globally between 2015 and 2016.
The estimated number of deaths from malaria globally was 655 000, 446 000 and 445 000 in 2010, 2015 and 2016 respectively. It was estimated that approximately 80% of these deaths were from Sub-Saharan African countries in 2015, while in 2016 the figure was estimated as 91%. Moreover, 70% of all those who died in 2016 were children under five years old (WHO, 2015; WHO, 2016).
Malaria was the fourth highest cause of mortality in Sub-Saharan Africa, accounting for 10% of children's deaths. This is the equivalent of approximately one child in Sub-Saharan Africa dying of malaria every two minutes (WHO, 2015). In Malawi, as one of the Sub-Saharan Africa countries, where malaria is endemic throughout the country, the disease remains a health problem. In this country, malaria most often affects individuals who live in the rural areas, which are hotter, wetter, more humid and tend to be low-lying, rather than those who live in the dry, urban, highland areas (Kazembe et al., 2006; Dzinjalamala, 2009; Chirombo et al., 2014; Kazembe and Mathanga, 2016).
In 2013, malaria in Malawi was the leading cause of hospital admissions and death in children under five years of age and pregnant women. The disease accounted for 20% of all deaths of children under five (WHO, 2016). The prevalence of malaria in Malawi has decreased from 43% in 2010 to 33% in 2014 and 24% in 2018 (NMCP and ICF, 2010; NMCP and ICF, 2014; NMCP and ICF, 2018). This reduction was due to the efforts of the Malawian government and the international sponsors who put more resources into fighting the burden of malaria among children under five years of age (Mathanga et al., 2012). In 2010, the Malawian government introduced indoor residual spraying (IRS) in various districts around the country as one of the methods of reducing malaria. In 2012 to 2014, the government of Malawi and the sponsors distributed free long-lasting insecticide-treated nets (LLIN) to the children and pregnant women in the whole country (Mathanga et al., 2012; Chanda et al., 2016). Although there has been a great reduction in malaria in Malawi, the disease remains a health problem, especially in children under five (NMCP and ICF, 2012; NMCP and ICF, 2018).
The study by Zgambo et al. (2017) used the 2012 and 2014 Malawi Malaria Indicator Surveys (MMIS) to compare the prevalence of and factors associated with malaria parasitaemia in children under five years of age in Malawi. Their findings showed that the prevalence of malaria had increased from 28% in 2012 to 33% in 2014. This reveals that malaria is still a health problem in the country and more research is needed using different methods to identify the risk factors associated with the disease, especially for children under five years of age in Malawi.
Post-2000 research about malaria in Malawi such as that by Buchwald et al. (2016); Chitunhu and Musenge (2016); Kazembe et al. (2006); Lazzerini et al. (2016); Hershey et al. (2017); Kabaghe et al. (2017); and Parvin et al. (2018) have used different parametric methods, such as logistic regression, generalized linear mixed models and other statistical models. These models are an amazing asset in modelling the relationship between the outcome variable and covariates. However, in numerous applications, this relationship between the outcome and some confounding covariates may have an unknown function form (Ayele et al., 2014a, b). Therefore, along these lines, with such kinds of parameters, it is very important to estimate non-parametrically. This prompted an investigation into non-parametric methods, which include semiparametric additive models. Thus, the current study used the generalized additive mixed model (GAMM) to overcome these challenges. The GAMM is an extension of the generalized additive model (GAM), which includes the random effect. The random effect is used to model the correlation between observations. The GAM does not include random effect, only the model covariate effect (Wang, 1998; Lin and Zhang, 1999). The GAMM is also an extension of the generalized linear mixed model (GLMM) which is a parametric model introduced by Breslow and Clayton (1993). The GAMM enables the parametric fixed effects from GLMM to be modelled as a non-parametric model using the additive smooth function (Hastie and Tibshirani, 1990).
According to our knowledge, researchers have not used the generalized additive mixed model (GAMM) nation-wide to identify the factors associated with malaria in children under five years of age in Malawi. The study by Chirombo et al. (2014) used structured additive regression models, which include GAMM and the geo-additive model in their research in Malawi for children under five years of age, using the 2010 MMIS data set. However, it must be stressed that the data set used is different from the 2017 MMIS data set used in the current study.
Therefore, this study aims to investigate the prevalence of and factors associated with malaria in children under five years old, using the MMIS for 2017 with the application of GAMM. The study also investigates the risk factors for malaria and whether or not they had remained the same after the study by Chirombo et al. (2014).
2. Methodology and material
2.1. Study area
Malawi is a Sub-Saharan African country situated south of the equator and is bordered by Tanzania in the north and northeast; by Mozambique to the east and southwest; and Zambia to the west and northwest (NMCP and ICF, 2018). The total area is approximately 118 484 square kilometres, in which 9 4276 square kilometres are land and the remaining area consists of Lake Malawi. The country is split into three regions and twenty-eight districts. The Northern region has six districts, the Central region nine and the Southern region comprises thirteen districts (NMCP and ICF, 2018). Malawi has a tropical continental climate with sea influences, where the variation of rain and temperature depends on altitude and proximity to Lake Malawi. The tropical climate is favourable for the breeding of Anopheles Mosquitoes and the breeding of Anopheles increases in the rainy season from November to April. The weather in Malawi becomes cool and dry from May to August and the transmission of malaria is not as high as in the rainy season (Kazembe, 2007; NMCP and ICF, 2012). The economy of Malawi is based on agriculture and it is one of the poorest countries in the world. Healthcare is poor compared to other African countries (WHO, 2016; Team, 2018).
2.2. Data sources
The study used secondary data from the 2017 Malawi Malaria Indicator Survey (MMIS) and was collected between 15 April and June 2017. The MMIS was implemented by the Malawi National Malaria Control Program (NMCP) through support from the President's Malaria Initiative (PMI). The United States Agency for International Development (USAID) provided financial support through the President's Malaria Initiative (PMI). They also funded the project by offering technical assistance in the implementation of population and health surveys as they do in countries worldwide (NMCP and ICF, 2018). The governing body of Malawi provided staff, office space and strategic help. Thereafter, the ICF provided technical support through the Demographic and Health Survey (DHS) program.
The 2017 MMIS data interviewed all residents or visitors who stayed in the selected households the night before the interview. The survey was population-based on a household cluster survey. The data sampling followed the two-stage sampling method. The first stage included a selection of 150 clusters from the enumeration areas (EAs) demarcated in the 2008 population and housing census. Out of the 150 clusters, 60 clusters were from urban and 90 from rural areas. The second stage sampling involved the systematic selection of a sample of 3 750 households. Out of the 3 750 households, 25 households were selected from each enumeration area (EA). All women aged 15–49 years who were living in or had visited the selected household the night before the survey were eligible to be interviewed. The children aged 6–59 months in these households were tested for malaria infection with the consent of their parents or guardians. The study used a total number of 2 724 children as a weighted sample in order to ascertain a national-level representation (NMCP and ICF, 2018). The survey sample of this study is representative at the national and regional level, as well as for urban and rural areas.
In the sampling process, the number of women surveyed in each region should contribute to the size of the total sample in proportion to the size of the region (NMCP and ICF, 2018). However, some regions may have small populations, and this unweighted distribution does not represent the exact population. To resolve this problem, regions with small populations are oversampled. Thus, the weighted sample used in the study to get statistics that are representative of the country and to account for the complex sample design from MMIS data set (NMCP and ICF, 2018). The SD Bioline Malaria Ag P.f/P, a rapid diagnostic test (RDT) was used to collect a blood sample from children's finger or heel-prick. This test is appropriate in detecting the histidine-rich protein II (HRP II), an antigen of Plasmodium falciparum and common Plasmodium lactate dehydrogenase (pLDH) of Plasmodium species in human blood (NMCP and ICF, 2018) The diagnostic test incorporates an expendable sample tool that comes in a standard package. A tiny volume of blood is caught on the instrument and placed in the well of a testing device. The RDTs for malaria offers the possibility to expand the arrangement of exact malaria diagnosis to the region where microscopy services are not accessible; for example in a remote area or after standard laboratory hours (Wongsrichanalai et al., 2007). Microscopic diagnosis does have some limitations such as insufficiently trained microscopists, lack of quality control; the chance of misdiagnosis because of low parasitaemia or blended diseases, and in some cases itis hard to determine the types of plasmodium (Ohrt et al., 2002). In the field, laboratory technicians were trained to use the RDT and results were available in 20 min. The children who tested positive were given medication by trained nurses according to the national guidelines (NMCP and ICF, 2018).
3. Data analysis
3.1. Dependent variable
The prevalence of malaria in children under the age of five years was detected using results from the RDT. Hence, the response variable (outcome of interest) was binary, where the child tested either positive (had malaria) or negative (did not have malaria).
3.2. Independent variables
The independent variables considered in this study include a number of socio-economic, demographic, and environmental or geographic factors. The demographic factors associated with the malaria status in children were the age of the child, the gender of the child and family size. These variables of interest were collected at an individual level (Ayele et al., 2014a; Zgambo et al., 2017).
The socio-economic variables were: type of place of residence; wealth quintile; mother's highest education level; source of drinking water; type of toilet facility; the main material of the walls, floors and roofs of the rooms; the total number of rooms inhabited; the total number of nets in dwellings; if mosquito nets were used for sleeping and if there had been antimalarial spraying. These were collected at the household level (Buchwald et al., 2016).
The environmental variables were the temperature; altitude; rainfall and humidity; the life cycle of the parasite in the mosquito, and the breeding and feeding habits of the vector (Bennett et al., 2013; Alegana et al., 2014).
4. Statistical analysis
The present study used bivariate procedures to show the association between independent variables and childhood malaria. The analysis for the bivariate method used cross-tabulation techniques with an application of SPSS version 2.50. The p-value and Chi-squared test were used to check whether the independent variables are significantly associated with childhood malaria or not. The variables from bivariate results with a p-value less than 5% level of significance were included in multivariate GAMM analysis (Gaston et al., 2018).
4.1. Model formulation
The generalized additive model (GAM) is the same as the semi-parametric additive model, which was developed by Hastie and Tibshirani (1986). The GAM is applied to the data to identify the relationship between the response and covariates variables. The parametric models also have powerful tools for modelling the relationship between the response and predictors variables, when their assumptions are not violated. The parametric models in applications such as determining the relationship between the response and covariates variables, may have unknown functional form and are complicated (Ayele et al., 2014a). The unknown functions may lead to applications of semiparametric additive models, which are flexible to allow non-normal error distributions. Furthermore, the semi-parametric additive model relaxes the assumption of normality and linearity in linear regression (Lin and Zhang, 1999; Ayele et al., 2014a). The use of a semiparametric additive model may allow the response variable to be modelled with Poisson and binomial distribution. Moreover, the nonparametric models are flexible for modelling the continuous predictor variables. The GAM extends the generalized linear model (GLM) by allowing the predictor function to include the unspecified nonlinear function for some or all of the covariate variables (Hastie and Tibshirani, 1990). The linear form for the conditional expectation expressed as follow:
| (1) |
Eq. (1) was replaced with the additive form and hence, the general equation for GLM as becomes ) in GAM. Thus, the equation of GAM is written as follows:
| (2) |
From Eq. (1), and distributed some exponential family distribution, is the designed matrix, while is the corresponding parameter vector and are the smooth functions of covariates, while g (.) is the monotonic differentiable function (Wood, 2017). If there is no linear component in Eq. (2), the model is known as nonparametric, whilst the models whose predictors have both linear and unspecified nonlinear function are semiparametric. To estimate the parameters, the standardized condition of the smooth functions should be satisfied such that E [] = 0, apart from that, each function will have free constants (Hastie and Tibshirani, 1990).
When the data has repeated measurement or correlations, the model includes a random variable and this leads to the extension of GAM. Hence, GAM becomes the generalized additive mixed model (GAMM) in the same way as the generalized linear mixed models GLMM are an extension of GLM (Hastie and Tibshirani, 1990). The GAMM was introduced by Breslow and Clayton (1993) to include the random effect in the GAM and model the correlation between the observations.
The equation of GAMM can be expressed as follows:
| (3) |
where g (.) is monotonic differentiable link function, are n covariate associated with fixed effects and vector of covariates associated with random effects. Thus, the given vector of random effect , the observations are assumed to be conditionally independent with means and variance, , where v (.) is the specified variance function and ψ is a scale parameter. Moreover, is a centred twice differentiable smooth function and the random effects is assumed to be distributed as and is a vector of variance components. In addition, when is a linear function, the GAMM reduces to GLMM (Lin and Zhang, 1999).
For a specified variance component, θ the log-likelihood function of is expressed by Lin and Zhang (1999) in the following equation:
| (4) |
where and define the conditional deviance function of given b. The statistical inference for GAMM on nonparametric function requires the estimate of smoothing parameter and the inference on variance component θ. It is known that the smoothing spline estimators and linear mixed models have close connections (Green and Silverman, 1993; Wang, 1998; Lin and Zhang, 1999). Moreover, the natural cubic smoothing spline estimators of function maximize the penalized log-likelihood for the same given and θ and give the following equation:
| (5) |
where the and indicate the range of covariate and are the smoothing parameters that manage the trade-off between goodness of fit and the smoothness of the estimated functions (Lin and Zhang, 1999; Ayele et al., 2014a). Moreover, is an unknown vector of the values of , estimated at ordered values of the where = (1,…, n) and is the smoothing matrix (Green and Silverman, 1993). By using the matrix form, the GAMM given in Eq. (3), can be written as:
| (6) |
where the vector of ones, matrix, such that, the component of and . In order to evaluate Eq. (7), the numerical integration is required. Additionally, to calculate the natural cubic smoothing spline estimators of by maximizing Eq. (6) is sometimes complicated. Consequently, Lin and Zhang, (1999) resolved this problem by suggesting the double penalized quasi-likelihood (DPQL) model as an alternative approach. Hence, the estimation of nonparametric function can be obtained by applying double quasi-likelihood. The function is re-parameterized in terms of and in one-to-one transformation as:
| (7) |
where is vector with the centred and ordered distinct values of the and and is an full rank matrix satisfying and . Thus, the double penalized quasi-likelihood with respect to and becomes:
| (8) |
where , and with . Note that the small values of correspond to over smoothing (Breslow and Clayton, 1993; Lin and Zhang, 1999).
5. Results
The present study used survey-weighted data in order to ascertain a national level presentation (NMCP and ICF, 2018). The results from cross-tabulation analysis are summarized in Table 1. The results indicated that all independent variables were significantly associated with childhood malaria (p-value<0.05). The age of child and altitude were categorized, however, in multivariate GAMM are considered as continuous. The results from Table 1 indicated that the prevalence of malaria was 25%, 40.6%, and 43.4% among children aged between 6-23, 24–41 and 42–59 months respectively. The prevalence of malaria in terms of the sex of the child was 36.5% for a male child and 35.8% for a female child.
Table 1.
Childhood malaria by categorical variables.
| Variable | Category | Malaria (Positive) | Malaria (Negative) | p-value |
|---|---|---|---|---|
| Region | North Central South |
62 (20.8%) 452 (39.8%) 500 (38.7%) |
236 (79.2%) 683 (60.2%) 791 (61.3%) |
0.000 |
| Place of residence | Rural Urban |
987 (41.9%) 27 (7.3%) |
1369 (58.1%) 341 (92.7%) |
0.000 |
| Wealth index | Poorer Middle Richer |
611 (48.0%) 204 (39.6%) 199 (21.3%) |
662 (52.0%) 311 (60.4%) 737 (78.7%) |
0.000 |
| Mother's education level | No education Primary Secondary Tertiary |
152 (46.3%) 557 (37.5%) 61 (17.4%) 1 (3.6%) |
176 (53.7%) 930 (62.5%) 290 (82.6%) 27 (96.4%) |
0.000 |
| Child's age in months | 6–23 24–31 32–59 |
200 (25.6%) 411 (40.6%) 403 (43.4%) |
581 (74.4%) 602 (59.4%) 526 (56.6%) |
0.000 |
| Anemia level | Anemic Not anemic |
706 (45.6%) 307 (26.1%) |
843 (54.4%) 867 (73.9%) |
0.000 |
| Sex of the child | Male Female |
463 (36.5%) 447 (35.8%) |
804 (63.5%) 800 (64.2%) |
0.001 |
| Altitude | 0–500metres 501–1000m >1000 |
119 (34.3%) 492 (43.8%) 403 (32.2%) |
228 (65.7%) 631 (56.2%) 850 (67.8%) |
0.000 |
| Toilet facility | Toilet with flush Pit latrine No facility |
88 (21.1%) 832 (39.3%) 95 (50.8%) |
330 (78.9%) 1287 (60.7%) 92 (49.2%) |
0.000 |
| Electricity | Yes No |
21 (7.3%) 992 (40.7%) |
265 (92.7%) 1445 (59.3%) |
0.000 |
| Main roof material | Thatch/Palm leaf Corrugated &Metal Stick & Mud |
686 (45.8%) 283 (25.8%) 45 (35.7%) |
812 (54.2%) 816 (74.2%) 81 (64.3%) |
0.000 |
| Main wall material | Wood/Mud Bricks Cement/block |
331 (43.2%) 467 (40.1%) 216 (27.2%) |
436 (56.8%) 697 (59.9%) 577 (72.8%) |
0.000 |
| Main floor material | Earth/Sand Mud block/wood Cement/block |
840 (43.5%) 74 (39.4%) 100 (16.6%) |
1092 (56.5%) 114 (60.6%) 504 (83.4%) |
0.000 |
| Sleep under mosquito bed net | All children Some None |
553 (33.6%) 88 (34.1%) 372 (45.4%) |
1093 (66.4%) 170 (65.9%) 447 (54.6%) |
0.000 |
It was observed that the prevalence of malaria was higher in the Central Region (39.8%), followed by the South Region (38.7) and lastly the North Region (20.8%). The results also showed that the prevalence of malaria was higher in children from poorer households (48.0%), middle income households (39.6%) and wealthy households (21.3%) respectively. It was found that the prevalence of malaria among the children with anaemia (45.6%) was higher compared to those without anaemia (26.1%). The results also showed that the prevalence of malaria in children living in rural areas is higher (41.9%) than in children living in urban areas (7.3%). The prevalence of malaria was highest in children from mothers with no education (46.3%), followed by those whose mothers had primary (37.5%), secondary (17.4) and tertiary education (3.6%) respectively.
5.1. Model fitting
The multivariate study used R software to analyze the data with the application of “mgcv” packages. The GAMM was used to model the effect of age and altitude non-parametrically, while other covariates were used as parametric factors. These factors have a continuous effect and might have non-linear relationships with malaria (Ayele et al., 2014a). The R software has packages with numerous choices for controlling the smoothness in the GAMM using splines. The various splines can be used such as the cubic smoothing splines, Bin smoothers, shrinkage smoothers, locally-weighted running line smoothers, kernel smoothers, among others (Hastie and Tibshirani, 1990; Ruppert et al., 2003). However, this study used shrinkage smoothers (splines) to fit the GAM model, due to advantages such as assisting to control the knot placement. Furthermore, the shrinkage smoother is constructed in such a way that the smooth terms are rebuffed away all around (Wood, 2006). The study also considered the fundamental impact and possible two-way interaction effect. The p-value of the individual smooth term and the AIC of each model, together with the inference of smooth were analyzed. The selection of the model was based on the smallest AIC, the higher value of degree of freedom and high statistical significance. Hence, the final model for this study is given in Eq. (9) as follows:
| (9) |
where, is the logit link function, are the parametric regression coefficients, are centred smooth functions, while is the random effects, which can be written as .
5.2. Interpretation of results
The results in model (9) are presented in Tables 2 and 3 and in Figure 1. Table 2 indicates the parameter estimates for the model, standard error, z-value, odds ratio and p-values. The study reported the variables with significant impact for malaria using a RDT such as anaemia, electricity, region, residence, wealth index, the toilet facilities and mother's education status. The study checked all possible interactions. However, the two-way interaction effect was not included, since it did not add any significant effect to the model with non-significant p-values.
Table 2.
The parameter estimates and Odds ratio of GAM model of the main parametric models.
| Variable | Estimate | Standard Error | z-value | Odds ratio | p-value |
|---|---|---|---|---|---|
| Intercept | -2.086 | 0.4620 | -4.514 | 0.124 | 0.000 |
|
Anaemia (Ref = Yes) No |
- -1.455 |
- 0.152 |
- -9.577 |
- 0.233 |
- 0.000 |
|
Region (Ref=North) Central South |
- 0.66755 0.14260 |
- 0.279 0.317 |
- 2.395 0.450 |
- 1.936 1.179 |
- 0.017 0.653 |
|
Residence (Ref= Urban) Rural |
1.463 | 0.293 | 4.994 | 4.318 | 0.000 |
|
Toilet facility (Ref=Flush toilet) Pit Latrine No facility |
- 0.329 1.078 |
- 0.226 0.343 |
- 1.456 3.143 |
- 1.389 2.938 |
- 0.145 0.002 |
|
Wealth Index (Ref=Poorer) Middle Richer |
- -0.298 -0.560 |
- 0.182 0.190 |
- -1.631 -2.956 |
- 0.743 0.571 |
- 0.103 0.003 |
|
Electricity (Ref=No) Yes |
-0.832 | 0.317 | -2.623 | 0.435 | 0.009 |
|
Mothers' education (Ref=No education) Primary Secondary Tertiary |
- -0.102 -0.541 -2.274 |
- 0.201 0.273 1.251 |
- -0.508 -1.982 -1.817 |
- 0.903 0.582 0.103 |
- 0.611 0.047 0.069 |
Table 3.
Approximate significance of the smooth terms.
| Source | Degree of freedom (Edf) | Chi squared | p-value |
|---|---|---|---|
| S (age) | 2.423 | 90.420 | 0.000 |
| S (altitude) | 2.875 | 22.340 | 0.000 |
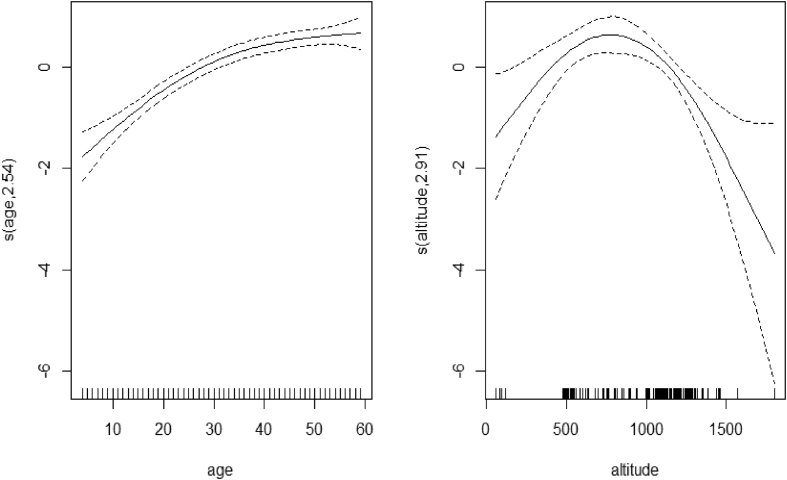
Figure 1.
Smoothing components of malaria RDT test with age and altitude.
Table 2 shows that the children with no anaemia were 0.233 times less likely to test positive for malaria using a RDT as compared with anaemic children. The results also revealed that the odds of positive malaria results in a RDT for children living in the Central Region were 1.936 times more likely than for those who lived in the North Region. Similarly, the odds of positive malaria in a RDT for children living in the South Region were 1.179 times more likely than for those who lived in the North Region. The children living in rural areas were 4.318 times more likely to test positive for malaria in terms of RDT results compared to those living in urban areas. The study also showed that the odds of positive malaria results in a RDT test for children from a household with no toilet facilities were 2.938 times more likely than those with flush toilets. Furthermore, the children from households with pit latrines were 1.389 times more likely to test positive for malaria in a RDT, compared to those with flush toilets. The results indicated that the children from the middle class were 0.743 times less likely to test positive for malaria using a RDT, compared to those from the poorer classes. In addition, the children from the wealthier classes were 0.571 times less likely to test positive for malaria in a RDT than those from the poorer classes. Lastly, the results indicated that the odds of positive malaria in a RDT for children from households with access to electricity were 0.435 times less likely than those from households with no access to electricity. Table 3 shows that the age of a child and the altitude of their region of residence has a significant impact on malaria using a RDT.
The letter S in Table 3 represents the smooth term and the number in parentheses shows the estimated degree of freedom (edf). The test statistics for child age and altitude of the region of residence (22.340; 90.420 respectively) together with their p-value (0.000; 0.000) shows that there is no linear trend associated either for child age or for altitude. This is confirmed in Figure 1, where the trend shows that the effect of malaria results in a RDT increases with age up to approximately 35 months and thereafter remains constant with no sign of decreasing. The same results indicate that the effect of malaria results in a RDT increases with the altitude of their region of residence up to approximately 750 m above sea level and above that starts decreasing.
6. Discussion
The present study utilized the generalized additive mixed model (GAMM) to investigate the risk factors associated with malaria using nationwide malaria survey data from Malawi. The previous studies had used the parametric models such as the generalized linear mixed model (GLMM) to analyze the malaria results using RDT (Ayele et al., 2013; Roberts and Matthews, 2016). The parametric models are useful to model the relationship between a response variable and covariance. However, non-parametric models are flexible enough to allow non-normal error distributions, modelling continuous predictor variable, relaxes the assumption of normality and linearity in linear regression (Lin and Zhang, 1999). The parametric and non-parametric models should complement each other, and for this reason the combination of the two methods is more useful (Wu and Zhang, 2006). Thus, the study first used the parametric model to create geographical and social-economic status variables such as type of place of residence, region, wealth quintile, mother's highest education level, type of toilet facility and availability of electricity.
The effect of age and altitude was modelled as non-parametric and was statistically significant. The interaction effect was not included in the model as it was not statistically significant to improve the original model. The results from the parametric part revealed that the probability of increasing a positive malaria RDT was lower in the richer and the middle classes compared to the poorer class. These results confirmed that the prevalence of malaria is linked to socio-economic conditions, where poorer people are more vulnerable (Hay et al., 2004; Chitunhu and Musenge, 2016). This is due to the limited access to healthcare and the affordability of treatment (Worrall et al., 2002). The study revealed that the households with access to electricity are less likely to increase the positive malaria RDT rates. Moreover, the households with no toilet facilities are more likely to increase the positive malaria RDT rates. This shows that the households with access to electricity and toilet facilities can more easily access the healthcare and afford the treatment (Hay et al., 2004). Hence, these factors that are indicators of socio-economic status are consistent with the study by Ayele et al. (2014a).
The results from the study also showed that the risk of malaria is lower in children from mothers with higher education. This might be linked to socio-economic status, as educated individuals are more likely to have a better standard of living and better understand health-related issues. Furthermore, the individuals with higher levels of education can more easily access healthcare and afford the use of mosquito nets, indoor residual spray and other preventive measures for malaria. These results were consistent with previous studies such as those by Snyman et al. (2015); Zgambo et al. (2017) and Sultana et al. (2017).
The study revealed that the households from rural areas have a higher prevalence of testing positive to malaria compared to those from urban areas. This may be explained by the individuals living in rural areas not having the same access to the many things that their urban counterparts have; such as proper formal houses, drinking water, education opportunities, access to health care and so forth. The individuals living in rural areas often drink water from rivers which may attract mosquitoes, as river water is often dirty. Moreover, it takes longer to pass through the bush to reach these rivers, which may increase susceptibility to mosquito bites and therefore contracting malaria. In addition, most of the individuals living in rural areas live in poor housing conditions. A particular issue could be holes in the walls of the houses where the Anopheles Mosquitoes could enter the houses increasing the chance of malaria transmission through its bite (Lwetoijera et al., 2013; Jenkins et al., 2015; Kazembe and Mathanga, 2016; Sultana et al., 2017).
The study indicated that children without anaemia have a lower prevalence of testing positive to malaria compared to that of anaemic children. This might be explained by the link between anaemia and malaria, as has been shown by previous studies, such as those of Biemba et al. (2000) and Sultana et al. (2017).
The study indicates a large variation among the three regions, where the households from the Central Region being most likely to test positive for malaria. This is due to the fact that the region is covered by a large plain of land and the low-lying zone along the lake. Moreover, the lake might be an area conducive to the breeding of malaria vectors (Minakawa et al., 2012; Zgambo et al., 2017).
The results from the non-parametric model indicate that the probability of a positive malaria RDT increases as the child's age increases. This could be due, in part, to the impact of maternal immunity in the child before one year of age. In addition, the children younger than one year old are more protected and well taken care of and this helps to fight any kind of disease. This reduces as the children get older. These results are consistent with the studies by Ayele et al. (2014a) and Chirombo et al. (2014).
The research reveals that the risk of having a positive malaria RDT result increases as the altitude increases, up to 750 m, and starts showing a decrease as altitude increases thereafter. This may be explained by the very high temperatures at lower altitudes as mosquitos develop in hotter areas. As the altitude increases, the temperatures decrease and this reduces the risk of having a positive malaria RDT result (Lindsay and Martens, 1998; Chirombo et al., 2014).
7. Conclusion
The aim of this study was to assess the prevalence of and factors associated with malaria in children under the age of five years in Malawi using GAMM. The current findings show that the government should consider other factors associated with malaria especially in children under five years of age; such as anaemia, region, residence type, toilet facilities, wealth index, the use of electricity, mothers' education, children's age and the altitude of the region of residence.
The findings from this study revealed that malaria is still a major problem and is linked to socio-economic factors as well as geographical location. The government should focus on poorer communities from rural and low altitude areas, especially in the Central Region, as their target group of individuals to educate, support and help change mindsets. In addition, children with anaemia should take priority in receiving the necessary health care and support. The key findings also show that there is a need to educate the population through workshops, mobile clinics and various social media platforms on how to prevent malaria in children under five years of age.
Moreover, the education of mothers should be considered and supported so that they can take better care of and protect their children, especially after the child's first six months from birth, as they are more likely to be exposed to malaria vectors.
The study will help the government and donors to control and possibly eliminate malaria in children under five years of age. The main focus should be on children with anaemia, mother's education level, wealth index, children's age, the altitude of the place of residence, region, place of residence, toilet facility and electricity facilities. Furthermore, the model used in this study will help other researchers to compare findings.
Future research could use the joint model to model malaria and anaemia simultaneously in order to examine the possible correlation between the two diseases, as there is a link between them (Ayele et al., 2014b; Adebayo et al., 2016).
8. Limitation
The current data set was cross-sectional and consequently cannot address causality. It would have been ideal to have a longitudinal data set to study the change in factors and prevalence over time.
Declarations
Author contribution statement
R.T. Gaston: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
S. Ramroop: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data.
Funding statement
This work was supported by the Health Economics and HIV/AIDS Research Division (HEARD).
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Acknowledgements
The authors acknowledge the National Malaria Control Programme and the ICF through the DHS programme for providing the data.
References
- Adebayo S.B., Gayawan E., Heumann C., Seiler C. Joint modelling of anaemia and malaria in children under five in Nigeria. Spatial Spatio Tempo Epidemiol. 2016;17:105–115. doi: 10.1016/j.sste.2016.04.011. [DOI] [PubMed] [Google Scholar]
- Alegana V.A., Wright J.A., Nahzat S.M., Butt W., Sediqi A.W., Habib N., Snow R.W., Atkinson P.M., Noor A.M. Modelling the incidence of Plasmodium vivax and Plasmodium falciparum malaria in Afghanistan 2006–2009. PloS One. 2014;9(7) doi: 10.1371/journal.pone.0102304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayele D.G., Zewotir T.T., Mwambi H.G. The risk factor indicators of malaria in Ethiopia. Int. J. Med. Med. Sci. 2013;5(7):335–347. [Google Scholar]
- Ayele D.G., Zewotir T.T., Mwambi H.G. Semiparametric models for malaria rapid diagnosis test result. BMC Publ. Health. 2014;14(1):31. doi: 10.1186/1471-2458-14-31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayele D.G., Zewotir T.T., Mwambi H.G. Modelling the joint determinants of a positive malaria Rapid Diagnosis Test result, use of mosquito nets and indoor residual spraying with insecticide. Occup. Health South Afr. 2014;20(4):20–27. [Google Scholar]
- Bennett A., Kazembe L., Mathanga D.P., Kinyoki D., Ali D., Snow R.W., Noor A.M. Mapping malaria transmission intensity in Malawi, 2000–2010. Am. J. Trop. Med. Hyg. 2013;89(5):840–849. doi: 10.4269/ajtmh.13-0028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biemba G., Dolmans D., Thuma P.E., Weiss G., Gordeuk V.R. Severe anaemia in Zambian children with Plasmodium falciparum malaria. Trop. Med. Int. Health. 2000;5(1):9–16. doi: 10.1046/j.1365-3156.2000.00506.x. [DOI] [PubMed] [Google Scholar]
- Breslow N.E., Clayton D.G. Approximate inference in generalized linear mixed models. J. Am. Stat. Assoc. 1993;88(421):9–25. [Google Scholar]
- Buchwald A.G., Walldorf J.A., Cohee L.M., Coalson J.E., Chimbiya N., Bauleni A., Nkanaunena K., Ngwira A., Kapito-Tembo A., Mathanga D.P., Taylor T.E. Bed net use among school-aged children after a universal bed net campaign in Malawi. Malar. J. 2016;15(1):127. doi: 10.1186/s12936-016-1178-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chanda E., Mzilahowa T., Chipwanya J., Ali D., Troell P., Dodoli W., Mnzava A.P., Ameneshewa B., Gimnig J. Scale-up of integrated malaria vector control: lessons from Malawi. Bull. World Health Organ. 2016;94(6):475. doi: 10.2471/BLT.15.154245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cibulskis R.E., Alonso P., Aponte J., Aregawi M., Barrette A., Bergeron L., Fergus C.A., Knox T., Lynch M., Patouillard E., Schwarte S. Malaria: global progress 2000–2015 and future challenges. Infect. Dis. Poverty. 2016;5(1):61. doi: 10.1186/s40249-016-0151-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chirombo J., Lowe R., Kazembe L. Using structured additive regression models to estimate risk factors of malaria: analysis of 2010 Malawi malaria indicator survey data. PloS One. 2014;9(7) doi: 10.1371/journal.pone.0101116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chitunhu S., Musenge E. Spatial and socio-economic effects on malaria morbidity in children under 5 years in Malawi in 2012. Spatial Spatio Temporal Epidemiol. 2016;16:21–33. doi: 10.1016/j.sste.2015.11.001. [DOI] [PubMed] [Google Scholar]
- Dzinjalamala F. Epidemiology of malaria in Malawi. Epidemiol. Malawi. 2009;203:21. [Google Scholar]
- Gaston R.T., Ramroop S., Habyarimana F. Determinants of factors associated with anemia among children under five years in Lesotho. Afr. Popul. Stud. 2018;32(1):3894–3895. [Google Scholar]
- Green P.J., Silverman B.W. CRC Press; Landon: 1993. Nonparametric Regression and Generalized Linear Models: a Roughness Penalty Approach. [Google Scholar]
- Hastie T.J., Tibshirani R. Generalized additive models. Stat. Sci. 1986;1:297–318. doi: 10.1177/096228029500400302. [DOI] [PubMed] [Google Scholar]
- Hastie T.J., Tibshirani R. CRC press; London: 1990. Generalized Additive Models. [DOI] [PubMed] [Google Scholar]
- Hay S.I., Guerra C.A., Tatem A.J., Noor A.M., Snow R.W. The global distribution and population at risk of malaria: past, present, and future. Lancet Infect. Dis. 2004;4(6):327–336. doi: 10.1016/S1473-3099(04)01043-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hershey C.L., Florey L.S., Ali D., Bennett A., Luhanga M., Mathanga D.P., Salgado S.R., Nielsen C.F., Troell P., Jenda G., Ye Y. Malaria control interventions contributed to declines in malaria parasitemia, severe anaemia, and all-cause mortality in children less than 5 years of age in Malawi, 2000–2010. Am. J. Trop. Med. Hyg. 2017;97(3Suppl):76–88. doi: 10.4269/ajtmh.17-0203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkins R., Omollo R., Ongecha M., Sifuna P., Othieno C., Ongeri L., Kingora J., Ogutu B. Prevalence of malaria parasites in adults and its determinants in malaria endemic area of Kisumu County, Kenya. Malar. J. 2015;14(1):263. doi: 10.1186/s12936-015-0781-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kabaghe A.N., Phiri M.D., Phiri K.S., van Vugt M. Challenges in implementing uncomplicated malaria treatment in children: a health facility survey in rural Malawi. Malar. J. 2017;16(1):419. doi: 10.1186/s12936-017-2066-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kazembe L.N., Kleinschmidt I., Holtz T.H., Sharp B.L. Spatial analysis and mapping of malaria risk in Malawi using point-referenced prevalence of infection data. Int. J. Health Geogr. 2006;5(1):41. doi: 10.1186/1476-072X-5-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kazembe L.N. Spatial modelling and risk factors of malaria incidence in northern Malawi. Acta Trop. 2007;102(2):126–137. doi: 10.1016/j.actatropica.2007.04.012. [DOI] [PubMed] [Google Scholar]
- Kazembe L.N., Mathanga D.P. Estimating risk factors of urban malaria in Blantyre, Malawi: a spatial regression analysis. Asian Pac. J. Trop. Biomed. 2016;6(5):376–381. [Google Scholar]
- Lazzerini M., Seward N., Lufesi N., Banda R., Sinyeka S., Masache G., Nambiar B., Makwenda C., Costello A., McCollum E.D., Colbourn T. Mortality and its risk factors in Malawian children admitted to hospital with clinical pneumonia, 2001–12: a retrospective observational study. Lancet Global Health. 2016;4(1):e57–e68. doi: 10.1016/S2214-109X(15)00215-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin X., Zhang D. Inference in generalized additive mixed models by using smoothing splines. J. Roy. Stat. Soc. B. 1999;61(2):381–400. [Google Scholar]
- Lindsay S.W., Martens W.J. Malaria in the African highlands: past, present and future. Bull. World Health Organ. 1998;76(1):33. [PMC free article] [PubMed] [Google Scholar]
- Lwetoijera D.W., Kiware S.S., Mageni Z.D., Dongus S., Harris C., Devine G.J., Majambere S. A need for better housing to further reduce indoor malaria transmission in areas with high bed net coverage. Parasites Vectors. 2013;6(1):57. doi: 10.1186/1756-3305-6-57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathanga D.P., Walker E.D., Wilson M.L., Ali D., Taylor T.E., Laufer M.K. Malaria control in Malawi: current status and directions for the future. Acta Trop. 2012;121(3):212–217. doi: 10.1016/j.actatropica.2011.06.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mhalu F.S. Burden of diseases in poor resource countries: meeting the challenges of combating HIV/AIDS, tuberculosis and malaria. Tanzan. J. Health Res. 2005;7(3):179–184. doi: 10.4314/thrb.v7i3.14257. [DOI] [PubMed] [Google Scholar]
- Minakawa N., Dida G.O., Sonye G.O., Futami K., Njenga S.M. Malaria vectors in Lake Victoria and adjacent habitats in western Kenya. PloS One. 2012;7(3) doi: 10.1371/journal.pone.0032725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Malaria Control Programme (NMCP) [Malawi] and ICF International . Lilongwe, Malawi & Calverton; Maryland, USA: 2010. Malawi Malaria Indicator Survey (MIS) [Google Scholar]
- National Malaria Control Programme (NMCP) [Malawi] and ICF International Malawi malaria indicator survey (MIS) 2012. Lilongwe: NMCP ICF Int. 2012 [Google Scholar]
- National Malaria Control Programme (NMCP) [Malawi] and ICF International Malawi malaria indicator survey (MIS) 2014. Lilongwe: NMCP ICF Int. 2014 [Google Scholar]
- National Malaria Control Programme (NMCP) [Malawi] and I.C.F. 2018. Malawi Malaria Indicator Survey 2017. Lilongwe: NMCP and ICF. [Google Scholar]
- Ohrt C., Sutamihardja M.A., Tang D., Kain K.C. Impact of microscopy error on estimates of protective efficacy in malaria-prevention trials. J. Infect. Dis. 2002;186(4):540–546. doi: 10.1086/341938. [DOI] [PubMed] [Google Scholar]
- Parvin H., Beygi S., Helm J.E., Larson P.S., Van Oyen M.P. Distribution of medication considering information, transshipment, and clustering: malaria in Malawi. Prod. Oper. Manag. 2018;27(4):774–797. [Google Scholar]
- Perkins D.J., Were T., Davenport G.C., Kempaiah P., Hittner J.B., Ong'echa J.M. Severe malarial anaemia: innate immunity and pathogenesis. Int. J. Biol. Sci. 2011;7(9):1427. doi: 10.7150/ijbs.7.1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts D, Matthews G. Risk factors of malaria in children under the age of five years old in Uganda. Malaria Journal. 2016;15(1):P.246. doi: 10.1186/s12936-016-1290-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruppert D., Wand M.P., Carroll R.J. Cambridge University Press; New York: 2003. Semiparametric Regression (No. 12) [Google Scholar]
- Semakula H.M., Song G., Achuu S.P., Zhang S. A Bayesian belief network modelling of household factors influencing the risk of malaria: a study of parasitaemia in children under five years of age in sub-Saharan Africa. Environ. Model. Software. 2016;75:59–67. [Google Scholar]
- Snyman K., Mwangwa F., Bigira V., Kapisi J., Clark T.D., Osterbauer B., Greenhouse B., Sturrock H., Gosling R., Liu J., Dorsey G. Poor housing construction associated with increased malaria incidence in a cohort of young Ugandan children. Am. J. Trop. Med. Hyg. 2015;92(6):1207–1213. doi: 10.4269/ajtmh.14-0828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sultana M., Sheikh N., Mahumud R.A., Jahir T., Islam Z., Sarker A.R. Prevalence and associated determinants of malaria parasites among Kenyan children. Trop. Med. Health. 2017;45(1):25. doi: 10.1186/s41182-017-0066-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Team M.C. 2018. Systematic country diagnostic: breaking the cycle of low growth and slow poverty reduction.http://documents.worldbank.org/curated/en/723781545072859945/Breaking-the-Cycle-of-Low-Growth-and-Slow-Poverty-Reduction Available at. [Google Scholar]
- Wang Y. Mixed effects smoothing spline analysis of variance. J. Roy. Stat. Soc. B. 1998;60(1):159–174. [Google Scholar]
- Wongsrichanalai C., Barcus M.J., Muth S., Sutamihardja A., Wernsdorfer W.H. A review of malaria diagnostic tools: microscopy and rapid diagnostic test (RDT) Am. J. Trop. Med. Hyg. 2007;77(6_Suppl):119–127. [PubMed] [Google Scholar]
- Wood S.N. Vol. 67. Chapman and Hall/CRC. Texts in Statistical Sciences; 2006. Generalized additive models: an introduction with R; p. 391. [Google Scholar]
- Wood S.N. second ed. Chapman and Hall/CRC; London, UK: 2017. Generalized Additive Models: an Introduction with R. [Google Scholar]
- World Health Organization . World Health Organization; Geneva: 2013. WHO Global Malaria Programme. World Malaria Report 2013; p. 255. [Google Scholar]
- World Health Organization . World Health Organization; Geneva: 2015. World Malaria Report 2015. [Google Scholar]
- World Health Organization . World Health Organization; Geneva: 2016. World Malaria Report 2016. [Google Scholar]
- World Health Organization . World Health Organization; Geneva: 2017. World Malaria Report 2017. [Google Scholar]
- Worrall E., Basu S., Hanson K. Vol. 56. School of Hygiene and Tropical Medicine; London: 2002. The relationship between socio-economic status and malaria: a review of the literature. (Background Paper for Ensuring that Malaria Control Interventions Reach the Poor). [Google Scholar]
- Wu H., Zhang J.T. Vol. 515. John Wiley & Sons; New York: 2006. (Nonparametric Regression Methods for Longitudinal Data Analysis: Mixed-Effects Modeling Approaches). [Google Scholar]
- Zgambo M., Mbakaya B.C., Kalembo F.W. Prevalence and factors associated with malaria parasitaemia in children under the age of five years in Malawi: a comparison study of the 2012 and 2014 Malaria Indicator Surveys (MISs) PloS One. 2017;12(4) doi: 10.1371/journal.pone.0175537. [DOI] [PMC free article] [PubMed] [Google Scholar]