Network Reconstruction and Community Detection from Dynamics

Abstract

We present a scalable nonparametric Bayesian method to perform network reconstruction from observed functional behavior that at the same time infers the communities present in the network. We show that the joint reconstruction with community detection has a synergistic effect, where the edge correlations used to inform the existence of communities are also inherently used to improve the accuracy of the reconstruction which, in turn, can better inform the uncovering of communities. We illustrate the use of our method with observations arising from epidemic models and the Ising model, both on synthetic and empirical networks, as well as on data containing only functional information.

The observed functional behavior of a wide variety large-scale system is often the result of a network of pairwise interactions. However, in many cases, these interactions are hidden from us, either because they are impossible to measure directly, or because their measurement can be done only at significant experimental cost. Examples include the mechanisms of gene and metabolic regulation [1], brain connectivity [2], the spread of epidemics [3], systemic risk in financial institutions [4], and influence in social media [5]. In such situations, we are required to infer the network of interactions from the observed functional behavior. Researchers have approached this reconstruction task from a variety of angles, resulting in many different methods, including thresholding the correlation between time series [6], inversion of deterministic dynamics [7–9], statistical inference of graphical models [10–14] and of models of epidemic spreading [15–20], as well as approaches that avoid explicit modeling, such as those based on transfer entropy [21], Granger causality [22], compressed sensing [23–25], generalized linearization [26], and matching of pairwise correlations [27,28].

In this Letter, we approach the problem of network reconstruction in a manner that is different from the aforementioned methods in two important ways. First, we employ a nonparametric Bayesian formulation of the problem, which yields a full posterior distribution of possible networks that are compatible with the observed dynamical behavior. Second, we perform network reconstruction jointly with community detection [29], where, at the same time as we infer the edges of the underlying network, we also infer its modular structure [30]. As we will show, while network reconstruction and community detection are desirable goals on their own, joining these two tasks has a synergistic effect, whereby the detection of communities significantly increases the accuracy of the reconstruction, which in turn improves the discovery of the communities, when compared to performing these tasks in isolation.

Some other approaches combine community detection with functional observation. Berthet et al. [31] derived necessary conditions for the exact recovery of group assignments for dense weighted networks generated with community structure given observed microstates of an Ising model. Hoffmann et al. [32] proposed a method to infer community structure from time-series data that bypasses network reconstruction by employing a direct modeling of the dynamics given the group assignments, instead. However, neither of these approaches attempt to perform network reconstruction together with community detection. Furthermore, they are tied down to one particular inverse problem, and as we will show, our general approach can be easily extended to an open-ended variety of functional models.

Bayesian network reconstruction.—We approach the network reconstruction task similarly to the situation where the network edges are measured directly, but via an uncertain process [33,34]: If $\mathcal{D}$ is the measurement of some process that takes place on a network, we can define a posterior distribution for the underlying adjacency matrix $\mathit{A}$ via Bayes’ rule

$$P(\mathit{A}|\mathcal{D})=\frac{P(\mathcal{D}|\mathit{A})P(\mathit{A})}{P(\mathcal{D})},$$ (1)

where $P(\mathcal{D}|\mathit{A})$ is an arbitrary forward model for the dynamics given the network, $P(\mathit{A})$ is the prior information on the network structure, and $P(\mathcal{D})={\sum }_{\mathit{A}}P(\mathcal{D}|\mathit{A})P(\mathit{A})$ is a normalization constant comprising the total evidence for the data $\mathcal{D}$. We can unite reconstruction with community detection via an, at first, seemingly minor, but ultimately consequential modification of the above equation where we introduce a structured prior $P(\mathit{A}|\mathit{b})$ where $\mathit{b}$ represents the partition of the network in communities, i.e., $\mathit{b}=\{b_i\}$, where $b_i\in \{1,\dots ,B\}$ is group membership of node $i$. This partition is unknown, and is inferred together with the network itself, via the joint posterior distribution

$$P(\mathit{A},\mathit{b}|\mathcal{D})=\frac{P(\mathcal{D}|\mathit{A})P(\mathit{A}|\mathit{b})P(\mathit{b})}{P(\mathcal{D})}.$$ (2)

The prior $P(\mathit{A}|\mathit{b})$ is an assumed generative model for the network structure. In our work, we will use the degree-corrected stochastic block model (DC-SBM) [35], which assumes that, besides differences in degree, nodes belonging to the same group have statistically equivalent connection patterns, according to the joint probability

$$P(\mathit{A}|\mathit{\lambda },\mathit{\kappa },\mathit{b})=\prod _{i<j}\frac{e^{-{\kappa }_i{\kappa }_j{\lambda }_{b_i,b_j}}({\kappa }_i{\kappa }_j{\lambda }_{b_i,b_j}{)}^{A_{ij}}}{A_{ij}!},$$ (3)

with ${\lambda }_{rs}$ determining the average number of edges between groups $r$ and $s$ and ${\kappa }_i$ the average degree of node $i$. The marginal prior is obtained by integrating over all remaining parameters weighted by their respective prior distributions,

$$P(\mathit{A}|\mathit{b})=\int P(\mathit{A}|\mathit{\lambda },\mathit{\kappa },\mathit{b})P(\mathit{\kappa }|\mathit{b})P(\mathit{\lambda }|\mathit{b})d\mathit{\kappa }d\mathit{\lambda },$$ (4)

which can be computed exactly for standard prior choices, although it can be modified to include hierarchical priors that have an improved explanatory power [36] (see Supplemental Material [37] for a concise summary.).

The use of the DC-SBM as a prior probability in Eq. (2) is motivated by its ability to inform link prediction in networks where some fraction of edges have not been observed or have been observed erroneously [34,39]. The latent conditional probabilities of edges existing between groups of nodes is learned by the collective observation of many similar edges, and these correlations are leveraged to extrapolate the existence of missing or spurious ones. The same mechanism is expected to aid the reconstruction task, where edges are not observed directly, but the observed functional behavior yields a posterior distribution on them, allowing the same kind of correlations to be used as an additional source of evidence for the reconstruction, going beyond what the dynamics alone says.

Our reconstruction approach is finalized by defining an appropriate model for the functional behavior, determining $P(\mathcal{D}|\mathit{A})$. Here, we will consider two kinds of indirect data. The first comes from a susceptible-infected-susceptible (SIS) epidemic spreading model [40], where ${\sigma }_i(t)=1$ means node $i$ is infected at time $t$, 0, otherwise. The likelihood for this model is

$$P(\mathit{\sigma }|\mathit{A},\mathit{\tau },\gamma )=\prod _t\prod _{i}P\mathbf{(}{\sigma }_i(t)|\mathit{\sigma }(t-1)\mathbf{)},$$ (5)

where

$$\begin{gathered} P\mathbf{(}{\sigma }_i(t)|\mathit{\sigma }(t-1)\mathbf{)} \\ =f\mathbf{(}{e}^{m_i(t-1)},{\sigma }_i(t){\mathbf{)}}^{1-{\sigma }_i(t-1)}\times f\mathbf{(}\gamma ,{\sigma }_i(t){\mathbf{)}}^{{\sigma }_i(t-1)} \end{gathered}$$ (6)

is the transition probability for node $i$ at time $t$, with $f(p,\sigma )=(1-p{)}^{\sigma }{p}^{1-\sigma }$, and where $m_i(t)={\sum }_j{A}_{ij}\ln (1-{\tau }_{ij}){\sigma }_j(t)$ is the contribution from all neighbors of node $i$ to its infection probability at time $t$. In the equations above, the value ${\tau }_{ij}$ is the probability of an infection via an existing edge $(i,j)$, and $\gamma$ is the $1\to 0$ recovery probability. With these additional parameters, the full posterior distribution for the reconstruction becomes

$$P(\mathit{A},\mathit{b},\mathit{\tau }|\mathit{\sigma })=\frac{P(\mathit{\sigma }|\mathit{A},\mathit{\tau },\gamma )P(\mathit{A}|\mathit{b})P(\mathit{b})P(\mathit{\tau })}{P(\mathit{\sigma }|\gamma )}.$$ (7)

Since ${\tau }_{ij}\in [0,1]$, we use the uniform prior $P(\mathit{\tau })=1$. Note, also, that the recovery probability $\gamma$ plays no role on the reconstruction algorithm, since its term in the likelihood does not involve $\mathit{A}$ [and, hence, gets cancelled out in the denominator $P(\mathit{\sigma }|\gamma )=P(\gamma |\mathit{\sigma })P(\mathit{\sigma })/P(\gamma )$]. This means that the above posterior only depends on the infection events $0\to 1$ and, thus, is also valid without any modifications to all epidemic variants susceptible-infected (SI), susceptible-infected-recovered (SIR), susceptible-exposed-infected-recovered (SEIR), etc., [40], since the infection events occur with the same probability for all these models.

The second functional model we consider is the Ising model, where spin variables on the nodes $\mathit{s}\in \{-1,1{\}}^N$ are sampled according to the joint distribution

$$P(\mathit{s}|\mathit{A},\beta ,\mathit{J},\mathit{h})=\frac{\exp (\beta \sum _{i<j}{J}_{ij}{A}_{ij}{s}_i{s}_j+\sum _i{h}_i{s}_i)}{Z(\mathit{A},\beta ,\mathit{J},\mathit{h})},$$ (8)

where $\beta$ is the inverse temperature, $J_{ij}$ is the coupling on edge $(i,j)$, $h_i$ is a local field on node $i$, and $Z(\mathit{A},\beta ,\mathit{J},\mathit{h})={\sum }_{\mathit{s}}\exp (\beta {\sum }_{i<j}{J}_{ij}{A}_{ij}{s}_i{s}_j+{\sum }_i{h}_i{s}_i)$ is the partition function. Note that this is not a dynamical model as each microstate $\mathit{s}$ is sampled independently according to the above distribution. Unlike the SIS model considered before, this distribution cannot be written in closed form since $Z(\mathit{A},\beta ,\mathit{J},\mathit{h})$ cannot be computed exactly, rendering the reconstruction problem intractable. Therefore, instead, we make use of the pseudolikelihood approximation [41], which is very accurate for the purpose at hand [14], where we approximate Eq. (8) as a product of (properly normalized) conditional probabilities for each spin variable $s_i$

$$P(\mathit{s}|\mathit{A},\beta ,\mathit{J},\mathit{h})=\prod _i\frac{\exp (\beta s_i\sum _j{J}_{ij}{A}_{ij}{s}_j+h_i{s}_i)}{2\cosh (\beta \sum _j{J}_{ij}{A}_{ij}{s}_j+h_i)}.$$ (9)

With the above likelihood, reconstruction is performed by observing a set of $M$ microstates $\overline{\mathit{s}}=\{{\mathit{s}}_1,\dots ,{\mathit{s}}_M\}$, sampled according to $P(\overline{\mathit{s}}|\mathit{A},\beta ,\mathit{J},\mathit{h})={\prod }_{l}P({\mathit{s}}_l|\mathit{A},\beta ,\mathit{J},\mathit{h})$, which yields the posterior distribution

$$\begin{gathered} P(\mathit{A},\mathit{b},\beta ,\mathit{J},\mathit{h}|\overline{\mathit{s}}) \\ =\frac{P(\overline{\mathit{s}}|\mathit{A},\beta ,\mathit{J},\mathit{h})P(\beta )P(\mathit{h})P(\mathit{J}|\mathit{A})P(\mathit{A}|\mathit{b})P(\mathit{b})}{P(\overline{\mathit{s}})}. \end{gathered}$$ (10)

In the above, we use uniform priors $P(\mathit{J}|\mathit{A})={\prod }_{ij}[-1/2<J_{ij}<1/2{]}^{A_{ij}}$, thus, forcing, without loss of generality, the values of $J_{ij}$ to lie in the shifted unit interval $[-1/2,1/2]$. For the remaining parameters, we use uniform priors, $P(\mathit{h})\propto 1$ and $P(\beta )\propto 1$, for $\beta \in [-\infty ,\infty ]$ and $\mathit{h}\in [-\infty ,\infty {]}^N$.

For any of the above posterior distributions, we perform sampling using a Markov chain Monte Carlo procedure: For each proposal $\mathit{A}\to {\mathit{A}}^{\prime }$, it is accepted with the Metropolis-Hastings probability [42,43]

$$\min (1,\frac{P({\mathit{A}}^{\prime },\mathit{b},\mathit{\theta }|\mathcal{D})}{P(\mathit{A},\mathit{b},\mathit{\theta }|\mathcal{D})}\frac{P({\mathit{A}}^{\prime }\to \mathit{A})}{P(\mathit{A}\to {\mathit{A}}^{\prime })}),$$

and likewise, for the node partition $\mathit{b}\to {\mathit{b}}^{\prime }$, and any of the remaining parameters $\mathit{\theta }\to {\mathit{\theta }}^{\prime }$. Note that the acceptance probability does not require the intractable normalization constant $P(\mathcal{D})$ to be computed. For both functional models considered, a whole sweep over $E$ entries of the adjacency matrix and $N$ nodes is done in time $O(EM+N⟨k⟩)$, where $M$ is the number of data samples per node, allowing the method to be applied for large systems. We summarize and give more details about the technical aspects of the algorithm in the Supplemental Material [37].

Synthetic networks.—We begin by investigating the reconstruction performance of networks sampled from the planted partition (PP) model, i.e., a DC-SBM with ${\kappa }_i=1$, ${\lambda }_{rs}={\lambda }_{\text{in}}{\delta }_{rs}+{\lambda }_{\text{out}}(1-{\delta }_{rs})$, with ${\lambda }_{\text{in}}=⟨k⟩[1+\epsilon (B-1)]/N$ and ${\lambda }_{\text{out}}=⟨k⟩(1-\epsilon )/N$, where $\epsilon =N({\lambda }_{\text{in}}-{\lambda }_{\text{out}})/⟨k⟩B$ controls the strength of the modular structure. The detectability threshold for this model is given by ${\epsilon }^{*}=1/\sqrt{⟨k⟩}$, below which it is impossible to recover the planted community structure [44]. Given a network ${\mathit{A}}^{*}$ from this model, we sample $M$ independent Ising microstates $\mathit{s}$ according to Eq. (8) using $J_{ij}=1$, $h_i=0$, and $\beta ={\beta }^{*}$ being the critical inverse temperature for the particular network. We compare two inference approaches: In the first, we sample both the reconstructed network as well as its community structure form the joint posterior of Eq. (10). In the second approach, we perform reconstruction and community detection separately, by first performing reconstruction in isolation, by replacing the DC-SBM prior $P(\mathit{A}|\mathit{b})$ by the likelihood of an Erdős-Rényi model. We evaluate the quality of the reconstruction via the posterior similarity $S\in [0,1]$, defined as

$$S({\mathit{A}}^{*},\mathit{\pi })=1-\frac{\sum _{i<j}|A_{ij}^{*}-{\pi }_{ij}|}{\sum _{i<j}|A_{ij}^{*}+{\pi }_{ij}|},$$ (11)

where ${\mathit{A}}^{*}$ is the true network and $\mathit{\pi }$ is the marginal posterior probability for each edge, i.e., ${\pi }_{ij}={\sum }_{\mathit{A},\mathit{b},\mathit{\theta }}{A}_{ij}P(\mathit{A},\mathit{b},\mathit{\theta }|\mathcal{D})$. A value $S=1$ means perfect reconstruction. We then perform community detection a posteriori by obtaining the maximum marginal point estimate

$${\widehat{A}}_{ij}=\{\begin{array}{ll}1& \text{if}{\pi }_{ij}>1/2,\\ 0& \text{if}{\pi }_{ij}<1/2.\end{array},$$ (12)

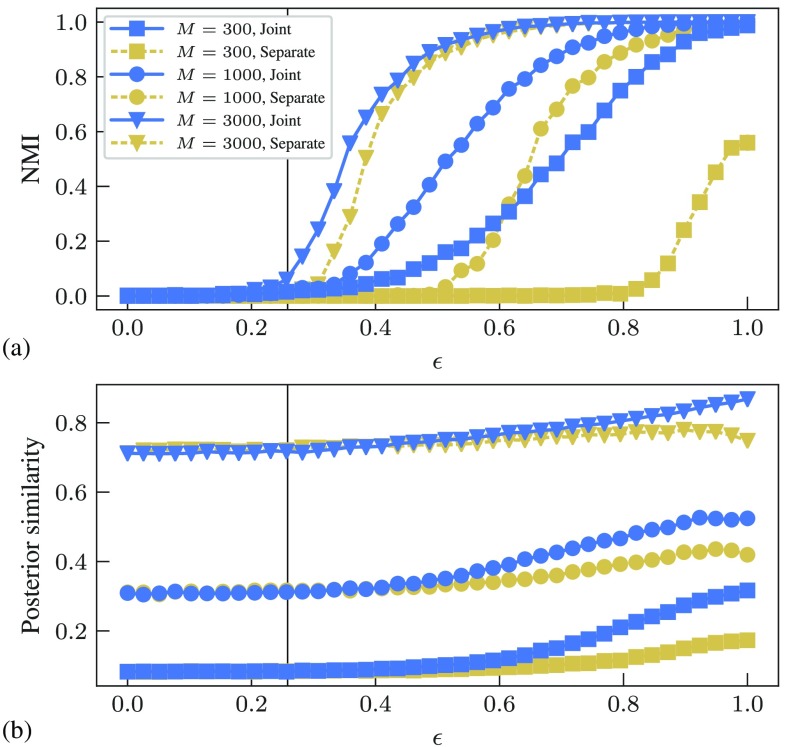
and then sampling from the posterior $P(\mathit{b}|\widehat{\mathit{A}})$. Figure 1 contains the comparison between both approaches for networks sampled from the PP model, which shows how sampling from the joint posterior improves both the reconstruction as well as community detection. For the latter, the joint inference allows the detection all the way down to the detectability threshold, for the examples considered, which, otherwise, is not possible with the separate method.

FIG. 1.

Comparison between joint and separate reconstruction with community detection for a PP model with $N=1000$, $⟨k⟩=15$, and $B=10$. (a) Normalized mutual information (NMI) between inferred and planted node partitions, as a function of the model parameter $\epsilon$, for several values of the number of samples $M$ from the Ising model described in the text. (b) Posterior similarity between planted and inferred networks, for the same cases as in (a). The vertical line marks the detectability threshold $\epsilon =1/\sqrt{⟨k⟩}$.

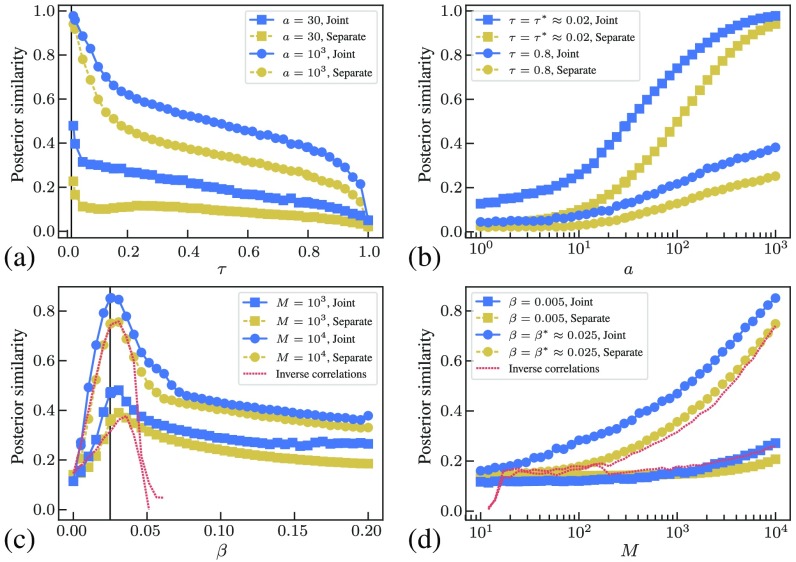
Real networks with synthetic dynamics.—Now, we investigate the reconstruction of networks not generated by the DC-SBM. We take two empirical networks, the worldwide network of $N=3286$ airports [45] with $E=39430$ edges, and a food web from Little Rock Lake [46], containing $N=183$ nodes and $E=2434$ edges, and we sample from the SIS (mimicking the spread of a pandemic) and Ising model (representing simplified interspecies interactions) on them, respectively, and evaluate the reconstruction obtained via the joint and separate inference with community detection, with results shown in Fig. 2. As is also the case for synthetic networks, the reconstruction quality is significantly improved by performing joint community detection [47]. The quality of the reconstruction peaks at the critical threshold for each model, at which the sensitivity to perturbations is the largest. As the number of observed samples increases, so does the quality of the reconstruction, and the relative advantage of the joint reconstruction diminishes, as the data eventually “washes out” the contribution from the prior. For the Ising model, we compare the results of our method with the mean-field inverse correlations method [14], i.e., $\beta A_{ij}{J}_{ij}=[{\mathit{C}}^{-1}{]}_{ij}$, where $C_{ij}=⟨{\sigma }_i{\sigma }_j⟩-⟨{\sigma }_i⟩⟨{\sigma }_j⟩$ is the connected correlation matrix. As seen in Fig. 2, this simpler reconstruction method can be just as accurate as our separate reconstruction approach, but only close to the critical point. For higher inverse temperatures, the reconstruction deteriorates rapidly and breaks down completely as the system becomes locally magnetized, with whole rows and columns of the matrix $\mathit{C}$ being equal to zero, causing it to be singular [48]. In such situations, this kind of approach requires explicit regularization techniques [49], which become unnecessary with our Bayesian method. The joint inference with community structure improves the reconstruction even further, beyond what is obtainable with typical inverse Ising methods, since it incorporates a different source of evidence.

FIG. 2.

Reconstruction results for simulated dynamics on empirical networks, comparing separate and joint reconstruction with community detection. (a) and (b) correspond to a SIS dynamics on global airport data, using ${\tau }_{ij}=\tau$, $\gamma =1$, for different values of the infection probability $\tau$ and node activity $a$ (defined as the number of infection events per node), and (c) and (d) the Ising model on a food web, using $J_{ij}=1$ and $h_i=0$. The dashed red line corresponds to the inverse correlation method for the Ising model. The solid vertical line marks the critical value for each model.

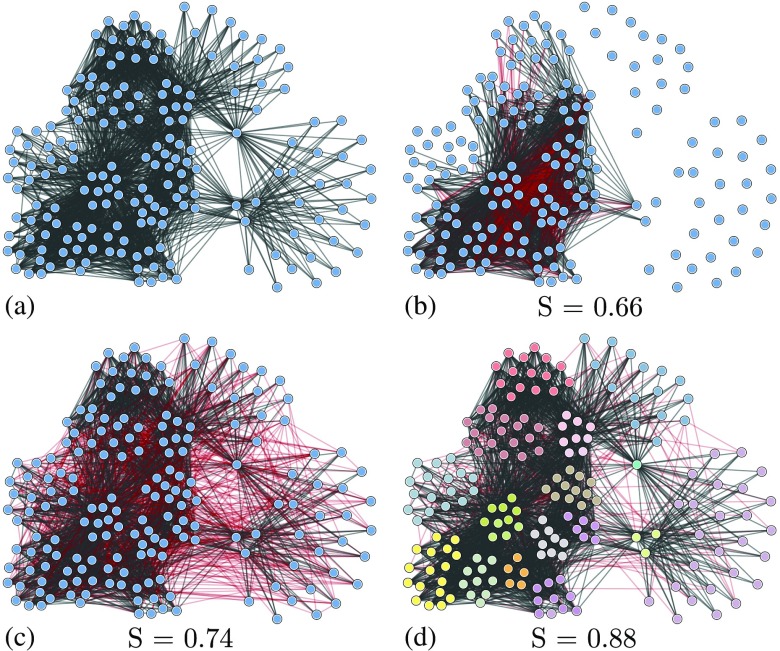
In Fig. 3, we show a comparison of the reconstruction of the food web network from a simulated Ising model, using different approaches. Optimal thresholding corresponds to the naive approach of imputing the existence of an edge to the connected correlation between two nodes exceeding a threshold $c^{*}$, i.e., ${\pi }_{ij}=\{1\text{if}{C}_{ij}>c^{*},0,\text{otherwise}\}$. The value of $c^{*}$ was chosen to maximize the posterior similarity, which represents the best possible reconstruction achievable with this method. Nevertheless, the network thus obtained is severely distorted. The inverse correlation method comes much closer to the true network, but is superseded by the joint inference with community detection.

FIG. 3.

Reconstruction of a food web network [46] from $M={10}^4$ samples of an Ising model at critical temperature. Edges marked in red are erroneous in the reconstruction. (a) Original network. (b) Optimal correlation thresholding. (c) Inverse correlations. (d) Joint reconstruction with community detection. The legends show the values of the posterior similarity [Eq. (11)].

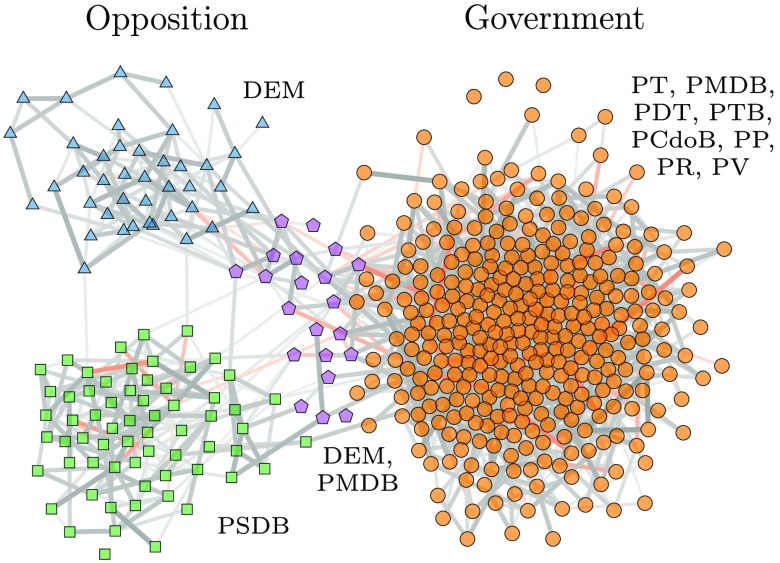
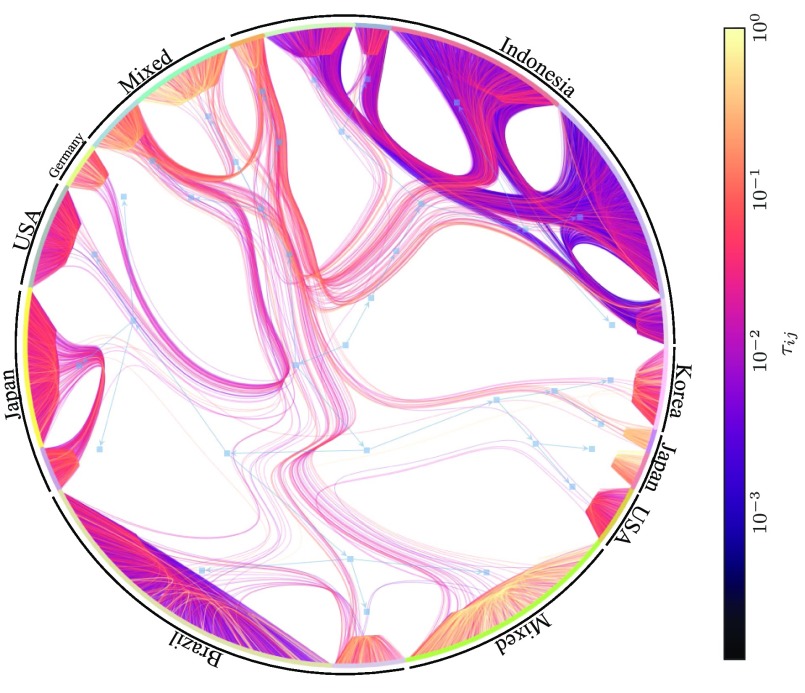
Empirical dynamics.—We turn to the reconstruction from observed empirical dynamics with unknown underlying interactions. The first example is the sequence of $M=619$ votes of $N=575$ deputies in the 2007 to 2011 session of the lower chamber of the Brazilian congress. Each deputy voted yes, no, or abstained for each legislation, which we represent as $\{1,-1,0\}$, respectively. Since the temporal ordering of the voting sessions is likely to be of secondary importance to the voting outcomes, we assume the votes are sampled from an Ising model [the addition of zero-valued spins changes Eq. (9) only slightly by replacing $2\cosh (x)\to 1+2\cosh (x)$]. Figure 4 shows the result of the reconstruction, where the division of the nodes uncovers a cohesive government and a split opposition, as well as a marginal center group, which correlates very well with the known party memberships and can be used to predict unseen voting behavior (see Supplemental Material [37] for more details). In Fig. 5, we show the result of the reconstruction of the directed network of influence between $N=1833$ twitter users from 58224 retweets [50] using a SI epidemic model (the act of “retweeting” is modeled as an infection event, using Eqs. (5) and (6) with $\gamma =0$) and the nested DC-SBM. The reconstruction uncovers isolated groups with varying propensities to retweet, as well as groups that tend to influence a large fraction of users. By inspecting the geolocation metadata on the users, we see that the inferred groups amount, to a large extent, to different countries, although clear subdivisions indicate that this is not the only factor governing the influence among users (see Supplemental Material [37] for more details).

FIG. 4.

Reconstruction of the interactions between members of the lower house of the Brazilian congress from the voting patterns of the 2007–2011 session, according to the Ising model. The node colors indicate the inferred groups. The edge thickness shows the posterior probability for each edge, and the color shows the magnitude of the coupling $J_{ij}$. The labels show the most frequent party membership for each group.

FIG. 5.

Reconstruction of the directed network of influence between $N=1833$ twitter users from 58224 retweets, using a SI infection model. The hierarchical division represents the inferred fit of the nested DC-SBM (see Refs. [51,52] for details on the layout algorithm), and the edge colors indicate the infection probabilities ${\tau }_{ij}$ as shown in the legend. The text labels show the dominating country membership for the users in each group.

Conclusion.—We have presented a scalable Bayesian method to reconstruct networks from functional observations that uses the SBM as a structured prior and, hence, performs community detection together with reconstruction. The method is nonparametric and, hence, requires no prior stipulation of aspects of the network and size of the model, such as number of groups. By leveraging inferred correlations between edges, the SBM includes an additional source of evidence and, thereby, improves the reconstruction accuracy, which in turn also increases the accuracy of the inferred communities. The overall approach is general, requiring only appropriate functional model specifications, and can be coupled with an open ended variety of such models other than those considered here.