Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jan 22;20(5):2973–2979. doi: 10.1021/acs.nanolett.9b04659

Tailored Nanoscale Plasmon-Enhanced Vibrational Electron Spectroscopy

Luiz H G Tizei †,*, Vahagn Mkhitaryan ‡, Hugo Lourenço-Martins †, Leonardo Scarabelli §,∥, Kenji Watanabe ⊥, Takashi Taniguchi ⊥, Marcel Tencé †, Jean-Denis Blazit †, Xiaoyan Li †, Alexandre Gloter †, Alberto Zobelli †, Franz-Philipp Schmidt #, Luis M Liz-Marzán §,○, F Javier García de Abajo ‡,◆, Odile Stéphan †, Mathieu Kociak †,*
PMCID: PMC7227010  PMID: 31967839

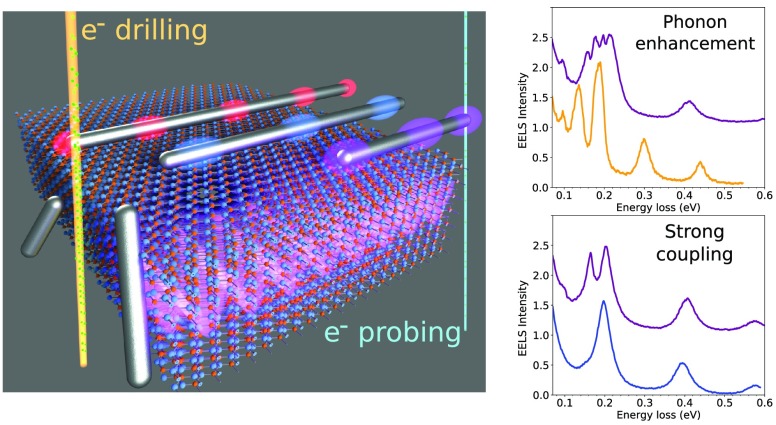
Abstract

graphic file with name nl9b04659_0004.jpg

Atomic vibrations and phonons are an excellent source of information on nanomaterials that we can access through a variety of methods including Raman scattering, infrared spectroscopy, and electron energy-loss spectroscopy (EELS). In the presence of a plasmon local field, vibrations are strongly modified and, in particular, their dipolar strengths are highly enhanced, thus rendering Raman scattering and infrared spectroscopy extremely sensitive techniques. Here, we experimentally demonstrate that the interaction between a relativistic electron and vibrational modes in nanostructures is fundamentally modified in the presence of plasmons. We finely tune the energy of surface plasmons in metallic nanowires in the vicinity of hexagonal boron nitride, making it possible to monitor and disentangle both strong phonon–plasmon coupling and plasmon-driven phonon enhancement at the nanometer scale. Because of the near-field character of the electron beam–phonon interaction, optically inactive phonon modes are also observed. Besides increasing our understanding of phonon physics, our results hold great potential for investigating sensing mechanisms and chemistry in complex nanomaterials down to the molecular level.

Keywords: electron energy-loss spectroscopy (EELS), plasmon−phonon coupling, Raman scattering, plasmon-enhanced vibrational spectroscopy (PEVES), Fuchs-Kliewer modes, strong coupling, h-BN

Vibrational spectroscopy is key in a wide range of research areas and technological applications, extending from molecular fingerprinting to fundamental solid-state physics.1,2 The discovery that plasmonic structures can increase the measured vibrational signal has driven the development of ultrasensitive analytical techniques capable of reaching single-molecule detection, such as in surface-enhanced Raman spectroscopy3,4 (SERS) and surface-enhanced infrared absorption5 (SEIRA). Typically, the molecules to be studied are dispersed on designed plasmonic substrates, leading to strongly enhanced signals associated with those molecules that are sitting on the so-called hotspots.4 Alternatively, a metallic tip can be scanned over a sample to induce SERS locally, leading to chemical mapping at submolecular scales, a technique known as tip-enhanced Raman scattering6 (TERS).

Vibrational electron energy-loss spectroscopy (EELS) has been performed for decades mainly as a surface technique7 using wide beams with poor spatial resolution. The recent development of a new family of electron monochromators8,9 has allowed vibrational mode measurements to be performed based on EELS,10−12 down to atomic spatial resolution in bulk materials.13 Unfortunately, the signal-to-noise ratio of vibrational EELS is low for materials that are sensitive to the electron beam, thus imposing a lower bound on the volume necessary for analysis. This jeopardizes the high-resolution mapping of fragile materials, such as organic molecules.14 Recently, theoretical studies15−17 have proposed the use of infrared plasmonic fields to develop a new form of enhanced vibrational EELS, which would overcome these limitations by making the molecules interact with the beam at a distance mediated by plasmons extended in a nanoparticle.

Here, we demonstrate plasmon-enhanced vibrational electron spectroscopy (PEVES) through the tailored coupling of plasmon resonances in metallic nanowires to phonon modes in h-BN thin flakes. Coupling is achieved by continuously shifting the energies of the plasmon modes of micrometer-long metallic nanowires (SI Figure 1) using electron-beam controlled milling to bring them into resonance with specific h-BN vibrational modes (SI Figure 2). We reveal three new effects when a plasmon–phonon resonance is encountered: (1) strong coupling between surface phonons and surface plasmons; (2) enhancement of the bulk vibrational EELS signal; and (3) emergence of geometry-forbidden dark phonon modes.

EELS measures the distribution of energy losses experienced by free electrons when interacting with a target.18 The energy resolution is determined by the energy spread of the electron source, typically ∼250 meV for a cold field emitter. This resolution can be improved down to a few millielectronvolts using an electron monochromator (SI Figure 3). To achieve subnanometer spatial resolution, the electron monochromator can be coupled to an electron microscope (SI Figure 3). Finally, an electron spectrometer is used to acquire the spectrum of the electron beam after interaction with the sample. Such a setup, implemented on a NION Hermes scanning transmission microscope (STEM), was used in this work (see Methods for more details).

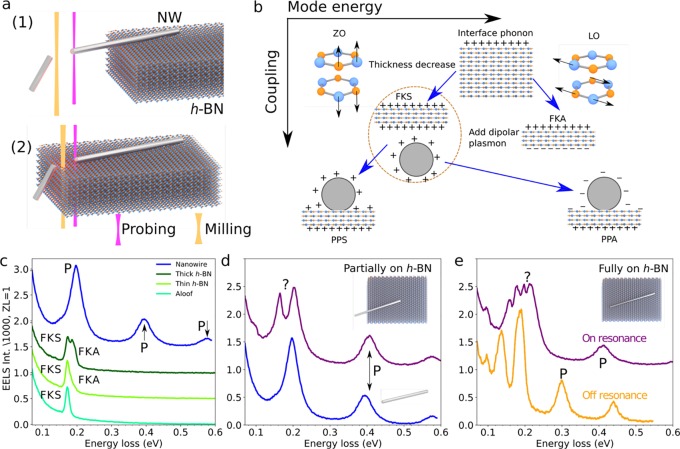
Plasmonic metallic nanowires were synthesized by chemical seeded growth as detailed elsewhere19,20 (Figure 1a) and subsequently deposited, either partially (configuration (1)) or entirely (configuration (2)), on an h-BN substrate.21 In total, 24 nanowires on h-BN have been analyzed, of which 10 nanowires have been milled to monitor the effect of coupling. In theory, extended h-BN possesses a variety of infrared-active transverse optical (TO) and longitudinal optical (LO) phonons. Because of the h-BN anisotropy, TO and LO phonons may possess different energies depending on whether they are polarized out- or in-plane.22 Bulk EELS is therefore highly dependent on the orientation of the electron beam relative to the h-BN crystallographic orientation. Indeed, when the electron propagates along the [0001] h-BN direction, mainly the in-plane LO bulk mode is excited, while the out-of-plane modes can only be excited in a tilted configuration. Additionally, thin h-BN substrates sustain two surface phonon modes: the charge-symmetric (FKS) and charge-antisymmetric (FKA) Fuchs-Kliewer modes, whose energies disperse as a function of thickness. A qualitative sketch of the energy hierarchy of the different modes discussed in the text is presented in Figure 1b. For very thin substrates, the former (FKS) arises at the in-plane TO phonon energy (around 169 meV) whereas the later (FKA) appears at the out-of-plane LO phonon energy (around 198 meV). In EELS experiments, the FKS (respectively FKA) energy varies between the TO (respectively LO) energy and that of the h-BN interface phonon (around 195 meV). Also, the FKA intensity is usually much smaller than that of the FKS23,24 (see Figure 1c, green curves). The FK modes usually overshadow the bulk modes, at least for the thickness range probed in this study (50–100 nm).24 Nanowire plasmons of well-defined energy are produced due to confinement, leading to modes that can be classified as dipolar, quadrupolar, and so forth, depending on the number of nodes in the induced-charge along the nanowire length. In the nanowire cross-section, the charge distribution is approximately homogeneous. EELS is extremely sensitive to surface plasmon modes and reveals their nearly uniform energy spacing (Figure 1c). Their energies are roughly proportional to the inverse of the nanowire length, which thus becomes a suitable parameter to tune the nanowire plasmon energies. Finally, note that both surface plasmons and surface phonons (FK modes) can also be excited in a configuration in which the beam does not directly hit the sample (“aloof geometry”).10,11,25,26

Figure 1.

Figure 1

Open in a new tab

(a) Samples consisting of silver nanowires deposited on h-BN were investigated with two different configurations: (1) nanowires partially supported by h-BN with one of their ends in vacuum; and (2) nanowires fully supported on h-BN. High-current (∼10 μA at 200 keV, orange) and low-current (∼10 pA at 60 keV, purple) electron beams were used for milling and probing, respectively. (b) Sketches of the different phonons, plasmons, and hybrid excitations discussed in the text. (c) Spectra of a 3.3 μm long metallic nanowire in vacuum (blue) and h-BN (green). The in-vacuum nanowire exhibits equally spaced surface plasmon modes labeled P. h-BN spectra are shown for the electron beam placed outside the material (aloof configuration), as well as thin and thick h-BN, where the FKS and FKA modes are observed. (d) Spectrum of a metallic nanowire in sample configuration (1) measured on the tip in vacuum (upper curve). The dipolar mode at ∼200 meV is split into two peaks compared with the nanowire in vacuum (lower curve). (e) Spectra for a metallic nanowire in configuration (2) under off- (orange) and on-resonance (purple) conditions.

Plasmon–phonon interaction was probed initially using the sample configuration (1) sketched in Figure 1a, where only surface phonons interact with surface plasmons, avoiding any potential overlap between surface and bulk effects. In this geometry, long silver nanowires with only one tip placed on different volumes of h-BN were modified in length by electron milling in order to bring their dipolar plasmon into and then out of resonance with respect to the h-BN FK modes.

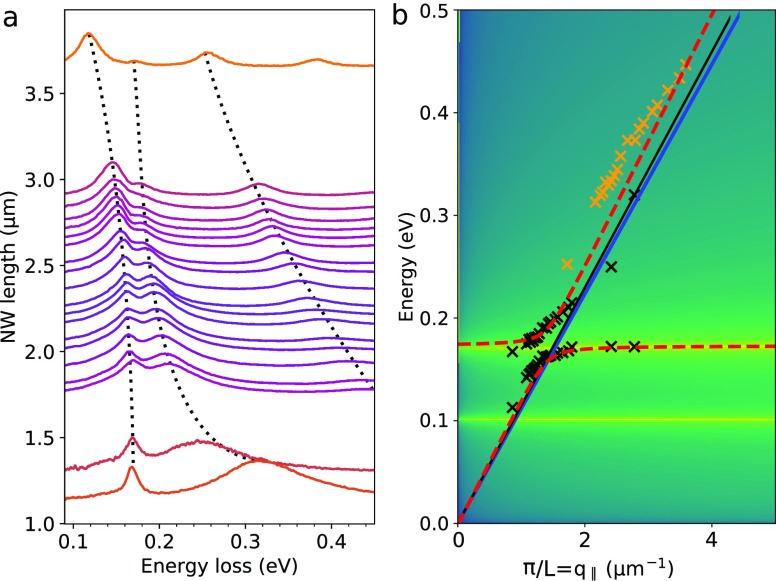
When their energies differ by more than ∼100 meV, phonons and surface plasmons do not interact (Figure 1d, blue curve, and Figure 2a, orange curves). As the nanowire length is shortened, the dipolar plasmon energy approaches that of the FKS mode. Close to resonance, a second peak is observed at the nanowire tip in vacuum, away from h-BN, at an energy close to 180 meV (Figures 1d and 2a, purple curves). The two peaks do not cross each other as the nanowire length is varied, exhibiting a minimum splitting of 37 meV (average splitting in the 1.7–2.9 μm nanowire length range), comparable to the full width at half-maximum of the two peaks (between 30 and 40 meV). The energy of the first peak continues to increase for nanowire lengths shorter than 2.9 μm. However, it does not disperse proportionally to the inverse of the nanowire length 1/L, as expected for plasmons on long metallic nanowires. This is analogous to previously observed energy shifts associated with plasmon–plasmon interaction.30 Such a behavior is in contrast to that of the higher-order plasmon modes that indeed disperse as expected, as 1/L (SI Figure 4). In Figure 2b, the positions of the two strongly coupled peaks (black crosses) and the plasmon quadrupolar mode (orange crosses) are shown for different values of the longitudinal momentum transfer (q∥ = π/L). The observed behavior has been previously predicted for strongly interacting phonons and plasmons.31 This way of presenting measured data produces excellent agreement with theoretical predictions (dashed lines). Peak-splitting is observed to vary between nanowires (in the 0–52 meV range in Figures S5–8). In order to assess the strength of coupling between plasmons and phonons, spectra were fitted using a two-oscillators model with Lorenztian shapes (as described in ref (32)) leading to resonance frequencies

graphic file with name nl9b04659_m001.jpg 1

where ω1 and ω2 are the energies of the two modes (plasmon and phonon in the present case) before coupling, γ1 and γ2 are their full width at half-maximum, and g is the coupling constant. From this fit, a coupling constant g = 18 meV was extracted for the configuration in which the largest splitting was measured (shown in Figure 1a). The full width at half-maximum of the two peaks was calculated to be γ1 = 23 meV and γ2 = 19 meV from the fit. From these values, one can then deduce g/|γ1 – γ2| = 4.4 ≥ 0.25 and g/|γ1 + γ2| = 0.4 ≥ 0.25, which are the two criteria certifying the observation of strong coupling.32 The strong coupling of plasmons with various excitations using electron spectroscopy is currently attracting increasing attention because of the high spatial resolution of electron beam techniques, which makes it easier to investigate coupling taking place at the nanoscale. Experimentally, the onset of strong coupling between plasmons and excitons has been demonstrated,33 but it turns out that in the present study the plasmon–phonon coupling is, relative to the excitation energy, stronger than the plasmon–exciton coupling.

Figure 2.

Figure 2

Open in a new tab

Plasmon–phonon strong coupling. (a) EELS spectra measured at the tip in vacuum of a metallic nanowire (under sample configuration (1) in Figure 1a) as a function of nanowire length. By changing through milling the length of the nanowire, its dipolar plasmon mode is brought in and out of strong coupling with the h-BN phonon modes at around 180 meV. The strong coupling is confirmed by the anticrossing of the two modes, indicated by the two dashed curves (added as guides to the eye) on the left of (a). (b) Theoretical calculations for the energies of the coupled modes (dashed-red curve) and the energy position measured in experiments (black and orange crosses for the dipolar and quadrupolar modes, respectively).27−29 The light line is marked in blue.

These observations indicate strong coupling between the dipolar surface plasmon and the FKS mode. For small detuning, the two peaks cannot be assigned as either a plasmon or a phonon but rather as hybrid plasmon–phonon (PP) modes, either charge-symmetric (low-energy, PPS) or charge-antisymmetric (high-energy, PPA), as illustrated in Figure 1b. Above the anticrossing, the nature of the modes is inverted, as expected for strong coupling: the lower (higher) energy peak changes continuously from the plasmon (phonon) to the phonon (plasmon) mode. Strong coupling evidences a coherent field across the whole nanowire, as its signature is observed at a region of the nanowire where no h-BN is present and the aloof signal from h-BN without the nanowire is not experimentally detectable. In fact, the coupled peaks are only observed where the dipolar mode is measurable, close to the nanowire tips (SI Figure 9). This can be more clearly observed in a line profile of the hyperspectral image going from the nanowire tip in vacuum to the region supported on thin h-BN (SI Figure 9). As the electron beam is moved away from the nanowire tip, the two coupled modes lose intensity. When it approaches h-BN, the lower energy FKS mode is observed at an intermediate energy between the two coupled modes. Finally, with the electron beam on h-BN, both FK modes are revealed.

The energy splitting due to coupling depends on the amount of h-BN contained inside the modal volume of the dipole surface plasmon.16 For small quantities, no splitting is observed (SI Figure 6). For intermediate amounts, a 17 meV splitting is observed in some measurements (SI Figure 7). The largest observed splitting in this study is 52 meV (SI Figure 8). These results support the hypothesis that the volume of h-BN within the dipole surface plasmon modal volume determines the splitting of the two strongly coupled peaks. Indeed, when intentionally removing hBN in the vicinity of a coupled nanowire, the splitting continuously decreases, starting from 52 meV and ending at 12 meV (SI Figure 8). Only removal of h-BN performed within 500 nm of the nanowire tip modified the splitting, while removal farther away did not affect the splitting, again indicating that the coupling is mediated by the overlap of the plasmon field lines and h-BN.

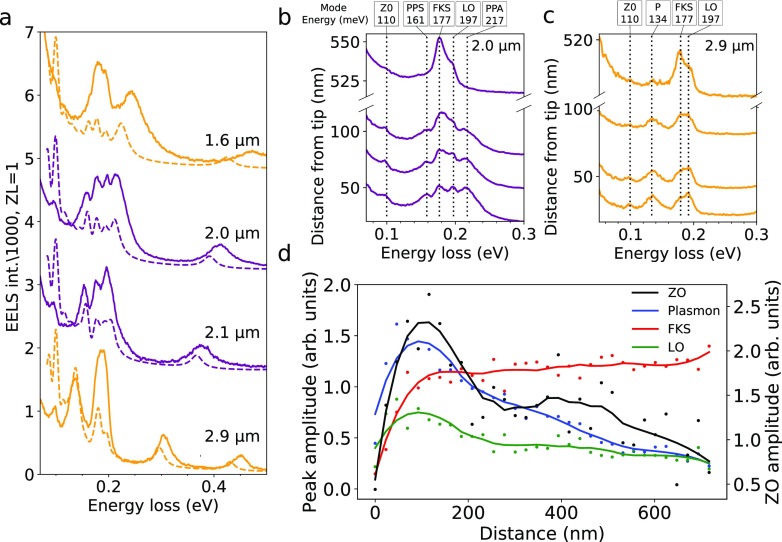
The behavior just described is also observed at the nanowire tip lying on h-BN but with the complicating factor that h-BN bulk losses are also present. To understand the signal when h-BN is present, a second sample geometry is used ((2) in Figure 1a), in which the nanowire is lying completely on an homogeneous piece of h-BN. The presence of plasmons with energies away from the phonon energies (Figure 1e, orange curve) does not affect the phonon spectra. Close to a plasmon–phonon resonance, the spectra change substantially (Figure 1e, purple curve and SI Figure 10) with the appearance of multiple peaks (Figure 3a–c). Under on-resonance conditions (Figure 3b), the peaks appear at 100, 161, 177, 197, and 217 meV (Figure 3b). For off-resonance conditions, four peaks are observed at 100, 134, 177, and 197 meV. This multiple peak structure is correctly reproduced by theoretical calculations (dashed curves in Figure 3a). While the energy position matches well, intensities are not expected to match, as the calculations show the projected local density of optical states (LDOS) instead of the loss function (i.e., the quantity actually measured in EELS experiments27). The 161 and 217 meV modes do disperse with nanowire length (their dispersion is confirmed by numerical calculations shown in SI Figure 11). They can be safely attributed to the previously discussed phonon–plasmon hybridized modes, namely the PPS and PPA modes. As the nanowire length increases (Figure 3 from panel b to c), the plasmons and phonons move out of resonance, and the PPS mode transforms into a plasmon mode (marked P in Figure 3c).

Figure 3.

Figure 3

Open in a new tab

Plasmon-enhanced phonon losses. (a) Experimental (full curves) and calculated (dashed curves) EELS spectra at one of the tips of a metallic nanowire fully supported on h-BN (configuration (2) in Figure 1a) for different lengths of the nanowire: 1.6, 2.0, 2.1, and 2.9 μm. When the dipolar plasmon mode is close to or on resonance with h-BN phonon modes, the latter are enhanced, leading to the appearance of multiple peaks. (b,c) Spectra as a function of distance from the nanowire tip for lengths 2.0 μm (b) and 2.9 μm (c). The ZO, PPS, FKS, LO, PPA, and uncoupled plasmon (P) modes are labeled as described in the main text. (d) Peak intensities retrieved from fits to spectra at different distances from the nanowire tip (data shown in SI Figure 13).

Therefore, three peaks which do not appear in configuration (1) but show up in configuration (2) are left to be identified (100, 177, and 197 meV). For the 2.0 μm long nanowire, where the peak intensities are the largest, peak energies do not change as a function of the distance away from the nanowire tip at which they are probed (Figure 3b and SI Figure 12) but their intensities do vary with this parameter.

The 177 meV mode intensity increases away from the nanowire surface, while the four other modes vanish (Figure 3b,c). The 177 meV mode can be interpreted as the FKS, excited in an aloof-like configuration when the beam is close to the nanowire tip. Close to the tip, the probability of exciting it obviously decreases because the PPA and PPS features, which are hybrid plasmon-FKS modes, are more intensely excited for this probe position.

Away from the influence area of the dipolar mode, the vanishing of the PPA and PPS signals is expected, as they are formed where the plasmon field lines are intense enough. Now, the 100 and 197 meV peaks show a similar spatial variation that is radically different from the PPA and PPS one, indicating that they have a common origin. The first of these energies matches that of the ZO normal mode34 (a longitudinal optical phonon polarized along the anisotropy axis), while the second one corresponds well with the LO mode polarized perpendicular to the anisotropy axis (see schematics in Figure 1b). Although the LO mode can be observed for thick h-BN samples, it is not detected in our relatively thin films, except close to the nanowires when the plasmon energy overlaps with that of the LO mode. Additionally, for symmetry reasons the ZO mode should not be observed in the sample geometry even if a small contribution may appear in spectra due to the finite convergence angle of the electron beam. The observation of these two modes can only be explained by their coupling to the plasmon mode. This is clearly seen in Figure 3b,c, which presents the variations of spectra taken at different positions away from the tip of a nanowire for two different lengths. In Figure 3c, the plasmon energy is closer to the ZO energy and a higher intensity of the ZO peak is measured, whereas in Figure 3b the plasmon energy is closer to the LO energy and a higher intensity of the LO peak is observed. Figure 3d summarizes the behavior of the intensity of the different modes as a function of distance of the electron-beam probe electron to the nanowire. It is clear that the LO and ZO modes are enhanced by the presence of the nanowire, passing from below the detection level to values comparable to that of a typical plasmon (∼10–3 of the ZLP). Furthermore, the intensities of the ZO and LO peaks follow that of the plasmon mode as a function of distance from the nanowire tip (see Figure 3d, where intensities were extracted from fits to the data set shown in SI Figure 13), therefore strengthening our interpretation in terms of plasmonic enhancement.

In summary, two main effects are observed: the possibility to detect a bulk phonon mode (the ZO mode), whose excitation in the absence of a nanowire is geometry-forbidden; and an extreme enhancement of the LO and ZO modes. The magnitude of this enhancement cannot be quantified, as in the absence of a nanowire both modes are not experimentally detectable.

The ZO and LO phonon modes are enhanced along the whole nanowire length, where the plasmon dipolar mode is present. In EELS spectra, the dipolar mode is only observed where its electric field has a nonzero component along the electron trajectory, that is, close to the nanowire tips. The fact that the ZO and LO modes are observed at the center of the nanowire, where the plasmon mode is not measurable due to its electric field direction, shows that it is the plasmon enhancement that allows their detection in this geometry. The PPS and PPA peaks are visible close to the nanowire tips (left and right of SI Figure 13), whereas others appear along the entire nanowire (SI Figure 13 ZO peak). In this respect, the symmetry of the plasmon electric field provides additional information about the phonons with which it interacts.

Controlled coupling between plasmon and phonon modes with precision below 10 meV opens the way to a new form of plasmon-enhanced vibrational spectroscopy (PEVES). Plasmon modes are highly localized in space, leading to stronger enhancement effects in volumes of the order of 103 nm3;15 only a technique with sub-10 nm spatial resolution can exploit this high localization. The plasmonic enhancement has the additional benefit that smaller sample volumes can be probed rather than using regular EELS. The difficulties involving cutting a nanowire, as used here to achieve coupling, can be overcome by more advanced sample designs. Those should eventually allow fingerprinting of molecular vibrational modes. Aiming at single-molecule spectroscopy is plausible, considering that single C60 and C70 molecules inside carbon nanotubes survive a long time under electron irradiation, enough to be identified by core-loss EELS.35 For specific analytes, two general approaches are feasible: (1) designing plasmonic nanoparticles36 with resonances matching vibrational modes of a targeted analyte; or (2) designing metallic structures with broad responses in the infrared37 to survey the vibrational spectrum of an unknown analyte. For example, one could produce dedicated slots in metallic structures, each of them containing different analytes, or a movable metallic tip could be added to the microscope holder (as demonstrated in a previous work38) to selectively enhance the vibrational modes along a molecule. Sequencing of DNA strands also appears as a possible application of PEVES by scanning both the tip and the electron beam.

Acknowledgments

This project has been funded in part by the European Union through the Horizon 2020 Research and Innovation Program (Grant Agreement 823717), the National Agency for Research under the program of future investment TEMPOS-CHROMATEM (reference no. ANR-10-EQPX-50), the Spanish MINECO (MAT2017-88492-R and SEV2015-0522), the ERC (Advanced Grants 789104-eNANO and 787510-4DBIOSERS), the Catalan CERCA Program, and Fundació Privada Cellex. The authors would like to thank Javier Aizpurua for helpful comments on strong coupling and Christoph Hanske for help in the nanowire sample preparation. L.H.G.T. would like to thank Andreia Hisi for help during experiments.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.9b04659.

  • Material and Methods and supporting Figures 1–14 (PDF)

Author Contributions

L.H.G.T., O.S., and M.K. conceived the experiment. L.H.G.T. performed the experiments and data analysis. V.M. performed the numerical calculations. V.M. and F.J.G.A. provided theoretical interpretation. L.H.G.T., V.M., F.J.G.A., O.S., and M.K. wrote the manuscript, which was discussed and updated by all authors. L.L.M. and L.S. prepared the metallic nanowires. K.W. and T.T. prepared the h-BN monocrystals. M.T., J.D.B., X.L., A.G., H.L.M., F.S. and A.Z. participated in the experiment.

The authors declare no competing financial interest.

Supplementary Material

nl9b04659_si_001.pdf (1.8MB, pdf)

References

  1. Zenobi R. Introduction: Vibrational nanoscopy. Chem. Rev. 2017, 117, 4943–4944. 10.1021/acs.chemrev.7b00107. [DOI] [PubMed] [Google Scholar]
  2. Verma P. Tip-enhanced raman spectroscopy: technique and recent advances. Chem. Rev. 2017, 117, 6447–6466. 10.1021/acs.chemrev.6b00821. [DOI] [PubMed] [Google Scholar]
  3. Fleischmann M.; Hendra P.J.; McQuillan A.J. Raman spectra of pyridine adsorbed at a silver electrode. Chem. Phys. Lett. 1974, 26, 163–166. 10.1016/0009-2614(74)85388-1. [DOI] [Google Scholar]
  4. Nie S.; Emory S. R. Probing single molecules and single nanoparticles by surface-enhanced raman scattering. Science 1997, 275, 1102–1106. 10.1126/science.275.5303.1102. [DOI] [PubMed] [Google Scholar]
  5. Osawa M.; Ikeda M. Surface-enhanced infrared absorption of p-nitrobenzoic acid deposited on silver island films: contributions of electromagnetic and chemical mechanisms. J. Phys. Chem. 1991, 95, 9914–9919. 10.1021/j100177a056. [DOI] [Google Scholar]
  6. Sonntag M. D.; Pozzi E. A.; Jiang N.; Hersam M. C.; Van Duyne R. P. Recent advances in tip-enhanced raman spectroscopy. J. Phys. Chem. Lett. 2014, 5, 3125–3130. 10.1021/jz5015746. [DOI] [PubMed] [Google Scholar]
  7. Ibach H.; Mills D. L.. Electron energy loss spectroscopy and surface vibrations; Academic Press: San Diego, 1982. [Google Scholar]
  8. Krivanek O. L.; Ursin J. P.; Bacon N. J.; Corbin G. J.; Dellby N.; Hrncirik P.; Murfitt M. F.; Own C. S.; Szilagyi Z. S. High-energy-resolution monochromator for aberration-corrected scanning transmission electron microscopy/electron energy-loss spectroscopy. Philos. Trans. R. Soc., A 2009, 367, 3683–3697. 10.1098/rsta.2009.0087. [DOI] [PubMed] [Google Scholar]
  9. Tizei L. H. G.; Lin Y.-C.; Mukai M.; Sawada H.; Lu A.-Y.; Li L.-J.; Kimoto K.; Suenaga K. Exciton mapping at subwavelength scales in two-dimensional materials. Phys. Rev. Lett. 2015, 114, 107601. 10.1103/PhysRevLett.114.107601. [DOI] [PubMed] [Google Scholar]
  10. Krivanek O. L.; Lovejoy T. C.; Dellby N.; Aoki T.; Carpenter R. W.; Rez P.; Soignard E.; Zhu J.; Batson P. E.; Lagos M. J.; Egerton R. F.; Crozier P. A. Vibrational spectroscopy in the electron microscope. Nature 2014, 514, 209–214. 10.1038/nature13870. [DOI] [PubMed] [Google Scholar]
  11. Lagos M. J.; Trugler A.; Hohenester U.; Batson P. E. Mapping vibrational surface and bulk modes in a single nanocube. Nature 2017, 543, 529–532. 10.1038/nature21699. [DOI] [PubMed] [Google Scholar]
  12. Senga R.; Suenaga K.; Barone P.; Morishita S.; Mauri F.; Pichler T.. Position and momentum mapping of vibrations in graphene nanostructures in the electron microscope. 2018, arXiv:1812.08294. [DOI] [PubMed]
  13. Hage F. S.; Kepaptsoglou D. M.; Ramasse Q. M.; Allen L. J. Phonon spectroscopy at atomic resolution. Phys. Rev. Lett. 2019, 122, 016103 10.1103/PhysRevLett.122.016103. [DOI] [PubMed] [Google Scholar]
  14. Rez P.; Aoki T.; March K.; Gur D.; Krivanek O. L.; Dellby N.; Lovejoy T. C.; Wolf S. G.; Cohen H. Damage-free vibrational spectroscopy of biological materials in the electron microscope. Nat. Commun. 2016, 7, 10945. 10.1038/ncomms10945. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Neubrech F.; Pucci A.; Cornelius T. W.; Karim S.; García-Etxarri A.; Aizpurua J. Resonant plasmonic and vibrational coupling in a tailored nanoantenna for infrared detection. Phys. Rev. Lett. 2008, 101, 157403. 10.1103/PhysRevLett.101.157403. [DOI] [PubMed] [Google Scholar]
  16. Konecna A.; Neuman T.; Aizpurua J.; Hillenbrand R. Surface-enhanced molecular electron energy loss spectroscopy. ACS Nano 2018, 12, 4775–4786. 10.1021/acsnano.8b01481. [DOI] [PubMed] [Google Scholar]
  17. Kordahl D.; Dwyer C. Enhanced vibrational electron energy-loss spectroscopy of adsorbate molecules. Phys. Rev. B: Condens. Matter Mater. Phys. 2019, 99, 104110. 10.1103/PhysRevB.99.104110. [DOI] [Google Scholar]
  18. Egerton R. F.Electron Energy-Loss Spectroscopy in the Electron Microscope; Plenum Press: New York, 1996. [Google Scholar]
  19. Mayer M.; Scarabelli L.; March K.; Altantzis T.; Tebbe M.; Kociak M.; Bals S.; García de Abajo F. J.; Fery A.; Liz-Marzán L. M. Controlled living nanowire growth: Precise control over the morphology and optical properties of agauag bimetallic nanowires. Nano Lett. 2015, 15, 5427–5437. 10.1021/acs.nanolett.5b01833. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Sanchez-Iglesias A.; Winckelmans N.; Altantzis T.; Bals S.; Grzelczak M.; Liz-Marzan L. M. Highyield seeded growth of monodisperse pentatwinned gold nanoparticles through thermally induced seed twinning. J. Am. Chem. Soc. 2017, 139, 107–110. 10.1021/jacs.6b12143. [DOI] [PubMed] [Google Scholar]
  21. Taniguchi T.; Watanabe K. Synthesis of high-purity boron nitride single crystals under high pressure by using ba–bn solvent. J. Cryst. Growth 2007, 303, 525–529. 10.1016/j.jcrysgro.2006.12.061. [DOI] [Google Scholar]
  22. Geick R.; Perry C. H.; Rupprecht G. Normal modes in hexagonal boron nitride. Phys. Rev. 1966, 146, 543–547. 10.1103/PhysRev.146.543. [DOI] [Google Scholar]
  23. Batson P. E.; Lagos M. J. Characterization of misfit dislocations in si quantum well structures enabled by stem based aberration correction. Ultramicroscopy 2017, 180, 34. 10.1016/j.ultramic.2017.03.002. [DOI] [PubMed] [Google Scholar]
  24. Lourenco-Martins H.; Kociak M. Vibrational surface electron-energy-loss spectroscopy probes confined surfacephonon modes. Phys. Rev. X 2017, 7, 041059 10.1103/PhysRevX.7.041059. [DOI] [Google Scholar]
  25. Nelayah J.; Kociak M.; Stéphan O.; García de Abajo F. J.; Tencé M.; Henrard L.; Taverna D.; Pastoriza-Santos I.; Liz-Marzán L. M.; Colliex C. Mapping surface plasmons on a single metallic nanoparticle. Nat. Phys. 2007, 3, 348–353. 10.1038/nphys575. [DOI] [Google Scholar]
  26. Govyadinov A. A.; Konecna A.; Chuvilin A.; Velez S.; Dolado I.; Nikitin A. Y.; Lopatin S.; Casanova F.; Hueso L. E.; Aizpurua J.; Hillenbrand R.; et al. Probing low-energy hyperbolic polaritons in van der waals crystals with an electron microscope. Nat. Commun. 2017, 8, 95. 10.1038/s41467-017-00056-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. García de Abajo F. J.; Kociak M. Probing the photonic local density of states with electron energy loss spectroscopy. Phys. Rev. Lett. 2008, 100, 106804. 10.1103/PhysRevLett.100.106804. [DOI] [PubMed] [Google Scholar]
  28. Novotny L.; Hecht B.. Principles of Nano-Optics; Cambridge University Press: New York, 2006. [Google Scholar]
  29. Ashley J. C.; Emerson L. C. Dispersion relations for non-radiative surface plasmons on cylinders. Surf. Sci. 1974, 41, 615–618. 10.1016/0039-6028(74)90080-6. [DOI] [Google Scholar]
  30. Batson P. E. Surface plasmon coupling in clusters of small spheres. Phys. Rev. Lett. 1982, 49, 936–940. 10.1103/PhysRevLett.49.936. [DOI] [Google Scholar]
  31. Marty R.; Mlayah A.; Arbouet A.; Girard C.; Tripathy S. Plasphonics: local hybridization of plasmons and phonons. Opt. Express 2013, 21, 4551–4559. 10.1364/OE.21.004551. [DOI] [PubMed] [Google Scholar]
  32. Autore M.; Li P.; Dolado I.; Alfaro-Mozaz F. J; Esteban R.; Atxabal A.; Casanova F.; Hueso L. E; Alonso-Gonzalez P.; Aizpurua J.; Nikitin A. Y; Velez S.; Hillenbrand R.; et al. Boron nitride nanoresonators for phonon-enhanced molecular vibrational spectroscopy at the strong coupling limit. Light: Sci. Appl. 2018, 7, 17172. 10.1038/lsa.2017.172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Yankovich A. B.; Munkhbat B.; Baranov D. G.; Cuadra J.; Olsen E.; Lourenco-Martins H.; Tizei L. H. G.; Kociak M.; Olsson E.; Shegai T. Visualizing spatial variations of plasmon-exciton polaritons at the nanoscale using electron microscopy. Nano Lett. 2019, 19, 8171. 10.1021/acs.nanolett.9b03534. [DOI] [PubMed] [Google Scholar]
  34. Serrano J.; Bosak A.; Arenal R.; Krisch M.; Watanabe K.; Taniguchi T.; Kanda H.; Rubio A.; Wirtz L. Vibrational properties of hexagonal boron nitride: Inelastic x-ray scattering and ab initio calculations. Phys. Rev. Lett. 2007, 98, 095503 10.1103/PhysRevLett.98.095503. [DOI] [PubMed] [Google Scholar]
  35. Tizei L. H. G.; Liu Z.; Koshino M.; Iizumi Y.; Okazaki T.; Suenaga K. Single molecular spectroscopy: Identification of individual fullerene molecules. Phys. Rev. Lett. 2014, 113, 185502. 10.1103/PhysRevLett.113.185502. [DOI] [PubMed] [Google Scholar]
  36. Myroshnychenko V.; Rodriguez-Fernandez J.; Pastoriza-Santos I.; Funston A. M.; Novo C.; Mulvaney P.; Liz-Marzan L. M.; Garcia de Abajo F. J. Modelling the optical response of gold nanoparticles. Chem. Soc. Rev. 2008, 37, 1792–14. 10.1039/b711486a. [DOI] [PubMed] [Google Scholar]
  37. Carminati R.; Cazé A.; Cao D.; Peragut F.; Krachmalnicoff V.; Pierrat R.; De Wilde Y. Electromagnetic density of states in complex plasmonic systems. Surf. Sci. Rep. 2015, 70, 1–41. 10.1016/j.surfrep.2014.11.001. [DOI] [Google Scholar]
  38. Ohnishi H.; Kondo Y.; Takayanagi K. Uhv electron microscope and simultaneous stm observation of gold stepped surfaces. Surf. Sci. 1998, 415, L1061. 10.1016/S0039-6028(98)00623-2. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl9b04659_si_001.pdf (1.8MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES