Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Apr 1;20(5):3263–3270. doi: 10.1021/acs.nanolett.0c00005

Hierarchical Nanotexturing Enables Acoustofluidics on Slippery yet Sticky, Flexible Surfaces

Ran Tao †,§, Glen McHale †, Julien Reboud ‡, Jonathan M Cooper ‡, Hamdi Torun †, JingTing Luo §, Jikui Luo , Xin Yang ⊥, Jian Zhou #, Pep Canyelles-Pericas †, Qiang Wu †, Yongqing Fu †,*
PMCID: PMC7227016  PMID: 32233442

Abstract

graphic file with name nl0c00005_0006.jpg

The ability to actuate liquids remains a fundamental challenge in smart microsystems, such as those for soft robotics, where devices often need to conform to either natural or three-dimensional solid shapes, in various orientations. Here, we propose a hierarchical nanotexturing of piezoelectric films as active microfluidic actuators, exploiting a unique combination of both topographical and chemical properties on flexible surfaces, while also introducing design concepts of shear hydrophobicity and tensile hydrophilicity. In doing so, we create nanostructured surfaces that are, at the same time, both slippery (low in-plane pinning) and sticky (high normal-to-plane liquid adhesion). By enabling fluid transportation on such arbitrarily shaped surfaces, we demonstrate efficient fluid motions on inclined, vertical, inverted, or even flexible geometries in three dimensions. Such surfaces can also be deformed and then reformed into their original shapes, thereby paving the way for advanced microfluidic applications.

Keywords: Hierarchical nanotexture, slippery surface, flexible devices, acoustofluidics, droplet transport

Precision control of microfluids on a small scale, particularly in a microdroplet format, underpins a range of smart microsystems, such as those for soft robotics and lab-on-chip.1−3 However, a major challenge remains in the complexity of assembling all the necessary functionalities using conventional microfluidic devices which are generally based upon rigid substrates and are thus unable to conform to the flexing of natural shapes.4−7 Future applications for the directional transport of fluids will require liquid actuation on flexible and deformable surfaces, on three-dimensional shapes, such as those in robotics.

Thin film piezoelectric surface acoustic wave (SAW) devices have previously been shown to enable all necessary microfluidic functions in diagnosis and sensing applications.8 Material stoichiometry, texture, and crystallinity can be easily controlled, while remaining biocompatible.9−11 They have previously been developed on conformable substrates and have been used for sensing and microfluidics with similar performances to their rigid counterparts.12−14 However, to date, their deformability has not been exploited due to challenges both in realizing long-range wave propagation across the surfaces as well as in implementing liquid handling on curved surfaces (where gravity causes the droplet to detach).

To address these issues, we now show that we can deposit and control the surface structures of ZnO on the nanoscale, on aluminum foils (with thickness from 50 to 600 μm) as flexible and acoustically actuated microfluidic devices, which can be deformed (and maintain their temporal shape) before being returned to their original shapes. Importantly, we show that the acoustic waves not only propagate over long distances of several centimeters without significant dissipation but also overcome the major challenge of enabling efficient liquid handling on curved surfaces—providing the designated slipperiness necessary for motion along the surface, while ensuring sufficient stickiness for the retention of the liquid when the surface is inclined, vertical, or even inverted.

Hydrophobic coatings such as CYTOP,15 or topographic structures (including roughness), have previously been combined with hydrophobic materials16−18 to create surfaces with superhydrophobicity, minimizing droplet pinning forces and creating a slippery surface. However, this also minimizes the surface contact area, which itself is directly related to the quanta of energy that can be transferred from the acoustic waves into the liquid.

The reduced contact area for superhydrophobic surfaces also necessarily results in a reduced droplet adhesion normal to the plane (“stickiness”). Additionally, as the surface oscillates with a nanometer-scale amplitude generated by the acoustic excitation, this increases the probability that the liquid penetrates the surface texture, resulting in an irreversible pinning of the droplet. Such issues are counterintuitive to the key design criteria for a three-dimensional and bendable smart system for droplet transport, which critically requires retaining droplets on the surface as the physical orientation is varied (e.g., either as the angle of inclination or curvature).

We demonstrate that, by engineering the material stack and surface texture of a ZnO/Al piezoelectric flexible sheet for our SAW-based devices, we can achieve droplet manipulation on large scales and conformable shapes not previously possible, opening a new way for flexible devices to perform complex smart microfluidic systems. We combine the microscale roughness of the metal foil substrate with the nanoscale structures of ZnO film to create a hierarchically textured surface, showing not only a low contact angle hysteresis (i.e., shear hydrophobicity19 allowing easy translation of droplets across the surface) but also a receding contact angle allowing droplets to be retained in a wide range of surface orientations (i.e., with sufficient tensile hydrophilicity19). Importantly, we not only demonstrate that such ZnO/Al sheets support low power wave propagation and efficiently drive liquids on horizontal, inclined, vertical, and arbitrarily shaped surfaces but also show that both the contact angle hysteresis and receding contact angle are key design parameters for requiring droplet transportation and adhesion.

Surface Design Considerations

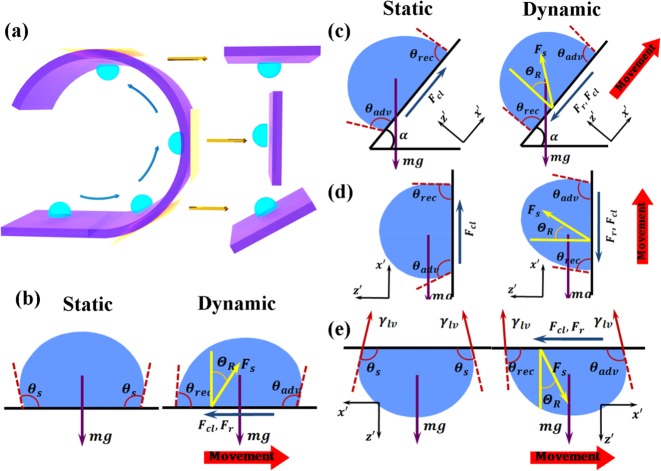
Figure 1a depicts a droplet in sequential positions along a curved surface driven by SAW propagating along the surface. For microliter-sized droplets (for instance 1 μL with a radius of ∼1 mm), the radius of curvature of surfaces conforming to geometric features can be considered infinitely large (>10 cm) as compared to the droplet, so that we can estimate the forces applied to the droplet by considering a flat sheet tangential to the curved surface. For a droplet placed on a horizontal flat surface (see Figure 1b), the idealized static equilibrium state is described using Young’s equation

graphic file with name nl0c00005_m001.jpg 1

where, γsl is the surface tension of the liquid–solid interface, γlv is the liquid surface tension, γsv is the solid surface tension, and θY is the contact angle in the idealized equilibrium state.

Figure 1.

Figure 1

Open in a new tab

Principles of droplets moving on a curved surface. (a) Schematic diagram of droplet movement on a curved surface, which can be treated as a sum of movements on tangential planes. (b–e) Force analysis of the water droplet retained and moving on hydrophobic surfaces: (b) placed horizontally, (c) tilted at angle α, (d) placed vertically (α = 90°), and (e) placed upsidedown (α = 180°) in static and dynamic (surface acoustic wave power is on) states.

When the SAW propagates, and thus moves a droplet along the horizontal surface, the advancing and receding contact angles, θadv, and θrec, define the contact hysteresis and the pinning of the contact line.20 To agitate and move the droplet, the externally applied driving force must overcome the pinning force of the droplet due to this contact angle hysteresis. Assuming there is a perfect circular contact line for the droplet, the lateral (radial) pinning force can be formulated as21,22

graphic file with name nl0c00005_m002.jpg 2

where D0 is the equivalent base diameter in a static state.

The force can be reduced by decreasing the difference between the advancing and receding contact angles, or by tuning the surface topography and hydrophobicity, thus enabling the liquid to ball up and changing the length of the contact line (represented in eq 2 by the equivalent base diameter).

Considering the case of driving a hanging droplet, e.g., perpendicular to a surface and upward, the actuation force must overcome both the work of adhesion (given by γlv(1 + cos θrec)19,23) and gravity. Use of a superhydrophobic surface is difficult to implement, because although droplets can be pushed on inclined or inverted superhydrophobic surfaces (at an angle α, 0° < α ≤ 180°), in practice, once the actuation force stops, gravity will often cause the moving liquid droplet to detach from the surface and fall off.

An alternative approach that reduces the contact line force is to reduce the contact angle hysteresis (i.e., increase shear hydrophobicity19), while retaining a receding contact angle at a value appropriate to ensure that the droplet adheres to the surface when subject to normal forces (i.e., tensile hydrophilicity19). In this approach, the reduction in contact angle hysteresis does not require the droplet to be balled-up or the contact line length to be reduced to achieve an easy droplet transport along the surface. Moreover, since the contact line length does not have to be reduced, the droplet-surface area is large enough for the acoustic wave to interact with the liquid droplet and, hence, enable an efficient wave energy dissipation; thus, low power actuation is maintained.

Once the droplet starts moving under agitation of a SAW, the viscous resistance force becomes significant due to a strain formed along the contact line. This force, Fr(v), can be written as24

graphic file with name nl0c00005_m003.jpg 3

where εc is the cutoff length to prevent the singularity at the contact line, μ is the liquid viscosity, v is the droplet velocity, and h(r) is the height of the droplet at a certain position dependent on the radial coordinate r. Fr(v) is equal to zero when the droplet is immobile.

Figure 1b–e compares the total SAW streaming forces, Fs, applied to the droplet in both static and dynamic states of different substrate orientations, induced by an acoustic pressure, which is defined as25−27

graphic file with name nl0c00005_m004.jpg 4

where A is the wave amplitude, ω is the angular velocity, and ki is the imaginary part of kl which is the wavenumber of the leaky surface acoustic wave. θ1 = jθ (with j2 = −1) is the attenuation constant where θ2 = 1 – (vLe/vl)2, vLe is the leaky wave velocity, while vl is the sound velocity in liquid.

The direction of the pressure/force follows the Rayleigh angle ΘR which is defined by

graphic file with name nl0c00005_m005.jpg 5

where vs is the sound velocity in the flexible substrate. The minimum force required to move the droplet can be written as

graphic file with name nl0c00005_m006.jpg 6

The relationship among the different forces applied to the droplet which are balanced during droplet movement can be described using the following equation:

graphic file with name nl0c00005_m007.jpg 7

where m is the mass of the droplet. This relationship predicts that the projection of acoustic force will be increased with the Rayleigh angle for a given input power. If the surface is tilted at a certain inclination angle 0° < α ≤ 180°, the gravitational force is involved at both static and dynamic states; thus, the force balance in both the z′ and x′ directions should be considered (Figure 1c–e). In the static state, the forces are balanced to keep the droplet stable in its position, and then, we have

graphic file with name nl0c00005_m008.jpg 8

where g is the acceleration of gravity. Accordingly, in a dynamic state, the acoustic force needed to initiate the droplet movement is

graphic file with name nl0c00005_m009.jpg 9

Meanwhile, eq 7, which describes the relationship between the droplet velocity and the forces, can be further modified as

graphic file with name nl0c00005_m010.jpg 10

Based upon the above discussion and analysis, in order to realize three-dimensional manipulations of droplets on inclined or even curved surfaces driven by SAW, the surface needs to be prepared not only with a low contact angle hysteresis for easy transportation of droplets but also with a suitable receding contact angle to retain the droplet on it.

The contact angle hysteresis and receding contact angle can be regarded as two key parameters describing a design space, with the first parameter controlling whether a droplet is pinned (thus preventing motion along it), and the second parameter controlling how strongly a droplet adheres in the direction perpendicular to the surface. Figure 2 summarizes these four fundamental combinations of slipperiness and stickiness (e.g., showing low/high pinning and low/high adhesion) and provides exemplars of potential applications.28−30 For our application in this study requiring droplet motion along a surface that can have multiple orientations including vertical and inverted, the surface wettability design requires ease of transport and sufficient adhesion, and this was achieved by creating a hierarchical texture of nano- and microscale features, as shown in Figure 3a,b.

Figure 2.

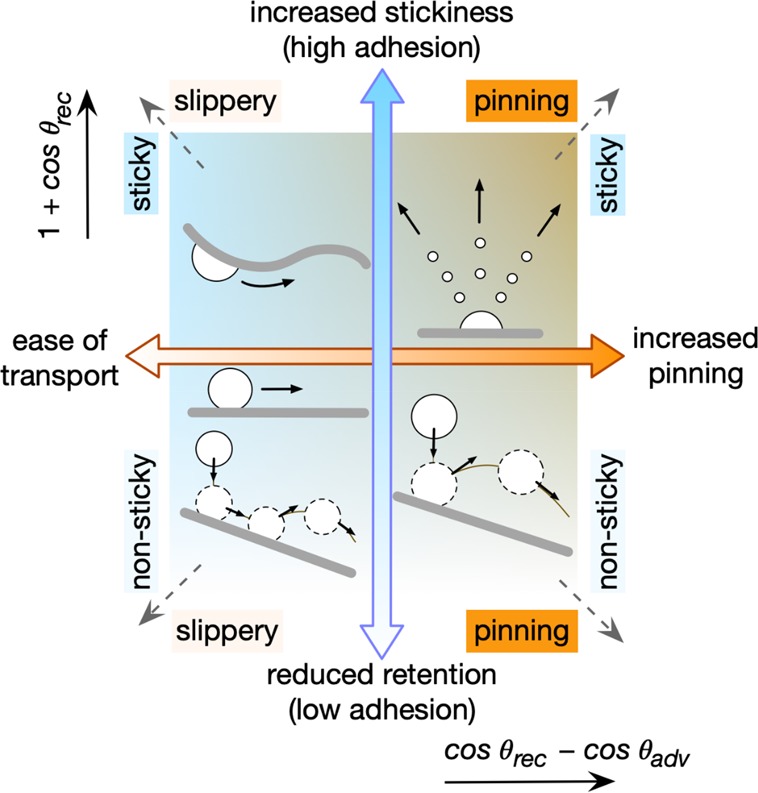
Figure 2

Open in a new tab

Combinations of four different surface types arising from contact angle hysteresis and receding contact angle. Scheme defining the design space of slippery/nonsticky,28 pinning/nonsticky,29 pinning/sticky,30 and slippery/sticky surface types with exemplars of possible applications.

Figure 3.

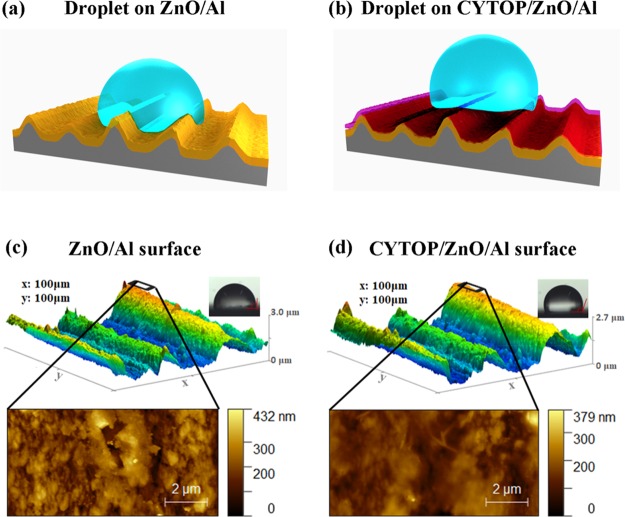
Figure 3

Open in a new tab

Surface morphology of hierarchical textures. (a) 3D schematic diagram of the bilayer structure composed of the Al substrate (gray) and ZnO thin film (orange). (b) 3D scheme of the trilayer structure composed of the Al substrate, ZnO thin film, and CYTOP coating (red). AFM images showing the root-mean-square (RMS) roughness of the hierarchical structure (c) before and (d) after CYTOP coating.

Hierarchically Textured Surface with Shear Hydrophobicity and Tensile Hydrophilicity

Here, we used Al sheets with a thickness of 600 μm as the underlying substrates. There are surface grooves with microscale roughness on the surface, generated by cold rolling manufacturing processes (Figure S1), and the root-mean-square roughness of grooved surfaces is in the range 0.72 ± 0.05 μm, measured using a profilometer. ZnO thin film was deposited on top of the microstructure, providing a hierarchical and fractal surface with an average roughness value of 73.6 nm (shown in Figure 3c—AFM image, 5 μm × 8 μm).

Sputtered ZnO thin films have a relatively low surface energy, and contact angles of a water droplet on such a surface vary between 70° and 100°.31 When the droplet is located on the ZnO/Al sheet structure, a Wenzel state is formed on the surface as shown in Figure 3a. This Wenzel state could be transformed into a Wenzel/Cassie–Baxter mixed state by coating the ZnO surface with a thin hydrophobic layer (300–500 nm thick) of CYTOP, an amorphous fluoropolymer with high transparency and water and oil repellency. Figure 3c,d shows that the nanoscale roughness is reduced after the surface is coated with CYTOP. For a comparison, we also measured the surface roughness of a ZnO film deposited onto a standard polished (100) Si wafer using the AFM and obtained a homogeneous and smooth surface with an average roughness of 15.05 ± 4.58 nm over an area of 100 μm × 100 μm, which is much smaller than those on the foil substrates.

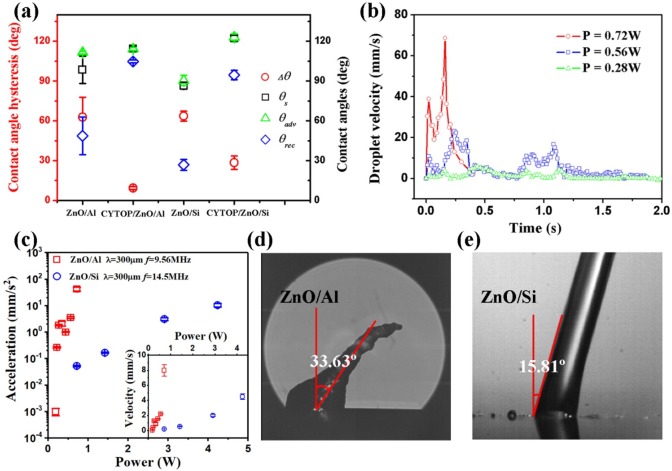
To further understand the wettability of the ZnO/Al sheet surface, we measured the static contact angle θs, and the advancing and receding contact angles, giving us a contact angle hysteresis, Δθ = θadv – θrec, for 1 μL water droplets with and without CYTOP treatment as shown in Figure 4a (values are tabulated in Table S1 in the Supporting Information). The untreated ZnO/Al sheet delivered good tensile hydrophilicity with a receding contact angle of 49° ± 14° retaining the droplet against any normal force. However, the droplet on such a surface is also pinned in the direction of movement due to the large contact angle hysteresis of 63° ± 15° and, hence, poor shear hydrophobicity. Similarly, the untreated ZnO/Si surface provides a smaller receding contact angle (27° ± 4°), indicating a better tensile hydrophilicity, while having poor shear hydrophobicity due to the contact angle hysteresis staying the same as the untreated ZnO/Al surface. After the surface was coated with CYTOP, the surface wetting properties were modified, and the shear hydrophobicity was enhanced with a decreased contact angle hysteresis of 28° ± 6°. The receding contact angle of the CYTOP/ZnO/Si surface increased to 95° ± 4° but was still able to prevent the droplet from being detached perpendicularly providing acceptable tensile hydrophilicity (adhesion) compared to superhydrophobic surfaces. By using the ZnO/Al surface, we could further optimize the shear hydrophobicity and reduce the contact angle hysteresis to 9° ± 2° while achieving a receding contact angle of 105° ± 1°, thus creating a surface that simultaneously has excellent shear hydrophobicity (slipperiness) and sufficient tensile hydrophilicity (adhesiveness). In such cases, the surface acoustic wave actuation force required to transport a droplet along a surface, which is proportional to γlv(cos θrec – cos θadv), is reduced, while the force normal to the surface required to remove a droplet, which is proportional to γlv(1 + cos θrec), remains sufficiently large to prevent droplet detachment.

Figure 4.

Figure 4

Open in a new tab

Contact angle measurements and pumping experiments on horizontal surfaces. (a) Comparison of the static contact angle θs, the receding contact angle θrec, and the advancing contact angle θadv, and hence the contact angle hysteresis, Δθ = θadv – θrec of water droplets (1 μL) on ZnO/Si and ZnO/Al surfaces before and after CYTOP coating. (b) Pumping velocity as a function of time with different input powers when the water droplet is driven by an acoustic wave on a 600 μm thick horizontal Al plate. (c) Average acceleration calculated from videos of horizontal pumping on ZnO coated 600 μm thick Al plates and ZnO coated Si wafer increasing with the input power. The wavelength of the acoustic wave was 300 μm for both devices. The inset figure shows the average velocity (over time). Rayleigh angles of the surface acoustic wave can be observed from the jetting trajectory of 2 μL water droplets on (d) the ZnO/Al device (jetted at 8 W) and (e) the ZnO/Si device (jetted at 14 W).

Droplet Transport Enhanced on Horizontal and Tilted Flat Surfaces

The input power determines the displacement amplitude of the Rayleigh wave and, thus, the streaming force Fs. According to eq 9, when Fs sin ΘR is larger than the lateral pinning force Fcl (mg sin α = 0 applied for a horizontal surface), the droplet starts to move forward. During the movement, eq 10 can be used to explain the behavior of the droplet shown in Figure 3b, where the instant velocity presents multiple peak values. The streaming force Fs decreases exponentially as the droplet moves away from the wave source due to its attenuation in the substrate. Meanwhile, the viscous resistance force Fr(v) is proportional to the instant velocity. At the starting point, Fs sin ΘR is much larger than the sum of Fcl, Fr, and mg sin α, creating a positive acceleration dv/dt. The instant velocity increases accordingly while Fs sin ΘR decreases, and Fr increases until the forces reach their first balance point, where dv/dt = 0. Afterward, the instant velocity decreases rapidly due to the negative acceleration, causing the fast decrease of Fr until once again Fs sin ΘR is dominant. This process would repeat several times before the droplet moves to the position where the damped acoustic wave cannot initiate the movement.

We also investigated the droplet transport characteristics of the hydrophobically treated ZnO/Al SAW devices by measuring average moving velocities and accelerations at different power levels (Figure 4c) and compared them with those on a ZnO/Si surface. The average accelerations on both the CYTOP/ZnO/Al and CYTOP/ZnO/Si surfaces are increased with the input power, reaching 42.1 ± 7.1 and 0.05 ± 0.003 mm/s2, respectively, for an applied power of 0.72 W, corresponding to average velocities (averaged over time) of 8.0 ± 0.8 and 0.2 ± 0.01 mm/s. Importantly, the threshold power to initiate droplet movement on the CYTOP/ZnO/Al surface is much smaller than that on the CYTOP/ZnO/Si device. In addition, the droplet average velocities are higher on the CYTOP/ZnO/Al surface than that on the CYTOP/ZnO/Si device at the same power, indicating that the acoustic devices on the ZnO/Al with a hierarchically textured surface are more efficient for droplet transport.

This enhanced performance can, in the first instance, be attributed to the hierarchical CYTOP/ZnO/Al surface, which reduces the contact angle hysteresis to 9°, significantly smaller than on the CYTOP/ZnO/Si surface at 28°, decreasing the threshold power required to initiate the droplet movement along the surface, and also reducing the power needed to overcome the lateral pinning force which could restrict the droplet movement. The surfaces also retained a receding contact angle of 105°, ensuring that droplets do not detach from the surface when curved/bent.

For completeness, the Rayleigh angle also plays an important part in the enhanced performance. We calculated it as 30.8° on ZnO/Al, as opposed to 19.7° on ZnO/Si (using phase velocities of 2868 m/s on the ZnO/Al sheet, 4351 m/s on ZnO/Si, and 1468 m/s in water) and verified experimentally (e.g., 33.6° and 15.8° as shown in Figure 4d,e). As predicted by eq 10, the driving force is the projection of the streaming force on the moving surface, which can be calculated by Fs sin ΘR. For ZnO/Al, sin ΘR is around 0.55, while it is around 0.27 for ZnO/Si. Therefore, given the same input power (same Fs), the driving force of ZnO/Al devices is twice that of ZnO/Si devices along the moving direction and, thus, is more efficient for droplet transport.

Furthermore, the enhanced actuation of the liquid can be attributed to the different ways in which the droplets interact with the substrate surface. For the droplet on the CYTOP/ZnO/Al substrate, assuming it is in a mixed Wenzel/Cassie–Baxter state, the entrapped air prevents the droplet from flowing into the surface’s topology and reduces the contact area between the liquid and the solid surface, thus lowering the friction and causing efficient transport. In contrast, there is little air entrapped under the droplet on the silicon substrates with smooth surfaces. The larger Rayleigh angle and smaller contact angle hysteresis for the CYTOP/ZnO/Al device during movement imply that liquid droplets move using a combination of rolling and sliding (Figure S2a). On the contrary, the droplet movement is dominated by sliding and jumping modes on the CYTOP/ZnO/Si surface (Figure S2b).

This mechanism enables us to demonstrate movement on inclined surfaces (Figure S3) by tilting the device plate into different orientations, e.g., inclined angled slopes, vertical, and upsidedown positions. Here, an important consideration is the droplet size, as it has a significant influence on pumping at different inclination angles due to the effect of gravity. This is especially important at inclination angles around 90°, and we experimentally determined a maximum volume for our device to be 3 μL. Larger droplets cannot be pumped upward but move downward due to gravity.

Demonstration of Programmable, Flexible, and Bendable Acoustofluidics

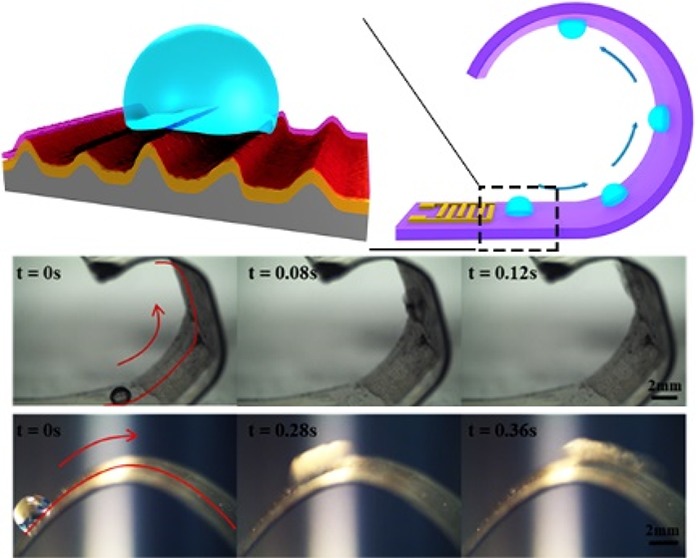
To demonstrate the concept of programmable, flexible, and bendable three-dimensional acoustofluidics using hierarchical CYTOP/ZnO/Al nanostructured surfaces, we deformed the CYTOP/ZnO/Al (600 μm thick) device into a circle (see schematic illustration in Figure 1a). Figure 5a–c shows that a water droplet could be efficiently pumped forward on different segments of its surface with a curvature varying from 54.5 to 85.7 m–1.

Figure 5.

Figure 5

Open in a new tab

Experimental demonstration of 3D pumping driven by the ZnO-based acoustic wave on bendable substrates. (a–c) 1 μL droplets moving at different stages on curved surfaces (P = 15 W). (d) 0.5 μL droplet moving on a “roller coaster” formed by curled acoustic wave devices (P = 20 W). (e) 2 μL droplet moving past a hilly surface (P = 6 W). (f) 0.5 μL droplet moving on a twisted surface (P = 3 W).

To further extend the flexibility of our platform, we reduced the thickness of Al sheets with the corresponding acoustic wave modes changing from those associated with Rayleigh waves to Lamb waves. Acoustic wave devices were designed and fabricated on 200 μm thick ZnO/Al sheets and deformed in shapes of a “roller coaster” (Figure 5d,e, and Movies S1 and S2). Finally, we also show that the droplet can be easily pumped along arbitrary topographies using a randomly twisted CYTOP/ZnO/Al (50 μm thick) sample (Figure 5f and Movie S3).

Conclusions

In summary, we designed nanostructured surfaces using hierarchical textures to optimize shear hydrophobicity and tensile hydrophilicity to tune droplet transport and adhesion on arbitrarily oriented devices. We demonstrated that the CYTOP/ZnO/Al sheets enabled a significantly better actuation performance when compared to conventional ZnO/Si acoustic wave devices. These CYTOP/ZnO/Al sheets were uniquely capable of efficiently driving droplets across a wide range of inclination angles (0° < α ≤ 180°). Our designed devices can be flexibly deformed and then maintain their shape, while enabling efficient liquid pumping. We envisage that the surface design principles and demonstrated devices/applications will be pivotal for liquid sampling for smart diagnostic systems within mobile and disposable settings.

Methods

Sample Preparation

ZnO/Al and ZnO/Si substrates were prepared using magnetron sputtering (NS3750, Nordiko). ZnO films with thicknesses of 5 μm were deposited on 50 μm thick Al foils, 200 and 600 μm thick Al thin plates, and 500 μm thick 4 in. (100) Si wafers in vacuum with a pressure of 0.65 Pa. A 99.99% pure Zn target was used while Ar/O2 gases with flow rates of 10/13 sccm were introduced to form a plasma and to provide oxygen ions (power, 400 W).

The acoustic wave devices included interdigital transducers (IDTs) on top of the ZnO thin films, fabricated through photolithography and lift-off processes. The Cr/Au electrodes with a thickness of 20 nm/100 nm were deposited using a thermal evaporator. For hydrophobic surface treatment, 1% CYTOP solution (L-809A) was dip-coated on the ZnO surface and heated to 180 °C for 1 min.

Experimental Methods

The surface roughness of all samples was characterized using an interferometer (Bruker Contour GT-K) and an AFM (Veeco Dimension 3100). The static, advancing, and receding contact angles were measured using sessile droplets and volume addition and withdrawal on a droplet shape analyzer (Kruss DSA30S). In the acoustofluidic experiments, the acoustic wave devices were connected to an RF signal generator (9 kHz–2.4 GHz 2024, Marconi Instruments) through a power amplifier (model 75A250, Amplifier Research). The movements of water droplets were imaged by both a high-speed camera (Phantom V2511, 3000 FPS) and a standard CMOS camera.

Acknowledgments

We gratefully acknowledge the microfluidic platforms in Northumbria University and the James Watt Nanofabrication Centre at the University of Glasgow. The work is also supported by the Special Interests Group for Acoustofluidics under the UK Fluids Network. We also acknowledge Mr. Yong Wang and Mr. Xiang Tao for their support in experiments. This work was financially supported by Research and Development Program of China (Grant 2016YFB0402705), the UK Engineering and Physical Sciences Research Council (EPSRC) grants, EP/P018998/1 and EP/K027611/1, Shenzhen Key Lab Fund (ZDSYS20170228105421966), Shenzhen Science & Technology Project (Grant JCYJ20170817100658231), the National Natural Science Foundation of China (51605485), as well as by the European Research Council Advanced Investigator Award 340117 (BioPhononics). All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supporting Information. Additional data related to this paper may be requested from the authors.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.0c00005.

  • Additional data and figures including surface morphology of the 600 μm thick Al substrate, deformation of a 1 μL droplet in the movement driven by acoustic waves, droplets moving on various tilted flat surfaces, and contact angle hysteresis measurements (PDF)

  • Movie S1: droplet moving on a “roller coaster” (AVI)

  • Movie S2: droplet moving past a hilly surface (AVI)

  • Movie S3: droplet moving on a twisted surface (AVI)

Author Present Address

⬢ Pep Canyelles-Pericas − Department of Integrated Devices and Systems, University of Twente, Enschede 7522 NB, The Netherlands

Author Contributions

Y.Q.F., G.M., J.R., and J.M.C. proposed the idea. R.T., Y.Q.F., J.T.L., and P.C.-P. performed the experimental work. R.T. and Y.Q.F. wrote the manuscript and performed analyses. G.M., J.R., H.T., Q.W., J.L., X.Y., J.Z., and J.M.C. were involved in writing, discussions, and modifications of the paper.

The authors declare no competing financial interest.

Author Status

Corresponding author: Prof. Richard Yongqing Fu, E-mail: richard.fu@northumbria.ac.uk.

Supplementary Material

nl0c00005_si_001.pdf (737.7KB, pdf)
nl0c00005_si_002.avi (9.9MB, avi)
nl0c00005_si_003.avi (11.3MB, avi)
nl0c00005_si_004.avi (116.5MB, avi)

References

  1. Kim J.; Campbell A. S.; de Ávila B. E. F.; Wang J. Wearable Biosensors for Healthcare Monitoring. Nat. Biotechnol. 2019, 37 (4), 389–406. 10.1038/s41587-019-0045-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Imani S.; Bandodkar A. J.; Mohan A. M. V.; Kumar R.; Yu S.; Wang J.; Mercier P. P. A Wearable Chemical-Electrophysiological Hybrid Biosensing System for Real-Time Health and Fitness Monitoring. Nat. Commun. 2016, 7 (11650), 11650. 10.1038/ncomms11650. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Zhang S.; Cicoira F. Flexible Self-Powered Biosensors. Nature 2018, 561, 466–467. 10.1038/d41586-018-06788-1. [DOI] [PubMed] [Google Scholar]
  4. Piraino F.; Selimović Š.; Iniewski K. K.. Diagnostic Devices with Microfluidics; CRC Press, 2017; 10.1201/9781315154442. [DOI] [Google Scholar]
  5. Yang Y.; Gao W. Wearable and Flexible Electronics for Continuous Molecular Monitoring. Chem. Soc. Rev. 2019, 48, 1465–1491. 10.1039/C7CS00730B. [DOI] [PubMed] [Google Scholar]
  6. Liu Y.; Pharr M.; Salvatore G. A. Lab-on-Skin: A Review of Flexible and Stretchable Electronics for Wearable Health Monitoring. ACS Nano 2017, 11 (10), 9614–9635. 10.1021/acsnano.7b04898. [DOI] [PubMed] [Google Scholar]
  7. Kim D.-H.; Ghaffari R.; Lu N.; Rogers J. A. Flexible and Stretchable Electronics for Biointegrated Devices. Annu. Rev. Biomed. Eng. 2012, 14 (1), 113–128. 10.1146/annurev-bioeng-071811-150018. [DOI] [PubMed] [Google Scholar]
  8. Jin H.; Zhou J.; He X.; Wang W.; Guo H.; Dong S.; Wang D.; Xu Y.; Geng J.; Luo J. K.; Milne W. I. Flexible Surface Acoustic Wave Resonators Built on Disposable Plastic Film for Electronics and Lab-on-a-Chip Applications. Sci. Rep. 2013, 3 (1), 2140. 10.1038/srep02140. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Zhang Y.; Nayak T.; Hong H.; Cai W. Biomedical Applications of Zinc Oxide Nanomaterials. Curr. Mol. Med. 2013, 13 (10), 1633–1645. 10.2174/1566524013666131111130058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Fu Y. Q.; Luo J. K.; Nguyen N. T.; Walton A. J.; Flewitt A. J.; Zu X. T.; Li Y.; McHale G.; Matthews A.; Iborra E.; Du H.; Milne W. I. Advances in Piezoelectric Thin Films for Acoustic Biosensors, Acoustofluidics and Lab-on-Chip Applications. Prog. Mater. Sci. 2017, 89, 31–91. 10.1016/j.pmatsci.2017.04.006. [DOI] [Google Scholar]
  11. Fu Y. Q.; Luo J. K.; Du X. Y.; Flewitt A. J.; Li Y.; Markx G. H.; Walton A. J.; Milne W. I. Recent Developments on ZnO Films for Acoustic Wave Based Bio-Sensing and Microfluidic Applications: A Review. Sens. Actuators, B 2010, 143 (2), 606–619. 10.1016/j.snb.2009.10.010. [DOI] [Google Scholar]
  12. Tao R.; Hasan S. A.; Wang H. Z.; Zhou J.; Luo J. T.; McHale G.; Gibson D.; Canyelles-Pericas P.; Cooke M. D.; Wood D.; Liu Y.; Wu Q.; Ng W. P.; Franke T.; Fu Y. Q. Bimorph Material/structure Designs for High Sensitivity Flexible Surface Acoustic Wave Temperature Sensors. Sci. Rep. 2018, 8 (1), 9052. 10.1038/s41598-018-27324-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Liu Y.; Li Y.; El-Hady A. M.; Zhao C.; Du J. F.; Liu Y.; Fu Y. Q. Flexible and Bendable Acoustofluidics Based on ZnO Film Coated Aluminium Foil. Sens. Actuators, B 2015, 221, 230–235. 10.1016/j.snb.2015.06.083. [DOI] [Google Scholar]
  14. Wang S. Y.; Ma J. Y.; Li Z. J.; Su H. Q.; Alkurd N. R.; Zhou W. L.; Wang L.; Du B.; Tang Y. L.; Ao D. Y.; Zhang S. C.; Yu Q. K.; Zu X. T. Surface Acoustic Wave Ammonia Sensor Based on ZnO/SiO2 Composite Film. J. Hazard. Mater. 2015, 285, 368–374. 10.1016/j.jhazmat.2014.12.014. [DOI] [PubMed] [Google Scholar]
  15. Jönsson-Niedziółka M.; Lapierre F.; Coffinier Y.; Parry S. J.; Zoueshtiagh F.; Foat T.; Thomy V.; Boukherroub R. EWOD Driven Cleaning of Bioparticles on Hydrophobic and Superhydrophobic Surfaces. Lab Chip 2011, 11 (3), 490–496. 10.1039/C0LC00203H. [DOI] [PubMed] [Google Scholar]
  16. Schutzius T. M.; Jung S.; Maitra T.; Graeber G.; Köhme M.; Poulikakos D. Spontaneous Droplet Trampolining on Rigid Superhydrophobic Surfaces. Nature 2015, 527 (7576), 82–85. 10.1038/nature15738. [DOI] [PubMed] [Google Scholar]
  17. Bird J. C.; Dhiman R.; Kwon H.-M.; Varanasi K. K. Reducing the Contact Time of a Bouncing Drop. Nature 2013, 503 (7476), 385–388. 10.1038/nature12740. [DOI] [PubMed] [Google Scholar]
  18. Lee W. K.; Jung W.-B.; Nagel S. R.; Odom T. W. Stretchable Superhydrophobicity from Monolithic, Three-Dimensional Hierarchical Wrinkles. Nano Lett. 2016, 16 (6), 3774–3779. 10.1021/acs.nanolett.6b01169. [DOI] [PubMed] [Google Scholar]
  19. Gao L.; McCarthy T. J. Teflon Is Hydrophilic. Comments on Definitions of Hydrophobic, Shear versus Tensile Hydrophobicity, and Wettability Characterization. Langmuir 2008, 24 (17), 9183–9188. 10.1021/la8014578. [DOI] [PubMed] [Google Scholar]
  20. Shirtcliffe N. J.; McHale G.; Atherton S.; Newton M. I. An Introduction to Superhydrophobicity. Adv. Colloid Interface Sci. 2010, 161 (1–2), 124–138. 10.1016/j.cis.2009.11.001. [DOI] [PubMed] [Google Scholar]
  21. Pilat D. W.; Papadopoulos P.; Schäffel D.; Vollmer D.; Berger R.; Butt H. J. Dynamic Measurement of the Force Required to Move a Liquid Drop on a Solid Surface. Langmuir 2012, 28 (49), 16812–16820. 10.1021/la3041067. [DOI] [PubMed] [Google Scholar]
  22. ElSherbini A. I.; Jacobi A. M. Retention Forces and Contact Angles for Critical Liquid Drops on Non-Horizontal Surfaces. J. Colloid Interface Sci. 2006, 299 (2), 841–849. 10.1016/j.jcis.2006.02.018. [DOI] [PubMed] [Google Scholar]
  23. De Souza E. J.; Gao L.; McCarthy T. J.; Arzt E.; Crosby A. J. Effect of Contact Angle Hysteresis on the Measurement of Capillary Forces. Langmuir 2008, 24 (4), 1391–1396. 10.1021/la702188t. [DOI] [PubMed] [Google Scholar]
  24. Ahmed G.; Sellier M.; Jermy M.; Taylor M. Modeling the Effects of Contact Angle Hysteresis on the Sliding of Droplets down Inclined Surfaces. Eur. J. Mech. B/Fluids 2014, 48, 218–230. 10.1016/j.euromechflu.2014.06.003. [DOI] [Google Scholar]
  25. Bruckenstein S.; Shay M. Experimental Aspects of Use of the Quartz Crystal Microbalance in Solution. Electrochim. Acta 1985, 30 (10), 1295–1300. 10.1016/0013-4686(85)85005-2. [DOI] [Google Scholar]
  26. Shiokawa S.; Matsui Y.; Ueda T. Study on Saw Streaming and Its Application to Fluid Devices. Jpn. J. Appl. Phys. 1990, 29 (S1), 137–139. 10.7567/JJAPS.29S1.137. [DOI] [Google Scholar]
  27. Alghane M.; Fu Y. Q.; Chen B. X.; Li Y.; Desmulliez M. P. Y.; Walton A. J. Streaming Phenomena in Microdroplets Induced by Rayleigh Surface Acoustic Wave. J. Appl. Phys. 2011, 109 (11), 114901. 10.1063/1.3586040. [DOI] [Google Scholar]
  28. Muschi M.; Brudieu B.; Teisseire J.; Sauret A. Drop Impact Dynamics on Slippery Liquid-Infused Porous Surfaces: Influence of Oil Thickness. Soft Matter 2018, 14 (7), 1100–1107. 10.1039/C7SM02026K. [DOI] [PubMed] [Google Scholar]
  29. Forsberg P. S. H.; Priest C.; Brinkmann M.; Sedev R.; Ralston J. Contact Line Pinning on Microstructured Surfaces for Liquids in the Wenzel State. Langmuir 2010, 26 (2), 860–865. 10.1021/la902296d. [DOI] [PubMed] [Google Scholar]
  30. Bartolo D.; Bouamrirene F.; Verneuil É.; Buguin A.; Silberzan P.; Moulinet S. Bouncing or Sticky Droplets: Impalement Transitions on Superhydrophobic Micropatterned Surfaces. Europhys. Lett. 2006, 74 (2), 299–305. 10.1209/epl/i2005-10522-3. [DOI] [Google Scholar]
  31. Dave P. Y.; Patel K. H.; Chauhan K. V.; Chawla A. K.; Rawal S. K. Examination of Zinc Oxide Films Prepared by Magnetron Sputtering. Procedia Technol. 2016, 23, 328–335. 10.1016/j.protcy.2016.03.034. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl0c00005_si_001.pdf (737.7KB, pdf)
nl0c00005_si_002.avi (9.9MB, avi)
nl0c00005_si_003.avi (11.3MB, avi)
nl0c00005_si_004.avi (116.5MB, avi)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES