Simultaneous T₁ and T₂ Mapping of Hyperpolarized ¹³C Compounds using the bSSFP Sequence

Abstract

As in conventional ¹H MRI, T₁ and T₂ relaxation times of hyperpolarized (HP) ¹³C nuclei can provide important biomedical information. Two new approaches were developed for simultaneous T₁ and T₂ mapping of HP ¹³C probes based on balanced steady state free precession (bSSFP) acquisitions: a method based on sequential T₁ and T₂ mapping modules, and a model-based joint T₁/T₂ approach analogous to MR fingerprinting. These new methods were tested in simulations, HP ¹³C phantoms, and in vivo in normal Sprague-Dawley rats. Non-localized T₁ values, low flip angle EPI T₁ maps, bSSFP T₂ maps, and Bloch-Siegert B₁ maps were also acquired for comparison. T₁ and T₂ maps acquired using both approaches were in good agreement with both literature values and data from comparative acquisitions. Multiple HP ¹³C compounds were successfully mapped, with their relaxation time parameters measured within heart, liver, kidneys, and vasculature in one acquisition for the first time.

Graphical Abstract

1. Introduction

The development of hyperpolarized (HP) ¹³C imaging with dissolution dynamic nuclear polarization, which provides a >10,000-fold signal enhancement for injected substrates, has enabled monitoring of various physiological processes for a wide range of diseases [1-3]. Probes such as pyruvate and urea inform on metabolism and perfusion [4-6], respectively, with several new probes currently being developed for additional applications [7-9]. Recent phase I and phase II human clinical trials have shown successful translation of [1-¹³C]pyruvate for monitoring metabolic conversion to [1-¹³C]lactate, [1-¹³C]alanine, and [1-¹³C]bicarbonate in prostate, brain, and liver cancer, and in the heart [10-15].

¹³C T₁’s and T₂’s are important parameters for characterizing new probes, pulse sequence optimization, calculations of rate constants such as k_PL [16], and could also be used for assessment of healthy versus diseased tissue, as is commonly done in ¹H imaging [17-20]. The development of quantitative MRI has indicated the advantage of direct quantitation of these parameters for a wide variety of clinical applications. Estimation of these parameters for ¹H has been well studied and can be done either individually [21-26] or simultaneously with MR fingerprinting with the balanced steady-state free precession (bSSFP) sequence [27-29]. High spatial resolution T₂ mapping has been recently developed for calculating in vivo ¹³C T₂’s using bSSFP [30-34], while T₁ values for ¹³C compounds, which represent decay of the hyperpolarization towards thermal equilibrium, have been reported on a non-localized basis. Furthermore, mapping the distribution of both parameters in vivo in one acquisition has not been investigated to our knowledge. Simultaneous acquisition of T₁ and T₂ data is challenging for multiple reasons, such as the limited lifetime of the HP magnetization, conversion of metabolically-active compounds, and flow.

bSSFP has previously been shown to provide high SNR imaging of ¹³C compounds [30,31,35] in an efficient and rapid fashion and has attractive properties for simultaneous mapping of T₁ and T₂ by analogy with its use in ¹H MR fingerprinting. In this study, we aimed to develop and apply simultaneous in vivo T₁ and T₂ mapping of multiple hyperpolarized ¹³C probes using two new approaches based on specialized bSSFP acquisitions: a method based on sequential T₁ and T₂ mapping modules, and a model-based joint T₁/T₂ approach analogous to MR fingerprinting. These two different approaches were successfully tested in HP ¹³C phantoms and normal rats, producing high spatial resolution T₁ and T₂ maps of heart, liver, kidneys, and vasculature.

2. Methods

2.1. Sample Preparation

[2-¹³C]pyruvate, [¹³C]urea, [¹³C,¹⁵N₂]urea, and HP001 were prepared as described previously [31,36]. The compounds were individually polarized in a HyperSense system (Oxford Instruments, Abingdon, UK) operating at 1.35 K and 3.35 T to achieve polarizations of ~15-20% for each compound. The compounds were then dissolved in appropriate media: 4.5 mL of 80 mM NaOH/40 mM Tris buffer for [2-¹³C]pyruvic acid resulting in 80 mM [2-¹³C]pyruvate (hereafter referred to as C₂-pyruvate); 5 mL of 1x phosphate-buffered saline for [¹³C]urea resulting in 110 mM [¹³C]urea; 5 mL of 1x phosphate-buffered saline for [¹³C,¹⁵N₂]urea resulting in 110 mM [¹³C,¹⁵N₂]urea; and 5 mL of 1x phosphate-buffered saline for HP001 resulting in 100 mM HP001.

2.2. Animal Preparation and Hardware

All animal studies were done under protocols approved by the University of California San Francisco Institutional Animal Care and Use Committee (IACUC). Normal female Sprague-Dawley rats (Charles River Laboratories, Wilmington, MA, Age: ~ 1 year old, Average Weight: ~284 g), anesthetized using isoflurane (1.5%, gas flow rate 1 L/min) and inserted with lateral tail vein catheters, were used during the course of these experiments.

All experiments were performed on a GE MR750 3 Tesla clinical MRI scanner (GE Healthcare, Waukesha, WI) using custom dual-tuned ¹³C/¹H quadrature transceiver radiofrequency (RF) coils with an 8 cm diameter. For the duration of the experiments, all animals were placed in a supine position on a heated pad within the coil, centered at the level of the kidneys. A 1 mL enriched [¹³C]urea vial phantom (6.0 M) was placed adjacent to the abdomen and used for frequency and power calibration.

2.3. MR Experiments

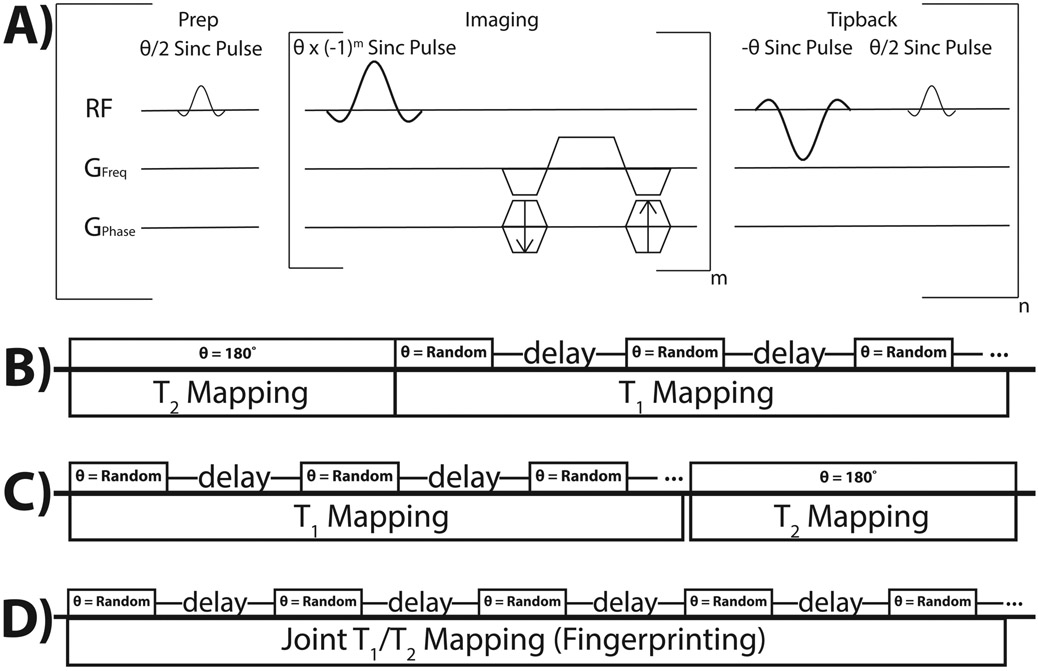
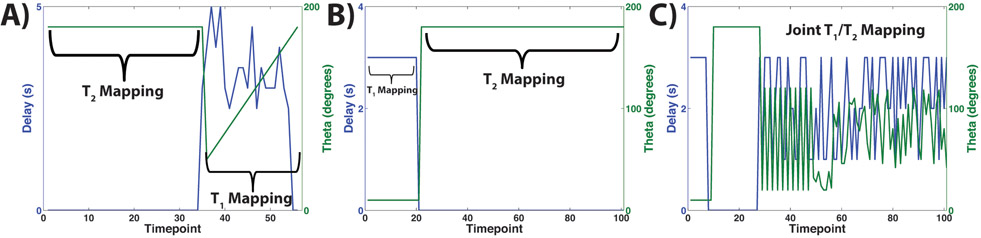
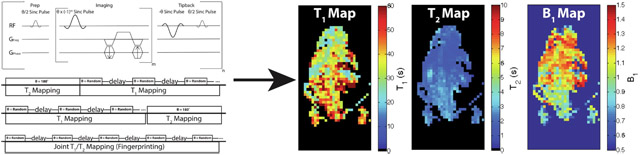
A custom bSSFP sequence was developed for this study, consisting of three portions for dynamic imaging (Figure 1A): preparatory portion consisting of a θ/2-TR/2 pulse for catalyzation, imaging portion consisting of alternating phase sinc pulses and balanced gradients, and a tipback portion consisting of a θ-TR-θ/2-TR/2 sequence for storing the magnetization along the longitudinal axis for imaging multiple time-points. Each acquisition consisted of one of two approaches: either two independent scanning modules (dual module) (Figure 1B and 1C) or modified MR fingerprinting (model-based joint T₁T₂ approach) (Figure 1D). The dual module approach featured one T₂ mapping module and one T₁ mapping module (in either order). The T₂ mapping module was acquired as described previously [31], The T₁ module specifically involved using delays between imaging, whereby the magnetization tipped back onto the longitudinal axis after imaging would decay by T₁. Initial studies utilized both constant and variable delays, ranging from 1-10 s, as well as constant and variable flip angles, ranging from 10-180° (θ) during the T₁ mapping module, to investigate potential in vivo SNR limitations and consequent signal fitting. Figure 2A shows an example set of delays and flip angles for a T₂ followed by T₁ mapping acquisition, with variable delays and flip angles for the T₁ mapping portion, while Figure 2B shows the delays and flip angles for a T₁ followed by T₂ mapping acquisition. Initial studies of the modified MR fingerprinting approach involved random delays between imaging, ranging from 1-9 s, and random flip angles, ranging from 10-180° (θ), throughout the entire acquisition, with Figure 2C showing an example set of delays and flip angles for one acquisition. Simulations were performed for the modified MR fingerprinting approach to generate potential combinations of flip angles, delays, and total time-points using the signal equation detailed below. All simulations had added Gaussian noise to mimic in vivo conditions and combinations resulting in calculated T₁ T₂, and B₁ values within 10% of the inputted values were subsequently utilized. The B₁ value represents the B₁ ratio, where a ratio of 1.0 would represent the exact flip angle intended.

Figure 1:

bSSFP-based methods for simultaneous T₁ and T₂ mapping of HP ¹³C probes. (A) Depiction of the bSSFP sequence used in this study, with the preparatory pulse, imaging portion, and tipback pulses for storing the magnetization during the delay portions. (B) Schematic of the dual module approach, with T₂ mapping followed by T₁ mapping. (C) Schematic of a different iteration of the dual module approach, with T₁ mapping followed by T₂ mapping. (D) Schematic of the modified MR fingerprinting approach that jointly estimated T₁, T₂, and B₁. The rectangles in B-D represent the image acquisition portions with the depicted θ.

Figure 2:

Depiction of representative sequence delays and flip angles used for each approach. (A) Delay and flip angles for a T₂ mapping module followed by a T₁ mapping module. The first 16 time-points represent the T₂ mapping module and featured no delay and θ = 180°. The rest of the time-points represent the T₁ mapping module, which featured random delays between 6 and 10 s, and a ramping variable flip angle scheme. (B) Delay and flip angles for a T₁ mapping module followed by a T₂ mapping module. The first 20 time-points represent the T₁ mapping module and featured a constant 3 s delay and θ = 10°. The rest of the time-points represent the T₂ mapping module, which featured no delay and θ = 180°. (C) Delay and flip angles for a modified MR fingerprinting approach. The first 8 time-points featured a constant 3 s delay and θ = 10° and served as a “mini” T₁ mapping module. The next 22 time-points featured no delay and θ = 180° and served as a “mini” T₂ mapping module. The rest of the time-points featured random delays between 1 and 3 s, and random flip angles between 20° and 120°.

All in vivo acquisitions were acquired as 2D coronal projections (no slice-select gradient) and featured the following parameters: 14 x 7 cm² FOV, 1.25 x 1.25 - 4 x 4 mm² in-plane spatial resolution, 1.6 ms sinc pulse with a TBW = 4, 5.6-6.4 ms TR, 40-90 time-points, scans starting at 30 s after start of injection, with ~3 mL injected over 12 s. For comparison, individual T₁ maps, T₂ maps, and B₁ maps were acquired using echo-planar imaging (EPI) [37], bSSFP [31], and Bloch-Siegert B₁ mapping [38,39], respectively. Single-shot echo-planar imaging (EPI) T₁ maps were also acquired as coronal projections and featured the following parameters: 2.5 x 2.5 mm² in-plane spatial resolution, 3.2 ms sinc pulse with a TBW = 4, constant 5° flip angle, 1 s TR, 80 time-points, scans starting at 30 s after start of injection. bSSFP T₂ maps were acquired with the following parameters: 14 x 7 cm² FOV, 2.5 x 2.5 mm² in-plane spatial resolution, 1.6 ms sinc pulse with a TBW = 4, 5.6 ms TR, 100 time-points, scans starting at 30 s after start of injection. Bloch-Siegert B₁ maps were acquired in the coronal plane with a single-band spectral-spatial excitation pulse and a single-shot spiral readout and featured the following parameters: 8.5 x 8.5 cm² FOV, 2.5 x 2.5 mm² in-plane spatial resolution, 1 cm slice thickness, fermi pulse duration T_RF of 12 ms, frequency offset ω_RF of ± 4.5 kHz, 10° flip angle, 200 ms TR, scans starting at 15 s after start of injection. Non-localized T₁ values were also acquired using a 500 μs hard pulse, 5° flip angle, 3 s TR, and 100 time-points. For anatomic reference, 3D bSSFP proton images (16 x 8 x 4.8 cm, 256 x 128 x 80, 5.1 ms TR, 50° flip angle) were acquired.

2.4. Phantom Experiments

All hyperpolarized phantom ([¹³C,¹⁵N₂]urea) acquisitions were also acquired as 2D coronal projections and featured the following parameters: 14 x 7 cm² FOV, 1 x 1 mm² in-plane spatial resolution, 1.6 ms sinc pulse with a TBW = 4, 7.7 ms TR, 80-110 time-points, scans starting at 20 s after the syringe was placed into the coil.

2.5. Signal Model and Fitting

All data was reconstructed and analyzed in Matlab (MathWorks, Natick, Massachusetts, USA). The signal train for each approach was modeled using the bSSFP signal equation developed by Scheffler [40], adopted for hyperpolarized ¹³C imaging (i.e. transient state with negligible T₁ recovery):

$$M_{xy,n}=M_{z,0}\ast \sin {}^{\theta }∕_2\ast {\left[(\cos {}^{\theta }∕_2{)}^{{}^2}+E_2(\sin {}^{\theta }∕_2{)}^{{}^2}\right]}^n$$ [1]

where θ is the flip angle, E₁ = exp(−TR/T₁), E₂ = exp(−TR/T₂), and n is the pulse number (i.e. phase encode). During the delay portion of the T₁ mapping module and the modified MR fingerprinting approach, the magnetization was assumed to decay by exp(−delay/T₁). M_z,0 corresponded to the initial longitudinal magnetization for each time-point, after accounting for the delay portion.

An initial SNR threshold, which varied from 5-20 depending on the compound, was used to filter out low SNR voxels. Additionally, respiratory motion correction in the superior/inferior direction was performed using rigid translation via mutual information, as described previously [41]. All fitting was done on a voxel-by-voxel basis and only voxels with fits of R²>0.9 were kept. The fitting of the dual module approach acquisitions was done by first fitting the T₂ mapping portion to a single exponential fit, and then feeding in the resulting values into the fitting of the T₁ mapping portion. The fitting for the T₁ mapping portions of the dual module approach, as well as the modified MR fingerprinting, was done using non-linear least squares with the trust-region-reflective algorithm. The initial guesses for the algorithm were based on known non-localized T₁ values for each compound, as well as previously acquired mean T₂ maps in the case of the modified MR fingerprinting. For comparison for the modified MR fingerprinting, T₁ and T₂ were fit using dictionary matching via the maximum inner product method [42], where the dictionary was created with a range of T₁’s (200 ms increments from 10-100 s), T₂’s (100 ms increments from 0.1 to 10 s), and B₁’s (2% increments from 50-150%), where B₁ is the ratio of the obtained flip angle to the desired flip angle [28].

EPI T₁ maps were calculated on a voxel-by-voxel basis by fitting to a mono-exponential curve after respiratory motion and flip angle correction. bSSFP T₂ maps were calculated as described previously [31], with the mean T₂ maps used for comparison.

3. Results

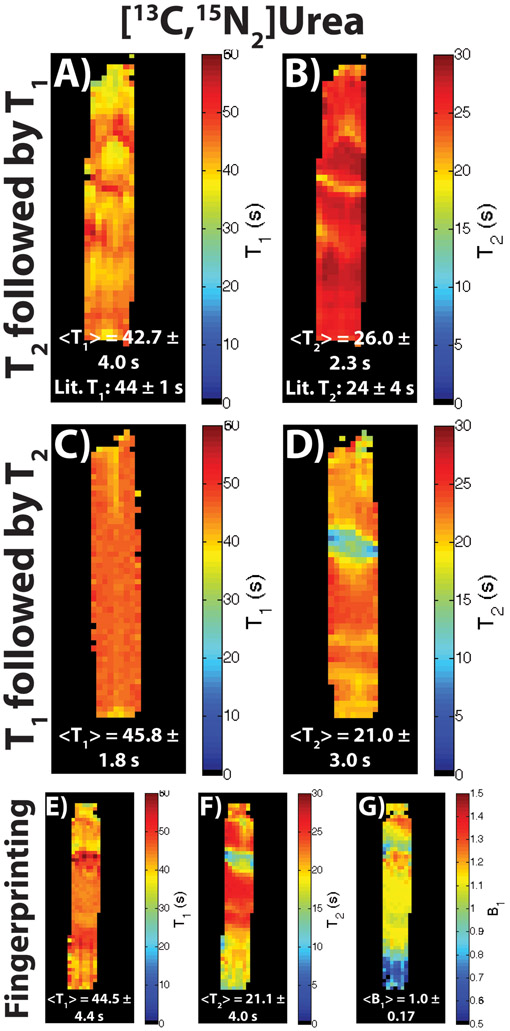
Figure 3 shows the calculated parameter maps for the hyperpolarized [¹³C,¹⁵N₂]urea phantom acquisitions of all three approaches. The dual module approach with the T₂ module followed by the T₁ module is shown in parts A and B, while the dual module approach with the T₁ module followed by the T₂ module is shown parts C and D. The modified MR fingerprinting approach is shown in parts E-G. The acquisitions were similar to those shown in Figure 2, albeit with more T₁ and T₂ mapping time-points due to the longer solution state T₁ and T₂ compared to in vivo for [¹³C,¹⁵N₂]urea. The mean and intra-map standard deviation of the T₁ and T₂ maps from all three acquisitions matched up well among each other and the literature values. The B₁ map in part G, with a mean value of 1.0, matched up well with the expected profile of the syringe within the volume coil, with some drop-off near the edge of the coil as seen at the bottom of the syringe. Deviations within the maps can be attributed to some B₀ inhomogeneity along the S/I dimension.

Figure 3:

Resulting T₁, T₂, and B₁ maps in a hyperpolarized [¹³C,¹⁵N₂]urea phantom for all three types of acquisitions described. (A,B) T₁ and T₂ maps for a dual module acquisition (T₂ mapping module followed by a T₁ mapping module). The acquisition was similar to the one depicted in Figure 2A, except with more T₂ time-points acquired due to the long solution state T₂ of the compound. (C,D) T₁ and T₂ maps for a different iteration of the dual module acquisition (T₁ mapping module followed by a T₂ mapping module). The acquisition was similar to the one depicted in Figure 2B, except with more T₁ and T₂ time-points acquired due to the long solution state T₁ and T₂ of the compound. (E-G) T₁, T₂, and B₁ maps for a modified MR fingerprinting approach, with the acquisition similar to the one depicted in Figure 2C, except with more T₁ and T₂ time-points acquired due to the long solution state T₁ and T₂ of the compound. For all three acquisitions, the resulting mean ± intra-map standard deviation agreed well with the literature value for all the T₁ and T₂ maps. The B₁ also had a mean of 1.0, which is expected with a stationary syringe centered in a volume coil. Deviations in values in the S/I direction for all maps can be attributed to some B₀ inhomogeniety, as well as some B₁ drop-off at the edge of the coil.

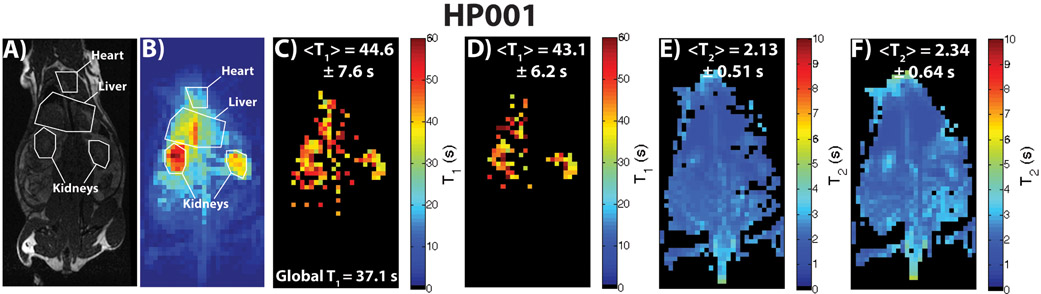
Figure 4 shows results for an HP001 acquisition of the dual module approach (T₂ mapping followed by T₁ mapping), including a ¹H anatomical slice (A), representative time-point (B), T₁ map (C), EPI T₁ map (D), T₂ Map (E), and bSSFP T₂ map (F). The T₁ mapping module featured variable delays and flip angles, as seen in Figure 2A. The relevant anatomical structures are outlined, with the location being similar in all in vivo acquisitions in the study. The mean and intra-map standard deviation of the T₁ map was 44.6 ± 7.6 s, which was close to the non-localized T₁ of 37.1 s, with the T₁ distribution matching well with the EPI T₁ map in the abdomen. The T₂ maps also agreed well with each other in terms of distribution and T₂’s and mean and intra-map standard deviation. The Bland-Altman plots in Supporting Figure 1A and 1B show good agreement between the dual module and comparative acquisitions on a voxel-by-voxel basis, with most voxels agreeing to within a few seconds (for T₁)/less than 0.5 s (for T₂) of each other, except for voxels corresponding to long T₁’s and T₂’s in the kidneys that can be attributed to both renal filtration effects and some low SNR fitting of the dual module approach. Supporting Video 1 shows all the time-points of the acquisition, along with the signal train for a representative voxel within the kidney, where rapid T₂ decay occurs first, followed by slower T₁ decay.

Figure 4:

Depiction of a ¹H anatomical slice (A), representative time-point (B), T₁ map (C), EPI T₁ Map (D), dual module T₂ map (E), and individually acquired T₂ map (F) for a dual module (T₂ mapping followed by T₁ mapping) HP001 acquisition in a normal Sprague-Dawley rat with 2.5 x 2.5 mm² in-plane spatial resolution (N = 3). The acquisition featured both a variable delay and flip angle during the T₁ mapping module, as seen in Figure 2A. The distribution as well as mean and intra-map standard deviation of the dual module T₁ map (C) matched up well with the EPI T₁ map (D), with the highest T₁ values seen within the kidneys. The T₂ maps in E and F also matched up well in terms of distribution and mean and intra-map standard deviation.

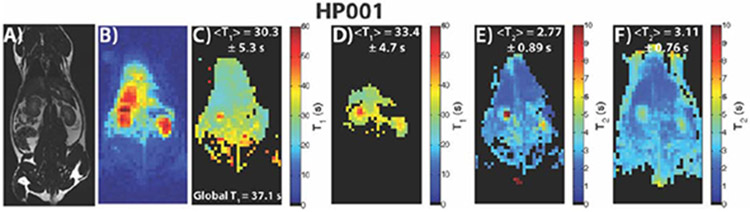
Figure 5 shows results for an HP001 acquisition of a different iteration of the dual module approach (T₁ mapping followed by T₂ mapping), including a ¹H anatomical slice (A), representative time-point (B), T₁ map (C), EPI T₁ Map (D), T₂ map (E), and bSSFP T₂ map (F). The T₁ mapping portion was done with a constant delay of 3 s and constant flip angle of 5° as illustrated in Figure 2B. The mean and intra-map standard deviation of the T₁ map was 30.3 ± 5.3 s, with the T₁ and T₂ distribution matching well with the EPI T₁ map and bSSFP T₂ map, respectively. As with the dual module approach in Figure 4, the Bland-Altman plots in Supporting Figure 1C and 1D show good agreement between this iteration of the dual module approach and the comparative acquisitions on a voxel-by-voxel basis, with most voxels agreeing to within a few seconds (for T₁)/less than 0.5 s (for T₂) of each other, except for voxels corresponding to long T₁’s and T₂’s in the kidneys. The T₂ maps in particular demonstrate the effects of renal filtration since the dual module T₂ map was effectively acquired at 1 minute after the start of the acquisition and compared to the start of the comparative bSSFP T₂ map, which gave rise to considerably longer T₂ values in the kidneys. Supporting Video 2 shows all the time-points of the acquisition, along with the signal train for a representative voxel within the kidney, where slower T₁ decay occurs first, followed by rapid T₂ decay.

Figure 5:

Depiction of a ¹H anatomical slice (A), representative time-point (B), T₁ map (C), EPI T₁ Map (D), dual module T₂ map (E), and individually acquired T₂ map (F) for a dual module (T₁ mapping followed by T₂ mapping) HP001 acquisition in a normal Sprague-Dawley rat with 2.5 x 2.5 mm² in-plane spatial resolution (N = 3). The distribution within the T₁ maps in parts C and D matched up well with each other within the liver and kidneys. The T₂ maps in parts E and F also matched up well, with renal filtration over the course of the acquisition resulting in comparatively longer T₂’s in the kidneys of part E.

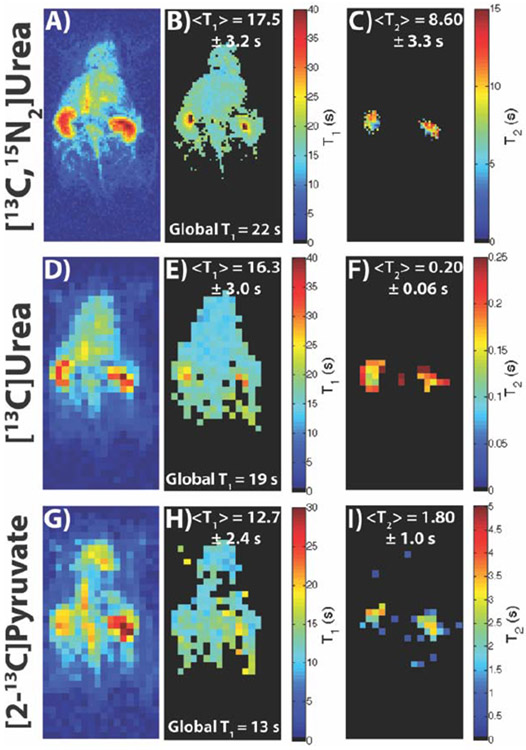
Figure 6 shows the representative time-point, T₁ map, and T₂ map of [¹³C,¹⁵N₂]urea (A-C), [¹³C]urea (D-F), and [2-¹³C]pyruvate (G-H) acquired with a dual module acquisition (T₁ mapping followed by T₂ mapping). The non-localized T₁ was close to or within the mean and intra-map standard deviation of the T₁ map, and T₂ maps matched up with previously acquired maps [30,31,41], although some of the longer T₂ values in the kidneys can be attributed to renal filtration over the course of the acquisition. Even with the relatively shorter T₁ and T₂’s of [2-¹³C]pyruvate, as well as the short T₂’s of [¹³C]urea, the tailored acquisition resulted in enough high SNR time-points for accurate fitting of both parameters in the kidneys.

Figure 6:

Depiction of a representative time-point, T₁ map, and T₂ map for [¹³C,¹⁵N₂]urea (A-C), [¹³C]urea (D-F), and [2-¹³C]pyruvate (G-I) from a dual module acquisition (T₁ mapping followed by T₂ mapping) (N = 1 for all compounds). The T₁ maps matched up well with the global T₁ as well as the HP001 T₁ maps in Figures 4-5, with the longest T₁’s seen in the kidneys. The T₂ maps of each compound matched up well with previously acquired maps, with the longest T₂ values seen in the kidneys due to renal filtration. Additionally, the [¹³C,¹⁵N₂]urea maps showed the capability of 1.25 x 1.25 mm² spatial resolution for T₁/T₂ mapping. For ¹H anatomical image, see Figure 7A.

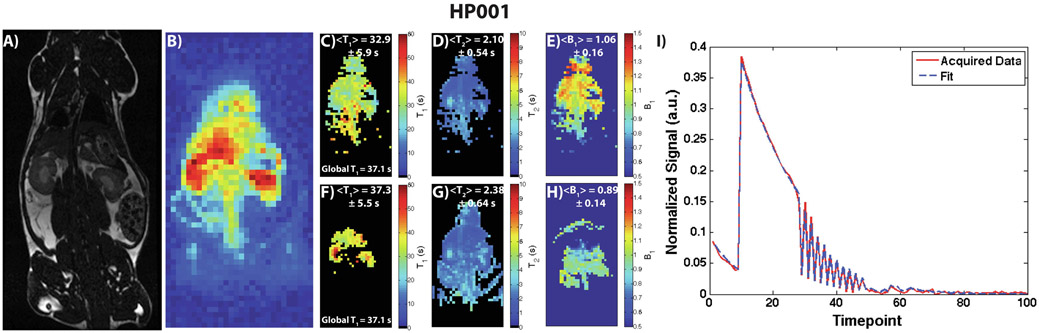
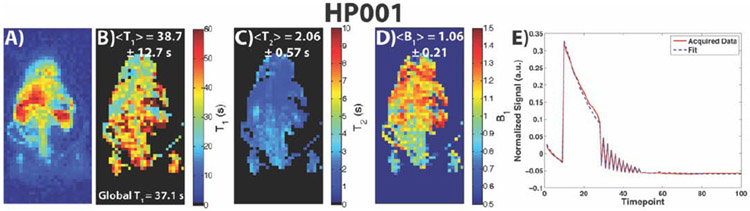
Figure 7 shows results for an HP001 acquisition of the modified MR fingerprinting approach and associated comparison maps, including a ¹H anatomical slice (A), representative time-point (B), T₁ map (C), T₂ map (D), B₁ Map (E), EPI T₁ map (F), bSSFP T₂ map (G), Bloch-Siegert B₁ map (H), and an example signal fit from a kidney voxel (I). The mean and intra-map standard deviation of the T₁ map was 32.9 ± 5.9 s, which is close to the non-localized T₁ of 37.1 s, and matches well with the EPI T₁ map. The Bland-Altman plot in Supporting Figure 1E indicates good agreement between the two acquisitions on a voxel-by-voxel basis as well, with most voxels agreeing to within a few seconds of each other, except for voxels corresponding to long T₁’s in the kidneys that can be attributed to renal filtration effects. Similarly, the calculated T₂ map matched up well with the bSSFP T₂ map based on the calculated means and intra-map standard deviations, as well as qualitatively based on the distribution of the T₂’s within the anatomy. The Bland-Altman plot in Supporting Figure 1F also indicates good agreement between the two acquisitions on a voxel-by-voxel basis, with most voxels agreeing to less than 0.5 seconds of each other. The additional B₁ map calculated with this approach matched up with the expected coil profile for a rat heart/abdomen acquisition and the Bloch-Siegert B₁ map within the kidneys, although deviation is visible within the liver due to potential motion effects during the readout of the Bloch-Siegert B₁ mapping. Supporting Video 3 shows all the time-points of the acquisition, along with the signal train for a representative voxel within the kidney, with the signal exhibiting initial T₁ decay and T₂ decay as part of the “mini” modules depicted in Figure 2C, followed by random flip angles and delays for the remaining time-points. Dictionary matching was also able to successfully calculate all three maps (Figure 8), although the spatial smoothness of the T₁ map was lower compared to non-linear least squares fit as evidenced by the larger intra-map standard deviation.

Figure 7:

Depiction of a ¹H anatomical slice (A), representative time-point (B), T₂ map (C), T₁ map (D), and B₁ Map (E), and for a modified MR fingerprinting HP001 acquisition in a normal Sprague-Dawley rat with 2.5 x 2.5 mm² in-plane spatial resolution (N = 3). The fitting was done using nonlinear least squares via the trust-region-reflective algorithm. An EPI T₁ map (F), bSSFP T₂ map (G), and Bloch-Siegert B₁ map (H) (resized for display purposes) are shown here for comparison. The distribution in the modified MR fingerprinting T₁ and T₂ maps match up well with the comparison maps, as well as maps in Figures 4 and 5. The B₁ map matches up well with the Bloch-Siegert map and with the expected coil profile of a rat acquisition, although some deviations do exist within the liver and kidneys. An example signal fit from a kidney voxel (I) is also shown here, indicating a good agreement between the acquired signal and least-squares fit.

Figure 8:

Depiction of a representative time-point (A), T₂ map (B), T₁ map (C), B₁ Map (D), and an example signal fit from a kidney voxel (E) for the same acquisition as Figure 7 (HP001 acquisition in a normal Sprague-Dawley rat with 2.5 x 2.5 mm² in-plane spatial resolution). The fitting was done using dictionary matching via the inner product method. The distribution in the T₂ and B₁ maps match up well with maps in Figure 7, while the T₁ map shows considerable difference from the T₁ map in Figure 7, with lower spatial smoothness and overestimation of the T₁ values based on the mean and intra-map standard deviation.

Table 1 shows a summary of the T₁ and T₂ values calculated here for the four compounds studied and the comparative global/gold standard/literature values. We also added values for [1-¹³C]pyruvate due to its importance in the hyperpolarized ¹³C community, although we did not use the compound here.

Table 1:

Compilation of T₁ and T₂ values calculated in this publication (Meas.) and comparative global/literature values (Global/Lit.). These values are for health Sprague-Dawley rats acquired at 3T. We also added literature values of [1-¹³C]pyruvate due its widespread use in HP ¹³C research and clinical trials. These values are strongly reflective of kidney parameter values, particularly T₂, and some discrepancies may be due to renal filtration (see discussion).

	[1-13C]Pyr	[2-13C]Pyr	HP001	[13C,14N2]Urea	[13C,15N2]Urea
T1 (s) (Meas.)	N/A	12.7	35.9 (mean of Fig. 4C, 5C, and 7C)	16.3	17.5
T1 (s) (Global/Lit.)	~30 [43]	13 (Global)	37.1 (Global) 37.9 (mean of Fig. 4D, 5D, and 7F) 32 [36]	19 (Global)	22 (Global)
T2 (s) (Meas.)	N/A	1.8	2.3 (mean of Fig. 4E, 5E, and 7D)	0.20	8.6
T2 (s) (Lit.)	~0.6 [33]	0.8 [31]	2.6 (mean of Fig. 4F, 5F, and 7G)	~0.25 [30]	See [30] for distributions in kidney

5. Discussion and Conclusion

We have developed two successful approaches for in vivo high spatial resolution simultaneous T₁ and T₂ mapping using the bSSFP sequence: dual module approach and modified MR fingerprinting. Two iterations of the dual module approach were demonstrated, with individual T₁ and T₂ mapping portions performed in a sequential manner, and with each portion being acquired in either order. The modified MR fingerprinting successfully extracted T₁, T₂, and B₁ maps by fitting the acquired signal to the analytical bSSFP model after a randomized delay/flip angle acquisition. The distribution of these parameters from several HP ¹³C compounds, with a wide range of T₁’s and T₂’s, was shown within the kidneys, liver, heart, and vasculature. The approaches developed here can be used for quantitative ¹³C MRI by using T₁ and T₂ relaxometry to monitor various biological processes, such as intracellular versus extracellular uptake [44] and renal urea handling [41]. We were also able to validate the initial implementation of these approaches in vivo using EPI (for T₁ values), bSSFP (for T₂ values), and Bloch-Siegert (for B₁ values).

Each of the described approaches has advantages that can be exploited for mapping specific compounds as well as achieving the highest in vivo distribution of these parameters. The advantage of the dual module approach was the straightforward manner of extracting the T₁ and T₂ maps since each parameter was sampled individually within different modules of the acquisition. Therefore only one parameter was being fit at one time, making the data analysis much less complicated. Furthermore, the exact timing of each module can be designed prior to the acquisition based on known estimates of the parameters for a given compound, thereby allowing proper sampling of each parameter, i.e. sampling for about 2-3 T₁’s and T₂’s for accurate fitting. Of the two iterations presented here, the one with the T₁ mapping module first via the acquisition detailed in Figure 5 was seen to be the most advantageous with regards to achieving a high and accurate distribution of each parameter at various spatial resolutions for multiple compounds. The magnetization usage of this approach was more optimal compared to acquiring the T₂ mapping module first because more magnetization remained for the T₂ mapping module as compared to the other iteration where the T₂ mapping module would use up considerable magnetization, thereby limiting the SNR of the subsequent T₁ mapping module. This is further illustrated in the Bland-Altman plot in Supporting Figure 1A, where some of the T₁ map voxels matched up poorly with the comparative EPI T₁ map due to some low SNR fits that led to some overfitting. A limitation of the dual module approach was the lack of sensitivity to high spatial resolution B₁ mapping since the acquisition did not have the necessary train of flip angles necessary for calculating B₁ variation accurately [28]. A variable flip angle T₁ mapping module would be a possibility for additionally mapping B₁, although we noticed difficulty in fitting both T₁ and B₁ simultaneously with this approach due to low SNR and limited time-points available for fitting.

The main advantage of the modified MR fingerprinting approach was the ability to map T₁, T₂, and B₁ at a high spatial resolution without any loss in the spatial distribution of any parameters, unlike what was seen in the dual module approach within the module that was acquired second. However, the data fitting was more difficult compared to the dual module approach since three parameters were being fit simultaneously. As with the dual module approach, the choice of temporal resolution between samples is crucial towards being sensitive in detecting the three parameters, with the set of variable flip angles and delays simulated prior to the acquisition. Based on the different schemes tried, the best results were seen with a delay ranging from 1-3 s and flip angles (theta) ranging from 20-120°, which allowed the magnetization to last for ~60-90 time-points or ~120-180 s (Figure 6). This scheme also featured additional “mini” T₁ and T₂ mapping modules (acquired on the order of one T₁ and one T₂) (Fig. 2C) that provided better initial estimates, as well as upper and lower bounds, for the non-linear least squares fit. This provided sufficient parameter sensitivity, due to long enough inter-imaging delays relative to the ¹³C T₁, and variation in low and high flip angles that provided additional sensitivity to T₁ (low flip angles), as well as T₂ (high flip angles) and B₁ (variation in the flip angles that induce signal oscillations). This scheme also provided a large amount of high SNR time-points, which was seen to be necessary for accurate fitting of the parameters as too few time-points, which was acquired in a few animals with long (up to 9 s) delay acquisitions or too many low flip angles, resulted in several voxels having visibly inaccurate T₁’s and T₂’s due to an inability of the algorithm to distinguish an expected fit from an inaccurate one (Supporting Fig. 2). Based on experience and literature, T₁ mapping requires ~2-3 T₁ of samples spaced ~3 s for accurate fitting. Therefore, design of the acquisition needs to have the required sensitivity to the T₁ of the probe via low flip angles and proper sampling timing. However, since SNR can be a limiting factor in all these acquisitions, and T₁ takes the longest amount of time to sample (whether in dual module approach or utilizing the “mini” modules), then T₁ becomes challenging to accurately measure when also trying to measure T₂ (and B₁) because the whole acquisition needs to be optimized to have accurate SNR and sampling to measure each parameter. T₁ measurement can also be very sensitive to the flip angle chosen as correcting for T₁ with an incorrect flip angle (even by a few degrees) can cause a change of ~5-10 s in the T₁ calculation. Based on these challenges, further work is needed to balance the length of the “mini” modules with the length of the random train of delays and flip angles to generate enough high SNR time-points for fitting, as well as further optimize the random train to improve B₁ sensitivity [45].

Based on the results of all three methods presented here, we believe the most stable approach is using the dual module approach with T₁ mapping followed by T₂ mapping because of the ease and stability of the subsequent fittings. This approach appeared to be best validated by our gold standards (EPI and bSSFP) compared to the other two. One aspect of future work will focus on improving the model for more accurate fitting of the acquired in vivo data. In general, this could help resolve some of the differences seen between the developed approaches and “gold” standard acquisitions (EPI, bSSFP, Bloch-Siegert) at long T₁ and T₂ values, as illustrated by via the Bland-Altman plots. The purpose of this study was to demonstrate the feasibility of mapping multiple parameters from one acquisition, and as such we used the simple, but straightforward, bSSFP analytical model for signal fitting and a fully sampled acquisition for easy reconstruction. We did not incorporate B₀ into the model because the frequency response of our acquisitions showed minimal variations over ±25 Hz based on the pulse width, time-bandwidth product, TR, and range of flip angles used (Supporting Fig. 3). Future acquisitions could incorporate a linear ramp of ~5 preparation pulses into the “prep” portion of the imaging sequence for additional off-resonance insensitivity [46,47]. B₀ can also be added to the model via Bloch simulations as is currently done in ¹H MR fingerprinting, at the expense of a more complicated data analysis. Additionally, based on the differences between the modified MR fingerprinting and Bloch-Siegert acquisitions, the B₁ term in the model can be considered a “nuisance” parameter that accounts for B₁, as well as other effects, such as B₀ and motion. The signal fits and parameter maps were better with the B₁ term included compared to without, but the calculated values might be slightly off of the true B₁ measured by the Bloch-Siegert, such as ~1.1 versus ~1 in a kidney voxel as seen in Figures 7D and 7G. However, incorporation of B₀ into the model could lead to an improved B₁ estimation by allowing us to tease out the effects of B₀ and B₁ on the calculation of T₁ and T₂.

We did not account for metabolism, such as for [2-¹³C]pyruvate, where conversion to compounds with short T₁’s and T₂’s, such as [2-¹³C]lactate, would result in an apparent decrease of the calculated [2-¹³C]pyruvate T₁’s and T₂’s, since we utilized an RF pulse with a wide spectral bandwidth. We also did not account for renal filtration, which causes a dynamic elongation of T₁ and T₂ in the kidneys, particularly in the renal pelvis (Fig. 6), due to a removal of red blood cells and proteins that causes T₁ and T₂ to lengthen back towards solution state values [30,41]. Metabolism can be accounted for by incorporating a metabolic conversion rate to the T₁ portion of the model as is currently done with calculation of k_PL [6]. Renal filtration can be accounted for within the kidney voxels by having T₁ and T₂ not be restricted to one value (representing a constant in vivo value), but to a vector of increasing values resulting in time-varying T₁ and T₂ maps. In general, the T₁’s and T₂’s measured here can be considered to be approximate or “apparent” values due to some confounding effects, such as RF transmitter variation and vascular contributions to some voxels [30].

Flow and perfusion are other sources of confounding effects that can cause deviations in relaxation measurements. The bSSFP sequence is first moment flow compensated along the frequency direction, so phase induced by flow along this direction should be fully rephased. However, flow along the phase encode direction will cause some dephasing in the voxel, which would lead to signal loss and a decrease in the apparent relaxation measurement, particularly T₂ [30]. Perfusion into tissues over the course of the imaging sequence would cause changes in the local microenvironment for a particular probe. This could have a variety of effects, such as elongation of the T₂ for urea due to perfusion within the kidneys, or perfusion into more metabolic regions of the body, which could be accounted for in the model as described above.

The clinical utility in this method can be looked at from two perspectives. One, as mentioned in the introduction, changes in these relaxation parameters can reveal differences in healthy versus diseased tissue, with a high resolution spatial distribution being necessary to identify where any abnormalities area, as demonstrated previously [32,34,41]. Second, we can use the distribution of relaxation parameters to help improve subsequent acquisitions, such as EPI or 3D bSSFP. For example, the spatial parameter information can be used to design an appropriate, on-the-fly, patient-specific, variable flip angle schedule to maximize the spatiotemporal SNR for and/or (if the same flip angle scheme is used for all patients) more accurately calculate other parameters that rely on these relaxation parameters, such as k_PL, post-acquisition. However, to obtain this parameter information, an additional injection would be required, which would make widespread use a challenge, although any information from patients would be beneficial for the hyperpolarized ¹³C community. Additionally, more work would need to be done to adapt our technique to [1-¹³C]pyruvate and associated metabolites due to these metabolites resonating close to one another at 3T.

Another aspect of future work will focus on adding undersampling to improve the spatial resolution. Undersampling ¹H parameter mapping [21,22] and MR fingerprinting acquisitions [27-29] is commonly done to speed up these acquisitions without any loss in pattern recognition and serves as a basis for undersampling HP acquisitions. While HP acquisitions are already fast due to rapid inherent decay of the HP signal, undersampling would reduce the number of phase encodes needed for higher spatial resolution (e.g. 1 x 1 mm²), thereby preserving more magnetization for acquisition of multiple time-points. We have previously showed both 2D and 3D T₂ mapping using a locally low rank plus sparse reconstruction that featured matrix sizes of 140x70x20 (2D) and 120x60x18x20 (3D). Several types of reconstructions can be leveraged, with some initial retrospective simulations (Supporting Fig. 4) indicating both a temporal subspace and low rank reconstruction [22] and model-based reconstruction [21] being viable options going forward.

Supplementary Material

5

Supporting Figure 1: Bland-Altman plots comparing the T₁ and T₂ maps from the developed approaches and comparison EPI/bSSFP maps. (A,B) Comparison of the dual module approach (T₂ mapping followed by T₁ mapping) T₁ map and EPI T₁ map (A), as well as T₂ map and bSSFP T₂ map (B) is shown here. The maps matched up well with each other in most voxels, although some differences occurred at long T₁/T₂ values due to renal filtration and some overfitting due to low SNR voxels in the dual module approach. (C,D) Comparison of the dual module approach (T₁ mapping followed by T₂ mapping) T₁ map and EPI T₁ map (C), as well as T₂ map and bSSFP T₂ map (D) is shown here. The maps matched up well with each other in most voxels, although some differences occurred at long T₁/T₂ values due to renal filtration elongating the T₁/T₂ over the course of the dual module acquisition. (E,F) Comparison of the modified MR fingerprinting T₁ map and EPI T₁ map (E), as well as T₂ map and bSSFP T₂ map (F) is shown here. As with A-D, the maps matched up well with each other in most voxels, although similar differences occurred at long T₁/T₂ values due to renal filtration and some overfitting due to low SNR voxels in the EPI acquisition for the T₁ map. For all plots, the zero line (i.e. no difference between voxels), and the mean ± 1.96*standard deviation (SD) (95% confidence interval) lines are displayed.

6

Supporting Figure 2: Comparison of fits for a modified MR fingerprinting acquisition of HP001 with long delays (up to 9 s) and only 20 high SNR time-points available for fitting in a kidney voxel, along with resulting parameter maps. Nonlinear least squares was used for fitting. (A) The calculated fit matched up very closely with the acquired signal, although the resulting values for T₁ and T₂ were lower and higher, respectively, than ideal values, such as those seen in Figures 3 and 4. A plot of the simulated signal trains for combinations of T₁ and T₂ values show how close all curves match up to one another when only 20 time-points are available for fitting, causing the fitting problem to be poorly conditioned due to lack of signal variation. (B-D) The resulting T₂, T₁, and B₁ maps are shown here, along with the mean and intra-map standard deviation. The mean of the T₁ map was considerably lower than the maps found in Figures 3-5, while the T₂ map had poor spatial smoothness owing to the high intra-map standard deviation (for comparison, Figure 2E had an intra-map standard deviation of 1.1). The difficulty in fitting illustrated in part A resulted in several voxels in the T₂ map with values close 10 s, which was chosen as the upper bound. Consequently, the T₁ values were shorter than expected in those voxels, indicating erroneous fits. Acquisition schemes for the modified MR fingerprinting approach with >~60-80 time-points provided fits closer to ideal values and resulted in smoother spatial variation within the parameter maps. Addition of “mini” modules, as depicted in Figure 2C, can help condition the fitting better by providing close initial estimates as well as upper and lower bounds for the fit.

7

Supporting Figure 3: Depiction of the simulated frequency response for different flip angles using the parameters described in the methods section (1.6 ms TBW = 4 sinc pulse played with a TR of 5.6 ms). For the simulations, θ was set to (A) 10°, (B) 20°, (C) 40°, (D) 60°, (E) 120°, and (F) 180°, which represents the range of the flip angles used in these studies. The variation within ±25 Hz was relatively minimal for both low and high flip angles, allowing us to ignore the contribution of B₀ during the signal modeling.

8

Supporting Figure 4: Comparison of different 50% undersampled reconstructions of a random flip angle and delay acquisition. The first image from the ground truth (A), temporal subspace and low rank recon (B), model-based (via nonlinear conjugate gradient) recon (C), and zero-filled recon (D) can be seen. The dictionary described in the methods section was used for the sparsifying transform. Both recons in B and C had low nRMSE and considerably outperformed the zero-filled recon. Qualitatively, both recons removed the aliasing artifacts present in part D.

9

Supporting Video 1: An iteration of a T₂ mapping followed by T₁ mapping acquisition in a normal Sprague-Dawley rat with 2.5 x 2.5 mm² in-plane spatial resolution is shown here along with the signal evolution for a representative kidney voxel. The delays and flip angles used in this acquisition are shown in Figure 2A and the results are shown in Figure 4. The first 16 time-points represent the T₂ mapping module, while the rest of the time-points represent the T₁ mapping module.

10

Supporting Video 2: An iteration of a T₁ mapping followed by T₂ mapping acquisition in a normal Sprague-Dawley rat with 2.5 x 2.5 mm² in-plane spatial resolution is shown here along with the signal evolution for a representative kidney voxel. The delays and flip angles used in this acquisition are shown in Figure 2B and the results are shown in Figure 5. The first 20 time-points represent the T₁ mapping module, while the rest of the time-points represent the T₂ mapping module.

11

Supporting Video 3: An iteration of a modified MR fingerprinting HP001 acquisition in a normal Sprague-Dawley rat with 2.5 x 2.5 mm² in-plane spatial resolution is shown here along with the signal evolution for a representative kidney voxel. The delays and flip angles used in this acquisition are shown in Figure 2C and the results are shown in Figures 7 and 8. The randomness of the signal evolution mimics the flip angle train in Figure 2C, with the longest signal lasting in the kidneys due to renal filtration characteristics that elongate the T₁ and T₂ over time. The first 8 time-points show T₁ decay as part of the “mini” T₁ mapping module, while the next 19 time-points (3 removed for overranging from original 22) featured show T₂ decay as part of the “mini” T₂ mapping module.

Highlights.

• Two new approaches were developed for simultaneous T₁ and T₂ mapping of HP ¹³C probes based on balanced steady state free precession (bSSFP) acquisitions: a method based on sequential T₁ and T₂ mapping modules, and a model-based joint T₁/T₂ approach analogous to MR fingerprinting

• T₁ and T₂ maps acquired using both approaches were in good agreement with both literature values and data from comparative acquisitions.

• Multiple HP ¹³C compounds were mapped, with their relaxation time parameters measured within heart, liver, kidneys, and vasculature in healthy rats.