Intra-aortic balloon counterpulsation timing: A new numerical model for programming and training in the clinical environment.

Highlights

• •The paper “Intra-Aortic Balloon Counterpulsation Timing: A New Numerical Model for Programming and Training in the Clinical Environment.”, is original research from our ongoing program on numerical simulation applied to the clinical environment.
• •In this work we present a new numerical model of the intraaortic balloon pump (IABP). The new model also allows us to simulate patient weaning from IABP assistance.
• •Furthermore, the cardiovascular network model in which the IABP is inserted, allows us to simulate also a mechanical ventilatory assistance that is very important in patients affected by COVID-19.

Abstract

Background and Objective

The intra-aortic balloon pump (IABP) is the most widely available device for short-term mechanical circulatory support, often used to wean off cardiopulmonary bypass or combined with extra-corporeal membrane oxygenation support or as a bridge to a left ventricular assist device. Although based on a relatively simple principle, its complex interaction with the cardiovascular system remains challenging and open to debate. The aim of this work was focused on the development of a new numerical model of IABP.

Methods

The new model was implemented in CARDIOSIM©, which is a modular software simulator of the cardiovascular system used in research and e-learning environment. The IABP is inserted into the systemic bed divided in aortic, thoracic and two abdominal tracts modelled with resistances, inertances and compliances. The effect induced by the balloon is reproduced in each tract of the aorta by the presence of compliances connected to P_IABP generator and resistances. P_IABP generator reproduces the balloon pressure with the option to change IABP timing. We have used literature data to validate the potential of this new numerical model.

Results

The results have shown that our simulations reproduced the typical effects induced during IABP assistance. We have also simulated the effects induced by the device on the hemodynamic variables when the IABP ratio was set to 1:1, 1:2, 1:4 and 1:8. The outcome of these simulations is in accordance with literature data measured in the clinical environment.

Conclusions

The new IABP module is easy to manage and can be used as a training tool in a clinical setting. Although based on literature data, the outcome of the simulations is encouraging. Additional work is ongoing with a view to further validate its features. The configuration of CARDIOSIM© presented in this work allows the simulation of the effects induced by mechanical ventilatory assistance. This facility may have significant importance in the management of patients affected by COVID-19 when they require mechanical circulatory support devices.

NOMENCLATURE

ABP (Pas)

Aortic blood pressure [mmHg]

EDP

End diastolic blood pressure [mmHg]

PDP

Peak diastolic blood pressure [mmHg]

LVP (Plv)

Left ventricular pressure [mmHg]

BSA

Body surface area [m²]

CI

Cardiac index [L/min/m²]

CO

Cardiac output [L/min]

EDV (Ved)

End-diastolic volume [ml]

ESV (Ves)

End-systolic volume [ml]

SV

Stroke volume [ml]

E_a

Arterial elastance [mmHg/ml]

E_es

Slope of ESPVR [mmHg/ml]

EDPVR (ESPVR)

End-diastolic (end-systolic) pressure volume relationship

EF%

Ejection fraction

MCBF

Mean coronary blood flow [ml/min]

HR

Heart rate [bpm]

RAP

Right atrial pressure [mmHg]

PAP

Pulmonary arterial pressure [mmHg]

PCWP

Pulmonary capillary wedge pressure [mmHg]

Ped (Pes)

End-diastolic (end-systolic) ventricular pressure [mmHg]

PVR

Pulmonary vascular resistance [mmHg · s/ml]

LVSW

Left ventricular stroke work [g · m⁻¹]

RVSW

Right ventricular stroke work [g · m⁻¹]

LVSWI

Left ventricular stroke work index [g · m · m⁻²]

RVSWI

Right ventricular stroke work index [g · m · m⁻²]

IABP

Intra-aortic balloon pump

MVA

Mechanical ventilator assistance

1. Introduction

The intra-aortic balloon pump (IABP) is a widely available in-series cardiac assist device. It consists of a double-lumen catheter with a polyurethane balloon attached at its distal end and a mobile pump console, which shuttles helium through the main lumen of the catheter. The tip of the catheter has a pressure sensor to monitor aortic blood pressure. The IABP is now inserted percutaneously through the femoral artery and positioned just below the origin of the left subclavian artery either under fluoroscopic guidance in the cath lab or under trans-oesophageal guidance in theatre.

The IABP is based on the principle of counterpulsation, which aims to optimize the balance between myocardial oxygen supply and demand in terms of endocardial viability ratio (EVR) [1],[2].

The functional relationship between stroke volume (SV), aortic mean diastolic pressure (MDP), tension time index (TTI), aortic end diastolic pressure (EDP), balloon inflation/deflation timing and heart rate (HR) is a key element for optimal pump control [1],[2].

The physiological advantage of intra-aortic balloon counterpulsation is increased aortic diastolic blood pressure. Rapid inflation of the balloon at the beginning of diastole generates proximal and distal blood displacement, which is proportional to the volume of the balloon. Diastolic blood pressure augmentation increases the intrinsic windkessel effect leading to storage of extra potential energy in the aorta and conversion to kinetic energy following the elastic recoil of the vessel [3]. This event has the potential to increase coronary blood flow. Rapid deflation of the balloon in early systole leads to afterload reduction or, to be more precise, to reduction of impedance to ventricular ejection and cardiac work [4],[5]. This is in accordance with a previous analytical model [5].

The ability to model the interactions between IABP and the cardiovascular system and how alterations of specific parameters such as timing can affect their coupling remains a key element for clinical application [6],[7].

Simulations of combined VA-ECMO and IABP support show an increase in pulsatility and LV stroke volume between 5% and 10% due to afterload reduction although PCWP and left ventricular EDV are only marginally affected. Significant LV unloading is achieved during combined VA-ECMO and Impella support although aortic valve opening and improved diastolic coronary perfusion pressure are not observed in comparison with IABP [8]. Nevertheless, the pulse contour is higher and more similar to the physiological pattern during partial ECMO support where some degree of LV ejection is allowed [9].

The concomitant use of IABP and VA-ECMO shows reduced in-hospital mortality in patients with cardiogenic shock secondary to post-cardiotomy failure, ischaemic heart disease and myocarditis [10], [11], which is in contrast with the questionable outcome of the SHOCK II trial [12], [13], [14]. The study was designed as a multicentre, randomised, open-label trial. Between 2009 and 2012, 600 patients with cardiogenic shock following acute myocardial infarction and requiring early revascularisation were randomised to IABP versus control. Long-term follow-up (6.2 years) showed no difference in mortality, recurrent myocardial infarction, stroke, repeat revascularisation or hospital readmission for cardiac reasons between the two groups. Nevertheless, the use of IABP in cardiogenic shock remains the subject of significant debate and controversy.

2. Material And Method

2.1. The heart and circulatory numerical network

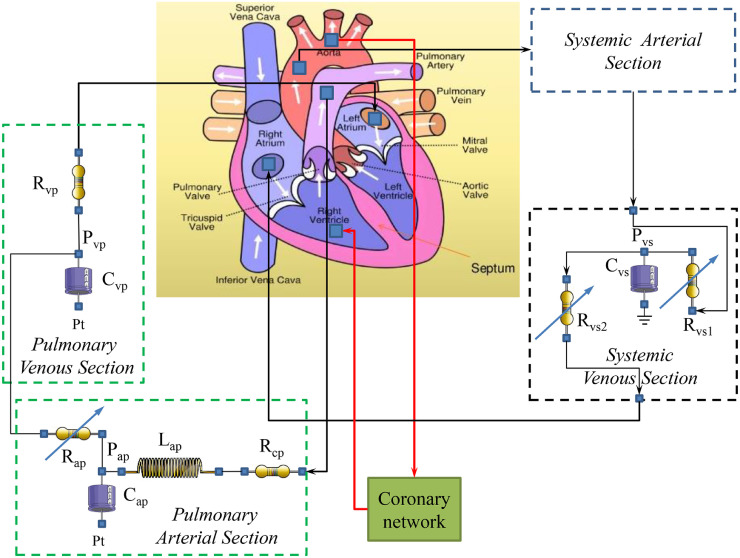
The electrical analogue of the cardiovascular system assembled inside the software simulator platform CARDIOSIM© is reported in Fig. 1 . The circuit consists of systemic and venous sections, coronary section and pulmonary arterial and venous sections. Each section is modelled by RLC electrical circuit based on 0-D numerical representation. The systemic venous section consists of a compliance (C_vs) and two variable resistances (R_vs1 and R_vs2); the pulmonary arterial section is modelled with a characteristic resistance (R_cp), a variable pulmonary arterial resistance (R_ap), a compliance (C_ap) and an inertance (L_ap). Finally, the behavior of the pulmonary venous section is reproduced with a resistance (R_vp) and a compliance (C_vp). Pt is the mean intrathoracic pressure.

Fig. 1.

Electrical analogue of the cardiovascular network. The key compartments and their relationship are highlighted: pulmonary (systemic) venous section to left (right) atrium via mitral (tricuspid) valve to left (right) ventricle; aortic (pulmonary) valve to systemic (pulmonary) arterial section. The coronary network is modelled using RC elements as already described in [22], [23], [24], [25], [26]. Pt is the mean intrathoracic pressure.

The following CARDIOSIM© module was selected to simulate the heart activity. The behavior of the left and right native ventricles is reproduced by the time-varying elastance model. The same theory is used to model both left and right atria and the septum [15], [16], [17], [18], [19]. Ventricles, atria and septum activities are synchronized with the electrocardiographic (ECG) signal [19]. The described model allows inter-ventricular and intra-ventricular dyssynchrony to be simulated [19], [20], [21].

2.2. IABP and systemic arterial numerical models

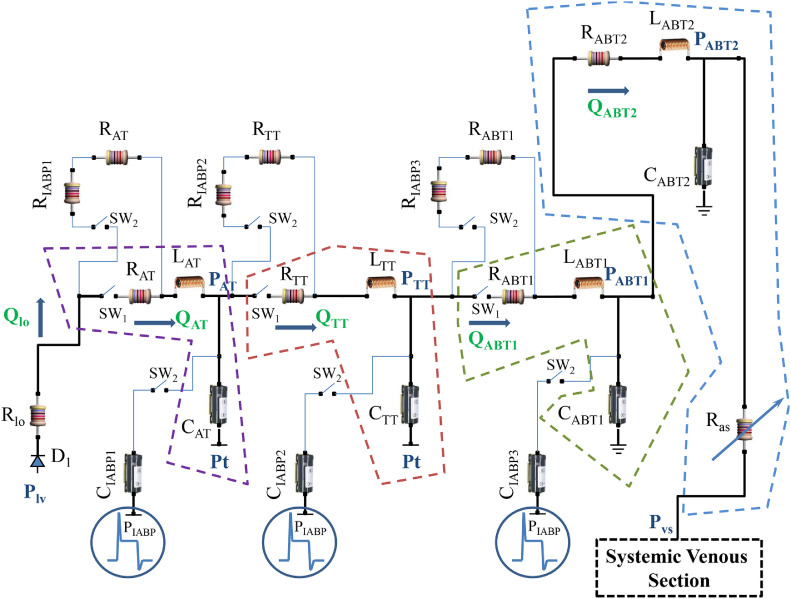
Figure 2 shows the electrical analogue of the systemic circulation and the IABP. The systemic bed is divided in aortic, thoracic and two abdominal tracts. When the IABP is “OFF” (SW₁=ON and SW₂=OFF), the aortic (thoracic) tract is modelled using resistance R_AT (R_TT), compliance C_AT (C_TT) and inertance L_AT (L_TT). The behavior of the first abdominal tract is reproduced by RLC elements (R_ABT1, L_ABT1 and C_ABT1) when the IABP is disabled. The second abdominal tract is modelled by R_ABT2, L_ABT2, C_ABT2 and by variable systemic arterial resistance (R_as). The switches SW₁ and SW₂ are set to OFF (ON) and ON (OFF) respectively, when the device is (not) working. The effect induced by the balloon is reproduced in each tract of the aorta by the presence of compliances (C_IABP1, C_IABP2 andC_IABP3) connected to P_IABP generator and resistances (R_IABP1, R_IABP2 and R_IABP3). P_IABP generator reproduces the balloon pressure with the option to change the IABP timing. The resistances (compliances) R_IABP1 (C_IABP1), R_IABP2 (C_IABP2) and R_IABP3 (C_IABP3) are connected in series (parallel) to R_AT (C_AT), R_TT (C_TT) and R_ABT1 (C_ABT1) in the aortic, thoracic and first abdominal tract. Figure 3 shows the waveform of the pressure produced by the generator that is defined as follows:

$$P_{IABP}\left(t\right)=\{\begin{array}{cc}\frac{P_{DRIVE}}{T_1}·(t-T_0)\hfill & T_0\le t<T_0+T_1\hfill \\ P_{DRIVE}\hfill & T_0+T_1\le t<T_0+T_2\hfill \\ P_{DRIVE}-\frac{P_{DRIVE}-P_{PLATEAU}}{T_3-T_2}·\left(t-T_0-T_2\right)\hfill & T_0+T_2\le t<T_0+T_3\hfill \\ P_{PLATEAU}\hfill & T_0+T_3\le t<T_0+T_4\hfill \\ P_{PLATEAU}-\frac{P_{PLATEAU}-P_{VACUUM}}{T_5-T_4}·\left(t-T_0-T_4\right)\hfill & T_0+T_4\le t<T_0+T_5\hfill \\ P_{VACUUM}\hfill & T_0+T_5\le t<T_0+T_6\hfill \\ P_{VACUUM}-\frac{0-P_{VACUUM}}{T_6-T_7}·\left(t-T_0-T_6\right)\hfill & T_0+T_6\le t<T_0+T_7\hfill \\ 0\hfill & T_0+T_7\le t\hfill \end{array}$$

Fig. 2.

Electrical analogue of systemic arterial section and IABP. The systemic compartment consists of aortic, thoracic and abdominal tract. The abdominal bed is divided in two parts modelled with R_ABD1, L_ABD1, C_ABD1 and R_ABD2, L_ABD2, C_ABD2 and R_as elements respectively. The aortic, thoracic and first abdominal tract is directly influenced by IABP activation. Qi (i=AT, TT, ABT1 and ABT2) represents the flow inside each compartment. R_AT, L_AT, and C_AT (R_TT, L_TT, and C_TT) reproduce the aortic (thoracic) bed. The compliances C_IABP1, C_IABP2 and C_IABP3 and the resistances R_IABP1, R_IABP2 and R_IABP3 with the generator P_IABP allow simulating the effects of the intra-aortic counterpulsation.

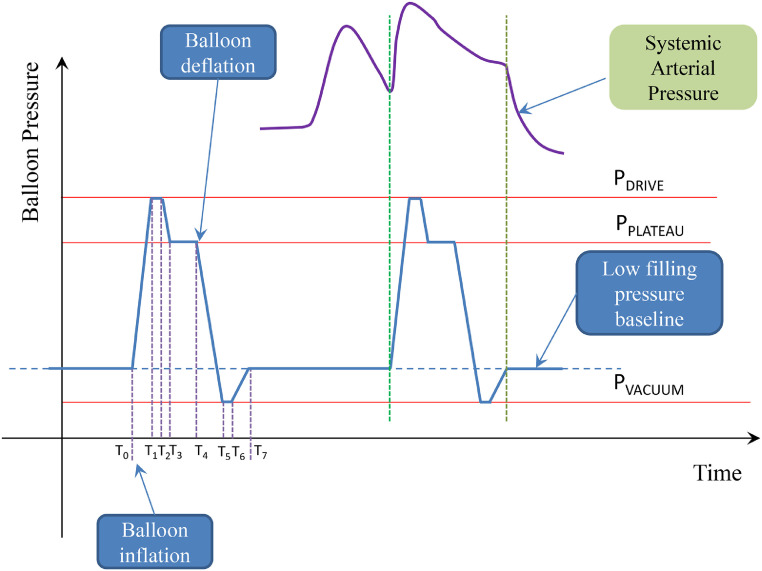
Fig. 3.

Schematic representation of the balloon pressure. T₀ starting balloon inflation, T₁ ending balloon inflation, T₁-T₂ inflation overshoot interval (P_DRIVE), T₃-T₄ maximal inflation interval, T₄ starting balloon deflation, T₅ ending balloon deflation, T₅-T₆ deflation overshoot interval, T₆ starting filling pressure baseline, T₇ ending filling pressure baseline (P_VACUUM).

When the IABP is OFF, the network showed in Fig. 2 is solved by the equations:

$$\begin{array}{c}{P}_{lv}-P_{AT}=Q_{lo}·\left(R_{lo}+R_{AT}\right)+\stackrel{•}{Q_{lo}}·L_{AT}\begin{array}{ccc}& & \end{array}{P}_{ABT1}-P_{ABT2}=Q_{ABT2}·R_{ABT2}+\stackrel{•}{Q_{ABT2}}·L_{ABT2}\hfill \\ \\ Q_{AT}=\stackrel{•}{P_{AT}}·C_{AT}+Q_{TT}\begin{array}{cccc}& & & \end{array}{Q}_{TT}\equiv Q_{lo}\begin{array}{cccc}& & & \end{array}{Q}_{TT}=\stackrel{•}{P_{TT}}·C_{TT}+Q_{ABT1}\hfill \\ \\ Q_{ABT1}=\stackrel{•}{P_{ABT1}}·C_{ABT1}+Q_{ABT2}\begin{array}{cccc}& & & \end{array}{Q}_{ABT2}=\underset{ABT2}{\overset{•}{P}}·C_{ABT2}+\left(\frac{P_{ABT2}-P_{vs}}{R_{as}}\right)\hfill \\ \\ P_{AT}-P_{TT}=Q_{TT}·R_{TT}+\stackrel{•}{Q_{TT}}·L_{TT}\begin{array}{ccc}& & \end{array}\left(P_{TT}+Pt\right)-P_{ABT1}=Q_{ABT1}·R_{ABT1}+\stackrel{•}{Q_{ABT1}}·L_{ABT1}\hfill \end{array}$$

If the IABP is ON, the equations are:

$$\begin{array}{c}{P}_{lv}-P_{AT}=Q_{lo}·\left(R_{lo}+R_{IABP1}+R_{AT}\right)+\stackrel{•}{Q_{lo}}·L_{AT}\begin{array}{ccc}& & \end{array}\left(P_{ABT1}-P_{ABT2}\right)=Q_{ABT2}·R_{ABT2}+\stackrel{•}{Q_{ABT2}}·L_{ABT2}\hfill \\ \\ P_{I1}=P_{AT}-P_{IABP}\begin{array}{cccc}& & & \end{array}{P}_{I2}=P_{TT}-P_{IABP}\begin{array}{cccc}& & & \end{array}{P}_{I3}=P_{ABT1}-P_{IABP}\hfill \\ \\ Q_{AT}=\underset{AT}{\overset{•}{P}}·C_{AT}+\underset{I1}{\overset{•}{P}}·C_{IABP1}+Q_{TT}\begin{array}{ccc}& & \end{array}{Q}_{TT}=\underset{TT}{\overset{•}{P}}·C_{TT}+\stackrel{•}{P_{I2}}·C_{IABP2}+Q_{ABT1}\hfill \\ \\ Q_{ABT1}=\underset{ABT1}{\overset{•}{P}}·C_{ABT1}+\underset{I3}{\overset{•}{P}}·C_{IABP3}+Q_{ABT2}\begin{array}{ccc}& & \end{array}{Q}_{ABT2}=\underset{ABT2}{\overset{•}{P}}·C_{ABT2}+\left(\frac{P_{ABT2}-P_{vs}}{R_{as}}\right)\hfill \\ \\ \left(P_{AT}-P_{TT}\right)=Q_{TT}·\left(R_{IABP2}+R_{TT}\right)+\stackrel{•}{Q_{TT}}·L_{TT}\begin{array}{ccc}& & \end{array}\hfill \\ \\ \left(P_{TT}+Pt\right)-P_{ABT1}=Q_{ABT1}·\left(R_{IABP3}+R_{ABT1}\right)+\stackrel{•}{Q_{ABT1}}·L_{ABT1}\hfill \end{array}$$

where P_lv is the left ventricular pressure. The resistance R_lo and the diode D₁ model the mitral valve (Fig. 2). The software simulator allows the IABP to be synchronized with either the ECG or the aortic pressure waveform. The frequency of balloon-assisted beats can be set from the maintenance 1:1 ratio to a weaning 1:2 ratio (every other systole is assisted). Depending on the clinician's judgment, weaning modes of 1:4 or even 1:8 may be initiated if a more gradual approach is needed. In addition, IABP driving and vacuum pressures can be changed.

The hemodynamic effects induced by the IABP may vary with assisting frequency and depend on balloon inflation/deflation timing. A range of settings T₁-T₇ is available in the software simulator. The IABP can be triggered to deflate during systole once the peak of the R wave is sensed. IABP inflation may be triggered to occur in the middle of the T wave, which corresponds to diastole. The simulator allows the setting of different delays. Changing IABP compliance and resistance allows the balloon volume to be modified.

2.3. Cardiogenic Shock Patients

Patients with acute myocardial infarction (AMI) and cardiogenic shock (CS) may require intra-aortic balloon counterpulsation as an adjunct to medical treatment [27]. For the purposes of our study, literature data [28], [29], [30] were used to reproduce the baseline conditions of CS patients and those following IABP assistance. The hemodynamic data used in this study have been listed in Table 1 .

Table 1.

Literature data for pathological and assisted conditions.

	Baseline conditions	IABP on [1:1]
PDP [mmHg]	67±7	75±7
EDP [mmHg]	55±6	42±9
HR [beat/min]	99±27	100±22
LV EDV [cc]	293±35	285±36
LV ESV [cc]	263±32	259±36
SV [cc]	29±4	26±4
PAP [mmHg]	42±11	32±6
PCWP [mmHg]	27±8	23±6
RA [mmHg]	10±5	10±5
CI [l·min−1/m2]	1.56±0.29	1.57±0.3
SVR [Wood]	21.67±5.2	16.42±11.8
PVR [Wood]	4.95±2.7	1.46±1.1
BSA [m2]	1.8±0.13	1.8±0.13
CO [l · min−1]	2.8±1.25	2.91±1.25

2.4. Simulation Protocol

The duration of the whole cardiac cycle was set at 1000 ms for all the simulations. Starting from the reproduced baseline conditions, the IABP was activated with a driving (vacuum) pressure of P_DRIVE = 240 mmHg (P_VACUUM= -10 mmHg). The plateau IABP pressure was set to P_PLATEAU = 150 mmHg. During the simulations, the IABP was synchronized with the ECG and its ratio was set to 1:1, 1:2, 1:4 and 1:8. During baseline conditions and when the IABP ratio was set to 1:1, the mean values for pressure, flow, EDV and ESV (for both ventricles) were calculated for one cardiac cycle. When the IABP ratio was set to 1:2 (1:4 or 1:8), the mean values for pressure, flow, EDV and ESV (for both ventricles) were calculated for two (four or eight) cardiac cycles.

3. Results

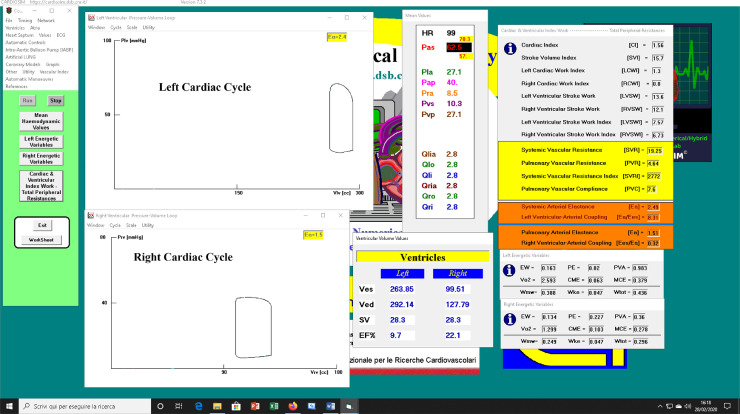
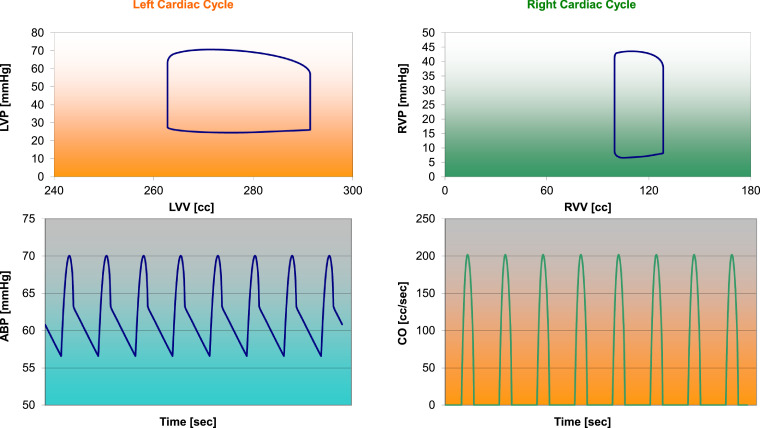
Figure 4a shows a screen output produced by CARDIOSIM© when patient's baseline conditions were reproduced using the data reported in Table 1. The left (right) ventricular loop has been plotted in the upper (lower) window. The first column on the left hand side is the command of the software. The middle column shows the mean value of pressures and flows. End systolic volume (ESV Ves), end diastolic volume (EDV Ved), stroke volume and ejection fraction are listed below the middle column. Finally, the last windows on the right hand side show the cardiac and ventricular work index with the left and right ventricular energetic variables.

Fig. 4.

(a) Screen output from CARDIOSIM© software simulator with data obtained when patient's baseline conditions were reproduced. The simulation was performed using literature data reported in Table 1. (b) Data obtained during baseline patient's simulation, which have been stored in excel file and subsequently processed. The left (right) upper window shows the left (right) ventricular loop plotted in the pressure-volume plane. Left (right) lower window shows the aortic blood pressure (cardiac output) during multiple cardiac cycles.

Figure 4b shows the data obtained during a simulation, which are stored in excel files and subsequently processed.

Table 2 shows the simulation results obtained when the IABP ratio was set to 1:1; 1:2; 1:4 and 1:8. When the IABP ratio was set to 1:2, the mean values of each parameter were calculated during two cardiac cycles (one with IABP set to “ON” and the other with IABP set to “OFF”). When the IABP ratio was set to 1:4 (1:8), the mean values were calculated during four (eight) cardiac cycles i.e. one cardiac cycle with IABP set to “ON” and three (seven) cardiac cycles with IABP set to “OFF”. The results obtained when the IABP ratio was set to 1:1 are comparable with the literature data reported in Table 1. The simulation results presented when the IABP ratio was set to 1:2, 1:4 and 1:8 were obtained after changing the IABP ratio from baseline conditions.

Table 2.

Simulation results.

	Baseline conditions	IABP on [1:1]	IABP on [1:2]	IABP on [1:4]	IABP on [1:8]
PDP [mmHg]	70.8	91	83.7±4.3	74.2±12.4	70.44±12.25
EDP [mmHg]	57.2	41.5	40.5±8.5	46.18±9.15	49.84±9.6
HR [beat/min]	99	99	99	99	99
LV EDV [cc]	293.35	267.92	262.3±0.3	270±2.4	276.06±4.05
LV ESV [cc]	264.9	231.92	224.8±8.4	236±9.25	244.77±10.43
RV EDV [cc]	128.37	139.98	138±0.6	133.46±1.4	129.44±2.11
RV ESV [cc]	99.92	103.98	102±0.3	100.0±0.32	98.48±0.49
SV [cc]	28.4	35.9	36.9±3.9	33.7±5.35	31.13±6.15
PAP [mmHg]	40.3	41	40.3±0.05	39.8±0.1	39.45±0.15
PCWP [mmHg]	27.2	24.8	23.95±0.2	24.75±0.3	25.3±0.35
RA [mmHg]	8.6	9.8	9.5±0.1	9.0±0.2	8.69±0.2
CI [l · min−1/m2]	1.56	1.98	1.84±0.2	1.68±0.3	1.56±0.31
SVR [Wood]	18.87	15.33	14.66±4.7	15.48±3.93	16.47±3.96
PVR [Wood]	4.64	4.64	5.11±1.58	4.93±1.26	4.8±1.2
BSA [m2]	1.8	1.8	1.8	1.8	1.8
CO [l · min−1]	2.82	3.56	3.65±0.4	3.34±0.53	3.08±0.61
Left Ea	2.49	1.71	1.66±0.32	1.93±0.43	2.14±0.51
Left Ea/Ees	8.31	5.68	5.52±1.05	6.42±1.43	7.13±1.67
Right Ea	1.51	1.22	1.18±0.03	1.26±0.05	1.34±0.07
Right Ees/Ea	0.32	0.39	0.41±0.01	0.38±0.02	0.36±0.01
LVSW [g · m−1]	13.4	19.3	16.25±3.15	14.63±4.2	13.64±4.6
RVSW [g · m−1]	12.2	15.4	15.2±0.4	14.0±0.45	13.06±0.6
LVSWI [g · m · m−2]	7.43	10.7	9.05±1.75	8.13±2.36	7.58±2.58
RVSWI [g · m · m−2]	6.8	8.55	8.72±1.97	7.9±2.15	7.28±2.37
PVC [ml · mmHg−1]	7.6	9.94	9.97±0.04	9.84±0.04	9.74±0.04
MCBF [ml/min]	58.3	70.5	55.3±4.8	53.4±4.4	53.6±3.8
Left EF%	9.7	13.4	14.3±3.3	12.58±3.5	11.38±3.8
Right EF%	22.2	25.7	26.25±0.45	25.05±0.6	24.05±0.85

Figure 5a shows a screen output produced by CARDIOSIM© during IABP assistance.

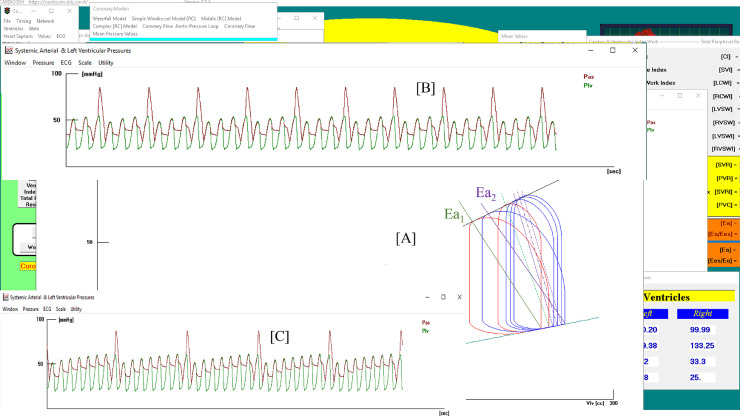
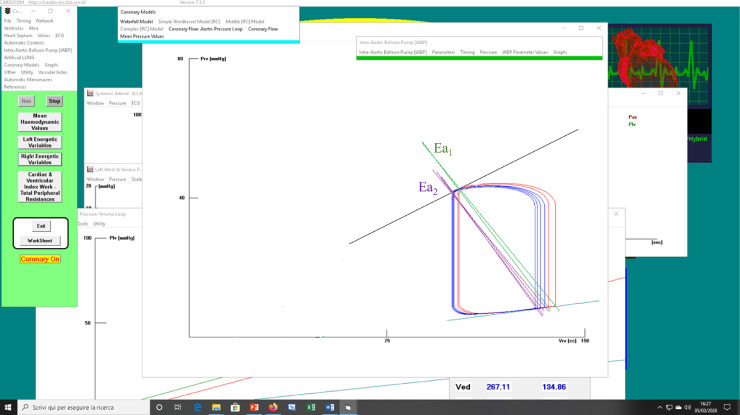
Fig. 5.

(a) Screen output from CARDIOSIM© software simulator with instantaneous values obtained during IABP assistance. Window [A] shows the left ventricular loops obtained when IABP ratio was set to 1:2 (red lines) and to 1:4 (blue lines). Ea₁, green lines (Ea₂, lilac lines) is the systemic arterial elastance plotted when IABP ratio was set to 1:2 (1:4). Window [B] ([C]) shows aortic (red lines) and ventricular pressures when IABP ratio was set to 1:4 (1:8). (b) Screen output from CARDIOSIM© software simulator showing right ventricular loops. The red (blue) loops were obtained when IABP ratio was set to 1:4 (1:8).

The middle window [A] shows the left ventricular loops following different assisted conditions. The two red loops are obtained when the IABP ratio is set to 1:2; in this case, two different values are obtained for the systemic arterial elastance Ea₁ (green lines): the first when the IABP is ON and the second when the IABP is OFF. The elastances have the same slope. When the IABP is active, the simulator reproduces the largest left ventricular loop. When the IABP ratio is set to 1:4, the software simulator plots the blue left ventricular loops. The wider loop corresponds to the cardiac cycle in which IABP is ON. In this case, the systemic arterial elastance Ea₂ (lilac lines) assumes four different values. The left ventricular elastance (Ees) does not change during circulatory assistance, so the variation in coupling (LEFT Ea/Ees) depends only on Ea.

Window [B] ([C]) shows the instantaneous left ventricular pressure (LVP Plv, green line) and aortic blood pressure (ABP Pas, red line) when the IABP ratio is set to 1:4 (1:8).

Fig. 5b shows the right ventricular loops during IABP assistance with ratio 1:2 (red loops) and 1:4 (blue loops). The pulmonary arterial elastance (Ea₁) assumed two values (green lines) when the ratio of the assistance was set to 1:2. The arterial elastance Ea₂ assumed four values (lilac lines) when IABP ratio was set to 1:4. The right ventricular end systolic volume (ESV) presents minimal changes on 1:2 and 1:4 assistance. The right ventricular elastance (Ees) does not change during IABP assistance.

4. Discussion

The numerical model for IABP assistance implemented in CARDIOSIM© produces an increase between 10% (1:8 ratio) and 25% (1:1 ratio) in CO following activation. It is estimated that IABP assistance with 1:1 ratio in the presence of sinus rhythm can increase cardiac output up to 20-25% of its initial value according to the available literature data. We point out that in the transition from IABP setting with 1:1 ratio to that with 1:8 ratio, the parameters of the simulator were not changed. Systemic vascular resistance (SVR) decreases from 23% to 18% when IABP is activated. The assistance induces about 10% reduction in EDV (when the ratio is 1:1) and about 5% reduction in the mean value of EDV (calculated on eight cardiac cycles) when the IABP ratio is set to 1:8. There is about 13% (7%) decrease in ESV when IABP is set to 1:1 (1:8). A 27% (13%) reduction in end diastolic blood pressure (EDP) is observed during IABP activation with 1:1 (1:8) ratio. The simulation results show a reduction in the left ventricular end-diastolic and end-systolic volumes with concomitant decrease in the left atrial filling and in the pulmonary capillary wedge pressures (PCWP) leading to reduced right ventricular afterload. These findings are completely in accordance with literature data. Besides, the PCWP reduction during the simulation can be up to 10%.

The peak diastolic blood pressure (PDP) increases by 30% when the IABP ratio is set to 1:1. The left ventricular arterial coupling (Ea/Eas) decreases by 32% (14%) when the assistance ratio is set to 1:1 (1:8). The mean coronary blood flow (MCBF) increases by 21% when the IABP ratio is set to 1:1 but it decreases by 8% when the ratio is set to 1:8. In this case, the MCBF is calculated over eight cardiac cycles where only one is assisted by IABP activation.

The limitations of this work are related to the use of incomplete data from the available literature, which affects the accurate reproduction of a patient's cardiovascular conditions. Furthermore, we were unable to obtain data related to the trend of the hemodynamic variables during different IABP operating modes. We believe these data would be useful to further validate our model. Nevertheless, the cardiovascular network used in this work has been previously validated [15],[16] and has led to the successful evaluation of the trend of the hemodynamic variables during patient weaning off the device.

We have also observed that the cardiovascular network outlined in Fig. 1 allows changes in the mean value of intrathoracic pressure to be made. This option may be used to evaluate the effects induced by mechanical ventilatory assistance (MVA) during IABP support. Simulating the effects induced by MVA may have significant importance in the management of patients affected by COVID-19 when they require mechanical circulatory support devices.

The recent events leading to the COVID-19 pandemic have confirmed how unprepared we are despite our level of knowledge and technology. Although a certain degree of uncertainty remains, the ability to model and simulate critical clinical conditions in advance with a view to treatment optimization and outcome prediction may be an option to consider on a more routine basis. The severe respiratory impairment caused by COVID-19 requiring mechanical ventilation and ECMO support has generated severe strain on intensive care units capacity and hospital resources. Redeployment of medical and nursing staff in different roles has required crash training for those not accustomed to a certain type of work. The ability to study and train through modelling and simulation may help with organization and rearrangement of working patterns. This may become part of the training of healthcare professionals with a view to focus on specific subjects with an open mind where the clinician remains the ultimate decision-maker.

5. Conclusion

We have developed an innovative IABP numerical model with potential for clinical application. The focus has been on IABP timing and the evaluation of the most appropriate weaning strategy in terms of device assist ratio. Its value as a training tool in a clinical setting has been proposed. Although based on literature data, the outcome of the simulations is encouraging. Additional work is ongoing with a view to further validate its features.

6. Funding And Conflict Of Interest

None

Declaration of Competing Interest

All authors have no conflicts of interest