From force-responsive molecules to quantifying and mapping stresses in soft materials

Embedded spiropyran mechanophores reveal and quantitatively map stresses in soft materials by changing their color.

Abstract

Directly quantifying a spatially varying stress in soft materials is currently a great challenge. We propose a method to do that by detecting a change in visible light absorption. We incorporate a spiropyran (SP) force–activated mechanophore cross-linker in multiple-network elastomers. The random nature of the network structure of the polymer causes a progressive activation of the SP force probe with load, detectable by the change in color of the material. We first calibrate precisely the chromatic change in uniaxial tension. We then demonstrate that the nominal stress around a loaded crack can be detected for each pixel and that the measured values match quantitatively finite element simulations. This direct method to quantify stresses in soft materials with an internal force probe is an innovative tool that holds great potential to compare quantitatively stresses in different materials with simple optical observations.

INTRODUCTION

When an object with an arbitrary shape is mechanically loaded, the strains and stresses in the material are spatially heterogeneous, and it is essential to identify regions of high stresses to predict at which macroscopic loading the object will break. If the material obeys linear elasticity, such information can be easily obtained by finite element simulations. However, there are situations where loading is complex and/or the material does not obey linear elasticity, motivating the development of advanced experimental methods to directly measure the stress rather than calculate it from the strain field.

One recent example is the mapping of forces exerted by cells on a soft gel where the position of fluorescent tracer beads is used to map local stresses in three dimensions (3D) by assuming linear elasticity and small strains (1–4). Yet, soft materials often deform substantially before failure, which leads to two important limitations:

(i) The methods determining displacement fields become less accurate when sharp gradients are present and require many images at intermediate deformations to obtain accurate values of displacements.

(ii) The constitutive model relating the stress and strain field is generally poorly known for very large strains, making the determination of the stress field from the strain field inaccurate.

There are few available methods that measure stresses directly in soft materials. Optical birefringence can be used but relies on molecular orientation, and the direct connection between stress and birefringence is only demonstrated for conventional elastic rubbers (5). Even with proper calibration, the use of this technique in regions of strong deformation gradients is problematic because of its thickness dependence (5). The amorphous halo of x-rays (6) can also be used to detect segmental orientation, but spatial mapping is difficult and requires a microfocused beam. Therefore, a molecular probe that would directly respond optically to the application of a force to the chemical bond is a promising path to obtain a pixel-by-pixel mapping of the stress.

Recent developments in mechanochemistry (7–8) have enabled force-sensitive molecules (mechanophores) to be incorporated into various polymeric materials, and their potential as sensors has been evaluated. When the mechanophores are activated by a critical force, they can exhibit changes in optical properties (5) such as fluorescence (9–10), luminescence (11), and color change (12–18). If incorporated in a polymer strand, scission-based mechanophores such as dioxetane (19), or pi-extended anthracenes (9), break into two parts upon the application of a high force and either emit light (19–20) or become fluorescent (9), providing information on material damage.

Non–scission type mechanophores, on the other hand, maintain the connectivity of the network chain, allowing these molecules to behave as stress sensors. A commonly used nonscission mechanophore is spiropyran (SP), which can be activated into merocyanine (MC) by force. Craig and co-workers demonstrated elegantly by single-molecule atomic force microscopy (AFM) experiments (21) that this transition occurs when the applied force exceeds ~240 pN. If SP is incorporated in a polymer material, a change in color (12, 14, 22–25) of the material can be used to detect a region of high stress, as for example, the activation of plastic deformation in polymer glasses (26), or to detect high-strain regions in impact experiments (27).

However, the progress from a qualitative detection to quantitative mapping of heterogeneous stress fields is not trivial and requires careful thought on the choice of the material, the incorporation of the mechanophore in the material, the data acquisition process, and the analysis at both the calibration and measurement stages. The incorporation of SP in the material must be random and homogeneous. The average force on the molecule must be directly related to the macroscopic stress and should activate before the material breaks. Furthermore, SP should be incorporated in elastic materials to avoid viscoelastic effects on mechanophore activation.

A good model system is interpenetrated multiple-network elastomers (19, 28, 29) made from one or more loosely cross-linked matrix networks interpenetrated with a well–cross-linked filler network that is isotropically prestretched. As previously demonstrated for hydrogels (30, 31), the prestretched filler network is stiffer than the matrix network and carries most of the load. It acts as a sacrificial network and dissipates energy by bond scission, delaying macroscopic crack propagation during deformation. If the T_g of the polymer is well below room temperature, it exhibits a very weak strain rate dependence. Hence, the purpose of this paper is to exploit recently developed mechanochemistry to propose an accessible and direct analytical method to quantify stress in elastomeric materials.

RESULTS

Fabrication and mechanical responsiveness

As previously described (19, 28, 29) and detailed in the Supplementary Materials, mechanochromic multiple-network elastomers were prepared by photopolymerizing an initial network containing ethyl acrylate (EA) monomers, SP, and 1,4-butanediol diacrylate (BDA) cross-linkers and 2-hydroxy-2-methylpropiophenone (HMP) photoinitiators. The fraction of cross-linker that is SP was adjusted to 10% of the total cross-linker to obtain the best results in imaging.

After drying, the loosely cross-linked interpenetrating network was synthesized by swelling the filler network with EA monomers, BDA cross-linkers, and HMP initiators and subsequently photopolymerizing them under ultraviolet (UV) light. This process of swelling and photopolymerization was carried out for each interpenetrated network added to the material system so that double-network (DN) and triple-network (TN) elastomers were synthesized as depicted in Fig. 1.

Fig. 1. Synthesis of multiple-network elastomers containing SP mechanophores.

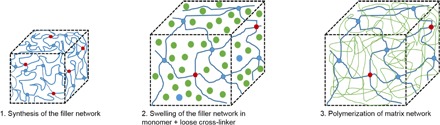
Red, blue, and green dots represent the SP cross-linker, BDA cross-linker, and the EA monomers, respectively. The blue and green networks denote the filler and matrix networks, respectively.

As previously reported (28, 29), the first polymerized network behaves analogously to a continuous filler network and controls the general mechanical properties of the material system. By adjusting the cross-linking level of the filler network, thereby changing the maximum extensibility of the polymer chain between cross-links and degree of swelling of the filler network, the onset of strain hardening of the elastomeric system can be tuned to different values of stretch. To reflect this, the sample nomenclature is represented by Ax-y(z) as shown in Table 1, where A, x, y, and z denote the monomer type in the filler network, the total cross-linker, the SP concentration in mole percent (mol %) relative to the monomer, and the degree of prestretched λ₀ in the filler network, respectively. The volume fraction of the filler network, ϕ_filler, in each molecular composite can be easily obtained from

$${\mathrm{\varphi }}_{\text{filler}}=\frac{1}{{\mathrm{\lambda }}_0^3}$$ (1)

Table 1. Nomenclature of materials used.

Family of materials	Single networks	DNs	TNs
EA0.5-0.05	EA0.5-0.05(1)	EA0.5-0.05(1.56)	EA0.5-0.05(2.23)
EA0.5-0.025	EA0.5-0.025(1)	EA0.5-0.025(1.60)	EA0.5-0.025(2.35)
EA0.5-0.0125	EA0.5-0.0125(1)	EA0.5-0.0125(1.58)	EA0.5-0.0125(2.36)
EA0.2-0.05	EA0.2-0.05(1)	EA0.2-0.05(1.70)	EA0.2-0.05(2.61)

Note that Ax-y represents a family of materials characterized by the filler network properties. For further details on the material properties and corresponding stress-strain curves, see table S1 and fig. S2A.

Chromatic changes and SP activation

As described in Fig. 2A, the SP cross-linker can be converted to MC by force activation, which is accompanied by a change in light absorption and a visible color change (transparent to blue). As mentioned earlier, the critical force f_act to activate SP has been determined from AFM studies (21) to be ~240 pN. This value can be used to estimate the average stress of activation by multiplying the activation force per molecule by the areal density Σ of strands crossing a plane normal to the tensile direction. From the cross-link density of the filler network, Σ can be estimated (29) at 0.3 × 10¹⁷ to 0.5 × 10¹⁷ chains/nm², and 50% of activated molecules should correspond to a stress of the order of 7 to 10 MPa. To observe a wide range of color change, we selected EA0.5-0.05(2.23) as a model mechanochromic system due to its relatively high failure stress in uniaxial tension (σ_f~15 MPa; fig. S2B). SP was incorporated into the filler network as a cross-linker because the filler network is primarily responsible for supporting high stresses in the material system (29).

Fig. 2. Quantification of color change.

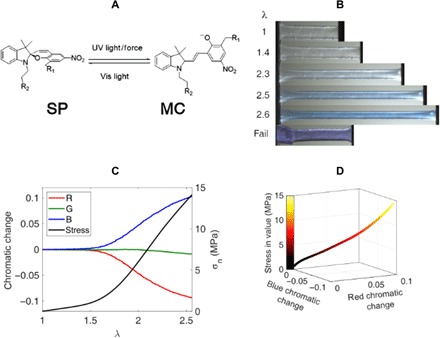
(A) Scheme of the SP and MC molecules. Vis, visible. (B) Images taken at different values of stretch. Photo credits: Yinjun Chen and C. Joshua Yeh (ESPCI Paris). (C) Chromatic change as a function of stretch for the images extracted from the video of uniaxial extension. (D) Calibration curve for the stress as a function of the blue and red chromatic change. All tests were carried out for the EA0.5-0.05(2.23) materials.

Color changes during uniaxial extension tests were recorded using a standard Red-Green-Blue (RGB) camera and postprocessed (32) in MATLAB (see section S3.2). As shown in Fig. 2B, the sample initially appears transparent until a uniaxial critical nominal stress is reached, in which the sample begins to turn blue. To quantitatively characterize the color of a pixel in the sample area, we use the chromaticity, S_ratio, defined as the ratio of a color channel intensity, S = R, G, or B, normalized by the total pixel intensity (33)

$$S_{\text{ratio}}=\frac{S}{\sum S}$$ (2)

where ∑ represents the summation of all the color channels. Chromatic changes (ΔR_ratio, ΔG_ratio, and ΔB_ratio) were calculated relative to the beginning of the experiment.

Note that the color state of a pixel is uniquely defined by two chromatic descriptors since the remaining chromatic value can be determined from Eq. 2. This quantitative approach for characterizing color is referred herein as RGB analysis. Details of the data acquisition and RGB analysis are given in section S3.

The results of the RGB analysis are plotted in Fig. 2C. During uniaxial stretching, the averaged blue chromaticity over the uniaxially stretched sample rapidly increased above a critical nominal stress of ~1.5 MPa, while the red chromaticity exhibited an opposite trend. The green chromaticity remained relatively constant throughout the whole process. From the color and stress state, a color-stress calibration curve can be constructed (see section S4) as shown in Fig. 2D, where the color bar represents the uniaxial nominal stress. The chromaticity increases linearly with stress, except at high stress levels, where nonlinearity in the absorbance and/or damage begins to influence the color response.

The chromatic change that we observe is due to the progressive activation of the SP mechanophores incorporated in the filler network into MC as the stress increases, resulting in a change in light absorption. Thus, changing the initial SP concentration will affect chromaticity. To examine the effects of SP concentration, we compare samples with different relative amounts of SP cross-linker in the filler network (at the same total cross-linking level) in Fig. 3A. Although the three types of materials have similar mechanical properties (fig. S4A), they show different chromatic behaviors as a function of stress due to the different initial concentration of SP. The red and blue chromaticity changes linearly as a function of applied nominal stress, which is not intuitively obvious considering that the information collected from an RGB camera is proportional to the integrated transmitted light from the sample (see eq. S8). However, the observed linearity in chromaticity for nominal stresses below 8 MPa suggests that a linear correction factor is sufficient to collapse the curves, as shown in Fig. 3 (A and B).

Fig. 3. Stress and stretch detection in uniaxial tension.

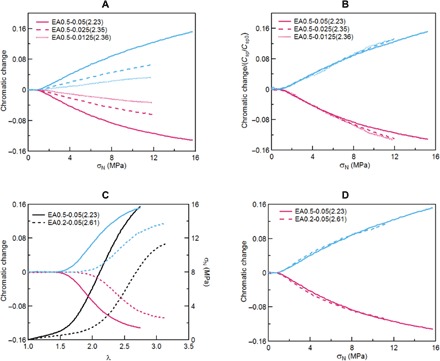
(A) Red and blue chromatic change plots as a function of nominal stress for the multiple-network elastomers with various SP concentrations. (B) Same data with the chromatic change renormalized by the SP concentration. (C) Stress-strain curves (black lines) and red and blue chromatic change as a function of stretch. (D) Red and blue chromatic change as a function of nominal stress for multiple-network elastomers with different cross-link densities in the filler network.

Although the changes in chromaticity are attributed to the activation of SP, thickness effects need to be considered. According to the Beer-Lambert law, the length of the optical path will have an equal effect as the changes in concentration. As the sample is being uniaxially stretched of λ, the thickness of the sample will decrease as λ^−1/2. This will give a logarithmic dependence of the chromaticity on stretch. To minimize the thickness dependence on chromaticity, we kept the initial sample thickness during fracture tests the same as the calibration tests.

From the calibration curve shown in Fig. 2D, the activation of the SP could be strain or stress sensitive. To address this question, we investigated the chromatic response between two different families of materials containing the same probe. Because the mechanical properties of multiple-network elastomers are characterized by the structure of the filler network (29), its cross-linking density was reduced from 0.5 to 0.2 mol % relative to moles of monomer while maintaining the same SP concentration relative to monomer. As shown in Fig. 3C, this new family of materials based on a less cross-linked filler network (EA0.2-0.05) displayed a lower elastic modulus and higher extensibility (black curves in Fig. 3C). More interesting are the associated chromatic changes during uniaxial extension that occur in these two materials, which are shown in Fig. 3C as a function of stretch and in Fig. 3D as a function of nominal stress. The change in color clearly occurs at a different extension ratio (Fig. 3C) but at the same stress (Fig. 3D). This shows that SP acts here as a molecular force sensor because the nominal stress (and not the true stress) in uniaxial extension represents the product of the average chain force (the measured quantity) with the loaded areal strand number (a material constant with increasing stretch).

Another example of stress versus strain sensing is shown in fig. S4. Additional factors that can influence chromaticity for a given nominal stress such as strain rate or color stability over time in relaxation tests modified little the chromatic response. These results are discussed in more detail in fig. S5.

Quantification of stress around crack tip

Having established the relationship between chromatic change and nominal stress, the color-stress calibration curve was used to quantify the spatially heterogeneous stress distribution in fracture tests performed in uniaxial tension with a single-edge notch geometry. The energy release rates ($\mathcal{G}$) can be calculated for each value of stretch λ by using the approach proposed by Rivlin and Thomas (34) and modified by Greensmith (35)

$$\mathcal{G}=\frac{6c}{\sqrt{\mathrm{\lambda }}}\times W\left(\mathrm{\lambda }\right)$$ (3)

where c is the initial notch length and W(λ) is the strain energy density in the unnotched sample under uniaxial tension with a stretch ratio of λ. An RGB camera was used to record the entire experiment during fracture tests from the side, and representative images are shown in Fig. 4A.

Fig. 4. Stress map around the crack tip.

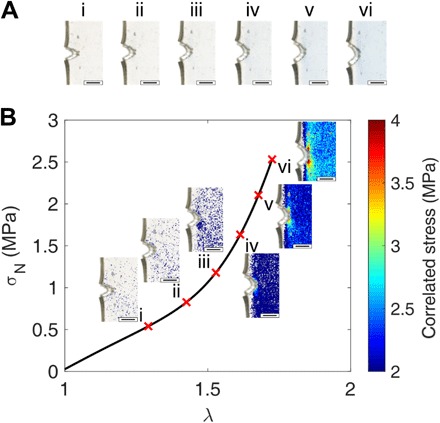
(A) Color-corrected images of a EA0.5-0.05(2.23) sample around the crack tip during a fracture test. i to vi correspond to different values of λ defined in (B). (B) Stress-strain curve of the same sample. Stress maps i to vi correspond to images in (A) with position-dependent stress values obtained with the RGB analysis. Scale bars, 1 mm. Photo credits: Yinjun Chen and C. Joshua Yeh (ESPCI Paris).

The chromatic zones were then quantified and converted to a stress value pixel by pixel on the basis of the color-stress calibration curve in uniaxial tension shown in Fig. 2D. Figure 4B shows the stress map of the EA0.5-0.05(2.23) sample around the crack tip [see section S5 for the construction of stress maps; (36)]. As the average stress increases, above 2 MPa, a stress concentration becomes directly visible at the crack tip and continues to grow with increasing applied strain. At the onset of crack propagation, the stress around the crack tip, within the spatial resolution of the technique, reached a maximum stress of 4 MPa, while the far-field regions sustained stresses above 2.5 MPa. (Note that stresses below ~1.5 MPa are below the detection limit of SP activation and appear colorless.)

Comparing stress maps between two different materials

The relevance of quantitative stress mapping by using an internal stress probe can be demonstrated by comparing the crack tip stress distribution between two different types of materials obtained with the same calibration curve. Figure 5 shows the value of the applied energy release rate $\mathcal{G}$ as a function of λ for single-edge notch samples made from the two materials containing the SP cross-linker described in Fig. 3 (C and D). The last point of each curve represents crack propagation, which corresponds to a critical energy release rate $\mathcal{G}$_c of 3.48 ± 0.48 and 5.1 ± 0.64 kJ/m² for EA0.5-0.05(2.23) and EA0.2-0.05(2.61), respectively. Figure 5 shows stress maps near the crack tip for different values of λ and $\mathcal{G}$. When comparing the measured stress fields of both materials at the same $\mathcal{G}$, the multiple network EA0.5-0.05(2.23) made from the more cross-linked filler network consistently displays much higher stresses near the crack relative to the material EA0.2-0.05(2.61) made from less cross-linked filler network. However, just before crack propagation, stresses are clearly higher and more delocalized for EA0.2-0.05(2.61), reflecting its higher value of $\mathcal{G}$_c and supporting the general intuition that a larger dissipation zone ahead of the crack tip leads to enhanced fracture toughness (37, 38).

Fig. 5. Stress maps at the same energy release rate.

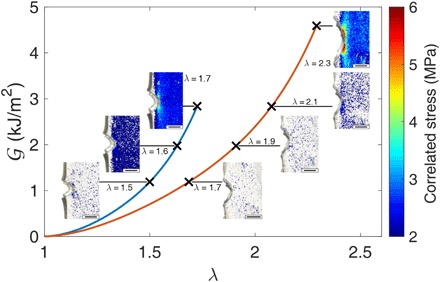
Stress mapping around a crack tip for two different materials: EA0.5-0.05(2.23) in blue and EA0.2-0.05(2.61) in red. Crosses correspond to different values of the supplied elastic energy at the crack tip (energy release rate) $\mathcal{G}$ = 1.18, 2.48, 3.57, and 5.1 kJ/m². Photo credits: Yinjun Chen and C. Joshua Yeh (ESPCI Paris).

Results of finite element simulations

Although Fig. 5 clearly shows that different intensities of blue can be detected near a defect, there is still no evidence that the measured value of stress is consistent with what one would expect from the knowledge of the mechanical properties of the material. To validate quantitatively our stress measurement, we performed finite element simulations. The stress-strain response obtained from uniaxial tension tests was first satisfactorily fitted with the incompressible Ogden model (39). Although there are other choices of hyperelastic models (40), a version of the Ogden model was able to provide an almost perfect fit with uniaxial tension data in the stress range of 0 to 6 MPa, as shown in fig. S10 for both materials [EA0.2-0.05(2.61) and EA0.5-0.05(2.23)]. It should be noted that such a model does not carry physical meaning and was used here to reproduce as closely as possible the mechanical behavior of the material by fitting data in uniaxial tension. The stress range where the Ogden model fits the uniaxial tension data well (i.e., 0 to 6 MPa) coincides with the range exhibited in experimental stress maps in Fig. 5.

The Ogden model with calibrated parameters was then fed into finite element simulations (FEM) through a commercial software ABAQUS (version 6.17, Simulia Inc., Providence, RI) with the macroscopic stretch λ as the only input and no further adjustable parameters. The FEM simulation determines the stress field near the crack tip, which is multiaxial in nature and consists of normal and shear components. Description of such multiaxial stress state requires a tensor, while the value of the stress determined by the chromatic change of SP is a scalar. In addition, FEM results typically provide true stress components defined in the deformed configuration, while the calibration curve in Fig. 2 relates the SP chromatic signal to the nominal stress defined using the undeformed cross-sectional area. These two differences between FEM results and experimental stress map lead to a question on exactly what stress is measured by the chromatic change. Because SP activation only depends on the average force applied on the polymer strand in the network, we hypothesize that the experimentally measured stress is the maximum principal nominal stress (41), which is equal to the ratio of the maximum principal true stress and the maximum principal extension: σ_max/λ_max (see section S6 for a detailed derivation). Note that σ_max/λ_max recovers the nominal tensile stress σ_N under uniaxial tension. The 2D FEM map of σ_max/λ_max immediately before crack propagation [i.e., λ = 1.7 for EA0.2-0.05(2.61) and λ = 2.3 for EA0.5-0.05(2.23)] is plotted in Fig. 6 using the same color coding for the stress and can be quantitatively compared with the stress field generated by the measurement of the chromatic change. It can be seen that for both materials, the experimental data and the FEM result match quantitatively well in stress values without any adjustable parameters, but that the experimental stress maps for both samples show a notable high stress region along the crack faces rather than directly in front of the crack tip. We believe that this difference is due to the crack front not being strictly perpendicular to the sample plane because the three-dimensionality close to the crack tip prevented accurate determination of color observed at the front sample surface. To support this hypothesis, we built a 3D FEM model where the crack front makes an angle with the surface plane of the sample, as shown in fig. S11. Consequently, the crack on the front surface is longer than the crack on the back surface of the sample. In the fracture experiments, the stress map measured from chromatic change reflects the averaged response across the sample thickness, which motivates us to average σ_max/λ_max across the thickness of the 3D FEM model and project the average stress contour on the front surface of the model, as illustrated in fig. S11. The FEM results based on the 3D model, shown in fig. S12, exhibit a high stress region on the crack surface rather than directly ahead of the crack tip. Both the location and magnitude of the high stress region are consistent with what is found from the experimental stress map. Together, the quantitative consistency between simulation results and experimental data with no adjustable parameter for such a difficult problem as the tip of a crack demonstrates the feasibility of using SP as an experimental quantitative approach for stress mapping.

Fig. 6. Comparison of experimental and simulated stress maps.

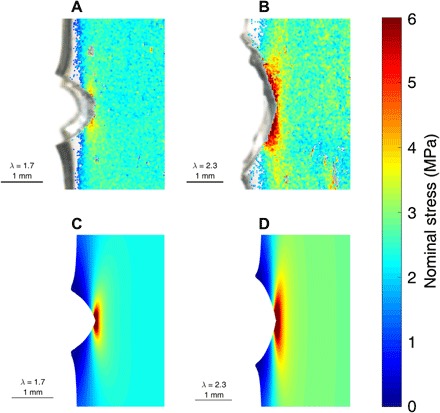
The experimentally obtained stress map of (A) the EA0.5-0.05(2.23) and (B) the EA0.2-0.05(2.61) fracture samples. The simulated stress map of (C) the EA0.5-0.05(2.23) and (D) the EA0.2–0.05(2.61) fracture samples.

DISCUSSION

Several points deserve a more detailed discussion. First, the successful quantitative mapping of the stress is due to the very specific structure of the multiple-network elastomers. As previously pointed out (29) and modeled (42, 43), the filler network carries most of the load in the material as soon as the deformation exceeds the strain hardening limit for the prestretched filler network. The matrix networks carry only a small portion of the total stress. As a result, the activation of the SP occurs well before macroscopic fracture occurs. Second, the elastomers that we use have a homogeneous composition and are elastic so that the color signal does not change over time. This combination, i.e., activation of SP before macroscopic fracture and absence of viscoelasticity, results in a quantitative stress mapping where SP acts as an internal force probe. Last, while the chromatic change is a scalar instead of a tensor, the use of the maximum principal nominal stress as the activation criterion makes it possible to apply the calibration curve obtained from uniaxial tension to more complex loading situations such as the crack tip region. The quantitative correspondence between the measured stress and the calculated one, without any adjustable parameters, is remarkable and demonstrates that the activation of the SP by force can be reliably used to quantify the local stress along the principal direction in transparent materials. Although we focused here on the use of an RGB camera to obtain a pixel-by-pixel map of the stress, a more sensitive spectrometer could be used to detect the stress more accurately in specific single points.

It is lastly worthwhile to discuss how this method could have advantages relative to an indirect method. The classical way of evaluating a stress field experimentally is through a measure of the strain field by digital image correlation and subsequent use of a constitutive model. The accuracy of the stress values obtained in this way depends crucially on the accuracy of both strain field data and model. In situations where there are sharp gradients and the material behaves very nonlinearly at high strain (strain hardening or damage by bond scission), both strain field measurements and constitutive model lack accuracy so that a direct stress measure relying on an internal force probe may be more accurate despite the inherent difficulty in incorporating the force probe in the material.

CONCLUSION

A novel method to map stress in soft materials by mechanochemistry has been proposed and carried out. We have quantitatively mapped the stress distribution in multiple-network elastomers by incorporating SP in the filler network as a cross-linker. The concept of chromaticity was used to track color change as the material is subjected to a uniaxial tension. By varying the concentration and mechanical properties within the filler network of TN elastomers, a calibration curve between the applied uniaxial nominal stress and the resulting chromatic change was established. This stress-color calibration curve was then implemented to determine the stress distribution around a crack tip for two model materials with different strain hardening properties. This example provides methodological challenges with the presence of strong localized stress gradients where the stress distribution would be much more difficult to obtain from the strain field.

To validate the mapping method, we compared experimental stress fields with FEM simulations on the basis of the incompressible Ogden model and showed an excellent agreement without any adjustable parameter, thereby validating our quantitative approach correlating chromatic analysis with nominal stresses to experimentally deduce stress distributions around a crack tip. By extending the quantitative value of SP as a molecular force probe, previously inaccessible insights into the physical mechanisms driving crack propagation can now be obtained experimentally and used to test statistical fracture modeling of soft, tough materials and more generally to quantify stresses in more complex geometries from simple optical observations with a color camera.

MATERIALS AND METHODS

Preparation of various SN

The identical filler network was prepared first by free-radical photopolymerization. SP was covalently incorporated into the first network along with BDA. To accomplish this, 1 mole percent (mol %) 2-hydroxy-2-methylpropiophenone (HMP) UV initiator and 0.5 mol % of cross-linker (0.05 mol % of SP and 0.45 mol % of BDA) were dissolved into EA, and a purple pre-gel solution was prepared. Note that molar percentages are respective to moles of EA in the first network. The solution was poured into a mold composed of two glass plates with a silicone spacer to control the film thickness. The whole device was tightened by two metal frames to seal the mold. Polymerization was initiated by UV light (by a Vilber Lourmat lamp: model VL-215.L). After polymerization, a uniform purple rubbery single network was formed and subsequently dried in a vacuum desiccator for 1 day to remove unreacted monomers. After drying, the single network exhibited a reddish color and was stored at room temperature in a dark environment for later use. Mechanical response is closely related to the mechanical properties of materials. According to previous reports (29), the filler network mainly controls the mechanical properties of multiple-network elastomers. To synthesize an SN containing 0.2 mol % of cross-linker while maintaining the same amount of SP, the BDA cross-linker was reduced to 0.15 mol %. Various filler networks with 0.5 mol % of cross-linker and varying SP concentrations were also prepared by tuning the ratio of SP and BDA. A summary of the material properties is shown in table S1.

Fabrication of multiple-network elastomers

Using the SNs described above, DNs and TNs were prepared by sequentially swelling and polymerizing. A piece of SN (0.67-mm thickness, 3-cm length, and 2-cm width) was swollen in a monomer solution with loose cross-linker BDA (0.01 mol %) and HMP (0.01 mol %) initiator. When the equilibrium swelling was reached, DNs were synthesized by polymerizing the swollen single network. After polymerization, sample was dried under vacuum for 1 day and then weighted. These two steps above were repeated on the DN to prepare TNs.

Uniaxial tension

Samples with dog-bone shape were subjected to uniaxial extension at an initial strain rate of 0.05 s⁻¹ on an Instron machine (model 5565 with a 100-N load cell). To measure the macroscopic strain during the uniaxial deformation, two black marks were made on the homogeneously deformed zone of the specimens. An RGB camera (SENTECH: STC-MCS241U3V; image sensor: SONY IMX174; cell size: 5.86 μm × 5.86 μm) with a frame rate of 25 fps was used to record the relative displacement of the two black markers. MATLAB scripts were used to analyze the position of the marks from the recorded videos, which allowed for accurate determination of the applied uniaxial stretch. The stretch was defined as λ = L/L₀, where L₀ and L are the distances between the two centroid of the marks before and after stretching, respectively. The macroscopic engineering stress was obtained from the Instron machine. Before performing tensile tests, all specimens were exposed to white light for 5 min to ensure that all of the mechanophores were in its inactivated SP form. More details on the mechanical tests can be found in section S2.

RGB analysis

Frames extracted from the recorded videos were used to perform color analysis. A static background region was defined and used to color correct each analyzed frame. After color correction, a sample region was chosen to quantify the color change in uniaxial extension. The red, green, and blue chromatic ratios are then calculated for each pixel using Eq. 2. To quantify chromatic changes, the red, green, and blue chromatic ratios were subtracted relative to the beginning of the experiment. By synchronizing the video and uniaxial extension with the stress data taken from the Instron machine, the corresponding nominal stress of each frame was obtained. Last, the color-stress calibration curves were constructed from the stress and chromaticity values. More details on the color analysis, the construction of the color-stress curves, and stress mapping around the crack tip can be found in sections S3, S4, and S5, respectively.

Simulation

To simulate the deformation and stress field of the mode I crack, a 2D plane stress finite element model (FEM) in ABAQUS (v6.17, Simulia Inc., Providence, RI) was constructed. Geometry of the model was set the same as the experiment fracture test, i.e., width W = 5 mm, height H = 10 mm, and crack length a = 0.75 mm for the EA0.5-0.05(2.23) material and a = 0.81 mm for the EA0.2-0.05(2.61) material. Because of symmetry, the FE model can be simplified as a half model with top surface loaded with uniform displacement and the bottom surface applied with symmetry boundary. The model was meshed with 6200 CPS4 elements with the smallest size set to 0.01 mm. The bulk mechanical response was implemented with the Ogden model using the fitting parameter shown in table S3. More details can be found in section S6.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/20/eaaz5093/DC1