Psi4 1.4: Open-source software for high-throughput quantum chemistry

Abstract

PSI4 is a free and open-source ab initio electronic structure program providing implementations of Hartree–Fock, density functional theory, many-body perturbation theory, configuration interaction, density cumulant theory, symmetry-adapted perturbation theory, and coupled-cluster theory. Most of the methods are quite efficient, thanks to density fitting and multi-core parallelism. The program is a hybrid of C++ and Python, and calculations may be run with very simple text files or using the Python API, facilitating post-processing and complex workflows; method developers also have access to most of PSI4’s core functionalities via Python. Job specification may be passed using The Molecular Sciences Software Institute (MolSSI) QCSCHEMA data format, facilitating interoperability. A rewrite of our top-level computation driver, and concomitant adoption of the MolSSI QCARCHIVE INFRASTRUCTURE project, makes the latest version of PSI4 well suited to distributed computation of large numbers of independent tasks. The project has fostered the development of independent software components that may be reused in other quantum chemistry programs.

I. INTRODUCTION

The PSI series of programs for quantum chemistry (QC) has undergone several major rewrites throughout its history. This is also true of the present version, PSI4,¹ which bears little resemblance to its predecessor, PSI3. While PSI3 is a research code aimed at providing a handful of high-accuracy methods for small molecules, PSI4 aims to be a user-friendly, general-purpose code suitable for fast, automated computations on molecules with up to hundreds of atoms. In particular, PSI4 has seen the introduction of efficient multi-core, density-fitted (DF) algorithms for Hartree–Fock (HF), density functional theory (DFT), symmetry-adapted perturbation theory (SAPT),^2,3 second- and third-order many-body perturbation theory (MP2, MP3), and coupled-cluster (CC) theory through perturbative triples [CCSD(T)].⁴ While PSI3 is a stand-alone program that carries the assumption that QC computations were the final desired results and so offered few capabilities to interface with other program packages, PSI4 is designed to be part of a software ecosystem in which quantum results may only be intermediates in a more complex workflow. In PSI4, independent components accomplishing well-defined tasks are easily connected, and accessibility of key results through a Python interface has been emphasized.

Although the PSI project was first known as the BERKELEY package in the late 1970s, it was later renamed to reflect its geographical recentering alongside Henry F. Schaefer III to the University of Georgia. The code was ported to hardware-independent programming languages (Fortran and C) and UNIX in 1987 for PSI2; rewritten in an object-oriented language (C++), converted to free-format user input and flexible formatting of scratch files, and released under an open-source GPL-2.0 license in 1999 for PSI3;⁵ reorganized around a programmer-friendly library for easy access to molecular integrals and related quantities and then unified into a single executable combining C++ for efficient QC kernels with Python for input parsing and for the driver code in 2009 for PSI4;⁶ and, most recently, converted into a true Python module calling core C++ libraries, reorganized into an ecosystem with narrow data connections to external projects, opened to public development and open-source best practices, and relicensed as LGPL-3.0 to facilitate use with a greater variety of computational molecular sciences (CMS) software in 2017 for PSI4 v1.1.¹

These rewrites have addressed challenges particular to quantum chemistry programs, including the following: (i) users want a fully featured program that can perform computations with the latest techniques; however, (ii) QC methods are generally complex and difficult to implement; even more challenging is that (iii) QC methods have a steep computational cost and therefore must be implemented as efficiently as possible; yet this is a moving target as (iv) hardware is widely varied (e.g., from laptops to supercomputers) and frequently changing. We also note an emerging challenge: (v) thermochemical,⁷ machine learning,⁸ force-field fitting,⁹ etc. applications can demand large numbers (10⁵–10⁸) of QC computations that may form part of complex workflows.

PSI4 has been designed with these challenges in mind. For (i)–(iii), we have created a core set of libraries that are easy to program with and that provide some of the key functionalities required for modern QC techniques. These include the LIBMINTS library that provides simple interfaces to compute one- and two-electron integrals, the DFHELPER library to facilitate the computation and transformation of three-index integrals for DF methods, and a library to build Coulomb and exchange (J and K) matrices in both the conventional and generalized forms that are needed in HF, DFT, SAPT, and other methods (see Refs. ¹ and ⁶ and Sec. V B for more details). These libraries are also intended to address challenge (iv) above, as they have been written in a modular fashion so that alternative algorithms may be swapped in and out. For example, the LIBMINTS library actually wraps lower-level integrals codes, and alternative integrals engines may be used as described in more detail in Sec. V G. Similarly, the object-oriented JK library is written to allow algorithms adapted for graphics processing units (GPUs) or distributed-parallel computing. Challenge (v) is tackled by allowing computations via a direct application programming interface (API) and by encouraging machine-readable input and output.

The PSI4NUMPY project¹⁰ further simplifies challenge (ii), the implementation of new QC methods in PSI4. By making the core PSI4 libraries accessible through Python, it is now considerably easier to create pilot or reference implementations of new methods, since Python as a high-level language is easier to write, understand, and maintain than the C++ code. Indeed, because the libraries themselves are written in an efficient C++ code, a Python implementation of a new method is often sufficient as the final implementation as well, except in the cases that require manipulations of three- or four-index quantities that are not already handled by the efficient core PSI4 libraries. For reasons of readability, maintainability, and flexibility, the entire codebase is migrated toward more top-level functions in Python.

Although the library design makes it easier for developers to add new methods into PSI4, we believe an even more powerful approach is to create a software ecosystem that facilitates the use of external software components. Our build system, driver, and distribution system have been rewritten specifically with this goal in mind, as discussed in Ref. 1 and Sec. VIII. The Python interface to PSI4 and the recently introduced ability to communicate via QCSCHEMA further enhance this interoperability. Our recent moves to the more permissive LGPL-3.0 license and to fully open development on a public GitHub site (https://github.com/psi4/psi4) are also meant to foster this ecosystem.

Our recent infrastructure work since Ref. 1 is mainly focused on challenge (v), so that QC calculations can be routinely undertaken in bulk for use in various data analysis pipelines. As discussed in Sec. IV, PSI4 has reworked its driver layout to simplify nested post-processing calls and greatly promote parallelism and archiving. Python within PSI4’s driver sets keywords according to the molecular system and method requested, allowing straightforward input files. Additionally, PSI4 as a Python module (since v1.1, one can import psi4) means that codes may easily call PSI4 from Python to perform computations and receive the desired quantities directly via Python, either through the application programming interface (PSIAPI) or through JavaScript Object Notation (JSON) structured data.

Below, we present an overview of the capabilities of PSI4 (Sec. II). We then discuss the performance improvements in PSI4’s core QC libraries (Sec. V), the expanding ecosystem of software components that can use or be used by PSI4 (Secs. VI and VII), and how the software driver has been rewritten to collect key quantities into a standard data format and to allow for parallel computation of independent tasks (Sec. IV).

II. CAPABILITIES

PSI4 provides a wide variety of electronic structure methods, either directly or through interfaces to external community libraries and plugins. Most of the code is threaded using OPENMP to run efficiently on multiple cores within a node. The developers regularly use nodes with about six to eight cores, so performance is good up to that number; diminishing returns may be seen for larger numbers of cores.

Hartree–Fock and Kohn–Sham DFT. Conventional, integral-direct, Cholesky, and DF algorithms are implemented for self-consistent field (SCF) theory. Thanks to the interface with the LIBXC library (see Sec. V A), nearly all popular functionals are available. The DF algorithms are particularly efficient, and computations on hundreds of atoms are routine. Energies and gradients are available for restricted and unrestricted Hartree–Fock and Kohn–Sham (RHF, RKS, UHF, UKS), and restricted open-shell Hartree–Fock (ROHF). RHF and UHF Hessians are available for both conventional and DF algorithms.

Perturbation theory. PSI4 features Møller–Plesset perturbation theory up to the fourth order. Both conventional and DF implementations are available for MP2, MP3, and MP2.5,¹¹ including gradients.^1,12,13 For very small molecules, the full configuration interaction (CI) code can be used^14,15 to generate arbitrary-order MPn and Z-averaged perturbation theory (ZAPTn)¹⁶ results. Electron affinities and ionization potentials can now be computed through second-order electron-propagator theory (EP2)¹⁷ and the extended Koopmans’s theorem (EKT).^18–20

Coupled-cluster theory. PSI4 supports conventional CC energies up to singles and doubles (CCSD) plus perturbative triples [i.e., CCSD(T)]⁴ for any single determinant reference (including RHF, UHF, and ROHF) and analytic gradients for RHF and UHF references.⁵ For the DF, energies and analytic gradients up to CCSD(T) are available for RHF references.^21–23 Cholesky decomposition CCSD and CCSD(T) energies²¹ and conventional CC2²⁴ and CC3²⁵ energies are also available. To lower the computational cost of CC computations, PSI4 supports²⁶ approximations based on frozen natural orbitals (FNOs)^27–30 that may be used to truncate the virtual space. Excited-state properties in PSI4 are supported with equation-of-motion CCSD^31,32 and the CC2 and CC3 approximations.³³ Linear-response properties, such as optical rotation,³⁴ are also available. PSI4 also supports additional CC methods through interfaces to the CCT3 (see Sec. VI C 6) and MRCC programs.³⁵

Orbital-optimized correlation methods. CC and Møller–Plesset perturbation methods are generally derived and implemented using the (pseudo)canonical Hartree–Fock orbitals. Choosing to instead use orbitals that minimize the energy of the targeted post-HF wavefunction has numerous advantages, including simpler analytic gradient expressions and improved accuracy in some cases. PSI4 supports a range of orbital-optimized methods, including MP2,³⁶ MP3,³⁷ MP2.5,³⁸ and linearized coupled-cluster doubles (LCCD).³⁹ DF energies and analytic gradients are available for all of these methods.^40–43

Symmetry-adapted perturbation theory. PSI4 features wavefunction-based SAPT through the third-order to compute intermolecular interaction energies (IEs) and leverages efficient, modern DF algorithms.^44–48 PSI4 also offers the ability to compute the zeroth-order SAPT (SAPT0) IEs between open-shell molecules with either UHF or ROHF reference wavefunctions.^49–51 In addition to conventional SAPT truncations, PSI4 also features the atomic⁵² and functional-group⁵³ partitions of SAPT0 (ASAPT0 and F-SAPT0, respectively), which partition SAPT0 IEs and components into contributions from pairwise atomic or functional group contacts. Furthermore, PSI4 also offers the intramolecular formulation of SAPT0 (ISAPT0),⁵⁴ which can quantify the interaction between fragments of the same molecule as opposed to only separate molecules. The extensive use of core library functions for DF Coulomb and exchange matrix builds and integral transformations (see Sec. V B) has greatly accelerated the entire SAPT module in PSI4, with all SAPT0-level methods routinely deployable to systems of nearly 300 atoms (∼3500 basis functions); see also Secs. V C–V F for a new SAPT functionality.

Configuration interaction. PSI4 provides configuration interaction singles and doubles (CISD), quadratic CISD (QCISD),⁵⁵ and QCISD with perturbative triples [QCISD(T)]⁵⁵ for RHF references. It also provides an implementation⁵⁶ of full configuration interaction (FCI) and the restricted active space configuration interaction (RASCI) approach.⁵⁷

Multi-reference methods. PSI4 provides conventional and DF implementations of the complete-active-space SCF (CASSCF)^58,59 and restricted-active-space SCF (RASSCF).⁶⁰ Through the CHEMPS2 code, the density-matrix renormalization group (DMRG)^61,62 based CASSCF⁶³ and CASSCF plus second-order perturbation theory (CASPT2)⁶⁴ are available. The state-specific multireference CC method of Mukherjee and co-workers (Mk-MRCC) is implemented in PSI4 with singles, doubles, and perturbative triples.⁶⁵ A complementary second-order perturbation theory based on the same formalism (Mk-MRPT2) also exists.⁶⁶ PSI4 can perform multireference CC calculations through an interface to the MRCC program of Kállay and co-workers,^35,67 where high-order excitations (up to sextuples) as well as perturbative methods are supported. Additional methods for strong correlation are available through the FORTE^68–70 and V2RDM_CASSCF⁷¹ (see Sec. VI C 5) plugins.

Density cumulant theory. PSI4 offers the reference implementation of Density Cumulant Theory (DCT), which describes electron correlation using the cumulant of the two-electron reduced density matrix (RDM) instead of a many-electron wavefunction.⁷² PSI4 includes an implementation⁷³ of the original DCT formulation,⁷² a version with an improved description of the one-particle density matrix (DC-12),⁷⁴ its orbital-optimized variants (ODC-06 and ODC-12),⁷⁵ and more sophisticated versions that include N-representability conditions and three-particle correlation effects [ODC-13 and ODC-13(λ₃)].⁷⁶ In particular, ODC-12 maintains CCSD scaling but is much more tolerant of open-shell character and mild static correlation.^77,78 Analytic gradients are available for DC-06, ODC-06, ODC-12, and ODC-13 methods.^75,76,79

Relativistic corrections. PSI4 can perform electronic structure computations with scalar relativistic corrections either by calling the external DKH library for up to fourth-order Douglas–Kroll–Hess (DKH)^80,81 or by utilizing the exact-two-component (X2C)^82–92 approach to supplement the one-electron Hamiltonian of a non-relativistic theory for relativistic effects. At present, only the point nuclear model is supported.

Composite and many-body computations. PSI4 provides a simple and powerful user interface to automate multi-component computations, including focal-point^93–95 approximations, complete-basis-set (CBS) extrapolation, basis-set superposition corrections [counterpoise (CP), no-counterpoise (noCP), and Valiron–Mayer functional counterpoise (VMFC)],^96–98 and many-body expansion (MBE) treatments of molecular clusters. These capabilities can all be combined to obtain energies, gradients, or Hessians, as discussed below in Sec. IV. For example, one can perform an optimization of a molecular cluster using focal-point gradients combining MP2/CBS estimates with CCSD(T) corrections computed in a smaller basis set, with counterpoise corrections. The MBE code allows for different levels of theory for different terms in the expansion (monomers, dimers, trimers, etc.) and also supports electrostatic embedding with point charges.

III. PSIAPI

Introduced in v1.1,¹ the PSI4 API (PSIAPI) enables deployment within custom Python workflows for a variety of applications, including quantum computing and machine learning, by making PSI4 a Python module (i.e., import psi4). Using PSI4 in this manner is no more difficult than writing a standard PSI4 input file, as shown in the middle and left panels of Fig. 1, respectively. The true power of the PSIAPI lies in the user’s access to PSI4’s core C++ libraries and data structures directly within the Python layer. The PSIAPI thereby can be used to, e.g., combine highly optimized computational kernels for constructing Coulomb and exchange matrices from HF theory with syntactically intuitive and verbose Python array manipulation and linear algebra libraries such as NUMPY.⁹⁹ An example of the PSIAPI for rapid prototyping is given in Sec. V I 1.

FIG. 1.

Input modes for PSI4. A coupled-cluster calculation is run equivalently through its preprocessed text input language (PSIthon; left), through the Python API (PSIAPI; middle), and through structured JSON input (QCSCHEMA; right).

A. Psi4NumPy

Among the most well-developed examples of the advantages afforded by the direct Python-based PSIAPI is the PSI4NUMPY project,¹⁰ whose goal is to provide three services to the CMS community at large: (i) to furnish reference implementations of computational chemistry methods for the purpose of validation and reproducibility, (ii) to lower the barrier between theory and implementation by offering a framework for rapid prototyping where new methods could be easily developed, and (iii) to provide educational materials that introduce new practitioners to the myriad of practical considerations relevant to the implementation of quantum chemical methods. PSI4NUMPY accomplishes these goals through its publicly available and open-source GitHub repository,¹⁰⁰ containing both reference implementations and interactive tutorials for many of the most common quantum chemical methods, such as HF, Møller–Plesset perturbation theory, CC, CI, and SAPT. Furthermore, since its publication in 2018, 17 separate projects to date have leveraged the PSI4NUMPY framework to facilitate their development of novel quantum chemical methods.^101–117 Finally, PSI4NUMPY is a thoroughly community-driven project; interested readers are highly encouraged to visit the repository¹⁰⁰ for the latest version of PSI4NUMPY and to participate in the “pull request” code review, issue tracking, or contributing the code to the project itself.

B. Jupyter notebooks

Inspired by notebook interfaces to proprietary computer algebra systems (e.g., Mathematica and Maple), a JUPYTER notebook is an open-source web application that allows users to create and share documents containing an executable code, equations, visualizations, and text.¹¹⁸ JUPYTER notebooks are designed to support all stages of scientific computing, from the exploration of data to the creation of a detailed record for publishing. Leveraging PSI4 within this interface, therefore, provides interactive access to PSI4’s data structures and functionalities. Visualization and analysis of properties such as geometry and orbitals can be facilitated with tools available within The Molecular Sciences Software Institute’s¹¹⁹ (MolSSI) QCARCHIVE^120,121 project. Additionally, the ability to combine executable code cells, equations, and text makes JUPYTER notebooks the perfect environment for the development and deployment of interactive educational materials, as illustrated by the PSI4NUMPY and PSI4EDUCATION¹²² projects, or for living supplementary material that allows readers to reproduce the data analysis.^123,124

IV. TASK-BASED DISTRIBUTED DRIVER

The recursive driver introduced in 2016 for PSI4 v1.0 to reorganize the outermost user-facing functions into a declarative interface has been refactored for PSI4 v1.4 into the distributed driver that emphasizes high-throughput readiness and discretized communication through schema. In the earlier approach, the user employed one of a few driver functions [energy(), gradient(), optimize(), hessian(), frequency()], and everything else was handled either by the driver behind the scenes [e.g., selecting analytic or finite-difference (FD) derivatives] or through keywords (e.g., “mp2/cc-pv[t,q]z,” “bsse_type=cp,” dertype=“energy”). When a user requested a composite computation that requires many individual computations (for example, a gradient calculation of a basis-set extrapolated method on a dimer with counterpoise correction), internal logic directed this into a handler function (one each for many-body expansion, finite-difference derivatives, and composite methods such as basis-set extrapolations and focal-point approximations) which broke the calculation into parts; then, each part re-entered the original function, where it could be directed to the next applicable handler (hence a “recursive driver”). At last, the handlers called the function on an analytic task on a single chemical system, at which point the actual QC code would be launched. However, the code to implement this functionality was complex and not easily extendable to the nested parallelism (among many-body, finite-difference, and composite) to which these computations are naturally suited. Because of these limitations, the internal structure of the driver has been reorganized so that all necessary QC input representations are formed before any calculations are run.

The motivation for the driver refactorization has been the shift toward task-based computing and particularly integration with the MolSSI QCARCHIVE^120,121 project to run, store, and analyze QC computations at scale. The QCARCHIVE software stack, collectively QCARCHIVE INFRASTRUCTURE, consists of several building blocks: QCSCHEMA¹²⁵ for JSON representations of QC objects, job input, and job output; QCELEMENTAL¹²⁶ for Python models (constructors and helper functions) for QCSCHEMA as well as fundamental physical constants and periodic table data; QCENGINE¹²⁷ for compute configuration (e.g., memory, nodes) and QCSCHEMA adaptors for QC programs; and QCFRACTAL¹²⁸ for batch compute setup, compute management, storage, and query.

PSI4 v1.1 introduced a psi4 --json input mode that took in a data structure of molecular coordinates, drivers, methods, and keyword strings and returned a JSON structure with the requested driver quantity (energy, gradient, or Hessian), a success boolean, QCVariables (a map of tightly defined strings such as CCSD CORRELATION ENERGY or HF DIPOLE to float or array quantities), and string output. Since then, QC community input under MolSSI guidance has reshaped that early JSON into the current QCSCHEMA AtomicInput model capable of representing most non-composite computations. (“Atomic” here refers not to an atom vs a molecule but to a single energy/derivative on a single molecule vs multistage computations.) PSI4 v1.4 is fully capable of being directed by and emitting MolSSI QCSCHEMA v1 (see Fig. 1, right) via psi4 --schema input or psi4.run_qcschema(input), where input is a Python dictionary, JSON text, or binary MESSAGEPACKed structure of NUMPY arrays and other fields. Since PSI4 speaks QCSCHEMA natively, its adaptor in QCENGINE is light, consisting mostly of adaptations for older versions of PSI4 and of schema hotfixes. Several other QC packages without QCSCHEMA input/ouput (I/O) have more extensive QCENGINE adaptors that construct input files from AtomicInput and parse output files into AtomicResult (discussed below). The distributed driver is designed to communicate through QCSCHEMA and QCENGINE so that the driver is independent of the community adoption of QCSCHEMA.

The AtomicInput data structure includes a molecule, driver function name, method and basis set (together “model”), and keyword dictionary, while the output data structure AtomicResult additionally includes the primary return scalar or array, any applicable of a fixed set of QCSCHEMA properties, as well as PSI4 specialties such as QCVariables. Importantly, the customary output file is included in the returned schema from a PSI4 computation. The driver has been revamped to use the AtomicInput and AtomicResult structures as the communication unit. In order for the above-mentioned handler procedures (now “Computer” objects) of the PSI4 driver to communicate, specialized schemas that are supersets of AtomicResult have been developed. New fields have been introduced, including bsse_type and max_nbody for ManyBodyComputer; stencil_size (the number of points in the finite-difference approximation) and displacement_space for FiniteDifferenceComputer; scheme and stage for CompositeComputer; and degeneracy and theta_vib for the vibrational procedure. These contents are being optimized for practical use in PSI4 and have been or will be submitted to MolSSI QCSCHEMA and QCELEMENTAL for community input and review. A recently official schema already implemented in PSI4 is for wavefunction data and encodes orbital coefficients, occupations, and other information in the standard common component architecture (CCA) format.¹²⁹ This new schema is supported by the native PSI4 infrastructure to permit serialization and deserialization of PSI4’s internal Wavefunction class that contains more fields than the schema stores. Although not yet used for communication, PSI4 can also emit the BasisSet schema. The layered procedures of the distributed driver involve sums of potentially up to thousands of schema-encoded results and are thus susceptible to numerical noise that a pure-binary data exchange would avoid. Nominally, JSON does not serialize NUMPY arrays or binary floats. However, the QCELEMENTAL/QCSCHEMA models support extended serialization through MESSAGEPACK¹³⁰ so that NUMPY arrays⁹⁹ can be transparently and losslessly moved through the distributed driver.

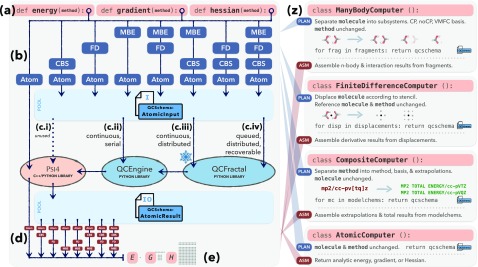
The task-oriented strategy for the distributed driver is illustrated in Fig. 2. The user interface with the customary driver functions, Fig. 2(a), remains unchanged. If a single analytic computation is requested, it proceeds directly into the core QC code of PSI4 (leftmost arrow), but if any of the handlers are requested, the driver diverts into successively running the “planning” function of each prescribed procedure [Fig. 2(b) with details in Fig. 2(z)] until a pool of analytic single-method, single-molecule jobs in the QCSCHEMA AtomicInput format is accumulated. Although these could be run internally through the API counterpart of psi4 --schema [Fig. 2(c.i)], PSI4 executes through QCENGINE so that other programs can be executed in place of PSI4 if desired [Fig. 2(c–ii)]. An additional strategic benefit of running through QCENGINE is that the job pool can be run through QCFRACTAL [Fig. 2(c–iv)], allowing for simultaneous execution of all jobs on a cluster or taking advantage of milder parallelism on a laptop, just by turning on the interface (∼5 additional Python lines). The database storage and QCSCHEMA indexing inherent to QCFRACTAL means that individual jobs are accessible after completion; if execution is interrupted and restarted, completed tasks are recognized, resulting in effectively free coarse-grained checkpointing. Alternatively, for the mild boost of single-node parallelism without the need to launch a QCFRACTAL database, one can run in the “snowflake” mode [Fig. 2(c.iii)], which employs all of QCFRACTAL’s task orchestration, indexing, and querying technology, except the internal database vanishes in the end. The use of these modes in input is shown in Fig. 3. When all jobs in the pool are complete (all QCSCHEMA AtomicResult are present), the “assemble” functions of each procedure are run in a reverse order of invocation [Fig. 2(d) with details in Fig. 2(z)]. That is, model chemistry energies are combined into composite energies by the CompositeComputer class, then composite energies at different displacements are combined into a gradient by the FiniteDifferenceComputer class, then gradients for different molecular subsystems and basis sets are combined into a counterpoise-corrected gradient by the ManyBodyComputer class, and finally, the desired energy, gradient, or Hessian is returned, Fig. 2(e). The schema returned by driver execution has the same apparent (outermost) structure as a simple AtomicResult with a molecule, return result, properties, and provenance, so it is ready to use by other software expecting a gradient (like a geometry optimizer). However, each procedure layer returns its own metadata and the contributing QC jobs in a specialized schema, which is presently informal, so that the final returned JSON document is self-contained. Ensuring maintainability by merging code routes was given high priority in the distributed driver redesign: parallel and serial executions take the same routes, intra-project (API) and inter-project communications use the same QCSCHEMA medium, and (in a future revision) a generic QC driver calling PSI4 can proceed through QCSCHEMA.

FIG. 2.

Structure of the distributed driver: see the final paragraph in Sec. IV for details. In brief, a user request (a) for a multi-molecule, multi-model-chemistry, or non-analytic derivative passes into planning functions (b) defined in procedure tiles (z) that generate a pool of QCSCHEMA for single-molecule, single-model-chemistry, analytic derivative inputs. These can run in several modes (c), depending on desired parallelism and recoverability. Completed QCSCHEMA passes through assembly functions (d) defined in procedure tiles (z) and denoted “ASM” that reconstitute (e) into the requested energy (“E”), gradient (“G”), or Hessian (“H”).

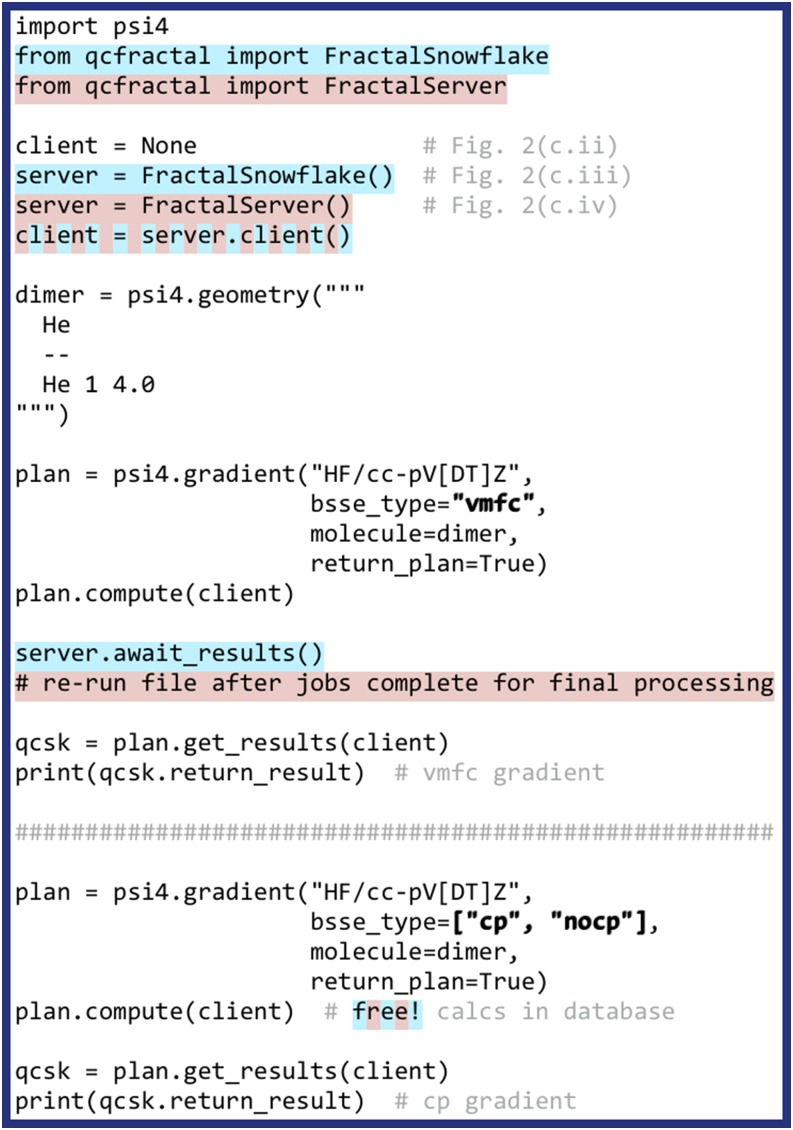
FIG. 3.

Input file illustrating a CBS and many-body gradient run through the distributed driver in the continuous mode [white-background lines; Fig. 2(c.ii)], distributed mode with FractalSnowflake [Fig. 2(c.iii); additional blue-background lines], and distributed mode with the full storage and queuing power of QCFRACTAL [Fig. 2(c.iv); additional red-background lines]. The lower example is “free” when using QCFRACTAL since the components required for BSSE corrections have already been computed during the upper VMFC. While this example exposes the returned QCSCHEMA AtomicResult, the traditional syntax of grad = psi4.gradient(“HF/cc-pV[DT]Z,” bsse_type=“vmfc”) runs in the mode as in Fig. 2(c.ii) and is identical to the upper example.

V. NEW FEATURES AND PERFORMANCE IMPROVEMENTS

A. DFT

The DFT module now uses LIBXC¹³¹ to evaluate the exchange-correlation terms. PSI4 thus has access to 400+ functionals, of which ∼100 are routinely tested against other implementations. Modern functionals, such as ωB97M-V¹³² and the SCAN family,¹³³ are now available. Support for hybrid LDA functionals such as LDA0, pending their release in a stable version of LIBXC, is also implemented. The new functional interface is Python-dictionary-based and uses LIBXC-provided parameters where possible. Additional capabilities for dispersion-inclusive, tuned range-separated, and double-hybrid functionals are defined atop LIBXC fundamentals. The interface also allows users to easily specify custom functionals, with tests and examples provided in the documentation.

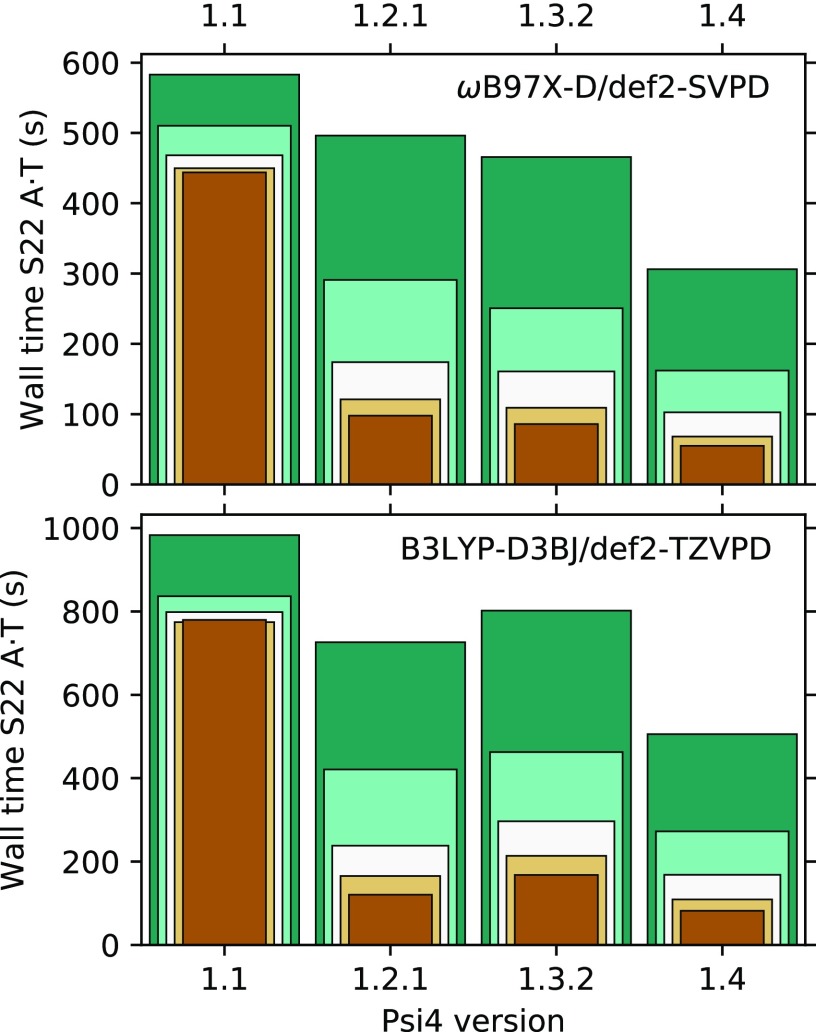
The DFT module in PSI4 v1.4 is significantly faster than the one in PSI4 v1.1, in both single-threaded and multi-threaded use cases. Recent versions are compared in Fig. 4, showing the speed improvements for the adenine·thymine (A·T) stacked dimer from the S22 database.¹³⁵ With ωB97X-D/def2-SVPD (Fig. 4, upper), this test case corresponds to 234 and 240 basis functions for each monomer and 474 for the dimer, while the problem size is approximately doubled in B3LYP-D3(BJ)/def2-TZVPD (Fig. 4, lower).

FIG. 4.

Wall-time comparison for the interaction energy of the adenine·thymine stacked dimer from the S22 database with various versions of PSI4 using 1 (darker green) to 16 (brown) threads, in multiples of two.¹³⁴ PSI4 v1.4 data are obtained with the robust grid pruning algorithm.

Much of the speed improvement is due to improved handling of the DFT grids. Collocation matrices between basis functions and the DFT grid are now formed by an optimized library (GAU2GRID; Sec. VI B 3) and are automatically cached if sufficient memory is available, thus removing the need for their re-computation in every iteration. The whole module, including the generation of quadrature grids and collocation matrices, is now efficiently parallelized. The overall speedup between v1.1 and v1.4 is 1.9× on a single core. Notable speedups are obtained for range-separated functionals (e.g., the ωB97X-D functional, see Fig. 4, upper), as the MemDFJK algorithm is now implemented for this class of methods (see Sec. V B).

As of PSI4 v1.4, grid screening based on exchange-correlation weights is applied with a conservative default cutoff of 10⁻¹⁵. Grid pruning schemes are also implemented, the default robust scheme removing ∼30% of the grid points. Grid pruning on its own is responsible for a 1.3× single-core speedup in the case of the A·T dimer with B3LYP-D3(BJ)/def2-TZVPD. However, a loss of accuracy can be expected in the pruning of smaller grids (<0.1 kcal mol⁻¹ for IEs in the A24 database¹³⁶).

B. MemDFJK algorithm

The SCF Coulomb (J) and exchange (K) builds are the cornerstone of all SCF-level operations in PSI4, such as SCF iterations, MP2 gradients, SAPT induction terms, SCF response, time-dependent DFT (TDDFT), and more. Over the past decade, the ability to perform raw floating point operations per second (FLOPS) of modern central processing units (CPUs) has grown much faster than the speed of memory I/O, which can lead to memory I/O rather than raw FLOPS limiting operations. A large data copy quickly became the bottleneck of the PSI4 v1.1 JK algorithm, especially when running on many concurrent cores.

Examining the canonical K equations with the DF shows the following (using the Einstein summation convention):

$$D_{\lambda \sigma }=C_{i\sigma }{C}_{i\lambda },$$ (1)

$${\zeta }_{P\nu i}=\left(P|\nu \lambda \right)C_{i\lambda },$$ (2)

$$K{\left[D_{\lambda \sigma }\right]}_{\mu \nu }={\zeta }_{P\mu i}{\zeta }_{P\nu i},$$ (3)

where i is an occupied index, P is the index of the auxiliary basis function, and μ, ν, λ, and σ are atomic orbital (AO) indices. The C, D, K, and (P|νλ) tensors are the SCF orbitals matrix, density matrix, exchange matrix, and three-index integral tensor (including auxiliary basis Coulomb metric term), respectively. Holding the (P|νλ) quantity in a tensor T_Pνλ offers the benefit of a straightforward optimized matrix–matrix operation in Eq. (2). However, this neglects the symmetricity and sparsity of the three-index integrals (P|νλ). Accounting for both of these properties leads to the previously stored form of $T_{P\nu {\lambda }^{\nu }}$ where the λ index was represented sparsely for each Pν pair by removing all duplicate or zero values; the sparsity of the index λ depends on the value of ν and hence the notation λ^ν. This form provides a highly compact representation of the (P|νλ) tensor; however, the matrix–matrix operation to form ζ_Pνi in Eq. (2) requires unpacking to a dense form, causing the previously mentioned data bottleneck.

To overcome this issue, the new J and K builds in PSI4 hold the (P|νλ) quantity in a $T_{\nu P{\lambda }^{\nu }}$ representation, where there is a unique mapping for the Pλ indices for each ν index. While full sparsity can also be represented in this form, the symmetry of the AOs is lost, leading to this quantity being twice as large in the memory or disk. This form requires the $C_{i{\lambda }^{\nu }}$ matrix to be packed for every ν index for optimal matrix–matrix operations in Eq. (2). While both the $T_{P\nu {\lambda }^{\nu }}$ and $T_{\nu P{\lambda }^{\nu }}$ forms require packing or unpacking of tensors, the former requires QN² operations, while the latter requires N²o operations, where Q is the size of the auxiliary index, N is the number of basis functions, and o is the size of the occupied index. In practice, o ≪ Q, often resulting in 15× less data movement, and generally all but removing the bottleneck.

This small data organization change combined with vectorization and parallelization improvements has led to performance increases, especially for a high number of cores and when the system is very sparse, with the drawback of doubling the memory footprint. For a system of two stacked benzene molecules in the cc-pVDZ basis set (228 basis functions), the new JK algorithm is 2.6, 3.6, 3.7, and 4.3× faster than the old algorithm for 1, 8, 16, and 32 threads, respectively. For a more extensive system of 20 stacked benzene molecules with cc-pVDZ (2280 basis functions), the respective speedups are 1.5, 1.7, 2.1, and 2.2×. PSI4 automatically detects which algorithm to use based on the amount of available memory.

C. Additive dispersion models

PSI4 specializes in providing convenient access to methods with additive dispersion corrections. Several have long been available, such as Grimme’s three-component corrections to mean-field methods, HF-3c¹³⁷ and PBE-3c¹³⁸ (external via DFTD3¹³⁹ and GCP¹⁴⁰ executables), and the simpler pairwise additive schemes -D2¹⁴¹ (internal code) and -D3^142,143 (external via a DFTD3 executable). Now also available are a similar correction to perturbation theory, MP2-D¹⁴⁴ (external via an MP2D¹⁴⁵ executable), and a non-local correction to DFT through the VV10 functional, DFT-NL¹⁴⁶ (internal code). These are simply called gradient(“mp2-d”) or energy(“b3lyp-nl”). See Table I for details of external software.

TABLE I.

Quantum chemistry software that PSI4 can use (upstream interaction).

Softwarea	Group	Added	License	Language	Comm.b	Citec		Capability
Upstream required C-link
LIBINT1	Valeev	v1.0d	LGPL-3.0	C	C API	163	…	Two-electron and properties integrals
LIBINT2	Valeev	v1.4	LGPL-3.0	C++	C++ API	164	…	Two-electron and properties integrals
LIBXC	Marques	v1.2	MPL-2.0	C	C API	179	131	Definitions, compositions of
								density functionals
GAU2GRID	Smith	v1.2	BSD-3-Cl	C/Py	C API	180	…	Gaussian collocation grids for DFT
Upstream required Py-link
QCELEMENTAL	MolSSI	v1.3	BSD-3-Cl	Py	Py API	126	121	Physical constants and molecule parsing
QCENGINE	MolSSI	v1.4	BSD-3-Cl	Py	Py API	127	121	QC schema runner with dispersion
								and opt engines
Upstream optional C-link
DKH	Reiher	v1.0	LGPL-3.0	Fortran	C API	181	80 and 81	Relativistic corrections
LIBEFP	Slipchenko	v1.0e	BSD-2-Cl	C	C API	182	183	Fragment potentials
GDMA	Stone	v1.0	GPL-2.0	Fortran	C API	184	185	Multipole analysis
CHEMPS2	Wouters	v1.0	GPL-2.0	C++	C++ API	186	187 and 188	DMRG and multiref. PT2 methods
PCMSOLVER	Frediani	v1.0	LGPL-3.0	C++/Fortran	C++ API	189	190	Polarizable continuum/implicit
								solvent modeling
ERD	QTP	v1.0d	GPL-2.0	Fortran	C API	191	192	Two-electron integrals
SIMINT	Chow	v1.1	BSD-3-Cl	C	C API	193	165	Vectorized two-electron integrals
AMBIT	Schaefer	v1.2	LGPL-3.0	C++/Py	C++ API	194	…	Tensor manipulations
Upstream optional Py-link or exe
DFTD3	Grimme	v1.0	GPL-1.0	Fortran	QCSCHEMA	139	142 and 143	Empirical dispersion for HF and DFT
MRCC	Kallay	v1.0	pty	C++/Fortran	Text file	…	35	Arbitrary order CC and CI
GCP	Grimme	v1.1	GPL-1.0	Fortran	Py intf./CLI	140	137 and 138	Small-basis corrections
PYLIBEFP	Sherrill	v1.3	BSD-3-Cl	C++/Py	Py API	195	…	Python API for libefp
MP2D	Beran	v1.4	MIT	C++	QCSCHEMA	145	144	Empirical dispersion for MP2
CPPE	Dreuw	v1.4	LGPL-3.0	C++/Py	Py API	196	197	Polarizable embedding/explicit
								solvent modeling
ADCC	Dreuw	v1.4	GPL-3.0+pty	C++/Py	Py API	198	113	Algebraic-diagrammatic
								construction methods

^aBinary distributions available from Anaconda Cloud for all projects except for MRCC. For the channel in conda install <project> -c <channel>, use psi4 except for ADCC from adcc and GAU2GRID, QCELEMENTAL, and QCENGINE from conda-forge, the community packaging channel.

^bMeans by which PSI4 communicates with the project.

^cThe first reference is a software repository. The second is theory or software in the literature.

^dNo longer used. LIBINT1 last supported before v1.4. ERD last supported before v1.2.

^eSince v1.3, LIBEFP called through PYLIBEFP.

PSI4 v1.4 uses the -D3 correction in a new method, SAPT0-D. While SAPT0 has long been applicable to systems with upward of 300 non-hydrogen atoms by leveraging optimized DF routines for both JK builds and MP2-like $E_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}^{\left(20\right)}$ and $E_{\mathrm{e}\mathrm{x}\mathrm{c}\mathrm{h}-\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}^{\left(20\right)}$ terms, it is limited by the $\mathcal{O}\left(N^5\right)$ scaling of the second-order dispersion (N proportional to the system size). By refitting the -D3 damping parameters against a large training set of CCSD(T)/CBS IEs and using the result in place of the analytic SAPT0 dispersion component, SAPT0-D at $\mathcal{O}\left(N^4\right)$ scaling achieves a 2.5× speedup for systems with about 300 atoms (increasing for larger systems).¹⁴⁷

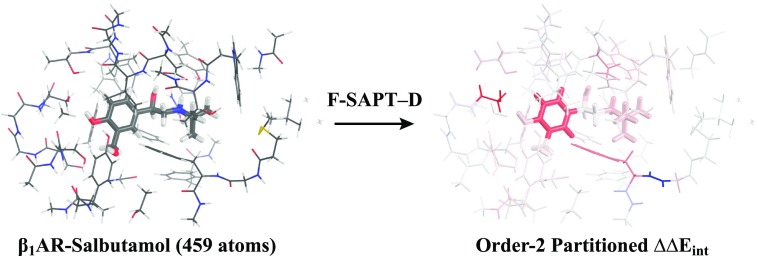
The SAPT0-D approach is also applicable to the functional group partition of SAPT.⁵³ The resulting F-SAPT0-D has been applied to understand the differential binding of the β₁-adrenoreceptor (β₁AR) (Fig. 5) in its active (G-protein coupled) vs inactive (uncoupled) forms to the partial agonist salbutamol. While experimentally determined ΔΔG_bind was previously justified with respect to changes in the binding site geometry upon β₁AR activation,¹⁴⁸ F-SAPT0-D quantifies the contribution of each functional group contact, revealing that differential binding is due in large part to cooperativity of distant amino acid residues and peptide bonds, rather than only local contacts.

FIG. 5.

F-SAPT0-DD3M(0)/jun-cc-pVDZ analysis of 459 atoms (5163 orbitals and 22 961 auxiliary basis functions) from the β₁AR–salbutamol co-crystal (PDB: 6H7M). (Left) Geometry of ligands (wide sticks) and residues (thin sticks) within 7 Å. (Right) Order-2 F-SAPT difference analysis of an active vs an inactive complex, with functional groups colored by contribution to ΔΔE_int (red: more attractive in the activated state; blue: more attractive in the inactive state; color saturation at ±10 kcal mol⁻¹).

D. SAPT(DFT)

PSI4 now provides SAPT(DFT),¹⁴⁹ also called DFT-SAPT,¹⁵⁰ which approximately accounts for the intramolecular electron correlation effects that are missed in SAPT0 by including correlation-like effects found in DFT. The Hartree–Fock orbitals are replaced with Kohn–Sham orbitals,¹⁵¹ and induction terms are solved using the coupled-perturbed Kohn–Sham equations. The long-range behavior that is important for dispersion interactions is known to be problematic for generalized gradient approximation (GGA) functionals, and in DFT-SAPT, this is corrected by gradient-regulated asymptotic correction (GRAC)¹⁵² in obtaining the Kohn–Sham orbitals. Dispersion energies are obtained by solving for the TDDFT propagator of each monomer and integrating the product of the propagators over the frequency domain.^153,154 In PSI4 1.4, we have improved the TDDFT dispersion capabilities to allow hybrid kernels in the TDDFT equations,¹⁵⁵ which can significantly improve accuracy when hybrid functionals are used to determine the orbitals.^150,156

E. SAPT0 without the single-exchange approximation

The SAPT module in PSI4 now has an option to compute the second-order SAPT0 exchange corrections $E_{\mathrm{e}\mathrm{x}\mathrm{c}\mathrm{h}-\mathrm{i}\mathrm{n}\mathrm{d},\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}}^{\left(20\right)}$ and $E_{\mathrm{e}\mathrm{x}\mathrm{c}\mathrm{h}-\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}^{\left(20\right)}$ without the use of the common S² approximation, that is, using the complete antisymmetrizer in the expressions instead of its approximation by intermolecular exchanges of a single electron pair. The working equations for the non-approximate second-order corrections were derived and implemented for the first time in Refs. ¹⁵⁷ and ¹⁵⁸ in the molecular-orbital (MO) form prevalent in the classic SAPT developments. We have recast the nonapproximate formulas for $E_{\mathrm{e}\mathrm{x}\mathrm{c}\mathrm{h}-\mathrm{i}\mathrm{n}\mathrm{d},\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}}^{\left(20\right)}$ and $E_{\mathrm{e}\mathrm{x}\mathrm{c}\mathrm{h}-\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}^{\left(20\right)}$ in Refs. ¹⁵⁷ and ¹⁵⁸ into the AO form and implemented them efficiently in PSI4 with DF. As these AO-based expressions have not been published before, we present them together with an outline of their derivation in the supplementary material. Thanks to this new development, the entire SAPT0 level of theory (but not higher levels such as the second-order, SAPT2) is now available in PSI4 without the single-exchange approximation. Preliminary numerical tests show^157–159 that the replacement of $E_{\mathrm{e}\mathrm{x}\mathrm{c}\mathrm{h}-\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}^{\left(20\right)}\left(S^2\right)$ with its nonapproximated counterpart introduces inconsequential changes to the SAPT0 interaction potentials at short intermolecular separations. In contrast, the full $E_{\mathrm{e}\mathrm{x}\mathrm{c}\mathrm{h}-\mathrm{i}\mathrm{n}\mathrm{d},\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}}^{\left(20\right)}$ values often deviate significantly from $E_{\mathrm{e}\mathrm{x}\mathrm{c}\mathrm{h}-\mathrm{i}\mathrm{n}\mathrm{d},\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}}^{\left(20\right)}\left(S^2\right)$ at short ranges, especially for interactions involving ions.¹⁶⁰ At the usual SAPT0 level (as defined, e.g., in Ref. 161), this difference between $E_{\mathrm{e}\mathrm{x}\mathrm{c}\mathrm{h}-\mathrm{i}\mathrm{n}\mathrm{d},\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}}^{\left(20\right)}$ and $E_{\mathrm{e}\mathrm{x}\mathrm{c}\mathrm{h}-\mathrm{i}\mathrm{n}\mathrm{d},\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}}^{\left(20\right)}\left(S^2\right)$ cancels out when the $\delta E_{\mathrm{H}\mathrm{F}}^{\left(2\right)}$ term that approximates the higher-order induction and exchange induction effects from a supermolecular HF calculation is taken into account. However, the removal of the S² approximation from second-order SAPT0 will significantly affect SAPT results computed without the $\delta E_{\mathrm{H}\mathrm{F}}^{\left(2\right)}$ correction.

F. SF-SAPT

An open-shell SAPT feature that is currently unique to PSI4 is the ability to compute the leading exchange term, $E_{\mathrm{e}\mathrm{x}\mathrm{c}\mathrm{h}}^{\left(10\right)}\left(S^2\right)$, for an arbitrary spin state of the interacting complex, not just its highest spin state. This spin-flip SAPT (SF-SAPT) method was introduced in Ref. 162 and so far applies to the interaction between two open-shell systems described by their ROHF determinants. Such an interaction leads to a bundle of asymptotically degenerate states of the interacting complex, characterized by different values of the spin quantum number S. These states share the same values of all electrostatic, induction, and dispersion energies, and the splitting between them arises entirely out of electron exchange. In such a case, the SF-SAPT approach implemented in PSI4 can provide an inexpensive [cost is similar to the standard $E_{\mathrm{e}\mathrm{x}\mathrm{c}\mathrm{h}}^{\left(10\right)}\left(S^2\right)$] and qualitatively correct first-order estimate of the splittings between different spin states of the complex. In addition, all terms can be computed using standard SCF JK quantities and have been implemented within PSI4 in a PSI4NUMPY formalism, as the best performance can be achieved without any additional compiled code.

G. Libint2 and Simint

The LIBINT package¹⁶³ has been the default engine for two-electron integrals since the development of PSI3 two decades ago. Allowing arbitrary levels of angular momentum and numerous integral kernels, LIBINT has proven to be a reliable tool for generating the integrals that are central to QC. However, modern CPUs increasingly derive their power from a combination of multi-core and single instruction, multiple data (SIMD) technologies, rather than the regular strides in clock speed that were realized around the time of PSI3’s development. While PSI4 has exploited multi-core technologies for some time via OPENMP, its SIMD capabilities were previously limited to the linear algebra libraries used to power SCF and post-HF methods. In PSI4 v1.4, the LIBINT package has been superseded by LIBINT2,¹⁶⁴ which partially exploits SIMD capabilities by vectorizing the work needed for a given shell quartet, making it better suited for modern computer architectures. LIBINT2 permits additional integral kernels, including the Yukawa- and Slater-type geminal factors, which expand the range of DFT and explicitly correlated methods that may be implemented. LIBINT2 is also preferable from a software sustainability perspective as it is actively maintained and developed, unlike the original LIBINT.

Although LIBINT2 is now the default integrals engine, PSI4 is written to allow the use of alternative integrals packages, and an interface to SIMINT^165,166 is also provided. SIMINT was designed from the beginning with SIMD parallelism in mind. By reordering shell pairs to be grouped by common angular momentum classes, SIMINT achieves a compelling level of vectorization on the latest AVX512 chipsets. The PSI4 integrals interface has been generalized to allow the shell pairs to be given in an arbitrary order and to account for the possibility of batching among them, thus allowing SIMINT to take full advantage of its approach to vectorization.

H. SCF guesses

The reliability of the atomic solver used for the superposition of atomic densities^167,168 (SAD) initial guess has been greatly improved in PSI4, and the SAD guess has been made the default also for open-shell and restricted open-shell calculations, resulting in significantly faster convergence, especially for systems containing heavy atoms such as transition metal complexes. Although powerful in many cases, the SAD guess does not yield molecular orbitals, and it may thereby be harder to build a guess with the wanted symmetry. The traditional alternatives to SAD that do yield molecular orbitals, the core orbital guess or the generalized Wolfsberg–Helmholz¹⁶⁹ modification thereof, fail to account for electronic screening effects whose importance increases rapidly with the increasing nuclear charge, resulting in horrible performance.¹⁷⁰ However, guesses that both account for electronic screening and yield guess orbitals have recently been described in Ref. 170 and are now implemented in PSI4: an extended Hückel guess employing the atomic orbitals and orbital energies from the SAD solver, the SAD natural orbitals (SADNO) guess, and the superposition of atomic potentials (SAP) guess that constructs a guess Fock matrix from a sum of atomic effective potentials computed at the complete-basis-set limit.^171,172 With the improvements to SAD and the introduction of the three novel guesses, PSI4 can be applied even to more challenging open-shell and transition metal systems. Calculations are now possible even in overcomplete basis sets, as redundant basis functions are removed automatically by default in PSI4 via the pivoted Cholesky decomposition procedure.^173,174

I. TDDFT

We have recently added time-dependent DFT capabilities using either the full TDDFT equations [also known as the random-phase approximation (RPA)] or the Tamm–Dancoff approximation (TDA).¹⁷⁵ The former yields a generalized eigenvalue problem, and our solver leverages the Hamiltonian structure of the equations to ensure robust convergence.¹⁷⁶ The latter corresponds to a Hermitian eigenvalue problem, and we employ a Davidson solver.¹⁷⁷ The excitation energies and vectors are obtained from the following generalized eigenvalue problem, also known as the response eigenvalue problem:

$$\left(\begin{array}{cc}\hfill \mathbf{A}\hfill & \hfill \mathbf{B}\hfill \\ \hfill {\mathbf{B}}^{*}\hfill & \hfill {\mathbf{A}}^{*}\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\mathbf{X}}_n\hfill \\ \hfill {\mathbf{Y}}_n\hfill \end{array}\right)={\omega }_n\left(\begin{array}{cc}\hfill \mathbf{1}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill -\mathbf{1}\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\mathbf{X}}_n\hfill \\ \hfill {\mathbf{Y}}_n\hfill \end{array}\right).$$ (4)

The excitation eigenvectors, ${\left({\mathbf{X}}_n,{\mathbf{Y}}_n\right)}^T$, provide information on the nature of the transitions and can be used to form spectroscopic observables, such as oscillator and rotatory strengths. The A and B matrices appearing on the left-hand side are the blocks of the molecular electronic Hessian¹⁷⁸ whose dimensionality is ($ov$)², with o and $v$ being the number of occupied and virtual MOs, respectively. Due to this large dimensionality, rather than forming A and B explicitly, one instead uses subspace iteration methods to extract the first few roots. In such methods, the solutions are expanded in a subspace of trial vectors b_i, and the most compute- and memory-intensive operations are the formation and storage of the matrix–vector products (A + B)b_i and (A − B)b_i. These matrix–vector products are equivalent to building generalized Fock matrices; the efficient JK-build infrastructure of PSI4 (Sec. V B) can thus be immediately put to use also for the calculation of TDDFT excitation energies. In fact, construction of these product vectors is the only part written in C++. All other components, including the subspace iteration techniques, are written in Python for easy readability and maintainability. Following our design philosophy, we have written the required subspace solvers for the response eigenvalue problems in a generic way, so that they may be reused for future features.

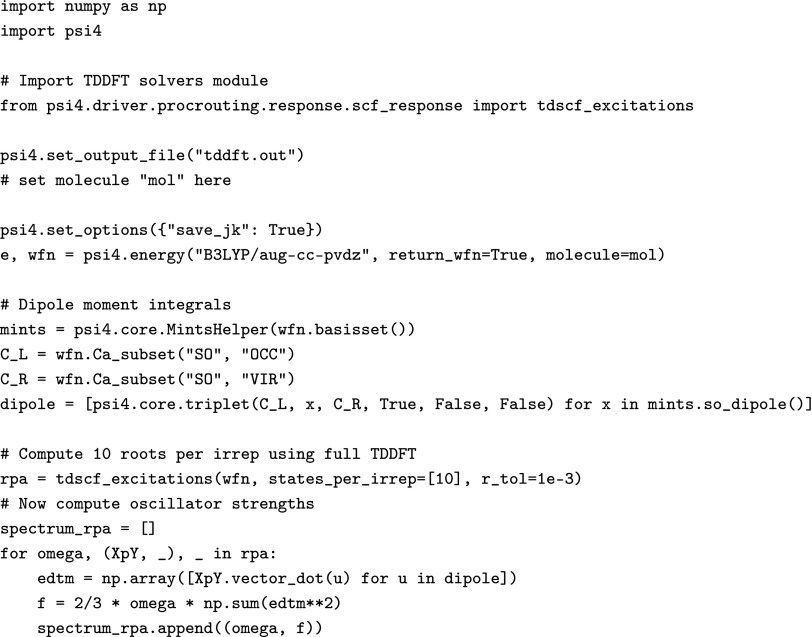
1. Example of rapid prototyping

To illustrate the use of PSI4 and PSI4NUMPY to rapidly implement new features, Fig. 6 shows an easy oscillator strength implementation at the Python layer. Excitations are obtained by calling the tdscf_excitations() function, and dipole moment integrals are calculated trivially in four lines of code by accessing the occupied and virtual parts of the SCF coefficient matrix and the dipole moment integrals from LIBMINTS. The oscillator strengths are then computed from the MO basis electric dipole moment integrals $⟨{\varphi }_a\left|\widehat{\mathit{\mu }}\right|{\varphi }_i⟩$ and the right excitation vectors X_n + Y_n as follows:

$$f=\frac{2}{3}{\omega }_n\sum _{u=x,y,z}\sum _i^{\text{occ}}\sum _a^{\text{vir}}|{\left({\mathbf{X}}_n+{\mathbf{Y}}_n\right)}_{ia}⟨{\varphi }_a\left|{\widehat{\mu }}_u\right|{\varphi }_i⟩{|}^2.$$ (5)

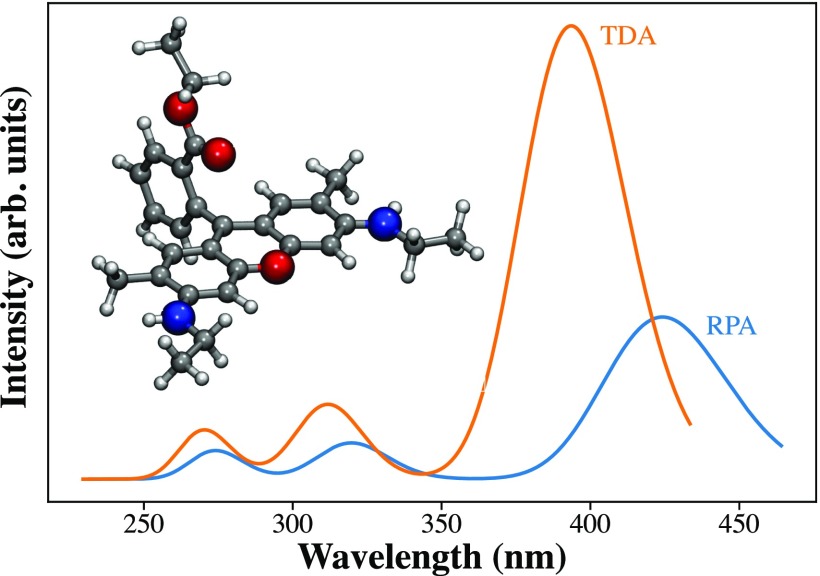
Figure 7 shows an example UV-Vis spectrum using these oscillator strengths, as fitted by applying a Gaussian-shaped broadening to the computed excitation energies. We are also working on the implementation of gauge-including atomic orbitals (London orbitals) to enable magnetic response evaluations needed to calculate properties such as optical rotation and electronic circular dichroism.

FIG. 6.

Example Python implementation of TDDFT oscillator strengths.

FIG. 7.

UV-Vis spectrum of rhodamine 6G at the PBE0/aug-pcseg-2 level of theory. The spectra computed using full TDDFT (RPA) and the Tamm–Dancoff approximation (TDA) are reported in blue and orange, respectively.

VI. SOFTWARE ECOSYSTEM

Like all QC packages, PSI4 strives to continuously expand its capabilities to advance research in both method development and applications. New methods are introduced frequently in electronic structure theory, and it would be a challenge to implement all the latest advances. The PSI4 team prefers to encourage the development of reusable libraries, so that new methods need to be implemented only once (by the experts) and can then be adopted by any QC code with merely a short, custom interface. This ecosystem-building approach has the advantages of (i) not binding a community library’s use to a single software package, (ii) encouraging smaller software projects that are more modular in function and ownership and more localized in (funding) credit, and (iii) facilitating the propagation of new features and bug fixes by using a generic interface rather than embedding a code snapshot. Since v1.1, PSI4 has added new projects to its ecosystem, contributed back to existing projects, and disgorged some of its own code into projects that are more tightly defined. Discussed below is a selection of illustrative or newly interfaced projects. The full ecosystem of external, connected software is collected into Table I, code used by PSI4 (upstream packages), and Table II, code that uses PSI4 (downstream packages).

TABLE II.

Chemistry software that can use PSI4 (downstream interaction).

Softwarea	Group	V.b	License	Language	Comm.c	Cited		PSI4 provides
Downstream optional C-link, plugins
V2RDM_CASSCF	DePrince	v1.0	GPL-2.0	C++/Fortran	C++ API	71	199	Backend for variational 2-RDM-driven CASSCF
FORTE	Evangelista	v1.0	LGPL-3.0	C++/Py	C++ API	70	68 and 69	Backend for multiref. many-body mtds and sel. CI
CCT3	Piecuch	v1.1	LGPL-3.0	Fortran	C++ API	200	201 and 202	Backend for actv-sp CCSDt, CC(t;3), CR-CC(2,3)
GPU_DFCC	DePrince	v1.2	GPL-2.0	C++/Cuda	C++ API	203	204	Backend for GPU-accelerated DF-CCSD and (T)
Downstream optional Py-link or exe
WEBMO	Polik	v1.0	pty	Java/Perl	PSIthon	…	205	QC engine for GUI/web server
MOLDEN	Schaftenaar	v1.0	pty	Fortran	Molden file	206	207	Orbitals for orbital/density visualization
JANPA	Bulavin	v1.0	BSD-4-Cl	Java	Molden file	208	209	Orbitals for natural population analysis (NPA)
PSI4NUMPY	Smith	v1.1	BSD-3-Cl	Py	PsiAPI	100	10	QC essentials for rapid prototyping and QC edu.
PSI4EDUCATION	McDonald	v1.1	BSD-3-Cl	Py	PsiAPI	210	122	QC engine for instructional labs
PSIOMM	Sherrill	v1.1	BSD-3-Cl	Py	PsiAPI	211	…	Self for interface betweenPSI4 and OPENMM
HTMD/PARAMETERIZE	Acellera	v1.1	pty	Py	PSIthon	212	213 and 214	QC engine for force-field parametrization for MD
GPUGRID	De Fabritiis	v1.1	pty	Py	PSIthon	215	216	QC torsion scans for MD-at-home
PYREX	Derricotte	v1.1	BSD-3-Cl	Py	PsiAPI	217	…	Engine for reaction coordinate analysis
SNS-MP2	D. E. Shaw	v1.2	BSD-2-Cl	Py	PsiAPI	218	219	Backend for spin-network-scaled MP2 method
RESP	Sherrill	v1.2	BSD-3-Cl	Py	PsiAPI	220	115	ESP for restrained ESP (RESP) fitting
QCENGINE	MolSSI	v1.2	BSD-3-Cl	Py	QCSCHEMA	127	121	QC engine for QC schema runner
QISKIT-AQUA	IBM	v1.2	Apache-2.0	Py	PSIthon	221	…	Engine for quantum computing algorithms
MS QUANTUM	Microsoft	v1.2	MIT	C#/Q#	PsiAPI	222	…	Engine for quantum computing algorithms
ORION	OpenEye	v1.2	pty	Go/Py	PsiAPI	…	…	QC engine for drug-design workflow
CRYSTALATTE	Sherrill	v1.2	LGPL-3.0	Py	PSIthon	223	224	QC and MBE engine for crystal lattice energies
OPENFERMION	Google	v1.3	Apache-2.0	Py	PSIthon	225	226	Engine for quantum computing algorithms
OPENFERMION-PSI4	Google	v1.3	LGPL-3.0	Py	PSIthon	227	226	Self for interface between PSI4 and OpenFermion
QCDB	Sherrill	v1.3	BSD-3-Cl	Py	QCSCHEMA	228	…	Engine for QC common driver
OPTKING	King	v1.3	BSD-3-Cl	Py	QCSCHEMA	229	…	Gradients for geometry optimizer
PSIXAS	Gryn’ova	v1.3	GPL-3.0	Py	PsiAPI	230	…	Backend for x-ray absorption spectra
FOCKCI	Mayhall	v1.3	BSD-3-Cl	Py	PsiAPI	231	116	CAS engine for Fock-space CI
ASE	ASE	v1.4	LGPL-2.1	Py	PsiAPI	232	233	QC engine for CMS code runner
I-PI	Ceriotti	v1.4	GPL-3.0	Fortran/Py	PsiAPI	234	235	QC gradients for MD runner
MDI	MolSSI	v1.4	BSD-3-Cl	C	PsiAPI	236	…	QC engine for standardized CMS API
GEOMETRIC	Wang	v1.4e	BSD-3-Cl	Py	QCSCHEMA	237	238	QC gradients for geometry optimizer
QCFRACTAL	MolSSI	v1.4	BSD-3-Cl	Py	QCSCHEMA	128	121	QC engine for database and compute manager

^aBinary distributions available from Anaconda Cloud for some projects. For the channel in conda install <project> -c <channel>, use psi4 for V2RDM_CASSCF, GPU_DFCC, SNS-MP2, RESP, OPENFERMION, and OPENFERMION-PSI4; acellera for HTMD/PARAMETERIZE; and conda-forge, the community packaging channel, for QCENGINE, ASE, MDI, GEOMETRIC, and QCFRACTAL.

^bEarliest version of PSI4 with which software works.

^cApart from compiled plugins that interact directly with PSI4’s C++ layer, downstream projects use established file formats such as Molden or one of the three input modes of Fig. 1.

^dThe first reference is a software repository. The second is theory or software in the literature.

^eGeomeTRIC has called PSI4 through PSIthon since v1.0. QCENGINE has driven geomeTRIC to drive PSI4 through QCSCHEMA since v1.3. PSI4 can itself call geomeTRIC through QCSCHEMA since v1.4.

A. Sustainability through community libraries

The introduction of LIBINT2 and LIBXC not only provides new features (see Secs. V G and V A, respectively) but also results in substantial simplifications to the codebase. The previous version of LIBINT only provided the recursion routines, relying on the calling program to provide the fundamental s-type integrals used as the starting point. There were also restrictions on the angular momentum ordering among the four centers, requiring bookkeeping to apply permutations to the resulting integrals in the case where reorderings were necessary to satisfy these requirements. Furthermore, LIBINT1 provided only the minimal number of integral derivatives required by translational invariance,^239,240 requiring the calling code to compute the missing terms by application of the relationships. The combination of applying permutations and translational invariance amounted to over 3000 lines of code in previous PSI4 versions, primarily due to the complexity introduced by second derivative integrals. In LIBINT2, the fundamental integrals are provided and the translational invariance is applied automatically for derivatives, and the shells can be fed in any order of the angular momenta. With these tasks outsourced to LIBINT2, the latest PSI4 codebase is significantly cleaner and more maintainable.

With the transition to the LIBXC¹³¹ library for DFT calculations, in accordance with the modular development model, PSI4 gains continuous fixes and new features, which is especially important as none of the primary PSI4 development groups specialize in DFT. Thanks to LIBXC, PSI4 now supports over 400 functionals of various rungs. Final DFT compositions suitable for energy() are now defined by LIBXC and are directly subsumed into PSI4’s functional list, making for a more maintainable code. In cooperation with the LIBXC upstream, the PSI4 authors have contributed an alternate CMAKE build system and a Python API, PYLIBXC, to LIBXC, and also provided help in porting to Windows.

B. Launching community libraries

1. QCElemental

When the needs of ongoing research projects outgrew LIBMINTS’s C++ parsing of molecule specification strings, a redesign was implemented in Python and transferred to QCELEMENTAL to serve as the backend to QCSCHEMA Molecule validation. The resulting code is easily extensible, mirrors the schema (though with additional fields to accomodate PSI4’s Z-matrix and deferred geometry finalization features), and accepts and returns dictionary-, schema-, array-, or string-based representations. Additionally, it performs strong physics-based validation and defaulting for masses, mass numbers, total and fragment charges and multiplicities, and basis function ghosting, saving considerable validation code in PSI4 as a QCELEMENTAL client.

QCELEMENTAL additionally provides a light Python interface over NIST CODATA and periodic table data and other “look-up” quantities such as van der Waals and covalent radii. By switching to QCELEMENTAL API calls in PSI4’s Python code and using its header-writing utilities for the C++ code, readability has improved, and datasets are easier to update.

2. QCEngine

PSI4 has long supplemented its internal empirical dispersion capabilities (Sec. V C) with external projects, namely, DFTD3 and MP2D executables. These were run via a Python interface that additionally stores fitting and damping parameters at the functional level, so that the programs are used solely for compute and not for internal parameters. Since operation is independent of PSI4, the Python interfaces have been adapted to QCSCHEMA and moved to the QCENGINE repository where they can be of broader use.

3. Gau2Grid

Improvements to the PSI4 DFT code highlighted a bottleneck at the computation of the collocation matrix between basis functions and the DFT grid. It was found that the simple loops existing in PSI4 did not vectorize well and exhibited poor cache performance. Much in the same way that modern two-electron libraries work, GAU2GRID¹⁸⁰ begins with a template engine to assist in writing unrolled C loops for arbitrary angular momentum and up to third-order derivatives. This template engine also allows multiple performance strategies to be employed and adjusted during code generation, depending on the angular momentum, the derivative level of the requested matrix, and the hardware targeted. GAU2GRID also has a Python interface to allow usage in Python programs that need fast collocation matrices.

4. PylibEFP

In the course of shifting control of SCF iterations from C++ to Python, it became clear that the effective fragment potential^241,242 (EFP) capabilities through Kaliman and Slipchenko’s LIBEFP library¹⁸³ would be convenient in Python. Since LIBEFP provides a C interface, a separate project of essentially two files, PYLIBEFP,¹⁹⁵ wraps it into an importable Python module. PYLIBEFP includes a full test suite, convenient EFP input parsing, and an interface amenable to schema communication (a QCENGINE adaptor is in progress). PSI4 employs PYLIBEFP for EFP/EFP energies and gradients and EFP/SCF energies.

C. Selected new features from community libraries

1. adcc

ADC-connect (ADCC),¹¹³ a hybrid Python/C++ toolkit for excited-state calculations based on the algebraic-diagrammatic construction scheme for the polarization propagator (ADC),^243–245 equips PSI4 with ADC methods (in-memory only) up to the third order in perturbation theory. Expensive tensor operations use an efficient C++ code, while the entire workflow is controlled by Python. PSI4 and ADCC can connect in two ways. First, PSI4 can be the main driver; here, method keywords are given through the PSI4 input file and ADCC is called in the background. Second, the PSI4 Wavefunction object from a SCF calculation can be passed to ADCC directly in the user code; here, there is more flexibility for complex workflows or for usage in a JUPYTER notebook.

2. SNS-MP2

McGibbon and co-workers²¹⁹ applied a neural network trained on HF and MP2 IEs and SAPT0 terms to predict system-specific scaling factors for MP2 same- and opposite-spin correlation energies to define the spin-network-scaled, SNS-MP2, method. This has been made available in a PSI4 pure-Python plugin²¹⁸ so that users can call energy(“sns-mp2”), which manages several QC calculations and the model prediction in the background and then returns an IE likely significantly more accurate than conventional MP2.²¹⁹ By using PSI4’s export of wavefunction-level arrays to Python, the developers were able to speed up calculations through custom density matrix manipulations of basis projection, fragment stacking, and fragment ghosting.

3. CPPE

PSI4 now supports the polarizable embedding (PE) model^246,247 through the CPPE library.¹⁹⁷ In the PE model, interactions with the environment are represented by a multi-center multipole expansion for electrostatics, and polarization is modeled through dipole polarizabilities usually located at the expansion points. The interface to the CPPE library is entirely written in Python and supports a fully self-consistent description of polarization for all SCF methods inside PSI4. In the future, PE will also be integrated in a fully self-consistent manner for molecular property calculations and TDDFT. Integration of CPPE motivated efficiency improvements to the electric field integrals and multipole potential integrals, which also benefit the related EFP method.

4. GeomeTRIC

Wang and Song^237,238 developed a robust geometry optimization procedure to explicitly handle multiple noncovalently bound fragments using a translation-rotation-internal coordinate (TRIC) system. Their standalone geometry optimizer, GEOMETRIC, supports multiple QC packages including PSI4 through a command-line interface. QCENGINE offers a GEOMETRIC procedure, allowing PSI4 and others to use the new optimizer with a Python interface. The latest PSI4 release adds native GEOMETRIC support, allowing users to specify the geometry optimizer within an input, e.g., optimize(…, engine=“geometric”).

5. v2rdm_casscf

PSI4 can perform large-scale approximate CASSCF computations through the v2rdm_casscf plugin,⁷¹ which describes the electronic structure of the active space using the variational two-electron RDM approach.^199,248,249 Version 0.9 of v2rdm_casscf can perform approximate CASSCF calculations involving active spaces as large as 50 electrons in 50 orbitals¹⁹⁹ and is compatible with both conventional four-center electron repulsion integrals (ERIs) and DF/Cholesky decomposition approximations. Active-space specification in v2rdm_casscf is consistent with other active-space methods in PSI4, and users can write RDMs to the disk in standard formats (e.g., FCIDUMP) for post-processing or for post-CASSCF methods. Geometry optimizations using analytic energy gradients can also be performed (with four-center ERIs).²⁵⁰ While most use cases of v2rdm_casscf involve calls to PSI4’s energy() or gradient() functions, key components of the plugin such as RDMs are also accessible directly through Python.

6. CCT3

The CCT3 plugin²⁰⁰ to PSI4 is capable of executing a number of closed- and open-shell CC calculations with up to triply excited (T₃) clusters. Among them are the active-space CC approach abbreviated as CCSDt,^251–254 which approximates full CCSDT by selecting the dominant T₃ amplitudes via active orbitals, and the CC(t;3) method, which corrects the CCSDt energies for the remaining, predominantly dynamical, triple excitations that have not been captured by CCSDt.^201,202 The CC(t;3) approach belongs to a larger family of methods that rely on the generalized form of biorthogonal moment expansions defining the CC(P;Q) formalism.^201,202

The CCSDt method alone is already advantageous, since it can reproduce electronic energies of near-CCSDT quality at a small fraction of the computational cost while accurately describing select multireference situations, such as single bond breaking. CC(t;3) improves on the CCSDt energetics even further, being practically as accurate as full CCSDT for both relative and total electronic energies at essentially the same cost as CCSDt. CCSDt and CC(t;3) converge systematically toward CCSDT as the active space is increased.

The CCT3 plugin can also be used to run CCSD and completely renormalized (CR) CR-CC(2,3) calculations. This can be done by making the active orbital set (defined by the user in the input) empty, since in this case CCSDt = CCSD and CC(t;3) = CR-CC(2,3). We recall that CR-CC(2,3) is a completely renormalized triples correction to CCSD, which improves the results obtained with the conventional CCSD(T) approach without resorting to any multireference concepts and being at most twice as expensive as CCSD(T).^255–257

VII. DOWNSTREAM ECOSYSTEM

A. Computational molecular science drivers

In addition to the closely associated ecosystem in Sec. VI, PSI4 is robust and simple enough that projects can develop interfaces that use it as a “black box,” and such programs are considered part of the downstream ecosystem. Of these, the one exposing the most PSI4 capabilities is the QCARCHIVE INFRASTRUCTURE project QCENGINE, which can drive almost any single-command computation (e.g., gradient or complete-basis-set extrapolation, in contrast to a structure optimization followed by a frequency calculation) through the QCSCHEMA specification. By launching PSI4 through QCFRACTAL, the QCARCHIVE database has stored 18M computations over the past year and is growing rapidly. A recent addition is the interface to the Atomic Simulation Environment^232,233 (ASE) through which energies and gradients are accessible as a Calculator. All PSI4 capabilities are available in the ASE by using the in-built psi4 module in the PSIAPI. Another MolSSI project, the MolSSI Driver Interface²³⁶ (MDI), devised as a light communication layer to facilitate complex QM/MM and machine learning workflows, has a PSI4 interface covering energies and gradients of HF and DFT methods. Finally, the I-PI universal force engine driver^234,235 has a PSI4 interface covering gradients of most methods.

B. Quantum computing

PSI4 is also used in several quantum computing packages to provide orbitals, correlated densities, and molecular integrals. Its flexible open-source license (LGPL) and Python API are factors that have favored its adoption in this area. For example, PSI4 is interfaced to the open-source quantum computing electronic structure package OPENFERMION^225,226 via the OPENFERMION-PSI4 plugin.²²⁷ The QISKIT AQUA suite of algorithms for quantum computing developed by IBM²²¹ is also interfaced to PSI4 via an input file. The Microsoft Quantum Development Kit²²² is another open-source project that takes advantage of PSI4’s Python interface to generate molecular integrals and then transform them into the Broombridge format, a YAML-based quantum chemistry schema.

C. Aiding force-field development for pharmaceutical infrastructure

Many classical simulation methods have been developed with the aid of PSI4. As an illustrative example, torsion scans have been performed⁹ using the OpenEye’s ORION platform to provide a first principles evaluation of conformational preferences in crystals, and the related methodology is used by the Open Force Field consortium²⁵⁸ to parameterize force fields within the QCARCHIVE framework. PSI4 has also found use in the development of nascent polarizable, anisotropic force fields by providing the distributed multipoles and MP2 electrostatic potentials (ESPs) needed to parameterize the AMOEBA force field.²⁵⁹ Moreover, the efficient SAPT code has been used in many recent developments in advanced force fields,²⁶⁰ including the emerging successors to AMOEBA.^261,262 In collaboration with Bristol Myers Squibb, we performed nearly 10 000 SAPT0 computations with PSI4 to train a pilot machine-learning model of hydrogen-bonding interactions,⁸ and a much larger number is being computed for a follow-up study.

The restrained electostatic potential (RESP) model²⁶³ is a popular scheme for computing atomic charges for use in force field computations. A Python implementation was initially contributed to the PSI4NUMPY project, and later, an independent open-source package was developed,^115,220 both of which employ PSI4 for the quantum electrostatic potential. The package supports the standard two-stage fitting procedure and multi-conformational fitting and also allows easy specification of complex charge constraints.

VIII. DEVELOPMENT AND DISTRIBUTION

A choose-your-own-adventure guide to obtaining PSI4 is available at http://psicode.org/downloads. Here, users and developers can select their operating system (Linux, Windows, Mac) and Python version and then choose between downloading standalone installers for production-quality binaries, using the CONDA²⁶⁴ package manager, and building the software from the source. While standalone installers are only provided for stable releases, the source and CONDA installations also support the development branch. A new and substantial access improvement has been the porting of PSI4 to native Windows by one of the authors (R.G.) for the Acellera company (previously it was only available via Windows Subsystem for Linux, WSL) for GPUGRID, a distributed computing infrastructure for biomedical research.²¹⁵ This involved separate ports of the required dependency projects and introduction of Windows continuous integration to conserve compatibility during the course of largely Linux-based development. The resulting uniform access to PSI4 in a classroom setting has been especially valuable for the PSI4EDUCATION project.

The cultivation of an ecosystem around PSI4 led to changes in the build system (Sec. 3 of Ref. 1), notably the maintain-in-pieces build-as-a-whole scheme where upstream and downstream dependencies remain in their own development repositories and are connected to PSI4 through a single-file footprint in the CMAKE build system. Through a “superbuild” setup, PSI4 and ecosystem projects can be flexibly built together upon a single command and use either pre-built packages or build dependencies from the source. For distribution, we rely upon Anaconda Python (and its associated package manager, CONDA), which specializes in cross-platform building and management of Python/C++/Fortran software for the scientific community. Conda packages for Linux and Mac of PSI4 and its dependencies (such that conda install psi4 -c psi4 yields a working installation) were in place by v1.1, when 11 packages were built for the psi4 channel.

Since the v1.1 era, PSI4 developers have focused on modernization and compatibility. With the release of CONDA-BUILD²⁶⁵ v3 in late 2017 supporting enhanced build recipe language and built-in sysroots, PSI4 has upgraded to use the same compilers as the foundational Anaconda defaults and community conda-forge channels. A substantial improvement is that, with the widespread availability of the Intel Math Kernel Library (MKL) through CONDA, PSI4 now uses the same libraries (mkl_rt) as those in packages such as NUMPY, rather than statically linking LAPACK, thereby eliminating a subtle source of import errors and numerical discrepancies. After these improvements, PSI4 today may be installed without fuss or incompatibility with other complex packages such as JUPYTER, OPENMM, and RDKIT. While maintaining compatibility with defaults and conda-forge channels, PSI4 packages additionally build with Intel compilers and use flags that simultaneously generate an optimized code for several architectures so that the same binary can run on old instruction sets such as SSE2 but also run in an optimal fashion on AVX2 and AVX512. In keeping with our ecosystem philosophy, PSI4 will help a project with CONDA distribution on their own channel or ours or the community channel, or leave them alone, whichever level of involvement the developers prefer. We presently manage 23 packages. Since distributing through CONDA, PSI4 has accumulated 68k package manager and 93k installer downloads.

With a reliable distribution system for production-quality binaries to users, PSI4 can allow fairly modern code standards for developers, including C++14 syntax, Python 3.6+, and OPENMP 3+. By streamlining the build, PSI4 can be compiled and tested within time limits on Linux and Windows with multiple compilers. By performing this continuous integration testing on cloud services, developers receive quality control feedback on their proposed code changes. These include the following: through testing, rough assurance that changes do not break the existing functionality; through coverage analysis, confidence that changes are being tested and a notice of testing gaps; and through static analysis, alerts that changes have incorrect syntax, type mismatches, and more. The last reflects the advantages of using standard CMAKE build tools: the static analysis tool correctly guesses how to build the PSI4 source purely by examining build-language files in the repository.

IX. LIMITATIONS

PSI4’s current focus on high-throughput quantum chemistry on conventional hardware has limited development of distributed parallel multi-node computing capabilities except for independent tasks managed by QCFRACTAL, as described in Sec. IV. GPU support is also limited beyond the GPU_DFCC module;^203,204 however, due to the plugin structure of PSI4, interfacing a GPU-based Coulomb (J) and exchange (K) code would enhance the majority of PSI4’s capabilities, and PSI4 is in discussions to integrate such a plugin. Several other features have been requested by users such as advanced algorithms for transition state searching, implicit solvent gradients, and additional implicit solvent methods. Beyond the above capability weaknesses, a primary downside of the open-source code is that there is no dedicated user support. While help can be found through a user forum at http://forum.psicode.org, a Slack workspace, and GitHub Issues, this support always comes from volunteers, and while questions are answered in the majority of cases, this is not guaranteed. On the other hand, the open-source software model empowers do-it-yourself fixes and extensions for power users and developers.

X. CONCLUSIONS

PSI4 is a freely available, open-source quantum chemistry (QC) project with a broad feature set and support for multi-core parallelism. The density-fitted MP2 and frozen natural orbital CCSD(T) codes are particularly efficient, even in comparison with commercial QC programs. PSI4 provides a number of uncommon features, including orbital-optimized electron correlation methods, density cumulant theory, and numerous intermolecular interaction methods in the symmetry-adapted perturbation theory family. With several input modes—text file, powerful Python application programming interface, and structured data—we can serve QC to traditional users, power users, developers, and database backends. The rewrite of our driver to work with task lists and integration with the MolSSI QCARCHIVE INFRASTRUCTURE project make PSI4 uniquely positioned for high-throughput QC.

Our development efforts and capabilities have been tremendously boosted by the “inversion” of PSI4 into a Python module in v1.1. We are able to rely more heavily on Python for driver logic, simplifying export of structured data and transition to the new distributed driver. The hybrid C++/Python programming strategy has also greatly aided development in the multiconfigurational SCF (MCSCF) and SAPT modules. We are able to transparently convert between NUMPY and PSI4 linear algebra structures and fully access performance-critical C++ classes, facilitating rapid prototyping of novel SAPT and orbital-optimized MPn methods. We are able to load into Python scripts and connect easily with other CMS software such as OPENMM and ASE.

Finally, we have fostered a QC software ecosystem meant to benefit the electronic structure software community beyond PSI4. Our adoption of the MolSSI QCSCHEMA should facilitate interoperability efforts, and our switch to a more permissive LGPL-3.0 license should aid developers and users who wish to deploy PSI4 as part of a larger toolchain or in cloud computing environments. We sincerely hope that the uptick in reusable software elements will continue in the future, so that new methods may be adopted quickly by many QC packages simply by interfacing a common implementation that is continuously updated, rather than developing redundant implementations in every code.

SUPPLEMENTARY MATERIAL

See the supplementary material for working equations for second-order SAPT0 without the single-exchange (S²) approximation using an atomic orbital formulation with density fitting.

DATA AVAILABILITY

Data sharing is not applicable to this article as no new data were created or analyzed in this study.